How to understand and report heterogeneity in a meta-analysis: The difference between I-squared and prediction intervals

Abstract

In any meta-analysis it is important to report not only the mean effect size but also how the effect size varies across studies. A treatment that has a moderate clinical impact in all studies is very different than a treatment where the impact is moderate on average, but in some studies is large and in others is trivial (or even harmful). A treatment that has no impact in any studies is very different than a treatment that has no impact on average because it is helpful in some studies but harmful in others. The majority of meta-analyses use the I-squared index to quantify heterogeneity. While this practice is common it is nevertheless incorrect. I-squared does not tell us how much the effect size varies (except when I-squared is zero percent). The statistic that does convey this information is the prediction interval. It allows us to report, for example, that a treatment has a clinically trivial or moderate effect in roughly 10 % of studies, a large effect in roughly 50 %, and a very large effect in roughly 40 %. This is the information that researchers or clinicians have in mind when they ask about heterogeneity. It is the information that researchers believe (incorrectly) is provided by I-squared.

1. Introduction

In any meta-analysis it is important to report not only the mean effect size but also how the effect size varies across studies. A treatment that has a moderate clinical impact in all studies is very different than a treatment where the impact is moderate on average, but in some studies is large and in others is trivial (or even harmful). A treatment that has no impact in any studies is very different than a treatment that has no impact on average because it is helpful in some studies but harmful in others.

Researchers recognize that information about heterogeneity is crucial, and therefore virtually all meta-analyses report heterogeneity. However, most do so in a manner that does not provide useful information about the dispersion in effects. Specifically, the majority of meta-analysis use the I² statistic to quantify heterogeneity. While this practice is ubiquitous it is nevertheless incorrect. The I² statistic does not tell us how much the effects vary. It was never intended to provide that information, and cannot do so except when I² is zero percent.

1.1. In this paper I will explain

• •How to think about heterogeneity in a meta-analysis
• •How to report heterogeneity using the prediction interval
• •That I² does not tell us how much the effect size varies
• •Why the system for classifying heterogeneity as low, moderate or high should be abandoned

This paper is adapted from a chapter in Common Mistakes in Meta-Analysis and How to Avoid Them.¹ A free PDF of the book is available at https://www.meta-analysis.com/KIOM.

2. How to think about heterogeneity in a meta-analysis

Heterogeneity in a meta-analysis is essentially the same as heterogeneity in a primary study. I will use a fictional primary study to review the basic concepts of heterogeneity, and then show how we can apply the same ideas to a meta-analysis.

2.1. Fictional primary study

Consider a primary study to assess the scores of students on a math test, where possible scores range from 0 to 100. Assume that scores can be used to classify students as shown in Table 1.

Table 1.

Classification of students in fictional example.

Score	Classification
0–30	Needs remediation
30–40	Somewhat below grade level, but acceptable
40–60	At grade level
60–70	Somewhat above grade level, but acceptable
70–100	Needs more challenging materials

2.2. Average score - the mean and confidence interval

Suppose that we draw a random sample of 20 students from the class, and report that mean score is 50 and the standard error is 2.0. The true mean usually falls within (roughly) two standard error of the estimated mean, so we can use the mean plus/minus two standard error to compute a confidence interval. This is an index of precision – it tells us how precisely we have estimated the mean. The standard error is 2.0 so the confidence interval is roughly 46–54. The class mean probably falls in this interval.

2.3. Distribution of scores – the prediction interval

The score for any single student usually falls within (roughly) two standard deviations of the mean, so we can use the mean plus/minus two standard deviations to compute a prediction interval. This is an index of dispersion – it tells us how widely the scores vary. This is called a prediction interval because if I were asked to predict the score for one student, selected at random from the class, I would predict that student would score within two standard deviations of the mean, and I would be correct roughly 95 % of the time.

• •If the standard deviation was 5 points the prediction interval would be 40–60.
• •If the standard deviation was 10 points the prediction interval would be 30–70.
• •If the standard deviation was 20 points the prediction interval would be 10–90.

While we rarely use the term prediction interval, we should all be familiar with the concept. When a paper reports the mean and standard deviation, we intuitively understand that most scores will fall within two standard deviations of the mean, and we compute the prediction in our heads.

On the one hand we have the mean and its confidence interval. On the other hand we have the prediction interval. Which do we care about? That depends on our goals.

Suppose that I am the school's principal. I need to submit a report to the department of education to document the progress of this class, and the department requires that all classes have a mean score of at least 40. In this case what matters is the average score. I can say that the average is 50. And, since the confidence interval excludes 40, I can confirm that the class meets the criterion.

By contrast, suppose that I am the class teacher and am concerned about the progress of each student. In this case I would want to know how widely the scores vary. For that, I would turn to the prediction interval.

• •If the prediction interval is 40–60, I would report that all students are performing at grade level
• •If the prediction interval is 30–70, I would report that some students are performing at grade level. Some are performing below or above grade level, but within an acceptable range.
• •If the prediction is 10–90, I would report that some students are performing at grade level. Some are performing below or above grade level, within an acceptable range. But the curriculum is not working for everyone. Some students are so far below grade level that they need remediation. And some are so far above grade level that they need a more challenging curriculum.

Thus, for some purposes we would focus on the mean and its confidence interval, while for other purposes we would focus on the prediction interval.

2.4. Meta-analysis

The same ideas apply in a meta-analysis. When the effect size is consistent across studies, in the sense that the clinical implications of the treatment are essentially the same in all studies, we can report that the effect size is consistent and then focus on the mean (or common) effect size.

By contrast, when the effect size varies substantially across studies, we need to consider the implications of that variation. The mean becomes less useful as a summary statistic for two reasons. First, there may be few studies where the effect actually falls near the mean, so the mean is not representative of many real populations. Second, when the effect size varies substantially we have an opportunity to explore the reasons for this variation. If the treatment works better in studies that enrolled certain types of patients, or that employed a specific variant of the intervention, we can study these potential moderators and improve the way we use the treatment.

For these purposes we need to be able to quantify the heterogeneity in a way that actually tells us about the distribution of effects. As was true in the fictional study, the relevant statistic is the prediction interval.

2.5. Motivating example

Hollingsworth et al.² performed a series of meta-analyses to assess the use of alpha blockers for treatment of ureteric stones. The researchers performed a separate analysis for studies where the “risk” of stone passage in the control group was classified as low (< 40%), middle (40% - 60%) or high (> 60%). While “risk” is something of a misnomer here (since it refers to a good outcome), I will retain these labels in this paper.

The effect-size index is a risk ratio. Risk ratios to the left of 1.0 indicate that the treatment was harmful while risk ratios to the right of 1.0 indicate that the treatment was helpful. Assume that for this diagnosis and treatment the following classifications apply. (These classifications are for illustrative purposes only, and not intended to provide any kind of clinical advice).

Risk ratio	Clinical impact
1.0−1.2	Trivial – Impact is not large to be useful
1.2–1.5	Moderate – Will help some patients
1.5–2.5	Large – Will have substantial benefit for many patients
2.5 +	Very large – Should be a first clinical option

2.6. Analysis 1- Low risk

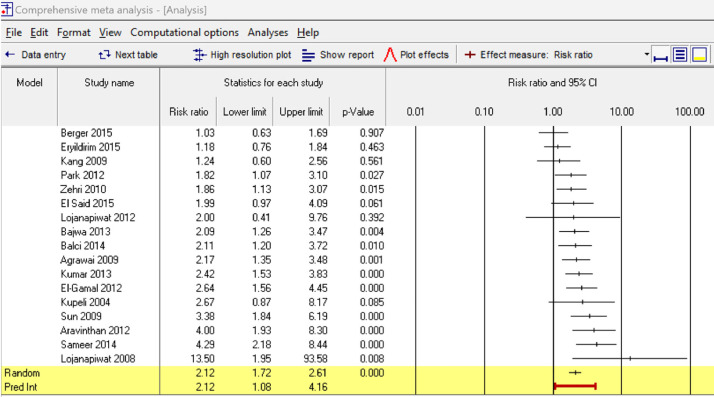
The authors performed a meta-analysis using studies where the patients were at low risk. The results are displayed in Fig. 1.

Fig. 1.

Analysis of low-risk studies.

There are two rows at the bottom of the plot

• •The line labeled “Random” (black) deals with the mean effect.
• •The line labeled “Prediction interval” (red) deals with the dispersion in effects.

2.7. Average effect – the mean and confidence interval

The mean risk ratio is 2.12 with a confidence interval of 1.72–2.61. The confidence interval speaks to the precision of the mean – we can be reasonably certain that the mean risk ratio falls in the interval 1.72–2.61. Using the classification system, the mean effect is probably large but could be very large.

2.8. Distribution of effects – the prediction interval

The prediction interval is 1.08–4.16. This speaks to the dispersion in effects and tells us that the treatment's impact varies across studies. At one extreme there are some studies where the impact will be trivial. At the other extreme there are some studies where the impact will be very large.

2.9. Confidence interval vs. prediction interval

It is critical to understand the difference between a confidence interval and a prediction interval. Most meta-analysis report a confidence interval but not a prediction interval, and readers sometimes assume that the confidence interval tells us how much the effect size varies. This is a mistake.

The confidence interval (on the line labeled Random, in black) is an index of precision, not an index of dispersion. It tells us how precisely we have estimated the effect size. It says nothing about how much the effect size varies. The confidence interval is sometimes displayed as a diamond rather than a line, but it has the same interpretation. The endpoints of the diamond represent the endpoints of the confidence interval, and say nothing about the dispersion in effects. The confidence interval, as an index of precision, is based on the standard error of the mean.

The prediction interval (on the line labeled Prediction Interval, in red) reflects the dispersion in effects. A 95 % prediction interval of 1.08–4.16 tells us that in some 95 % of studies comparable to those in the analysis, the true effect size will fall in the interval 1.08–4.16. This is called a prediction interval because if we were asked to predict the true effect size for any one study, selected at random from the universe of comparable studies, we would predict that effect size would fall between 1.08 and 4.16, and we would be correct roughly 95 % of the time. The prediction interval, as an index of dispersion, is based on the standard deviation of the effects.

2.10. Analysis 2 – Middle risk

The authors performed a meta-analysis using studies where the patients were at middle risk. The results are displayed in Fig. 2.

Fig. 2.

Analysis of middle-risk studies.

2.11. Average effect – the mean and confidence interval

For studies that enrolled patients at middle risk, the mean risk ratio is 1.52 with a confidence interval of 1.42–1.62. We know the mean effect very precisely and it falls on the border of moderate and large.

2.12. Distribution of effects – the prediction interval

There is no prediction interval displayed because there is no evidence of any variation in effects. In all studies comparable to those in the analysis, the impact of the treatment is expected to be essentially the same. This might seem odd since the effects do appear to vary, and I will return to this point later.

2.13. Analysis 3 – High risk

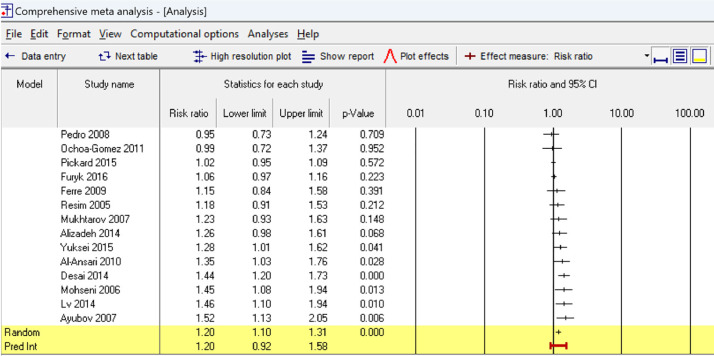
Finally, the authors performed a meta-analysis using studies where the patients were at high risk. The results are displayed in Fig. 3.

Fig. 3.

Analysis of high-risk studies.

2.14. Average effect – the mean and confidence interval

For studies that enrolled high-risk patients the mean risk ratio is 1.20 with a confidence interval of 1.10–1.31. The average effect is either trivial or moderate.

2.15. Distribution of effects – the prediction interval

The prediction interval is 0.92–1.58. At one extreme there are some populations where the treatment impact is trivial (or nil). At the other extreme there are a few populations where the effect is large.

3. How to compute the prediction interval

For each meta-analysis we reported the prediction interval. One might assume that to estimate the prediction interval we could simply pick the lowest and highest effects seen on the plot, but this approach is wrong for three reasons.

• •The interval would be based on the two most extreme two studies while ignoring the information in all the others.
• •The effects displayed in the plot are subject to sampling error, and therefore we cannot assume that the effects reported by each study are accurate. In Fig. 1 one study reported a risk ratio of 13.50 but the confidence interval for that study was very wide and the true effect in that study could have been substantially lower. Indeed, the prediction interval based on the information from all studies assigns relatively little weight to that outlier and yields an upper limit of 4.2 for the prediction interval.
• •Our intention is to generalize from the studies in the analysis to the universe of comparable studies. If our analysis includes only a handful of studies, we would expect that the range of effects in the universe would be wider than the range we see in our sample.

Therefore, the way we compute a prediction interval is similar to the approach we use in a primary study, which is to use the mean plus/minus two standard deviations. While this is the way to think about the prediction interval, the actual computation is a bit more complicated.

3.1. Expanding the interval

If we actually knew the mean and variance of true effects for the universe of comparable studies we could compute the 95 % interval using

$$PI=\mu \pm Z^{\alpha }\sqrt{{\tau }^2},$$

where

• •µ is the actual mean
• •τ² is the actual variance of true effects.

In fact, however, we are working with an estimate of the mean and an estimate of the variance. Therefore, we expand the interval to account for the fact that the true mean may be lower or higher than our estimate, and that the variance may be higher than our estimate. A recommended formula for prediction interval is

$$PI=M\pm t_{df}^{\alpha }\sqrt{T^2+V_M},$$

where

• •M is the random-effects estimate of the mean
• •T² is the estimate of the variance of true effects
• •V_M is the (random-effects) error variance of the mean (i.e., the standard error of the mean, squared).

For the 95 % prediction interval the t-value is based on alpha = 0.05 with df equal to the number of studies minus 2. In Excel™, the function =TINV(0.05, 1000) will yield a t-value of 1.96.

The effect of this adjustment is to expand the interval, and thus increase the likelihood that the interval will incorporate at least 95 % of the true effects.

For more detailed information see.^1,3, 4, 5, 6, 7

3.2. Working with transformed data

When we are working with some effect-size indices (such as a difference in means) the value of T² is in the same metric as the value of the mean, and so these values may be employed in the formula. By contrast, when we are working with risk ratios (as in the motivating example) T² is reported in log units while the risk ratio is reported in risk ratio units. We need to transform all values to log units, compute the prediction interval, and then convert the results back to risk ratio units. The same idea applies to analyses of prevalence (where the variance may be in logit units or arcsin units) and correlations (where the variance may be Fisher's Z units).³

3.3. Computer programs

Given these technical issues, it is a good idea to use a computer program to compute the prediction interval. Most popular programs for meta-analysis have recently introduced the option to compute prediction intervals. Figs. 1–3 are screen-shots from Comprehensive Meta-Analysis (CMA)⁸ but similar options are available in Metafor⁹ and Stata.¹⁰

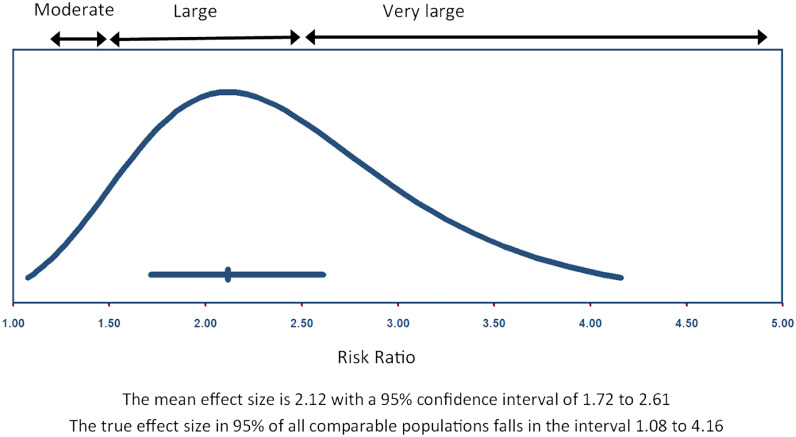
CMA also allows the user to create the plot shown in Fig. 4, which displays the distribution of effects for the low-risk patients. In this plot –

• •The horizontal line toward the bottom of the plot reflects the confidence interval and corresponds to the line labeled Random in Fig. 1. The mean effect probably falls in this interval.
• •The normal curve reflects the distribution of true effects. The endpoints of this distribution correspond to the prediction interval in Fig. 1. In any single study the true effect size is expected to fall in this interval

Fig. 4.

Distribution of effects for the low-risk patients.

This plot contains the same information as the two summary lines in Fig. 1. The difference is that whereas Fig. 1 shows the prediction interval as a line, Fig. 4 shows it as a distribution of effects.

• •Where Fig. 1 told us that the true effect size in some studies will be trivial or moderate, Fig. 4 shows that it will be trivial in only to a tiny fraction of studies, and moderate in roughly 10 % of studies.
• •Where Fig. 1 told us that the true effect size in some studies will be large or very large, Fig. 4 shows that roughly 90 % of studies fall into these categories.

While Fig. 4 was created using Comprehensive Meta-Analysis, a free program to create this plot may be downloaded at https://www.meta-analysis.com/KIOM. This program will work with any software for meta-analysis. The user simply provides a few statistics that are reported by all programs, and the program creates the plot.

4. Caveats

When we report the prediction interval we need to be aware of its limitations.³

4.1. Reasonable number of studies

We need a reasonable number of studies to yield a reliable estimate of the prediction interval. For purposes of estimating the dispersion in effects, each study yields one estimate regardless of how many people are included in that study. If the meta-analysis includes five studies with a thousand people in each. the effective sample size for estimating heterogeneity is five, not five thousand.

There is no consensus on how many studies are needed to yield a useful estimate of heterogeneity, but a prediction interval based on less than ten studies may be suspect and one based on less than five studies is not likely to be informative. As noted earlier, the formula will expand the interval to take account of this uncertainty. While this makes it more likely that the interval will include 95 % of all populations, it can also lead to a very wide interval. This does not mean that the effects vary widely. Rather, it reflects the uncertainty of our estimates.

4.2. Estimate is subject to error

The estimate of the prediction interval, like all statistics, is subject to error. Since the interval will play a role in evaluating the utility of the intervention, it is important to ensure that the key elements of the interval are correct. Specifically, if the interval suggests that the intervention is helpful in some cases but harmful in others, we should check and see if this is supported by the data.

For example, in Fig. 3 the prediction interval is 0.92–1.58 which suggests that there are some studies where the risk ratio is harmful (i.e., less than 1.0). If we report this, some clinicians might hesitate to use the treatment. If we look at the forest plot we can see where this came from – there are actually two studies with risk ratios less than 1.0. However, both of those studies have confidence intervals that include 1.0 and so neither of them provide proof that the treatment is harmful. In this case it would make sense to report the prediction interval but also explain that there is no evidence of actual harm in any studies.

4.3. When T² is estimated as zero

In the analysis of middle-risk studies (Fig. 2) the variance of true effects (T²) was estimated as zero, and so there was no prediction interval displayed. When the studies are based on unique populations it is not plausible to assume that they share precisely the same effect size, so we recognize that the value of zero must be an underestimate of the true value. We hope that the true value, while not really zero, is small enough to be unimportant. This assumption makes sense when (a) our knowledge of the subject matter suggests that the dispersion will be trivial and (b) we have sufficient studies in the analysis so that the estimate of variance has a credible reliability.

5. What about I²

To this point I have explained that the correct way to quantify heterogeneity is to use the prediction interval. However, only a small number of meta-analyses follow this practice. Rather, the vast majority of meta-analyses use the I² index to quantify heterogeneity. This is a mistake, based on a fundamental misunderstanding I². The I² index does not tell us how much the effect size varies (except when I² is zero)11, 12, 13 So, what does I² tell us?

5.1. True effects vs. observed effects

In any meta-analysis we distinguish between true effects and observed effects. A true effect is the effect size that a study would report if that study had an infinitely large sample size and no error. An observed effect is the effect size that the study reports. It serves as an estimate of the true effect size but invariably falls below or above the true effect size due to sampling error.

The variance of the observed effects tends to be greater than the variance of true effects. Why? Consider a hypothetical meta-analysis where all studies are based on random samples from the same population and are identical to each other in all material respects. The variance of true effects is zero by definition (since all studies are estimating the same population value) but the observed effects would still vary because of sampling error. So, the variance of observed effects would be greater than the variance of true effects. While this concept is most intuitive in the example where there is no variance in true effects, the same idea holds true in an analysis where the true effects do vary. The variance of observed effects tends to be greater than the variance of true effects.

Since we are looking at the distribution of observed effects but we really care about the distribution of true effects, we might want to ask about the relationship between the two. This is the domain of the I² index. It tells us what proportion of the variance that we see in the forest plot represents variance in true effects rather than sampling error.

5.2. Prediction interval vs. I²

Fig. 5 is based on the low-risk analysis (at left) and the high-risk analysis (at right). In each case –

• •The top row (in red) is the prediction interval. The length is proportional to T, the standard deviation of true effects.
• •The bottom row (in blue) reflects the dispersion of observed effects. The length is proportional to S, the standard deviation of observed effects.

Fig. 5.

Prediction intervals using the low-risk and the high-risk analyses.

Results for the low-risk patients (at left)

• •If we want to know about the distribution of true effects, this is given by the prediction interval – effects vary from 1.08 to 4.16.
• •If we want to know the relationship between the two distributions (true effects and observed effects), that is given by the ratio of the two lines. The ratio of the two lengths is 0.700, which is the ratio of the two standard deviations. We can square that to get the ratio of the two variances (I²) which is 49 %.

Results for the high-risk patients (at right)

• •If we want to know about the distribution of true effects, this is given by the prediction interval – effects vary from 0.92 to 1.58.
• •If we want to know the relationship between the two distributions (true effects and observed effects), that is given by the ratio of the two lines. The ratio of the two lengths is 0.773, which is the ratio of the two standard deviations. We can square that to get the ratio of the two variances (I²) which is 60 %.

5.3. Two separate questions

The key point here is that the prediction interval and the I² index address two entirely separate questions. We need to be clear about what question we want to ask, and then apply the appropriate statistic to address that question. When someone asks about heterogeneity, they are almost certain to be asking how much the effects vary. That question is addressed by the prediction interval, and not by I².

With reference to Fig. 5, when someone asks about heterogeneity, they are almost certain to be asking about the line labeled “Prediction interval”. By contrast, I² tells us the relationship between that line and the line below it, which is something else entirely.

5.4. What I² does not tell us

Critically, I² is a proportion, not an absolute amount. Suppose that we were told that I² is 50 %. That does not tell us how much the true effects vary. If the observed effects have a variance of 100, the true effects have a variance of 50. But if the observed effects have a variance of 50, the true effects have a variance of 25.

• •For the low-risk patients I² is 49 % but that tells us nothing useful about the distribution of effects.
• •For the high-risk patients I² is 60 % but that tells us nothing useful about the distribution of effects.

Most researchers would assume that the effects vary more widely for the high-risk patients (where I² is 60 %) than for the low-risk patients (where I² is 49 %). However, in this case, this is incorrect. In Fig. 5, the prediction interval (which does reflect the amount of dispersion) is much wider for the low-risk patients (at left), where I² was lower. This makes no sense if we think that I² is an index of dispersion but is not a problem when we recognize that it is actually a proportion.

• •For the low-risk patients the observed effects (in blue) vary widely. Only 49 % of that variance reflects variance in true effects, but 49 % of a large amount is still a large amount (in red).
• •For the high-risk patients the observed effects (in blue) fall in a relatively narrow range. Some 60 % of that variance reflects variance in true effects, but 60 % of a small amount is still a small amount (in red).

In sum, the I² index does not tell us how much the effect size varies. Indeed, as in this example, it cannot even tell us which of two analyses has greater heterogeneity than the other.

5.5. An analogy

It might be helpful to present an analogy. Suppose a person shopping for an item asks the dealer “How much do I need to pay?” The dealer responds that the person will pay only 80 % of the usual cost. The person still does not know how much they need to pay. If the usual cost is $100 the person will need to pay $80 but if the usual cost is $1000 the person will need to pay $800.

In this tale, the usual cost is analogous to the dispersion of observed effects, the proportion the person needs to pay is analogous to I², and the actual amount the person needs to pay is analogous to the dispersion of true effects. We need to multiply 80 % by the usual cost to get the actual price. We need to multiply I² by the variance of observed effects to get the variance of true effects.

The most important part of the analogy is the following. If the dealer tells the person that she needs to pay 80 %, she will not write a check for 80 %. Rather, she will insist on being told what she actually needs to pay. By contrast, when a paper reports that I² is 80 % the reader may assume that they know how much the effects vary. In fact, however, this makes no more sense for the reader than it does for the shopper. The I² statistic simply does not provide that information.

6. Classifying heterogeneity as being low, moderate or high

6.1. Classifications based on I²

In many papers researchers use I² to classify heterogeneity as being low, moderate or high based on the value of I². This practice should be abandoned for three reasons.

• •If we wanted to classify the amount of heterogeneity based on some criterion, that criterion would need to reflect the actual amount of dispersion. I² does not serve that function. An analysis classified as low heterogeneity (based on an I² of 25 %) could actually have more heterogeneity than analysis classified as high heterogeneity (based on an I² of 75 %).
• •The idea of these classifications makes no sense even if they were based on an index of actual dispersion such as the standard deviation. The reason is that the terms low, moderate and high are understood in a clinical context. An amount of heterogeneity that is considered trivial in one clinical context may be considered large in another clinical context. Therefore, any classification system that fails to account for clinical context (as does this one) cannot be useful.
• •This system treats heterogeneity as an issue that is separate from the mean, but to understand the potential impact of dispersion we need to think of that dispersion in the context of the mean. A risk difference that varies from 0.20 to 0.60 has the same dispersion as one that varies from -0.20 to +0.20 but the clinical implications are very different in the two cases.

6.2. Classifications based on the prediction interval

By contrast, consider a classification system based on the prediction interval. This would not reflect the dispersion perse but rather the clinical implications of the interval. Thus, working with plots that show the distribution of effects we might report that

• •For low-risk patients the treatment has a trivial or moderate effect in roughly 10 % of studies, a large effect in roughly 50 %, and a very large effect in roughly 40 %.
• •For moderate-risk patients the treatment effect falls on the border or moderate and large, and is consistent for all studies
• •For high-risk patients the impact is trivial for 50 % of patients and moderate for the other 50 %.

This approach avoids the three problems with the current system. Under the proposed system -

• •The amount of dispersion is based on an index of actual dispersion
• •The classifications are based on the clinical question at hand
• •The classifications reflect the position of the distribution on the scale and not merely its width.

As such, the prediction interval provides information not only about the dispersion but also about the actual effect. This is the information we need to assess the potential utility of the intervention.

7. Summary

The concept of heterogeneity in a meta-analysis is essentially similar to the concept of heterogeneity in a primary study. We want to know the distribution of effects, and the statistic that conveys this information is the prediction interval. In a primary study we report the mean and standard deviation, and researchers intuitively understand what the prediction interval looks like. In a meta-analysis the computation is a bit more complicated and so the paper should actually report the prediction interval. But in either case, the concept is the same.

Critically, the prediction interval addresses the question that researchers or clinicians have in mind when they ask about heterogeneity. They want to know (for example) if the treatment effect is always large, or if it varies from moderate in some studies to trivial (or even harmful) in others. This is the information they need to assess the potential utility of the intervention. The prediction interval provides this information. It provides it in a format that is clear and intuitive. Indeed, it reports the distribution in the same units as the mean and confidence interval.

Ironically, relatively few meta-analyses report the prediction interval. Rather, most quantify heterogeneity using the I² statistic. The I² statistic is a ratio, not an absolute amount. It tells us what proportion of the variance in observed effects is due to variance in true effects. It does not tell us how much that variance is (except when I² is 0 %).

When a meta-analyst uses I² to quantify heterogeneity they do not actually understand how much the effect size varies. Therefore, they typically focus on the mean effect size. The paper might say that “there was a lot of heterogeneity” but then this is ignored in the discussion since it is not really informative. This carries through to discussion among clinicians who are using the meta-analysis to set policy.

Suppose a group of clinicians is discussing the potential utility of the treatment for low-risk patients. Consider two possible scenarios.

• •In one scenario the clinicians are told that the mean risk ratio is 2.2 but I² is 49 %. The discussants will try to reach a consensus on how to proceed, while each will be working with their own set of facts – each will have their own idea of what the distribution looks like, and none of these ideas are necessarily correct.
• •In the other scenario the clinicians are told that the mean risk ratio is 2.2 but the effects vary from 1.1 to 4.6. The treatment has a trivial or moderate effect in roughly 10 % of studies, a large effect in roughly 50 %, and a very large effect in roughly 40 %. In this case the discussants will be working with a common set of facts – they will all understand what the distribution of effects actually is.

Clearly, the second scenario is the only reasonable choice.

This paper is intended as an overview of these issues. A video with additional explanation and examples of how how to report heterogeneity in papers is available at: https://www.Meta-Analysis.com/KIOM