Abstract
Analyses of genetic variation typically assume that rare variants within a population are inherited from a single common ancestral event identity-by-descent (IBD). However, there are genetic and technical processes through which rare variants in population genetic data may deviate from this simple evolutionary model, including recurrent mutations, gene conversions and genotyping error. All these processes can decrease the expected length of shared background haplotype surrounding a rare variant if that variant was inherited from a single event descending from a common ancestor. No method exists to computationally infer rare variants inconsistent with this simple model–denoted here as ‘IBD-inconsistent’–using unphased population sequencing data.
We hypothesized that the difference in shared haplotype background length can distinguish variants consistent and inconsistent with this simple IBD transmission population sequencing data without pedigree information. We implemented a Bayesian hierarchical model and used Gibbs sampling to estimate the posterior probability of IBD state for rare variants, using simulated recurrent mutations to demonstrate that our approach accurately distinguishes rare variants consistent and inconsistent with a simple IBD inheritance model.
Applying our method to whole-genome sequencing data from 3,621 human individuals in the UK10K consortium, we found that IBD-inconsistent variants correlated with higher local mutation rates and genomic features like replication timing. Using a heuristic to categorize IBD-inconsistent variants as gene conversions, we found that potential gene conversions had expected properties such as enriched local GC content.
By identifying IBD-inconsistent variants, we can better understand the spectrum of recent mutations in human populations, a source of genetic variation driving evolution and a key factor in understanding recent demographic history.
Keywords: population genetics, bioinformatics, molecular evolution, evolutionary biology, Bayesian methods
1 |. BACKGROUND
Population genetics inference studies typically invoke a simple origin and transmission of alleles at polymorphic sites segregating in a population, that is, a single mutational event from which alleles, when subsequently transmitted to the next generation, are passed on faithfully and directly from parent to offspring. These assumptions are mathematically useful, as an allele state shared by sampled chromosomes can be traced to an originating mutation event.
Large-scale population data suggest that these assumptions are reasonable on average but not universally. One example is the frequency of recurrent mutations, which has been studied at length in population genetics (e.g. Haldane, 1933; Wright, 1931, 1937). In the Exome Aggregation Consortium, Lek et al. noted a marked depletion of singleton CpG transitions relative to other mutation types (Lek et al., 2016). This observation could be explained by the presence of recurrent mutations saturating these highly mutable sites in this large sample, resulting in two or more sampled individuals segregating identical-by-state alleles at CpG sites. Beyond this, there are other types of population phenomena (e.g. gene conversion) but also technical artefacts (e.g. genotyping error) that can create alleles that appear in the same state but whose origin and genealogy is more complex. We refer to the cases of alleles segregating at a polymorphic site that do not descend from a simple model of identity-by-descent (IBD) as ‘IBD-inconsistent’ events.
Estimating the frequency and identifying specific examples of IBD-inconsistent variants is important to improve statistical analyses of population genetic data and infer mechanisms. For example, distinguishing recurrent mutations from variants with single event mutational origins is important for understanding the causes of variation in germline mutation rates and for population genetic methods that make inferences based on the observed number of variants in a population. Many population genetics methods use the site frequency spectrum (SFS) to infer the demographic history of a sample (Bhaskar et al., 2015; Excoffier et al., 2013; Gutenkunst et al., 2009; Jouganous et al., 2017; Lukic & Hey, 2012), approaches which generally assume an infinite sites model with no recurrent mutations (Harpak et al., 2016). This could impact the accuracy of demographic parameter inference. Recent work has described the SFS allowing for recurrent mutations but relies on observed recurrent mutations detectable as tri-allelic sites, not those in the same allele state (Jenkins et al., 2014; Jenkins & Song, 2011; Ragsdale et al., 2016). Finally, the magnitude of purifying selection may be underestimated if the frequencies of rare variants are overestimated due to undetected recurrent mutation.
Below, we present a computational approach to infer the presence of an IBD-inconsistent variant at a genomic site. The key idea underlying our approach is to use genetic variation linked to rare variants to distinguish alleles carried at that variant position as consistent or inconsistent with our model for IBD. In our model, rare variants inherited IBD are flanked by a shared haplotype on all chromosomes carrying the variant (i.e. an IBD segment) as all segregating alleles derive from a recent ancestral mutation. If the variant arose recently, recombination will have had little time to shorten this shared segment. Thus, the length of the IBD segment shared across carriers is inversely related to the age of the variant (Haldane, 1919; Mathieson & McVean, 2014). In contrast, alleles that are IBD-inconsistent could occur on a random haplotype background; thus, we expect that their local time to the most recent common ancestor (TMRCA) will be older than an IBD variant of the same frequency. Leveraging this relationship, we can infer rare variants that segregate alleles similar in state with haplotype lengths inconsistent with simple transmission. Thus, rare variants that fall on the short end of the distribution of shared IBD segment lengths are older than expected and we explore the possible causes of these IBD-inconsistent variants (e.g. recurrent mutation, non-crossover gene conversion, proximity to a region of extremely high local recombination rate and/or genotyping errors).
While previous efforts have leveraged IBD tracts to infer mutation and gene conversion rates (Palamara et al., 2015), as well as to estimate allele ages (Albers & McVean, 2020; Mathieson & McVean, 2014; Palamara et al., 2012; Platt et al., 2019), we are not aware of any previous method designed to specifically identify IBD-inconsistent variants events at specific genomic positions across the entire genome. Such a method could be applied to flag potentially erroneous rare variant genotype calls in large-scale sequencing datasets. We implement a Bayesian hierarchical model to identify IBD-inconsistent rare variants, using population genetic simulations to assess its precision and accuracy. We then apply our approach to sequencing data of 3,621 individuals from the UK10K dataset, and partition high-confidence IBD-inconsistent rare variants as those likely to be recurrent mutations or gene conversions.
2 |. A BAYESIAN HIERARCHICAL MODEL TO IDENTIFY RARE GENETIC VARIANTS INCONSISTENT WITH IBD
We hypothesized that the expected difference in the TMCRA between IBD and non-IBD allele pairs can distinguish between these two states. While the TMRCA of a genetic variant is not directly observable, it can be estimated by the length of the haplotype shared by carriers of the variant. As our purpose here is to distinguish between IBD consistency and inconsistency of alleles at rare variant sites, there will be few if any linked mutations more recent than the focal variant. Thus, we rely solely on the recombination clock for inference. The distance to the nearest recombination event on either side of a genetic variant between a pair of alleles can be modelled as exponentially distributed with rate proportional to the TMRCA (Mathieson & McVean, 2014; Palamara et al., 2012). The expected difference in the TMRCA between a rare variant segregating with IBD alleles and a variant position with non-IBD mutations translates into IBD alleles having longer expected distances to the nearest recombination event compared to IBD-inconsistent alleles of the same allele frequency (Supplementary Figure S1). Recent methods have inferred the age of alleles in large-scale population datasets by leveraging this relationship between haplotype background and the TMRCA (Albers & McVean, 2020; Palamara et al., 2012; Platt et al., 2019) and by constructing local genealogies (Kelleher et al., 2019; Speidel et al., 2019). However, these approaches require known haplotypic phase and do not explicitly attempt to identify IBD-inconsistent variants. Existing approaches to identify recurrent mutations rely on family relationships or assume that variants present at very low frequencies in distantly related populations are recurrent without explicitly identifying IBD-inconsistent variants (e.g. Pagnier et al., 1984; The 1000 Genomes Project Consortium, 2012). Thus, our goal was to develop an approach to identify IBD-inconsistent variants that scales to large, whole-genome population sequencing studies with thousands of individuals.
While recombination breakpoints cannot be directly observed in population sequencing data, patterns of genetic variation can provide an estimate of the location of these events without haplotype phase being known. Our method utilizes unphased diploid genotypes to estimate the recombination distances on either side of a pair of alleles. With diploid genotypes for a pair of individuals each carrying a focal allele, one can measure the obligate recombination distance: the genetic distance to the first opposite homozygote genotype between the two individuals (Figure 1A; Hudson & Kaplan, 1985). No genealogy without recombination is compatible with the observed genotypes of these two sites, and thus we assume a recombination event has occurred between them (Mathieson & McVean, 2014). Thus, the obligate recombination distance gives an upper bound for the IBD segment length around the target variant.
FIGURE 1.

Description of the EVICORD model. (a) Measuring the obligate recombination distance with unphased diploid genotypes. The orange dot represents the focal variant and blue dots additional variants present in these two individuals. Each individual A and B has two chromosomes (dashed lines), and the red boxes highlight the nearest opposite homozygote genotypes. The purple lines highlight the extent of the shared haplotype of the chromosomes carrying the focal variant. The boxes at the bottom illustrate these two individual’s diploid genotypes. (b) The generative model underlying our Bayesian hierarchical model to distinguish identity-by-descent (IBD)-consistent and inconsistent variants. Step 1: Each variant is assigned as IBD () or non-IBD (. Each variant has allele pairs, calculated from its allele count (ac). Step 2: If the variant is IBD , all allele pairs are also . If the variant is non-IBD, depending on the non-IBD partition there are possible permutations of assignments , each of which are equally likely. Step 3: For an IBD variant, a single time to the most recent common ancestor (TMRCA) is sampled. If the variant is non-IBD, a TMRCA for the non-IBD allele pairs is sampled (), and potentially a TMRCA for one or more IBD sub-clades ) depending on allele count and partition. Step 4: for each allele pair, recombination distances to the left and right are sampled independently.
We considered a Bayesian hierarchical model for the pairwise recombination distances from a sample of variants of a given allele count, illustrated in Figure 1B. We denote each -th variant’s IBD-consistent or IBD-inconsistent state with parameter , and modelled the sampled variants as a finite mixture of IBD-consistent or IBD-inconsistent (, with each possible partition of alleles for an IBD-inconsistent variant given a different value of ) with mixture proportions . For example, we model an IBD-inconsistent variant of allele count = 4 as one of two possible partitions: a singleton and an IBD tripleton (1:3), or two IBD doubletons (2:2). Each variant of allele count = A has allele pairs. While partitions of more than two groups (e.g. 2:1:1) are possible, we model only two groups, as simulations suggest this simplified approach identifies both the simple and complex partitions (Supplementary Table S1). The TMRCA, denoted by , for each allele pair was sampled from a Gamma distribution with shape parameter and rate parameter , with one Gamma distribution used to model for IBD-consistent allele pairs and one for IBD-inconsistent allele pairs . We chose Gamma distributions to model the TMRCA due to the availability of a conjugate prior as well as the fact that the Gamma distribution models the TMRCA of a pair sequences given the mutation rate, number of pairwise differences and sequence length in the coalescent (Hein et al., 2005). For IBD-inconsistent allele pairs, we estimated and from multiallelic sites, and for IBD allele pairs we fixed and performed sampling for over a range of possible values for . We modelled the left and right recombination distances () for each allele pair using an exponential distribution with rate proportional to . We used Gibbs sampling to sample from the marginal posterior density of each parameter, as we could estimate these densities from the full conditional distributions. We outline these expressions below.
2.1 |. Mixture proportions
Using a multinomial likelihood for the probability of each variant i’s assignment as IBD () or IBD-inconsistent , with the possible values of depending on allele count) based on mixture proportions , we used the Dirichlet distribution as the conjugate prior to obtain the posterior probability of given the observed assignments. The likelihood function is
| (1) |
We used a Dirichlet prior for π:
| (2) |
The resulting posterior probability follows a Dirichlet distribution, with representing the vector of variant assignments :
| (3) |
2.2 |. TMRCA
The likelihood of the pairwise recombination distance (; could be left or right, ) to one side of a variant (in centiMorgans), given the TMRCA scaled by genetic distance, follows an exponential distribution (Palamara et al., 2012):
| (4) |
We used a Gamma distribution for the prior of , the TMRCA for each allele pair, dependent on the assignment for allele pair as IBD-consistent or IBD-inconsistent :
| (5) |
The resulting posterior is also Gamma distributed, with representing the number of allele pairs and the vector of allele pair distances d:
| (6) |
We determined that for a range of values, fixing and sampling from the posterior did not affect the performance of our approach (Supplementary Methods), allowing us to use the conjugate priors for a Gamma distribution with shape parameter and rate parameter , which is a second Gamma distribution:
| (7) |
The posterior for is also Gamma, with representing a vector of length of the TMRCA estimates for :
| (8) |
2.3 |. Full conditional distributions
To sample from the posterior for each unknown parameter, we derived the full conditional distributions, ignoring conditionally independent terms. In each iteration of the Gibbs sampler, we sample each parameter from its full conditional distribution, conditioned on the current values of all other parameters. The sampling algorithm is described in the Supplementary Methods.
represents a vector of mixture proportions of (the vector of assignments ), with representing the possible assignments of and the vector of allele pair assignments :
| (9) |
, rate parameter of TMRCA distributions:
| (10) |
, the TMRCA for variant , with representing the subset of allele pair distances and representing the subset of allele pair assignments for variant :
| (11) |
, variant label for variant (: IBD-consistent; : IBD-inconsistent), with representing the vector of prior estimates for proportions of :
| (12) |
, the partition assignments for allele pairs from IBD-inconsistent variants, modelled as a Multinomial distribution with equal prior probabilities for all permutations of possible assignments:
| (13) |
3 |. RESULTS
3.1 |. Application to simulated recurrent mutations
To evaluate our approach, we applied it to simulated genetic data which included recurrent mutations identical by state (and thus, inconsistent with our IBD model). Using SLiM (Haller & Messer, 2017), we generated genomic segments of length with uniform mutation and recombination rates ( mutations per site per generation, events per site per generation), without selection, following a European demographic model (Bhaskar et al., 2015) and sample size of 3,621 diploids (the size of the UK10K dataset analysed subsequently). We measured the pairwise obligate recombination distances of recurrent and non-recurrent mutation sites with allele count for a window in the middle of each simulated segment, reporting the number of recurrent mutations (Supplementary Figure S2). We applied our method to the obligate recombination distances from these simulations, calculating the posterior probability of a variant being IBD-inconsistent as the fraction of posterior samples with (Supplementary Figure S3). We evaluated the ability of this posterior estimate to distinguish between recurrent and non-recurrent mutations. Receiver operating characteristic (ROC) curves in Figure 2 show the relationship between true- and false-positive rates for allele counts 2–10 (Supplementary Table S2). The precision and recall of our approach depends on the fraction of variants that are IBD-inconsistent (Figure 2), with higher recurrent fractions having superior performance.
FIGURE 2.

Power of EVICORD using simulated data. (a) Precision-recall plots and (b) ROC plots for the Bayesian hierarchical model applied to distinguish recurrent and identity-by-descent (IBD) variants in simulated data. In (a), each panel represents the application to variants of a given allele count (AC). The precision-recall relationship depends on the fraction of true positives (‘Fraction recurrent’) in the simulated sample of variants. In (b), the dashed line represents the identity line.
We next performed a battery of sensitivity studies, simulating population genomic features known to influence patterns of genetic variation that could impact robustness of our estimates. First, we simulated genomic segments including genes and deleterious mutations to test the effect of background selection on our approach (Methods). We observed that background selection had little impact on the power of our approach (Supplementary Figure S4; Table S2). We suspect that the recent ages of rare variants (Supplementary Figure S5) cause the difference in recombination distances of recurrent vs. non-recurrent mutations to not be strongly altered by the presence of weak negative selection.
Next, we considered variable recombination rates, sampling from a human recombination map (Methods). At allele count = 2, the area under the ROC curve (AUC) was greater for the variable recombination map than the uniform map (Supplementary Table S2), though performance was worse for variable recombination rates at the lowest end of false-positive rates (Supplementary Figure S6A). For all larger allele counts tested, power was reduced in simulations with variable recombination maps relative to uniform maps (Supplementary Figure S6A and Table S2). Increasing the sample size to 10,000 diploids with a variable recombination map demonstrated that the power to identify recurrent variants was similar between sample sizes for allele count = 2, but improved for all larger allele counts tested (Supplementary Figure S6B; Table S2).
3.2 |. Comparison to variant age estimates to identify IBD-inconsistent variants
IBD-inconsistent variants could potentially be identified as age estimate outliers within each allele frequency class from methods that estimate variant ages using large scale genome-wide sequencing data (Albers & McVean, 2020; Platt et al., 2019). To evaluate the utility of these approaches to identify IBD-inconsistent variants, we estimated the ages of simulated variants using runtc (Platt et al., 2019; Methods). We used these age estimates to potentially identify recurrent mutations, by sliding an age estimate threshold and calling variants older than the threshold as IBD-inconsistent. We plot the performance of this approach in Supplementary Figure S7. We find that the age estimates have limited power to identify IBD-inconsistent recurrent mutation events, and that runtc’s performance at this task (Supplementary Table S3)–a task the method was not explicitly designed for–performs poorly compared to our Bayesian hierarchical approach (Supplementary Table S2).
3.3 |. Application of Bayesian hierarchical model to UK10K sequencing data
We applied our method to identify IBD-inconsistent variants in whole-genome sequencing data in 3,621 individuals from the UK10K project (Methods; The UK10K Consortium, 2015). We measured the obligate recombination distance for biallelic and multiallelic single nucleotide variants that passed the UK10K quality filters, focusing on variants of allele count based on performance of our method in simulations.
We applied our approach to a mixture of 80% biallelic and 20% multiallelic sites to use multiallelic sites as a positive control for IBD-inconsistent mutations. We compared the empirical cumulative distribution of posterior probabilities for multiallelic and biallelic sites, and as expected we observed that multiallelic sites had higher posterior probabilities of IBD-inconsistency (Supplementary Figure S8). We used these distributions to determine the threshold for posterior probabilities we denote as ‘IBD-inconsistent’ used in downstream analyses. Here, we focus on biallelic variants with allele counts between 2 and 5 (inclusive).
3.4 |. IBD-inconsistent variants correlate with local sequence context
To assess the accuracy of our IBD-inconsistent variant calls, we took advantage of the relationship between local sequence context and mutation rate (Aggarwala & Voight, 2016). Under a Poisson model of mutation, sequence contexts with a higher mutation rate should have a higher probability of recurrent mutation relative to other contexts. If IBD-inconsistent variant calls reflect largely recurrent mutations, we would expect to see a correlation between the fraction of IBD-inconsistent variants and the mutability of sequence contexts. Using sequence-context estimated polymorphism probabilities calculated from the UK10K dataset, we calculated an expected fraction of recurrent variants for each 5 base-pair nucleotide (5-mer) sequence context window and allele count (Methods).
Across all 5-mer sequence contexts, we observed a significant correlation between expected and observed fractions of IBD-inconsistent calls (Pearson’s correlation coefficient for allele count = 2; Figure 3; Supplementary Tables S4 and S5). The observed fraction of sites called IBD-inconsistent was higher than expected for contexts, and lower than expected for contexts (Figure 3; Supplementary Tables S4 and S5). Within contexts, we also observed a significant correlation between expected and observed fractions for allele count = 2), though for all contexts calls were fewer than expected (Supplementary Figure S9; Tables S4 and S5). Within contexts, the correlation between expected and observed was significant for all allele counts except for variants of allele count = 5, which had the smallest sample size ( for allele count = 2; Supplementary Figure S10; Tables S4 and S5). These results suggest that at sequence contexts with relatively lower polymorphism probabilities, there was a higher rate of IBD-inconsistent calls. contexts represent 82% of the polymorphic sites tested, but 68% of sites called IBD-inconsistent.
FIGURE 3.
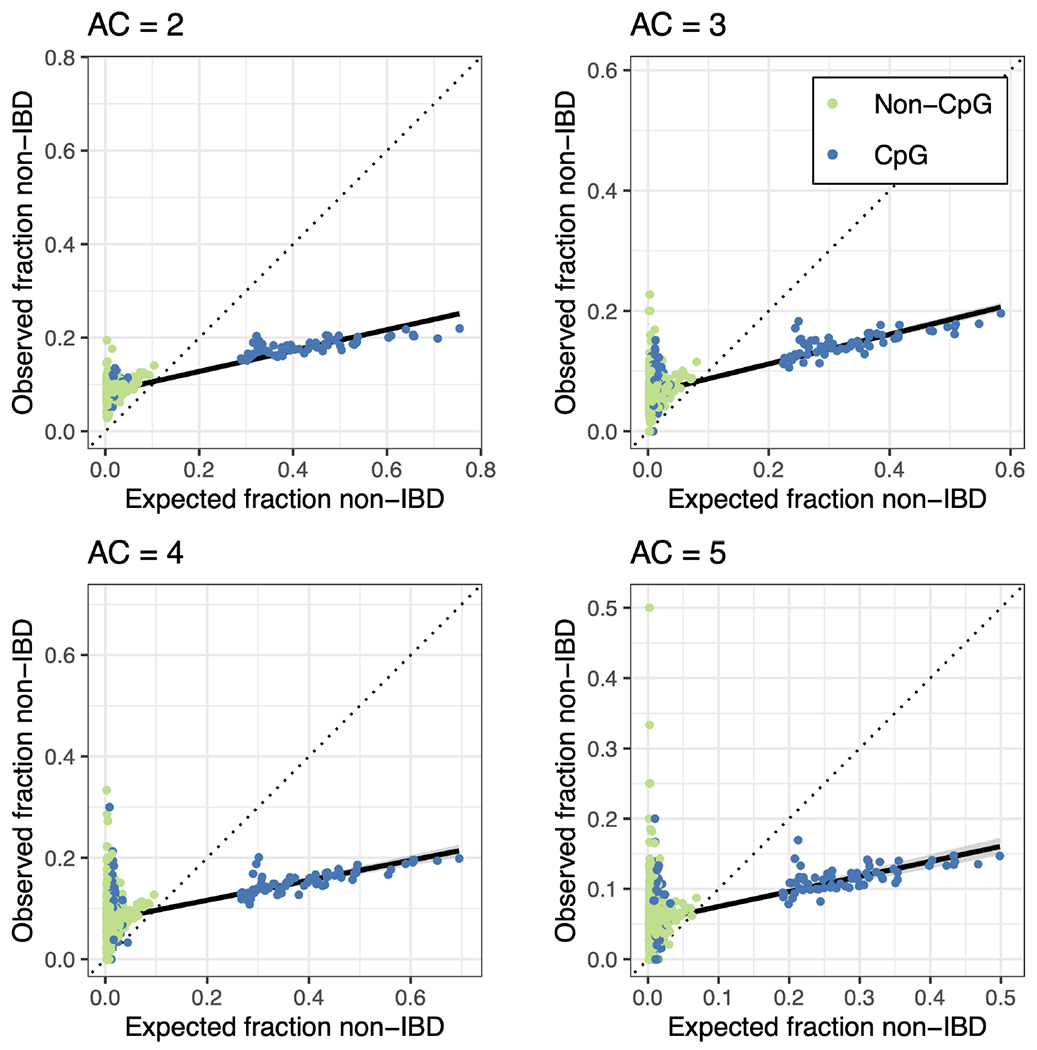
Calibration of EVICORD detected rates of identity-by-descent (IBD)-inconsistent calls in UK10K data. The expected and observed fraction of sites called IBD-inconsistent for UK10K variants, for allele counts (AC) 2–5. Each dot represents a 5-mer sequence context. Dot colours represent whether the sequence context is a CpG context (blue) or not (light green). The expected fraction was calculated from each sequence context’s polymorphism probability. The solid black line is a linear regression line for all sequence contexts, and the dotted line is the identity line.
We next assessed whether IBD-inconsistent variants were localized to specific sequence contexts or dispersed proportionally to the polymorphism probabilities of larger sequence contexts. We compared polymorphism probabilities estimated from IBD-variants to probabilities derived from allele counts 2–5 IBD-inconsistent variants in 7-mer sequence context models. Due to the small sample size of some 7-mer windows, we employed a dynamic programming algorithm to only consider contexts in our models where at least 100 mutations and 20,000 instances of the context were present in the dataset. For contexts where either criterion fails, the algorithm uses the next largest nucleotide window where both criteria are satisfied (Methods). Probabilities from IBD-consistent and inconsistent variants were strongly rank correlated (Spearman’s correlation = 0.93, ) but with a concerted shift towards IBD compared to IBD-inconsistent polymorphisms for the most mutable mutation types, and (Figure 4). These observations suggest that there is a global shift proportional to the underlying mutability of each context which is not localized to any specific 7-mer contexts.
FIGURE 4.
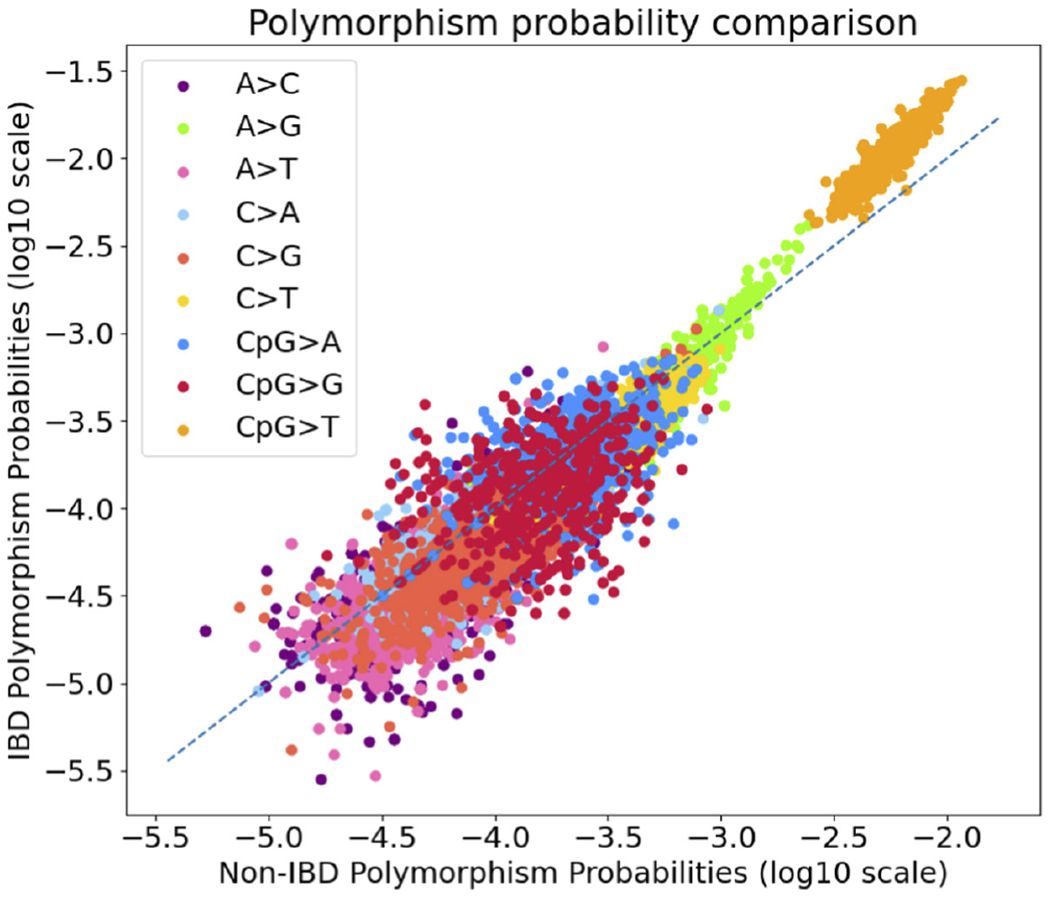
7-mer sequence context polymorphism probabilities for sites called identity-by-descent (IBD)-inconsistent vs. IBD-consistent for UK10K variants. Each dot represents the polymorphism probability estimated for each 7-mer sequence context using our dynamic programming algorithm. The dashed blue line represents the expected polymorphism probabilities under a model of no differences between IBD-consistent and inconsistent variants. Polymorphism probabilities were strongly rank correlated (Spearman’s correlation ).
3.5 |. Additional genomic annotations correlated with IBD-inconsistent variants
To infer genomic features correlated with IBD-inconsistent variants, we performed a logistic regression with IBD-consistent/inconsistent calls for each variant as the response variable (6,763,324 sites; with 665,340 called IBD-inconsistent). In separate regressions for each allele count, we included 7-mer polymorphism probabilities, background selection, GC content, replication timing, local recombination rate, distance to a recombination hotspot, germline CpG methylation levels, the variant calling quality measure VQSLOD and read depth as predictors. We transformed the values of each annotation to -scores and report the odds ratios and 95% confidence interval for each annotation in Figure 5 (Supplementary Table S6). All annotations were significantly associated with the outcome (multiple logistic regression coefficient ). We also performed regressions with sites only (Supplementary Figure S11, Table S6). Below, we highlight the annotations included as predictors, our prior hypotheses about their relationships with IBD-inconsistent rare variants, and the results of the regression models.
FIGURE 5.
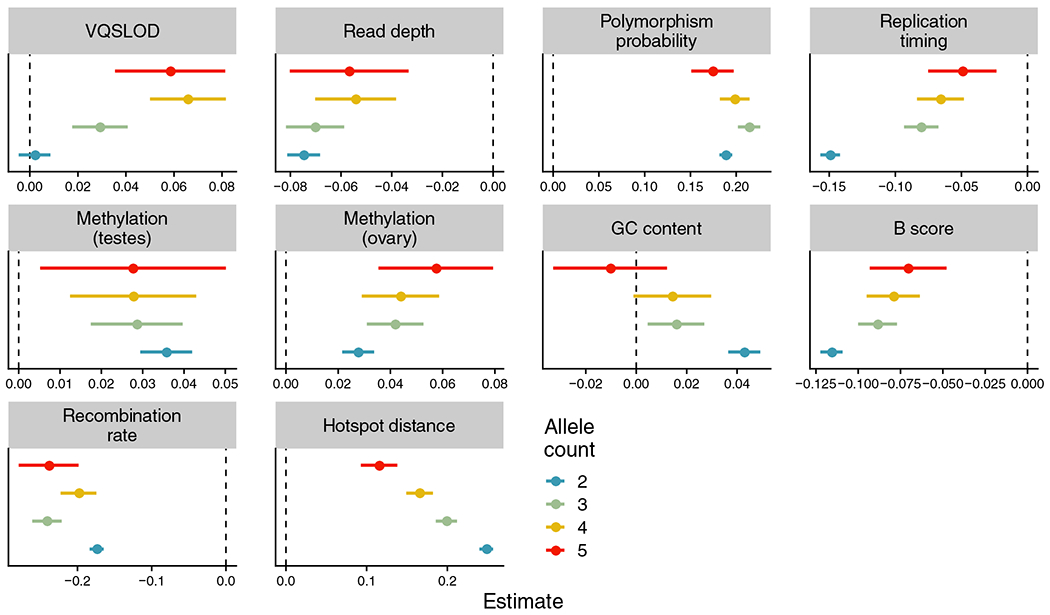
Correlations between genomic annotations and identity-by-descent (IBD)-inconsistent variant calls. Depicted are summaries of multiple logistic regression models of genomic annotations (predictor variables) vs. IBD-inconsistent variant calls (outcome) for all variant sites, grouped by allele count. Dot colours represent allele count, and a separate regression was run for variants of each allele count. Each dot’s position denotes its regression coefficient estimate, with error bars representing the estimate . The vertical dashed line represents a coefficient estimate of zero. Hotspot distance: physical distance to nearest recombination hotspot z-score; Recombination rate: local recombination rate z-score; B score: McVicker’s B statistic z-score; Replication timing: replication timing z-score; GC content: local GC content z-score; Methylation (ovary): ovary CpG methylation z-score; Methylation (testes): testes CpG methylation z-score; Read depth: read depth z-score; VQSLOD: variant quality z-score.
3.5.1 |. Polymorphism probability
As shown above, polymorphism probability was strongly positively correlated with IBD-inconsistent status. As previous work has shown that a 7-mer model explains additional variation in genetic variation over a 5-mer model (Aggarwala & Voight, 2016), we find that a 7-mer polymorphism probability calculated in UK10K in the logistic regression model was associated with our IBD-inconsistent calls (multiple regression coefficient for variants of allele count = 2).
3.5.2 |. GC content
GC content varies across the human genome, and is correlated with gene content, repetitive elements, DNA methylation, recombination rates and substitution probabilities (Arndt et al., 2005). In our regression model, increased local GC content (measured at a 1 kb scale) was associated with increased probability IBD-inconsistency (multiple regression coefficient for variants of allele count = 2).
3.5.3 |. Replication timing
Later replication timing has been linked to higher rates of de novo mutation in the human genome, specifically in the offspring of relatively younger fathers (Francioli et al., 2015). Our regression model with replication timing estimates (Koren et al., 2012) was consistent with these results, with variants in late replicating regions significantly more likely to be called as recurrent (multiple regression coefficient for variants of allele count = 2.
3.5.4 |. Background selection
We included B-values (McVicker et al., 2009), a measure of background selection, or purifying selection due to linkage with deleterious alleles, with lower B-values indicative of stronger background selection. We expected that increased background selection would be associated with increased recurrent mutation, as linkage to deleterious alleles would result in variants being removed from the population and thus present at lower frequencies. Recurrent mutations would then be more likely to be present as they effectively shift the SFS towards more rare alleles. Our results are consistent with this expectation, with an odds ratio less than one for -values (multiple regression coefficient for variants of allele count = 2). This relationship could also potentially be caused by older IBD variants maintained at low frequencies due to negative selection being identified as IBD-inconsistent.
3.5.5 |. Local recombination rate and distance to recombination hotspots
We observed that both an increased local recombination rate and a shorter distance to a recombination hotspot were correlated with a lower probability of a site being called as recurrent (multiple regression coefficient for local recombination rate for variants of allele count = 2).
3.5.6 |. Methylation levels at CpG sites
Spontaneous deamination of 5-methylcytosine at CpG sites results in a substantial increase in C-to-T transition mutations. We included CpG methylation levels measured in testes and ovaries in our model, expecting that CpG sites with higher methylation levels are more likely to spontaneously deaminate, increasing mutation rates generally and thus increase recurrent mutation probabilities. Methylation levels in testes and ovaries were correlated (Pearson’s ), but we note that increased methylation in both tissue types independently predicted an increased posterior probability of a variant being IBD-inconsistent (e.g., ovarian CpG methylation levels: multiple regression coefficient ; testes CpG methylation levels: multiple regression coefficient ; both for variants with allele count = 2).
3.5.7 |. VQSLOD and read depth
We observed a significant relationship between sequencing quality, measured both by read depth and variant quality score, and the probability of a site being IBD-inconsistent (multiple regression coefficient for read depth of variants of allele count = 2). Under a simple model for genotyping error, where errors are distributed randomly (without respect to haplotype), this result suggests that our approach also identifies some number of genotyping errors in regions of low read depth or sequencing quality.
3.6 |. IBD-inconsistent calls and gene conversion events
As non-crossover gene conversions are thought to be more frequent than de novo mutations in the human genome (Halldorsson et al., 2016), we expect that a subset of our IBD-inconsistent variant calls reflect gene conversion events. After a non-crossover gene conversion event encompassing a rare variant, the copied allele resides on the existing haplotype background of the acceptor chromosome, which may reduce the surrounding shared IBD segment. We devised a heuristic to identify likely gene conversions, based on the intuition that two IBD-inconsistent variants in close physical proximity in the same individuals are more likely to reflect variants copied along a gene conversion tract, rather than two independent recurrent point mutations. If a gene conversion tract contains only a single rare variant, this signature would be indistinguishable from a recurrent point mutation with our approach. However, if a gene conversion contained no rare variants, it would not be identified in our analysis as a potential recurrent mutation or gene conversion.
Limiting our results to tracts with two or more IBD-inconsistent variants present in the same individuals, we identified 42,203 variants within 18,971 putative gene conversion tracts, representing 6.3% of IBD-inconsistent variants (Supplementary Figure S12). We performed logistic regression with all IBD-inconsistent variants labelled as potential gene conversions or not as the outcome, and the genomic annotations listed above as predictor variables (Figure 6, Supplementary Table S7). We additionally included the posterior probability of a variant being IBD-inconsistent as a predictor variable. Compared to IBD-inconsistent variants not in putative gene conversion tracts, these variants were associated with lower polymorphism probability, higher variant quality score, increased posterior probability of being IBD-inconsistent, smaller distance to a recombination hotspot and lower recombination rate. We also observed a GC bias in putative gene conversion variants, as measured by the fraction of variants containing an or mutation (37% in putative gene conversions vs. 27% in all other IBD-inconsistent variants; Fisher’s exact test ).
FIGURE 6.
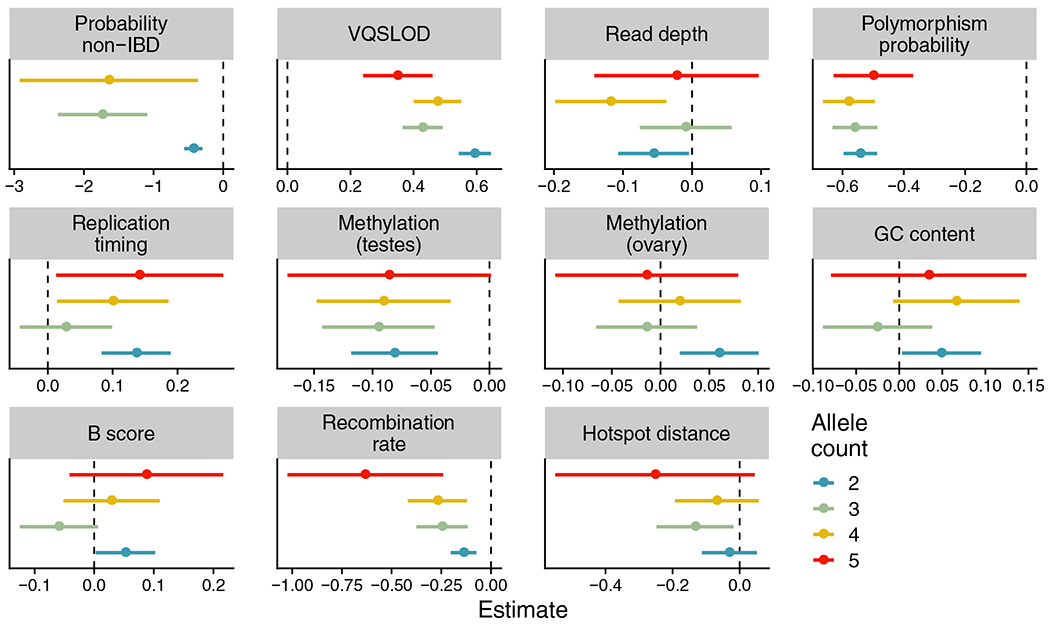
Correlations between genomic annotations and putative calls of gene conversion events. Results of a logistic regression using genomic annotations to distinguish putative gene conversions from other identity-by-descent (IBD)-inconsistent variants in UK10K data. Separate regressions were performed for variants of each allele count. The annotation of variants’ probability of being IBD-inconsistent for allele count was left off to improve the visualization (Estimate: ). Dot colours represent allele count. Each dot’s position denotes its regression coefficient estimate, with error bars representing the 95% confidence interval (estimate ). The vertical dashed line represents a regression coefficient estimate of zero. Hotspot distance: physical distance to nearest recombination hotspot z-score; Recombination rate: local recombination rate z-score; B score: McVicker’s B statistic z-score; Replication timing: replication timing z-score; GC content: local GC content z-score; Methylation (ovary): ovary CpG methylation z-score; Methylation (testes): testes CpG methylation z-score; Read depth: read depth z-score; VQSLOD: variant quality z-score; Probability non-IBD: posterior probability of variant being IBD-inconsistent.
3.7 |. Rescaling the site frequency spectrum with IBD-inconsistent mutations
With our set of high-confidence IBD-inconsistent variants, we rescaled the SFS for very rare variants. Considering the power of our approach on simulated data, we plot the original and rescaled SFS for variants with allele count in (Figure 7a; Methods). Rescaling the SFS resulted in a 3% increase in the fraction of singleton variants, from 46.6% to 49.6%. As expected, most of this shift is due to the relatively large fraction of variants that were called as IBD-inconsistent (Figure 7b). For variants alone, the fraction of singleton variants increased from 43.6% to 49.9%. We note that this rescaling is incomplete, as we identified IBD-inconsistent variants at only allele counts 2 to 5, which represent 38% of the non-singleton variants in the UK10K dataset.
FIGURE 7.
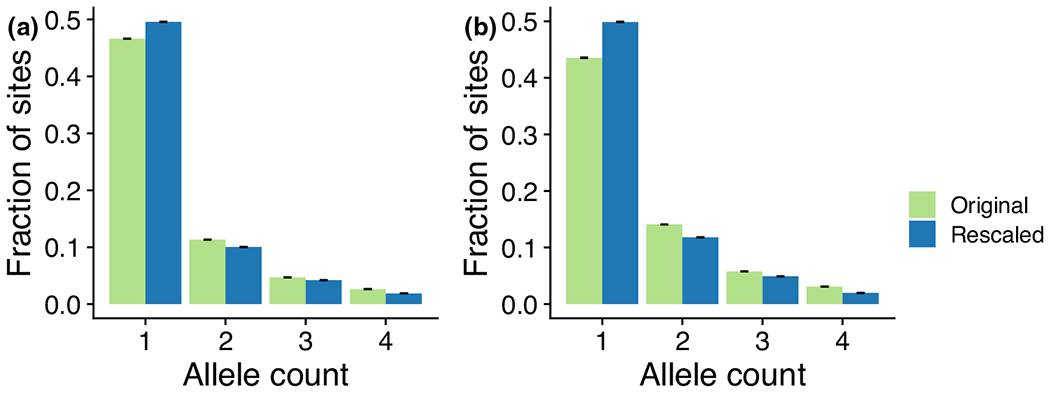
Rescaling the site frequency spectrum (SFS) with identity-by-descent (IBD)-inconsistent calls. Shown here are the UK10K SFS for variants of allele count , before and after rescaling to incorporate IBD-inconsistent variants. (a) The original and rescaled SFS for all variants. (b) The original and rescaled SFS for variants only.
4 |. DISCUSSION
We describe a novel approach designed to identify variants inconsistent with IBD transmission of alleles using whole-genome sequencing data, leveraging the expected difference in the obligate recombination distance between rare alleles transmitted under a simple IBD transmission model, relative to those with more complex patterns of inheritance. Our approach uses a Bayesian hierarchical model and Gibbs sampling to jointly infer the TMRCA distributions of these two scenarios and identify variants with a high posterior probability of being IBD-inconsistent. In simulated data, we find that the posterior probabilities of IBD-inconsistency can discriminate between recurrent mutation and non-recurrent mutational events up to allele count 5 in a population sample of 3,621 individuals.
Our approach assumes that we lack phase assignment of the rare allele to the maternally or paternally inherited chromosome. If we had true phase information, we could more accurately measure recombination breakpoints, potentially improving the performance of our method by eliminating the measurement error caused using the obligate recombination distance. We assumed a single, exponentially growing population, though extensions to rare variants shared by multiple populations may be possible. In the scenario of a very rare variant present in two populations, the null hypothesis may be recurrence rather than single mutational event, especially at hypermutable sites, but would need to model migration. Simulations modelling this scenario would be required to test the applicability of our approach to variants shared across populations. We assume a ‘star-shaped’ genealogy for IBD rare variants, though in the true genealogy of an IBD variant, the TMRCA for some allele pairs could be much more recent than the clade TMRCA for variants with allele count . This assumption reduced the complexity of our model and sped up computation, but future work could model this variation in TMRCA across allele pairs. We did not model the effect of genotyping error on our estimate of the shared haplotype length between pairs of rare alleles. These errors could result in underestimation of shared haplotype length and potentially false calls of truly IBD variants as IBD-inconsistent. Future work could explicitly model and investigate the impact of these errors on our approach. We also focused on inference of IBD-inconsistent variants for allele counts of 5 or less, as the performance of our method decreases with increasing allele count. Our simulations with a larger sample size of 10,000 (versus 3,621) confirmed that increasing sample size provides a boost in power for variants of a given allele count. Thus, we expect that applying our method to even larger sequencing datasets will improve its performance.
The negative correlation we observed between local recombination rate and the probability of a site being called IBD-inconsistent suggests that our method is confounded by local recombination rate. In simulated data, we observed that we had lower power to identify recurrent mutations when there was a variable recombination rate. We also note that we found a significant relationship between sequencing quality, measured by read depth and variant quality score, and the probability of a site being called IBD-inconsistent. The signature of an IBD-inconsistent variant used here could also be that of a genotyping error, as genotyping errors also may occur on any random haplotype background in a population. This could be a potential application of our method. Our current recommendation is to remove variants of low quality until this relationship is not significant. However, distinguishing genotyping errors from true non-IBD variants remains an important problem. Additionally, though we heuristically identified a number of likely gene conversions, this approach can only identify gene conversions encompassing at least two rare variants, a small fraction of true gene conversion events.
5 |. MATERIALS AND METHODS
5.1 |. Forward genetic simulations with SLiM
We used the software program SLiM version 2.5 (Haller & Messer, 2017), to simulate genetic data following a European demographic model (Bhaskar et al., 2015): an ancestral population size of 10,000 (burn-in of 100,000 generations); a population bottleneck to 200 individuals at generation 200; population size rebounds to 10,000; a second bottleneck to 500 individuals at generation 4280; population size rebounds to 5800 ; exponential growth starting at generation 4870 at 3.89% per generation; random sampling of 3,621 individuals at generation 5000. SLiM simulations had a uniform rate of mutations per base pair per generation. We identified recurrent mutations as base positions with two or more mutations in the SliM output. We performed 1000 simulations with uniform recombination rate of events per base pair per generation, and an additional 500 simulations with selection or variable recombination rate.
For simulations with selection, we generated genomic segments using a recipe from the SLiM manual (Haller & Messer, 2017): (1) sample non-coding region; (2) sample exon; (3) sample intron and exon pairs in a loop with 20% probability of stopping after each pair; (4) repeat steps 1–3 while chromosome length ; and (5) sample final non-coding region. Exonic mutations were synonymous or non-synonymous at a ratio of , and 10% of non-synonymous mutations were neutral. Deleterious non-synonymous mutation selection coefficients were sampled from a Gamma distribution with mean and shape parameter . Exon lengths were sampled from a Lognormal distribution with mean and standard deviation . Non-coding regions were neutral and their lengths were sampled from a uniform distribution between 100 and 5000. Intronic mutations were neutral and intron lengths were sampled from a Lognormal distribution with mean and standard deviation .
For each simulation with a variable recombination map, we randomly sampled a segment from chromosome 2 of the 1000 Genomes Project CEU genetic map (The 1000 Genomes Project Consortium, 2012) and used the given recombination rates for the simulated segment. All other parameters for the variable recombination simulations were as described above with no selection.
5.2 |. UK10K dataset
We applied our method to identify IBD-inconsistent mutations in whole-genome sequencing data in 3,621 individuals from the UK10K project (The UK10K Consortium, 2015). These individuals were sequenced to average depth , passed the UK10K project quality control filters, and come from the ALSPAC and TWINSUK studies. We measured the recombination distance for biallelic and multiallelic single nucleotide variants that passed the UK10K quality filters that were present at allele count in these individuals.
5.3 |. Measuring the obligate recombination distance
For simulated data, we generated diploid genotypes by randomly combining pairs of haploid genomes and calculated the recombination distances for variants within the central of each genomic segment. In both simulated and UK10K data, we measured the obligate recombination distances for variants with allele count and all carriers as heterozygotes. For each pair of carriers, we identified the nearest variant upstream and downstream with opposite homozygote genotype (Figure 1A). We then converted the physical distance to a genetic distance using a genetic map. For UK10K, we used the Project CEU genetic map (The 1000 Genomes Project Consortium, 2012).
5.4 |. Applying the Bayesian hierarchical model
To apply our model to simulated or UK10K recombination distances, we first estimated the parameter for IBD-inconsistent variants from multiallelic sites. Using Gibbs sampling on non-IBD allele pairs from multiallelic variants, we used a simplified version of the hierarchical model which sampled the TMRCA for each allele pair and the parameter in each Gibbs iteration. We repeated this procedure to estimate for a range of values from multiallelic sites’ recombination distances. To test whether the choice of affected our ability to discriminate IBD-consistent and IBD-inconsistent variants, we applied the model with different IBD-inconsistent values to UK1OK variants on chromosome 22. The posterior estimates of were highly correlated across values of , Supplementary Table S8). When applying the full model to data, we used for IBD allele pairs, with and the corresponding value of inferred from multiallelic sites () for non-IBD allele pairs. We ran 10,000 iterations of the Gibbs sampler for each run of the model, thinned the chains until autocorrelation was below 0.01, and assessed convergence of the chains by comparing the thinned samples from the first and second half of the chain via a Wilcoxon rank-sum test. A chain was determined to have converged if the Wilcoxon test -value was .
We parallelized the application of our model by breaking down the genome into segments, rather than including all variants of a given allele count in a single run of the Gibbs sampler. To test the effect of the number of variants included in a Gibbs sampling run, we applied the model to segments on chromosome 22 and to all variants on chromosome 22 together. For smaller allele counts with thousands of variants in each segment, we observed no effect, but for larger allele counts we did see an effect of applying the model to small numbers of variants. Thus, for allele counts , we grouped segments together until at least 1000 variants were included in each run of the model.
5.5 |. Variant age estimation with runtc
We obtained the runtc software to perform age estimation (see URLs) (Platt et al., 2019). The output from 100 simulations from SLiM with uniform recombination and mutation rates was converted to VCF format, and then runtc was applied to the vcf files with the commands: -range 2 10, rec 1e-8, mut 2.5e-8.
5.6 |. Area under the ROC curve
For all ROC curves from simulated data, we calculated the AUC as, for all possible pairs of one IBD and one recurrent variant, the percent of pairs with the recurrent variant with a higher value of the statistic being evaluated. For each AUC, we calculated a confidence interval by generating 10,000 bootstrap samples of 5,000 variants (with the same ratio of IBD:recurrent variants as the simulated sample). We then sorted the 10,000 AUC estimates and took the 2.5th and 97.5th percentiles to get a 95% confidence interval.
5.7 |. Calculating an expected fraction of recurrent mutations from polymorphism probabilities
As a proxy for the mutation rate, we estimated the polymorphism probability for 5-mer sequence contexts (i.e. two bases up and downstream of the focal base) as the fraction of sites with that context that were variable in the UK10K dataset. These polymorphism probabilities were highly correlated with those calculated previously with the 1000 Genomes dataset (Aggarwala & Voight, 2016) (Pearson’s correlation , Supplementary Table S5).
To predict the fraction of sites that should be called recurrent based on sequence context polymorphism probabilities, we used a simple Poisson model of mutation. With the polymorphism probability for a context as the Poisson rate parameter and the number of mutations at a site , the probability of a recurrent mutation is the probability of two or more mutations at a site:
| (14) |
As we are only considering sites where there has been at least one mutation event, that is, polymorphic sites, the probability of a recurrent mutation at a site is then:
| (15) |
We calculated this probability for each 5-mer sequence context. We then calculated the expected fraction by scaling the overall fraction of sites called IBD-inconsistent by each context’s probability of a recurrent mutation, relative to all the other contexts.
We used 5-mer sequence contexts for this analysis so that we would have a reasonable number of variants classified as IBD or not for each sequence context. For the regression models to predict IBD-inconsistent variants using multiple genomic annotations, we used 7-mer sequence contexts, as there is significant mutation rate variation beyond 5-mer contexts (Aggarwala & Voight, 2016).
5.8 |. Identifying putative gene conversions
Within the set of variants called as IBD-inconsistent, we called putative gene conversion tracts that contained 2 or more variants that were (1) present in the same individuals, (2) at the same allele count and (3) within of each other.
5.9 |. Estimating polymorphism probabilities from IBD-consistent and inconsistent variants
Variants with allele count between 2 and 5 were combined and then separated into two groups according to IBD status. All putative gene conversion variants were removed. The IBD-inconsistent variant group was down-sampled to match the sample size of the IBD variant group, and then both groups were normalized to the overall polymorphism probability. Polymorphism probabilities for each group were then separately modelled up to a 7-mer sequence context size. For each model, an inclusion criterion was set, requiring a minimum sample size of 20,000 genomic instances and 100 total mutations across all three possible mutation types (e.g. ). If either criterion was not met, a smaller context window was considered instead and again tested given these specifications. The nested relationship of contexts was leveraged to yield the final model, containing a subset possible 7-mer contexts and a collection of smaller window sizes.
5.10 |. Genomic annotation datasets
We used the B statistic (McVicker et al., 2009) to measure background selection, which estimates the proportion of neutral variation in a region. VQSLOD and read depth were extracted from the UK10K VCF files. We used a recombination rate map estimated for Europeans from the 1000 Genomes Project, downloaded from the below given URL (The 1000 Genomes Project Consortium, 2012). We used human recombination hotspots identified in the HapMap project (The International Hapmap Consortium, 2007), and downloaded from the below given URL. Replication timing data were obtained from Koren et al. (2012). CpG methylation levels were downloaded from using accession numbers GSM1010980 (ovary), and GSM1127119 (testis). URLs for downloaded sites are provided below (see URLs).
5.11 |. Rescaling the SFS with IBD-inconsistent mutations
Starting with the SFS calculated from all UK10K biallelic sites included in our study, for allele counts 2–5 for and all other mutation types we calculated the fraction called as IBD-inconsistent. We then divided this fraction by the power of our method, estimated by the percent of multiallelic sites identified as IBD-inconsistent at the chosen posterior threshold. From this fraction of IBD-inconsistent sites for the two mutation types, we apportioned the IBD-inconsistent mutations into lower allele counts based on the relative frequency of allele counts 1–5. For example, to determine what fraction of IBD-inconsistent 4-ton variants would be assigned partition 1:3 vs. 2:2, we used the relative frequencies:
Where is the relative frequency of the 1:3 partition, and is the frequency of singletons in the original SFS. In the rescaled SFS, the number of singletons increased by the number of variants of allele count 2–5 that were identified with partition 1:(n – 1); the number of doubletons decreased by the number of doubletons that were identified as IBD-inconsistent, and increased by the number of variants of allele count 3–5 that had partition 2: and so on through allele count 4. Allele count 5 was excluded from the rescaled SFS plots because we did not identify IBD-inconsistent variants at allele counts greater than 5.
Supplementary Material
ACKNOWLEDGEMENTS
This work was supported by the US National Institutes of Health (grant numbers DK101478 and DK126194 to B.F.V.; T32 GM008216 for K.E.J.) and a Linda Pechenik Montague Investigator award (to B.F.V.). This study makes use of data generated by the UK10K Consortium, derived from samples from ALSPAC and TWINSUK. A full list of the investigators who contributed to the generation of the data is available from www.UK10K.org. Funding for UK10K was provided by the Wellcome Trust under award WT091310.
Funding information
National Institute of Diabetes and Digestive and Kidney Diseases, Grant/Award Number: DK101478 and DK126194; National Institute of General Medical Sciences, Grant/Award Number: T32 GM008216; Perelman School of Medicine, University of Pennsylvania; Wellcome Trust, Grant/Award Number: WT091310
Footnotes
CONFLICT OF INTEREST
The authors declare no competing interest.
SUPPORTING INFORMATION
Additional supporting information can be found online in the Supporting Information section at the end of this article.
URLS
runtc software: https://github.com/jaredgk/runtc
B statistic: http://www.phrap.org/othersoftware.html
Recombination maps: http://ftp.1000genomes.ebi.ac.uk/vol1/ftp/technical/working/20130507_omni_recombination_rates, https://github.com/auton1/Campbell_et_al
GEO access for methylation accessions GSM1010980 (ovary), and GSM1127119 (testis): https://www.ncbi.nlm.nih.gov/geo/
DATA AVAILABILITY STATEMENT
We have created the R package EVICORD (eValuating IBD Consistency via Obligate Recombination Distance) containing the Gibbs sampler for our Bayesian hierarchical model (Johnson, 2022). The code is available at https://doi.org/10.5281/zenodo.7090677. The hierarchical model input data (pairwise obligate recombination distances) and output (posterior probabilities and IBD in/consistent calls) from simulations and UK10K are available at http://coruscant.itmat.upenn.edu/data/johnson-voight-nIBD-v2.tar.gz.
REFERENCES
- Aggarwala V, & Voight BF (2016). An expanded sequence context model broadly explains variability in polymorphism levels across the human genome. Nature Genetics, 48, 349–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albers PK, & McVean G (2020). Dating genomic variants and shared ancestry in population-scale sequencing data. PLoS Biology, 18, e3000586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arndt PF, Hwa T, & Petrov DA (2005). Substantial regional variation in substitution rates in the human genome: Importance of GC content, gene density, and telomere-specific effects. Journal of Molecular Evolution, 60, 748–763. [DOI] [PubMed] [Google Scholar]
- Bhaskar A, Wang YXR, & Song YS (2015). Efficient inference of population size histories and locus-specific mutation rates from large-sample genomic variation data. Genome Research, 25, 268–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L, Dupanloup I, Huerta-Sánchez E, Sousa VC, & Foll M (2013). Robust Demographic inference from genomic and SNP data. PLoS Genetics, 9, e1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francioli LC, Polak PP, Koren A, Menelaou A, Chun S, Renkens I, Genome of the Netherlands Consortium, Van Duijn CM, Swertz M, Wijmenga C, Van Ommen G, Slagboom PE, Boomsma DI, Ye K, Guryev V, Arndt PF, Kloosterman WP, de Bakker PIW, & Sunyaev SR (2015). Genome-wide patterns and properties of de novo mutations in humans. Nature Genetics, 47, 822–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst RN, Hernandez RD, Williamson SH, & Bustamante CD (2009). Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genetics, 5, e1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane JBS (1919). The combination of linkage values and the calculation of distances between the loci of linked factors. Journal of Genetics, 8, 229–309. [Google Scholar]
- Haldane JBS (1933). The part played by recurrent mutation in evolution. The American Naturalist, 67, 5–19. [Google Scholar]
- Halldorsson BV, Hardarson MT, Kehr B, Styrkarsdottir U, Gylfason A, Thorleifsson G, Zink F, Jonasdottir A, Jonasdottir A, Sulem P, Masson G, Thorsteinsdottir U, Helgason A, Kong A, Gudbjartsson DF, & Stefansson K (2016). The rate of meiotic gene conversion varies by sex and age. Nature Genetics, 48, 1377–1384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller BC, & Messer PW (2017). SLiM 2: Flexible, interactive forward genetic simulations. Molecular Biology and Evolution, 34, 230–240. [DOI] [PubMed] [Google Scholar]
- Harpak A, Bhaskar A, & Pritchard JK (2016). Mutation rate variation is a primary determinant of the distribution of allele frequencies in humans. Eyre-Walker A, editor. PLOS Genetics, 12, e1006489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hein J, Schierup MH, & Wiuf C (2005). Gene genealogies, variation and evolution: A primer in coalescent theory. Oxford University Press. [Google Scholar]
- Hudson RR, & Kaplan NL (1985). Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics, 111, 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins PA, Mueller JW, & Song YS (2014). General triallelic frequency spectrum under demographic models with variable population size. Genetics, 196, 295–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins PA, & Song YS (2011). The effect of recurrent mutation on the frequency spectrum of a segregating site and the age of an allele. Theoretical Population Biology, 80, 158–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson KE (2022). EVICORD (EValuating IBD Consistency via Obligate Recombination Distance). 10.5281/zenodo.7090677 [DOI] [Google Scholar]
- Jouganous J, Long W, Ragsdale AP, & Gravel S (2017). Inferring the joint demographic history of multiple populations: Beyond the diffusion approximation. Genetics, 206, 1549–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelleher J, Wong Y, Wohns AW, Fadil C, Albers PK, & McVean G (2019). Inferring whole-genome histories in large population datasets. Nature Genetics, 51, 1330–1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koren A, Polak P, Nemesh J, Michaelson JJ, Sebat J, Sunyaev SR, & McCarroll SA (2012). Differential relationship of DNA replication timing to different forms of human mutation and variation. American Journal of Human Genetics, 91, 1033–1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lek M, Karczewski KJ, Minikel EV, Samocha KE, Banks E, Fennell T, O’Donnell-Luria AH, Ware JS, Hill AJ, Cummings BB, Tukiainen T, Birnbaum DP, Kosmicki JA, Duncan LE, Estrada K, Zhao F, Zou J, Pierce-Hoffman EP, Berghout J, … MacArthur DG (2016). Analysis of protein-coding genetic variation in 60,706 humans. Nature, 536, 285–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukic S, & Hey J (2012). Demographic inference using spectral methods on SNP data, with an analysis of the human out-of-Africa expansion. Genetics, 192, 619–639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathieson I, & McVean G (2014). Demography and the age of rare variants. PLoS Genetics, 10, e1004528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVicker G, Gordon D, Davis C, & Green P (2009). Widespread genomic signatures of natural selection in hominid evolution. PLoS Genetics, 5, e1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagnier J, Mears JG, Dunda-Belkhodja O, Schaefer-Rego KE, Beldjord C, Nagel RL, & Labie D (1984). Evidence for the multicentric origin of the sickle cell hemoglobin gene in Africa. Proceedings of the National Academy of Sciences of the United States of America, 81, 1771–1773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palamara PF, Francioli LC, Wilton PR, Genovese G, Gusev A, Finucane HK, Sankararaman S, Sunyaev SR, De Bakker PIW, Wakeley J, Pe’er I, & Price AL (2015). Leveraging distant relatedness to quantify human mutation and gene-conversion rates. American Journal of Human Genetics, 97, 775–789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palamara PF, Lencz T, Darvasi A, & Pe’er I (2012). Length distributions of identity by descent reveal fine-scale demographic history. American Journal of Human Genetics, 91, 809–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt A, Pivirotto A, Knoblauch J, & Hey J (2019). An estimator of first coalescent time reveals selection on young variants and large heterogeneity in rare allele ages among human populations. PLoS Genetics, 15, e1008340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ragsdale AP, Coffman AJ, Hsieh P, Struck TJ, & Gutenkunst RN (2016). Triallelic population genomics for inferring correlated fitness effects of same site nonsynonymous mutations. Genetics, 203, 513–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speidel L, Forest M, Shi S, & Myers SR (2019). A method for genome-wide genealogy estimation for thousands of samples. Nature Genetics, 51, 1321–1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium. (2012). An integrated map of genetic variation from 1,092 human genomes. Nature, 491, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International Hapmap Consortium. (2007). A second generation human haplotype map of over 3.1 million SNPs. Nature, 449, 851–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The UK10K Consortium. (2015). The UK10K project identifies rare variants in health and disease. Nature, 526, 82–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S (1931). Evolution in mendelian populations. Genetics, 16, 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S (1937). The distribution of gene frequencies in populations. Proceedings of the National Academy of Sciences of the United States of America, 23, 307–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We have created the R package EVICORD (eValuating IBD Consistency via Obligate Recombination Distance) containing the Gibbs sampler for our Bayesian hierarchical model (Johnson, 2022). The code is available at https://doi.org/10.5281/zenodo.7090677. The hierarchical model input data (pairwise obligate recombination distances) and output (posterior probabilities and IBD in/consistent calls) from simulations and UK10K are available at http://coruscant.itmat.upenn.edu/data/johnson-voight-nIBD-v2.tar.gz.


