Deep learning based automated left ventricle segmentation and flow quantification in 4D flow cardiac MRI

Abstract

Background

4D flow MRI enables assessment of cardiac function and intra-cardiac blood flow dynamics from a single acquisition. However, due to the poor contrast between the chambers and surrounding tissue, quantitative analysis relies on the segmentation derived from a registered cine MRI acquisition. This requires an additional acquisition and is prone to imperfect spatial and temporal inter-scan alignment. Therefore, in this work we developed and evaluated deep learning-based methods to segment the left ventricle (LV) from 4D flow MRI directly.

Methods

We compared five deep learning-based approaches with different network structures, data pre-processing and feature fusion methods. For the data pre-processing, the 4D flow MRI data was reformatted into a stack of short-axis view slices. Two feature fusion approaches were proposed to integrate the features from magnitude and velocity images. The networks were trained and evaluated on an in-house dataset of 101 subjects with 67,567 2D images and 3030 3D volumes. The performance was evaluated using various metrics including Dice, average surface distance (ASD), end-diastolic volume (EDV), end-systolic volume (ESV), LV ejection fraction (LVEF), LV blood flow kinetic energy (KE) and LV flow components. The Monte Carlo dropout method was used to assess the confidence and to describe the uncertainty area in the segmentation results.

Results

Among the five models, the model combining 2D U-Net with late fusion method operating on short-axis reformatted 4D flow volumes achieved the best results with Dice of 84.52% and ASD of 3.14 mm. The best averaged absolute and relative error between manual and automated segmentation for EDV, ESV, LVEF and KE was 19.93 ml (10.39%), 17.38 ml (22.22%), 7.37% (13.93%) and 0.07 mJ (5.61%), respectively. Flow component results derived from automated segmentation showed high correlation and small average error compared to results derived from manual segmentation.

Conclusions

Deep learning-based methods can achieve accurate automated LV segmentation and subsequent quantification of volumetric and hemodynamic LV parameters from 4D flow MRI without requiring an additional cine MRI acquisition.

Graphical Abstract

1. Background

Four-dimensional flow magnetic resonance imaging (4D flow MRI) is an advanced imaging technique that allows for comprehensive assessment of cardiovascular hemodynamics [1]. The magnitude and velocity images in 4D flow MRI provide both anatomic and intra-cardiac blood flow velocity information, enabling a better understanding of cardiovascular function and pathology. Several quantitative left ventricular (LV) hemodynamic parameters can be derived from the acquired data, including intra-cardiac kinetic energy (KE), vorticity and functional flow components [2], [3]. Quantitative assessment of these parameters relies on accurate segmentation of the LV cavity. However, the contrast between the blood pool and the surrounding tissue is typically extremely poor in the acquired magnitude images of a 4D flow acquisition. For this reason, the segmentation is usually performed using the images of an additionally acquired balanced Steady State Free Precession (b-SSFP) cine MR acquisition [4], [5]. Based on the known spatial relation between the two acquisitions, the obtained segmentation can be transferred to the domain of the 4D flow acquisition. Bustamante et al. proposed a multi-atlas registration method to automatically generate a segmentation of the entire thoracic cardiovascular system using eight 3D phase-contrast MR angiogram volumes as atlases [6]. A disadvantage of this approach is the high computational cost of the required image registration. Additionally, due to breath-hold inconsistency and differences in heart rate, the cine MR images are prone to a spatial and temporal misalignment resulting in sub-optimal segmentation of the 4D flow acquisition. Therefore, it would be advantageous when the segmentation could be performed directly from the 4D flow acquisition, not requiring any additional acquisition. Moreover, employing an automatic segmentation method directly from the 4D flow MRI data offers the advantage of time efficiency compared to registration-based methods. Despite the limitation posed by the lower spatial resolution in 4D flow MRI, there is potential to compensate the drawback by extracting and fusing additional information from the magnitude and velocity images together.

In recent years, deep learning-based segmentation methods have been proposed and achieved immense success in medical image segmentation tasks. U-Net, consisting of a contracting and expanding path, has demonstrated excellent performance in segmentation of MR imaging data of the heart, brain and various other organs [7]. Benefiting from these convolutional neural networks (CNNs), a few studies reported the use of deep learning for the segmentation of 4D flow MRI. Berhane et al. developed a 3D U-Net with DenseNet-based dense blocks to segment the aortic arch from 4D flow MRI [8]. Based on U-Net and attention gate mechanism, Wu et al. demonstrated that incorporating the information from the combination of magnitude and velocity images results in improved performance in LV myocardium segmentation in 4D myocardial velocity mapping MRI [9]. Corrado et al. applied a fine-tuned CNN model trained on short-axis cine b-SSFP MRI data and used registration to derive segmentation of intra-cardiac 4D flow MRI [10]. However, this approach relies on the availability of a cine MRI acquisition. Bustamante et al. recently reported a 3D U-Net based method for segmentation of the cardiac chambers and great thoracic vessels directly from 4D flow MRI magnitude images, ignoring the velocity images [11]. An excellent geometric agreement with manual segmentation results was reported (DICE ≥ 0.9) and also good agreement of the derived quantitative results, such as end-diastolic (ED) and and-systolic (ES) volumes and blood flow kinetic energy. However, since the employed 4D flow acquisition was acquired directly after gadolinium contrast administration it remains unknown whether the presented method performs equally well on non-contrast-enhanced imaging data.

In this study, we sought to develop and evaluate deep learning-based methods for fully automated LV segmentation directly from 4D flow MRI. Our aim was to enable fast and reliable assessment of blood flow related clinical metrics such as KE and flow components, without the need for manual interaction or cine MRI. Specifically, we aimed to investigate a dedicated deep learning model that incorporates both magnitude and velocity images as input, with the goal of achieving improved segmentation performance compared to using magnitude images alone. Furthermore, we explored the performance of CNN models on both contrast-enhanced and non-contrast-enhanced 4D flow MRI data acquired without respiratory motion compensation, allowing for a comprehensive evaluation of their capabilities. We hypothesized that, despite the relative low image quality of 4D flow MRI, utilizing CNN-based models for LV segmentation may provide an efficient workflow while maintaining reasonable performance compared to manual analysis. Our main contributions are summarized as follows: (1) We evaluated multiple strategies to take advantage of the magnitude and velocity images of the 4D flow MRI acquisition. (2) We compared the performance of five different U-Net-based networks on both subjects with and without post-contrast. (3) We used a Monte Carlo dropout method to evaluate the segmentation uncertainty of the implemented CNN models.

2. Methods

2.1. Study cohort and imaging protocol

The dataset used in the study included 101 subjects, including 75 post-myocardial infarction (MI) patients (11 females, 64 males; mean age 69 ± 12 years, range 40–94) and 26 healthy volunteers (10 females, 16 males; mean age 50 ± 17, range 24–81). The study was approved by the local medical ethical committee of the University of Leeds, UK, and all participants provided written informed consent. All subjects underwent a comprehensive cardiac MR imaging protocol on a 1.5 T MR system (Philips Healthcare), including cine MR imaging in standard cardiac views and 4D flow MR with whole-heart coverage. Table 1 summarizes the demographics derived from the short-axis cine MRI.

Table 1.

Population characteristics of the dataset derived from the short-axis cine. Data is presented as mean ± standard deviation or count. EDV: End-diastolic volume, ESV: End-systolic volume, SV: Stroke volume, EF: Ejection fraction. Mass: Myocardium Mass.

Characteristic	Patients (n = 75)	Volunteers (n = 26)
Gender (Male, n)	64	16
EDV (ml)	186.72 ± 66.54	157.96 ± 39.32
ESV (ml)	99.93 ± 61.16	60.28 ± 17.17
SV (ml)	86.83 ± 17.51	97.68 ± 25.29
EF (%)	49.86 ± 12.43	61.74 ± 4.48
LV mass (g)	110.50 ± 32.40	98.03 ± 25.91

A short-axis cine stack was acquired with a slice thickness of 8–10 mm and an inter-slice gap of 2 mm using 10–17 slices to cover the LV from the apex to the base. Imaging was performed during breath-holding in end-expiration. Other imaging parameters were a field of view (FOV) 300 × 300 mm² to 470 × 470 mm², slice thickness 8 mm, acquired pixel spacing 1.7 mm (reconstructed pixel spacing 0.83–1.19 mm), flip angle 60°, echo time (TE) 1.27–1.62 ms, repetition time (TR) 2.55–3.25 ms and receiver bandwidth 950 Hz/pixel. Using retrospective gating 30 phases were reconstructed to cover a full cardiac cycle. 4D flow MRI was acquired using an echo-planar imaging (EPI) accelerated sequence with retrospective electrocardiogram gating during free-breathing without using respiratory motion compensation [20], [21]. The 3D volume of the acquisition was planned in an oblique orientation with a voxel size of 3 × 3 × 3 mm³, a field of view of 370–400 × 370–400 mm² and 33–52 reconstructed slices to cover the whole heart. The orientation of the acquired 3D volume varied from subject to subject and was adjusted such as to encompass the complete heart and proximal aorta using a minimal number of slices. The number of reconstructed cardiac phases was 30. In all subjects, correction for background velocity offset errors was performed as provided by the scanner software. Other scan parameters of the 4D flow MRI acquisition were TE 3.1–3.8 ms, TR 7.4 − 13.9 ms, flip angle 10˚ and velocity encoding (VENC) 150 cm/s. A more detailed description of the scan parameters can be found in previous work [12]. In patients, the 4D flow acquisition was added to a regular clinical scan protocol, including late-gadolinium enhancement (LGE) imaging. Typically, the 4D flow acquisition was obtained post-contrast (Magnevist, 0.2 mmol/kg) in the waiting period between contrast administration and LGE imaging. In the vast majority of patients (59/75) the delay was less than 15 min. However, in 16 cases the delay was more than 15 min. In these patients the scanner operator opted for acquiring the late-enhancement scan prior to performing the 4D flow acquisition. The volunteer subjects were obtained without the use of contrast.

2.2. Ground truth generation

One experienced observer semi-automatically defined the LV endocardial contours in all slices and phases of the short-axis cine stack using in-house developed Mass research software (Version V2017-EXP; Leiden University Medical Center, Leiden, the Netherlands). Following SCMR recommendations, papillary muscles and trabeculations were included within the defined contours in order to derive a consistent and time-continuous segmentation of the LV geometry. Correction for spatial misalignment, resulting from patient movement between the cine MR and 4D flow acquisition, was performed using rigid registration using Elastix software as previously described [13], [14]. The registration process focused on a single phase that provided the best depiction of LV in the 4D flow magnitude images. The outcome of this registration procedure was subsequently applied to all phases of the 4D flow acquisition. Following this, the registered contours were visually reviewed to identify potential registration or projection errors. Whenever necessary, manual corrections were performed to rectify these issues.

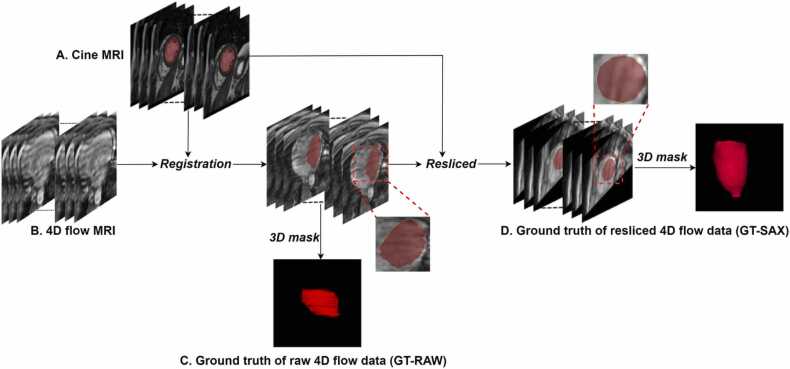
Subsequently, we generated two types of LV blood pool masks for the 4D flow MRI acquisition. The first type of mask, further labelled as RAW, was generated by labelling the pixels of the original slices of the 4D flow acquisition as either blood pool or background according to the nearest labelled pixel in the short-axis cine acquisition. Due to the relatively low through-plane resolution of the short-axis stack and the varying orientation of the acquired 4D flow volumes, the resulting RAW masks frequently suffer from jagged boundaries and are less smooth compared to the original contours as defined in the short-axis stack. Therefore, a second type of mask, further labelled as SAX, was generated by reformatting the volume of the 4D flow acquisition into a stack of short-axis slices. Given the known short-axis orientation, the original 4D flow acquisition was resliced into a short-axis view using a slice spacing of 3 mm and a fixed number of 41 slices. The in-plane resolution was chosen to be equal to that of the cine short-axis stack and ranged from 0.83 × 0.83 mm² to 1.19 × 1.19 mm². Subsequently, the SAX mask was generated by labelling the pixels in the reformatted 4D flow images as either blood pool or background, following the same approach as for the RAW mask. The resulting blood pool regions are smoother compared to the RAW mask regions and vary less in shape since all masks are defined in short-axis orientation. Accordingly, two ground truths are available for training and testing: GT-RAW for the original 4D flow data and GT-SAX for the resliced 4D flow data. Fig. 1 describes the procedure of the ground truth generation, illustrating the more irregular GT-RAW masks compared to the GT-SAX masks. After excluding the images without LV, the dataset contained 89,659 SAX 2D image pairs, 67,567 RAW 2D image pairs and 3030 (101 ×30) 3D volumes.

Fig. 1.

The procedure of ground truth generation. A: The mask of left ventricle was first annotated in the short-axis cine MRI. B, C: it was propagated to original 4D flow MRI using rigid registration method. D: Given the orientation of short-axis cine MRI, the raw 4D flow MRI was resliced into short-axis view.

2.3. Networks

We compare five deep learning models to investigate the effect of data preprocessing, information fusion strategies and network structures on the segmentation performance. The five proposed methods are summarized in Table 2. RAW and SAX represent the two different input orientations. RAW used the original 4D flow data to train the network, either as a 3D volume, or as individual 2D slices and SAX used 4D flow data resliced into the short-axis orientation. Each 2D slice was center cropped to a fixed size of 256 × 256. The number of slices in the 3D volume of the original 4D flow data varies from 33 to 52. The middle 32 slices in the original 4D flow data are stacked as the input of RAW3D. In the resliced dataset with fixed number of 41 slices, the last 40 slices are stacked as the input of SAX3D after excluding the first slice, resulting in an even number of spatial input dimension, which is convenient for the repeated down-sampling operations with a factor of 2.

Table 2.

Different methods with different networks and inputs. SAX indicates that the resliced data in the short-axis view was used as input to the network. RAW indicates that the raw 4D flow data was used as input.

Method	Input orientation	Ground truth	Network	Input Size	Output Size
SAX2D	SAX	GT-SAX	2D U-Net	(256,256,4)	(256,256,1)
RAW2D	RAW	GT-RAW	2D U-Net	(256,256,4)	(256,256,1)
SAX3D	SAX	GT-SAX	3D U-Net	(256,256,40,4)	(256,256,40,1)
RAW3D	RAW	GT-RAW	3D U-Net	(256,256,32,4)	(256,256, 32,1)
SAX2DF	SAX	GT-SAX	2D Fusion Network	(256,256,1), (256,256,3)	(256,256,1)

SAX2D and RAW2D models are adapted from 2D U-Net, an encoder-decoder CNN model with long-skip connections. The architecture includes five-scaled resolutions. Each level contains two convolutional blocks composed of a convolution layer with kernel size of 3 × 3 followed by an instance normalization (IN) layer, a rectified linear unit (ReLU) and one dropout layer. In the encoder feature maps are down-sampled by a max-pooling layer with kernel size of 2 × 2, while in the decoder transposed convolution layers are used to increase the resolution to its original scale. The long-skip connections are used to concatenate the features from fine to coarse scales at each level. Finally, a convolution layer with kernel size of 1 × 1, followed by a Sigmoid function, is used to generate the probability map. The final segmentation results are determined by choosing the class with the highest probability at each pixel.

RAW3D and SAX3D models employ a 3D U-Net architecture, which is used to investigate the performance of varying volumetric inputs. The 3D volume generated from each phase is considered as an independent input of 3D U-Net. Compared to 2D U-Net, the kernel size of all convolution layers in 3D U-Net is set to 3 × 3 × 3. The 3D U-Net introduced four max-pooling layers for the down-sampling operations. The kernel size of all pooling layers in RAW3D are set to 2 × 2 × 2. Whereas in SAX3D the first three pooling layers are set to 2 × 2 × 2 and last pooling layer is set to 2 × 2 × 1 because the spatial dimension will be reduced to 5 after three down-sampling operations.

Magnitude and velocity images can be considered as different modalities providing different information for the segmentation. To fuse the information from these two modalities, we introduce two approaches named early fusion and late fusion, respectively. SAX2D, SAX3D, RAW2D and RAW3D use the early fusion method where the magnitude and velocity images are concatenated along the channel dimension as the input. Whereas SAX2DF uses the late fusion method. As illustrated in Fig. 2, separate encoders are used to extract the features from these two modalities. Thereafter, features in the same level from two encoders are added together. The aggregated features in the bottleneck are up-sampled to the original resolution. The other multi-scale aggregated feature maps are then concatenated with the features up-sampled from the lower level. The structure of decoder used in SAX2DF is the same as that in 2D U-Net.

Fig. 2.

The network architecture of SAX2DF. SAX2DF separates magnitude and the three velocity images as two inputs and uses two encoders to extract the features from each input. The late fusion method is used to integrate those features.

Dice loss and cross-entropy were jointly used as the loss function to train the models. All the experiments were implemented using Pytorch [19] with the following parameters: batch size= 50; learning rate= 0.0001; optimizer=Adam. Five-fold cross-validation was applied to assess the performance and the averaged values are reported. All the experiments were implemented on a machine equipped with an NVIDIA Quadro RTX 6000 GPU with 24 GB internal memory.

2.4. Evaluation metrics

The performance of the automated methods was evaluated using segmentation accuracy, uncertainty score and volumetric and flow related clinical metrics.

2.5. Segmentation accuracy

Dice and average surface distance (ASD) were used to assess the segmentation accuracy. Dice measures the overlap between the prediction and the ground truth. ASD is the average of all the distances from all surface points on the boundary of the predicted region to the boundary of the ground truth, which can be described as formula (1):

$$ASD=\frac{1}{n_S+n_{S\prime }}(\sum _{p=1}^{n_S}d(p,S\prime )+\sum _{p\prime =1}^{n_{S\prime }}d(p\prime ,S))$$ (1)

where $d(p,S\prime )=\underset{p\prime \in S\prime }{\min }||p-p\prime |{|}_2$ is the minimum of the Euclidean distance between a point $p$ on surface S and the surface S′. Dice and ASD reported in this work are computed based on each 3D volume and averaged over all phases.

2.6. Clinical metrics

End-diastolic volume (EDV), end-systolic volume (ESV), LV ejection fraction (LVEF) and kinetic energy (KE) were derived as clinical metrics. The KE was computed as formula (3) with ${\rho }_{blood}$ being the density of the blood (1.06 g/cm³), $V_{voxel}$ the voxel volume and $v$ the velocity magnitude of one voxel. The total KE is the summation of the KE of each voxel within the LV region. The total KE values were indexed for LV EDV and averaged over the complete cardiac cycle.

$$KE=\frac{1}{2}{\rho }_{blood}\cdot V_{voxel}\cdot v^2$$ (3)

Additionally, three phasic KE parameters were derived: peak systolic, peak E-wave and peak A-wave KE. The result of LV segmentation was also used for LV flow component analysis. Based on previously described methods by Eriksson et al. [4] the segmented LV blood pool at the ED moment was used to define seeding particles of size 3 × 3 × 3 mm³ and particle pathlines were derived using particle tracing in forward (until the next ES moment) and backward (until the previous ES moment) direction. The particle position at the two ES moments was then used to classify the defined pathlines as either direct flow (DIR), delayed ejection flow (DEL), retained inflow (RET) or residual volume (RES). The relative size of each flow component was expressed as a percentage of the ED volume. The clinical parameters derived from automated LV segmentation were compared to the results derived of manual segmentation.

2.7. Uncertainty score

Segmentation of anatomical structures is inherently ambiguous especially near an object border which is not clearly defined due to the poor contrast or restriction imposed by the image acquisition. The uncertainty score can give some insights into the confidence of a model in its predicted segmentation results [15]. In case of a high uncertainty score, it is more likely that the segmentation result is inaccurate. Usually, a CNN model only produces a single segmentation map without any information to explain its confidence in its prediction. A high probability value in a segmentation map doesn’t imply a high confidence score. A model also can be uncertain in pixels with high probability. In order to investigate the segmentation uncertainty of the different models we applied the Monte Carlo (MC) dropout method [16] to quantify the model’s confidence in the segmentation result.

Generally during the testing phase, the dropout layers in the network are removed. The uncertainty score can be derived by preserving the dropout layers during testing while executing multiple inference runs. In our experiments the drop rate in the middle-level dropout layers was set to 0.5 and the testing was repeated 20 times resulting in 20 predictions denoted as $P_i(i=1,2,\cdots 20)$. The uncertainty score can be derived using Eq. (2) where$P=\frac{1}{20}\sum _{i=1}^{20}{P}_i$.

$$UQ=-P\times {\log }_{2}P-(1-P)\times {\log }_2(1-P)$$ (2)

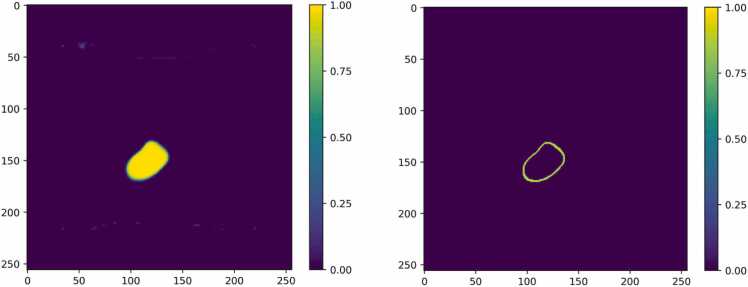
Fig. 3 shows an example of a segmentation probability map and its corresponding uncertainty map. The uncertainty score for the pixels within the LV chamber is low, implying a high confidence of the models’ prediction, but due to the poor contrast between the heart chamber and myocardium the uncertainty near the ambiguous LV border with a corresponding probability varying from 0.4 to 0.6 is substantially higher. To compute the mean of uncertainty and to quantify the segmentation quality, we first computed the uncertainty score for the whole LV chamber where each pixel’s prediction probability is larger than 0.5. Then to highlight the higher uncertainty in the boundary region, we further computed the score for this area with a prediction probability ranging from 0.4 to 0.6.

Fig. 3.

An example of segmentation probability and its corresponding uncertainty map. Left: Probability map derived from the last layer of RAW2D. Right: Corresponding uncertainty map derived from MC method.

2.8. Statistical analysis

The correlation of the clinical metrics derived from the manual and predicted segmentation results were assessed using the Pearson correlation coefficient (PCC). Additionally, bias and limits of agreement (LOA, 1.96 ×standard deviation) were used to describe the agreement of prediction and ground truth.

2.9. Intra-observer variability

For quantitative evaluation of human performance, we assessed the intra-observer variability. A set of 20 subjects (10 patients and 10 volunteers) were randomly selected. The same observer conducted manual analysis on each subject twice (M1, M2). The difference of clinical measurements was computed between M1 and M2.

For the experiments, first, we compared the results derived by the five models on various evaluation metrics. Second, we explored the impact of the fusion methods on the uncertainty score. Lastly, we investigated the performance of the best model on the KE and flow components.

3. Results

3.1. Segmentation results

Table 3 summarizes the segmentation performance derived from different models. SAX2DF achieved the best results with Dice of 84.52%, ASD of 3.14 mm and absolute error of ESV and LVEF of 17.38 ml, 7.37%, respectively. The best results in an absolute error of EDV and KE were obtained using the model of SAX2D, yielding an error of 19.93 ml and 0.07 mJ, respectively.

Table 3.

Segmentation performance derived from different methods. The reported clinical results are represented using the absolute error and relative error between the ground truth and prediction. The best results are shown in bold. SAX2D-M and SAX3D-M represent models that only use the magnitude images as the input. The other methods use both magnitude and velocity images as the input.

Method	Dice (%)	ASD (mm)	EDV (ml)	ESV (ml)	LVEF (%)	KE (mJ)
SAX2D	84.44 ± 6.31	3.31 ± 1.90	19.93(10.39%)	19.43(25.45%)	9.44(18.41%)	0.07(5.61%)
RAW2D	80.02 ± 7.39	4.01 ± 1.87	29.57(17.97%)	32.61(44.54%)	10.92(21.60%)	0.19(13.93%)
SAX3D	82.81 ± 6.69	4.43 ± 4.72	22.80(12.80%)	24.66(32.21%)	10.06(19.07%)	0.14(11.61%)
RAW3D	79.79 ± 7.57	3.68 ± 1.65	24.66(14.32%)	26.82(35.01%)	10.41(21.91%)	0.16(11.61%)
SAX2DF	84.52 ± 6.61	3.14 ± 2.35	20.29(10.55%)	17.38(22.22%)	7.37(13.93%)	0.09(7.04%)
SAX2D-M	81.39 ± 7.42	4.13 ± 2.93	26.26(13.45%)	32.51(45.40%)	21.04(39.37%)	0.15(11.83%)
SAX3D-M	80.71 ± 0.09	5.29 ± 4.80	24.96(13.97%)	38.41(57.66%)	18.88(34.86%)	0.17(13.31%)

Due to the different ground truth masks used, a direct comparison of the performance using Dice and ASD derived from RAW and SAX data is not easily possible. Therefore, also clinical parameters were used to compare the performance of the models. Table 3 shows that SAX2D outperformed RAW2D and SAX3D performed better than RAW3D in all clinical metrics including EDV, ESV, LVEF and KE, demonstrating the models using images in short-axis view orientation can generate a better prediction.

We further compared the results derived from only using magnitude images (SAX2D-M and SAX3D-M) and combining magnitude and velocity images. The comparison was restricted to the models using the short-axis view data, since these models provided the best performance. Table 3 reveals that the Dice derived from models using the combination of magnitude and velocity data is 3% higher compared to the models using the magnitude images only. More specifically, for the 2D model, SAX2D outperforms SAX2D-M in terms of Dice in 81 out of the 101 individual cases (80.20%). Similarly, SAX2DF outperforms SAX2D-M in terms of Dice in 86 out of the 101 cases (85.15%). For the 3D model, SAX3D outperforms SAX3D-M in terms of Dice in 65 out of 101 cases (64.36%). Therefore, adding velocity images as input to the model is clearly shown to be beneficial. The variation in Dice and ASD over the cardiac phases for each model is illustrated in Fig. 4. All models achieved the best Dice and ASD in phases 1, 2 and 30 which is around the ED phase. The lowest performance is observed in the phases varying between phase 11–13, which is around the ES phase. These results demonstrate that LV segmentation from 4D flow data is more accurate in the ED phase than in the ES phase.

Fig. 4.

Average Dice and ASD results plotted over time (averaged over all subjects). The x-axis is the phase number, y-axis is the averaged Dice (left) and ASD (right) derived from different models.

Table 4 reports the performance of five models on both patients (contrast-enhanced data) and volunteers (non-contrast-enhanced data). The segmentation methods of SAX2D, RAW2D, RAW3D, and SAX2DF showed improved results in terms of the Dice similarity coefficient when applied to contrast-enhanced data. In terms of ASD, these same models demonstrated better performance on the volunteers compared to the patients. However, in terms of EDV and ESV, the volunteers outperformed the patients across all five models. Similarly, the patients achieved better results in terms of LVEF and KE, regardless of the segmentation methods used.

Table 4.

Segmentation performance derived from different models on two groups. The clinical results are represented using the absolute error and relative error.

Method	Group	Dice (%)	ASD (mm)	EDV (ml)	ESV (ml)	EF (%)	KE (mJ)
SAX2D	Patients	84.71 ± 5.91	3.39 ± 1.95	20.20(10.35%)	21.64(26.89%)	8.76(18.29%)	0.06(5.51%)
	Volunteers	83.75 ± 7.29	3.07 ± 1.73	19.14(10.54%)	13.06(21.31)	11.41(18.75)	0.09(6.02%)
RAW2D	Patients	80.20 ± 6.98	4.01 ± 1.65	32.76(19.56%)	33.28(45.12%)	10.40(22.13%)	0.15(12.44%)
	Volunteers	79.53 ± 8.43	4.01 ± 2.41	20.04(13.12%)	28.65(45.11%)	11.26(18.24%)	0.31(18.39%)
SAX3D	Patients	82.74 ± 6.72	4.57 ± 5.04	23.12(12.67%)	24.32(31.53%)	9.04(18.39%)	0.12(10.20%)
	Volunteers	83.01 ± 6.58	4.03 ± 3.63	21.87(13.17%)	20.10(34.19%)	12.99(21.01%)	0.22(15.93%)
RAW3D	Patients	80.01 ± 7.10	3.68 ± 1.68	26.57(14.88%)	28.55(34.10%)	10.52(23.87%)	0.14(11.24%)
	Volunteers	78.89 ± 8.74	3.68 ± 1.57	18.03(13.66%)	22.52(37.68%)	10.73(16.23%)	0.20(12.86%)
SAX2DF	Patients	85.20 ± 5.81	2.86 ± 1.66	20.53(10.32%)	18.55(21.99%)	6.34(12.91%)	0.09(6.89%)
	Volunteers	82.58 ± 8.22	3.93 ± 3.56	19.57(11.20%)	13.62(22.92%)	10.29(16.92%)	0.12(7.37%)

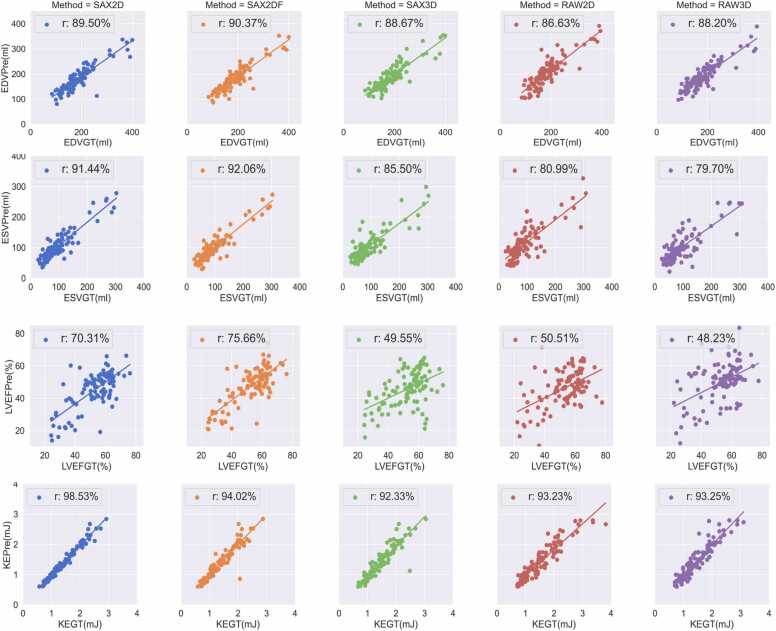
The PCC, bias and LOA of clinical evaluation metrics comparing manual with automatic segmentation results are reported in Table 5. Fig. 5 and Fig. 6 show the scatter plots, including PCC and Bland-Altman plots of four clinical metrics. SAX2DF achieved the highest correlation of 90.37%, 92.06% and 75.66% for EDV, ESV and LVEF, respectively. The best PCC for KE was achieved using SAX2D method. Although the PCC in LVEF derived from all five methods are lower than 80%, the results in the other three metrics demonstrate a good linear correlation with the results derived from manual segmentation. Notably, all five models achieved a PCC for KE higher than 90%. Although there is a significant variation in the performance of EDV and ESV estimation derived from the different methods, the biases for those two metrics derived from SAX2D, RAW3D and SAX2DF are smaller than 10 ml. The smallest biases in EDV and ESV are 1.99 ml and 3.24 ml derived from SAX3D and SAX2DF, respectively. RAW2D achieved the worst performance, with a bias of 19.62 ml and 20.51 ml in EDV and ESV, respectively. RAW3D and SAX2DF achieved the smallest bias in LVEF and KE with 3.08% and 0.005 mJ, respectively.

Table 5.

PCC and Bias of clinical metrics from the prediction against the reference. The best results are shown in bold.

Method	PCC				Bias± LOA
	EDV (%)	ESV (%)	LVEF (%)	KE (%)	EDV (ml)	ESV (ml)	LVEF (%)	KE (mJ)
SAX2D	89.50	91.44	70.31	98.53	6.95 ± 57.08	-8.17 ± 47.04	7.59 ± 17.93	0.04 ± 0.18
RAW2D	86.63	80.99	50.51	93.23	-19.62 ± 62.69	-20.51 ± 68.06	6.50 ± 23.36	0.11 ± 0.46
SAX3D	88.67	85.50	49.55	92.33	-1.99 ± 58.49	-11.17 ± 59.34	6.81 ± 22.81	0.06 ± 0.41
RAW3D	88.20	79.70	48.23	93.25	-7.45 ± 60.08	-7.25 ± 69.62	3.08 ± 25.11	0.01 ± 0.42
SAX2DF	90.37	92.06	75.66	94.02	7.74 ± 54.59	-3.24 ± 46.16	5.03 ± 16.02	0.005 ± 0.36

Fig. 5.

Correlation of clinical metrics derived from manual and automated segmentation. Each column represents one CNN model. The four rows denote four clinical metrics including EDV, ESV, LVEF and KE. For each plot, the x-axis represents the manual segmentation and y-axis represents the results derived from automated prediction.

Fig. 6.

Bland-Altman plots of clinical metrics comparing automated and manual segmentation. The columns represent five models and the rows show the results of EDV, ESV, LVEF and KE, respectively. In each Bland-Altman plot, the x-axis denotes the average of two measurements and the y-axis represents the difference between two measurements. The black line represents the bias and the two red lines denote the LOA.

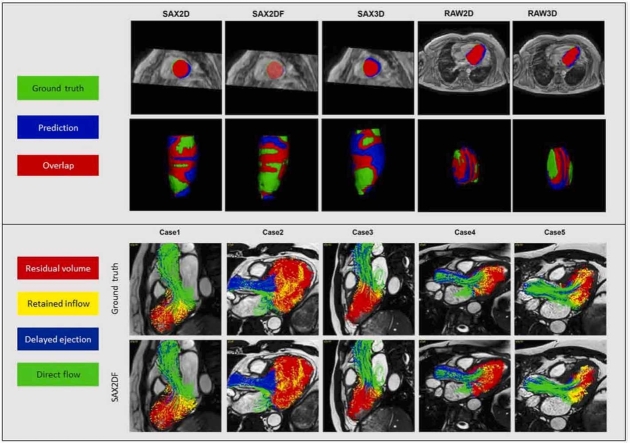
Examples of 2D and 3D segmentation masks derived from the five models are shown in Fig. 7.

Fig. 7.

Examples of automated LV segmentation results in 2D and 3D. The two rows illustrate the results of 2D and 3D segmentation results. Green color represents the ground truth, blue color is the prediction, and red parts represents the overlap between the prediction and ground truth.

3.2. Uncertainty results

Table 6 reports the averaged uncertainty scores both in the LV blood pool and the defined boundary area over 3030 phases (30 phases per subject, 101 subjects in total) derived from the five proposed models. SAX2DF achieved the lowest uncertainty scores with 0.12 and 0.75 in the whole LV and boundary area. SAX3D has lower uncertainty than SAX2D (0.13 vs. 0.15, 0.76 vs. 0.83). Similarly, RAW3D has a lower uncertainty than RAW2D (0.13 vs. 0.20, 0.77 vs. 0.82). The 3D models are shown to be more confident in its predictions than the 2D models. When comparing SAX2D and SAX2DF, it can be concluded that the late fusion method resulted in a lower uncertainty score.

Table 6.

The averaged uncertainty value derived from different defined areas. The LV chamber refers to the area with a probability larger than 0.5. Boundary area refers to the area with probability ranging from 0.4 to 0.6.

Area	SAX2D	SAX3D	RAW2D	RAW3D	SAX2DF
LV chamber	0.15 ± 0.03	0.13 ± 0.04	0.20 ± 0.09	0.13 ± 0.04	0.12 ± 0.44
Boundary area	0.83 ± 0.03	0.76 ± 0.05	0.82 ± 0.07	0.77 ± 0.03	0.75 ± 0.02

3.3. Flow quantitative analysis

SAX2DF is the best segmentation model among the proposed five models, according to the performance on segmentation accuracy, clinical metrics and uncertainty score. Therefore, we further investigated the performance of SAX2DF in quantifying KE and flow components. The low averaged error of indexed KE ranging from − 0.01 mJ to 0.05 mJ and flow components varying from − 4.58% to 2.98%, as reported in Table 7, shows a good agreement between the prediction and ground truth. A detailed summary of the PCC of KE and flow components derived from the automatic and manual methods is illustrated in Fig. 8.

Table 7.

The averaged difference and PCC between the automatic and manual methods in flow components quantification and KE. RES: Residual volume; RET: retained inflow; DEL: delayed ejection flow; DIR: direct flow.

	flow components (%)				KE (mJ)
	RES	RET	DEL	DIR	Max RR	Max Systole	Max E-wave	Max A-wave
Mean± SD	2.98 ± 5.97	0.80 ± 2.61	0.80 ± 2.69	-4.58 ± 4.35	-0.01 ± 0.38	0.05 ± 0.51	0.03 ± 0.46	0.02 ± 0.30
PCC (%)	86.91	91.10	89.24	94.29	97.45	88.65	96.85	95.43

Fig. 8.

Correlation of left ventricle kinetic energy and four flow components derived from the SAX2DF and manual method. First row: flow components including residual volume, retained inflow, delayed ejection and direct flow. Second row: kinetic energy including maximum KE over full RR-interval, systolic period, E-wave and A-wave period.

Fig. 9 visualizes the result of LV flow component analysis derived from manual and CNN based segmentation in five subjects. The results demonstrate a good agreement between those two segmentation methods. More flow components visualization videos and segmentation result videos can be found in https://github.com/xsunn/4DflowLVSegmentation.

Fig. 9.

Visualization of the left ventricular flow components generated from particle tracing derived from the manual segmentation and the method of SAX2DF. Green: direct flow. Yellow: retained inflow. Blue: delayed ejection flow. Red: residual volume.

3.4. Intra-observer variability

The difference between the intra-observer, as well between the automated and manual results are reported in Table 8. It shows that the variation in volume metrics was lower in intra-observer comparisons (M1vs. M2) than between the CNN and manually derived measurements. But for the flow components and KE, the variation between the CNN and manual annotation is less than that within the intra-observer.

Table 8.

The average absolute difference in clinical metrics derived from repeated manual segmentations, as well as between automated and manual segmentation. M1 and M2: first and second manual analysis. P1: analysis derived from SAX2DF using M1 as ground truth. EDV: LV end-diastolic volume, ESV: LV end-systolic volume. EF: LV ejection fraction. RES: Residual volume; RET: retained inflow; DEL: delayed ejection flow; DIR: direct flow.

		M1vs. M2	M1vs. P1
Volume (ml)	EDV	4.81 ± 4.54	18.87 ± 22.24
	ESV	4.24 ± 3.43	12.70 ± 9.29
	EF (%)	2.02 ± 1.24	5.98 ± 4.79
Flow components (%)	RES	4.44 ± 3.72	8.51 ± 5.34
	RET	4.66 ± 4.01	3.92 ± 2.59
	DEL	8.25 ± 5.46	3.61 ± 2.32
	DIR	5.49 ± 4.74	3.37 ± 2.83
KE (mJ)	Max RR	0.34 ± 0.31	0.23 ± 0.19
	Max Systole	0.64 ± 0.63	0.38 ± 0.35
	Max E-wave	0.20 ± 0.27	0.19 ± 0.19
	Max A-wave	0.18 ± 0.22	0.13 ± 0.16

4. Discussion

In this work, we developed and evaluated CNN-based methods for automatic segmentation and LV flow assessment from 4D flow cardiac MRI. The main findings of our study were (1) CNN models showed good performance in LV segmentation with an average Dice of 84.52% across 101 subjects; (2) Data preprocessing has an impact on the segmentation results; (3) Combining the features from magnitude and velocity images together can benefit the segmentation performance in 4D flow MRI; (4) High correlation and low bias of EDV, ESV, KE and flow components analysis demonstrate CNN-based segmentation can provide reliable quantification of LV flow in 4D flow data.

Segmentation in 4D flow cardiac MRI is challenging due to the poor contrast between the heart chamber and its surrounding tissue. Few approaches have been proposed to overcome this challenge. Atlas-based methods [4] and registration-based methods [10] are two prevailing traditional approaches. The atlas-based method relies on image registration to generate accurate transformation between a labelled atlas and the images. Registration-based segmentation methods rely on the registration between labelled cine MRI data and 4D flow data. Both methods require additional data and high computational costs due to the registration. Bustamante et al. [11] employed a 3D U-Net architecture for LV segmentation, but in their proposed method, only the magnitude images were used as input and information from velocity images were ignored. Hussaini et al. [22] conducted a comparative analysis of time-averaged (TA) and time-resolved (TR) 4D flow segmentation methods to assess the accuracy of kinetic energy (KE) measurement. The TA method involved segmenting the time-averaged image obtained over a complete cardiac cycle, while the TR method considered segmentation at each time point throughout the entire cardiac cycle. Although qualitatively similar, notable quantitative differences were observed. The KE values obtained through TA segmentation consistently exceeded those from TR segmentation, particularly during systole and in the left ventricle (LV). Their studies demonstrate that TA segmentation is well-suitable for clinical applications that do not rely on precise KE measurements and precise KE values still require the use of accurate time-resolved segmentation. In this work, we compared five fully automatic segmentation models named SAX2D, SAX3D, RAW2D, RAW3D and SAX2DF to segment the LV from 4D flow MRI without any additional cine MRI and we also investigated the impact of different data pre-processing approaches, feature fusion methods and model structure on the segmentation results.

Interestingly, our model SAX3D-M and Bustamante’s model share the same architecture, utilizing the 3D U-Net and taking the magnitude images as input. But the performance derived from SAX3D-M is not as good as that of Bustamante’s. The data cohort used in their work is much larger than ours; in our work, around 2400 out of 3030 3D volumes are employed for training in each running, which is significantly smaller than Bustamante’s 5760 3D volumes. Meanwhile, our results are averaged over 3030 3D volumes using five-fold cross-validation, whereas their results were directly derived from 1640 3D volumes. Furthermore, by simply using the magnitude images as input allowed them to introduce various data augmentation techniques to enlarge the training data. However, the conventional data augmentation methods such as rotation, Gaussian noise and transformation cannot directly work on our proposed approach because the velocity images are more complicated than the magnitude images. Therefore, compared to their work, we trained the model with fewer data but evaluated the performance on a larger data set. In Bustamante’s work all 4D flow acquisitions were obtained directly post-contrast administration in both patients and volunteers and navigator gating breathing motion was applied. In contrast, in our dataset, volunteer scans were obtained without contrast administration and in patients the timing of the 4D flow acquisition was not directly after contrast-administration. Additionally our 4D flow data was acquired without respiratory motion compensation. Therefore, it is expected that the image quality of the obtained magnitude images in Bustamante’s study was higher than in our study. Our model SAX2DF, which incorporates a late fusion method, outperformed SAX3D-M, which implies that if applied to the same dataset, our SAX2DF model has the potential to achieve superior results compared to Bustamante’s method.

For data preparation, given the known orientation, the original 4D flow MRI acquisition volume was resliced into short-axis slices. The raw data and resliced short-axis data served as two independent training data sets to train the networks. Improved segmentation results were derived when using the resliced short-axis data as the training data, demonstrating resliced short-axis data provided more accurate information for the segmentation, which could be explained by the more various shapes and ambiguous borders in the raw data when compared to the more consistent convex left ventricular shape in the short-axis view.

Considering magnitude and velocity images as two different modalities in 4D flow MRI, we proposed two approaches named early fusion and late fusion to fuse the information from these modalities. SAX2D, SAX3D, RAW2D and RAW3D employed early fusion by concatenating two modalities along the channel dimension as the input. While for the late fusion, SAX2DF employed two encoders to extract features from two modalities and then concatenated the features along the spatial dimension. A modestly improved performance was observed in SAX2DF when compared to the other methods, revealing that late fusion works better. We also compared the segmentation performance between 2D and 3D U-Net based methods. The results show that compared to SAX3D, SAX2D achieved better performance in all evaluation metrics. Constrained to the input spatial dimension, in SAX3D the kernel size of the final pooling layer was set to 2 × 2 × 1, resulting in the spatial features not being extracted completely. Moreover, a total of 3030 resliced 3D samples (101 subjects, 30 phases in each subject) were used to train and test the 3D U-Net, which is much less than 89,659 2D samples. As a result, the smaller training data size may be the primary reason why SAX3D did not outperform the SAX2D model.

CNN models produce a pixel-level prediction without any knowledge about the confidence of the model in its predictions. In this work, we introduced the Monte Carlo dropout method to estimate the uncertainty of the model in its segmentation results. The uncertainty score assesses segmentation reliability and offers the quantification of error to increase trust into CNN models. The results showed that the most uncertain area in the prediction is near the LV endocardial boundary, which can be explained by the poor contrast in the magnitude images and also because of the low blood flow velocity near the LV wall. Segmenting the myocardium in addition to the LV blood pool may reduce the uncertainty but cannot eliminate the uncertainty. When analyzing the uncertainty scores derived from different models, it reveals that the 3D models (SAX3D and RAW3D) performed better than the 2D models (SAX2D and RAW2D). Because 3D models are able to extract more spatial information from the input than the 2D models. It can be observed that although SAX2DF is a 2D model, benefiting from the late fusion method, SAX2DF achieved the lowest uncertainty score among all five models. A further evaluation of the results derived from the best model, SAX2DF, was performed by comparing the KE and flow components. The results show a good agreement between the ground truth and prediction.

The average Dice and ASD results over time show that the segmentation results may be more acceptable during the ED phase than in the other phases. This can be explained by several reasons. Firstly, during ED phase, the LV is in a relaxed state and filled with the maximum amount blood. This phase often provides a well-defined boundary between the myocardium and the blood pool, making it easier to segment the ventricular structures accurately. Secondly, the ED phase is relatively less effected by motion artifacts compared to the other phases, resulting in less distortion and improved segmentation performance. Thirdly, the LV appears brighter due to the inflow of fresh blood, while the myocardium appears darker. Therefore, the increased contrast in ED phase makes it easier to differentiate the boundary between the LV and myocardium. Additionally, the left ventricle's anatomy is relatively stable during ED phase. The ventricular walls are in a more uniform position, and variations in shape and position due to contraction or relaxation are minimized. This anatomical consistency can contribute to improved segmentation results during this phase.

There are several limitations in our work. The major limitation is the lack of generalization of the proposed models. The data used in this study was acquired from one vendor and one center. Meanwhile, there is no publicly available 4D flow MRI dataset currently. Therefore the model might not generalize well to other datasets from different vendors or centers. As Bai [17] pointed out, a CNN model can perform well in other datasets using fine-tuning or transfer learning. Additionally, exploiting advanced data augmentation methods utilizing domain knowledge is also crucial for model generalization and robustness [18]. However, the velocity images have complicated structure. which represents the directional information of each pixel as a vector and are aligned with the magnitude images. When the magnitude images undergo rotation, the direction of velocity needs to be adjusted accordingly. Additionally, the intensity of the magnitude image is associated with the velocity. Introducing Gaussian noise to the magnitude image is expected to influence the velocity values, although the exact nature of this impact remains unclear. Therefore, the commonly used data augmentation methods are not suitable for 4D flow data. Moreover, integrating the temporal information such as dynamic changes in the cardiac structures and their motion throughout the cardiac cycle can also provide valuable insights and improve the accuracy of the segmentation process [23], [24].

5. Conclusions

In conclusion, we developed multiple deep learning-based 4D flow MRI LV segmentation models that do not require additional cine MRI. The proposed CNN models were evaluated on a large in-house dataset, achieving good performance on several metrics. The results demonstrate that a model employing late fusion and trained on resliced short-axis view data generates the best performance for left ventricular segmentation in 4D flow MRI.

Ethics approval and consent to participate

The study was approved by the local medical ethical committee of the University of Leeds, UK and all participant provided written informed consent.

Funding

XS is supported by the China Scholarship Council No. 201808110201. LC is supported by the RISE-WELL project under H2020 Marie Skłodowska-Curie Actions.

CRediT authorship contribution statement

Garg Pankaj: Data curation, Writing – review & editing. van der Geest Rob J: Conceptualization, Data curation, Funding acquisition, Project administration, Software, Supervision, Writing – review & editing. Sun Xiaowu: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Writing – original draft, Writing – review & editing. Cheng Li-Hsin: Methodology, Writing – review & editing. Plein Sven: Data curation, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.