Robot-Induced Perturbations of Human Walking Reveal a Selective Process of Generation of Motor Adaptation

Iahn Cajigas; Alexander Koenig; Giacomo Severini; Maurice Smith; Paolo Bonato

doi:10.1126/scirobotics.aam7749

. Author manuscript; available in PMC: 2024 Jun 29.

Published in final edited form as: Sci Robot. 2017 May 24;2(6):eaam7749. doi: 10.1126/scirobotics.aam7749

Robot-Induced Perturbations of Human Walking Reveal a Selective Process of Generation of Motor Adaptation

Iahn Cajigas ^†,^*, Alexander Koenig ^†,^*, Giacomo Severini ^†,^¥,^*, Maurice Smith ^‡, Paolo Bonato ^†,^Ŧ

PMCID: PMC11213998 NIHMSID: NIHMS1035724 PMID: 33157871

Abstract

The processes underlying the generation of motor adaptation in response to mechanical perturbations during human walking have been subject to debate. In this study, we used a robotic system to apply mechanical perturbations to step length and step height over consecutive gait cycles. Specifically, we studied perturbations affecting only step length, only step height, and step length and height in combination. Both step-length and step-height perturbations disrupt normal walking patterns, but step-length perturbations have a far greater impact on locomotor stability. We discovered a selective process of motor adaptation in that participants failed to adapt to step-height perturbations but strongly adapted to step-length perturbations, even when these adaptations increased metabolic cost. These results indicate that motor adaptation during human walking is primarily driven by locomotor stability, and only secondarily by energy expenditure and walking pattern preservation. These findings have significant implications for the design of protocols for robot-assisted gait rehabilitation.

Introduction

Previous studies have investigated how human subjects adapt motor plans in response to sudden or gradual changes in the environment. These studies have often referred to Shadmehr and Mussa-Ivaldi’s seminal work on upper-limb motor adaptation (1). The authors used a robotic manipulandum to produce a velocity-dependent force and affect subjects’ upper-limb point-to-point movements. Subjects showed motor adaptation countering the predicted effect of the robot-produced force, hence suggesting the generation of error-driven adjustments derived from internal models. The central nervous system (CNS) utilizes such models to predict the outcome of a given motor plan in the task space in which the experiment takes place (2–4). Several investigators have proposed experimental paradigms to extend Shadmehr and Mussa-Ivaldi’s study to the lower limbs either by using robotic systems to produce external forces as a means to produce a mechanical perturbation (5–10) or by relying upon treadmill walking based protocols to create the conditions in which motor adaptation could be observed (11–15).

Emken et al (5), van Asseldonk et al (7), and our own research group (8) utilized robotic systems to generate forces affecting the foot trajectory of one leg during treadmill walking. Emken et al (5) interpreted motor adaptation in response to a velocity-dependent upward force during the swing phase of the gait cycle as the result of a trade-off between restoring the baseline foot trajectory and minimizing the metabolic cost of locomotion (6). Van Asseldonk et al (7) studied the response to sudden and gradual downward forces produced during the swing phase. The authors interpreted the responses to sudden forces as aimed to assure locomotor stability and the responses to gradual forces as a strategy to preserve baseline foot trajectory. Our own work (8) showed responses to mechanical perturbations orthogonal to the trajectory of movement in the joint coordinate space (i.e. knee vs. hip angle). We argued that the experimental observations reflected a bias toward maintaining the baseline trajectory of movement. Lam et al (9) and Selinger et al (10) used robotic systems to produce resistive forces during the swing phase. Lam et al (9) observed rapid changes in the electromyographic activity consistent with feedback mechanisms aimed to assure locomotor stability and slow changes consistent with feed-forward mechanisms to restore baseline kinematics. Selinger et al (10) used robotic knee braces to produce a resistive torque that varied with the step frequency. They observed that subjects adjusted their step frequency to achieve minimum metabolic cost of locomotion.

Prokop et al (11), Reisman et al (12), and Choi and Bastian (13) used a split-belt treadmill to study motor behaviors when the belts were moved at different speeds or in different directions. Prokop et al (11) argued that changes in inter-limb coordination observed when the belts were moved at different speeds were primarily caused by the need for assuring locomotor stability. Reisman et al (12) looked upon motor adaptation when subjects walked with the belts moving at different speeds as associated with optimal locomotor stability and metabolic cost of locomotion. Choi and Bastian (13) tested subjects during backward walking and hybrid walking (i.e. walking forward with one leg and backward with the other). They observed motor adaptation that was leg specific and direction specific. They suggested that inter-limb coordination is the result of a synchronized modulation of the activity of leg-specific locomotor networks. Savin et al (14) used a single-belt treadmill and studied motor adaptation by connecting/disconnecting a weight to one leg using a pulley. They observed bilateral adaptation and suggested that motor adaptation should be considered in the context of the goals and task constraints associated with the experiment rather than as indicative of the relevance of inter-limb over intra-limb control. Lastly, Finley et al (15) demonstrated that there is a linear relationship between the time-course of the motor adaptation and the metabolic cost of walking.

This body of work points at three potential principles used by the CNS to generate lower-limb motor adaptation: 1) maintaining the gait patterns observed in absence of perturbations; 2) minimizing the metabolic cost of locomotion; and 3) preserving locomotor stability. However, the significant differences in motor adaptation observed under different experimental constraints and our limited understanding of the interplay among the principles utilized by the CNS to generate motor adaptation make it difficult to predict how patients would respond to the interaction with a robotic system for gait rehabilitation. Herein, we present the results of a systematic study on the effects of mechanical perturbations produced using an exoskeleton system for treadmill-based gait rehabilitation (Lokomat by Hocoma AG, Zurich, Switzerland) (Figure 1A). This work was motivated by the observation that the modification of gait patterns is an important goal of physical therapy and that the study of motor adaptation has significant potential for assessing the ability of patients to modify their gait patterns (16). Our work was focused on characterizing motor adaptation in healthy subjects as a necessary step before motor adaptation could be investigated in patients. Study volunteers were instructed to walk at 3 km/h at a pace of approximately 86 steps per minute. The system produced mechanical perturbations that were applied to the subjects’ right lower limb during the swing phase of the gait cycles. Tests were performed using the robotic system to produce net perturbation forces (herein referred to as perturbation force vectors) at the foot with different orientations in the sagittal plane. We hypothesized that we would have observed motor adaptation for all the orientations of the perturbation force vector should the underlying goal of the CNS be to preserve only baseline gait kinematics. To our surprise, the results of the study revealed instead a selective process of generation of motor adaptation.

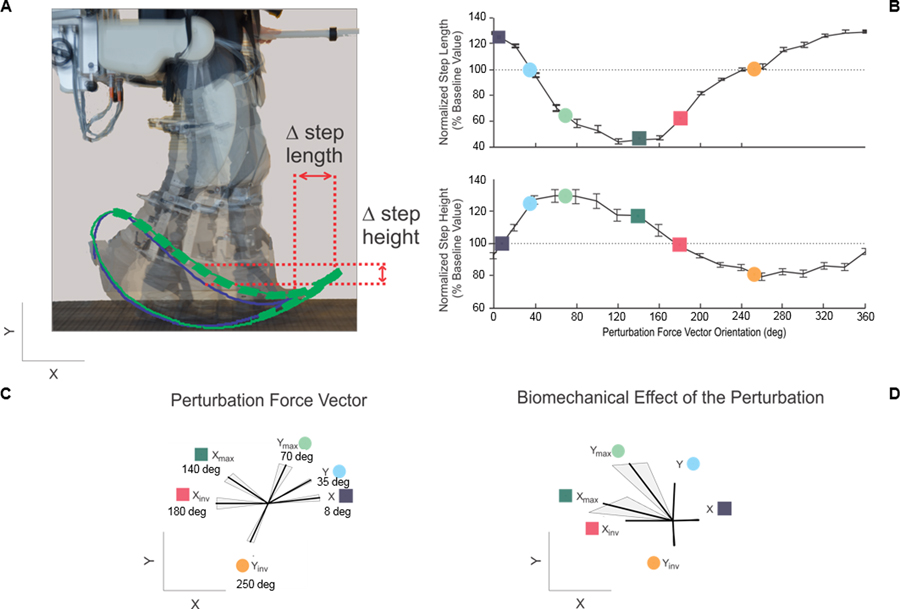
Figure 1. — Schematic representation of the effects of the mechanical perturbations generated by the robot used in the study (A). The robot was used to cause the foot trajectory to change (green line) compared to baseline (blue line). Forces were generated by the robot during a portion of the gait cycle approximately corresponding to the swing phase (bold dashed green line). Step-length and step-height values were estimated during the perturbation phase of the experiments and compared to baseline values. Panel (B) shows the results of the single-step perturbation experiments for step length and step height. The bottom plots show the orientation of the perturbation force vectors selected for the motor adaptation experiments (C) and their biomechanical effects on step length and step height (D). The shaded areas in (C) show the variability across subjects (i.e. standard error) in the orientation of the vectors that resulted in the desired effects (i.e. X, X_inv, Y, Y_inv, X_max, and Y_max). The shaded areas in (D) show the variability across subjects in the resultant biomechanical effect (i.e. effects on step length and step height).

Results

We performed two sets of experiments. The first set of experiments was focused on assessing the biomechanical effects of robot-induced perturbations applied over non-consecutive gait cycles. We refer to these perturbations as “single-step perturbations”. The second set of experiments was designed to study if healthy subjects adapt to mechanical perturbations applied over consecutive gait cycles. We refer to this second set of experiments as motor adaptation experiments.

Single-Step Perturbation Experiments

Single-step perturbations were induced by the robot for one randomly-selected gait cycle every ten cycles. They were generated using the hip and knee actuators of the robot’s right leg to result in a net force (herein referred to as perturbation force vector) at the distal end of the robotic leg that affected the foot trajectory. We tested the effect of nineteen different orientations of the perturbation force vector in the sagittal plane ranging from 0° to 360° by increments of 20° (with the vectors at 0° and 360° oriented horizontally in the forward direction). This set of experiments allowed us to evaluate the effects of the orientation of the perturbation force vector. Our analyses focused on changes in step length and step height.

Figure 1 shows the results of the single-step perturbation experiments performed in 15 study volunteers. Figure 1B shows the group average and standard error of the normalized step-length and step-height values observed for the gait cycles during which mechanical perturbations were applied by the robot. The step-length and step-height values were normalized by the average step-length and step-height values observed when no perturbations were present.

When plotted as a function of the orientation of the perturbation force vector, the normalized step-length and step-height values showed a non-symmetric, but roughly sinusoidal pattern. Interpolation of the experimental results allowed us to choose values of the orientation of the perturbation force vector corresponding to the following biomechanical effects: 1) an increase in step length without affecting step height (vector orientation = 8°); 2) a decrease in step length without affecting step height (vector orientation = 180°); 3) an increase in step height without affecting step length (vector orientation = 35°); 4) a decrease in step height without affecting step length (vector orientation = 250°); 5) a maximal step-length deviation from baseline with a combined effect on step length and step height (vector orientation = 140°); and 6) a maximal step-height deviation from baseline with a combined effect on step length and step height (vector orientation = 70°). We refer to these testing conditions as X, X_inv, Y, Y_inv, X_max, and Y_max, respectively. Figures 1C and D show a schematic representation of the perturbation force vectors corresponding to these testing conditions and their biomechanical effects.

Motor Adaptation Experiments

Data was gathered over 240 gait cycles divided in three blocks of 80 gait cycles. During the first block, the robot was programmed to minimize the interaction forces between the subject and the robot (baseline phase). During the second block, the robot generated a perturbation force vector aimed to affect the trajectory of the right foot (perturbation phase). During the last block (aftereffect phase), the robot was programmed as during the baseline phase. This experimental protocol was repeated six times during two separate sessions to study subjects’ motor adaptation in response to perturbation force vectors with the six above-mentioned vector orientations.

These experiments were performed in a group of 15 study volunteers. Figures 2–4 show the step-length and step-height data collected during the motor adaptation experiments. To test if step-length and step-height changes observed during the experiments were significant, we performed Friedman tests followed by post-hoc analyses using the Minimum Significant Difference test. The significance level α was set to 0.05. Besides, an exponential function was used to fit the group data for each of the three phases of the experiments (baseline, perturbation, and aftereffect) in each testing condition and derive the time constants associated with behaviors observed for each of these phases. Details about the statistical analyses performed on the results of all testing conditions can be found in the Supplementary Materials section.

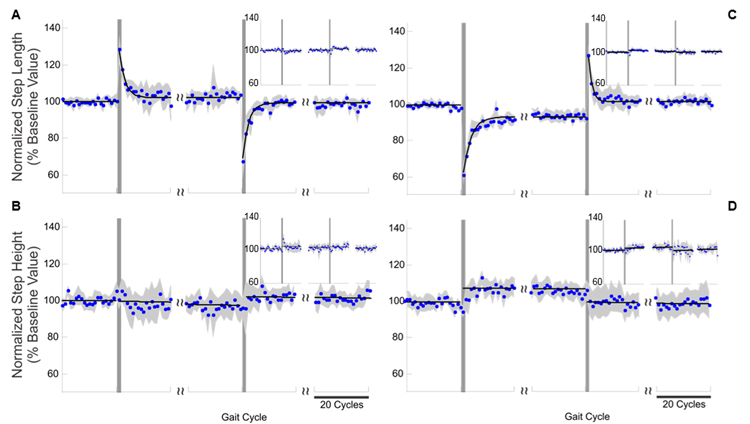
Figure 2. — Results of the experiments in the X (A and B) and X_inv (C and D) testing conditions. Step-length (A and C) and step-height (B and D) values observed during the experiments for the right lower limb (large plots) and the left lower limb (insets). The blue dots represent the average normalized step-length and step-height values (aggregate data across subjects), the gray shaded areas represent the standard error, and the black solid line represents the line or exponential function best fitting the points for each phase of the experiment. The vertical lines represent the onset and end of the perturbation phase. The perturbation force vector generated by the robot during these experiments affected only the step length of the right lower limb. Motor adaptations are apparent for step length.

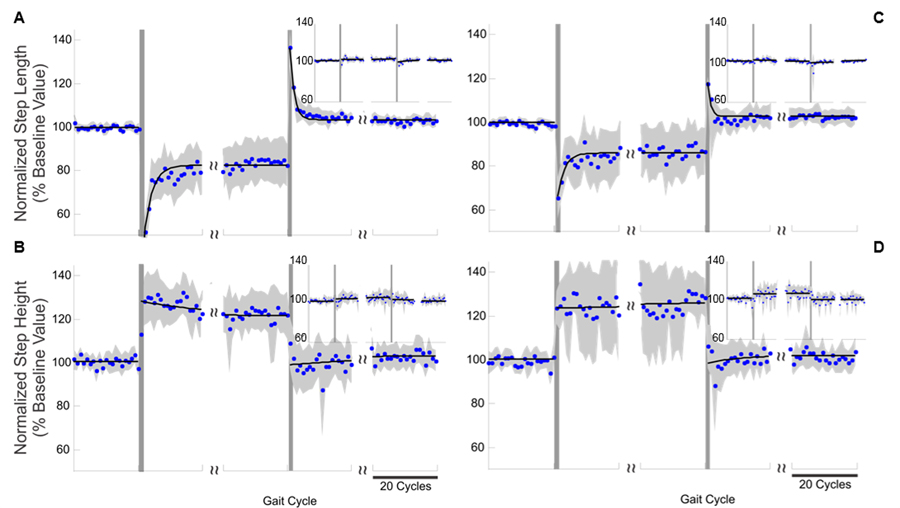
Figure 4. — Results of the experiments in the X_max (A and B) and Y_max (C and D) testing conditions. Step-length (A and C) and step-height (B and D) values observed during the experiments for the right lower limb (large plots) and the left lower limb (insets). The blue dots represent the average normalized step-length/height values (aggregate data across subjects), the gray shaded areas represent the standard error, and the black solid line represents the line or exponential function best fitting the points for each phase of the experiment. The vertical lines represent the onset and end of the perturbation phase. The perturbation force vector generated by the robot during these experiments affected both the step length and the step height of the right lower limb. However, only motor adaptations to compensate for step-length changes are apparent in these plots.

Adaptations to pure step-length perturbations

We found that when the robot produced a perturbation force vector that, by design, led to a significant increase or a decrease in step length without affecting step height (i.e. X and X_inv conditions), subjects displayed systematic step-length motor adaptation that compensated for these perturbations. After the change in step length that occurred at the onset of the perturbation phase of the experiments, we observed a gradual but systematic return to the baseline step length (Figure 2). Because the observed reductions in the kinematic effects of the perturbations could be caused by increased feedback corrections, limb stiffness, or predictive feed-forward motor adaptation, we examined the aftereffects that occurred when perturbations were withheld following training (i.e. the perturbation phase of the experiments). We found a remarkably close match between the aftereffect amplitude and the amount of perturbation compensation observed during training. This observation indicates that the compensatory reduction of the displacement observed during the perturbation phase of the X and X_inv perturbation experiments is due to a predictive feed-forward motor adaptation. Exponential fitting of the results of these experiments provided estimates of the time constants associated with the time-course of the motor behaviors that marked the perturbation and aftereffect phases of the experiments. We defined as steady state the step-length value reached at three times the value of the time constants for each of the above-mentioned phases of the experiments. The results showed that approximately 10 gait cycles were needed to adapt to the perturbation force vector for both the X and X_inv perturbations. Aftereffects persisted for approximately 7 gait cycles in both the X and X_inv perturbations.

Adaptations to pure step-height perturbations

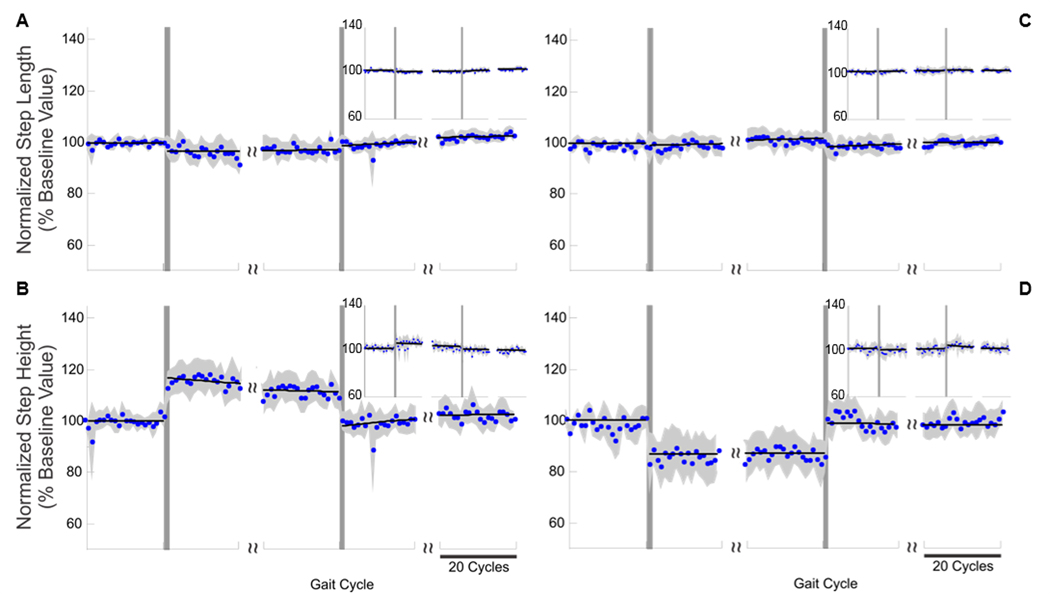
In stark contrast to step-length perturbations, we found that subjects displayed little to no adaptive compensation when robot-generated perturbations led, by design, to an increase or a decrease in step height without affecting step length (i.e. Y and Y_inv conditions). The results of these experiments are shown in Figure 3. Step-height displacements observed during the first gait cycle after perturbation onset persisted for the duration of the perturbation phase of the experiments. Correspondingly, we found no aftereffects when the Y and Y_inv perturbations were withdrawn. These results indicate that there is little to no adaptation for perturbations that specifically increase or decrease step height. Comparison of the motor adaptation induced by pure step-length (X and X_inv) vs. pure step-height (Y and Y_inv) reveals that the human motor system adaptively compensates for external perturbations that affect step length but does not for perturbations that affect step height.

Results of the experiments in the Y (A and B) and Y_inv (C and D) testing conditions. Step-length (A and C) and step-height (B and D) values observed during the experiments for the right lower limb (large plots) and the left lower limb (insets). The blue dots represent the average normalized step-length and step-height values (aggregate data across subjects), the gray shaded areas represent the standard error, and the black solid line represents the line or exponential function best fitting the points for each phase of the experiment. The vertical lines represent the onset and end of the perturbation phase. The perturbation force vector generated by the robot during these experiments affected only the step height of the right lower limb. No motor adaptations are apparent in these plots.

Adaptations to combined step-length, step-height perturbations

We investigated whether the contrast between no adaptation to step-height perturbations and strong adaptation to step-length perturbations would persist if these perturbations were simultaneously experienced. We thus applied gait perturbations that simultaneously affected step height and step length. We chose perturbation directions with maximal effect on step length and step height (X_max and Y_max). Figure 4 shows the results of these experiments. During the perturbation phase in the X_max condition, we observed a highly selective motor adaptation. At the end of the perturbation phase, we observed a significant adaptation in step length but little adaptation in step height. Besides, the step-length decrease observed during the first gait cycle of the perturbation phase was mirrored by a step-length increase during the first gait cycle of the aftereffect phase of the experiments, followed by a gradual, nearly-complete return to baseline step length. In contrast, step height during the first gait cycle of the aftereffect phase showed no significant deviation from the baseline step-height value. The results of the experiments carried out in the Y_max condition confirmed the observation from the experiments carried out in the X_max condition. Subjects showed motor adaptation to compensate for the effect of the perturbation on step length but not for the effect on step height. Subjects required approximately 15 gait cycles to adapt to the X_max perturbation and approximately 23 gait cycles to adapt to the Y_max perturbation. Aftereffects persisted for approximately 9 gait cycles in the X_max condition and for approximately 13 gait cycles in the Y_max condition.

A Selective Process of Generation of Motor Adaptation

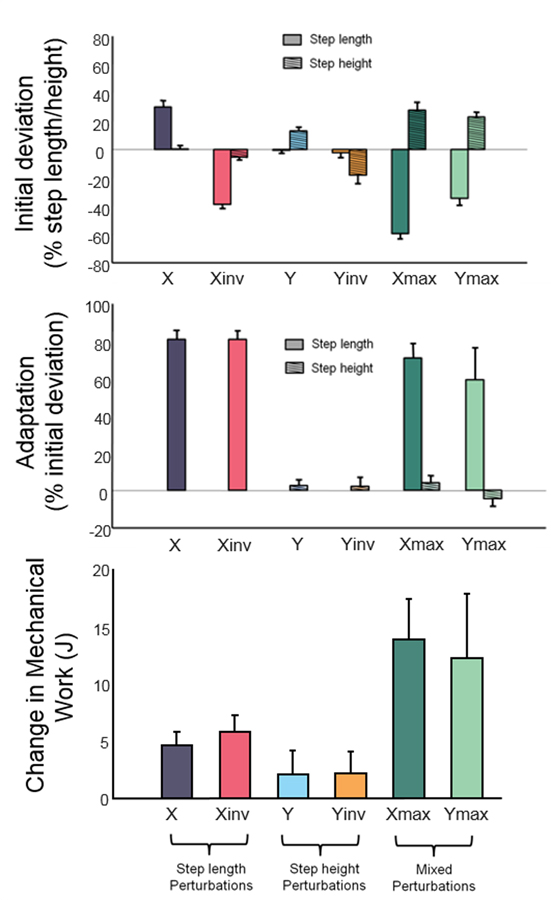
Figure 5 summarizes the results for all testing conditions. The top panel shows the initial deviations (i.e. observed during the first gait cycle of the perturbation phase) in step length and step height caused by the mechanical perturbations. The panel in the middle shows the percentage of the initial deviations in step length and step height that subjects compensated for. The bottom panel shows the change in mechanical work observed in response to the perturbation force vector produced by the robot. The results are grouped by perturbations with effect only on step length (i.e. “step-length perturbations”, X and X_inv), only on step height (i.e. “step-height perturbations”, Y and Y_inv), and with combined effects on step length and step height (i.e. “mixed perturbations”, X_max and Y_max).

Table 1 shows the results of the statistical analyses (Wilcoxon’s signed rank tests) that we performed to assess if the magnitude of the adaptation was different from zero. While significant step-length adaptations (p < 0.05) were observed for all the testing conditions associated with a robot-induced change in step length (i.e. X, X_inv, X_max and Y_max), no significant step-height adaptation was observed for the testing conditions associated with a robot-induced change in step height (i.e. Y, Y_inv, X_max and Y_max). Table 1 also shows the results of Wilcoxon’s signed rank tests that we performed to evaluate if the work that subjects performed in response to the perturbation force vector produced by the robot was different from zero. Significant changes (p < 0.05) were observed only for the perturbation conditions affecting step length. Subjects generated additional 5–15 J of work per gait cycle to counter the perturbations. Taken together, the results of these experiments demonstrate a striking selectivity whereby motor adaptation is observed for perturbations of step length but not step height, regardless of whether perturbations have an effect on step length and step height in isolation or in combination.

Table 1.

Statistical analysis of the changes in step length and step height as well as the changes in net mechanical work observed during the perturbation phase of the experiments.

	Adaptation
Testing Condition	Step Length	Step Heigth	Mechanical Work
X	< 0.01 (^**)	n.a.	< 0.01 (^**)
X_inv	< 0.01 (^**)	n.a.	< 0.01 (^**)
Y	n.a.	0.19	n.a.
Y_inv	n.a.	0.72	n.a.
X_max	< 0.01 (^**)	0.12	< 0.01 (^**)
Y_max	< 0.01 (^**)	0.63	< 0.01 (^**)

Open in a new tab

^**

indicates p values < 0.01. These values were estimated using the Wilcoxon’s signed rank test.

Discussion

Our results revealed a selective process of generation of motor adaptation in response to robot-induced perturbations of human walking. Namely, motor adaptation was observed in response to changes in step length but not to changes in step height. What is the origin of this selective process? Previous studies have suggested three principles possibly underlying the generation of motor adaptation: 1) maintaining the baseline gait patterns; 2) minimizing the metabolic cost of locomotion; and 3) preserving locomotor stability.

Preservation of Locomotor Stability

Our results are at odds with the hypothesis that adaptation is driven solely by the aim of maintaining the baseline walking patterns since adaptations were not observed for perturbations in step height. The results are also at odds with the hypothesis that adaptation is driven solely by the objective of minimizing the metabolic cost of locomotion. In fact, the mechanical work generated by subjects in the X, X_inv, X_max and Y_max conditions increased during the perturbation phase of the experiments as subjects countered the robot-induced perturbations. In contrast, the results are consistent with the hypothesis that motor adaptation aims to preserve locomotor stability. This explanation appears to account for the fact that subjects did not compensate for perturbations with effect on step height. Changes in step height of the magnitude tested in the study appear to be similar to those observed while negotiating an obstacle, a task that would not challenge the stability of human walking. Vice versa, step-length control is highly relevant to preserving locomotor stability. Stability boundaries during walking have been related to the position and velocity of the center of mass (CoM) relative to the base of support (BoS) (17). Several studies (18–22) have highlighted the importance of the placement of the foot on the ground at heel strike to maintain the projection of the CoM inside the BoS and thus preserve locomotor stability (23). Interestingly, this concept has been applied to the control of bipedal robots (24–29). Furthermore, experiments in which healthy individuals were exposed to perturbations designed to challenge their balance during walking, showed that subjects respond to perturbations by altering the trajectory of the CoM (30–31) and/or the area of the BoS (32–33). The former response is primarily achieved by modifying the position of the trunk, while the latter is mainly achieved by controlling the position of the foot on the ground at the time of heel strike. Furthermore, it has been shown that walking speed, cadence and step length are jointly controlled to maximize locomotor stability (34). In our experiments, in which speed and cadence were controlled, motor adaptation restoring baseline step length would preserve the preferred relationships among walking speed, cadence and step length.

Locomotor Stability over Multiple Steps

One could notice that subjects could not fall when strapped to the exoskeleton system utilized in our experiments. Also, the step-length changes caused by the robot in our experiments do not appear to be of a magnitude sufficient to cause an immediate loss of balance. Then, why would the CNS process the perturbations as challenging locomotor stability?

Previous studies with focus on the control of bipedal robots could provide the answer. Pratt and co-authors introduced the concept of N-step capture points and regions as a fundamental principle to enable long-term stability of bipedal robots and a stable N-step stopping strategy during robotic locomotion (26–28). In this framework, the stability of the bipedal robot is defined by the number of steps (N) required to stop without falling. N strictly depends on foot placement for each step that the robot takes. By applying this conceptual framework to human walking, one would conclude that a mechanical perturbation that alters step length may affect the long-term (i.e. over multiple steps) stability of the subject even if the mechanical perturbation does not challenge the subject’s immediate stability. Then subjects would develop a motor plan to assure locomotor stability on the basis of the prediction of the effects of that perturbation over several gait cycles.

Comparison with Previous Studies

At a first glance, our results appear to be in disagreement with previous studies by Emken et al (5) and van Asseldonk et al (7) in which motor adaptation was observed in response to robot-induced changes in step height. However, in these studies, the authors utilized exoskeleton systems that differ in one fundamental aspect from the one that we utilized. While the robotic system that we used constrained the movement of the pelvis, the ones utilized in previous studies did not. We argue that, in the experiments performed by Emken et al (5) and by van Asseldonk et al (7), the mechanical perturbations generated by the robots caused movements of the pelvis and upper body resulting in a significant acceleration of the CoM. We speculate that these mechanical perturbations were processed by the CNS as challenging the stability of locomotion, thus triggering the generation of motor adaptation. In this context, one would expect that perturbations causing a deviation from the baseline foot trajectory of large magnitude would produce a significant acceleration of the CoM and thus trigger a motor adaptation in response to the balance perturbation. In contrast, perturbations causing a deviation of small magnitude would not trigger a motor adaptation since they would not be processed as challenging locomotor stability. These considerations are consistent with the results of the above-referenced studies. Conversely, the robotic system used in our experiments constrained the movement of the pelvis, hence preventing a significant acceleration of the CoM. Consequently, we did not observe any motor adaptation.

Clinical Implications

The experimental paradigm utilized in this study could result in the development of a method to assess the ability of patients undergoing rehabilitation to process and respond to perturbations generated by an exoskeleton system for robot-assisted treadmill-based gait rehabilitation. Such method would be of great interest in a clinical context if the ability of patients to process and respond to perturbations could be used to predict the responsiveness of each patient to robot-assisted gait training interventions. In addition, it would be of great interest to evaluate if the paradigm herein proposed could be utilized to assess the stability boundaries of individuals with motor impairments. If so, one could envision designing individualized gait training interventions driven by criteria such as the long-term stability of locomotion. Finally, the results of this study suggest that motor adaptation can be leveraged only to change those aspects of patients’ gait patterns that are processed by the CNS as challenging locomotor stability. We hypothesize that other feedback modalities would be necessary to induce changes in gait patterns along other dimensions.

Materials and Methods

Study Design

Two cohorts of subjects were recruited in the study. The first cohort of subjects was recruited to investigate the response to single-step perturbations. For this study, we recruited 9 male and 6 female subjects, age 32.7 ± 8.0 years (mean ± standard deviation), weight 74 ± 14 kg, and height 174 ± 11 cm. The second cohort of subjects was recruited to investigate motor adaptation. For this study, we recruited 10 male and 5 female subjects, age 30.5 ± 6.5 years (mean ± standard deviation), weight 72 ± 10 kg, and height 174 ± 9 cm. Thirteen subjects participated in both sets of experiments.

The first set of experiments took place during a single session. Subjects underwent three trials. The first trial was performed to identify control settings that minimized the interaction forces between the subjects and the robotic legs using a method previously proposed by Vallery et al (35). The second trial was performed to collect data that was later used to track the point of the gait cycle that subjects were at using an algorithm previously developed by Aoyagi et al (36). During the third trial, we instructed subjects to walk for a period of time corresponding to the performance of 770 gait cycles. Subjects walked freely for the first 10 gait cycles. After that, we performed four blocks of 190 gait cycles each. During each block, we generated 19 single-step perturbations with 19 different orientation values of the perturbation force vector randomly selected among pre-defined values spanning the range from 0° to 360° by steps of 20°. Gait cycles randomly selected to produce a perturbation were marked by a minimum separation of five gait cycles and a maximum separation of eight gait cycles. For each orientation value of the perturbation force vector, we collected four data points, namely one for each of the four blocks of 190 gait cycles. The four data points were averaged to generate a single data point per subject. The average and standard error values estimated across subjects were used to derive the relationship between the orientation of the perturbation force vector and the changes in step length and step height compared to baseline.

The motor adaptation experiments took place over two sessions. During each session, subjects underwent five trials. The first two trials were identical to the first two trials performed during the session devoted to the study of single-step perturbations. The following three trials were devoted to investigate motor adaptation. Subjects were instructed to walk for a period of time corresponding to the performance of 420 gait cycles for each trial. After the first 20 gait cycles, during which the robotic system was programmed to minimize the interaction forces between the subjects and the robot, we generated nine single-step perturbations over randomly selected gait cycles out of 160 gait cycles. Gait cycles during which a mechanical perturbation was applied were separated by a minimum of eight gait cycles. The remaining 240 gait cycles of each trial were divided into three blocks of 80 gait cycles. Each of these three blocks consisted of the baseline, perturbation, and aftereffect phases of the motor adaptation experiments described above. All perturbations within a trial were marked by the same orientation of the perturbation force vector.

Data Analysis

Step length was defined as the maximum value of the foot position in the antero-posterior direction in a coordinate system positioned at the center of rotation of the robotic joint connecting the pelvis and thigh components of the exoskeleton system. Step height was defined as the distance between the foot and the belt of the treadmill during the mid-swing phase of the gait cycle. This definition of step height allowed us to measure it where the effect of the perturbation led to a maximum deviation from the baseline value.

Step-length and step-height data collected during the single-step perturbations were analyzed to determine the relationship between the orientation of the perturbation force vector and the magnitude of the changes in step length and step height observed in response to the perturbations. The experimental data points were interpolated using cubic splines to determine the orientation values of the perturbation force vector corresponding to the six conditions described in the Results section. These orientation values were used in the motor adaptation experiments.

Step-length and step-height values were estimated for different phases of the motor adaptation experiments. Specifically, we estimated the following step-length and step-height values: 1) average during the baseline phase; 2) value for the first gait cycle of the perturbation phase; 3) value for the last gait cycle of the perturbation phase; 4) value for the first gait cycle of the after-effect phase; and 5) value for the last gait cycle of the after-effect phase. Statistical comparisons among the above-listed step-length and step-height values were performed using Friedman tests followed by post-hoc analyses using the Minimum Significant Difference test (see the Supplementary Materials section of the manuscript). Besides, we estimated the magnitude of the adaptation, as the percentage of the initial deviation that was compensated for at the end of the perturbation phase. This analysis was performed for step length and step height when statistically significant differences were observed between the value observed at baseline and the value observed for the first step of the perturbation phase of the experiments. Wilcoxon’s signed rank tests were performed to assess if the magnitude of the adaptation was different from zero. Mechanical work was estimated from the angular displacements and the interaction torques recorded by the exoskeleton at the hip and the knee (see the Supplementary Materials section for details). Wilcoxon’s signed rank tests were performed to estimate differences in mechanical work between the baseline phase and the last 10 steps of the perturbation phase for conditions showing motor adaptation. The significance level α was set to 0.05 for all the tests described above.

Supplementary Material

main

Figure S01. Schematic representation of the motor adaptation experiments.

Figure S02. Comparison of the robot joint angles during the baseline phase of the experiments and normative joint angle data collected during over-ground walking.

Figure S03. Comparison of joint interaction torque and power values during the baseline phase of the experiments and normative data collected during over-ground walking.

Figure S04. Diagram of the controller of the exoskeleton.

Figure S05. Effect of the metronome on the variability in the ankle velocity.

Figure S06. Kinematics and kinetics of motion for the right lower limb during all testing conditions.

Figure S07. Kinematics and kinetics of motion for the left lower limb during all testing conditions.

Figure S08. Aggregate results for changes in step length and step height for the X testing condition.

Figure S09. Aggregate results for changes in step length and step height for the X_inv testing condition.

Figure S10. Aggregate results for changes in step length and step height for the Y testing condition.

Figure S11. Aggregate results for changes in step length and step height for the Y_inv testing condition.

Figure S12. Aggregate results for changes in step length and step height for the X_max testing condition.

Figure S13. Aggregate results for changes in step length and step height for the Y_max testing condition.

Table S01. Statistical analysis to test for step-length and step-height differences observed during the motor adaptation experiments for all testing conditions.

Table S02. Time constants of adaptation calculated from the aggregate data (mean ± standard error).

Table S03. Comparisons of the values of the time constants derived from individual data associated with motor adaptation for the X, X_inv, X_max and Y_max testing conditions.

Table S04. Analysis of the symmetry indices for step length, step height, and the net mechanical work generated by subjects during the baseline and perturbation phases of the motor adaptation experiments.

NIHMS1035724-supplement-main.pdf^{(1.4MB, pdf)}

Acknowledgments:

The authors would like to thank Alexander Duschau-Wicke, Robert Riener, Heike Vallery and the R&D team at Hocoma AG for providing access to software algorithms utilized to control the robotic system used in the study.

Funding:

This project was partially supported by the Wyss Institute for Biologically-Inspired Engineering at Harvard University. Iahn Cajigas was partially supported by the National Institute of Neurological Disorders and Stroke (award # 1F31NS058275-01A2).Alexander Koenig was partially supported by the Swiss National Science Foundation (award # PBEZ3_137336).

Footnotes

Competing interests: The authors have no financial interests related to the content of this manuscript.

Data and materials availability: Please contact PB to obtain a copy of the data collected during the study.

References

1.Shadmehr R, Mussa-Ivaldi FA, Adaptive representation of dynamics during learning of a motor task, J Neurosci 14, 3208–3224 (May, 1994). [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Wolpert DM, Miall RC, Forward models for physiological motor control, Neural Networks 9, 1265–1279 (Nov, 1996). [DOI] [PubMed] [Google Scholar]
3.Kawato M, Internal models for motor control and trajectory planning, Curr Opin Neurobiol 9, 718–727 (Dec, 1999). [DOI] [PubMed] [Google Scholar]
4.Thoroughman KA, Shadmehr R, Learning of action through adaptive combination of motor primitives, Nature 407, 742–747 (Oct 12, 2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Emken JL, Reinkensmeyer DJ, Robot-enhanced motor learning: accelerating internal model formation during locomotion by transient dynamic amplification, IEEE Trans Neural Syst Rehabil Eng 13, 33–39 (Mar, 2005). [DOI] [PubMed] [Google Scholar]
6.Emken JL, Benitez R, Sideris A, Bobrow JE, Reinkensmeyer DJ, Motor adaptation as a greedy optimization of error and effort, J Neurophysiol 97, 3997–4006 (Jun, 2007). [DOI] [PubMed] [Google Scholar]
7.van Asseldonk EH, Koopman B, van der Kooij H, Locomotor adaptation and retention to gradual and sudden dynamic perturbations, IEEE Int Conf Rehabil Robot, 1–5 (2011). [DOI] [PubMed] [Google Scholar]
8.Cajigas I, Goldsmith MT, Duschau-Wicke A, Riener R, Smith MA, Brown EN, Bonato P, Assessment of lower extremity motor adaptation via an extension of the force field adaptation paradigm, Conf Proc IEEE Eng Med Biol Soc 2010, 4522–4525 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Lam T, Anderschitz M, Dietz V, Contribution of feedback and feedforward strategies to locomotor adaptations, J Neurophysiol 95, 766–773 (Feb, 2006). [DOI] [PubMed] [Google Scholar]
10.Selinger JC, O’Connor SM, Wong JD, Donelan JM, Humans can continuously optimize energetic cost during walking, Curr Biol 25, 2452–2456 (Sep 21, 2015). [DOI] [PubMed] [Google Scholar]
11.Prokop T, Berger W, Zijlstra W, Dietz V, Adaptational and learning processes during human split-belt locomotion: interaction between central mechanisms and afferent input, Exp Brain Res 106, 449–456 (1995). [DOI] [PubMed] [Google Scholar]
12.Reisman DS, Block HJ, Bastian AJ, Interlimb coordination during locomotion: what can be adapted and stored?, J Neurophysiol 94, 2403–2415 (Oct, 2005). [DOI] [PubMed] [Google Scholar]
13.Choi JT, Bastian AJ, Adaptation reveals independent control networks for human walking, Nat Neurosci 10, 1055–1062 (Aug, 2007). [DOI] [PubMed] [Google Scholar]
14.Savin DN, Tseng SC, Morton SM, Bilateral adaptation during locomotion following a unilaterally applied resistance to swing in nondisabled adults, J Neurophysiol 104, 3600–3611 (Dec, 2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Finley JM, Bastian AJ, Gottschall JS, Learning to be economical: the energy cost of walking tracks motor adaptation, J Physiol 591, 1081–1095 (Feb 15, 2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Bastian AJ, Understanding sensorimotor adaptation and learning for rehabilitation, Curr Opin Neurol 21, 628–633 (Dec, 2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Pai YC, Patton J, Center of mass velocity-position predictions for balance control, J Biomech 30, 347–354 (Apr, 1997). [DOI] [PubMed] [Google Scholar]
18.Hof AL, The ‘extrapolated center of mass’ concept suggests a simple control of balance in walking, Hum Mov Sci 27, 112–125 (Feb, 2008). [DOI] [PubMed] [Google Scholar]
19.Patla AE, Strategies for dynamic stability during adaptive human locomotion, IEEE Eng Med Biol Mag 22, 48–52 (Mar-Apr, 2003). [DOI] [PubMed] [Google Scholar]
20.Winter DA, Human balance and posture control during standing and walking, Gait and Posture 3, 193–214 (1995). [Google Scholar]
21.Winter DA, Sagittal plane balance and posture in human walking, IEEE Eng Med Biol Mag 6, 8–11 (1987). [DOI] [PubMed] [Google Scholar]
22.Perry J, Burnfield J, Gait analysis: normal and pathological function. (Slack Incorporated, 2010). [Google Scholar]
23.Hof AL, Gazendam MG, Sinke WE, The condition for dynamic stability, J Biomech 38, 1–8 (Jan, 2005). [DOI] [PubMed] [Google Scholar]
24.Geyer H, Herr H, A muscle-reflex model that encodes principles of legged mechanics produces human walking dynamics and muscle activities, IEEE Trans Neural Syst Rehabil Eng 18, 263–273 (2010). [DOI] [PubMed] [Google Scholar]
25.Kajita S, Kanehiro F, Kaneko K, Yokoi K, Hirukawa H, The 3D Linear Inverted Pendulum Mode: A simple modeling for a biped walking pattern generation, Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems 1, 239–246 (2001). [Google Scholar]
26.Koolen T, De Boer T, Rebula J, Goswami A, Pratt J, Capturability-based analysis and control of legged locomotion, Part 1: Theory and application to three simple gait models, The International Journal of Robotics Research 31, 1094–1113 (2012). [Google Scholar]
27.Pratt J, Koolen T, De Boer T, Rebula J, Cotton S, Carff J, Johnson M, Neuhaus P, Capturability-based analysis and control of legged locomotion, Part 2: Application to M2V2, a lower-body humanoid, The International Journal of Robotics Research 31, 1117–1133 (2012). [Google Scholar]
28.Pratt JE, Tedrake R, Velocity-based stability margins for fast bipedal walking, Fast Motions in Biomechanics and Robotics 340, 299–324 (2006). [Google Scholar]
29.Townsend MA, Biped gait stabilization via foot placement, J Biomech 18, 21–38 (1985). [DOI] [PubMed] [Google Scholar]
30.Reynolds RF, Bronstein AM, The broken escalator phenomenon. Aftereffect of walking onto a moving platform, Exp Brain Res 151, 301–308 (Aug, 2003). [DOI] [PubMed] [Google Scholar]
31.You J, Chou Y, Lin C, Su F, Effect of slip on movement of body center of mass relative to base of support, Clin Biomech 16, 167–173 (Feb, 2001). [DOI] [PubMed] [Google Scholar]
32.Cham R, Redfern MS, Lower extremity corrective reactions to slip events, J Biomech 34, 1439–1445 (Nov, 2001). [DOI] [PubMed] [Google Scholar]
33.Cham R, Redfern MS, Changes in gait when anticipating slippery floors, Gait and Posture 15, 159–171 (Apr, 2002). [DOI] [PubMed] [Google Scholar]
34.Latt MD, Menz HB, Fung VS, Lord SR, Walking speed, cadence and step length are selected to optimize the stability of head and pelvis accelerations, Exp Brain Res 184, 201–209 (Jan, 2008). [DOI] [PubMed] [Google Scholar]
35.Vallery H, Duschau-Wicke A, Riener R, Generalized elasticities improve patient-cooperative control of rehabilitation robots, IEEE Int Conf Rehabil Robot, 535–541 (2009). [Google Scholar]
36.Aoyagi D, Ichinose WE, Harkema SJ, Reinkensmeyer DJ, Bobrow JE, A robot and control algorithm that can synchronously assist in naturalistic motion during body-weight-supported gait training following neurologic injury, IEEE Trans Neural Syst Rehabil Eng 15, 387–400 (Sep, 2007). [DOI] [PubMed] [Google Scholar]
37.Riener R, Lünenburger L, Maier IC, Colombo G, Dietz V, Locomotor training in subjects with sensori-motor deficits: an overview of the robotic gait orthosis lokomat, Journal of Healthcare Engineering 1, 197–216 (2010). [Google Scholar]
38.Duschau-Wicke A, von Zitzewitz J, Caprez A, Lunenburger L, Riener R, Path control: a method for patient-cooperative robot-aided gait rehabilitation, IEEE Transactions on Neural Systems and Rehabilitation Engineering 18, 38–48 (2010). [DOI] [PubMed] [Google Scholar]
39.Aoyagi D, Ichinose WE, Harkema SJ, Reinkensmeyer DJ, Bobrow JE, A robot and control algorithm that can synchronously assist in naturalistic motion during body-weight-supported gait training following neurologic injury, IEEE Transactions on Neural Systems and Rehabilitation Engineering 15, 387–400 (2007). [DOI] [PubMed] [Google Scholar]
40.Scheidt RA, Conditt MA, Secco EL, Mussa-Ivaldi FA, Interaction of visual and proprioceptive feedback during adaptation of human reaching movements, J Neurophysiol 93, 3200–3213 (Jun, 2005). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials