Hydrogen isotope fractionation is controlled by CO₂ in coccolithophore lipids

Significance

The ²H/¹H ratio of marine algal lipids has been proposed to serve as a chemical fossil of the ²H/¹H ratio of the ocean, tracking changes in the environmental water cycle and ocean salinity. Yet, our culture experiments and a numerical model of cellular H sources in lipid synthesis reveal how the CO₂ concentration and temperature strongly affect the hydrogen isotopic fractionation of acyl lipids by altering the photosynthetic fixation rate and nicotinamide adenine dinucleotide phosphate hydrogen (NADPH) residence time in the chloroplast. This suggests that hydrogen isotope fractionation in acyl lipids may provide insight into the modern and past cellular regulation of algal photosynthesis and the carbon concentrating mechanism.

Abstract

Hydrogen isotope ratios (δ²H) represent an important natural tracer of metabolic processes, but quantitative models of processes controlling H-fractionation in aquatic photosynthetic organisms are lacking. Here, we elucidate the underlying physiological controls of ²H/¹H fractionation in algal lipids by systematically manipulating temperature, light, and CO₂(aq) in continuous cultures of the haptophyte Gephyrocapsa oceanica. We analyze the hydrogen isotope fractionation in alkenones (α_alkenone), a class of acyl lipids specific to this species and other haptophyte algae. We find a strong decrease in the α_alkenone with increasing CO₂(aq) and confirm α_alkenone correlates with temperature and light. Based on the known biosynthesis pathways, we develop a cellular model of the δ²H of algal acyl lipids to evaluate processes contributing to these controls on fractionation. Simulations show that longer residence times of NADPH in the chloroplast favor a greater exchange of NADPH with ²H-richer intracellular water, increasing α_alkenone. Higher chloroplast CO₂(aq) and temperature shorten NADPH residence time by enhancing the carbon fixation and lipid synthesis rates. The inverse correlation of α_alkenone to CO₂(aq) in our cultures suggests that carbon concentrating mechanisms (CCM) do not achieve a constant saturation of CO₂ at the Rubisco site, but rather that chloroplast CO₂ varies with external CO₂(aq). The pervasive inverse correlation of α_alkenone with CO₂(aq) in the modern and preindustrial ocean also suggests that natural populations may not attain a constant saturation of Rubisco with the CCM. Rather than reconstructing growth water, α_alkenone may be a powerful tool to elucidate the carbon limitation of photosynthesis.

The stable isotope composition of hydrogen of lipids produced by photosynthetic organisms has often been employed to estimate variations in the isotopic composition of the growth water to reconstruct the hydrological cycle over time (1, 2) because lipid C-H bonds do not further exchange with environmental water after biosynthesis. Lipids feature a lower ²H/¹H than the growth water, and a complication is that the magnitude of this ²H/¹H fractionation depends strongly on physiological factors that change from one compound to another, among species and among different environmental conditions within a given species (3, 4).

Experimental studies have evaluated the influence of several growth conditions on algal lipid hydrogen isotope fractionations relative to growth water. Fractionation is typically expressed by the fractionation factor α, where a lower α indicates more deuterium (²H or D)-depleted lipids relative to the hydrogen isotope ratio of growth water. In freshwater green algae harvested in the range from 15 to 25 °C, increasing temperature intensifies ²H/¹H fractionation in acyl lipids, lowering α (5). Higher salinity led to higher α in the acyl lipids of the haptophyte Emiliania huxleyi (6), and increasing light intensity in cultures led to higher α-values in the acyl lipids of marine diatom Thalassiosira pseudonana and in E. huxleyi (7, 8). In chemostat cultures, as cell growth rates were slowed by progressive N- or P-nutrient limitation, hydrogen isotope fractionation of acyl lipids in E. huxleyi decreased (9). However, apparent discrepancies between the influence of a given environmental factor in culture and natural samples, such as contrasting temperature influence (10) or much higher (11) sensitivity to salinity, challenge simple empirical explanations of the controls on fractionation.

The overall deuterium depletion of algal biomass relative to the water (12) has its root in the large kinetic isotope effect (KIE) of NADPH generation via the ferredoxin-NADP⁺ reductase (FNR) enzyme at the photosystem I (PSI) of the chloroplast, with an apparent fractionation (δ²H_NADPH/PSI) of around −600‰ from growth water (13). NADPH produced through other pathways, such as the oxidative pentose phosphate pathway (oxPPP), is less depleted, with a δ²H_NADPH/oxPPP around −250‰ (9), consistent with the observation that heterotrophy leads to ²H-enriched biomass compared to phototrophic growth in plants (14, 15). Consequently, previous explanations (9) proposed that algal lipid ²H/¹H fractionation depends on the relative flows of photosynthetic ²H-depleted NADPH, extrachloroplastic NADPH, and exchange with intracellular ²H-enriched water. Another potential mechanism attenuating this strongly negative chloroplastic δ²H_NADPH could be NADPH exchange with intracellular water. This process has been observed during ²H-labeling experiments in eukaryotic cell lines catalyzed by flavin-dependent enzymes such as glutathione reductase (16) and could change δ²H_NADPH in the chloroplast directly. Yet, despite wide interest in δ²H application in algal systems, a quantitative evaluation of these hypotheses has not been performed.

Here, to elucidate the underlying physiological controls of fractionation, we provide a set of experimental data from algal lipids grown in continuous culture, in which we systematically manipulate temperature, light, and CO₂(aq). We focus on a specific lipid class, the alkenones, which are ketone alkenes commonly C₃₇/C₄₀-long and di- or triunsaturated. These biomarkers are unique to certain haptophyte algae, allowing their ²H/¹H signal to be attributed to a specific group among mixed populations in the ocean. Alkenones are hypothesized to form from fatty acid precursors synthesized in the chloroplast that would further elongate in the endoplasmic reticulum (17, 18) (SI Appendix, Fig. S1). Both alkenones and fatty acids, during their acetogenic synthesis by the multienzyme fatty acid synthase (FAS) complex, obtain almost half of their hydrogen atoms from the redox cofactor NADPH, about a quarter from the precursor acetyl-CoA and the remaining from intracellular water (19, 20). The knowledge of alkenone synthesis allows us to model the variations of ²H/¹H fractionation. Most importantly, alkenones are well-preserved molecular fossils and can be successfully recovered not only from cultures but also from ocean suspended particulate organic matter (SPOM), and marine sediments dating back tens of millions of years (21).

We carried out continuous cultures of Gephyrocapsa oceanica RCC1303, an alkenone-producing species contributing significantly to modern and ancient coccolithophore calcite production. Compared with the batch cultures in most previous works, in which increasing cell concentrations progressively deplete dissolved CO₂ levels and increasingly self-shade, steady-state cultures maintain constant cell density. Continuous cultures therefore maintain a more stable CO₂ and light environment, which facilitates full separation of the different environmental influences on α_alkenone. We also reevaluate whether the influence of CO₂(aq), temperature, and salinity on α_alkenone in natural environmental samples is coherent with our findings in cultures. To diagnose the processes responsible for the influence of CO₂(aq), temperature, and light on α, we develop a model to simulate the hydrogen isotope ratio of lipids, incorporating the sensitivity of key cellular metabolic rates to temperature, CO₂(aq), and light. Our findings provide a template for the interpretation of alkenone hydrogen isotope ratios as an indicator of physiological response to environmental pressures and thus inform about central metabolic pathways such as photosynthesis.

Hydrogen Isotope Fractionation as a Function of CO₂, Light, and Temperature

Continuous cultures of G. oceanica RCC1303 were grown in photobioreactors under a wide range of CO₂(aq) (5 to 90 µM), light intensities (50 to 200 µE), and temperatures (15 to 27 °C) (SI Appendix, Figs. S2 and S3 and Table S1). Harvested cells from photobioreactors had alkenone δ²H values ranging from −241.4 to −313.3‰, reported as abundance-weighted average of methyl ketones C37:3 and C37:2, and ethyl ketone C38:2Et (SI Appendix, Fig. S4). The seawater media spanned −72.7 to −76.1‰, resulting in an α_alkenone range of 0.743 to 0.821 for our 29 samples (Dataset S1), where the fractionation factor α is defined relative to growth water as detailed in Material and Methods.

The impacts of CO₂(aq), light, and temperature on α_alkenone are evaluated individually in data subsets in which variation in the other factors is limited (Fig. 1). At 18 °C and a low light of 50 µE, the CO₂(aq) sensitivity of α_alkenone is −9.0 × 10⁻⁴ µM⁻¹. Remarkably, at higher light intensities of 100 µE and 200 µE, this CO₂(aq) sensitivity is halved: −4.5 × 10⁻⁴ µM⁻¹ and −5.1 × 10⁻⁴ µM⁻¹, respectively (Fig. 1A). While we express the sensitivity in linear terms, we cannot exclude the possibility of a logarithmic or other nonlinear dependence of α_alkenone on CO₂(aq) from our data. These possibilities will be subsequently explored in our model simulations. Increasing temperature decreases α_alkenone, with a slope of −4.9 × 10⁻³ °C⁻¹ in experiments at 200 µE light and 8 to 18 µM CO₂(aq) (Fig. 1B). In contrast, higher light generally increases α_alkenone, with the greatest sensitivity of 2.4 × 10⁻⁴ µE⁻¹ at very high CO₂(aq) levels above 20 µM, and no sensitivity to light at low 5 to 20 µM CO₂(aq) (Fig. 1C).

Fig. 1.

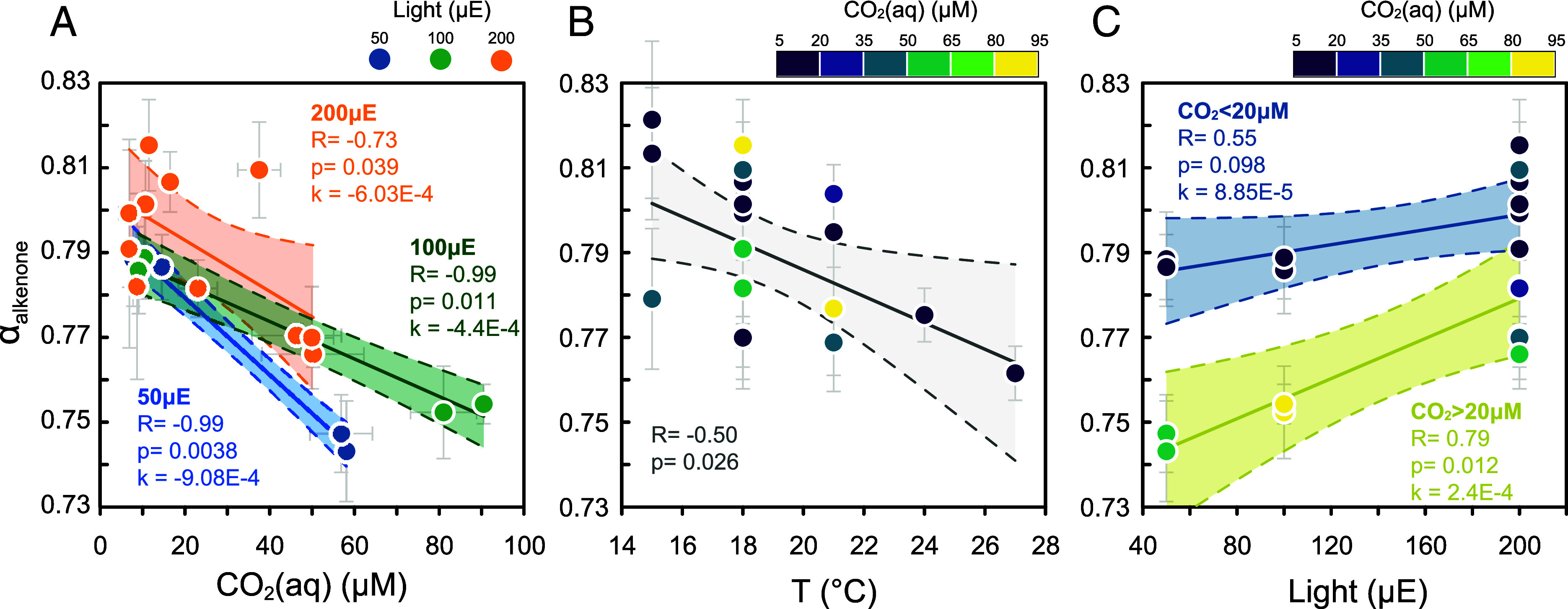
Alkenone α changes in cultures due to CO₂, temperature, and light. (A) CO₂ effect: subset growing at 18 °C in different lights. (B) Temperature effect in the subset at 200 µE at different CO₂(aq) levels (N = 20). (C) Light effect in the subset at 18 °C at different CO₂(aq) ranges. Means of N ≥ 2 and error bars represent one SD. The solid line represents simple regression and dashed lines, 95% CI. The slope of the linear regression is annotated as k and p is the confidence value. It should be noted that the linear relationship between α_alkenone and light is insignificant when CO₂ concentration is smaller than 20 μM.

Multiple linear regressions (MLR) were also carried out to account for the combination of the above environmental influences on α_alkenone (SI Appendix, Table S2). The best prediction of α_alkenone using environmental parameters had an R² of 0.615:

$$\begin{array}{c}{\mathrm{\alpha }}_{\text{alkenone}}=0.8526-6.017 {10}^{-4}{C}_e\hfill \\ +8.815·{10}^{-5}\mathrm{L}-3.566·{10}^{-3}\mathrm{T}.\hfill \end{array}$$ [1]

Using a log(CO₂) in MLR results in a comparably strong prediction of α_alkenone (R² = 0.58):

$$\begin{array}{c}{\mathrm{\alpha }}_{\text{alkenone}}=0.8807-3.672·{10}^{-4}\text{log}(C_e)\hfill \\ +1.258·{10}^{-4}\mathrm{L}-3.714·{10}^{-3}\mathrm{T},\hfill \end{array}$$ [2]

where CO₂(aq) (C_e), light (L), and temperature (T) have units of µM, µE, and °C, respectively. These regressions highlight the complex relationship between environment parameters and hydrogen isotope ratios in lipids.

In addition to media carbonate system and lipid hydrogen isotope ratios, a large array of biological parameters were analyzed to characterize algal composition (SI Appendix and Dataset S1). We performed a cross-correlation analysis (SI Appendix, Fig. S5) to gain insight into the different relationships among all the cellular and environmental variables. Along with the previously described correlation of α_alkenone to CO₂(aq) (Pearson r = −0.623, P-value < 0.001) and light intensity as previously reported (7), we also find that lower α_alkenone correlates with higher alkenone content (Pearson r = −0.650, P-value = 0.002) and higher calcification (Pearson r = −0.571, P-value = 0.003). To a lesser extent, chlorophyll per cell also correlates to lower α_alkenone. These correlations indicate that the extracellular environmental variations could influence α_alkenone via metabolic processes such as photosynthesis and carbon fixation. We do not find any significant correlation between growth rate and α_alkenone in our culture data (SI Appendix, Fig. S6).

Temperature and CO₂ Influence on α_alkenones in Previous Culture and Environmental Samples

Previous culture studies of α_alkenone have not focused on manipulating CO₂(aq) and only one prior culture experiment of E. huxleyi cultures (22) reported carbon system parameters, namely pH and alkalinity at the start and end of the batch culture. For this experiment, we estimate CO₂(aq) and find a weak negative correlation between α_alkenone and average CO₂(aq) [Fig. 2A in green, SI Appendix, Fig. S7A; basis of CO₂(aq) calculation in SI Appendix, Table S2]. In cultures with no reported carbon system measurements, it is possible that manipulations of culture temperature, salinity, and culture alkalinity, as well as differences in cell growth rate and cell density at harvest, have also led to systematic variation of CO₂(aq) which has contributed to some reported variations in α_alkenone (SI Appendix, SI Materials and Methods).

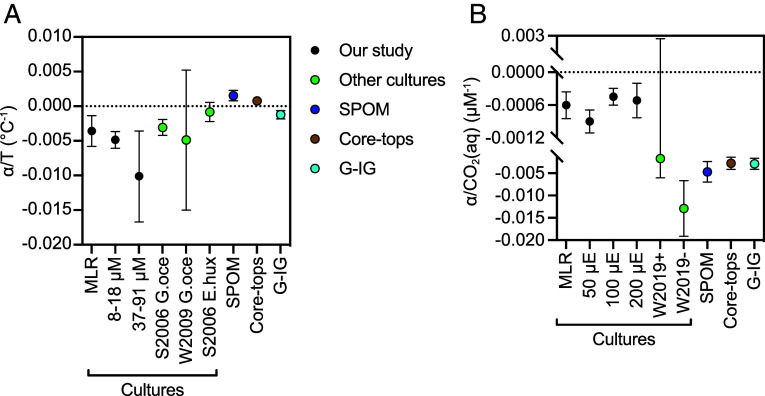
Fig. 2.

Comparison between α_alkenone in this work and in published datasets. (A) Comparison of linear regressions of α_alkenone on CO₂(aq) (µM). Slopes cover a CO₂(aq) range of 5 to 90 µM for our MLR. Culture 50, 100, and 200 µE are the slopes calculated on our data subset at 18 °C and indicate light intensity. W2019 is the slope for Weiss et al. cultures (22) at a range from 5.4 to 10.3 µM (excluding Exp. 6, W2019-) or to 12.8 µM (including Exp. 6 datapoint, W2019+). SPOM, surface ocean suspended particulate organic material, is the slope at the 10 to 16 µM range for Gould et al. (23). Core-tops are surface sediments (0 to 1 cm) between 7 and 14 µM from Weiss et al. (24). G-IG, glacial-interglacial, are deep ocean sediments from present-153.1 ky from the Chile margin, and have a range of 7 to 11 µM (11). (B) Comparison of linear regressions of α_alkenone on temperature (°C). Slopes cover a temperature range of 15 to 27 °C for the MLR of our culture study. Cultures in the CO₂(aq) range of 8 to 18 or 37 to 91 µM are all at 200 µE. S2006 G. oce are G. oceanica cultures from Schouten et al. (25), W2009 G. oce are also G. oceanica cultures from Wolhowe et al. (26) and S2006 E. hux are E. huxleyi cultures from Schouten et al. (25). Datapoints represent slopes and error bars are 95% CIs (Materials and Methods).

Where environmental samples with published α_alkenone originated in regions of the ocean characterized by air–sea CO₂ equilibrium, we estimated the CO₂(aq) characterizing surface ocean environments above published core-top sediments (24) and surface particulate organic matter, SPOM, samples from the euphotic zone (23) (SI Appendix, Table S3). In these sets of samples, α_alkenone negatively correlates with CO₂(aq) (Fig. 2 and SI Appendix, Fig. S7). In both of these sample sets, the range in CO₂(aq) results only from the higher solubility of CO₂ in colder ocean surface waters, and therefore α_alkenone is also significantly positively correlated with SST (P = 0.0001 for SPOM, P = 0.0009 for core-tops), as described previously (22). However, in our cultures, where the CO₂(aq) and temperature vary independently, α_alkenone correlates negatively with temperature, as found in several other culture studies (25–27) (Fig. 2B and SI Appendix, Fig. S7E). Therefore, the spatial gradients in α in the ocean are consistent with the sign of α covariation with CO₂(aq) in cultures but inconsistent with sign of α covariation with temperature in cultures. While our cultures exhibit a decrease of α_alkenone with rising CO₂ for a single G. oceanica strain, the prevalence of similar inverse relationships in natural ocean populations suggests that the main physiological drivers of the relationship are not unique to this G. oceanica strain.

Over late Pleistocene glacial cycles, glacial periods of low atmospheric CO₂ coincide with low temperature, as well as high ice volume and salinity. Based on our cultures and previous results on salinity (6, 10), all of these factors could contribute to higher α_alkenone during glacial times. Previous studies find larger magnitude increases in δ²H alkenone during glacial time periods (11, 28) than would be expected given modest ocean salinity changes. Low temperature and low CO₂(aq) might be additional drivers of high glacial α_alkenone; α_alkenone vs. CO₂(aq) is negative in slope similar to that of the cultures, assuming sites were at air–sea equilibrium and using CO₂ solubility from alkenone SST and SSS from ice volume (Fig. 2).

Mechanism of α_alkenone Varying with CO₂, Temperature, and Light

Our results highlight an influence of CO₂(aq) on δ²H fractionation, in addition to temperature and light influences on fractionation. Previous conceptual explanations for variable fractionation proposed that algal lipid ²H/¹H fractionation depends on the relative flows of photosynthetic ²H-depleted NADPH, extrachloroplastic NADPH, and exchange with intracellular ²H-richer water (9), i.e., the major source of alkenone and fatty acid δ²H is the hydrogen transferred during the redox reactions to NADP⁺. We extend this conceptual mechanism by considering the enzymatic H exchange between the ²H-depleted NADPH in the chloroplast with H₂O by flavoproteins (16) (Fig. 3A and SI Appendix, Fig. S1). We hypothesize that the activity level of these enzymes and the turnover of the generated NADPH determine its residence time in the chloroplast (τ_NADPH). The NADPH residence time, τ_NADPH, is defined as the NADPH amount in chloroplast divided by the NADPH generation rate or consumption rate with a unit of second (SI Appendix, Eq. S38). A longer NADPH residence time would allow a more exchange with the heavier isotopic intracellular water, leading to more positive δ²H_NADPH,x, and thereby larger α_alkenone (15). We therefore propose that the τ_NADPH,x is the major factor controlling hydrogen isotope fractionation of alkenones, and the residence time is systematically affected by the CO₂(aq), temperature, and light conditions which regulate the photosynthetic process.

Fig. 3.

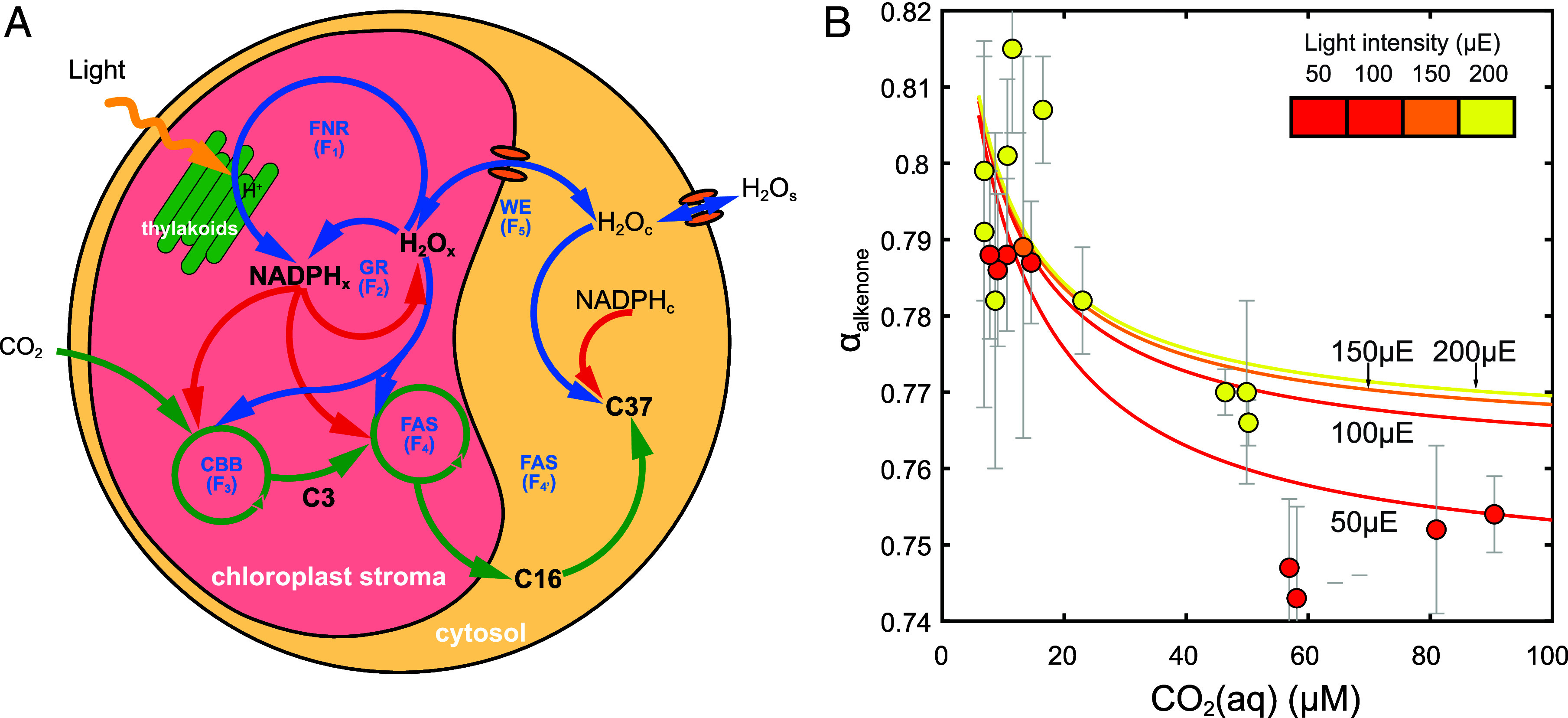
Model structure and comparison between simulations and laboratory cultures. (A) Structure of the hydrogen fractionation model in this work. There are two simulated compartments: the chloroplast and cytoplasm. The hydrogen isotope ratios of NADPH in chloroplast (NADPH_x), intracellular water (H₂O_x and H₂O_c), production of small C3 carbon metabolites, fatty acid precursors from chloroplast (C16), and alkenones from cytoplasm (C37) are simulated. In different colors, the six fluxes affecting the hydrogen isotope ratios of alkenones are highlighted: in red, fluxes using NADPH as a substrate; in green, fluxes using carbon molecules, and in blue, fluxes with water. The ferredoxin-NADP reductase (FNR) introduces a δ²H in NADPH_x of −600‰ relative to the stromal water (H₂O_x) (flux F₁). This ²H-depleted H from NADPH_x exchanges with the ²H-enriched H₂O_x via flavoproteins such as glutathione reductase (GR) (fluxes F₂). NADPH_x is mainly consumed by the CBB cycle and the FAS complex (fluxes F₃ and F₄), whose competition with flavoproteins (GR) determines NADPH residence time (τ_NADPx). The CBB produces C3 compounds that can generate acetyl-CoA for fatty acid production by the FAS. These fatty acids can be exported to the cytoplasm for further elongation to produce alkenones. The different H₂O channels and pumps influence the water δ²H by exchanging water (WE) between the chloroplast and cytoplasm (fluxes F₅). (B) Comparison between simulation and laboratory culture results on CO₂(aq) and light effect at 18 °C. The lines are simulation results at fixed 18 °C temperature at varying CO₂(aq). The circles are measurements in laboratory culture. Gray bars represent the SD of hydrogen isotope fractionations calculated from C37:3, C37:2, and C38:2Et alkenones (α_alkenone). Only the cultures carried out at 18 °C are presented in this panel to remove the temperature effect. The color of circles and lines represents the light intensity in µE and shares the same colormap.

To test our hypothesis, we construct a numerical model (SI Appendix, SI Material and Methods) to simulate how environmental factors affect the variations of cell metabolism causing hydrogen isotope fractionations in lipids. The model focuses on the key processes influencing hydrogen isotope ratios of NADPH in chloroplast (Fig. 3A and SI Appendix, Fig. S8) and reproduces several important aspects of the observations in experiments (Fig. 3B). First, at constant temperature, the negative correlation between CO₂(aq) and α_alkenone is well reproduced in simulations. Second, a larger α_alkenone characterizes high light conditions in both simulation and laboratory culture. Third, the model captures the higher sensitivity of α_alkenone to light under high CO₂ conditions, while the light effect is negligible in a low CO₂ environment.

We can diagnose that these responses are driven by variations in τ_NADPH,x (Fig. 4). Higher CO₂(aq) and higher temperature can decrease the τ_NADPH,x by enhancing the carbon fixation rate and lipid synthesis rate (red fluxes in Fig. 4A). In this case, the consumption rate of NADPH is higher than the NADPH-water exchange rate (Fig. 4A). Thus, higher CO₂(aq) and higher temperature result in stronger fractionations (more negative δ²H_alkenone and lower α_alkenone). More generally, a higher carbon fixing rate and hydrogen exchange rate ratio (F₃/F₂ in Figs. 3 and 4) leads to lower α_alkenone, which would also enhance alkenone content. That could explain the inverse correlation between α_alkenone and the cellular alkenones/POC (SI Appendix, Fig. S5).

Fig. 4.

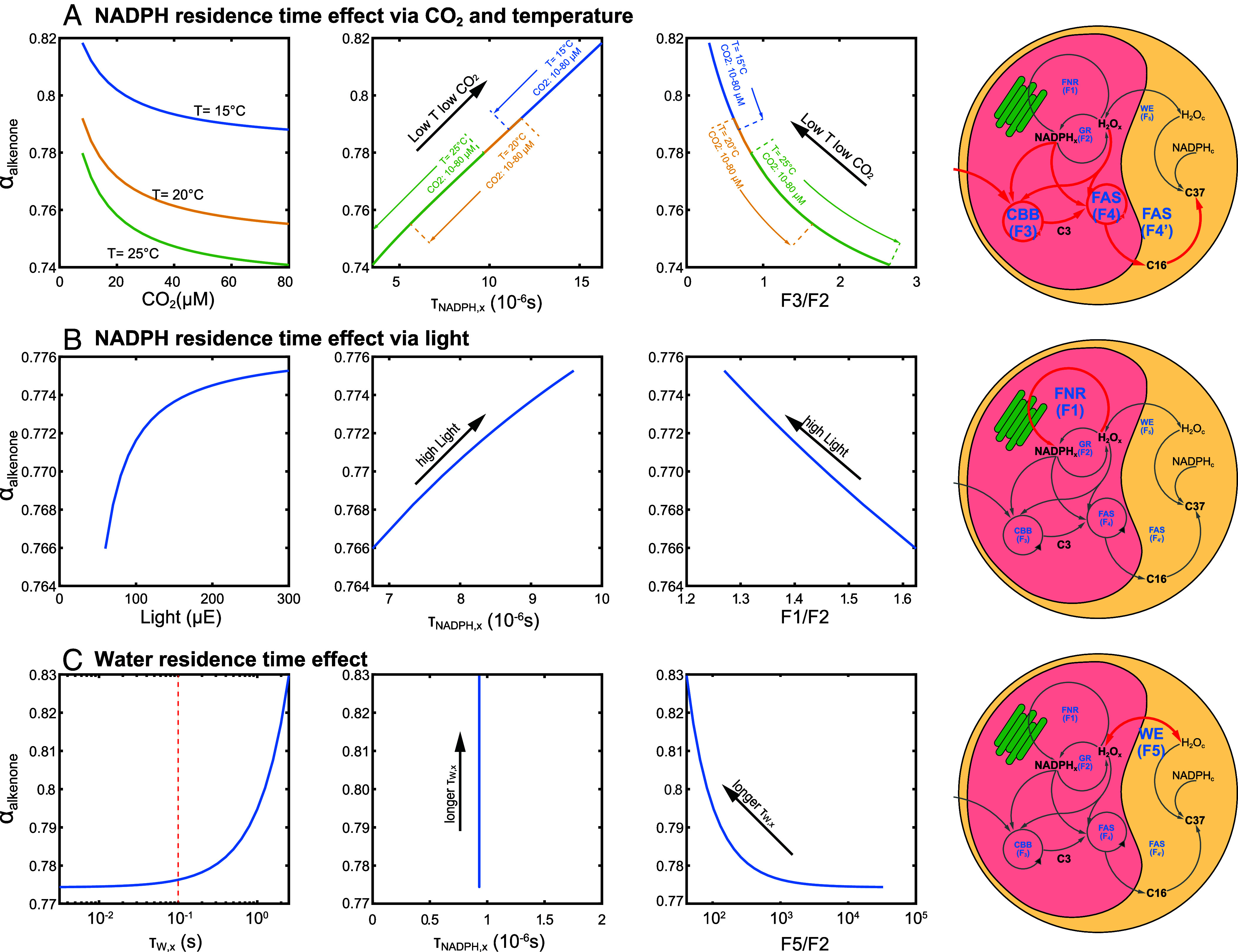
Sensitivity tests on temperature, CO₂(aq), light, and water residence time on α_alkenone. (A) Simulating faster alkenone synthesis at high CO₂(aq) and/or high temperature. The different lines represent simulated α_alkenone as a function of CO₂(aq) at increasing temperatures (1st panel), as a function of NADPH residence time in the chloroplast (2nd plot) and as a function of the ratio between simulated fluxes 3 and flux 2 (3rd plot). It should be noted that the lines of different temperature and CO₂(aq) combinations in the 2nd and 3rd panels are overlapping. This overlap results from dual temperature and CO₂ control on carbon fixation rate which affects hydrogen isotope fractionation. (B) Simulating faster NADPH_x reduction at high light intensity. Here, the Left panel shows α_alkenone in function of the ratio between simulated fluxes 1 and 2 (F1/F2). The red line in the Right panel represents the generation of NADPH is enhanced in high light conditions. (C) Simulating lower water residence time at slow water exchange between chloroplast and cytoplasm. Here, the 3rd panel shows α_alkenone in function of the ratio between simulated fluxes 5 and 2 (F5/F2). The red lines in the right cell diagram represent enhanced carbon fixation and lipid synthesis in high temperature and high CO₂ conditions.

Light fuels the photosynthetic chain providing the energy to reduce the NADP⁺ stromal pool and keeps a high NADPH/NADP ratio in the chloroplast (29). A higher NADPH concentration would increase the residence time of chloroplast NADPH (SI Appendix, Eq. S38), allowing more time for hydrogen exchange between water and NADPH (Fig. 4B). Therefore, a higher light intensity results in a smaller fractionation and a higher α_alkenone. As illustrated in Fig. 1C, the light effect is muted at very low CO₂(aq) conditions when the consumption of NADPH in the chloroplast is very low due to the CO₂ limitation of the Calvin–Benson–Bassham cycle (CBB). Thus, the NADPH levels in the chloroplast are still very high even during low light conditions (SI Appendix, Fig. S9). In this case, the light effect on τ_NADPH,x and α_alkenone is not significant. This explanation fits with previous studies with low CO₂/high light conditions suggesting that light intensity does not have a direct effect on NADPH hydrogen isotopic fractionation (30).

An increase in the abundance of glutathione reductase with higher light could also lead to the light dependence of α_alkenone. The primary function of glutathione reductase is to maintain the cellular redox balance by catalyzing the reduction of oxidized glutathione to its reduced form using NADPH as a cofactor. This process helps to protect cells from oxidative stress by scavenging reactive oxygen species (31) and maintaining the antioxidant capacity of the cell. Higher content of glutathione reductase can accelerate the exchange of hydrogen between NADPH and water resulting in a smaller fractionation between alkenone and water. Because a high content of glutathione reductase has the same effect as the high NADPH generation rate in high light, these two effects are combined in our model parameterization to reduce the degrees of freedom.

Potential Influences from Other Processes

Salinity correlates positively with α_alkenone in some laboratory culture experiments (6, 25), but the detailed mechanism of the salinity effect is still under debate (2). Moreover, most experimental manipulation of culture media salinity has also affected alkalinity, which alters the carbon system and complicates the distinction between the salinity effect and potential CO₂ effects (30). Salinity could play a minor role in lipid hydrogen isotope ratios via changing the water residence time in the chloroplast (τ_W) (32, 33). During NADP⁺ reduction via FNR, more ¹H goes into NADPH resulting in a more ²H-enriched chloroplast water. If the chloroplast water has a low exchange rate with external water, thus a longer water residence time in chloroplast (τ_W,x), then the enrichment of ²H would be greater and finally lead to a smaller hydrogen isotope fractionation in alkenones (higher α_alkenone). Since there is no accurate estimation of the water residence time in coccolithophores, we test a large range of τ_W,x from 0.01 to 1 s, but we do not suggest that the τ_W,x would vary dynamically in a single cell over such a large range. Based on our simulation, selection of a τ_W,x of 0.001 to 10 s results in α_alkenone changing from 0.775 to 0.8, which is equivalent to ~25‰ increase in hydrogen isotope ratio (Fig. 3C). The observed change in fractionation correlated with salinity in culture is equivalent to ~5‰ from 25 to 35 practical salinity units (6, 25). This suggests that, if the fractionation change is due to a salinity effect on τ_W,x, the variation of τ_W,x with salinity should be in a much narrower range than our sensitivity test. Recent works using surface sediment samples have found that there is only a weak correlation between surface water salinity and α_alkenone. Thus, the salinity effect on α_alkenone could be overwhelmed by other environmental factors, such as light and CO₂, in most of natural samples.

In some chemostat culture experiments under 24-h illumination, as nutrient limitation is relieved and growth rates increase, α_alkenone decreases (9). If in these experiments the growth rate is proportional to the gross C fixation rates, this response is consistent with our modeled decrease in α_alkenone with higher gross C fixation (Fig. 4A) which lowers τ_NADPH,x. At the same time, in our experiments (SI Appendix, Fig. S6) and across all published datasets reporting growth rate, there is no significant correlation between growth rate and α_alkenone (SI Appendix, Fig. S10). One explanation is that the balance of gross photosynthetic fixation and respiration may vary under different experimental conditions, decoupling measured cell growth rates from gross C fixation and decoupling α_alkenone from growth rate.

Our model accounts for the core processes in chloroplast affecting α_alkenone, which are more related to the carbon fixation, and simulates the main trends in the dataset (SI Appendix, Fig. S11). Other sources of NADP⁺ reduction from respiration, such as the tricarboxylic acid cycle and the oxidative pentose phosphate pathway (oxPPP), are not simulated in our model. The NADPH generated in chloroplast and cytoplasm could also exchange with each other via malic acid shuttle and triose phosphate shuttle to meet metabolic needs (34). Thus, the source of NADPH can also vary with cellular metabolic processes. For example, nutrient limitation might decrease growth rate and increase respiration rate, resulting in a higher oxPPP contribution and increasing the hydrogen isotope ratios of lipids as suggested by Sachs and Kawka (9).

Further complexity could be added to the model to evaluate the effects of oxPPP contributing to the isotope composition of NADPH (35), for example, by allowing fractionation between NADPH and water in chloroplast (α_w-N,x) to vary with the fraction of oxPPP involvement. If the oxPPP contribution were constant, it would affect the absolute value of α_alkenone, and would affect our parameter tuning, but it would not affect the α_alkenone response to environmental variables. On the other hand, if the relative contribution of the oxPPP were variable, it could contribute to variation in α_alkenone in response to environmental variables like CO₂. Implementation into the model would require independent constraints on the drivers of the varying relative contribution of the oxPPP.

It should be noted that some KIE used in our simulations (SI Appendix, Table S5) are also not well constrained by independent experimental data, which could increase the uncertainty of our simulations. Also, the model is limited to acyl lipids, and quantitative simulation of α in other biosynthesis pathways may require additional model complexity.

Implications of α_alkenone-CO₂ Sensitivity on CCMs

In our reference simulations illustrated in Figs. 3 and 4, we set the CO₂(aq) at the site of Rubisco (CO_2,x) as 1.5 fold higher than the CO₂(aq) in the seawater. An assumption of elevated CO₂ at the site of photosynthesis compared to that in extracellular media is consistent with evidence that coccolithophores, like many other eukaryotic and prokaryotic algae, can operate a CO₂-concentrating mechanism (CCM) (36–38). However, there is as of yet no direct means to quantify the degree of CO₂ enhancement at the site of Rubisco by a growing cell. A limited number of studies on diatoms provide indirect estimations of the CO₂ at the site of photosynthesis from modeling gas fluxes during incubations but are subject to significant uncertainties (39–41).

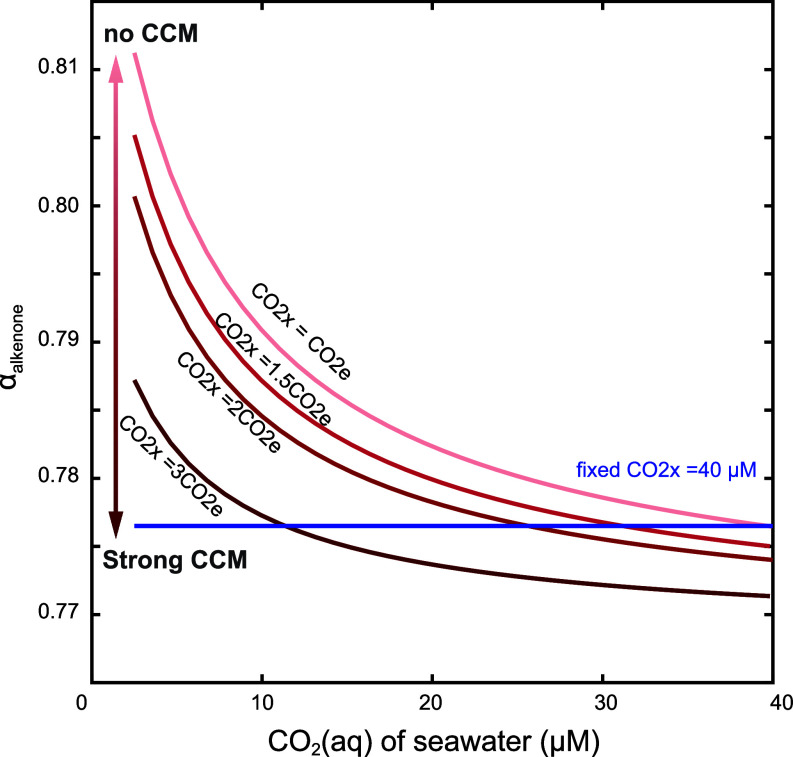
An optimal CCM would be expected to maintain the CO_2,x at a level nearly saturating Rubisco, such that at a given temperature, the CO_2,x would be constant regardless of external CO₂(aq). We have simulated such a case of a CCM at constant saturation and find that, in this case, α_alkenone would be insensitive to CO₂(aq) during culture (blue lines in Fig. 5). Thus, the persistent decline in α_alkenone with an increase of external CO₂(aq) in, not only our culture experiments (Fig. 1A), but also the global surface sediment samples (Fig. 2), indicates that these alkenone producers do not feature a CCM fully up-regulating to attain a constant saturation of Rubisco. At the same time, at constant temperature and light, a portion of the variability in α_alkenone for a given CO₂(aq) may be caused by different intensity of the CCM and the CO₂(aq) of the chloroplast (Fig. 5).

Fig. 5.

Influence of CCM strategies on α_alkenone. The intensity of CCM affects CO₂ concentration in the chloroplast (CO2x). The pink lines represent different intensities of CCM resulting in a varying CO2x and thereby different α_alkenone. The left arrow shows the CCM intensity from non-CCM to strong CCM. The blue line represents that α_alkenone does not respond to CO₂(aq) if the cells employ a constant CCM (set as 40 µM in this test).

Our finding of an unsaturated CCM is consistent with previous field measurements which indicate that the high energetic cost of CCM operation may lead to running the CCM at a lower intensity (40). Previous field experiments suggested that the CCM may not operate close to saturation in cold conditions due to the low enzyme turnover rates (41). However, our results at 18 °C suggest that the limited operation of a CCM may be a more general strategy, not only at cold temperature. Indeed, the persistent inverse correlation of α_alkenone with CO₂(aq) in the modern and preindustrial ocean (Fig. 2A) also suggests that natural populations may not attain a constant saturation of Rubisco through the CCM. Furthermore, the apparent sensitivity of α_alkenone to CO₂(aq) variations for the past 153 ky (SI Appendix, Fig. S7) may indicate that the CCM has not been fully up-regulated to compensate for glacial minima in CO₂(aq), an observation important to document in additional locations of expected air–sea equilibrium.

Our results also provide additional constraints on the role of light in the CCM. Previous studies suggested that higher light intensity may lead to higher CO_2,x by providing energy for the CCM or via light-dependent transporters (42, 43). If this mechanism were dominant, then higher light would lead to lower α_alkenone by enriching CO_2,x concentrations (red lines in Fig. 5) and increasing the carbon fixation rate (Fig. 3A). In contrast, our data suggest that higher light may not be ubiquitously correlated to higher CO_2,x, or that a CO_2,x enrichment could be masked by high NADPH concentrations. Future studies with experimental CO₂ conditions spanning the CO₂(aq) range of highest model sensitivity of α_alkenone and including additional strains of alkenone producers could be used to more clearly elucidate the CCM via hydrogen isotopic fractionations of lipids.

Conclusions

Our culture results document an important influence of CO₂ on α_alkenone which suggests that α_alkenone may not be suited for simple application as a proxy for salinity. The positive covariation of salinity and temperature, and their inverse correlation with CO₂ spatially in the modern ocean complicates efforts to empirically derive the dependence of α_alkenone on any one of these variables purely from core-top or SPOM measurements. Future culture studies carefully controlling for carbon system variation may improve constraints on the direct temperature and salinity effects in a broader range of alkenone-producing species and strains. If the temperature effect is similar and reproducible across species, it may be possible to account for its influence on α in studies on environmental samples. At the same time, our simulations indicate that the NADPH residence time in the chloroplast is a dominant control on α_alkenone. Thus, rather than a passive recorder of environmental parameters, α_alkenone may be well suited to provide a key perspective on the cellular regulation of photosynthesis and the CO₂ availability in the chloroplast in the modern and past oceans.

Materials and Methods

Continuous Cultivation.

Gephyrocapsa oceanica RCC1303 (Roscoff Culture Collection) cells were inoculated into 1 or 3-L photobioreactors (FMT150, Photon Systems Instruments) aerated at different pCO₂ levels. Light intensity of a cool-white LED panel was set in sinusoid mode for a diurnal rhythm of 8 h dark/16 h light plateauing at 50 to 200 µE (SI Appendix, Fig. S3). An array of different combinations of temperature, pCO₂, and light (SI Appendix, Fig. S2 and Table S1) was imposed to grow 29 cultures. Photobioreactors were operated in turbidostat mode by automatic dilution triggered above an optical density at 680 nm (OD680) equivalent to 1 to 2 × 10⁵ cells mL⁻¹ (log phase). Cells were kept in suspension with gentle magnet stirring, air bubbling, and thorough daily manual resuspension of precipitate cells. More details about cell density, carbonate system control, and particulate organic/inorganic carbon measurements, lipids extraction, and identifications can be found in SI Appendix.

Hydrogen Isotope Analysis.

The stable hydrogen isotopic compositions of alkenones were analyzed by a gas chromatograph (Thermo Scientific Trace GC Ultra) coupled to an isotope ratio mass spectrometer (Thermo Scientific Delta V) using a pyrolysis interface (Thermo Scientific Isolink). Samples were injected with a GC PAL autosampler system (CTC Analytics AG) in splitless mode with a PTV injector (Gerstel CIS 6). Helium gas with a flow rate of 1 mL/min was used as the carrier gas. Separation of alkenones was performed with a 105 m × 0.32 mm capillary column (Rtx-200, 0.5 µm film thickness, Restek) with the following temperature program: 1 min at 50°, temperature gradient of 25 °C min⁻¹ to 250 °C and 2 °C min⁻¹ to 305 °C, hold for 25 min, then to 310 °C at 10 °C min⁻¹ and hold for 5 min. For each sample, triplicate measurements were performed to determine the δ²H value of alkenones and FAMEs, respectively, and reported as per mil relative to Vienna Standard Mean Ocean Water (VSMOW). Our in-house alkenones standard and A7 (purchased from Indiana University) were used as standards.

Water hydrogen isotope ratios were analyzed on a Picarro L2120-i cavity ringdown spectrometer using reference waters SLAP2, GRESP, and VSMOW2. Accuracy (2σ) for δ²H was 1‰ based on reproducibility of 6 measurements of international standard USGS W-67400-S. The apparent lipid-water fractionation factor α was calculated as

$${\mathrm{\alpha }}_{\text{alkenone}}=\frac{{\mathrm{\delta }}^2{\mathrm{H}}_{\text{alkenone}}+1000}{{\mathrm{\delta }}^2{\mathrm{H}}_{\mathrm{water}}+1000},$$ [3]

where δ²H_lipid is the weighted average of the most abundant alkenone species: methyl ketones C37:3 and C37:2 and ethyl ketone C38:2Et. The δ²H of each alkenone is shown in SI Appendix, Fig. S4. The three alkenones show very similar α. Thus, further α analysis applies to the abundance-weighted average of the three alkenones and only for the cultures with a low analytical error (SD <3%). This allowed us to calculate a reproducible δ²H across all samples, because for cases where one of these three alkenones was too low in abundance for precise isotopic measurement, its low abundance would preclude the alkenone having appreciable influence on the weighted average isotopic value.

Inferring CO₂(aq) from Other Studies.

The approach for calculation of CO₂(aq) from environmental samples and from one culture is summarized in SI Appendix, Table S2. For cultures from Weiss et al. (22), CO₂(aq) was estimated from CO2SYS excel macro (44) based on reported alkalinity and pH, and using the total scale, 35‰ salinity, 7 µM phosphate, and 0 µM silicate. From these E. huxleyi batch cultures (22), we included data where calculated CO₂(aq) variations from initial to final measurement varied by <5 µM. Among these experiments, we compared the 11 cultures with similar cell growth effect on alkalinity (consumed by 238 ± 118 µM) (conditions 1 to 5). For environmental samples, we used the temperature-dependent solubility and equilibrium with atmosphere of 280 ppmv for core-tops and 400 ppm for recent suspended particulate matter. The CO₂ ranges of environmental samples are in the lower range (7 to 16 µM) of our culture samples (5 to 90 µM), and we cannot determine the nonlinearity of the CO₂ effect from our cultures. Consequently, we cannot distinguish whether the CO₂(aq) is higher in environmental samples or whether our culture’s linear regression has underestimated sensitivity at the lower range (Fig. 2A).

We did not estimate CO₂(aq) from culture experiments in which no carbon system variables were reported. However, CO₂(aq) may have varied in many culture studies, in some cases in systematic ways with the experimentally manipulated variables. Due to the temperature influence on CO₂ solubility, increasing temperature without modifying the carbon chemistry would naturally feature lower CO₂(aq), a situation that will counteract the temperature effect on α_alkenone and attenuate its manifestation in cultures, potentially contributing to debate over the importance of temperature in previous culture experiments (22). Because reducing salinity from 35 to 25 g/kg increases CO₂ solubility and CO₂(aq) increases from 14.3 µM to 17.3 µM, α_alkenone decreases at lower salinity may also be influenced by the salinity effect on CO₂(aq) solubility. More rigorous quantification of such variation in, for example, alkalinity, may help distinguish salinity from carbon system effects in future studies.

Model Structure.

We quantitatively test this hypothesis in a numerical hydrogen isotope model for alkenone producers. Briefly, the model simulates NADPH production during photosynthesis and its subsequent consumption to synthesize alkenones (SI Appendix, SI Materials and Methods). Production of alkenones (C37) uses the hydrogen from NADPH and water in the cytoplasm by elongating fatty acid precursors (C16) imported from the chloroplast. Both C37 and C16 compounds are made by the FAS complex, but C16 production consumes NADPH and water from the chloroplast and acetyl-CoA. The C16 is derived from the C3 compounds produced during CO₂ fixation by the CBB cycle. We use this framework to test how variations of α_alkenone are driven by the dynamics of the chloroplast NADPH hydrogen isotope ratios (δ²H_NADPH,x) and water hydrogen isotope ratios (δ²H_W,x).

The δ²H_NADPH,x is controlled by the relative intensities of five different metabolic fluxes within the chloroplast (SI Appendix, Table S4), which in turn are systematically influenced by temperature, light, and CO₂(aq). Higher light intensity is used to oxidize more water, which increases the linear electron flow of the photosynthetic chain, and passes more electrons on to NADP⁺, the final electron acceptor, via the ferredoxin-NADP⁺ reductase (FNR, F₁ in Fig. 3A), increasing the generation rate of NADPH:

$$\begin{array}{c}2 \mathrm{reduced} \mathrm{ferredoxin} +{\mathrm{NADP}}^{+} + {\mathrm{H}}^{+}\hfill \\ \to 2 \mathrm{oxidized} \mathrm{ferredoxin} +\mathrm{NADPH}.\hfill \end{array}$$ [4]

This chloroplastic NADPH exchanges with intracellular water via flavoproteins such as glutathione reductase (GR, F₂ in Fig. 3A) at a rate dependent on NADPH residence time (τ_NADPH,x), which is affected by its redox turnover. The major consumption of NADPH in the chloroplast is the carbon fixation in the CBB cycle (F₃ in Fig. 3A), and the fatty acid synthetase (FAS, F₄, and F_4’ in Fig. 3A):

$$\begin{array}{c}3{\text{CO}}_2+9\text{ATP}+6\text{NADPH}+5{\text{H}}_2\text{O}\\ \to \text{G}3\text{P}\left(\text{C}3\right)+9\text{ADP}+8\text{Pi}+6{\text{NADP}}^{+}+2{\text{H}}^{+},\end{array}$$ [5]

$$\begin{array}{c}8\text{acetyl-CoA}+{\text{CO}}_2+14\text{NADPH}+13{\text{H}}^{+}+7\text{ATP}\\ \to \text{Palmitate}\left(\text{C}16\right)+8\text{CoA}-\text{SH}+6{\text{H}}_2\text{O}+14{\text{NADP}}^{+}+7\text{ADP}+7\text{Pi}\end{array}.$$ [6]

The rate of the first reaction (Eq. 5) is limited by the CO₂(aq) at the site of Rubisco, the core CBB enzyme. In our reference simulation, we estimate that the CO₂(aq) at the site of Rubisco is elevated 1.5-fold relative to the external CO₂(aq) in the seawater, and therefore the consumption of NADPH increases with higher seawater CO₂(aq). We evaluate this CO₂ assumption in a later section. Higher temperature increases the catalytic turnover rate of Rubisco (45), and therefore NADPH consumption. When NADPH turnover is slow, the enzymatic exchange between NADPH and water (F₂) is higher, resulting in a higher δ²H_NADPH,x value as the initial FNR isotopic depletion in the NADPH is attenuated by exchange with the large H reservoir in chloroplast water. The hydrogen isotopic composition of chloroplast water (δ²H_W,x) is also simulated dynamically (SI Appendix, SI Materials and Methods). The hydrogen isotope ratio of water in cytoplasm is assumed to be the same as seawater based on the rapid water exchange facilitated by aquaporins (46). Our model configuration captures the core fluxes and exchanges occurring in the synthesis of acyl lipids such as alkenones and evaluates whether these processes are sufficient to cause the observed variation in α_alkenone (SI Appendix, Fig. S11).

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (XLSX)

Data, Materials, and Software Availability

All study data are included in the article and/or supporting information.