In many randomised trials researchers measure a continuous variable at baseline and again as an outcome assessed at follow up. Baseline measurements are common in trials of chronic conditions where researchers want to see whether a treatment can reduce pre-existing levels of pain, anxiety, hypertension, and the like.
Statistical comparisons in such trials can be made in several ways. Comparison of follow up (post-treatment) scores will give a result such as “at the end of the trial, mean pain scores were 15 mm (95% confidence interval 10 to 20 mm) lower in the treatment group.” Alternatively a change score can be calculated by subtracting the follow up score from the baseline score, leading to a statement such as “pain reductions were 20 mm (16 to 24 mm) greater on treatment than control.” If the average baseline scores are the same in each group the estimated treatment effect will be the same using these two simple approaches. If the treatment is effective the statistical significance of the treatment effect by the two methods will depend on the correlation between baseline and follow up scores. If the correlation is low using the change score will add variation and the follow up score is more likely to show a significant result. Conversely, if the correlation is high using only the follow up score will lose information and the change score is more likely to be significant. It is incorrect, however, to choose whichever analysis gives a more significant finding. The method of analysis should be specified in the trial protocol.
Some use change scores to take account of chance imbalances at baseline between the treatment groups. However, analysing change does not control for baseline imbalance because of regression to the mean1,2: baseline values are negatively correlated with change because patients with low scores at baseline generally improve more than those with high scores. A better approach is to use analysis of covariance (ANCOVA), which, despite its name, is a regression method.3 In effect two parallel straight lines (linear regression) are obtained relating outcome score to baseline score in each group. They can be summarised as a single regression equation:
follow up score=
constant+a×baseline score+b×group
where a and b are estimated coefficients and group is a binary variable coded 1 for treatment and 0 for control. The coefficient b is the effect of interest—the estimated difference between the two treatment groups. In effect an analysis of covariance adjusts each patient's follow up score for his or her baseline score, but has the advantage of being unaffected by baseline differences. If, by chance, baseline scores are worse in the treatment group, the treatment effect will be underestimated by a follow up score analysis and overestimated by looking at change scores (because of regression to the mean). By contrast, analysis of covariance gives the same answer whether or not there is baseline imbalance.
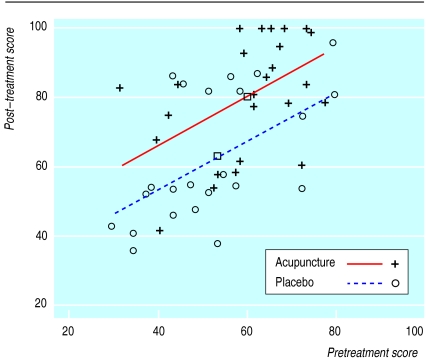
As an illustration, Kleinhenz et al randomised 52 patients with shoulder pain to either true or sham acupuncture.4 Patients were assessed before and after treatment using a 100 point rating scale of pain and function, with lower scores indicating poorer outcome. There was an imbalance between groups at baseline, with better scores in the acupuncture group (see table). Analysis of post-treatment scores is therefore biased. The authors analysed change scores, but as baseline and change scores are negatively correlated (about r=−0.25 within groups) this analysis underestimates the effect of acupuncture. From analysis of covariance we get:
follow up score=
24+0.71×baseline score+12.7×group
(see figure). The coefficient for group (b) has a useful interpretation: it is the difference between the mean change scores of each group. In the above example it can be interpreted as “pain and function score improved by an estimated 12.7 points more on average in the treatment group than in the control group.” A 95% confidence interval and P value can also be calculated for b (see table).5 The regression equation provides a means of prediction: a patient with a baseline score of 50, for example, would be predicted to have a follow up score of 72.2 on treatment and 59.5 on control.
An additional advantage of analysis of covariance is that it generally has greater statistical power to detect a treatment effect than the other methods.6 For example, a trial with a correlation between baseline and follow up scores of 0.6 that required 85 patients for analysis of follow up scores, would require 68 for a change score analysis but only 54 for analysis of covariance.
The efficiency gains of analysis of covariance compared with a change score are low when there is a high correlation (say r>0.8) between baseline and follow up measurements. This will often be the case, particularly in stable chronic conditions such as obesity. In these situations, analysis of change scores can be a reasonable alternative, particularly if restricted randomisation is used to ensure baseline comparability between groups.7 Analysis of covariance is the preferred general approach, however.
As with all analyses of continuous data, the use of analysis of covariance depends on some assumptions that need to be tested. In particular, data transformation, such as taking logarithms, may be indicated.8 Lastly, analysis of covariance is a type of multiple regression and can be seen as a special type of adjusted analysis. The analysis can thus be expanded to include additional prognostic variables (not necessarily continuous), such as age and diagnostic group.
Table.
Results of trial of acupuncture for shoulder pain4
| Pain scores (mean and SD)
|
Difference between means (95% CI) | P value | ||
|---|---|---|---|---|
| Placebo group (n=27) | Acupuncture group (n=25) | |||
| Baseline | 53.9 (14) | 60.4 (12.3) | 6.5 | |
| Analysis | ||||
| Follow up | 62.3 (17.9) | 79.6 (17.1) | 17.3 (7.5 to 27.1) | 0.0008 |
| Change score* | 8.4 (14.6) | 19.2 (16.1) | 10.8 (2.3 to 19.4) | 0.014 |
| ANCOVA | 12.7 (4.1 to 21.3) | 0.005 | ||
Analysis reported by authors.4
Figure.
Pretreatment and post-treatment scores in each group showing fitted lines. Squares show mean values for the two groups. The estimated difference between the groups from analysis of covariance is the vertical distance between the two lines
Acknowledgments
We thank Dr J Kleinhenz for supplying the raw data from his study.
References
- 1.Bland JM, Altman DG. Regression towards the mean. BMJ. 1994;308:1499. doi: 10.1136/bmj.308.6942.1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bland JM, Altman DG. Some examples of regression towards the mean. BMJ. 1994;309:780. doi: 10.1136/bmj.309.6957.780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Senn S. Baseline comparisons in randomized clinical trials. Stat Med. 1991;10:1157–1159. doi: 10.1002/sim.4780100715. [DOI] [PubMed] [Google Scholar]
- 4.Kleinhenz J, Streitberger K, Windeler J, Gussbacher A, Mavridis G, Martin E. Randomised clinical trial comparing the effects of acupuncture and a newly designed placebo needle in rotator cuff tendonitis. Pain. 1999;83:235–241. doi: 10.1016/s0304-3959(99)00107-4. [DOI] [PubMed] [Google Scholar]
- 5.Altman DG, Gardner MJ. Regression and correlation. In: Altman DG, Machin D, Bryant TN, Gardner MJ, editors. Statistics with confidence. 2nd ed. London: BMJ Books; 2000. pp. 73–92. [Google Scholar]
- 6.Vickers AJ. The use of percentage change from baseline as an outcome in a controlled trial is statistically inefficient: a simulation study. BMC Med Res Methodol. 2001;1:16. doi: 10.1186/1471-2288-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Altman DG, Bland JM. How to randomise. BMJ. 1999;319:703–704. doi: 10.1136/bmj.319.7211.703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bland JM, Altman DG. The use of transformation when comparing two means. BMJ. 1996;312:1153. doi: 10.1136/bmj.312.7039.1153. [DOI] [PMC free article] [PubMed] [Google Scholar]