Skip to main content
PMC home page
Veterinary Medicine and Science logoLink to Veterinary Medicine and Science
. 2024 Jul 2;10(4):e1521. doi: 10.1002/vms3.1521

Application of ultrasonographic human estimated foetal weight formulas to cynomolgus monkeys (Macaca fascicularis) at 129–132 days of gestation: A comparative study of estimated and actual birthweight

Dong‐Ho Lee 1,2, Seung‐Bin Yoon 1, Ji‐Su Kim 1, Jun Won Mo 1, Yu‐Jin Jo 1, Jeongwoo Kwon 1, Sang Il Lee 1, Jungkee Kwon 2,✉, Chan‐Wook Park 3,4,✉
PMCID: PMC11217594  PMID: 38952271

Abstract

Background

Cynomolgus monkeys (Macaca fascicularis) are essential in biomedical research, including reproductive studies. However, the application of human estimated foetal weight (EFW) formulas using ultrasonography (USG) in these non‐human primates is not well established.

Objectives

This study aims to evaluate the applicability of human EFW formulas for estimating foetal weight in cynomolgus monkeys at approximately 130 days of gestation.

Methods

Our study involved nine pregnant cynomolgus monkeys. We measured foetal parameters, including biparietal diameter, head circumference, abdominal circumference and femur length using USG. The EFW was calculated using 11 human EFW formulas. The actual birthweight (ABW) was recorded following Cesarean section, the day after the EFW calculation. For comparing EFW and ABW, we employed statistical methods such as mean absolute percentage error (APE) and Bland–Altman analysis.

Results

The ABW ranged between 200.36 and 291.33 g. Among the 11 formulas, the Combs formula showed the lowest APE (4.3%) and highest correlation with ABW (p < 0.001). Notably, EFW and ABW differences for the Combs formula were ≤5% in 66.7% and ≤10% in 100% of cases. The Bland–Altman analysis supported these results, showing that all cases fell within the limits of agreement.

Conclusions

The Combs formula is applicable for estimating the weight of cynomolgus monkey fetuses with USG at approximately 130 days of gestation. Our observations suggest that the Combs formula can be applied in the prenatal care and biomedical research of this species.

Keywords: cynomolgus monkey, human estimated foetal weight formulas, pregnancy, ultrasonography

Ultrasonography (USG) is a crucial tool in human prenatal care for determining gestational age and evaluating foetal development. In our study, we measured foetal parameters in cynomolgus monkey fetuses at around 130 days of gestation using USG and applied 11 human estimated foetal weight formulas. Among these, the Combs formula showed a mean absolute percentage error of 4.3% and performed excellently across various statistical analyses, suggesting its applicability in prenatal care and research for cynomolgus monkeys.

graphic file with name VMS3-10-e1521-g001.jpg

1. INTRODUCTION

Preterm birth, which accounts for approximately 10%–11% of all live births worldwide, is a global concern associated with increased neonatal mortality and long‐term morbidity, posing significant implications for maternal and child health (World Health Organization, 2023a; Osterman et al., 2023; Walani, 2020). Preterm infants are at a higher risk of complications and developmental delays with potentially long‐lasting effects on their health and well‐being (Blencowe et al., 2013; World Health Organization, 2023b). Exact confirmation of gestational age is necessary for the determination and management of preterm birth. Additionally, precise assessment of foetal weight is crucial in both clinical prenatal care and research settings, specifically given the occurrence of preterm births (Chauhan et al., 1998). This assessment provides critical information on foetal growth and development, aids in identifying potential complications during pregnancy and delivery, and guides decision‐making on the appropriate interventions to be applied (Boulet et al., 2003; Husslein et al., 2012; Ugwa et al., 2015).

Cynomolgus monkeys (Macaca fascicularis) are valuable animal models in various areas of biomedical research, including reproductive studies (Abee et al., 2012; Li et al., 2023; Wolfe‐Coote, 2005). With a known pregnancy duration of approximately 165 days (Abee et al., 2012; Wolfe‐Coote, 2005), monitoring foetal weight during this entire gestation period is essential for understanding normal foetal growth patterns, evaluating the impact of interventions or treatments on foetal development, and assessing potential risks to offspring (Kiserud et al., 2017). However, direct foetal weight measurement through Cesarean section in live animals is impractical and invasive. Therefore, non‐invasive ultrasound‐based estimation formulas could be a practical alternative.

Ultrasonography (USG), introduced in 1958, has become a widely utilized tool for determining gestational age and assessing foetal growth, development and well‐being (Skinner & Mount, 2023; Woo, 2002). The development of estimated foetal weight (EFW) formulas, based on USG measurements of various foetal body parts such as abdominal circumference (AC), biparietal diameter (BPD), femur length (FL) and head circumference (HC), has been crucial in this field. Over the years, numerous EFW formulas have been proposed in the context of specific gestational age and race/ethnicity. The choice of a particular formula often depends on the accuracy of specific measurements in the clinical context in which it is applied within a given population.

In veterinary medicine, USG has also been applied to various animal species (Kähn, 1992), such as dogs (Khatti et al., 2017; Lopate, 2008), horses (Ortega‐Ferrusola et al., 2022; Reef et al., 1996) and non‐human primates (Conrad et al., 1995; D'Mello et al., 2023; Jang et al., 2023; Jaquish et al., 1995; Lee et al.; Morgan et al., 1987; Oerke et al., 1996; Redmond & Evans, 2012; Tarantal, 1990; Tarantal & Hendrickx, 1988a, 1988b, 1988c, 1988d; VandeVoort & Tarantal, 1991) (Table 1), for reproductive management and research, including monitoring foetal development. Currently, there is no information about the foetal weight in non‐human primates, except only one study in the baboon (Van Calsteren et al., 2009). However, whether foetal weight estimation in cynomolgus monkeys with human EFW formulas is applicable remains unknown.

TABLE 1.

Comparative overview of foetal development confirmation studies using ultrasonography in non‐human primates.

Previous studies Species Parameters Foetal weight
Tarantal and Hendrickx (1988a) Macaca fascicularis Cardiac motion, embryo, GL, GS, YS N/A
Tarantal and Hendrickx (1988b) M. fascicularis, Macaca mulatta BPD, FL, GL, GS N/A
Tarantal and Hendrickx (1988c) M. fascicularis, Macaca mulatta Embryo, GS, heart, YS N/A
Lee et al. (1991) Pan troglodytes BPD N/A
Conrad et al. (1995) Macaca nemestrina BPD, FL, HA, HL N/A
Van Calsteren et al. (2009) Papio anubis AC, BPD, FL, GL, HC, TCD Yes
Redmond and Evans (2012) Chlorocebus sabaeus AC, BPD, CRL, FL, GS, HC N/A
D'Mello et al. (2023) M. mulatta AC, AFI, BPD, FL, HC, Hemodynamics N/A
Open in a new tab

Abbreviations: AC, abdominal circumference; AFI, amniotic fluid index; BPD, biparietal diameter; CRL, crown‐rump length; FL, femur length; GL, greatest length; GS, gestational sac; HA, head area; HC, head circumference; HL, humerus length; N/A, not available; TCD, transverse cerebellar diameter; YS, yolk sac.

Therefore, this study aimed to evaluate the accuracy of EFW formulas utilized in human medicine for predicting the weight of cynomolgus monkey fetuses using USG. The main objective was to compare the EFW derived from these formulas with the actual birthweight (ABW) obtained from direct measurements.

2. MATERIALS AND METHODS

2.1. Animal subjects

Nine female cynomolgus monkeys, imported from China, were included in this study. The monkeys were aged 81–102 months and weighed 2.70–4.56 kg. All monkeys were nulliparous. They were housed as a group (one male and multiple females) under standard laboratory conditions with continuous full contact. Upon pregnancy confirmation, the pregnant female was transitioned to single housing. The monkeys had ad libitum access to water and were fed a primate‐specific diet supplemented with multivitamins twice daily, along with fruits or vegetables provided once daily. Qualified animal caretakers observed all animals at least twice daily for injuries and illnesses. In addition, signs of any abnormalities, including abnormal sexual behaviour and abnormal vaginal excretions, were reported to the veterinarians. Health and medical records were kept for each animal. The Institutional Animal Care and Use Committee reviewed and approved the study protocol at the Korea Research Institute of Bioscience and Biotechnology to ensure that the study complied with the ethical guidelines and relevant regulations. This study reports additional discoveries derived from the approved study protocol.

2.2. Study design

A comparative design was employed to assess the accuracy of 11 EFW formulas commonly utilized in human pregnancy for predicting the weight of cynomolgus monkey fetuses. USG was performed on the monkeys during the early stages of pregnancy to confirm the gestational day (GD) and measure foetal parameters for calculating foetal weight. Monkey weight was measured at each USG session. The EFW was calculated at GD 129–132 for each of the nine monkeys. The specific pregnancy date – the 130th day of gestation (approximately 80% of term gestation) – was designated as the EFW measurement date based on the development and utilization of preterm birth models comparable to 32‐week preterm birth in humans. Subsequently, the ABW data were obtained through a scheduled Cesarean section, approximately 16 h after the calculation of EFW.

2.3. Determination of gestational days

The GDs of the pregnant cynomolgus monkeys were accurately determined through a scheduled process using USG under anaesthesia (10 mg/kg ketamine), referencing previous researches (Abee et al., 2012; Tarantal & Hendrickx, 1988a, 1988c). Within 21–25 days after mating, the assessment of pregnancy began by confirming the presence of key indicators such as gestational sac, yolk sac and cardiac motion. Subsequently, 4–7 days later, the greatest length (GL) was measured to confirm the GD more precisely. Finally, 1 week after the GD confirmation, GL measurements were conducted to ensure the accuracy of GD.

2.4. Data collection

USG was conducted on the pregnant monkeys using a high‐resolution USG machine (LOGIQ e, GE Healthcare Technologies, Inc.) equipped with a 12.0 MHz probe. The settings were optimized for image quality, with a depth of 4–6 cm, and the gain settings were adjusted for clear visualization of foetal structures. Prior to USG, abdominal hair was shaved, and ultrasound gel was applied to facilitate probe‐skin contact. Each foetal parameter was measured once, following standardized measurement protocols (Kuile et al.). Head measurements were obtained from a horizontal section at the level of the thalami and cavum septum pellucidum, that is, transthalamic plane. BPD was measured by placing the caliper's intersection from the outer border of the near skull to the inner edge of the far skull, at the widest part of the skull. HC was derived using an ellipse, encompassing the outer edge of the skull bone at the transthalamic plane. AC was measured in a transverse section of the foetal abdomen, identifying three key abdominal structures: the stomach, umbilical and portal vein and spine. The ellipse tool was applied to draw a line around the outer border of the abdomen. FL measurements were obtained when the entire length of the femur bone was visible in the horizontal plane. The intersection of the calipers was placed at the outer borders of the femoral bone, excluding the trochanter (Figure 1). Single experienced veterinarian (Dong‐Ho Lee) conducted all USG measurements under animal anaesthesia.

FIGURE 1.

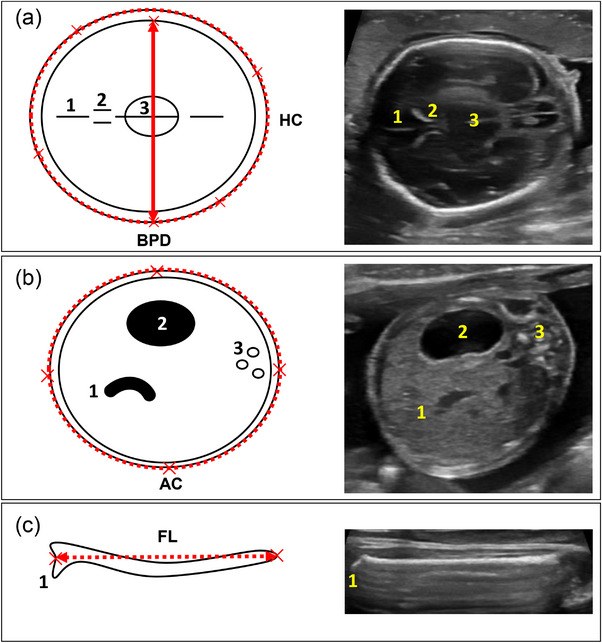
FIGURE 1

Open in a new tab

Schematic diagram and ultrasonography image illustrating the measured foetal parameters. (a) Biparietal diameter (BPD, indicated by a solid bidirectional arrow) and head circumference (HC, represented by a dotted line) with anatomical landmarks: (1) falx cerebri, (2) cavum septum pellucidum and (3) thalamus; (b) Abdominal circumference (AC) alongside labelled structures: (1) umbilical vein connecting to portal vein, (2) stomach and (3) spine; and (c) Femur length (FL) with marked (1) trochanter.

2.5. Estimated foetal weight formulas

The eleven valid and commonly utilized EFW formulas, such as Campbell and Wilkin (1975), Combs et al. (1993), Hadlock (I, II, III, IV, V, VI) (Hadlock et al., 1984, 1985), Ott et al. (1986), Scott et al. (1996) and Shepard et al. (1982) formulas (Table 2), were selected for comparative analysis based on their widespread usage and previous validation in human populations (Abele et al., 2010; Ayad et al., 2016; Chaudhury et al., 2010; Dakwar Shaheen et al., 2019; Hiwale et al., 2019; Hoopmann, Abele et al., 2010; Hoopmann, Bernau et al., 2010; Schild et al., 2004).

TABLE 2.

Foetal weight estimation models employed in the comparative analysis.

Author Components Formula
Campbell AC Ln(EFW) = − 4.564 + 0.282 × AC − 0.00331 × AC2 [kg, cm]
Combs HC, AC, FL EFW = 0.23718 × AC2 × FL + 0.03312 × HC3 [g, cm]
Hadlock I BPD, HC, AC, FL Log(EFW) = 1.3596 + 0.0064 × HC + 0.0424 × AC + 0.174 × FL + 0.00061 × BPD × AC − 0.00386 × AC × FL [g, cm]
Hadlock II AC, FL Log(EFW) = 1.304 + 0.05281 × AC + 0.1938 × FL − 0.004 × AC × FL [g, cm]
Hadlock III BPD, AC, FL Log(EFW) = 1.335 − 0.0034 × AC × FL + 0.0316 × BPD + 0.0457 × AC + 0.1623 × FL [g, cm]
Hadlock IV HC, AC, FL Log(EFW) = 1.326 − 0.00326 × AC × FL + 0.0107 × HC + 0.0438 × AC + 0.158 × FL [g, cm]
Hadlock V BPD, AC Log(EFW) = 1.1134 + 0.05845 × AC − 0.000604 × AC2 − 0.007365 × BPD2 + 0.000595 × BPD × AC + 0.1694 × BPD [g, cm]
Hadlock VI HC, AC, FL Log(EFW) = 1.5662 − 0.0108 × HC + 0.0468 × AC + 0.171 × FL + 0.00034 × HC2 − 0.0003685 × AC × FL [g, cm]
Ott HC, AC, FL Log(EFW) = −2.0661 + 0.04355 × HC + 0.05394 × AC − 0.0008582 × HC × AC + 1.2594 × FL/AC [kg, cm]
Scott HC, AC, FL Log(EFW) = 0.66 × log(HC) + 1.04 × log(AC) + 0.985 × log(FL) [g, cm]
Shepard BPD, AC Log(EFW) = −1.7492 + 0.166 × BPD + 0.046 × AC − 0.002546 × AC × BPD [kg, cm]
Open in a new tab

Abbreviations: AC, abdominal circumference; BPD, biparietal diameter; FL, femur length; HC, head circumference.

2.6. Actual birthweight measurements

The ABW of each fetus was obtained using a calibrated digital scale; the measurements were immediately recorded following the Cesarean section, which was performed under aseptic conditions by a team of experienced veterinarians.

2.7. Statistical analysis

Several statistical methods were applied to evaluate the accuracy and agreement between the EFW and ABW of fetuses (i.e. mean percentage error [PE], mean absolute PE [APE], standard deviation [SD], Pearson's correlation coefficient, significance, the frequency distribution of differences between EFW/ABW and Bland–Altman analysis). The PE and APE were calculated to assess the overall accuracy of the EFW formulas, using the formulas PE = (EFW − ABW)/ABW × 100 and APE = |EFW − ABW|/ABW × 100. Additionally, the SD was computed to analyse the variability within the EFW formulas. These methods have been widely employed in human studies to evaluate the performance of the EFW formulas (Abele et al., 2010; Geerts & Widmer, 2011; Hart et al., 2010; Hiwale et al., 2019; Hoopmann, Abele et al., 2010; Hoopmann, Bernau et al., 2010). Pearson's correlation coefficient was applied to examine the strength and direction of the relationship between EFW and ABW (Dimassi et al., 2015; Schild et al., 2004; Van Mieghem et al., 2009; Warshafsky et al., 2021), and the significance of the correlation was determined using p‐values. Statistical significance was set at p < 0.05. Furthermore, the frequency distribution of differences between EFW and ABW was analysed. Differences were calculated as (EFW − ABW)/ABW and presented as the proportions of cases with discrepancies within ±5%, ±10%, ±15% and ±20% of the ABW. Bland–Altman analysis was employed to assess the mean difference and limits of agreement (Anderson et al., 2007; Bland & Altman, 1986; Chaudhury et al., 2010; Schild et al., 2004), as a high correlation does not necessarily imply good agreement between values (Bland & Altman, 2003; Giavarina, 2015). A strong indication of good agreement in Bland–Altman analysis is generally defined by the presence of 95% of data points falling within the limits of agreement (Bland & Altman, 2003). These statistical analyses were conducted in SPSS version 25 and GraphPad Prism 8, comprehensively evaluating the agreement, accuracy and variability between the EFW and ABW.

3. RESULTS

3.1. Demographic characteristics of pregnant animals and newborns

The demographic data of nine pregnant cynomolgus monkeys are described in Table 3 (i.e., maternal age and weight, parity, GD at USG, newborn sex and ABW). The average weight gain of the monkeys throughout pregnancy was 0.60 ± 0.28 kg (range: 0.20–1.00 kg). The EFW was measured through the USG examinations performed at a mean GD of 130.4 ± 1.2 days (range: 129–132 days). The ABW was measured after Cesarean section the following day. The average ABW was 236.48 ± 28.19 g (range: 200.36–306.08 g).

TABLE 3.

Demographic characteristics of pregnant animals and newborns (n = 9).

Mean ± SD (range) Median
Maternal age (month) 88.9 ± 6.3 (81–102) 88
Nullparity (n) 9
Maternal weight
Before pregnancy (kg) 3.22 ± 0.59 (2.70–4.56) 3.18
Gain during pregnancy (kg) 0.60 ± 0.28 (0.20–1.00) 0.70
The day before delivery (kg) 3.82 ± 0.68 (3.08–5.35) 3.76
GD at USG 130.4 ± 1.2 (129–132) 130
Newborn sex (female:male) 6:3
ABW (g) 236.48 ± 28.19 (200.36–291.33) 233.91
Open in a new tab

Abbreviations: ABW, actual birthweight; GD, gestational day; SD, standard deviation; USG, ultrasonography.

3.2. Comparison of the EFW formulas: PE, APE and correlation analysis

Table 4 compares the EFW derived from the 11 different formulas with the corresponding ABW. The PE ranged from −13.3% (Campbell formula) to 21.1% (Hadlock VI formula). The APE ranged from 4.3% to 21.1%. The Combs formula exhibited the smallest error, whereas the Hadlock VI formula showed the highest error. Among the 11 formulas evaluated, 5 formulas had an APE <10%. The correlation coefficients between EFW and ABW varied among the formulas, with values ranging from 0.714 (Hadlock VI formula) to 0.911 (Combs formula). The Combs formula showed the highest correlation coefficient among all the formulas. Furthermore, all formulas demonstrated statistically significant correlations (p < 0.05), with the Combs formula having the lowest p‐value (p < 0.001).

TABLE 4.

Percentage error, absolute percentage error and correlation between the estimated foetal weight and actual birthweight.

Formula PE (%, mean) APE (%, mean) Correlation coefficients
Combs −3.3 ± 4.6 4.3 ± 3.6 0.911***
Shepard 1.2 ± 6.9 5.8 ± 3.4 0.851**
Hadlock V −5.2 ± 6.0 6.2 ± 4.9 0.854**
Hadlock IV 6.6 ± 8.2 8.7 ± 5.6 0.786*
Scott 7.4 ± 7.8 9.3 ± 4.9 0.811**
Hadlock I 9.1 ± 8.9 10.6 ± 6.7 0.761*
Hadlock III 9.2 ± 9.1 10.7 ± 7.0 0.755*
Ott 11.7 ± 7.3 11.8 ± 7.0 0.895**
Hadlock II 9.7 ± 10.3 12.1 ± 6.9 0.723*
Campbell −13.3 ± 9.3 13.3 ± 9.3 0.804**
Hadlock VI 21.1 ± 11.0 21.1 ± 11.0 0.714*
Open in a new tab

Note: Data are presented as mean ± standard deviation. The results are arranged in accordance with the APE values.

Abbreviations: APE, absolute percentage error; PE, percentage error.

*p < 0.05.

**p< 0.01.

***p < 0.001.

3.3. Distribution of differences between the EFW and ABW

Table 5 presents the frequency distribution according to the differences between the EFW and ABW for each formula. Among the considered formulas, only the Combs and Shepard formula exhibited the difference within 10% or less in a high proportion, approximately 90%. Specifically, based on the Combs formula, all cases showed the difference 10% or less. In contrast, when using the Hadlock VI formula, the difference within 10% or less between EFW and ABW was present in only 11.1% of the study subjects.

TABLE 5.

The frequency of study population distribution according to the differences between the estimated foetal weight (EFW) and actual birthweight (ABW).

Formula Difference between EFW and ABW ≤5% ≤10% ≤15% ≤20%
Combs 66.7% 100.0% 100.0% 100.0%
Shepard 33.3% 88.9% 100.0% 100.0%
Hadlock V 55.6% 66.7% 100.0% 100.0%
Hadlock IV 22.2% 66.7% 88.9% 100.0%
Scott 22.2% 66.7% 88.9% 100.0%
Hadlock I 22.2% 44.4% 88.9% 88.9%
Hadlock III 11.1% 55.6% 88.9% 88.9%
Ott 22.2% 44.4% 55.6% 100.0%
Hadlock II 11.1% 33.3% 88.9% 88.9%
Campbell 22.2% 44.4% 44.4% 88.9%
Hadlock VI 11.1% 11.1% 22.2% 33.3%
Open in a new tab

Note: The results are organized based on the absolute percentage error values, as listed in Table 4.

3.4. Assessing agreement between the EFW and ABW: Bland–Altman analysis

The Bland–Altman analysis revealed the mean difference and limits of agreement between the EFW and ABW (Figure 2). Although all data points fell within the limits of agreement indicating a good agreement between the EFW and ABW in the seven formulas such as Combs, Shepard, Hadlock V, Hadlock IV, Hadlock I, Hadlock III and Ott, 95% of the data points did not fall within the limits of agreement in the remaining four formulas (i.e. Scott, Hadlock II, Campbell and Hadlock VI).

FIGURE 2.

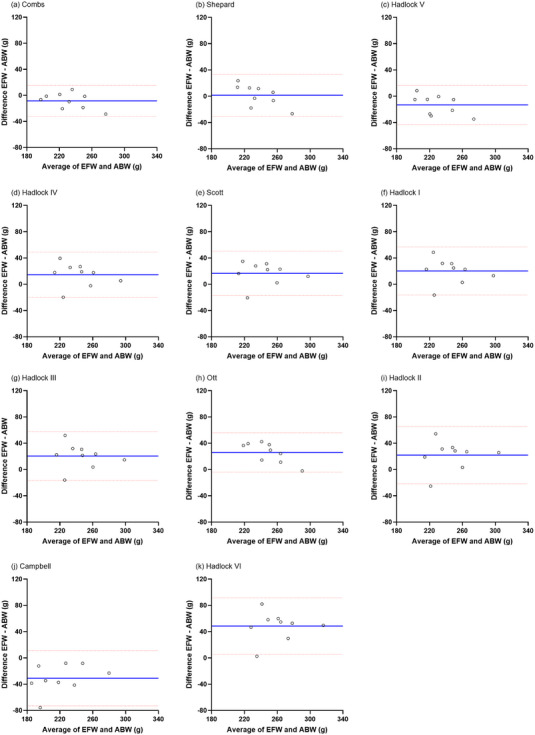
FIGURE 2

Open in a new tab

Bland–Altman plot demonstrating the agreement between estimated foetal weight (EFW) and actual birthweight (ABW). The plots include: (a) Combs, (b) Shepard, (c) Hadlock V, (d) Hadlock IV, (e) Scott, (f) Hadlock I, (g) Hadlock III, (h) Ott, (i) Hadlock II, (j) Campbell, and (k) Hadlock VI. The blue line represents the mean difference between EFW and ABW (in g), and the red dotted lines indicate the limits of agreement (±1.96 standard deviation [SD]). Figures are organized according to the absolute percentage error (APE) values listed in Table 4.

4. DISCUSSION

4.1. Principal observations of the study

In this study, we applied 11 well‐established EFW formulas in human obstetric clinical practice to cynomolgus monkey fetuses at approximately 130 days of gestation. The Combs formula demonstrated the most favourable results among the 11 formulas.

4.2. Limitation of previous studies

Although previous studies have primarily focused on assessing foetal development in cynomolgus monkeys (Tarantal & Hendrickx, 1988a, 1988b, 1988c, 1988d) and other non‐human primate species (Conrad et al., 1995; D'Mello et al., 2023; Lee et al., 1991; Redmond & Evans, 2012), they have predominantly measured specific parameters using USG, such as BPD, but not the EFW. Indeed, in veterinary research, estimating foetal weight is not commonly practiced. Instead, researchers tend to directly measure the foetal weight usually through Caesarean section (Chellman et al., 2009; Roberts et al., 2023).

4.3. How does the combs formula perform in humans and other non‐human primate species?

The EFW formula with an APE less than 10% is considered accurate (Nguyen et al., 2012). Among the applied formulas in our study, 10% or less in an APE was present in five formulas, and especially, the Combs formula demonstrated the most outstanding performance capability for estimating the weight of cynomolgus monkey fetuses at approximately 130 GD in our study (Tables 4 and 5).

The Combs formula was initially reported to provide accurate estimates at the extremes as well as the normal range of human foetal weight (Combs et al., 1993). However, the accuracy of the Combs formula varies in small human fetuses, with subsequent studies reporting high accuracy (Esinler et al., 2015; Eze et al., 2015; Warshafsky et al., 2021), whereas others report lower accuracy (Abele et al., 2010; Dudley, 2005; Hammami et al., 2018; Hiwale, 2017; Warrander et al., 2020). It is noteworthy that some studies demonstrate high accuracy, despite the potential for decreased precision when EFW formula is applied to populations different from those for which the formula was initially developed (Akinola et al., 2009). Parameters, such as AC, FL and HC, exhibit remarkable similarities between humans and cynomolgus monkeys up to mid‐pregnancy (Figure S1), highlighting the foetal morphological and developmental similarities between the two species. Direct evidence of the performance of the Combs formula in cynomolgus monkeys may be limited. However, given these observations, the Combs formula's accuracy in estimating the weight of small human fetuses, along with biological similarities, suggests a possible basis for its application to cynomolgus monkeys.

In a study on baboons (Papio anubis) (Van Calsteren et al., 2009), another species of Old World monkeys (Table S1), the Combs formula was the most accurate among the compared formulas for estimating foetal weight. However, the baboon study differs from our study in the following aspects: (1) the baboon study showed a broader GD range 71–167, compared to GD range of 130–133 in our study (Figure S2); (2) There was a 3‐day gap in the baboon study between USG and ABW measurements, whereas our study had a noticeably shorter 16‐h interval. This 3‐day interval is a critical weakness, as the fetus continues to develop during this period. Although obtaining USG measurements on the day of delivery might pose challenges, a shorter interval between USG and ABW measurements results in a more meaningful temporal relationship. Interestingly, this baboon study also demonstrated high accuracy within the GD range of 122–142 days, which is similar to our results (Table S2). This suggests that the Combs formula for EFW can be applied both to cynomolgus monkeys and to other species at approximately 130 days of gestation.

4.4. Application of the combs formula to previous studies in cynomolgus monkey

Chellman et al.’s (2009) study documented the body weight and foetal parameters of cynomolgus monkey fetuses at GD 100 in the context of DART study. However, it is important to acknowledge methodological differences between our and Chellman et al.’s study as follows: (1) foetal parameters were measured directly, not with USG and (2) AC was not measured in Chellman et al.’s study. Of note, chest circumference might be replaceable in place of AC in the Combs formula, considering there was no significant difference between the two foetal parameters (Johnson et al., 1987; Roberts et al., 2023). We found substituting these foetal parameter values in Chellman et al.’s study into the Combs formula revealed a close resemblance between the EFW and the body weight, with an APE of 1.1% (Table S3). Therefore, our observation indicates the potential applicability of the Combs formula to cynomolgus monkey fetuses at GD 100.

Moreover, the application of previously published foetal biometric parameters to the Combs formula may make it possible to predict EFW between GD 110 and GD 165 in cynomolgus monkeys. Therefore, we can estimate GD through the newborn body weight based on the predicted value for foetal weight (Figure S3). Determining the GD, especially in cases of preterm birth or stillbirth with the unknown exact GD, offers valuable information for the researchers and veterinarians managing pregnant cynomolgus monkeys and their fetuses.

4.5. Strengths and weaknesses of the study

The major strengths of the study are as follows: (1) Our study possesses distinct benefits from only a 16 h difference between the USG measurement and the ABW confirmation. This is in marked contrast to previous studies in human populations, where differences of over 2 days resulted in nearly 50% variances in the performance of foetal weight formulas (Hoopmann, Abele et al., 2010). This reduced time gap between USG measurements and weight confirmation in our study enhances the precision and reliability of our evaluation of foetal weight formulas; (2) All USG examinations performed by a single operator (Dong‐Ho Lee, D.V.M.) ensure a consistent and standardized measurement approach throughout this study. This eliminates inter‐observer variability, which can occur when multiple examiners are involved (Chang et al., 1993; Westerway, 2012), and results in more reliable and reproducible results. The weaknesses of our study are as follows. One weakness of our study is the relatively small sample size, which may restrict the generalizability of our observations to larger subjects. Another weakness of our study is that it is limited to the USG measurement at GD 129–132, but not during the entire pregnancy. Fetuses at these specific GD of late pregnancy may have different growth patterns and characteristics from those of early or mid‐pregnancy (Tarantal et al., 1995). Therefore, the results obtained at GD 129–132 in our study may not fully represent the accuracy and variability of the EFW formulas at different GDs in cynomolgus monkeys.

4.6. Unanswered questions and proposals for future study

Whether the Combs formula is applicable across all GDs in cynomolgus monkeys remains unproven, and subsequently, further confirmation of its applicability throughout the pregnancy with a specialized formula is necessary. Moreover, the applicability of the formula to other non‐human primate species needs to be verified. Finally, a multidisciplinary team approach (i.e. researchers, veterinarians and statisticians) is essential for improving the accuracy and reliability of weight estimation formulas.

5. CONCLUSION

To the best of our knowledge, this is the first study to apply a weight formula designed for human fetuses to cynomolgus monkey fetuses and investigate its accuracy. It has been confirmed that among the human EFW formulas, the Combs formula is sufficiently applicable to cynomolgus monkeys at approximately GD 130. These observations contribute to the cynomolgus monkey management and research, providing a foundation for developing new EFW methods tailored for this species.

AUTHOR CONTRIBUTIONS

Dong‐Ho Lee: Investigation; data curation; formal analysis; methodology; visualization; writing – original draft preparation; writing – review and editing. Seung‐Bin Yoon: Investigation; formal analysis; writing – original draft preparation. Jun Won Mo and Sang Il Lee: Investigation; resources. Yu‐Jin Jo and Jeongwoo Kwon: Investigation; visualization. Ji‐Su Kim: Funding acquisition; project administration; writing – review and editing. Jungkee Kwon: Conceptualization; supervision; project administration; writing – review and editing. Chan‐Wook Park: Conceptualization; funding acquisition; methodology; supervision; project administration; writing – review and editing.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

ETHICS STATEMENT

The authors confirm that the ethical policies of the journal, as noted on the journal's author guidelines page, have been adhered to and the appropriate ethical review committee approval has been received. The study was approved by the Institutional Animal Care and Use Committee (IACUC) of the Korea Research Institute of Bioscience and Biotechnology (KRIBB).

PEER REVIEW

The peer review history for this article is available at https://www.webofscience.com/api/gateway/wos/peer-review/10.1002/vms3.1521.

Supporting information

Supporting Information

VMS3-10-e1521-s001.docx (394.2KB, docx)

ACKNOWLEDGEMENTS

The authors would like to express heartfelt gratitude to Taehyun Kim, Yoojin Kim and Young Jeon from GE Healthcare Korea for their invaluable assistance and unwavering support. This research was supported by the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HI21C1871) and by a grant from the Korea Research Institute of Bioscience and Biotechnology (KRIBB) Research Initiative Program (KGM5162423).

Lee, D.‐H. , Yoon, S.‐B. , Kim, J.‐S. , Mo, J. W. , Jo, Y.‐J. , Kwon, J. , Lee, S. I. , Kwon, J. , & Park, C.‐W. (2024). Application of ultrasonographic human estimated foetal weight formulas to cynomolgus monkeys (Macaca fascicularis) at 129–132 days of gestation: A comparative study of estimated and actual birthweight. Veterinary Medicine and Science, 10, e1521. 10.1002/vms3.1521

Dong‐Ho Lee and Seung‐Bin Yoon contributed equally to this work.

Contributor Information

Jungkee Kwon, Email: jkwon@jbnu.ac.kr.

Chan‐Wook Park, Email: cspark99@snu.ac.kr.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

REFERENCES

  1. Abee, C. R. , Mansfield, K. , Tardif, S. D. , & Morris, T. (2012). Nonhuman primates in biomedical research: Biology and management. Academic Press. [Google Scholar]
  2. Abele, H. , Hoopmann, M. , Wagner, N. , Hahn, M. , Wallwiener, D. , & Kagan, K. O. (2010). Accuracy of sonographic fetal weight estimation of fetuses with a birth weight of 1500 g or less. European Journal of Obstetrics Gynecology and Reproductive Biology, 153, 131–137. [DOI] [PubMed] [Google Scholar]
  3. Akinola, R. , Akinola, O. , & Oyekan, O. (2009). Sonography in fetal birth weight estimation. Educational Research and Review, 4, 16–20. [Google Scholar]
  4. Anderson, N. G. , Jolley, I. J. , & Wells, J. E. (2007). Sonographic estimation of fetal weight: Comparison of bias, precision and consistency using 12 different formulae. Ultrasound in Obstetrics & Gynecology, 30, 173–179. [DOI] [PubMed] [Google Scholar]
  5. Ayad, C. E. , Ibrahim, A. A. M. , Garelnabi, M. E. M. , Ahmed, B. H. , Abdalla, E. A. , & Saleem, M. A. E. (2016). Assessment of used formulae for sonographic estimation of fetal weight in sudanese population. Open Journal of Radiology, 6, 113–120. [Google Scholar]
  6. Bland, J. M. , & Altman, D. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. The Lancet, 327, 307–310. [PubMed] [Google Scholar]
  7. Bland, J. M. , & Altman, D. G. (2003). Applying the right statistics: Analyses of measurement studies. Ultrasound in Obstetrics & Gynecology, 22, 85–93. [DOI] [PubMed] [Google Scholar]
  8. Blencowe, H. , Cousens, S. , Chou, D. , Oestergaard, M. , Say, L. , Moller, A. B. , Kinney, M. , & Lawn, J. , Born Too Soon Preterm Birth Action Group . (2013). Born too soon: The global epidemiology of 15 million preterm births. Reproductive Health, 10(Suppl 1), S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Boulet, S. L. , Alexander, G. R. , Salihu, H. M. , & Pass, M. (2003). Macrosomic births in the United States: Determinants, outcomes, and proposed grades of risk. American Journal of Obstetrics and Gynecology, 188, 1372–1378. [DOI] [PubMed] [Google Scholar]
  10. Campbell, S. , & Wilkin, D. (1975). Ultrasonic measurement of fetal abdomen circumference in the estimation of fetal weight. British Journal of Obstetrics and Gynaecology, 82, 689–697. [DOI] [PubMed] [Google Scholar]
  11. Chang, T. , Robson, S. C. , Spencer, J. A. , & Gallivan, S. (1993). Ultrasonic fetal weight estimation: Analysis of inter‐and intra‐observer variability. Journal of Clinical Ultrasound, 21, 515–519. [DOI] [PubMed] [Google Scholar]
  12. Chaudhury, P. , Haeri, S. , Horton, A. L. , Wolfe, H. M. , & Goodnight, W. H. (2010). Ultrasound prediction of birthweight and growth restriction in fetal gastroschisis. American Journal of Obstetrics and Gynecology, 203, e391–395. [DOI] [PubMed] [Google Scholar]
  13. Chauhan, S. P. , Hendrix, N. W. , Magann, E. F. , Morrison, J. C. , Kenney, S. P. , & Devoe, L. D. (1998). Limitations of clinical and sonographic estimates of birth weight: experience with 1034 parturients. Obstetrics & Gynecology, 91, 72–77. [DOI] [PubMed] [Google Scholar]
  14. Chellman, G. J. , Bussiere, J. L. , Makori, N. , Martin, P. L. , Ooshima, Y. , & Weinbauer, G. F. (2009). Developmental and reproductive toxicology studies in nonhuman primates. Birth Defects Research Part B: Developmental and Reproductive Toxicology, 86, 446–462. [DOI] [PubMed] [Google Scholar]
  15. Combs, C. A. , Jaekle, R. K. , Rosenn, B. , Pope, M. , Miodovnik, M. , & Siddiqi, T. A. (1993). Sonographic estimation of fetal weight based on a model of fetal volume. Obstetrics and Gynecology, 82, 365–370. [PubMed] [Google Scholar]
  16. Conrad, S. , Ha, J. , Lohr, C. , & Sackett, G. (1995). Ultrasound measurement of fetal growth in Macaca nemestrina . American Journal of Primatology, 36, 15–35. [DOI] [PubMed] [Google Scholar]
  17. D'Mello, R. J. , Lo, J. O. , Hagen, O. L. , Castro, J. N. , Graham, J. A. , Frias, A. E. , & Roberts, V. H. J. (2023). Ultrasound evaluation of normal rhesus macaque fetal biometry and uteroplacental hemodynamics. American Journal of Primatology, 85, e23504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dakwar Shaheen, J. , Hershkovitz, R. , Mastrolia, S. A. , Charach, R. , Eshel, R. , Tirosh, D. , Shaheen, N. , & Baron, J. (2019). Estimation of fetal weight using Hadlock's formulas: Is head circumference an essential parameter? European Journal of Obstetrics Gynecology and Reproductive Biology, 243, 87–92. [DOI] [PubMed] [Google Scholar]
  19. Dimassi, K. , Douik, F. , Ajroudi, M. , Triki, A. , & Gara, M. F. (2015). Ultrasound fetal weight estimation: How accurate are we now under emergency conditions? Ultrasound in Medicine & Biology, 41, 2562–2566. [DOI] [PubMed] [Google Scholar]
  20. Dudley, N. (2005). A systematic review of the ultrasound estimation of fetal weight. Ultrasound in Obstetrics and Gynecology, 25, 80–89. [DOI] [PubMed] [Google Scholar]
  21. Esinler, D. , Bircan, O. , Esin, S. , Sahin, E. G. , Kandemir, O. , & Yalvac, S. (2015). Finding the best formula to predict the fetal weight: Comparison of 18 formulas. Gynecologic and Obstetric Investigation, 80, 78–84. [DOI] [PubMed] [Google Scholar]
  22. Eze, C. U. , Egwuanumku, K. I. , Agwuna, K. K. , Odidi, L. , Ochie, K. , & Nwadike, I. U. (2015). Validity of common ultrasound methods of fetal weight estimation in late pregnancy among women in Kwale, Niger Delta region, Nigeria. African Health Sciences, 15, 206–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Geerts, L. , & Widmer, T. (2011). Which is the most accurate formula to estimate fetal weight in women with severe preterm preeclampsia? The Journal of Maternal‐Fetal & Neonatal Medicine, 24, 271–279. [DOI] [PubMed] [Google Scholar]
  24. Giavarina, D. (2015). Understanding Bland Altman analysis. Biochemia Medica, 25, 141–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hadlock, F. P. , Harrist, R. B. , Carpenter, R. J. , Deter, R. L. , & Park, S. K. (1984). Sonographic estimation of fetal weight. The value of femur length in addition to head and abdomen measurements. Radiology, 150, 535–540. [DOI] [PubMed] [Google Scholar]
  26. Hadlock, F. P. , Harrist, R. B. , Sharman, R. S. , Deter, R. L. , & Park, S. K. (1985). Estimation of fetal weight with the use of head, body, and femur measurements—A prospective study. American Journal of Obstetrics and Gynecology, 151, 333–337. [DOI] [PubMed] [Google Scholar]
  27. Hammami, A. , Mazer Zumaeta, A. , Syngelaki, A. , Akolekar, R. , & Nicolaides, K. H. (2018). Ultrasonographic estimation of fetal weight: Development of new model and assessment of performance of previous models. Ultrasound in Obstetrics & Gynecology, 52, 35–43. [DOI] [PubMed] [Google Scholar]
  28. Hart, N. C. , Hilbert, A. , Meurer, B. , Schrauder, M. , Schmid, M. , Siemer, J. , Voigt, M. , & Schild, R. L. (2010). Macrosomia: A new formula for optimized fetal weight estimation. Ultrasound in Obstetrics & Gynecology, 35, 42–47. [DOI] [PubMed] [Google Scholar]
  29. Hiwale, S. S. (2017). A systematic evaluation of ultrasound‐based fetal weight estimation models on Indian population. Journal of Medical Ultrasound, 25, 201–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hiwale, S. , Misra, H. , & Ulman, S. (2019). Fetal weight estimation by ultrasound: Development of Indian population‐based models. Ultrasonography, 38, 50–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hoopmann, M. , Abele, H. , Wagner, N. , Wallwiener, D. , & Kagan, K. O. (2010). Performance of 36 different weight estimation formulae in fetuses with macrosomia. Fetal Diagnosis and Therapy, 27, 204–213. [DOI] [PubMed] [Google Scholar]
  32. Hoopmann, M. , Bernau, B. , Hart, N. , Schild, R. , & Siemer, J. (2010). Do specific weight formulas for fetuses ≤1500 g really improve weight estimation? Ultraschall in der Medizin‐European Journal of Ultrasound, 31, 48–52. [DOI] [PubMed] [Google Scholar]
  33. Husslein, H. , Worda, C. , Leipold, H. , & Szalay, S. (2012). Accuracy of fetal weight estimation in women with diet controlled gestational diabetes. Geburtshilfe und Frauenheilkunde, 72, 144–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Jang, H. Y. , Kwak, J. , Lee, S. J. , Wu, J. , Jiang, H. , Choi, E. S. , Park, C. W. , Kang, B. C. , & Kim, J. H. (2023). Ultrasonographic monitoring of fetal eye growth parameters throughout gestation in the common marmoset (Callithrix jacchus). American Journal of Primatology, 85, e23532. [DOI] [PubMed] [Google Scholar]
  35. Jaquish, C. E. , Toal, R. L. , Tardif, S. D. , & Carson, R. L. (1995). Use of ultrasound to monitor prenatal growth and development in the common marmoset (Callithrix jacchus). American Journal of Primatology, 36, 259–275. [DOI] [PubMed] [Google Scholar]
  36. Johnson, A. , Callan, N. A. , Bhutani, V. K. , Colmorgen, G. H. , Weiner, S. , & Bolognese, R. J. (1987). Ultrasonic ratio of fetal thoracic to abdominal circumference: An association with fetal pulmonary hypoplasia. American Journal of Obstetrics and Gynecology, 157, 764–769. [DOI] [PubMed] [Google Scholar]
  37. Kähn, W. (1992). Ultrasonography as a diagnostic tool in female animal reproduction. Animal Reproduction Science, 28, 1–10. [Google Scholar]
  38. Khatti, A. , Jena, D. , Singh, S. K. , Mondal, T. , & Singh, S. V. (2017). Application of ultrasonography in canine pregnancy—An overview. International Journal of Livestock Research, 7, 20–27. [Google Scholar]
  39. Kiserud, T. , Piaggio, G. , Carroli, G. , Widmer, M. , Carvalho, J. , Neerup Jensen, L. , Giordano, D. , Cecatti, J. G. , Abdel Aleem, H. , Talegawkar, S. A. , Benachi, A. , Diemert, A. , Tshefu Kitoto, A. , Thinkhamrop, J. , Lumbiganon, P. , Tabor, A. , Kriplani, A. , Gonzalez Perez, R. , Hecher, K. , … Platt, L. D. (2017). The World Health Organization fetal growth charts: A multinational longitudinal study of ultrasound biometric measurements and estimated fetal weight. PLOS Medicine, 14, e1002220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Kuile, F. T. , Tinto, H. , Sevene, E. , Dellicour, S. , d'Alessandro, U. , Stergachis, A. , & Sangaré, L. (2012). Ultrasound Reference Manual for Pregnancy Dating. Malaria in Pregnancy Consortium. https://stacks.cdc.gov/view/cdc/36626/cdc_36626_DS5.pdf
  41. Lee, D. R. , Kuehl, T. J. , & Eichberg, J. W. (1991). Real‐time ultrasonography as a clinical and management tool to monitor pregnancy in a chimpanzee breeding colony. American Journal of Primatology, 24(3–4), 289–294. [Google Scholar]
  42. Li, J. , Zhu, Q. , Cao, J. , Liu, Y. , Lu, Y. , Sun, Y. , Li, Q. , Huang, Y. , Shang, S. , Bian, X. , Li, C. , Zhang, L. , Wang, Y. , Nie, Y. , Fu, J. , Li, W. , Mazid, M. A. , Jiang, Y. , Jia, W. , … Liu, Z. (2023). Cynomolgus monkey embryo model captures gastrulation and early pregnancy. Cell Stem Cell, 30, 362–377.e367. [DOI] [PubMed] [Google Scholar]
  43. Lopate, C. (2008). Estimation of gestational age and assessment of canine fetal maturation using radiology and ultrasonography: A review. Theriogenology, 70, 397–402. [DOI] [PubMed] [Google Scholar]
  44. Morgan, P. M. , Hutz, R. J. , Kraus, E. M. , Cormie, J. A. , Dierschke, D. J. , & Bavister, B. D. (1987). Evaluation of ultrasonography for monitoring follicular growth in rhesus monkeys. Theriogenology, 27, 769–780. [DOI] [PubMed] [Google Scholar]
  45. Nguyen, T. M. , Nakamura, H. , Wakabayashi, A. , Kanagawa, T. , Koyama, S. , Tsutsui, T. , Hamasaki, T. , & Kimura, T. (2012). Estimation of mouse fetal weight by ultrasonography: Application from clinic to laboratory. Laboratory Animals, 46, 225–230. [DOI] [PubMed] [Google Scholar]
  46. Oerke, A. K. , Einspanier, A. , & Hodges, J. K. (1996). Noninvasive monitoring of follicle development, ovulation, and corpus luteum formation in the marmoset monkey (Callithrix jacchus) by ultrasonography. American Journal of Primatology, 39, 99–113. [DOI] [PubMed] [Google Scholar]
  47. Ortega‐Ferrusola, C. , Gómez‐Arrones, V. , Martín‐Cano, F. E. , Gil, M. C. , Peña, F. J. , Gaitskell‐Phillips, G. , & Da Silva‐Álvarez, E. (2022). Advances in the ultrasound diagnosis in equine reproductive medicine: New approaches. Reproduction in Domestic Animals, 57, 34–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Osterman, M. , Brady, E. , Martin, J A. , Driscoll, A K. , & Valenzuela, C P. (2023). Births: Final data for 2021. National Vital Statistics Reports, 72(1), 1–53. [PubMed] [Google Scholar]
  49. Ott, W. J. , Doyle, S. , & Flamm, S. (1986). Accurate ultrasonic estimation of fetal weight. Effect of head shape, growth patterns, and amniotic fluid volume. American Journal of Perinatology, 3, 193–197. [DOI] [PubMed] [Google Scholar]
  50. Redmond D. E., Jr. , & Evans, L. (2012). Determination of fetal age by ultrasonography in St. Kitts green monkeys. American Journal of Primatology, 74, 433–441. [DOI] [PubMed] [Google Scholar]
  51. Reef, V. B. , Vaala, W. E. , Worth, L. T. , Sertich, P. L. , & Spencer, P. A. (1996). Ultrasonographic assessment of fetal well‐being during late gestation: Development of an equine biophysical profile. Equine Veterinary Journal, 28, 200–208. [DOI] [PubMed] [Google Scholar]
  52. Roberts, V. H. , Castro, J. N. , Wessel, B. M. , Conrad, D. F. , Lewis, A. D. , & Lo, J. O. (2023). Rhesus macaque fetal and placental growth demographics: A resource for laboratory animal researchers. American Journal of Primatology, 85(8), e23526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Schild, R. L. , Fell, K. , Fimmers, R. , Gembruch, U. , & Hansmann, M. (2004). A new formula for calculating weight in the fetus of < or = 1600 g. Ultrasound in Obstetrics & Gynecology, 24, 775–780. [DOI] [PubMed] [Google Scholar]
  54. Scott, F. , Beeby, P. , Abbott, J. , Edelman, D. , & Boogert, A. (1996). New formula for estimating fetal weight below 1000 g: Comparison with existing formulas. Journal of Ultrasound in Medicine, 15, 669–672. [DOI] [PubMed] [Google Scholar]
  55. Shepard, M. J. , Richards, V. A. , Berkowitz, R. L. , Warsof, S. L. , & Hobbins, J. C. (1982). An evaluation of two equations for predicting fetal weight by ultrasound. American Journal of Obstetrics and Gynecology, 142, 47–54. [DOI] [PubMed] [Google Scholar]
  56. Skinner, C. , & Mount, C. A. (2023). Sonography assessment of gestational age. StatPearls. [PubMed] [Google Scholar]
  57. Tarantal, A. F. (1990). Interventional ultrasound in pregnant macaques: Embryonic/fetal applications. Journal of Medical Primatology, 19, 47–58. [PubMed] [Google Scholar]
  58. Tarantal, A. , Gargosky, S. , Ellis, D. , O'Brien, W. Jr. , & Hendrickx, A. (1995). Hematologic and growth‐related effects of frequent prenatal ultrasound exposure in the long‐tailed macaque (Macaca fascicularis). Ultrasound in Medicine & Biology, 21, 1073–1081. [DOI] [PubMed] [Google Scholar]
  59. Tarantal, A. F. , & Hendrickx, A. G. (1988a). Characterization of prenatal growth and development in the crab‐eating macaque (Macaca fascicularis) by ultrasound. Anatomical Record, 222, 177–184. [DOI] [PubMed] [Google Scholar]
  60. Tarantal, A. F. , & Hendrickx, A. G. (1988b). Prenatal growth in the cynomolgus and rhesus macaque (Macaca fascicularis and Macaca mulatta): A comparison by ultrasonography. American Journal of Primatology, 15, 309–323. [DOI] [PubMed] [Google Scholar]
  61. Tarantal, A. F. , & Hendrickx, A. G. (1988c). The use of ultrasonography for evaluating pregnancy in macaques. In Non‐human primates—Developmental biology and toxicology Ueberreuter Wissenschaft, Berlin (pp. 91–111) Open Library. [Google Scholar]
  62. Tarantal, A. F. , & Hendrickx, A. G. (1988d). Use of ultrasound for early pregnancy detection in the rhesus and cynomolgus macaque (Macaca mulatta and Macaca fascicularis). Journal of Medical Primatology, 17, 105–112. [PubMed] [Google Scholar]
  63. Ugwa, E. A. , Gaya, S. , & Ashimi, A. (2015). Estimation of fetal weight before delivery in low‐resource setting of North‐west Nigeria: Can we rely on our clinical skills? The Journal of Maternal‐Fetal & Neonatal Medicine, 28, 949–953. [DOI] [PubMed] [Google Scholar]
  64. Van Calsteren, K. , De Catte, L. , Devlieger, R. , Chai, D. , & Amant, F. (2009). Sonographic biometrical normograms and estimation of fetal weight in the baboon (Papio anubis). Journal of Medical Primatology, 38, 321–327. [DOI] [PubMed] [Google Scholar]
  65. Van Mieghem, T. , Deprest, J. , Klaritsch, P. , Gucciardo, L. , Done, E. , Verhaeghe, J. , & Lewi, L. (2009). Ultrasound prediction of intertwin birth weight discordance in monochorionic diamniotic twin pregnancies. Prenatal Diagnosis, 29, 240–244. [DOI] [PubMed] [Google Scholar]
  66. VandeVoort, C. A. , & Tarantal, A. F. (1991). The macaque model for in vitro fertilization: Superovulation techniques and ultrasound‐guided follicular aspiration. Journal of Medical Primatology, 20, 110–116. [PubMed] [Google Scholar]
  67. Walani, S. R. (2020). Global burden of preterm birth. International Journal of Gynaecology and Obstetrics, 150, 31–33. [DOI] [PubMed] [Google Scholar]
  68. Warrander, L. K. , Ingram, E. , Heazell, A. E. , & Johnstone, E. D. (2020). Evaluating the accuracy and precision of sonographic fetal weight estimation models in extremely early‐onset fetal growth restriction. Acta Obstetricia et Gynecologica Scandinavica, 99, 364–373. [DOI] [PubMed] [Google Scholar]
  69. Warshafsky, C. , Ronzoni, S. , Quaglietta, P. , Weiner, E. , Zaltz, A. , Barrett, J. , Melamed, N. , & Aviram, A. (2021). Comparison of sonographic fetal weight estimation formulas in patients with preterm premature rupture of membranes. BMC Pregnancy and Childbirth, 21, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Westerway, S. C. (2012). Estimating fetal weight for best clinical outcome. Australasian Journal of Ultrasound in Medicine, 15, 13–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Wolfe‐Coote, S. (2005). The laboratory primate. Elsevier. [Google Scholar]
  72. Woo, J. (2002). A short history of the development of ultrasound in obstetrics and gynecology. History of Ultrasound in Obstetrics and Gynecology, 3, 1–25. [Google Scholar]
  73. World Health Organization (WHO) . (2023a). Born too soon: Decade of action on preterm birth . World Health Organization. [Google Scholar]
  74. World Health Organization (WHO) . (2023b). Preterm birth . World Health Organization. https://www.who.int/news‐room/fact‐sheets/detail/preterm‐birth [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information

VMS3-10-e1521-s001.docx (394.2KB, docx)

Data Availability Statement

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Articles from Veterinary Medicine and Science are provided here courtesy of Wiley

RESOURCES