Physical analysis of aspirin in different phases and states using density functional theory

Abstract

This study analyzed the aspirin molecule (C9H8O4) using Density Functional Theory (DFT) on Gaussian 09W software. First, the structure of aspirin was optimized using the DFT method with the B3LYP functional and the 6-311+G (d,p) basis set. A global reactivity study was employed to understand the reactivity of aspirin in gas and solvent water for both anion and neutral states. To understand the involvement of orbitals in chemical stability and electron conductivity, we calculated the HOMO-LUMO. The thermodynamic function of a molecule was understood using thermochemistry. Molecular Electrostatic Potential (MEP) was employed to understand the physiochemical properties of aspirin. We observed the Mulliken atomic charge to calculate the atomic charge of aspirin. Finally, the title molecule's UV–Vis, FTIR, and Raman spectra are analyzed and compared with the experimental data.

1. Introduction

Aspirin, also known as acetylsalicylic acid, is an aromatic homocyclic compound prepared through the chemical synthesis of salicylic acid through acetylation and acetic anhydride. Aspirin is a non-narcotic drug widely used for medical purposes [1]. Aspirin is an odorless, white crystalline powder with the chemical formula C9H8O4. Aspirin is an analgesic, an antipyretic drug that reduces cardiovascular disease (CVD) and strokes by preventing blood clots [2,3]. Aspirin is a non-steroid anti-inflammatory drug (NSAIDs). It prevents the activity of an enzyme called cyclooxygenase (COX), which forms prostaglandins (PGs), leading to inflammation, swelling, pain, and fever. Aspirin may help prevent some cancers, especially colorectal cancer. Aspirin-containing metal complex crystals have additional therapeutic properties in biological systems, including anti-ulcer, anti-cancer, antimutagenic, and antioxidative properties. Some effects of using aspirin could include an increased risk of renal insufficiency and worsening of hypertension control [[4], [5], [6]].

Previously, computational studies have been conducted on researching and discovering medical drugs [7]. Similarly, aspirin molecules have gone through numerous computational studies, like in the research paper D.A. Safin et al. explored computational analysis of aspirin molecules, where the molecular docking method was employed to understand the interaction of aspirin with the SARS-COV-2 protein [8]. Rashid et al. performed geometry optimization, MEP, Mulliken charge distribution, and global reactivity descriptor of aspirin, and a molecular docking study was carried out with the human COX-2 enzyme in the basis set of 6-31G (d,p) [9]. V. Renganayaki et al. worked on computational FTIR spectroscopy of aspirin using semi-empirical methods “Austin model 1” and “parametric method 3” and compared them with experimental data. It resulted in a minimal difference in computational and experimental data for the wave number of most fundamental modes [10]. R. Mathew et al. studied a combined experimental and computational approach to distinguish between polymorphs of aspirin. They used AIRRS (a DFT-based structure prediction method) and NMR techniques to identify the molecular environment of polymorphs present in the sample [11].

DFT is a computational method that aids experimental research, providing insights into their structure, dynamics, and interaction. It bridges the gap between theory and experiment, accelerating understanding and developing discoveries. DFT analysis aids hypothesis generation, targeted experiment design, optimized conditions, and cost and time savings [12].

These works inspired us to study the aspirin molecule; we created the optimized aspirin molecule using the Density Functional Theory (DFT) method with B3LYP/6-311+G (d,p) basis set, where we have analyzed the physical properties, including Global reactivity descriptors, Frontier Molecular Orbitals, DOS, MEP, Mulliken atomic charge of aspirin. We compared those properties for different neutral and anionic states in different phases, such as the gas phase and solvent water. Vibrational spectroscopy, like FTIR, Raman, and UV–Vis spectroscopy, was studied and compared for the same parameters. To the best of our knowledge, these properties of aspirin have not been studied in terms of its anion state or the water solvent.

2. Methodology

In this research, the quantum physical calculation was performed by adopting the DFT method using the Becke-3-Lee–Yang–Parr (B3LYP) with 6-311+G (d,p) basis set that is implemented in the Gaussian 09W program package [[13], [14], [15], [16]]. Further structural optimization was achieved through Gauss View 5.0.8 software [17]. The optimized structure was employed to calculate vibrational analysis, and Potential Energy Distribution (PED) and Raman spectroscopy were calculated using the VEDA 4.0 program [18]. The graphs of electronic absorption spectra were obtained through GaussSum 3.0 software [19].

3. Result and discussion

3.1. Optimized geometry

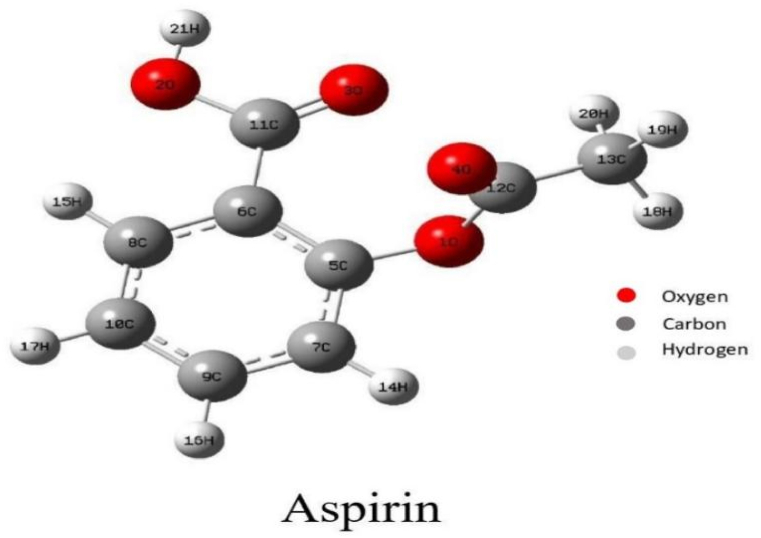
The geometrical optimization of the aspirin molecule [20] is done using Gaussian 09W software. The optimized geometry structure of aspirin is shown in Fig. 1.

Fig. 1.

Optimized structure of aspirin with labelled atoms.

The standardized structural parameters, such as observed bond lengths and angles, are tabulated in Table 1. In the title molecule aspirin (C₉H₈O₄), the C–C distance of the benzene ring is around 1.39 Å for the neutral state and 1.40 Å for the anion state. The C–O bond with a length of 1.36 Å and 1.41 Å shows a single bond character, and the C O bond with a length of 1.20 Å and 1.21 Å shows the double bond character in the neutral and anion state, respectively. The bond angles of the benzene ring are around 120° for the neutral state and 121° for the anion state; this suggests that benzene is a planer molecule. The dihedral angle of H21–O2–C11–C6 is 179.34° for the neutral state and 178.00° for the anion state, which shows its antiperiplanar arrangement. C7–C5–C6–C8 dihedral angle in the benzene ring has a value of 0.45° for the neutral state and 1.06° for the anion state. Adding extra electrons, which influence the high electron density compared with the neutral state, alters bond length in the anion state. The increase in bond length shows more electron density, while the decrease in bond length shows low electron density.

Table 1.

Optimized structural parameter of aspirin with bond length, bond angle, and dihedral angle for neutral and anion states.

Parameters	Bond Length (Å)		Parameters	Bond Angle (°)		Parameters	Dihedral Angle (°)
Atoms	Neutral	Anion	Atoms	Neutral	Anion	Atoms	Neutral	Anion
C6–C11	1.49	1.42	O3–C11–C6	126.51	129.78	H21–O2–C11–C6	179.34	178.00
O2–C11	1.36	1.41	O2–C11–O3	121.17	116.48	C5–C6–C11–O3	−2.43	−1.55
C11–O3	1.21	1.25	C5–O1–C12	118.61	119.25	C8–C6–C11–O2	−2.03	−0.53
O1–C5	1.38	1.41	O1–C12–O4	122.86	124.94	C5–O1–C12–O4	9.66	18.85
O4–C12	1.20	1.21	O1–C12–C13	109.99	109.93	C7–C5–C6–C8	0.45	1.06
H18–C13	1.09	1.09	O1–C5–C6	121.93	119.48	O1–C5–C7–H14	3.52	4.43
C7–C9	1.39	1.41	H20–C13–H18	107.99	108.39	O1–C5–C6–C11	−2.89	−3.48
			C5–C7–H14	118.49	118.04	C11–C6–C8–H15	−0.80	−1.24
			C5–C7–C9	120.16	121.06	O1–C12–C13–C18	−43.59	−40.12

From Table 2, we see that the total energy of the title molecule was continuously decreasing from the gas phase of the neutral state to the water solvent phase of the anion state. It indicates that the molecule is more stable in an anion state than in a neutral state. The dipole moment of Aspirin was continuously increasing from the gas phase of the neutral state to the solvent water phase of the anion state.

Table 2.

Total energy (EB3LYP) and corresponding dipole moment of aspirin.

tate	Solvent	Total Energy (B3LYP) (eV)	Dipole (Debye)
Neutral	Gas	−17657.10	2.14
	Water	−17657.43	2.32
Anion State	Gas	−17657.58	2.36
	Water	−17659.86	3.69

3.2. Frontier molecular orbitals [HOMO-LUMO] and global reactivity descriptors

Global reactivity descriptors are used to characterize the electronic structure and properties of the system as a whole, which is crucial for understanding and predicting its reactivity [21,22]. The energy gap and global parameters were calculated using Koopman's closed-shell orbit [23]. The equation for energy gap = E_LUMO-E_HOMO; for chemical hardness (η) = $\frac{1}{2}$ (I-A), where ‘A’ is electron affinity and ‘I’ is ionization energy; for chemical softness (S) = $\frac{1}{\mathrm{\eta }}$ ; chemical potential (μ) = -$\frac{1}{2}$ (I + A); global electrophilicity index (ω) = $\frac{{\mu }^2}{2\eta }$. These chemical reactivity descriptors, besides HOMO and LUMO, such as electronegativity (χ), chemical hardness (η), chemical potential (μ), and the global electrophilicity index of the aspirin molecule, are shown in Table 3 for both neutral and anion states.

Table 3.

Global reactivity descriptors of aspirin compound for neutral, anion state in the gas phase and solvent water.

Parameters	Reactivity descriptor value (eV)
	Neutral State		Anion State
	Gas phase	Solvent water	Gas phase	Solvent water
Electron Affinity (A) (alpha)	1.95	2.0	−0.97	0.16
Ionization Energy (I) (alpha)	7.32	7.45	2.90	2.83
Chemical Hardness (η) (alpha)	2.68	2.72	1.93	1.33
Chemical Softness (S) (alpha)	0.37	0.36	0.51	0.74
Chemical Potential(μ) (alpha)	−4.63	−4.72	−0.96	−1.49
Electrophilicity index (ω) (alpha)	4.0	4.10	0.23	0.84
Electron Affinity (A) (beta)	–	–	−2.82	0.94
Ionization Energy (I) (beta)	–	–	2.38	6.21
Chemical Hardness (η) (beta)	–	–	2.6	2.63
Chemical Softness (S) (beta)	–	–	0.38	0.37
Chemical Potential(μ) (beta)	–	–	0.22	−3.57
Electrophilicity index (ω) (beta)	–	–	0.01	2.42

The electrophilicity index measures the amount of energy that is lost when there is a maximum amount of electron movement between LUMO and HOMO [24]. The electrophilicity index in the solvent water phase has increased in neutral and anion states, indicating a higher tendency to accept electrons. A similar result can be observed in electron affinity, which suggests that the molecule is more stable in the water solvent phase than in the gas phase. Chemical hardness is a descriptor that measures the stability and reactivity of a molecule [25]. Observation shows that the hardness of the molecule is highest in solvent water in its neutral state compared to others, suggesting more excellent stability. Ionization energy is highest for the neutral state in a water solvent, suggesting that more energy is required to knock off the electron from the molecule in a water solvent. The result from chemical softness suggests that the solvent water phase in the anion state is more prone to undergo chemical changes than other states and phases.

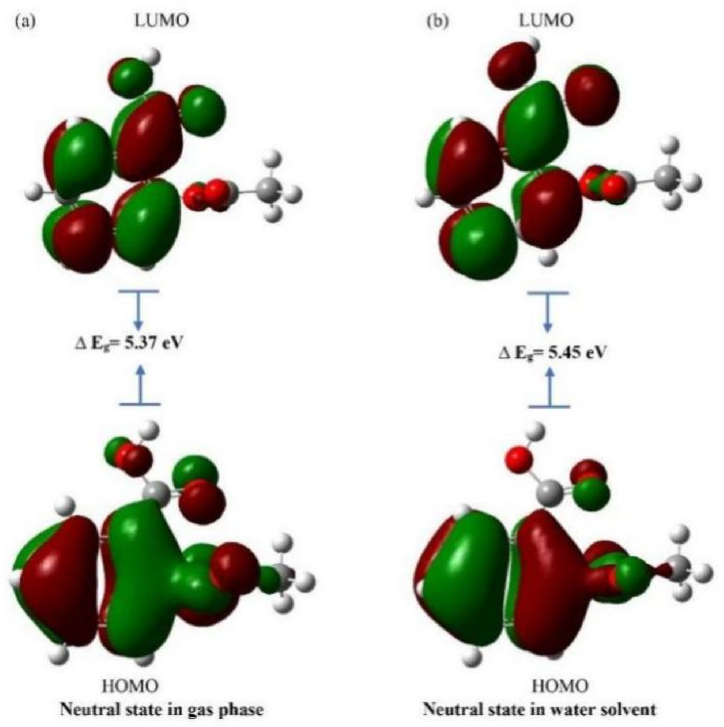
The HOMO (Highest Occupied Molecular Orbital) and LUMO (Lowest Unoccupied Molecular Orbital) are called Frontier Molecular Orbitals (FMOs) as they are located at the outermost boundaries of molecules [26,27]. They are the primary orbitals involved in chemical stability [28]. The energy difference between them is typically the lowest-energy electronic excitation that a molecule is capable of experiencing [29,30].

From the difference between alpha HOMO and alpha LUMO, we can obtain the energy gap for up spin. Since in the neutral state, there is no spin polarization, both alpha and beta HOMO and

LUMO has the same value as Table 4 and Fig. 2. We see similar energy differences between LUMO and HUMO in the neutral state for both the gas and water solvent phases.

Table 4.

HOMO, LUMO, and their energy gap (eV) in neutral and anion state for aspirin molecule.

Parameters (eV)	Neutral State		Anion State
	Gas phase	Solvent water	Gas phase	Solvent water
HOMO(a1pha)	−7.32	−7.45	−2.90	−2.83
LUMO (alpha)	−1.95	−2.00	0.97	−0.16
HOMO (beta)	–	–	−2.38	−6.21
LUMO (beta)	–	–	2.82	−0.94
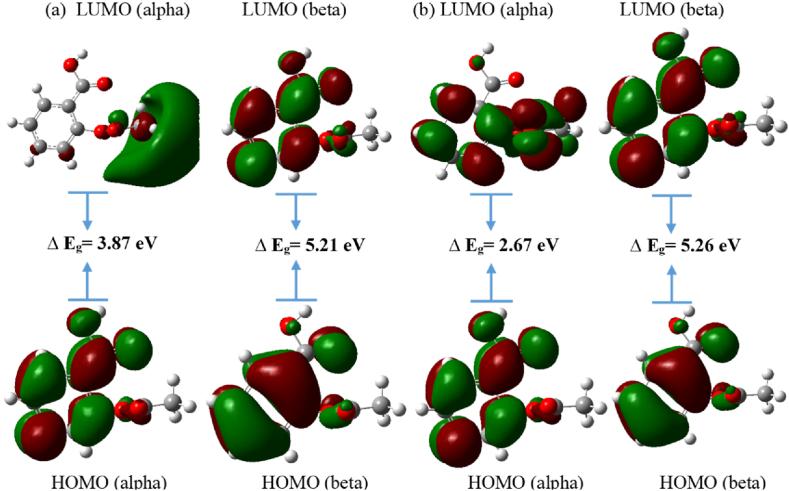
Energy gap (alpha)	5.37	5.45	3.87	2.67
Energy gap (beta)	–	–	5.20	5.27

Fig. 2.

HOMO, LUMO and energy gap of aspirin in neutral state in (a) gas phase (b) water solvent.

For the anion state, there is spin polarization, so we get the values of both alpha and beta HOMO and LUMO, and their respective differences give us the energy gap, as presented in Table 4.

A figure representing the respective energy gaps for alpha and beta HOMO and LUMO for anion states in the gas phase and in solvent water is presented in Fig. 3. In the anion state; the alpha LUMO and alpha HOMO spectra show a minor energy difference than the beta LUMO and beta HOMO spectra in the gas and water solvent phases, which indicates that molecules in the up-spin state have a lower energy gap, indicating greater electron acceptability and chemical reactivity than those in the down-spin state.

Fig. 3.

HOMO, LUMO, and energy gap of aspirin in anion state in (a) gas phase b) solvent water.

3.3. Thermochemistry

Molecular electronic, translational, rotational, and vibrational motions contribute to thermodynamic function. The statistical thermodynamic functions such as thermal energy, specific heat, and entropy for each molecular motion plus zero-point vibrational energy (ZPVE) are calculated using a basis set in Gaussian for neutral and anion states with the presence of water in both cases. The sum of each molecular motion (electronic, translational, rotational, and vibrational) is calculated for each thermodynamic function for both neutral and anion states [31].

Total internal energy (U), which is a thermodynamic function, can be described in terms of contribution from translational, vibrational, rotational, and electronic motion [32].

U = U_trans + U_vib + U_rot + U_elec

where U_trans = translational contribution to internal energy.

U_vib = vibrational contribution to internal energy.

U_rot = rotational contribution to internal energy.

U_elec = electronic contribution to internal energy.

Theoretically, the entropy due to electronic motion is given by S_e R (ln q_e), where R is the ideal constant and q_e is the electronic partition function. The electronic heat capacity and the internal thermal energy resulting from electronic motion are zero since the partition function does not contain a temperature-dependent factor [33]. Similar to theory, from Table 5, we can see that electronic motion has no contribution except for the entropy of the anion state. The similar contribution of electronic, translational, and rotational means these motions are not affected by the addition of electrons. But vibrational motion shows a change in the neutral and the anion states. A molecule's vibrational motion refers to atoms' oscillation about their equilibrium position. Each vibration corresponds to specific energy level, and the distribution of these energy to specific energy level, and the distribution of these energy levels depends on the molecular structure and electronic configuration. Thus, the difference signifies changes in molecular structure and energy level due to adding energy. The zero-point vibrational energy was found to be 98.07 eV for the neutral state and 95.57 eV for the anion state.

Table 5.

Thermochemistry of aspirin molecule in neutral and anion states.

Parameters	Thermal Energy (kcal/mol)		Specific Heat (cal/mol-K)		Entropy (cal/mol-K)
	Neutral	Anion	Neutral	Anion	Neutral	Anion
Electronic	0	0	0	0	0	1.38
Translational	0.89	0.89	2.98	2.98	41.47	41.47
Rotational	0.89	0.89	2.98	2.98	31.00	31.03
Vibrational	103.67	101.37	37.29	39.34	36.58	35.74
Total	105.45	103.15	43.26	45.29	109.06	109.62
Zero-point Vibrational Energy	98.07	95.57	–	–	–	–

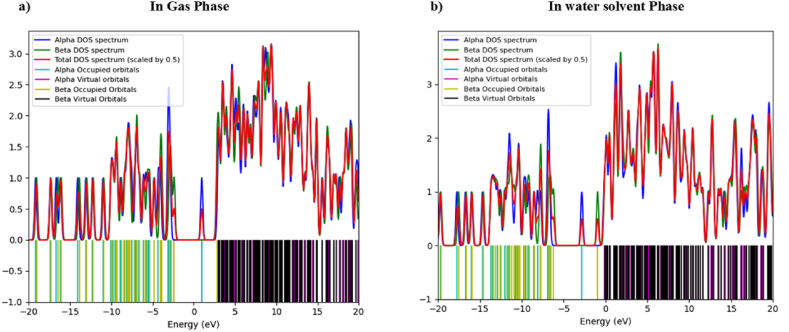
3.4. DOS and total density

The Density of State (DOS) spectrum explains the energy level per unit energy increase. That means several possible states per energy interval at each energy level can be occupied. High DOS at a given energy means more states are available for occupation [34,35]. The DFT with a basis set of B3LYP, 6-311+ G (d,p), was used in Gaussian 09W to calculate the required data, and GausSum was employed to analyze and plot the DOS spectrum.

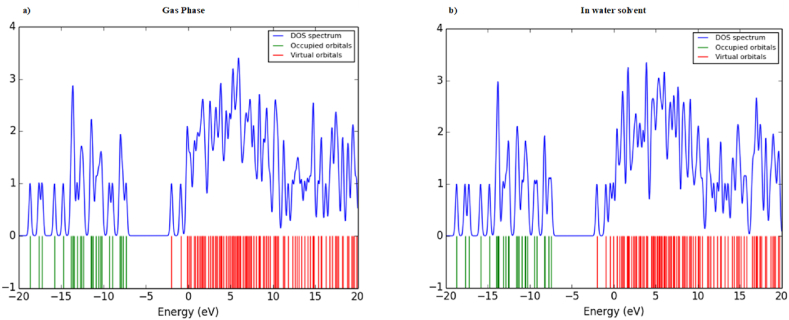
DOS of aspirin in a neutral state and anion state are represented in Fig. 4, Fig. 5, respectively, in the energy range of −20 eV–20 eV. The energy range of −20 eV to −7.5 eV is called the filled or donor orbital, and from −2 eV to 20 eV is called the virtual or acceptor orbital in DOS.

Fig. 4.

DOS spectra of aspirin molecule in a a neutral state in a) gas phase and b) water solvent.

Fig. 5.

DOS spectra of aspirin molecule in anion state a) gas phase a) water solvent.

In DOS, the difference between the virtual and occupied states gives the energy gap between the lowest unoccupied states. For a neutral state in the gas phase (from Fig. 4a), the difference in energy of the lowest virtual orbital and the energy of the highest occupied orbital is 5.44 eV, which is consistent with the values of difference of LUMO (alpha) and HUMO (alpha), which is 5.37 eV. For a neutral state in a water solvent (from Fig. 4b), the difference of energy between the lowest virtual orbital and the energy of the highest occupied orbital is 5.56 eV, which is consistent with the difference of LUMO (alpha) HUMO (alpha), which is 5.45 eV.

From Fig. 5, for DOS of the anion state in the gas phase, the difference in energy of alpha occupied orbital and alpha virtual orbital is 3.92 eV. The difference in energy of beta-occupied orbital and beta-virtual orbital is 5.85 eV. Similarly, in DOS in a water solvent, the difference in alpha-occupied orbital energy and alpha virtual-orbital energy is 2.67 eV, and the difference in beta-occupied orbital energy and beta-virtual orbital energy is 5.58 eV. Both are consistent differences of LUMO HUMO for anion state.

The neutral state has similar energy differences in the gas and water solvent phases. However, anion state spin polarization splits the DOS spectrum into alpha and beta spectra. The alpha DOS spectrum shows a minor energy difference in the gas and water solvent phases, suggesting that molecules in the up-spin state have a lower energy gap, greater chemical reactivity, and greater likelihood of accepting or donating electrons than those in the spin-down state.

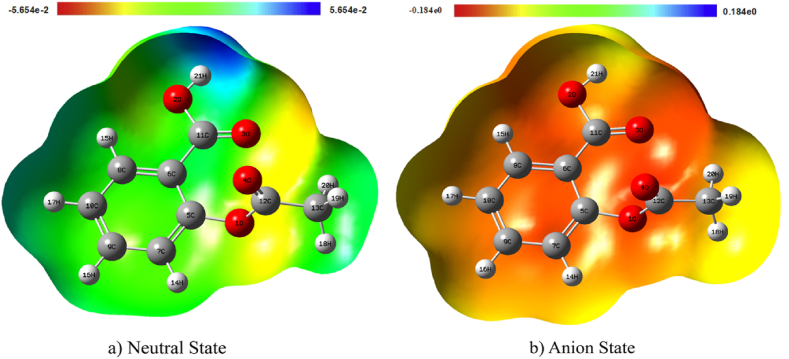
3.5. Molecular electrostatic potential

The MEP can determine a molecule's electrical and structural characteristics, including its bond, ring, and crucial points used to determine the molecular structure of atomic connectivity [36]. It has been discovered that molecular electrostatic potential is a beneficial tool for examining the relationship between a molecule's molecular structure and its physiochemical properties, including those of pharmaceuticals and bio-molecules [37,38].

FromFig. 6, the MEP plot shows that the hierarchical arrangement of the surface region is red < orange < yellow < green < blue for neutral and anion states. The aspirin-colored map ranges from −5.65 e⁻² to 5.65 e⁻² in the neutral state and −0.184 e⁰ to 0.184 e⁰ in the anion state. The neutral state is predominantly electrophilic, with regions around H21 being more electrophilic, suggesting they are likely to accept electrons, and regions around O4, C12, and O1, being more nucleophilic, are more likely to donate electrons. Similarly, most of the region in the anion state is nucleophilic since most of the map shows the color red and orange, and regions around H18, H19, H21, and H17 are less nucleophilic sites than regions around O3, C7, C5, and C6.

Fig. 6.

MEP map of aspirin in a) neutral state and b) anion state.

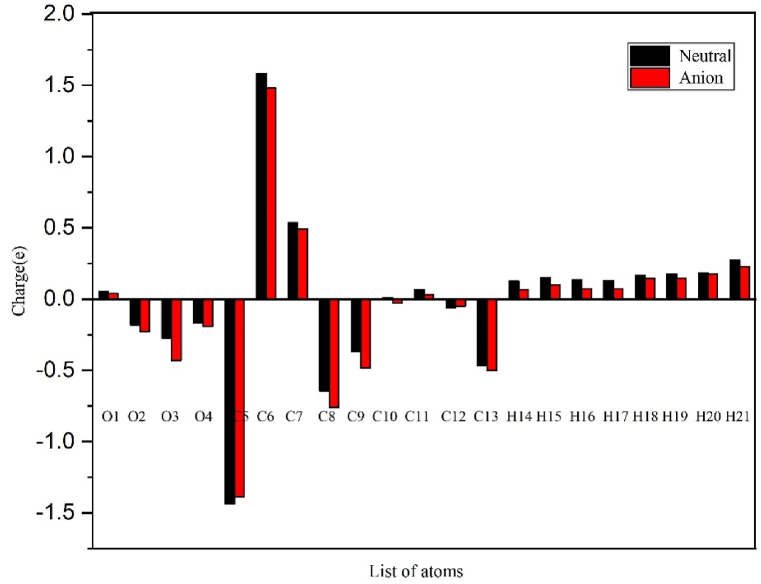
3.6. Mulliken atomic charge

The Mulliken atomic charge is defined by using orbitals. For each atom, the electronic charge contribution of the orbital surrounding the atom is added, and the electronic charge due to overlapped clouds of two or more atoms is divided equally between individual atoms [39,40]. The atomic charge directly affects electronic structure, polarizability, dipole moment, and other molecular properties [41]. The negative charge is distributed among carbon and oxygen atoms; the C5 atom has the highest negative charge in the neutral and anion states. The positive charge is distributed among all their carbon, hydrogen, and oxygen atoms, with C6 having the highest positive charge for neutral and anion states. The computed Mulliken atomic charge is presented in Fig. 7.

Fig. 7.

Mulliken charge distribution chart of the aspirin molecule in neutral and anion state.

3.7. Vibrational analysis

The total number of potentially active observable basics in a non-linear molecule with N atoms has 3N–6 normal modes of vibration. The aspirin molecule has 21 atoms and 57 modes of vibration, including 20 stretching, 18 bending, 13 torsions, and 4 out-of-plane vibrations. Among all these vibrations, the frequencies that contributed the most to the Raman spectra are picked and tabulated in Table 6. The vibrational modes for the region of frequency range 0–4000 cm⁻¹ were computed for the Total Energy Distribution (TED) and their percentage contribution for the neutral and anion states for the gas and water solvent phases.

• •C–H vibration: It determines the presence of an aromatic ring in the molecule, whose frequency range is 2800–3200 cm⁻¹. Our study found the C–H vibration at 3219 cm⁻¹ with 93 and 91 percent contributions in the neutral state for the gas and water solvent phases, respectively. In the anion state for the gas phase, the vibration was found at 3196 cm-1 with 96 percent contribution, and for the solvent water phase, at 3200 cm⁻¹ with 90 percent contribution.
• •C–O vibration: The maximum peak for C–O vibration occurs at 1710-1680 cm^-1. In the neutral state, for aspirin, the C–O vibration was found at 1784 cm^-1 with an 82 percent contribution for the gas phase and 1744 cm-1 with an 83 percent contribution for the water solvent phase. In the anion state, for the gas phase, the vibration was found at 1690 cm⁻¹ with a 35 percent contribution, and for the solvent water phase, 1666 cm⁻¹ with a 24 percent contribution.
• •O–H vibration: The maximum peak occurs at 3690-3100 cm-1 for O–H vibration. For aspirin, the O–H vibration was found at 3774 cm⁻¹ and 3753 cm⁻¹ with 100 percent contribution in the neutral state for gas and water solvent, respectively; in the anion state for gas and water solvent phase, it was found at 3805 cm⁻¹ and 3792 cm⁻¹ with 100 percent contribution, respectively.

Table 6.

Vibrational assignments of frequencies with their TED and percentage contribution of aspirin molecule for neutral and anion state. (S = stretching, B = bending, T = torsion, O = out of plane).

Modes of vibration	Frequency (cm−1) with percentage contribution
	Neutral state [TED%]		Anion state [TED%]
	Gas Phase	Water solvent	Gas Phase	Water solvent
S(O2–H21)	3774 [100]	3753 (100]	3805 [100]	3792 [100]
S(C8–H15)	3219 [93]	3219 [91]	3196 [96]	3200 [90]
S(O3–C11)	1784 [82]	1744 [83]	1690 [35]	1666 [24]
S(C5–C11)	1645 [30]	1640 [31]	1510 [22]	1510 [18]
B(C11–C6–C8)	230 [9]	225 [60]	221 [59]	218 [59]
B(H18–C13–H20)	1396 [41]	1392 [46]	1376 [38]	1387 [43]
B(O3–C11–O2)	645 [37]	643 [38]	613 [33]	613 [22]
T (H18–C13–C12–O1)	1061 [16]	1058 [16]	1055 [20]	1055 [21]
T (C5–C7–C9–C10)	667 [12]	666 [12]	603 [14]	603 [13]
T (H17–C10–C9–C7)	1005 [33]	1016 [32]	932 [38]	953 [62]
O(O4–C13–O1–C12)	1061 [17]	1058 [21]	1055 [21]	1055 [20]

3.7.1. Vibrational spectroscopy

Vibrational spectroscopy provides a dynamic picture of the molecule. It primarily concerns transitions from electromagnetic radiation's absorption or emission [42]. Vibration spectroscopy includes several techniques, the most important of which are infrared and Raman spectroscopy.

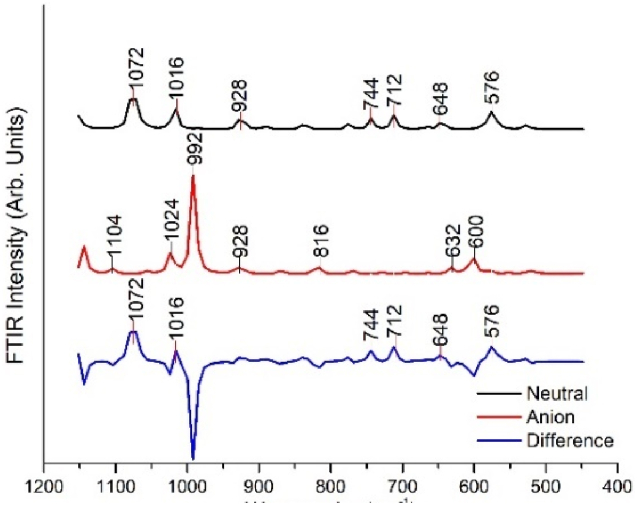
3.7.1.1. Fourier transform infrared (FT-IR) spectroscopy

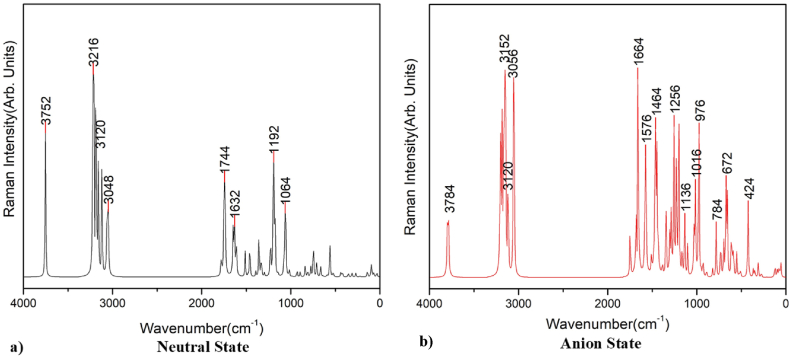
Infrared spectroscopy is best at detecting the asymmetric vibrations of polar groups [43]. Being of high resolution and scanning speed, FTIR is not limited to middle infrared; its spectrum ranges from ultraviolet to far infrared [44]. From Fig. 8, peaks in the 685–995 cm-1 range are due to C–H bending with small intensity. Peaks below 700 are due to the aromatic ring of benzene.

Fig. 8.

FT-IR spectra of aspirin in the gas phase for fingerprint region.

In Fig. 8, the peak at 1104 cm-1 for the anion state is associated with the stretching vibration of the C–O bond in the carboxylic acid functional group, but the neutral state doesn't show any peaks at that range. Both neutral and anion states show peaks in the 1016 cm⁻¹ and 1024 cm⁻¹ associated with the ester group. Since both carboxylic and ester groups are present in the compound, it shows that aspirin is a polar molecule.

FT-IR spectra of aspirin for water solvent were not performed since water has strong absorption characteristics in the infrared spectrum region, especially in the fingerprint region.

3.7.1.2. Raman spectroscopy

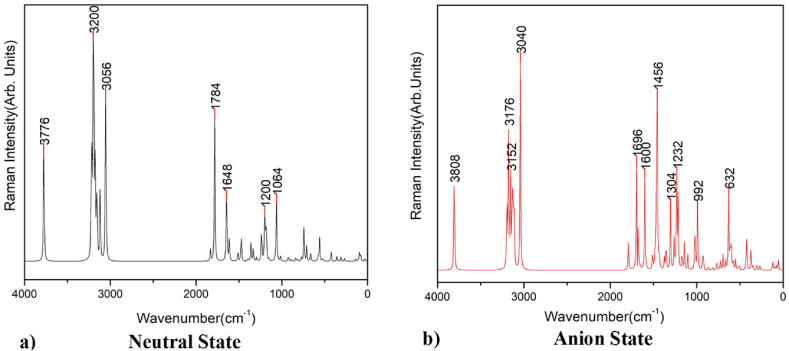
Raman spectroscopy is best for symmetric vibrations of nonpolar groups. Raman spectroscopy is a method that is extremely sensitive to structural change and is used to understand molecular bonding in materials [45]. The Raman peak at 1200 cm⁻¹ is due to characteristics of CH₂ and CH₃ deformation vibrations; the peak at 1750 cm⁻¹ is due to C C stretching vibrations; and the peak of 3000–3300 cm⁻¹ is due to C–H stretching modes, respectively, presented in Fig. 9 and Fig. 10.

Fig. 9.

Raman spectra of aspirin for a) neutral and b) anion state in gas phase.

Fig. 10.

Raman spectra of aspirin for a) neutral and b) anion state in solvent water.

From the comparison of the above figures, there is not much difference in the plot since every state and phase contains almost the same kind of deformation vibration spectra. Every plot contains O–H vibration in the range of 3700–3800 cm⁻¹ and C–H vibration in the range of 3000–3200 cm⁻¹. Similarly, every plot contains a cluster of peaks in the range of 400–1800 cm⁻¹, This is consistent with the data obtained from TED and their percent contribution to each frequency. The experimental Raman spectrum of aspirin shows a peak around 2700-3300 cm⁻¹ and a cluster of peaks 500-1800 cm⁻¹, which is also consistent with our finding [46].

3.8. UV–Vis absorption spectra

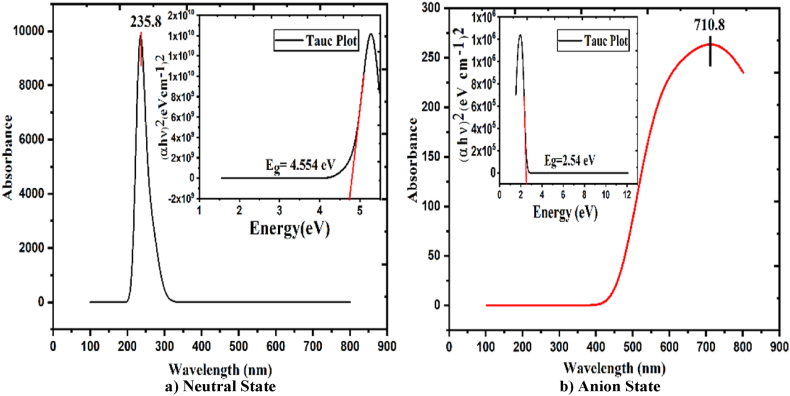
Radiation interacts with matter in several ways, including reflection, refraction, absorbance, phosphorescence, and photochemical reactions. In this study, we measure absorbance in a neutral water solvent state; we get maximum absorption of wavelength max = 235.8 nm, which falls in the region of the UV-C spectrum. Similarly, in anion water solvent state λ_max = 710.8 nm, which falls into the deep red visible light, from Fig. 11. Longer wavelength in the anion state than in the neutral state indicates a lower-energy transition involving changes in the electronic configuration due to the presence of additional electrons.

Fig. 11.

UV–Vis spectra and Tauc plot of aspirin for a) neutral and b) anion state in water solvent.

Fig. 11 shows that the title molecule significantly absorbs light of wavelength 235 nm and 710 nm for neutral and anion states, respectively. Higher wavelength (nm) values absorb more light with low transmittance. The optical energy gap Eg and absorption coefficient (α) are calculated from UV–Vis data to plot Tauc's relation, (αhν) ² = A (hν-E_g) [47]. The optical band gap shows 4.5 and 2.5 eV for the neutral and anion states, respectively. The value of a band gap greater than 3 eV is considered an insulator, also called dielectric material. The packing material that reflects and absorbs UV–visible light with a similar optical band gap can be selected to achieve maximum efficiency in medicine.

4. Conclusion

The Characterization study of the aspirin molecule is carried out using the B3LYP method in the Gaussian software together with the 6-311+G (d,p) basis set using Density Functional Theory. The total energy of the optimized aspirin molecule decreased from −17657.10 eV to −17657.58 eV for the gas phase and −17657.43 eV to −17659.86 eV for water solvent for neutral and anion state, respectively. From FMO, the alpha LUMO and alpha HOMO spectrums in anion states show a minor energy difference, indicating greater electron acceptability and chemical reactivity in molecules at the up-spin than in molecules at the down-spin. Similarly, the electrophilicity index in the solvent water phase of the neutral state is highest, indicating a higher tendency to accept electrons. The chemical hardness of the aspirin molecule is highest in the water solvent phase in its neutral state, implying more excellent stability. From the result of thermochemistry, we found that the zero-point vibrational energy was 98.07 eV for the neutral state and 95.57 eV for the anion state. When comparing the neutral and the anion states, a change in vibrational contribution to total energy was observed due to the change in electronic configuration. The DOS of the molecule provided a consistent result of energy difference with the difference in HOMO and LUMO for both neutral and anion states. The MEP plot suggested that the neutral state is predominantly electrophilic, and the anion state is nucleophilic. The vibrational analysis gave information about different modes of vibrations with their percentage TED. FT-IR and RAMAN studies confirmed the presence of various functional groups associated with this molecular organic crystal. The experimental UV–Vis Spectrum of aspirin at around 256 nm is consistent with our computational finding for a neutral state in the gas phase. Similarly, the experimental Raman spectrum of aspirin shows a peak around 2700-3300 cm⁻¹ and a cluster of peaks 500-1800 cm⁻¹, which is also consistent with our finding [46].

Data availability statement

Data will be made available on request.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Additional information

No additional information is available for this paper.

CRediT authorship contribution statement

Manoj Sah: Writing – original draft, Data curation. Mukesh Khadka: Software, Investigation, Formal analysis. Hari Prasad Lamichhane: Validation, Supervision. Hari Shankar Mallik: Methodology, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.