SUMMARY
We assessed the mechanism of mammalian breathing rhythmogenesis, in the preBötzinger Complex (preBötC) in vitro, where experimental tests remain inconsistent with hypotheses of canonical rhythmogenic cellular or synaptic mechanisms, i.e., pacemaker neurons or inhibition. Under rhythmic conditions, in each cycle an inspiratory burst emerges, as (presumptive) preBötC rhythmogenic neurons transition from aperiodic uncorrelated population spike activity to become increasingly synchronized during preinspiration (for ~50–500 ms), which can trigger inspiratory bursts that propagate to motoneurons. In nonrhythmic conditions, antagonizing GABAA receptors can initiate this synchronization while inducing a higher conductance state in nonrhythmogenic preBötC output neurons. Our analyses uncover salient features of preBötC network dynamics where inspiratory bursts arise when and only when the preBötC rhythmogenic subpopulation strongly synchronizes to drive output neurons. Furthermore, downstream propagation of preBötC network activity, ultimately to motoneurons, is dependent on the strength of input synchrony onto preBötC output neurons exemplifying synchronous propagation of network activity.
Keywords: Breathing, rhythm, central pattern generator, preBötzinger Complex, synchrony, synaptic correlation, network dynamics, synfire chain
eTOC Blurb
The preBötzinger Complex is the kernel for inspiratory rhythm generation in mammals whose mechanisms remain unresolved. Ashhad and Feldman show that the rhythm emerges as the network reorganizes from random tonic activity towards periodic short-term synchronization.
Graphical Abstract
INTRODUCTION
In the early 19th century, a focus of what we now call neuroscience was to discover the noeud vital, i.e., the site where the rhythm of breathing originates; ~200 years later the preBötzinger Complex (preBötC) in the medulla was hypothesized to be the kernel for breathing (Smith et al., 1991). Considerable data supports this role (Del Negro et al., 2018). Still, the longstanding question of how the rhythm is generated remains unanswered (Del Negro et al., 2018). Critically, two long-favored hypotheses for rhythmogenesis, i.e., that rhythm is generated by pacemaker neurons or by simple circuits dependent on inhibition are not supported by experimental tests (Baertsch et al., 2018; Bongianni et al., 2010; Del Negro et al., 2018; Feldman et al., 2013; Feldman and Kam, 2015; Janczewski et al., 2013; Rekling and Feldman, 1998; Sherman et al., 2015). Specifically, neither the pharmacological blockade of amplifying currents such as the persistent sodium current (INaP) or the calcium-activated cation nonspecific current (ICAN) that are present in preBötC inspiratory-modulated (I-M) neurons (Del Negro et al., 2005; Pace et al., 2007a, b) nor blocking inhibition within preBötC (Janczewski et al., 2013; Sherman et al., 2015) abolishes inspiratory rhythm. Based on these observations that such cellular or synaptic properties cannot (fully, if at all) account for rhythmogenesis, we considered the possibility that a key element is a network level mechanism. Here, we explored an alternative (though nonexclusive) hypothesis for preBötC rhythmogenesis that the rhythm is an emergent property of the preBötC microcircuit (Del Negro et al., 2018; Feldman and Kam, 2015; Kam et al., 2013a; Kam et al., 2013b).
To study neuronal microcircuit function, it is paramount that its constituents are clearly identifiable. The fact that for breathing essential elements lie within the preBötC is of great advantage, as we know where to look. However, the preBötC lacks a regular cytoarchitecture to allow location and/or morphology to serve as markers of diverse neuronal subtypes (Del Negro et al., 2018; Feldman and Kam, 2015). To elaborate, in rodents the preBötC contains ~3000 neurons with near equal proportion of excitatory (expressing the vesicular glutamate transporter 2 (vGluT2) (Wallen-Mackenzie et al., 2006)) and inhibitory (expressing the GABAergic enzyme glutamate decarboxylase (GAD) or the glycinergic transporter GlyT2) subtypes (Koizumi et al., 2013; Winter et al., 2009). A key subset of the excitatory neuronal population expresses the developing brain homeobox1 (Dbx1) protein (Bouvier et al., 2010; Gray et al., 2010; Picardo et al., 2013; Wu et al., 2017), a subpopulation of which expresses the peptide somatostatin (SST; (Bouvier et al., 2010; Gray et al., 2010; Stornetta et al., 2003; Tan et al., 2010)). In vivo stimulation of Dbx1+ neurons induces a large increase in breathing frequency and tidal volume. In contrast, stimulating preBötC SST+ neurons only modestly affects breathing frequency, though when these neurons are stimulated in early inspiration there is a substantial increase in tidal volume (Cui et al., 2016). Thus, while Dbx1+ neurons can affect both breathing frequency, i.e., rhythm, and pattern, e.g., tidal volume, SST+ neurons predominantly effect breathing pattern. These experiments suggest that the rhythmogenic population of preBötC consists of Dbx1+ SST− neurons which lie upstream of SST+ neurons (Cui et al., 2016).
preBötC inhibitory neurons, some of which are inspiratory-modulated, release gamma-aminobutyric acid (GABA), glycine or both (Koizumi et al., 2013; Morgado-Valle et al., 2010). Disinhibition of preBötC microcircuits does not eliminate inspiratory rhythm, suggesting that inhibitory neurons are not essential for rhythmogenesis (Bongianni et al., 2010; Feldman and Smith, 1989; Janczewski et al., 2013; Sherman et al., 2015). Nonetheless, inhibition plays a significant role in modulating breathing frequency and pattern, including effects on the duration and shape of inspiratory bursts (I-bursts) and in effecting changes in breathing pattern resulting from proprioceptive feedback, e.g., Breuer-Hering lung inflation reflexes (Baertsch et al., 2018; Janczewski et al., 2013; Sherman et al., 2015). Thus, the preBötC consists of spatially intermixed population neurons of various molecular subtypes (Figure 1A) with overlapping physiological subtypes, i.e., inspiratory vs non-inspiratory/tonic, and rhythmogenic vs patternogenic neurons. This renders the elucidation and localization of rhythmogenic components challenging.
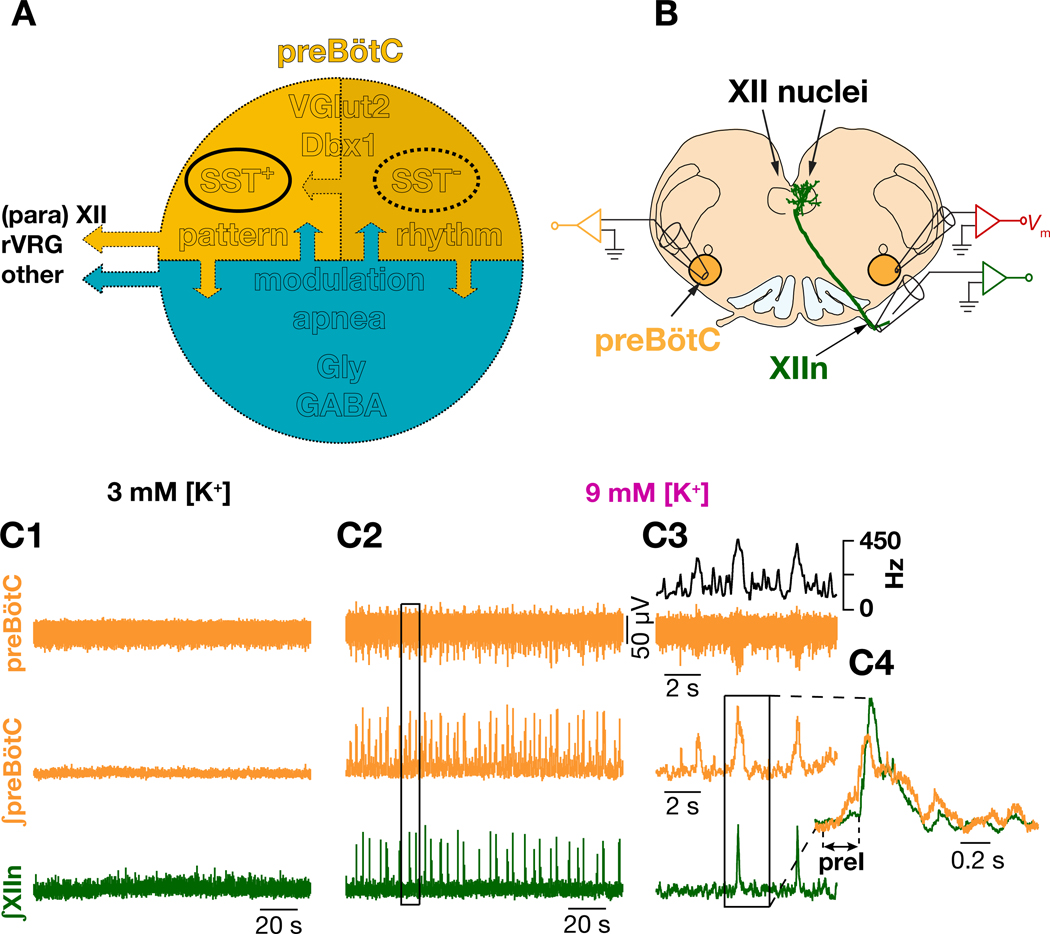
Figure 1. Diverse neuronal subtypes contribute to initiation and propagation of inspiratory rhythm in preBötzinger Complex.
(A) Schematic representation of various preBötC neuronal subtypes whose roles in the generation and propagation inspiratory rhythm and patterns are discussed in the text (see Introduction). Upper half, yellow, represents excitatory neurons and the lower half, blue, represents the inhibitory neurons of preBötC. SST; somatostatin; Vglut2: vesicular glutamate transporter 2; Dbx1: developing brain homeobox protein 1; Gly; Glycinergic; GABA: γ-amino butyric acid; XII: hypoglossal nucleus, rVRG: rostral ventral respiratory group. Arrows indicate synaptic interactions. Both excitatory and inhibitory subpopulations send efferent projections (outward left arrows). (B) Configuration for simultaneous recording of preBötC SST+ neurons along with hypoglossal nerve (XIIn) and contralateral preBötC population activity. preBötC neurons project to XII premotor and motor neurons. (C) preBötC population activity (orange: integrated preBötC (∫preBötC)); green: integrated XIIn (∫XIIn)) in 3 mM [K+]ACSF, i.e., control, (C1), and in 9 mM [K+]ACSF (C2); (C3) expanded boxed region from (C2), top black trace: instantaneous preBötC population firing frequency. (C4) expanded boxed region from (C3) with ∫preBötC and ∫XIIn I-burst overlaid.
SST+ preBötC neurons, necessary for breathing in vivo (Tan et al., 2008), are preBötC output neurons that project widely to inspiratory premotor neurons (Cui et al., 2016; Stornetta et al., 2003; Tan et al., 2010; Yang and Feldman, 2018). Being preBötC output neurons driven by a rhythmic source, we reasoned that the synaptic activity impinging upon them would serve as a reliable indicator of the network dynamics underlying preBötC rhythmogenesis. Hence, we explored the network dynamics underlying the generation of I-bursts by recording the membrane potential () of preBötC SST+ neurons as they transitioned from nonrhythmic, i.e., control, to inspiratory-modulated (I-M) rhythmic activity. To target these neurons for recording, we used knock-in mice expressing the fluorophore tdTomato in SST+ neurons. Time-frequency decomposition of of I-M SST+ neurons revealed a spectrotemporal reorganization of their synaptic inputs that transitioned from randomly tonic in the nonrhythmic control condition to periodically synchronized in the rhythmic condition. Furthermore, a comparison of simultaneous whole-cell current clamp recordings between pairs of I-M SST+ neurons with preBötC population and downstream hypoglossal nerve outputs (quadruple electrode recordings) revealed their inputs become synchronized with short-latency correlated EPSPs (with ~0–125 ms correlation lags) during preinspiration (preI) and subsequent I-burst. This suggests that network synchronization of rhythmogenic neurons underlies initiation and maintenance of preI and emergence of I-bursts. Exploring network mechanisms underlying synchronization, we uncovered a shift in the excitation-inhibition balance towards excitation, which further promotes preBötC synchronization. Assessing connectivity profiles of preBötC SST+ neurons, together with pharmacological perturbations, spectrotemporal analyses and computational modeling, we conclude that the hallmark of preBötC rhythmogenesis and I-burst initiation is the switch from asynchronous to synchronous activity and not the overall level of synaptic inputs. Our analyses uncover a mechanism acting at the microcircuit level that reflects intricate interactions among various neuronal subtypes leading to periodic network assembly underlying breathing rhythmicity.
RESULTS
preBötC rhythm consists of burstlets and bursts
Acute slices from neonatal brainstem of rodents containing the preBötC bathed in artificial cerebrospinal fluid (ACSF) with near physiological [K+] and [Ca2+] (3 mM and 1.5 mM, respectively) are typically nonrhythmic (Smith et al., 1991) (Figures 1B–C). However, with elevated [K+]ACSF (9 mM), rhythmic I-bursts emerge in preBötC that in almost all (≳90%) instances produce motor-related I-bursts in hypoglossal nerve (XIIn). In each cycle, for up to a few hundred milliseconds prior to the rapid onset of I-bursts, preBötC population activity grows slowly (~250 ms in vitro); this epoch is designated preinspiration (preI) and can be detected by extracellular field potential recordings (the ensemble of synaptic and action potentials recorded with a glass electrode covering the preBötC). Furthermore, the integral of this activity (∫preBötC) reliably captures the changes in the instantaneous firing frequency of the preBötC population (c.f. black and middle orange traces in Figure 1C3; also see STAR Methods). Notably, when preI fails to induce a preBötC I-burst, the result is a low amplitude preBötC burstlet with no associated XIIn I-burst (Figure 1C3) (Kam et al., 2013a).
Inspiratory activity is correlated with a spectrotemporal reorganization of inputs onto preBötC I-M SST+ neurons
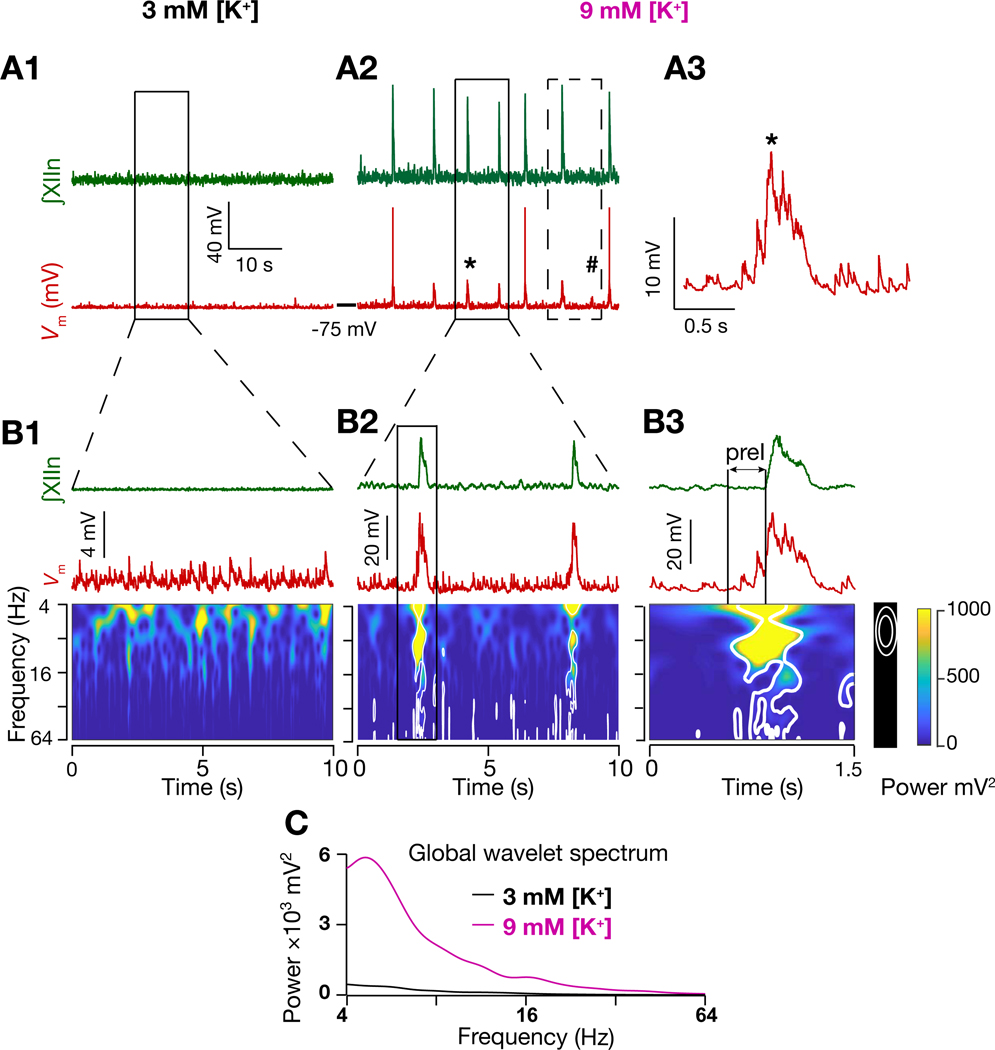
To unravel rhythmogenic mechanisms underlying breathing, we posed several questions: i) What network dynamics underlie the onset and progression of preI activity? ii) What are the threshold mechanisms that transforms preI activity into I-bursts? iii) Which neuronal subpopulations of the preBötC microcircuit contribute to preI and I-burst activity? To address these questions, we took advantage of the unique position SST+ neurons as an intermediary population in the transmission chain of inspiratory signals. By recording their membrane potentials, we could evaluate the dynamics of their synaptic inputs and, consequently, that of the rhythmogenic neurons. Under nonrhythmic conditions, where preBötC population bursts were absent or sporadic (3 mM [K+]ACSF; Figures 1C1, 2A1), preBötC SST+ neurons received asynchronous synaptic inputs that rarely summated to produce action potentials (APs; Figures 2A1, B1). However, by increasing [K+]ACSF to 9 mM, their excitatory postsynaptic potentials (EPSPs) became periodic and clustered, producing more APs at shorter intervals; this activity increased slowly at first during preI, ultimately transforming into I-bursts (Figures 2A2–A3; S1A1–A2). Using wavelet analysis to ascertain the EPSP spectrotemporal structure, we found that the membrane potential () power in the frequency range 4–64 Hz of preBötC I-M SST+ neurons (n=15/29 of recorded SST+ neurons were inspiratory-modulated) significantly increased during preI and even further in subsequent I-bursts (Figure 2B2–B3). During run-up to an I-burst, synchronization of EPSPs progressively increased, with inputs at lower frequencies appearing first during preI (Figures 2B3). Two notable points: i) preBötC I-M SST+ neurons rarely fired APs during preI (Figure S1A1–A2; similar to inspiratory Type-2 neurons (Rekling et al., 2000)) making them an unlikely source for preI activity, and; ii) the frequency of synaptic inputs in the interburst intervals (IBIs) preceding each preI was lower than that during nonrhythmic conditions where low frequency inputs (4–8Hz) were only sporadically present (Figure 2B1–B2). Furthermore, the global wavelet spectrum power, i.e. time-averaged power, of I-M SST+ neuron also increased in higher [K+]ACSF (Figure 2C) indicative of an increase in the overall frequency of inputs.
Figure 2. Inspiratory activity is correlated with spectrotemporal reorganization of inputs onto preBötC I-M SST+ neurons.
(A1-A2) ∫XIIn (green) and I-M SST+ neuron membrane potential (; red) in 3 mM [K+]ACSF (A1) and in 9 mM [K+]ACSF (A2); (A3) expanded from (A2) marked by *. Dashed box in (A2) represents the deflection corresponding to a missed burst in the XIIn, marked by #, which resulted in a longer interburst interval for the next burst. (B1-B3) ∫XIIn, and associated frequency-time plot for I-M SST+ neuron in 3 mM [K+]ACSF (nonrhythmic; B1) and in 9 mM [K+]ACSF (rhythmic, B2); expanded traces from solid boxed region in (A1) and (A2), as indicated. (B3) expanded boxed region from (B2). White contours in frequency-time plots enclose regions where local power was significantly higher (95% confidence level) than background spectrum, i.e., global wavelet spectrum of in (B1). Note in (B3) emergence of input synchrony in preI period well before the emergence of I-burst in XIIn. (C) global wavelet spectrum of in 3 mM K+ (B1) and 9 mM K+ (B2). Also, see Figure S1.
Increased synaptic correlation between I-M SST+ neuron pairs during preI and I-bursts is concurrent with their increased input synchrony
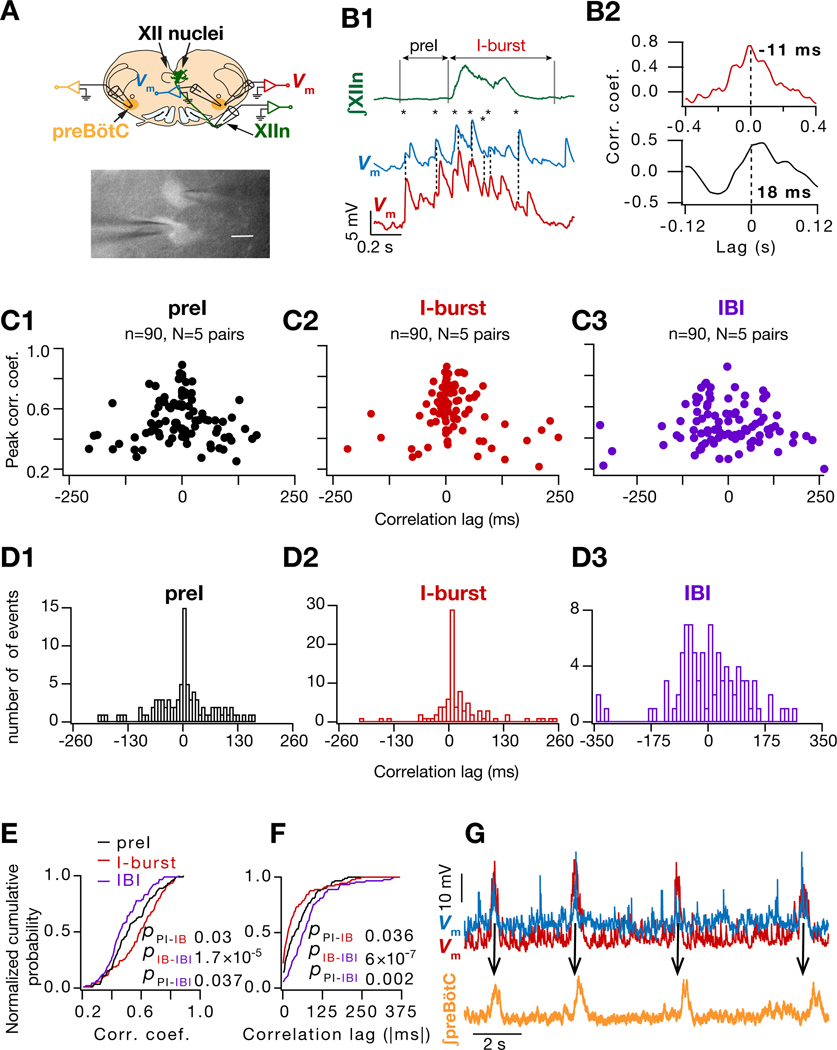
Next we asked, what kind of network interactions result in the emergence of synchronous inputs onto I-M SST+ neurons? We speculated that the emergence of synchronous inputs onto I-M SST+ neurons was a consequence of recurrent excitatory connections (Guzman et al., 2016; Miles and Wong, 1986) among these I-M SST+ neurons. However, as only 1/50 pairs (2%) of preBötC SST+ neurons tested was synaptically coupled, this did not appear to be the case, (Figure S2 A1–A6; Note: the chemical synapse was unidirectional with a rectifying electrical coupling in the reverse direction (Figure S2 B1–B2; (Rekling et al., 2000)). Given this sparse connectivity among SST+ neurons, we postulated that their input synchrony resulted from convergent inputs arising from afferent rhythmogenic preBötC neurons, consistent with our previous hypothesis (Cui et al., 2016; Feldman and Kam, 2015). Putatively rhythmogenic inspiratory preBötC Type-1 neurons (SST− ) interact through excitatory synapses with ~13% probability of any pair having a one-way connection (Rekling et al., 2000). Notably, in each cycle, Type-1 neurons have a progressive slow increase in their firing rate that starts before preI and continues through the I-burst (Gray et al., 1999). In each cycle among pairs of simultaneously recorded I-M SST+ neurons (Figure 3A), an increase in their correlation was associated with the emergence of preI input synchrony (Figures 3B1–B2, S2C1–C4). This manifested as an increase in the correlation coefficients of their during preI epochs, which further increased during the I-burst (Figure 3C1–C2). Following each I-burst, their correlations decreased in the IBI (Figure 3C3) revealing desynchronization of their inputs. Importantly, the increase in the correlation was a consequence of an increase in short-latency correlated EPSPs during preI and I-bursts (8/90, 23/90 and 35/90 events had <10 ms correlation lags in the IBI, preI and I-burst epochs respectively; Figures 3D1–D3). These changes resulted in a significant leftward shift in the cumulative histograms of the correlation coefficients (Figure 3E) and a rightward shift in the cumulative histograms of the correlation lags (Figure 3F) during IBI, preI and I-burst epochs. Furthermore, the peak of deflections of simultaneously recorded I-M SST+ pairs lead the peak of ∫preBötC activity during I-bursts (Figure 3G) revealing that the input synchrony-mediated firing of I-M SST+ neurons drives preBötC I-bursts. Taken together, these results indicate that input synchrony onto I-M SST+ neurons results from (upstream) synchronization within the preBötC subnetwork generating inspiratory rhythm. Thus, the emergence of periodic synchronous EPSPs in I-M SST+ neurons (Figure 2) represents a significant spectrotemporal reorganization in the activity of their input population, i.e., presumptive rhythmogenic neurons. Consequently, this induced synchronous firing of I-M SST+ neurons inherent in preBötC output.
Figure 3. Increased synaptic correlation between I-M SST+ neuron pairs during preI and I-bursts is concurrent with their increased input synchrony.
(A) Top, Configuration for simultaneous recording of preBötC SST+ neuronal pairs with hypoglossal nerve (XIIn) and contralateral preBötC population activity; bottom, fluorescent micrograph of simultaneously patched SST+ neurons. (B1) ∫XIIn (green) and of two simultaneously recorded I-M SST+ neurons (blue, red) along with the crosscorrelograms (B2) during preI (black) and I-burst (red). Temporally aligned EPSP peaks indicated by dashed line and *. (C1-C3) Plots for peak correlation vs time lag for of I-M SST+ pairs (90 cycles from 5 pairs) during preI, I-burst and interburst interval (IBI) epochs. (D1-D3) Histogram of crosscorrelation lags for of I-M SST+ pairs for data in (C1-C3). (E-F) normalized cumulative histogram of crosscorrelation peaks (E) and lags (F) for events in (C1-C3). Kruskal Wallis test (E, p = 5×10–5; F, p = 9×10–8) followed by Wilcoxon signed rank test for pairwise comparisons (p values for color-coded pairwise comparisons). (G) of simultaneously recorded I-M SST+ pair (blue, red) along with ∫preBötC (orange) showing that ∫preBötC activity peaks after the peak of in each cycle. Also, see Figure S2.
Input synchrony during an I-bursts is specific to I-M SST+ neurons
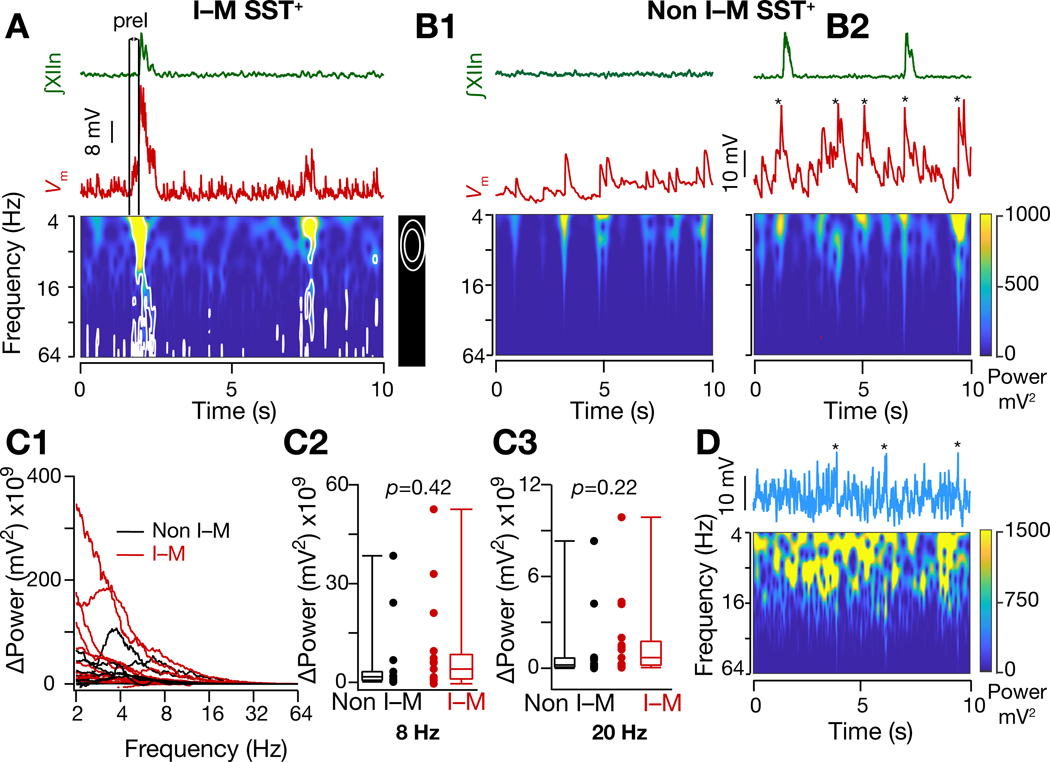
This emergence of a strong synchronous input structure of I-M SST+ neurons only occurs under rhythmic conditions, suggesting that network synchronization is causal to both rhythmogenesis and I-burst generation. Accordingly, when input synchrony (henceforth used as a proxy for network synchrony) onto these neurons was present but weak, there was no resultant I-burst and, consequently, there were longer intervals between XIIn bursts (Figures 2A2 and 4A). Furthermore, the increase in membrane potential power, which signifies an increase in the average input frequency, in non-I-M SST+ neurons (n=14; Figures 4B1–B2, S1B1–B2) was indistinguishable from that of I-M SST+ neurons (Figure 4C1–C3), despite the fact that non-I-M SST+ neurons did not show structured input synchrony, i.e., significant increases in spectrotemporal power (compare Figure 4A with 4B1–B2; S3A1–A2). This further demonstrates strong synchronized inputs as a necessary condition for the substantial increase in I-M SST+ neuronal activity underlying I-bursts.
Figure 4. Input synchrony during an I-burst is specific to I-M SST+ neurons.
(A) Frequency-time plot of of an I-M SST+ neuron (from dashed box region of Figure 2(A2)) under rhythmic conditions showing reduced synchrony during I-burst failure compared to production of I-burst (first peak), i.e., corresponding to preI activity not followed by an I-burst (second smaller peak). (B1-B2) Same as (A) but for non I-M SST+ neuron under control (3mM [K+]ACSF) (B1) and rhythmic (9mM [K+]ACSF) (B2) conditions. median filtered to remove APs (indicated by *). (C1- C3) Change in power of I-M and non-I-M SST+ neurons when brainstem slices were shifted from nonrhythmic to rhythmic conditions; p values for Wilcoxon rank sum test. (D) Frequency-time plot of median filtered of a model neuron when 10 excitatory synapses were activated randomly with 15 Hz mean frequency. Note absence of bursting. * indicate median filtered APs. Also, see Figure S3.
We considered the possibility that this synchrony was epiphenomenal, resulting from increased firing rates of individual afferent neurons, such that random alignment of more APs appears as synchronous input. As a proof of principle, we tested this computationally in a biophysically realistic model neuron that had inputs from 10 afferent neurons, each with a Poisson-distributed 2–20 Hz mean AP frequency (see STAR Methods – Simulations). We found no indication of any spectrotemporal reorganization from uncorrelated activity to significant input synchrony (Figure 4D) and no bursting (Figures 4D, S3B). We conclude that synchrony is not simply the result of an increase in network excitability but is a manifestation of network assembly (Buzsaki and Draguhn, 2004) necessary for generation of preBötC population preI activity and I-bursts. To elaborate, the emergence of temporally aligned EPSPs and correlation between I-M SST+ neurons (Figures 3, S2C1–C4) reflect the onset of output synchrony of their afferent rhythmogenic neurons. The resultant synchronous firing of I-M SST+ neurons then leads to I-bursts (Figure 3G), with a subsequent decrease in input synchrony, as evident in the decorrelation of the of neuronal pairs in IBI epochs, contributing to I-burst termination.
GABAAR inhibition regulates preBötC synchronization and conductance state of I-M SST+ neurons
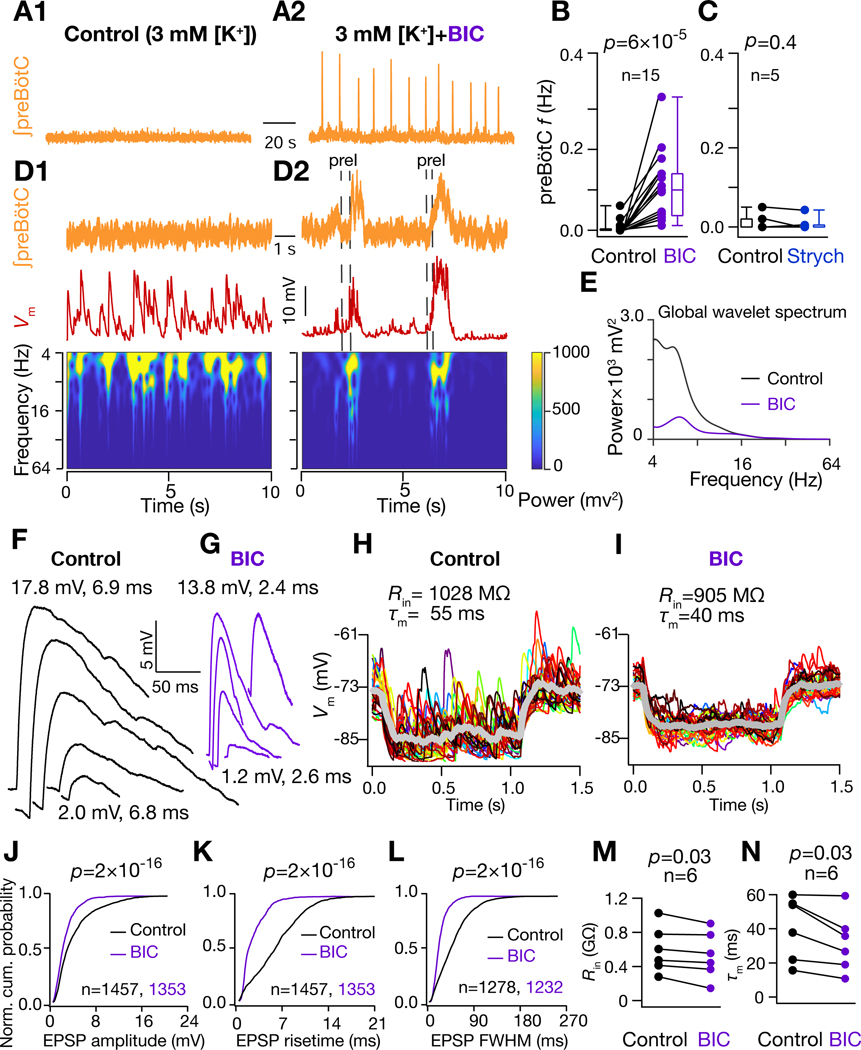
What network mechanism(s) leads to the emergence of preBötC synchrony essential for generation of bursts? Evidently, an overall (uncorrelated) increase in the neuronal firing is insufficient (Figures 4B1–D, S3). Given that the excitation-inhibition balance is, in general, a critical determinant of network output (Bartos et al., 2002), including for breathing (Baertsch et al., 2018; Baertsch et al., 2019; Janczewski et al., 2013; Sun et al., 2019), we hypothesized that the net impact of elevated [K+]ACSF is to shift the excitation-inhibition balance towards higher excitation, thus favoring preBötC synchronization. To test this hypothesis, we disinhibited the preBötC network by antagonizing GABAA or glycinergic receptors. Surprisingly, antagonism of GABAA, but not glycine, receptors in a nonrhythmic slice resulted in rhythmic I-bursts associated with synchronous EPSPs in I-M SST+ neurons (5A-D, S4A-G). Strikingly, for I-M SST+ neurons, at the onset of rhythmic bursting, despite the emergence of input synchrony, global wavelet power decreased (Figure 5E), as did EPSP amplitude, durations, and 20%–80% rise times (Figure 5F–G, J–L). In a subset of these experiments, we continuously monitored input resistance () and membrane time constant () (n=6 neurons from 6 mice) during the transition from nonrhythmicity to the emergence of input synchrony and rhythmicity in response to GABAAR blockade, and found that values for both decreased (Figure 5H–I, M–N). These changes are consistent with a shift to a higher conductance state.
Figure 5. GABAAR inhibition regulates preBötC synchronization and conductance state of preBötC I-M SST+ neurons.
(A) preBötC activity under nonrhythmic control (3 mM [K+]; A1) and after addition of 10 μM Bicuculline (BIC) rhythmic (A2) conditions. (B-C) preBötC burst frequency under control and BIC (B) and 2 μM strychnine (Strych) (C) conditions. (D) Frequency-time plot for of I-M SST+ neuron under control (D1) and BIC rhythmic (D2) conditions. (E) Global wavelet spectrum of in (D1-D2). Note decrease in global wavelet power under rhythmic conditions with BIC. (F) and (G) spontaneous EPSPs extracted from traces in (D1) and (D2) respectively. Amplitude and 20%−80% rise times of largest (top) and smallest (bottom) EPSPs are indicated. (H-I) of I-M SST+ neuron in response to a 10 pA hyperpolarizing current under control (H) and under 10 μM BIC (I); individual traces span 30 trials (different colors) and thick grey traces represent averages. (J-L) Normalized cumulative probability for spontaneous EPSP amplitude (J), 20%−80% rise time (K), and full width at half maximum duration, FWHM (L), under control (black) and BIC rhythmic (purple) conditions; N=8 neurons from 8 brain slices. (M) Input resistance, , and (N) membrane time constant, , of I-M SST+ neurons recorded in control and BIC. For (B-C) and (M-N), p-values are for Wilcoxon signed rank test; for (J-L), p-values for Wilcoxon rank sum test. Also, see Figure S4.
Simultaneous application of GABA and glycine receptor antagonists partially reversed the higher conductance state of I-M SST+ neurons induced by GABAAR blockade only
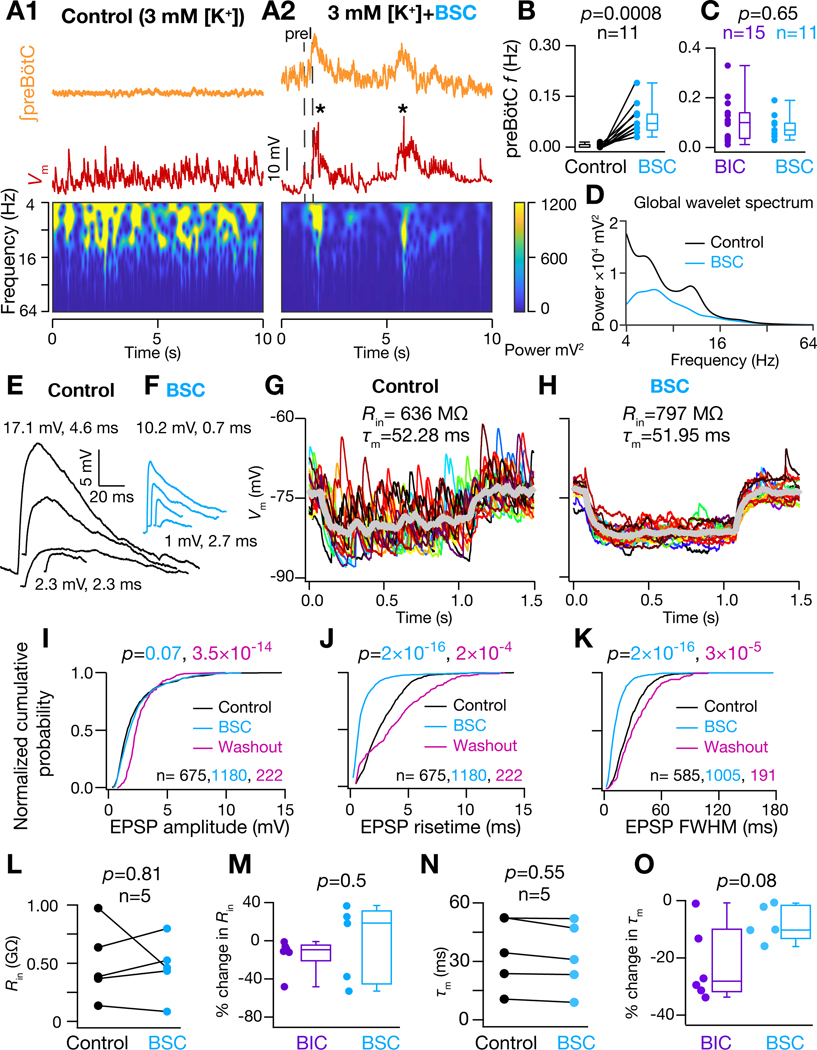
The induction of a higher conductance state in preBötC neurons by GABAAR blockade contrasts with the neocortex, where activated inhibitory conductances are instead dominant determinants of high conductance state (Destexhe et al., 2003). Therefore, we further explored roles of GABAergic and glycinergic receptors in effectuating higher conductance state of I-M SST+ neurons. We recorded in the presence of bicuculline (10 μM), strychnine (2 μM), and CGP55845 (2 μM), to block GABAA, glycine, and GABAB receptors, respectively. In the presence of this cocktail of antagonists (BSC), in 3 mM [K+]ACSF, the preBötC rhythm emerged with the characteristic spectrotemporal reorganization of inputs onto I-M SST+ neurons, i.e., input synchrony was concurrent with the preI period (Figure 6A1–A2). Importantly, there was no significant difference in the preBötC frequency compared to GABAAR blockade only (Figure 6B–C), suggesting that under these conditions network synchronization and rhythmogenesis are predominately if not exclusively modulated by GABAA-mediated inhibition. Under this condition, the time averaged power of the of I-M SST+ neurons decreased with the emergence of rhythmogenesis (Figure 6D), possibly due to the decrease in tonic firing of their input neurons during the IBI. Furthermore, even when the peak amplitude of largest spontaneous EPSPs was lower, most spontaneous EPSP amplitudes were very similar to the control condition (3 mM [K+]ACSF) albeit with faster rise times and shorter durations (Figure 6E–F). Thus, there was no change in the cumulative probability distribution of spontaneous EPSP amplitudes (Figure 6I) despite a rightward shift in their rise times and full width half maximum (FWHM) duration (Figure 6J–K) as compared to control.
Figure 6. Blocking GABA and Glycine receptors partially reversed impact of higher conductance state of I-M SST+ neurons.
(A1) Frequency-time plot for of I-M SST+ neuron under control and (A2) with 10 μM Bicuculline, 2 μM Strychnine and 2 μM CGP55845 (cocktail abbreviated as BSC) in ACSF to block GABAA, glycinergic and GABAB receptors, respectively; * indicates filtered APs (B) preBötC burst frequency recorded under control and under BSC, respectively. (C) comparison of preBötC frequency under control, BIC and BSC conditions. (D) global wavelet spectrum of in (A1-A2), note decrease in global wavelet power under rhythmic conditions with BSC. (E) and (F) spontaneous EPSPs extracted from traces in (A1) and A2) respectively. (G-H) of I-M SST+ neuron in response to a 10 pA hyperpolarizing current under control (G) and under BSC condition (H); individual traces (different colors) span 16–20 trials and thick grey traces represent averages. (I-K) Normalized cumulative probability for spontaneous EPSP amplitude (I), 20%−80% rise time (J), and full width at half maximum duration, FWHM (K), under control (black) and rhythmic with BSC (cyan) conditions and after washout of BSC with control ACSF (pink); p values for comparison of color-coded experimental sets vs. control; N=5 neurons from 5 brain slices. (L) of I-M SST+ neurons recorded in control and BSC conditions. (M) % change in of I-M SST+ neurons recorded under BIC and BSC conditions. (N) of I-M SST+ neurons recorded in control and BSC conditions. (O) % change in of I-M SST+ neurons recorded under BIC and BSC conditions. For (B), (L) and (N), p-values are for Wilcoxon signed rank test; for (C), (I-K), (M) and (O), p-values for Wilcoxon rank sum test.
We further probed the underlying biophysical mechanism for this behavior of spontaneous EPSPs, and found that with the blockade of all three receptors, there was no significant change in the (Figure 6G–H, L), which accounts for the observation of no change in amplitude of spontaneous EPSPs. Specifically, in 3/5 I-M SST+ neurons, BSC resulted in an increase in , in contrast to the decrease in of all neurons tested with GABAAR blockade only (Figures 5M, 6M). Furthermore, under SBC, the decrease in was not statistically significant (Figure 6G–H, N). This decrease in the , under SBC, was also smaller when compared to that during GABAAR blockade only (Figures 6O). This suggests that integrative neuronal properties may be also regulated by excitatory synaptic and/or calcium-dependent intrinsic conductances under rhythmic conditions (Del Negro et al., 2010), which would contribute to a decrease in the EPSP rise time and duration (Figure 6J–K). Importantly, changes in EPSP rise time and duration were reversible (Figure 6J–K), ruling out the possibility that these changes were primarily due to plasticity in neuronal response dynamics caused by increased cytosolic Ca2+ mobilization with increased network excitability (Ashhad et al., 2015; Ashhad and Narayanan, 2019; Narayanan et al., 2010). Taken together, these results uncover a significant and novel dichotomy in the roles of GABAergic and glycinergic inhibition in breathing rhythmogenesis. Furthermore, I-M SST+ neurons can transition to a higher conductance state and show rhythmicity in going from 3 mM to 9 mM [K+]ACSF (Figure S5), possibly as a consequence of increased activity of both excitatory and inhibitory neurons as higher extracellular [K+]-induced neuronal depolarization should increase the activity of all neuronal preBötC subtypes. Thus, the network synchronization and increased conductance state of these neurons are tightly coupled, representing an emergent feature of the preBötC microcircuit common across experimental conditions employed to induce rhythmicity.
Propagation of preBötC bursts to XIIn is dependent upon strength of input synchrony onto I-M SST+ neurons
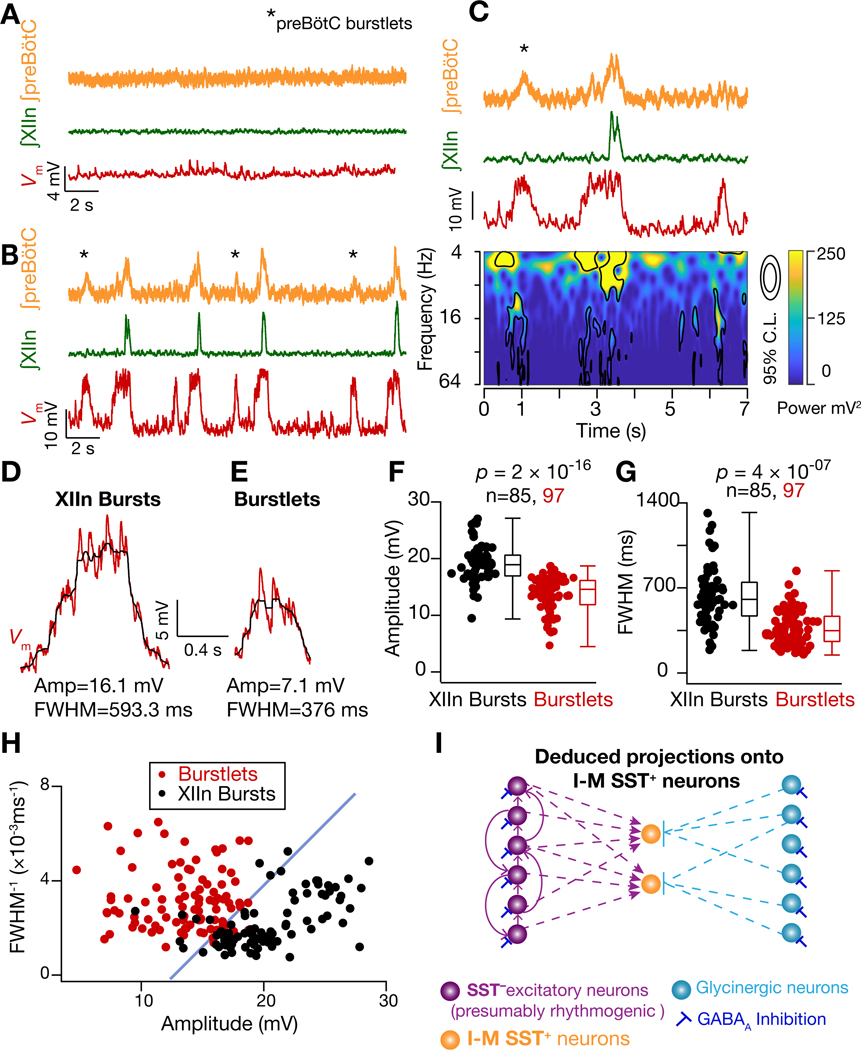
Given the central role of network synchronization in the generation of preBötC I-bursts, we considered its role in their efferent propagation to motor nuclei that control inspiratory muscles. We noticed that under rhythmic conditions ~16% I-M SST+ neurons (4/25 neurons recorded in 9 mM [K+]ACSF) received more bouts of synchronous inputs than the number of I-bursts that concurrently propagated to XIIn (Figures 2A2 (dashed box), 3G blue trace, 4A, 7A-C). Thus, when the input synchrony was weak or short-lived, i.e., reduced area of significant increase in the power in frequency-time plot, preBötC burstlet activity (Kam et al., 2013a) did not propagate to the XIIn. This observation is reminiscent of a synfire chain, where propagation of synchronous activity along successive neuronal populations is governed by the temporal compactness of population activity and the total number of spiking neurons in each population (Diesmann et al., 1999; Kumar et al., 2010). Under such an arrangement, the output synchrony of a given network serves as input synchrony for neurons in the downstream network, so that the stable propagation of population bursts along a linear network is a consequence of its input synchrony and the total activity of its afferent network (Diesmann et al., 1999). In support of this theory, we found that when the input synchrony onto I-M SST+ neurons was weak, preBötC I-burst activity failed to initiate resulting in a burstlet (Figure 7B–C). Additionally, bouts of synchronous EPSPs associated with XIIn I-bursts were sustained for significantly longer compared to those bouts that failed to produce XIIn I-bursts (Figure 7D–G). Furthermore, successful propagation of preBötC activity was dependent on both the duration of input synchrony and the resultant amplitude of deflections (Figure 7H), which is a function of temporal compactness as well total activity of the presynaptic population.
Figure 7. Propagation of preBötC bursts to XIIn is dependent upon strength of input synchrony onto I-M SST+ neurons.
(A-B) preBötC activity, XIIn activity and of an I-M SST+ neuron under control (3 mM [K+]ACSF) (A) and rhythmic (9 mM [K+]ACSF) (B) conditions. Note more bouts of input synchrony in than preBötC and/or XIIn I-bursts in B, i.e., burstlets. (C) Frequency-time plot concurrent with recordings of first 7 seconds from (B). (D-E) Representative (raw (red) and median filtered (black)) from another neuron during an XIIn I-burst (D) and when preBötC input synchrony was not accompanied by an I-burst (E). (F-G) Summary plots for measurements in (D-E); n = number of events. (H) plot of FWHM−1 vs amplitude of deflections from I-M SST+ neurons (n=4) during bouts of input synchrony. The data is color coded for synchronous inputs that resulted in XIIn I-bursts (black) and those that did not (red). An arbitrary blue line with slope of ~1 ms x mV separates the data into the two groups. (I) Schematic representation of inputs onto I-M SST+ neurons (as inferred from data); these neurons receive synchronized inputs from SST− glutamatergic neurons, some of which are presumptively rhythmogenic and connected through excitatory synapses among themselves (Rekling et al., 2000). I-M SST+ neurons also receive glycinergic inputs. Glycinergic neurons are in turn regulated by GABAA inhibition.
DISCUSSION
Reorganization of neuronal dynamics underlies preBötC rhythmogenesis
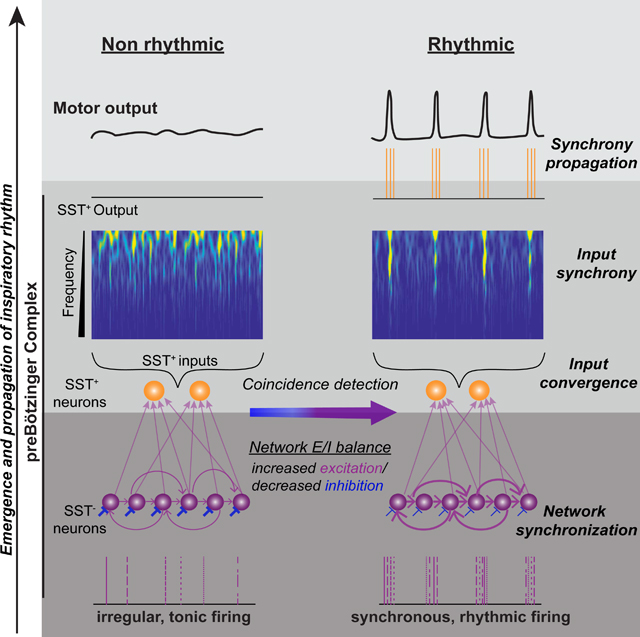
Delineating essential features of network dynamics underlying inspiratory rhythmogenesis is a critical missing link in the endeavor to understand the neural basis of breathing behavior. Here, we exploited a unique experimental preparation where the rhythmogenic kernel is localized within the preBötC, which via local connections to separate output populations that include nonrhythmogenic SST+ neurons, has paucisynaptic projections to motoneurons. By direct comparison of network activity under nonrhythmic and rhythmic conditions, we found that strong network synchronization on a short time scale among rhythmogenic neurons is essential for rhythmicity and its propagation to motor nerves (Figures 7I and 8). The appearance of (near) instantaneously correlated inputs onto the pairs of I-M SST+ neurons (Figure 3) suggests that network synchronization emerges as a consequence of synchronous firing of upstream rhythmogenic neurons initiating the preI period that eventually drives I-bursts. Thus, the synchrony here is the mode of network assembly and not mere increase in the average firing rates of preBötC neurons during I-bursts (Carroll and Ramirez, 2013; Wittmeier et al., 2008). Notably, during buildup of input synchrony during preI and I-burst, the synaptic inputs onto I-M SST+ neurons resemble the firing profile of pre-inspiratory, including Type-1, neurons (Gray et al., 1999)). Type-1 neurons are synaptically interconnected with a unidirectional connection probability of 13% (Rekling et al., 2000), which is substantially higher than the 2% unidirectional synaptic connectivity of preBötC SST+ neurons. We hypothesize that Type-1 neurons can synchronize through recurrent synaptic excitation with high reliability as a population of the order of 1000 neurons, to serve as the rhythmogenic preBötC neuronal kernel.
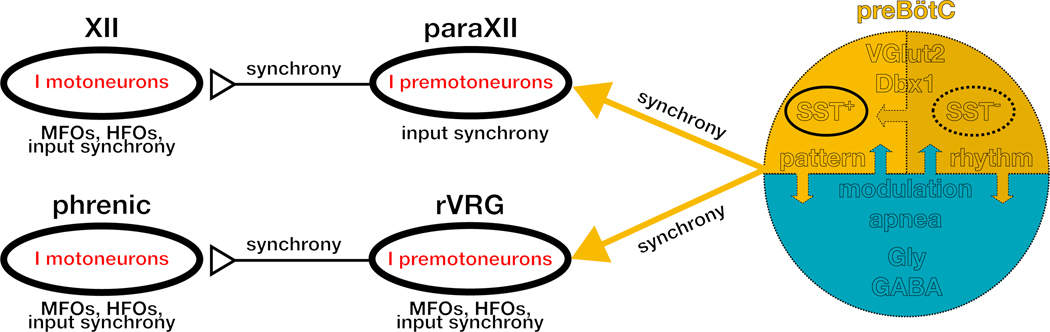
Figure 8. Synchronous propagation of preBötC activity to motor nuclei.
Diagrammatic representation of synchronized preBötC output that propagates through premotor and motor inspiratory networks. Synchrony arises from correlated activity of preBötC rhythmogenic neurons, which are SST−, and propagates via preBötC output neurons, a subset of which are SST+, to inspiratory premotoneurons, in, e.g., parahypoglossal nucleus (paraXII) and rostral ventral respiratory group (rVRG) to inspiratory motoneurons, e.g., XII and phrenic motor nucleus. MFOs = Medium Frequency (15–50 Hz) Oscillations; HFO = High Frequency (50–120 Hz) Oscillations. The schematic is based on data presented here as well as in (Christakos et al., 1991; Ellenberger et al., 1990; Feldman et al., 1980; Funk and Parkis, 2002; Huang et al., 1996; Liu et al., 1990; Mitchell and Herbert, 1974; Parkis et al., 2003; Schmid et al., 1990; Tan et al., 2010; Wang et al., 2002; Yang and Feldman, 2018).
Under nonrhythmic conditions, the synaptic noise onto I-M SST+ was higher compared to rhythmic conditions, brought about by either increased network excitation (9mM [K+]ACSF) or inhibitory blockade (Figures 2A, 5D,H–I and 6A, G–H). This suggests that that their presynaptic neurons (including Type-1 neurons) are tonically active under nonrhythmic conditions. We postulate that this could be due interactions between the background tonic inputs and intrinsic properties, such as the persistent Na conductance, which is active at near resting membrane potentials (−60 mV) and can critically regulate suprathreshold excitability in neurons (Carter et al., 2012; Del Negro et al., 2002a; Del Negro et al., 2005; Mishra and Narayanan, 2019; Pace et al., 2007a). Once network excitability was increased or inhibition blocked, rhythmogenic neurons could synchronize to give rise to preI and I-bursts (Figures 2, 3, 5 and 6). The onset of rhythmic bursting was concomitant with a decrease in their activity during interburst intervals, marking a refractory period for their synchronization. This postburst refractory period is typical of Type-1 preBötC neurons (Baertsch et al., 2018; Del Negro et al., 2010; Feldman et al., 2013) and provides another line of evidence that they are rhythmogenic neurons.
Under nonrhythmic conditions, rhythmogenic neurons were tonically active with no underlying rhythmicity, as evident by high synaptic noise in the I-M SST+ neurons (Figures 2B1,5D1, 5H, 6A1, 6G). Rhythm emerges only when rhythmogenic neurons synchronize, periodically, to drive outputs of the downstream I-M SST+ neurons (Figure 2A, 4A, 5D,6A). Thus, our results suggest that inspiratory rhythm is an emergent network property where several synaptic and intrinsic components interact to produce strong network synchronization and consequent synchrony propagation (Del Negro et al., 2018; Del Negro et al., 2010; Del Negro et al., 2002b). It is important to note that our proposed mechanism of inspiratory rhythmogenesis depends on spike correlation-based evolution of network dynamics for which pacemaker(-like) or post-inhibitory-rebound potential-induced firing is not necessary. This is in contrast with many rate-based models of inspiratory rhythmogenesis where I-bursts arise due to mechanisms based on average firing rate of neurons over a broad temporal window, e.g., (Butera et al., 1999a, b; Del Negro et al., 2005; Morgado-Valle et al., 2010; Phillips et al., 2019; Rekling and Feldman, 1998).
Dynamic formation of neuronal ensembles in every inspiratory cycle
While synchronous inputs reliably drive each inspiratory cycle, the underlying evolution of the EPSP correlation between I-M SST+ neurons varies on a cycle-to-cycle basis (Figure 3C1–C3), implying that detailed network dynamics vary, i.e., in each cycle the network synchronizes through reliable formation of dynamical cell assemblies (Buzsaki and Draguhn, 2004; Carroll and Ramirez, 2013; Tsukada et al., 1996) that has a random or chaotic element in terms of which neurons seed the synchronization. The inherent variability in the evolution of synchrony in this microcircuit could manifest as jitter in preI duration (which marks the onset of network synchronization) observed in slices (240 ± 10 ms; mean ± sem; range = 63 ms to 588 ms; data for preI events in Figure 3C1) (also compare Figures 2B3, 4A and 7C), as well as in the preceding IBIs that reflects the time necessary for the network to (re)assemble. Additionally, the preI duration mirrors the latency to induce ectopic I-bursts following synchronous stimulation of very few (3–9) randomly chosen preBötC neurons during the IBI in vitro (Kam et al., 2013b); we hypothesize that this latency to I-burst onset reflects the same process as underlying preI, where synchronization is seeded by random onset in activity of a few neurons in the preBötC rhythmogenic microcircuit. Similarly, under conditions of reduced network drive, cycle-to-cycle temporal variability in the evolution of network synchrony can contribute to increased jitter in the period of I-bursts, i.e., breathing frequency (Wang et al., 2014) (Figure S4A–B). Since synchronization can be initiated by only a few neurons, the fact that the rhythmogenic microcircuit has ~600–1000 neurons (in rodents; (Gray et al., 2001)) assures robustness as a statistical consequence (Strogatz and Stewart, 1993).
GABAergic and glycinergic inhibition regulate distinct aspects of rhythm and pattern generation respectively
Activity of GABAergic neurons appears to regulate synchronization of rhythmogenic (SST−) preBötC neurons. Thus, under control conditions, active GABAA inhibition can prevent synchronization of these neurons. Once GABAARs were blocked, these rhythmogenic SST− neurons could synchronize periodically to give rise to rhythmic I-bursts. These results rule out the possibility that postinhibitory rebound in essential for inspiratory burst generation. Counterintuitively, even when the inhibition was substantially reduced (by GABAAR blockade), the overall synaptic activity onto I-M SST+ neurons decreased during the IBI (Figures 5D, H–I). Consequently, global wavelet power of the of I-M SST+ neurons also decreased (Figure 5E). Thus, the emergence of periodic input synchrony onto I-M SST+ neurons along with a decrease in the input frequency during IBI, with GABAAR blockade, suggests GABAA inhibition is a critical regulator of emergent preBötC network dynamics, not simply a gain modulator. Antagonizing GABAARs also led to a higher conductance state in I-M SST+ neurons that was abolished, at least in part, upon blockade of glycinergic and GABAB receptors. As the higher conductance state resulted in a decrease in EPSP amplitude (Figure 5F–G, J), this could also contribute to the decrease in spectral power in the of I-M SST+ neurons upon GABAAR blockade (Figure 5E). These observations are direct evidence that network synchronization, irrespective of any generic increase in average population firing rate, is a key driving force for preBötC rhythmicity (Figures 5D–E, 6A1–A2, D). Furthermore, these experiments reveal complex interactions among various neuronal subtypes underlying the switch from a nonrhythmic (asynchronous) state to a rhythmic (synchronous) state of the preBötC microcircuit (Figure 7I). Thus, GABAA regulates network synchrony, but glycinergic and GABAB do not, while still able to affect mechanisms that shape pattern and assure propagation of I-bursts.
The higher conductance state resulting from antagonizing GABAA receptors appears to be a consequence of increased activation of glycinergic neurons, possibly due to disinhibition of these neurons resulting in increased glycinergic inputs onto I-M SST+ neurons. Since the of recorded neurons was close to the reversal potential of chloride conductances (Shao and Feldman, 1997), we hypothesize that the induction of the higher conductance state in I-M SST+ neurons is through shunting inhibition; this is consistent with the previously described roles of shunting inhibition in regulation of neuronal subthreshold membrane voltage as well as their firing rates (Brizzi et al., 2004; Mitchell and Silver, 2003). That I-M SST+ neurons transition to a higher conductance state in going from 3 mM to 9 mM [K+]ACSF (Figure S5) suggests that network synchronization and increased conductance state of these neurons are tightly coupled. This represents an emergent feature of the preBötC microcircuit common across experimental conditions employed to induce rhythmicity.
Higher conductance state, co-incidence detection and synchrony propagation
Input synchrony and higher conductance state in the I-M SST+ neurons concurrently interact to produce rhythmic I-bursts. This is a manifestation of efficient cellular and circuit level coordination (Barlow, 1961; Das and Narayanan, 2017; Deneve et al., 2017). The higher conductance state changes neuronal integrative properties such that a shorter and an increased temporal resolution renders them more responsive to higher frequency inputs, thereby favoring coincidence detection and enhancing their selectivity to synchronous inputs (Contreras and Steriade, 1996; Destexhe et al., 2003; Fernandez et al., 2011; Ratte et al., 2013; Rudolph and Destexhe, 2003; Stevens and Zador, 1998). This selectivity, especially during preI and I-bursts, facilitates propagation of synchronous population activity in the downstream efferent neuronal populations (Diesmann et al., 1999; Kumar et al., 2010; Ratte et al., 2013). In agreement with this mechanism, synchrony propagation in the inspiratory motor network (Figure 8) is seen in medullary inspiratory premotoneurons (Mitchell and Herbert, 1974) projecting onto hypoglossal (Wang et al., 2002) and phrenic (Parkis et al., 2003) motoneurons, as well as in the high frequency (HFO; 50–100 Hz) and medium frequency (MFO; 20–50 Hz) oscillations present during inspiration in the: i) discharge patterns of inspiratory premotoneurons and motoneurons (Christakos et al., 1991; Ellenberger et al., 1990; Feldman et al., 1980; Huang et al., 1996; Tan et al., 2010; Yang and Feldman, 2018), and; ii) motor nerves projecting to inspiratory muscles (Christakos et al., 1991; Funk and Parkis, 2002; Schmid et al., 1990). Taken together, strong association between the network dynamics and neuronal properties that facilitate synchrony transfer (Ratte et al., 2013) is compelling evidence that the inspiratory motor command is a form of temporal neuronal code (Buzsaki and Draguhn, 2004; Srivastava et al., 2017) that, among other possibilities, increases the reliability of propagation of inspiratory drive from its source, i.e., preBötC, to the ultimate neural output, i.e., motoneurons
While our study focuses on mechanisms of inspiratory rhythmogenesis, I-burst initiation and propagation, the mechanisms of I-burst termination and control of IBI remain open questions. Both burstlets and I-bursts self-terminate, even when all inhibition is blocked (Figures 6A2, B). We speculate that an important contributing factor is a decrease in synaptic efficacy following network synchronization, e.g., due to increased neuronal conductance (Bernander et al., 1994). Moreover, while not essential to rhythmogenesis, inhibition originating in the preBötC does powerfully regulate the duration and shape of I-bursts, and modulates breathing frequency (Baertsch et al., 2018; Baertsch et al., 2019; Janczewski et al., 2013; Shao and Feldman, 1997; Sherman et al., 2015).
Finally, recent studies have uncovered widespread coupling of breathing rhythms with many other brain regions regulating or affecting behaviors, e.g., whisking (Moore et al., 2013), attention control (Yackle et al., 2017), and possibly higher cognitive function through bottom-up respiratory modulation of neuronal activity in hippocampus and prefrontal cortex (Karalis and Sirota, 2018). In the light of divergent ascending projections of preBötC output neurons through mono- and oligo-synaptic connections (Yang and Feldman, 2018), synchronized oscillations in inspiratory motoneurons (Christakos et al., 1991; Funk and Parkis, 2002) and entrainment of limbic neurons by respiratory corollary discharge (Karalis and Sirota, 2018), we hypothesize that preBötC synchrony plays a critical role in the extraordinary reliability and robustness of networks underlying respiratory motor output as well as in the suprapontine propagation of breathing rhythms that can serve for binding of activity with and across higher brain regions that can affect emotional state and cognitive function.
The unique studies here, where we explored the mechanisms underlying a directly measurable output (motoneuronal activity) of a critical behavior, i.e., breathing rhythmogenesis, were possible because the preBötC is the only mammalian kernel of rhythmicity that is clearly localized. The mechanisms of synchrony revealed in this novel probing of neuronal circuits underlying breathing movements represent a fundamental principle of network signal processing that might be expanded to understand other mammalian neuronal circuits underlying behavior.
STAR METHODS
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jack L Feldman (feldman@g.ucla.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Mice
Animal use was in compliance with the guidelines approved by the UCLA Institutional Animal Care and Use Committee. Mice were housed in vivarium with 12-hour light/dark cycle and food and water was supplied ad libitum. Adult SST-Cre (IMSR Cat# JAX:013044, RRID: IMSR_JAX:013044) mice were crossed to Ai14 Cre-reporter mice (IMSR Cat# JAX:007914, RRID: IMSR_JAX:007914) to generate the SST reporter line used for in vitro slice experiments. All experiments were performed using the reporter line neonates between postnatal 0 to postnatal 7 days old.
METHOD DETAILS
In Vitro slice preparation and electrophysiological recordings.
The neuraxis containing the brainstem and the spinal cord from neonatal mice of either sex was isolated and one transverse brainstem slice (550 μm-600 μm thick) was cut that contained the preBötC along with respiratory premotor and hypoglossal (XII) respiratory motor neurons and XII nerve (XIIn) rootlets. The slice was cut (using a Leica VT1200 slicer) such that the preBötC was on the surface of the slice when placed rostral side facing upwards and contained anatomical landmarks as described in (Ruangkittisakul et al., 2014). The slices were cut in chilled ACSF containing (in mM): 124 NaCl, 3KCl, 1 MgSO4, 25 NaHCO3, 0.5 NaH2PO4 and 30 D-glucose, bubbled with 95% CO2 and 5% O2, at 7.4 pH
For electrophysiological recordings, slices were perfused with ACSF (32–34°C) at 4 ml/min in the recording chamber where they were allowed to recover for at least 30 minutes in normal ACSF before the start of recordings. To record preBötC and XIIn population activity, ACSF-filled suction electrodes were used (~150 μm tip diameter) pulled from borosilicate glass (1.2 mm outer diameter with 0.52 mm wall thickness) using a P-97 puller (Sutter Instruments). Data was acquired through a differential AC amplifier (A-M Systems, Model 1700), filtered at 1–5 kHz and digitalized using a MultiClamp 700B (Molecular Devices). The sampling frequency was either 20 or 40 kHz. The population recording time series was full wave rectified and integrated using a custom built analog Paynter filter with a time constant of 15 ms. The integrated data lacked scale for comparisons across experiments and, thus, was represented as normalized arbitrary units (Kam et al., 2013a).
For intracellular whole-cell current-clamp clamp recordings, fluorescently labeled (tdTomato) somatostatin-positive (SST+) neurons were patched under visually guided video microscopy using an upright microscope (either Zeiss Examiner A1or Olympus BX51W1) fitted with DIC optics and CCD camera (Andor Technology iXon or Hamamatsu C11440). The preBötC boundary was ventral to nucleus ambiguous and lateral to the principle loop of inferior olive. Neurons were patched with glass electrodes of ~1μm tip diameter with electrode resistance of 5–8 MΩ. Electrodes were pulled from borosilicate glass capillary (1.5 mm outer diameter, 0.64 mm wall thickness) using a P-97 microelectrode puller (Sutter Instruments) and filled with intracellular solution containing (in mM): 120 K-gluconate, 20 KCl,10 HEPES, 4 NaCl, 4 Mg-ATP,0.3 Na-GTP, and 7 K2-phosphocreatine (pH= 7.3 adjusted with KOH, osmolarity ~310 mOsm). Whole-cell current-clamp recordings were performed on SST+ neuronal somata using a Dagan IX2–700 amplifier and data was digitalized using a MultiClamp 700B at either 20 or 40 kHz. Measured liquid junction potential (LJP) between the pipette solution and ACSF was 16–20 mV and it was not compensated during the experiment. Unless otherwise noted, all neurons were hyperpolarized to ~–75 mV by negative current injection to record synaptic inputs and minimize their generation of APs. Resting membrane potential at break-in (without LJP compensation) was between –48 mV to –60 mV. Series resistance () and series capacitance (Cs) was monitored by examining the voltage response of the patched neurons to a hyperpolarizing current injection of 10 pA and was compensated online through bridge balance, though high synaptic noise and hence fluctuating membrane potential meant that the compensation was only approximate. range was between 13 MΩ−40 MΩ.
Pharmacology.
To block γ-aminobutyric acid (GABA) type A receptors (GABAAR), glycine receptors (GlyR) and GABAB receptors 10 μM (−)Bicuculline methiodide (Tocris Bioscience), 2 μM Strychnine hydrochloride (Tocris Bioscience) and 2 μM CGP55845 (Tocris Bioscience) were used, respectively.
To induce inspiratory rhythm in preBötC slices either [K+]ACSF was increased to 9 mM or inhibition was pharmacologically blocked in normal, i.e., 3 mM [K+]ACSF.
Simulations.
A biophysically realistic conductance based single-compartmental (isopotential) model of preBötC neuron was simulated as a cylinder 20 μm in diameter and 20 μm long with the following passive parameters: membrane capacitance, μF/cm2; specific membrane resistance and axial resistivity . These parameters were chosen such that the input resistance, , of the model neuron was 350 MΩ, which falls in the range of experimentally observed values of for I-M SST+ neurons (Figures 3I and 3M). Two voltage-gated ion channels, i.e., a fast sodium (NaF) and a delayed rectifier potassium (KDR), were incorporated into the model. Each ion channel was modeled using a Hodgkin-Huxley formulation adopted from (Migliore et al., 1999). NaF channel density was 45 mS/cm2 and KDR channel density was 15 mS/cm2. Current through α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptors was modeled as a combination of sodium and potassium currents:
| (8) |
where,
| (9) |
| (10) |
where is the maximum permeability of AMPAR that was set to 1×10−7 cm/s so that the resultant EPSP amplitude was 2.5 mV, which approximates the mean amplitude of spontaneous EPSPs of I-M SST+ neurons under normal ACSF (Figures 3F and 3O). was set equal to (Dingledine et al., 1999). determined the kinetics of current through AMPAR and was defined as:
| (11) |
where is a normalization constant to ensure that . ms and ms(Narayanan and Johnston, 2010).
All simulations were performed in the NEURON simulation environment (Hines and Carnevale, 1997) with the integration time step of 25 μs. Resting membrane potential was set at −75 mV, simulation temperature was 34°C and ion channel kinetics were adjusted per their experimentally determined coefficients.
Data analysis.
To estimate input resistance, , a hyperpolarizing pulse of 10 pA, 1s duration was applied for 10–30 trials (Figure S3G-H). The average membrane potential deflection was then divided by the injected current to estimate . To compute membrane time constant, , the repolarizing phase of the averaged trace was fitted with an exponential function of form:
| (1) |
where , A and are fit coefficients and is the steady-state value of at the end of repolarization. For these estimates, only trials in the interburst intervals were considered.
To compute population firing rate from population recordings (Figure S1 A3), the raw signal was first band-pass filtered between 300 Hz to 3 kHz to get multiunit activity (MUA). From this MUA, extracellular action potentials, exhibiting positive and negative polarity, were detected as peaks that were greater than a predetermined threshold in either direction and were separated from each other by at least 1.5 ms (to avoid multiple detection of same spike). The threshold for spike detection was determined by the noise level (representing neuronal + signal noise) present under the non-rhythmic condition (in normal ACSF) and in this case (Figure S1A3) was set to 10 μV. Spike times of detected spikes was converted into instantaneous firing frequency which was then box smoothed twice, with a window of 2 ms, to give rise to the final population firing rate trace.
Wavelet analysis.
Time frequency decomposition of neuronal by continuous wavelet transform (CWT) was implemented through guidelines presented in (Torrence and Compo, 1998). Briefly, was subtracted from its mean and normalized by its standard deviation. Thereafter, CWT was performed on the resultant time series, , defined as the convolution of with scaled and translated version of the wavelet function :
| (2) |
where the (*) indicates complex conjugate. The minimum scale, , was fixed at 0.0153 s (corresponding to 64 Hz). Subsequent scales were determined as:
| (3) |
| (4) |
Where, determined the largest scale and , i.e., increment of , was fixed at 0.025. Thus, the total number of scales was . is the normalized version of which is the complex Morlet wavelet defined as:
| (5) |
Where is the nondimensional frequency chosen to be 6 to satisfy the admissibility criterion for a Morlet wavelet(Torrence and Compo, 1998). is the nondimensional time parameter. was normalized to give so that at each scale, s, the wavelet function has unit energy irrespective of the scale size:
| (6) |
This made it possible to directly compare the wavelet transform at each scale and to the wavelet transforms of other time series (Torrence and Compo, 1998), i.e., wavelet transforms of of a given neuron under inspiratory rhythmic and non-rhythmic conditions. The global wavelet spectrum was computed as the time averaged wavelet spectrum over entire time multiplied by the variance of the original signal. For significance testing the global wavelet spectrum of under nonrhythmic conditions (normal ACSF) was chosen as background spectrum for each neuron. Peaks in the wavelet spectrum of the of the same neuron under rhythmic condition was then considered to be above the background spectrum with 5% significance level (or 95% confidence level) if it was above the product of background spectrum with 95th percentile value for chi-square distribution having two degrees of freedom (Torrence and Compo, 1998). Wavelet software was provided by C. Torrence and G. Compo: http://paos.colorado.edu/research/wavelets/.
Unless otherwise stated, only epochs of without APs were analyzed. When containing APs was used, they were removed through median filtering in a two-step process. First, in a large window of 10–13 ms all data points greater than 3 mV from the median were replaced by the median. This selectively removed AP peaks with sharp transients at the base of the truncated APs. The filtered signal was again median filtered with a 2 ms window to remove these transients. This process ensured that only APs were removed from the trace without distorting synaptic potentials. To get the envelope of deflections during the epochs of synchronous inputs (Figure 7 D–H), traces were median filtered with a 25 ms window.
For paired whole-cell patch-clamp recordings, fluorescently labelled SST+ neuronal pairs were patched at intersomatic distance of 10–100 μm. The normalized cross-correlation between two time series, and ( of paired neurons for our analysis), was calculated as follows (Graupner and Reyes, 2013):
| (7) |
where, is the total length of the signal, and and and are means and standard deviations of and respectively. The value of varies from −1 to 1 such that two identical signals will have a value of 1 at zero time lag . PreI duration was determined as the time between the onset of preBötC activity and the onset of an I-burst in the XIIn. The onset of preBötC activity was determined by the start of positive inflection in the differentiated ∫preBötC trace. For one I-M SST+ pair. XIIn was not active, hence the preI period was determined by the initial slope of ∫preBötC trace (Figure S2 B4) (Kam et al., 2013a). Epochs of interburst intervals (IBI) extracted from trace were ~1 second after the termination of the I-burst and did not overlap with the subsequent preBötC burstlet. For direct comparison, the duration of analyzed IBI epochs was fixed at the duration of the preI period preceding it.
To probe synaptic connections between the recorded neurons, a depolarizing current pulse was injected sequentially in each neuron to produce APs. The spike triggered average of in non-firing neurons was computed to ascertain synaptic connectivity. To probe electrical coupling a hyperpolarizing current was injected in sequentially in each neuron while both the neurons of the pair was recorded simultaneously. The coupling coefficient was computed as the ratio of peak voltage deflection in the unstimulated neuron vs that in the stimulated neuron.
For quantification of spontaneous excitatory postsynaptic potentials (EPSPs), 100–300 s epochs of from I-M SST+ neurons were used. Custom semi-automated peak detection software was used to select for spontaneous EPSPs. Due to very high synaptic noise, the start and end of each EPSP was manually specified to avoid temporally clustered EPSPs being falsely detected as a unitary EPSP. Only those EPSPs which did not have any visually detectable inflections in their rising phase were considered for analysis. When there were overriding EPSPs in the decay phase of a selected EPSP, its full width at half maximal (FWHM) duration was not computed. This resulted in a reduced number of events that were analyzed for FWHM as compared to EPSPs amplitude and rise time (cf. Figures 3 F–H and 3 O–Q). EPSP amplitude was defined as the difference of peak from the baseline value for each event. 20%−80% rise time was defined as the duration in which the EPSP grew from 20% to 80% of peak amplitude. For non-I-M SST+ neurons, the recording duration was shorter and hence 50–100 s epochs were used for EPSP analysis.
QUANTIFICATION AND STATISTICAL ANALYSIS
Data was analyzed using custom software in Igor Pro (version 7.4; WaveMetrics Inc.). Statistical analyses were performed using R software (www.r-project.org). Sample size was not predetermined. Normality was neither tested nor assumed and hence, for statistical testing, non-parametric tests were used. For box-and-whisker plots, center line represents the median; box limits, upper and lower quartiles and whiskers represent 90 and 10 percentile range.
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| N/A | ||
| Bacterial and Virus Strains | ||
| N/A | ||
| Biological Samples | ||
| N/A | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| (−)Bicuculline methiodide | Tocris Bioscience | Cat#2503; CAS#40709–69-1 |
| Strychnine hydrochloride | Tocris Bioscience | Cat#2785; CAS# 1421–86-9 |
| CGP55845 hydrochloride | Tocris Bioscience | Cat# 1248; CAS# 149184–22-5 |
| Critical Commercial Assays | ||
| N/A | ||
| Deposited Data | ||
| N/A | ||
| Experimental Models: Cell Lines | ||
| N/A | ||
| Experimental Models: Organisms/Strains | ||
| Mouse: SST-Cre also known as Sst-IRES-Cre | The Jackson Laboratory | RRID: IMSR_JAX:013044 |
| Mouse: Ai14 Cre-reporter | The Jackson Laboratory | RRID: IMSR_JAX:007914 |
| Oligonucleotides | ||
| N/A | ||
| Recombinant DNA | ||
| N/A | ||
| Software and Algorithms | ||
| Wavelet analysis software | Torrence and Compo, 1998 | http://paos.colorado.edu/research/wavelets/ |
| NEURON Simulation environment | Hines and Carnevale, 1997 | https://www.neuron.yale.edu/neuron/ |
| Igor Pro version 7.4 | WaveMetrics Inc | https://www.wavemetrics.com |
| R Software | The R Project for Statistical Computing | www.r-project.org |
| Other | ||
| N/A | ||
Highlights.
Mechanisms underlying rhythm generation in preBötzinger Complex are unknown
Rhythm emerges via spike synchronization of neurons in the rhythmogenic microcircuit
Excitation-inhibition balance within the microcircuit regulates synchrony
Reliable propagation of inspiratory command to motoneurons enhanced by synchrony
Acknowledgements
This work was supported by NIH-NHLBI grant 1R35HLI35779. We thank D.V.Buonomano, A. Kumar and R. Narayanan for their insights and discussion on this project and R. Abreu, D.N. Chiu, Hailan Hu, K. Kam, C.T. Pérez, M. Shao and C.F. Yang for their comments on earlier versions of this manuscript.
Footnotes
Declaration of interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
DATA AND CODE AVAILABILITY
The datasets generated during this study are available from the corresponding author upon reasonable request.
References
- Ashhad S, Johnston D, and Narayanan R. (2015). Activation of InsP3 receptors is sufficient for inducing graded intrinsic plasticity in rat hippocampal pyramidal neurons. J Neurophysiol 113, 2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashhad S, and Narayanan R. (2019). Stores, Channels, Glue, and Trees: Active Glial and Active Dendritic Physiology. Mol Neurobiol 56, 2278–2299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baertsch NA, Baertsch HC, and Ramirez JM (2018). The interdependence of excitation and inhibition for the control of dynamic breathing rhythms. Nat Commun 9, 843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baertsch NA, Severs LJ, Anderson TM, and Ramirez JM (2019). A spatially dynamic network underlies the generation of inspiratory behaviors. Proc Natl Acad Sci U S A 116, 7493–7502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barlow HB (1961). Possible principles underlying the transformation of sensory messages. In Sensory communication, Rosenblith WA, ed. (Cambridge, MA: The MIT Press; ), pp. 217–234. [Google Scholar]
- Bartos M, Vida I, Frotscher M, Meyer A, Monyer H, Geiger JR, and Jonas P. (2002). Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks. Proc Natl Acad Sci U S A 99, 13222–13227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernander O, Koch C, and Usher M. (1994). The Effect of Synchronized Inputs at the Single Neuron Level. Neural Computation 6, 622–641. [Google Scholar]
- Bongianni F, Mutolo D, Cinelli E, and Pantaleo T. (2010). Respiratory responses induced by blockades of GABA and glycine receptors within the Botzinger complex and the pre-Botzinger complex of the rabbit. Brain Res 1344, 134–147. [DOI] [PubMed] [Google Scholar]
- Bouvier J, Thoby-Brisson M, Renier N, Dubreuil V, Ericson J, Champagnat J, Pierani A, Chedotal A, and Fortin G. (2010). Hindbrain interneurons and axon guidance signaling critical for breathing. Nat Neurosci 13, 1066–1074. [DOI] [PubMed] [Google Scholar]
- Brizzi L, Meunier C, Zytnicki D, Donnet M, Hansel D, Lamotte D’Incamps B, and Van Vreeswijk C. (2004). How shunting inhibition affects the discharge of lumbar motoneurones: a dynamic clamp study in anaesthetized cats. J Physiol 558, 671–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butera RJ Jr., Rinzel J, and Smith JC (1999a). Models of respiratory rhythm generation in the pre-Botzinger complex. I. Bursting pacemaker neurons. J Neurophysiol 82, 382–397. [DOI] [PubMed] [Google Scholar]
- Butera RJ Jr., Rinzel J, and Smith JC (1999b). Models of respiratory rhythm generation in the pre-Botzinger complex. II. Populations Of coupled pacemaker neurons. J Neurophysiol 82, 398–415. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, and Draguhn A. (2004). Neuronal oscillations in cortical networks. Science 304, 1926–1929. [DOI] [PubMed] [Google Scholar]
- Carroll MS, and Ramirez JM (2013). Cycle-by-cycle assembly of respiratory network activity is dynamic and stochastic. J Neurophysiol 109, 296–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter BC, Giessel AJ, Sabatini BL, and Bean BP (2012). Transient sodium current at subthreshold voltages: activation by EPSP waveforms. Neuron 75, 1081–1093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christakos CN, Cohen MI, Barnhardt R, and Shaw CF (1991). Fast rhythms in phrenic motoneuron and nerve discharges. J Neurophysiol 66, 674–687. [DOI] [PubMed] [Google Scholar]
- Contreras D, and Steriade M. (1996). Spindle oscillation in cats: the role of corticothalamic feedback in a thalamically generated rhythm. J Physiol 490 ( Pt 1), 159–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui Y, Kam K, Sherman D, Janczewski WA, Zheng Y, and Feldman JL (2016). Defining preBotzinger Complex Rhythm- and Pattern-Generating Neural Microcircuits In Vivo. Neuron 91, 602–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das A, and Narayanan R. (2017). Theta-frequency selectivity in the somatic spike triggered average of rat hippocampal pyramidal neurons is dependent on HCN channels. J Neurophysiol 118, 2251–2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Negro CA, Funk GD, and Feldman JL (2018). Breathing matters. Nat Rev Neurosci 19, 351–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Negro CA, Hayes JA, Pace RW, Brush BR, Teruyama R, and Feldman JL (2010). Synaptically activated burst-generating conductances may underlie a group-pacemaker mechanism for respiratory rhythm generation in mammals. Prog Brain Res 187, 111–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Negro CA, Koshiya N, Butera RJ Jr., and Smith JC (2002a). Persistent sodium current, membrane properties and bursting behavior of pre-botzinger complex inspiratory neurons in vitro. J Neurophysiol 88, 2242–2250. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Morgado-Valle C, and Feldman JL (2002b). Respiratory rhythm: an emergent network property? Neuron 34, 821–830. [DOI] [PubMed] [Google Scholar]
- Del Negro CA, Morgado-Valle C, Hayes JA, Mackay DD, Pace RW, Crowder EA, and Feldman JL (2005). Sodium and calcium current-mediated pacemaker neurons and respiratory rhythm generation. J Neurosci 25, 446–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deneve S, Alemi A, and Bourdoukan R. (2017). The Brain as an Efficient and Robust Adaptive Learner. Neuron 94, 969–977. [DOI] [PubMed] [Google Scholar]
- Destexhe A, Rudolph M, and Pare D. (2003). The high-conductance state of neocortical neurons in vivo. Nat Rev Neurosci 4, 739–751. [DOI] [PubMed] [Google Scholar]
- Diesmann M, Gewaltig MO, and Aertsen A. (1999). Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533. [DOI] [PubMed] [Google Scholar]
- Dingledine R, Borges K, Bowie D, and Traynelis SF (1999). The glutamate receptor ion channels. Pharmacol Rev 51, 7–61. [PubMed] [Google Scholar]
- Ellenberger HH, Feldman JL, and Goshgarian HG (1990). Ventral respiratory group projections to phrenic motoneurons: electron microscopic evidence for monosynaptic connections. J Comp Neurol 302, 707–714. [DOI] [PubMed] [Google Scholar]
- Feldman JL, Del Negro CA, and Gray PA (2013). Understanding the rhythm of breathing: so near, yet so far. Annu Rev Physiol 75, 423–452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman JL, and Kam K. (2015). Facing the challenge of mammalian neural microcircuits: taking a few breaths may help. J Physiol 593, 3–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman JL, and Smith JC (1989). Cellular mechanisms underlying modulation of breathing pattern in mammals. Ann N Y Acad Sci 563, 114–130. [DOI] [PubMed] [Google Scholar]
- Feldman JL, Sommer D, and Cohen MI (1980). Short time scale correlations between discharges of medullary respiratory neurons. J Neurophysiol 43, 1284–1295. [DOI] [PubMed] [Google Scholar]
- Fernandez FR, Broicher T, Truong A, and White JA (2011). Membrane voltage fluctuations reduce spike frequency adaptation and preserve output gain in CA1 pyramidal neurons in a high-conductance state. J Neurosci 31, 3880–3893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funk GD, and Parkis MA (2002). High frequency oscillations in respiratory networks: functionally significant or phenomenological? Respir Physiol Neurobiol 131, 101–120. [DOI] [PubMed] [Google Scholar]
- Graupner M, and Reyes AD (2013). Synaptic input correlations leading to membrane potential decorrelation of spontaneous activity in cortex. J Neurosci 33, 15075–15085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray PA, Hayes JA, Ling GY, Llona I, Tupal S, Picardo MC, Ross SE, Hirata T, Corbin JG, Eugenin J, and Del Negro CA (2010). Developmental origin of preBotzinger complex respiratory neurons. J Neurosci 30, 14883–14895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray PA, Janczewski WA, Mellen N, McCrimmon DR, and Feldman JL (2001). Normal breathing requires preBotzinger complex neurokinin-1 receptor-expressing neurons. Nat Neurosci 4, 927–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray PA, Rekling JC, Bocchiaro CM, and Feldman JL (1999). Modulation of respiratory frequency by peptidergic input to rhythmogenic neurons in the preBotzinger complex. Science 286, 1566–1568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guzman SJ, Schlogl A, Frotscher M, and Jonas P. (2016). Synaptic mechanisms of pattern completion in the hippocampal CA3 network. Science 353, 1117–1123. [DOI] [PubMed] [Google Scholar]
- Hines ML, and Carnevale NT (1997). The NEURON simulation environment. Neural Comput 9, 1179–1209. [DOI] [PubMed] [Google Scholar]
- Huang WX, Cohen MI, Yu Q, See WR, and He Q. (1996). High-frequency oscillations in membrane potentials of medullary inspiratory and expiratory neurons (including laryngeal motoneurons). J Neurophysiol 76, 1405–1412. [DOI] [PubMed] [Google Scholar]
- Janczewski WA, Tashima A, Hsu P, Cui Y, and Feldman JL (2013). Role of inhibition in respiratory pattern generation. J Neurosci 33, 5454–5465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kam K, Worrell JW, Janczewski WA, Cui Y, and Feldman JL (2013a). Distinct inspiratory rhythm and pattern generating mechanisms in the preBotzinger complex. J Neurosci 33, 9235–9245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kam K, Worrell JW, Ventalon C, Emiliani V, and Feldman JL (2013b). Emergence of population bursts from simultaneous activation of small subsets of preBotzinger complex inspiratory neurons. J Neurosci 33, 3332–3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karalis N, and Sirota A. (2018). Breathing coordinates limbic network dynamics underlying memory consolidation. bioRxiv doi: 10.1101/392530 [DOI] [Google Scholar]
- Koizumi H, Koshiya N, Chia JX, Cao F, Nugent J, Zhang R, and Smith JC (2013). Structural-functional properties of identified excitatory and inhibitory interneurons within preBotzinger complex respiratory microcircuits. J Neurosci 33, 2994–3009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A, Rotter S, and Aertsen A. (2010). Spiking activity propagation in neuronal networks: reconciling different perspectives on neural coding. Nat Rev Neurosci 11, 615–627. [DOI] [PubMed] [Google Scholar]
- Liu G, Feldman JL, and Smith JC (1990). Excitatory amino acid-mediated transmission of inspiratory drive to phrenic motoneurons. J Neurophysiol 64, 423–436. [DOI] [PubMed] [Google Scholar]
- Migliore M, Hoffman DA, Magee JC, and Johnston D. (1999). Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J Comput Neurosci 7, 5–15. [DOI] [PubMed] [Google Scholar]
- Miles R, and Wong RK (1986). Excitatory synaptic interactions between CA3 neurones in the guinea-pig hippocampus. J Physiol 373, 397–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra P, and Narayanan R. (2019). Conjunctive changes in two distinct ion channels induce activity-dependent intrinsic plasticity in rat dentate gyrus granule cells. bioRxive doi: 10.1101/747550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell RA, and Herbert DA (1974). Synchronized high frequency synaptic potentials in medullary respiratory neurons. Brain Res 75, 350–355. [DOI] [PubMed] [Google Scholar]
- Mitchell SJ, and Silver RA (2003). Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron 38, 433–445. [DOI] [PubMed] [Google Scholar]
- Moore JD, Deschenes M, Furuta T, Huber D, Smear MC, Demers M, and Kleinfeld D. (2013). Hierarchy of orofacial rhythms revealed through whisking and breathing. Nature 497, 205–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgado-Valle C, Baca SM, and Feldman JL (2010). Glycinergic pacemaker neurons in preBotzinger complex of neonatal mouse. J Neurosci 30, 3634–3639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Dougherty KJ, and Johnston D. (2010). Calcium Store Depletion Induces Persistent Perisomatic Increases in the Functional Density of h Channels in Hippocampal Pyramidal Neurons. Neuron 68, 921–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, and Johnston D. (2010). The h current is a candidate mechanism for regulating the sliding modification threshold in a BCM-like synaptic learning rule. J Neurophysiol 104, 1020–1033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace RW, Mackay DD, Feldman JL, and Del Negro CA (2007a). Inspiratory bursts in the preBotzinger complex depend on a calcium-activated non-specific cation current linked to glutamate receptors in neonatal mice. J Physiol 582, 113–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pace RW, Mackay DD, Feldman JL, and Del Negro CA (2007b). Role of persistent sodium current in mouse preBotzinger Complex neurons and respiratory rhythm generation. J Physiol 580, 485–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkis MA, Feldman JL, Robinson DM, and Funk GD (2003). Oscillations in endogenous inputs to neurons affect excitability and signal processing. J Neurosci 23, 8152–8158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips RS, John TT, Koizumi H, Molkov YI, and Smith JC (2019). Biophysical mechanisms in the mammalian respiratory oscillator re-examined with a new data-driven computational model. Elife 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Picardo MC, Weragalaarachchi KT, Akins VT, and Del Negro CA (2013). Physiological and morphological properties of Dbx1-derived respiratory neurons in the pre-Botzinger complex of neonatal mice. J Physiol 591, 2687–2703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratte S, Hong S, De Schutter E, and Prescott SA (2013). Impact of neuronal properties on network coding: roles of spike initiation dynamics and robust synchrony transfer. Neuron 78, 758–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rekling JC, and Feldman JL (1998). PreBotzinger complex and pacemaker neurons: hypothesized site and kernel for respiratory rhythm generation. Annu Rev Physiol 60, 385–405. [DOI] [PubMed] [Google Scholar]
- Rekling JC, Shao XM, and Feldman JL (2000). Electrical coupling and excitatory synaptic transmission between rhythmogenic respiratory neurons in the preBotzinger complex. J Neurosci 20, RC113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruangkittisakul A, Kottick A, Picardo MC, Ballanyi K, and Del Negro CA (2014). Identification of the pre-Botzinger complex inspiratory center in calibrated “sandwich” slices from newborn mice with fluorescent Dbx1 interneurons. Physiol Rep 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudolph M, and Destexhe A. (2003). A fast-conducting, stochastic integrative mode for neocortical neurons in vivo. J Neurosci 23, 2466–2476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid K, Bohmer G, and Weichel T. (1990). Concurrent fast and slow synchronized efferent phrenic activities in time and frequency domain. Brain Res 528, 1–11. [DOI] [PubMed] [Google Scholar]
- Shao XM, and Feldman JL (1997). Respiratory rhythm generation and synaptic inhibition of expiratory neurons in pre-Botzinger complex: differential roles of glycinergic and GABAergic neural transmission. J Neurophysiol 77, 1853–1860. [DOI] [PubMed] [Google Scholar]
- Sherman D, Worrell JW, Cui Y, and Feldman JL (2015). Optogenetic perturbation of preBotzinger complex inhibitory neurons modulates respiratory pattern. Nat Neurosci 18, 408–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JC, Ellenberger HH, Ballanyi K, Richter DW, and Feldman JL (1991). PreBotzinger complex: a brainstem region that may generate respiratory rhythm in mammals. Science 254, 726–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava KH, Holmes CM, Vellema M, Pack AR, Elemans CP, Nemenman I, and Sober SJ (2017). Motor control by precisely timed spike patterns. Proc Natl Acad Sci U S A 114, 1171–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens CF, and Zador AM (1998). Input synchrony and the irregular firing of cortical neurons. Nat Neurosci 1, 210–217. [DOI] [PubMed] [Google Scholar]
- Stornetta RL, Rosin DL, Wang H, Sevigny CP, Weston MC, and Guyenet PG (2003). A group of glutamatergic interneurons expressing high levels of both neurokinin-1 receptors and somatostatin identifies the region of the pre-Botzinger complex. J Comp Neurol 455, 499–512. [DOI] [PubMed] [Google Scholar]
- Strogatz SH, and Stewart I. (1993). Coupled oscillators and biological synchronization. Sci Am 269, 102–109. [DOI] [PubMed] [Google Scholar]
- Sun X, Thorn Perez C, Halemani DN, Shao XM, Greenwood M, Heath S, Feldman JL, and Kam K. (2019). Opioids modulate an emergent rhythmogenic process to depress breathing. Elife 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan W, Janczewski WA, Yang P, Shao XM, Callaway EM, and Feldman JL (2008). Silencing preBotzinger complex somatostatin-expressing neurons induces persistent apnea in awake rat. Nat Neurosci 11, 538–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan W, Pagliardini S, Yang P, Janczewski WA, and Feldman JL (2010). Projections of preBotzinger complex neurons in adult rats. J Comp Neurol 518, 1862–1878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torrence C, and Compo GP (1998). A practical guide to wavelet analysis. B Am Meteorol Soc 79, 61–78. [Google Scholar]
- Tsukada M, Ichinose N, Aihara K, Ito H, and Fujii H. (1996). Dynamical Cell Assembly Hypothesis - Theoretical Possibility of Spatio-temporal Coding in the Cortex. Neural Netw 9, 1303–1350. [PubMed] [Google Scholar]
- Wallen-Mackenzie A, Gezelius H, Thoby-Brisson M, Nygard A, Enjin A, Fujiyama F, Fortin G, and Kullander K. (2006). Vesicular glutamate transporter 2 is required for central respiratory rhythm generation but not for locomotor central pattern generation. J Neurosci 26, 12294–12307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Irnaten M, Venkatesan P, Evans C, Baxi S, and Mendelowitz D. (2002). Synaptic activation of hypoglossal respiratory motorneurons during inspiration in rats. Neurosci Lett 332, 195–199. [DOI] [PubMed] [Google Scholar]
- Wang X, Hayes JA, Revill AL, Song H, Kottick A, Vann NC, LaMar MD, Picardo MC, Akins VT, Funk GD, and Del Negro CA (2014). Laser ablation of Dbx1 neurons in the pre-Botzinger complex stops inspiratory rhythm and impairs output in neonatal mice. Elife 3, e03427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter SM, Fresemann J, Schnell C, Oku Y, Hirrlinger J, and Hulsmann S. (2009). Glycinergic interneurons are functionally integrated into the inspiratory network of mouse medullary slices. Pflugers Arch 458, 459–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittmeier S, Song G, Duffin J, and Poon CS (2008). Pacemakers handshake synchronization mechanism of mammalian respiratory rhythmogenesis. Proc Natl Acad Sci U S A 105, 18000–18005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J, Capelli P, Bouvier J, Goulding M, Arber S, and Fortin G. (2017). A V0 core neuronal circuit for inspiration. Nat Commun 8, 544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yackle K, Schwarz LA, Kam K, Sorokin JM, Huguenard JR, Feldman JL, Luo L, and Krasnow MA (2017). Breathing control center neurons that promote arousal in mice. Science 355, 1411–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang CF, and Feldman JL (2018). Efferent projections of excitatory and inhibitory preBotzinger Complex neurons. J Comp Neurol 526, 1389–1402. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during this study are available from the corresponding author upon reasonable request.