Abstract
In causal mediation analysis, nonparametric identification of the natural indirect effect typically relies on, in addition to no unobserved pre-exposure confounding, fundamental assumptions of (i) so-called “cross-world-countterfactuals” independence and (ii) no exposure-induced confounding. When the mediator is binary, bounds for partial identification have been given when neither assumption is made, or alternatively when assuming only (ii). We extend existing bounds to the case of a polytomous mediator, and provide bounds for the case assuming only (i). We apply these bounds to data from the Harvard PEPFAR program in Nigeria, where we evaluate the extent to which the effects of antiretroviral therapy on virological failure are mediated by a patient’s adherence, and show that inference on this effect is somewhat sensitive to model assumptions.
Keywords: Cross-world counterfactual, Mediation, Natural indirect effect, Partial identification, Pure direct effect, Single World Intervention Graph
1. Introduction
Causal mediation analysis seeks to determine the role that an intermediate variable plays in transmitting the effect from an exposure to an outcome. An indirect effect refers to the effect that goes through the intermediate variable; a direct effect is a measure of the effect that does not. The study of causal mediation has enjoyed an explosion in popularity in recent years (Petersen, Sinisi, and van der Laan, 2006, Imai, Keele, and Tingley, 2010, Tchetgen Tchetgen and Shpitser, 2012, Shpitser, 2013, VanderWeele, 2015), not only in terms of theoretical developments, but also in practice. This has been most notable in the fields of epidemiology and social sciences. This strand of work is based on ideas originating from Robins and Greenland (1992) and Pearl (2001) grounded in the language of potential outcomes (Splawa-Neyman, Dabrowska, Speed et al., 1990, Rubin, 1974, 1978) to give nonparametric definitions of effects involved in mediation analysis, allowing for settings where interactions and nonlinearities may be present.
Consider an intervention which sets the exposure of interest for all subjects in the population to one of two possible values: a reference value or an active value. The total effect of such an intervention corresponds to the change of the counterfactual outcome mean if the exposure were set to the active value compared with if it were set to the reference value. Robins and Greenland (1992) formalized the concept of effect decomposition of the total effect into direct and indirect effects by describing pure direct and indirect effects using counterfactual language. Pearl (2001) further formalized this concept, giving general definitions using counterfactual notation to what he termed natural direct and indirect effects, as well as general identification results. The pure direct effect (PDE) corresponds to the change in the counterfactual outcome mean under an intervention which changes a person’s exposure status from the reference value to the active value, while maintaining the person’s mediator at the value it would have had under the exposure reference value. In contrast, the natural indirect effect (NIE) corresponds to the change in the average counterfactual outcome under an intervention that sets a person’s exposure value to the active value, while changing the value of the mediator from the value it would have had under the reference exposure value, to its value under the active exposure value. The PDE and NIE sum to give the total effect.
Identification of these natural effects has been somewhat controversial as it requires assumptions that may be overly restrictive for many applications. First, identification invokes a so-called cross-world-counterfactuals-independence assumption, which by virtue of involving counterfactuals under conflicting interventions on the exposure, cannot be enforced experimentally (Pearl, 2001, Robins and Richardson, 2010). Secondly, a necessary assumption for identification rules out the presence of exposure-induced confounding of the mediator’s effect on the outcome, even if all confounders are observed. While this assumption is in principle testable provided no unmeasured confounding, more often than not, post-exposure covariates are altogether ignored in routine application, in which case mediation analyses may be invalid. These issues have been considered recently, and some work has been done on partial or point identification under a weaker assumption. Specifically, on the one hand Robins and Richardson (2010) and Tchetgen Tchetgen and VanderWeele (2014) provide conditions for point identification of the PDE and NIE when a confounder is directly affected by the exposure. On the other hand, Robins and Richardson (2010) give bounds for the PDE and NIE for binary mediator without making the cross-world-counterfactual-independence assumption, but assuming no exposure-induced confounding of the mediator-outcome relation, and Tchetgen Tchetgen and Phiri (2014) extend these bounds to account for exposure-induced confounding. Bounds are commonly employed in causal inference when structural assumptions are not sufficiently strong to give point identification of a causal parameter of interest (Robins, 1989, Balke and Pearl, 1997, Zhang and Rubin, 2003, Kaufman, Kaufman, MacLehose, Greenland, and Poole, 2005, Cheng and Small, 2006, Cai, Kuroki, Pearl, and Tian, 2008, Sjölander, 2009, Taguri and Chiba, 2015). We build on this previous work to provide a number of new nonparametric bounds for the PDE and NIE allowing for a polytomous mediator under relaxations of the assumptions of (i) cross-world-counterfactuals independence, and (ii) no exposure-induced confounding, both separately and jointly. In particular, we relax assumption (ii) to allow for exposure-induced confounders when these confounders are measured and discrete. We apply these bounds to data from the Harvard PEPFAR program in Nigeria, where we evaluate the extent to which the effects of antiretroviral therapy on virological failure are mediated by a patient’s adherence.
2. Preliminaries
For a directed acyclic graph (DAG) consisting of nodes , and a given intervention assigning a subset of nodes to a fixed value , we denote the counterfactual value of a distinct node under this intervention by . In order to link these counterfactuals to the observed , we adopt the standard set of consistency assumptions that for any , and , if , then with probability one. Various causal models may be associated with a given DAG. We will focus on two in particular: the Nonparametric Structural Equation Model with Independent Errors (NPSEM-IE) of Pearl (2000) and the Finest Fully Randomized Causally Interpretable Structured Tree Graph (FFRCISTG) of Robins (1986). Let pa denote the parents of in the DAG, and denote the subset of corresponding to the subset , where gives the support of its argument. The NPSEM-IE is defined as the set of all probability distributions for which
are mutually independent; the FFRCISTG is the set of all probability distributions for which
are mutually independent for each . The NPSEM-IE associated with a particular DAG is then a subset of the associated FFRCISTG, as the former condition contains the latter. To illustrate the difference in these models, consider the directed acyclic graph (DAG) displayed in Fig. 1.A. The NPSEM-IE associated with this graph implies mutual independence of , , and for all , , and , whereas the associated FFRCISTG merely implies mutual independence of , , and for all and , i.e., when . When , , and are “cross-world counterfactuals” in the sense that they arise under conflicting interventions that could not occur simultaneously in the same world. Thus, the NPSEM-IE makes independence assumptions about cross-world counterfactuals, whereas the FFRCISTG only makes assumptions about counterfactuals in the “same world”.
Figure 1:
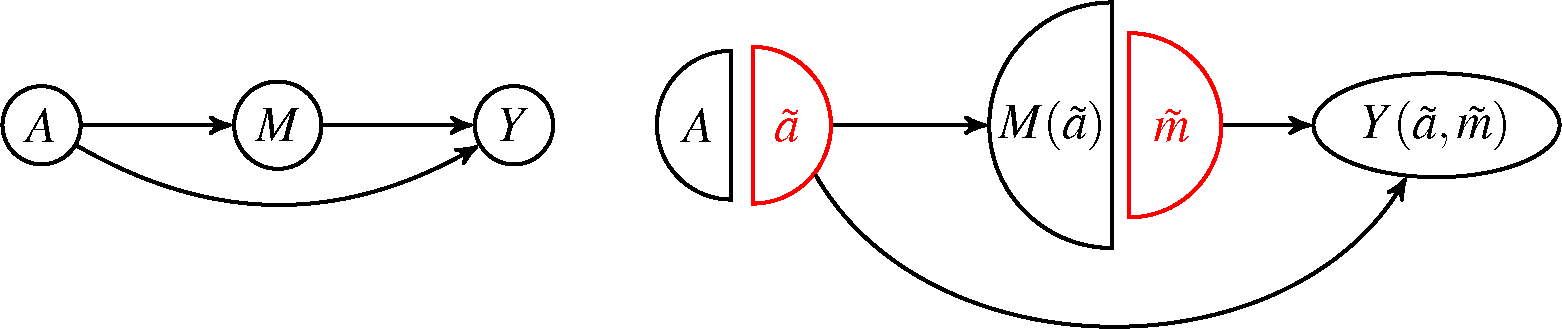
A. The three-node mediation directed acyclic graph in a setting with no confounding. The nodes represent random variables, and the arrows represent possible causal effects of one random variable on another. B. The single-world intervention graph in the setting of (a) under the intervention setting to and to . The black nodes represent random variables under this intervention, the red nodes represent the level an intervened random variable takes under this intervention, and the arrows represent possible causal effects of one variable under this intervention on another.
To view the NPSEM-IE another way, consider the nonparametric structural equations associated with the graph in Fig. 1.A. These provide a nonparametric algebraic interpretation of this DAG corresponding to three equations – one for each variable in the graph. Each random variable on the graph is associated with a distinct, arbitrary function, denoted , and a distinct random disturbance, denoted , each with a subscript corresponding to its respective random variable. Each variable is generated by its corresponding function, which depends only on all variables that affect it directly (i.e., its parents on the graph), and its corresponding random disturbance, as follows:
The NPSEM-IE conditions are equivalent to the condition that the random disturbances are mutually independent, hence the name “Nonparametric Structural Equation Model With Independent Errors”. The FFRCISTG can be formulated in the same way, but with weaker conditions on the random disturbances.
The graph in Fig. 1.A illustrates the simplest possible mediation setting, where is defined to be the exposure taking either baseline value or comparison value , is defined to be the (potential) mediator, and is defined to be the outcome. This DAG assumes randomization of the exposure, which for expositional simplicity we maintain throughout. Results in this paper can be extended to settings with observed pre-exposure confounders, and are given at the end of Section 3. The graph also encodes no unobserved confounding of the effect of on given . The effect along the path on the diagram is generally referred to as direct with respect to , and the effect along the path on the diagram as indirect with respect to . In terms of counterfactuals, the randomization assumption encoded by the DAG in Fig. 1.A is for all and ; the assumption of no unobserved confounding of given is for all and .
Richardson and Robins (2013) propose another form of causal graphs, known as Single-World Intervention Graphs (SWIGs). A SWIG is essentially a DAG that has been modified under a particular intervention to graphically encode the Markov factorization of the counterfactual distribution under that intervention. Operationally, for an intervention assigning a subset of nodes to a particular level , a SWIG splits each intervention node into two. The first is a “pre-intervention” node that has the value this random variable, say , would be observed to take under this intervention “just prior” to the intervention on this particular node, i.e., when all other nodes in besides are intervened on. This node will be counterfactual (potentially trivially) based on the other nodes being intervened on, and inherits only the edges entering its corresponding node in the DAG. The second is a “post-intervention” node that is the value that the node is actually set to under this intervention. Its value is deterministic, and inherits only the edges exiting its corresponding node in the DAG. The remaining non-intervention nodes are replaced by their corresponding counterfactual variables under this intervention.
These graphs manage to clear up some of the ambiguity inherent to DAGs by graphically representing the counterfactuals themselves, allowing independence statements of counterfactuals to be read directly from the graph using the rules of -separation (Pearl, 2000). These rules are applied just as in DAGs, with the exception that paths through deterministic-valued nodes are no longer considered to be -connecting. Consider the SWIG in Fig. 1.B. By -separation, it is clear that for all and , however no such statement can be made from the graph about and when . In fact, cross-world counterfactual independence statements are never implied by SWIGs, as each SWIG is defined only for a single intervention, hence the name “Single-World Intervention Graph”. Thus, SWIGs correspond only to FFRCISTGs and not NPSEM-IES.
For both full and partial identification of the PDE and NIE, we require the following positivity assumptions to be satisfied for and . Additionally, when exposure-induced confounding is present and sufficiently controlled for by measured variables , we require that and .
We will consider as well defined the nested counterfactual , i.e., the counterfactual outcome under an intervention which sets the exposure to the comparison value , and the mediator to the value it would have taken under the conflicting baseline exposure value . We may now define the pure/natural direct effect and natural indirect effect (Robins and Greenland, 1992, Pearl, 2001), which form the following decomposition of the average causal effect:
The terms , for all , are identified under randomization of . The parameter is identified under the NPSEM-IE interpretation of the DAG in Fig. 1.A. Under particular interventions, structural equations with independent errors naturally encode independences of cross-world counterfactuals. Consider, for example, two interventions, one setting , and another setting and . The structural equations then become
This model then implies that for all , (i) , (ii) , and (iii) , which in turn suffice for identification of (Pearl, 2001). Independence condition (iii) can be seen to hold under the model by observing that the only source of randomness in is and the only source of randomness in is . Thus, the cross-world-counterfactual-independence statement follows directly from independence of exogenous disturbances.
Cross-world counterfactual independence statements, however, are not experimentally enforceable (Robins and Richardson, 2010). This issue has been discussed extensively (Robins and Richardson, 2010, Richardson and Robins, 2013), and in large part motivated the development of SWIGs. Under the FFRCISTG corresponding to the SWIG in Fig. 1.B, independence between and is not assumed, and hence is not point identified. Robins and Richardson (2010) provide the following bounds for its partial identification in the setting where is binary and FFRCISTG independence assumptions and hold for all and :
In Section 3, we extend this result to the setting of a polytomous .
As previously mentioned, another often-overlooked condition required for identification of is that there is no confounder of the mediator’s effect on the outcome that is affected by the exposure. Such a confounder is present in the setting illustrated in the DAG in Fig. 2.A.
Figure 2:
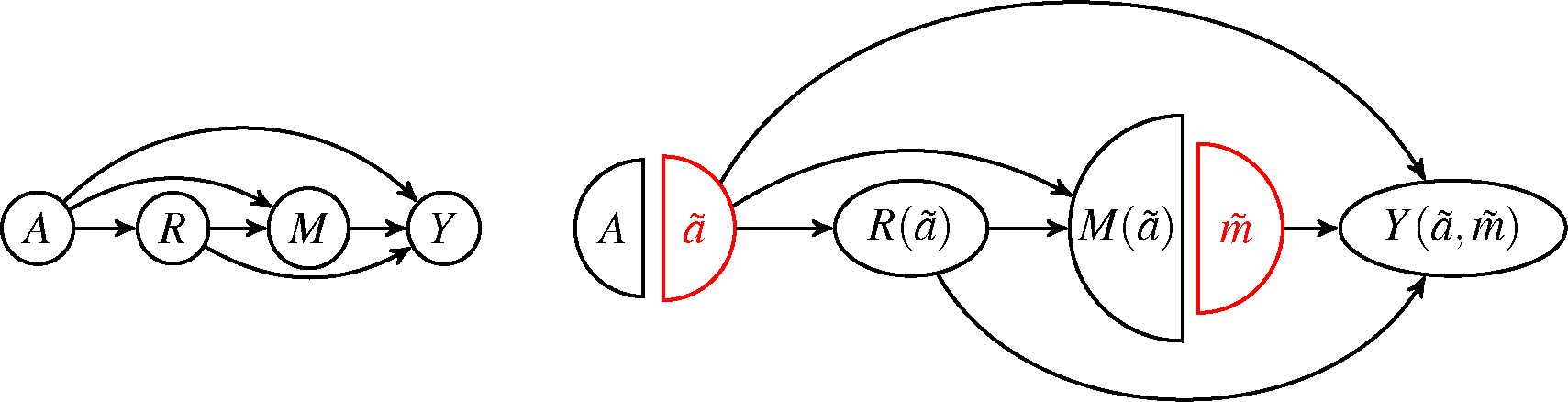
A. A mediation directed acyclic graph in which is an exposure-induced confounder. The nodes represent random variables, and the arrows represent possible causal effects of one random variable on another. B. The single-world intervention graph in the setting of (a) that has been intervened on to set to and to . The black nodes represent random variables under this intervention, the red nodes represent the level an intervened random variable takes under this intervention, and the arrows represent possible causal effects of one variable under this intervention on another.
Generally, even under an NPSEM-IE interpretation of this DAG, will not be identified in this setting. This is readily seen by considering the following representation under this model given by Robins and Richardson (2010):
| (1) |
Clearly the joint probability term can never be identified from observed data, since we will never be able to observe and for the same individual. Note however that the presence of poses no trouble if there is no direct effect of on . In this case, almost everywhere for all , and (1) reduces to
which is in fact identical to the identification formula under the NPSEM-IE with baseline confounders and no exposure-induced confounders. Thus, it is only when the confounders are directly affected by that is not identified.
A few conditions for identification in this setting have been proposed. Robins and Richardson (2010) give two. The first is that , in which case the troublesome term in (1) will factor, giving
It seems biologically unlikely, however, that in a scenario in which affects , the counterfactual under would not be predictive of the counterfactual under . The other condition is that the counterfactual outcome under one exposure value is a deterministic function of the counterfactual for the other treatment, i.e., . In this case,
The above assumption is implied by rank preservation (Robins and Richardson, 2010), which is unlikely to hold in social and health sciences as it rules out individual-level effect heterogeneity (Tchetgen Tchetgen and VanderWeele, 2014). As none of these conditions are experimentally verifiable, the authors themselves “do not advocate blithely adopting such assumptions in order to preserve identification of the PDE in [this setting]” (Robins and Richardson, 2010).
Tchetgen Tchetgen and VanderWeele (2014) give two testable conditions for identification of when is present. The first is of monotonicity, i.e., for Bernoulli , . If is a vector of Bernoulli random variables whose structural equations have independent errors, and if monotonicity holds for each element,
where
Their second condition is no additive mean interaction, i.e.,
for all levels and of and and of . For discrete and , this yields
Eschewing the cross-world-counterfactual assumptions of the NPSEM-IE, Tchetgen Tchetgen and Phiri (2014) extend the bounds of Robins and Richardson (2010) under an FFRCISTG to allow for the presence of an exposure-induced confounder when the mediator is binary:
We extend these bounds as well to allow for polytomous in Section 3. Additionally, we construct bounds for under an NPSEM-IE that account for an observed discrete exposure-induced confounder, but require no further assumption.
3. New partial identification results
We begin by extending the bounds of Robins and Richardson (2010) and Tchetgen Tchetgen and Phiri (2014) to settings with discrete mediator and outcome. Proofs can be found in the Appendix.
Theorem 1.
Under the FFRCISTG corresponding to the SWIG in either Fig. 1.B or Fig. 2.B with discrete and and arbitrary ,
The upper and lower bounds coincide when or is degenerate, which follows from the properties of joint probability mass functions. The upper and lower bounds are achieved only if and are perfectly dependent or perfectly negatively dependent, respectively, for each . This is formalized by the requirement that these counterfactuals be comonotone or countermonotone, respectively, for each . Comonotonicity of and holds if , where denotes the joint (or marginal) cumulative distribution function of a random vector (or scalar) ; countermonotonicity holds if (Nelsen, 2007). A straightforward application of the -formula under the DAGs in Fig. 1 and 2 yields the following corollaries:
Corollary 1.
For polytomous and , is partially identified under the FFRCISTG corresponding to the SWIG in Fig. 1.B by the bounds in Theorem 1 with and . It is partially identified under the FFRCISTG corresponding to the SWIG in Fig. 2.B by the same bounds, but with and .
The second part of the corollary continues to hold even when there is a hidden common cause of and as in Fig. 3, since the same -formula applies in this setting.
Figure 3:
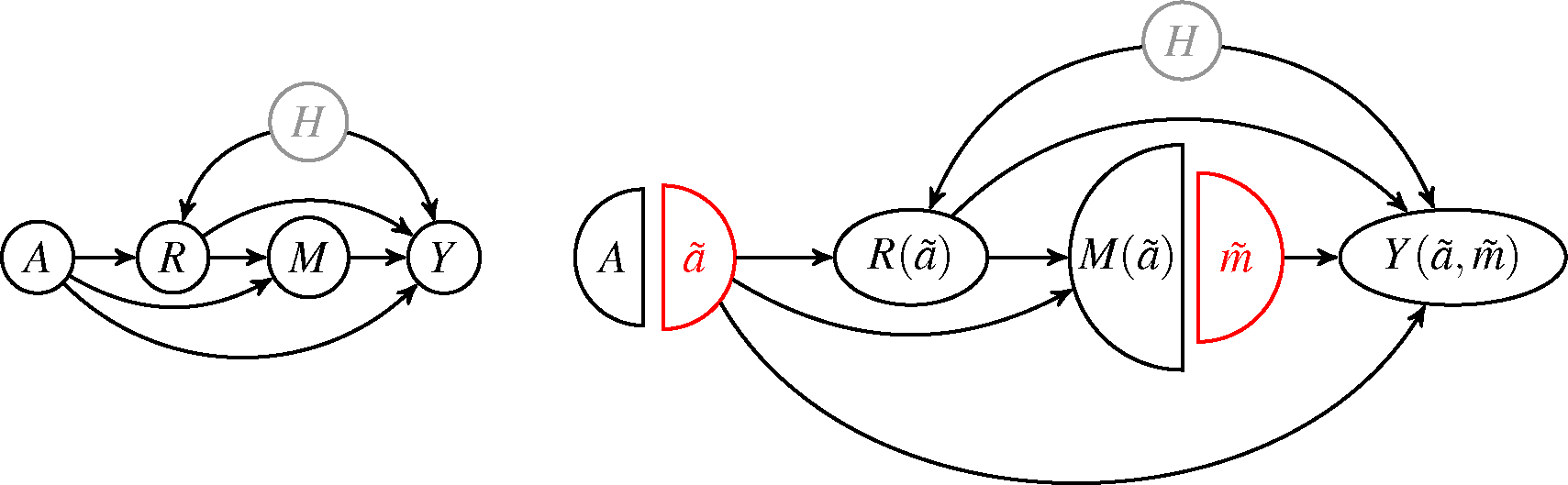
A. A mediation directed acyclic graph in which an unobserved variable affects , an exposure-induced confounder, and . The black nodes represent observed random variables, and the arrows represent possible causal effects of one random variable on another. B. The single-world intervention graph in the setting of (a) that has been intervened on to set to and to . The black nodes represent random variables under this intervention, the red nodes represent the level an intervened random variable takes under this intervention, and the arrows represent possible causal effects of one variable under this intervention on another. In each panel, the gray node represents a hidden random variable.
Whereas the previous results invoked no cross-world-counterfactual independences under the FFRCISTG interpretation of the DAG in Fig. 2.A, sharper bounds are available under Pearl’s NPSEM-IE interpretation of these DAGs. We introduce some notation before stating the result. Let be discrete taking values in be the vectorization of the matrix
, be the vectorization of the matrix , and be the vectorization of the matrix , i.e., the matrix with row and column removed. Equation (1) can then be expressed as , which is identified in , but not . Given the marginal probabilities, which are identified, the joint probabilities have degrees of freedom, and can be expressed in terms of the -dimensional vector as , where is the matrix
where
and is the -dimensional vector
The following result states that bounds for can be obtained by optimizing in via linear programming.
Theorem 2.
Under the NPSEM-IE corresponding to the DAG in Fig. 2.A, where and can be either continuous or discrete, is partially identified by , where and are the minimizing and maximizing solutions respectively to the linear programming problem with objective function subject to the Fréchet inequality constraints
where denotes the th element of .
Similar to the previous result, these bounds coincide if either or is degenerate. The upper bound is achieved when and are comonotone; the lower bound is achieved when they are countermonotone. These bounds are available in closed form only when is binary; otherwise they can be solved using standard software, such as with the lp_solve function, which uses the revised simplex method and is accessible from a number of languages, including R, MAT-LAB, Python, and C. While the method used by this software is not guaranteed to converge at a polynomial rate (Klee and Minty, 1970), it is quite efficient in most cases (Schrijver, 1998). Under monotonicity with binary , the identifying functional given by Tchetgen Tchetgen and VanderWeele (2014) is recovered at the upper bound in Theorem 2.
As mentioned, all results given here can be extended to settings with observed pre-exposure confounders, which we denote . The following assumes that previous assumptions hold conditionally on , and that the positivity assumptions conditional on hold almost everywhere. The bounds in Theorem 1 become
The identification formulas in Corollary 1 are the same, but conditional on . The bounds in Theorem 2 become , where and are simply and respectively, but conditional on . For each , and minimize and maximize respectively the objective function subject to the Fréchet inequality constraints
When is of moderate size, can be solved for each covariate pattern of , i.e., without modeling the dependence of the cross-world-counterfactual joint distribution on . Each of these bounds remains sharp, since satisfaction of the Fréchet inequality constraints on the marginal joint probabilities is implied by satisfaction of those on the conditional joint probabilities.
4. Application to Harvard PEPFAR data set
We now consider an application to a data set collected by the Harvard President’s Emergency Plan for AIDS Relief (PEPFAR) program in Nigeria. The data set consists of HIV-1 infected adult patients who had not previously received antiretroviral therapy (ART), began ART in the program, and were followed at least one year following initiation. Patients without reliable viral load data at two of the hospitals were excluded. Only complete cases initially prescribed to either TDF+3TC/FTC+NVP or AZT+3TC+NVP1 were considered for this analysis. Thus, the data set we consider consists of 6627 patients, 1919 of whom were prescribed to TDF+3TC/FTC+NVP, and the remaining 4708 prescribed to AZT+3TC+NVP.
There has accumulated evidence of a differential effect on virologic failure between these two first-line antiretroviral treatment regimens (Tang, Kanki, and Shafer, 2012). Virologic failure is defined by the World Health Organization as repeat viral load above 1000 copies/mL. We base this on measurements at 12 and 18 months of ART duration in our analysis. A natural question of scientific interest is what role adherence plays in mediating this differential effect. We are primarily interested in learning about the scientific mechanism of this effect on the individual level. The natural indirect effect best captures this mechanism in that it captures an isolated effect difference mediated by adherence by, in a sense, deactivating effect differences along all other possible causal pathways. We specifically examine the effect through adherence over the second six months since treatment assignment, i.e., the six months prior to the first viral load measurement. Identification is complicated by the presence of treatment toxicity, which clearly affects adherence directly, and has the potential to modify the effect of the treatment assignment on virologic failure. Thus, toxicity measured at six months after treatment assignment is an exposure-induced confounder of the effect of the mediator on the outcome. Further, toxicity and virologic failure are likely to be rendered dependent by unobserved underlying biological common causes as in Fig. 3, where represents these hidden biological mechanisms. Because we define the mediator to be adherence over the second six months, adherence over the first six months is also an exposure-induced confounder along with toxicity, and must be accounted for. Had we defined the mediator to be adherence over the full year, measurement of the mediator and toxicity would have overlapped, violating the principle of temporal ordering.
Let denote the vector consisting of baseline covariates sex, age, marital status, WHO stage, hepatitis C virus, hepatitis B virus, CD4+ cell count, viral load, the tertiary hospital affiliated with the patient’s clinic, and whether the patient visited that tertiary hospital or an affiliated clinic. Let be an indicator of ART assignment taking levels for TDF+3TC/FTC+NVP and for AZT+3TC+NVP; be a vector consisting of an indicator variable of the presence of any lab toxicity at six months following initiation of therapy, and a categorization of average adherence over the first six months following initiation of therapy into three groups: exceeding 95%, between 80% and 95%, and not exceeding 80%; be a categorization of average adherence over the subsequent six months into the same ranges as in ; and be an indicator of virologic failure at one year, i.e., repeat viral load above 1000 copies/mL at one year and at 18 months.
Here we estimate the natural indirect effect of on through , as defined above, on the risk difference scale using the various sets of identifying and partially-identifying assumptions given above. Throughout, estimation is performed using maximum likelihood. There is a growing literature on inference methods for partially-identified parameters, many of which are reviewed in Tamer (2010). In particular, Chernozhukov, Hong, and Tamer (2007), Romano and Shaikh (2008), Andrews and Guggenberger (2009) propose methods for obtaining uniformly-valid confidence sets for moment condition models by inverting a test whose critical value is obtained by subsampling the test statistic. While the models considered in this paper can be framed as moment condition models, subsampling is unfortunately not possible due to the rarity of virologic failure. Additionally, Andrews and Guggenberger (2009) propose an alternative method for obtaining a critical value under the asymptotically least-favorable null model, however this yields uninformative confidence sets in our setting as it does not account for models such as ours in which moment conditions cannot hold as equalities simultaneously. Instead, we construct confidence intervals using the weighted bootstrap (van der Vaart and Wellner, 1996), which accounts for the rare outcome, but does not produce confidence sets that are valid uniformly, due to the bounds under consideration not being pathwise-differentiable parameters. The results are summarized in Fig. 4.
Figure 4:
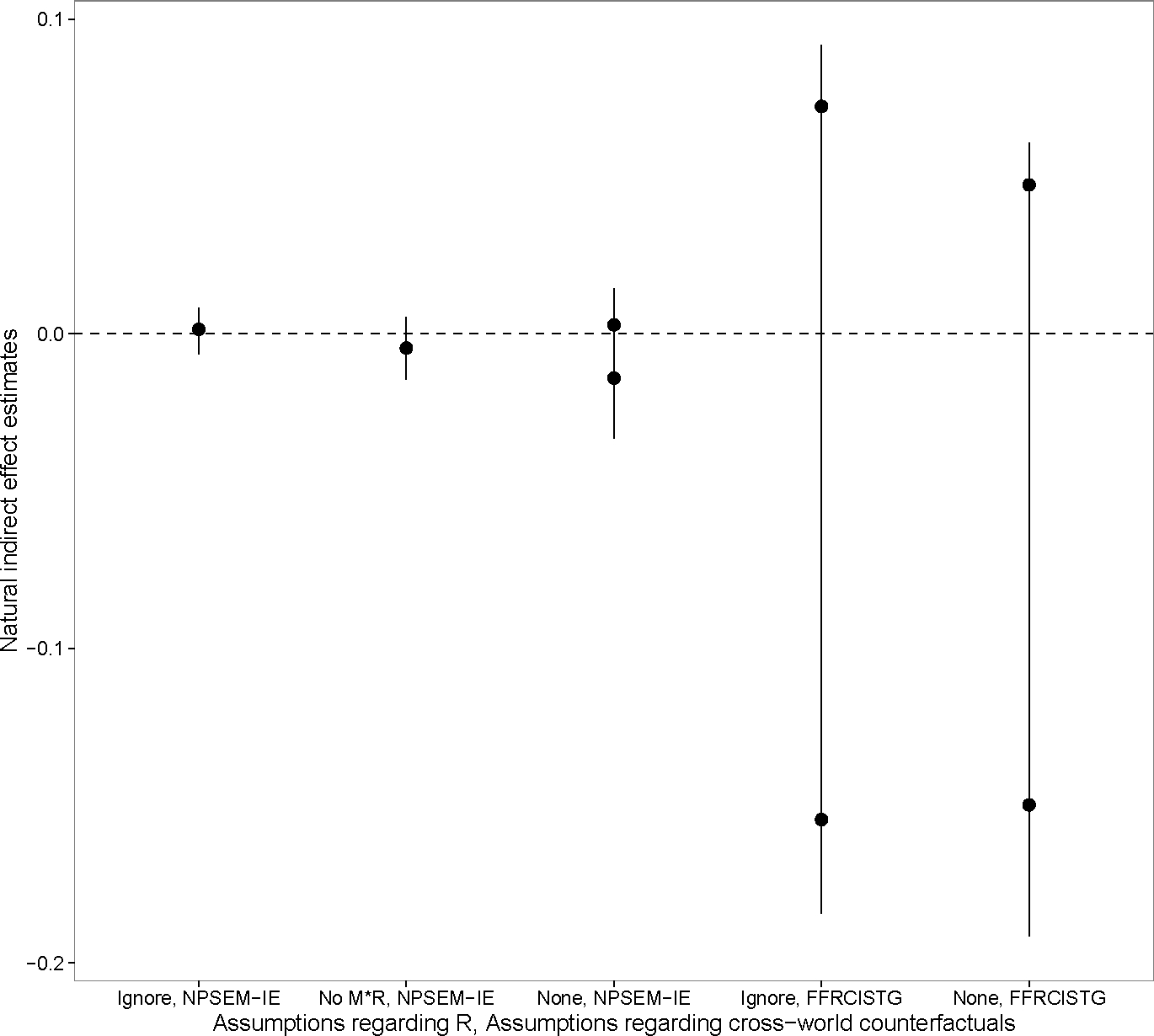
A plot showing the estimated natural indirect effect of ART assignment on virologic failure with respect to adherence under the various assumptions. The assumptions vary across the horizontal axis, with the first part of the label indicating the assumption regarding the exposure-induced confounder, , and the second part indicating the assumption regarding cross-world counterfactuals. For the assumptions regarding , “Ignore” means that the presence of is ignored altogether, “No M*R” means the no interaction assumption in Section 1, and “None” means that was accounted for without additional assumptions. For the assumptions regarding cross-world counterfactuals, “NPSEM-IE” means a NPSEM-IE was assumed, and “FFRCISTG” means an FFRCISTG was assumed, i.e., no cross-world-counterfactual independences were assumed. When the assumptions give partial identification, the two dots represent the point estimates of the upper and lower bound for the natural indirect effect, and the vertical bar represents the bootstrap 95% confidence interval for the interval. When the assumptions give full identification, the single dot represents the point estimate of the natural indirect effect, and the vertical bar represents its bootstrap 95% confidence interval.
It is immediately apparent that range of uncertainty for the NIE is sensitive to which identifying assumptions are made. Consider an investigator who might be willing to rely on cross-world-counterfactual independences. By ignoring the presence of toxicity, she would find a small, insignificant positive effect. Conversely, were she to make the no interaction assumption, she would find a small, insignificant negative indirect effect. (An empirical test of this assumption reveals that it is unlikely to apply, however we present this result for the sake of comparison.) The identification result under monotonicity does not extend to the case where is polytomous, and hence could not be applied in this setting. Incorporating with no assumptions results in bound estimates corresponding to Theorem 2 that roughly match the confidence interval achieved under the no interaction assumption, and a confidence interval that is about three times wider.
Another investigator unwilling to impose cross-world-counterfactual independence assumptions is left with little to say as the bounds are considerably wider, regardless of how toxicity is handled. These bounds easily contain the null hypothesis of no NIE, as well as all confidence intervals obtained under the NPSEM-IE. Thus, cross-world-counterfactual-independences appear to have stronger empirical implications in the current analysis than assumptions regarding exposure-induced confounders. Interestingly, the point estimates of the bounds that result from making no assumptions about the joint distribution of the cross-world counterfactuals are narrower than those that result from ignoring . This is because even though we do not impose any restrictions on the distribution of or its counterfactuals a priori, observing is clearly informative. The bounds accounting for correspond to Theorem 1, and have the added advantage of being the only identifying formula that remains valid when toxicity and virologic suppression are affected by an unobserved common cause, as in Fig. 3. If it is indeed the case that this manner of unobserved confounding is present, then the other estimates will be biased.
5. Discussion
We have shown that PEPFAR results are sensitive to the choice of assumptions made, consequently, we counsel investigators employing mediated effects to exercise caution in considering the basis for point identification and to explicitly state the assumptions required for validity. Where assumptions are empirically untestable, they should be argued for on the basis of scientific understanding, and ideally the alternative should be explored by employing partial identification bounds given both here and elsewhere. While some work has been done to develop sensitivity analyses for unmeasured confounding of the mediator (Tchetgen Tchetgen, 2011, Tchetgen Tchetgen and Shpitser, 2012, Vansteelandt and VanderWeele, 2012), sensitivity analyses for ranges of plausible associations between cross-world counterfactuals remain undeveloped. Further development of sensitivity analyses of both forms would be highly beneficial for practical use, and is fertile ground for future work. Additionally, interest is growing in mediation analysis in longitudinal settings with repeated measures of the exposure, confounders, and mediator. Extending this work to such settings is also a fruitful direction for future research. We hope that the work presented here will inspire deeper consideration and transparency regarding underlying identifying assumptions in the practice of mediation analysis.
Acknowledgments
The authors gratefully acknowledge the hard work and dedication of the clinical, data, and laboratory staff at the PEPFAR supported Harvard/AIDS Prevention Initiative in Nigeria (APIN) hospitals that provided secondary data for this analysis. This work was funded, in part, by the US Department of Health and Human Services, Health Resources and Services Administration (U51HA02522), the Centers for Disease Control and Prevention (CDC) through a cooperative agreement with the AIDS Prevention Initiative in Nigeria (APIN) (PS 001058), and by the National Institutes of Health (R01AI104459–01A1). The contents are solely the responsibility of the authors and do not represent the official views of the funding institutions. We thank the anonymous referees for their helpful comments, which greatly improved the clarity of this article.
Glossary
- 3TC
lamivudine
- AZT
zidovudine
- FTC
emtricitabine
- NVP
nevirapine
- TDF
tenofovir
Appendix
Proofs of theorems
Proof of Theorem 1.
Applying the (sharp) Fréchet inequalities
to each summand in
yields the result.
Proof of Theorem 2.
Since is linear in and each element of is constrained linearly, the proposed linear programming problem will yield the that optimizes , and hence . Thus, will be bounded by evaluated at the minimizing and maximizing linear programming solutions and .
Contributor Information
Caleb Miles, Department of Biostatistics, University of California, Berkeley 94720-7358.
Phyllis Kanki, Department of Immunology and Infectious Diseases, Harvard School of Public Health, Boston, MA 02115..
Seema Meloni, Department of Immunology and Infectious Diseases, Harvard School of Public Health, Boston, MA 02115..
Eric Tchetgen Tchetgen, Departments of Biostatistics and Epidemiology, Harvard School of Public Health, Boston, MA 02115..
References
- Andrews DW and Guggenberger P (2009): “Validity of subsampling and “plug-in asymptotic” inference for parameters defined by moment inequalities,” Econometric Theory, 25, 669–709. [Google Scholar]
- Balke AA and Pearl J (1997): “Probabilistic counterfactuals: semantics, computation, and applications,” Technical report, DTIC Document. [Google Scholar]
- Cai Z, Kuroki M, Pearl J, and Tian J (2008): “Bounds on direct effects in the presence of confounded intermediate variables,” Biometrics, 64, 695–701. [DOI] [PubMed] [Google Scholar]
- Cheng J and Small DS (2006): “Bounds on causal effects in three-arm trials with non-compliance,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68, 815–836. [Google Scholar]
- Chernozhukov V, Hong H, and Tamer E (2007): “Estimation and confidence regions for parameter sets in econometric models,” Econometrica, 75, 1243–1284. [Google Scholar]
- Imai K, Keele L, and Tingley D (2010): “A general approach to causal mediation analysis.” Psychological Methods, 15, 309. [DOI] [PubMed] [Google Scholar]
- Kaufman S, Kaufman JS, MacLehose RF, Greenland S, and Poole C (2005): “Improved estimation of controlled direct effects in the presence of unmeasured confounding of intermediate variables,” Statistics in Medicine, 24, 1683–1702. [DOI] [PubMed] [Google Scholar]
- Klee V and Minty GJ (1970): “How good is the simplex algorithm,” Technical report, DTIC Document. [Google Scholar]
- Nelsen RB (2007): An Introduction to Copulas, Springer Science & Business Media. [Google Scholar]
- Pearl J (2000): Causality: Models, Reasoning and Inference, Cambridge University Press, New York. 2nd edition, 2009. [Google Scholar]
- Pearl J (2001): “Direct and indirect effects,” in Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, Morgan Kaufmann Publishers Inc., 411–420. [Google Scholar]
- Petersen ML, Sinisi SE, and van der Laan MJ (2006): “Estimation of direct causal effects,” Epidemiology, 17, 276–284. [DOI] [PubMed] [Google Scholar]
- Richardson TS and Robins JM (2013): “Single world intervention graphs (SWIGs): A unification of the counterfactual and graphical approaches to causality,” Center for the Statistics and the Social Sciences, University of Washington Series. Working Paper. [Google Scholar]
- Robins JM (1986): “A new approach to causal inference in mortality studies with a sustained exposure period-application to control of the healthy worker survivor effect,” Mathematical Modelling, 7, 1393–1512. [Google Scholar]
- Robins JM (1989): “The analysis of randomized and non-randomized AIDS treatment trials using a new approach to causal inference in longitudinal studies,” Health service research methodology: a focus on AIDS, 113, 159. [Google Scholar]
- Robins JM and Greenland S (1992): “Identifiability and exchangeability for direct and indirect effects,” Epidemiology, 143–155. [DOI] [PubMed] [Google Scholar]
- Robins JM and Richardson TS (2010): “Alternative graphical causal models and the identification of direct effects,” Causality and Psychopathology: Finding the Determinants of Disorders and Their Cures, 103–158. [Google Scholar]
- Romano JP and Shaikh AM (2008): “Inference for identifiable parameters in partially identified econometric models,” Journal of Statistical Planning and Inference, 138, 2786–2807. [Google Scholar]
- Rubin DB (1974): “Estimating causal effects of treatments in randomized and nonrandomized studies.” Journal of Educational Psychology, 66, 688. [Google Scholar]
- Rubin DB (1978): “Bayesian inference for causal effects: The role of randomization,” The Annals of Statistics, 34–58. [Google Scholar]
- Schrijver A (1998): Theory of linear and integer programming, John Wiley & Sons. [Google Scholar]
- Shpitser I (2013): “Counterfactual graphical models for longitudinal mediation analysis with unobserved confounding,” Cognitive Science, 37, 1011–1035. [DOI] [PubMed] [Google Scholar]
- Sjölander A (2009): “Bounds on natural direct effects in the presence of confounded intermediate variables,” Statistics in Medicine, 28, 558–571. [DOI] [PubMed] [Google Scholar]
- Splawa-Neyman J, Dabrowska D, Speed T, et al. (1990): “On the application of probability theory to agricultural experiments. Essay on principles. Section 9,” Statistical Science, 5, 465–472. [Google Scholar]
- Taguri M and Chiba Y (2015): “A principal stratification approach for evaluating natural direct and indirect effects in the presence of treatment-induced intermediate confounding,” Statistics in Medicine, 34, 131–144. [DOI] [PubMed] [Google Scholar]
- Tamer E (2010): “Partial identification in econometrics,” Annu. Rev. Econ, 2, 167–195. [Google Scholar]
- Tang MW, Kanki PJ, and Shafer RW (2012): “A review of the virological efficacy of the 4 World Health Organization–recommended tenofovir-containing regimens for initial HIV therapy,” Clinical Infectious Diseases, 54, 862–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ (2011): “On causal mediation analysis with a survival outcome,” The International Journal of Biostatistics, 7, 1–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ and Phiri K (2014): “Bounds for pure direct effect,” Epidemiology, 25, 775–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ and Shpitser I (2012): “Semiparametric theory for causal mediation analysis: Efficiency bounds, multiple robustness and sensitivity analysis,” The Annals of Statistics, 40, 1816–1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tchetgen Tchetgen EJ and VanderWeele TJ (2014): “On identification of natural direct effects when a confounder of the mediator is directly affected by exposure,” Epidemiology (Cambridge, Mass.), 25, 282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Vaart AW and Wellner JA (1996): Weak Convergence and Empirical Processes, Springer. [Google Scholar]
- VanderWeele T (2015): Explanation in Causal Inference: Methods for Mediation and Interaction, Oxford University Press. [Google Scholar]
- Vansteelandt S and VanderWeele TJ (2012): “Natural direct and indirect effects on the exposed: effect decomposition under weaker assumptions,” Biometrics, 68, 1019–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang JL and Rubin DB (2003): “Estimation of causal effects via principal stratification when some outcomes are truncated by “death”,” Journal of Educational and Behavioral Statistics, 28, 353–368. [Google Scholar]


