Robust Rain-Repellency and Droplet Bouncing Properties of Bauhinia Fresh and Aged Leaves Up to 6 Months

Abstract

Robust rain-repellent surfaces are useful in roofs, solar panels, windshields, etc. Herein, excellent rain-repellency and droplet bouncing properties of Bauhinia Variegata leaves are presented. They possess surface microbumps (l ∼ 13 μm, w ∼ 8 μm, h ∼ 3 μm), which in turn comprise nanoplatelets (l ∼ 741 nm, t ∼ 59 nm) and Wenzel roughness (r_w) of ∼2.2. The leaf’s surface energy was estimated to be 9.47 ± 0.03 mJ·m^–2 by incorporating r_w into the van Oss–Good–Chaudhary theory. The leaves exhibited static contact angle of 157 ± 1°, roll-off angle of 9 ± 1°, and contact angle hysteresis of 12 ± 4°, which retained as they aged up to 186 days in the natural weather and laboratory conditions. The water droplets (10 μL, 40 μL) bounced off for free-fall heights from 5 cm to ∼13 m (Weber no. 36 to ∼2990) and displayed robust rain-repellency (Weber no. ∼4500), similar to that of a lotus leaf. Also, Bauhinia leaves survived pressurized water jets (Weber no. ∼4240). Nevertheless, underwater hydrophobicity has been persistent only for up to 3 h when submerged in 20 cm (∼1.96 kPa gauge pressure) deep water, while lotus leaves retained for >7 h. Such robust Bauhinia leaf’s nanoplatelets and wax chemistries can be replicated onto glass/metals for preparing rain-repellent surfaces.

1. Introduction

Superhydrophobic surfaces have triggered notable interest in the research community, as they provide self-cleaning,^1,2 anti-corrosion,^3,4 anti-fouling,⁵ anti-icing,⁶ anti-fogging,⁷ water energy harvesting,⁸ and blood repellency.⁹ In nature, there are many examples of superhydrophobic surfaces such as lotus leaves,¹⁰ taro leaves,¹¹ India canna leaves,¹² shark skin,^13,14 water strider legs,¹⁵ gecko feet,¹⁶ cicadas,¹⁷ viola tricolor petals,¹⁸ periwinkle petals,¹⁹ rice leaves,²⁰ and rose petals.²¹ Fundamentally, the presence of micro/nano/hierarchical features and low-surface-energy materials aid in achieving superhydrophobicity.

The surface topographies and wetting properties of several superhydrophobic surfaces are widely reported in the literature. The rain-repellency and subsequent self-cleaning properties of a surface depend on the droplet impact dynamics. Thus, detailed investigations were conducted to reveal the Cassie–Wenzel transition on several superhydrophobic surfaces. As reported in the literature,²² the Cassie–Wenzel transition at the macroscopic scale happens when the impacting droplet irreversibly moves from the Cassie to Wenzel configuration, and the complete droplet or the residual of the droplet gets stuck on the surface.

The Weber number (We) is an important dimensionless parameter, which is defined as the ratio of the drop’s kinetic energy just before impacting the solid substrate and its surface energy. It is mathematically expressed as .²³ The critical Weber number (We_c) is defined as the minimum Weber number at which the Cassie to Wenzel transition occurs for a surface. A larger We_c for a surface implies that a relatively higher kinetic energy/impact pressure is required for the drop to penetrate into the air cavities of the surface and undergo a Cassie to Wenzel transition.

A couple of theoretical models were proposed and developed to explain the Cassie to Wenzel transitions due to impacting liquid droplets.^22,24 Among them, one model²² proposed that the transition happens when the sum of hammer and dynamic pressures exceeds the capillary pressure. Here, the hammer pressure is the thrust generated by the compressed liquid droplet at the impact, whereas the dynamic pressure is due to the velocity of the droplet, and the capillary pressure is due to the trapped air between the microfeatures.

In another study,²⁴ the equation for liquid drop pressure is derived by equating the three forces (force exerted by the rigid substrate on the pillar, the force due to surface tension at the triple line, and force due to impact pressure) for conical, hemispherical-topped, and flat-topped cylindrical pillars. Further, the equations for the Wenzel pressure (P_w) and pull-off pressure (P_out) are derived. It is found that conical pillars have zero P_out, due to which the liquid drops can easily detach and bounce off the surface, whereas P_out has a higher value for hemispherical-topped and flat-topped cylindrical pillars. On the contrary, due to lower P_w for the conical pillars, the probability of the Cassie to Wenzel transition is higher as compared to cylindrical pillars.

The lotus leaf surface comprises microconical pillars possessing a base diameter of ∼8 μm, height of ∼10 μm, and pitch of ∼19.5 μm. They are covered with hydrophobic wax-based nanorods, which have a length of ∼530 nm and diameter of ∼100 nm.²⁵ They showcase high water static contact angles (SCAs) of ∼164°, contact angle hysteresis (CAH) of ∼3°, and roll-off angles (RAs) of ∼3°.²⁶ A study revealed that Cassie to Wenzel transition did not occur for lotus leaves up to a We of 22 for impacting water droplets.²⁷ However, when they were immersed in water for 2 h at a depth of 50 cm (∼4.9 kPa), the surface was completely wetted.²⁸ Also, another study revealed that an external pressure of ∼13.5 kPa applied for only 30 min resulted in a transition from Cassie to Wenzel configuration.²⁹ Thus, it was concluded that both hydrostatic pressure and submersion time could be responsible for the Cassie to Wenzel transition.^28,29

The taro leaves have two-tier honeycomb-like microwell structures with nanoplatelets covering the full surface. These differ from the lotus leaf’s two-tier micropillars.¹¹ Despite the absence of microbumps, they showcase high water SCAs of ∼150° and low CAH of ∼9°, demonstrating superhydrophobicity. In the taro leaves, the Cassie to Wenzel transition did not occur up to a We of 15.9, and drops were bouncing on the surface. Taro’s bioinspired surface was made from silicon wafer that comprised hexagonal-shaped cavities without any nanoplatelets. The droplet impact studies on these biomimicked surfaces revealed that water drops were in the Wenzel configuration for all of the We from 1.1 to 15.9.¹¹

In a study, microscales called dermal denticles were found on the shark skin.¹⁴ Thereafter, a superhydrophobic surface was fabricated by replicating the surface features of dermal denticles on poly(dimethylsiloxane) (PDMS), followed by flame treatment to form hierarchical micro/nanofeatures. The replicated surfaces showcase a water SCA of ∼160° and a roll-off angle of ∼1°. Further, the drop impact studies indicate a We_c of 34. In another study,³⁰ shark (Carcharhinus brachyurous) skin’s surface structures were replicated by combining hot embossing and replica molding. The negative replica was made on poly(methyl methacrylate) (PMMA) by hot embossing the shark skin. Then, Sylgard PDMS solution was poured on the negative replica to obtain the positive replica of the shark skin. The riblets on the dermal denticles were replicated. Further, drag reduction studies in a water tunnel were conducted, and 8.25% of drag reduction efficiency was achieved for the biomimicked surface. When water flows over the biomimicked surface, the vortices are formed, interacting only with the riblets’ tip. The water does not penetrate the valleys of the riblets, due to which the viscous forces are reduced, and sharks can easily move underwater. However, the droplet impact tests and underwater hydrophobicity are not evaluated for the shark skin.

The rice leaves have anisotropic ridge-like topographies, which are due to the arrangement of conical microbumps in a longitudinal direction.²⁰ These bumps are covered with dense nanoplatelets. The rice leaves showcase water SCAs of ∼143° and RA of ∼11° when measured in the longitudinal direction. Nevertheless, higher SCA of ∼166° and higher RA of ∼37° were reported when measured in the transverse direction. The water drops bounced off the surface, revealing a robust Cassie configuration for We of up to 68.4 and 66.7 in the longitudinal and transverse directions, respectively.

The rose petals comprise tightly packed microbumps with nanostriae (i.e., wrinkled folds) on the top of the bumps. Rose petals are parahydrophobic surfaces with a high water SCA of ∼151°, wherein the water droplets experience high normal adhesion and do not glide on the surface even when the surface is tilted upside down (i.e., 180°). Although rose petals exhibit sticky hydrophobicity, the water drops bounced off for small We of up to 16. As the We was increased to 50, the drop was completely stuck on the surface without displaying bouncing.²¹ Thus, We_c for the rose petal is <50. On the other hand, underwater hydrophobicity was not reported for taro leaves, rice leaves, and rose petals.

Thus, it is evident that “rain-repellency” is explicitly not reported for any of the aforementioned surfaces. Herein, we report the rain-repellency and superhydrophobicity of the Bauhinia leaves and compare them with those of lotus leaves. A thorough literature survey indicates that there are only two reports on the evaluation of the wetting properties of Bauhinia leaves. In the first study,³¹ microbumps with nanoplatelets were found on the top surface of the Bauhinia leaf. The water drops displayed SCAs of ∼140° and RAs of ∼7.5°. A biomimicked surface was prepared on AISI 316L stainless steel by laser texturing. It comprised microbumps with a tiny hole on the top and nanoparticles covering the microbumps. Further, wetting properties were evaluated for the biomimicked surface.

The second work³² reports the presence of microbumps covered with nanoplatelets on the bottom surface of the leaf. The water SCAs of ∼148°, CAH of ∼8°, and RAs of ∼9° were found. The leaf’s surface topographies were replicated on the Sylgard PDMS. It was observed that only the microbumps were replicated as the nanoplatelets could be loosely attached to the leaf’s surface. Based on the available two studies, the rain-repellency, droplet impact dynamics, and Cassie–Wenzel transition in Bauhinia leaves were not investigated.

Thus, this article will present the microstructural and wetting properties of the freshly plucked leaves as a function of aging time (0 day to 157 days). Furthermore, the water droplet impact dynamics will be discussed for freely falling drops in the laboratory and outside weather conditions. These results will be compared with those of lotus leaves. Additionally, underwater hydrophobicity and pressurized water jet tests were conducted to investigate the robustness of the Cassie configuration. Finally, the We_c for the Bauhinia leaf is compared with that of the various superhydrophobic surfaces, namely, taro leaves, rose petals, rice leaves, goose feathers, etc., that were reported in the literature.

2. Experimental Details

2.1. Materials

The fresh Bauhinia and lotus leaves were plucked from the IIT Gandhinagar campus. Ultrapure deionized (DI) water having a resistance of 18 MΩ was collected from a Milli-Q ultrapure water purifying system. The DI water was used for cleaning the leaves before performing the wetting and droplet impact tests. The formamide (99.5% purity) and diiodomethane (99% purity) were procured from LOBA Chemie Pvt. Ltd. and Sigma-Aldrich respectively, for surface energy estimations. A Runwet garden sprayer (1 L) was purchased from Flipkart and was used to conduct pressurized water jet tests.

2.2. Specimen Preparation

The fresh Bauhinia and lotus leaves were plucked and rinsed with running DI water to remove dust particles and contamination from their surfaces. Following that, pressurized N₂ gas was gently blown to remove any tiny water droplets that may have been adherent to the ridges on the leaves. In this article, the investigations on the bottom side of the Bauhinia leaf are generally reported unless otherwise mentioned. The droplet impact and underwater hydrophobicity tests for the lotus leaves will also be reported for comparison.

2.3. Surface Morphologies

2.3.1. Scanning Electron Microscopy

The surface features were investigated in a JEOL JSM7600F scanning electron microscope (SEM) at an operating accelerating voltage of 5–10 keV and beam current of 48.6 μA. Prior to the imaging, the moisture content of freshly cleaned leaves was removed by drying at 35 °C for 40 min in a vacuum oven and stored in a vacuum desiccator for 12 h until the microscopy investigations were carried out. A thin platinum coating was deposited over the leaf surface in a sputtering machine (JEOL JFC-1600 auto fine coater) at 10 mA for 60 s. The images were captured at different locations on the leaf surface in secondary electron (SE) mode.

2.3.2. 3D Noncontact Optical Profilometry

The surface of the leaf was characterized with a Bruker Contour GT-K three-dimensional (3D) noncontact profilometer (NOP) using white light. A scan area of 582 × 436 μm² was probed with a lateral resolution of 910 nm and a vertical resolution of ∼110 nm. As a result, features smaller than 910 nm in lateral dimensions would not be detected in this method. The measurements were performed at two locations on the surface to ensure repeatability.

2.3.3. Atomic Force Microscopy

3D topographical images were taken using the tapping mode in a Multimode 8.0 Bruker Corporation atomic force microscope (AFM). A scan area of 5 × 5 μm² was taken with a lateral resolution of 19.53 nm, vertical resolution of 0.1 nm, and scan rate of 0.8 Hz. This measurement complements the NOP data by providing information from nanoplatelets having dimensions <910 nm.

2.4. Surface Chemistry

2.4.1. Fourier Transform Infrared Spectroscopy

Fourier transform infrared spectroscopy (FTIR) measurements were carried out on the Bauhinia leaf at 25 °C and 65% RH in a UATR-IR Perkin-Elmer Fourier transform infrared spectroscope to identify the surface functional groups on the leaf as a function of aging time (1 day, 123 days, 151 days). The wavenumber in the spectra varies from 4000 to 400 cm^–1 with a resolution of 4 cm^–1. The diamond crystal stage was first cleaned with 1-isopropanol and wiped with lint-free tissue before conducting the measurements. For reproducibility, the FTIR spectra were captured at three locations on the leaf’s surface.

2.4.2. X-ray Photoelectron Spectroscopy

The X-ray photoelectron spectrum (XPS) of the Bauhinia leaf surface was obtained from a ThermoFisher Scientific (Nexsa base) X-ray photoelectron spectrometer. X-rays were generated using a monochromatic source Al Kα (λ = 8.34 Å). A beam diameter of 400 μm, power of 72 W, and voltage of 12,000 V were employed.

2.5. Wetting Properties

2.5.1. Contact Angle Measurements

The SCAs, advancing contact angles (ACAs), receding contact angles (RCAs), and RAs were measured in a contact angle goniometer (DSA25 KRÜSS, Germany) at room temperature of 25 °C using the sessile drop method. The DI water droplets (5 μL) were used to measure the SCAs with a stainless steel needle (diameter = 0.51 mm) attached to a poly(tetrafluoroethylene) syringe SY3601. The leaves were cut into 1 × 1 cm² to avoid bigger ridges, as they are hindrances while measuring the contact angles. Since the surfaces were bulging out, they were first attached to the glass slide with double-sided tape to make them flat. The SCAs were measured by fitting a Young–Laplace fitting algorithm to the digital images.³³ For the reproducibility of the data, SCAs were measured at five different locations, and an average value is reported in this work.

For surface energy estimations, the SCAs of diiodomethane (3 μL) and formamide (4 μL) were measured 5 times at different locations, and an average value was used in the van Oss–Chaudhary–Good model (vOCG).³⁴ The DCAs and RAs of water droplets were measured by tilting the specimen from 0 to 30° at a rate of 1°·s^–1 and capturing the droplet motion videos with a frame rate of 40 fps. Water droplets of 5 μL volume were deposited on the leaves before tilting the specimens. For repeatability, three measurements were taken at different locations, and the average value was reported.

2.5.2. Droplet Impact Tests in Laboratory Conditions

The DI water droplet (10, 40 μL) impact dynamics were recorded using a Photron fast cam mini UX 100 high-speed camera with a frame rate of 5000 fps. For 10 μL water droplets, the release heights were 5, 10, 15, 20, 25, 50, 100, and 150 cm. While for 40 μL droplets, the release heights were 25, 50, 100, and 150 cm.The 10 μL droplet was formed with the help of a P’fact autoclavable microvolume pipette, which is capable of producing droplets of 10–100 μL. For making a 40 μL droplet, first, 40 μL volume was taken in the micropipette and then inserted into a 3 mL dropper. Further, the dropper was gradually squeezed to form a 40 μL drop. Additionally, a pressurized water jet was allowed to strike the leaf surface by using a garden sprayer. The sprayer nozzle knob (diameter of 1 mm) was placed ∼10 cm above the leaf surface, and the water jet struck the surface at ∼54° angle.

2.5.3. Droplet and Natural Rainfall Impact Tests in Outside Weather Conditions

For these tests, both the Bauhinia and lotus leaves were cleaned with DI water and then placed at the bottom of the building, with a height of 13.058 m. The DI water was poured from the top of the building. The videos of the water droplets striking the leaf surfaces were captured with a Canon EOS 5D Mark IV DSLR camera at a frame rate of 100 fps. The raindrops impacting the leaf surface were imaged in July 2020 and August 2022. From the weather report, the mean relative humidity was 99%, the temperature was 20 °C, and the wind speed was 10 m·s^–1 during that period.³⁵

2.5.4. Underwater Hydrophobicity Tests

The cleaned and dried Bauhinia and lotus leaves were submerged at a depth of 20 cm in DI water. The Bauhinia leaf was removed at time intervals of 5, 15, 30, 45, 60, and 180 min. The lotus leaf was removed at time intervals of 5, 15, 30, 45, 60, 180, 420, and 1440 min. These leaves’ surfaces were imaged, and videos were captured to investigate their wettability and spreading of water films.

3. Results and Discussion

3.1. Surface Topographies

The surface topographies of both the top and bottom surfaces of the leaf were investigated to study their influence on wettability. Figure S1, Supporting Information, presents SEM images of the top surface. ImageJ software was used to measure the dimensions of the surface features. Based on the SEM analyses, the top surface was found to comprise elliptical-shaped microbumps/cavities possessing lengths of ∼18 μm and widths of ∼11 μm. They are covered with densely populated nanoplatelets having length of ∼721 nm and width of ∼52 nm. Figure S2, Supporting Information, shows the two-dimensional (2D) and 3D surface profiles of the top surface obtained from NOP. The conical microbumps with varying heights were found on the surface.

Figure 1a shows the digital image of the bottom surface of Bauhinia leaf with few DI water and rain droplets residing. Figure 1b shows an overview SEM image of the bottom surface possessing regularly arranged big ridges, small ridges, and trichomes. Figure 1c showcases a single trichome that has a length of 53 ± 11 μm and width of 11 ± 2 μm, which was covered by regularly arranged microbumps. The widths of the big and small ridges are 157 ± 7 and 55 ± 8 μm, respectively. The big ridge has parallel grooves, as shown in Figure 1d. On the other hand, the small ridges and regions surrounded by them have microbumps and cavities that are fully covered by the nanoplatelets, as observed in Figure 1e,f. The microbumps are elliptical-shaped, possessing length and width of 13 ± 2 and 8 ± 2 μm, respectively. They are periodic with an interspacing distance (referred to as pitch) of 17 ± 3 μm.

Figure 1.

(a) Digital image of water drops on Bauhinia leaf (bottom) with insets showing a single raindrop and water drop. (b–g, j–l) SEM images of the leaf showing big and small ridges, trichomes, stomata, microbumps, and nanoplatelets. (h) Scheme of two-step replica molding from the leaf to epoxy. (i) SEM image of the replicated epoxy surface showing microbumps and cavities. (m) Color-coded surface profile and (n) line profile of the leaf obtained from NOP. (o) 3D surface profile obtained from AFM. (p) Dimensions of big ridges, small ridges, trichomes, microbumps, stomata, and nanoplatelets.

In a recent study,¹⁹ it was reported that periwinkle flower petals’ microtopographies were shrunk from conical pillars to platelet-like structures due to the removal of moisture during the specimen preparation, which is similar to this present study (see Section 2.3). In order to verify this shrinkage in Bauhinia leaves, the surface topographies from fresh leaves were replicated into epoxy. For this, first, the Sylgard 184 PDMS solution was prepared by mixing a 10:1 ratio of base/curing agent and poured onto the leaf surface at 25 °C. After 48 h of curing, the PDMS was peeled off from the leaf, ultrasonicated in a water bath for 10 min, and dried at room temperature. Subsequently, Technovit 3040 epoxy was mixed in the ratio of 1:1 (base/curing agent) and poured on the PDMS replica. The resultant cured epoxy replica was obtained after 10 min of curing at 25 °C. Figure 1h shows the scheme of this two-step replication process.

The representative SEM images of the epoxy replica are displayed in Figure 1i. It clearly shows that both microbumps and microcavities are present in approximately equal numbers. This implies that the Bauhinia leaf also contains both microbumps and cavities, as revealed by the SEM images (Figure 1f), wherein fewer bumps are observed, possibly due to the shrinkage in the leaf during the drying process. These topographies are very unique to this leaf and distinguish it from the superhydrophobic lotus leaf.³⁶

The SEM image of the nanoplatelets is showcased in Figure 1j. They have an average length of 741 ± 164 nm and width of 59 ± 5 nm. Previously, similar microbumps and nanoplatelets were found on the bottom surface of Bauhinia X blakeana.³² Similar nanoplatelets were also observed on other hydrophobic leaf surfaces, namely, taro leaves,¹¹ India canna leaves,³⁷ rice leaves,²⁰ Euphorbia myrsinites,¹⁰ etc. In addition to nanoplatelets, stomata were found to be distributed all over the surface, as evident from Figure 1k. The magnified image of one stoma is shown in Figure 1l, wherein the number density of nanoplatelets is relatively smaller. The stomata are elliptical-shaped with average length and width of 7 ± 1 and 2.5 ± 1 μm, respectively. Briefly, it can be concluded that the top and bottom surfaces of the Bauhinia leaves have similar topographies.

3.2. Measured Wenzel Roughness

Wenzel roughness (r_w) plays an important role in governing the wetting properties of a surface. Recently, a combination of noncontact optical profilometry and AFM techniques was used to measure the Wenzel roughness of banana leaf that comprised two-tier roughness.³⁸ The same protocol is employed in this present work to measure the Wenzel roughness of the Bauhinia leaf. Figure 1m shows a representative color-coded surface profile of Bauhinia leaf obtained from a noncontact optical profilometer on areas of 582 × 436 μm². The orange-colored connected regions are from small ridges, while the marked dots correspond to microbumps/cavities. A line profile (marked by the blue line) is shown in Figure 1n, which confirms bumps instead of cavities. Figure S3, Supporting Information, presents the 3D surface profile obtained from NOP, which also confirms the presence of conical microbumps on the bottom surface.

The measured bottom diameter, height, and pitch of microbumps are 16 ± 1, 3.3 ± 0.6, and 15 ± 1 μm, respectively. Thus, the diameter is overestimated from the NOP data as compared to the SEM images (11 ± 2 μm). This could also be attributed to the differences in both leaves that were examined by NOP and SEM. Nevertheless, the pitches from both NOP and SEM are similar.

The lateral resolution of the NOP is only ∼910 nm. Thus, nanoplatelets that are ∼740 nm long and ∼60 nm wide cannot be resolved in NOP but can significantly contribute to the Wenzel roughness. Thus, AFM measurements were taken on scan areas of 5 × 5 μm². The 3D surface profile obtained from AFM is displayed in Figure 1o. The scan dimensions are smaller than a microbump. Indeed, the partial area from the top of the bump is shown in Figure 1o, which clearly indicates nanoroughness. The measured dimensions of big ridges, small ridges, trichomes, microbumps, stomata, and nanoplatelets from SEM images are graphically summarized in Figure 1p. The Wenzel roughness (r_w) is mathematically defined by eq 1.³⁹

1

For the Bauhinia leaf, eq 1 is further expressed by eq 2.

2

where 3D and 2D represent the 3D surface areas and 2D surfaces area of small ridges, trichomes, micro bumps, stomata, and nanoplatelets. This can be further simplified to eq 3, similar to that developed in the literature.³⁸

3

Here, r_w,NOP and r_w,AFM are the Wenzel roughnesses calculated from NOP and AFM, respectively. Gwydion software was used to analyze the (X, Y, and Z) coordinates obtained from NOP and AFM for obtaining the roughnesses. Here, ⌀_{nanoplatelets} is the area fraction of nanoplatelets on the leaf’s surface. It was calculated from the SEM images and found to be 0.37.

The measured r_w,NOP is 1.35 ± 0.1, while the measured r_w,AFM is 2.17. Therefore, the net r_w calculated using eq 3 from AFM+NOP is 2.15 ± 0.1, which is approximately twice the r_w,NOP (1.35). This shows that the presence of nanoplatelets greatly enhances the r_w.

3.3. Estimation of Chemical Composition and Surface Free Energy (SFE)

In addition to surface roughness, surface chemistry affects the wettability.^39,40 In order to reveal the surface bonds, the FTIR spectrum of the fresh leaf (day 1) surface was recorded and is shown in Figure 2a. Prominent peaks at 3356, 2917, 2849, 1463, 1637, and 1037 cm^–1 were observed. A broad peak at 3356 cm^–1 can be attributed to the OH group. The sharp peaks at 2917 and 2849cm^–1 could be from the primary C–H stretching. Lower intense peaks at 1637, 1463, and 1037 cm^–1 could be from C=O stretching, C–H bending in the CH₃ group, and C–O alcoholic stretching, respectively. These bonds are similar to those found on the lotus leaf.^41,42

Figure 2.

(a) FTIR spectra of the Bauhinia leaf (bottom) as a function of aging time: 1 day, 123 days, and 151 days, (b) XPS spectrum of the fresh Bauhinia leaf (1 day) and (c) estimated surface free energy and its components of the Bauhinia leaf by using the vOGC model.

To complement the FTIR data, the XPS spectrum was collected and is presented in Figure 2b. Prominent peaks at binding energies of 285, 347, and 532 eV were observed. They correspond to the carbon (C 1s), calcium (Ca 2p), and oxygen (O 1s) elements. The highest intense peak at 285 eV could be linked to the presence of numerous C–C bonds, which in turn hints at the presence of saturated hydrocarbons on the surface. The two peaks at 284.77 and 532.4 eV were reported for carbon and oxygen in the lotus leaf.⁴¹ The peaks at approximately the same binding energies of 285 and 532 eV were also observed on the XPS spectrum of the Bauhinia leaf.

The surface free energy (SFE) of the leaf was estimated using the van Oss–Good–Chaudhury (vOGC) model,³⁴ which is mathematically expressed by eq 4. This model estimates the total surface energy (γ_s) of the leaf and its acid (γ⁺_s), base (γ^–_s), and dispersive (γ^d_s) components. Here, the SCAs (θ_flat) of three liquids, namely, DI water, formamide, and diiodomethane, are required to estimate the three unknowns γ^d_s, γ⁺_s, and γ^–_s. Eventually, the total SFE can be estimated by eq 5.

4

5

In eqs 4 and 5, subscripts “s” and “l” stand for the solid substrate and liquid, respectively. The values of γ_l, γ^p_l, γ^d_l, γ⁺_l, and γ^–_l for DI water, formamide, and diiodomethane are listed in Table S1, Supporting Information.

The θ_flat values in eq 4 are the SCAs of three liquids on ideally flat surfaces. However, the Bauhinia leaf has a Wenzel roughness of 2.15 ± 0.1. Therefore, the measured SCAs of liquid droplets on the leaf are on the rough surface. This has been recently addressed in the literature³⁸ by employing Cassie–Baxter’s⁴⁰ or Wenzel model³⁹ to theoretically deduce the SCAs on flat surfaces. The same strategy is adapted to this present work. The Cassie–Baxter equation (eq 6)⁴⁰ was used for DI water drops resting on the Bauhinia leaf, as they exhibited high SCAs of ∼157° and small RAs of ∼9° and small CAHs of ∼12° (refer to Section 3.4).

6

Here, θ_CB = measured water SCA on the leaf, r_w = measured Wenzel roughness (2.15 ± 0.1), and f_sl = area fraction of the solid–liquid interface. The calculated value of f_sl is 0.37, while θ_flat is the deduced SCA on the flat surface.

The f_sl was calculated by using ImageJ software. The SEM image was opened in the software and then subjected to the threshold color (by clicking image–adjust–threshold). The threshold color level was adjusted to cover the surface except the nanoplatelets. Then, the area fraction was measured by clicking analyze–measure. The area fraction obtained is the fraction of the solid that is not in contact with the liquid. This value is subtracted from one to obtain f_sl. It should be noted here that we are considering that water drops are in the Cassie state and not penetrating the nanoplatelets.

However, the θ_flat of formamide and diiodomethane droplets are deduced by employing Wenzel’s equation (eq 7), as they exhibit low SCAs of ∼138 and ∼126°, respectively, and stuck to the leaf surface (refer to Figure S5, Supporting Information).

7

Here, θ_W = measured SCAs of formamide and diiodomethane on the direct leaf surface, which has roughness.

The measured SCAs and deduced θ_flat of DI water, formamide, and diiodomethane droplets on the Bauhinia leaf are tabulated in Table 1. It can be observed that the deduced SCAs are smaller than the measured SCAs with a considerable difference. This is because the SCAs increase with roughness.

Table 1. Measured and Deduced SCAs on the Bauhinia Leaf.

water		formamide		diiodomethane
θCB (°)	θflat (°)	θW (°)	θflat (°)	θW (°)	θflat (°)
157 ± 1	111 ± 1	138 ± 2	109 ± 1	121 ± 14	103 ± 5

These deduced θ_flat are plugged in eqs 4 and 5 to calculate the surface free energy and their components, which are presented in Figure 2c. The estimated total SFE is 9.5 ± 0.03 mJ·m^–2 by employing the vOGC model. The acid, base, and dispersive components of SFE are 0.65 ± 0.005, 1.40 ± 0.04, and 7.59 ± 1.9 mJ·m^–2, respectively. To complement, OWRK and Wu’s models were also employed. These models also lead to similar values. More details can be found in Section S3, Supporting Information. It can be found that the dispersive component is greater than the polar component. This can be due to the presence of higher no. of nonpolar bonds (C–H) as compared to polar bonds (C=O, O–H, C–O; see Figure 2a).

3.4. Wetting Studies

In our observations, the Bauhinia leaves show rain-repellency and superhydrophobicity in outside weather conditions (see Video S1, Supporting Information). The aged Bauhinia leaves also show superhydrophobic properties. Thus, the water SCAs, RAs, and CAHs for the fresh and aged Bauhinia leaves (bottom surface) are presented in this section. Video S2, Supporting Information, shows water droplets rolling off the smaller ridges but sticking to bigger ridges and veins. The presence of nanoplatelets on the small ridges (refer to Section 3.1) results in the Cassie–Baster state of water drops, due to which they easily roll off. On the contrary, nanoplatelets are absent on big ridges (refer to Section 3.1), and drops stick, as they are in the Wenzel state.

The water droplets make SCAs of 157 ± 1° on the fresh leaf (referred to as day 1), as presented in Figure 3a. For measuring the dynamic contact angles (DCAs) and RAs, the leaf specimen was tilted from 0 to 30°. A software named Free video to jpg converter was used to get every frame of the droplet motion videos. The frames were then analyzed in ImageJ software to measure the RAs, ACAs, and RCAs. The CAH is the difference between ACA and RCA.⁴³ The RA is 9 ± 1°, and CAH is 12 ± 4° for the fresh leaf (day 1), as shown in Figure 3b,c.

Figure 3.

Measured water (a) equilibrium SCAs, (b) RAs, and (c) CAHs for the bottom surface of the 1-, 59-, 127-, 155-, and 186-day-old Bauhinia leaves.

The temporal images of droplets as a function of specimen tilt angle for fresh leaves are showcased in Figure S6(b), Supporting Information. The droplets quickly rolled off at a specimen tilt angle of ∼8° (see Video S2, Supporting Information). This implies that the droplets are in the Cassie–Baxter state and do not penetrate the surface features. The high SCAs, low RA, and CAH on the surface show that it has superhydrophobic properties.

It was observed that Bauhinia leaves that fall from the tree show water-repelling properties. Therefore, we report the SCAs, RAs, and CAHs on the 59-, 127-, 155-, and 186-day-aged leaves, which are presented in Figure 3. The temporal images of water droplets as a function of specimen tilt angle for the aged leaf are shown in Figure S6(c–f), Supporting Information. It can be observed that the SCA, RA, and CAH values for the aged leaf are very close to those measured for the fresh leaf and are plotted in Figure 3a–c. Even after 186 days, the surface has high SCA, easy roll-off, and low CAH, showing that it retains superhydrophobic properties with aging (see Video S2, Supporting Information). The lotus leaf also retains superhydrophobicity with aging, similar to the Bauhinia leaf. We found that ∼12-month-aged lotus leaf showed water SCA of ∼142° and a roll-off angle of ∼5°, as shown in Figure S6(g), Supporting Information.

The possible reason for the superhydrophobic properties is the presence of microbumps, nanoplatelets, and low-surface-energy material on the leaf surface. The presence of nonpolar bonds reduces the van der Waals force of attraction between droplets and the surface. Further, it results in easy roll-off of droplets due to low adhesion to the surface. Therefore, it can be concluded that the combination of surface features (microbumps and nanoplatelets) and the presence of low-surface-energy material make the leaf surface superhydrophobic. Additionally, the SCAs, RAs, and CAHs for the leaf’s top surface are measured and included in Figure S7, Supporting Information. The bottom surface’s SCA, RA, and CAH are slightly better than those of the top surface.

The aged Bauhinia leaves, which are yellow-green, show rain-repellency. Thus, we studied the aged leaves to investigate the reasons for retaining superhydrophobic properties. The fresh leaf was plucked and stored in an open box under room conditions (25 °C and 50–80% RH) for 186 days. With time, the leaf changed color from green to yellow-green, which shows that something has changed in the leaf. The surface topographies of the 157-days-old leaf are showcased in Figure S4, Supporting Information. It is found that the shape and dimensions of microbumps/cavities and nanoplatelets are similar for fresh and aged Bauhinia leaves. Interestingly, with aging, the leaf shrunk to some extent at the macro level due to the loss of water, but the microbumps/cavities and nanoplatelets retained their shape and dimensions.

Further, the FTIR spectra for 123- and 151-day-aged leaves were recorded to reveal any changes in surface chemistry due to aging and are shown in Figure 2a. Prominent peaks were observed at the same wavenumbers as fresh leaves, but the peak’s intensity was reduced. The possible reason for the fall in peak intensity can be the reduction of bonds for the corresponding wavenumbers. It can be observed that the peak intensity corresponding to the O–H bond is reduced, which can be due to the drying of the leaf. Drying resulted in the loss of H₂O molecules from the leaf surface and a reduced number of O–H bonds. The intensity for C–H and C=O does not reduce, whereas the intensity for C–O increases.

Therefore, the surface topographies and surface chemistry are retained with the aging of the leaf. Due to this possible reason, the water SCAs, RAs, and CAHs also do not vary with aging time. Similar to the Bauhinia leaf, a previous study⁴⁴ reported the retention of superhydrophobicity and rain repellency of the 1-month-old lotus leaf. It was found that the microbumps and nanorods were retained on the aged leaf. Further, the FTIR and XPS spectra revealed the same surface chemistry of fresh and aged lotus leaf. On the contrary, the canna leaf that possesses nanoplatelets similar to the Bauhinia leaf lost the superhydrophobicity and rain repellency after 1 month of outdoor exposure due to the loss of nanoplatelets.⁴⁴ Thus, we can conclude that the superhydrophobic properties of the Bauhinia leaf are preserved because of unchanged surface topographies and surface chemistry.

3.5. Drop Impact Tests

As per the definition in the literature,²² the Cassie to Wenzel transition was reported to occur at the macroscopic scale when the impacting droplet irreversibly moves from a Cassie configuration to a Wenzel configuration and the complete droplet or the residual of the droplet gets stuck on the surface. Herein, the metastable Wenzel configuration that a droplet may be experiencing at the micron scales i.e., during its contact with the solid substrate, is merely an intermediate state. If this droplet eventually rebounds from the surface, then it is not termed as Cassie–Wenzel transition. Accordingly, we conducted drop impact tests to evaluate the critical Weber number for the Cassie–Wenzel transition by analyzing the macroscopic droplet configurations. A similar methodology was followed in the previous literature^{11,20−22,27} to study the Cassie–Wenzel transition.

In the laboratory experiments, 10 and 40 μL water droplets were released from different heights. The impact dynamics of droplets was recorded using a high-speed camera. The droplets (10 μL) were dropped from release heights (H) of 5, 10, 15, 20, 25, 50, 100, and 150 cm. For 40 μL droplets, the release heights were 25, 50, 100, and 150 cm. The corresponding Weber numbers (We) and Reynolds numbers (Re) for both 10 and 40 μL droplets are presented in Table 2, as calculated by eqs 8(23) and 9,⁴⁵ respectively. Reynolds number (Re) is an important dimensionless number that dominates the spreading dynamics of the droplet, at high Re values. It is the ratio of the inertial force to the viscous force.

8

9

Here, ρ = density of water, d = diameter of the droplet, u = velocity of the droplet before it impacts the leaf’s surface, γ = surface tension of water, and μ = dynamic viscosity of water.

Table 2. We/Re^1/2 at Different Release Heights for Droplet Volumes of 10 and 40 μL.

	droplet volume = 10 μL			droplet volume = 40 μL
release height (H), cm	Weber no. (We)	Reynolds no. (Re)	We/Re1/2	Weber no. (We)	Reynolds no. (Re)	We/Re1/2
5	36	2669	0.70
10	72	3775	1.17
15	109	4624	1.60
20	145	5339	1.98
25	181	5970	2.34	288	9481	2.95
50	363	8442	3.95	577	13408	4.98
100	727	11940	6.65	1155	18962	8.38
150	1090	17910	8.14	1731	28443	10.26

The videos were captured at 5000 fps and were converted to images using free video to JPG converter software. Here, the temporal digital images of the 10 μL impacting droplet atop the Bauhinia leaf are displayed in Figure 4a–d as a function of release height, i.e., for only H = 5, 20, 50, and 150 cm, while the temporal digital images for H = 10, 15, 25, and 100 cm are presented in Figure S8, Supporting Information.

Figure 4.

Droplet impact tests with a droplet volume of 10 μL at dropping heights of (a) 5, (b) 20, (c) 50, and (d) 150 cm (scale bar at the left is the same for all of the images in that row).

For H = 5 cm, the water droplet initially spreads up to 4 ms, later recedes, and eventually rebounds at 9 ms without breaking into smaller droplets (Figure 4a). Also, all of the frames captured from 0 to 4.8 ms, with time intervals of 0.2 ms, are shown in Figure S9, Supporting Information. Video S3, Supporting Information, shows the slow-speed video of the droplet (10 μL) released from a height of 5 cm. Similar behaviors were observed for H = 10 and 15 cm (see Figure S8, Supporting Information). This is attributed to lower kinetic energy that causes spreading, as compared to its surface tension that pulls inward. For H ≥ 20 cm, the droplet initially spreads with showcasing fingering⁴⁶ and then recedes but in parallel splits into one main droplet and a few smaller satellite droplets.⁴⁷ All of these main and subdroplets bounced off the surface.

For H = 150 cm, the droplet spread and exhibited corona splash.⁴⁶⁻⁴⁸ The impacting droplet was ruptured into smaller droplets, which eventually bounced off the surface. A compilation of the droplet dynamics for H = 5, 20, 50, and 150 cm is presented as Video S3, Supporting Information. Based on the macroscopic droplet configuration, we can conclude that the irreversible Cassie to Wenzel transition has not occurred until a We of 1090.

The maximum release height feasible in the laboratory setup was only 150 cm. Thus, further experiments were conducted with a higher droplet volume of 40 μL. Temporal digital images of the 40 μL impacting droplet are showcased in Figure S10, Supporting Information for release heights of 25, 50, 100, and 150 cm. The 40 μL impacting droplet shows similar bouncing behavior as the 10 μL droplet, as observed in compiled Video S3, Supporting Information. The droplets spread, showcasing fingering, later recede, and subsequently break into smaller satellite droplets surrounding the main droplet, which bounce off the surface. As the dropping height is increased, corona splash and internal rupture^49,50 are observed during spreading. Thus, the irreversible Cassie to Wenzel transition has not occurred for We of up to 1731.

From the above observations, the maximum spreading diameter (D_max) of the droplet on the substrate before it starts retracting and the maximum contact time (t_c) for 10 μL and 40 μL droplets for different release heights (i.e., different We) are measured. Figure 5a,b showcases D_max at different We and Re for 10 μL droplets. It can be observed that D_max increases with an increase in We and Re, as the impacting droplets have a higher kinetic energy. For 10 μL droplets and for We of 36, 72, 109, 145, 181, 363 and 727, the corresponding D_max are 4.2, 6.9, 7.4, 8, 9, 32, and 44.3 mm, respectively. The D_max for a We of 1090 could not be measured due to the corona splash, wherein the droplets lose contact with the surface during spreading. Figure S11, Supporting Information, showcases D_max at different We and Re for 40 μL droplets.

Figure 5.

(a) Maximum spreading diameter (D_max) versus Weber number (We), (b) maximum spreading diameter (D_max) versus Reynolds number (Re) for 10 μL water droplets. Contact time (t_c) versus Weber number (We) for (c) 10 and (d) 40 μL water droplets. Contact time (t_c) versus impact velocity (u) for (e) 10 and (f) 40 μL water droplets.

Previously, Fedorchenko et al.⁵¹ reported the effect of viscous forces on the droplet spreading during the impact. They found that for We/Re^1/2 < 1, droplet spreading is governed by We, whereas for We/Re^1/2 > 1, viscous forces cannot be neglected and therefore are controlled by Re. They further proposed that for We/Re^1/2 > 1, D_max is directly proportional to Re^1/5. In order to verify this mathematical correlation in our study, the We/Re^1/2 values were calculated and are presented in Table 2. For both droplet volumes, it can be observed that We/Re^1/2 > 1, for all release heights except H = 5 cm. This suggests that the droplet spreading is mainly controlled by Re, and thereby, the effect of viscous forces cannot be neglected. For a 10 μL droplet, the mathematical fitting relations between D_max and We and Re are expressed by eqs 10 and 11 in Table 3, and the fitted curves are shown in Figure 5a,b, respectively. Clearly, these equations suggest different exponent values instead of 0.2 as suggested by Fedorchenko et al..⁵¹ Nevertheless, for 25 < We < 200, Antonini et al.⁵² reported a fitting equation—D_max ∝ (We)^0.40, for superhydrophobic Teflon surface, similar to that of ours.

Table 3. Expression of D_max and t_c as a Function of We, Re, and u for 10 and 40 μL Droplets.

droplet volume (μL)	conditions (u in m/s)	expression
10	36 < We < 181	10
10	2669< Re < 5970	11
10	181< We < 1090	12
40	288< We < 1731	13
10	181< We < 1090	14
	2.23< u < 5.47
40	288< We < 1731	15
	2.23 < u < 5.47

Figure 5c,d shows droplet contact time (t_c) at different We for both 10 and 40 μL droplets. It includes the time when the droplet hits the surface, spreads, and retracts and, finally, when the last contact point of the drop is detached. For 10 μL droplets, for We of 36, 72, 109, 145, 181, 363, 727, and 1090, t_c are 14.8, 11, 15, 14, 9.4, 6.8, 6, and 4.6 ms, respectively. For 40 μL droplets, for We of 288, 577, 1155, and 1731, t_c are 11, 9.4, 7.8, and 7 ms, respectively. As We increases, the impacting droplets have more kinetic energy, due to which the spreading and retraction events are faster, thus reducing the contact time. Also, the kinetic energy of impacting droplets increases with the droplet volume, due to which more spreading takes place to dissipate the kinetic energy. This eventually results in higher D_max and t_c for larger drop diameters.

For the 10 μL droplet, the contact time does not depend on We (36 < We < 145). The mathematical fitting relations show that for the 10 μL droplet, t_c ∝ (We)^−0.39 for 181 < We < 1090, and for the 40 μL droplet, t_c ∝ (We)^−0.25 for 288 < We < 1731. Antonini et al.⁵² also reported that spreading time (t_s) does not depend on We for We < 200 and t_s ∝ (We)^−0.25 for We > 200. The mathematical relations of t_c with We for 10 and 40 μL droplets are expressed by eqs 12 and 13 in Table 3.

Figure 5e,f showcases contact time (t_c) at different impact velocities (u) for both 10 and 40 μL droplets. For 10 μL droplets, the contact time for the impact velocities of 1 (H = 5 cm) to 2 m.s^–1 (H = 20 cm) is almost constant. This is because the viscous forces are not dominant in this velocity range. For u = 1.41 m/s(H = 10 cm), the contact time reduces because the droplet falls on the big ridge (see Video S3, Supporting Information), due to which the retraction time reduces. Richard et al.⁵³ also found that for the bouncing droplets, the contact time does not depend on the impact velocity in the range of 0.2–2.30 m/s. For u > 2 m·s^–1, the contact time reduces with an increase in the impact velocity for both 10 and 40 μL droplets. The contact time, t_c ∝ (u)^−0.71 for the 10 μL droplet and t_c ∝ (u)^−0.5 for the 40 μL droplet. Equations 14 and 15 in Table 3 show the mathematical fitted relations between t_c and u for 10 and 40 μL droplets, respectively.

In the literature,^54,55 we found that the contact time of an impacting droplet falling on the ridge is significantly reduced. Bauhinia leaves have a distributed network of big and small ridges. Thus, we studied the effect of ridges on the hydrodynamics during the spreading and retraction stages. It was found that at the maximum spreading, if the local droplet height is much higher than the small ridge height, then during the retraction stage, the three-phase contact line retracts inward isotropically, as observed for release heights of 5 and 20 cm for 10 μL droplets (see Video S3, Supporting Information).

However, when the local droplet height at the maximum spreading is comparable to the ridge height (big or small), the retraction speed of the three-phase contact line is different along the ridge and perpendicular to the ridge. Along the ridge, the retraction speed is higher due to less mass in the thinner region. The three-phase contact line along the ridge was retracting faster as compared to the perpendicular direction, which resulted in drop fragmentation (see Video S3, Supporting Information). It was also observed that as the impact velocity increases, the local droplet height at the maximum spreading reduces, and the possibility of different retraction speeds of the three-phase contact line increases. Previously, Bird et al.⁵⁴ fabricated two superhydrophobic surfaces, namely, silicon coated with trichloro (1H,1H,2H,2H-perfluorooctyl) silane, with and without the ridge. It was found that the droplet striking the flat surface retracted uniformly. However, water droplets showcased nonaxisymmetric retraction after hitting the ridge with a retraction speed higher along the ridge. The droplet contact time on the surface possessing the ridge was 7.8 ms, which is 0.63 times smaller than that on the flat surface (12.4 ms). Therefore, it can be concluded that the droplet striking the ridge shows different hydrodynamics during retraction as compared to that of the flat surface, which results in reduced contact time.

3.6. Pressurized Water Jet Test and Drop Impact Test from 13 m Height

Furthermore, pressurized water jet tests were conducted to analyze the Cassie to Wenzel transition. The pressurized water jet was created with the help of a garden sprayer, as schematically depicted in Figure 6a. In Video S4, Supporting Information, it can be observed that the continuous jet is converted into several droplets before they strike the leaf’s surface. The water jet comes out of the sprayer with a flow rate (Q) of 9279 mm³·s^–1 and an inlet velocity (v_inlet) of 11.8 m.s^–1. First, water is filled in the sprayer, and then water pressure is created by pumping in 4 times. The water is sprayed in the beaker (volume capacity of 1000 mL) to fill up to 300 mL, and the time taken is noted. The flow rate is calculated by . Further, the inlet velocity is calculated by . The measurements were repeated 2 times, and average values were used for calculations.

Figure 6.

(a) Pressurized water jet test on Bauhinia. (b) Drop impact test from a height of 13.058 m and (c) underwater hydrophobicity test on Bauhinia and lotus leaves.

The droplets (diameter = 3.35 mm) strike the leaf surface with an impact velocity of 11.9 m·s^–1, which is calculated by applying energy conservation. The vertical component of the impact velocity is used for calculating the corresponding We of ∼4240. After striking, the droplets initially spread, then recede and break into smaller droplets that bounce off the surface (see the marked rectangular region). Thus, irreversible Cassie to Wenzel transition has not occurred even for We of up to 4240.

Thus, we performed the drop impact test from 13.058 m height, i.e., from the top of a building in the outside weather conditions, as schematically shown in Figure 6b. This test is unique and novel in our study as compared to that in the literature. In the literature, water drops were never released from such heights and that too in outside weather conditions. As the drops were falling from a large height of ∼13 m, thus they were assumed to be broken in smaller drops of 10 μL, which struck the leaf’s surface with an impact velocity of ∼9 m·s^–1. The corresponding We is 2990.

These highly energized differently sized water droplets strike the Bauhinia leaf, as observed in Figure 6b. The readers can also refer to Video S5, Supporting Information. The impacted droplets finally rested on the leaf surface after losing all of their kinetic energy. They rolled off the surface when tilted by 10–15°. Nevertheless, some droplets were stuck on the veins and ridges of the leaf, as they did not contain nanoplatelets (refer to Section 3.1). Thus, irreversible Cassie to Wenzel transition did not occur for We of up to 2990.

The falling raindrops bounced off the aged yellowish chlorophyll deficient Bauhinia leaf’s surface in July 2020 time, where the RH was 99% and temperature was 20 °C. As raindrops bounced off the leaf’s surface, the corresponding We is calculated. It was reported that the raindrops have diameters of 0.6–4 mm and terminal velocities of 2–9 m·s^–1 in the Western Ghats of India.^56,57 Thus, the maximum We is 4500, as calculated from eq 8. Thus, the irreversible Cassie to Wenzel transition has not occurred for We of up to 4500. It is evident that the critical We will be higher than 4500, at which droplets will penetrate the topographies.

The impact tests from 13.058 m and pressurized water jet tests were also conducted for the lotus leaf. Video S4, Supporting Information, shows the bouncing behavior of droplets on a lotus leaf in pressurized water jet test. The temporal digital images for the impact test are added in Figure 6b for comparison with that of the Bauhinia leaf. It can be concluded that lotus leaf and Bauhinia leaf showcased similar behaviors. The readers can refer to Video S5 in the Supporting Information. Also, lotus leaves are known to be rain-repellent. Here, it is to be noted that Cassie to Wenzel transition investigations on lotus leaf were conducted only up to We of 22.²⁷ Thus, this study shows that the lotus leaf will not have irreversible Cassie to Wenzel transition for We of up to 4500.

The surface topographies of the Bauhinia and lotus leaves are very different. Thus, we attempted to investigate the quantitative reasons for the rain-repellency and robust Cassie configuration in Bauhinia leaves. We adapt the model reported in the literature,²⁴ which aids in calculating the Wenzel pressure (P_w) and pull-off pressure (P_out) for the conical pillars. Basically, P_w is the critical pressure required for the Cassie to Wenzel transition, while P_out is the critical pressure needed to dewet the penetrated liquid droplet from the cavities. Higher is required for superhydrophobic windshields and self-cleaning glasses, which are subjected to high impact pressures, while negligible P_out is required in biker helmets, microfluidic chips, and chemical reactors wherein easy detachment and bouncing of drops on the substrate are desirable. In our study, we found that Bauhinia leaves have conical microbumps covered with nanoplatelets (see Figure 1). Due to the conical geometry of the microbumps, the equations derived from the model are applicable in our study.

Equation 16 presents the dimensionless liquid drop pressure (ṕ) exerted on the conical textured pillars.^24,58 This is derived by equating the three forces: the normal force exerted by the rigid substrate on the pillar, force due to surface tension at the triple line, and force due to impact pressure of the drop acting on a single conical pillar.

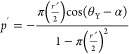16

Here, and ŕ = r_L/λ. ṕ is the dimensionless liquid drop pressure, p is liquid drop pressure, λ is linear semi-spacing (i.e., pitch/2) between pillars, γ_LA is the interfacial surface tension between the liquid and air, r_L is the radial position of the triple line, α is the semicone angle of the pillar, and θ_Y is Young’s contact angle.

The values of α, θ_Y, λ, r_L, ŕ, ṕ, and p obtained from NOP and SEM data are tabulated in Table 4. In this study, the value of θ_Y is 157° as obtained from wetting studies (see Figure 3a). The semicone angle, , was estimated from NOP data (Figure 1p) to be ∼70°, where D and h are the bottom diameter and height of the conical microbumps, respectively. When the drop is in Wenzel configuration, then r_L = D/2 = 8 μm and p = Wenzel pressure, whereas in the Cassie state, r_L = 0, i.e., the drop is suspended over the bumps. By using eq 16, the calculated values of ŕ, ṕ, and p for the Wenzel state are 1.06, 0.815, and 7911 Pa, respectively, and are listed in Table 4.

Table 4. Measured Parameters in Equation 16.

from NOP							from SEM
α (°)	θY (°)	λ (μm)	rL (μm)	ŕ	ṕ	p (Pa)	α (°)	θY (°)	λ (μm)	rL (μm)	ŕ	ṕ	p (Pa)
70	157	7.5	8	1.06	0.815	7911	N/A	157	8.5	6.5	0.764	0.116	993

Alternatively, considering SEM observations, the microbumps appeared to be elliptical shaped with a major diameter of 13 μm and minor diameter of 8 μm. For the Wenzel configuration, we have taken the bigger diameter, i.e., r_L = D/2 = 6.5 μm. As we do not have height information for microbumps from SEM, we used α = 70° as obtained from NOP. Thus, the calculated values of ŕ, ṕ, and p for the Wenzel state are 0.764, 0.116, and 993 Pa, respectively, and are presented in Table 4.

The dynamic droplet impacting pressure (ΔP_D) before it strikes the substrate is expressed by ΔP_D = 0.5 × ρ × u², where ρ is density of the liquid drop and is 1000 kg/m³ (for DI/rainwater), and is the droplet impact velocity.²² For a water droplet released from H = 5 cm, the dynamic impacting pressure is 490 Pa, which is smaller than the Wenzel pressure (P_w) values of 993 Pa (from SEM data) and 7911 Pa (from NOP data, Table 4). Therefore, the dynamic impact pressure is insufficient to cause a Cassie–Wenzel transition. Thus, the Cassie state is a thermodynamically stable configuration. However, for the raindrops (u ∼ 9 m/s), the dynamic impacting pressure is 40,500 Pa, which is 5–40 times higher than the Wenzel pressure (i.e., 993 or 7911 Pa). Thus, it can be hypothesized that the droplets penetrated the topographies, went to the metastable Wenzel configuration, and subsequently dewetted to cause a reversible transition to the Cassie configuration.

For the Bauhinia leaf, the liquid drop pressure (ṕ) becomes equal to pull-off pressure (P_out) by approximating ŕ = 0 in eq 16, as the water droplets were observed to be in the Cassie state (refer to Section 3.5 and Figures 6a and S6, Supporting Information). Thus, it can be safely assumed that the drops do not penetrate into the valleys between the nanoplatelets. Thus, P_out = 0 indicates that no external energy is required to dewet the drop from the air cavities. Typically, ŕ = 0 is applicable for sharp conical pillars.^24,58 However, round, shorter conical microbumps are observed in the Bauhinia leaf (Figure 1), but covered by nanoplatelets, which aid in suspending the water droplets. Therefore, ŕ = 0 is a valid assumption. In other words, the highly energetic striking droplets may have penetrated the microbumps and nanoplatelets and went into a metastable state. Nevertheless, due to negligible P_out, they can easily dewet and bounce off the surface.

3.7. Underwater Hydrophobicity Tests

A robust Cassie configuration was demonstrated by the Bauhinia leaf and is on par with the lotus leaf during the impact tests in the laboratory, outside weather conditions, as well as with pressurized water jets. In the latter, the droplet pressure acts for a very short time. However, the Cassie–Wenzel transition may happen if continuous pressure is applied for a longer time. To study the effect of continuous pressure on the surface, underwater retention of the hydrophobicity of the Bauhinia leaf was investigated.

Figure 6c presents a scheme showing the submersion of a cleaned and dried leaf in a cuboidal container filled with DI water up to a height of 20 cm (gauge pressure of 1.962 kPa). Also, the temporal digital images of the Bauhinia leaf as a function of time (0 min to 3 h) are presented after they were taken out of the water. Similarly, the temporal digital images of lotus leaves are shown as a function of submersion time (0 min to 24 h). The Bauhinia leaf retained the hydrophobicity until 30 min, as there were no attached water droplets. The reader can refer to Video S6, Supporting Information as well as Figure S12, Supporting Information, to observe the retention of the silver/shiny effect until 30 min. Beyond 30 min, the shiny effect disappeared and drops were stuck. The leaf was completely wetted after 3 h of submersion.

However, lotus leaves possessing microcones with an aspect ratio of 1.25²⁵ outperformed the Bauhinia leaf by retaining the hydrophobicity for up to 7 h submersion time (see also Video S6, Supporting Information). The lotus leaf showed complete wetting for 24 h of submersion time. Although the Bauhinia leaf’s micro topographies have an aspect ratio of 0.21, the presence of nanoplatelets significantly aided in the robust hydrophobicity, similar to that explained in the literature.²⁹ The complete wetting occurred between 7–24 h in the lotus leaf, while just within 3 h for the Bauhinia leaf. Higher transition time in the lotus leaf could be attributed to higher aspect ratios (1.25) of the microcones as compared to that of the Bauhinia leaf (0.21), which could have led to a relatively higher amount of trapped air in the lotus leaf’s cavities. Therefore, the diffusion of this trapped air to the surrounding water^59,60 will take a longer duration in the lotus leaf as compared to that of the Bauhinia leaf.

It was reported that the Cassie to Wenzel transition occurred for the lotus leaf within 30 min when it was subjected to an external pressure of 13.5 kPa when immersed at ∼5 mm depth.²⁹ In another study, lotus leaves are completely wetted when immersed at a depth of 50 cm for 2 h.²⁸ Bobji et al.⁵⁹ investigated the effect of immersion time on the trapped air pockets in the cavities of a superhydrophobic textured silicon surface under a constant hydrostatic pressure of ∼600 Pa by using the total internal reflection (TIR) of the light. It is found that air pockets completely disappear after 100 min. Also, Xiang et al.⁶⁰ studied the effect of immersion time and dissolved gas saturation degree (s) in water on the trapped air pockets in the cavities of lotus leaves using confocal microscopy. They found that when s = 1, there is negligible diffusion of air molecules to the surrounding water for up to 240 min. But, for s = 0.67 (i.e., water is 67% saturated with air), the Cassie to Wenzel transition occurred within 2 min due to the diffusion of trapped air molecules to the surrounding water.

Herein, solid surfaces are exposed to continuous hydrostatic pressures for much longer times, i.e., in minutes to hours. However, in droplet impact tests, the liquid is in contact with the substrate only for ∼4–15 ms. Therefore, it can be concluded that the applied hydrostatic pressure, the dissolved gases/air concentration in water, and immersion/contact time have a combinatorial effect on the Cassie to Wenzel transition.

To compare the mechanical robustness of the Bauhinia leaf’s topographies with other hydrophobic surfaces, We_c are plotted in Figure 7. The data presented for the taro leaf indicates that transition was not observed for We of up to 15.9.¹¹ Similarly, for the lotus leaf, there was no transition for We of up to 22.²⁷ This is superimposed with the data from the present study where the lotus leaf did not show transition for We of up to 4500 and more. Similarly, the Cassie–Wenzel transition did not occur in rice leaves for We of up to 68.4.²⁰

Figure 7.

Critical Weber numbers (We_c) of rose petals,²¹ dual-scale nanograss (NG),²⁷ flame-treated shark skin replica (SSR),¹⁴ and goose feather⁶¹ as collected from the literature. Maximum reported We for the taro leaf,¹¹ rice leaf,²⁰ and lotus leaf²⁷ are also added along with that of the lotus and Bauhinia leaves from this present work.

However, rose petals,²¹ dual nanograss (NG),²⁷ flame-treated shark skin replica (SSR),¹⁴ and goose feathers⁶¹ display easy Cassie–Wenzel transitions. Their critical We are 16, 24, 34, and 900, respectively. Interestingly, in rose petals, the water drops showcased sticky superhydrophobicity when they were deposited with negligible pressure i.e., during SCA measurements.^62,63 However, the droplet impact studies were conducted, and the water drops bounced for a We of 4.²¹ From this comparison, it is evident that Bauhinia leaves have extremely high We_c than all of the superhydrophobic surfaces reported so far and are on par with the lotus leaf. Thus, promising alternative topographies are showcased in this study for developing synthetic rain-repellent surfaces by biomimicking them.

4. Conclusions

We report the superhydrophobicity and rain-repellency of Bauhinia leaf and compare it with that of lotus leaf. The surface consists of hierarchical conical microbumps covered by dense nanoplatelets distributed throughout, which remained intact with the aging time tested up to 157 days. Also, the nature and intensity of the chemical bonds have been retained with aging time, as confirmed by the FTIR analyses. Further, a combination of AFM and NOP techniques was employed to quantify the r_w, similar to that recently reported in the literature.³⁸ The water SCAs, RAs, and CAHs also do not vary with aging time. Therefore, we conclude that the superhydrophobicity is preserved for a very long time both in the laboratory and outside weather conditions (32 °C, 50–80% RH).

We also found that irreversible Cassie to Wenzel transition did not occur for We of up to 4500 when impacted by high energetic droplets falling from ∼13 m as well as from pressurized water jets and natural rainfall. These topographies show high potential in retaining a robust Cassie state and outperformed dual-scale nanograss,²⁷ flame-treated shark skin replica,¹⁴ and goose feathers⁶¹ and on par with lotus leaves’ topographies. The biomimicked surfaces containing these topographies can be useful in making rain-repellent roofs, solar panels, and windshields. These rain-repellent surfaces can be fabricated by creating microbumps on a range of materials, including metals and polymers using hot embossing. Additionally, low-surface-energy nanoplatelets can be grown by self-assembly of alkane deposited through thermal evaporation.⁶⁴

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c01623.

• Surface topographies of the Bauhinia leaf (top and bottom) (Section S1); gliding of diiodomethane and formamide droplets on the Bauhinia bottom surface (Section S2); surface energy estimations of the Bauhinia leaf (bottom) by OWRK and Wu’s models (Section S3); water wetting properties on bottom and top surfaces of the Bauhinia leaf (Section S4); droplet impact tests (Section S5); and temporal images of the submerged Bauhinia leaf (Section S6) (PDF)

• Rainfall tests on a green and yellow-colored Bauhinia leaf (Video S1) (AVI)

• Rolling of water drops on the Bauhinia leaf with aging time (Video S2) (AVI)

• Drop impact tests for 10 and 40 μL drops falling from different heights (Video S3) (AVI)

• Pressurized water jet test on Bauhinia and lotus leaves (Video S4) (AVI)

• Drop impact test on Bauhinia and lotus leaves from 13 m height (Video S5) (AVI)

• Submerged Bauhinia and lotus leaves in DI water for different time intervals (Video S6) (AVI)

Author Contributions

S.R. discovered the rain-repellency in the Bauhinia leaves. S.R. is the principal investigator, acquired the funding, supervised, aided in interpretation of the data, and reviewed and edited the manuscript. R.C. performed all of the experiments except noncontact optical profilometry and carried out data analyses and interpretation. R.C. drafted the original manuscript, edited it, and reviewed it. Both the authors had technical and scientific discussions throughout the project.

The authors acknowledge IIT Gandhinagar for providing financial support under project number RIG/0301.

The authors declare no competing financial interest.