Abstract
COVID-19 (Coronavirus), an acute respiratory disorder, is caused by SARS-CoV-2 (coronavirus severe acute respiratory syndrome). The high prevalence of COVID-19 infection has drawn attention to a frequent illness symptom: olfactory and gustatory dysfunction. The primary purpose of this manuscript is to create a Computer-Assisted Diagnostic (CAD) system to determine whether a COVID-19 patient has normal, mild, or severe anosmia. To achieve this goal, we used fluid-attenuated inversion recovery (FLAIR) Magnetic Resonance Imaging (FLAIR-MRI) and Diffusion Tensor Imaging (DTI) to extract the appearance, morphological, and diffusivity markers from the olfactory nerve. The proposed system begins with the identification of the olfactory nerve, which is performed by a skilled expert or radiologist. It then proceeds to carry out the subsequent primary steps: (i) extract appearance markers (i.e., and order markers), morphology/shape markers (i.e., spherical harmonics), and diffusivity markers (i.e., Fractional Anisotropy (FA) & Mean Diffusivity (MD)), (ii) apply markers fusion based on the integrated markers, and (iii) determine the decision and corresponding performance metrics based on the most-promising classifier. The current study is unusual in that it ensemble bags the learned and fine-tuned ML classifiers and diagnoses olfactory bulb (OB) anosmia using majority voting. In the 5-fold approach, it achieved an accuracy of 94.1%, a balanced accuracy (BAC) of 92.18%, precision of 91.6%, recall of 90.61%, specificity of 93.75%, F1 score of 89.82%, and Intersection over Union (IoU) of 82.62%. In the 10-fold approach, stacking continued to demonstrate impressive results with an accuracy of 94.43%, BAC of 93.0%, precision of 92.03%, recall of 91.39%, specificity of 94.61%, F1 score of 91.23%, and IoU of 84.56%. In the leave-one-subject-out (LOSO) approach, the model continues to exhibit notable outcomes, achieving an accuracy of 91.6%, BAC of 90.27%, precision of 88.55%, recall of 87.96%, specificity of 92.59%, F1 score of 87.94%, and IoU of 78.69%. These results indicate that stacking and majority voting are crucial components of the CAD system, contributing significantly to the overall performance improvements. The proposed technology can help doctors assess which patients need more intensive clinical care.
Keywords: Anosmia, COVID-19, Computer aided design (CAD) diffusion tensor imaging (DTI), Features selection (FS), Fluid-attenuated inversion recovery (FLAIR), Spherical harmonics (SH), Texture analysis
1. Introduction
COVID-19 (Coronavirus-19) is an acute respiratory illness caused by the coronavirus severe acute respiratory syndrome (SARS-CoV-2). The COVID-19 pandemic has been the most menacing global health issue the world has faced since the Spanish flu, with the coronavirus SARS-CoV-2 spreading rapidly throughout the world, leading to more than 2 million deaths in a year according to the World Health Organization (WHO), in addition to enormous socioeconomic burden [1]. Human-to-human (H2H) transmission is characterized by a worrying exponential rate, which has led to explosive outbreaks throughout the world [2]. The severity of SARS-CoV-2 infection ranges from mild to severe, and the severity of infection depends on each person's immune system, age, and comorbidities [3].
COVID-19 infection and ramifications affect several organs, including the lung, heart, brain, kidney, and others [4]. In addition, there are neurological symptoms of COVID-19 that involve the central nervous system and the peripheral system, including a defect or loss of the sense of smell [5]. Based on the results of various forms of medical imaging that many COVID-19 patients with anosmia have experienced, several investigations have indicated that COVID-19 has substantial consequences for the olfactory bulb (OB). Whereas the findings of several tests conducted through various research revealed that COVID-19 produces olfactory dysfunction due to the presence of a change in the shape and size of the OB in some patients with COVID-19-induced anosmia [6], [7]. Kim et al. [8] discovered that anosmia continues to be a risk factor that should be closely monitored in COVID-19 infection. It was also revealed as a significant predictor in predicting the severity of COVID-19. Hence, grading the severity of OB dysfunction is considered an essential task.
The OB can be examined using different modalities such as magnetic resonance imaging (MRI), fluid-attenuated inversion recovery (FLAIR), and diffusion tensor imaging (DTI) [9]. Kandemirli et al. [10] attempted to understand the underlying etiology of persistent olfactory disturbance associated with COVID-19. They employed MRI to assess 23 anosmic patients with chronic COVID-19 olfactory dysfunction who had at least a one-month interval between the onset of olfactory dysfunction and the evaluation. Their findings revealed that COVID-19 anosmia had olfactory cleft and OB anomalies, as well as a relatively high percentage of OB degeneration. Further, Chiu et al. [11] compared pre-COVID imaging to a COVID-19 anosmic case with definite OB atrophy. After a positive MRI diagnosis of COVID-19 and 2 months of anosmia, an MRI revealed obvious interval OB atrophy. This predictive finding indicated that the olfactory entrance site to the brain should be examined further to better our understanding of COVID viral pathogenesis. Notably, Nagamine [12] discovered no abnormalities in the head computed tomography (CT), but MRI revealed brain contusions in the bilateral orbitofrontal lobes on the FLAIR images.
Regarding the dysfunction of smell and taste investigation, Lechien et al. [13] examined 417 COVID-19 cases from 12 European hospitals who were laboratory-confirmed. They studied the epidemiological and clinical results of the patients in terms of comorbidities, age, general symptoms, gender, and otolaryngological symptoms. The patients also underwent a smell and taste test. About 85.6% of patients notified a defect in their sense of smell, 88% of patients notified a defect in taste. Although 18.2% of the infected do not suffer from nasal congestion or rhinorrhea, 79.7% of them suffer from a hyposmia or anosmia. The study proved that the defect in the sense of smell or taste is one of the common symptoms in European people infected with COVID-19 and may not show nasal symptoms refers to COVID-19 infection.
Although artificial intelligence (AI) is applied excessively to detect and examine COVID-19 cases [14], few preliminary research and case reports are examining the application of AI to plain radiography and CT of the OB for early diagnosis of anosmia. Machine learning (ML) can be used, in collaboration with radiologists, to improve anosmia detection outcomes by increasing the speed and accuracy of prognostication, diagnosis, and classification, as well as exploring anonymous functions. It has the potential to be a valuable tool for defining and measuring lesions in medical images, as well as tracking longitudinal changes between scans, which is critical for precision medicine. Unfortunately, Computer Aided Design (CAD) systems for anosmia diagnosis of patients by olfactory bulbs imaging are limited in the literature [15].
Lu et al. [16] determined the subtle structural alterations in the brain caused by COVID-19. The study was applied to 60 people recovered from COVID-19 and 39 people without COVID-19 using DTI where the Mean Diffusivity (MD), Fractional Anisotropy (FA), Radial Diffusivity (RD), and Axial Diffusivity (AD) values for the DTI were recorded. By applying covariance analysis (ANCOVA), they compared the regional volumes between voxel-based morphometry (VBM) DTI measurements. The study found that nearly 55% of patients had neurological signs. Furthermore, Callejon-Leblic et al. [17] utilized ML models that involved a logistic regression (LR), random forest (RF), and support vector machine (SVM) to evaluate the prognostic values of COVID-19-related olfactory and taste dysphoria. Their study comprised 777 infected individuals who received real-time reverse transcription–polymerase chain reaction (RT-PCR) testing as well as a questionnaire about the existence and severity of their symptoms, such as loss of smell and taste. Based on visual analog scales (VAS), the ML algorithms achieved an accuracy of 80%, a sensitivity of 82%, and a specificity of 78%.
Moreover, Roland et al. [18] included 145 +ve COVID-19 cases and 157 -ve COVID-19 cases. The study relied on a Stepwise LR to identify symptoms that predict +ve COVID-19 infection. The study used receiver operating characteristic curve (ROC) analysis to evaluate the identified classifiers for making prediction. The study found a disturbance in the sense of smell, taste, and myalgias indicates positive COVID-19, while difficulty breathing and a sore throat indicate a negative COVID-19. When the prediction model depended on five symptoms, it gave aloft accuracy with a predictive value of 82% and a low sensitivity, and when it only took two symptoms out of the five, obtained aloft sensitivity 70%, accuracy 75%, and a prediction of 75%.
As far as we are aware, the previous studies and CAD systems faced various limitations that are addressed by the current research. Most of the approaches mentioned above did not consider developing a grading system to predict the OB severity of infection (Normal, Mild, Moderate, or Severe). Most of the aforementioned studies have low diagnostic accuracy because they developed their CAD system upon a single imaging modality. Most existing studies did not consider the appearance, diffusivity, and shape markers to assess the OB infection severity. The goal of the proposed CAD system is to overcome these limitations by enhancing and extending the current state-of-the-art in OB infection diagnosis. By incorporating multiple imaging modalities and a grading system, the proposed system is expected to improve the diagnostic accuracy of OB infection and provide more detailed information about the severity of the infection. Additionally, the use of appearance, diffusivity, and shape markers can provide a more comprehensive analysis of the infection characteristics. Overall, the proposed CAD system aims to enhance the current capabilities of OB infection diagnosis and provide a more advanced tool for medical professionals to accurately assess and treat patients with OB infection. The contributions of the current study can be listed as follows:
-
-
Proposed a novel Computer-Assisted Diagnostic (CAD) system to diagnose olfactory bulb (OB) infection severity in COVID-19 patients using fluid-attenuated inversion recovery (FLAIR) Magnetic Resonance Imaging (MRI) and Diffusion Tensor Imaging (DTI).
-
-
Overcame limitations of previous studies by incorporating multiple imaging modalities and a grading system to improve diagnostic accuracy and provide more comprehensive analysis of infection characteristics.
-
-
Demonstrated improved performance metrics using markers stacking and majority voting, with potential to help doctors assess which patients need more intensive clinical care.
The rest of this paper is organized as follows: Section 2 discusses the materials while Section 3 methods. Section 4 presents the experimental results. Section 5 discusses the results and study problem. Section 6 mentions the current study limitations. Finally, Section 7 presents the conclusions, and future work.
2. Materials
Study Design and Ethical Considerations: The proposed study underwent rigorous verification and validation utilizing a dataset obtained from Mansoura University in Egypt. Ethical approval for the research plan was granted by the institutional review boards at both the University of Louisville (IRB: R.22.02.1622.R1.R2 - 2022/04/14) and Mansoura University. The study strictly adhered to established rules and regulations, ensuring all methods were conducted in accordance with ethical standards. Informed consent was explicitly obtained from all patients involved in the study.
Patient Selection and Characteristics: A diverse cohort of 71 patients participated in the study, contributing to a comprehensive understanding of olfactory disorders. The patient distribution included 27 classified as “Normal,” 29 with “Mild Anosmia,” and 15 with “Severe Anosmia.” Each patient underwent thorough examination through two imaging modalities: Diffusion Tensor Imaging (DTI) and Fluid-Attenuated Inversion Recovery (FLAIR).
Imaging Techniques: State-of-the-art imaging technology was employed, utilizing a 1.5 Tesla Magnetic Resonance (MR) device (Ingenia, Philips Medical Systems, Nederland). The 3D-Fluid Attenuated Inversion Recovery (FLAIR) sequence parameters were finely tuned: Repetition Time (TR)/Echo Time (TE) = 8000/133 milliseconds (ms), bandwidth = 120 Hertz per pixel (Hz/pixel), Turbo Spin Echo (TSE) factor = 80, section thickness = 2 millimeters (mm), inter-slice gap = 0.5 mm, Field of View (FOV) = 230 × 230 × 20 mm2, matrix = 240 × 240, Echo Train Length (ETL) = 220 with variable flip angles, and an acquisition time of 270 seconds. Diffusion Tensor Imaging (DTI), a crucial component of our investigation, utilized a single-shot echo-planar sequence with a TR/TE of 3200/90 ms. Diffusion gradients were applied along 32 axes, with scanning parameters including FOV = 184 × 184 mm2, voxel dimensions = 1.8 × 1.8 × 18 mm3, number of averages = 14, and a data matrix of 92 × 88, resulting in 48 slices with no inter-slice gap.
-
-
Exemplar samples from the dataset are thoughtfully illustrated in Fig. 1.
-
-
The meticulous analysis of images was performed by two highly skilled neuroradiologists.
-
-
Subsequent to image acquisition, the data underwent detailed analysis on a specialized workstation, particularly focusing on the DTI maps co-registered and positioned at the Olfactory Bulb (OB) alongside the 3D-FLAIR pictures.
-
-
Quantitative measurements of Mean Diffusivity (MD) and Fractional Anisotropy (FA) were undertaken on the right and left OBs, respectively.
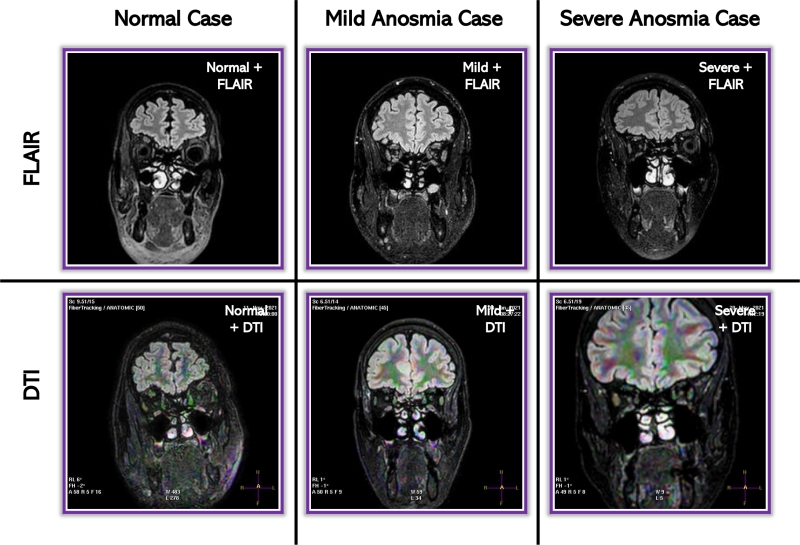
Figure 1.
Diffusion Tensor Imaging (DTI) and Fluid Attenuated Inversion Recovery (FLAIR) samples from the dataset. Left: Normal case. Middle: Anosmia case. Right: Severe anosmia case. Top row: FLAIR images. Bottom row: DTI images.
Data Collection and Analysis: The collected data underwent a systematic and thorough analysis, employing advanced statistical and computational methods to derive meaningful insights into olfactory disorders. This comprehensive approach ensured the reliability and robustness of our findings.
Data Categorization: The data was categorized meticulously, considering various parameters such as patient demographics, imaging modalities, and diagnostic classifications. This categorization enhances the granularity of our analysis.
Data Availability: The datasets generated and analyzed during the current study are available upon reasonable request.
3. Methods
The current study suggests a Computer-Assisted Diagnostic (CAD) system that categorizes a COVID-19 patient as either having normal smell, mild anosmia, or severe anosmia. Hence, there are three categories. The system is designed to detect anosmia, a medical condition characterized by loss of smell. It comprises of a complex pipeline with three distinct stages, each performing a specific task to improve the accuracy of the final diagnosis. In the first stage, the system extracts various appearance markers, including both first and second-order markers, morphology/shape markers such as spherical harmonics, and diffusivity markers like Fractional Anisotropy (FA) and Mean Diffusivity (MD). These markers provide information about the texture, shape, and diffusion characteristics of the olfactory bulbs, which can help differentiate between normal and anosmic individuals.
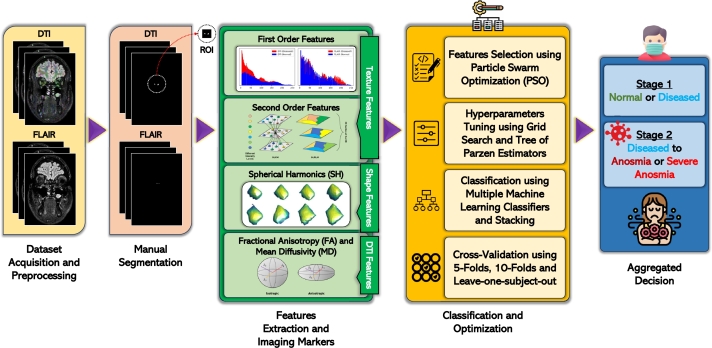
In the second stage, the system applies marker fusion techniques to integrate the extracted markers from the first stage. This fusion process optimizes the information gained from the markers and improves the system's ability to detect anosmia. In the third and final stage, the system determines the diagnosis and corresponding performance metrics based on the most promising classifier. Using the integrated markers from stage two, the system categorizes the diagnosis as “Normal,” “Mild Anosmia,” or “Severe Anosmia,” depending on the severity of the condition. The current study is unique in that it ensemble bagging the trained and fine-tuned ML classifiers together and makes the OB anosmia diagnosis based on majority voting. The suggested CAD framework is summarized graphically in Fig. 2.
Figure 2.
Graphical summarization of the suggested CAD framework that categorizes a COVID-19 patient as either having normal smell, mild anosmia, or severe anosmia.
From Fig. 2, the study unfolds in stages that encompass “dataset acquisition and preprocessing”, “manual segmentation”, and “features extraction, and imaging markers”, including first order and second order features, spherical harmonics (SH), FA, and MD. The process further delves into texture features, shape features, and DTI features. The “classification and optimization” phase follow, involving features selection using particle swarm optimization (PSO) and hyperparameters tuning through grid search and tree of parzen estimators. Classification culminates with multiple machine learning classifiers and stacking. The study employs cross-validation techniques, including 5-folds, 10-folds, and leave-one-subject-out, contributing to an aggregated decision-making process.
3.1. Pre-processing
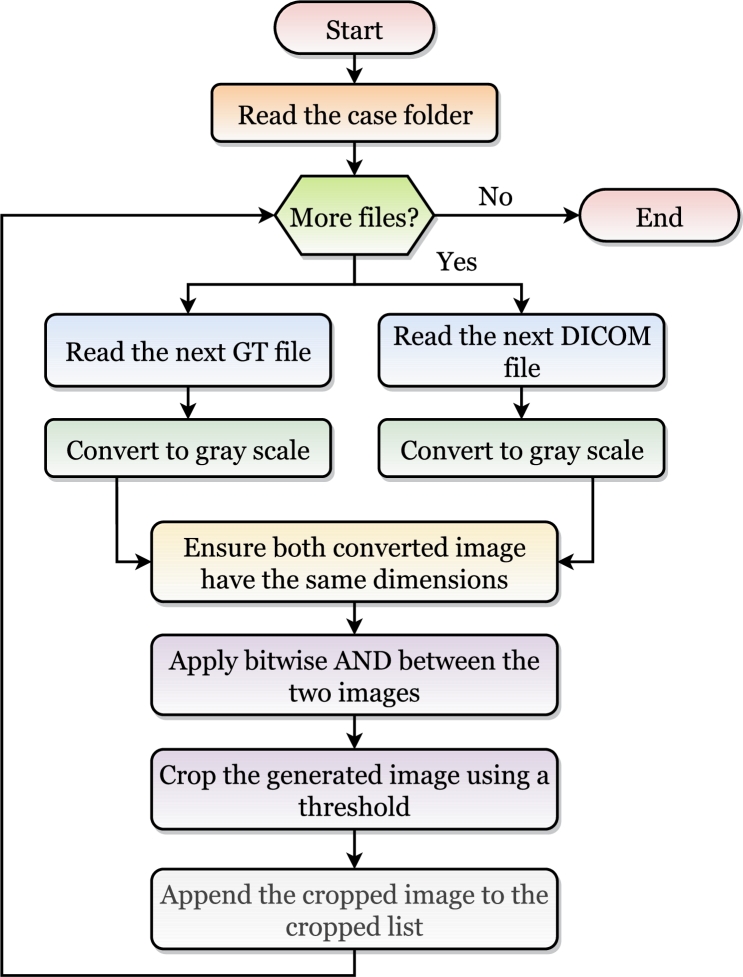
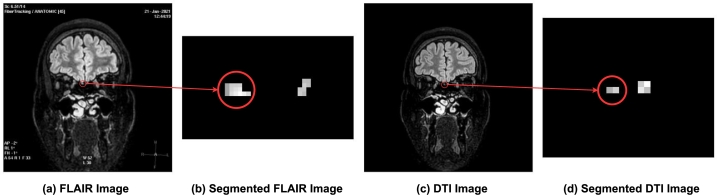
The DICOMs and masks were pre-processed before extracting the features from them. Fig. 3 showed a flowchart of the applied steps for each case. Refer to Fig. 4 for visual representations of samples from the delineated dataset. The DICOMs (Fig. 4 a and c) and masks (Fig. 4 b and d) of a case were read as images and converted to grayscale. The images could be found in different dimensions, and hence the images were resized to be equal in size (i.e., width and height). After that, for each DICOM image and its corresponding mask, a bitwise AND operation was applied to them. To capture only the olfactory bulbs, the black portion was cropped.
Figure 3.
Pre-processing the DICOMs and masks before extracting the features.
Figure 4.
Sample from the used dataset and their delineations. (a) FLAIR Image, (b) Delineated FLAIR Images, (c) DTI Image, and (d) Delineated DTI Image.
For DTI and FLAIR cases, similar pre-processing steps were applied. This involved resizing different images to equal dimensions and converting all cases to grayscale. Manual delineation was carried out to facilitate the extraction of the Region of Interest (ROI).
3.2. Markers extraction
A marker (i.e., feature) is an independently measurable attribute of an observation in machine learning (ML). There are different approaches to extract the markers such as textural, morphological, and topological markers extraction techniques. A major challenge is to select the most suitable markers that can increase the machine learning classifier chance to distinguish between the different classes. In the current study, three marker types are extracted from the delineated ROIs. They are appearance markers (i.e., and order markers), morphology/shape markers (i.e., spherical harmonics), and diffusivity markers (i.e., Fractional Anisotropy (FA) & Mean Diffusivity (MD)). The different markers are summarized in Table 1 and discussed in detail in the following subsections.
Table 1.
The different combinations of the extracted markers including textural markers, morphological shape markers, and DTI markers.
| Type | Technique | Modality | No. of Markers |
|---|---|---|---|
| Textural Markers | First-order Markers | DTI and FLAIR | 44 |
| Second-order Markers using GLCM | DTI and FLAIR | 56 | |
| Second-order Markers using GLRLM | DTI and FLAIR | 16 | |
| Morphological Shape Markers | Spherical Harmonics (SH) | DTI and FLAIR | 85 |
| DTI Markers | MD-FA | DTI | 4 |
| Total (BOTH) | 201 × 2 + 4 = 406 | ||
3.2.1. Appearance markers
The first- and second-order markers are exploited in the current study. First-order markers, such as the mean and standard deviation concern with the properties of individual pixels. Second-order markers concern the spatial co-occurrence (or inter-dependency) of 2 pixels at specific relative positions. The extracted first-order markers are (1) mean, (2) median, (3) median absolute deviation (MAD), (4) variance, (5) skewness, (6) kurtosis, (7) Pearson kurtosis, (8) Fisher kurtosis, (9) Shannon entropy, (10) descriptive statistics, (11) cumulative frequency, (12) relative frequency, (13) cumulative distribution function (CDF), (14) empirical cumulative distribution function (ECDF), (15) percentiles, and (16) interquartile range. The total number of extracted markers per record is 44. The drawback of the first-order markers is that they do not capture the homogeneity between the pixels which is solved by the second-order markers [19].
The Gray Level Co-occurrence Matrix (GLCM) markers are 24 markers that describe the order joint probability function of a specific image region restricted by the applied mask. The extracted markers are (1) autocorrelation, (2) cluster prominence, (3) cluster shade, (4) cluster tendency, (5) contrast, (6) correlation, (7) difference average, (8) difference entropy, (9) difference variance, (10) joint energy, (11) joint entropy, (12) Informational Measure of Correlation (IMC), (13) Inverse Difference Moment (IDM), (14) Maximal Correlation Coefficient (MCC), (15) Inverse Difference (ID), (16) Inverse Difference Normalized (IDN), (17) inverse variance, (18) maximum probability, (19) Sum Average, (20) sum entropy, and (21) sum of squares. The total number of extracted markers per record is 56 [20], [21].
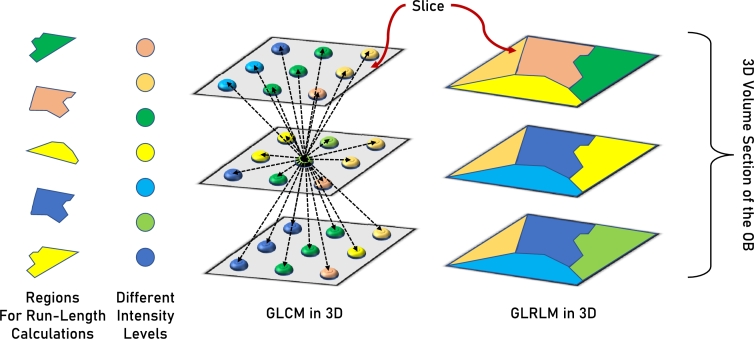
The Gray Level Run-Length Matrix (GLRLM) is the set of continuous pixels that have the same gray level. The run-length is the neighboring gray levels number in a specific direction [21]. It is used to capture the homogeneity in a pattern based on the order relationships and pairwise interactions. 16 markers are extracted from the GLRLM that quantify the gray level runs. They are: Short and Long Run Emphasis (LRE and SRE), Gray Level Non-Uniformity and Non-Uniformity Normalized (GLN and GLNN), Run Length Non-Uniformity and Non-Uniformity Normalized (RLN and RLNN), Run Percentage (RP), Gray-Level Variance (GLV), Run Variance and Entropy (RV and RE), Low and High Gray Level Run Emphasis (LGLRE and HGLRE), Short Run Low and High Gray Level Emphasis (SRLGLE and SRHGLE), and Long Run Low and High Gray Level Emphasis (LRLGLE and LRHGLE). Fig. 5 shows a visualization of the differences between GLCM and GLRLM.
Figure 5.
Visualization of the differences between Gray Level Co-occurrence Matrix (GLCM) and Gray Level Run Length Matrix (GLRLM) for a 3D volume. Each square-like region represents a slice in the volume. Polygons in the GLRLM slices represent regions for run-length calculations. Circles in the GLCM slices represent pixels with different intensity levels.
GLCM and GLRLM are texture analysis techniques employed in both 2D (single image) and 3D (entire volume or case) imaging scenarios. In 2D, GLCM quantifies spatial relationships between pixel pairs by calculating the occurrence of intensity values at specified pixel distances and angles. This matrix provides information about texture patterns, aiding in the characterization of image structures such as edges and textures. On the other hand, GLRLM, in its 2D form, focuses on the consecutive occurrence of pixel intensities along specific directions, revealing information about the length and distribution of runs in an image. When extended to 3D, these techniques are adapted to analyze volumetric data. 3D GLCM considers the co-occurrence of voxel intensities in three-dimensional space, capturing spatial relationships along multiple axes. This extension enhances the analysis of complex structures within volumetric data, such as medical imaging volumes. Similarly, 3D GLRLM extends the run-length analysis to three dimensions, providing insights into the length and distribution of voxel runs within the entire volume.
3.2.2. Morphology/shape markers
The motivation for using morphological markers relies on the hypothesis that anosmia and severe anosmia have different sizes and shapes depending on the severity of inflammation. Spherical harmonics (SH) are utilized in the current study to extract morphological markers. It is believed that the number of SHs will differ between the cases severity. In other words, the number of SHs in a severe case will be more that the number of SHs in a normal case. The origin reference point is chosen at random from the interior of the region convex kernel. The surface of the region can be considered a function of the polar and azimuth angle (i.e., . The new coordinate system can be written as a linear collection of base functions described in the unit sphere. The attraction–repulsion approach is used to map a triangulated mesh approximating the surface of the scan to the unit sphere in the modelling of spherical harmonics [22]. This approach allows precise modelling since the unit distance between each remapped node and the origin is maintained while the distances between the neighboring nodes are preserved.
Each attraction–repulsion cycle α operates as follows. Assume that represents the coordinates of the node on the unit sphere corresponding to mesh vertex i at the beginning of cycle α. Let (Equation (1)) represent the vector directed from node i to node j. Then, the Euclidean distance between the nodes i and j is defined as . Assume that represents the index group of the neighbors of a vertex i in the triangulated mesh. Then, the attraction step updates the node's locations to maintain it in the center with its neighbors concerning Equation (2) where and are parameters of the attractive force strength, , and .
| (1) |
| (2) |
The repulsion step then enlarges the spherical mesh to prevent it from deteriorating, as shown in Equation (3), where is a repulsion parameter that specifies the shift incurred concerning each other surface node and keeps the processing time and accuracy in balance. A small value of CR maintains the accuracy while increasing the processing time. The nodes are then projected back onto the unit sphere using the unit norm, and these are the new coordinates to work with at the start of the next cycle as shown in Equation (4).
| (3) |
| (4) |
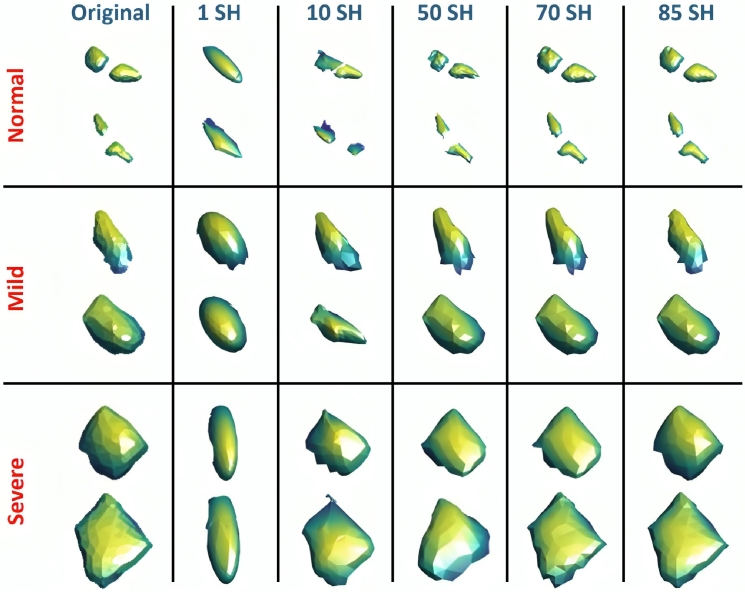
In the final cycle of the attraction–repulsion approach, the surface has a one-to-one relationship with the unit sphere. Every point of the initial mesh has been mapped to a corresponding point with a polar angle and an azimuth angle . At this time, it is more suitable to represent the scan by a SH series . A SH series is created by solving an isotropic heat equation for a surface that is modelled as a function on the unit sphere. The of degree τ with an order β is identified concerning Equation (5) where is the SH factor and represents the relevant Legendre polynomial of a τ degree with a β order. Anosmia and severe anosmia scans are defined by a higher-order integration of SH series because their shapes are heterogeneous and more complicated, whereas normal scans are represented by a lower-order integration of SH series because their shapes are homogeneous and less complex. As a result, the number of SH is equal to the total number of markers indicating the shape complexity of the recognized scans. In the suggested CAD system, 85 SHs are adequate to properly reconstruct the scan geometry. Fig. 6 shows the visualization of the SHs for the “Normal”, “Anosmia”, and “Severe Anosmia” cases.
| (5) |
Figure 6.
Visualzation of the Spherical Harmonics (SHs) for the “Normal”, “Anosmia”, and “Severe Anosmia” cases. Rows represent the categories, while columns represent the different numbers of added SHs.
3.2.3. Diffusivity markers
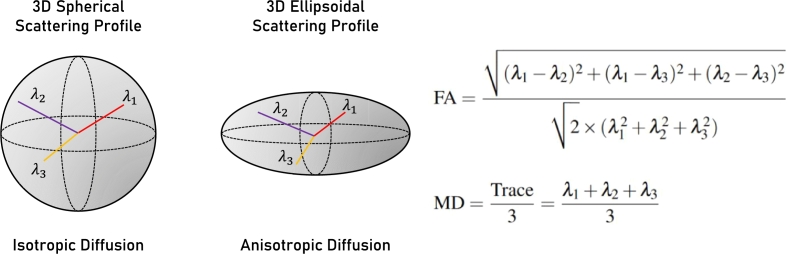
Diffusion Tensor Imaging (DTI) is a sophisticated MRI modality that characterizes the diffusion tensor of a voxel and provides the essential data by using the Brownian motion of water molecules in at least 6 directions [23]. The Fractional Anisotropy (FA) and Mean Diffusivity (MD) are extracted from the DTI using Equations (6) and (7) respectively where , , and are the eigenvalues (i.e., displacement/diffusion value for each specific vector) [24]. The MD determines the tissue's overall diffusivity, while the FA determines the degree of directional limitation in water diffusion. The eigenvalues are presented graphically in Fig. 7. In it, the left sub-figure shows an isotropic diffusion profile because the tensor has about equal eigenvalues for each primary vector while the right sub-figure presents an anisotropic diffusion profile.
| (6) |
| (7) |
Figure 7.
Visualization of the isotropic and anisotropic shapes alongside the Fractional Anisotropy (FA) and Mean Diffusivity (MD) equations, which are based on the lambda values. The isotropic shape represents a 3D spherical profile, while the anisotropic shape represents a 3D ellipsoidal profile.
3.3. Evolutionary features selection using particle swarm optimization (PSO)
The current study employed Particle Swarm Optimization (PSO) as a powerful technique for Evolutionary Feature Selection (EFS). PSO is a nature-inspired optimization algorithm that simulates the social behavior of birds (or fish) [25]. In the context of feature selection, PSO is utilized to identify the most promising subset of features from a given feature space. The algorithm starts with a population of potential feature subsets, represented as particles, and iteratively updates their positions based on the fitness of the subsets in improving the performance of a specified machine learning model. Through this iterative process, PSO effectively explores the feature space, converging towards an optimal set of features that enhances the model's predictive capability [26].
Algorithm 1 outlines the Evolutionary Feature Selection using Particle Swarm Optimization (PSO) algorithm [26]. It iteratively updates the positions of particles (representing feature subsets) in the search space based on their fitness, aiming to converge towards the optimal feature subset that maximizes the performance of the specified machine learning model. The PSO algorithm employs acceleration coefficients, inertia weight, and randomization to guide particles through the search space efficiently. The best feature subset is determined by evaluating the fitness of each particle, and the algorithm continues until a specified maximum number of iterations is reached.
Algorithm 1.
Evolutionary Feature Selection using Particle Swarm Optimization (PSO) [26].
In Algorithm 1: The dataset is denoted by , representing the input dataset containing records for the machine learning task. The population size is represented by N, indicating the number of particles (feature subsets) in the swarm. The maximum number of iterations is denoted by T, defining the total number of iterations the PSO algorithm will perform. Acceleration coefficients are represented by and , influencing the impact of personal and global best positions on particle movement. The inertia weight is denoted by w, regulating the impact of the previous velocity on the current velocity. Particle positions and velocities are represented by and for each particle i. Personal best positions and fitness values are denoted by and , respectively. The global best position is represented by . The algorithm iteratively updates these parameters to guide the swarm toward an optimal feature subset that maximizes the performance of the machine learning model.
3.4. Classification and optimization
The markers fusion is utilized in this multiclass classification problem to distinguish between “Normal”, “Mild Anosmia”, and “Severe Anosmia”. Eleven machine learning algorithms are utilized in the current study to obtain state-of-the-art results. They are (1) decision trees (DT), (2) extra tree (ET), (3) adaptive boosting (AdaBoost), (4) random forest (RF), (5) support vector machine (SVM), (6) gradient boosting (GB), (7) histogram gradient boosting (HGB), (8) eXtreme gradient boosting (XGB), (9) light gradient boosting model (LGBM), (10) k-nearnest neighbors (KNN), and (11) multilayer perception (MLP) [27].
Table 2 shows the different ranges for the ML algorithms hyperparameters. In addition to the mentioned hyperparameters and their ranges, different scaling techniques are used to find the most suitable on the dataset. They are (1) L1 normalization , (2) L2 normalization , (3) max normalization , (4) standardization , (5) min-max scaling , (6) max-absolute scaling , and (7) robust scaling .
Table 2.
The utilized hyperparameters ranges for ML algorithms.
| ML Algorithm | Hyperparameters | Utilized Range |
|---|---|---|
| DT | Criterion | Gini and Entropy |
| Splitter | Best and Random | |
| Max Depth | 1 to # Features | |
| SVM | C | Log-Normal distribution (0,1.0) |
| Kernel | Linear, RBF, Poly, Sigmoid | |
| Gamma | Scale, Auto | |
| Degree | 1, 2, 3, 4, 5 | |
| LR | C | Log-Normal distribution (0,1.0) |
| Solver | Liblinear, LBFGS | |
| RF | Max Depth | 1 to # Features |
| # Estimators | 1 to 100 | |
| Criterion | Gini and Entropy | |
| KNN | # Neighbours | 1 to 0.5 × # Samples |
| Weights | Uniform and Distance | |
| Algorithm | Ball Tree, KDTree, Brute Force | |
| Distance Metrics | Minkowski, Euclidean, Manhattan, Chebyshev | |
| LGBM | # Estimators | 1 to 100 |
| Max Depth | 1 to # Features | |
| Learning Rate | Log-Normal distribution (0.01,1.0) | |
| XGB | Subsample | Uniform distribution (0.1,1) |
| # Estimators | 1 to 100 | |
| Max Depth | 1 to 50 | |
| Learning Rate | Log-Normal distribution (0.01,1.0) | |
| GB | Max Depth | 1 to # Features |
| Learning Rate | Log-Normal distribution (0.01,1.0) | |
| # Estimators | 1 to 100 | |
| AdaBoost | # Estimators | 1 to 100 |
| Learning Rate | Log-Normal distribution (0.01,1.0) | |
| MLP | Activation | Logistic, ReLU, Tanh |
| Learning Rate | Constant, Adaptive, Invscaling | |
| Solver | LBFGS, SGD, Adam | |
| Hidden Layer Sizes | 16 to 512 (multiple of 16) | |
| ET | Max Depth | 1 to # Features |
| Criterion | Gini and Entropy | |
| # Estimators | 1 to 100 | |
Hyperparameter tuning is a critical aspect of ML model development, aiming to find the optimal configuration of hyperparameters that maximizes model performance. Two commonly utilized techniques for this purpose are Grid Search (GS) and Tree of Parzen Estimators (TPE). Grid Search involves exhaustively evaluating the model's performance over a predefined grid of hyperparameter values. This method is straightforward to implement and provides a systematic exploration of the entire search space. On the other hand, Tree of Parzen Estimators, a Bayesian optimization algorithm, offers a more efficient approach. TPE builds a probabilistic model of the objective function and uses an exploit-explore strategy to balance between refining known promising regions and exploring uncertain areas of the hyperparameter space. This technique tends to require fewer evaluations compared to Grid Search, making it particularly useful in high-dimensional spaces [28].
Algorithm 2 outlines the TPE optimization algorithm [28]. It involves iteratively sampling configurations, evaluating the objective function, updating the set of observed configurations, and refining the probabilistic model based on Bayesian principles. The final step selects the best hyperparameter set based on the observed objective function values. Adjustments to the exploration-exploitation balance can be made through the ρ parameter.
Algorithm 2.
Tree of Parzen Estimators (TPE) for Hyperparameters Optimization [28].
In Algorithm 2: represent the dataset, n denotes the number of iterations, p signifies the hyperparameter space, ξ stands for the acquisition function guiding exploration-exploitation trade-offs, and ρ is a parameter influencing this balance. The set keeps track of observed configurations and their objective function values. Hyperparameter sets, represented by θ, are sampled from p and evaluated with associated objective function values denoted by r. The algorithm iteratively updates and refines its probabilistic model to efficiently search for the optimal hyperparameter set. The final result, , corresponds to the hyperparameter set maximizing the objective function based on observed values, with the ρ parameter allowing practitioners to fine-tune exploration-exploitation dynamics.
Algorithm 3 outlines the GS optimization algorithm [29]. It systematically explores the hyperparameter grid, evaluates the objective function for each configuration, and updates the best hyperparameter set based on the observed objective function values. The final result is the hyperparameter set that yields the highest objective function value during the search.
Algorithm 3.
Grid Search Hyperparameters Optimization Algorithm [29].
In Algorithm 3: The hyperparameter grid is denoted by , representing a predefined set of hyperparameter values to be explored. Each θ in represents a specific configuration of hyperparameters. The objective function, denoted by r, is evaluated for each configuration, reflecting the performance metric to be optimized. represents the best hyperparameter set encountered during the search, while corresponds to the highest observed objective function value. The algorithm systematically iterates through the hyperparameter grid, evaluating configurations and updating the best set based on the objective function values, ultimately identifying the hyperparameters that optimize the chosen performance metric.
3.5. Model evaluation and performance metrics
K-fold cross-validation is used to evaluate the ML algorithms and compare them together. This is utilized by dividing the dataset into k portions where are used for training and 1 is used for testing. The current study uses 5 and 10 folds, and leave-one-subject-out (LOSO). LOSO uses all records in the dataset unless one observation in the training and that one is left for testing. LOSO is used as it provides a reduced biased measure.
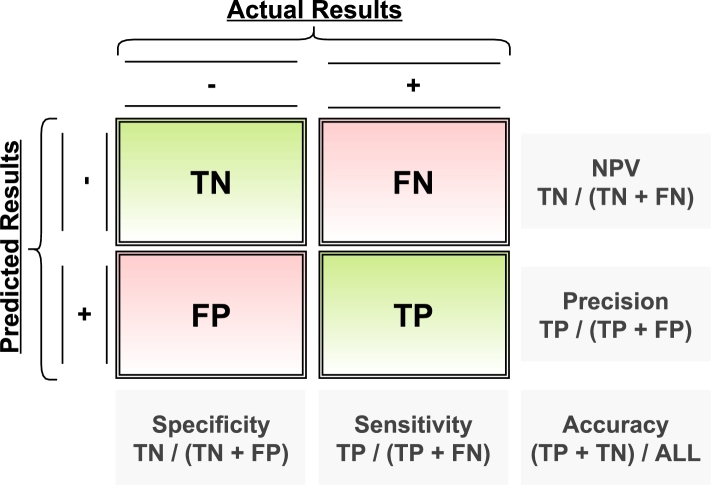
During the learning and optimization process, various performance metrics are computed to assess the model's effectiveness. Accuracy is the proportion of correctly predicted observations (true values) to the total number of observations, providing a comprehensive overview of overall correctness. Sensitivity, also known as Recall, measures the ratio of correctly predicted positive instances to the total actual positive instances, emphasizing the model's ability to capture all relevant cases. Specificity quantifies the ratio of true negatives to the total actual negatives, offering insights into the model's capability to correctly identify non-positive instances. Precision represents the ratio of correctly predicted positive instances to the total predicted positive instances, emphasizing the precision of positive predictions. The F1-score, a harmonic mean of Precision and Recall, provides a balanced assessment of the model's performance. Additionally, the Receiver Operating Characteristic (ROC) curve illustrates the trade-off between Sensitivity and Specificity across different threshold values. This comprehensive set of metrics, as illustrated in Fig. 8, ensures a nuanced evaluation of the model's performance, capturing various aspects of classification effectiveness.
Figure 8.
Summary on the performance metrics from the confusion matrix.
4. Experimental results
To highlight the innovation of this system, as discussed earlier, the current study suggests a CAD system that categorizes a COVID-19 patient as being either normal or having mild or severe anosmia as shown in Fig. 2. It overcomes the discussed limitations. To highlight the prediction of the OB infection severity, the CAD system multi-classifies the severity into normal, moderate, and severe as presented in Fig. 1. To highlight the modalities and markers contributions, the CAD utilizes the FLAIR and DTI images. It extracts first and higher-order appearance markers as well as shape and diffusivity markers as shown in Table 1. To confirm the accuracy of the proposed CAD approach, the experiments are performed using 5-folds, 10-folds, and LOSO to validate the performance. In each category, 11 ML classifiers are trained on the extracted markers and tuned using the grid search to select the most promising hyperparameters (as presented in Table 2). The features are stacked together and the decision is made based on the majority voting. To report the performance, different performance metrics are used such as accuracy as sensitivity. The different experimental configurations are summarized in Table 3.
Table 3.
The utilized experimental configurations in the current study.
| Configuration | Value |
|---|---|
| No. of Cases | 71 Cases |
| Markers Categories | First Order, Second Order, SH, MD-FA, and Concatenated |
| Classes | Normal, Mild Anosmia, and Severe Anosmia |
| Modalities | DTI and FLAIR |
| Segmentation Mechanism | Manual Segmentation |
| Hyperparameters Optimization Approach | Grid Search (GS) and Tree of Parzen Estimators (TPE) |
| Features Selection Technique | Particle Swarm Optimization (PSO) (Evolutionary Feature Selection) |
| Machine Learning Algorithms | DT, ET, AdaBoost, RF, GB, HGB, XGB, LGBM, SVM, KNN, and MLP |
| Scaling Techniques | Normalization (L1, L2, and Max), Standardization, Min-Max, Max-Absolute, and Robust |
| Hyperparameters Range | Presented in Table 2 |
| Evaluation Approach | cross-validation and Performance Metrics (Fig. 8) |
| No. of Folds | 5-Folds, 10-Folds, and Leave-one-subject-out (LOSO) |
| No. of Trials | 100 trials to report means and 95% CI |
Table 4 showcases the performance metrics resulting from the application of PSO feature selection within the framework of 5-fold cross-validation. Each approach is associated with various classifiers or combinations thereof, and the metrics include accuracy, BAC, precision, recall, specificity, F1 score, and IoU.
Table 4.
The reported performance metrics that reflect the outcomes of the PSO feature selection applied within the context of 5-fold cross-validation.
| Approach | Accuracy | BAC | Precision | Recall | Specificity | F1 | IoU |
|---|---|---|---|---|---|---|---|
| AdaBoost | 87.02% ± 0.0007 | 84.49% ± 0.0009 | 81.55% ± 0.001 | 80.54% ± 0.0011 | 88.45% ± 0.0007 | 80.26% ± 0.0012 | 68.19% ± 0.0014 |
| DT | 76.83% ± 0.0055 | 73.15% ± 0.006 | 65.8% ± 0.0081 | 65.52% ± 0.0083 | 80.79% ± 0.004 | 65.18% ± 0.0078 | 50.25% ± 0.0081 |
| ET | 71.69% ± 0.0053 | 67.34% ± 0.0056 | 60.36% ± 0.0091 | 59.68% ± 0.0072 | 75.01% ± 0.004 | 58.12% ± 0.0066 | 41.85% ± 0.0069 |
| GB | 74.27% ± 0.0019 | 70.81% ± 0.0021 | 64.08% ± 0.0024 | 61.99% ± 0.0028 | 79.63% ± 0.0015 | 62.72% ± 0.0027 | 47.25% ± 0.0026 |
| KNN | 71.43% ± 0.0 | 66.91% ± 0.0 | 62.6% ± 0.0 | 59.15% ± 0.0 | 74.67% ± 0.0 | 54.77% ± 0.0 | 39.47% ± 0.0 |
| MLP | 80.94% ± 0.0021 | 77.13% ± 0.0022 | 75.51% ± 0.0058 | 72.3% ± 0.0029 | 81.95% ± 0.0016 | 70.2% ± 0.0027 | 55.53% ± 0.0033 |
| RF | 72.56% ± 0.0062 | 68.2% ± 0.0066 | 65.47% ± 0.0093 | 61.44% ± 0.0081 | 74.96% ± 0.0051 | 59.59% ± 0.008 | 43.22% ± 0.0085 |
| SVM | 78.42% ± 0.0 | 74.4% ± 0.0 | 74.09% ± 0.0 | 69.01% ± 0.0 | 79.8% ± 0.0 | 66.6% ± 0.0 | 51.16% ± 0.0 |
| XGB | 88.26% ± 0.0 | 85.28% ± 0.0 | 81.17% ± 0.0 | 81.69% ± 0.0 | 88.87% ± 0.0 | 80.05% ± 0.0 | 69.12% ± 0.0 |
| LGBM-AdaBoost | 93.47% ± 0.0005 | 92.34% ± 0.0007 | 90.68% ± 0.0008 | 90.23% ± 0.0009 | 94.45% ± 0.0005 | 90.3% ± 0.0009 | 82.7% ± 0.0014 |
| MLP-ET | 79.31% ± 0.0031 | 75.44% ± 0.0035 | 69.85% ± 0.0059 | 69.68% ± 0.0046 | 81.2% ± 0.0025 | 67.93% ± 0.0047 | 53.09% ± 0.0051 |
| MLP-RF | 81.07% ± 0.003 | 77.53% ± 0.0033 | 73.78% ± 0.0067 | 72.45% ± 0.0045 | 82.62% ± 0.0021 | 71.05% ± 0.0045 | 56.25% ± 0.005 |
| XGB-AdaBoost | 89.17% ± 0.001 | 86.58% ± 0.0012 | 82.72% ± 0.0019 | 83.17% ± 0.0016 | 89.98% ± 0.0008 | 82.05% ± 0.0017 | 71.33% ± 0.0021 |
| Best Stacked | 94.1% ± 0.0021 | 92.18% ± 0.0027 | 91.6% ± 0.003 | 90.61% ± 0.0032 | 93.75% ± 0.0021 | 89.82% ± 0.0037 | 82.62% ± 0.0055 |
Each row corresponds to a specific approach, with individual classifiers or combinations thereof applied in both the first and second stages of the experiment. For instance, a single keyword like “AdaBoost” indicates the use of the AdaBoost classifier in both stages, while combined keywords like “LGBM-AdaBoost” signify a two-stage application with LGBM in the first stage and AdaBoost in the second. The term “Stacked” represents a majority voting ensemble involving classifiers such as “LGBM-AdaBoost,” “MLP-ET,” “MLP-RF,” and “XGB-AdaBoost”, collectively yielding the best metrics across various evaluation criteria. To enhance the robustness of the findings, the records provide mean and 95% confidence interval values, derived from 100 experiment trials, offering a more comprehensive understanding of the approach's stability and consistency.
Analyzing the reported metrics, it is evident that the “Stacked” ensemble approach consistently outperforms individual classifiers in terms of accuracy, BAC, precision, recall, specificity, F1 score, and IoU. This underscores the effectiveness of combining diverse classifiers to achieve superior predictive performance. The approach exhibits notable outcomes with an accuracy of 94.1% ± 0.0021, BAC of 92.18% ± 0.0027, precision of 91.6% ± 0.003, recall of 90.61% ± 0.0032, specificity of 93.75% ± 0.0021, F1 score of 89.82% ± 0.0037, and IoU of 82.62% ± 0.0055.
In the first stage of the “Stacked” ensemble approach, the MLP is configured with the following hyperparameters: ReLU activation function, hidden layer sizes at 384, constant learning rate, and Adam optimizer. For the XGB classifier, the hyperparameters include a learning rate of 0.7876, maximum depth set to 14, number of estimators at 85, and subsample of 0.9868. The LGBM in the first stage is configured with a learning rate of 0.5188, a maximum depth of 156, and 96 estimators. In the second stage, the hyperparameters for the ensemble classifiers are as follows: For AdaBoost, the learning rate is set to 1.0010, and the number of estimators is 53. The ET classifier uses Gini as the criterion, has a maximum depth of 8, and employs 31 estimators. The RF classifier, on the other hand, utilizes Entropy as the criterion, has a maximum depth of 74, and is configured with 86 estimators.
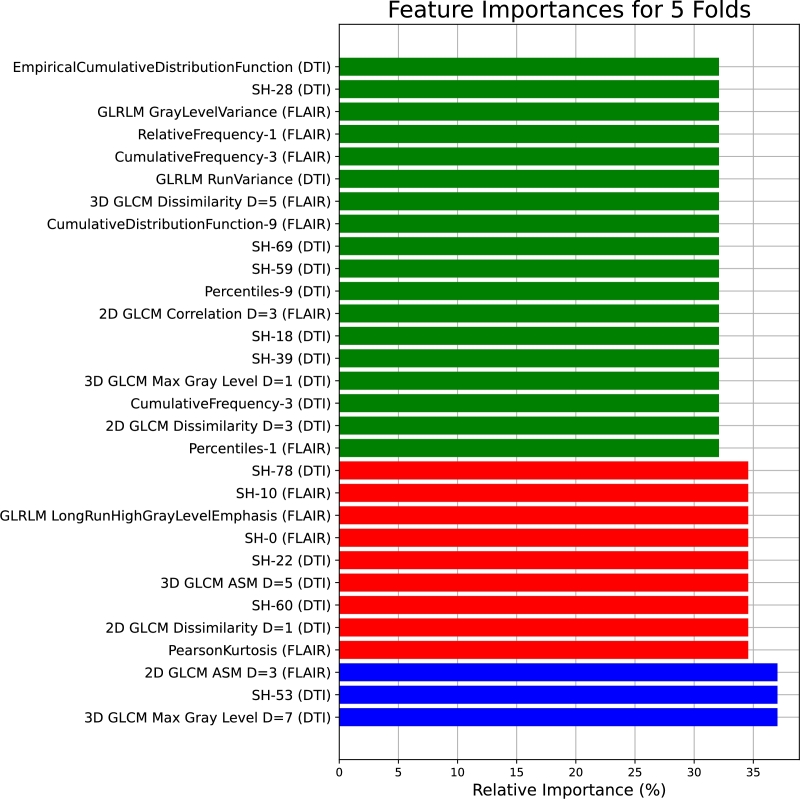
Regarding scaling, in the first stage, MinMax scaling is applied to MLP, STD scaling to XGB, and MaxAbs scaling to LGBM. In the second stage, AdaBoost uses L2 scaling, ET uses L1 scaling, and RF uses Max scaling. In terms of feature configurations, the first stage involves MLP with 213 features, XGB with 198 features, and LGBM with 208 features. Moving to the second stage, the AdaBoost classifier operates with 201 features, the Extra Trees (ET) classifier with 187 features, and the Random Forest (RF) classifier with 207 features. Fig. 9 presents the top 30 features shared between the tuned classifiers.
Figure 9.
The most promising 30 features shared between the tuned classifiers based on the 5-folds cross-validation.
By observing Fig. 9, the feature importances for the 5 folds reveal a diverse set of influential features across different imaging modalities and measurements. Notably, 3D GLCM Max Gray Level D=7 and SH-53 from DTI, as well as 2D GLCM ASM D=3 and PearsonKurtosis from FLAIR, demonstrate high relative importance. The inclusion of features like SH-0, GLRLM LongRunHighGrayLevelEmphasis, and SH-10 from FLAIR, and SH-60, SH-22, and SH-78 from DTI, underscores the significance of texture and statistical metrics in capturing meaningful information. The list also encompasses percentile-based features, such as Percentiles-1 and Percentiles-9 from FLAIR, and CumulativeFrequency-3, CumulativeDistributionFunction-9, and RelativeFrequency-1 from DTI.
Table 5 showcases the performance metrics resulting from the application of PSO feature selection within the framework of 10-fold cross-validation. Each approach is associated with various classifiers or combinations thereof, and the metrics include accuracy, BAC, precision, recall, specificity, F1 score, and IoU.
Table 5.
The reported performance metrics that reflect the outcomes of the PSO feature selection applied within the context of 10-fold cross-validation.
| Approach | Accuracy | BAC | Precision | Recall | Specificity | F1 | IoU |
|---|---|---|---|---|---|---|---|
| AdaBoost | 81.21% ± 0.0004 | 76.83% ± 0.0005 | 66.52% ± 0.0005 | 70.32% ± 0.0007 | 83.34% ± 0.0002 | 67.72% ± 0.0005 | 57.09% ± 0.0005 |
| DT | 77.88% ± 0.0053 | 74.49% ± 0.0058 | 67.28% ± 0.0081 | 67.51% ± 0.0078 | 81.48% ± 0.0039 | 66.98% ± 0.0076 | 51.68% ± 0.0083 |
| ET | 73.67% ± 0.0047 | 69.43% ± 0.005 | 63.8% ± 0.0082 | 62.42% ± 0.0065 | 76.44% ± 0.0036 | 60.85% ± 0.006 | 44.68% ± 0.0065 |
| GB | 70.36% ± 0.0044 | 66.21% ± 0.0052 | 58.09% ± 0.007 | 57.49% ± 0.0067 | 74.92% ± 0.0039 | 56.94% ± 0.007 | 40.64% ± 0.0062 |
| HGB | 83.61% ± 0.0 | 78.63% ± 0.0 | 83.38% ± 0.0 | 74.65% ± 0.0 | 82.6% ± 0.0 | 66.69% ± 0.0 | 58.35% ± 0.0 |
| KNN | 76.27% ± 0.0 | 73.13% ± 0.0 | 68.07% ± 0.0 | 66.2% ± 0.0 | 80.07% ± 0.0 | 66.24% ± 0.0 | 49.73% ± 0.0 |
| LGBM | 90.16% ± 0.0 | 86.9% ± 0.0 | 88.77% ± 0.0 | 84.51% ± 0.0 | 89.3% ± 0.0 | 82.21% ± 0.0 | 73.27% ± 0.0 |
| MLP | 81.27% ± 0.0022 | 77.17% ± 0.0026 | 78.62% ± 0.002 | 72.69% ± 0.0031 | 81.66% ± 0.0021 | 69.68% ± 0.004 | 55.53% ± 0.0043 |
| RF | 71.0% ± 0.0043 | 66.83% ± 0.0046 | 60.59% ± 0.0072 | 59.17% ± 0.0059 | 74.5% ± 0.0034 | 58.19% ± 0.0057 | 41.62% ± 0.0058 |
| SVM | 78.34% ± 0.0 | 74.35% ± 0.0 | 74.11% ± 0.0 | 69.01% ± 0.0 | 79.69% ± 0.0 | 66.61% ± 0.0 | 51.16% ± 0.0 |
| XGB | 85.16% ± 0.0 | 81.66% ± 0.0 | 78.35% ± 0.0 | 77.46% ± 0.0 | 85.85% ± 0.0 | 75.68% ± 0.0 | 63.27% ± 0.0 |
| LGBM-AdaBoost | 90.97% ± 0.0004 | 88.93% ± 0.0005 | 85.95% ± 0.0008 | 85.82% ± 0.0007 | 92.03% ± 0.0002 | 85.56% ± 0.0007 | 76.56% ± 0.0009 |
| LGBM-DT | 89.8% ± 0.0025 | 88.31% ± 0.0029 | 84.85% ± 0.0037 | 83.93% ± 0.004 | 92.7% ± 0.0019 | 84.24% ± 0.0039 | 74.66% ± 0.0049 |
| LGBM-KNN | 93.65% ± 0.0 | 91.67% ± 0.0 | 92.06% ± 0.0 | 90.14% ± 0.0 | 93.19% ± 0.0 | 89.6% ± 0.0 | 82.2% ± 0.0 |
| XGB-DT | 83.08% ± 0.0027 | 80.26% ± 0.003 | 74.63% ± 0.0041 | 74.11% ± 0.0044 | 86.41% ± 0.0018 | 74.2% ± 0.0041 | 60.9% ± 0.0045 |
| Best Stacked | 94.43% ± 0.0017 | 93.0% ± 0.0021 | 92.03% ± 0.0031 | 91.39% ± 0.0028 | 94.61% ± 0.0015 | 91.23% ± 0.0029 | 84.56% ± 0.0044 |
Each row corresponds to a specific approach, with individual classifiers or combinations thereof applied in both the first and second stages of the experiment. For instance, a single keyword like “AdaBoost” indicates the use of the AdaBoost classifier in both stages, while combined keywords like “LGBM-AdaBoost” signify a two-stage application with LGBM in the first stage and AdaBoost in the second. The term “Stacked” represents a majority voting ensemble involving classifiers such as “LGBM-AdaBoost,” “LGBM-DT,” “LGBM-KNN,” and “XGB-DT”, collectively yielding the best metrics across various evaluation criteria. To enhance the robustness of the findings, the records provide mean and 95% confidence interval values, derived from 100 experiment trials, offering a more comprehensive understanding of the approach's stability and consistency.
Analyzing the reported metrics reveals that the “Stacked” ensemble approach consistently outperforms individual classifiers in terms of accuracy, BAC, precision, recall, specificity, F1 score, and IoU. This underscores the effectiveness of combining diverse classifiers to achieve superior predictive performance. The approach demonstrates impressive results, with an accuracy of 94.43% ± 0.0017, BAC of 93.0% ± 0.0021, precision of 92.03% ± 0.0031, recall of 91.39% ± 0.0028, specificity of 94.61% ± 0.0015, F1 score of 91.23% ± 0.0029, and IoU of 84.56% ± 0.0044.
Concerning the “Stacked” ensemble approach, the hyperparameters for the first stage of the ensemble classifiers are as follows: For LGBM, the parameters include a Min-Max scaler, a learning rate of 0.4047, a maximum depth of 5, and 84 estimators. HGB is configured with a Min-Max scaler, a learning rate of 0.4078, and a maximum depth of 44. The hyperparameters for the second stage classifiers include: AdaBoost with a Standard scaler, a learning rate of 0.9285, and 29 estimators, and KNN using a Max scaler, brute algorithm, Euclidean metric, 5 neighbors, and Uniform weights. Additionally, DT utilizes a Max scaler, Gini as the criterion, a maximum depth of 58, and “Best” as the splitter.
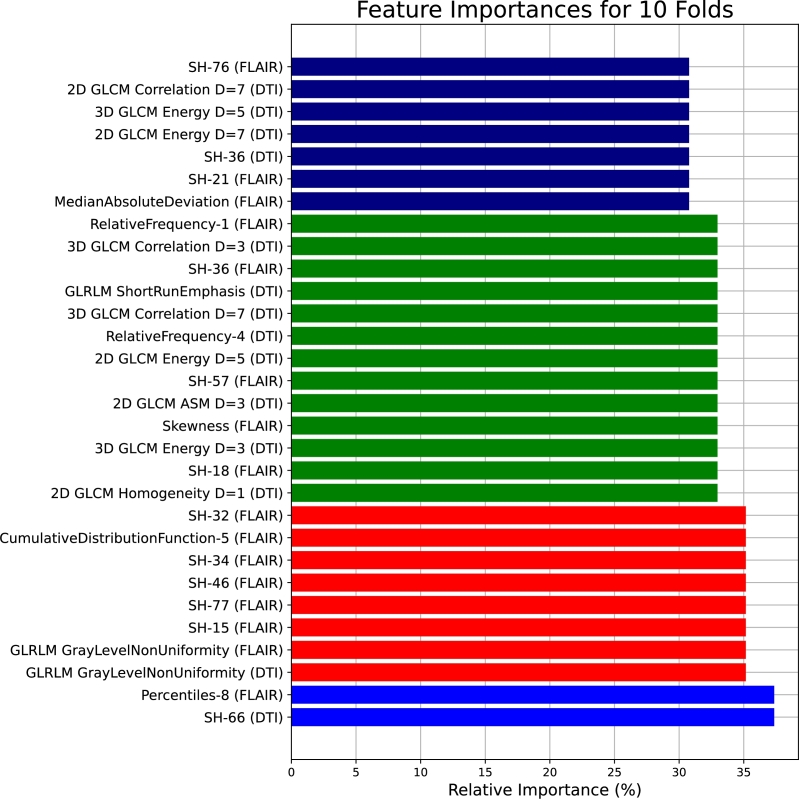
Moreover, the selected feature configurations for the ensemble classifiers in the first and second stages are detailed as follows: In the first stage, LGBM operates with 206 features, HGB with 206 features. Transitioning to the second stage, AdaBoost employs 193 features, KNN utilizes 197 features, and DT operates with 210 features. Fig. 10 presents the top 30 features shared between the tuned classifiers.
Figure 10.
The most promising 30 features shared between the tuned classifiers based on the 10-folds cross-validation.
By observing Fig. 10, the feature importances for 10 folds showcase a distinct set of influential features, revealing the complexity and variability within the dataset. Notably, SH-66 from DTI and Percentiles-8 from FLAIR exhibit significant relative importance, indicating their relevance across different folds. The inclusion of texture metrics, such as GLRLM GrayLevelNonUniformity in both DTI and FLAIR, SH-15, SH-77, SH-46, and SH-34 from FLAIR, and CumulativeDistributionFunction-5 from FLAIR, suggests the importance of capturing textural nuances in the analysis. Features like SH-32 from FLAIR, 2D GLCM Homogeneity D=1 from DTI, and 3D GLCM Energy D=3 from DTI contribute to the diverse array of impactful metrics. The list also includes statistical measures like Skewness from FLAIR and MedianAbsoluteDeviation from FLAIR, indicating the importance of assessing data distribution characteristics.
Table 6 showcases the performance metrics resulting from the application of PSO feature selection within the framework of LOSO-fold cross-validation. Each approach is associated with various classifiers or combinations thereof, and the metrics include accuracy, BAC, precision, recall, specificity, F1 score, and IoU.
Table 6.
The reported performance metrics that reflect the outcomes of the PSO feature selection applied within the context of LOSO cross-validation.
| Approach | Accuracy | BAC | Precision | Recall | Specificity | F1 | IoU |
|---|---|---|---|---|---|---|---|
| AdaBoost | 90.75% ± 0.0011 | 89.97% ± 0.0013 | 87.38% ± 0.0018 | 87.37% ± 0.0017 | 92.57% ± 0.0009 | 87.35% ± 0.0018 | 77.64% ± 0.0028 |
| DT | 81.31% ± 0.004 | 78.58% ± 0.0046 | 72.88% ± 0.0065 | 72.89% ± 0.006 | 84.26% ± 0.0033 | 72.59% ± 0.0063 | 57.64% ± 0.0073 |
| ET | 72.06% ± 0.0038 | 67.58% ± 0.0039 | 59.87% ± 0.0074 | 59.94% ± 0.0053 | 75.21% ± 0.0027 | 57.76% ± 0.0047 | 41.9% ± 0.0048 |
| GB | 83.75% ± 0.0033 | 80.99% ± 0.0036 | 74.83% ± 0.0046 | 75.3% ± 0.0047 | 86.68% ± 0.0025 | 74.93% ± 0.0046 | 61.57% ± 0.0058 |
| HGB | 84.65% ± 0.0 | 81.41% ± 0.0 | 79.7% ± 0.0 | 77.46% ± 0.0 | 85.36% ± 0.0 | 76.23% ± 0.0 | 62.98% ± 0.0 |
| KNN | 81.91% ± 0.0 | 77.76% ± 0.0 | 78.23% ± 0.0 | 73.24% ± 0.0 | 82.28% ± 0.0 | 69.43% ± 0.0 | 55.85% ± 0.0 |
| LGBM | 78.14% ± 0.0 | 72.94% ± 0.0 | 75.7% ± 0.0 | 67.61% ± 0.0 | 78.28% ± 0.0 | 59.92% ± 0.0 | 48.44% ± 0.0 |
| MLP | 80.92% ± 0.0015 | 76.96% ± 0.0018 | 77.0% ± 0.0014 | 72.23% ± 0.0022 | 81.69% ± 0.0015 | 69.31% ± 0.003 | 54.86% ± 0.003 |
| RF | 70.0% ± 0.004 | 65.27% ± 0.0042 | 58.41% ± 0.0082 | 57.38% ± 0.0056 | 73.17% ± 0.0029 | 55.36% ± 0.005 | 39.35% ± 0.005 |
| SVM | 78.3% ± 0.0 | 74.3% ± 0.0 | 74.21% ± 0.0 | 69.01% ± 0.0 | 79.58% ± 0.0 | 66.65% ± 0.0 | 51.24% ± 0.0 |
| XGB | 77.19% ± 0.0 | 73.62% ± 0.0 | 68.15% ± 0.0 | 66.2% ± 0.0 | 81.04% ± 0.0 | 66.49% ± 0.0 | 51.48% ± 0.0 |
| ET-AdaBoost | 73.1% ± 0.0043 | 69.45% ± 0.0047 | 61.55% ± 0.0072 | 61.62% ± 0.0061 | 77.28% ± 0.0034 | 60.94% ± 0.0063 | 44.32% ± 0.0064 |
| GB-DT | 84.26% ± 0.0039 | 81.49% ± 0.0042 | 75.7% ± 0.0057 | 76.04% ± 0.0058 | 86.95% ± 0.0029 | 75.56% ± 0.0055 | 62.46% ± 0.0068 |
| XGB-KNN | 83.3% ± 0.0 | 79.87% ± 0.0 | 82.29% ± 0.0 | 76.06% ± 0.0 | 83.68% ± 0.0 | 74.88% ± 0.0 | 60.67% ± 0.0 |
| Best Stacked | 91.6% ± 0.0023 | 90.27% ± 0.0029 | 88.55% ± 0.0038 | 87.96% ± 0.0037 | 92.59% ± 0.0022 | 87.94% ± 0.0039 | 78.69% ± 0.0059 |
Each row corresponds to a specific approach, with individual classifiers or combinations thereof applied in both the first and second stages of the experiment. For instance, a single keyword like “AdaBoost” indicates the use of the AdaBoost classifier in both stages, while combined keywords like “XGB-KNN” signify a two-stage application with XGB in the first stage and KNN in the second. The term “Stacked” represents a majority voting ensemble involving classifiers such as “ET-AdaBoost,” “AdaBoost-AdaBoost,” “GB-DT,” and “XGB-KNN”, collectively yielding the best metrics across various evaluation criteria. To enhance the robustness of the findings, the records provide mean and 95% confidence interval values, derived from 100 experiment trials, offering a more comprehensive understanding of the approach's stability and consistency.
Analyzing the reported metrics reveals that the “Stacked” ensemble approach consistently outperforms individual classifiers in terms of accuracy, BAC, precision, recall, specificity, F1 score, and IoU. This underscores the effectiveness of combining diverse classifiers to achieve superior predictive performance. The approach showcases notable outcomes, achieving an accuracy of 91.6% ± 0.0023, BAC of 90.27% ± 0.0029, precision of 88.55% ± 0.0038, recall of 87.96% ± 0.0037, specificity of 92.59% ± 0.0022, F1 score of 87.94% ± 0.0039, and IoU of 78.69% ± 0.0059.
In the context of the “Best Stacked” ensemble, the hyperparameters for the initial stage of the ensemble classifiers are specified as follows: For GB, the parameters consist of a Min-Max scaler, a learning rate of 6.2040, a maximum depth of 81, and 49 estimators. AdaBoost is configured with a Min-Max scaler, a learning rate of 0.1106, and 92 estimators. XGB employs a Min-Max scaler, a learning rate of 0.0679, a maximum depth of 45, 67 estimators, and a subsample rate of 0.8870. ET uses a Max scaler, Gini as the criterion, a maximum depth of 85, and 89 estimators. Furthermore, the hyperparameters for the second stage classifiers include: KNN with a Max scaler, ball tree algorithm, Manhattan metric, 7 neighbors, and distance-based weights. AdaBoost utilizes a L1 scaler, a learning rate of 0.6917, and 77 estimators. DT operates with a Max scaler, Gini as the criterion, a maximum depth of 129, and “Best” as the splitter.
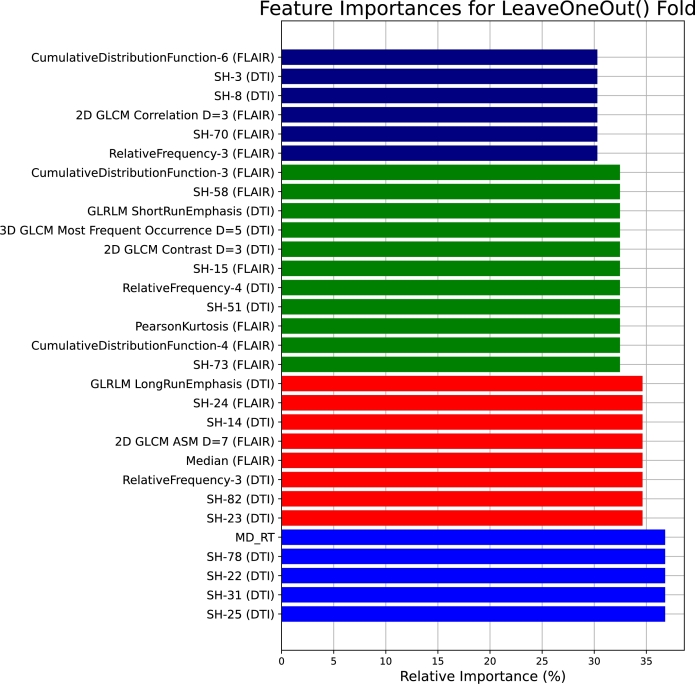
For the scalers used in the ensemble classifiers, in the first stage, GB, AdaBoost, XGB, and ET are applied with L1, L1, L1, and Max scalers, respectively. Moving to the second stage, KNN, AdaBoost, and DT are equipped with L2, L1, and Max scalers, respectively. Additionally, the chosen feature configurations for the ensemble classifiers in the first and second stages are outlined as follows: In the initial stage, GB operates with 192 features, AdaBoost with 189 features, XGB with 205 features, and ET with 191 features. Transitioning to the second stage, KNN employs 203 features, AdaBoost utilizes 189 features, and DT operates with 183 features. Fig. 11 presents the top 30 features shared between the tuned classifiers.
Figure 11.
The most promising 30 features shared between the tuned classifiers based on the LOSO cross-validation.
By examining Fig. 11, the feature importances for LOSO folds reveal a distinctive set of influential features, highlighting the intricate and varied nature of the dataset. Notably, SH-25, SH-31, SH-22, and SH-78 from DTI and MD from the right region demonstrate significant relative importance, underscoring their relevance across different folds. The incorporation of texture metrics, such as GLRLM LongRunEmphasis in DTI, SH-24 from FLAIR, SH-14, SH-82, and SH-23 from DTI, GLCM ASM at distance 7 from FLAIR, RelativeFrequency-3 from DTI, and Median from FLAIR, emphasizes the significance of capturing textural nuances in the analysis.
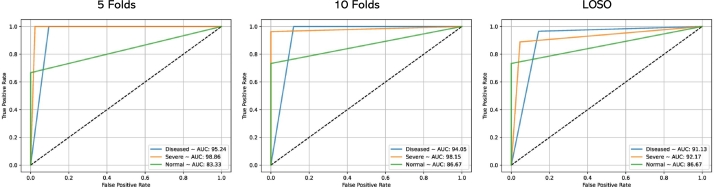
Fig. 12 provides a visual comparison of the performance of three cross-validation techniques: 5-folds, 10-folds, and LOSO. The graphical representation illustrates the varying effectiveness of these cross-validation methods in evaluating our proposed model. Each curve corresponds to a specific cross-validation technique, offering insights into their respective performance trends. Moreover, Fig. 13 displays ROC curves, portraying the model's discriminative ability, across the three cross-validation scenarios: 5-folds (Left), 10-folds (Middle), and LOSO (Right). The accompanying legends specify the corresponding Area Under the Curve (AUC) values for the three distinct classes, providing a comprehensive view of the model's predictive accuracy across different validation strategies. These figures collectively contribute to a nuanced understanding of our model's robustness and generalization capabilities under various cross-validations.
Figure 12.
Graphical comparison between the performance of the three cross-validations: 5-folds, 10-folds, and LOSO.
Figure 13.
ROC curves displaying the model's discriminative ability across three cross-validation scenarios: 5-folds (Left), 10-folds (Middle), and Leave-One-Subject-Out (LOSO) (Right). The legends specify the corresponding Area Under the Curve (AUC) values for the three distinct classes, providing a comprehensive view of the model's predictive accuracy across different validation strategies.
Comparison with Convolutional Neural Networks (CNNs): In comparing the performance metrics of the presented model with CNN, the model achieves an accuracy of 56.67%. The precision was 37.40% while the recall was 37.54%. The specificity was 64.86% and the F1 score was 36.93%. The IoU was 23.21% and the BAC was 51.20%. The “Stacked” ensemble approach consistently outperforms individual classifiers across various metrics, highlighting the efficacy of combining diverse classifiers for enhanced predictive performance. The ensemble approach consistently demonstrates superior performance, these results underscore the importance of selecting the most suitable models, hyperparameters, and features.
5. Overall discussion
The COVID-19 pandemic, caused by the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), has emerged as a global health crisis, claiming over 2 million lives within a year. The WHO identifies it as a formidable threat, with human-to-human transmission occurring exponentially, leading to widespread outbreaks. The severity of infection varies, influenced by factors such as an individual's immune system, age, and comorbidities.
COVID-19 manifests in various organs, including the OB, giving rise to neurological symptoms like anosmia, or loss of smell. Studies indicate significant consequences for the OB, impacting its shape and size. Anosmia has been identified as a risk factor and predictor of COVID-19 severity. However, existing studies face limitations, including a lack of grading systems, low diagnostic accuracy, and neglect of appearance, diffusivity, and shape markers.
In response to these limitations, this manuscript proposes a comprehensive CAD system for diagnosing OB infection severity in COVID-19 patients. The proposed system introduces a novel approach by incorporating FLAIR-MRI and DTI. It addresses previous shortcomings by utilizing multiple imaging modalities, introducing a grading system, and incorporating appearance, diffusivity, and shape markers.
The proposed CAD system makes several significant contributions. Firstly, it introduces a novel approach for OB infection severity diagnosis. Secondly, it overcomes limitations of existing studies through the integration of multiple imaging modalities and the introduction of a grading system. Lastly, the system demonstrates improved performance metrics through the utilization of marker stacking and majority voting.
The CAD system categorizes patients into “Normal,” “Mild Anosmia,” or “Severe Anosmia” through a complex pipeline involving three stages. These stages include the extraction of appearance markers (i.e., first and second-order), morphology/shape markers (i.e., spherical harmonics), and diffusivity markers (i.e., FA and MD). The integration of these markers is optimized through marker fusion techniques, and machine learning ensemble classifiers make diagnoses based on the integrated markers.
The study emphasizes the uniqueness of its approach, utilizing ensembling of bagged machine learning classifiers and making diagnoses based on majority voting. The proposed CAD framework spans dataset acquisition, pre-processing, manual segmentation, feature extraction, imaging markers, classification, and optimization. It addresses challenges in selecting suitable markers and provides insight into the motivation behind morphology/shape markers. Diffusivity markers extracted from DTI play a vital role in understanding OB characteristics.
Furthermore, the manuscript delves into the evolutionary features selection using PSO, classification and optimization using eleven machine learning algorithms, and the challenges associated with selecting suitable markers. Hyperparameter tuning is explored through TPE and GS, each offering a unique approach to optimization. Model evaluation is conducted through K-fold cross-validation, ensuring a robust assessment of the system's performance.
6. Limitations
While the proposed system exhibits promising results in grading the severity of olfactory bulb (OB) dysfunction in COVID-19 patients using MRI-based markers, several limitations should be acknowledged. Firstly, the sample size utilized in this study is relatively small, potentially limiting the generalizability of our findings to the broader population. To address this, future research should aim to test the proposed system on a more extensive and diverse dataset to ensure robustness and reliability.
Secondly, it is crucial to note that the proposed system is currently tailored specifically for the diagnosis of anosmia in COVID-19 patients. The extension of its applicability to diagnose other medical conditions or diseases remains uncertain and warrants further investigation.
Thirdly, despite the improvement demonstrated in diagnosing OB dysfunction, the system still relies on expert radiologists for the delineation of the olfactory nerve. The manual nature of this process introduces inter-observer variability, and future developments could explore automation to enhance precision and reduce variability.
Finally, while our proposed system shows promise, its clinical utility requires thorough testing and validation in a real-world setting. Additionally, the absence of demographic data, such as sex, age, and race, limits our ability to explore potential correlations and incorporate these factors into the model, which could further enhance its machine learning performance. We recognize these limitations and emphasize the need for ongoing research to address these aspects and refine the proposed system for broader clinical applications.
7. Conclusions and future work
The COVID-19 pandemic, caused by the SARS-CoV-2 virus, has prompted a global health crisis with significant mortality rates. The World Health Organization recognizes its exponential H2H transmission, leading to widespread outbreaks with varying infection severity influenced by individual factors. The virus manifests in various organs, including the OB, resulting in neurological symptoms like anosmia. Anosmia has been identified as a predictor of COVID-19 severity, but existing studies face limitations, such as a lack of grading systems and neglect of appearance, diffusivity, and shape markers.
In response, this work proposes a CAD system that categorizes patients into “Normal,” “Mild Anosmia,” or “Severe Anosmia” using a three-stage pipeline involving appearance markers, morphology/shape markers, and diffusivity markers. Marker fusion techniques optimize the integration of these markers, and machine learning ensemble classifiers make diagnoses based on the integrated markers. The study emphasizes the uniqueness of its approach, utilizing bagged machine learning classifiers and making diagnoses based on majority voting. The CAD framework spans dataset acquisition, pre-processing, manual segmentation, feature extraction, imaging markers, classification, and optimization, addressing challenges in selecting suitable markers and providing insight into the motivation behind morphology/shape markers. Diffusivity markers extracted from DTI play a vital role in understanding OB characteristics. The manuscript explores evolutionary feature selection using PSO, classification and optimization using eleven machine learning algorithms, and challenges associated with selecting suitable markers. Hyperparameter tuning is conducted through TPE and GS. Model evaluation is robustly performed through K-fold cross-validation, showcasing the system's consistent performance.
In the 5-fold cross-validation, the “Stacked” approach achieves an accuracy of 94.1%, BAC of 92.18%, precision of 91.6%, recall of 90.61%, specificity of 93.75%, F1 score of 89.82%, and IoU of 82.62%. Similar trends are observed in the 10-fold and LOSO cross-validation, where the “Stacked” ensemble consistently outperforms individual classifiers, achieving an accuracy of 94.43% and 94.1%, respectively. The feature importance analysis reveals influential features across different imaging modalities and measurements. Texture and statistical metrics, such as GLCM Max Gray Level, SH-53, 2D GLCM ASM, and PearsonKurtosis, demonstrate high relative importance. The inclusion of features like SH-0, GLRLM LongRunHighGrayLevelEmphasis, and percentile-based features underscores the significance of capturing textural nuances and distribution characteristics in the analysis.
Future research should focus on developing deep learning models that utilize CNNs and data augmentation techniques to improve the accuracy of the CAD system. In addition, the proposed system can be expanded to include other neurological symptoms associated with COVID-19, allowing for a more comprehensive diagnosis and clinical management of COVID-19 patients.
Declarations
Author agreement statement
We, the undersigned authors, declare that this manuscript is original, has not been published before, and is not currently being considered for publication elsewhere. We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the order of authors listed in the manuscript has been approved by all of us. We understand that the “Corresponding Author” is the sole contact for the editorial process. He is responsible for communicating with the other authors about progress, submissions of revisions, and final approval of proofs.
Intellectual property
We confirm that, we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, concerning intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property.
Authorship
We confirm that the manuscript has been read and approved by all named authors. We confirm that the order of authors listed in the manuscript has been approved by all named authors.
Compliance with ethical standards
The proposed approach underwent rigorous verification and validation utilizing a dataset obtained from Mansoura University in Egypt. Ethical approval for the research plan was granted by the institutional review boards at both the University of Louisville (IRB: R.22.02.1622.R1.R2 - 2022/04/14) and Mansoura University. The study strictly adhered to established rules and regulations, ensuring all methods were conducted in accordance with ethical standards. Informed consent was explicitly obtained from all patients involved in the study.
CRediT authorship contribution statement
Hossam Magdy Balaha: Writing – review & editing, Writing – original draft, Visualization, Validation, Software, Methodology, Investigation, Formal analysis, Conceptualization, Data curation. Mayada Elgendy: Writing – original draft, Visualization, Investigation, Data curation. Ahmed Alksas: Visualization, Validation, Software, Data curation. Mohamed Shehata: Data curation. Norah Saleh Alghamdi: Visualization, Validation, Resources, Funding acquisition, Data curation. Fatma Taher: Visualization, Validation, Funding acquisition, Data curation. Mohammed Ghazal: Visualization, Validation, Resources, Funding acquisition, Data curation. Mahitab Ghoneim: Visualization, Validation, Investigation, Data curation. Eslam Hamed Abdou: Visualization, Validation, Data curation. Fatma Sherif: Data curation. Ahmed Elgarayhi: Validation, Data curation. Mohammed Sallah: Investigation, Data curation. Mohamed Abdelbadie Salem: Visualization, Validation, Data curation. Elsharawy Kamal: Data curation. Harpal Sandhu: Visualization, Validation, Investigation, Data curation. Ayman El-Baz: Supervision, Project administration, Funding acquisition, Formal analysis, Conceptualization.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
Princess Nourah bint Abdulrahman University Researchers Partial Supporting Project Number (PNURSP2024R40), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on a reasonable request.
References
- 1.World Health Organization Coronavirus disease (COVID-19) pandemic. 2024. https://www.who.int/europe/emergencies/situations/covid-19
- 2.Wu Yi-Chi, Chen Ching-Sung, Chan Yu-Jiun. Overview of the 2019 novel coronavirus (2019-nCoV): the pathogen of severe specific contagious pneumonia (SSCP) J. Chin. Med. Assoc. 2020;83(3):217–220. doi: 10.1097/JCMA.0000000000000270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Mohammed Mazin Abed, Al-Khateeb Belal, Yousif Mohammed, Mostafa Salama A., Kadry Seifedine, Abdulkareem Karrar Hameed, Garcia-Zapirain Begonya. Novel crow swarm optimization algorithm and selection approach for optimal deep learning COVID-19 diagnostic model. Comput. Intell. Neurosci. 2022;2022(22) doi: 10.1155/2022/1307944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jain Uday. Effect of covid-19 on the organs. Cureus. 2020;12(8) doi: 10.7759/cureus.9540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Doyle Margaret F. Central nervous system outcomes of covid-19. Translational Research. 2022;241:41–51. doi: 10.1016/j.trsl.2021.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Aragão Maria de Fátima Viana Vasco, Carvalho Leal M., Cartaxo Filho O. Queiroga, Fonseca Tatiana Moreira, Valença Marcelo Moraes. Anosmia in COVID-19 associated with injury to the olfactory bulbs evident on MRI. Am. J. Neuroradiol. 2020;41(9):1703–1706. doi: 10.3174/ajnr.A6675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tsivgoulis G., Fragkou P.C., Lachanis S., Palaiodimou L., Lambadiari V., Papathanasiou M., Sfikakis P.P., Voumvourakis K.I., Tsiodras S. Olfactory bulb and mucosa abnormalities in persistent COVID-19 induced anosmia: a magnetic resonance imaging study. Eur. J. Neurol. 2020 doi: 10.1111/ene.14537. [DOI] [PubMed] [Google Scholar]
- 8.Kim Doo Hwan, Kim Min Gul, Yang Seong J., Lee Eun Jung, Yeom Sang Woo, You Yeon Seok, Kim Jong Seung. Influenza and anosmia: important prediction factors for severity and death of COVID-19. J. Infect. 2021;83(5):e10–e13. doi: 10.1016/j.jinf.2021.08.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yildirim Duzgun, Kandemirli Sedat Giray, Tekcan Sanli Deniz Esin, Akinci Ozlem, Altundag Aytug. A comparative olfactory mri, dti and fmri study of covid-19 related anosmia and post viral olfactory dysfunction. Acad. Radiol. 2022;29(1):31–41. doi: 10.1016/j.acra.2021.10.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Giray Kandemirli Sedat, Altundag Aytug, Yildirim Duzgun, Tekcan Sanli Deniz Esin, Saatci Ozlem. Olfactory bulb MRI and paranasal sinus CT findings in persistent COVID-19 anosmia. Acad. Radiol. 2021;28(1):28–35. doi: 10.1016/j.acra.2020.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chiu Andrew, Fischbein Nancy, Wintermark Max, Zaharchuk Greg, Yun Paul T., Zeineh Michael. COVID-19-induced anosmia associated with olfactory bulb atrophy. Neuroradiology. 2021;63(1):147–148. doi: 10.1007/s00234-020-02554-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nagamine Takahiko. Beware of traumatic anosmia in COVID-19 pandemic. Canadian Journal of Emergency Medicine. 2021;23(4):567–568. doi: 10.1007/s43678-021-00135-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lechien Jerome R., Chiesa-Estomba Carlos M., De Siati Daniele R., Horoi Mihaela, Le Bon Serge D., Rodriguez Alexandra, Dequanter Didier, Blecic Serge, El Afia Fahd, Distinguin Lea, et al. Olfactory and gustatory dysfunctions as a clinical presentation of mild-to-moderate forms of the coronavirus disease (COVID-19): a multicenter European study. Eur. Arch. Oto-Rhino-Laryngol. 2020;277(8):2251–2261. doi: 10.1007/s00405-020-05965-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Elgendy Mayada, Balaha Hossam Magdy, Shehata Mohamed, Alksas Ahmed, Ghoneim Mahitab, Sherif Fatma, Mahmoud Ali, Elgarayhi Ahmed, Taher Fatma, Sallah Mohammed, et al. Role of imaging and AI in the evaluation of COVID-19 infection: a comprehensive survey. Front. Biosci. (Landmark edition) 2022;27(9):276. doi: 10.31083/j.fbl2709276. [DOI] [PubMed] [Google Scholar]
- 15.Alsunaidi Shikah J., Almuhaideb Abdullah M., Ibrahim Nehad M., Shaikh Fatema S., Alqudaihi Kawther S., Alhaidari Fahd A., Khan Irfan Ullah, Aslam Nida, Alshahrani Mohammed S. Applications of big data analytics to control covid-19 pandemic. Sensors. 2021;21(7):2282. doi: 10.3390/s21072282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lu Yiping, Li Xuanxuan, Geng Daoying, Mei Nan, Wu Pu-Yeh, Huang Chu-Chung, Jia Tianye, Zhao Yajing, Wang Dongdong, Xiao Anling, et al. Cerebral micro-structural changes in COVID-19 patients–an MRI-based 3-month follow-up study. EClinicalMedicine. 2020;25 doi: 10.1016/j.eclinm.2020.100484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Callejon-Leblic Maria A., Moreno-Luna Ramon, Del Cuvillo Alfonso, Reyes-Tejero Isabel M., Garcia-Villaran Miguel A., Santos-Pena Marta, Maza-Solano Juan M., Martín-Jimenez Daniel I., Palacios-Garcia Jose M., Fernandez-Velez Carlos, et al. Loss of smell and taste can accurately predict COVID-19 infection: a machine-learning approach. J. Clin. Med. 2021;10(4):570. doi: 10.3390/jcm10040570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roland Lauren T., Gurrola Jose G., Loftus Patricia A., Cheung Steven W., Chang Jolie L. Smell and taste symptom-based predictive model for COVID-19 diagnosis. 2020;10(7):832–838. doi: 10.1002/alr.22602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wati Masna, Puspitasari Novianti, Budiman Edy, Rahim Robbi, et al. First-order feature extraction methods for image texture and melanoma skin cancer detection. 2019;1230(1) doi: 10.1088/1742-6596/1230/1/012013. [DOI] [Google Scholar]
- 20.Iqbal Naveed, Mumtaz Rafia, Shafi Uferah, Hassan Zaidi Syed Mohammad. Gray level co-occurrence matrix (glcm) texture based crop classification using low altitude remote sensing platforms. PeerJ Comput. Sci. 2021;7:e536. doi: 10.7717/peerj-cs.536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Preetha K., Jayanthi S.K. GLCM and GLRLM based feature extraction technique in mammogram images. Int. J. Eng. Technol. 2018;7(2.21):266–270. doi: 10.14419/ijet.v7i2.21.12378. [DOI] [Google Scholar]
- 22.Nitzken Matthew Joseph, et al. 2015. Shape analysis of the human brain. Ph.D. Thesis. [DOI] [Google Scholar]
- 23.Le Bihan Denis, Mangin Jean-François, Poupon Cyril, Clark Chris A., Pappata Sabina, Molko Nicolas, Chabriat Hughes. Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging. 2001;13(4):534–546. doi: 10.1002/jmri.1076. [DOI] [PubMed] [Google Scholar]
- 24.Prčkovska Vesna, Descoteaux Maxime, Poupon Cyril, Romeny Bart M., Vilanova Anna. 2012. Classification Study of DTI and HARDI Anisotropy Measures for HARDI Data Simplification; pp. 229–251. [DOI] [Google Scholar]
- 25.Garcia-Gonzalo Esperanza, Fernandez-Martinez Juan Luis. A brief historical review of particle swarm optimization (PSO) Journal of Bioinformatics and Intelligent Control. 2012;1(1):3–16. doi: 10.1166/jbic.2012.1002. [DOI] [Google Scholar]
- 26.Liu Yuanning, Wang Gang, Chen Huiling, Dong Hao, Zhu Xiaodong, Wang Sujing. An improved particle swarm optimization for feature selection. J. Bionics Eng. 2011;8(2):191–200. [Google Scholar]
- 27.Baghdadi Nadiah A., Malki Amer, Abdelaliem Sally F., Magdy Balaha Hossam, Badawy Mahmoud, Elhosseini Mostafa. An automated diagnosis and classification of COVID-19 from chest CT images using a transfer learning-based convolutional neural network. Comput. Biol. Med. 2022;144 doi: 10.1016/j.compbiomed.2022.105383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bergstra James, Bardenet Rémi, Bengio Yoshua, Kégl Balázs. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011;24 [Google Scholar]
- 29.Alibrahim Hussain, Ludwig Simone A. 2021. Hyperparameter Optimization: Comparing Genetic Algorithm Against Grid Search and Bayesian Optimization; pp. 1551–1559. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on a reasonable request.