Correlation between Dzyaloshinskii-Moriya interaction and orbital angular momentum at an oxide-ferromagnet interface

Abstract

We report on the Dzyaloshinskii-Moriya (DMI) interaction at the interface between a ferromagnet and an oxide. We demonstrate experimentally that oxides can give rise to DMI. By comparison of systems comprised of Pt/Co₉₀Fe₁₀/oxide and Cu/Co₉₀Fe₁₀/oxide, we also show how oxidation of one interface can enhance and add to the total DMI of that generated by the Pt interface. This is due to the fact that the DMI on both interfaces promotes left-handed chirality. Finally, by use of ferromagnetic resonance spectroscopy, we show that the DMI and the spectroscopic splitting factor, which is a measure of the orbital momentum, are correlated. This indicates the importance of hybridization and charge transfer at the oxide interface for the DMI.

I. INTRODUCTION

The interface between heavy metals such as Pt and a ferromagnet can give rise to a variety of phenomena, where the strong spin-orbit coupling in the heavy metal plays an important role. These phenomena include perpendicular anisotropy, Dzyaloshinskii-Moriya interaction (DMI), and spin-orbit torques [1–6]. The DMI gives rise to a rich variety of chiral magnetic structures in thin magnetic films. For sufficiently large DMI, chiral spin chains, chiral domain walls, and skyrmions can be stabilized. Such spin textures are now being explored for electronic applications [7,8].

Fundamentally, the DMI is an antisymmetric exchange interaction that requires a broken inversion symmetry in combination with spin-orbit interaction [1–3,9,10]. The interface formed between a ferromagnet and a heavy metal provides both the necessary symmetry breaking of the system and the large spin-orbit coupling. The DMI energy E for two neighboring spins ${\overrightarrow{S}}_i$ and ${\overrightarrow{S}}_j$ at the interface is given by $E=-{\overrightarrow{D}}_{ij}\cdot \left({\overrightarrow{S}}_i\times {\overrightarrow{S}}_j\right)$, where ${\overrightarrow{D}}_{ij}$ is the DMI vector. The relation between the DMI vector and the symmetry of the interface is given by the Moriya rules [9,11]. For highly symmetric interfaces such as (111)-oriented interfaces, the DMI vector ${\overrightarrow{D}}_{ij}$ is perpendicular to the plane of the triangle formed by ${\overrightarrow{S}}_i$ and ${\overrightarrow{S}}_j$ and a third atom in the heavy metal.

So far, not much is known about the underlying physics of DMI. Recently, a direct proportionality between the antisymmetric and the symmetric Heisenberg exchange was shown in the Ni₈₀Fe₂₀/Pt system [12]. Such proportionality was theoretically predicted for bulk metallic spin-glasses and bulk magnetic oxides [9,10]. Kim et al. [13] have found that the DMI and the Heisenberg exchange have a similar temperature dependence in the Pt/Co/MgO system. Moreover, they used x-ray circular dichroism to determine the temperature dependence of the orbital momentum and established a correlation with the DMI. Ryu et al. propose that the DMI and the proximity magnetization at the interface are closely related [14]. Finally, the correlation of the DMI and spin-mixing conductance was studied by Ma et al. [15,16]. Relativistic first principles calculations by Belabbes et al. have shown that the sign and magnitude of the DMI in 3d-5d systems are correlated to the band filling determined by Hund’s first rule [17]. Most experimental work on interfacial DMI has been confined to metallic materials, where the heavy metal is, for example, Pt or Ir [12]. It has also been found that the interface generated between graphene and a ferromagnet can exhibit a measurable DMI [18]. However, it is well known that bulk oxides can also have chiral spin structures that originate from DMI. An example is Hematite, α-Fe₂O₃, where the canted spin-structure gives rise to weak ferromagnetism [19,20]. Moriya found that the DMI is proportional to the symmetric superexchange J in magnetic oxides [9]: $\left|{\overrightarrow{D}}_{ij}\right|\sim \Delta g/g$ · J, where g the spectroscopic splitting factor and Δg its deviation from the free electron value g_e = 2. The deviation Δg = 2 · l/s itself is proportional to the orbital momentum l of the electron with spin s, implying a relationship between the DMI and the orbital momentum [1,9].

Recent density functional theory calculations (DFT) by Belabbes et al. for oxide/ferromagnet interfaces show a correlation of the DMI with an electric dipole moment at the interface [21]. This electrical dipole moment is the result of hybridization of the 3d orbitals of the ferromagnet and the p orbitals of the oxygen together with the associated charge transfer. The hybridization will also change the orbital angular momentum, which will alter the spectroscopic splitting factor. Thus, the interface between an oxide and a ferromagnet can give rise to DMI, while simultaneously modifying the orbital momentum at the interface. In this work, we show experimentally that the interface formed between an oxide and a metallic ferromagnet can give rise to DMI, and we gain deeper insight into the underlying physics that generates DMI through the comparison of the spectroscopic splitting factor g (related to the orbital momentum) to the magnitude of the DMI as the interface becomes increasingly oxidized. Here, we find a change of g, and thus a change in the orbital momentum, as the oxide forms. This change most likely originates from hybridization together with charge transfer at the interface. This implies a correlation of an electrical dipole moment at the interface with the DMI as predicted in previous DFT calculations [21].

II. EXPERIMENT

We prepared two series of samples to experimentally determine the influence of oxide coverage of a ferromagnet on the DMI. One series had a Pt underlayer and a second, the control series, had a Cu underlayer. The Cu underlayer was chosen since it has small spin-orbit coupling compared to Pt. As a result, the presence of any DMI measured in the control samples would demonstrate that it originates at the oxide interface. The sample structure consists of substrate/Ta (3 nm)/Pt(6 nm)/Co₉₀Fe₁₀(2 nm)/Cu (3 nm)/Ta(2 nm) and substrate/Ta (3 nm)/Cu (6 nm)/Co₉₀Fe₁₀(2 nm)/ Cu (3 nm)/Ta(2 nm) and were sputter deposited on thermally oxidized Si substrates. The oxide layer on the substrate is about 150-nm thick. Ta serves as an adhesion layer and induces a (111) texture. Following deposition of the CoFe layer, we exposed the CoFe surface to a gas mixture of 99% Ar and 1% oxygen for a time t ranging from 0 to 1000 s. This allowed us to systematically vary the amount of oxide formation. Following the oxidation process, the chamber was pumped for 5 min to a pressure better than 13 × 10⁻⁹ Pa (1 × 10⁻⁸ Torr) before continuing with the deposition of a Cu (3 nm)/Ta(2 nm) capping layer to prevent any additional oxidation.

We used x-ray diffraction to characterize structural changes of the samples during the oxidation process. The unoxidized Pt/Co₉₀Fe₁₀ sample has a smaller in-plane lattice constant of 0.3586 ± 0.0004 nm relative to Cu/Co₉₀Fe₁₀, which has a lattice constant of 0.3597 ± 0.0002 nm. The lattice constants for both sample series is continuously strained with increasing oxidation and after 1000 s of oxidation both sample series have within error bars the same in-plane lattice constant (0.3604 ± 0.0006 nm for Pt/Co₉₀Fe₁₀ and 0.3606 ± 0.0001 nm for Cu/Co₉₀Fe₁₀). Thus, the oxide interface strains the Cu/Co₉₀Fe₁₀ lattice less than the Pt/Co₉₀Fe₁₀ lattice, see Ref. [22] for the x-ray data.

Measurements with a magnetometer based on a super-conducting quantum interference device (SQUID), where the magnetic field is applied parallel to the sample surface, show that the magnetic moment per area decreases with oxidation time. This trend is consistent with the thickness of the Co₉₀Fe₁₀ layer being reduced as a result of the formation of Co oxide and Fe oxide at the interface. The thickness reduction for the samples with the longest oxidation time of 1000 s is 13% and 12% for the Pt/Co₉₀Fe₁₀ and for the Cu/Co₉₀Fe₁₀ sample, respectively, or about 1.3 monolayer. This is consistent with the assumption that only one to two monolayers become oxidized. We do not expect the saturation magnetization M_s itself would change significantly due to the strain induced during the oxidation process. This assumption is supported by the fact that μ₀M_s, where μ₀ is the permeability of vacuum, for the unoxidized samples is (1.898 ± 0.001) T for the Pt/Co₉₀Fe₁₀ series and (1.851 ± 0.009) T for the Cu/Co₉₀Fe₁₀ series are within 2% of each other despite difference in their respective lattice constants. The induced magnetic moment in the Pt layer is small and might explain the small difference for both samples [21]. As a result, for a given sample series, we use the value of M_s for the unoxidized sample for all calculations.

Broadband ferromagnetic resonance (FMR) was used in both the in-plane and in the out-of-plane geometries, where the magnetic field was swept through the resonance for a given frequency. The perpendicular anisotropy field H_k and the spectroscopic splitting factors g^∥ and g^⊥ for the in-plane and out-of-plane geometry were determined from fits to the Kittel equations for the in-plane and out-of-plane geometries, respectively:

$$f=\frac{{\mu }_0{\mu }_B{g}^{\parallel }}{h}\sqrt{H\cdot \left(H+M_{\text{eff}}\right),}$$ (1)

$$f=\frac{{\mu }_0{\mu }_B{g}^{\perp }}{h}(H-M_{\text{eff}}),$$ (2)

where M_eff = M_s − H_k is the effective magnetization, H is the applied magnetic field, μ_B is the Bohr magneton, and h is the Planck constant. We obtain M_eff directly from fits to the Kittel equations, and further refine the values for g^∥ and g^⊥ using an asymptotic analysis [23], see the Supplemental Material [22] (also Refs. [23,24], therein). In Figs. 2(a) and 2(b), g^⊥ is shown for both samples series. g^∥ was not used in the correlation analysis since it has significantly larger error bars, which prohibits the determination of clear trend with the oxidation time. (See Ref. [22] for the data of g^∥). This is especially true for the Pt/Co₉₀Fe₁₀ series, where the spin-pumping significantly increases the linewidth and damping. The FMR data together with the SQUID magnetometry shows that the perpendicular anisotropy field μ₀H_k is reduced during the oxidation process from (1.110 ± 0.003) T to (0.73 ± 0.01) T for the Pt/Co₉₀Fe₁₀ and from (0.627 ± 0.009) T to (0.17 ± 0.01) T for the Cu/Co₉₀Fe₁₀ series. After an oxidation time of 1000 s, the anisotropy of the oxide interface favors an in-plane orientation of the magnetization. Oxides are known to induce anisotropy. Easy-plane anisotropy has been found in the past for the CoFe/CoFeO_x system [25], which is in agreement with findings in this study. These results are in contrast to interfaces of ferromagnets with MgO and Al₂O₃, which induce perpendicular anisotropy [5,26].

FIG. 2.

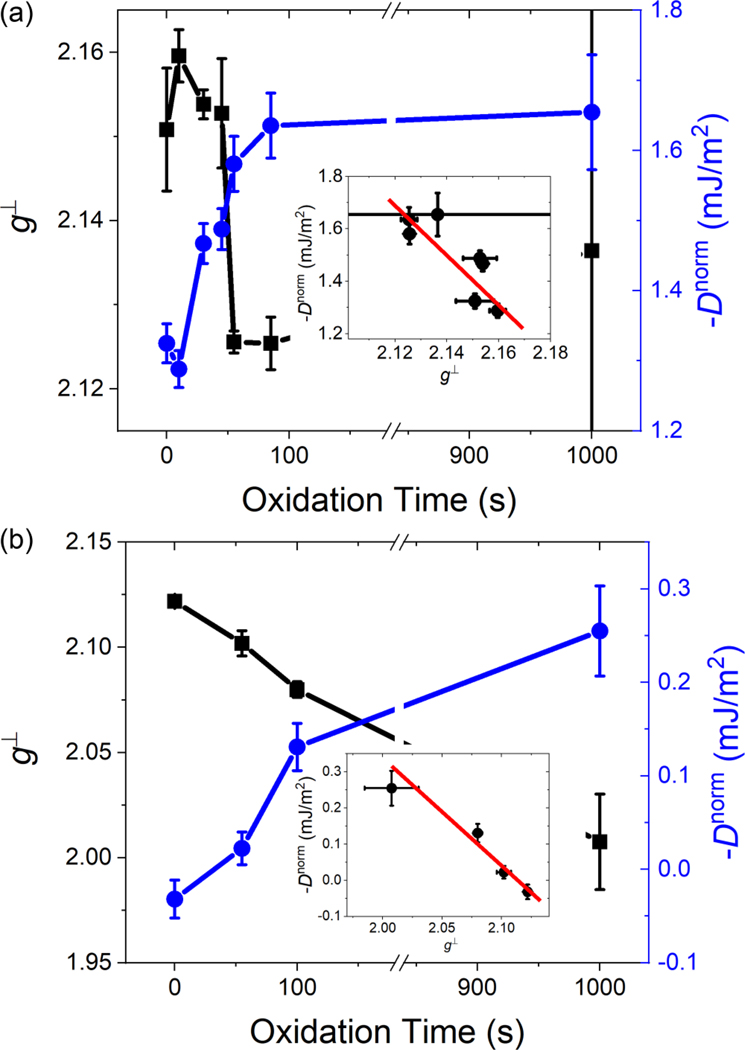
Spectroscopic splitting factor g^⊥ and normalized DMI D^norm as a function of the oxidation time. We normalized the DMI D^norm to a CoFe layer thickness of 1 nm to take the thickness reduction during the oxidation into account. (The not normalized values are shown in Fig. S4.) The change of the magnitude of the DMI is shown in (a) for the Pt/Co₉₀Fe₁₀ and in (b) for the Cu/Co₉₀Fe₁₀ sample series with increasing oxidation time (blue circles). The spectroscopic splitting factor g^⊥ is represented by the black squares in the two respective graphs. g^⊥ shows the opposite trend than D^norm with oxidation time. The insets in (a) and (b) show D^norm vs g^⊥ for the two sample series. The insets demonstrate the correlation between these two quantities. The red line is a guide to the eye.

The DMI can be determined from the asymmetric spin-wave dispersion [27,28]. We used Brillouin-Light scattering spectroscopy (BLS) with a 532-nm-wavelength laser to measure the spin-wave frequencies. The photons are inelastically scattered by magnons, while energy and momentum are conserved. The angle of incidence in our experiment is 45 degrees, which fixes the wave vector k of the magnons at 16.7μm⁻¹. The frequency f for spin waves propagating perpendicular to the applied magnetic field, the so-called Damon-Eshbach modes, in the presence of DMI is given by[29]

$$f=\frac{{\mu }_0{\mu }_B{g}^{\parallel }}{h}\sqrt{\left(H+\frac{2A}{{\mu }_0{M}_s}{k}^2-H_k+M_s\frac{1-e^{-t\left|k\right|}}{t\left|k\right|}\right)\cdot \left(H+\frac{2A}{{\mu }_0{M}_s}{k}^2+M_s\left(1-\frac{1-e^{-t\left|k\right|}}{t\left|k\right|}\right)\right)}+sgn\left(M\right)\frac{{\mu }_B{g}^{\parallel }}{h}\cdot \frac{2D_{\text{DMI}}}{M_s}k,$$ (3)

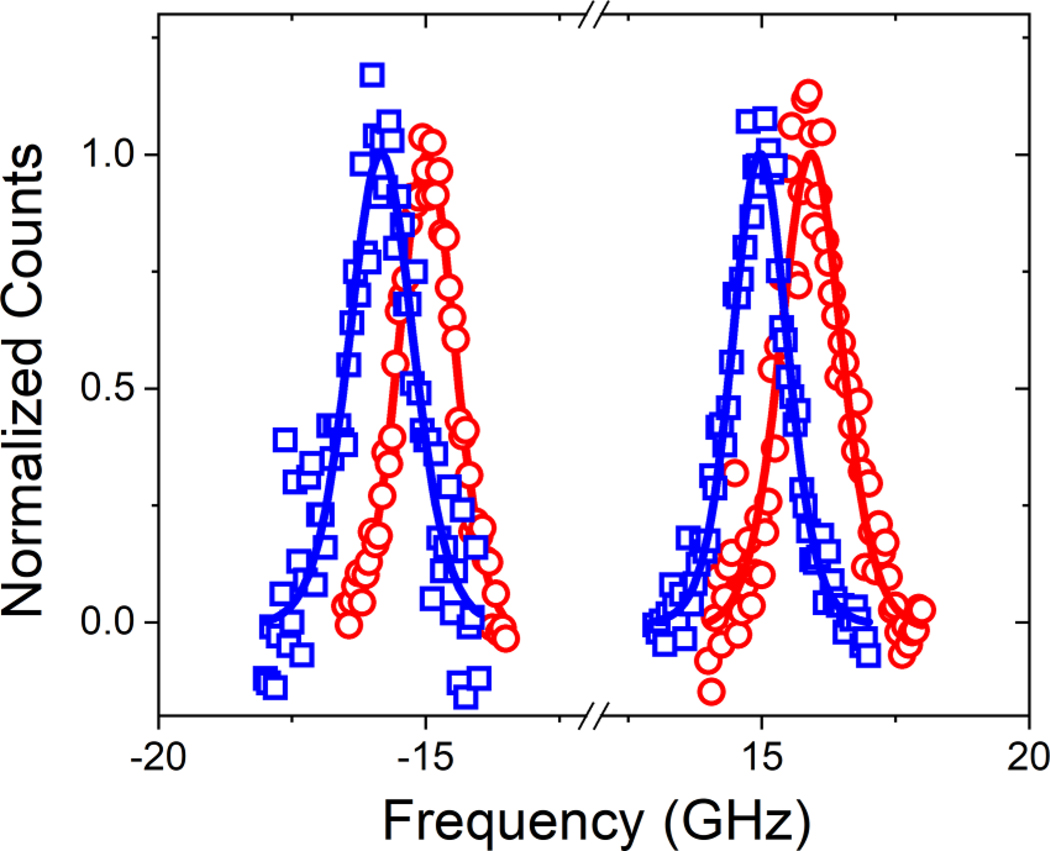
where t is the thickness of the ferromagnetic layer, A is the exchange constant, and D_DMI is the volumetric DMI constant. D_DMI gives the effective strength of the DMI, as if it would be a volume effect and not interfacial. The last term in this equation is dependent on both the spin-wave propagation direction (sign of the wavevector k) and field polarity. We measure the spin-wave frequency for the Stokes and the anti-Stokes peak for positive and negative field polarity with the BLS and obtain the frequency shift Δf_DMI = (f (+H) − f (−H))/2 due to the presence of the DMI for both peaks separately. This frequency shift is equal to the last term in Eq. (3) and is shown in Fig. 1, where we plot the BLS spectra for the unoxidized sample of the Pt/Co₉₀Fe₁₀ series for both field polarities. The spin-wave frequencies for positive and negative fields are clearly distinguishable and shifted from one another due to the DMI at the Pt/Co₉₀Fe₁₀ interface. The reported DMI values are the average of the DMI for the Stokes and the anti-Stokes. The error bars are based on one standard deviation.

FIG. 1.

BLS spectra for the two field polarities for the unoxidized Pt/Co₉₀Fe₁₀ sample for positive field (blue squares) and negative field (red circles). The amplitude of the spectra is normalized to one.

It is also important to consider that Damon-Eshbach spin waves have a nonuniform profile through the thickness of the ferromagnet with the largest amplitude at the top or the bottom interface depending on their propagation direction [30,31]. Consequently, in the presence of interfacial anisotropy, Damon-Eshbach spin waves propagating in opposite directions can have different frequencies due to their nonreciprocal character. In order to estimate the frequency shift caused by the change of the interfacial perpendicular anisotropy during the oxidation, we used the equation derived by Gladii et al. [32]

$$\Delta f_{\text{ani}}\simeq \frac{8\gamma }{{\pi }^3}\frac{\Delta K}{M_s}\cdot \frac{k}{1+\frac{{\Lambda }^2{\pi }^2}{t^2}},$$ (4)

where $\Lambda =\sqrt{2A/{\mu }_0{M}_s^2}$ is the exchange length, ΔK is the difference of the anisotropy of the top and bottom interfaces induced by the oxidation (see the Supplemental Material [22] for details), and A is the exchange constant. We calculated the oxide induced Δf_ani using the changes of the perpendicular anisotropy measured by FMR and the spin-wave stiffness D_stiff = 7.4 × 10⁻⁴⁰ Jm² from Grimsditch et al. [33], with A = D_stiffM_s/2g^∥μ_B. D_stiff is not an interfacial property and we do not expect any change with oxidation. The largest anisotropy-induced frequency shift is Δf_ani ≃ 10 MHz, which is small compared to the total oxide induced frequency shift of about 100 MHz. In Fig. 2 we plot the DMI, which is calculated from the frequency shift after correcting for the anisotropy-induced shift, for both sample series. We used g^∥ determined by FMR for each sample and the saturation magnetization for the respective unoxidized sample from each series for the calculation. For both sample series the DMI is increasing with the oxidation time. The presence of a significant DMI for the control series after oxidation demonstrates that a ferromagnet/oxide interface can give rise to DMI. The DMI for the unoxidized Pt/Co₉₀Fe₁₀ sample originates from the DMI at the Pt interface. The oxidation further increases the total DMI indicating that the DMI of the oxide interface promotes the same left-handed chirality as the DMI at the Pt interface. We are using the convention that positive DMI gives rise to clockwise rotation of the spins (right-handed chirality), see the Supplemental Material [22] for more details. Describing the DMI by its chirality has the advantage that it does not depend on careful definition on sign conventions. The total increase of the frequency shift is larger for the Pt/Co₉₀Fe₁₀ series than for Cu/Co₉₀Fe₁₀ series. The fractional contribution of the DMI from the Pt interface increases as the thickness of the ferromagnet decreases with the oxidation time. The maximum increase of the volume averaged DMI from the Pt interface is ∼0.1mJ/m². All considered, both sample series show within error bars the same contribution to the DMI from the oxide interface.

III. RESULTS AND DISCUSSION

In Figs. 2(a) and 2(b), g^⊥ and D^norm both show a monotonic dependence with increasing oxidation time. g^⊥ has both a volume and an interfacial contribution, which would require a Co₉₀Fe₁₀ thickness series to deconvolute these two contributions. However, since the film thickness is on the order of the exchange length, a clear distinction between bulk and interfacial contributions to g^⊥ is not possible and we will not attempt to separate the two contributions. The DMI, on the other hand, originates from the interface. Here, we compare the as measured values for g^⊥ and D_DMI in order to avoid any ambiguity by correcting only D_DMI for the thickness reduction during the oxidation. In the Supplemental Material [22], we also show a similar analysis, where instead we normalized D_DMI to a constant thickness of 1 nm Co₉₀Fe₁₀. We use the magnetic moment measured by SQUID to determine the relative thickness for the oxidized samples. The overall trend between the two methods of thickness normalization remains unchanged. Only the quantitative change of D_DMI becomes dependent on the method used. Furthermore, we quantify the correlation between D_DMI and g^⊥ through the Pearson correlation coefficients, which assesses the linear relationship between two parameters. The Pearson correlation coefficient for D_DMI and g^⊥ is $r_s^{Pt}=-0.88$ for the Pt/Co₉₀Fe₁₀/oxide and $r_s^{Cu}=-0.98$ for the Cu/Co₉₀Fe₁₀/oxide series. These values indicate that D_DMI and g^⊥ are indeed correlated. This can be visualized in the plots of D_DMI vs g^⊥ as shown in the insets of Figs. 2(a) and 2(b). Again, we do not pursue a correlation analysis of g^∥ due to the larger scatter of the data.

DFT calculations for the Ir/Fe/oxide system show that the presence of an oxide at the interface gives rise to DMI and is correlated with an electric dipole moment at the interface [21]. This electric dipole moment originates from hybridization and the associated charge transfer at the interface between the oxygen and metal atoms. This finding is in agreement with DFT calculations by Yang et al., which showed that the DMI for a Pt/Co/MgO trilayer is enhanced compared to a Pt/Co bilayer [34]. Moreover, they found that application of an electric field perpendicular to the surface of the trilayer structure further increases the DMI, when the positive electric field points from the insulator to the metal. The electric field gives rise to a charge redistribution in a manner similar to a material with high electronegativity. Oxygen, for example, has a Pauling electronegativity of 3.44, much higher than the electronegativity of elemental 3d ferromagnets, which have an electronegativity of about 1.9 [35].

During the oxidation the 3d orbitals of the Co and the Fe, which point towards the interface (d_xz, d_yz, and $d_{z^2}$), will hybridize with the oxygen p_z orbitals. The d_xy and d_x2−y2 orbitals are oriented within the interface plane, and as such, hybridize to a much lesser degree with the oxygen orbitals. The bonding between Co and O was confirmed by photoelectron x-ray spectroscopy for the Co/AlO_x systems [36]. The hybridization shifts the energy levels of the 3d orbitals and changes their respective occupation. This also changes the associated total orbital momentum. Thus, the change of g^⊥, which originates from a change in the orbital momentum l, is indirect evidence of the hybridization and the associated charge transfer at the oxide interface. This charge transfer, which depends on the difference of the electronegativity of the materials on both sides of the interface, increases the asymmetry of the electronic structure at the interface. Such a lack of inversion symmetry is a critical requirement for DMI.

The hybridization at the oxide interface is also related to the change of the interfacial anisotropy. The respective band levels depend on the orientation of the magnetization, which gives rise to an orientation dependence of the orbital momentum. The difference of the orbital momentum for the out-of-plane plane and in-plane geometry Δl^{⊥–∥ =} l^⊥ – l^∥ is, according to Bruno’s theory, directly related to the interfacial perpendicular anisotropy and was extensively studied for many systems experimentally and theoretically [5,37–39]. Tetragonal distortion often contributes to the orbital asymmetry.

The orbital asymmetry Δl^⊥–∥ is proportional to the difference of the out-of-plane and in plane g factors. In Fig. 3 we plot the perpendicular anisotropy field H_k vs g^⊥ – g^∥ for the Cu/Co₉₀Fe₁₀/oxide series and find qualitative agreement with Bruno’s model. However, the large scatter and the larger error bars for g^∥ found in the data for the Pt/Co₉₀Fe₁₀/oxide series obscures any relationship between H_k and g^⊥ – g^∥.

FIG. 3.

Perpendicular anisotropy vs the difference between the spectroscopic g factor for the out-of-plane geometry and the in-plane geometry, which is proportional to the difference of the orbital momentum for these two geometries, for the Cu/Co₉₀Fe₁₀ sample series.

The theory by Moriya predicts a correlation of D_DMI with g. A direct comparison between Moriya’s theory and our result is difficult. First, Moriya’s theory was developed for ionic bonds between oxygen and Fe in the bulk, where the spins are interacting by superexchange and g is considered isotropic. Here, the DMI is interfacial and the bonds are characterized by hybridization between the Co and Fe d orbitals and the oxygen p orbitals. Thus, it is not necessarily expected that the DMI shows the same trend with g as Moriya’s theory predicts. Nevertheless, we still find that g^⊥ and D_DMI are correlated as originally predicted. It is important to keep in mind that there are other contributing factors that determine the magnitude of the DMI. For example, the strength of the Heisenberg exchange can also affect the magnitude of the DMI. Therefore, all of these factors must be taken into consideration.

IV. SUMMARY

We have demonstrated that ferromagnetic / oxide interfaces can induce DMI. Metal/ Co₉₀Fe₁₀/oxide systems give rise to left-handed chiral spin chains (negative DMI value). Thus, it will lead to an enhancement of the total DMI in a Pt/Co₉₀Fe₁₀/oxide trilayer system. Moreover, g^⊥ follows the same trend as the DMI with the oxidation time. This is in agreement with DFT calculations by Belabbes et al. for the Fe/oxide system, which show an increase of hybridization at the interface together with charge transfer and gives rise to DMI. The electric dipole moment, which results from the charge transfer, is correlated to the DMI. Finally, we show that the orbital asymmetry for the Cu/Co₉₀Fe₁₀/oxide series is correlated with the anisotropy.