Abstract
Drought is one of the foremost outcomes of global warming and global climate change. It is a serious threat to humans and other living beings. To reduce the adverse impact of drought, mitigation strategies as well as sound projections of extreme events are essential. This research aims to strengthen the robustness of anticipated twenty-first century drought by combining different Global Climate Models (GCMs). In this article, we develop a new drought index, named Maximum Relevant Prior Feature Ensemble index that is based on the newly proposed weighting scheme, called weighted ensemble (WE). In the application, this study considers 32 randomly scattered grid points within the Tibetan Plateau region and 18 GCMs of Coupled Model Intercomparison Project Phase 6 (CMIP6) of precipitation. In this study, the comparative inferences of the WE scheme are made with the traditional simple model averaging (SMA). To investigate the trend and long-term probability of various classes, this research employs Markov chain steady states probability, Mann–Kendall trend test, and Sen’s Slope estimator. The outcomes of this research are twofold. Firstly, the comparative inference shows that the proposed weighting scheme has greater efficiency than SMA to conflate GCMs. Secondly, the research indicates that the Tibetan Plateau is projected to experience “moderate drought (MD)” in the twenty-first century.
Keywords: Drought, Global warming, Multiple global climate models (GCMs), Coupled model intercomparison project Phase 6 (CMIP6)
Subject terms: Climate sciences, Hydrology, Natural hazards
Introduction
Global warming refers to the rapidly increasing temperature on the earth’s surface over a long period1. Global warming is mostly caused by rises in greenhouse gases, including methane (), hydrogen (H), nitrous oxide (O), carbon dioxide (), and sulfur dioxide (). emissions in the atmosphere from power plants, factories, vehicles, volcanic eruptions, and burning of coal and gas are the key issues of global warming2. It will affect the earth’s geology3, ocean, and atmosphere4. One of the adverse effects of global warming is that the reservoir of freshwater resources has been depleted at an unprecedented ratio. Pakistan is also experiencing the effects of global warming5. In several undeveloped areas, death rates have been reported in many parts of the country due to global warming6. Thousands of people died due to harsh conditions resulting from the scarcity of clean water in Tharparker, particularly in the 2010s7. This scarcity is closely related to climate change, which has made the region’s already dry conditions even worse. Significant reductions in rainfall lead to prolonged droughts in Tharparker. These droughts dried water sources, making it difficult for the local population to access clean drinking water6. Furthermore, many researchers noted the decreasing trend of rainfall in Pakistan attributable to climate change8. This trend has been observed over the past few decades5,9. Drought has also harmed many aspects of life in the majority of the world as a result of global warming10. Drought is an extreme event of climate that occurs when the precipitation is below than average level. The global agricultural sector faces severe drought risk due to rapid changes in the global warming environment. It is posing significant threats to pollution levels11, agriculture, livestock12, ecosystems, and human health13. Nevertheless, effective planning and drought moderation techniques can mitigate these adverse effects to some extent. Drought moderation techniques include methods like rainwater harvesting, building reservoirs and dams, and planting drought-resistant crops.
A Global Climate Model (GCM) is a mathematical depiction of the Earth’s atmosphere designed to simulate the Earth's climate system and ocean circulations14,15. It is essential for climate studies, as it enables the refinement of our comprehension and projecting capabilities regarding the atmosphere16, ocean, and climate behavior17. GCM simulations are commonly employed for assessing future drought risks. These GCM simulations have been utilized by various researchers, including18–20. Numerous researchers have utilized hydrological data to evaluate drought indices for estimating drought severity. Examples include the Palmer Drought Severity Index (PDSI)21, the Normalized Ecosystem Drought Index (NEDI)22, and the Standardized Precipitation Index (SPI)23. Similarly,24 also utilized precipitation data of GCMs to study future conditions of drought. GCM models exhibit significant biases, particularly for the variables influencing hydrology.
The assessment of climate variables in the Coupled Model Intercomparison Project phase 5 (CMIP5) and CMIP6 models is prone to a certain amount of uncertainty and fluctuation. CMIP5 and CMIP6 simulate Earth's climate system and are used to project future climate scenarios under different greenhouse gas emission scenarios24. Numerous authors have found that it is challenging to accurately estimate extreme hydrological occurrences because of the uncertainty of climate projection models25. Using a single climate model decreases the reliability of the results in analyzing meteorological events26. Numerous researchers suggested that using ensemble models might help to reduce the uncertainty27,28.
Drought has been evaluated in a range of climate simulation scenarios using the ensemble approach many times. For instance,29 employed statistical and machine-learning techniques to construct an ensemble approach for thirty-four CMIP5 climate models30. Utilized the multi-model ensemble and the delta method to project future temperature changes. Ruan et al.31 examined potential fluctuations in temperature, precipitation, and drought characteristics using the CMIP5 optimum ensemble of GCMs. However, biases and some estimation errors are inherent in every model ensemble, lowering the reliability of models32. Hence, to accurately estimate drought conditions, it is necessary to use methods that can project droughts efficiently. This ensures a more comprehensive understanding of drought dynamics. Therefore, this research aims to propose a comprehensive technique for studying future drought conditions for the time 2015–2100 at different time scales (i.e., 1, 3, 6, 9, 12, 24, and 48 months). Time scales help to evaluate which type of drought it is. Short-term precipitation deficits indicate meteorological drought, medium-term soil moisture deficits point to agricultural drought, and long-term reductions in water bodies signal hydrological drought. Socioeconomic drought can encompass various time scales, depending on its impact on society and the economy.
The resulting Maximum Relevant Prior Feature Ensemble (MRPFE) drought index allows for efficient and accurate drought estimations.
Data and methods
The methods and study areas utilized in this study briefly explained in the following sub-sections. However,32,33 utilized the same study area for studying drought. Whereas, the standardization procedure is selected, based on34 research. Moreover,24 also studied the long-term statistic of precipitation by using Steady state probabilities.
K-component Gaussian mixture distribution (K-CGMD)
The Standardized Drought Index (SDI) is a crucial measure for assessing drought severity. Fitting an appropriate probability distribution to time series precipitation data is a key point in measuring the SDI. The meteorological variables data follow a multimodal distribution, which means that the distribution of the data has more than one peak. The current SDI estimation methodology is based on an unimodal distribution. In such cases, insufficient distribution fitting reduces the accuracy of drought assessment. In past research, unimodal distributions were commonly employed to compute drought indices such as the Standardized Precipitation Index (SPI)23 and standardized Precipitation Evapotranspiration Index (SPEI)35. However, these indices are multimodal5. On another aspect, multimodal distributions can improve computational accuracy. The R packages ‘fitdistrplus’ and ‘propagate’ are used to select the appropriate probability function in this study. Recently,36,37 fitted 32 probability distributions for the calculation of various drought indices using the ‘R’ package. Ali et al.5 used K-CGMD based on a standardization method to model precipitation time series and achieve the highest computational accuracy. K-CGMD is a type of mixture model that has been used in a variety of studies to simulate various random events24,37. Mathematically, the K-CGMDs are presented as:
| 1 |
| 2 |
| 3 |
where denotes the quantity and number of components, specifies the weight of the mixture component of ith element with the restraint . show the mean and variance of the ith component24.
Steady-state probability of Markov chain
A discrete stochastic process (Markov chain) describes a possible sequence of events38. Markov chain models can be used to predict the probabilities of incoming process states. It plays an important role in projecting future droughts. To assess drought conditions of different climatic regions, several authors used Markov chain stochastic process models, including;39–42. The Markov chain, Transition Probability Matrix (TPM), and steady-state probabilities are explained briefly below:
Let Z = {} be the possible process states. The process may begin in one of these states and move sequentially from one to another state. If the current position of the chain is in the state , then it proceeds to the next step, by passing to the state with probability . The TPM provides the probabilities of changing states42. TPM assumes that it is always in a square matrix, where rows show the initial state and columns show the next state. Each element of TPM is a probability, which means all values are nonnegative (0 1) and the sum of rows is equal to 1.
The following conditions satisfy each formulated TPM.
| 4 |
for all and .
These probabilities are expressed in matrix form as follows.
Let be the number of transitions, in which (initial state) transit to state (Next state). The different states of the transition probabilities are:
| 5 |
TPM is a square matrix with elements that are both real and non-negative, which are as follows:
| 6 |
The above-mentioned matrix's elements assess the transient probabilities in the process state space. The stationary probabilities of the process quantify the long-term behavior of the process states. Such types of probabilities are known as steady-state probabilities. After a certain number of steps, a Markov process's probabilities tend towards a stable steady state. Let represent the limiting probability of step after “n” steps. The mathematical definition of the steady-state probability is defined below.
| 7 |
In another way,
| 8 |
The criteria by which MRPFE index values are categorized into different drought classes are provided in24.
Mann–Kendall (MK) test
Mann–Kendall (MK) trend test has several applications in environmental and hydrological research and uses test statistics for assessing trends in time series data43. The MK trend test identifies statistically significant increasing or decreasing trends in long-term temporal data and detects climate trends in meteorological and hydrological time series data44. Several researchers have employed the MK test to identify trends, for example,45 used the modified MK test to detect trends in annual precipitation and temperature for nine states of the northeastern United States. The modified MK test is a statistical method that is built upon the original MK trend test by incorporating adjustments or enhancements to better suit specific research contexts.46 analyzed the long-term spatio-temporal variations in rainfall from 1901 to 2015 in India using the MK test to identify the pattern of precipitation (rainfall). Vicente-Serrano t al.36 employed the MK test to determine the monthly and annual patterns (trends) of the Yangtze River flows at the Zhutuo and Cuntan stations of China over 35 years (1980–2015). Praveen et al.47 employed the MK test to identify potential trends and analyze monthly and annual trends in streamflow, rainfall, and temperature within the Urmia Lake (UL) basin over 42 years from 1971 to 2013. The MK test can be mathematically described as follows:
| 9 |
where of Eq. (9) can be calculated by using Eq. (10).
| 10 |
The positive S values represent an upward trend, negative values indicate a downward trend, and zero signifies the absence of a trend. The following test statistics are formulated to appraise trends within the complete time series data.
| 11 |
In Eq. (11), can be calculated by the following equation:
| 12 |
where m is the difference in the number of compared values and n represents the overall amount of data points.
Sen’s slope estimator (SSE)
Sen's Slope Estimator (SSE) serves as a nonparametric statistical test widely utilized for determining trend magnitudes in time series data48. SSE finds application in hydro-meteorological time series for both trend analysis44, and the prediction of trend magnitude49,50. SSE has been employed in several studies to gain insight into time series data trends. For example,51 examined spatiotemporal trends in annual rainfall utilizing SSE. Harka et al.52 calculated trends in the time series data of identified COVID-19 cases in India using SSE. Additional applications are found by51,53–56. Sen’s Slope Estimator (SSE) was introduced by57. A brief mathematical description of SSE is as follows:
| 13 |
where and denote data values at times t and i, respectively in the context of t > i, signifies the slope of the estimator between the data points and . Here varies from 2 to and varies from 1 to , and n denotes the total number of data points in the temporal data.
For an individual datum in every period, there will be slope estimates. For several observations in one or more periods, then .
The median of n values of calculated by the following equation:
| 14 |
| 15 |
The Positive value of indicate an upward (increasing) trend, while a negative value of indicate a downward (decreasing) trend.
Application
This research applies temporal data of precipitation from 18 climate models of CMIP6, emphasizing 32 grid points located on the Tibetan Plateau which national territory of China. However, we selected these models are grid points by following the study of24. Tibetan plateau encompasses an area of more than 2.5 million km2 (26.00–39.47 N, 73.19–104.47 E), this is the world’s largest plateau58. This region is also called the “world water tower”59. The Tibetan Plateau is a region in southwest China, and a large number of Asian rivers originate there. However, the region of the Tibetan Plateau is prone to global warming and climate change60. The temperature on the Tibetan Plateau has significantly increased over the last few decades61. So, it is beneficial to measure and assess drought with respect to global warming and climate change. Several researchers have performed spatial–temporal analyses associated with drought forecasting, assessment, and monitoring, in Tibetan Plateau regions. Including;62–66. In this study, we use simulated monthly time series of precipitation data of the CMIP6 models, which range from 1961 to 2014. We utilized CN05.1 model data as the observational data set of precipitation32. In addition, we utilize three different future scenarios i.e., SSP1-2.6, SSP2-4.5, and SSP5-8.5. Information on the selected models is available in24.
The proposed method
In this section, we used precipitation data ranging from 1961 to 2014 from several GCMs corresponding to CN05.1 as observational data. Moreover, this section describes the process involved in the development of the MRPFE index. Figure 1 shows the flowchart of the MRPFE index. Here, the proposed weighting scheme aims to reduce the impact of extreme values on the aggregated data. The mathematical expressions for the suggested weighting scheme for combining precipitation time series data obtained from various CMIP6 models are shown in this section. The proposed weighting scheme distinguishes itself by giving more weight to those values whose frequency contributes more to homogeneity among them. In contrast, divergent values will be given lower weights. This implicates minimization of the impact of extreme values in the aggregation process. The proposed weighting scheme is implemented in the following steps:
Figure 1.
Flowchart of the proposed index.
Let D (,, ,….) be the time series data of precipitation simulated by various models in a specific region. And is the observed time series data. Where shows the total number of GCMs. The primary goal of the weighting scheme is to reduce the effect of extreme values. Our proposed scheme is based on three major phases. The explanation of each phase is described below:
Phase 1. Weighting each model
This phase assigns each model weight based on its difference from observed values. Below is a description of these steps:
Step 1. The absolute difference between simulated and observed
In this stage, we are taking the absolute difference of data simulated from GCM models and observed data :
| 16 |
Step 2. Combining observed and simulated data
In this stage, we are adding the absolute of to the absolute of each model value:
| 17 |
Step 3. Assigning weights
This stage assigns weights to each model by taking the ratio of Eqs. (16) and (17):
| 18 |
Here, will be the weight of ith model.
Step 4. Standardization of weights
This stage standardizes the weights assigned to each model. For standardization, each assigned weight is divided by the sum of the weights of each model:
| 19 |
Here represents the standardized weights for each model.
Phase 2. Assigning spatiotemporal weights to each value
This phase assigns values of each model a relevant weight based on its location and time. This phase includes the following steps:
Step 1. Exponentials of the absolute differences
As a1 in Eq. (16) represents the difference in the observed value and ith GCM data, the first step of this phase then suggests calculating the exponent of ith differences. This equation aims to maximize the differences.
| 20 |
Step 2. Estimation of weights
In this step, we assign a high weight to small deviated values and a low weight to large deviated values:
| 21 |
Step 3. Standardizing weights
In this stage, we standardize as follows:
| 22 |
Under certain conditions that Phase 2 is iterated for each model.
Phase 3. Hybridization of Phases 1 & 2
To combine both weights, we are taking an average of Eqs. (19) and (22):
| 23 |
Here are representing the proposed weights and we name this weighting technique “Weighted Ensemble”.
Phase 4. Data aggregation
This phase aggregates the data of various CMIP6 GCM simulations under proposed weights:
| 24 |
After the aggregation of data, now we perform multiple linear regression models for future projections.
After this, we will standardize the under K-CGMD, this is the 12-component combined Cumulative Distribution Function (CDF):
| 25 |
Here, we selected 12 components as there are 12 months in a year. In Eq. 25, is the CDF of K-CGMD. To standardize this CDF for the calculation of the proposed drought index MRPFRE, the following method is applied:
| 26 |
| 27 |
Here , when
| 28 |
| 29 |
where
| 30 |
Here , when
| 31 |
= 2.515517, = 0.802853, = 0.010328, = 1.432788, = 0.985269, and = 0.001308 are constants. This index and the included constants were developed based on the spatiotemporally weighted combination of precipitation time series. It is named the Maximum Relevant Prior Feature Ensemble (MRPFE) index.
Comparative statistics
Simple model averaging (SMA)
Simple model averaging (SMA) is a type of simple mean that gives equal importance to each value in the dataset67, which has been used many times to combine GCM ensembles29,68. In this study, it is applied as a comparative method to the proposed weighting scheme. The calculation is based on the following equation:
| 32 |
where is the SMA of GCMs, is the precipitation projection for the ith GCM and is the number of GCMs.
Relative absolute error (RAE) and mean absolute error (MAE)
Relative Absolute Error (RAE), a statistical tool, assesses the accuracy and precision of projections relative to a reference value. RAE is calculated by dividing the absolute difference between the predicted and the reference value. In contrast, MAE, another statistical performance metric, represents the average of the absolute differences between predicted and corresponding reference values. These methods are frequently used in various recent studies69.24,69 have explained these methods mathematically in their studies.
Results
Estimation of weights of the proposed index
In this study, a novel weighting index is proposed to address biases and reduce the impact of extreme precipitation values by placing greater emphasis on values that deviate less from observational data. Figure 2 presents the selected locations of the Tibetan Plateau. A temporal representation of observed and simulated models data is shown in Fig. 3. Table 1 provides the resolution of each selected model and summary statistics of weights assigned to all selected GCMs at one random point. The GCMs and their corresponding weights are listed in rows, and the columns show the minimum, maximum, and average weights assigned to each GCM. It can be observed that the average weights assigned to the GCMs range from 0.046 to 0.054. The minimum and maximum weights assigned to each GCM also vary, with some GCMs having weights as low as 0.023 and as high as 0.057. The maximum average weight (0.054) is assigned to MPI-ESM1-2-LR, minimum average weight (0.046) to CNRM-CM6-1. Overall, the table provides useful information about the weights assigned to the GCMs and their relative importance in the ensemble. Furthermore, Fig. 4 displays the assigned weights of each CMIP6 model at one random grid point. Table 2 shows the monthly weights that are assigned to all selected GCMs at one random point. From the table, we can see that the maximum weights were assigned to the ACCESS-ESM1-5 model in December and, the minimum to the MPI-ESM1-2-LR model in July.
Figure 2.
The geographical locations of the selected study area.
Figure 3.
Temporal representation of observed and selected GCM data of precipitation (kgms−2).
Table 1.
Resolution of models and summary statistics of weights assigned to each GCM at one random point.
| Sr. No. | Models | Resolution (longitude × latitude) | Minimum | Maximum | Average |
|---|---|---|---|---|---|
| 1 | ACCESS-CM2 | 1.875° × 1.25° | 0.0261 | 0.0491 | 0.0483 |
| 2 | ACCESS-ESM1-5 | 1.875° × 1.2143° | 0.0318 | 0.0567 | 0.0524 |
| 3 | AWI-CM-1–1-MR | 0.9375° × 0.9375° | 0.0374 | 0.0526 | 0.0512 |
| 4 | BCC-CSM2-MR | 1.125° × 1.125° | 0.0467 | 0.0529 | 0.0519 |
| 5 | CanESM5 | 2.8125° × 2.8125° | 0.0470 | 0.0516 | 0.0508 |
| 6 | CanESM5-CanOE | 2.8125° × 2.8125° | 0.0466 | 0.0508 | 0.0500 |
| 7 | CNRM-CM6-1 | 1.40625° × 1.40625° | 0.0449 | 0.0471 | 0.0464 |
| 8 | EC-Earth3-Veg | 0.703125° × 0.703125° | 0.0463 | 0.0518 | 0.0508 |
| 9 | GFDL-ESM4 | 1.25° × 1° | 0.0300 | 0.0554 | 0.0523 |
| 10 | HadGEM3-GC31-LL | 2° × 2.25° | 0.0447 | 0.0474 | 0.0467 |
| 11 | INM-CM4-8 | 2° × 1.5° | 0.0427 | 0.0484 | 0.0476 |
| 12 | INM-CM5-0 | 2° × 1.5° | 0.0419 | 0.0544 | 0.0530 |
| 13 | IPSL-CM6A-LR | 2.5° × 1.25874° | 0.0473 | 0.0545 | 0.0530 |
| 14 | MIROC6 | 1.40625° × 1.40625° | 0.0483 | 0.0515 | 0.0506 |
| 15 | UKESM1-0-LL | 0.9375° × 0.9375° | 0.0371 | 0.0514 | 0.0505 |
| 16 | MPI-ESM1-2-LR | 1.875° × 1.875° | 0.0430 | 0.0555 | 0.0537 |
| 17 | MRI-ESM2-0 | 1.125° × 1.125° | 0.0435 | 0.0477 | 0.0470 |
| 18 | NESM3 | 1.875° × 1.875° | 0.0235 | 0.0476 | 0.0465 |
| 0.703125° × 0.703125° |
Figure 4.
Weights assigned to each model at one random location.
Table 2.
Monthly summary statistics of weights of all selected GCMs at one random point.
| Sr. No. | Models | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ACCESS-CM2 | 0.054 | 0.054 | 0.054 | 0.054 | 0.054 | 0.053 | 0.055 | 0.055 | 0.055 | 0.054 | 0.054 | 0.054 |
| 2 | ACCESS-ESM1-5 | 0.062 | 0.061 | 0.059 | 0.056 | 0.052 | 0.049 | 0.060 | 0.060 | 0.059 | 0.057 | 0.061 | 0.062 |
| 3 | AWI-CM-1-1-MR | 0.058 | 0.058 | 0.058 | 0.057 | 0.058 | 0.057 | 0.055 | 0.055 | 0.057 | 0.058 | 0.058 | 0.058 |
| 4 | BCC-CSM2-MR | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.059 | 0.059 | 0.059 | 0.058 | 0.058 | 0.058 | 0.058 |
| 5 | CanESM5 | 0.056 | 0.056 | 0.057 | 0.057 | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 | 0.057 | 0.056 | 0.056 |
| 6 | CanESM5-CanOE | 0.055 | 0.056 | 0.056 | 0.056 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.056 | 0.055 | 0.055 |
| 7 | CNRM-CM6-1 | 0.051 | 0.052 | 0.052 | 0.052 | 0.052 | 0.053 | 0.053 | 0.053 | 0.052 | 0.052 | 0.052 | 0.051 |
| 8 | EC-Earth3-Veg | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.055 | 0.057 | 0.057 | 0.057 |
| 9 | GFDL-ESM4 | 0.052 | 0.052 | 0.052 | 0.052 | 0.052 | 0.053 | 0.053 | 0.053 | 0.053 | 0.052 | 0.052 | 0.052 |
| 10 | HadGEM3-GC31-LL | 0.053 | 0.053 | 0.053 | 0.053 | 0.054 | 0.053 | 0.054 | 0.054 | 0.054 | 0.053 | 0.053 | 0.053 |
| 11 | INM-CM4-8 | 0.059 | 0.059 | 0.059 | 0.059 | 0.059 | 0.060 | 0.059 | 0.059 | 0.058 | 0.059 | 0.059 | 0.059 |
| 12 | INM-CM5-0 | 0.059 | 0.059 | 0.058 | 0.058 | 0.059 | 0.060 | 0.060 | 0.059 | 0.059 | 0.060 | 0.060 | 0.059 |
| 13 | IPSL-CM6A-LR | 0.056 | 0.056 | 0.056 | 0.057 | 0.057 | 0.057 | 0.058 | 0.058 | 0.057 | 0.056 | 0.056 | 0.056 |
| 14 | MIROC6 | 0.056 | 0.056 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.057 | 0.055 | 0.056 | 0.056 | 0.056 |
| 15 | UKESM1-0-LL | 0.053 | 0.053 | 0.053 | 0.053 | 0.053 | 0.053 | 0.054 | 0.053 | 0.053 | 0.053 | 0.053 | 0.053 |
| 16 | MPI-ESM1-2-LR | 0.052 | 0.052 | 0.053 | 0.053 | 0.053 | 0.053 | 0.048 | 0.049 | 0.052 | 0.052 | 0.052 | 0.052 |
| 17 | MRI-ESM2-0 | 0.057 | 0.057 | 0.057 | 0.058 | 0.058 | 0.058 | 0.055 | 0.055 | 0.057 | 0.058 | 0.057 | 0.057 |
| 18 | NESM3 | 0.052 | 0.052 | 0.052 | 0.053 | 0.053 | 0.053 | 0.049 | 0.050 | 0.052 | 0.052 | 0.052 | 0.052 |
Validation of the proposed WE scheme
Table 3 shows the summary statistics of MAE and RAE of the WE weighting scheme and SMA technique. The results show that the errors of the WE scheme are significantly less than SMA scheme. Based on these findings, it can be stated that our proposed weighting scheme is more efficient than the traditional SMA scheme.
Table 3.
Summary statistics of RAE and mean absolute error.
| SSP1-2.6 | SSP2-4.5 | SSP5-8.5 | ||||
|---|---|---|---|---|---|---|
| Time scale | Unimodal | K-CGMD | Unimodal | K-CGMD | Unimodal | K-CGMD |
| 1 |
− 222.27 (Skewed Normal) |
− 742.13 |
− 158.65 (Skewed-normal) |
− 743.43 |
− 129.03 (Skewed-normal) |
− 840.03 |
| 3 |
− 323.31 (GEV) |
− 2355.23 |
− 291.91 (Triangular) |
− 2346.92 |
− 283.19 (Triangular) |
− 2559.56 |
| 6 |
− 318.68 (GEV) |
− 3139.93 |
− 300.10 (GEV) |
− 3096.39 |
− 252.11 (GEV) |
− 3325.64 |
| 9 |
-315.88 (Logistic) |
− 3232.43 |
− 301.87 (Normal) |
− 3043.03 |
− 255.50 (Logistic) |
− 3293.38 |
| 12 |
− 353.10 (Laplace) |
− 3276.15 |
− 263.96 (Logistic) |
− 2972.94 |
− 297.35 (Johnson SU) |
− 3194.17 |
| 24 |
− 524.45 (Johnson SU) |
− 3921.03 |
− 381.67 (Normal) |
− 3579.21 |
− 449.68 (3P Weibull) |
− 3771.39 |
| 48 |
− 355.58 (Johnson SU) |
− 4492.90 |
− 556.60 (Gumbel) |
− 4112.98 |
− 381.56 (3P Weibull) |
− 4418.03 |
Estimation of MRPFE using K-CGMD under a different scenario
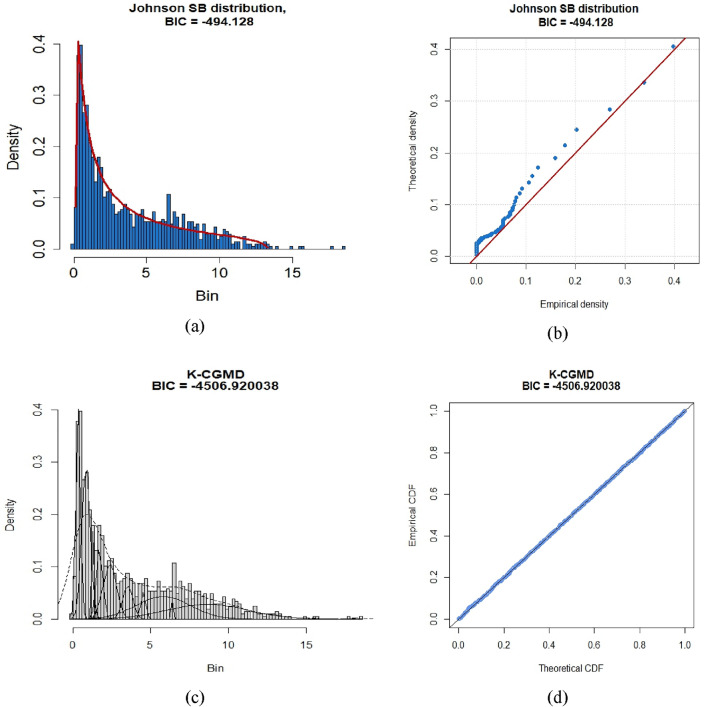
In this section, we examine the effectiveness of K-CGMD for modeling drought index values. The accuracy of K-CGMD at different time scales is compared with different univariate probability distributions using the Bayesian Information Criterion (BIC). BIC is used to evaluate models and determine which trade-off between model fit and complexity is optimal. A more favorable model fit is indicated by lower BIC values. Table 4 represents the BIC values for univariate distributions and the K-CGMD model for various time scales of three different scenarios. The findings reveal that, for SSP1-2.6, SSP2-4.5, and SSP5-8.5, the K-CGMD model consistently exhibits lower BIC values across all time scales compared to unimodal. This consistent pattern recommends that the K-CGMD model is a superior fit for the data for most of the time scales within all three scenarios. Consequently, the K-CGMD model proves to be a more reliable and effective approach for standardizing drought indices compared to unimodal distributions. In Fig. 5, probability and Q-Q plots visually demonstrate K-CGMD's superiority over unimodal probability models in modeling drought indices for scenario SSP1-2.6. Furthermore, Figs. 6 and 7 present probability and Q-Q plots for scenarios SSP1-2.6, SSP2-4.5, and SSP5-8.5, respectively, providing additional evidence of K-CGMD's superior fit for the data.
Table 4.
BIC of Unimodal and K-CGMD at different time scales for three different scenarios at one location.
| Metrics | Proposed | SMA | ||||
|---|---|---|---|---|---|---|
| Minimum | Average | Maximum | Minimum | Average | Maximum | |
| RAE | 0.4500 | 2.8892 | 22.7670 | 0.4650 | 2.9710 | 23.6250 |
| MAE | 0.411 | 1.629 | 6.575 | 0.439 | 1.666 | 6.804 |
Figure 5.
Probability and QQ-plot of univariate and K-CGMM for SSP1-2.6 future scenarios at time scale-1 on 76.5° E and 36° N location.
Figure 6.
Probability and QQ-plot of univariate and K-CGMM for SSP2-4.5 future scenarios at time scale-1 on 76.5° E and 36° N location.
Figure 7.
Probability and QQ-plot of univariate and K-CGMM for SSP5-8.5 future scenarios at time scale-1 on 76.5° E and 36° N location.
Trend assessment under Mann–Kendall and Sen’s slope
The significance of future drought trends and direction is evaluated using Sen’s slope and seasonal Mann–Kendall approaches36. This specific method is used to evaluate the drought conditions on the Tibetan Plateau. Table 5 presents trend analyses utilizing Mann–Kendall and Sen’s slope methods for three scenarios across various time scales. Each scenario and time scale combination includes the Kendall Z-value, Sen’s slope, p-value, significance level, and trend direction. The direction of the trend, whether it is increasing or decreasing, is determined by the trend analysis. Additionally, the p-value i.e., p < 0.05 establishes the significance level of the trend in this analysis. The results indicate a predominantly decreasing trend across all time scales for SSP1-2.6, with an exception at time scale 1, which exhibits an increasing trend. For SSP2-4.5, the trend is mostly increasing for smaller time scales (Scale-1, Scale-3, and Scale-6) and decreasing for larger time scales (Scale-24 and Scale-48). For SSP5-8.5, the trend is consistently decreasing for all time scales and is statistically significant for all except for Scale-1.
Table 5.
Mann–Kendall and Sen’s Slope values for trend evaluation under three different future scenarios at each time scale.
| Scenarios | Time Scales | z-value | Slope | p-value | Significance | Direction |
|---|---|---|---|---|---|---|
| SSP1-2.6 | 1 | 0.109 | 0.000 | 0.913 | p > 0.10 | Increasing |
| 3 | − 0.105 | 0.000 | 0.917 | p > 0.10 | Decreasing | |
| 6 | − 1.392 | − 0.001 | 0.164 | p > 0.10 | Decreasing | |
| 9 | − 2.332 | − 0.003 | 0.020 | p < 0.05 | Decreasing | |
| 12 | − 2.304 | − 0.003 | 0.021 | p < 0.05 | Decreasing | |
| 24 | − 2.827 | − 0.004 | 0.005 | p < 0.05 | Decreasing | |
| 48 | − 6.008 | − 0.009 | 0.000 | p < 0.05 | Decreasing | |
| SSP2-4.5 | 1 | 0.169 | 0.000 | 0.866 | p > 0.10 | Increasing |
| 3 | 0.550 | 0.000 | 0.583 | p > 0.10 | Increasing | |
| 6 | 0.137 | 0.000 | 0.891 | p > 0.10 | Increasing | |
| 9 | − 0.404 | 0.000 | 0.686 | p > 0.10 | Decreasing | |
| 12 | − 1.033 | − 0.001 | 0.302 | p > 0.10 | Decreasing | |
| 24 | − 2.511 | − 0.003 | 0.012 | p < 0.05 | Decreasing | |
| 48 | − 6.144 | − 0.009 | 0.000 | p < 0.05 | Decreasing | |
| SSP5-8.5 | 1 | − 1.582 | − 0.002 | 0.114 | p > 0.10 | Decreasing |
| 3 | − 3.247 | − 0.003 | 0.001 | p < 0.05 | Decreasing | |
| 6 | − 5.366 | − 0.005 | 0.000 | p < 0.05 | Decreasing | |
| 9 | − 7.410 | − 0.008 | 0.000 | p < 0.05 | Decreasing | |
| 12 | − 8.496 | − 0.012 | 0.000 | p < 0.05 | Decreasing | |
| 24 | − 11.537 | − 0.016 | 0.000 | p < 0.05 | Decreasing | |
| 48 | − 14.593 | − 0.020 | 0.000 | p < 0.05 | Decreasing |
Estimation of drought using steady-state probabilities
The steady-state probability of the Markov chain is employed in this study to measure the long-term impact of random events. Precipitation is classified into seven classes, namely Extreme Wet (EW), Severe Wet (SW), Moderate Wet (MW), Near Normal (NN), Moderate Drought (MD), Severe Drought (SD), and Extreme Drought (ED). Table 6, evaluates the steady-state probabilities for the various drought classes under three different scenarios at each time scale. From this information, we conclude that the probability of ED is greater than the probability of EW the probability of MD is less than the probability of MW, and the probabilities SD is greater than the probabilities of SW at SSP1-2.6. After analyzing the probabilities of SSP2-4.5 and SSP5-8.5 across different time scales we noticed that the probability of dry conditions is more probable than that of wet conditions. It is anticipated that in all locations, drought conditions will be more prevalent than wet conditions.
Table 6.
Steady State Probabilities for various drought classes in various time scales at all the locations by using three different scenarios.
| Scenario | Time scales | ED | EW | MD | MW | NN | SD | SW |
|---|---|---|---|---|---|---|---|---|
| SSP1-2.6 | 1 | 0.0156 | 0.0019 | 0.0873 | 0.0989 | 0.6702 | 0.0641 | 0.0621 |
| 3 | 0.0293 | 0.0155 | 0.0802 | 0.1047 | 0.6710 | 0.0411 | 0.0582 | |
| 6 | 0.0234 | 0.0234 | 0.0897 | 0.0858 | 0.6803 | 0.0478 | 0.0497 | |
| 9 | 0.0247 | 0.0234 | 0.0881 | 0.0867 | 0.6827 | 0.0438 | 0.0506 | |
| 12 | 0.0207 | 0.0205 | 0.0985 | 0.0840 | 0.6728 | 0.0468 | 0.0566 | |
| 24 | 0.0216 | 0.0236 | 0.0996 | 0.0777 | 0.6809 | 0.0473 | 0.0492 | |
| 48 | 0.0224 | 0.0285 | 0.0844 | 0.1037 | 0.6829 | 0.0478 | 0.0305 | |
| SSP2-4.5 | 1 | 0.0204 | 0.0116 | 0.0951 | 0.0912 | 0.6906 | 0.0388 | 0.0524 |
| 3 | 0.0194 | 0.0243 | 0.1079 | 0.0914 | 0.6676 | 0.0418 | 0.0476 | |
| 6 | 0.0224 | 0.0185 | 0.1023 | 0.0965 | 0.6676 | 0.0448 | 0.0478 | |
| 9 | 0.0176 | 0.0215 | 0.0792 | 0.0919 | 0.6892 | 0.0567 | 0.0440 | |
| 12 | 0.0206 | 0.0225 | 0.0990 | 0.0922 | 0.6775 | 0.0431 | 0.0451 | |
| 24 | 0.0227 | 0.0243 | 0.0770 | 0.0936 | 0.6914 | 0.0464 | 0.0445 | |
| 48 | 0.0246 | 0.0225 | 0.0984 | 0.1012 | 0.6763 | 0.0359 | 0.0411 | |
| SSP5-8.5 | 1 | 0.0310 | 0.0155 | 0.1018 | 0.0824 | 0.6857 | 0.0252 | 0.0582 |
| 3 | 0.0204 | 0.0253 | 0.0943 | 0.0865 | 0.6851 | 0.0447 | 0.0437 | |
| 6 | 0.0224 | 0.0283 | 0.0906 | 0.0838 | 0.6930 | 0.0458 | 0.0361 | |
| 9 | 0.0244 | 0.0235 | 0.0978 | 0.0880 | 0.6794 | 0.0420 | 0.0450 | |
| 12 | 0.0161 | 0.0224 | 0.0837 | 0.0849 | 0.6829 | 0.0612 | 0.0488 | |
| 24 | 0.0238 | 0.0185 | 0.0928 | 0.0876 | 0.6686 | 0.0571 | 0.0516 | |
| 48 | 0.0295 | 0.0250 | 0.1005 | 0.0872 | 0.6832 | 0.0404 | 0.0341 |
Discussion
The analysis of the proposed MRPFE drought index and the novel weighting scheme WE demonstrate significant improvements in the accuracy of drought estimation. The application of the WE scheme to the CMIP6 dataset shows a marked reduction in both comparative measures compared to the SMA approach.
CMIP models have various uncertainties and this unpredictability is an essential part of climate modeling. Understanding these uncertainties is integral for making informed decisions regarding climate change mitigation. By utilizing MME, probabilistic approaches, and transparent communication, we can better manage uncertainties and enhance the robustness of climate projections. Variations in the analysis results of drought trends under different scenarios arise from the varying assumptions and projections related to future greenhouse gas emissions, land use changes, and other socio-economic factors. Each scenario reflects a different trajectory of human activity and its impact on the climate system, leading to variations in the projected severity, frequency, and spatial distribution of droughts. And the guiding significance of utilizing different emission scenarios is to help policymakers and to get insight into better risk management. The proposed index employs the K-CGMD and Markov Chain steady-state probability analysis, provides a robust framework for estimating the likelihood of various drought states. The results indicate that the MRPFE index effectively captures the temporal dynamics of drought conditions, offering a more nuanced understanding of drought trends in this region. Furthermore, the study’s findings highlight the importance of considering multiple emission scenarios when projecting future drought conditions. The variations in drought trends observed under different scenarios underscore the influence of future greenhouse gas emissions, land use changes, and other socio-economic factors on drought severity, frequency, and spatial distribution. This insight is crucial for policymakers and stakeholders involved in climate change mitigation and adaptation planning.
Conclusion
Drought is a naturally occurring phenomenon, that is caused by irregularities in climate variables such as precipitation patterns. There are numerous ecological causes concerned with classifying drought conditions at the particular monitoring station. Therefore, proper pattern processing methods are required to project and investigate the periodic data about the occurrences of drought classes. This study provides a novel weighting scheme, “WE” to combine multiple models and a new drought index “MRPFE” to project drought. The novel weighting scheme WE utilize time-series precipitation data from various GCMs at a specific georeferenced point. In application, simulated time-series precipitation data of CMIP6 from 18 GCMs at thirty-two random locations of the Tibetan Plateau region of China has been used. The methodology of the MRPFE drought index is based on K-CGMD. To estimate the probability of specific drought states, the study includes a steady-state probability analysis applying the Markov Chain approach. The MAE and RAE have been used as relative measures to assess the performance of the proposed weighting scheme. The comparative inference shows that the proposed weighting scheme has greater efficiency than SMA in combining GCMs. Looking ahead, the findings suggest that the Tibetan Plateau region may experience increase in frequency of drought due to declining pattern of precipitation.
Acknowledgements
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under Grant number RGP. 2/115/45 "And this study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).
Author contributions
A.G. and Z.A. conceived the idea. S.Q. supervised the research. M.Y. provided technical assistance. Z.A. reviewed the findings and validated the results. M.A. and S.O.H. provided technical and financial assistance to revise the manuscript. All authors contributed equally.
Data and codes availability
The data and code that support the findings of this study are available from the corresponding author upon reasonable request. Declaration of generative AI and AI-assisted technologies in the writing process. During the preparation of this work the authors used ChatGBT in order to improve the readability of the article. This tool was used in the review and editing stages of drafts only. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Pörtner, H. O., Roberts, D. C., Adams, H., Adler, C., Aldunce, P., Ali, E. & Birkmann, J. Climate change 2022: Impacts, adaptation and vulnerability. IPCC Sixth Assessment Report, 37–118 (2022).
- 2.Singh, B. R. & Singh, O. Study of impacts of global warming on climate change: rise in sea level and disaster frequency. Global Warm.—Impacts and Fut. Perspect. (2012).
- 3.Toebelmann D, Wendler T. The impact of environmental innovation on carbon dioxide emissions. J. Clean. Prod. 2020;244:118787. doi: 10.1016/j.jclepro.2019.118787. [DOI] [Google Scholar]
- 4.Friedlingstein P, Jones MW, O’Sullivan M, Andrew RM, Bakker DC, Hauck J, Zeng J. Global carbon budget 2021. Earth Syst. Sci. Data. 2022;14(4):1917–2005. doi: 10.5194/essd-14-1917-2022. [DOI] [Google Scholar]
- 5.Ali Z, Ellahi A, Hussain I, Nazeer A, Qamar S, Ni G, Faisal M. Reduction of errors in hydrological drought monitoring–a novel statistical framework for spatio-temporal assessment of drought. Water Resour. Manag. 2021;35(13):4363–4380. doi: 10.1007/s11269-021-02952-x. [DOI] [Google Scholar]
- 6.Sadiq S, Saboor A, Mohsin AQ, Khalid A, Tanveer F. Ricardian analysis of climate change–agriculture linkages in Pakistan. Clim. Dev. 2019;11(8):679–686. doi: 10.1080/17565529.2018.1531746. [DOI] [Google Scholar]
- 7.Khan, A. W. & Taylor-Robinson, A. Persistent disease outbreaks and malnutrition in Tharparkar, Pakistan: Natural disaster or man-made public health crisis?. CQUniversity. J. Contrib.https://hdl.handle.net/10018/1260933 (2018).
- 8.Khattak MS, Ali S. Assessment of temperature and rainfall trends in Punjab province of Pakistan for the period 1961–2014. J. Himal. Earth Sci. 2015;48(2):42. [Google Scholar]
- 9.Ahmed K, Shahid S, Nawaz N. Impacts of climate variability and change on seasonal drought characteristics of Pakistan. Atmos. Res. 2018;214:364–374. doi: 10.1016/j.atmosres.2018.08.020. [DOI] [Google Scholar]
- 10.Ahmed N, Turchini GM. Recirculating aquaculture systems (RAS): environmental solution and climate change adaptation. J. Clean. Prod. 2021;297:126604. doi: 10.1016/j.jclepro.2021.126604. [DOI] [Google Scholar]
- 11.Shi L, Zhang J, Yao F, Zhang D, Guo H. Temporal variation of dust emissions in dust sources over Central Asia in recent decades and the climate linkages. Atmos. Environ. 2020;222:117176. doi: 10.1016/j.atmosenv.2019.117176. [DOI] [Google Scholar]
- 12.Islam ARMT, Tasnuva A, Sarker SC, Rahman MM, Mondal MSH, Islam MMU. Drought in Northern Bangladesh: Social, agroecological impact and local perception. Int. J. Ecosyst. 2014;4(3):150–158. [Google Scholar]
- 13.Salvador C, Nieto R, Linares C, Díaz J, Gimeno L. Effects of droughts on health: Diagnosis, repercussion, and adaptation in vulnerable regions under climate change. Challenges for future research. Sci. Total Environ. 2020;703:134912. doi: 10.1016/j.scitotenv.2019.134912. [DOI] [PubMed] [Google Scholar]
- 14.Meehl, G. A. et al. Global climate projections. In Climate Change, 2007: The Physical Science Basis. Contribution of Working group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (eds Solomon, S. et al.) 747–845 (Cambridge University Press, Cambridge, UK; New York, NY, 2007).
- 15.Allen, E., Yorgey, G., Rajagopalan, K. & Kruger, C. Modeling environmental change: A guide to understanding model results that explore the impacts of climate change on regional environmental systems. FS159E (WSU Peer Reviewed Extension Publication, 2015).
- 16.Sailor DJ, Hu T, Li X, Rosen JN. A neural network approach to local downscaling of GCM output for assessing wind power implications of climate change. Renew. Energy. 2000;19(3):359–378. doi: 10.1016/S0960-1481(99)00056-7. [DOI] [Google Scholar]
- 17.Benestad RE. Empirical-statistical downscaling in climate modeling. EOS Trans. Am. Geophys. Union. 2004;85(42):417–422. doi: 10.1029/2004EO420002. [DOI] [Google Scholar]
- 18.Johnson F, Sharma A. What are the impacts of bias correction on future drought projections? J. Hydrol. 2015;525:472–485. doi: 10.1016/j.jhydrol.2015.04.002. [DOI] [Google Scholar]
- 19.Ahmed K, Shahid S, Chung ES, Wang XJ, Harun SB. Climate change uncertainties in seasonal drought severity-area-frequency curves: Case of arid region of Pakistan. J. Hydrol. 2019;570:473–485. doi: 10.1016/j.jhydrol.2019.01.019. [DOI] [Google Scholar]
- 20.Kirono DGC, Kent DM, Hennessy KJ, Mpelasoka F. Characteristics of Australian droughts under enhanced greenhouse conditions: Results from 14 global climate models. J. Arid Environ. 2011;75(6):566–575. doi: 10.1016/j.jaridenv.2010.12.012. [DOI] [Google Scholar]
- 21.Palmer, W. C. Meteorological Drought, Vol. 30. Washington D. C, US: US Department of Commerce, Weather Bureau (1965).
- 22.Chang KY, Xu L, Starr G. A drought indicator reflecting ecosystem responses to water availability: The normalized ecosystem drought index. Agricult. For. Meteorol. 2018;250:102–117. doi: 10.1016/j.agrformet.2017.12.001. [DOI] [Google Scholar]
- 23.McKee, T. B., Doesken, N. J. & Kleist, J. The relationship of drought frequency and duration to time scales. In: Proceedings of the 8th Conference on Applied Climatology (Vol. 17, No. 22, pp. 179–183). Boston, MA: American Meteorological Society (1993).
- 24.Yousaf M, Ali Z, Mohsin M, Ilyas M, Shakeel M. Development of a new hybrid ensemble method for accurate characterization of future drought using multiple global climate models. Stoch. Environ. Res. Risk Assess. 2023;37:4567–4587. doi: 10.1007/s00477-023-02526-w. [DOI] [Google Scholar]
- 25.Slingo J, Palmer T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011;369(1956):4751–4767. doi: 10.1098/rsta.2011.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yuanbin, S. et al. A new ensemble index for extracting predictable drought features from multiple historical simulations of climate. Tellus A: Dyn. Meteorol. Oceanogr.74(1), 236–249 (2022).
- 27.Li T, Hasegawa T, Yin X, Zhu Y, Boote K, Adam M, Bouman B. Uncertainties in predicting rice yield by current crop models under a wide range of climatic conditions. Glob. Chang. Biol. 2015;21(3):1328–1341. doi: 10.1111/gcb.12758. [DOI] [PubMed] [Google Scholar]
- 28.Zumwald M, Knüsel B, Baumberger C, Hirsch Hadorn G, Bresch DN, Knutti R. Understanding and assessing uncertainty of observational climate datasets for model evaluation using ensembles. Wiley Interdiscipl. Rev. Climat. Chang. 2020;11(5):e654. doi: 10.1002/wcc.654. [DOI] [Google Scholar]
- 29.Crawford J, Venkataraman K, Booth J. Developing climate model ensembles: A comparative case study. J. Hydrol. 2019;568:160–173. doi: 10.1016/j.jhydrol.2018.10.054. [DOI] [Google Scholar]
- 30.Ruan Y, Liu Z, Wang R, Yao Z. Assessing the performance of CMIP5 GCMs for projection of future temperature change over the lower Mekong Basin. Atmosphere. 2019;10(2):93. doi: 10.3390/atmos10020093. [DOI] [Google Scholar]
- 31.Chhin R, Oeurng C, Yoden S. Drought projection in the Indochina Region based on the optimal ensemble subset of CMIP5 models. Clim. Chang. 2020;162(2):687–705. doi: 10.1007/s10584-020-02850-y. [DOI] [Google Scholar]
- 32.Baseer A, Ali Z, Ilyas M, Yousaf M. A new Monte Carlo feature selection (MCFS) algorithm-based weighting scheme for multi-model ensemble of precipitation. Theor. Appl. Climatol. 2024;155(1):513–524. doi: 10.1007/s00704-023-04648-1. [DOI] [Google Scholar]
- 33.Mukhtar, A., Ali, Z., Kartal, V., Karakoyun, E., Yousaf, M., & Sammen, S. S. (2024). Development of divergence and interdependence-based hybrid weighting scheme (DIHWS) for accurate assessment of regional drought. Theor. Appl. Climatol., 1–18.
- 34.Batool A, Ali Z, Mohsin M, Shakeel M. A generalized procedure for joint monitoring and probabilistic quantification of extreme climate events at regional level. Environ. Monit. Assess. 2023;195(10):1223. doi: 10.1007/s10661-023-11717-5. [DOI] [PubMed] [Google Scholar]
- 35.Vicente-Serrano SM, Begueria S, Lopez-Moreno JI. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim. 2010;23(7):1696–1718. doi: 10.1175/2009JCLI2909.1. [DOI] [Google Scholar]
- 36.Ali R, Kuriqi A, Abubaker S, Kisi O. Long-term trends and seasonality detection of the observed flow in Yangtze River using Mann-Kendall and Sen’s innovative trend method. Water. 2019;11(9):1855. doi: 10.3390/w11091855. [DOI] [Google Scholar]
- 37.Batool, A., Ali, Z., Mohsin, M., Masmoudi, A., Kartal, V. & Satti, S. Assessing the generalization of forecasting ability of machine learning and probabilistic models for complex climate characteristics. Stoch. Environ. Res. Risk Assess., 1–21 (2024).
- 38.Ye N, Zhang Y, Borror CM. Robustness of the Markov-chain model for cyber-attack detection. IEEE Trans. Reliab. 2004;53(1):116–123. doi: 10.1109/TR.2004.823851. [DOI] [Google Scholar]
- 39.Rahmat SN, Jayasuriya N, Bhuiyan MA. Short-term droughts forecast using Markov chain model in Victoria, Australia. Theor. Appl. Climatol. 2017;129(1):445–457. doi: 10.1007/s00704-016-1785-y. [DOI] [Google Scholar]
- 40.Khalili D, Farnoud T, Jamshidi H, Kamgar-Haghighi AA, Zand-Parsa S. Comparability analyses of the SPI and RDI meteorological drought indices in different climatic zones. Water Resour. Manag. 2011;25(6):1737–1757. doi: 10.1007/s11269-010-9772-z. [DOI] [Google Scholar]
- 41.Rezaeianzadeh M, Stein A, Cox JP. Drought forecasting using Markov chain model and artificial neural networks. Water Resour. Manag. 2016;30(7):2245–2259. doi: 10.1007/s11269-016-1283-0. [DOI] [Google Scholar]
- 42.Paulo AA, Ferreira E, Coelho C, Pereira LS. Drought class transition analysis through Markov and Loglinear models, an approach to early warning. Agricult. Water Manag. 2005;77(1–3):59–81. doi: 10.1016/j.agwat.2004.09.039. [DOI] [Google Scholar]
- 43.Blain GC. The Mann-Kendall test: The need to consider the interaction between serial correlation and trend. Acta Sci. Agron. 2013;35:393–402. doi: 10.4025/actasciagron.v35i4.16006. [DOI] [Google Scholar]
- 44.Da Silva RM, Santos CA, Moreira M, Corte-Real J, Silva VC, Medeiros IC. Rainfall and river flow trends using Mann-Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards. 2015;77(2):1205–1221. doi: 10.1007/s11069-015-1644-7. [DOI] [Google Scholar]
- 45.Karmeshu, N. Trend detection in annual temperature & precipitation using the Mann Kendall test–a case study to assess climate change on select states in the northeastern United States (2012).
- 46.Praveen B, Talukdar S, Mahato S, Mondal J, Sharma P, Islam ARM, Rahman A. Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches. Sci. Rep. 2020;10(1):1–21. doi: 10.1038/s41598-020-67228-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nourani V, Danandeh Mehr A, Azad N. Trend analysis of hydroclimatological variables in Urmia lake basin using hybrid wavelet Mann–Kendall and Şen tests. Environ. Earth Sci. 2018;77:1–18. doi: 10.1007/s12665-018-7390-x. [DOI] [Google Scholar]
- 48.Neeti N, Eastman JR. A contextual mann-kendall approach for the assessment of trend significance in image time series. Trans. GIS. 2011;15(5):599–611. doi: 10.1111/j.1467-9671.2011.01280.x. [DOI] [Google Scholar]
- 49.Satish Kumar K, Venkata Rathnam E. Analysis and prediction of groundwater level trends using four variations of Mann Kendall tests and ARIMA modelling. J. Geol. Soc. India. 2019;94:281–289. doi: 10.1007/s12594-019-1308-4. [DOI] [Google Scholar]
- 50.Gibrilla A, Anornu G, Adomako D. Trend analysis and ARIMA modelling of recent groundwater levels in the White Volta River basin of Ghana. Groundw. Sustain. Dev. 2018;6:150–163. doi: 10.1016/j.gsd.2017.12.006. [DOI] [Google Scholar]
- 51.Harka AE, Jilo NB, Behulu F. Spatial-temporal rainfall trend and variability assessment in the Upper Wabe Shebelle River Basin, Ethiopia: Application of innovative trend analysis method. J. Hydrol. Reg. Stud. 2021;37:100915. doi: 10.1016/j.ejrh.2021.100915. [DOI] [Google Scholar]
- 52.Pavan Kumar ST, Lahiri B, Alvarado R. Multiple change point estimation of trends in Covid-19 infections and deaths in India as compared with WHO regions. Spatial Stat. 2022;49:100538. doi: 10.1016/j.spasta.2021.100538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Romanić D, Ćurić M, Jovičić I, Lompar M. Long-term trends of the ‘Koshava’wind during the period 1949–2010. Int. J. Climatol. 2015;35(2):288–302. doi: 10.1002/joc.3981. [DOI] [Google Scholar]
- 54.Dawood M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Climat. Dyn. 2017;48(3–4):783–797. [Google Scholar]
- 55.Gao F, Wang Y, Chen X, Yang W. Trend analysis of rainfall time series in Shanxi Province, Northern China (1957–2019) Water. 2020;12(9):2335. doi: 10.3390/w12092335. [DOI] [Google Scholar]
- 56.Alashan S. Combination of modified Mann–Kendall method and Şen innovative trend analysis. Eng. Rep. 2020;2(3):e12131. doi: 10.1002/eng2.12131. [DOI] [Google Scholar]
- 57.Sen PK. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968;63(324):1379–1389. doi: 10.1080/01621459.1968.10480934. [DOI] [Google Scholar]
- 58.Wang Z, Li J, Liang L. Ecological risk in the TibetTibetanan Plateau and influencing urbanization factors. Environ. Chall. 2022;6:100445. doi: 10.1016/j.envc.2022.100445. [DOI] [Google Scholar]
- 59.Liu Y, Li Y, Huang J, Zhu Q, Wang S. Attribution of the TibetTibetanan Plateau to northern drought. Natl. Sci. Rev. 2020;7(3):489–492. doi: 10.1093/nsr/nwz191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tang L, Duan X, Kong F, Zhang F, Zheng Y, Li Z, Hu S. Influences of climate change on area variation of Qinghai Lake on Qinghai-TibetTibetanan Plateau since 1980s. Sci. Rep. 2018;8(1):7331. doi: 10.1038/s41598-018-25683-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zha X, Niu B, Li M, Duan C. Increasing impact of precipitation on alpine-grassland productivity over last two decades on the TibetTibetanan Plateau. Remote Sens. 2022;14(14):3430. doi: 10.3390/rs14143430. [DOI] [Google Scholar]
- 62.Zhao S, Cong D, He K, Yang H, Qin Z. Spatial-temporal variation of drought in China from 1982 to 2010 based on a modified temperature vegetation drought index (mTVDI) Sci. Rep. 2017;7(1):1–12. doi: 10.1038/s41598-017-17810-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mokhtar A, Jalali M, He H, Al-Ansari N, Elbeltagi A, Alsafadi K, Rodrigo-Comino J. Estimation of SPEI meteorological drought using machine learning algorithms. IEEE Access. 2021;9:65503–65523. doi: 10.1109/ACCESS.2021.3074305. [DOI] [Google Scholar]
- 64.Duan H, Xue X, Wang T, Kang W, Liao J, Liu S. Spatial and temporal differences in alpine meadow, alpine steppe and all vegetation of the Qinghai-TibetTibetanan Plateau and their responses to climate change. Remote Sens. 2021;13(4):669. doi: 10.3390/rs13040669. [DOI] [Google Scholar]
- 65.Yudan WANG, Yunfeng KONG, Hao CHEN, Yongjian DING. Spatial-temporal characteristics of drought detected from meteorological data with high resolution in Shaanxi Province, China. J. Arid Land. 2020;12(4):561–579. doi: 10.1007/s40333-020-0066-x. [DOI] [Google Scholar]
- 66.Wu X, Zhang R, Bento VA, Leng S, Qi J, Zeng J, Wang Q. The effect of drought on vegetation gross primary productivity under different vegetation types across China from 2001 to 2020. Remote Sens. 2022;14(18):4658. doi: 10.3390/rs14184658. [DOI] [Google Scholar]
- 67.Jitmaneeroj B. Beyond the equal-weight framework of the Social Progress Index: Identifying causal relationships for policy reforms. Int. J. Soc. Econ. 2017;44:2336–2350. doi: 10.1108/IJSE-01-2016-0011. [DOI] [Google Scholar]
- 68.Dey A, Sahoo DP, Kumar R, Remesan R. A multimodel ensemble machine learning approach for CMIP6 climate model projections in an Indian River basin. Int. J. Climatol. 2022;42(16):9215–9236. doi: 10.1002/joc.7813. [DOI] [Google Scholar]
- 69.Smith AW, Forsyth C, Rae IJ, Garton TM, Bloch T, Jackman CM, Bakrania M. Forecasting the probability of large rates of change of the geomagnetic field in the UK: Timescales, horizons, and thresholds. Space Weather. 2021;19(9):e2021SW002788. doi: 10.1029/2021SW002788. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data and code that support the findings of this study are available from the corresponding author upon reasonable request. Declaration of generative AI and AI-assisted technologies in the writing process. During the preparation of this work the authors used ChatGBT in order to improve the readability of the article. This tool was used in the review and editing stages of drafts only. After using this tool, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.