Combining Multiple Biomarkers Linearly to Minimize the Euclidean Distance of the Closest Point on the ROC Surface to the Perfection Corner in Trichotomous Settings

Abstract

The performance of individual biomarkers in discriminating between two groups, typically the healthy and the diseased, may be limited. Thus, there is interest in developing statistical methodologies for biomarker combinations with the aim of improving upon the individual discriminatory performance. There is extensive literature referring to biomarker combinations under the two-class setting. However, the corresponding literature under a three-class setting is limited. In our study, we provide parametric and nonparametric methods that allow investigators to optimally combine biomarkers that seek to discriminate between three classes by minimizing the Euclidean distance from the ROC surface to the perfection corner.

Using this Euclidean distance as the objective function allows for estimation of the optimal combination coefficients along with the optimal cutoff values for the combined score. An advantage of the proposed methods is that they can accommodate biomarker data from all three groups simultaneously, as opposed to a pairwise analysis such as the one implied by the three-class Youden index. We illustrate that the derived true classification rates (TCRs) exhibit narrower confidence intervals than those derived from the Youden-based approach under a parametric, flexible parametric, and nonparametric kernel-based framework. We evaluate our approaches through extensive simulations and apply them to real data sets that refer to liver cancer patients.

Introduction

ROC analysis is a popular method for evaluating the discriminatory ability of continuous biomarkers. Initially, ROC methods were restricted to the two-class setting, where the groups (classes) under consideration typically refer to a healthy group and a diseased group. ROC methods have been extended to include three or more classes.^1,2 In the three-class or $k$—class setting, an ROC surface or hypersurface is used, rather than ROC curves, which are employed in the two-class setting. Accounting for more than two groups is useful in certain scenarios, as some studies are designed to account for the progressive nature of the disease and thus, they might include three (or more) groups for discrimination. In the three class-setting, biomarker studies typically consider a healthy/control group (group 1), the benign group (group 2), and an aggressive stage of the disease (group 3). For example, liver cancer studies often consider three groups: healthy individuals, individuals with cirrhosis of the liver or liver cysts, and individuals with liver cancer.^{3, 4, 5}

In the two-class setting, the random variable that refers to the continuous biomarker scores for the healthy group is denoted with X₁. The random variable that refers to the diseased group is denoted with X₂. The specificity, at a given cutoff c, is defined as spec(c) = P(X₁ < c) and the sensitivity as sens(c) = P(X₂ > c). The ROC curve is a plot of the sensitivity versus 1-specificity across all thresholds. There are a variety of measures used in ROC analysis to determine the diagnostic performance of a biomarker. The most popular is the area under the ROC curve (AUC). It can be shown that it is the average sensitivity across all levels of specificity, or likewise the average specificity across all levels of sensitivity.⁶ Equivalently, the AUC is equal to $P\left(X_1<X_2\right)$ for a continuous biomarker.⁶

The Youden index is another popular measure to gauge the performance of a biomarker, which is commonly denoted, $J$.⁷ Its expression is given by: $J={\mathit{max}}_c\left\{\mathit{sens}\right(c)+\mathit{spec}(c)-1\}$, where $c$ is the cutoff value. This expression corresponds to the maximum of the sum of the sensitivity and specificity. This is graphically represented by the maximum vertical distance of the ROC curve to the main diagonal. Another measure is the closest point on the ROC curve to the perfection corner. We will refer to this measure as the Euclidean distance.⁸ It yields a more balanced set of true classification rates for the two groups than the Youden index.⁹ Depending on the context, this may or may not be desirable. It is defined by: ${D^{\mathrm{*}}=\mathit{min}}_c\sqrt{(1-\mathit{sens}(c){)}^2+(1-\mathit{spec}\left(c\right){)}^2}$.

While the AUC provides insight regarding the overall diagnostic performance of a marker, it is unable to provide information about the performance of a marker at the optimal point on the ROC curve. The Youden index and the Euclidean distance provide information about the diagnostic performance of a marker at an ”optimal” operating point. These measures also estimate the corresponding optimal cutoff values, which are valuable for diagnostic testing. The Youden index has a clear clinical interpretation, while the Euclidean distance does not, but instead enjoys an appealing geometrical interpretation¹⁰. In a recent paper, it was demonstrated that in the 3-class setting, the Euclidean distance can yield narrower confidence intervals for the estimated optimal cutoffs compared to the 3-class Youden index.¹¹ This is due to its ability to accommodate data from all three groups simultaneously as opposed to the 3-class Youden index. Additionally, in some settings, it outperforms the Youden index with regard to the sum of the true classification rates (TCRs) when evaluated under independent testing data.¹¹

It is common that multiple biomarkers are measured for each individual in a study, with each individual biomarker having inadequate diagnostic performance. By collecting multiple measurements, more information is provided on the disease status of the patient than any individual biomarker can provide.

As the individual performance of a biomarker may be limited, there is clinical interest in finding optimal combinations of biomarkers that are simultaneously assayed on the same individuals.^{12, 13} In the two-class setting, several methods have been explored to combine biomarkers using optimization procedures under a variety of objective functions. Methods for combining biomarkers to maximize the AUC have been explored extensively.^{14, 15, 16} Proposed biomarker-combination methods aiming to maximize the AUC include the min-max approach,¹⁴ stepwise approaches based on the empirical ROC curve,^{14, 15} the logistic regression model,¹⁴ and methods using the Fisher’s discriminant coefficient under the assumption of normality.¹⁶ Authors have also explored combining biomarkers to maximize the Youden index (YI) and the partial area under the curve (pAUC).^{17, 18} Biomarker combinations driven by the maximization of the Youden index involve stepwise procedures based on the empirical ROC curve, nonparametric methods based on kernel smoothing, and methods based on the assumption of normality.¹⁷ For combinations that are based on the maximization of the pAUC, authors have considered parametric approaches, as well as non-parametric kernel-based approaches.¹⁸ When assuming normality, if the covariance matrices for the healthy and diseased groups are proportional, there is a combination of biomarkers that leads to a dominant ROC curve across all levels of specificity.¹⁶ This would lead to an optimal ROC curve under any measure/objective function. A similar result exists for the three-class setting, where a closed form solution for a dominant ROC surface exists. This result is discussed in Section 3.1 and proof is available in Web Appendix A. Such an assumption is very strict, and thus more flexible methods are needed. However, by exploring scenarios that meet these assumptions, we have the luxury of knowing the true optimal linear combinations of scores. This allows to see how well our methods perform, not only compared to each other, but also with regard to the theoretically dominant ROC surface, and thus there is value in exploring such scenarios.

In the three-class setting, the literature is more limited. There are three ordered groups, for which, the random variables corresponding to the continuous biomarkers are denoted $X_1,X_2$, and $X_3$. The ROC surface is the collection of the triplets $(x,y,z)=\left(TC{R}_1\left(c_1\right),TC{R}_3\left(c_2\right),TC{R}_2\left(c_1,c_2\right)\right)$ for all $c_1<c_2$, where $TC{R}_1\left(c_1\right)=P\left(X_1\le c_1\right),TC{R}_2\left(c_1,c_2\right)=P\left(c_1<\left.X_2\le c_2\right)\right.$, and $TC{R}_3=P\left(X_3>c_2\right)$. See also Nakas and Yiannoutsos, 2004 and Nakas, Bantis, and Gatsonis, 2023 for more details.^{2, 19}

Authors have explored linear combinations of biomarkers to maximize the volume under the surface (VUS). These methods include the cumulative logistic model, a min-max combination approach, a penalized/scaled stochastic distance based on the assumption of normality, and a stepwise procedure based on the empirical ROC surface.²⁰ Additionally, authors have explored strategies that involve the maximization of pairwise AUCs.²¹ While maximizing the VUS provides the best average performance of a biomarker across all thresholds, the diagnostic performance at an optimal operating point may be inferior to alternative combinations. Additionally, VUS-based combination methods do not provide estimates of an optimal pair of cutoff points. As such, the clinical utility of such strategies might be questionable.

In a recent paper, authors explore the use of the Youden index for combining biomarkers in the 3-class setting.²² For individual biomarkers, the Euclidean distance has been shown to provide substantially shorter confidence intervals around the corresponding cutoffs compared to the 3-class Youden index.¹¹ In settings with low sample size, the cutoff values estimated using the Youden index may suffer from excessively wide confidence intervals and therefore they may not be very informative. The advantage of the Euclidean method to simultaneously accommodate the scores of all groups is strengthened when we are dealing with k–class problems with (k > 3). The reason being that the k–class Youden index operates pairwisely, regardless of the value of k, thus excluding k − 2 groups at a time (k > 3). In such instances, the Euclidean distance may be a better choice for cutoff-estimation.

This paper is organized as follows: In section 2 we refer to an easy to use approach based on the cumulative logistic model that allows combinations of biomarkers under a 3-class setting. This approach has been used in order to combine biomarkers to improve the VUS.²⁰ Due to its computational simplicity, along with its popularity, we briefly discuss it and include it to our comparisons throughout the paper. In section 3 we discuss our proposed methods that involve parametric and non-parametric techniques for finding optimal combinations that are driven by the minimization of the Euclidean distance of the ROC surface to the perfection corner. In section 4 we evaluate our approaches through extensive simulations and we further compare them to strategies that involve the cumulative logistic regression model and the three-class Youden index. In section 5 we present an application that refers to liver cancer patients. We end with a discussion.

Known Approaches for Combining Biomarkers in the Three-Class Setting

Logistic regression is the most common method for linearly combining biomarkers. Due to its popularity and its robust performance, it may be of interest as a method for finding optimal combinations to minimize the Euclidean distance or maximize the three-class Youden index. Its popularity makes it a method of interest to compare with our proposed methods. In contrast with the normality assumption in Section 3.1, the logistic regression approach is a two-step process. First, the combination coefficients are estimated using the logistic model, then based on the combined score, the optimal cutoff values are estimated using the empirical estimates of the ROC surface. The cumulative logistic model is of the form $\mathit{log}\left(\frac{P\left(D=1\mid {\mathit{Y}}_p\right)}{P\left(D=2\mid {\mathit{Y}}_p\right)+P\left(D=3\mid {\mathit{Y}}_p\right)}\right)=a_0+{\mathit{Y}}_p\mathit{\beta },\mathit{log}\left(\frac{P\left(D=1\mid {\mathit{Y}}_p\right)+P\left(D=2\mid {\mathit{Y}}_p\right)}{P\left(D=3\mid {\mathit{Y}}_p\right)}\right)=b_0+{\mathit{Y}}_p\mathit{\beta }$, where $\mathit{\beta }$ is a vector of coefficients of length $p$, and $a_0$ and $b_0$ are intercepts. In order to combine the biomarkers with one set of combination coefficients, we discard the intercepts, so the obtained pseudoscore in practice is simply ${\mathit{Y}}_p\stackrel{\mathit{ˆ}}{\mathit{\beta }}$.

Once the pseudoscore is obtained, the optimal cutoff values can be estimated in order to minimize the shortest distance from the ROC surface to the perfection corner. Note that since the combination coefficients are derived using cumulative logistic regression, they are not optimized with respect to this distance.

Other previously explored approaches aim to maximize the volume under the ROC surface (VUS) under various algorithms.²⁰ Unless very strict assumptions are imposed on the ROC surface, a larger VUS for one marker does not necessarily imply better performance at its ”optimal” operating point than the optimal operating point for another marker. Our approaches combine biomarkers under the notion of minimizing the Euclidean distance from the ROC surface to the perfection corner, which aims directly to a combination that will yield an optimal operating point. As a result: (1) we simultaneously estimate optimal combination coefficients and cutoff values corresponding to the optimal operating point (2) we simultaneously accommodate data from all three groups, as opposed to a strategy that uses the data in a pairwise fashion, e.g., the 3-class Youden index or a strategy that attempts to maximize the sum of pairwise AUCs.

Proposed Approaches for Combining Biomarkers

We propose a variety of approaches, which aim to minimize the shortest Euclidean distance from the ROC surface to the perfection corner. The following equation is the general form of the equation:

$$D^{\text{*}}={\mathit{\text{min}}}_{c_1,c_2;c_1<c_2}{\left\{{\left(1-F_1\left(c_1\right)\right)}^2+{\left(1-\left\{F_2\left(c_2\right)-F_2\left(c_1\right)\right\}\right)}^2+{\left(F_3\left(c_2\right)\right)}^2\right\}}^{1/2}.$$ (1)

Parametric Approach Under Multivariate Normality

Let ${\mathit{Y}}_i,i=\mathrm{1,2},3$ be the random variables referring to the collection of $p$ biomarker scores for the healthy, moderate diseased, and severe diseased individuals, respectively. Assume that ${\mathit{Y}}_i\sim MV{N}_p\left({\mathit{\theta }}_i,{\mathbf{\Sigma }}_i\right)$. Given the combination vector $\mathit{\beta }$, the combined score $X_i={\mathit{\beta }}^T{\mathit{Y}}_i$ follows a univariate normal distribution, that is, $X_i\sim N\left({\mu }_i,{\sigma }_i\right)$, where ${\mu }_i={\mathit{\beta }}^T{\mathit{\theta }}_i$, and ${\sigma }_i^2={\mathit{\beta }}^T{\mathbf{\Sigma }}_i\mathit{\beta }$.

The Euclidean distance for the combined score is therefore

$$D^{\ast }=mi{n}_{\mathit{\beta },c_1,c_2;c_1<c_2}\{{\left\{1-\text{Φ}\left(\frac{c_1-{\mu }_1}{{\sigma }_1}\right)\right\}}^2+(1-\{\text{Φ}\left(\frac{c_2-{\mu }_2}{{\sigma }_2}\right)-{\text{Φ}\left(\frac{c_1-{\mu }_2}{{\sigma }_2}\right)\})}^2+{{\left\{\text{Φ}\left(\frac{c_2-{\mu }_3}{{\sigma }_3}\right)\right\}}^2\}}^{1/2}.$$ (2)

Note that in contrast to equation (1), $D^{\mathrm{*}}$ in equation (2) is a function of $\mathit{\beta }$, along with $c_1$ and $c_2$. Note that estimates for ${\mathit{\theta }}_i$ and ${\mathbf{\Sigma }}_i$ can be obtained using maximum likelihood and plugged into (2). We can then use numerical optimization techniques, such as the Nelder-Mead method, which is implemented in the fminsearch function in Matlab or various packages in R, for estimating the optimal combination, $\mathit{\beta }$, and the optimal cutoffs $c_1$, and $c_2$. In order to standardize the optimal combination, we restrict our search to the interval [$\mathrm{1,1}]$, and allow the marker with the largest value in absolute value to be either 1 or −1. This is because ROC surfaces are unchanged under monotone transformations. As such, the combined score, $X=Y\mathit{\beta }$ is equivalent to the combined score, $X^{\mathrm{*}}=Y{\mathit{\beta }}^{\mathrm{*}}$, where ${\mathit{\beta }}^{\mathrm{*}}=\alpha \mathit{\beta }$ and $\alpha$ is a positive constant. For example, the combination coefficients $\mathit{\beta }=\left[\mathrm{1,0.50,0.02}\right]$ are equivalent to ${\mathit{\beta }}^{\mathrm{*}}=[\mathrm{100,5},2]$. Therefore, restricting our search to the interval $[-\mathrm{1,1}]$ allows us to search over the range of all possible combinations, while standardizing the result, which eliminates any redundant combinations. We implement the following algorithm.

1. Set the coefficient for the first marker to be 1, i.e. ${\beta }_1=1$, and then search for the remaining combination coefficients in the interval $[-\mathrm{1,1}]$ to minimize $D^{\mathrm{*}}$ using equation (3). For this iteration, ${\beta }_1$ is the ”anchor” for the combination.

2. Repeat step 1, but with the coefficient for the first marker set to −1, i.e. ${\beta }_1=-1$.

3. Repeat steps 1 and 2 for each of the remaining biomarkers, first letting ${\beta }_2$ be the anchor, and then going through the remaining markers, and ending with ${\beta }_p$ as the anchor. Choose the combination with the smallest value of $D^{\mathrm{*}}$ from equation (3).

In the two-class setting, combinations for a dominant ROC curve have been derived when normality is assumed and the two groups have proportional covariance matrices.¹⁶ In such a configuration, the ROC curve will have higher sensitivity across all levels of specificity compared to any other linear combination. It is also the case in the three-class setting, that if ${\mathit{\mu }}_2-{\mathit{\mu }}_1={\mathit{\mu }}_3-{\mathit{\mu }}_2=\mathit{\delta }$ and ${\mathbf{\Sigma }}_1={\mathbf{\Sigma }}_2={\mathbf{\Sigma }}_3=\mathbf{\Sigma }$, then the best set of linear combination coefficients is $\mathit{\beta }\propto {\mathit{\delta }}^T{\mathbf{\Sigma }}^{-1}$, which results in an ROC surface dominating all others. Proof of this result is found in Web Appendix A and a visualization of a linear combination of markers corresponding to a dominant ROC surface is displayed in Figure 1. By using such configurations, we can evaluate the performance of each of the approaches in comparison with the true optimal values.

Figure 1.

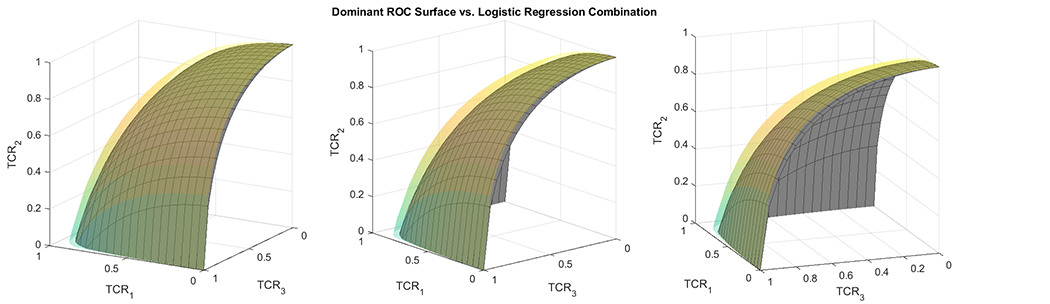
A plot comparing the ROC surface using the true optimal combination (transparent yellow/green) versus an ROC surface using a combination estimated from logistic regression (grey). The yellow/green ROC surface dominates the grey surface. The surfaces were constructed using the true CDFs of the combined scores.

Box-Cox Approach

It is often the case that the biomarkers for each disease state (group) do not comply with the normality assumption. It may be the case that the biomarkers can be transformed to normality using the Box-Cox transformation, which is a monotone transformation. Such an approach may allow us to achieve approximate normality for the transformed data and thus may be convenient, both computationally and in terms of more efficient estimation over a non-parametric approach. The Box-Cox transformation is defined by

$$Y^{(\lambda )}=\{\begin{array}{ll}\frac{Y^{\lambda }-1}{\lambda }\hfill & \lambda \ne 0\hfill \\ \text{log}(Y)\hfill & \lambda =0\hfill \end{array}.$$ (3)

A single transformation parameter, ${\lambda }_m$ is estimated for biomarker $m$, where $m=1,\dots ,p$. This allows us to use a single Box-Cox transformation for each individual biomarker to transform all three groups $\left(Y_{1,\left(m\right)},Y_{2,\left(m\right)},Y_{3,\left(m\right)}\right)$ so that the transformed scores for each of the markers, $Y_{1,\left(m\right)}^{\left(\lambda \right)},Y_{2,\left(m\right)}^{\left(\lambda \right)}$, and $Y_{3,\left(m\right)}^{\left(\lambda \right)}$ are approximately normally distributed. The Box-Cox transformation is demonstrated in Figure 2. The optimal value of ${\lambda }_m$ can be estimated via maximum likelihood.²³ Under an ROC setting, a profile likelihood can be used for the derivation of ${\lambda }_m$. This results in a computationally easier version of the full likelihood to be used solely for estimating ${\lambda }_m$.²⁴ For a single marker $Y_{\left(m\right)}$, this profile likelihood can be written as:

$$\begin{gathered} l\left({\lambda }_m\right)=-\frac{n_1}{2}\text{log}{\left(\frac{{\sum }_{i=1}^{n_1}{\left(Y_{1i,(m)}^{(\lambda )}-\frac{{\sum }_{i=1}^{n_1}{Y}_{1i,(m)}^{(\lambda )}}{n_1}\right)}^2}{n_1}\right)}^2 \\ -\frac{n_2}{2}\text{log}\left(\frac{{\sum }_{j=1}^{n_2}{\left(Y_{2j,(m)}^{(\lambda )}-\frac{{\sum }_{j=1}^{n_2}{Y}_{2j,(m)}^{(\lambda )}}{n_2}\right)}^2}{n_2}\right) \\ -\frac{n_3}{2}\text{log}\left(\frac{{\sum }_{k=1}^{n_3}{\left(Y_{3k,(m)}^{(\lambda )}-\frac{{\sum }_{k=1}^{n_3}{Y}_{3k,(m)}^{(\lambda )}}{n_3}\right)}^2}{n_3}\right) \\ +(\lambda -1)\left(\sum _{i=1}^{n_1}\text{log}{Y}_{1i,(m)}+\sum _{j=1}^{n_2}\text{log}{Y}_{2j,(m)}+\sum _{k=1}^{n_3}\text{log}{Y}_{3k,(m)}\right)+k. \end{gathered}$$ (4)

Figure 2.

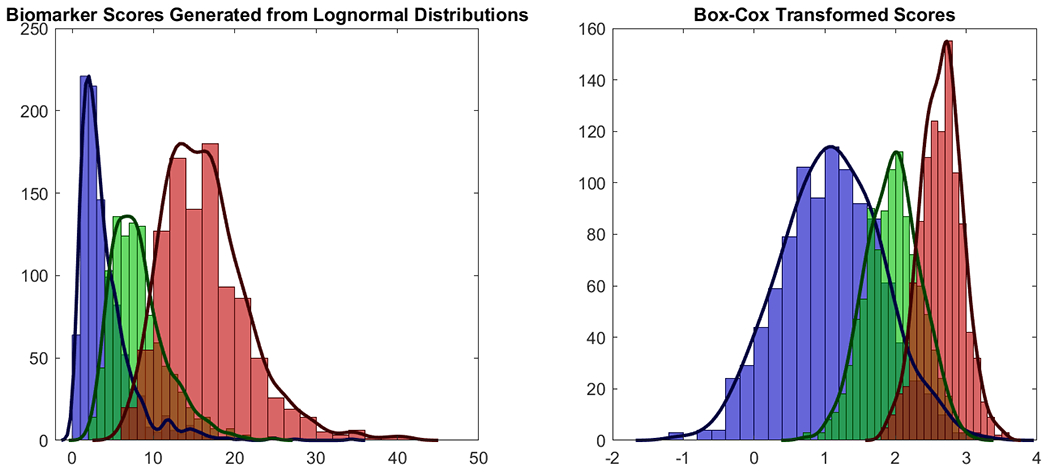
The plot demonstrates the use of the Box-Cox transformation in the context of ROC analysis. A single biomarker with 3 groups uses a single value of λ to transform all 3 groups to normality. When using this approach to combine p biomarkers, we obtain p separate λ’s to transform each biomarker to normality.

After the scores are transformed, equation (2) can be used as the objective function to combine the scores. This approach implements the same algorithm as the normality assumption, but it does so for the transformed scores.

It is often the case that biomarkers are not normally distributed and cannot be adequately transformed to approximate normality. In such cases, the performance of methods that rely on normality may not be appropriate. As a result, other methods are required for developing linear combinations. Various nonparametric approaches have been explored for combining biomarkers to optimize different objective functions, such as AUC, pAUC, Youden index, and VUS. We will explore using adapted versions of some of these methods to combine biomarkers under the notion of minimizing the Euclidean distance.

Stepwise Procedure Based on Empirical ROC Surface

This method is a stepwise down procedure for combining biomarkers that has been used to maximize the Youden index in the two-class setting.¹⁷ It starts with the combining the best two performing individual biomarkers pairwisely and works its way down to the worst performing biomarkers. The algorithm implements the following steps:

1. Calculate the empirical estimate of Euclidean distance for each of the $p$ biomarkers.

2. Order these $p$ biomarkers based on the values of the empirical Euclidean distance estimates from smallest to largest. Denote the corresponding values for the healthy group as ${\left({\mathit{Y}}_{1i}=\right.\left(Y_{1i,\left(p\right)},Y_{1i,(p-1)},\dots ,Y_{1i,\left(1\right)}\right)}^T$ for $i=\mathrm{1,2},\dots ,n_1$, the values for the moderate disease progression group as ${\mathit{Y}}_{2j}={\left(Y_{2j,\left(p\right)},Y_{2j,(p-1)},\dots ,Y_{2j,\left(1\right)}\right)}^T$ for $j=\mathrm{1,2},\dots ,n_2,$, and the values for the advanced disease progression group as $\left({\mathit{Y}}_{3k}=\right.{\left(Y_{3k,\left(p\right)},Y_{3k,(p-1)},\dots ,Y_{3k,\left(1\right)}\right)}^T$ for $k=\mathrm{1,2},\dots ,n_3$.

3. Combine the first two biomarkers empirically using the objective function

   $${\hat{D}}_{w_{p-1}}^{\text{*}}=\{{\left(1-\frac{{\sum }_{i=1}^{n_1}I\left(Y_{1i,(p)}+w_{p-1}{Y}_{1i,(p-1)}\le {\hat{c}}_{1,w_{p-1}}\right)}{n_1}\right)}^2+(1-(\frac{{\sum }_{j=1}^{n_2}I\left(Y_{2j,(p)}+w_{p-1}{Y}_{2j,(p-1)}\le {\hat{c}}_{2,w_{p-1}}\right)}{n_2}-{\frac{{\sum }_{j=1}^{n_2}I\left(Y_{2j,(p)}+w_{p-1}{Y}_{2j,(p-1)}\le {\hat{c}}_{1,w_{p-1}}\right)}{n_2}))}^2+{{\left(\frac{{\sum }_{k=1}^{n_3}I\left(Y_{3k,(p)}+w_{p-1}{Y}_{3k,(p-1)}\le {\hat{c}}_{2,w_{p-1}}\right)}{n_3}\right)}^2\}}^{1/2}.$$ (5)

   which is evaluated on 201 equally spaced values of $w_{p-1}$ in $[-\mathrm{1,1}]$ as follows. For each given value of $w_{p-1}$, first the optimal cutoff value, ${\hat{c}}_{w_{p-1}}$ is empirically searched by minimizing ${\hat{D}}_{w_{p-1}}^{\mathrm{*}}$; then, the value of ${\hat{D}}_{w_{p-1}}^{\mathrm{*}}$ is calculated at the selected optimal cutoff for each $w_{p-1}$.
4. Similar to step 3, combine the first two biomarkers empirically as

   $${\hat{D}}_{r_{p-1}}^{\text{*}}={\left(1-\frac{{\sum }_{i=1}^{n_1}I\left(r_{p-1}{Y}_{1i,(p)}+Y_{1i,(p-1)}\le {\hat{c}}_{1,r_{p-1}}\right)}{n_1}\right)}^2+(1-(\frac{{\sum }_{j=1}^{n_2}I\left(r_{p-1}{Y}_{2j,(p)}+Y_{2j,(p-1)}\le {\hat{c}}_{2,r_{p-1}}\right)}{n_2}-{\frac{{\sum }_{j=1}^{n_2}I\left(r_{p-1}{Y}_{2j,(p)}+Y_{2j,(p-1)}\le {\hat{c}}_{1,r_{p-1}}\right)}{n_2}))}^2+{\left(\frac{{\sum }_{k=1}^{n_3}I\left(r_{p-1}{Y}_{3k,(p)}+Y_{3k,(p-1)}\le {\hat{c}}_{2,r_{p-1}}\right)}{n_3}\right)}^2.$$ (6)

5. Choose the coefficient, $w_{p-1}$ or $r_{p-1}$, which gives the smallest Euclidean distance value as the optimal combination coefficient for the first two markers.

6. Having derived the univariate combined score of the first two biomarkers in step 5, combine it with the third marker, that is, the $(p-2{)}^{th}$ ordered marker, using the same procedure in steps 3-5. Proceed in the same way until all biomarkers are included in the linear combination.

This approach was shown to perform well in simulations when evaluated under training data in the two-class setting with the Youden index as the objective function.¹⁷ In our simulation section, we evaluate its performance under independent testing data to avoid any issues of overfitting.

Kernel-Based Method

This method is a modification of a method proposed by Yan et. al. to maximize pAUC in the two-class setting.¹⁸ The method has been modified to optimize the Euclidean distance as the objective function.

Given a set of biomarkers for healthy, moderate disease, and advanced disease groups, ${\mathit{Y}}_1,{\mathit{Y}}_2$, and ${\mathit{Y}}_3$, respctively, and given linear coefficients $\mathit{\beta }$, we consider using normal kernels to estimate the cumulative distributions of the combined scores for each of the groups, denoted $X_1,X_2$, and $X_3$. The kernel-based cumulative distribution estimate for group $i$ is given by:

$${\hat{F}}_i(x)=\frac{1}{n_i}\sum _{j=1}^{n_i}\text{Φ}\left(\frac{x-X_{ij}}{h_i}\right),$$ (7)

where $n_i$ is the sample size of group $i,X_{ij}$ is the combined score of the $j_{th}$ individual in group $i$, and $h_i$ is the bandwidth for group $i$. We employ a Gaussian kernel²⁴, and for the bandwidth we use:

$$h_i=0.9\text{min}\left(sd\left(X_i\right),iqr\left(X_i\right)/1.34\right)n_i^{-0.2},$$

where sd and iqr are the standard deviation and interquartile range of group i.²⁵

The kernel-based estimate of the Euclidean distance is therefore,

$${\hat{D}}^{\text{*}}={\mathit{\text{min}}}_{\mathit{\beta },c_1,c_2;c_1<c_2}{\left\{{\left(1-{\hat{F}}_1\left({\hat{c}}_1\right)\right)}^2+{\left(1-\left({\hat{F}}_1\left({\hat{c}}_2\right)-{\hat{F}}_1\left({\hat{c}}_1\right)\right)\right)}^2+{\left({\hat{F}}_3\left({\hat{c}}_2\right)\right)}^2\right\}}^{\frac{1}{2}},$$ (8)

where ${\hat{c}}_1$ and ${\hat{c}}_2$ are the estimated optimal cutoff values. The proposed method implements the following steps

1. Set the coefficient for the first marker to be 1, i.e. ${\beta }_1=1$, and then search for the remaining combination coefficients in the interval $[-\mathrm{1,1}]$ to minimize $D^{\mathrm{*}}$ using equation (8).

2. Repeat step 1, but with the coefficient for the first marker set to −1, i.e. ${\beta }_1=-1$.

3. Repeat steps 1 and 2 for each of the remaining biomarkers. Choose the combination with the smallest value of $D^{\mathrm{*}}$.

Kernel-density estimation can accommodate a wide variety of distributions. In the context of ROC analysis, kernel density estimates of the ROC curve tend to give a more conservative estimate of performance than empirical estimates in terms of AUC.²⁶ As such, their results when evaluated under training data are less prone to over-estimating the performance of biomarkers. Additionally, kernel-based estimates tend to provide smaller MSE for $D^{\mathrm{*}}$ than empirical based estimates, which is demonstrated in Figure 3.

Figure 3.

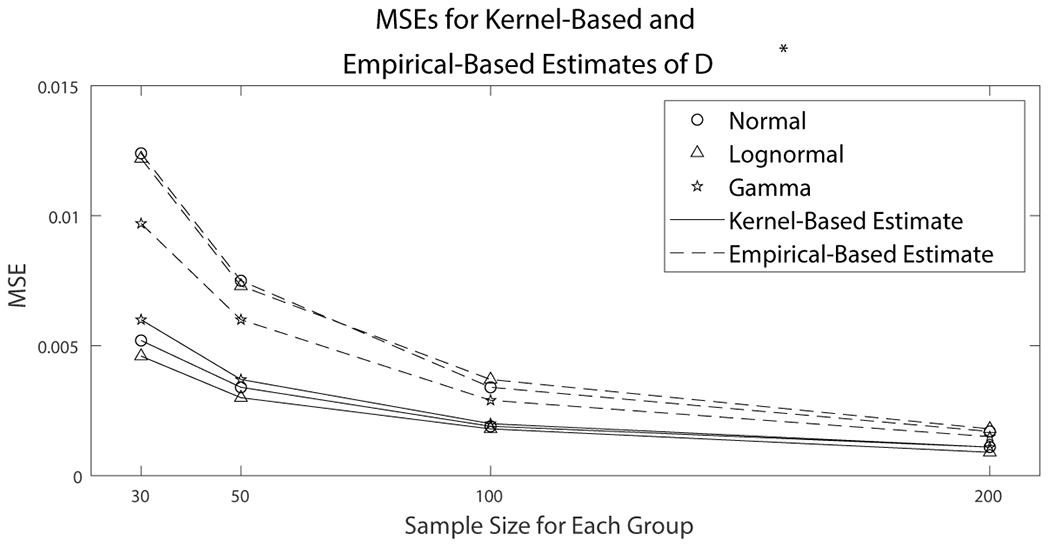
Data were simulated from normal, lognormal, and gamma distributions with sample sizes of (30, 30, 30), (50, 50, 50), (100, 100, 100), and (200, 200, 200). Point estimates of $D^{\mathrm{*}}$ were obtained using a kernel-based estimate and an empirical estimate. Mean squared errors were estimated for both estimators. The kernel-based estimator had smaller MSE than the empirical estimator for all explored distributions and sample sizes.

Simulation Study

In this section we present the results from an extensive simulation study to compare the performance of the combinations of biomarkers based on the Euclidean distance and Youden index as objective functions. We implement five methods of combining biomarkers, including the normality assumption and the Box-Cox transformation where appropriate, the logistic regression model, the stepwise procedure, and the kernel-based method. In all scenarios explored, we consider three biomarkers to combine. We explore scenarios where data are generated from normal, log-normal, and gamma distributions. We generate groups with sample sizes of (30,30,30), (50,50,50), (100,100,100), (200,200,200), and (200,50,50). We consider scenarios with correlations between biomarkers of 0.3, 0.5, and 0.7.

In the simulation study we generate training data and estimate both the combination coefficients, as well as the optimal cutoff values for the combination. Evaluating the performance of the combination based on training data leads to overly optimistic results that are unlikely to accurately reflect how the combinations would perform in the population. For validation, we generate independent datasets with sample sizes of 100,000 for each of the three groups in order to evaluate the performance of the combination methods. This is analogous to estimating combination coefficients and cutoff values in a given study and then evaluating their performance in the population. It is through the independent testing data that we can see the true performance of the estimated combination coefficients and their associated cutoff values.

In the scenarios where the data are generated from normal distributions, we explore configurations where the combination coefficients for a dominant ROC surface can be derived in closed form. In the two-class setting, combinations for a dominant ROC curve have been derived when normality is assumed and the two groups have proportional covariance matrices.¹⁶ McIntosh and Pepe (2002) also discuss that in the two-class setting, it is not necessary to specify the constituent distributions because rules based on the density ratio are equivalent to rules based on $P(D=1\mid Y)$, which can be approximated with binomial regression tools.²⁷ It is the case in the three-class setting, that if ${\mathit{\mu }}_2-{\mathit{\mu }}_1={\mathit{\mu }}_3-{\mathit{\mu }}_2=\mathit{\delta }$ and ${\mathbf{\Sigma }}_1={\mathbf{\Sigma }}_2={\mathbf{\Sigma }}_3=\mathbf{\Sigma }$, then the best set of linear combination coefficients is $\mathit{\beta }=\mathit{\delta }{\mathbf{\Sigma }}^{-1}$, which results in an ROC surface dominating all others. Proof of this result is found in Web Appendix A. By using such configurations, we can evaluate the performance of each of the approaches in comparison with the true optimal values.

In order to compare the performance of the Euclidean distance and the Youden index as objective functions to be optimized for the combined score, we explore the following measures for all of the explored scenarios:

1. Variance of the TCRs.

2. Percent difference in total classification (sum of TCRs).

3. Total classification for each method/approach.

Because the scale of the combined score is affected by the estimated combination coefficients, directly comparing the variance of the cutoff values is not meaningful, as the scale of the combined scores may vary between approaches. By comparing the variance of the TCRs, we remain in the ROC space, and thus lie on the same scale for both methods.

For the scenarios generated from normal distributions, where a dominant ROC surface is known, we can also explore the bias, variance, and MSE of the estimated combination coefficients, cutoff values, TCRs, and sum(TCRs). These measures will provide us with insight as to how each of the methods perform in estimating the true optimal combination coefficients and cutoff values.

Scenarios with a dominant ROC surface

Comparing performance of the Euclidean distance and Youden index as objective functions

When the data are generated from normal distributions in configurations where a dominant ROC surface exists and is known, both combination methods seek to find the same set of combination coefficients. This allows us to compare the use of the Euclidean method and Youden index as objective functions for combining biomarkers under fair conditions. We focus on results for the scenarios with covariance matrices, $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. Results for $\mathbf{\Sigma }=0.5\mathit{I}+0.3\mathit{J}$ and $\mathbf{\Sigma }=0.3\mathit{I}+0.7\mathit{J}$ are discussed briefly in the text and full results are included in the Web Appendix B. In Figure 4, we see that in most explored scenarios, the $\widehat{\mathit{TCR}}s$ have smaller bias, variance, and mean squared error (MSE) under the Euclidean method than the Youden index for each of the approaches. In a few select scenarios, the Youden index exhibits smaller bias than the Euclidean method. When $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,50,50}\right)$, logistic regression exhibits larger bias than the Youden index. The stepwise procedure results in higher bias for the Euclidean method when sample sizes are $\left(n_1,n_2,n_3\right)=\left(\mathrm{100,100,100}\right),\left(\mathrm{200,200,200}\right)$, and $\left(\mathrm{200,50,50}\right)$. While the bias for these scenarios is larger for the Euclidean method, we observe substantially smaller variances, and as a result, smaller MSE. For instance, when using logistic regression and the sample size is $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,50,50}\right)$, the bias, variance, and MSE for the Euclidean method are $\mathrm{0.0174,0.0037}$, and 0.0045, respectively. For the Youden index, they are $\mathrm{0.0145,0.0095}$, and 0.0100. While on average, the Youden index has a smaller bias on for the $\widehat{\mathit{TCR}}s$, the average variance is 2.57 times larger. This results in MSEs for the $\widehat{\mathit{TCR}}s$ derived using the Youden index that are 2.22 times larger on average. Similarly, when using the stepwise procedure and the sample size is $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,50,50}\right)$, the bias, variance, and MSE for the Euclidean method are $\mathrm{0.0412,0.0033}$, and 0.0055. For the Youden index, they are $\mathrm{0.0230,0.0083}$, and 0.0092. Again, while the bias for the Youden index is smaller on average, its variance is 2.52 times larger. This results in an MSE that is 1.67 times larger for the Youden index. In all scenarios where $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$, the Euclidean method exhibits smaller variance and MSE for the $\widehat{\mathit{TCR}}s$ than the Youden index. In the majority of scenarios, the Euclidean method also exhibits smaller bias on average than the Youden index.

Figure 4.

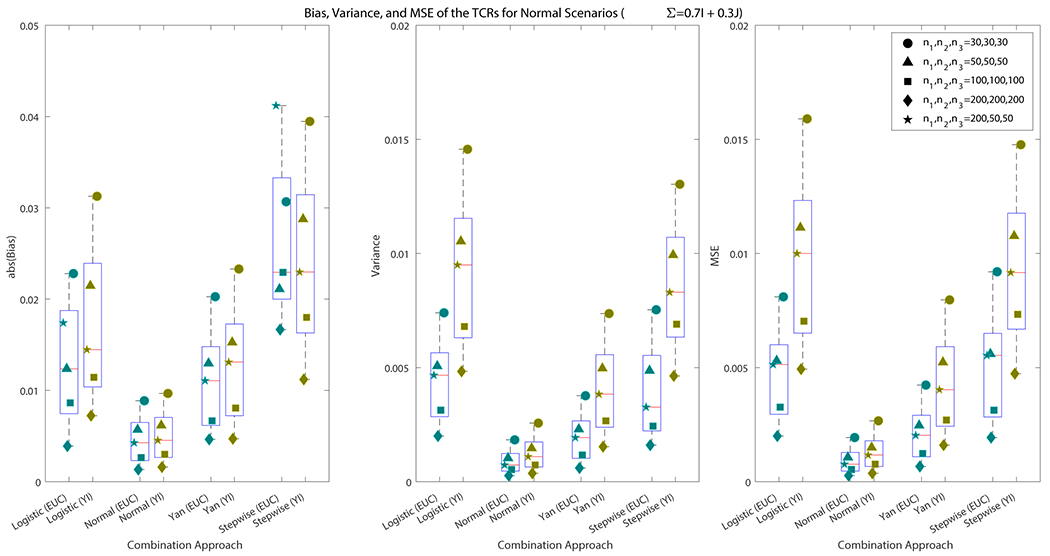
The first panel in the figure displays the average of $\left|\mathit{bias}\left({\widehat{\mathit{TCR}}}_1\right)\right|,\left|\mathit{bias}\left({\widehat{\mathit{TCR}}}_2\right)\right|$, and $\left|\mathit{bias}\left({\widehat{\mathit{TCR}}}_3\right)\right|$ for each of the explored sample sizes. The second panel displays the average of $\mathit{var}\left({\widehat{\mathit{TCR}}}_1\right),\mathit{var}\left({\widehat{\mathit{TCR}}}_2\right)$, and $\mathit{var}\left({\widehat{\mathit{TCR}}}_3\right)$ for each scenario. The third panel displays the average of $\mathit{MSE}\left({\widehat{\mathit{TCR}}}_1\right),\mathit{MSE}\left({\widehat{\mathit{TCR}}}_2\right)$, and $\mathit{MSE}\left({\widehat{\mathit{TCR}}}_3\right)$ for each scenario. We see that for most scenarios, the Euclidean method had smaller bias than the Youden index. For all scenarios, the Euclidean method had smaller variance and MSE.

When $\mathbf{\Sigma }=0.5\mathit{I}+0.5\mathit{J}$, there are several instances where the $\widehat{\mathit{TCR}}s$ derived by the Euclidean method exhibit larger bias on average than those derived by the Youden index when using logistic regression or the stepwise procedure. Full results are available in Table B.5 in Web Appendix B. For logistic regression, this occurs when $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,50,50}\right)$. For the stepwise procedure, this occurs when $\left(n_1,n_2,n_3\right)=\left(\mathrm{100,100,100}\right),\left(\mathrm{200,200,200}\right)$, and $\left(\mathrm{200,50,50}\right)$. For each of these scenarios, the Youden index has higher variance and MSE than the Euclidean method. When the normality assumption or Yan’s method are used, the bias is smaller for the Euclidean method for all sample sizes.

When $\mathbf{\Sigma }=0.3\mathit{I}+0.7\mathit{J}$, the stepwise procedure is the only combination approach with higher average absolute bias for the $\widehat{\mathit{TCR}}s$ when using the Euclidean method out for select sample sizes. Full results are available in Table B.6 in Web Appendix B. The higher bias occurs when $\left(n_1,n_2,n_3\right)=\left(\mathrm{100,100,100}\right),\left(\mathrm{200,200,200}\right)$, and $\left(\mathrm{200,50,50}\right)$. While these scenarios have higher bias for the Euclidean method, the Youden index has higher variance and MSE.

In Figure 5, we see that the difference in sum(TCRs), or total classification, between the two methods is minimal. For the logistic regression approach, the Euclidean method actually provides higher total classification in independent testing data than the Youden index for all scenarios except when the sample size is 200 for each of the groups. When this combination approach is used and the sample size is 30 for each group, the Euclidean method has a total classification that is $0.87\mathrm{\%}$ higher than the Youden index. When the sample size is 200, the Euclidean method has a total classification that is $0.17\mathrm{\%}$ lower than the Youden index. For normally distributed biomarkers, this result, along with the smaller variance of the $\widehat{\mathit{TCR}}s$ provides strong justification for using the Euclidean method when using logistic regression to combine biomarkers.

Figure 5.

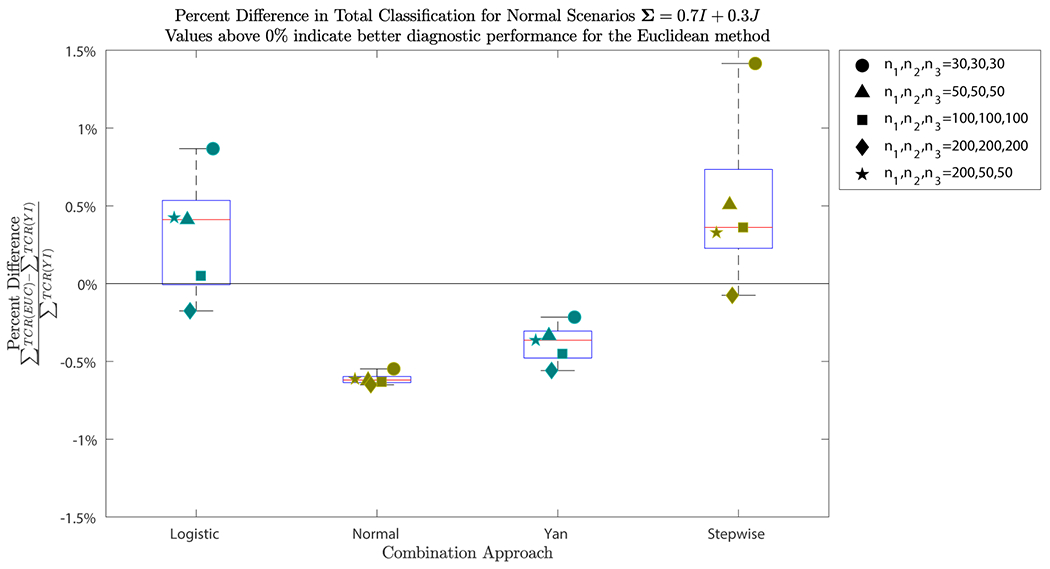
The plot displays the percent difference in ${\sum }_{i}TC{R}_i,i=1,2,3$, i.e. total classification, for the Euclidean method (EUC) versus the Youden index (YI) for each of the combination approaches and sample sizes, where $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. The percent difference is calculated by $\frac{\sum \mathit{TCR}\left(EUC\right)-\sum \mathit{TCR}\left(YI\right)}{\sum \mathit{TCR}\left(YI\right)}$. Values above $0\mathrm{\%}$ correspond to a higher total classification for the Euclidean method than the Youden index, indicating better diagnostic performance for the Euclidean method. Both logistic regression and the stepwise procedure saw higher total classification than the Youden index for all sample sizes except when $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,200,200}\right)$. For the normality assumption and Yan’s method, the Youden index saw higher total classification that was less than $1\mathrm{\%}$ higher than that of the Euclidean method.

For Yan’s method, the Youden index provides higher total classification than the Euclidean method in all cases. The largest difference is seen where sample sizes are 200 for each of the groups. Here the Euclidean method has a total classification that is $0.56\mathrm{\%}$ lower than that of the Youden index. When sample sizes are 30 for each group, this percent difference is only $0.22\mathrm{\%}$. While the gain in total classification when using the Youden index is minimal, its increase in variance for the $\widehat{\mathit{TCR}}s$ is substantial.

For the normality assumption, again, the Euclidean method provides lower total classification than the Youden index in all explored scenarios. This corresponding percent difference ranges from $0.55\mathrm{\%}$ to $0.65\mathrm{\%}$ lower total classification for the Euclidean method than the Youden index.

For the stepwise procedure we see similar results to those when using logistic regression. For all scenarios explored, except when the sample size is 200 for each group, the Euclidean method outperforms the Youden index in terms of total classification. Here, the Euclidean method has total classification that is $0.08\mathrm{\%}$ lower than the Youden index. When the sample size is 30 for each group, the Euclidean method provides total classification that is $1.41\mathrm{\%}$ higher than the Youden index.

We see that for each of the methods, little is lost in terms of total classification when using either of the methods. For the normality assumption and Yan’s method, the Youden index provides higher total classification that is less than $1\mathrm{\%}$ higher than for the Euclidean method. On the other hand, for the logistic regression and stepwise procedure approaches of combining biomarkers, the Euclidean method provides higher total classification than the Youden index for all explored sample sizes, except when the sample size is 200 for each of the groups.

Comparing the performance of the explored combination approaches

In order to compare the performance of the combination approaches, it is valuable to know what the true optimal combination coefficients are, as well as the true optimal cutoff values for the combination. This allows us to compare the bias, variance, and MSE of the combination coefficients and the cutoff values for each of the approaches. Under the normality assumption, the scenarios were configured so that there is a known dominant ROC surface. Population parameters and optimal combination coefficients/cutoff values are displayed in Table 1. Table 2 displays the corresponding bias, variance, and MSE of each of the approaches for the combination coefficients.

Table 1.

The table contains population parameters and optimal combination coefficients for the scenarios generated from normal distributions with a dominant ROC curve.

${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\mathit{\mu }}_3$	$\mathbf{\Sigma }$	$\mathit{\beta }$
$(\mathrm{0,0},0)$	$(\mathrm{0.9,1},1.1)$	$(\mathrm{1.8,2},2.2)$	$0.7\mathit{I}+0.3\mathit{J}$	$\left(\mathrm{0.6279,0.8140,1.0000}\right)$
$(\mathrm{0,0},0)$	$(\mathrm{0.9,1},1.1)$	$(\mathrm{1.8,2},2.2)$	$0.5\mathit{I}+0.5\mathit{J}$	$\left(\mathrm{0.4286,0.7143,1.0000}\right)$
$(\mathrm{0,0},0)$	$(\mathrm{0.9,1},1.1)$	$(\mathrm{1.8,2},2.2)$	$0.3\mathit{I}+0.7\mathit{J}$	$\left(\mathrm{0.1111,0.5556,1.0000}\right)$

Table 2.

The table provides results for the normal scenarios with $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. Included are the bias, variance, and MSE for ${\hat{\beta }}_1,{\hat{\beta }}_2$ and ${\hat{\beta }}_3$ for each of the explored approaches.

Method	Approach	${\mathit{n}}_1,{\mathit{n}}_2,{\mathit{n}}_3$	${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_1$			${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_2$			${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_3$
			Bias	Variance	MSE	Bias	Variance	MSE	Bias	Variance	MSE
Euclidean	Logistic	$\mathrm{30,30,30}$	−0.0506	0.0766	0.0792	−0.0607	0.0596	0.0633	−0.1131	0.0336	0.0464
		$\mathrm{50,50,50}$	−0.0238	0.0567	0.0572	−0.0451	0.0464	0.0484	−0.0741	0.0191	0.0246
		$\mathrm{100,100,100}$	−0.0133	0.0334	0.0336	−0.0111	0.0275	0.0276	−0.0334	0.0060	0.0071
		$\mathrm{200,200,200}$	0.0000	0.0194	0.0194	−0.0003	0.0171	0.0171	−0.0134	0.0017	0.0019
		$\mathrm{200,50,50}$	−0.0082	0.0397	0.0397	−0.0290	0.0317	0.0325	−0.0426	0.0086	0.0104
	Yan	$\mathrm{30,30,30}$	−0.0923	0.1469	0.1554	−0.1414	0.1176	0.1376	−0.1928	0.0815	0.1187
		$\mathrm{50,50,50}$	−0.0485	0.1129	0.1153	−0.0942	0.0862	0.0951	−0.1547	0.0514	0.0753
		$\mathrm{100,100,100}$	−0.0365	0.0710	0.0723	−0.0346	0.0547	0.0559	−0.0837	0.0231	0.0301
		$\mathrm{200,200,200}$	−0.0024	0.0484	0.0484	−0.0073	0.0376	0.0377	−0.0471	0.0109	0.0131
		$\mathrm{200,50,50}$	−0.0384	0.1029	0.1044	−0.0814	0.0828	0.0894	−0.1274	0.0460	0.0622
	Normal	$\mathrm{30,30,30}$	−0.0547	0.0825	0.0855	−0.0759	0.0657	0.0715	−0.1288	0.0391	0.0557
		$\mathrm{50,50,50}$	−0.0297	0.0633	0.0642	−0.0539	0.0514	0.0543	−0.0843	0.0224	0.0295
		$\mathrm{100,100,100}$	−0.0160	0.0364	0.0367	−0.0123	0.0302	0.0303	−0.0374	0.0068	0.0082
		$\mathrm{200,200,200}$	−0.0016	0.0219	0.0219	−0.0020	0.0182	0.0182	−0.0157	0.0022	0.0024
		$\mathrm{200,50,50}$	−0.0168	0.0540	0.0543	−0.0501	0.0437	0.0463	−0.0643	0.0147	0.0189
	Stepwise	$\mathrm{30,30,30}$	−0.1768	0.1607	0.1920	−0.2366	0.1487	0.2047	−0.2681	0.1145	0.1864
		$\mathrm{50,50,50}$	−0.1207	0.1415	0.1561	−0.1767	0.1238	0.1550	−0.2349	0.0834	0.1386
		$\mathrm{100,100,100}$	−0.0937	0.1220	0.1308	−0.1051	0.0845	0.0956	−0.1532	0.0481	0.0716
		$\mathrm{200,200,200}$	−0.0391	0.0915	0.0930	−0.0697	0.0670	0.0718	−0.1170	0.0316	0.0452
		$\mathrm{200,50,50}$	−0.1271	0.1364	0.1525	−0.1542	0.1120	0.1358	−0.2041	0.0754	0.1170
Youden	Logistic	$\mathrm{30,30,30}$	−0.0506	0.0766	0.0792	−0.0607	0.0596	0.0633	−0.1131	0.0336	0.0464
		$\mathrm{50,50,50}$	−0.0238	0.0567	0.0572	−0.0451	0.0464	0.0484	−0.0741	0.0191	0.0246
		$\mathrm{100,100,100}$	−0.0133	0.0334	0.0336	−0.0111	0.0275	0.0276	−0.0334	0.0060	0.0071
		$\mathrm{200,200,200}$	0.0000	0.0194	0.0194	−0.0003	0.0171	0.0171	−0.0134	0.0017	0.0019
		$\mathrm{200,50,50}$	−0.0082	0.0397	0.0397	−0.0290	0.0317	0.0325	−0.0426	0.0086	0.0104
	Yan	$\mathrm{30,30,30}$	−0.0907	0.1334	0.1416	−0.1294	0.1076	0.1244	−0.1897	0.0793	0.1153
		$\mathrm{50,50,50}$	−0.0387	0.1071	0.1086	−0.0851	0.0850	0.0922	−0.1460	0.0468	0.0681
		$\mathrm{100,100,100}$	−0.0376	0.0677	0.0691	−0.0379	0.0541	0.0555	−0.0788	0.0224	0.0286
		$\mathrm{200,200,200}$	0.0070	0.0522	0.0523	−0.0033	0.0363	0.0363	−0.0478	0.0110	0.0133
		$\mathrm{200,50,50}$	−0.0324	0.0976	0.0987	−0.0792	0.0793	0.0856	−0.1168	0.0425	0.0561
	Normal	$\mathrm{30,30,30}$	−0.0482	0.0792	0.0815	−0.0657	0.0618	0.0661	−0.1187	0.0348	0.0489
		$\mathrm{50,50,50}$	−0.0252	0.0583	0.0590	−0.0490	0.0481	0.0505	−0.0767	0.0195	0.0254
		$\mathrm{100,100,100}$	−0.0148	0.0337	0.0340	−0.0110	0.0286	0.0287	−0.0337	0.0058	0.0070
		$\mathrm{200,200,200}$	−0.0005	0.0196	0.0196	0.0003	0.0171	0.0171	−0.0137	0.0018	0.0020
		$\mathrm{200,50,50}$	−0.0104	0.0482	0.0483	−0.0411	0.0390	0.0406	−0.0546	0.0120	0.0150
	Stepwise	$\mathrm{30,30,30}$	−0.2503	0.1613	0.2240	−0.2243	0.1435	0.1938	−0.2661	0.1114	0.1823
		$\mathrm{50,50,50}$	−0.1853	0.1420	0.1763	−0.1876	0.1171	0.1523	−0.2164	0.0836	0.1304
		$\mathrm{100,100,100}$	−0.1498	0.1123	0.1347	−0.1229	0.0780	0.0931	−0.1410	0.0448	0.0647
		$\mathrm{200,200,200}$	−0.0922	0.0845	0.0930	−0.0658	0.0550	0.0594	−0.0949	0.0246	0.0336
		$\mathrm{200,50,50}$	−0.1407	0.1278	0.1476	−0.1487	0.1025	0.1246	−0.1708	0.0610	0.0902

With regard to the combination coefficients, the logistic regression method provides the smallest values of bias, variance, and MSE for all explored scenarios. The normal approach exhibits a bias for the combination coefficients that is similar to logistic regression. However, the former exhibits higher variance and MSE than the latter. We see that each of the approaches provide estimates of the combination coefficients that are biased downwards. As the sample size increases, the estimates approach the true optimal values. Unsurprisingly, the stepwise procedure and kernel-based approach perform worse than the logistic regression and normality-based approaches. We see that the stepwise approach provides the largest values of bias, variance, and MSE.

With regard to the first optimal cutoff value, $c_1$, there are mixed results. Full results are presented in Table 3. For all sample sizes excluding $\left(n_1,n_2,n_3\right)=\left(\mathrm{50,50,50}\right)$, the stepwise procedure has the smallest bias. On the other hand, the normal assumption provides the smallest variance and MSE for all sample sizes. While the logistic approach has the smallest bias, variance, and MSE for each of the combination coefficients, it exhibits the largest variance and MSE for $c_1$. The variance of the estimate from the logistic approach is more than double the variance of the estimate from Yan’s method for several of the sample sizes. For example, when $\left(n_1,n_2,n_3\right)=\left(\mathrm{100,100,100}\right)$, the variance of $c_1$ for Yan’s method is 0.0460, while it is 0.1017 for the logistic approach. With regard to the second optimal cutoff value, $c_2$, the stepwise procedure provides the largest bias for all sample sizes. Additionally, it also has the largest MSE of all of the approaches. The normal assumption has the smallest bias for $c_2$ for all sample sizes except $\left(n_1,n_2,n_3\right)=\left(\mathrm{200,50,50}\right)$, where it has a bias of −0.2202, and the logistic approach has a bias of −0.1816. With regard to variance and MSE, the normal assumption provides the smallest values for $c_2$.

Table 3.

The table provides results for the normal scenarios with $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. Included are the bias, variance, and MSE for the cutoff values, $c_1$ and $c_2$, for each of the explored approaches.

Method	Approach	${\mathit{n}}_1,{\mathit{n}}_2,{\mathit{n}}_3$	${\mathit{c}}_1$			${\mathit{c}}_2$
			Bias	Variance	MSE	Bias	Variance	MSE
Euclidean	Logistic	$\mathrm{30,30,30}$	−0.1126	0.2018	0.2145	−0.4859	0.4447	0.6808
		$\mathrm{50,50,50}$	−0.0635	0.1452	0.1492	−0.2957	0.3222	0.4097
		$\mathrm{100,100,100}$	−0.0189	0.1017	0.1021	−0.1446	0.2212	0.2421
		$\mathrm{200,200,200}$	−0.0099	0.0605	0.0606	−0.0420	0.1537	0.1554
		$\mathrm{200,50,50}$	0.0623	0.1160	0.1199	−0.1816	0.2937	0.3267
	Yan	$\mathrm{30,30,30}$	−0.1907	0.1010	0.1374	−0.7236	0.5345	1.0581
		$\mathrm{50,50,50}$	−0.1439	0.0696	0.0904	−0.4901	0.4182	0.6583
		$\mathrm{100,100,100}$	−0.0826	0.0460	0.0528	−0.2498	0.2852	0.3476
		$\mathrm{200,200,200}$	−0.0454	0.0304	0.0325	−0.0805	0.2173	0.2237
		$\mathrm{200,50,50}$	−0.0896	0.0570	0.0650	−0.3962	0.4245	0.5815
	Normal	$\mathrm{30,30,30}$	−0.1024	0.0572	0.0677	−0.4509	0.3104	0.5137
		$\mathrm{50,50,50}$	−0.0719	0.0388	0.0439	−0.2877	0.2489	0.3317
		$\mathrm{100,100,100}$	−0.0305	0.0217	0.0226	−0.1132	0.1664	0.1793
		$\mathrm{200,200,200}$	−0.0131	0.0126	0.0127	−0.0360	0.1122	0.1135
		$\mathrm{200,50,50}$	−0.0400	0.0244	0.0260	−0.2202	0.2193	0.2678
	Stepwise	$\mathrm{30,30,30}$	−0.0888	0.0771	0.0850	−1.1444	0.4898	1.7995
		$\mathrm{50,50,50}$	−0.1860	0.1141	0.1487	−0.9142	0.4116	1.2474
		$\mathrm{100,100,100}$	−0.0135	0.0625	0.0626	−0.5736	0.3859	0.7149
		$\mathrm{200,200,200}$	0.0080	0.0507	0.0508	−0.3582	0.3197	0.4480
		$\mathrm{200,50,50}$	0.0335	0.0686	0.0697	−0.7967	0.4410	1.0758
Youden	Logistic	$\mathrm{30,30,30}$	−0.3275	0.3552	0.4625	−0.4990	0.5443	0.7933
		$\mathrm{50,50,50}$	−0.1939	0.2692	0.3068	−0.3365	0.3918	0.5050
		$\mathrm{100,100,100}$	−0.1157	0.2015	0.2149	−0.1453	0.2712	0.2924
		$\mathrm{200,200,200}$	−0.0789	0.1285	0.1347	−0.0569	0.2111	0.2144
		$\mathrm{200,50,50}$	−0.0069	0.2303	0.2304	−0.1971	0.4077	0.4465
	Yan	$\mathrm{30,30,30}$	−0.2819	0.2030	0.2825	−0.6182	0.5326	0.9148
		$\mathrm{50,50,50}$	−0.1792	0.1604	0.1925	−0.4075	0.4043	0.5703
		$\mathrm{100,100,100}$	−0.0955	0.0985	0.1076	−0.2411	0.2817	0.3398
		$\mathrm{200,200,200}$	−0.0362	0.0659	0.0672	−0.0708	0.2235	0.2285
		$\mathrm{200,50,50}$	−0.1088	0.1325	0.1444	−0.3358	0.4329	0.5456
	Normal	$\mathrm{30,30,30}$	−0.1589	0.0871	0.1123	−0.3372	0.2840	0.3977
		$\mathrm{50,50,50}$	−0.1138	0.0597	0.0726	−0.2213	0.2140	0.2630
		$\mathrm{100,100,100}$	−0.0476	0.0346	0.0369	−0.0851	0.1394	0.1466
		$\mathrm{200,200,200}$	−0.0179	0.0195	0.0198	−0.0200	0.0939	0.0943
		$\mathrm{200,50,50}$	−0.0707	0.0431	0.0481	−0.1468	0.1892	0.2107
	Stepwise	$\mathrm{30,30,30}$	−0.4349	0.2281	0.4173	−1.1462	0.4646	1.7782
		$\mathrm{50,50,50}$	−0.3295	0.1957	0.3043	−0.8778	0.4531	1.2236
		$\mathrm{100,100,100}$	−0.2084	0.1767	0.2201	−0.6420	0.3861	0.7983
		$\mathrm{200,200,200}$	−0.1550	0.1200	0.1440	−0.3821	0.3118	0.4578
		$\mathrm{200,50,50}$	−0.1716	0.1746	0.2040	−0.7022	0.5060	0.9991

Next, we explore the performance of each of the approaches with regard to the $\widehat{\mathit{TCR}}s$. The bias, variance, and MSE of the $\widehat{\mathit{TCR}}s$ are displayed in Table 4, along with the mean total classification (sum of $\widehat{\mathit{TCR}}s$) for each of the approaches. We see that the normality assumption leads to the smallest bias, variance, and MSE for the $\widehat{\mathit{TCR}}s$. Additionally, the normality assumption has the highest total classification when compared to all other approaches. The difference in total classification is minimal when compared to the logistic approach. For instance, when the sample size is 100 for each group, the normality assumption provides a total classification that is equal to 1.9984, while the logistic approach has total classification of 1.9912. Yan’s method provides smaller MSE than the logistic approach for all explored sample sizes, but has smaller total classification than the logistic approach. This is partially due to smaller variances in the $\widehat{\mathit{TCR}}s$ than those of the logistic approach. The stepwise approach provides smaller MSE than the logistic approach for ${\widehat{\mathit{TCR}}}_1$ and ${\widehat{\mathit{TCR}}}_3$, but has a larger MSE for ${\widehat{\mathit{TCR}}}_2$. This approach performs notably worse than all of the other approaches in terms of total classification. When the sample size is 30 for each group, the stepwise approach has total classification of 1.9281, while it is 1.9454 for Yan’s method, 1.9654 for the logistic approach, and 1.9796 for the normal assumption. As sample sizes increase, the difference in performance between the methods decreases.

Table 4.

The table provides results for the normal scenarios with $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. Included are the bias, variance, and MSE for $TC{R}_1,TC{R}_2$, and $TC{R}_3$ for each of the explored approaches.

Method	Approach	${\mathit{n}}_1,{\mathit{n}}_2,{\mathit{n}}_3$	$\mathit{T}\mathit{C}{\mathit{R}}_1$			$\mathit{T}\mathit{C}{\mathit{R}}_2$			$\mathit{T}\mathit{C}{\mathit{R}}_3$			$\mathit{Sum}\left(\mathit{T}\mathit{C}\mathit{R}\mathit{s}\right)$
			Bias	Variance	MSE	Bias	Variance	MSE	Bias	Variance	MSE	Mean
Euclidean	Logistic	$\mathrm{30,30,30}$	−0.0148	0.0082	0.0085	−0.0398	0.0070	0.0086	0.0138	0.0070	0.0072	1.9654
		$\mathrm{50,50,50}$	−0.0083	0.0054	0.0055	−0.0239	0.0048	0.0054	0.0049	0.0050	0.0050	1.9788
		$\mathrm{100,100,100}$	−0.0031	0.0035	0.0035	−0.0173	0.0027	0.0030	0.0055	0.0032	0.0033	1.9912
		$\mathrm{200,200,200}$	−0.0029	0.0021	0.0021	−0.0077	0.0017	0.0017	0.0011	0.0022	0.0022	1.9966
		$\mathrm{200,50,50}$	0.0137	0.0039	0.0041	−0.0354	0.0042	0.0054	0.0031	0.0059	0.0059	1.9875
	Yan	$\mathrm{30,30,30}$	−0.0197	0.0039	0.0043	−0.0255	0.0035	0.0044	−0.0107	0.0039	0.0040	1.9454
		$\mathrm{50,50,50}$	−0.0144	0.0025	0.0027	−0.0225	0.0021	0.0023	−0.0105	0.0023	0.0024	1.9672
		$\mathrm{100,100,100}$	−0.0091	0.0013	0.0014	−0.0084	0.0010	0.0010	−0.0061	0.0012	0.0013	1.9862
		$\mathrm{200,200,200}$	−0.0070	0.0007	0.0008	−0.0032	0.0005	0.0005	−0.0060	0.0006	0.0007	1.9941
		$\mathrm{200,50,50}$	−0.0060	0.0016	0.0016	−0.0389	0.0017	0.0019	−0.0118	0.0025	0.0026	1.9730
	Normal	$\mathrm{30,30,30}$	−0.0065	0.0020	0.0020	−0.0176	0.0015	0.0018	−0.0025	0.0020	0.0020	1.9796
		$\mathrm{50,50,50}$	−0.0052	0.0012	0.0012	−0.0093	0.0008	0.0009	−0.0026	0.0011	0.0011	1.9891
		$\mathrm{100,100,100}$	−0.0027	0.0006	0.0006	−0.0040	0.0004	0.0004	−0.0012	0.0006	0.0006	1.9984
		$\mathrm{200,200,200}$	−0.0019	0.0003	0.0003	−0.0017	0.0002	0.0002	−0.0004	0.0003	0.0003	2.0022
		$\mathrm{200,50,50}$	−0.0005	0.0006	0.0006	−0.0089	0.0005	0.0006	−0.0034	0.0011	0.0011	1.9935
	Stepwise	$\mathrm{30,30,30}$	0.0234	0.0024	0.0030	−0.0888	0.0053	0.0132	−0.0127	0.0057	0.0058	1.9281
		$\mathrm{50,50,50}$	−0.0109	0.0051	0.0052	−0.0462	0.0049	0.0070	−0.0062	0.0046	0.0046	1.9430
		$\mathrm{100,100,100}$	0.0176	0.0017	0.0020	−0.0418	0.0027	0.0044	−0.0094	0.0029	0.0030	1.9726
		$\mathrm{200,200,200}$	0.0141	0.0013	0.0015	−0.0266	0.0017	0.0024	−0.0093	0.0018	0.0019	1.9844
		$\mathrm{200,50,50}$	0.0372	0.0016	0.0030	−0.0730	0.0037	0.0090	−0.0134	0.0045	0.0046	1.9570
Youden	Logistic	$\mathrm{30,30,30}$	−0.0569	0.0138	0.0170	−0.0255	0.0197	0.0203	0.0114	0.0102	0.0104	1.9485
		$\mathrm{50,50,50}$	−0.0341	0.0090	0.0102	−0.0225	0.0149	0.0154	0.0078	0.0077	0.0078	1.9707
		$\mathrm{100,100,100}$	−0.0234	0.0060	0.0066	−0.0084	0.0095	0.0096	0.0025	0.0049	0.0049	1.9902
		$\mathrm{200,200,200}$	−0.0173	0.0038	0.0041	−0.0032	0.0068	0.0068	0.0012	0.0039	0.0039	2.0001
		$\mathrm{200,50,50}$	−0.0030	0.0064	0.0064	−0.0389	0.0136	0.0151	0.0015	0.0085	0.0085	1.9791
	Yan	$\mathrm{30,30,30}$	−0.0335	0.0071	0.0082	−0.0168	0.0087	0.0090	−0.0196	0.0063	0.0067	1.9496
		$\mathrm{50,50,50}$	−0.0201	0.0048	0.0052	−0.0114	0.0060	0.0061	−0.0143	0.0041	0.0044	1.9738
		$\mathrm{100,100,100}$	−0.0096	0.0025	0.0025	−0.0091	0.0032	0.0033	−0.0055	0.0023	0.0023	1.9952
		$\mathrm{200,200,200}$	−0.0058	0.0014	0.0015	−0.0042	0.0019	0.0020	−0.0041	0.0013	0.0013	2.0053
		$\mathrm{200,50,50}$	−0.0088	0.0032	0.0033	−0.0164	0.0042	0.0045	−0.0141	0.0041	0.0043	1.9802
	Normal	$\mathrm{30,30,30}$	−0.0150	0.0024	0.0026	−0.0023	0.0030	0.0030	−0.0117	0.0023	0.0024	1.9905
		$\mathrm{50,50,50}$	−0.0113	0.0014	0.0015	0.0003	0.0017	0.0017	−0.0069	0.0013	0.0013	2.0015
		$\mathrm{100,100,100}$	−0.0052	0.0007	0.0007	0.0003	0.0009	0.0009	−0.0035	0.0006	0.0007	2.0111
		$\mathrm{200,200,200}$	−0.0030	0.0003	0.0003	0.0003	0.0005	0.0005	−0.0015	0.0003	0.0003	2.0153
		$\mathrm{200,50,50}$	−0.0062	0.0008	0.0009	−0.0001	0.0012	0.0012	−0.0073	0.0013	0.0014	2.0058
	Stepwise	$\mathrm{30,30,30}$	−0.0445	0.0118	0.0138	−0.0508	0.0172	0.0198	−0.0231	0.0101	0.0107	1.9012
		$\mathrm{50,50,50}$	−0.0288	0.0082	0.0090	−0.0326	0.0135	0.0146	−0.0249	0.0081	0.0087	1.9332
		$\mathrm{100,100,100}$	−0.0150	0.0058	0.0060	−0.0306	0.0100	0.0110	−0.0084	0.0049	0.0050	1.9655
		$\mathrm{200,200,200}$	−0.0138	0.0037	0.0039	−0.0118	0.0067	0.0068	−0.0080	0.0035	0.0035	1.9859
		$\mathrm{200,50,50}$	−0.0042	0.0052	0.0052	−0.0484	0.0117	0.0140	−0.0163	0.0080	0.0083	1.9506

Additionally, we compare the performance of each of these methods with respect to training data. Here, we compare the sum of $\widehat{\mathit{TCR}}s$ under training and testing for each method and approach. Here, we discuss the scenarios with $\mathbf{\Sigma }=0.7\mathit{I}+0.3\mathit{J}$. Full results are available in Tables B.7, B.8, and B.9

The stepwise procedure had the highest sum of $\widehat{\mathit{TCR}}s$ out of all the approaches under training data, being 2.1371 and 2.1609 for the Euclidean and Youden methods, on average across all sample sizes. This approach led to a sum of $\widehat{\mathit{TCR}}s$ under training data that ranged from $4.0\mathrm{\%}$ to $15.3\mathrm{\%}$ (average of $9.2\mathrm{\%}$ across all sample sizes) higher than for testing data for the Euclidean method. For the Youden index, these values ranged from $5.1\mathrm{\%}$ to $17.6\mathrm{\%}$ higher, with an average of $11.0\mathrm{\%}$ across all sample sizes.

Logistic regression had the next highest sum of $\widehat{\mathit{TCR}}s$ on average, being 2.1089 and 2.1279 for the Euclidean method and Youden index. This approach led to a sum of $\widehat{\mathit{TCR}s}$ under training data that ranged from $3.0\mathrm{\%}$ to $10.3\mathrm{\%}$ (average of $5.4\mathrm{\%}$ across all sample sizes) higher than for testing data for the Euclidean method and a range of $3.6\mathrm{\%}$ to $12.4\mathrm{\%}$ (average of $7.6\mathrm{\%}$ across all sample sizes) for the Youden index.

Yan’s method had the second lowest sum of $\widehat{\mathit{TCR}}s$ on average, being 2.0538 and 2.0779 for the Euclidean method and Youden index, respectively. This approach led to a sum of $\widehat{\mathit{TCR}}s$ under training data that ranged from $1.4\mathrm{\%}$ to $7.6\mathrm{\%}$ (average of $4.1\mathrm{\%}$ across all sample sizes) higher than for testing data for the Euclidean method and a range of $1.8\mathrm{\%}$ to $8.7\mathrm{\%}$ (average of $4.9\mathrm{\%}$ across all sample sizes) for the Youden index.

The normality assumption had the lowest sum of $\widehat{\mathit{TCR}}s$ across all approaches, being on average, 2.0217 and 2.0359 for the Euclidean method and Youden index, respectively. This approach led to a sum of $\widehat{\mathit{TCR}}s$ under training data that ranged from $0.4\mathrm{\%}$ to $2.7\mathrm{\%}$ (average of $1.5\mathrm{\%}$ across all sample sizes) higher than for testing data for the Euclidean method and a range of $0.5\mathrm{\%}$ to $2.9\mathrm{\%}$ (average of $1.6\mathrm{\%}$ across all sample sizes).

In short, while it provided the lowest sum of $\widehat{\mathit{TCR}}s$ under training data, it had the performance closest to what was seen under testing data, where it saw the best performance of all approaches. Yan’s method performed the next closest between training and testing data. The logistic model and stepwise procedure significantly overestimate the performance under training data, when compared to their performance under independent testing data. As such, investigators should be wary of the results of these methods when evaluated under training data. Additionally, the Youden index tended to overestimate the performance in training data when compared to testing data. For instance, when Yan’s method was used, the Euclidean method overestimated performance by $4.1\mathrm{\%}$, while the Youden index overestimated it by $4.9\mathrm{\%}$. Similar trends were seen for each of the approaches, implying the Youden index is more prone to overfitting than the Euclidean method.

Scenarios without a known dominant ROC surface

When the data are generated from lognormal or gamma distributions, we do not know the distribution of the linear combination, and thus, we cannot derive the best linear combination of biomarkers. In order to compare the performance of the Euclidean method versus the Youden index, we can explore the variance of the $\widehat{\mathit{TCR}}s$, as well as the total classification of both methods. Results for the lognormal scenarios are available in Tables C.1, C.2, and C.3, as well as Figures 5–10 in Web Appendix C. Results for the gamma scenarios are available in Tables C.4, C.5, and C.6, as well as Figures 11–16 in Web Appendix C.

Data generated from lognormal distributions

When the data are generated from lognormal distributions, the data lies within the power-normal family, and thus, the data can be transformed to normality using the Box-Cox transformation. Full results are available in Tables C.1, C.2, and C.3 in the Web Appendix. In Figure 5 in Web Appendix C, we see that the Box-Cox approach provides the best performance in terms of variability of the $\widehat{\mathit{TCR}}s$. Additionally, it provides the best performance in terms of total classification. With regard to the variance of the $\widehat{\mathit{TCR}}s$, the Euclidean method provides smaller variances than the Youden index. On average, the Euclidean method has variances for the $\widehat{\mathit{TCR}}s$ that are 2.70 times smaller than those from the Youden index. Averaging across the sample sizes, on average, the Euclidean method has a total classification of 1.7908, while the Youden index has a total classification of 1.8148. This result is apparent in Figure 6 in Web Appendix C. This equates to a sum of $\widehat{\mathit{TCR}}s$ that is $1.34\mathrm{\%}$ higher for the Youden index than for the Euclidean method. Little is lost in terms of the total classification when using the Euclidean method, but the variance of the $\widehat{\mathit{TCR}s}$ is much smaller for the Euclidean method.

For Yan’s method of combining biomarkers, the Euclidean method exhibits smaller variances for the $\widehat{\mathit{TCR}}s$ than for the Youden index. On average, the variance of the $\widehat{\mathit{TCR}}s$ are 3.86 times larger for the Youden index than for the Euclidean method. The total classification for the Euclidean method is on average $1.47\mathrm{\%}$ lower than for the Youden index. Again, the Euclidean method has minimal loss in total classification, but the variance of the $\widehat{\mathit{TCR}}s$ is greatly reduced when compared to the Youden index.

When the logistic regression approach for combining biomarkers is used, the Euclidean method provides smaller variances for the $\widehat{\mathit{TCR}}s$ than the Youden index does. On average, the variance of the $\widehat{\mathit{TCR}}s$ is 2.39 times smaller for the Euclidean method than for the Youden index. On average, the sum of $\widehat{\mathit{TCR}}s$ for the Euclidean method is 1.7317, whereas it is 1.7399 for the Youden index. This equates to a gain of $0.47\mathrm{\%}$ in terms of total classification for the Youden index. In fact, when the sample size is 30 for each group, the Euclidean method sees a sum of $\widehat{\mathit{TCR}}s$ equal to 1.7162, whereas the Youden index has a sum of $\widehat{\mathit{TCR}}s$ equal to 1.7153. When the sample size is limited, the Euclidean method is able to outperform the Youden index with regard to total classification.

When the stepwise procedure is used to combine biomarkers, the Euclidean method sees variances of the $\widehat{\mathit{TCR}}s$ that are 2.27 times smaller on average than for the Youden index. In terms of total classification, on average, the Euclidean method estimates the sum of $\widehat{\mathit{TCR}}$ to be 1.7099, whereas the Youden index estimates the sum of $\widehat{\mathit{TCR}}s$ to be 1.7201. This equates to an increase of $0.60\mathrm{\%}$ in terms of total classification for the Youden index.

For each of the explored approaches of combining biomarkers, the Euclidean method has variances of the $\widehat{\mathit{TCR}}s$ that are less than half those from the Youden index. The higher variance of the $\widehat{\mathit{TCR}}s$ when using the Youden index leads to uncertainty regarding the estimation of the optimal combination coefficients and the optimal cutoff values. On average, the Youden index provides a higher sum of $\widehat{\mathit{TCR}}s$ than the Euclidean method, but at best, this equates to an improvement of $1.34\mathrm{\%}$. This increase in total classification is minor, whereas the improvement in variance of the $\widehat{\mathit{TCR}}s$ seen when using the Euclidean method is substantial.

In terms of comparing the performance of the approaches when the data are generated from lognormal distributions, the Box-Cox approach significantly outperforms all of the other approaches. This approach has an average sum of $\widehat{\mathit{TCR}}s$ equal to 1.7908. The next best performing approach is the logistic regression approach, with a total classification of 1.7317. This is followed by Yan’s method and the stepwise procedure, with sums of $\widehat{\mathit{TCR}}s$ equal to 1.7122 and 1.7099, respectively. The Box-Cox approach outperforms the next best performing approach by $3.41\mathrm{\%}$, which is a substantial gain in terms of total classification. Additionally, the Box-Cox approach has the smallest variance for the $\widehat{\mathit{TCR}}s$, being equal to 0.0012. Yan’s method has the next smallest variance for the $\widehat{\mathit{TCR}}s$, being equal to 0.0026. This is followed by the stepwise procedure and the logistic regression approach, with variances of the $\widehat{\mathit{TCR}}s$ equal to 0.0055 and 0.0061, respectively. Interestingly, the logistic regression approach has the highest variance for the $\widehat{\mathit{TCR}}s$.

We also compare the results of the methods in terms of training data. Full results are available in Tables C.4, C.5, and C.6 in the Web Appendix. These results were similar to what we saw for the scenarios generated under the normality assumption. The stepwise procedure had the highest sum of $\widehat{\mathit{TCR}}s$ out of the methods, but had the worst performance in terms of testing data. Next was logistic regression, then Yan’s method, and then the Box-Cox approach. In general, parametric methods overfit much less than nonparametric, and particularly, empirical-based methods.

Data generated from gamma distributions

When the data are generated from gamma distributions, we are operating in the power-normal family. In some instances, the Box-Cox transformation can still suitably approximate normality after transforming the data. The scenarios explored in this simulation study showed poor performance of the Box-Cox approach when the data are generated from gamma distributions. Full results are available in Tables C.7, C.8, and C.9 in the Web Appendix.

When using the Box-Cox approach, we see in Figure 11 in Web Appendix C that the Euclidean method provides smaller variance for the $\widehat{\mathit{TCR}}s$ than for the Youden index. On average, the variance of the $\widehat{\mathit{TCR}}s$ is 0.0010 for the Euclidean method, whereas it is 0.0014 for the Youden index. This corresponds to variances that are $43\mathrm{\%}$ higher for the Youden index. The sum of $\widehat{\mathit{TCR}}s$ for the Euclidean method is 2.0728, whereas it is 2.0795 for the Youden index. This corresponds to a $0.32\mathrm{\%}$ higher total classification for the Youden index, which can be visualized in Figure 12 in Web Appendix C.

Under Yan’s combination method, the $\widehat{\mathit{TCR}}s$ have on average, a variance of 0.0017 and 0.0031 when using the Euclidean distance and Youden index as objective functions, respectively. The Youden index has variances that are 1.9936 times larger than for the Euclidean distance. The sum of $\widehat{\mathit{TCR}}s$ for the Euclidean method is 2.1099, whereas it is 2.1093 for the Youden index. When the sample sizes are $\left(\mathrm{30,\; 30,\; 30}\right)$, and $\left(\mathrm{50,50,50}\right)$, the Euclidean method has a higher sum of $\widehat{\mathit{TCR}}s$ than the Youden index. For all other explored sample sizes, the Youden index has higher total classification.

When using logistic regression to combine the biomarkers, the variance of the $\widehat{\mathit{TCR}}s$ is 0.0037 for the Euclidean method and 0.0078 for the Youden index. On average, the variance of the $\widehat{\mathit{TCR}}s$ when using the Youden index is 2.1171 times larger than when using the Euclidean method. The sum of $\widehat{\mathit{TCR}}s$ for the Euclidean method is 2.1090 and 2.0994 for the Youden index. For all explored sample sizes, the Euclidean method provides higher total classification.

The stepwise procedure saw smaller variances for the Euclidean method. The Youden index has variances that are 2.0675 times larger on average than for the Euclidean method. The sum of $\widehat{\mathit{TCR}}s$ for the Euclidean method is 2.0925, whereas it is 2.0820 for the Youden index. For all explored sample sizes, the Euclidean method provides higher total classification.

The Box-Cox approach fails to perform well compared to the other approaches in terms of sum of $\widehat{\mathit{TCR}}s$. Yan’s method and the logistic regression approach have the best performance in terms of sum of $\widehat{\mathit{TCR}}$. They perform similarly in this regard. For instance, when the sample sizes are $\left(\mathrm{30,30,30}\right)$, and $\left(\mathrm{200,\; 50,\; 50}\right)$, the logistic regression approach has higher total classification. For all other explored sample sizes, Yan’s method has higher total classification. The Box-Cox approach and the stepwise procedure perform similarly in terms of total classification, but underperform compared to the other two approaches.

In terms of variance of the $\widehat{\mathit{TCR}}s$, the Box-Cox approach has the smallest variance, followed by Yan’s approach, then the logistic regression approach, and lastly the stepwise procedure.

In instances where the data cannot be adequately transformed to normality, Yan’s method shows the best performing approach to combine biomarkers. It has a comparable sum of $\widehat{\mathit{TCR}}s$ to the logistic regression approach for small sample sizes, and even has a higher total classification when sample sizes are $\left(\mathrm{50,50,50}\right)$, $\left(\mathrm{100,100,100}\right)$, and $\left(\mathrm{200,200,200}\right)$. Yan’s method provides variances for the $\widehat{\mathit{TCR}}s$ that are 2.50 times smaller than the variances from using logistic regression.

Interestingly, the Euclidean method has higher total classification than the Youden index in several instances. For the logistic regression approach and the stepwise procedure, the Euclidean method has higher total classification than the Youden index for all explored sample sizes. Additionally, this was the case for Yan’s method, when sample sizes are 30 for each group and 50 for each group.

For the gamma scenarios, the Box-Cox method showed the worst performance in terms of results under training data, but performed almost as well as logistic regression in terms of results from testing data. Again, the stepwise procedure overfitted the most, followed by logistic regression. In these scenarios, Yan’s method had the third highest sum of $\widehat{\mathit{TCR}}s$ based on training data, but had the best performance based on testing data. Full results are available in Tables C.10, C.11, and C.12 in the Web Appendix.

Additional simulations

In addition to the above scenarios, we ran a small simulation study to explore scenarios in which the markers in each group were generated from different families of distributions. Full results are available in Table C.13 in the Web Appendix. In these scenarios, group 1 was generated from lognormal distributions, group 2 was generated from gamma distributions, and group 3 was generated from mixture normal distributions. The correlation between groups was set to be $\rho =0.5$ and the sample size was set to $n_1,n_2,n_3=\mathrm{50,50,50}$.

The Box-Cox approach provided the highest sum of $\widehat{\mathit{TCR}}s$, being 2.2010 for the Euclidean method and 2.2514 for the Youden-index method. Logistic regression had the next highest sum of $\widehat{\mathit{TCR}}s$, being 2.1703 and 2.1890 for the Euclidean and Youden index, respectively. The kernel-based approach had the next highest $\widehat{\mathit{TCR}}s$, being 2.1549 and 2.1721, respectively. Last was the stepwise procedure, with $\widehat{\mathit{TCR}}s$ being 2.1465 and 2.1627, respectively.

In terms of variances of the $\widehat{\mathit{TCR}}s$, the Box-Cox approach saw the smallest average variance for the $\widehat{\mathit{TCR}}s$, being 0.0011 for both the Euclidean and Youden index methods. For logistic regression, the average variance of the $\widehat{\mathit{TCR}}s$ were 0.0045 and 0.0068, respectively. For the kernel-based approach, the average variances were 0.0020 and 0.0039, respectively. For the stepwise procedure, the variances were 0.0039 and 0.0055, respectively.

It should be noted that while the Box-Cox approach had the best performance overall for these scenarios, it is still sensitive to distributional assumptions. This was observed in the previous scenarios that were generated from gamma distributions, where it was outperformed by the kernel-based approach, as well as logistic regression. The Box-Cox approach has been used in different ROC settings before and therein the authors discuss its robustness when data are generated from Gamma as well as its limitations for severe violations of normality induced by bimodal distributions.^{28, 29, 30, 31, 32} Therein, it is highlighted that if normality is not justified for the Box-Cox transformed scores then non-parametric kernel-based alternatives should be considered, which is also the strategy that we recommend in our framework.

Summary of simulation results

The simulation section demonstrates the benefits of using the Euclidean distance as the objective function, rather than the Youden index when combining biomarkers. We see substantially smaller variances and MSEs for the $\widehat{\mathit{TCR}}s$ when using the Euclidean method. In addition, the potential benefit from using the Youden index is minimal in terms of sum of the $\widehat{\mathit{TCR}}s$. At best, the Youden index provides a sum of $\widehat{\mathit{TCR}}s$ that is less than $2\mathrm{\%}$ higher than when using the Euclidean method. In many instances, the Euclidean method is able to outperform the Youden index in terms of total classification when evaluated under independent testing data. In particular, when the logistic regression model or the stepwise procedure are used, the Euclidean method frequently outperforms the Youden index in terms of sum of $\widehat{\mathit{TCR}}$. These results provide strong justification for the use of the Euclidean method by providing substantially smaller variance of the $\widehat{\mathit{TCR}}s$, as well as similar sums of $\widehat{\mathit{TCR}}s$.

When the data are generated from normal distributions, the normality assumption has the best performance in terms of bias, variance, and MSE of the $\widehat{\mathit{TCR}}$. In addition, it has the highest total classification out of each of the approaches. For the explored scenarios, the Youden index has a total classification that is at most $0.65\mathrm{\%}$ higher than the Euclidean method. For both the Youden index and the stepwise procedure, the Euclidean method provides a higher sum of $\widehat{\mathit{TCR}}s$ than the Youden index, while having smaller bias, variance, and MSE for the $\widehat{\mathit{TCR}}s$.

When the data are generated form lognormal distributions, the Box-Cox approach outperforms all of the other explored approaches. The Euclidean method has smaller variance for the $\widehat{\mathit{TCR}}s$ than the Youden index. The Youden index provides higher total classification than the Euclidean method for each of the approaches, but this is at most $1.37\mathrm{\%}$ higher when using the preferred Box-Cox approach.

When the data are generated from gamma distributions, Yan’s approach performs comparably to logistic regression with regard to total classification, but has smaller variances for the $\widehat{\mathit{TCR}}s$, making it the preferred method when the data cannot be adequately transformed to normality. When sample sizes are $\left(\mathrm{30,30,30}\right)$ or $\left(\mathrm{50,50,50}\right)$, the Euclidean method has higher total classification than the Youden index when using Yan’s approach. When the sample sizes are $\left(\mathrm{200,50,50}\right)$, the sum of $\widehat{\mathit{TCR}}s$ for the Youden index is $;0.01\mathrm{\%}$ higher than for the Euclidean method. For smaller sample sizes, the Euclidean method can outperform the Youden index in both variance of $\widehat{\mathit{TCR}}s$ and total classification.

At the request of an anonymous reviewer, we explored the use of the normality assumption when the data are generated from lognormal and gamma distributions. For the considered lognormal scenarios, the Box-Cox approach has a sum of $\widehat{\mathit{TCR}}s$ that is $4.9\mathrm{\%}$ higher than for the normality assumption. For different explored gamma scenarios, we also saw unsatisfactory performance. The combined results from the lognormal and gamma scenarios demonstrate that when normality is not met, it is best to use alternative methods. Additionally, the reviewer requested we explore the performance of our methods with regard to the VUS of the resulting combination. For the normal scenarios, on average, the VUS was 0.0013 lower for our proposed method compared to the Youden index. For the lognormal and gamma scenarios, our proposed combination method had a higher VUS than combinations based on the Youden index, being 0.0015 and 0.0011 higher, respectively. That is, we do not observe any meaningful differences with respect to the VUS.

We suggest the following guidance for when each approach is more appropriate. If the markers are each approximately normally distributed, the normality assumption should be used. If the markers are not normally distributed, but can each be successfully transformed using the Box-Cox transformation, the Box-Cox approach should be used. When the data cannot be successfully transformed to normality, Yan’s method, the kernel-based approach should be used, although logistic regression performed nearly as well in our simulations for these scenarios. The stepwise procedure performed the worst on average, and we would not recommend using it.

If logistic regression is used to find a combination of scores, our method provides a higher sum of TCRs than the Youden index on average. As such, we would suggest using our method to derive optimal cutoff values when logistic regression is the combination method used.

While the difference in total classification between the Euclidean method and Youden index is minimal, the methods provide different sets of $\mathit{TCR}s$. In general, the Euclidean method provides a more balanced set of $\mathit{TCR}s$ than the Youden index. Thus, if the clinical setting has preference for this, such a combination would be preferred. If there is preference for higher classification of one group, then the Youden index may provide a better set of $\mathit{TCR}s$ for that clinical setting.

Application to Liver Cancer

A biomarker study was conducted for application to liver cancer at the Shanghai Chang-zheng Hospital in China. This dataset has previously been used to combine biomarkers in the two-class setting where groups were evaluated pairwisely, or where patients with chronic liver disease and hepatoma were combined into one group.³³ In the three-class setting it was used in application of cubic splines for ROC surface estimation.³⁴ Biomarker scores were generated by the surface-enhanced laser desorption/ionization time of flight mass spectrometer. The study includes 236 markers, along with 52 healthy individuals, 39 individuals with chronic liver disease, and 54 individuals with hepatoma. Three biomarkers were selected to be combined: markers 11646.52674, 11675.92167, and 11866.94047. Normality of the scores was evaluated before and after Box-Cox transformation using the Kolmogorov-Smirnov test (KS test). The estimated $D^{\mathrm{*}}$ and KS test p-values after Box-Cox transformation are displayed in Table 5.

Table 5.

The selected biomarkers, along with their $D^{\mathrm{*}}$ values and Kolmogorov-Smirnov test $p$-values after Box-Cox transformation (denoted $p_i$ for group $i,i=\mathrm{1,2},3$.)

Marker	${\mathit{D}}^{\mathbf{*}}$	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$
11646.52674	0.5349	0.5073	0.5439	0.4148
11675.92167	0.5639	0.2870	0.1683	0.2468
11866.94047	0.6092	0.4701	0.5007	0.4202

We explore the use of the Box-Cox approach, logistic regression, Yan’s method, and the stepwise procedure for combining these scores. The point estimates of the optimal combination coefficients are displayed in Table 6. The point estimates of $D^{\mathrm{*}}$, the TCRs, and the sum of the TCRs are displayed in Table 7. Based on the point estimates in Table 7, the combination estimated using the stepwise procedure appears to be the best performing of all of the approaches. We see that it has the smallest value for $D^{\mathrm{*}}$, as well as the highest sum(TCRs). Logistic regression had the next best performance in training, followed by Yan’s method, and finally, the Box-Cox approach. These training-based estimates of performance are not sufficient for evaluating their true performance. In simulation we saw that the stepwise procedure and logistic regression are more prone to overfitting than the other approaches, and thus cross-validation is required to get a better estimate of their performance.

Table 6.

The estimated combination coefficients for each of the approaches for the Euclidean method.

Method	${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_1$	${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_2$	${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_3$
Box-Cox	1.0000	0.2081	0.8492
Logistic	1.0000	0.0435	0.4283
Yan	1.0000	0.0833	0.6134
Stepwise	1.0000	0.2700	0.1700

Table 7.

The table includes the point estimates and the estimates based on testing data for the Euclidean distance, $D^{\mathrm{*}}$, the true classification rates, $TC{R}_i,i=\mathrm{1,2},3$, and the total classification (${\sum }_{i}TC{R}_i,i=\mathrm{1,2},3$) for the Euclidean method and Youden index.

Estimate Type	Method	Approach	${\stackrel{\mathit{ˆ}}{\mathit{D}}}^{\mathbf{*}}$	${\widehat{\mathit{T}\mathit{C}\mathit{R}}}_1$	${\widehat{\mathit{T}\mathit{C}\mathit{R}}}_2$	${\widehat{\mathit{T}\mathit{C}\mathit{R}}}_3$	${\sum }_{\mathit{i}}{\widehat{\mathit{T}\mathit{C}\mathit{R}}}_{\mathit{i}},\mathit{i}=\mathrm{1,2},3$
Point Estimate	Euclidean	Box-Cox	0.5270	0.7849	0.7262	0.6110	2.1221
		Logistic	0.4850	0.7885	0.7692	0.6296	2.1873
		Yan	0.5003	0.7902	0.7747	0.6057	2.1706
		Stepwise	0.4547	0.7692	0.7436	0.7037	2.2165
	Youden	Box-Cox		0.8667	0.7683	0.5148	2.1498
		Logistic		0.7855	0.8718	0.5556	2.2158
		Yan		0.8120	0.8120	0.5598	2.1812
		Stepwise		0.7500	0.7949	0.7037	2.2486
Testing	Euclidean	Box-Cox	0.5755	0.7054	0.6880	0.6165	2.0902
		Logistic	0.6235	0.7692	0.5263	0.6667	2.0176
		Yan	0.6323	0.7542	0.6466	0.5699	1.9708
		Stepwise	0.6360	0.7209	0.5918	0.6492	1.9620
	Youden	Box-Cox		0.8470	0.7377	0.5232	2.1078
		Logistic		0.7455	0.6976	0.5634	2.0064
		Yan		0.7884	0.6968	0.4943	1.9795
		Stepwise		0.7757	0.6826	0.5301	1.9884

For this reason, we also use repeated cross-validation by resampling training/testing datasets 1000 times. We use half of the data for training and half for testing. The results are also displayed in Table 7. We see that when evaluated using cross-validation, the Box-Cox approach has the best performance. Its estimated $D^{\mathrm{*}}$ is 0.5755, and the sum(TCRs) is 2.0902. Logistic regression saw an estimated $D^{\mathrm{*}}$ of 0.6235, and a sum(TCRs) of 2.0176. In both measures, the Box-Cox approach has better performance. Lastly, we estimate the variance of the TCRs for each of the approaches. In Table 8, we see that on average, the Euclidean method provides smaller variances for the $\widehat{\mathit{TCR}}s$ than the Youden index. For the Box-Cox approach, the estimated variance for ${\widehat{\mathit{TCR}}}_1$ is 0.0014 for the Euclidean method and 0.0013 for the Youden index. For $TC{R}_2$ and $TC{R}_3$, the variance of their estimators are 1.47 and 2.68 times larger for the Youden index, respectively. For all other approaches, the Euclidean method saw smaller estimated variances for each of the $\widehat{\mathit{TCR}}$. In several instances, the Youden index has variances that are multiple times larger than the Euclidean method. For the stepwise procedure, the estimated variances of ${\widehat{\mathit{TCR}}}_1,{\widehat{\mathit{TCR}}}_2$, and ${\widehat{\mathit{TCR}}}_3$ when using the Youden index are 1.86, 3.33, and 5.48 times larger than the corresponding estimates based on the Euclidean method.

Table 8.

The bootstrap-based estimates of the variances of the $\widehat{\mathit{TCR}}s$.

Approach	$\mathit{var}\left({\widehat{\mathit{TCR}}}_1\right)$	$\mathit{var}\left({\widehat{\mathit{TCR}}}_2\right)$	$\mathit{var}\left({\widehat{\mathit{TCR}}}_3\right)$
Box-Cox	0.0014	0.0017	0.0022
Logistic	0.0037	0.0050	0.0050
Yan	0.0034	0.0042	0.0042
Stepwise	0.0021	0.0021	0.0027
Box-Cox	0.0013	0.0025	0.0059
Logistic	0.0047	0.0079	0.0094
Yan	0.0053	0.0087	0.0179
Stepwise	0.0039	0.0070	0.0148

In conclusion, when the approaches applied to this dataset are evaluated using cross-validation, the Box-Cox approach provides the smallest value for $D^{\mathrm{*}}$, the highest total classification, and the lowest variance of the estimates of TCRs on average. This approach is preferred to the commonly used logistic regression when markers can be transformed to approximate normality. For this dataset, logistic regression outperforms both Yan’s method and the stepwise procedure. It provides a higher total classification than both approaches. The Euclidean method has comparable performance to the Youden index when evaluated under independent testing data and provides smaller variances for the $\widehat{\mathit{TCR}}$. For the Box-Cox approach, the total classification is 2.0902 for the Euclidean method and 2.1078 for the Youden index. This corresponds to total classification that is $0.84\mathrm{\%}$ higher for the Youden index, while its variance is 1.78 times larger. Logistic regression has higher total classification for the Euclidean method than the Youden index. The corresponding values are 2.0176 and 2.0064 for the Euclidean method and Youden index, respectively.

The Box-Cox approach is the preferred method of combining biomarkers for these data since the biomarkers could be adequately transformed to normality. It exhibits both the highest total classification, as well as the smallest variance for the $\widehat{\mathit{TCR}}s$. The Euclidean method has comparable sums of $\widehat{\mathit{TCR}}s$ to the Youden index, while providing smaller variances for the $\widehat{\mathit{TCR}}s$.

Discussion

The Youden index has been used in the literature as an objective function for combining biomarkers while simultaneously selecting optimal cutoff values. In the three-class setting, this has well known drawbacks. For such settings, when estimating cutoffs for a single biomarker, the Youden index ignores information from one of the groups. The Euclidean method considers information from all three groups (i.e. all available data), as opposed to the pairwise nature of the Youden index. When combining biomarkers, the Youden index indirectly gains information from all three groups through the combination coefficients. We demonstrate that while this is the case, the Euclidean method still provides smaller variance for the $\widehat{\mathit{TCR}}s$. In our extensive simulation studies, we observe many cases where the Youden index exhibits variances for the $\widehat{\mathit{TCR}}s$ that are over twice those of the Euclidean method. In addition, the Euclidean method provides comparable sums of TCRs to the Youden index. When using the logistic regression or the stepwise procedure, the Euclidean method actually provides a higher sum than the Youden index in independent testing data. For Yan’s method and the normality/Box-Cox approaches, the difference in sum of $\mathit{TCR}s$ is less than $1\mathrm{\%}$. This makes the Euclidean distance an attractive alternative to the Youden index as an objective function for combining biomarkers.

When we applied our methods to the liver cancer dataset, we show that the logistic regression underperforms. The Box-Cox approach outperforms the logistic regression model as well as the other approaches in terms of both $\sum \widehat{\mathit{TCR}}s$ and variance of the $\widehat{\mathit{TCR}}s$.

We provide a variety of combination approaches that can accommodate biomarkers from a wide range of distributions. The normality assumption and Box-Cox approach are preferred to logistic regression when the data justify these assumptions. When these assumptions are not met, the more flexible kernel-based approach is appropriate and exhibits better performance compared to the logistic regression.

Combining markers in the three-class setting is a relatively new topic, which is in need of further research. Additional topics may include maximizing different objective functions, including covariates to the models, or constructing nonlinear combinations of markers. There are many possible paths of research for both of these topics. Additionally, to make this work accessible, a Matlab package has been uploaded to https://github.com/BrianMosier/dstar.