Calculation of OTF, NPS, and DQE for Oblique X-Ray Incidence on Turbid Granular Phosphors

Abstract

Digital breast tomosynthesis (DBT) is an imaging modality in which tomographic sections of the breast are generated from a limited range of x-ray tube angles. One drawback of DBT is resolution loss in the oblique projection images. The purpose of this work is to extend Swank’s formulation of the transfer functions of turbid granular phosphors to oblique x-ray incidence, using the diffusion approximation to the Boltzmann equation to model the spread of light in the phosphor. As expected, the modulation transfer function (MTF) and noise power spectra (NPS) are found to decrease with projection angle regardless of frequency. By contrast, the dependence of detective quantum efficiency (DQE) on projection angle is frequency dependent. DQE increases with projection angle at low frequencies, and only decreases with projection angle at high frequencies. Importantly, the x-ray quantum detection efficiency (A_Q) and the Swank information factor (A_S) are also found to be angularly dependent.

1. Introduction

Digital breast tomosynthesis (DBT) is an emerging 3D imaging modality in which x-ray images of the compressed breast are acquired over a limited range of projection angles. Using digital image reconstruction techniques, tomographic sections at all depths of the breast volume can then be generated. Preliminary studies indicate that DBT provides increased sensitivity and specificity for the early detection of breast cancer in women relative to conventional 2D digital mammography [1].

One trade-off of DBT is resolution loss in the projection images as a result of oblique x-ray incidence. Although the degradation in image quality due to oblique x-ray incidence has been studied in columnar cesium iodide phosphors doped with thallium (CsI:Tl) with empirical data [2] and amorphous selenium (a-Se) direct converting detectors using Monte Carlo simulations [3], to our knowledge no one has performed a theoretical analysis of the consequences of oblique x-ray incidence. The purpose of this work is to extend Swank’s analytical formulation [4] of the transfer functions of x-ray fluorescent screens to oblique x-ray incidence. To this end, we have considered a non-structured turbid granular phosphor such as gadolinium oxysulfide doped with terbium (Gd₂O₂S:Tb), which is commonly used in breast imaging and which can reasonably approximate other detector materials.

2. Methods

The optical transfer function (OTF), noise power spectra (NPS), and detective quantum efficiency (DQE) of a turbid granular phosphor irradiated obliquely are now derived from first principles. The spread of visible light in a scintillator can be described by the Boltzmann transport equation. A first-order, steady state solution to the Boltzmann transport equation is a diffusion equation of the form [5]

$$-{\nabla }^2\varphi \left(\mathbf{\text{r}}\right)+{\sigma }^2\varphi \left(\mathbf{\text{r}}\right)=S\left(\mathbf{\text{r}}\right),$$ (1)

where $\varphi \left(\mathbf{\text{r}}\right)$ is the product of the density of the secondary carriers (i.e., the optical photons) with the diffusion constant, σ is the reciprocal of the mean diffusion length of the secondary carriers, and S(r) is the source function. The source function S(r) may be modeled as point-like and positioned on ($z_0\tan \theta$, 0, z₀), where z₀ is the depth of the phosphor of total thickness T and where θ is the projection angle relative to normal x-ray incidence. In terms of Dirac delta functions, S(r) can be written as

$$S\left(\mathbf{\text{r}}\right)=\delta \left(x-z_0\tan \theta \right)\delta \left(y\right)\delta \left(z-z_0\right).$$ (2)

In the Fourier domain, the source function can be written as the integral

$$S(r)=\delta \left(z-z_0\right){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{e}^{2\pi i\left[\left(x-z_0\tan \theta \right)v_x+y{v}_y\right]}d{v}_{x}d{v}_y.$$ (3)

Assuming solutions to Eq. (1) of the form

$$\varphi (x,y,z)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\psi }_{\mathbf{k}}(z)e^{2\pi i\left(x{v}_x+y{v}_y\right)}d{v}_{x}d{v}_y,$$ (4)

one finds

$$-\frac{d^2{\psi }_{\mathbf{\text{k}}}}{d{z}^2}+q^2{\psi }_{\mathbf{\text{k}}}=e^{-i{k}_x{z}_0\tan \theta }\delta \left(z-z_0\right),q^2={\sigma }^2+k_x^2+k_y^2,$$ (5)

where ν is the 2D spatial frequency vector and k = 2πν. To solve this differential equation, one can apply integral transform techniques. Denoting the Laplace transform of ${\psi }_{\mathbf{k}}\left(z\right)$ as ${\Psi }_{\mathbf{k}}\left(p\right)$, the transform of the differential equation is

$$\left(-p^2+q^2\right){\text{Ψ}}_{\mathbf{k}}(p)+C_{1}p+C_2=e^{-i{k}_x{z}_0\tan \theta }{e}^{-p{z}_0},$$ (6)

where C₁ and C₂ are the constants of integration. Solving for ${\text{Ψ}}_{\mathbf{k}}\left(p\right)$ and taking the inverse transform generates the following piece-wise expression for ${\psi }_{\mathbf{k}}\left(z\right)$.

$${\psi }_{\mathbf{\text{k}}}(z)=\{\begin{array}{l}{C}_1\cosh (qz)+\frac{C_2}{q}\sinh (qz),0\le z\le z_0\hfill \\ C_1\cosh (qz)+\frac{C_2}{q}\sinh (qz)-\frac{e^{-i{k}_x{z}_0\tan \theta }}{q}\sinh \left(q\left(z-z_0\right)\right),z_0<z\le T\hfill \end{array}$$ (7)

The constants C₁ and C₂ can now be determined from boundary conditions concerning secondary carrier currents directed toward the planes at z = 0 and z = T. In terms of the inverse relaxation length τ, the secondary carrier currents across any plane of constant z are

$$j_{\text{left}}(z)=\frac{1}{2}\left[\varphi \tau +\frac{d\varphi }{dz}\right],j_{\text{right}}(z)=\frac{1}{2}\left[\varphi \tau -\frac{d\varphi }{dz}\right].$$ (8)

In the right-hand side of the two equations, the first term models the effusion current, while the second term comes from Fick’s law. The first boundary condition is determined by the reflectivity r₀ of the plane at z = 0. Noting that j_right(0) = r₀ j_left(0), one finds

$${\frac{d\varphi }{dz}|}_{z=0}={\tau {\rho }_0\varphi |}_{z=0},{\rho }_0\equiv \frac{1-r_0}{1+r_0}.$$ (9)

The second boundary condition is determined from the reflectivity r₁ of the boundary at z = T, as stipulated by the expression j_left(T) = r₁ j_right(T). Defining ρ₁ similar to ρ₀ and noting that the boundary conditions hold for each Fourier component ψ_k of ϕ, it can be shown that

$$C_1=\left[\frac{\left(q+\tau {\rho }_1\right)e^{q\left(T-z_0\right)}+\left(q-\tau {\rho }_1\right)e^{-q\left(T-z_0\right)}}{\left(q+\tau {\rho }_0\right)\left(q+\tau {\rho }_1\right)e^{qT}-\left(q-\tau {\rho }_0\right)\left(q-\tau {\rho }_1\right)e^{-qT}}\right]e^{-i{k}_x{z}_0\tan \theta },$$ (10)

$$C_2=\tau {\rho }_0{C}_1.$$ (11)

Defining z = T as the plane of the photocathode, the OTF of the scattering process, T_s(ν, z₀), can now be determined for a point source from the expression

$$T_S\left(\mathbf{\nu },z_0\right)={\left[\frac{{\rho }_1}{1+{\rho }_1}\right]\left[{\psi }_{\mathbf{\text{k}}}\tau -\frac{d{\psi }_{\mathbf{\text{k}}}}{dz}\right]|}_{z=T},$$ (12)

giving

$$T_S\left(\mathbf{\nu },z_0\right)=\tau {\rho }_1\left[\frac{\left(q+\tau {\rho }_0\right)e^{\left(q-i{k}_x\tan \theta \right)z_0}+\left(q-\tau {\rho }_0\right)e^{-\left(q+i{k}_x\tan \theta \right)z_0}}{\left(q+\tau {\rho }_0\right)\left(q+\tau {\rho }_1\right)e^{qT}-\left(q-\tau {\rho }_0\right)\left(q-\tau {\rho }_1\right)e^{-qT}}\right]\text{.}$$ (13)

To calculate the OTF of the entire phosphor, one multiplies Eq. (13) by the relative number of x-ray absorptions as a function of the depth z₀

$$N\left(z_0\right)=\frac{\mu e^{-\mu z_0\sec \theta }\sec \theta }{1-e^{-\mu T\sec \theta }},$$ (14)

where μ is the x-ray linear attenuation coefficient of the phosphor, and then integrates from z₀ = 0 to z₀ = T. The OTF is thus

$$T_S(\mathbf{\nu })=\frac{\beta \mu \sec \theta }{1-e^{-\mu T\sec \theta }}\left[\frac{\left(q+\tau {\rho }_0\right)\left(e^{\left({\gamma }_{-}-i{k}_x\tan \theta \right)T}-1\right)}{{\gamma }_{-}-i{k}_x\tan \theta }-\frac{\left(q-\tau {\rho }_0\right)\left(e^{-\left({\gamma }_{+}+i{k}_x\tan \theta \right)T}-1\right)}{{\gamma }_{+}+i{k}_x\tan \theta }\right],$$ (15)

where

$$\beta \equiv \frac{\tau {\rho }_1}{\left(q+\tau {\rho }_0\right)\left(q+\tau {\rho }_1\right)e^{qT}-\left(q-\tau {\rho }_0\right)\left(q-\tau {\rho }_1\right)e^{-qT}},{\gamma }_{\pm }\equiv q\pm \mu \sec \theta .$$ (16)

The normalized modulus of the OTF of Eq. (15) gives the modulation transfer function (MTF). In the absence of other noise sources, the quantum NPS or W_Q(ν) is calculated by integrating the product of N(z₀) with |T_s(ν, z₀)|² from z₀ = 0 to z₀ = T.

$$W_Q(\mathbf{\nu })=\frac{{\beta }^2\mu \sec \theta }{1-e^{-\mu T\sec \theta }}\left[\frac{{\left(q+\tau {\rho }_0\right)}^2\left(e^{\left(q+{\gamma }_{-}\right)T}-1\right)}{q+{\gamma }_{-}}+\frac{2\left(q^2-{\tau }^2{\rho }_0^2\right)\left(1-e^{-\mu T\sec \theta }\right)}{\mu \sec \theta }+\frac{{\left(q-\tau {\rho }_0\right)}^2\left(1-e^{-\left(q+{\gamma }_{+}\right)T}\right)}{q+{\gamma }_{+}}\right]$$ (17)

With Eqs. (15)–(17), one now has all the tools required for determining the DQE of the phosphor. From the work of Nishikawa, DQE can be formulated as the product of four terms [6]

$$DQE(\mathbf{\nu })=A_Q{A}_S{R}_C(\mathbf{\nu })R_N(\mathbf{\nu }),$$ (18)

where A_Q is the x-ray quantum detection efficiency determined from the Lambert-Beer Law as 1 – e^-μTsecθ, A_S is the Swank information factor given by |T_s(0)|²/W_Q(0), R_C(ν) is the Lubberts fraction found by normalizing the quotient |T_s(ν)|²/W_Q(ν) to unity at ν = 0, and R_N(ν) is the ratio of the x-ray quantum noise power W_Q(ν) to the total noise power W_T(ν). Outside of x-ray quantum noise, additional sources of noise which contribute to W_T(ν) include optical-detector noise due to silver granules in the phosphor or thermal noise in the photocathode, secondary quantum noise arising from stochastic variation in the number of secondary carriers produced for each incident x-ray, and screen-structure noise [7]. Assuming a quantum-limited imaging system, we treat R_N(ν) as unity in this work.

3. Results

The preceding results are now illustrated for a phosphor possessing 90% x-ray quantum detection efficiency at normal incidence, a reflective backing, a non-reflective photocathode, and optical scatter at the diffusion limit (τ → ∞). Assuming that the frequency vector is oriented along the x direction (ν_y = 0), Figures 1A–1B show MTF and normalized NPS (NNPS) versus frequency at multiple angles of x-ray incidence for a phosphor with no optical absorption (σ = 0) and a phosphor with high optical absorption (σ = 2T⁻¹). Figures 1A–1B demonstrate that increasing the optical absorption increases both MTF and NNPS, which is consistent with Swank’s prior work at normal incidence. In addition, Figures 1A–1B indicate that increasing the projection angle decreases both MTF and NNPS, with the relative decrease as a function of projection angle being most predominate at high frequencies. The projection angle dependence of the NNPS is slightly less pronounced than the projection angle dependence of the MTF. For example, comparing 30° incidence to normal incidence at 5 line pairs per millimeter (lp/mm) in a scintillator with 100 μm thickness and no optical absorption, the MTF decreases by 20% whereas the NNPS decreases by only 14% (19% and 8.9%, respectively, with high optical absorption).

Fig. 1.

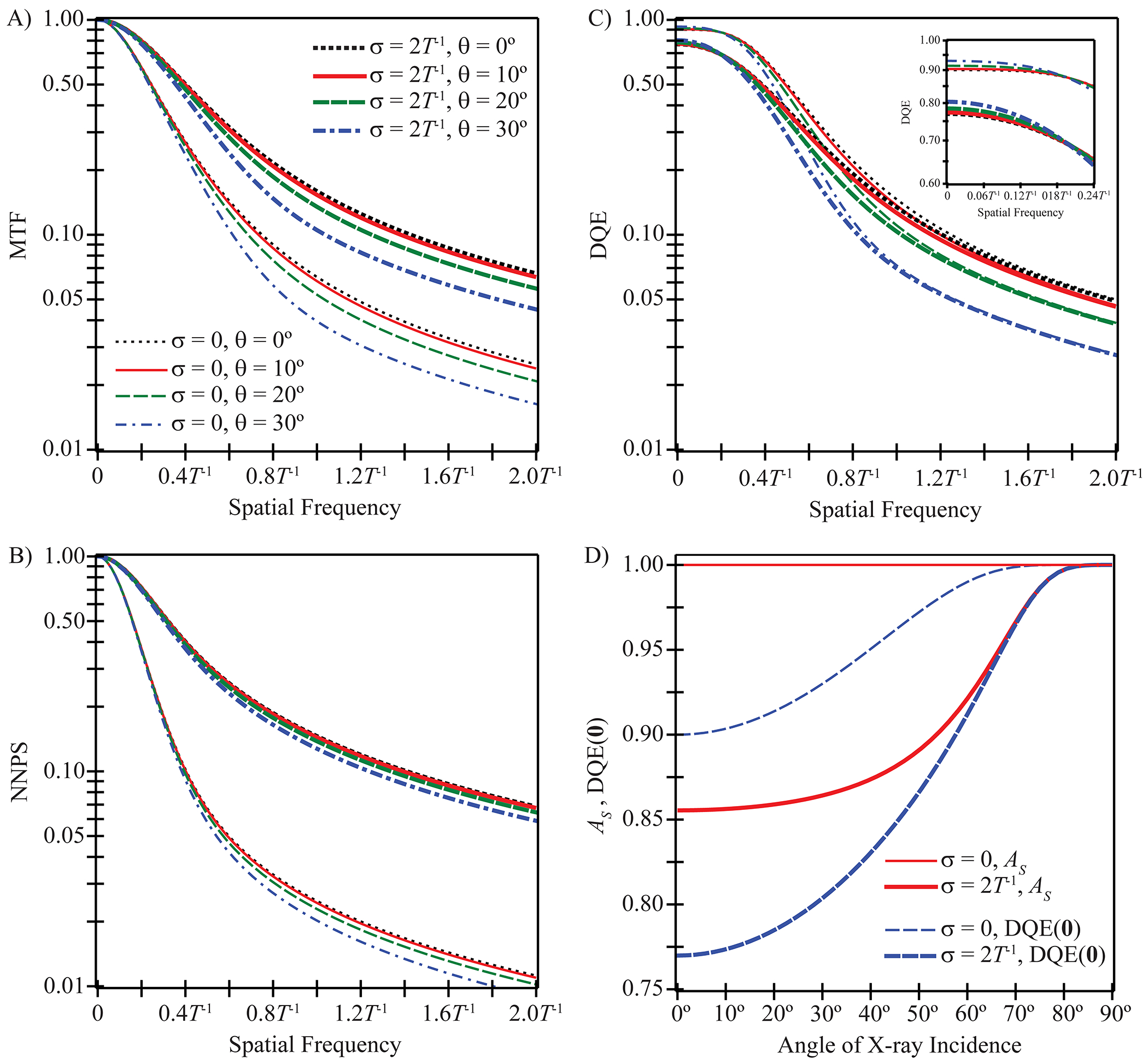
Assuming that the frequency vector is oriented along the x direction, the modulation transfer function (MTF), normalized noise power spectra (NNPS), and detective quantum efficiency (DQE) are plotted versus frequency in units of inverse phosphor thickness (T⁻¹) in subplots (A)-(C) for multiple projection angles (θ = 0°, 10°, 20°, 30°) and two optical absorption parameters (σ = 0, 2T⁻¹). The phosphor possesses 90% x-ray quantum detection efficiency at normal incidence, a reflective backing, a non-reflective photocathode, optical scatter at the diffusion limit, and quantum-limited noise. Subplots (A)-(C) implicitly share a common legend. In (D), the explicit dependence of the Swank information factor (A_S) and DQE(0) on the angle of x-ray incidence is studied for the two optical absorption parameters.

Figure 1C shows DQE versus frequency for the same phosphor. Consistent with Swank’s previous observations, Figure 1C indicates that increasing the optical absorption reduces the DQE at low frequencies but has a smaller effect on the DQE at high frequencies. In addition, Figure 1C demonstrates that unlike MTF and NNPS which decrease with projection angle at all frequencies, DQE actually increases with projection angle at low frequencies and only decreases with projection angle at high frequencies. The DQE degradation with projection angle at high frequencies is slightly more pronounced than either the MTF or NNPS degradation. For example, at 5 lp/mm in a scintillator of 100 μm thickness irradiated at a 30° angle, the DQE decreases by 24% relative to normal incidence for both optical absorption parameters shown in the figure.

In Figure 1D, the Swank information factor (A_S) and DQE(0) are plotted versus the angle of x-ray incidence. Swank has shown that A_S provides a measure of the fluctuation in signal generated from each x-ray due to variability in the absorbed energy of each interacting x-ray and in the number of optical photons generated from each interacting x-ray [8]. Figure 1D demonstrates that in a phosphor with no optical absorption, A_S is unity for all projection angles, but in a phosphor with high optical absorption, A_S increases with projection angle from 0.86 at normal incidence to unity at shearing incidence. In the typical range of projection angles used in DBT, the projection angle dependence of A_S is slight. For example, comparing 30° incidence to normal incidence in a phosphor with high optical absorption, A_S increases by merely 1.0%. Unlike A_S, DQE(0) is projection angle dependent for all possible optical absorption parameters. The projection angle dependence of DQE(0) is more pronounced than the projection angle dependence of A_S. In Figure 1D, DQE(0) increases from 0.90 (no optical absorption) and 0.77 (high optical absorption) at normal incidence to unity at shearing incidence. Comparing 30° incidence to normal incidence, the relative increase in DQE(0) is 3.3% in a phosphor with no optical absorption and 4.4% in a phosphor with high optical absorption.

4. Discussion

This work develops analytical models of OTF, NPS, and DQE for a turbid granular phosphor irradiated obliquely. In agreement with Mainprize et al. who studied CsI:Tl phosphors experimentally [2], we show that at high frequencies, oblique x-ray incidence gives rise to considerable degradation in MTF and hence poorer resolution. We have also observed that NPS is degraded with projection angle for all frequencies, where the NPS degradation is much less pronounced than the MTF degradation. Although Mainprize et al. did not study the dependency of NPS on projection angle, our finding of small changes in NPS with increasing projection angle is qualitatively concordant with the prior work of Hajdok and Cunningham in their Monte Carlo simulations of a-Se detectors [3]. As a final point, we have demonstrated that DQE increases with projection angle at low frequencies but decreases with projection angle at high frequencies. Consistent with the observations of Hajdok and Cunningham, the DQE degradation with projection angle at high frequencies is more pronounced than the MTF degradation, reflecting the dependency of DQE on the square of MTF.

In this work, it has been observed that the Swank information factor (A_S) is angularly dependent, but its dependency is small over the angles used in DBT. This observation is consistent with Monte Carlo simulations of columnar CsI:Tl phosphors conducted by Badano et al., who show that the variation in A_S over projection angles typical of DBT is minimal [9]. While the relative change in A_S with angle is slim, the relative increase in DQE(0) is more substantial, as it includes the influence of increasing x-ray quantum detection efficiency (A_Q) with increasing angle.