Abstract
In order to predict the smoke backlayering length of double-source fire in tunnels, this paper deduced the dimensional expressions for smoke backlayering length by theoretical analysis and proposed a prediction formula for smoke backlayering length in single-source fire on the basis of the Fire Dynamics Simulator. Based on the results, the paper proposed a method for studying the smoke backlayering length of double-source fire in the tunnel. By introducing the fire power influence coefficient α and the distance influence coefficient β, the formula for predicting smoke backlayering length in single-source fire was revised to obtain a new formula for predicting the smoke backlayering length of double-source fire. By comparing the formula prediction value with the simulation value, it is found that the prediction formula is almost accurate. This study will be helpful for understanding the multisource tunnel fire and predicting the smoke backlayering length of double-source fire in tunnels, which can provide guidance for tunnel fire rescue.
1. Introduction
Subways, highway tunnels, and railway tunnels are the main facilities and structures of underground space. Due to its particularity in construction, it often leads to serious accidents in case of a fire.1 In the course of a tunnel fire, due to the narrowness of the tunnel and the lack of entrance and exit, under certain ventilation conditions, the fire smoke may exhibit a reverse flow phenomenon, which may affect personnel escape and emergency rescue in some instances.2 The critical wind velocity and smoke backlayering are not only the main parameters that determine the degree of impact but also the main basis for arranging reasonable evacuation routes and rescue plans. Therefore, they are one of the research hotspots in the field of underground space fires.
For the calculation and prediction of smoke backlayering length in tunnels, the current research generally focuses on the single-source fire condition. By analyzing the Froude number under the critical conditions, the buoyancy and inertial force should be equal. Based on that, a formula for predicting the smoke backlayering length is put forward as follows.3
| 1 |
The static pressure difference between the smoke front and the ambient drives the smoke front; when the static pressure difference is equal to the hydraulic pressure, the upstream backlayering front stops propagating. Then, Hu proposed an equation to predict the smoke backlayering flow length by full-scale burning testing and CFD simulation.4 Gannouni5 found that the backlayering length is also related to the value of the heat release rate and proposed a model for predicting the backlayering length combined with small-scale testing. The backlayering length depends on both the dimensionless heat release rate and the dimensionless ventilation velocity when the dimensionless heat release rate is lower than 0.15, while it only depends on the dimensionless ventilation velocity when the dimensionless heat release rate is larger than 0.15. In order to study the influence of metro trains on the smoke back-layering in the subway tunnel fires, Zhang6 delivered a model including the factor of metro train length to predict the length of smoke back-layering flow in the tunnel based on the smoke temperature distribution and fire dynamics theory. By studying the smoke movement in the metro tunnel with a nonaxisymmetric (semiarched) cross-section, two new prediction models for the dimensionless back-layering length and the critical ventilation velocity in semiarched metro tunnel fires were proposed by FDS simulation.7 When investigating the smoke back-layering length and the critical ventilation velocity in curved subway tunnels with different turning radius and found that the back-layering length increases significantly with the decrease of tunnel curve radius at the same air speed, two prediction models were improved based on the simulation results by considering the turning radius.8 Tian9 used FDS fire simulation to establish a mine tunnel model including the middle section and the ramp and study the development rule of smoke back-layering under different operating conditions (fire source power, wind speed, and slope), the results show that the wind speed in the middle section has a significant effect on the suppression of smoke backlayering. Under a single-source fire condition, a formula for the length of smoke backlayering in the roadway based on simulated parameters such as internal temperature distribution, smoke velocity pressure, and return length was derived by analyzing the thermodynamic change law and employing the factor analysis method that analyzed the vertical attenuation law of the temperature of the ceiling jet flow and the distance from the fire source based on the test data of a full-scale single-source fire in an actual highway tunnel and derived the prediction formula of the smoke backlayering length.10 Employing the numerical simulation method to analyze the relationship between the critical wind velocity and smoke backlayering length, the corresponding prediction models of smoke backlayering length were proposed.5,11
The above research results are helpful for further understanding the phenomenon of smoke backlayering, but the relevant research is based on the single-source fire. When a tunnel fire occurs, a large amount of hot smoke spreads to both sides of the tunnel, causing the fire to spread in a “jumping” pattern, easily affecting combustibles that are far away from the point of ignition, which may lead to multisource fires. For example, the spread of flames after a multivehicle collision in a highway tunnel can easily lead to a fire accident with multiple sources of ignition.12 Due to the interaction and influence of different sources of smoke during the catastrophic event of a multiple-source fire, the phenomenon of smoke backlayering is more complicated. The existing formulas for predicting the smoke backlayer length of a single-source cannot be applied appropriately.
For the backflow of smoke during multiple-source fire, the current research mainly focuses on the combustion and its dynamic parameters between the multiple fire sources. Weng et al.13 studied the relationship between the number of fire sources and the flame height and heat release rate under multiple-source fire and found that with the same heat release rate for each burner, more fire sources lead to a higher flame height. The higher heat release rate also results in a higher flame height with the same fire source configuration. Kamikawa et al.14 used propane and a wood crib to study merged flames for multifire sources and found that increasing the separation distance for wood crib burners and multifire sources enhances combustion efficiency. Delichatsio et al.15 studied two point source fire plumes of equal size and derived the relation between the merging height of the plumes with separation distance and the densities of the flames and the ambient environment. Heidarinejad et al.16 used FDS to study various arrangements of different vehicles upstream of two sources of fire in both lateral and longitudinal directions and found that when there is a short distance between fires and medium obstructions, less air ventilation is needed to prevent smoke back-layering. Huan et al.17 studied the XPS fire propagation rate under double-source fire conditions. It was found that both the fire propagation rate and the mass loss rate rose slowly with the fire source spacing increasing and then slowly decreased, and it was concluded that the change of fire propagation rate with fire source spacing was mainly controlled by the thermal coefficient. Tsai et al.18 studied the mutual coupling of the double-source fires in the tunnel and the changing rules of the critical wind velocity and found that the two fire source flames approach each other within the effective distance, and the changes in the two combustion states will affect each other. Yu et al.19 conducted a FDS numerical analysis of the double-source fire scene in the tunnel and studied the effect of double-source fire on the critical wind velocity. Liu20 used PyroSim to study the combustion behavior and fire environment under fire conditions of double fire sources inside the tunnel. The results show that the temperature distribution between the double fire sources demonstrates a concave distribution pattern, and the double-fire source distance would have a large effect on the temperature distribution. He et al.21 investigated ceiling smoke temperature attenuation in naturally ventilated tunnels with dual fires of different sizes and distances and showed that the interaction between the two flames affects the excess gas temperature attenuation. The above research has deepened our understanding of double- or multiple-source fire combustion characteristics. However, there is still a lack of research on the method for predicting smoke backlayering length in double-source fire.
In summary, many domestic and foreign scholars conducted studies based on single-source fire scenarios in terms of the smoke backlayering length, which cannot be adapted to the specific conditions of multiple-source fire and cannot provide effective guidance for the rescue during the catastrophic event of multiple-source fire. In view of this situation, this paper studied the smoke backflow phenomenon of double-source fire by a numerical simulation method and analyzed the change law of smoke backlayering length with fire source spacing and the power of double-source fire in tunnels. Based on the results, a prediction formula for the smoke backlayering length was deduced. The research results will be helpful for further understanding the phenomenon of smoke backlayering in multiple-source tunnel fire and scientifically determining the range of smoke backflow.
2. Theoretical Analysis
2.1. Smoke Backlayering Length of Single-Source Fire
Previous research works4,22 have shown that the governing parameters influencing backlayering length in a longitudinally ventilated tunnel are the heat release rate, longitudinal ventilation velocity, the characteristic hydraulic diameter of the tunnel, air density, ambient temperature, the thermal capacity of air, and gravitational acceleration. On this basis, the dimensional analysis method was adopted to derive the relationship between the smoke backlayering length, the source power, and the vertical wind velocity in single-source tunnel fire. The main physical quantities that need to be considered in the derivation process are shown in Table 1. Since the tunnel selected in this paper is a horizontal tunnel, the slope effect is not considered here.
Table 1. Physical Quantity Influencing Smoke Backlayering Length.
| serial number | name | symbol | unit | dimension |
|---|---|---|---|---|
| 1 | smoke backlayering length | L | m | L |
| 2 | longitudinal wind velocity | V | m/s | LT–1 |
| 3 | gravitational acceleration | g | m/s2 | LT–2 |
| 4 | ambient temperature | Ta | K | Θ |
| 5 | air density | ρa | kg/m3 | ML–3 |
| 6 | thermal capacity of air | cp | J/(kg·K) | L2T–2Θ–1 |
| 7 | tunnel hydraulic diameter | H̅ | m | L |
| 8 | fire source heat release rate | Q | kW | ML2T–3 |
| 9 | tunnel slope | θ | % | — |
According to the influencing factors of the smoke backlayering length in tunnel fire, the general functional relationship between the physical quantities can be determined, as shown in eq 2.
| 2 |
The length, time, temperature, and mass are selected as the basic quantities, and the corresponding dimensions are L, T, Θ, and M, respectively. Then, eq 2 can be changed into a dimensional relationship equation, as shown in eq 3.
| 3 |
According to the Π- theorem,23 dimensionless treatment of the physical quantities in eq 3 is achieved, and dimensionless relation is obtained as shown in eq 4.
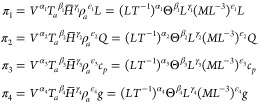 |
where α, β, γ, and ε are the variable coefficients. The above equation is simplified by the similarity theory and calculated to give eq 4.
| 4 |
If simplifying the dimensionless quantities in eq 4, the smoke backlayering length of a single-source fire in a tunnel can be expressed in eq 5.
| 5 |
where,  ,
,  ,
,  .
.
The derived dimensionless relationship eq 5 indicates that the dimensionless smoke backlayering length (L*) has a functional relationship with the ratio of the dimensionless (Q*) of 1/3 power and dimensionless longitudinal wind velocity (V*).
2.2. Smoke Backlayering Length of Double-Source Fire
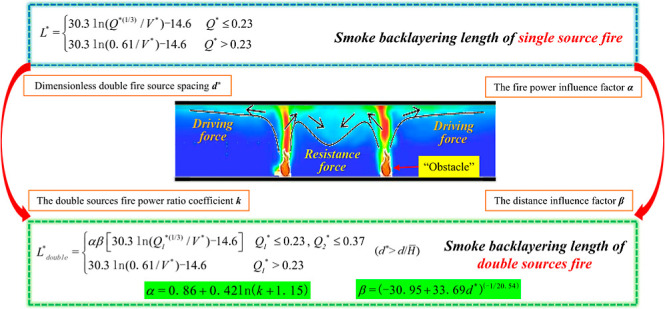
In the presence of multiple sources of fire, the relationship between the length of the smoke backlayering length and the influential parameters is ambiguous, but it will affect the spread of smoke when there are obstacles near the fire sources. Multifire source includes dual-fire source situation; dual-fire source is the most basic multifire source situation, as the object of study has a certain degree of representativeness, to provide support for the subsequent multifire source research. Therefore, this paper proposes a new method to study the smoke backlayering length. The essential idea is to identify a single point fire (a small area fire can be seen as a single-source fire) and then regard the rest of the fire as a dual-attribute “obstacle” which not only blocks the movement of smoke around the fire source but also generates hot wind pressure to drive the smoke movement. In the course of fire development, the hot air pressure formed by the high-temperature gas around the fire source will affect the surrounding other fire source smoke movement and finally lead to the coupling effect of resistance and driving force. The smoke between the two fire sources, influenced by the resistance of the smoke from the opposite source, is turned downward at the smoke junction, as shown in Figure 1. With the continuous accumulation of smoke in the middle of the two fire sources, the temperature gradually increases, forming a thermal driving force for the nearby fire sources and promoting the movement of smoke to the two sides of the fire sources.
Figure 1.

Smoke movement diagram at the smoke junction of double-source fire.
Therefore, for the smoke backflow phenomenon in double-source fire, it is considered to add the correction coefficient based on the forecast formula of smoke backlayering length of single-source fire to obtain the counter formula of double-source fire. The physical quantities involved in the process of formula derivation include the dimensionless double fire source spacing d* (eq 6), the distance influence factor β (eq 7), the double-source fire power ratio coefficient k (eq 8), and the fire power influence factor α (eq 9).
| 6 |
| 7 |
| 8 |
| 9 |
where (L*single)βj is the dimensionless smoke backlayering length under different longitudinal wind velocities when d = 0, which can be considered a single-source fire, and the equivalent fire source power value is the sum of Q1 and Q2. (L*double)βij is the dimensionless smoke backlayering length under different longitudinal wind velocities when d > 0, which is double-source fire. (L*single)αj is the dimensionless smoke backlayering length under different longitudinal wind velocities when k = 0 (i.e., Q2 = 0). (L*double)αij is the dimensionless smoke backlayering length under different longitudinal wind velocities when k > 0 in double-source fire. Both i and j indicate different fire conditions.
On this basis, and according to the dimensionless relationship of the smoke backlayering length of single-source fire derived in Section 2.1, the formula for the smoke backlayering length of double-source fire can be obtained in eq 10.
| 10 |
3. Numerical Simulation
3.1. FDS Model
In this paper, the experiments were conducted using FDS 6.1.0, and the simulated model was designed as a rectangular section tunnel with a length of 368 m, a width of 3.65 m, and a height of 4.8 m. One end of the tunnel which is away from the fire source was set as the wind velocity entrance boundary, and the end near fire source was set as the open boundary, as shown in Figure 2. The grid, which was about 15 m from the fire source, is locally encrypted as 0.35 × 0.35 × 0.35 m, and the other part was 0.4 × 0.4 × 0.4 m. 366 thermocouples were arranged 10 mm below the top of the tunnel. The distance between the two thermocouples was 1 m, as shown in Figure 3. Heptane was used as the fuel, and it was set as the steady-state fire source, and the fire source reached the maximum heat release rate within 10 s and then maintained stable combustion. Fire source 1 was located at a constant distance of 62 m from the right open boundary, fire source 2 was not uncertain, and it was adjusted according to the fire source spacing. The wind flow direction was from fire source 2 to fire source 1, with longitudinal wind speeds ranging from 0.9 to 2.5 m/s and fire power ranging from 2.5 to 30 MW. The initial ambient temperature, atmospheric pressure, and simulation time were set at 20 °C, 101,325 Pa, and 1500 s, respectively.
Figure 2.

Tunnel model in FDS.
Figure 3.
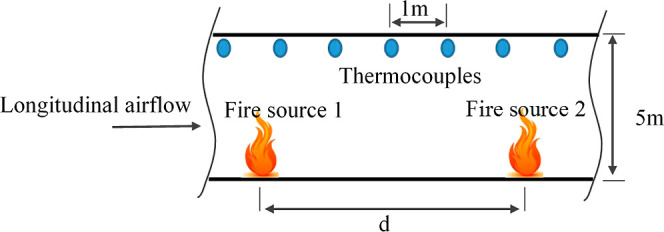
Sketch map of the thermocouple layout.
3.2. Simulation Project
This paper mainly studied the effect of fire source power and the distance between fire sources on the smoke backlayering length in double-source fire scenarios under longitudinal ventilation in a tunnel. A total of 197 simulation experiments were conducted. The first 65 groups were the control groups, in which only one fire source was set up to simulate the smoke backlayering phenomenon in single-source fire under different wind velocities of longitudinal ventilation. The 66th to 137th groups simulated the smoke backlayering phenomenon of double-source fire under different fire source spacing conditions. The 138–197th groups simulated the smoke backlayering phenomenon of double-source fire under different fire source power conditions. The specific settings of the simulation experiment variable are shown in Table 2.
Table 2. FDS Numerical Simulation Schemes.
| groups | fire source 1 (MW) | fire source 2 (MW) | fire source spacing d (m) | longitudinal velocity V (m.s–1) |
|---|---|---|---|---|
| 1–5 | 2.5 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7 |
| 6–12 | 5 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1 |
| 13–20 | 7.5 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3 |
| 21–29 | 10 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5 |
| 30–38 | 12.5 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5 |
| 39–47 | 15 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5 |
| 48–56 | 20 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5 |
| 57–65 | 30 | 0 | \ | 0.9, 1.1, 1.3, 1.5, 1.7, 1.9, 2.1, 2.3, 2.5 |
| 66–83 | 5 | 2.5 | 0, 5, 15, 30, 45, 60 | 0.9, 1.3, 1.7 |
| 84–101 | 5 | 10 | 0, 5, 15, 30, 45, 60 | 0.9, 1.3, 1.7 |
| 102–119 | 10 | 5 | 0, 5, 15, 30, 45, 60 | 0.9, 1.3, 1.7 |
| 120–137 | 10 | 20 | 0, 5, 15, 30, 45, 60 | 0.9, 1.3, 1.7 |
| 138–152 | 5 | 1.25, 2.5, 5, 10, 15 | 5 | 0.9, 1.3, 1.7 |
| 153–167 | 5 | 1.25, 2.5, 5, 10, 15 | 15 | 0.9, 1.3, 1.7 |
| 168–182 | 10 | 2.5, 5, 10, 20, 30 | 5 | 0.9, 1.3, 1.7 |
| 183–197 | 10 | 2.5, 5, 10, 20, 30 | 15 | 0.9, 1.3, 1.7 |
4. Results and Discussion
4.1. Smoke Backlayering Length of Single-Source Fire
According to the simulation results, the relationship between the smoke back-layering length of single-source fire, the longitudinal wind velocity, and the source power is shown in Figures 4 and 5. It indicates that the smoke backlayering length is inversely proportional to the longitudinal wind velocity. The smaller the longitudinal wind velocity, the greater the increase of the smoke backlayering length. While the smoke backlayering length is directly proportional to the power of the fire source. The higher the fire source power, the smaller the increase of the smoke backlayering length. When the fire source power is more than 12.5 MW, the smoke backlayering length does not change significantly with the power of the fire source.
Figure 4.
Relationship between smoke backlayering length and longitudinal wind velocity in different fire source powers.
Figure 5.
Relationship between smoke backlayering length and fire power at different longitudinal wind velocities.
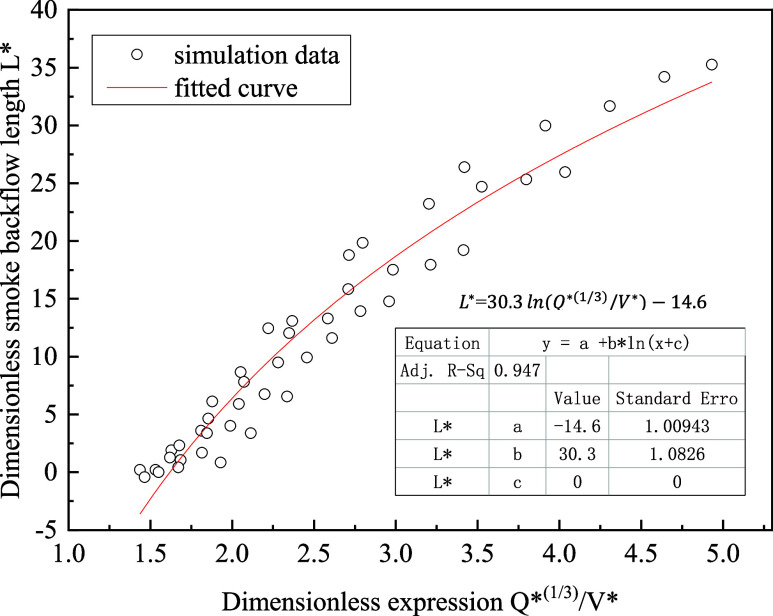
Based on eq 5, the dimensionless smoke backlayering length (L*) has a functional relationship with the ratio of the dimensionless (Q*) of 1/3 power to the dimensionless longitudinal wind velocity (V*). Combined with the simulation results, a fitting method was used to obtain a specific relationship, as shown in Figure 6. For the single-source fire, dimensionless smoke backlayering length (L*) is logarithmic to Q*1/3/V* when the fire source power is below 12.5 MW, as shown in eq 11.
| 11 |
Figure 6.
Relationship between dimensionless smoke backlayering length and.
When the fire source power is more than 12.5 MW, it has little effect on the smoke backlayering length. At this situation, Q*1/3 is equal to 0.61. Therefore, the formula of the smoke backlayering length of single-source fire can be summarized as the piecewise function, as shown in eq 12.
| 12 |
4.2. Smoke Backlayering Length of Double-Source Fire
4.2.1. Influence of Fire Source Spacing on the Smoke Backlayering Length
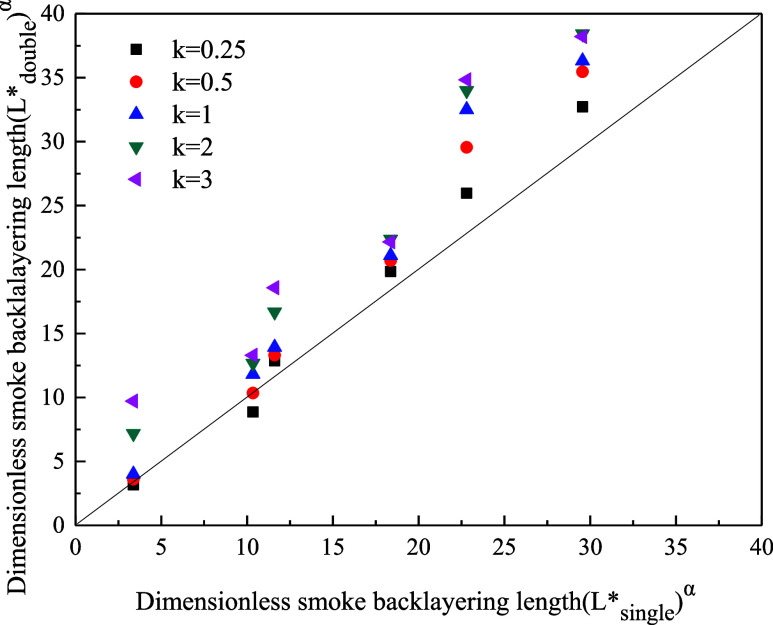
In order to derive β by eliminating the influence of the fire source power on the smoke backlayering length, the double-source fire power ratio coefficient k was set at 0.5 and 2 for analysis. Figure 7 (k = 0.5) and Figure 8 (k = 2) show the comparison results between simulation values of dimensionless smoke backlayering length and the single-source smoke backlayering length prediction eq 12 calculation value when d takes different values. Due to the increase of the distance between the two fire sources, the dimensionless smoke backlayering length is lower than the dimensionless smoke backlayering length of single-source fire. Moreover, as the value of the distance between the fire sources increases, the simulation value of the dimensionless smoke backlayering length decreases. It can be attributed to the increase of the distance between two fire sources causing a decrease of the coupling power value of the double-source fire, which leads to the maximum temperature drop of tunnel ceiling and reduces the driving force of smoke backlayering. The upstream fire source Q1 shows greater resistance than the driving effect to the smoke movement.
Figure 7.
Comparison of simulation values of the dimensionless backlayering length of smoke with eq 15 at different values of “d” (k = 0.5).
Figure 8.
Comparison of simulation values of the dimensionless smoke backlayering length with eq 15 at different values of “d” (k = 2).
According to the simulation results, it can be seen that the distance influence coefficient β decreases with the increase of dimensionless double fire source spacing d*, but the magnitude of the decrease is decreasing, and the two variables are power function relations, as shown in Figure 9. By nonlinear fitting, the function between distance influence coefficient β and dimensionless double fire source spacing d* can be obtained in eq 13.
| 13 |
Figure 9.
Relationship between the smoke backlayering length growth coefficient β and dimensionless double-source fire distance.
4.2.2. Influence of Fire Source Power on the Smoke Backlayering Length
In order to eliminate the influence of the fire source spacing on the smoke backlayering length, the fire source spacing d was set at 5 and 15 m for analysis. Figure 10 (d = 5) and Figure 11 (d = 15) are the comparison results between simulation values of dimensionless smoke backlayering length and the single-source smoke backlayering length prediction eq 12 calculation value when double-source fire power ratio coefficient k takes different values. Due to the increase of fire source 2 power, the dimensionless smoke backlayering length is greater than the dimensionless smoke backlayering length of the single-source fire. It can be attributed to the increase of the Q2 value causing the temperature of the smoke in tunnel to rise and enhancing the driving force of the smoke backflow.
Figure 10.
Comparison of simulation values of dimensionless smoke backlayering length with eq 15 at different values of “k” (d = 5 m).
Figure 11.
Comparison of simulation values of dimensionless smoke backlayering length with eq 15 at different values of “k” (d = 15 m).
According to the simulation results, it can be seen that the fire source power influence factor α increases with the increase of double-source fire power ratio coefficient k, but the magnitude of increase is decreasing, and the two variables are logarithmic function relation, as shown in Figure 12. By nonlinear fitting, the function between fire power influence factor α and double-source fire power ratio coefficient k can be obtained in eq 14.
| 14 |
Figure 12.
Relationship between the flue smoke backlayering length growth coefficient α and the double-source fire ratio coefficient k.
As known, when Q* > 0.23 (Q > 12.5), dimensionless smoke backlayering length is only related to Longitudinal wind velocity V. In cases where the sum of Q1 and Q2 is more than 12.5 MW, the fire source power is still regarded as 12.5 MW. Considering the influence of double fire source spacing and fire source power on the smoke backlayering length and adding the coefficients fire power influence factor α and distance influence coefficient β to modify the eq 12 of the smoke backlayering length in the single-source fire, the formula for predicting the smoke backlayering length of double-source fire can be obtained, as shown in eq 15.
| 15 |
In order to verify the accuracy of eq 15, six sets of data were selected for simulation verification. The comparison results are listed in Table 3. It indicates that the matching degree between the predicted value of eq 15 and the numerical simulation value is extremely high. Therefore, it can be considered that eq 15 can accurately predict the smoke backlayering length of the double-source fire.
Table 3. Comparison of the Numerical Simulation Results of the Smoke Backlayering Length with Prediction of eq 15.
| serial number | Q1 (MW) | V (m/s) | k | d (m) | smoke backlayering length (m) |
||
|---|---|---|---|---|---|---|---|
| simulation value | prediction formula (18) | deviation | |||||
| 1 | 5 | 0.9 | 3 | 15 | 132 | 126.756.8 | –0.040 |
| 2 | 5 | 1.3 | 2 | 30 | 63 | –0.098 | |
| 3 | 5 | 1.7 | 0.25 | 5 | 15 | 14.9 | 0.006 |
| 4 | 10 | 1.7 | 0.25 | 5 | 42 | 45.7 | 0.088 |
| 5 | 10 | 1.3 | 0.5 | 30 | 73 | 72.8 | –0.003 |
| 6 | 10 | 0.9 | 2 | 15 | 158 | 152.6 | –0.034 |
5. Conclusions
-
(1)
In single-source fire, it indicates that the smoke backlayering length is inversely proportional to the longitudinal wind velocity and directly proportional to the power of the fire source. The larger the fire source power, the smaller the increase of smoke backlayering length. When the fire source power is greater than 12.5 MW, it has little effect on the smoke backlayering length. Therefore, the formula of smoke backlayering length of single-source fire can be summarized as a piecewise function.
-
(2)
A new idea to study the smoke backlayering length of double-source fire was proposed. It is found that, as the value of the distance between the fire sources increases, the simulation value of dimensionless smoke backlayering length decreases. The distance influence factor β decreases with the increase of dimensionless double fire source spacing d*, and the two variables are power function relation. The higher the double-source fire power, the longer the smoke backlayering length. Fire power influence factor α increases with the increase of double-source fire power ratio coefficient k, and the two variables are logarithmic function relations. By introducing α and β, the formula for predicting the smoke backlayering length of double-source fire is proposed. The predicted value of the formula is compared with the simulated value, and it is found that the prediction formula is almost accurate.
 |
Acknowledgments
The authors deeply appreciate the financial support provided by the National Natural Science Foundation of China (no. 52174219, 51774275, and U1810106) and the Fundamental Research Funds for the Central Universities (no. 2023ZDPYRH01).
The authors declare no competing financial interest.
References
- Wang Z. N.; Chen J.; Cheng W. C.; Arulrajah A.; Horpibulsuk S. Investigation into the tempo-spatial distribution of recent fire hazards in China. Nat. Hazard. 2018, 92 (3), 1889–1907. 10.1007/s11069-018-3264-5. [DOI] [Google Scholar]
- Huang Y.; Bao Y. J.; Wang Y. H. Analysis of geoenvironmental hazards in urban underground space development in Shanghai. Nat. Hazard. 2015, 75 (3), 2067–2079. 10.1007/s11069-014-1414-y. [DOI] [Google Scholar]
- Thomas P. H. The movement of buoyant fluid against a stream and the venting of underground fires. Fire Saf. Sci. 1958, 351, 1. [Google Scholar]
- Hu L. H.; Huo R.; Chow W. K. Studies on buoyancy-driven back-layering flow in tunnel fires. Exp. Therm Fluid Sci. 2008, 32 (8), 1468–1483. 10.1016/j.expthermflusci.2008.03.005. [DOI] [Google Scholar]
- Gannouni S.; Maad R. B. Numerical study of the effect of blockage on critical velocity and backlayering length in longitudinally ventilated tunnel fires. Tunnelling Underground Space Technol. 2015, 48, 147–155. 10.1016/j.tust.2015.03.003. [DOI] [Google Scholar]
- Zhang S. G.; Cheng X. D.; Yao Y. Z.; Zhu K.; Li K. Y.; Lu S.; Zhang R. F.; Zhang H. P. An experimental investigation on blockage effect of metro train on the smoke back-layering in subway tunnel fires. Appl. Therm. Eng. 2016, 99, 214–223. 10.1016/j.applthermaleng.2015.12.085. [DOI] [Google Scholar]
- Zhao S. Z.; Liu F.; Wang F.; Weng M. C.; Zeng Z. A numerical study on smoke movement in a metro tunnel with a non-axisymmetric cross-section. Tunnelling Underground Space Technol. 2018, 73, 187–202. 10.1016/j.tust.2017.12.002. [DOI] [Google Scholar]
- Zhang S. G.; Yang H.; Yao Y. Z.; Zhu K.; Zhou Y.; Shi L.; Cheng X. Numerical Investigation of Back-Layering Length and Critical Velocity in Curved Subway Tunnels with Different Turning Radius. Fire Technol. 2017, 53 (5), 1765–1793. 10.1007/s10694-017-0656-0. [DOI] [Google Scholar]
- Tian M. Y.; Lu G.; Liu B.; Zhao J. Numerical Simulation Study on the Laws of Smoke Backlayering of Fire in Level Roadway of Metal Mine. IOP Conf. Ser.: Earth Environ. Sci. 2020, 558 (2), 022030. 10.1088/1755-1315/558/2/022030. [DOI] [Google Scholar]
- a Zhou F. B.; Wang D. M. Non-dimensional expression for backflow distances of smoke and hot gases in roadway or tunnel fire. J. China Univ. Min. Technol. 2003, 30 (5), 407–410. 10.3321/j.issn:1000-1964.2003.04.014. [DOI] [Google Scholar]; b Zhou Y.; Wang D. M. Experimental Study on Length of Smoke Back-Flow Layer of Fire in Horizontal Tunnel. J. China Univ. Min. Technol. 2001, 30 (5), 446–448. 10.3321/j.issn:1000-1964.2001.05.006. [DOI] [Google Scholar]; c Wang Y. F.; Jiang J. C.; Gong Y. F. Test research of full-scale tunnel fire and theoretical prediction on the distance of smoke regressing. China Saf. Sci. J. 2007, 17 (08), 37–41. 10.3969/j.issn.1003-3033.2007.08.007. [DOI] [Google Scholar]
- a Weng M. C.; Lu X. L.; Liu F.; Shi X. P.; Yu L. X. Prediction of backlayering length and critical velocity in metro tunnel fires. Tunnelling Underground Space Technol. 2015, 47, 64–72. 10.1016/j.tust.2014.12.010. [DOI] [Google Scholar]; b Liu J.; Wang Y. H.; Jing L. I.; Zong-Xiang L. I. Numerical simulation for the countercurrent fire change regularity in the inclined tunnel. J. Saf. Environ. 2015, 15 (4), 94–97. 10.13637/j.issn.1009-6094.2015.04.020. [DOI] [Google Scholar]
- Xu H. Z.Experimental and Numerical Simulation Study on Combustion Characteristics of Tunnel Fire on the Basic of Two Fire Sources Interaction. M.S.; Soochow University, 2020. [Google Scholar]
- Weng W. G.; Kamikawa D.; Fukuda Y.; Hasemi Y.; Kagiya K. Study on flame height of merged flame from multiple fire sources. Combust. Sci. Technol. 2004, 176 (12), 2105–2123. 10.1080/00102200490514949. [DOI] [Google Scholar]
- Kamikawa D.; Weng W. G.; Kagiya K.; Fukuda Y.; Mase R.; Hasemi Y. Experimental study of merged flames from multifire sources in propane and wood crib burners. Combust. Flame 2005, 142 (1–2), 17–23. 10.1016/j.combustflame.2005.02.004. [DOI] [Google Scholar]
- Delichatsios M. A. A Correlation for the Flame Height in “Group” Fires. Fire Sci. Technol. 2007, 26 (1), 1–8. 10.3210/fst.26.1. [DOI] [Google Scholar]
- Heidarinejad G.; Mapar M.; Pasdarshahri H. A comprehensive study of two fire sources in a road tunnel: Considering different arrangement of obstacles. Tunnelling Underground Space Technol. 2016, 59, 91–99. 10.1016/j.tust.2016.06.016. [DOI] [Google Scholar]
- Huan Z. F.; Zhou X. D.; Zhang T. L.; Peng F.; Wu Z. B.; Yang L. Z. Flame spread rate over two parallel extruded polystyrene (XPS) foam slabs. Fire Saf. Sci. 2014, 23 (4), 189–194. 10.3969/j.issn.1004-5309.2014.04.01. [DOI] [Google Scholar]
- Tsai K. C.; Chen H. H.; Lee S. K. Critical ventilation velocity for multi-source tunnel fires. J. Wind Eng. Ind. Aerodyn. 2010, 98 (10–11), 650–660. 10.1016/j.jweia.2010.06.006. [DOI] [Google Scholar]
- Yu M. G.; Su G. F.; J C. Numerical studies on the effect of double fire sources upon critical ventilation velocity in tunnel fires. Fire Saf. Sci. 2017, 26 (01), 20–28. 10.3969/j.issn.1004-5309.2017.01.03. [DOI] [Google Scholar]
- Liu S. T.; Zhao J. L.; Wei W. B. Experimental and Simulation Study on Dual-Source Fire with Different Spacing in Tunnels. China J. Highway Transp. 2022, 35 (7), 193–202. 10.19721/j.cnki.1001-7372.2022.07.016. [DOI] [Google Scholar]
- He K.; Shi L.; Zhang S.; Cong W.; Yang H.; Cheng X. Experimental study on temperature attenuation of smoke flow driven by dual fire sources in a tunnel. Tunnelling Underground Space Technol. 2023, 134, 105004. 10.1016/j.tust.2023.105004. [DOI] [Google Scholar]
- a Ingason H.; Li Y. Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45 (6–8), 371–384. 10.1016/j.firesaf.2010.07.004. [DOI] [Google Scholar]; b Li Y. Z.; Lei B.; Ingason H. Study of critical velocity and backlayering length in longitudinally ventilated tunnel fires. Fire Saf. J. 2010, 45 (6–8), 361–370. 10.1016/j.firesaf.2010.07.003. [DOI] [Google Scholar]
- Ming L. The Π Theorem and Its Application to Dimensional Analysis. J. Jiangsu Inst. Petrochem. Technol. 2000, (04), 59–61. 10.3969/j.issn.2095-0411.2000.04.019. [DOI] [Google Scholar]