Abstract
Developing efficient catalysts for syngas-based higher alcohol synthesis (HAS) remains a formidable research challenge. The chain growth and CO insertion requirements demand multicomponent materials, whose complex reaction dynamics and extensive chemical space defy catalyst design norms. We present an alternative strategy by integrating active learning into experimental workflows, exemplified via the FeCoCuZr catalyst family. Our data-aided framework streamlines navigation of the extensive composition and reaction condition space in 86 experiments, offering >90% reduction in environmental footprint and costs over traditional programs. It identifies the Fe65Co19Cu5Zr11 catalyst with optimized reaction conditions to attain higher alcohol productivities of 1.1 gHA h−1 gcat−1 under stable operation for 150 h on stream, a 5-fold improvement over typically reported yields. Characterization reveals catalytic properties linked to superior activities despite moderate higher alcohol selectivities. To better reflect catalyst demands, we devise multi-objective optimization to maximize higher alcohol productivity while minimizing undesired CO2 and CH4 selectivities. An intrinsic trade-off between these metrics is uncovered, identifying Pareto-optimal catalysts not readily discernible by human experts. Finally, based on feature-importance analysis, we formulate data-informed guidelines to develop performance-specific FeCoCuZr systems. This approach goes beyond existing HAS catalyst design strategies, is adaptable to broader catalytic transformations, and fosters laboratory sustainability.
Subject terms: Heterogeneous catalysis, Chemical engineering, Computational science
Developing efficient catalysts for syngas-based higher alcohol synthesis (HAS) remains challenging. Here the authors successfully demonstrate an active learning strategy by integrating Bayesian optimization into experimental workflows to accelerate the design of highly active and stable FeCoCuZr catalysts for HAS.
Introduction
Higher alcohol synthesis (HAS) via the thermocatalytic hydrogenation of syngas remains an aspiring technology for defossilizing the production of valuable chemicals and fuel additives while fostering a circular economy and mitigating climate change concerns1,2. Although catalyst patents were first filed in the late 1920s3,4 and a few pilot plants followed sixty years later5,6; these efforts have not materialized into a commercial process5. Key catalytic performance metrics worth consideration are productivity and selectivity. The highest literature-reported values for space-time yields to higher alcohols (STYHA) lie in the vicinity of 0.3 gHA h−1 gcat−1 5–7, in contrast to STYHA > 1 gHA h−1 gcat−1 for the related commercialized methanol synthesis, while selectivity to higher alcohols (SHA) typically remain below 30%5,8,9.
The low yields and selectivity of higher alcohols from CO hydrogenation arise from its mechanistic complexity and competing side-reactions which produce appreciable amounts of hydrocarbons and undesired CH4 and CO25,6,9. HAS requires catalytic surfaces with multiple functionalities in close proximity to each other—typically linked to different metals—to simultaneously perform C-O dissociation, C-C coupling, and CO insertion steps over specific active sites6,9. Tailored synthesis10,11, advanced characterization tools such as microscopy12,13 or operando spectroscopy14,15, and theoretical modeling16,17 have been explored to deduce performance descriptors for these complex multimetallic catalysts without achieving the anticipated benefits, necessitating alternative approaches.
The potential of artificial intelligence and machine learning (ML) to handle high-dimensional and intricate systems offers promise to address the above challenge18–20. At the intersection of ML and parallel experimentation lies active learning, suitable for expediting material design and process optimization21–23 through a closed-loop framework of small data—machine intelligence—human decision-making. Although gaining traction in material sciences24–28, drug discovery and biosystems engineering29–31, this methodology remains underexplored in catalysis. Notable studies include active learning accelerated density functional theory simulations for screening multimetallics for electrocatalytic CO2 reduction32 and alkyne semi-hydrogenation33, based on electronic or structural or descriptors. Experimental studies in optimizing multicomponent catalyst formulations for oxygen reduction34, methanol synthesis35, water gas shift36, and hydrogen evolution37 reactions have also been reported, but limited to single performance indicator. The predictive nature of these tools offer promise to reduce experimentation time, and more importantly, improve economic and environmental sustainability during catalyst development, which traditionally require hundreds to thousands of screening experiments35,36,38.
Despite the potential benefits, the applicability of active learning-aided approaches is not yet clear for highly complex catalyst systems for HAS, such as the extensively-investigated modified Fischer-Tropsch (m-FTS) family2,6. Comprising Fe39,40 or Co12,41 for C-O dissociation and carbon chain growth, in addition to Cu14,42 which facilitates non-dissociative CO insertion, these active metals have typically been anchored on oxide or carbonaceous supports and further promoted by alkali or noble metals in multicomponent formulations6,43,44. Our recent discovery of ZrO2 as a versatile activity promoter for m-FTS systems has led to promising STYHA > 0.3 gHA h−1 gcat−1, with all active metal pairings (CoCuZr, FeCuZr, FeCoZr) outperforming Zr-free and monometallic counterparts45. This prompts further exploration of FeCoCuZr catalysts where interactions between active metals and resultant activity could be further enhanced. However, the extensive chemical space and complex reaction dynamics of these materials, and the lack of established descriptors, pose a significant challenge.
In this study, we pioneer an active learning strategy to accelerate the development of highly active FeCoCuZr catalysts. Key features include (i) high prediction power leading to the Fe65Co19Cu5Zr11 catalyst and its optimal reaction conditions with stable STYHA of 1.1 gHA h−1 gcat−1 for at least 150 h, the highest reported for direct HAS from syngas, (ii) a substantial reduction in time and resources by identifying the optimal system in 86 experiments from the vast space of ca. five billion potential combinations, (iii) multi-objective optimization to reveal intrinsic performance trade-offs and recommended Pareto-optimal catalysts that minimize selectivity towards CO2 and CH4 while still maintaining high STYHA. These results underscore the potential of data-driven approaches to sustainably expedite efficient multicomponent catalyst development and foster innovation in catalysis research32,36.
Results
Overview and scope of the active learning framework
We devised an active learning approach by integrating data-driven algorithms with experimental workflows, which continuously learns from existing and newly-generated data from iterative experimental cycles, to explore and identify FeCoCuZr compositions and reaction conditions optimizing catalyst performance metric(s) of interest (Fig. 1)36,37,46. The core of the data-driven model combines Gaussian process (GP) and Bayesian optimization (BO) algorithms, along with human decision-making in order to accomplish single or multi-objective tasks46,47.
Fig. 1. Scheme of active learning workflow to develop FeCoCuZr catalysts.
The study is developed in three phases with progressive increases in the number of target performance metrics and variables (right). In each phase, iterative cycles comprising the depicted experimentation and modeling steps are performed (left).
To showcase the feasibility of this approach to HAS, the study was systematically conducted in three distinct phases by progressively increasing the model complexity. In Phase 1, the catalyst composition was varied with the objective of maximizing STYHA at fixed reaction conditions. In Phase 2, the dimensionality of the problem was increased by concurrently exploring the catalyst compositions and reaction conditions to maximize STYHA. This approach was subsequently extended towards multi-objective capabilities by simultaneously maximizing STYHA while minimizing combined selectivity to carbon dioxide and methane () in Phase 3. Iterative cycles comprising of six experiments were conducted during each phase, until the target performance metric(s) were achieved or reached saturation.
Phase 1: Optimal catalyst formulations for productivity
The first phase aimed to explore the suitability of the active learning framework in identifying optimal FeCoCuZr formulations for maximizing STYHA under fixed reaction conditions, specifically the H2:CO ratio (H2:CO), reaction temperature (T), pressure (P), and the gas hourly space velocity (GHSV). This strategy enabled the exploration of a space containing >175,000 unique compositional possibilities, known as the chemical space34,36 (Supplementary Note 1), and helped understand the sensitivity of higher alcohols productivity to catalyst composition in this family of materials. Without a priori composition and performance data for FeCoCuZr formulations, the initial model training was performed using 31 data points on the FeCoZr, FeCuZr, and CuCoZr catalysts recently reported by our group45, denoted as seed experiments for Phase 1 (Supplementary Note 2, Supplementary Table 1). Reaction conditions were fixed at H2:CO = 2.0, T = 533 K, P = 50 bar, and GHSV = 24,000 cm3 h−1 gcat−1 across cycles to match those in the seed dataset (Supplementary Note 2).
In each cycle, the GP-BO model was trained using the molar content values of the four elements (Fe, Co, Cu, Zr) and the corresponding STYHA of all catalysts in the dataset. Subsequently, we evaluated the expected improvement (EI) and predictive variance (PV) acquisition functions separately under specific constraints to generate candidate compositions (see Methods section, “Gaussian process and Bayesian optimization”, Supplementary Table 2). Six suitable catalysts were manually selected for experimentation by balancing the number of recommendations from EI, which searches for compositions maximizing the STYHA objective (i.e., exploitation), and from PV, which seeks potential candidates in the unexplored chemical space (i.e., exploration)23,48. Here, it is important to acknowledge the key role of human decision-making in providing a judgement and selection from the suggested compositions, which allowed us to supervise and fine-tune the implementation of active learning at this early stage. The experimentally evaluated performance together with measured compositions of these six catalysts were added to the dataset to re-train the model for the next cycle.
Five iterative cycles were performed (30 catalysts, see Supplementary Tables 3-7), which mapped the chemical space and identified regions with high STYHA (Fig. 2a). Progressive improvements in STYHA across cycles were achieved (Fig. 2b, Supplementary Tables 3-7), with the Fe69Co12Cu10Zr9 catalyst in Cycle 3 attaining the highest STYHA = 0.39 gHA h−1 gcat−1, a 1.2-fold improvement over the Fe79Co10Zr11 seed benchmark (STYHA = 0.32 gHA h−1 gcat−1). This performance was retained for at least 100 h on stream with no visible sign of deactivation (Supplementary Fig. 1). Similar compositions and performances obtained by the best catalysts in Cycles 4 and 5 confirmed the convergence of results.
Fig. 2. Exploration of catalyst compositions to maximize STYHA at fixed reaction conditions.
a Performance plot based on the chemical space of FeCoCuZr catalysts, with the sum of Fe, Co, and Cu molar contents normalized to 100% and excluding the Zr content. Compositions of catalysts evaluated during five active learning cycles are depicted as circles, and contours are generated from measured STYHA values of selected catalysts containing 10 ± 5 mol% Zr. b Evolution of the performance obtained from the best catalyst in each cycle and its associated composition (units in mol%). The catalysts are benchmarked vs. the reference Fe79Co10Zr11 catalyst from seed experiments. c Performance-based clustering of the catalysts. The catalysts with the highest STYHA in each cycle are colored in a–c. d Violin plots of catalyst compositions for the clusters identified in c, with individual data points shown as gray dots. Source data are provided in the source data file.
To reveal compositional trends driving performance, we used the k-means clustering algorithm21,34. This allowed us to identify catalysts that had high STYHA and SHA - both being key performance metrics, and enabled informed decision making regarding experiment selection in subsequent phases. Four distinct clusters were observed (Fig. 2c, d). Catalysts in the Zr-rich and equimolar clusters exhibit low STYHA, likely due to low contents and suboptimal ratios of the active metals, respectively. Fe stands out as a key active metal, as maximum STYHA up to 0.39 gHA h−1 gcat−1 was attained by Fe-rich catalysts, while those in the Fe-Co rich cluster exhibit the highest SHA up to 17%. Notably, Zr content converged towards 10% in the highest performing Fe-rich catalysts, mimicking that obtained over the seed catalysts45. Irrespective of compositional differences, product distributions of best performing catalysts in each cycle largely resembled each other, with SHA = 14 ± 2%, = 13 ± 5%, = 25 ± 5%, and = 48 ± 4% (Supplementary Fig. 2, Supplementary Table 8).
The superior STYHA of the Fe69Co12Cu10Zr9 optimal catalyst compared to the Fe79Co10Zr11 seed benchmark stemmed from an increase in XCO (45% vs. 36%), since they showed similar SHA ∼ 13%. We thus conducted characterization studies to identify key features behind the activity gain. STEM-EDX maps of both catalysts (Fig. 3a, b, Supplementary Figs. 3, 4) identified small domains of ZrO2 in intimate contact with larger active metal nanoparticles. These defect-rich ZrO2 domains, as indicated by the presence of Zrδ+ contributions in the Zr 3d region of XPS spectra (Fig. 3c), were previously identified to enhance surface iron and cobalt carbide formation in line with the C 1s signal of XPS spectra (Fig. 3d)49. Carbides are known active phases in CO hydrogenation, and their interface with partially reduced iron oxide species is thought to enhance non-dissociative CO activation and higher alcohol formation in iron-rich catalysts45,49,50. Notably, elemental distributions of Fe and Co suggest that these two metals are inter-dispersed and not segregated in both catalysts whether as calcined or after use (Fig. 3a, b, Supplementary Figs. 3, 4), in line with their tendency to form intermetallic alloys or mixed oxides. Initially dispersed Cu in the fresh Fe69Co12Cu10Zr9 catalyst agglomerated into distinct 10–20 nm-sized agglomerates in contact with Fe-Co nanoparticles following reduction and reaction (Fig. 3b, Supplementary Figs. 3, 4), accompanied by a decrease in surface area (Supplementary Table 9) and confirmed by XRD patterns (Supplementary Fig. 5). Such architectural features have also been observed for similar FeCoCu materials prepared by a sol-gel method without Zr present in the composition51.
Fig. 3. Characterization of the best performing catalyst in Phase 1 and the reference seed catalyst.
STEM-EDX elemental maps after reaction of (a) the reference Fe79Co10Zr11 and (b) the best performing Fe69Co12Cu10Zr9 catalyst identified in Phase 1. Scale bars represent 50 nm. XPS spectra around (c) Zr 3d and (d) C 1s regions after reaction with deconvoluting signals indicated. e H2-TPR profiles with deconvoluted peaks corresponding to the reduction of oxides indicated. For iron oxide: Fe2O3 → Fe3O4 → FeO → Fe. Temperature-programmed H2-D2 exchange profiles of (f) Fe79Co10Zr11, (g) Fe69Co12Cu10Zr9 with the exchange temperature (at the maximum rate of HD formation) marked. Reaction conditions: H2:CO = 2.0, T = 533 K, P = 50 bar, and GHSV = 24,000 cm3 h−1 gcat−1. Source data are provided in the source data file.
The presence of copper enhances the surface reducibility of Fe69Co12Cu10Zr9 as demonstrated by H2-TPR (Fig. 3e), where oxidic Cu is readily reduced in the presence of H2 to the metallic state, which in turn enhances hydrogen splitting and spillover to neighboring Fe-Co oxide domains51. Temperature-programmed H2-D2 exchange experiments also showed a 40 K decrease in the exchange temperature for Fe69Co12Cu10Zr9 (Fig. 3f, g) compared to Fe79Co10Zr11, suggesting that Cu nanoparticles improve hydrogen activation and thus play a similar role as in other Cu-catalyzed reactions such as methanol or olefin synthesis from COx51,52. As such, the increase in XCO, formation rates of each alcohol (Supplementary Table 10) and therefore STYHA attainable over iron-rich FeCoCuZr catalysts originates from its enhanced H2 activation ability from copper, while retaining the characteristics imparted by well-mixed, carbide-rich Fe-Co phases promoted by dispersed and defective ZrO2. Under reaction conditions, *CHx, CH3O*, and CH3CH2O* intermediates were detected by in situ DRIFTS (Supplementary Fig. 6), in line with the expected mechanisms of *CHx coupling and non-dissociative *CO insertion for HAS over m-FTS catalysts.
It is worth noting that the model formulation did not include any explicit chemical information guiding the iterative cycle. Nevertheless, it was able to provide performance predictions with high accuracy. The overall performance was influenced by the balance between EI and PV functions used in the GP-BO algorithm23,24,48, as the latter exhibits higher uncertainty leading to lower accuracy, and vice versa for the former. A total of 13 and 17 catalysts were evaluated based on recommendations from the EI and PV acquisition functions, respectively (Supplementary Fig. 7, Supplementary Table 11), progressively improving model performance from an initial coefficient of determination R2 = 0.36 in Cycle 1 to R2 = 0.84 by the final cycle. This improvement resulted from the expansion of available data generated during the active learning cycles and an increased number of experimental evaluations guided by the exploitation function probing regions of high performance. Accurate predictions on catalyst performance could be made owing to the standardized synthesis method that ensured consistency in structural properties.
Phase 2: Optimal catalyst formulations and reaction conditions for productivity
While basic reactivity patterns and the relevance of operating conditions are well known for HAS, there are no universally applicable set of optimal conditions as the influence of each parameter is catalyst-specific. The second phase of this study tackles this by expanding the exploration space to include reaction conditions, including H2:CO, T, and GHSV, defined as the parametric space (Supplementary Note 1). As Phase 1 did not include variation of reaction conditions, 20 additional experiments were performed to broaden the range of reaction conditions initially covered by the model, denoted as seed experiments for Phase 2 (Supplementary Note 3, Supplementary Table 12). Phase 2 was initiated by training the GP-BO algorithm using these 50 data points under compositional and parametric constraints based on knowledge from previous experiments and the literature (Supplementary Note 4, Supplementary Table 13).
Reaction conditions were found to exert a significant impact on STYHA, as Fe61Co20Cu9Zr10 identified as the best performer in Cycle 1 was already able to exceed 0.5 gHA h−1 gcat−1 at H2:CO = 1.8, T = 552 K, P = 50 bar, and GHSV = 32,550 cm3 h−1 gcat−1, almost 1.5-fold higher compared to the seed data used in Phase 1. Over the next two active learning cycles, STYHA reached ~0.7 gHA h−1 gcat−1, nearly doubling productivity compared to the maximum achieved in Phase 1 (Fig. 4a, Supplementary Tables 14–16). We noticed that by the end of Cycle 3, the optimizer was locally constrained at the GHSV upper bound of 50,000 cm3 h−1 gcat−1. As it is typically observed in literature that an increase in GHSV concurrently increases STYHA owing to higher reactant flows despite a slight reduction in XCO5,7,9, the upper bound was set to 100,000 cm3 h−1 gcat−1 in Cycle 4 to observe the behavior of the model. This adjustment led to the GP-BO extrapolating to previously unexplored GHSV values, suggesting catalytic systems that provided higher STYHA of up to 0.9 gHA h−1 gcat−1. By Cycle 5, our framework recommended the highly active Fe65Co19Cu5Zr11 catalyst that attained STYHA = 1.1 gHA h−1 gcat−1 at operating conditions of H2:CO = 2.2, T = 551 K, P = 50 bar, and GHSV = 90,000 cm3 h−1 gcat−1, marking a significant 3.5-fold increase from the original Phase 1 seed benchmark (Fig. 4a, Supplementary Table 18). The stability of this catalyst was evaluated in a 150-h catalytic run (Fig. 4b), where XCO ≥ 40% and STYHA ≥ 1 gHA h−1 gcat−1 were maintained throughout. Phase 2 concluded upon the completion of Cycle 6, during which catalytic systems yielding approximately 1 gHA h−1 gcat−1 were achieved once more, suggesting repeatability of results as well as model saturation (Fig. 4a, Supplementary Table 19).
Fig. 4. Identification of catalyst compositions and reaction conditions maximizing STYHA.
a Evolution of the performance obtained from the best catalyst in each cycle and its respective composition and reaction conditions. All reactions were conducted at P = 50 bar. b Stability test of the most productive Fe65Co19Cu5Zr11 catalyst over 150 h on stream. c Comparison of the performance of best FeCoCuZr catalytic systems developed in each active learning cycle across Phase 1 and 2, with over 120 Rh-, Mo-, and m-FTS based catalysts reported in literature. The horizontal dashed line represents average literature reported STYHA values. d Parity plots depicting the model performance through the active learning phases. Source data are provided in the source data file.
Benchmarking FeCoCuZr catalytic systems from Phases 1 and 2 with literature-reported catalysts across various families such as Rh-based, Mo-based, and m-FTS-based revealed notable differences. The literature-reported catalysts (a total of 125 catalysts were examined) exhibited an average STYHA ≈ 0.1 gHA h−1 gcat−1 with top performers in the 90th percentile reaching 0.18 gHA h−1 gcat−1. Conversely, the best performing FeCoCuZr catalysts in the different cycles of Phases 1 and 2 had an average STYHA of approximately 0.6 gHA h−1 gcat−1 highlighting significantly enhanced productivity compared to literature-reported counterparts for direct hydrocarbon synthesis from syngas for direct HAS from syngas6,8 (Fig. 4c). For comparative analysis, selectivity to higher alcohols exhibited a less responsive nature than productivity in this family. Regardless of the diverse set of compositions and reaction conditions investigated, SHA = 11 ± 2% was the mean of the most active systems in Phase 2 (Supplementary Fig. 8, Supplementary Table 20), similar to the observation made in Phase 1 and pointing to an intrinsic feature of the FeCoCuZr family.
The impact of varying reaction conditions on performance in Phase 2 could be visualized by mapping catalyst compositions and their respective STYHA attained in four clusters dictated by GHSV and T ranges (Supplementary Fig. 9). The highest-performing catalytic systems share similar compositions to the iron-rich catalysts discovered to be optimal in Phase 1 (Fig. 2c, d), hinting that they retain the same catalytic features previously determined to boost activity. The model recommendations of maximizing GHSV, T = 550–570 K, and moderate H2:CO ∼ 2 are also in line with established heuristics for syngas-based HAS (Supplementary Note 4). The accuracy remained high with R2 = 0.78 in Phase 2, comparable to that in Phase 1. Progressive improvements in accuracy were evident in Phase 2, with the mean absolute percentage error (MAPE) between predicted and measured STYHA for each cycle in Phase 2 decreasing from 33% in Cycle 1 to 7.6% in Cycle 6 (Supplementary Table 21). Considering predicted and measured STYHA across both phases resulted in an overall performance accuracy of R2 = 0.91 (Fig. 4d) with a low root mean squared error (RMSE) of 0.09 g h−1 gcat−1.
Phase 3: Maximized productivity and minimized selectivity to by-products
The third phase of this study aimed to apply active learning to search for catalytic systems that could meet multiple performance criteria, better reflecting the real-world demands on catalysts. Given the modest SHA across all catalysts developed in Phase 1 and 2, we focused on selectivities towards carbon dioxide and methane , considered as the least valuable products in HAS5,9. The 86 data points in Phase 1 and 2 exhibited = 16 ± 6% and = 25 ± 4%, highlighting the significance of the water-gas shift (WGS) and CO methanation reactions, especially at conditions favoring high XCO and therefore STYHA. (Supplementary Note 4, Supplementary Fig. 10). A plot of STYHA vs. suggested an intrinsic trade-off in the form of a Pareto front (Fig. 5a), in which the improvement of one metric would likely be at the expense of the other53,54.
Fig. 5. Uncovering Pareto-optimal catalysts and performance drivers.
a Visual depiction of Pareto-optimal catalytic performances before and after multi-objective active learning. The Pareto front delimits the zone available by catalysts developed in Phase 1 and 2. b Product distribution for FeCoCuZr catalysts across Phase 3. c Relative feature-importance of catalyst compositions and reaction conditions on each of the performance metrics as determined by SHAP analysis. Source data are provided in the source data file.
This scenario was explored in Phase 3 by varying the catalyst compositions and reaction conditions simultaneously to maximize STYHA and minimize . For this purpose, the GP-BO algorithm was trained with data from Phases 1 and 2 with STYHA and as target metrics, using the Expected Hypervolume Improvement (EHVI) acquisition function, which guides the optimization process to recommend catalyst composition and reaction conditions that are likely to lead to better trade-offs among conflicting objectives23,35.
During Cycle 1, a significant discrepancy between predicted and measured values of STYHA and was observed (Supplementary Fig. 11, Supplementary Table 26) with none of the catalysts evaluated near the Pareto barrier (Fig. 5a, Supplementary Table 22). Upon entering Cycle 2, two of the six catalysts evaluated were situated on the Pareto front (Fig. 5a, Supplementary Table 23), while the model exhibited enhanced prediction accuracy. The highest performing system notably attained STYHA = 1.04 gHA h−1 gcat−1, only 5% lower than the maximum attained in Phase 2 but with a drastically reduced = 40% vs. 46%. By Cycle 3, model recommendations improved significantly as five of the six catalysts evaluated lie directly on the Pareto frontier without crossing it (Fig. 5a, Supplementary Table 24) attaining = 34 ± 2% and STYHA = 0.65 ± 0.05 gHA h−1 gcat−1. Herein, while the productivity remained ca. two times higher than average literature values, we highlight the selectivity of undesired CO2 and CH4 was minimized by around 10% (Fig. 5b), in comparison to some of the catalysts developed in Phase 2, suggesting an optimal trade-off between STYHA and . Notably, we identified optimal systems along the Pareto frontier, suggesting an intrinsic limitation of this family of HAS catalysts to achieve < 30% without compromising STYHA. However, within this constraint, our strategy eventually uncovered five Pareto-optimal catalytic systems which are otherwise non-intuitive and not easily accessed by human experts55, thereby underscoring its versatility and significance.
Performance drivers and data-informed guidelines
We sought to elucidate the main performance drivers among the set of input features impacting STYHA and . However, an inherent challenge with most ML algorithms, including the GP regressor used in this study, lies in the complexity of deciphering the internal rationale behind predictions—rendering them black-box in nature. To address this challenge and make the model interpretable, we utilized the agnostic ML explainer, SHapley Additive exPlanations (SHAP)56. This methodology facilitates the extraction of interpretable insights from the GP algorithm through the computation of feature-importance scores57,58. Akin to sensitivity analysis, SHAP determines the individual or combined contributions of features to the model’s prediction, enabling catalysis practitioners to quantify the relative importance of different features affecting performance, that can be corroborated with existing knowledge or lead to testable hypotheses.
The overall influence of each feature was expressed by normalized SHAP values, revealing that reaction conditions and catalyst compositions contributed to ca. 60% and 40%, respectively, to the model predictions for both targeted metrics in Phases 2 and 3 (Fig. 5c). In the case of STYHA, GHSV and T emerged as the two most important parameters, in alignment with earlier intuition in Phase 2 as well as findings in the literature for similar C1 transformations36,57. Fe content ranked as the most prominent compositional input, in line with the high productivities only attained by iron-rich catalysts, as highlighted in the discussion of Phase 1 and given the claimed role of Fe phases in C-C coupling6. For , T was identified as the most significant variable, followed by Fe and Co contents. The role of T in dictating selectivity patterns could be ascribed to the coexistence of competing reaction networks, each with different temperature-dependent kinetic and thermodynamic barriers including HAS, WGS, or methanation. This highlights the importance of optimizing T to fine-tune the selectivity towards higher alcohols or by-products. The Fe-Co-rich cluster determined in Phase 1 (Fig. 2c) catered most favorably to HA selectivity, with Fe-Co surface carbides previously identified as a key feature for selective higher alcohol production from catalyst characterization45.
Despite demonstrating the efficacy of active learning in uncovering catalytic systems that enhance multiple performance metrics for HAS, it is essential to acknowledge its scope and limitations in its current form. The lack of electronic or structural descriptors as inputs to the model and its inability to optimize performance metrics which are intrinsically unresponsive to screened variables, such as SHA in this work, can be mentioned (see Supplementary Note 5 for extended discussion). Nonetheless, in the course of this study, three categories of catalytic systems within the FeCoCuZr family emerged exhibiting distinct performance characteristics, namely high STYHA and (STYHA = 0.97 ± 0.08 gHA h−1 gcat−1, = 44 ± 2%, SHA = 10 ± 1%), low STYHA and (STYHA = 0.25 ± 0.07 gHA h−1 gcat−1, = 31 ± 3%, SHA = 14 ± 2%), and Pareto-optimal catalysts (STYHA = 0.63 ± 0.06 gHA h−1 gcat−1, = 34 ± 2%, SHA = 14.6 ± 0.3%) (Fig. 6). Each category favors unique catalyst compositions and reaction conditions; for instance, systems displaying high STYHA and are characterized by high molar Fe content, H2:CO, and GHSV values, whereas the low STYHA and counterparts are favored at equimolar Fe-Co contents, low H2:CO, and milder T. The Pareto-optimal catalysts feature a combination of the aforementioned traits, recommending high Fe contents and operation at high GHSV and mild T. These quantitative guidelines, especially those relating to operating conditions, align with literature findings and are likely not dependent on specific catalyst formulations and could be relevant to HAS catalysts in general6,9. However, the exact compositional guidelines provided herein apply to the FeCoCuZr catalysts investigated in this study and would arguably not be directly relevant in designing HAS systems with different active metals, promoters, and architectures prepared by different synthesis methods. Importantly, this methodology based on data analysis can be extended to other potential HAS systems or even other multi-product chemical transformations, provided sufficient experimental data is available. Other users are thus recommended to formulate specific guidelines for their application during the active learning process. Overall, in the absence of quantifiable techno-economic data and community consensus on practically relevant productivities or selectivities for HAS, this approach provides guidelines for optimizing key metrics, serving as valuable assets to catalysis practitioners and industry stakeholders to accelerate research efforts by assisting in the selection of appropriate catalytic systems and experiments, ultimately saving time and resources.
Fig. 6. Establishment of guidelines for developing performance-specific catalysts.
Data-informed guidelines aimed towards the development of FeCoCuZr catalytic systems belonging to three performance categories. The box plots present a statistical summary of the composition and reaction condition requirements for each category, showing the minimum, interquartile range, and maximum values. Outliers are indicated as points outside the boundary of the whiskers wherever applicable. The corresponding performance metrics are shown below as horizontal bars. Source data are provided in the source data file.
Active learning and sustainable laboratories
While the possible chemical and parametric space of the FeCoCuZr systems is in the order of billion combinations, practical and real-world studies on multicomponent catalysts range between hundreds to thousands screening experiments35,36,38. By employing active learning we mapped the vast space of FeCoCuZr catalysts to a cumulative 104 experiments, across Phases 1–3 to meet the desired performance objectives, confirming the growing body of literature that claim active learning accelerates experimental efforts34–36. This has a profound impact on the environmental and economic sustainability of catalyst development programs that has not been explored.
To this context, assuming this study as representative of a catalyst development endeavor, we assessed the degree to which active learning could impact both sustainability pillars in laboratories (see scope in Supplementary Note 6). Our analysis suggests average reductions exceeding 90% in carbon footprint and costs on benchmarking with traditional campaigns (Fig. 7, Supplementary Tables 27–29). We also observe a very mild dependency of this result with regional variations across the globe affecting, for example, composition of the energy mix or laboratory operational expenditure (Supplementary Fig. 12). Thus, by reducing consumption of chemicals and energy, and optimizing resource utilization, active learning remarkably fosters sustainable catalysis laboratories.
Fig. 7. Impact of active learning on laboratory sustainability.
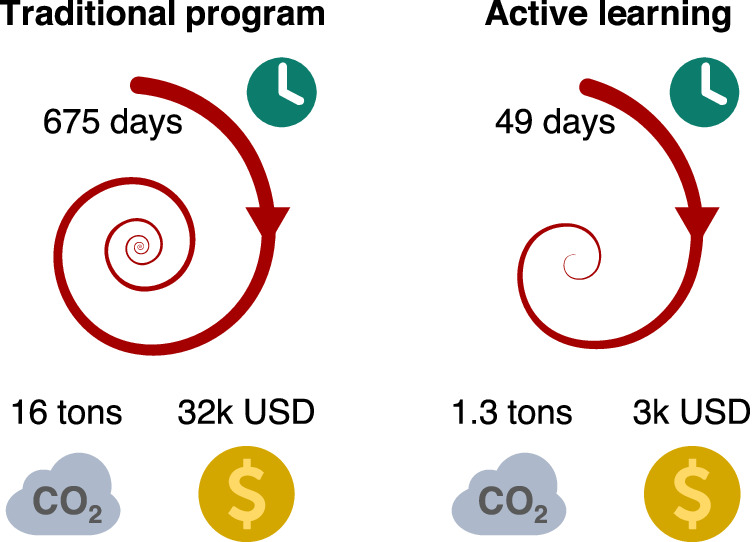
Schematic illustration of the reduction in work-days, CO2 footprint, and operating costs on a global average basis fostered by the adoption of active learning framework over traditional catalyst development programs, calculated from results obtained in this study. The spirals represent experimental efforts, and the derivation of the sustainability metrics shown are detailed in Supplementary Note 6 and regional variations in Supplementary Fig. 12.
Discussion
In this study, we advance research on multimetallic catalysts for HAS, exemplified by the novel FeCoCuZr catalyst family, by integrating digital tools in experimental catalysis in the form of active learning. It drastically narrows down the vast chemical and reaction condition space of multimetallic systems, in our case from around 5 × 109 combinations to 86 experiments, significantly accelerating experimental workflows. This strategy identified the Fe65Co19Cu5Zr11 catalyst and its optimized reaction conditions (H2:CO = 2.2, T = 551 K, P = 50 bar, and GHSV = 90,000 cm3 h−1 gcat−1) able to achieve STYHA = 1.1 gHA h−1 gcat−1, the highest reported in literature for direct thermocatalytic HAS from syngas. Representative catalytic materials were characterized to uncover reasons behind the outstanding performance, discovering the interplay between H2 activation on Cu and well-mixed, carbide-rich Fe-Co nanoparticles to boost activities. This strategy was also successful in identifying catalysts optimizing multiple performance metrics, by adapting the model to search for systems maximizing STYHA while minimizing , in view of the insensitivity of SHA to compositional and operational variations for this family of materials. This task uncovered an intrinsic trade-off between the two performance metrics and aided in the discovery of Pareto-optimal catalysts, a challenge not easily tackled by human experts. Finally, key performance drivers were quantified via SHAP analysis, and based on the insights gathered, formulate data-informed guidelines to assist catalysis practitioners in developing performance-specific FeCoCuZr catalysts for HAS.
The presented active learning framework can be expanded to carry out further optimization within this catalyst family such as adding carrier materials or promoters. Nevertheless, given the data-driven nature of this active learning framework, independent of the reaction or specific catalyst properties, it can be extended beyond the FeCoCuZr family and HAS. From a broader perspective, this work demonstrates active learning as an innovative tool that can go beyond traditional design strategies to largely accelerate catalyst development, while minimizing economic and environmental resource utilization, advocating towards more sustainable laboratories.
Methods
Catalyst synthesis
FexCoyCuzZra catalysts with molar Fe, Co, Cu, and Zr contents of x, y, z and a (metals basis, units of mol%), respectively, were prepared via a sol-gel method. Appropriate amounts of metal precursors [Fe(NO3)3·9H2O (Sigma-Aldrich, 98%), Co(NO3)2·6H2O (abcr, 98%), Cu(NO3)2·3H2O (Sigma-Aldrich, 98%), and ZrO(NO3)2·xH2O (Thermo Fischer Scientific, 99.5%)] required for a total metal concentration of 0.25 M with the targeted nominal metal contents were dissolved in 100 cm3 of ethanol (Fisher Scientific, 99.8%) in a 500 cm3 round bottom flask. A 100 cm3 solution of 0.5 M L-(+)-tartaric acid (99.5%, Sigma-Aldrich) was added dropwise to the metal precursor solution under magnetic stirring (ca. 1000 rpm) for 12 h. The resulting gel containing a metal-tartrate complex was separated from excess solvent using a Büchi Rotavapor R-114 instrument at 323 K and 100 mbar. The colloids obtained were dried in a vacuum oven at 383 K for 12 h, ground into a fine powder and calcined in static air at 673 K (2 K min−1) for 3 h.
Catalyst evaluation
The direct conversion of syngas to higher alcohols was conducted using a PID Eng&Tech high-pressure continuous-flow setup comprising four parallel fixed-bed reactors (main features in Supplementary Fig. 13). Sieved powder catalyst as calcined (50 mg, particle size = 0.15–0.30 mm) were diluted with quartz sand (75 mg, particle size = 0.15–0.30 mm) and loaded into each reactor tube (internal diameter 4 mm), held in place by a 2 mm bed of quartz wool set on a quartz frit. Catalysts were activated in situ to reduce surface metal oxides under a 20 cm3 min–1 flow of 50 vol.% H2 (PanGas, purity 5.0) in Ar (PanGas, 5.0) at atmospheric pressure and T = 623 K (5 K min–1) for 4 h. After the reactors were cooled to the reaction temperature and pressurized to the reaction pressure of 50 bar under Ar flow, the reaction mixture of CO (Messer, 3.0) H2, and Ar with the desired composition was fed into each reactor at the desired volumetric flow rates, with the fraction of Ar fixed at 10 mol% as an internal standard.
Effluent streams were analyzed by gas chromatography (GC, Agilent 8890) every 2 h, with calculations performed taking average values of 3 measurements between ca. 8 and 12 h on stream. Response factors, Fi, for each compound i, respective to the internal standard Ar, in the GC analysis were determined by calibration using Eq. (1),
| 1 |
where Ai is the integrated area determined for the peak of compound i measured by the respective detector, and ciin is the corresponding known molar concentration in the sampled calibration mixture. Representative GC results are shown in Supplementary Fig. 14.
The unknown effluent molar flow of compound i, niout, was determined using Eq. (2),
| 2 |
where is the known flow of Ar at the reactor outlet.
The overall CO conversion (XCO) was calculated using Eq. (3),
| 3 |
where nCO,in and nCO,out are the inlet and outlet CO molar flows, respectively. The selectivity for product i (Si) was calculated using Eq. (4),
| 4 |
where ni,out and NC,i are the molar flow and the number of carbon atoms in product i, respectively. The selectivity to higher alcohols and hydrocarbons were obtained summing the individual selectivity to alcohols and hydrocarbons with two or more carbon atoms. The space time yield of higher alcohols (STYHA) expressed in gHA h−1 gcat−1 was calculated using Eq. (5),
| 5 |
where mcat is the mass of the catalyst and MWj,HA is the molecular weight of higher alcohols containing j carbon atoms.
The carbon balance (δC) was determined according to Eq. 6 and showed always less than a 5% difference between the reactant and product streams.
| 6 |
Catalyst characterization
X-ray fluorescence spectroscopy (XRF) was performed with an Orbis Micro-EDXRF spectrometer equipped with a Rh source and a silicon drift detector operated at 35 kV and 500 μA.
X-ray diffraction (XRD) was conducted using a Rigaku SmartLab diffractometer with a D/teX Ultra 250 detector using Cu Kα radiation (λ = 0.1541 nm) and operating in a Bragg-Brentano geometry. Data were acquired in the 5–80°2θ range with an angular step size of 0.025° and a counting time of 1.5 s per step.
Temperature-programmed reduction with hydrogen (H2-TPR) was performed at ambient pressure using a Micromeritics AutoChem HP II analyzer. Samples were loaded into a quartz tube, dried at 423 K in Ar for 1 h (10 K min–1), and cooled to 313 K (20 K min–1) in Ar. The temperature-programmed reduction was then carried out using 5 vol.% H2 in N2 (Messer) and increasing the temperature to 1073 K (5 K min–1) with H2 consumption quantified by a thermal conductivity detector.
Temperature-programmed H2-D2 exchange was performed using a Micromeritics AutoChem HP II analyzer coupled to a Pfeiffer OMNIStar mass spectrometer (MS). Used samples were loaded into a quartz tube, dried at 423 K in Ar for 1 h (10 K min–1), and cooled to 313 K (20 K min–1) in Ar. The H2-D2 exchange reaction was then carried out under 10 vol.% D2 (Sigma-Aldrich, 99.8%) and 5 vol.% H2 in N2 (Messer) and increasing the temperature to 873 K (5 K min–1), with the outlet flow of H2, D2 and HD quantified by online MS.
High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) coupled to energy-dispersive X-ray (EDX) spectroscopy and elemental mapping were conducted using a Talos F200X instrument equipped with four silicon drift detectors (SDD) operated at an acceleration potential of 200 kV.
X-ray photoelectron spectroscopy (XPS) was performed using a Physical Electronics (PHI) Quantum 2000 X-ray photoelectron spectrometer featuring monochromatic Al Kα radiation, generated from an electron beam operated at 15 kV and 32.3 W and a hemispherical capacitor electron-energy analyzer equipped with a channel plate and a position-sensitive detector. Analyses were conducted at 2 × 10–7 Pa, with an electron takeoff angle of 45°, operating the analyzer in the constant pass energy mode. Prior to the measurements, used samples diluted with quartz sand were ground and pressed firmly onto indium foil. The energy scale of the instrument was calibrated using Au and Cu as reference samples.
Diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) was performed using a Bruker Invenio S FT-IR spectrometer. The pre-reduced sample was mixed with α-Al2O3 in a 1:2 mass ratio and inserted into the cell, subjected to in situ reduction in flowing H2/He (50 vol.%) at 623 K for 2 h, and cooled down to 493 K in He. After pressurizing the cell to 20 bar under He flow, the background was collected once the pressure and IR signal stabilized. Continuous spectra at 1-min intervals with a resolution of 4 cm−1 were collected upon switching to the CO/H2 reaction mixture.
Gaussian process and Bayesian optimization
As the mathematical relationship between the catalyst composition and reaction conditions to the catalyst performance metrics (STYHA and/or ) is unknown, the optimization procedure is treated as a black-box function. In this study, Gaussian processes (GP) and Bayesian optimization (BO) were utilized to solve such black-box functions. We opt for a BO with GP surrogate model for the following reasons: (i) the input features and target variable are continuous in nature, (ii) implementation of GP-BO is less sensitive to the initial choice of hyperparameter, (iii) BO is known to require smaller initial datasets and fewer iterations to reach the optimal than genetic algorithms, and (iv) the uncertainty of GP surrogate model enables effective trade-off selection between exploration and exploitation, which can eventually foster efficient sampling of the chemical and parametric space of the catalyst23,25,46.
A GP is a non-parametric and probabilistic model that defines a distribution over possible functions on the observed data, as described in Eq. (7),
| 7 |
where m(x) is the mean function and k(x,x’) is the covariance function.
The mean and covariance kernel function in the Gaussian process was chosen and tuned during the model building process. Common kernel functions include constant, linear, square exponential, etc. We assume a constant mean function for simplicity and choose the squared exponential kernel to capture the smooth functions sampled by the GP, according to Eqs. (8)–(9),
| 8 |
| 9 |
where is a constant, is the variance parameter, is the lengthscale parameter and is the squared Euclidean distance between the two input datapoints. Details of the lengthscale parameters and their optimal values are presented in Supplementary Note 7 and Supplementary Table 30, respectively.
The acquisition function of BO is a key attribute used to guide the selection of the optimal set of solutions by balancing exploration (sampling regions where the objective function is uncertain) and exploitation (sampling regions where the objective function is likely to be optimal). Depending on single or multi-objective optimization, and to strike a balance between exploration and exploitation, various acquisition functions can be selected, such as expected improvement (EI), predictive variance (PV), upper confidence bound (UCB), and expected hypervolume improvement (EHVI), etc23,35,46.
The BO campaigns with local penalization was implemented to recommend a batch of 30 data points to align with the experimental setup. For single objective optimization in Phase 1 and 2, we use a combination of EI and PV as acquisition functions given by Eq. (10)-,
| 10 |
| 11 |
where x is the point at which the objective function is evaluated, is the predicted mean of the objective function at point x, is the best observed value, denotes the expected value, and is a small positive constant, that controls model improvement.
In Phase 3, the EHVI acquisition function was selected for multi-objective optimization, as described by Eq. (12),
| 12 |
where x is the point at which the objective function is evaluated, is the hypervolume of the dominated space by the current Pareto front D, is the hypervolume of the dominated space when x is added to the current Pareto front, and denotes the expected value. We highlight that the configuration of multi-objective optimization herein holds distinctive features from those reported in literature35,37,54,59. In our work, target variables are optimized by simultaneously varying the chemical composition and reaction conditions of the catalysts, which is computationally expensive and experimentally challenging. Another aspect is the indirect approach of the multi-objective optimization. Despite the initial goal being to simultaneously maximize STYHA and SHA, the modest improvements to the latter, likely induced by intrinsic limitations of these catalysts, motivated us to minimize (undesired products), which is an indirect approach to improve overall selectivity to valuable products, including higher alcohols, alkanes, and olefins. However, devising such strategies requires mechanistic understanding of higher alcohols synthesis and product distribution, which were effectively incorporated to identify several Pareto-optimal FeCoCuZr catalysts. Details of the model architecture and hyperparameter tuning for the GP-BO algorithms along with the optimal hyperparameters in each active learning cycle across all the three Phases are presented in Supplementary Note 7 and Supplementary Table 30.
Implementation of the active learning loop
The generic workflow of the active learning across the various phases in this study followed a systematic sequence as described below:
-
(i)
an initial set of experiments is planned and a series of catalysts with unique formulations is synthesized.
-
(ii)
these catalysts are subjected to varying reaction conditions and their catalytic performance measured in terms of STYHA, SHA, XCO, etc., are evaluated,
-
(iii)
the experimental data (i.e., XRF-measured catalyst composition and reaction conditions) are used to train a GP regressor model, such that it predicts the performance metrics of interest (e.g., STYHA)
-
(iv)
the output of the GP prediction feeds to a BO algorithm, which in turn recommends the next set of experiments worth investigating. For each cycle Phases 1 and 2, a list of 30 catalytic systems is generated by using the EI function. This is followed by the generation of separate list of 30 candidates by using the PV function. In Phase 3, the EHVI function was used to generate 30 recommendations per cycle.
-
(v)
The combined set of recommended catalysts from the step (iv) are manually screened and 6 catalysts are selected worth experimentation based on human-decision making the following criteria: high STYHA yielding catalysts (based on EI), diverse catalyst composition and reaction condition (based on PV), and avoid repetition from previous cycles as much as possible.
-
(vi)
the steps (i)-(v) are iteratively performed until the performance metric(s) of interest is achieved or no further improvements are observed, eventually leading to the stop criterion.
Model quantification
To evaluate model performance, the predicted values of STYHA and were compared with their respective experimentally measured counterparts, and the R2, RMSE, and MAPE values were calculated using Eqs. (13)–(15). Conceptually, high values of R2 and low values of RMSE and MAPE indicate high model accuracy57,60.
| 13 |
| 14 |
| 15 |
where and are the predicted and measured values of the target variable, respectively, is the mean of all measured values of the target variable, and n is the total number of datapoints.
In addition to experimental verification, the evaluation of the predictive reliability of the Gaussian process model was performed by cross-validation at the end of each Phase. Given the small sample size i.e., 30, 36 and 18 datapoints, generated from the active learning loop, in Phases 1, 2, and 3 respectively, the stratified cross-validation technique was applied for this task. (See Supplementary Note 8 and Supplementary Table 31 for an extended discussion).
Composition-productivity relationship
The unsupervised k-means algorithm was used to investigate the effect of varying composition on STYHA, such that all the catalysts synthesized and tested in Phase 1 were grouped into distinct clusters. This algorithm identifies homogeneous subgroups of features in a given dataset60. In an n-dimensional space with m features, the algorithm divides the features into k clusters (where k ≤ n), minimizing the sum of squares within each cluster. Similarity between features within a cluster is determined by their distance, commonly measured using Euclidean distance. The objective function of k-means is expressed in Eq. (14) and the optimal number of k clusters was identified using the Elbow method.
| 16 |
where J is the objective function, is the ith datapoint, is jth cluster centre (centroid), and k is the number of clusters.
Feature-importance analysis
We employed a posteriori feature-importance using the SHAP (SHapley Additive exPlanations) on the GP algorithm to quantitatively estimate the contributions of each input feature on the model predictions, referred as interpretability. For each experimental datapoint, this methodology perturbs the features and determines importance value for every prediction. Furthermore, by averaging SHAP values across the entire dataset, the overall importance of input features is determined. As such, it facilitates local and global interpretability, respectively, with higher-ranked features exhibiting larger SHAP values and vice versa56–58.
All modeling activities were performed in Python (version 3.6), using libraries including Pandas 2.0.3 and NumPy 1.24.3 for data analysis, scikit-learn 1.3.0 for performing k-means clustering and data analysis, GPflow 2.9.0 and Trieste 1.2.0 for implementing the GP and BO algorithms, respectively and Shap 0.40.0 for model interpretation.
Supplementary information
Acknowledgements
This study was created as part of NCCR Catalysis (grant number 180544), a National Centre of Competence in Research funded by the Swiss National Science Foundation and was supported by Sulzer Chemtech AG. T.Z. thanks the Agency for Science, Technology and Research (A*STAR) Singapore for support through a graduate fellowship. The Scientific Center for Optical and Electron Microscopy (ScopeM) at ETH Zurich is thanked for access to their facilities. Dr. D. Faust Akl, Dr. F. Krumeich, and V. Giulimondi are acknowledged for STEM-EDX and XPS measurements. We are grateful to Dr. P. Preikschas and A. Nabera for fruitful discussions on the manuscript and assistance with environmental and economic cost calculations. C. Ko is thanked for help with illustrations.
Author contributions
M.S., T.Z., A.J.M., and J.P.R. conceptualized the stages of this project. M.S. developed the software codes and performed data analysis with assistance from S.H.C. T.Z. and S.H.C. synthesized the catalysts and performed the catalytic tests. T.Z. and Y.G. conducted catalyst characterization experiments and analyzed the data. A.J.M supervised the work and reviewed the manuscript. J.P.R. conceived and supervised the entire project, reviewed the manuscript, and managed resources and funding. All the authors provided inputs to the manuscript and approved the final version.
Peer review
Peer review information
Nature Communications thanks Hao Liu, Joshua Schrier and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Data availability
The curated dataset generated in this study have been deposited in the Zenodo database (10.5281/zenodo.11113829). Further data supporting the findings of this study are provided in the Supplementary Information and Source Data file.
Code availability
The curated dataset and the Python codes for data pre-processing and fine-tuning the Bayesian optimization along with necessary instructions to run the model can be found on GitHub at https://github.com/ssuvarnamanu/active-learning-for-HAS.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Manu Suvarna, Tangsheng Zou.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-50215-1.
References
- 1.Xu D, et al. Advances in higher alcohol synthesis from CO2 hydrogenation. Chem. 2021;7:849–881. doi: 10.1016/j.chempr.2020.10.019. [DOI] [Google Scholar]
- 2.Zeng F, et al. Catalysts design for higher alcohols synthesis by CO2 hydrogenation: trends and future perspectives. Appl. Catal. B Environ. 2021;291:120073. doi: 10.1016/j.apcatb.2021.120073. [DOI] [Google Scholar]
- 3.Lazier, W. A. Catalytic process (US1746783A) (1928).
- 4.Henry, D. Manufacture of oxygenated organic compounds (US1963119A) (1930).
- 5.Subramani V, Gangwal SK. A review of recent literature to search for an efficient catalytic process for the conversion of syngas to ethanol. Energy Fuels. 2008;22:814–839. doi: 10.1021/ef700411x. [DOI] [Google Scholar]
- 6.Luk HT, et al. Status and prospects in higher alcohols synthesis from syngas. Chem. Soc. Rev. 2017;46:1358–1426. doi: 10.1039/C6CS00324A. [DOI] [PubMed] [Google Scholar]
- 7.Xiaoding X, Doesburg EBM, Scholten JJF. Synthesis of higher alcohols from syngas - recently patented catalysts and tentative ideas on the mechanism. Catal. Today. 1987;2:125–170. doi: 10.1016/0920-5861(87)80002-0. [DOI] [Google Scholar]
- 8.Mäki-Arvela P, Aho A, Simakova I, Yu. Murzin D. Sustainable aviation fuel from syngas through higher alcohols. ChemCatChem. 2022;14:e202201005. doi: 10.1002/cctc.202201005. [DOI] [Google Scholar]
- 9.Spivey JJ, Egbebi A. Heterogeneous catalytic synthesis of ethanol from biomass-derived syngas. Chem. Soc. Rev. 2007;36:1514–1528. doi: 10.1039/b414039g. [DOI] [PubMed] [Google Scholar]
- 10.Guo L, Guo X, He Y, Tsubaki N. CO2 heterogeneous hydrogenation to carbon-based fuels: recent key developments and perspectives. J. Mater. Chem. A. 2023;11:11637–11669. doi: 10.1039/D3TA01025B. [DOI] [Google Scholar]
- 11.Bhat S, Pagán-Torres YJ, Nikolla E. Strategies for designing the catalytic environment beyond the active site of heterogeneous supported metal catalysts. Top. Catal. 2023;66:1217–1243. doi: 10.1007/s11244-023-01835-2. [DOI] [Google Scholar]
- 12.Xiang Y, et al. Long-chain terminal alcohols through catalytic CO hydrogenation. J. Am. Chem. Soc. 2013;135:7114–7117. doi: 10.1021/ja402512r. [DOI] [PubMed] [Google Scholar]
- 13.Xiang Y, Kovarik L, Kruse N. Rate and selectivity hysteresis during the carbon monoxide hydrogenation over promoted Co/MnOx catalysts. Nat. Commun. 2019;10:3953. doi: 10.1038/s41467-019-11836-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li Y, et al. Interfacial Fe5C2-Cu catalysts toward low-pressure syngas conversion to long-chain alcohols. Nat. Commun. 2020;11:61. doi: 10.1038/s41467-019-13691-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hu J, et al. Edge-rich molybdenum disulfide tailors carbon-chain growth for selective hydrogenation of carbon monoxide to higher alcohols. Nat. Commun. 2023;14:6808. doi: 10.1038/s41467-023-42325-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Medford AJ, et al. Activity and selectivity trends in synthesis gas conversion to higher alcohols. Top. Catal. 2014;57:135–142. doi: 10.1007/s11244-013-0169-0. [DOI] [Google Scholar]
- 17.Yang N, et al. Intrinsic selectivity and structure sensitivity of rhodium catalysts for C2+ oxygenate production. J. Am. Chem. Soc. 2016;138:3705–3714. doi: 10.1021/jacs.5b12087. [DOI] [PubMed] [Google Scholar]
- 18.Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature. 2018;559:547–555. doi: 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
- 19.Peng J, et al. Human- and machine-centred designs of molecules and materials for sustainability and decarbonization. Nat. Rev. Mater. 2022;7:991–1009. doi: 10.1038/s41578-022-00466-5. [DOI] [Google Scholar]
- 20.Kitchin JR. Machine learning in catalysis. Nat. Catal. 2018;1:230–232. doi: 10.1038/s41929-018-0056-y. [DOI] [Google Scholar]
- 21.Toyao T, et al. Machine learning for catalysis informatics: recent applications and prospects. ACS Catal. 2020;10:2260–2297. doi: 10.1021/acscatal.9b04186. [DOI] [Google Scholar]
- 22.Suvarna, M. & Pérez-Ramírez, J. Embracing data science in catalysis research. Nat. Catal. 7, 624–635 (2024).
- 23.Lookman T, Balachandran PV, Xue D, Yuan R. Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design. Npj Comput. Mater. 2019;5:1–17. doi: 10.1038/s41524-019-0153-8. [DOI] [Google Scholar]
- 24.Sun S, et al. Accelerated development of perovskite-inspired materials via high-throughput synthesis and machine-learning diagnosis. Joule. 2019;3:1437–1451. doi: 10.1016/j.joule.2019.05.014. [DOI] [Google Scholar]
- 25.Yuan X, et al. Active learning-based guided synthesis of engineered biochar for CO2 capture. Environ. Sci. Technol. 2024;58:6628–6636. doi: 10.1021/acs.est.3c10922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.MacLeod BP, et al. Self-driving laboratory for accelerated discovery of thin-film materials. Sci. Adv. 2020;6:eaaz8867. doi: 10.1126/sciadv.aaz8867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kusne AG, et al. On-the-fly closed-loop materials discovery via Bayesian active learning. Nat. Commun. 2020;11:5966. doi: 10.1038/s41467-020-19597-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Jablonka KM, Jothiappan GM, Wang S, Smit B, Yoo B. Bias free multiobjective active learning for materials design and discovery. Nat. Commun. 2021;12:2312. doi: 10.1038/s41467-021-22437-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Murphy RF. An active role for machine learning in drug development. Nat. Chem. Biol. 2011;7:327–330. doi: 10.1038/nchembio.576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.HamediRad M, et al. Towards a fully automated algorithm driven platform for biosystems design. Nat. Commun. 2019;10:5150. doi: 10.1038/s41467-019-13189-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tallorin L, et al. Discovering de novo peptide substrates for enzymes using machine learning. Nat. Commun. 2018;9:5253. doi: 10.1038/s41467-018-07717-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhong M, et al. Accelerated discovery of CO2 electrocatalysts using active machine learning. Nature. 2020;581:178–183. doi: 10.1038/s41586-020-2242-8. [DOI] [PubMed] [Google Scholar]
- 33.Ge, X. et al. Atomic design of alkyne semihydrogenation catalysts via active learning. J. Am. Chem. Soc. 146, 4993–5004 (2024). [DOI] [PubMed]
- 34.Moon J, et al. Active learning guides discovery of a champion four-metal perovskite oxide for oxygen evolution electrocatalysis. Nat. Mater. 2024;23:108–115. doi: 10.1038/s41563-023-01707-w. [DOI] [PubMed] [Google Scholar]
- 35.Ramirez, A. et al. Accelerated exploration of heterogeneous CO2 hydrogenation catalysts by Bayesian-optimized high-throughput and automated experimentation. Chem Catal. 4, 100888 (2024).
- 36.Wang G, et al. Accelerated discovery of multi-elemental reverse water-gas shift catalysts using extrapolative machine learning approach. Nat. Commun. 2023;14:5861. doi: 10.1038/s41467-023-41341-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim M, et al. Searching for an optimal multi-metallic alloy catalyst by active learning combined with experiments. Adv. Mater. 2022;34:2108900. doi: 10.1002/adma.202108900. [DOI] [PubMed] [Google Scholar]
- 38.Nguyen TN, et al. High-throughput experimentation and catalyst informatics for oxidative coupling of methane. ACS Catal. 2020;10:921–932. doi: 10.1021/acscatal.9b04293. [DOI] [Google Scholar]
- 39.Luk HT, et al. Role of carbonaceous supports and potassium promoter on higher alcohols synthesis over copper-iron catalysts. ACS Catal. 2018;8:9604–9618. doi: 10.1021/acscatal.8b02714. [DOI] [Google Scholar]
- 40.Xu J, et al. Precisely synergistic synthesis of higher alcohols from syngas over iron carbides. Chem. Catal. 2023;3:100584. doi: 10.1016/j.checat.2023.100584. [DOI] [Google Scholar]
- 41.Xiang Y, Kruse N. Tuning the catalytic CO hydrogenation to straight- and long-chain aldehydes/alcohols and olefins/paraffins. Nat. Commun. 2016;7:13058. doi: 10.1038/ncomms13058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Prieto G, et al. Design and synthesis of copper-cobalt catalysts for the selective conversion of synthesis gas to ethanol and higher alcohols. Angew. Chem. Int. Ed. 2014;53:6397–6401. doi: 10.1002/anie.201402680. [DOI] [PubMed] [Google Scholar]
- 43.Liu G, Yang G, Peng X, Wu J, Tsubaki N. Recent advances in the routes and catalysts for ethanol synthesis from syngas. Chem. Soc. Rev. 2022;51:5606–5659. doi: 10.1039/D0CS01003K. [DOI] [PubMed] [Google Scholar]
- 44.Ao M, Pham GH, Sunarso J, Tade MO, Liu S. Active centers of catalysts for higher alcohol synthesis from syngas: a review. ACS Catal. 2018;8:7025–7050. doi: 10.1021/acscatal.8b01391. [DOI] [Google Scholar]
- 45.Ge Y, Zou T, Martín AJ, Pérez-Ramírez J. ZrO2-promoted Cu-Co, Cu-Fe and Co-Fe catalysts for higher alcohol synthesis. ACS Catal. 2023;13:9946–9959. doi: 10.1021/acscatal.3c02534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shields BJ, et al. Bayesian reaction optimization as a tool for chemical synthesis. Nature. 2021;590:89–96. doi: 10.1038/s41586-021-03213-y. [DOI] [PubMed] [Google Scholar]
- 47.Tran K, Ulissi ZW. Active learning across intermetallics to guide discovery of electrocatalysts for CO2 reduction and H2 evolution. Nat. Catal. 2018;1:696–703. doi: 10.1038/s41929-018-0142-1. [DOI] [Google Scholar]
- 48.Kunkel C, Margraf JT, Chen K, Oberhofer H, Reuter K. Active discovery of organic semiconductors. Nat. Commun. 2021;12:2422. doi: 10.1038/s41467-021-22611-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ge, Y., et al. Defective zirconia promotes monometallic iron catalysts for higher alcohol synthesis. Chem. Catal. 4, 101010 (2024).
- 50.Chen Y, et al. Carbon-supported Fe catalysts with well-defined active sites for highly selective alcohol production from Fischer-Tropsch synthesis. Appl. Catal. B Environ. 2022;312:121393. doi: 10.1016/j.apcatb.2022.121393. [DOI] [Google Scholar]
- 51.Ning, S. et al. Natural sunlight-driven CO2 hydrogenation into light olefins at ambient pressure over bifunctional Cu-promoted CoFe alloy catalyst. Adv. Funct. Mater. 34, 2400798.
- 52.Jung K-D, Bell AT. Role of hydrogen spillover in methanol synthesis over Cu/ZrO2. J. Catal. 2000;193:207–223. doi: 10.1006/jcat.2000.2881. [DOI] [Google Scholar]
- 53.Torres JAG, et al. A multi-objective active learning platform and web app for reaction optimization. J. Am. Chem. Soc. 2022;144:19999–20007. doi: 10.1021/jacs.2c08592. [DOI] [PubMed] [Google Scholar]
- 54.MacLeod BP, et al. A self-driving laboratory advances the Pareto front for material properties. Nat. Commun. 2022;13:995. doi: 10.1038/s41467-022-28580-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schrier J, Norquist AJ, Buonassisi T, Brgoch J. In pursuit of the exceptional: research directions for machine learning in chemical and materials science. J. Am. Chem. Soc. 2023;145:21699–21716. doi: 10.1021/jacs.3c04783. [DOI] [PubMed] [Google Scholar]
- 56.Lundberg SM, et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020;2:56–67. doi: 10.1038/s42256-019-0138-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Suvarna M, Araújo TP, Pérez-Ramírez J. A generalized machine learning framework to predict the space-time yield of methanol from thermocatalytic CO2 hydrogenation. Appl. Catal. B Environ. 2022;315:121530. doi: 10.1016/j.apcatb.2022.121530. [DOI] [Google Scholar]
- 58.Esterhuizen JA, Goldsmith BR, Linic S. Interpretable machine learning for knowledge generation in heterogeneous catalysis. Nat. Catal. 2022;5:175–184. doi: 10.1038/s41929-022-00744-z. [DOI] [Google Scholar]
- 59.Bennett JA, et al. Autonomous reaction Pareto-front mapping with a self-driving catalysis laboratory. Nat. Chem. Eng. 2024;1:240–250. doi: 10.1038/s44286-024-00033-5. [DOI] [Google Scholar]
- 60.Suvarna M, Preikschas P, Pérez-Ramírez J. Identifying descriptors for promoted rhodium-based catalysts for higher alcohol synthesis via machine learning. ACS Catal. 2022;12:15373–15385. doi: 10.1021/acscatal.2c04349. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The curated dataset generated in this study have been deposited in the Zenodo database (10.5281/zenodo.11113829). Further data supporting the findings of this study are provided in the Supplementary Information and Source Data file.
The curated dataset and the Python codes for data pre-processing and fine-tuning the Bayesian optimization along with necessary instructions to run the model can be found on GitHub at https://github.com/ssuvarnamanu/active-learning-for-HAS.








