Evaluating synthetic neuroimaging data augmentation for automatic brain tumour segmentation with a deep fully-convolutional network

Abstract

Gliomas observed in medical images require expert neuro-radiologist evaluation for treatment planning and monitoring, motivating development of intelligent systems capable of automating aspects of tumour evaluation. Deep learning models for automatic image segmentation rely on the amount and quality of training data. In this study we developed a neuroimaging synthesis technique to augment data for training fully-convolutional networks (U-nets) to perform automatic glioma segmentation. We used StyleGAN2-ada to simultaneously generate fluid-attenuated inversion recovery (FLAIR) magnetic resonance images and corresponding glioma segmentation masks. Synthetic data were successively added to real training data (n = 2751) in fourteen rounds of 1000 and used to train U-nets that were evaluated on held-out validation (n = 590) and test sets (n = 588). U-nets were trained with and without geometric augmentation (translation, zoom and shear), and Dice coefficients were computed to evaluate segmentation performance. We also monitored the number of training iterations before stopping, total training time, and time per iteration to evaluate computational costs associated with training each U-net. Synthetic data augmentation yielded marginal improvements in Dice coefficients (validation set +0.0409, test set +0.0355), whereas geometric augmentation improved generalization (standard deviation between training, validation and test set performances of 0.01 with, and 0.04 without geometric augmentation). Based on the modest performance gains for automatic glioma segmentation we find it hard to justify the computational expense of developing a synthetic image generation pipeline. Future work may seek to optimize the efficiency of synthetic data generation for augmentation of neuroimaging data.

1. Introduction

Gliomas are cancerous tumors that predominantly originate within the brain and sometimes occur in the spinal cord. They represent 33% of all brain tumors and 80% of malignant brain tumors (Ostrom et al., 2015). Patients with glioma require immediate medical attention, and time is a crucial aspect of successful treatment (Ostrom et al., 2019). Surgical options and other therapeutic courses of action vary widely due to heterogeneity in glioma presentation among patients (Wu et al., 2021). Analysis of tumor morphology, density and regional distribution observed from medical images forms a key component of treatment planning and monitoring. Fast and accurate volumetric assessments of glioma are desirable for these purposes, leading to the development of computational tools for automatic analysis of neuroimaging data that are capable of evaluating gliomas.

Deep learning models are studied for analyzing gliomas in magnetic resonance (MR) images. These have been employed to extract features, analyze patterns, and classify neuroimaging data with high accuracy (Dang et al., 2022, Shaver et al., 2019). They have been used pre-treatment to analyze tumor genotype, perform grading or severity checks, and predict the best course of action; they have also been used post-treatment to monitor progress and predict survivability (Shaver et al., 2019). Unfortunately, data availability limits the development of fully-generalizable deep learning approaches for glioma analysis. Sufficient quantities of labelled neuroimaging data from glioma patients are difficult to obtain due to privacy-related concerts, scarcity of qualified annotators, time required to label data, and heterogeneity of tumor presentation, which can also lead to imbalanced datasets (Anaya-Isaza et al., 2021, Perone and Cohen-Adad, 2019).

Geometric and synthetic data augmentation are two strategies for overcoming data availability limitations for training deep neural networks (Dang et al., 2022, Shorten and Khoshgoftaar, 2019). Geometric data augmentation involves randomly altering images in the training dataset with geometric transformations (e.g., translation, rotation, zooming and shear), thereby amplifying the number of unique pixel arrangements used for training, which can improve generalization to out-of-sample data. These were implemented by leading entries in the Multimodal Brain Tumor Segmentation (BraTS) Challenge 2018 (Nalepa et al., 2019b), which highlighted affine, pixel-level and elastic deformations as particularly effective for application to glioma segmentation (Isensee et al., 2019, McKinley et al., 2019, Myronenko, 2019). However, it has been argued that these traditional image processing techniques generate augmented data with limited diversity (Basaran et al., 2022, Shin et al., 2018, Zhang et al., 2023). In contrast, synthetic data augmentation involves generating a set of new artificial images, rather than simply altering existing ones, that are added to the training dataset, potentially yielding more diverse augmented images. Synthetic data augmentation is an area of active research, with differences in implementation details (e.g., method of synthetic image generation, and data management) potentially yielding variable results (Carver et al., 2021, Cha et al., 2019, Foroozandeh and Eklund, 2020, Larsson et al., 2022, Subramaniam et al., 2022). However, synthetic and geometric data augmentation are not mutually exclusive, and can be combined in an effort to improve their value for training deep neural networks.

Generative adversarial networks (GANs) were proposed by Goodfellow et al. (2014). These are generative models designed to produce artificial data, closely associated with synthetic image generation. The concept of GAN training is based on game theory, whereby a generator network outputs artificial images and a discriminator network classifies them as either genuine or counterfeit. Generator and discriminator are trained in competition such that they both gradually become proficient. After training the generator can be used to synthesize data. In the domain of image generation, both generator and discriminator are generally convolutional neural networks (CNNs), whose design is inspired by the hierarchical organisation of the visual cortex (LeCun et al., 1998). Interestingly, GANs might also have a neurobiological counterpart as postulated by predictive coding theory (Friston, 2005, O’Reilly, 2022, O’Reilly, 2021, Rao and Ballard, 1999). These artificial neural networks have been reciprocally applied to support research in the field that inspired their development, including application to neuroimaging data for image synthesis, segmentation, pathology diagnosis, and image reconstruction (Ali et al., 2022, Chen et al., 2021, Dang et al., 2022, Nguyen et al., 2022).

Several studies have employed GANs for assisting in glioma segmentation for volumetric analysis. Yu et al. (2018) used a conditional GAN (cGAN) to generate T2 fluid-attenuated inversion recovery (FLAIR) images from T1-weighted MR images, and then used the higher-contrast generated images to segment brain tumors. A somewhat similar approach was taken by Hamghalam et al. (2020a), who trained a CycleGAN (Zhu et al., 2017) to translate low-contrast MR images into high-contrast equivalent images to enhance brain tumour segmentation. The same group also used a cGAN to enhance data for pixel-wise segmentation, achieving a Dice coefficient of 0.89 (Hamghalam et al., 2020b). Lee et al. (2020) attempted to address the issue of data scarcity by using a CycleGAN to transfer the style of MR images to brain tumour segmentation masks, and then evaluate the benefits of using that synthetic data for automatic segmentation. Carver et al. (2021) later trained GANs to generate four types of brain MR image (T1, post-contrast T1, T2, and FLAIR) to accompany manually altered tumour segmentation masks. These were used for synthetic data augmentation for a U-net (Ronneberger et al., 2015) trained to perform automatic tumour segmentation, reportedly improving Dice coefficient by 4.8%. The human-in-the-loop requirement for manual manipulation of segmentation masks introduces a potential source of bias and greater workload that limits the practicality of this approach.

In this study, we aimed to develop a fully-automatic synthetic data augmentation and segmentation pipeline for volumetric assessment of gliomas in FLAIR neuroimaging data. We investigated the computational costs and benefits of synthetic data augmentation with state-of-the-art StyleGAN2-ada (Karras et al., 2020, Karras et al., 2019), and compared this with and without geometric data augmentation. This research therefore provides evidence concerning appropriate data augmentation strategies for automatic glioma segmentation.

2. Materials and Methods

2.1. Data

The dataset used in this study was originally derived from The Cancer Imaging Archive (TCIA) (Clark et al., 2013, Pedano et al., 2016). It consists of multi-sequence MR images of lower grade glioma patient brains with corresponding manual segmentation masks. Genetic cluster information included with this dataset was not used in the present study. Collectively, there were 110 scans from different patients. Two of the MR sequences (T1 and T2) were unavailable for some patients, although the FLAIR sequences were completed for all patients. The same dataset has been used previously for identifying genetically influenced morphological subtypes of gliomas (Buda et al., 2019, Mazurowski et al., 2017).

The FLAIR sequence images (8-bit) were extracted and paired with their binary tumor segmentation masks. These were uniformly sized 256 × 256 pixels. The masks encoded tumor and non-tumor pixels with values 0 and 1, respectively. Images that did not contain tumor tissue initially did not have corresponding masks, so these were produced automatically by populating matrices of equal size with zeros. For preprocessing, scans were loaded and standardized before clipping in the range [− 2, 7] then normalizing to the range [0,255]. From 110 scans there were 3929 images. These were listed consecutively in scan order and the first 2751 (70%) were assigned for training, the next 590 (15%) were assigned for validation, and the remaining 588 (15%) were set aside for testing. This approach mitigates data leakage that could otherwise occur with random image splitting; importantly, this excluded the possibility of data leakage between training and testing datasets.

2.2. Generative model

2.2.1. Data pre-processing

The aforementioned training dataset was used to train a generative model (StyleGAN2-ada; Karras et al., 2020). Validation and test sets were not used to avoid potential data leakage that could affect performance of segmentation models subsequently trained with synthetic data augmentation and evaluated using the same validation and test sets. Three-channel images were prepared from the training dataset to train the GAN, as illustrated in Fig. 1. The FLAIR sequence images were copied into green and blue channels, while the corresponding masks were inserted into red channels. This approach allows the GAN to simultaneously generate neuroimaging and labelling data after training, rather than requiring manually manipulated tumour segmentation masks (Carver et al., 2021). When it was time to augment data for training the segmentation model, these three-channel GAN-generated images were separated into greyscale FLAIR and mask images. Green and blue channels were averaged to produce artificial FLAIR images, and binary thresholding (>128) was applied to red channels to obtain binary segmentation masks.

Fig. 1.

FLAIR images and associated glioma segmentation masks were combined to produce colour images. The FLAIR image was copied and inserted into green and blue channels, while the segmentation mask was inserted into the red channel. This was applied to the training dataset to produce a set of 2751 colour images for generative modelling with StyleGAN2-ada.

2.2.2. Model architecture

StyleGAN2 is a generative model that gives state-of-the-art results in image synthesis tasks (Karras et al., 2019). Its generator comprises two main components; a mapping network and a synthesis network. The mapping network consists of 8 fully connected layers. It generates a disentangled style vector of size 512 from a random latent vector of the same size, which is then used to control the styles of the generated feature maps through CNN operations in the synthesis network (Karras et al., 2019). Our synthesis network consisted of five blocks, each of which doubles the resolution of feature maps, producing output images at the requisite size of 256 × 256. There are two “style blocks” within each block, except for the first one. The first style block contains an upsampling layer to increase the resolution of feature maps, followed by two convolutional layers with 3 × 3 filters, one of which is included in the second style block. The weights of the convolutional layers are modulated using the style vector and normalized through weight demodulation. Random Gaussian noise and biases were added to feature maps after every style block. Skip connections between blocks are used to generate high-resolution images while avoiding phase artifacts caused by a progressively growing approach (Karras et al., 2019).

The discriminator consisted of five convolutional blocks with residual connections. Each block had two 3 × 3 convolution layers and a downsampling layer. Feature maps get downsampled by multiples of two. Towards the classification end of the network, two blocks before flattening the feature maps, a mini-batch standard deviation layer is applied to calculate the standard deviation of each feature map across a mini-batch. The average of all the standard deviations is then appended to the feature maps as an additional feature. The last feature map gets flattened and fed through a fully connected layer to produce a scalar value representing the probability of the “realness” of the input image.

StyleGAN2 requires a large training dataset to avoid overfitting the discriminator, which limits its practicality. Karras et al. (2022) introduced adaptive discriminator augmentations (StyleGAN2-ada), designed to overcome this limitation. They effectively prevented the leakage of augmentations used on the training images into the generated images by applying stochastic discriminator augmentation, in which a set of augmentations are applied to images only before they are fed to the discriminator. Using this approach, the discriminator learns to identify real and fake images with the same augmentation. Meanwhile, the generator learns to produce images without these augmentations. Eighteen different image manipulations are applied to a certain percentage of input images to the discriminator, which has empirically been found to not compromise the quality of generated images. To avoid manually tuning the strength of each augmentation, heuristics are used to detect overfitting in the discriminator and adjust the percentage of images that augmentations are applied to during training (Karras et al., 2020, Situ et al., 2021).

2.2.3. Model hyperparameters and training scheme

We trained the StyleGAN2-ada model on an NVIDIA Tesla T4 GPU with CUDA version 11.2 and 25 GB of RAM, using PyTorch library version 1.8.1 and torchvision version 0.9.1. The training dataset consisted of 2751 images, each sized 256 × 256 pixels, as described above. We employed the Adam optimizer with a learning rate of 0.0025, betas= [0, 0.99]. The loss function was StyleGAN2Loss with r1_gamma parameter of 0.8192. During the training process, we applied a custom data augmentation pipeline that included flipping, rotation, scaling, and colour adjustments. We implemented transfer learning with a network that was previously trained on FFHQ dataset images with a resolution of 256 × 256 (Karras et al., 2020). The batch size used was 32 and the model was saved every 3 ticks, with a snapshot of the generated images taken for visual inspection.

2.2.4. Model evaluation criteria

The GAN was evaluated using a combination of subjective and objective methods. Firstly, we visually examined a sample of 100 generated images to subjectively evaluate their appearance; a representative, randomly selected sub-sample is shown in Fig. 3. Additionally, we thoroughly searched all of the generated data to identify any lower-quality generated images, which are shown in Fig. 5. Secondly, we calculated Fréchet Inception Distance (FID), which provides a quantitative metric of GAN performance (Heusel et al., 2017). The FID metric is based on the activations of an Inception V3 trained on the ImageNet dataset (O’Reilly and Asadi, 2021; Szegedy et al., 2016). The activations are extracted from a pooling layer and are assumed to be approximately multivariate normal distributions. The FID score is calculated as the distance between the means of the activations of the real and generated images, minus the trace of the product of the covariance matrices of the real and generated images. The smaller the FID score, the more similar the generated images are to the real images.

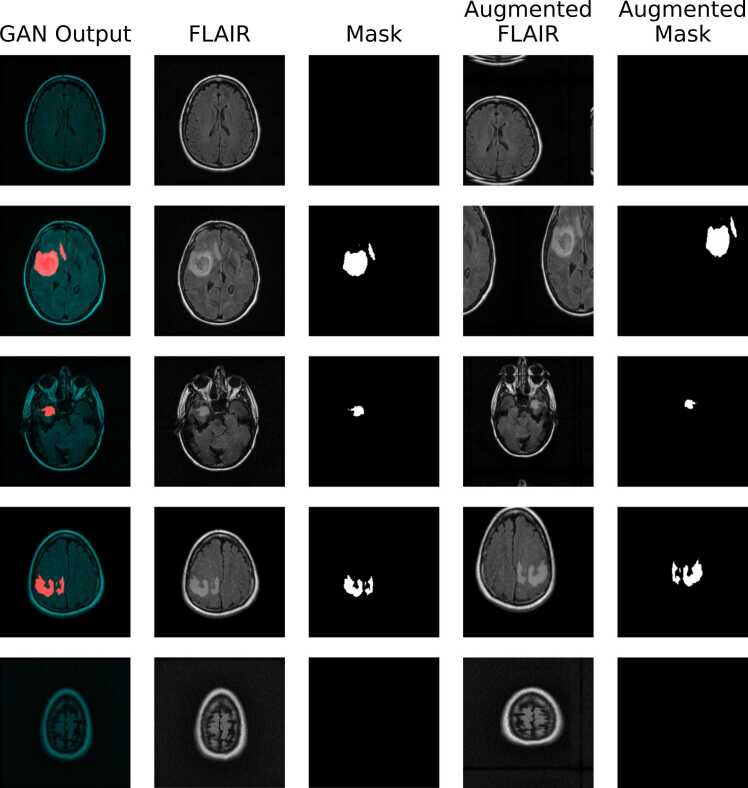
Fig. 3.

Representative sample of synthetic data, decomposed into FLAIR sequence and binary segmentation mask images, before and after applying geometric augmentations. The generated images are essentially indistinguishable from genuine images based on visual inspection, and the GAN achieved an FID score of 14.39. Following geometric augmentations, some of the image compositions are clearly irregular, with brain tissue spread across image boundaries; while this appearance may seem odd to human observers, it is not necessarily deleterious for training CNNs.

Fig. 5.

Selected examples of genuine, subjectively good and subjectively poor-quality synthetic images. Obtaining this sample of low-quality synthetic images required scouring all of the generated images. Issues identified from this sample include lack of FLAIR image detail, faded and noisy segmentation masks.

2.3. Segmentation model

2.3.1. Data pre-processing

Grayscale FLAIR images and binary segmentation masks were normalized to the range [0,1]. They were kept at a size of 256 × 256 pixels.

2.3.2. Model architecture

U-net (Ronneberger et al., 2015) models were trained to perform automatic image segmentation. These consisted of four encoding blocks, each with repeated convolution (3 ×3 filter, with zero-padding), batch normalization and rectified linear unit (ReLU) activation layers followed by max pooling (2 ×2 kernel, stride of 2). The number of filters in each of these consecutive encoding blocks was 64, 128, 256 and 512. These were connected to another convolutional block, although excluding max pooling, with 1024 filters, which fed into a decoding section. The decoder had four blocks with convolutional transpose layers that scaled up spatial dimensions by a factor of two. The number of filters in the decoding blocks mirrored those in the encoder (i.e., 512, 256, 128, 64), and data from equivalent stages of the encoder were concatenated before feeding into another convolutional layer with the same number of filters. Output was taken from a final convolutional layer with one filter with size 1 × 1 and sigmoid activation function.

2.3.3. Model hyperparameters and training scheme

The withheld validation dataset was used to monitor performance at the end of each training iteration. Dice loss and adaptive moment estimation optimizer were used for training. The learning rate started at 1 × 10⁻⁴ and reduced by a factor of 0.1 in response to plateau in validation loss with minimum limit of learning rate 1 × 10⁻⁷. Maximum number of training iterations was set to 1000, with batch size of 32, although early stopping occurred when no decrease in validation loss was observed for 50 iterations. Evaluation metrics calculated at the end of each training step included dice coefficient, intersection over union (IoU), recall, and precision. The best model in terms of validation set dice coefficient was saved. In the results section we report dice coefficient values, which are representative of the other metrics.

Firstly, a model was trained without any data augmentation, using only the real training set to evaluate baseline performance. Then fourteen models were trained while adding successive batches of 1000 synthetic images, as illustrated in Fig. 2, to evaluate the performance of synthetic data augmentation. Subsequently, this process was repeated with geometric data augmentation. Thus, baseline performance with and without geometric augmentation was determined, and model performance with synthetic data augmentation with and without geometric data augmentation was determined. The specific geometric manipulations that were randomly applied were horizontal and vertical flips, horizontal and vertical translations (max. 30% of image size), shearing (range of 0.2), zooming (range of 0.2), brightness adjustment (range of [0.5, 1.05]). New edge pixels were filled in with 'wrap' mode.

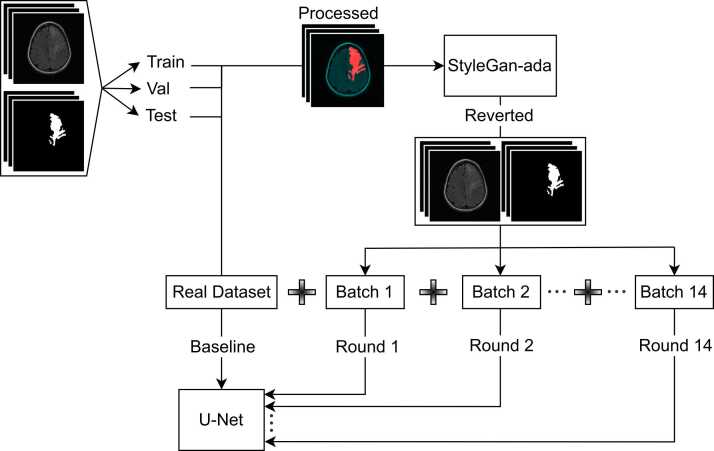
Fig. 2.

Study method overview. The initial dataset contained FLAIR images and glioma segmentation masks, illustrated in the upper-left. After preprocessing scans (standardising, clipping and normalising) these were split into training, validation and test sets. Colour images were produced from the training data, as illustrated in Fig. 1, and then used to train StyleGAN2-ada. After training, artificial images produced by the GAN were split into grayscale FLAIR (average of green and blue channels) and mask (thresholded red channel) images used for synthetic data augmentation. Fourteen batches of 1000 synthetic images and masks were generated using the trained StyleGAN2-ada; as such, they can be viewed as coming from the same distribution. A U-net was trained solely using real images from the training set to establish baseline performance. The same architecture was also trained for 14 rounds with consecutive addition of batches of synthetic data. All of the U-nets were trained with early stopping, using peak validation set dice coefficient as the monitoring criteria, and a patience of 50 iterations. Out-of-sample performance was evaluated with the withheld test set.

2.3.4. Model evaluation criteria

Computational costs of U-net training were quantified with the total number of completed training iterations, total training time (hours) and time per iteration (minutes). This data is plotted in Fig. 6. We used dice coefficient as the primary evaluation metric for segmentations. This metric assesses overlap between the predicted and ground truth segmentations, with a value ranging from 0 (no overlap) to 1 (perfect overlap). A higher dice coefficient therefore reflects better segmentations. Training and validation set metrics were calculated at the end of each training iteration and used to plot learning curves (Fig. 7). After completing training, models were evaluated with the test set. The influence of synthetic and geometric data augmentation relative to the baseline (using only real images) was then evaluated in terms of training, validation and test set dice coefficients (Fig. 8). Pearson’s correlation coefficient (r) was used to evaluate correlations between these metrics and the amount of synthetic data.

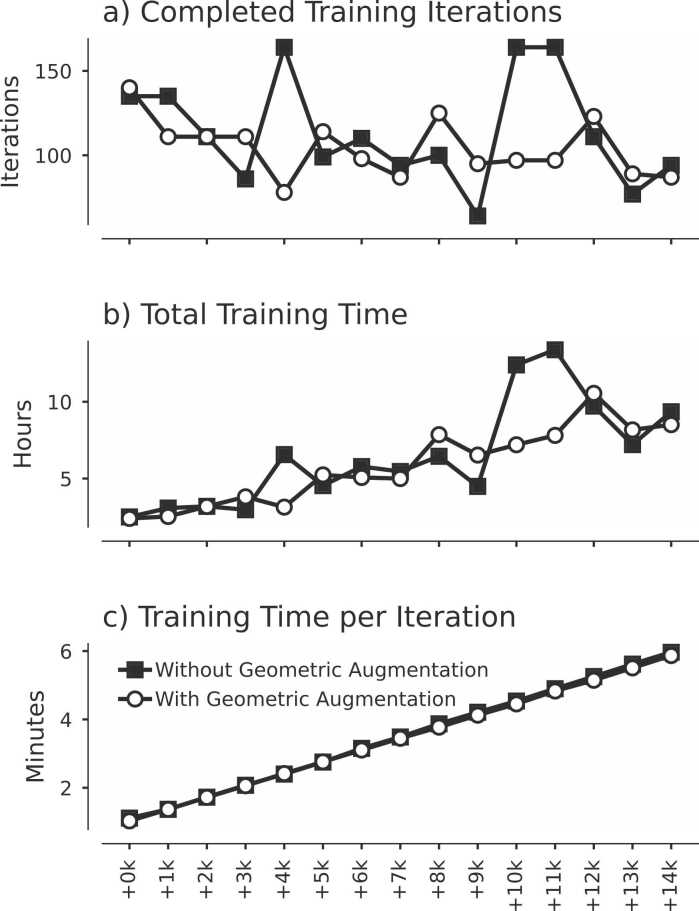
Fig. 6.

Training time increases with addition of synthetic images with and without geometric augmentation. The completed number of training iterations (a) does not exhibit a notable statistically significant trend, whereas the total training time (b) and time per iteration (c) both demonstrate statistically significant correlation with the amount of additional synthetic images. Real training data consisted of 2751 image-mask samples; these were augmented with 0 to 14,000 synthetic image-mask pairs, as illustrated on the x-axis.

Fig. 7.

Training loss converges faster with additional synthetic images with and without geometric augmentation. Learning curves for training set loss are shown on the top panels, and those for validation set loss are shown on the bottom panels. Models trained without geometric data augmentation are represented on the left, and those trained with geometric augmentation are represented on the right. Colour-coded learning curves illustrate how U-net losses evolve when trained with only real (+0k) and cumulative additional batches of synthetic (+1k to +14k) images. Increasing synthetic data augmentation correlates with training loss convergence rate. Furthermore, geometric augmentation increased training loss and decreased validation loss slightly relative to synthetic data augmentation alone.

Fig. 8.

Segmentation performance does not increase with additional synthetic images with or without geometric augmentation. From the top panel it can be noted that synthetic data augmentation does not substantially improve generalization from training to validation and test sets. In contrast, geometric augmentation does improve generalization, causing the U-net performance to converge for training, validation and test sets. Dashed lines show the line of best fit from least squares linear regression.

2.4. Distribution of image vector representations

Image vector representations were produced using a pre-trained Inception V3 model (Szegedy et al., 2016) with input size of 256 × 256 as a feature extractor. Image vectors of size 2048 were derived by collapsing the final convolutional layer filter activations with average pooling. All of the real images (2751) and a random sample of 2751 generated images were transformed into their vector representations using this approach. These vectors were transformed into two-dimensional space with t-Stochastic Neighbor Embedding (t-SNE) (Van Der Maaten and Hinton, 2008). The results from this analysis are visualized inFig. 4.

Fig. 4.

Distribution of genuine and synthetic image vector representations plotted in two-dimensional space using t-SNE. It may be noted that vector representations of these 2751 real and randomly-sampled 2751 fake images occupy largely overlapping regions in this space, without any obvious outliers.

2.5. Software

Python 3 was used with NiBabel, NumPy, OpenCV, MatPlotLib, PyTorch and TensorFlow. StyleGAN2-ada was developed using PyTorch, and U-net models were developed using TensorFlow. Code and data used in this study are openly available from https://osf.io/yr56s/?view_only=bf0cd961e56e44c391bc0a27d6511b5a.

3. Results

After training, the GAN reached an FID score of 14.39. It took approximately two days of continuous training to achieve this FID score; another day of fine-tuning did not improve the FID score. Randomly selected images generated by the trained GAN are shown in Fig. 3. These are effectively indistinguishable from the training set distribution. Importantly, none of the synthetic images were identical to any of those in the training set. Generated FLAIR sequence images and glioma segmentation masks appear to correspond well, with higher intensity pixels indicating tumour tissue that are overlapped by the mask. There is also diversity in the location and morphology of tumour regions among healthy brain tissue. Fourteen batches of 1000 synthetic images were produced, as illustrated in Fig. 2, and split into their corresponding FLAIR images and glioma segmentation masks. These were used cumulatively in fourteen rounds to augment real data and explore the influence of synthetic data augmentation on performance of U-nets trained to perform automatic glioma segmentation.

Fig. 4 displays vector representations of 2751 real and 2751 randomly-sampled fake images transformed into two-dimensional space using tSNE. This analysis indicates that genuine and synthetic image vector representations occupy largely overlapping distributions, accounting for the relatively low FID score. However, Fig. 5 illustrates examples of well-generated and poorly-generated synthetic images, alongside real images for reference; the quality of these synthetic images was judged by visual inspection. Identifying this small sample of poorly-generated images required thoroughly searching through all of the generated data, thus the vast majority of synthetic images were of high quality.

Analysis of the completed number of training iterations and computation time for U-nets trained with successive rounds of additional synthetic data augmentation are plotted in Fig. 6. The number of completed training iterations did not significantly correlate with the amount of synthetic data augmentation (Fig. 6a; r = −0.201, p = 0.472 and r = −0.426, p = 0.113 without and with geometric augmentation, respectively). However, total training time (Fig. 6b; r = 0.776, p = 6.76 ×10⁻⁴ without, and r = 0.937, p = 2.69 ×10⁻⁷ with geometric augmentation) and time per iteration (Fig. 6c; r = 1.0, p = 4.65 ×10⁻²⁴ without, and r = 1.0, p = 1.83 ×10⁻²⁹ with geometric augmentation) both significantly correlated with rounds of synthetic data augmentation. This is due to the dependence between the amount of training data and number of batches, and also between the number of batches and computation time for backpropagation.

Learning curves for U-nets trained with different amounts of synthetic data augmentation are plotted in Fig. 7. These depict patterns of training and validation set losses during training from models trained with and without geometric augmentation. Training set losses converge more quickly with increasing amounts of synthetic data augmentation. Rate of change in loss was evaluated by differentiating these learning curves, which showed that initial convergence rate of training loss significantly correlated with the amount of synthetic data, both with (r = −0.991, p = 9.18 ×10⁻¹³) and without geometric augmentation (r = −0.989, p = 2.86 ×10⁻¹²). Initial convergence rates for the validation set were also significantly correlated with the amount of synthetic data, both with (r = −0.943, p = 1.4 ×10⁻⁷) and without geometric augmentation (r = −0.67, p = 0.00629). However, by the second training iteration validation loss convergence rates no longer correlated with the amount of synthetic data (r = −0.228, p = 0.413 without, and r = 0.369, p = 0.176 with geometric augmentation).

Dice coefficients for U-nets trained with different amounts of synthetic data augmentation are plotted in Fig. 8. Without geometric augmentation (Fig. 8a), segmentation performance does not correlate significantly with the amount of synthetic data used for augmentation in terms of the training (r = −0.235, p = 0.4), validation (r = 0.332, p = 0.226) or test (r = 0.299, p = 0.279) sets. With geometric augmentation (Fig. 8b) these correlations were also not statistically significant (training set r = −0.269, p = 0.332; validation set r = 0.144, p = 0.609; test set r = −0.101, p = 0.721). Synthetic data augmentation did not noticeably improve model generalization, with there being relatively consistent gaps among training and validation and test set performances. Geometric data augmentation did, however, close these gaps and improve model generalization.

For real data without geometric augmentation, Dice coefficients were training 0.932, validation 0.819 and test 0.877. With synthetic data augmentation, these reached 0.944, 0.86 and 0.912, respectively, showing improvement of 0.0409 for validation and 0.0355 for test sets. With geometric augmentation, real data produced training 0.912, validation 0.878 and test 0.897; then combined geometric and synthetic augmentation achieved 0.91, 0.898 and 0.911, with improvements of 0.0196 and 0.0144 for validation and test sets, respectively. Standard deviation of Dice coefficients from U-nets trained without geometric augmentation was 0.0406, in contrast with 0.0104 for U-nets trained with geometric augmentation, demonstrating improved generalization.

4. Discussion

Synthesized FLAIR images and corresponding glioma segmentation masks were effectively indistinguishable from genuine images, illustrated with the sample in Fig. 3. The FID score of 14.39 is comparable with the range of values reported in the literature for GANs used to synthesize neuroimaging data (Kossen et al., 2022, Kossen et al., 2021, Subramaniam et al., 2022). Although direct comparison of this metric calculated in different contexts is not always informative, as the FID score can vary with image size, sample size, and software implementation (Nunn et al., 2021; O’Reilly and O’Reilly and Asadi, 2022, O’Reilly and Asadi, 2021). On visual inspection of the synthetic images no artifacts were detected. This contrasts with other architectures such as deep convolutional (DC)-GAN and progressively grown (PG)-GAN that are known to propagate unnatural artifacts to generated images (Asadi and O’Reilly, 2021, Carver et al., 2021, Foroozandeh and Eklund, 2020, Park et al., 2021). Absence of artifacts in generated images is one of the advantages of using the StyleGAN2 architecture (Karras et al., 2020, Karras et al., 2019), removing the need to identify and remove obviously artificial images from the synthetic dataset prior to use in downstream applications (O’Reilly and Asadi, 2022). While some relatively lower quality images were identified by visual inspection, as shown in Fig. 5, image vector representations plotted in Fig. 4 suggest that genuine and synthetic images occupy largely overlapping distributions. This is also supported by recent work demonstrating state-of-the-art performance of StyleGAN2-ada for generating synthetic medical images (Woodland et al., 2022). Issues identified from synthetic images that were subjectively judged to be poorly generated (Fig. 5) included lack of detail in FLAIR images, and noisy or faded segmentation masks; the latter of which were remedied by thresholding.

There is a trade-off between the computational costs of training a GAN then generating thousands of synthetic images versus the benefits obtained from using the resulting synthetic images. Estimation of these costs should include time, energy and memory requirements associated with training the GAN and subsequent training of the U-net with a larger amount of data. For the benefits, we can consider segmentation performance improvements attained by using synthetic data augmentation. The results presented in Fig. 6 display statistically significant positive correlations between dataset size and computation time, without corresponding changes in the number of completed training iterations. This demonstrates that although training takes longer with inclusion of larger amounts of synthetic data, the U-net is optimized to achieve its best performance within the same number of iterations through that training data.

Viewed alone this suggests that additional synthetic data does not contain substantially more information for the U-net to learn from than the real data used to train the GAN. However, the learning curves plotted in Fig. 7 indicate that larger amounts of synthetic data augmentation increase the initial convergence rate, such that the negative gradient at the beginning of the learning curve descent is significantly correlated with the amount of additional synthetic images. Taken together, these findings suggest that U-net optimization initially benefits from synthetic data augmentation, but fine-tuning of its weights requires a similar number of iterations through the training data before the early stopping criteria is reached. Returning to the question of the trade-off between the costs of implementing synthetic data augmentation versus the benefits gained in terms of U-net performance: it is difficult to argue on the basis of these findings that the benefits of synthetic data augmentation are worth the additional expense. In contrast, geometric augmentation provides a clear benefit for model generalization, as shown in Fig. 8, without the additional computational load associated with training and running a GAN to produce synthetic images.

These findings are generally in agreement with recent studies using PGGAN and an ensemble of GANs (Foroozandeh and Eklund, 2020, Larsson et al., 2022), which found marginal improvements in brain tumour segmentation provided by GAN-based synthetic data augmentation. Although an ensemble of 10 GANs produced significantly better U-net segmentations than without data augmentation (mean Dice coefficient 0.735 vs. 0.729), the inefficiency of this approach makes it difficult to justify based on the relatively small improvement reported. Nevertheless, we can consider other potential benefits of using synthetic neuroimaging data. In particular, artificial medical images synthesized by a GAN trained using data from a cohort of patients are considered to be more ethical for sharing among researchers because they cannot be identified as belonging to an individual patient (Kossen et al., 2022, Kossen et al., 2021, Subramaniam et al., 2022). In this sense, neuroimage synthesis can be interpreted as an enhanced standard of data anonymization. Therefore, where patient privacy is of paramount concern, application of GAN technology is advantageous.

StyleGAN2-ada (Karras et al., 2020) includes a truncation hyperparameter that controls the trade-off between diversity (0) and fidelity (1) of its generated images. In the current study this was fixed at 0.65, which is considered to be sufficient in most applications. It is feasible that altering this parameter, for example lowering it to increase the diversity of synthetic images at the expense of their fidelity, could influence the usefulness of images generated by the GAN after training. We can speculate that higher diversity of images would provide greater benefits from synthetic data augmentation, thus improving upon the marginal performance gains observed. However, corresponding decreases in the fidelity of synthetic images could potentially have deleterious effects due to compromised quality and co-registration of FLAIR and glioma segmentation image channels. It is unclear which of these possibilities would be more likely, or whether further, unforeseen conditions would emerge while tuning this hyperparameter. Ultimately, however, a systematic investigation of the effects of StyleGAN2-ada’s truncation parameter on downstream U-net segmentation performance with synthetic data augmentation was beyond the scope of this study.

Four different MRI sequences are available to support brain tumour segmentation in the BraTS challenge dataset. These include pre-contrast (T1), post-contrast T1-weighted (T1c), T2-weighted (T2), and FLAIR scans (Nalepa et al., 2019b). The methods presented in the current study have limited ability to synthesize multiple of these neuroimage modalities simultaneously. The StyleGAN2-ada model is designed for generating three-channel colour images; thus, at most it could synthesize two MRI sequences and one tumour segmentation mask simultaneously. By making significant changes to network architectures, pre-training procedures and supporting code it could be possible to expand the number of image channels to work with, although this is beyond the scope of the present study. Nevertheless, the FLAIR sequence provides sufficient contrast between healthy and tumour tissue for brain tumour delineation using convolutional neural networks (Ribalta Lorenzo et al., 2019, Zeineldin et al., 2020), which may improve clinical efficiency compared with acquiring multiple MRI scans.

In addition to geometric augmentation, several other methods of image augmentation have been proposed in the literature. For instance, Anaya-Isaza and Mera-Jimenez (2022) proposed a strategy based on principal component analysis, whereby random contributions from principal components are applied to original images to generate novel variants. This report did not quantitatively evaluate the similarity between synthesized and original images (Anaya-Isaza and Mera-Jimenez, 2022), obstructing comparison with GAN-based synthetic image augmentation methods that typically report FID scores (Kossen et al., 2022, Kossen et al., 2021, Subramaniam et al., 2022). Nalepa et al. (2019a) highlighted convergence of GANs as a potential issue with regards to their practical implementation, proposing diffeomorphic medical image registration as a viable alternative for data augmentation. This approach avoided generating unrealistic data using a recommendation algorithm (Nalepa et al., 2019a). Zhao and colleagues (Zhao et al., 2019) also proposed an image registration-based method for augmenting brain scans, whereby unlabelled data is transformed in spatial extent and appearance to match a labelled template scan. They applied this method to generate brain scans for training a model to perform one-shot segmentation of 30 neuroanatomical structures. We view this as potentially having limited generalization due to the sampling of initial labelled training data, particularly if applied for segmenting brain tumours, which have less predictable appearance than common neuroanatomical structures. Image mixing-based techniques have also been proposed for brain lesion segmentation, such as CarveMix (Zhang et al., 2023). In this approach, two existing annotated images are stochastically combined to create new labelled images, which was shown to improve segmentation performance of a U-net trained with addition of these images to training data. As seen from this review of relevant literature, innovative medical image augmentation techniques are actively under development. Implementation of diverse approaches will presumably enhance the robustness of artificial intelligence systems designed to encounter multiple sources of variance within medical images.

5. Conclusions

The StyleGAN2-ada approach produced realistic FLAIR sequence neuroimaging data and accompanying glioma segmentation masks. Cumulatively adding up to 14,000 of these generated image and mask pairs to the training data did not substantially improve segmentation performance of U-nets evaluated on held-out validation and test sets that were excluded from the GAN training data. Synthetic data augmentation marginally improved Dice coefficients (validation set +0.0409, test set +0.0355), whereas geometric augmentation improved generalization (SD among training/validation/test sets of 0.01 with, and 0.04 without geometric augmentation). We can conclude for the data used in this study that synthetic data augmentation using StyleGAN2-ada for glioma segmentation with the U-net does not significantly improve model performance. This can be attributed to partially non-overlapping distributions of imaging data in training, validation and test sets. The considerable computational costs associated with training the GAN and subsequently using it for synthetic data augmentation were not balanced by the marginal benefits attained by downstream application of the synthetic data. We cannot rule out that synthetic data augmentation may improve segmentation performance in other contexts more substantially than observed in this study. Furthermore, there are potentially more appropriate uses for state-of-the-art GAN technology in neuroimaging, such as sharing data with enhanced anonymity.

CRediT authorship contribution statement

FA: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing – original draft, Visualization. TA: Supervision. JAO: Conceptualization, Methodology, Software, Formal analysis, Resources, Data curation, Writing – original draft, Writing – review & editing, Visualization, Supervision.