Substrate Rigidity Modulates Segmentation Clock Dynamics in Isolated Presomitic Mesoderm Cells

Summary

The segmentation clock, a genetic oscillator in the presomitic mesoderm (PSM), is known to be influenced by biochemical signals, yet its potential regulation by mechanical cues remains unclear. The complex PSM microenvironment has made it challenging to isolate the effects of mechanical perturbations on clock behavior. Here we investigated how mechanical stimuli affect clock oscillations by culturing zebrafish PSM cells on PDMS micropost arrays with tunable rigidities (0.6–1200 kPa). We observed an inverse sigmoidal relationship between surface rigidity and both the percentage of oscillating cells and the number of oscillation cycles, with a switching threshold between 3–6 kPa. The periods of oscillating cells showed a consistently broad distribution across rigidity changes. Moreover, these cells exhibited distinct biophysical properties, such as reduced motility, contractility, and sustained circularity. These findings highlight the crucial role of cell-substrate interactions in regulating segmentation clock behavior, providing insights into the mechanobiology of somitogenesis.

Introduction

The rhythmic formation of somites during vertebrate embryogenesis is regulated by the segmentation clock, a genetic oscillator operating in the presomitic mesoderm (PSM) that relies on the periodic expression of cyclic genes from various signaling pathways, including the Hes/Her family, Delta/Notch, Wnt, and Fgf^1–4. This clock exhibits notable spatiotemporal changes along the anterior-posterior (AP) axis of the PSM, such as period elongation as it moves anteriorly and a transition from asynchrony to synchrony^5–8. While biochemical regulation plays a crucial role in governing the segmentation clock’s dynamics, it alone is insufficient to fully explain these spatial phenomena. Recent studies suggest that tissue mechanics may contribute to the regulation of the segmentation clock’s spatiotemporal properties^9–13. In this study, we investigate how modulating mechanical forces changes the segmentation clock’s temporal properties, which remain largely unknown.

The mechanical properties of the PSM microenvironment undergo significant changes during somitogenesis. Zebrafish embryos possess a unique foam-like PSM architecture, with little or no extracellular matrix (ECM) between cells in the posterior region^13,14. As clock-active progenitor cells migrate from the posterior to the anterior region of the PSM, they encounter a stiffening process known as the “jamming transition.” This transition is characterized by posterior to anterior spatiotemporal changes in the ECM composition, cell density, and motility¹⁴. In the posterior PSM, the ECM primarily contains hyaluronic acid, while in the anterior region, the ECM becomes dense and stiff due to the increasing abundance of fibronectin and collagen fibers¹². These observations suggest that in addition to the three-tier model of single-cell oscillators, cell-cell communications, and morphogen gradients, the mechanical gradient of the PSM microenvironment may act as a potential fourth tier of regulation, significantly impacting the properties of the segmentation clock. This notion is further supported by in vitro cultures of mouse PSM cells, where Hubaud et al. demonstrated that these dissociated PSM cells can sense substrate adhesion and switch between quiescent and oscillatory states by manipulating the transcriptional co-activator YAP pathway, suggesting a link between mechanical signal and the oscillatory dynamics of the clock¹⁰. However, these studies were conducted on highly rigid glass surfaces. It remains unclear how the dynamical properties of the oscillator respond to varying mechanical stimuli within a physiological dynamic range. Furthermore, how the mechanical properties of the PSM microenvironment, which play a critical role in shaping the cellular physical properties, such as morphology and migration, may correspond to the changing oscillatory behavior of individual cells remains unclear.

In recent studies, YAP has emerged as a key mediator of mechanical signals from the extracellular matrix to the nucleus¹⁵. YAP translocation to the nucleus has been shown to be dependent on substrate rigidity, with stiffer substrates above a rigidity threshold of 5 kPa promoting nuclear localization¹⁶. This mechanosensing mechanism is mediated by talin, a cytoskeletal protein that allows force transmission to the nucleus only above a threshold in substrate rigidity¹⁶. In the context of the segmentation clock, this suggests that individual cell oscillations may depend on a specific stiffness threshold mediated by YAP signaling. Notably, YAP activity has been linked to the regulation of the Delta/Notch pathway, which plays a crucial role in the synchronization and persistence of the segmentation clock. An increase in YAP activity has been shown to cause ‘in cis’ inhibition of the Notch signaling¹⁷, suggesting that mechanical regulation mediated by YAP can influence the oscillatory dynamics of the segmentation clock. This could lead to varying responses to rigidity between isolated cells and cell aggregates. Although single PSM cells function as self-autonomous oscillators with minimal cell-to-cell contact or juxtacrine Delta/Notch activity⁴, they may undergo cis-inhibition of Notch due to mechanical interactions with the extracellular matrix (ECM). In comparison, cell aggregates within the PSM tissue may modulate the spatiotemporal features of the segmentation clock through the antagonistic interplay between trans-activation of Notch via Delta/Notch interactions among neighboring cells and YAP-mediated cis-inhibition of Notch via mechanical feedback.

In this study, we investigated how mechanical cues affect the oscillatory behavior of isolated and aggregated zebrafish PSM cells, dissociated from transgenic zebrafish embryos expressing cyclic Her1-Venus⁶, by culturing them on polydimethylsiloxane (PDMS) micropost arrays with tunable surface stiffness. By varying the height and diameter of the microposts, we precisely controlled the substrate rigidity and investigated cellular responses to a range of mechanical environments¹⁸. This approach enabled us to decouple the effects of mechanical cues from those of morphogen gradients and cell-cell communication, which are known to influence the segmentation clock in vivo¹⁹. We focused specifically on the intrinsic her1 negative feedback loop that drives cell-autonomous oscillations⁴ providing a unique opportunity to study the role of mechanical cues in regulating the segmentation clock at the single-cell level.

We report that the segmentation clock exhibits a switch-like response to changes in surface rigidity, with a significantly reduced oscillation percentage beyond 6 kPa. However, the period, ranging widely between 60 to 100 minutes, shows no clear trend of changing in response to varying mechanical stimuli. This suggests that individual PSM cells may determine the period through an intrinsic pacemaker, likely driven primarily by transcriptional delays in the her1/7 negative feedback loop²⁰ and influenced by other position-dependent biochemical signals. In contrast, mechanical factors may provide a gating mechanism to determine whether the cells remain quiescent or oscillate. Furthermore, compared to isolated cells, cell aggregates exhibit a higher probability of oscillations across all rigidity conditions without a clear switching threshold, suggesting that the restoration of cellular interactions and tissue-level mechanics can co-modulate the segmentation clock dynamics. This mechanical regulation of the segmentation clock could represent an additional tier of control, complementing the existing models based on genetic circuits, cell-cell communication, and morphogen gradients.

Results

Substrate Rigidity Modulates Single-Cell Segmentation Clock Oscillations

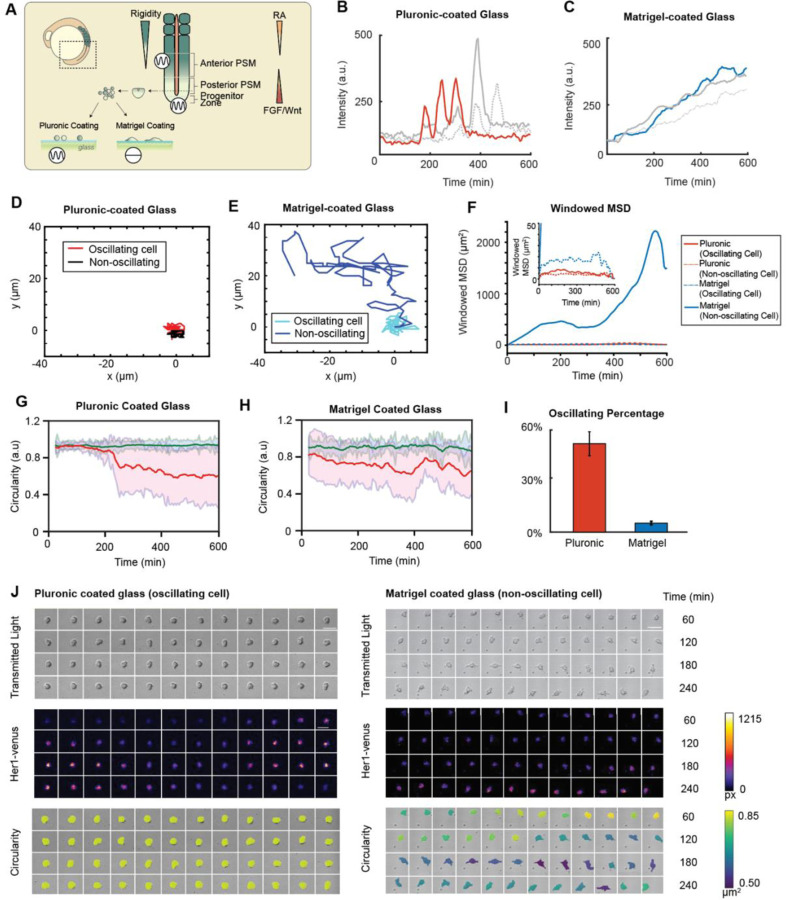
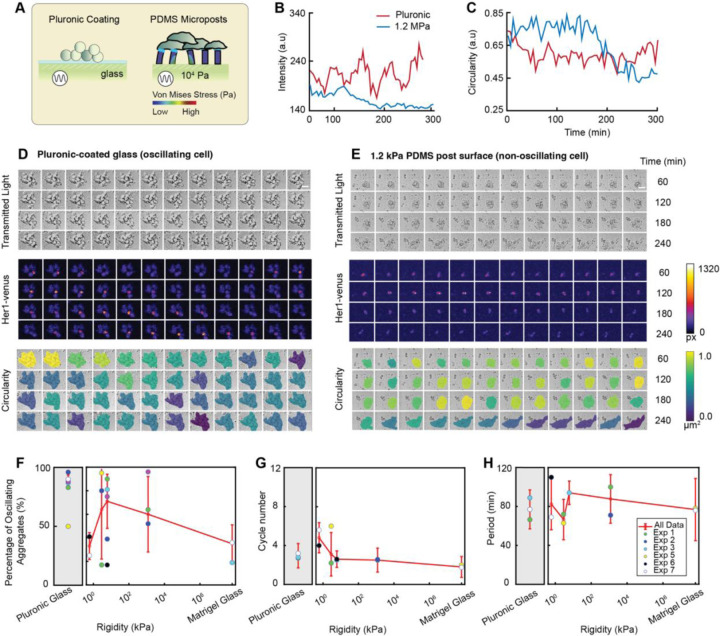
To examine the influence of substrate rigidity on the oscillatory behavior of isolated zebrafish presomitic mesoderm (PSM) cells, we modified a single-cell assay⁴ by using mechanical dissociation to minimize the potential effects of chemical dissociation. Cells were dissociated from PSM tailbuds of embryos at the 5- to 8-somite stage containing the Tg(her1:her1-Venus) transgene⁶ and cultured on two distinct surfaces: Pluronic-coated glass, which inhibits cell-surface adhesion, and Matrigel-coated glass, which enhances cell-surface adhesion (Figure 1A). Notably, cells isolated from the anterior PSM (A-PSM) exhibited earlier Her1-Venus oscillation peaks compared to those from the posterior PSM (P-PSM), suggesting that the oscillation dynamics of individual cells may vary depending on their original location within the presomitic mesoderm, potentially indicating that cells retain positional information from their endogenous tissue environments (Figure S1A). For the remaining results presented in this study, we utilize P-PSM cells. The Her1-Venus oscillatory behavior and morphology of single cells displayed marked differences between these two surface conditions (Figure 1B-J; Movie S1). On Pluronic-coated glass, around 55% of isolated cells exhibited self-sustained Her1-Venus oscillations (Figure 1B; Figure 1I, red; Figure 1J, left), while on Matrigel-coated glass, majority of cells are non-oscillatory (Figure 1C; Figure 1J, right) with around 4% of cells exhibiting oscillations (Figure 1I, blue). Moreover, on Pluronic-coated glass, both oscillating (Figure 1D, red; Figure 1F, solid red) and non-oscillating (Figure 1D, black; Figure 1F, dotted red) cells exhibited relatively low mean squared displacement (MSD); however, on Matrigel-coated glass, non-oscillating cells demonstrated significantly greater cell migration areas (Figure 1E) and MSD values that were orders of magnitude higher compared to oscillating cells (Figure 1F). On both Pluronic-coated and Matrigel-coated conditions, oscillating cells maintained high circularity throughout the time (Figure 1G-H, green; Figure 1J, left), while non-oscillating cells eventually became polarized after cell seeding (Figure 1G-H, red; Figure 1J, right), suggesting a potential relation between cell polarity and oscillatory state. These findings suggest that the surface coating significantly influences the oscillatory behavior of isolated cells, with cells that could perform self-sustained, autonomous oscillations on Pluronic-coated glass losing their oscillatory capability when attached to glass via Matrigel-coating (Figure S1B). The observed differences in oscillatory behavior and morphology between cells cultured on low-adhesion Pluronic-coated and high-adhesion Matrigel-coated glass surfaces suggest that mechanical cues, such as cell shape and spreading, play a potential role in regulating the segmentation clock.

Figure 1: Her1 negative-feedback loop exhibits sustained limit cycle oscillations on low-adhesion surfaces.

(A) Schematic of the zebrafish tail during somitogenesis. The segmentation clock in the presomitic mesoderm is known to respond to morphogen gradients (RA, Fgf) and a potential extracellular matrix mediated mechanical gradient. Progenitor cells harvested from the tailbud are exposed to surfaces with varying rigidities. (B) Sustained Her1-Venus expression in oscillating cells on a Pluronic- (hydrophobic) coated glass surface and (C) Matrigel-coated glass surface. The red line indicates the cell shown in the pluronic montage panel. Gray lines represent cells from independent experiments. The blue line indicates the cell shown in the Matrigel montage panel. (D-E) Tracked cell trajectories of an oscillating and non-oscillating cell on Pluronic- and Matrigel-coated surfaces. Red and blue lines represent cells shown in the respective montage panels. (F) Windowed mean squared displacement of oscillating and non-oscillating cells on pluronic and Matrigel-coated glass surfaces. Red and blue lines indicate the respective cells shown in the montages. (G-H) Circularity traces of isolated oscillating (red) and non-oscillating (blue) cells on Pluronic-coated and Matrigel-coated glass surfaces. (I) The percentage of oscillating cells on pluronic and Matrigel-coated surfaces across experiments. (J) Montage of a single cell on Pluronic- and Matrigel-coated glass surfaces. Transmitted light indicates cell viability, Her1-venus intensities indicate oscillations, and circularity demonstrates the PSM cell maintaining a low contact area and spherical conformation on the Pluronic-coated glass surface, while completely spreading on the Matrigel-coated glass surface.

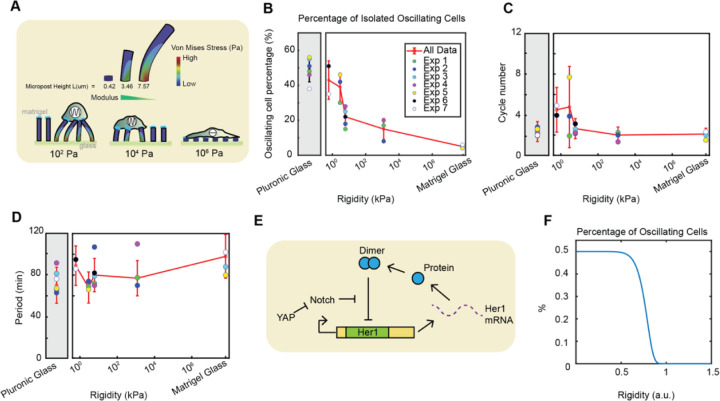
Compared to the stiff surface of a typical imaging cover glass, which has a reported elastic modulus of 48 GPa²¹, the tissue stiffness of the posterior PSM (P-PSM) measured using atomic force microscopy (AFM) was approximately 0.67 ± 0.04 kPa (Figure S2A-B). To investigate how the Her1-Venus oscillatory behavior may change across a gradient of rigidity covering the range of biological tissues, we cultured the PSM cells on Matrigel-coated PDMS micropost arrays with varying stiffness: 0.6 kPa, 2.9 kPa, 6 kPa, and 1.2 MPa¹⁸ (Figure 2A, Movies S2 and S3) as well as on Pluronic-coated and Matrigel-coated glass surfaces, as two control conditions. We found that cells on soft surfaces (0.6 and 2.9 kPa) maintained a high percentage of oscillations, about 40–50%, comparable to the Pluronic-coated control condition. However, as surface rigidity increased, the oscillation percentage exhibited a pronounced drop to 20% between 2.9–6 kPa and remained low with further increases in rigidity (Figure 2B). This switch-like characteristic was independent of selection criteria and remained consistent regardless of whether one-cycle cells were considered oscillatory(Figure S2C-D). This suggests a critical rigidity threshold on the order of a few kPa, where PSM cells are most sensitive to mechanical variations in the microenvironment, determining whether they oscillate or not. In line with this observation, the number of clock cycles exhibited a higher mean and variations on soft substrates (0.6–2.9 kPa) and dropped in a switch-like manner with increasing rigidity (Figure 2C). Furthermore, we examined the distribution of single-cell periods under various rigidity conditions. As a control, dissociated PSM cells on Pluronic-coated glass typically exhibited a wide distribution of periods, which were longer and more variable compared to in vivo segmentation clock oscillations, with a period distribution of 70.9 ± 16.8 minutes (mean ± SD), consistent with the reported values for chemically-dissociated cell cultures⁴. The cells on different surface conditions maintained a broad range of periods that are comparable to the Pluronic-coated glass condition and did not exhibit a clear dependency on rigidity (Figure 2D). This suggests that while cells can transition between quiescent and oscillatory states in response to mechanical cues, the period of the segmentation clock may depend on an intrinsic timing mechanism that is robust to mechanical perturbations. The pie charts in Figure S3A provide a comprehensive overview of the distribution of cell behaviors across different experimental conditions in this study.

Figure 2: Increasing surface rigidity reduces the percentage of oscillating cells, the number of cycles, and modulates the segmentation clock period in isolated zebrafish tailbud cells.

(A) Schematic of the PDMS micropost arrays. Single cells from zebrafish tailbuds were cultured on micropost arrays with varying Young’s modulus: 0.6 kPa, 2.9 kPa, 6 kPa, 1.2 MPa. Pluronic and Matrigel coatings on glass served as extreme controls for the rigidity range, with Matrigel-coated glass exhibiting the highest rigidity and Pluronic-coated glass displaying low cell adhesion. (B) Semi-log plot of the percentage of oscillating cells across varying rigidities. Grey and white backgrounds indicate Pluronic vs Matrigel surface coatings, respectively. Isolated cells on micropost arrays with rigidity <10⁴ Pa showed a higher percentage of oscillating cells compared to more rigid micropost arrays. The percentage of oscillating cells exhibits a switch-like drop between 2.9–6 kPa. (C) Semi-log plot displaying a decrease in oscillation cycles with increasing rigidity. (D) Semi-log plot depicting the segmentation clock period response to increasing surface rigidity. (E) Illustration of the proposed mechanism for YAP-mediated regulation of the Her1 negative feedback loop in the segmentation clock. (F) A time-delayed genetic oscillator model captured the decrease in the percentage of oscillating cells with increasing surface rigidity. Surface rigidity may exhibit a switch-like threshold to modulate the segmentation clock in single cells. Number of cells in each condition are provided in SI Figure 3.

To explain the switch-like response of oscillations to rigidity, we propose a mechanism involving YAP-mediated regulation of the her1 negative feedback loop in response to surface rigidity (Figure 2E). The specific mechanical threshold observed between 2.9–6 kPa may represent a critical point at which YAP activity switches, leading to the suppression of oscillations. This hypothesis coincides with the switch-like nuclear translocation of YAP observed at a threshold of 5 kPa in mouse embryonic fibroblast cells¹⁶. Furthermore, a previous study modeled the mouse segmentation clock as an activator-repressor oscillator based on the FitzHugh-Nagumo (FHN) model and proposed that the Yap pathway modulates the excitability threshold, effectively acting as a gate for Notch signaling as an external current¹⁰. To model our system, we used a time-delayed genetic oscillator model²² incorporating the effects of Notch and YAP signaling on her1 production. The model incorporates a Gaussian distribution of her1 production rates, a critical production rate threshold modulated by mechanical forces acting through YAP, and the rescue of oscillations by Notch signaling. The model predicts a sigmoidal decrease in the percentage of oscillating cells as rigidity increases, consistent with our experimental observations (Figure 2F).

Oscillating and Non-Oscillating Cells Exhibit Distinct Biophysical Properties

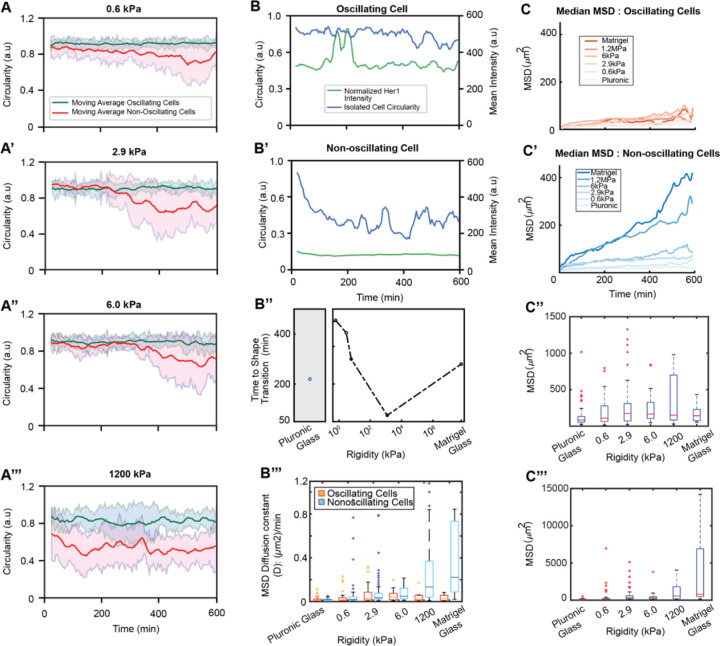
We further explored the relationship between cell morphology and oscillatory behavior on surfaces of varying rigidity. Similar to our observations in the two control conditions, oscillating and non-oscillating cells exhibited distinct morphological and biophysical properties on surfaces of varying rigidity. Across all tested rigidities (0.6 kPa-1.2 MPa), and consistent with the controls (Figure 1G-H), oscillating cells consistently maintained higher and more persistent circularity compared to their non-oscillating counterparts (Figure 3A-A’’’; Figure S4A-B). Distinct patterns of circularity changes were associated with oscillatory behavior. Actively oscillating cells maintained high circularity (Figure 3B) while non-oscillating cells exhibited low circularity (Figure 3B’). Cells took longer to spread on softer substrates, with non-oscillating cells decreasing their circularity more rapidly on increasingly rigid surfaces (Figure 3B’’).

Figure 3: Surface rigidity modulates morphological dynamics and migratory behavior in isolated PSM cells exhibiting distinct oscillation states.

(A-A’’’) Single-cell circularity traces over time on 0.6 kPa (A), 2.9 kPa (A’), 6.0 kPa (A’’), and 1.2 MPa (A’’’) surfaces. Oscillating cells (green) maintain higher and more persistent circularity than non-oscillating cells (red), indicating a key morphological feature that links to a cell’s oscillatory potential. Non-oscillating cells progressively lose circularity as they spread and crawl on surfaces over time. (B-B’) Circularity and Her1-Venus intensity traces of single cells on a 1.2 MPa micropost -arrays surface. The oscillating cell (B) maintains high circularity, while the non-oscillating cell (B’) progressively loses circularity. (B’’) Time for single non-oscillating cells to reach a distinct geometry (change in circularity) from their oscillating counterpart. Non-oscillating cells decrease circularity faster with increasing rigidity. (B’’’) MSD diffusion coefficient (D) analysis indicating oscillating cells maintain a low D regardless of surface conditions while non-oscillating cells increase D with increasing rigidity. (C-C’’’) Mean squared displacement (MSD) analyses of cells on varying surface rigidities, including median MSD of oscillating (C) and non-oscillating (C’) cells and maximum MSD of oscillating cells (C’’) and non-oscillating cells (C’’’). Oscillating cells maintain a relatively low MSD across all rigidity conditions, while non-oscillating cells increase displacement with increasing rigidity.

Analysis of mean square displacement (MSD), including windowed MSD (Figure S4C) and real-time MSD (Figure S4D), revealed that oscillating cells exhibited lower MSD values compared to non-oscillating cells across all rigidity conditions, suggesting that reduced motility may be favorable for the persistence of clock oscillations. Comparing the median values of windowed MSD for oscillating and non-oscillating cells across rigidity conditions, we found that oscillating cells maintained low MSD values all the time that are independent of rigidity (Figure 3C); in contrast, non-oscillating cells displayed a significantly increasing MSD over time, with the slope higher for more rigid surfaces (Figure 3C’). These differences are demonstrated in the MSD diffusion coefficient (D) analysis, indicating that oscillating cells have low D regardless of surface conditions, while non-oscillating cells have increased D with increasing rigidity (Figure 3B’’’). Maximum MSD values followed similar trends for oscillating (Figure 3C’’’) and non-oscillating cells (Figure 3C’’’).

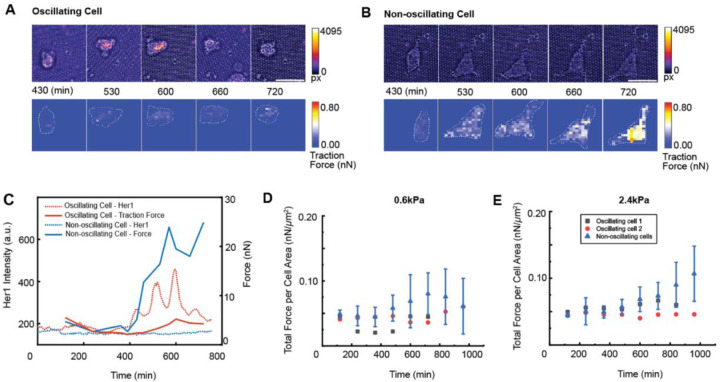
To provide a detailed view of cell-substrate interactions for oscillating and non-oscillating cells, we captured higher-resolution images of cells on 0.6 kPa and 2.4 kPa micropost arrays and analyzed the traction forces they exerted on the substrates as they attached and migrated. The subcellular level traction forces were quantified based on the deflection of the microposts¹⁸. In Figure 4A-C, we showed that an oscillating cell on 0.6 kPa micropost arrays maintained a round shape and exerted low traction forces (Figure 4A; Figure 4C, red; Movie S4A), whereas a non-oscillating cell on the same substrate became polarized and increased traction forces approximately 4 hours after seeding (Figure 4B; Figure 4C, blue; Movie S4B). These differences were consistent on 2.4 kPa micropost arrays (Movie S4C-D). The traction force normalized by cell spread area indicated that oscillating cells exhibited lower contractility compared to non-oscillating cells on both 0.6 kPa and 2.4 kPa micropost arrays (Figure 4D-E).

Figure 4: Oscillating and non-oscillating PSM cells exhibit distinct traction force profiles across substrate rigidities.

(A-B) Her1-Venus intensity and traction force heat maps of oscillating (A) and non-oscillating (B) isolated cells on 0.6 kPa micropost arrays. Oscillating cells maintain lower traction forces, while non-oscillating cells progressively increase traction force. (C) Her1 intensity and force profiles over time for the oscillating (red) and non-oscillating (blue) cells. (D) Quantitative analysis of total force per cell area for oscillating (N = 2) and non-oscillating (N = 5) isolated PSM cells cultured on 0.6 kPa micropost arrays. Oscillating cells maintain lower total force per cell area, while non-oscillating cells show a wide range of total force per cell area over time. (E) Quantitative analysis of total force per cell area for oscillating (N = 2) and non-oscillating (N = 5) isolated PSM cells cultured on 2.4 kPa micropost arrays. Similar to the 0.6 kPa condition, oscillating cells maintain lower total force per cell area compared to non-oscillating cells, which exhibit a wide range of total force per cell area over time.

These findings suggest that cell morphology, spreading dynamics, motility, and mechanical tension are closely linked to the oscillatory behavior of the segmentation clock. The morphological and biophysical differences between oscillating and non-oscillating cells may be linked to the activation of the YAP pathway, which is known to respond to mechanical cues and cell stretches¹⁶. Collectively, these results highlight the importance of mechanical cues from the microenvironment in modulating the oscillatory dynamics of the segmentation clock through changes in cell shape, contractility, and mechanical tension.

Multicellular Aggregates Display Emergent Oscillatory Properties Influenced by Cell-Cell Interactions and Mechanical Cues

To investigate the oscillatory behavior of multicellular systems, we cultured cell aggregates on PDMS micropost arrays and compared their properties to those of single cells across different surface conditions (Figure 5A). Similar to isolated cells, cell aggregates displayed oscillatory behavior linked to morphology and substrate conditions, suggesting the continued influence of mechanical signals in cell clusters As an example, we showed two cell clusters (Figure 5B-E; Movie S5A). The colony on Pluronic-coated glass exhibited sustained Her1-Venus oscillations and stable circularity over time (Figure 5B-C, red), with a slight reduction in circularity from the beginning due to the protrusion of peripheral cells (Figure 5D). In contrast, the cell aggregates on 1.2 MPa PDMS microposts were non-oscillatory (Figure 5B, blue) and experienced a significant reduction in circularity over time (Figure 5C, blue; Figure 5E; Movie S5B).

Figure 5: Surface rigidity modulates clock dynamics and morphological properties of PSM cell aggregates.

(A) Schematic of cell aggregates cultured on PDMS micropost arrays. (B) Her1-Venus intensity traces of cell aggregates on Pluronic-coated glass surfaces (black) and 1.2 MPa PDMS micropost arrays (red). (C) Circularity traces of the representative cells in (B). (D) Montage of a cell aggregate on Pluronic-coated glass and (E) 1.2MPa micropost surfaces. Transmitted light indicates aggregate viability, Her1-Venus intensities reflect segmentation clock oscillations, and circularity demonstrates the aggregate maintaining a low contact area on the Pluronic-coated glass surface while spreading more on the 1.2MPa micropost array surface. (F) Semi-log plot of the percentage of oscillating cell aggregates on surfaces of varying rigidities. The percentage of oscillating cell aggregates is lower on rigid micropost arrays (1.2 MPa) and Matrigel-coated glass compared to soft micropost arrays (0.6 kPa and 2.9 kPa), suggesting that increasing surface rigidity may suppress oscillations in cell aggregates. (G) The number of oscillation cycles decreases with increasing surface rigidity, indicating the segmentation clock is sensitive to mechanical cues, with stiffer surfaces leading to fewer oscillation cycles. (H) The segmentation clock oscillation period is modulated by surface rigidity, with a sensitive range between 10⁰-10² kPa, suggesting that the timing of oscillations can be fine-tuned by the mechanical properties of the surrounding environment within this rigidity range.

Additionally, we analyzed the oscillation properties of cell aggregates across all surface conditions and found that as rigidity increased, the percentage of oscillations and the number of cycles decreased (Figure 5F-G). However, the period remained widely distributed between 60 to 100 minutes and did not show a clear dependency on rigidity (Figure 5H). These observations were generally consistent with the behavior of isolated oscillating cells. However, the sigmoidal dependency of oscillation percentage on rigidity was no longer observable. Instead, we found that across all rigidity conditions, cell aggregates showed a significantly higher percentage of oscillations compared to single cells, suggesting that the oscillatory state may be influenced not only by cell mechanics but also by cell-cell communications.

These findings highlight the complex interplay between cellular interactions and the mechanical environment in regulating the segmentation clock dynamics in multicellular contexts. The observed differences in the oscillatory response to rigidity between cell aggregates and single cells may be attributed to the enhanced Notch signaling in the aggregates, which positively regulates her1, coupled with the antagonistic effect of mechano-transduced YAP activity on the segmentation clock. Another possibility could be the difficulty in activating YAP signaling in cell aggregates compared to isolated cells, due to the inhibited cell spreading or stretching of the cells in the middle. This may also explain the heterogeneous pattern of oscillations observed in aggregates on hard surfaces, where cells at the center are more likely to oscillate while cells in the periphery tend to spread and do not oscillate.

Discussion

Our study reveals that the segmentation clock is sensitive to mechanical cues from the microenvironment, with substrate rigidity playing a crucial role in modulating the oscillatory behavior of isolated PSM cells. Notably, we observed a critical rigidity threshold between 2.9–6 kPa, where the percentage of oscillating cells exhibits a switch-like drop, suggesting that the segmentation clock is finely tuned to respond to specific mechanical ranges.

The use of PDMS micropost arrays in our study provides a unique and powerful tool to investigate the role of mechanics in regulating the segmentation clock at the single-cell level and in multicellular aggregates. This approach allows for precise control over the mechanical environment, enabling us to explore a wide range of rigidities and their effects on oscillatory behavior. Other methods, such as hydrogels, require adjusting the densities of the coating, which impacts not only rigidity but also ligand concentration and other complex factors like biochemical signaling, cell adhesion properties, and matrix porosity. These complexities make it difficult to distinguish biochemical effects from mechanical effects on cellular responses. In our study, we cultured cells on micropost arrays with a uniform 2% Matrigel coating across all rigidity conditions to isolate mechanical rigidity from other matrix properties. This approach enables a clearer interpretation of cellular responses specifically to bulk mechanical changes. Additionally, this method could be extended to investigate the role of mechanics in segmentation clock systems across different species, providing a valuable tool for comparative studies and deepening our understanding of the conserved and divergent mechanisms that regulate the segmentation clock across vertebrates.

Our findings also highlight the importance of cell morphology, motility, and mechanical tension in regulating the oscillatory dynamics of the segmentation clock. We observed that oscillating cells exhibit distinct biophysical properties, such as sustained circularity, reduced spreading, lower motility, and decreased mechanical tension. In contrast, non-oscillating cells display altered morphology, increased spreading, higher motility, and elevated traction forces and contractility. These results suggest that the mechanical state of individual cells, as well as their ability to sense and respond to mechanical cues from the microenvironment, are critical factors in determining the oscillatory behavior of the segmentation clock.

Furthermore, our study reveals that cell-cell contacts and the mechanical environment within multicellular aggregates may coordinate, resulting in the segmentation clock of the aggregates less sensitive to rigidity changes compared to isolated cells. These findings underscore the importance of investigating the segmentation clock dynamics in multicellular contexts, as the interplay between cell-cell communication and mechanical cues can give rise to emergent behaviors that are not observed in isolated cells.

Methods

Data and materials availability:

The raw imaging data and corresponding MATLAB files containing segmentation, tracks, and data analysis are available upon request, please contact the corresponding author. MATLAB scripts for data analysis are deposited on GitHub.

Fish husbandry and tailbud cell dissociation

Zebrafish Tg(her1:her1-Venus) embryos were maintained at 28°C in E3 buffer without methylene blue until 50% epiboly and then held at 19°C overnight before in vitro experiments. Tailbud dissections were performed at the 5- to 8-somite stage. Embryos were dechorionated in E3 buffer using sharp tweezers and transferred to L15 medium with penicillin-streptomycin for cell dissociation and subsequent imaging. The tissue below the notochord, including the progenitor zone and parts of the posterior PSM, was cut using two syringe needles (30G x 1/2” - BD 305106 PrecisionGlide Needle) where one needle was used to fix the embryo in place within the Petri dish and another one to scrap the yolk away and cut the tailbud. Three tails were collected in a microcentrifuge tube with 10 µL of L15 medium and mechanically dissociated by pipetting using a P20 pipette for 5 minutes. Dissociated cells were plated on glass-bottom dishes pre-coated with F-127 Pluronic and 2% Matrigel. Cell culture droplets were mounted with mineral oil to prevent medium evaporation. The dissociation process produced a mixture of single cells and cell aggregates, both of which were used for the analysis in this study.

Confocal time-lapse microscopy

Images were acquired using an inverted Olympus FV1200 confocal microscope equipped with a 20x objective (Olympus UCPlanFL 20x / 0.70 NA), PMT detectors, and a Z-direction compensation autofocus function. Her1-Venus was excited using a 515 nm laser with 10% power and a scan speed of 12 μs/pixel (pixel dwell time) and detected with a high-sensitivity GaAsP detector. Transmitted light images were captured using a transmitted light photomultiplier detector. The image size was 512 × 512 pixels, resulting in a resolution of 1.242 pixels/µm. Both transmitted light and YFP channels were imaged at 5-minute intervals for a minimum duration of 20 hours. The sample dish was maintained at 28°C using the Tokai Hit Stage Top Incubation System. Multiposition scanning was configured to capture up to 14 positions per experiment.

Image analysis

Isolated cell Her1-Venus expression was tracked using Manual tracking with TrackMate in Fiji. The tracked circle diameter was set to 10–15 µm to ensure coverage of the entire cell area across all frames. Peak detection and period statistics were obtained using a custom Matlab script with the findpeaks function, which smoothens the time series and identifies peaks based on local maxima, minimum period distance, and minimum prominence. The period was defined as the peak-to-peak time interval. Oscillating cell percentage statistics were calculated using a 10-hour cutoff, with non-tracked cells including touched and dead cells, excluded. Pie plots were used to show the percentage of all cell types from the first frame and tracked cells at 10 hours for each dataset (Figure S3).

Cell aggregates were defined as having at least 4 cells at the first frame and surviving for 10 hours. Oscillating cell aggregates were defined as having at least one oscillating cell, with peaks detected using the custom Matlab script within the 10-hour window. If cells split from the aggregates, all separated parts containing more than 4 cells were tracked. Cell aggregates were manually tracked using the Fiji/ImageJ plugin, Mastodon, with the tracked circle diameter set to approximately 4 µm larger than the object to minimize background noise impact on average intensity calculation. The algorithm smooths the time series and identifies peaks based on local maxima, minimum period distance, and minimum prominence.

Fabrication of PDMS micropost arrays

Photolithography and deep reactive ion-etching (DRIE) techniques were used for the fabrication of the Si micropost mold. The PDMS micropost array was generated by replica molding^18,23. PDMS prepolymer with a 10:1 base-to-curing agent ratio was poured into the Si micropost mold and cured at 110°C for 30 min. The negative PDMS template containing an array of holes was formed after peeling off from the Si micropost. Then the template was oxidized with oxygen plasma and passivated with trichloro (1H, 1H, 2H, 2H-perfluorooctyl) silane vapor overnight. PDMS prepolymer with a 10:1 base-to-curing agent ratio was poured over the negative PDMS template, then covered by the cover glass (Fisher Scientific 12542B), and cured at 110°C overnight. The final PDMS micropost array was peeled from the negative PDMS template and subjected to sonication in 100% ethanol for 30 seconds, followed by dry-release with liquid CO₂ using a critical point dryer (Samdri^®-PVT-3D, Tousimis, Rockville, MD) to recover collapse of PDMS microposts during peeling process.

The array surface rigidities selected for PSM cell culture included 1.2 MPa (post diameter: 0.8 µm, post-to-post diameter: 1.6 µm, post height: 0.42 µm), 6 kPa (post diameter: 0.8 µm, post-to-post diameter: 1.6 µm, post height: 3.46 µm), 2,9 kPa (post diameter: 0.8 µm, post-to-post diameter: 1.6 µm, post height: 4.49 µm), and 0.6 kPa (post diameter: 0.8 µm, post-to-post diameter: 1.6 µm, post height: 7.57 µm). To attach cells to micropost tops, we functionalized Matrigel on the tops by contact printing. Firstly, PDMS stamps with a 30:1 base-to-curing agent ratio were generated and immersed in a solution containing Matrigel (2%; Corning) for 1 hour. Matrigel-coated PDMS stamps were then placed in contact with the PDMS micropost array pre-treated with UV-ozone (UV-ozone cleaner, Jelight, Irvine, CA) to transfer adhesive Matrigel from stamps to the tops of PDMS microposts. To avoid undesired cell adhesion to the side surfaces of microposts, PDMS micropost arrays were submerged sequentially in 100% ethanol (10 seconds), DI water (three times washing), and 0.2% w/v Pluronics^® F-127 solution (Sigma-Aldrich; 30 minutes). Matrigel-coated PDMS micropost arrays could be stored in phosphate-buffered saline (PBS; Invitrogen) solution for up to a week before cell culture.

Quantification of cell contractility of PSM cells

To quantify the traction forces exerted by isolated cells, we employed PDMS micropost arrays. The PDMS microposts beneath the isolated cells were stained with Fibrinogen, Alexa Fluor^™ 647 Conjugate (Invitrogen^™) and imaged using an inverted Olympus FV1200 confocal microscope equipped with an Olympus UPlanSApo 40× 1.25 Sil objective. Time-lapse images were analyzed using a custom-developed MATLAB script^18,23. The script fitted the deviation of each post’s centroid from its original position, determined by the free and undeflected posts. The horizontal traction force was then calculated by multiplying the post centroid deviation by the nominal spring constant K, which was generated through finite element model (FEM) simulations^18,23,24.

Oscillator model

We modeled the her1 genetic oscillator based on a time-delayed negative feedback model adapted from Negrete et al.²⁵, which is described by the delay differential equation (DDE):

$$\frac{dY}{dt}=-Y\left(t\right)+\chi H_{\infty }^{-}\left(Y\left(t-t_d\right)\right)$$

Here Y is the her1 protein concentration, $H_{\infty }^{-}\left(Y\left(t-t_d\right)\right)$ is the negative feedback with an explicit time delay $t_d$, and $\chi$ is the production rate. We assume $\chi$ to be constant for a free-running oscillator without any mechanical effects and $H_{\infty }^{-}\left(Y\right)=\text{1}-\theta \left(Y-\text{1}\right)$ where $\theta$ is the Heaviside step function.

While our model assumes constant production, we assume this production varies from cell to cell, with a Gaussian distribution. It has been observed in similar contexts that mechanical forces, acting through the YAP pathway, can create a thresholding effect for the onset of oscillations, and that Notch can help rescue these oscillations¹⁰. With these prior results and our experimental findings in this study, we treat $\chi$ as a function of Notch and Yap such that $\chi =f\left(Notch\right)g\left(YAP\right)$ where $f$ is a monotonically increasing function of Notch and $g$ is a monotonically decreasing function of YAP. Additionally, we modeled YAP following a Hill function relationship with rigidity, aligning with the experimental observation of switch-like YAP translocation in response to increasing rigidity¹⁶.

For this DDE with constant production, there is a thresholding effect here at $\chi =1$. For $\chi <1$ there are no oscillations. Under these assumptions, and with this thresholding effect, one observes that the percentage of oscillating cells decreases as rigidity increases. This reflects what is seen in our experimental results.

This model also coincides with our results from the cell aggregated data. Cell aggregates engage in Notch signaling, which increases $\chi$ in the model, and leads to a greater number of cell aggregates cells oscillating.

Mean squared displacement

The mean squared displacement (MSD) gives a measure for the type of motion displayed by particles in a given time interval²⁶. For each stage position, a background fixed point was tracked to account for slide movements from the stage. These displacements were subtracted from the cell tracking data in that position. Windowed MSD plots were generated for oscillating and non-oscillating cells on varying rigidity. The equation $MSD\left(t\right)=<r^2>=<{\left(\left|r\left(t+\mathit{to}\right)-r\left(\mathit{to}\right)\right|\right.}^2>$ and time from 0 to 600 min was used to produce plots. A windowed MSD calculation was also generated for each individual cell to generate span plots using the equation $MSD\left(Tau\right)=<{\left(\left|r\left(t+Tau\right)-r\left(t\right)\right|\right.}^2>$. We selected all time frames and Tau values to generate smooth MSD estimates for each cell. The windowed MSD was verified with two separate algorithms and MSD at to = 0 was compared to the windowed MSD. Span plot areas were colored by 10% quantiles in MSD data.

Diffusion coefficients (D) were calculated using equation MSD=2pDt where p=2 is the number of dimensions. We performed a linear least squares fit centered at the origin for each individual cell displacement track to evaluate diffusion in each condition. Span plot areas were colored by 10% quantiles in MSD data.

Circularity

Isolated cell circularity was collected manually by tracing the boundaries of cells in Fiji (Image J) software. Circularity was collected for 120 frames over 10 hours for the selected cells. The degree of circularity was calculated using the equation $\text{4}\pi \left({Area/Perimeter}^2\right)$.

Time to shape transition was calculated as follows: a time-lapse was divided into 40-minute windows, a given frame for non-oscillating cells was considered to have undergone a significant shape transition if it’s 5-frame moving average circularity was 2 standard deviations less than the moving average of the oscillating cells’ circularity; If an entire 40-minute window consisted of frames designated as having undergone a shape transition, the first frame was marked as the time to shape transition for the condition.

Highlights:

• The oscillatory behaviors of single PSM cells respond to substrate rigidity in a switch-like manner, with a critical threshold between 2.9 kPa and 6 kPa.

• As rigidity increases, both the oscillation percentage and the number of cycles decrease, while the period does not show a clear dependency on rigidity.

• Oscillating cells exhibit distinct biophysical properties compared to non-oscillating cells, including higher and more sustained circularity, lower motility, and reduced contractility.

• Cell aggregates exhibit similar trends in response to rigidity, except for significantly increased oscillation percentages across different rigidity conditions, suggesting a potential interplay between cell-cell communications and rigidity in influencing cell aggregate behavior.