Effective intervention of brucellosis prevention in developing countries: A dynamic modelling study

Abstract

Objective

Brucellosis has a considerable impact on human health and the economy in developing countries. In China, the biggest developing country, brucellosis shifted spread of the epidemic from northern to southern regions. Understanding the transmission characteristic of brucellosis on Hunan province, located in central China, is of great significance for successful control.

Methods

We developed a multi-population and multi-route dynamic model (MPMRDM), which is an animal-human-environment coupled model. The model is an extension of the SEIR model, taking into account direct transmission and indirect transmission. We used the model to explore the spread of brucellosis and evaluate the effectiveness of various intervention strategies.

Results

The animal-to-animal transmission rate was the highest at 5.14 × 10⁻⁸, while the environment-to-person transmission rate was the lowest at 9.49 × 10⁻¹². The mean R₀ was 1.51. The most effective intervention was taking personal protection, followed by shortening the infection period. Shortening the infection period combined with personal protection is the most effective two-combined intervention strategy. After any comprehensive intervention strategy was implemented, TAR dropped by 90% or more.

Conclusion

The results demonstrate that animal transmission route is essential for controlling human brucellosis. Strengthening personal protection, early detection, and early treatment can effectively control the trend of brucellosis. These results can provide an important reference for optimizing brucellosis intervention plans.

List of abbreviations

MPMRDM	Multi-population and multi-route dynamic model
SEIR	Susceptible-exposed-infectious-recovered model
R0	Basic regeneration number
TAR	Total attack rate

1. Introduction

Brucellosis is a zoonotic disease caused by Brucella. Among four types of bacteria [1], Brucella melitensis is the major cause of brucellosis epidemics and is the highest level of virulence. Animals were infected primarily through direct contact with infected animals or indirect exposure Brucella in the environment [2,3]. In humans, common routes of include direct contact with infected animals, or inhalation of infectious aerosols, and ingestion of infectious unpasteurized milk or other dairy products [4]. Brucellosis is widespread, but the clinical symptoms of infection in humans are not obvious [5], so the disease is commonly underreported and misdiagnosed.

Globally, brucellosis has emerged a serious public health problem, posing a threat to all countries [6]. Based on studies on the global burden of brucellosis, it is estimated that over 500,000 new cases are reported yearly, resulting in significant healthcare burdens for both governments and individuals. Many developing countries, such as Kenya (203.07/100,000), Yemen (89.96/100,000), and Syria (47.26/100,000) [7], show a high incidence of brucellosis infection, which is higher than that in developed countries. In recent years, the incidence of brucellosis remains at a high level in China, the biggest developing country. According to monitoring data from the China Information Network System of Disease Prevention and Control, the highest incidence was still concentrated in the northern regions, such as the Inner Mongolia, Ningxia, and Xinjiang [8,9]. However, the epidemic area of brucellosis continues to expand and there is a trend of spreading to southern provinces. The epidemic of human brucellosis is becoming serious in Hunan Province, a province in central China. The incidence of human brucellosis showed an increasing trend year by year, with a particularly notable increase observed since 2015 [10]. We chose Hunan Province as our study site to explore the transmission of brucellosis.

Prior to this study, some dynamic models have been used in the study of brucellosis, which study the transmission and provide referable advice for disease control. For example, Lou et al. [11] proposed a susceptible-exposed-infected-vaccinated model (SEIV) to study the brucellosis transmission among sheep/cattle and from sheep/cattle to humans. Sun et al. [12] presented a dynamic brucellosis model considered direct and indirect transmission with infected animals and the environment. Huang et al. [13] established a model to design control methods for brucellosis, taking into account the goat-to-person route and the differences between nanny goats and other goats. Li et al. [14] established a model with an indirect transmission rate to assess the strategies to control brucellosis. Hou et al. [15] developed a dynamic model involving sheep, human and environment and evaluated the preventive measures of animal brucellosis. Ma et al. [16] established a dynamic model of the coupling of humans and sheep in discrete time to study the impact of different control measures (including disinfection and public education) on the spread of brucellosis. Dustin G. et al. [17] combined landscape ecology and dynamic models to study the impact of land conversion factors on the spread of zoonotic diseases. Zeng et al. [18] considered environmental noise, established a deterministic cattle brucellosis model with abortion-infected individuals and carriers, and proposed a corresponding stochastic model. Liu et al. [19] constructed a spatially heterogeneous reaction-diffusion model with non-local time delays based on age structure for sheep brucellosis, providing new control strategies for the spread of brucellosis. However, few studies have studied the brucellosis transmission among animals and from animals to humans based on a multi-population and multi-route dynamic model with environmental transmission pathway. In China, the biggest developing country, brucellosis shifted spread of the epidemic from northern to southern regions. Due to regional and environmental differences, it is necessary to simulate the spread of brucellosis in Hunan Province, a province in central China in order to implement more effective prevention and control measures. Therefore, we proposed a multi-population and multi-route dynamic model (MPMRDM), which is an animal-human-environment coupled model. The model is an extension of the SEIR model, taking into account direct transmission and indirect transmission.

In this study, the MPMRDM was used to simulate the dataset of Hunan Province, China. We analyzed the transmission and evaluated the effectiveness of different intervention strategies. Separate intervention considered were shortening the infection period, vaccinating susceptible animals, environmental disinfection, and taking personal protection.

2. Methods

2.1. Study site

China is the biggest developing country. We selected Hunan province, a city in central China, as our study site. Hunan Province is located between 24°38′ and 30°08′ north latitude and 108°47′ to 114°157′ east longitude. Hunan ranks first among the provinces in central China，covering a total area of 21,800 km². Its strategic geographical location connects the southern and northern regions of the country. In addition, Hunan boasts abundant and diverse land resources, making it favorable for the development of animal husbandry.

2.2. Data collection

This study collected information regarding cases of brucellosis in Hunan Province from January 1, 2015, to December 31, 2019. Data were provided by the Hunan Provincial Center for Disease Control, and a brucellosis epidemic dataset (variables included number, gender, age, and occupation) was established. Demographic and animal data were obtained by consulting the Statistical Yearbook of Hunan Province.

2.3. Model without intervention

The environmental transmission pathway plays a significant role in the transmission of brucellosis, so the environmental transmission is introduced into our model. This study investigated four transmission routes: animal-to-animal, animal-to-person, environment-to-animal, and environment-to-person. In the animal-to-animal route, susceptible animals are infected through direct contact with exposed and infected animals. In the animal-to-person route, individuals become infected from eating undercooked meat and unpasteurized dairy products contaminated with Brucella and from direct contact with infected animals. Exposed and infected animals can excrete brucella into the environment through miscarriage or animal secretions. Brucella can survive in feces or contaminated environments under the right conditions. In environmental to human/animal route, and humans/animals become infected by Brucella in the environment.

Based on the characteristics of the epidemic in Hunan Province, we developed the MPMRDM among animals and from animals to humans to simulate the transmission in key populations. The key population includes farmers and herdsmen, and animals include cattle, buffaloes, goats, and sheep.

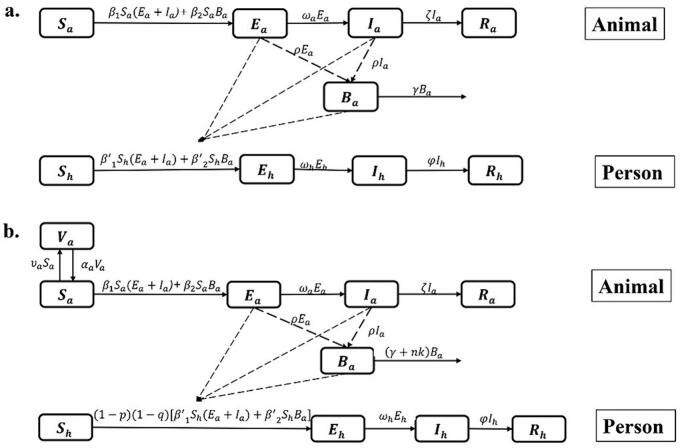
In the model, we adopted the subscripts h and a to represent human and animal, respectively. Animal-to-person transmission route includes the following: susceptible person (S_h), exposed person (E_h), infectious person (I_h), and recovered person (R_h). B_a represents the number of Brucella in the environment. The unit of B_a is defined as IU, which is a new bacterial unit that refers to the number of bacteria that can infect a susceptible animal or person. Animal-to-animal transmission includes the following: susceptible animal (S_a), exposed animal (E_a), infectious animal (I_a), and removed animal (R_a). (Model 1 in Fig. 1a). The model was based on the following assumptions:

• (1)Exposed (E_a) and infected (I_a) animals have the same transmission rate.
• (2)(2)A susceptible animal is infected through “animal-to-animal” and “environment-to-animal” routes, and the transmission rates are β₁ and β₂, respectively. A susceptible person is infected through “animal-to-person” and “environment-to-person” routes, and the transmission rates are β₁^’ and β₂^’, respectively.
• (3)The incubation period of an exposed person (E_h) is 1/ω_h. The rate (per month) at which an exposed person became infected was ω_hE_h.
• (4)Infected people will recover after an infection period of 1/φ. According to Chinese brucellosis epidemic data released by the Ministry of Health in 2021, the disease mortality rate of brucellosis was low. We therefore did not include the case fatality rate in the model for this study.
• (5)An exposed animal (E_a) and an infected animal (I_a) can all excrete Brucella, and it is assumed that both coefficients of Brucella excretion are ρ.
• (6)Brucella will cease to exist after a certain period in the environment, and the survival time is 1/γ.
• (7)The incubation period of the exposed animal (E_a) was 1/ω_a, and the rate (per month) at which an exposed animal became infected was ω_aE_a. The time from animal infection to slaughter is 1/ζ.

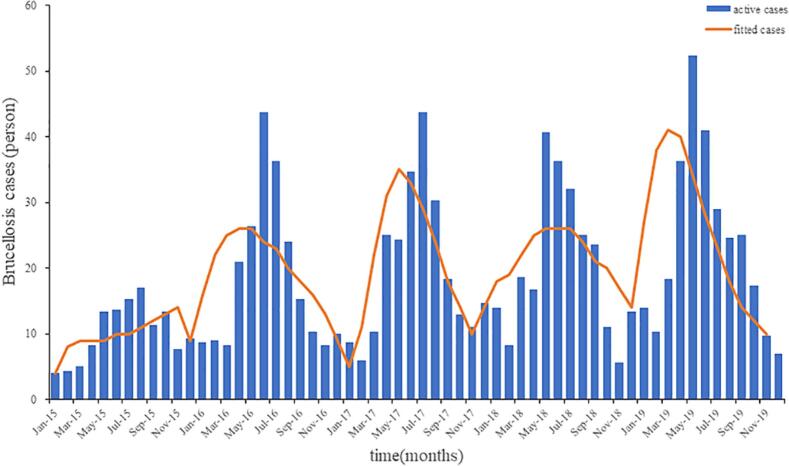
Fig. 1.

Flow chart of the model of brucellosis: a. Model 1; b. Model 2.

The equations of the model containing the four transmission routes are as follows:

$$\left\{\begin{array}{c}\mathrm{d}{\mathrm{S}}_{\mathrm{a}}/\mathrm{dt}=-{\mathrm{\beta }}_1{\mathrm{S}}_{\mathrm{a}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)-{\mathrm{\beta }}_2{\mathrm{S}}_{\mathrm{a}}{\mathrm{B}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{E}}_{\mathrm{a}}/\mathrm{dt}={\mathrm{\beta }}_1{\mathrm{S}}_{\mathrm{a}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)+{\mathrm{\beta }}_2{\mathrm{S}}_{\mathrm{a}}{\mathrm{B}}_{\mathrm{a}}-{\mathrm{\omega }}_{\mathrm{a}}{\mathrm{E}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{I}}_{\mathrm{a}}/\mathrm{dt}={\mathrm{\omega }}_{\mathrm{a}}{\mathrm{E}}_{\mathrm{a}}-\mathrm{\zeta }{\mathrm{I}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{R}}_{\mathrm{a}}/\mathrm{dt}=\mathrm{\zeta }{\mathrm{I}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{B}}_{\mathrm{a}}/\mathrm{dt}=\mathrm{\rho }{\mathrm{E}}_{\mathrm{a}}+\mathrm{\rho }{\mathrm{I}}_{\mathrm{a}}-\mathrm{\gamma }{\mathrm{B}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{S}}_{\mathrm{h}}/\mathrm{dt}=-{\mathrm{\beta }}_1^{\prime }{\mathrm{S}}_{\mathrm{h}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)-{\mathrm{\beta }}_2^{\prime }{\mathrm{S}}_{\mathrm{h}}{\mathrm{B}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{E}}_{\mathrm{h}}/\mathrm{dt}={\mathrm{\beta }}_1^{\prime }{\mathrm{S}}_{\mathrm{h}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)+{\mathrm{\beta }}_2^{\prime }{\mathrm{S}}_{\mathrm{h}}{\mathrm{B}}_{\mathrm{a}}-{\mathrm{\omega }}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{h}}\\ \mathrm{d}{\mathrm{I}}_{\mathrm{h}}/\mathrm{dt}={\mathrm{\omega }}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{h}}-\mathrm{\phi }{\mathrm{I}}_{\mathrm{h}}\\ \mathrm{d}{\mathrm{R}}_{\mathrm{h}}/\mathrm{dt}=\mathrm{\phi }{\mathrm{I}}_{\mathrm{h}}\end{array}\right)$$

3. Model with intervention

We built a new model (Model 2) to estimate the different intervention strategies effects (Fig. 1b) by adding the following assumptions to Model 1:

• (1)We assumed that the vaccination coefficient of the vaccine is υ_a. The rate (per month) at which a susceptible animal became vaccinated was υ_aS_a. The antibodies after vaccination can only last for a certain period (antibody maintenance period, 1/α_a); thereafter, V_a becomes S_a again.
• (2)For taking personal protection, q was the effective rate of protection, representing the effectiveness of protective measures. p was the population protection rate, representing the proportion of individuals taking protective measures against brucellosis.
• (3)For environmental disinfection, we assumed that the effective disinfection rate was k and the disinfection times was n.

The equations of the model with interventions are as follows:

$$\left\{\begin{array}{c}\mathrm{d}{\mathrm{S}}_{\mathrm{a}}/\mathrm{dt}=-{\mathrm{\beta }}_1{\mathrm{S}}_{\mathrm{a}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)-{\mathrm{\beta }}_2{\mathrm{S}}_{\mathrm{a}}{\mathrm{B}}_{\mathrm{a}}+{\mathrm{\alpha }}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{a}}-{\mathrm{\upsilon }}_{\mathrm{a}}{\mathrm{S}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{E}}_{\mathrm{a}}/\mathrm{dt}={\mathrm{\beta }}_1{\mathrm{S}}_{\mathrm{a}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)+{\mathrm{\beta }}_2{\mathrm{S}}_{\mathrm{a}}{\mathrm{B}}_{\mathrm{a}}-{\mathrm{\omega }}_{\mathrm{a}}{\mathrm{E}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{I}}_{\mathrm{a}}/\mathrm{dt}={\mathrm{\omega }}_{\mathrm{a}}{\mathrm{E}}_{\mathrm{a}}-\mathrm{\zeta }{\mathrm{I}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{R}}_{\mathrm{a}}/\mathrm{dt}=\mathrm{\zeta }{\mathrm{I}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{V}}_{\mathrm{a}}/\mathrm{dt}={\mathrm{\upsilon }}_{\mathrm{a}}{\mathrm{S}}_{\mathrm{a}}-{\mathrm{\alpha }}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{B}}_{\mathrm{a}}/\mathrm{dt}=\mathrm{\rho }{\mathrm{E}}_{\mathrm{a}}+\mathrm{\rho }{\mathrm{I}}_{\mathrm{a}}-\left(\mathrm{\gamma }+\mathrm{nk}\right){\mathrm{B}}_{\mathrm{a}}\\ \mathrm{d}{\mathrm{S}}_{\mathrm{h}}/\mathrm{dt}=-\left(1-\mathrm{p}\right)\left(1-\mathrm{q}\right)\left[{\mathrm{\beta }}_1^{\prime }{\mathrm{S}}_{\mathrm{h}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)+{\mathrm{\beta }}_2^{\prime }{\mathrm{S}}_{\mathrm{h}}{\mathrm{B}}_{\mathrm{a}}\right]\\ \mathrm{d}{\mathrm{E}}_{\mathrm{h}}/\mathrm{dt}=\left(1-\mathrm{p}\right)\left(1-\mathrm{q}\right)\left[{\mathrm{\beta }}_1^{\prime }{\mathrm{S}}_{\mathrm{h}}\left({\mathrm{E}}_{\mathrm{a}}+{\mathrm{I}}_{\mathrm{a}}\right)+{\mathrm{\beta }}_2^{\prime }{\mathrm{S}}_{\mathrm{h}}{\mathrm{B}}_{\mathrm{a}}\right]-{\mathrm{\omega }}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{h}}\\ \mathrm{d}{\mathrm{I}}_{\mathrm{h}}/\mathrm{dt}={\mathrm{\omega }}_{\mathrm{h}}{\mathrm{E}}_{\mathrm{h}}-\mathrm{\phi }{\mathrm{I}}_{\mathrm{h}}\\ \mathrm{d}{\mathrm{R}}_{\mathrm{h}}/\mathrm{dt}=\mathrm{\phi }{\mathrm{I}}_{\mathrm{h}}\end{array}\right)$$

3.1. Evaluating the effectiveness of different intervention strategies

We considered four separate interventions, including shortening the infection period, vaccinating susceptible animals, environmental disinfection, and taking personal protection. This study simulates separate-intervention strategies, two-combined intervention strategies, and integrated-intervention strategies, with the aim of assessing the effectiveness. We compared the differences under the following scenarios:

3.1.1. Scenario 1: shortening the infection period

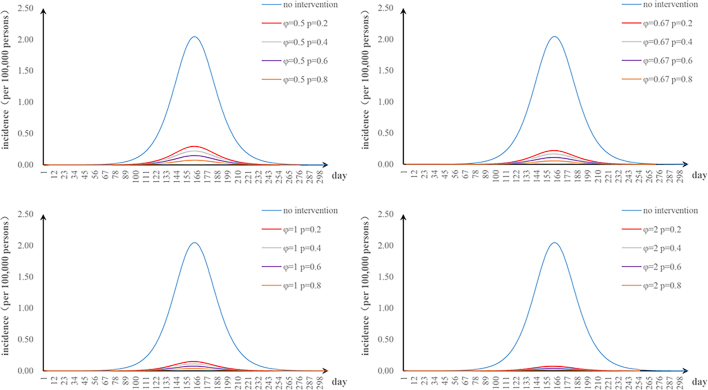
When an infected patient receives treatment promptly after symptoms appear, the time of treatment is shortened. The recovery period 1/φ will also be shortened. The recovery period was shortened from 2.2 months to 2, 1.5, 1, and 0.5 months respectively. We adjusted φ to 0.5, 0.67, 1, and 2. The other parameter settings remained unchanged.

3.1.2. Scenario 2: vaccinating susceptible animals

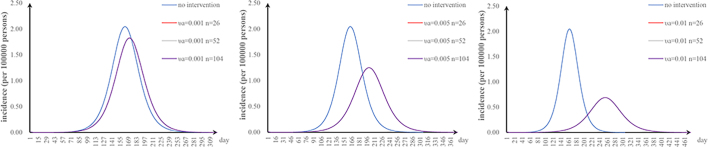
The vaccine intervention model has one more warehouse than the original model; we used V_a to denote those animals who were vaccinated. We set υ_a to 0.005, 0.001, and 0.01, respectively. All other parameters remained unchanged.

3.1.3. Scenario 3: environmental disinfection

The survival time of Brucella in the environment was reduced when disinfecting the external environment. We set n to 26, 52, and 104 times per year, respectively. The other parameter settings remained unchanged.

3.1.4. Scenario 4: Taking personal protection

Measures to take personal protection, such as masks and gloves, will reduce the transmission of brucellosis. We set p to 0.2, 0.4, 0.6, and 0.8, respectively. All other parameters remained unchanged.

3.1.5. Scenario 5: the two-combined intervention

There were six combinations of two interventions. When one of two-combined intervention strategies was implemented, we changed the parameters of the two interventions. All other parameters remained unchanged.

3.1.6. Scenario 6: the integrated intervention

Integrated interventions were considered simultaneously. While integrated interventions were implemented, we changed the parameters of the corresponding interventions. The other parameter settings remained unchanged.

3.2. Parameter estimation

We set all other parameters according to the literature (Table 1) and only fitted the values for β₁, β₂, β₁^’, and β₂^’. The Runge–Kutta method of order 4 with tolerance set at 0.001 was used to perform curve fitting of the root mean square deviation between the data and best run so far.

Table 1.

Parameter definitions and values.

Parameter	Description	Unit	Value	Parameter source
β1	Animal-to-animal transmission rate	(Animals·month)−1	3.98 × 10−8	Curve fitting
β2	Environment-to-animal transmission rate	(Animals·month)−1	1.12 × 10−10	Curve fitting
β1’	Animal-to-person transmission rate	(Persons·month)−1	1.27 × 10−9	Curve fitting
β2’	Environment-to-person transmission rate	(Persons·month)−1	6.60 × 10−12	Curve fitting
ωa	Incubation relative rate of animal	Month−1	0.98	Reference [20]
ωh	Incubation relative rate of person	Month−1	1.78	Reference [21]
ρ	Coefficient of Brucella excretion	Month−1	0.21	Artificial setting
φ	Recovery rate of infected person	Month−1	0.45	Reference [22]
ζ	Slaughtered rate of infected animals	–	0.82	Reference [23]
υa	Monthly vaccination ratio	–	0.001,0.005,0.01	Artificial setting
αa	Antibody elimination rate	–	0.21	Reference [24]
q	Effective rate of protection	–	0.8	Artificial setting
p	Population protection rate	–	0.2,0.4,0.6,0.8	Artificial setting
γ	Pathogen lifetime relative rate	Month−1	0.34	Reference [20]
k	Effective disinfection rate	–	0.95	Reference [25]
n	Disinfection times	–	26,52,104	Artificial setting

3.3. Evaluation index

The basic reproduction number (R₀) is the critical threshold in the deterministic model, representing the average number of infections generated by a single case over its entire infection period. We calculated the R₀ value in the Model 1 using the next-generation matrix method [26]. The new infectious terms and transition terms are given by.

$\mathcal{F}=\left(\begin{array}{c}{\beta }_1{S}_a\left(E_a+I_a\right)+{\beta }_2{S}_a{B}_a\\ 0\\ 0\end{array}\right)$, $\mathcal{V}=\left(\begin{array}{c}{\omega }_a{E}_a\\ -{\omega }_a{E}_a+\zeta I_a\\ -\rho E_a-\rho I_a+\gamma B_a\end{array}\right)$.

We find the F and V as.

$F=\left(\begin{array}{ccc}{\beta }_1{S}_a& {\beta }_1{S}_a& {\beta }_2{S}_a\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$, $V=\left(\begin{array}{ccc}{\omega }_a& 0& 0\\ -{\omega }_a& \zeta & 0\\ -\rho & -\rho & \gamma \end{array}\right)$.

It follows that.

$F{V}^{-1}=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$.

Where.

$a_{11}=\frac{{\beta }_1{S}_a}{{\omega }_a}+\frac{{\beta }_1{S}_a}{\zeta }+\frac{{\beta }_2{S}_a\rho \left({\omega }_a+\zeta \right)}{{\omega }_a\mathit{\zeta \gamma }}$, $a_{12}=\frac{{\beta }_1{S}_a}{\zeta }+\frac{{\beta }_2{S}_a\rho }{\mathit{\zeta \gamma }}$, $a_{13}=\frac{{\beta }_2{S}_a}{\gamma }$.

Because R₀ is the same as the FV⁻¹ spectrum radius, the R₀ formula is as follows:

$$R_0=\frac{{\beta }_1{S}_a\left({\omega }_a+\zeta \right)}{{\omega }_a\zeta }+\frac{{\beta }_2{S}_a\rho \left({\omega }_a+\zeta \right)}{{\omega }_a\mathit{\zeta \gamma }}$$

$$R_{0a}=\frac{{\beta }_1{S}_a\left({\omega }_a+\zeta \right)}{{\omega }_a\zeta }，R_{0e}=\frac{{\beta }_2{S}_a\rho \left({\omega }_a+\zeta \right)}{{\omega }_a\mathit{\zeta \gamma }}$$

R₀ was divided into two parts (R_0a and R_0e). R_0a denotes the transmission of infection originating from animals with the disease. R_0e denotes the transmission infection through a contaminated environment.

Evaluation index of effectiveness of interventions was a total attack rate (TAR) [27,28]. The formula is as follows:

$$\mathit{TAR}=\mathit{TN}/N\times K$$

$$K=\mathrm{100,000}/\mathrm{100,000}$$

In the equation, TN and N refer to the total number of new cases and the total population number, respectively.

3.4. Simulation methods and statistical analysis

In this study, Excel was used for data summary and chart drawing. Berkeley Madonna (Version 8.3.18) was used for fitting existing data and models and estimating the transmissibility rate under different transmission routes. AnyLogic (Version 8.7.8) was used for evaluation conducted for intervention effects.

4. Results

4.1. Epidemiological characteristics

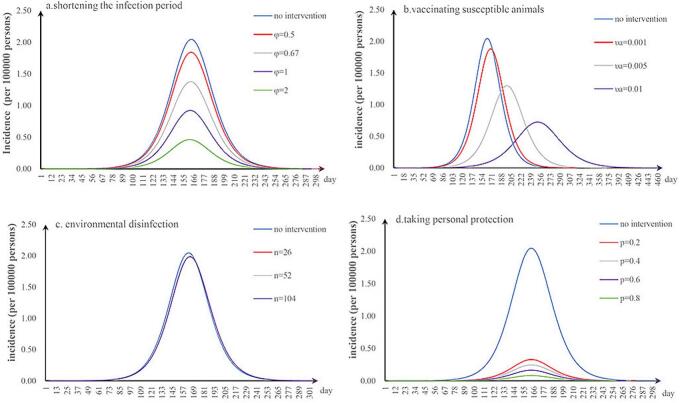
A total of 837 cases of brucellosis were reported in Hunan Province, China, from 2015 to 2019 (average annual incidence of 0.25/100,000). The highest incidence of brucellosis in Hunan Province was 0.31/100,000 in 2019, and the lowest incidence was 0.14/100,000 in 2015. The overall annual incidence rates showed an upward trend. Regarding the gender breakdown, there were 606 males and 231 females. The age of onset was concentrated between 45 and 65 years, accounting for 56.75% of the total number of patients. The most infected people were farmers, accounting for 61.17% of all case types. The results of curve fitting showed that the MPMRDM fits the data well (Fig. 2).

Fig. 2.

Fitting results of human brucellosis cases of Hunan Province.

4.2. Transmissibility of brucellosis

The values of β₁, β₂, β₁^’, and β₂^’ from 2015 to 2019 were obtained by fitting the curve and model (Table 2). The mean values were 5.14 × 10⁻⁸, 2.70 × 10⁻¹⁰, 1.06 × 10⁻⁹ and 9.49 × 10⁻¹², respectively. We calculated the R₀ from 2015 to 2019 (Table 3). The highest R₀ was in 2016 (1.92), and the mean R₀ was 1.51 from 2015 to 2019. The highest and the lowest R_0a were in 2016 (1.91) and 2015 (1.12), respectively. The highest R_0e was in 2016 (0.01).

Table 2.

Transmission rate of different transmission routes of brucellosis.

Year	β1	β2	β1’	β2’
2015	3.98 × 10−8	1.12 × 10−10	1.27 × 10−9	6.60 × 10−12
2016	4.08 × 10−8	3.17 × 10−10	5.46 × 10−10	1.15 × 10−11
2017	4.16 × 10−8	4.24 × 10−10	2.21 × 10−10	7.30 × 10−12
2018	5.69 × 10−8	1.24 × 10−10	2.30 × 10−9	8.14 × 10−12
2019	7.80 × 10−8	3.71 × 10−10	9.52 × 10−10	1.39 × 10−11

Table 3.

R₀ from 2015 to 2019.

Year	R0a	R0e	R0
2015	1.12	0.0019	1.12
2016	1.91	0.0101	1.92
2017	1.49	0.0078	1.50
2018	1.35	0.0022	1.35
2019	1.65	0.0046	1.65

4.3. Effectiveness of different intervention strategies

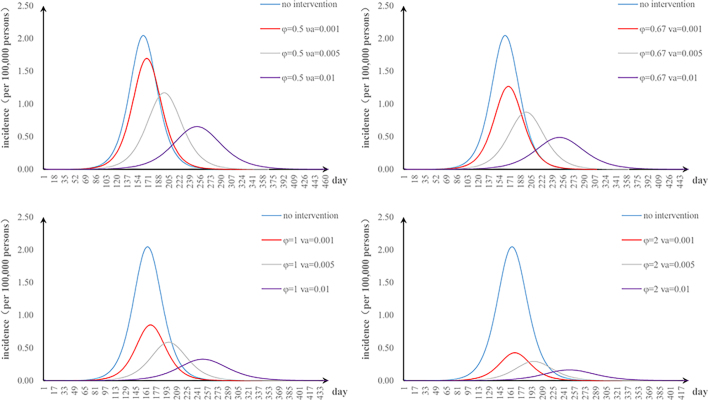
The effectiveness of different intervention strategies was investigated by setting some parameters. We first simulated the incidence without intervention based on the MPMRDM and an outbreak in 2015. Without intervention, the TAR per 100,000 people was 2.05.

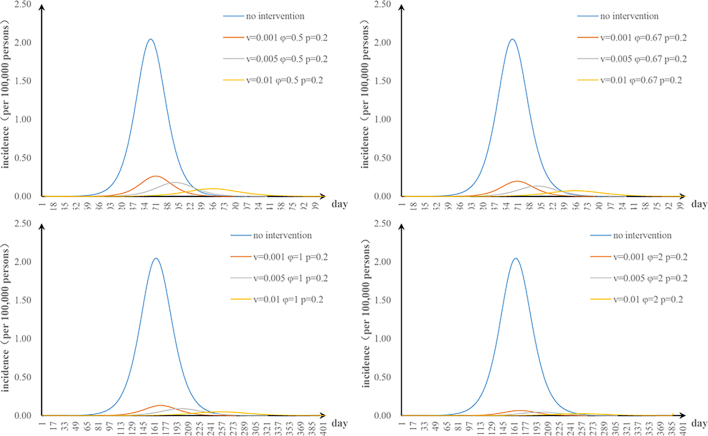
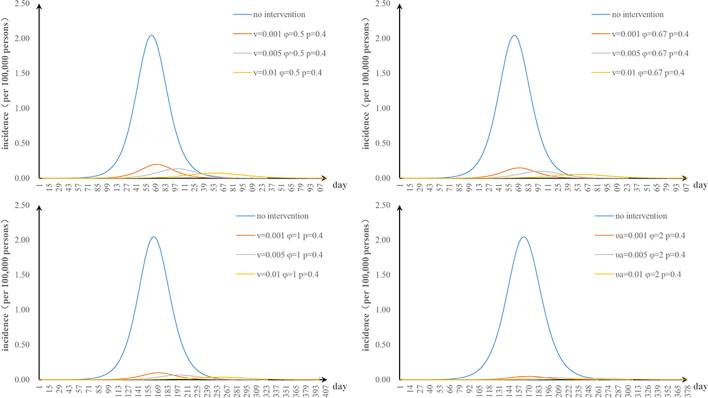
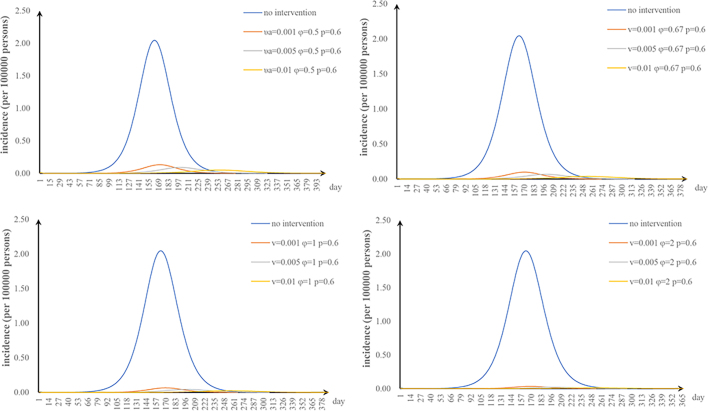
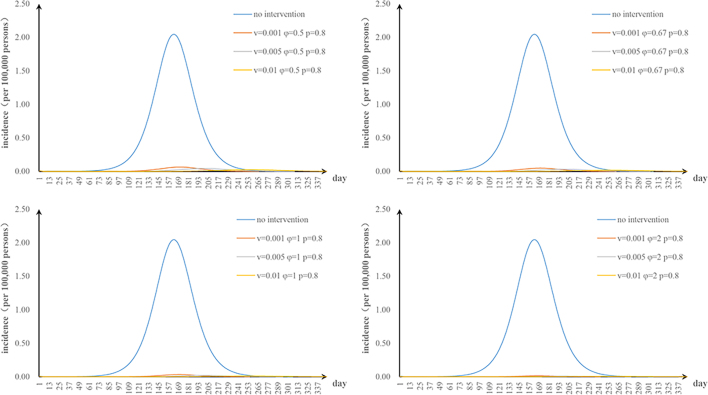
The first scenario has only one parameter φ changed: when we adjusted φ to 0.5, 0.67, 1, and 2, the TAR values (and reduced proportion) per 100,000 people were 1.84 (9.90%), 1.38 (32.64%), 0.92 (54.80%), and 0.46 (77.38%), respectively (Fig. 3a); the second scenario has only one parameter υ_a changed: when υ_a was 0.001, 0.005, and 0.01, the TAR values (and reduced proportion) per 100,000 people were 1.88 (7.99%), 1.30 (36.51%), and 0.73 (64.52%), respectively (Fig. 3b); the third scenario has only one parameter n changed: when n was 26, 52, and 104, the reduction of TAR values were 2.90%, 2.92%, and 2.93%, respectively (Fig. 3c); and the fourth scenario has only one parameter p changed: when p was 0.2, 0.4, 0.6, and 0.8, the reduction of TAR values were 83.95%, 87.96%, 91.97%, and 95.99%, respectively (Fig. 3d).

Fig. 3.

Effects of separate-intervention strategies. a. shortening the infection period; b. vaccinating susceptible animals; c. environmental disinfection; d. taking personal protection.

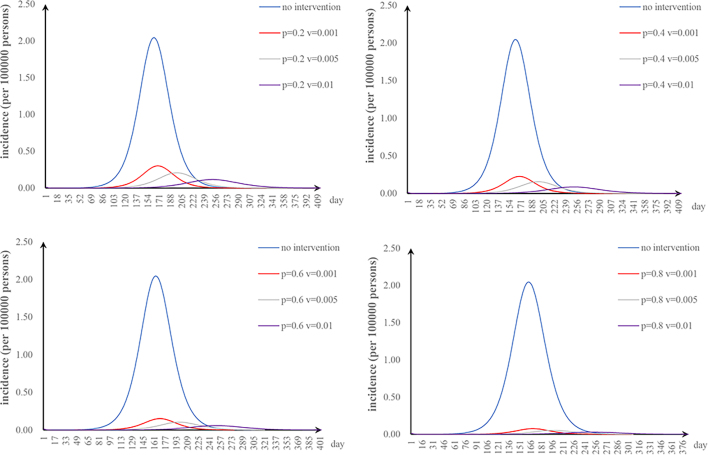
The fifth scenario is that two parameters are changed. The values of φ and υ_a were changed: when φ = 2 and υ_a = 0.01, the TAR value (and reduced proportion) per 100,000 people was 0.16 (92.00%) (Fig. S1). The values of φ and n were changed: when φ = 2 and n = 52, the TAR (and reduced proportion) per 100,000 people was 0.45 (78.05%) (Fig. S2). When φ = 2 and p = 0.8, the TAR (and reduced proportion) per 100,000 people was 0.02 (99.09%) (Fig. S3). The values of υ_a and n were changed: when υ_a = 0.01 and n = 52, the reduction of the TAR was 66.30% (Fig. S4). The values of υ_a and p were changed: when υ_a = 0.01 and p = 0.8, the reduction of the TAR was 98.58% (Fig. S5). The values of p and n were changed: when p = 0.8 and n = 52, the reduction of the TAR was 96.10% (Fig. S6).

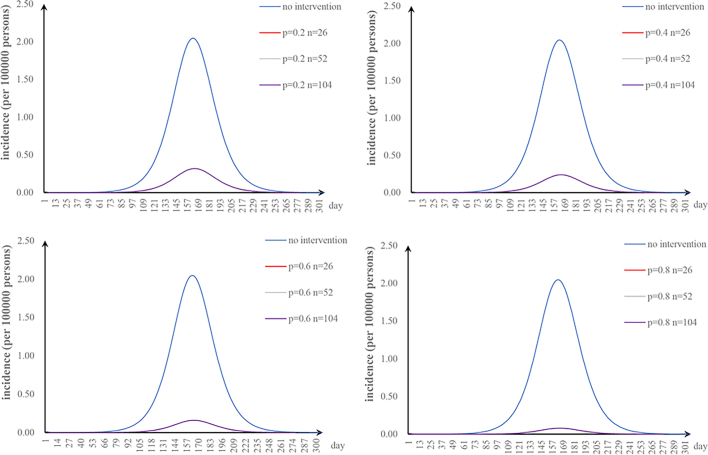
The effect of environmental disinfection was not obvious. Therefore, for integrated intervention strategies, the frequency of disinfection was assumed to be once a week. The TAR values are shown in Fig. S7–10. When p = 0.2 and φ = 0.67, the reduction of the TAR reaches over 90%.

5. Discussion

Our study showed an obvious increase in the incidence of brucellosis in Hunan Province between 2015 and 2019. There are more cases in men than in women, and the majority of infected individuals were farmers. In reality, men are more involved in breeding than women. Farmers are closest to diseased animals and their contaminants. It indicated that the main route of human brucellosis remains associated with contact with animals and their products.

Among four transmission rates, the highest was β_1, followed by β₁^’. This result indicated that the key to control the spread of human brucellosis is to control the transmission paths of animal-to-animal and animal-to-person. The transmission rates of the environmental transmission pathway are lower. Compared with other provinces, the transmission rates are lower than those in the Inner Mongolia [21] and Jilin [29], and roughly similar with that in Zhejiang [30].

The results showed that β₁ increased year by year, perhaps because the rising demand for meat, particularly beef and mutton, driven by improvements in people's quality of life [31,32]. β₂ and β₂^’ fluctuated between years because of environmental factors. The survival duration of Brucella varies in diverse soil [2]; the ambient temperature, air temperature, and UV intensity affect its survival time [[33], [34], [35]]. Another study [36] has found that meteorological factors affect the spread of brucellosis. β₁^’ varies annually, but there was an overall upward trend, which was related to β_1. The mean R₀ value was 1.51, lower than that of most northern provinces [15,37]. The more cases among animals, the higher R_0a is. R_0e increased with upward trend of R_0a, and their overall trend was similar.

The most effective separate intervention strategy was taking personal protection, followed by shortening the infection period. When taking personal protection, the incidence rate rapidly decreases. A study has shown that the behavior with the greatest risk of infection was helping cattle, goats or sheep give birth [38]. Individuals at high risk can effectively prevent infection by taking personal protection. Shortening the infection period refers to early detection and early treatment, which can effectively control the spread of brucellosis. Our study also showed that the higher the vaccination coefficient is, the more the incidence rate decreases. However, the increase in the vaccination coefficient will prolong the duration of the outbreak due to variations in animal immunity [30]. We should vaccinate the animals on demand. Environmental disinfection resulted in minimal reduction in incidence, possibly due to the low environmental transmission rate in our study.

The effectiveness of separate-intervention strategies in controlling outbreaks were limited, whereas we developed the two-combined intervention strategies and integrated-intervention strategies. For the two-combined intervention strategies, the combination of shortening the infection period and taking personal protection had the best effect. The integrated intervention strategies demonstrated significantly greater effectiveness, leading to a reduction of more than 90%. These results suggest that strengthening personal protection, early detection and early treatment can effectively control brucellosis.

Measures aimed at preventing brucellosis suggest several key aspects. Firstly, strengthen personal protection. High-risk occupational groups, such as farmers, should be equipped with suitable protective gear, including masks, goggles, gloves, and protective clothing. Additionally, raising awareness about self-protection is also crucial for enhancing personal protection. Secondly, early detection and early treatment. Individuals infected with brucellosis should receive immediate medical attention upon the onset of symptoms. Regular serological monitoring is advised for high-risk groups, and surveillance for brucellosis should be conducted. Furthermore, increasing public awareness of the early symptoms and modes of transmission of brucellosis is crucial to encourage individuals to seek medical assistance.

There were some limitations in this study. First, this study failed to separate the types of Brucella when we established the model. Second, some parameters of our model were collected from the literature instead of first-hand data. This may have influenced the accuracy of the model. Third, natural factors and social factors were not considered. Further studies that model a larger variety of brucellosis interventions and explore different factors, would be useful.

6. Conclusion

The results indicated that the spread of brucellosis will persist in Hunan Province. The main route of human brucellosis transmission is from animals to humans. The transmission rate through animal contact exceeds that through environmental exposure. It is crucial to minimize human contact with animals in order to control human brucellosis. Integrated intervention strategies are the most effective approach in developing countries. Taking personal protection, early detection, and early treatment can effectively control the trend of human brucellosis. These results can provide a reliable quantitative basis for further optimizing intervention strategies for brucellosis.

The following are the supplementary data related to this article.

Supplementary Fig. S1.

Effectiveness of a strategy combining shortening the infection period and vaccinating susceptible animals.

Supplementary Fig. S2.

Effectiveness of a strategy combining shortening the infection period and environmental disinfection.

Supplementary Fig. S3.

Effectiveness of a strategy combining shortening the infection period and taking personal protection.

Supplementary Fig. S4.

Effectiveness of a strategy combining vaccinating susceptible animals with environmental disinfection

Supplementary Fig. S5.

Effectiveness of a strategy combining vaccinating susceptible animals with taking personal protection

Supplementary Fig. S6.

Effectiveness of a strategy combining environmental disinfection with taking personal protection

Supplementary Fig. S7.

Effectiveness of integrated strategies when p = 0.2.

Supplementary Fig. S8.

Effectiveness of integrated strategies when p = 0.4.

Supplementary Fig. S9.

Effectiveness of integrated strategies when p = 0.6.

Supplementary Fig. S10.

Effectiveness of integrated strategies when p = 0.8.

Ethics approval and consent to participate

Not applicable.

Consent for publication

All authors in our study (Han Ni, Haoyun Dai, Xuewen Yang, Jin Zhao, Yuxi He, Shanghui Yi, Xiuqin Hong, Wenting Zha, Yuan Lv) agree to the publication.

Availability of data and materials

The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.

Funding

This work was supported by the Key Project of Hunan Provincial Science and Technology Innovation [2020SK1010], Natural Science Foundation of Hunan Province of China [2022JJ40285], Scientific Research Project of Health Commission of Hunan Province [202212054651], Key Project of Hunan Provincial Education Department [21A0023], Changsha Natural Science Foundation [kq2202254] and Hunan Province Degree and Graduate Teaching Reform Research Project [202201002020]. The funders had in our study were the correspondence author (Yuan Lv, Wenting Zha).

CRediT authorship contribution statement

Han Ni: Writing – original draft, Visualization, Methodology, Formal analysis, Conceptualization. Haoyun Dai: Writing – original draft, Visualization, Methodology, Formal analysis, Conceptualization. Xuewen Yang: Investigation, Data curation. Jin Zhao: Investigation, Data curation. Yuxi He: Methodology, Formal analysis. Shanghui Yi: Supervision, Project administration. Xiuqin Hong: Supervision, Project administration. Wenting Zha: Writing – review & editing, Funding acquisition. Yuan Lv: Writing – review & editing, Funding acquisition.

Declaration of competing interest

On behalf of all authors, the corresponding author states that there are no competing interests to declare.

Data availability

The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.