A lipidomic based metabolic age score captures cardiometabolic risk independent of chronological age

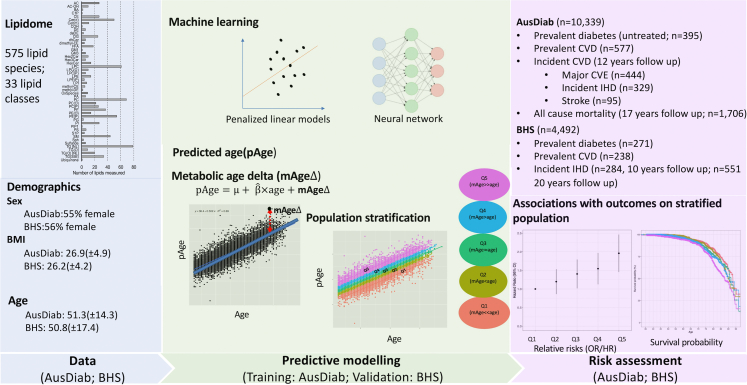
Summary

Background

Metabolic ageing biomarkers may capture the age-related shifts in metabolism, offering a precise representation of an individual’s overall metabolic health.

Methods

Utilising comprehensive lipidomic datasets from two large independent population cohorts in Australia (n = 14,833, including 6630 males, 8203 females), we employed different machine learning models, to predict age, and calculated metabolic age scores (mAge). Furthermore, we defined the difference between mAge and age, termed mAgeΔ, which allow us to identify individuals sharing similar age but differing in their metabolic health status.

Findings

Upon stratification of the population into quintiles by mAgeΔ, we observed that participants in the top quintile group (Q5) were more likely to have cardiovascular disease (OR = 2.13, 95% CI = 1.62–2.83), had a 2.01-fold increased risk of 12-year incident cardiovascular events (HR = 2.01, 95% CI = 1.45–2.57), and a 1.56-fold increased risk of 17-year all-cause mortality (HR = 1.56, 95% CI = 1.34–1.79), relative to the individuals in the bottom quintile group (Q1). Survival analysis further revealed that men in the Q5 group faced the challenge of reaching a median survival rate due to cardiovascular events more than six years earlier and reaching a median survival rate due to all-cause mortality more than four years earlier than men in the Q1 group.

Interpretation

Our findings demonstrate that the mAge score captures age-related metabolic changes, predicts health outcomes, and has the potential to identify individuals at increased risk of metabolic diseases.

Funding

The specific funding of this article is provided in the acknowledgements section.

Research in context.

Evidence before this study

While chronological age is the greatest risk factor for many diseases, it’s non-modifiable and may not accurately reflect an individual’s health status over time. Metabolic ageing biomarkers may capture the age-related shift in metabolism, offering a more precise representation of an individual’s overall metabolic health. Further, current metabolic age models have suffered from a limited prediction accuracy, possibly due to their focus on a limited subset of metabolites that may not fully capture the complexity of age-related changes. Lipidomics, a subset of metabolomics, has been demonstrated to show strong associations with age. A Google scholar search was performed, using the key words “Biological age” OR “Metabolic age” OR “machine learning” OR “Cardiovascular disease” OR “Metabolomics” AND “Lipidomics”. There was no study to describe a lipidome based metabolic age.

Added value of this study

We employed different machine learning models, to predict age, and calculated metabolic age scores. Upon stratification of the population into quintiles by mAgeΔ (the difference between metabolic age and age), we observed that participants in the top quintile had more than a two-fold increased risk of 12-year incident cardiovascular events and a 1.56-fold increased risk of 17-year all-cause mortality, relative to the individuals in the bottom quintile. Survival analysis further revealed that men in the top quintile faced the challenge of reaching a median survival rate due to cardiovascular events more than six years earlier and reaching a median survival rate due to all-cause mortality more than four years earlier than men in the bottom quintile.

Implications of all the available evidence

The lipidome based metabolic age can efficiently identify individuals at a higher risk of CVE and mortality, highlighting those who may benefit from early lifestyle or clinical intervention. The metabolic age score has the potential to serve as a health score that is modifiable and may identify individuals that are at high risk of age-related disease.

Introduction

Over recent decades, the human lifespan has steadily increased. However, health span – years lived free of disease – has not experienced a commensurate growth. Consequently, age-rated diseases, along with their associated morbidity and mortality, have now become a global challenge.¹

Longevity research^2,3 has started to focus on understanding the biological mechanisms underlying the ageing process, with the ultimate goal of enhancing the healthspan.⁴ This has led to the introduction of the concept of ‘biological ageing’, a quantitative and tangible measurement of ageing that captures an individual’s physiological status.⁵ Driven by the availability of large-scale omics data, multiple molecular ageing biomarkers have emerged, including epigenetic age,6, 7, 8, 9 transcriptomic age,10, 11, 12 proteomic age,13, 14, 15 and metabolic age.16, 17, 18, 19 These ageing signatures are often produced using machine/deep learning methods, most commonly variants of penalised linear models, gradient boosting tree, random forest, and neural networks. Previous studies have compared biological ages derived from different molecular features, revealing only mild correlations between them.^20,21 These findings suggest that different omics technologies may capture distinct ageing signals.

While chronological age is the greatest risk factor for many diseases, it’s non-modifiable and may not accurately reflect an individual’s health status due to influences such as lifestyle, environmental factors, and diseases.²² Relatively, metabolic ageing biomarkers may capture the age-related shift in metabolism, offering a more precise representation of an individual’s overall health, and potentially serving as a superior predictor of health outcomes. Therefore, the difference between the estimated metabolic age and chronological age (delta) can provide insights into age-related metabolic changes.²⁰ Individuals with a positive metabolic age delta are hypothesised to be metabolically older than their chronological age suggests, and therefore are at higher risk of age-related diseases.

The low cost and accessibility of metabolomics has driven the application of metabolic age to population levels.^17,23,24 However, current metabolic age models have suffered from a limited prediction accuracy, possibly due to their focus on a limited subset of metabolites that may not fully capture the complexity of age-related changes. Lipidomics, a subset of metabolomics, has been demonstrated to show strong associations with age.^25,26 In a recent publication, we observed strong linear and non-linear associations of lipid species with age in a large population.²⁵ Given the intimate link between lipid species and age, the lipidome may serve as a better metabolic ageing biomarker, particularly when the non-linearity is properly leveraged.

In this study, we have utilised comprehensive lipidomic profiles of two large population cohorts: the Australian Diabetes, Obesity and Lifestyle Study (AusDiab, n = 10,339) and the Busselton Health Study (BHS, n = 4494), to create metabolic age scores (metabolic age; mAge). We demonstrate the construction of metabolic age using penalised linear models (ridge and LASSO) and deep neural networks. The association of metabolic age delta (mAgeΔ) was then examined for prevalent and incident cardiovascular disease, type-2 diabetes, and all-cause mortality. We propose that mAge and mAgeΔ will provide a means to measure and monitor an individual’s metabolic health, allowing early intervention to reduce risk of age-related disease.

Methods

Study design and participants

Australian Diabetes, Obesity and Lifestyle Study (AusDiab): The AusDiab served as our primary training dataset for all our models. The AusDiab cohort represents a sample of the Australian population and focuses on studying the prevalence and risk factors associated with diabetes. The baseline survey took place in 1999/2000, involving 11,247 participants aged ≥ 25 years. These individuals were randomly selected from six states and the Northern Territory, encompassing 42 urban and rural areas across Australia, using a stratified cluster sampling method.²⁷ Measurement techniques for clinical lipids including fasting serum total cholesterol, HDL-C, and triglycerides as well as for height, weight, BMI, and other behavioural risk factors have been described previously.^27,28 We utilised all baseline fasting plasma samples from the AusDiab cohort (n = 10,339) after excluding samples from pregnant women (n = 21), those with missing data (n = 277), for technical reasons (n = 19) or whose fasting plasma samples were unavailable (n = 591). The average age of the cohort at baseline was 51.3 years, with a standard deviation (SD) of 14.3 years, and women accounted for 55% of the participants. Notably, the excluded samples (excluding pregnant women; n = 887) exhibited similar distributions for clinical variables as the included samples, indicating their missingness is likely at random.

The busselton health study (BHS)

The BHS cohort was utilised as a validation cohort for our study. The BHS is a community-based population study recruited in Western Australia since 1966. This cohort contains extensive phenotype data, particularly related to cardiovascular disease (CVD) traits. In our analysis, we included a total of 4492 subjects from the 1994/95 survey of this ongoing epidemiological study (see Table 1). The mean age of the 1994/95 BHS cohort was 50.8 years, with a standard deviation (SD) of 17.4 years, and women constituted 56% of the participants. The details of the study and measurements for HDL-C, triglycerides, total cholesterol, and BMI were previously described.^29,30

Table 1.

Characteristics of participants from the Australian Diabetes, Obesity and Lifestyle Study (AusDiab) and the Busselton Health Study (BHS).

	AusDiab	BHS
#Subjects	10,339	4492
Demographic
Sex (%male)	4654 (45.0)	1976 (44.0)
Age (years, mean ± sd)	51.3 (±14.3)	50.8 (±17.4)
BMI (kg/m2, mean ± sd)	26.9 (±4.9)	26.2 (±4.2)
Clinical lipids
Cholesterol (nmol/L, mean ± sd)	5.66 (±1.07)	5.58 (±1.11)
HDL-C (nmol/L, mean ± sd)	1.44 (±0.39)	1.39 (±0.39)
Triglycerides (nmol/L, mean ± sd)a	1.28 (±0.92)	1.18 (±0.90)
Other cardiometabolic risk factors
SBP (mmHg)	129.2 (±18.6)	124.0 (±17.9)
DBP (mmHg)	70.0 (±11.7)	74.5 (±10.2)
FBG (mmol/L)	5.2 (±1.1)	5.0 (±1.4)
2 h-PLG (mmol/L)	6.3 (±2.7)	–
Prevalent clinical outcomes at baseline
Prevalent diabetes (%)b	395 (3.8)	271 (6.0)
Prevalent CVD (%)	577 (5.6)	238 (5.3)
Incident clinical outcomes
Major CVE (%) (12 years follow up)	444 (4.3)	–
Incident IHD (%)	329 (3.2)c	284 (2.8)d/551 (5.3)e
Stroke (%) (12 years follow up)	95 (0.9)	–
All-cause mortality (%) (17 years follow up)	1706 (16.5)	–

^aData in Median, (IQR) as Triglyceride distribution was right skewed.

^bPrevalent diabetes only include the untreated prevalent cases.

^cIncident IHD cases with 12 years follow up in AusDiab.

^dIncident IHD cases with 10 years follow up in BHS.

^eIncident IHD cases with 20 years follow up in BHS.

Fasting plasma cholesterol and lipoprotein concentration including total cholesterol, high density cholesterol, (HDL-C), low density lipoprotein cholesterol (LDL-C) and triglycerides, fasting plasma glucose (FPG) and 2 h post load glucose (2 h-PLG) were measured using standard protocols.³¹

In Table 1, we presented the baseline characteristics of participants from both the AusDiab and BHS cohorts for comparison.

Clinical outcomes

In the AusDiab cohort, prevalent CVD (defined as history of heart attack and stroke combined; n = 577), incident cardiovascular events (CVE; n = 444) recorded over 12 years of follow-up and all-cause mortality over 17 years of follow-up were included. All nonfatal clinical data were collected through self-report, which was subsequently confirmed and adjudicated using medical records. Death in the cohorts were identified via the National Death Index. Incident CVEs included ischaemic heart disease (angina pectoris, myocardial infarction, coronary artery bypass grafting and percutaneous transluminal coronary angioplasty; n = 329) and cerebrovascular disease (intracerebral haemorrhage, cerebral infarction and stroke; n = 95). The CVE outcomes were defined based on the international classification of diseases (ICD) codes and ascertained through linkage to the National Death Index (deaths) and medical records (nonfatal events). There were 686 prevalent type 2 diabetes (T2D) cases (including newly diagnosed, untreated and treated diabetes). Participants with newly diagnosed prevalent diabetes are those who meet three criteria: 1) They were not diagnosed with diabetes when they entered the study; 2) They haven’t taken any diabetes medicine; 3) They have FPG or 2 h-PLG measurements over the diabetes cut-off range (FPG ≥ 7.0 mmol/L or 2 h-PLG ≥ 11.1 mmol/L after a 75-g oral glucose load).³² Out of 686 prevalent diabetes cases, there were 395 newly diagnosed/untreated diabetes and 291 treated diabetes. In this study, we excluded the treated diabetes at baseline to avoid the bias driven by the diabetes-related medication. All-cause mortality (n = 1706) within a 17-year follow-up period was also included.

In the BHS cohort, there were 238 prevalent CVD cases and 4254 controls at baseline and 284/551 IHD events (including myocardial infarction, angina, coronary artery bypass grafting and percutaneous transluminal coronary angioplasty) over 10/20 years of follow-up. Furthermore, there were 271 prevalent diabetes cases (the combination of newly diagnosed/untreated diabetes).

The definition of clinical outcomes for AusDiab and BHS is detailed in the Supplementary Fig. S1.

Lipidomic profiling

Targeted lipidomic analysis was performed using liquid chromatography electrospray ionization tandem mass spectrometry (LC-ESI-MS/MS). An Agilent 6490 triple quadrupole (QQQ) mass spectrometer [(Agilent 1290 series HPLC system and a ZORBAX eclipse plus C18 column (2.1 × 100 mm 1.8 μm, Agilent)] in positive ion mode were used. Details of the method and chromatography gradient have been described previously.^33,34 The LC-MS/MS conditions and settings with the respective MRM transitions for each lipid (n = 747) can be found in Supplementary Table S1. For the BHS cohort, lipidomic profiling was performed using the standardised methodology as described previously^33,35 and detailed by Huynh et al.^25,33 Overall, 596 lipid species were quantified; 575 of which were common to AusDiab cohort (highlighted in Supplementary Table S1).

Construction of metabolic age score (mAge)

We randomly split AusDiab into 10 folds to create a 10-fold cross-validation framework, where we repeatedly selected one-fold as the validation set and combined all others as the training set. For each iteration of the training set, we employed ridge regression (ridge),³⁶ LASSO (Least Absolute Shrinkage and Selection Operator),³⁷ and neural network³⁸ to model the associations between age and the 575 lipid species (common between AusDiab and BHS datasets), while adjusting for sex and BMI:

$$\text{age}\sim \text{sex}+\text{bmi}+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\hat{\mathrm{\beta }}}_{\mathrm{i}}\times {\text{lipid}}_{\mathrm{i}}+\mathrm{e}$$ (1)

Here $\mathrm{n}$ is the number of lipids. All the predictors were scaled to zero-mean and unit-variance. Under the model (1), we utilised the R package ‘glmnet’³⁹ to perform ridge and LASSO respectively. The lambda parameters under the restricted range from 0.001 to 10 were selected according to the minimum cross-validated RMSE (Root mean square error).

To account for the non-linearity of the lipidome over time, we also implemented a two-layer neural network using the R package ‘keras’ and ‘tensorflow’. We utilised an optimised parameter set, including a dropout rate of 0.4, 128 units in each layer, the ReLU activation function, and a kernel regularizer with an L2 penalty of 0.001.

Subsequently, using these models, we generated three sets of predicted age values for each individual respectively, referred to as ‘pAge’. We assessed the performance of each model by calculating the coefficient of determination (R²), which represents the squared Pearson correlation between pAge and Age. This metric provides an indication of how much of the age variance is captured by the models. The predicted age in BHS (the external validation cohort) was calculated by taking the average of predicted values across the model-folds developed in AusDiab.

We introduced the term ‘mAgeΔ’, which was calculated as the difference between pAge and the line of best fit between pAge and Age: $pAge\sim \mu +\hat{\beta }\times age+e$. In this equation, the term e represents the residuals (mAgeΔ). For more detailed information, please refer to Supplementary Material S1.

Finally, we defined the term ‘mAge’ as the sum of age and mAgeΔ.

Derivation of lipidome based CVD risk score

To evaluate the comparative performance of mAgeΔ and a CVD-specific risk score in predicting CVD, we developed a novel CVD risk score using the full lipidome, following a similar approach proposed by Wu et al.⁴⁰ We employed a ridge regression model to analyse the lipidomic data for predicting incident CVD in the AusDiab study. The lambda parameters, ranging from 0.001 to 10, were optimised to maximise the area under the curve (AUC). We externally validated this model in the BHS study, which refined our approach and solidified the CVD risk score derivation.

Statistical analysis

Linear regression models were used to examine the association of mAgeΔ or Age with the plasma lipidomic profile adjusting for sex, and BMI. The p-values were corrected for multiple comparison using the Benjamini-Hochberg procedure.⁴¹

We employed logistic regression models⁴² (R package ‘glm’) or time-to-event Cox proportional hazard regression models⁴³ (R package ‘survival’) to assess the associations between clinical outcomes and mAgeΔ, while adjusting for age, sex, and BMI. The derived odds ratios or hazard ratios were utilised to evaluate the strength of the associations, with p-values indicating the level of significance. Additionally, we categorised mAgeΔ into quintiles (Q1-Q5) and used these quintiles instead of mAgeΔ as the main predictor in the logistic regression or Cox regression models. The Akaike information criterion (AIC) was used to assess the relative quality of individual models with and without mAgeΔ. Additionally, we carried out time-to-event Cox proportional hazard regression models to examine the associations between incident CVD and CVD risk score, adjusting for age, sex, and BMI.

We also performed Kaplan–Meier survival analysis (R package ‘survival’ 3.1–12)⁴⁴ to evaluate the survival rates of individuals across Q1-Q5 with regards to either incident major CVE or all-cause mortality. In these analyses, age was treated as the time scale, and the quintiles of mAgeΔ served as the predictor.

We conducted a sensitivity analysis to examine the performance of mAge models using a sex-stratified population. Driven by this, we derived sex-specific metabolic age scores for male and female groups separately, employing a ridge regression model with the entire lipidome as predictors to predict age.

Additionally, we conducted another set of sensitivity analysis to assess the performance of a comprehensive set of covariates, including age, sex, BMI, smoking status, HDL-C, Cholesterol, Triglycerides, prevalent diabetes, and Systolic Blood Pressure (SBP), in deriving the metabolic age score. To achieve this, we applied the ridge regression model to predict age using this extensive covariate set and the whole lipidome, subsequently generating mAge and mAgeΔ. Furthermore, we employed a time-to-event Cox regression model to investigate the associations between the derived mAgeΔ and incident diseases, with adjustments made for age, sex and BMI. In the analysis, we have excluded LDL-C from the clinical lipid panel as it’s a calculated measure from total cholesterol and triglyceride levels.⁴⁵

Ethics

This study used datasets from the AusDiab biobank (project grant APP1101320) approved by the Alfred Human Research Ethics Committee, Melbourne, Australia (project approval number, 41/18) and the BHS cohort (informed consent obtained from all participants, and the study was approved by the University of Western Australia Human Research Ethics Committee [UWA-HREC; approval number, 608/15]). The current study was also approved by UWA HREC (RA/4/1/7894) and the Western Australian Department of Health HREC (RGS03656). Both studies were conducted in accordance with the ethical principles of the Declaration of Helsinki. No participant compensation was provided.

Role of funders

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Results

Population cohorts

Targeted lipidomic profiling was performed in fasting plasma samples of the AusDiab cohort (n = 10,339)²⁵ and fasting serum samples of the BHS cohort (n = 4492).⁴⁶ Both cohorts have similar distributions of age, sex, and BMI and clinical lipid measures (Table 1). In total, 747 lipid species were measured in AusDiab samples, and 596 lipid species in BHS samples. After alignment, 575 lipid species (from 33 lipid classes) were measured in both cohorts, including the major species from the glycerophospholipid, sphingolipid, glycerolipid and sterol classes.

To evaluate the associations of mAge with heath determinants, we included a range of clinical outcomes in AusDiab and BHS consisting of prevalent cardiovascular disease (CVD), prevalent diabetes, incident major cardiovascular events (CVE), and incident all-cause mortality (Table 1; Fig. 1).

Fig. 1.

The study design incorporating the AusDiab cohort as the training dataset and the BHS as the validation dataset. The study design includes: 1) Build predictive models using different machine learning methods, treating age as the outcome, and all the lipidomic data as the predictors adjusting for sex and BMI. Different machine learning methods included linear models (ridge and LASSO), and non-linear models (neural network). To reduce the overfitting, all these models were developed within a ten-fold cross validation framework. The fit of the models was assessed with R² (the associations between pAge and age). 2) Standardise pAge to the population to determine metabolic age (mAge). mAgeΔ was calculated using the residuals between pAge and the line of best fit of pAge against age. 3) Use mAgeΔ to stratify the population (quintiles). 4) Risk assessment – examine the associations of mAgeΔ with clinical outcomes on the stratified populations (Q1-Q5).

We further characterised the distribution of incident ischaemic heart disease (IHD) cases with age and sex over a 10 year follow up period. There were 329 incident IHD cases in AusDiab and 284 in BHS respectively over 10 years of follow up. There was a higher proportion of females in the >70 years group in BHS, while, in AusDiab, there were more males in the 50–70 years group developing IHD (Supplementary Fig. S2).

Deriving a metabolic age score

The metabolic age (mAge) scores were constructed in the AusDiab dataset, using penalised linear models (ridge and LASSO), and nonlinear models (neural network), incorporating the whole lipidome, sex, and BMI as predictors of age (Fig. 1).

Model performance was assessed using ten-fold cross-validation within the AusDiab cohort and external validation in the BHS cohort. For external validation, the average predicted age across the model-folds was used for association analysis.

While the ridge model contained all 575 lipid species, the LASSO model selected between 373 and 421 lipid species between the cross-validation folds. The predictive performance of these models was determined using R² (the variance in age explained by the lipidome), which was calculated as the square of the Pearson correlation between the average predicted age (pAge) and chronological age (Fig. 2; Supplementary Table S2). In AusDiab, the neural network model showed the highest correlation with age (R² = 0.73), while the ridge (R² = 0.68) and LASSO (R² = 0.69) models showed similar performance. However, external validation in BHS, reversed this trend, with the ridge (R² = 0.71) and LASSO (R² = 0.70) models performing better than the neural network (R² = 0.65) model (Fig. 2; Supplementary Fig. S3). Across both cohorts, the ridge and LASSO models showed consistent predictive performance, while the neural network model showed diminished performance in the external validation cohort, indicating possible overfitting of this model. We further derived sex-specific metabolic age scores for male and female groups separately, employing a ridge regression model with the entire lipidome as predictors to predict age. Interestingly, we found that the female-specific mAge score (R² = 0.68) showed similar performance as the whole population-based mAge score, while the male-specific mAge score (R² = 0.64) exhibited weaker performance relative to the whole population-based mAge score.

Fig. 2.

The performance of ridge, Lasso and neural network in AusDiab and BHS cohorts. All models were trained on AusDiab data within a 10-fold cross validation framework and externally validated on the BHS cohort. a. The comparison of prediction accuracy of ridge, LASSO, and neural network models by R² in AusDiab. The R² values were calculated by the squares of the Pearson’s correlations between predicted age (pAge) and actual age. The 95% CI for the R² values were based on 10,000 bootstrapped confidence intervals. b. The comparison of prediction accuracy of ridge, LASSO, and neural network models by R² in the external validation cohort BHS. c. The scatter plots of pAge (derived from ridge) against chronological age in AusDiab (Training set under 10 folds CV). d. The scatter plots of pAge (derived from ridge) against chronological age in BHS (Testing set).

The weights of individual lipid species in the ridge and LASSO models showed that lipid species from acylcarnitine (AC), sphingomyelin (SM), alkenylphosphatidylcholine (PCP), lysophosphatidylcholine (LPC), lysoalkylphosphatidylcholine (LPC(O)) were major predictors in both models (Supplementary Fig. S4 and Table S3).

To assess the predictive performance of lipid species relative to clinical lipids (HDL-C, cholesterol, and triglycerides), we repeated the penalised linear model creation, replacing lipid species with clinical lipids as predictors. Both ridge and LASSO models built with clinical lipids explained only a small proportion of age variance (R² = 0.06 for ridge and LASSO). External validation of clinical lipid models showed similar patterns (Supplementary Fig. S5 and Table S4). As a part of our sensitivity analysis, we conducted ridge regression analysis that incorporated an extended set of predictors, which included sex, BMI, smoking status, HDL-C, cholesterol, triglycerides, prevalent diabetes, systolic blood pressure (SBP), and the lipidome. This expanded ridge model, with all these predictors, exhibited the capacity to explain up to 71% of the variance in age (R²) – 3% higher relative to our original ridge model including only sex, BMI, and the lipidome (Supplementary Table S5). When we excluded the lipidome from this predictor set, the model’s prediction ability was reduced to only 30% (Supplementary Table S5). The external validation of such a model in BHS demonstrated a similar prediction performance.

Based on these predicted age values (pAge) derived from the different models, we further introduced the term ‘mAgeΔ’ to quantify the additional information captured by the lipidome, independent of age. mAgeΔ was calculated as the difference between pAge and the line of best fit between pAge and Age. Further details can be found in the Methods section. The distribution of mAgeΔ in the AusDiab and BHS has been detailed in the Supplementary Fig. S6a and b.

Chronological age and mAgeΔ show the same associations with lipid species

To better understand the lipid biology captured by mAgeΔ, we performed linear regression of age and mAgeΔ against all lipid species, in the AusDiab cohort. Of the 575 lipid species tested, 504 were significantly associated with age – independent of sex and BMI – after correction for multiple comparisons (Fig. 3).

Fig. 3.

The associations of lipid species with chronological age and mAge$\Delta$from ridge. Associations of 575 lipid species with age (a), or mAgeΔ derived from a ridge model (b) were estimated using linear regression adjusted for sex, BMI and age (mAgeΔ only). Pearson correlations of the beta coefficients from a-b are shown (c).

Comparing the associations of lipid species with chronological age and mAgeΔ, we observed that the coefficients were highly correlated (R² = 0.99 for ridge; R² = 1.0 for LASSO; And R² = 0.93 for neural network) (Supplementary Fig. S7 and Table S6), indicating that mAgeΔ captures the same lipid biology as age.

Ridge regression models effectively estimate mAgeΔ

We hypothesised that as the additional biological information captured by the lipidome was independent of age, mAgeΔ would also be significantly associated with cardiometabolic risk. Driven by this, we performed logistic regression to evaluate the relationship of mAgeΔ from different machine learning models with prevalent disease, including CVD and diabetes. The logistic regression models were adjusted for age, sex, and BMI. In AusDiab, mAgeΔ derived from the ridge model showed a slightly higher odds ratio (OR) for CVD per unit change in mAgeΔ (OR = 1.33, 95% CI = 1.22–1.45, p = 1.43 × 10⁻¹⁰) compared to both the LASSO (OR = 1.30, 95% CI = 1.19–1.42, p = 2.93 × 10⁻⁰⁹) and neural network (OR = 1.31, 95% CI = 1.21–1.43, p = 2.45 × 10⁻¹¹) models (Supplementary Fig. S8a). Relative to CVD, mAgeΔ showed weaker associations with diabetes, although here also the mAgeΔ from the ridge model had a slightly higher odds ratio for diabetes than either the LASSO or neural network models (Supplementary Fig. S8a). Additionally, we introduced an extended covariate set (including age, sex, BMI, smoking status, HDL-C, triglycerides, cholesterol, and systolic blood pressure [SBP]) to adjust the model. We observed that the associations of mAge with prevalent CVD and diabetes, after adjustment with the extended covariates, were similar to the associations observed with adjustment for age, sex, and BMI alone (Supplementary Table S7).

To further validate these findings, we examined these associations in BHS (Supplementary Fig. S9a). Here, we also observed stronger associations of the mAgeΔ (ridge model) compared to LASSO and neural network models with prevalent IHD (ridge, OR = 1.21, 95% CI = 1.05–1.40, p = 6.81 × 10⁻⁰³; LASSO, OR = 1.19, 95% CI = 1.04–1.37, p = 1.32 × 10⁻⁰², neural network, OR = 1.12, 95%CI = 0.98–1.28, p = 9.29 × 10⁻⁰²). In the BHS, mAgeΔ from all three models was not significantly associated with prevalent diabetes.

To assess the ability of mAgeΔ to predict incident disease risk, we performed Cox regression between mAgeΔ and incident CVD outcomes in AusDiab (Supplementary Fig. S8b), adjusted for age, sex, and BMI. We calculated the hazard ratio (HR) of mAgeΔ with incident CVE, IHD, and stroke (12 years follow-up) and all-cause mortality (17 years follow-up). We observed that mAgeΔ from all three models had similar performance in terms of the magnitude of effect. For example, for incident CVE (n = 444), we observed that mAgeΔ (ridge) had a hazard ratio (HR; per unit change in mAgeΔ) of 1.30 (95% CI = 1.18–1.42, p = 5.39 × 10⁻⁰⁸), with mAgeΔ (LASSO) having a HR of 1.29 (95%CI = 1.17–1.41, p = 9.77 × 10⁻⁰⁸) and mAgeΔ (neural network) having HR of 1.28 (95%CI = 1.18–1.28, p = 5.77 × 10⁻⁰⁹). The same finding was also observed for all-cause mortality – very consistent results were observed across the three models (ridge model, HR = 1.18, 95% CI = 1.13–1.24, p = 6.64 × 10⁻¹²; LASSO model HR = 1.17, 95%CI = 1.12–1.23, p = 3.10 × 10⁻¹¹; and neural network model, HR = 1.18, 95%CI = 1.13–1.23, p = 4.92 × 10⁻¹⁵). Furthermore, we observed that the associations of mAge with incident outcomes, after adjustment with the extended covariates (age, sex, BMI, smoking status, HDL_C, Triglycerides, Cholesterol, and systolic blood pressure SBP), closely resembled the associations observed with adjustment for age, sex, and BMI alone (Supplementary Table S7). The assessment of the proportional hazard assumptions of the Cox model for incident CVE outcomes and mAgeΔ, adjusted for these extended covariates revealed no violations of the proportional hazard assumption for any of the variables included in the model (Supplementary Table S8).

In our sensitivity analysis, we further investigated the associations between these incident outcomes and mAgeΔ, which was derived from a comprehensive set of predictors (including sex, BMI, smoking status, HDL-C, cholesterol, triglycerides, prevalent diabetes, SBP, and the lipidome). In comparison to the previous associations observed with mAgeΔ (derived from BMI, sex, and the lipidome), mAgeΔ derived from the full set exhibited enhanced associations with incident CVE (HR = 1.38, 95%CI = 1.25–1.51, p = 5.62 × 10⁻¹¹) and IHD (HR = 1.35, 95%CI = 1.21–1.51, p = 1.46 × 10⁻⁰⁷) (Supplementary Table S9). However, it showed diminished associations with incident all-cause mortality (HR = 1.15, 95%CI = 1.10–1.21, p = 5.74 × 10⁻⁰⁹) (Supplementary Table S9).

We further applied the Cox regression models in BHS to validate the above findings. Only IHD with both 10- and 20-years follow-up in BHS shared the similar definition as in AusDiab. Therefore, we evaluated the associations of mAgeΔ with incident IHD independent of age, sex, and BMI (Supplementary Fig. S9b). In comparison to the results observed in the AusDiab dataset, we noted weaker associations in the BHS dataset, characterised by significantly reduced hazard ratios (HR) and diminished statistical significance (p values). When we compared the performance across different machine learning models, mAgeΔ from the ridge model (20-years incident IHD: HR = 1.13, 95%CI = 1.04–1.23,p = 4.73 × 10⁻⁰³; 10-years incident IHD: HR = 1.14, 95%CI = 1.01–1.29, p = 2.81 × 10⁻⁰²) and LASSO model (20-years incident IHD: HR = 1.13, 95%CI = 1.03–1.22, p = 8.22 × 10⁻⁰³;10-years incident IHD: HR = 1.13, 95%CI = 1.01–1.28, p = 3.73 × 10⁻⁰²) showed significant associations, while mAgeΔ from the neural network models (20-years incident IHD: HR = 1.05, 95%CI = 0.97–1.14, p = 2.68 × 10⁻⁰¹;10-years incident IHD: HR = 1.02, 95%CI = 0.91–1.14,p = 7.58 × 10⁻⁰¹) were not significantly associated with incident IHD. These findings demonstrated mAge from ridge and LASSO models had more consistent performance across the two cohorts than mAge from the neural network model, in terms of incident IHD risk prediction.

Addition of mAgeΔ enhances the predictive performance of the models for clinical outcomes

To evaluate the significance of incorporating mAgeΔ into the prediction of clinical outcomes in the AusDiab cohort, we compared two nested models using Akaike’s information criterion (AIC) and Likelihood ratio test (LRT). Specifically, we compared one model including age, sex, and BMI as predictors with another model adding mAgeΔ alongside age, sex, and BMI. Our analysis revealed that models with mAgeΔ demonstrated a superior fit in predicting prevalent CVD, as evidenced by smaller AIC values (AIC = 3619.21 with mAgeΔ vs. AIC = 3658.56 without mAgeΔ) and a significant LRT p-value of 1.26 × 10⁻¹⁰. Similarly, for predicting CVE, the model incorporating mAgeΔ exhibited a significantly better fit (AIC = 7033.96 with mAgeΔ vs. AIC = 7061.46 without mAgeΔ) with an LRT p-value of 5.60 × 10⁻⁰⁸. Additionally, the model with mAgeΔ showed improved fit for predicting incident all-cause mortality compared to the model without mAgeΔ (Supplementary Table S10).

mAgeΔ shows similar associations with incident IHD in men and women

We observed different distributions of incident IHD cases between the sex- and age-stratified populations of BHS and AusDiab (Supplementary Fig. S2). We then examined the associations of mAgeΔ with incident IHD in sex-stratified populations of both cohorts. Due to the relatively consistent performance across cohorts, mAgeΔ (ridge) was selected for the subsequent analyses.

In AusDiab, there were 329 incident IHD cases, with 222 and 107 in men and women, respectively. In the sex-stratified population, the association of mAgeΔ with incident IHD was marginally stronger in men (HR = 1.29, 95%CI = 1.13–1.48, p = 1.68 × 10⁻⁰⁴) than women (HR = 1.25, 95%CI = 1.04–1.50, p = 1.92 × 10⁻⁰², Supplementary Fig. S10). However, in the BHS cohort, out of 284 incident IHD cases (10 years follow-up), there were equivalent numbers of female (n = 134) and male cases (n = 150). Both male (HR = 1.10, 95%CI = 0.93–1.30, p = 2.73 × 10⁻⁰¹) and female (HR = 1.16, 95%CI = 0.987–1.38, p = 9.29 × 10⁻⁰²) showed weaker associations with incident IHD (Supplementary Fig. S10 and Table S11).

In our sensitivity analysis, we further examined the associations of incident IHD with sex-specific mAge scores using a Cox regression model adjusted for age and BMI in men and women. Interestingly, we observed similar associations of incident IHD with mAge score that were derived either on the whole population or sex-specific population in AusDiab. In the female group, the mAge score modelled exclusively on females showed an HR of 1.27 (95% CI: 1.04–1.51) with p = 6.38 × 10⁻⁰². Similarly, in the male group, the mAge score modelled exclusively on males had an HR of 1.26 (95% CI: 1.10–1.45) with p = 7.06 × 10⁻⁰⁴ (Supplementary Table S11). Upon validation in BHS, sex-specific mAge scores did not exhibit significant associations with incident IHD.

mAgeΔ shows strong associations with cardiometabolic risk factors

To assess the relationship between mAgeΔ and cardiometabolic risk factors, including BMI, HDL-C, triglycerides, cholesterol, SBP, DBP, fasting blood glucose (FBG), and 2-h post-load glucose (2 h-PLG), we conducted linear regression analyses. In AusDiab, we observed strong associations of mAgeΔ with all cardiometabolic traits, especially for cholesterol (beta = 0.12, 95% CI = 0.11–0.14, p = 6.85 × 10⁻³⁹) and 2-h post load glucose (beta = 0.07, 95% CI = 0.05–0.09, p = 2.82 × 10⁻¹⁴) (Supplementary Table S12). These associations were validated in the BHS cohort, revealing similarly strong associations of mAgeΔ with most traits. However, two exceptions were noted: 1) the absence of records for 2-h post-load glucose in the BHS dataset, and 2) the lack of significant associations of mAgeΔ with SBP and DBP (Supplementary Table S12). Surprisingly, positive associations of mAgeΔ with HDL-C were observed in both cohorts. This may be related to higher total lipoprotein load of older participants compared to younger participants. Indeed, when HDL-C was expressed relative to LDL-C we observed a negative association with mAgeΔ in AusDiab (beta = −0.07, 95% CI = −0.13 to −0.01, p = 1.72 × 10⁻⁰²) and BHS (beta = −0.06, 95% CI = −0.08–0.03, p = 2.55 × 10⁻⁰⁵).

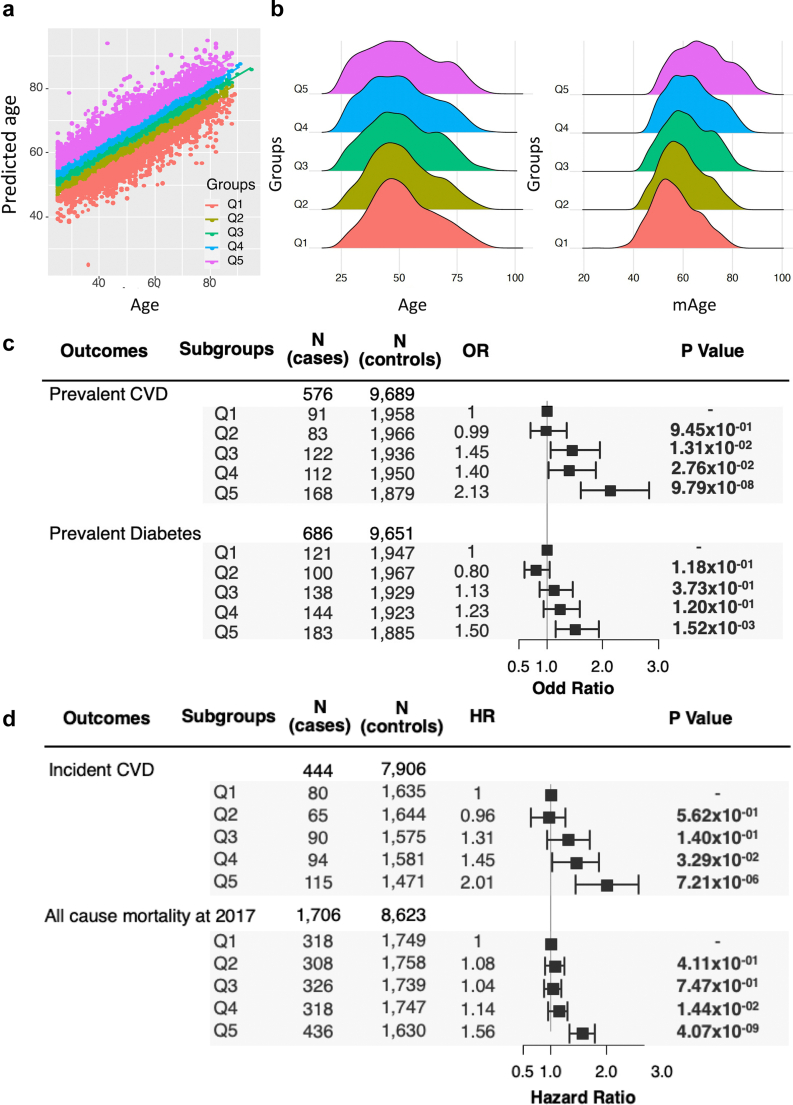
We stratified the AusDiab cohort into quintiles of the mAgeΔ (Q1-Q5). As expected, the distributions of age across the quintiles were comparable, while the mAge and mAgeΔ values progressively increasing from Q1 to Q5 (Fig. 4; Supplementary Table S13). We performed linear regression analyses, treating cardiometabolic risk factors as outcomes, quintiles of the mAgeΔ as the predictor (Q5 relative to Q1) with the covariate set of age, sex and BMI. Individuals in Q5 relative to Q1 had significantly elevated levels of cholesterol (beta = 0.32, 95% CI = 0.26–0.38, p = 8.82 × 10⁻²⁵), triglycerides (beta = 0.24, 95% CI = 0.18–0.29, p = 1.41 × 10⁻¹⁵) and 2 h-PLG (beta = 0.16, 95% CI = 0.10–0.22, p = 8.69 × 10⁻⁰⁸) in the AusDiab cohort (Supplementary Table S14). Notably, we also observed reduced level of the ratio of HDL to LDL in Q5 (related to Q1) (beta = −0.07, 95% CI = −0.13 to −0.01, p = 1.72 × 10⁻⁰²). The validation results in BHS were consistent with those in AusDiab.

Fig. 4.

The associations of mAgeΔ with cardiovascular disease, diabetes and all-cause mortality outcomes in the AusDiab cohort. a. The population was stratified into quintiles using mAgeΔ. b. The distributions of age (left) and mAge (right) within mAgeΔ quintiles. c. The associations of mAgeΔ quintiles with prevalent CVD and prevalent diabetes were examined using logistic regression models including age, sex, and BMI as covariates. d. The associations of mAgeΔ quintiles with incident CVE and all-cause mortality were examined using Cox regression models treating time-to-event as the outcome, mAgeΔ as the predictor, and age, sex, and BMI as covariates.

Stratification by mAgeΔ identifies individuals at increased risk of CVD and diabetes

In the stratified populations by mAgeΔ, we performed logistic regression of the quintiles of mAgeΔ with prevalent CVD and diabetes, treating Q1 (the lowest mAgeΔ) as the reference. After adjusting for age, sex, and BMI, we observed a progressive increase in the OR of CVD from Q1 to Q5 (Fig. 4). Individuals in Q5 (the largest mAgeΔ values) relative to Q1 had 2.13-fold higher odds for prevalent CVD (OR = 2.13, 95% CI = 1.62–2.83, p = 9.79 × 10⁻⁰⁸) (Fig. 4c). In contrast, only weak, non-significant, associations were observed with prevalent diabetes.

Next, we validated the associations with prevalent IHD in the stratified BHS cohort, where we observed a comparable progressive increase in the strength of association with prevalent IHD from Q1 to Q5 of mAgeΔ (Supplementary Fig. S11).

Higher mAgeΔ is associated with increased risk of incident CVE events and all-cause mortality

To assess whether the quintiles of mAgeΔ were associated with incident major CVD events and all-cause mortality, we performed Cox regression between mAgeΔ quintiles and these outcomes in the AusDiab dataset. As shown in Fig. 4d, the individuals in Q5 (the highest mAgeΔ group) had a 2.01-fold (95%CI = 1.45–2.57, p = 7.2 × 10⁻⁰⁶) increased risk of 12-year incident CVD and 1.56-fold (95%CI = 1.34–1.79, p = 2.07 × 10⁻⁰⁹) increased risk of 17-years all-cause mortality relative to Q1 (reference group). We validated these findings against 10-year and 20-year incident IHD in the BHS cohort (Supplementary Fig. S11d). Additionally, assessment of the proportional hazard assumptions of the Cox model for incident CVE outcomes and mAgeΔ quintiles revealed that no variables included in the model violated the proportional hazard assumption (Supplementary Table S15).

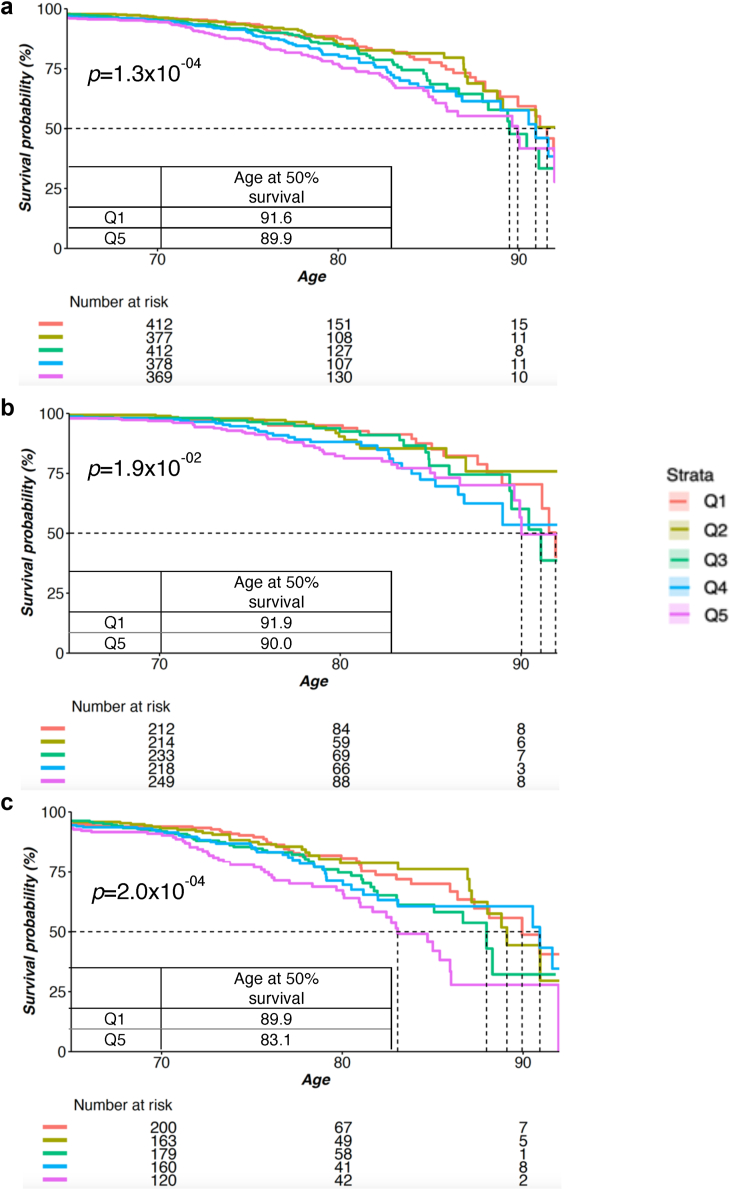
We then performed Kaplan–Meier survival analyses to compare the different survival probabilities for death due to major CVE across the quintiles of mAgeΔ in both the total and sex-stratified AusDiab cohorts. The survival curves revealed a higher rate of mortality for Q5 relative to other groups in both the whole population and the male group, while differences between Q5 and Q1 in the female sub-cohort were smaller (Fig. 5). The difference in survival curves between Q5 and Q1 became distinct from 70 years onwards. In the whole population, participants in Q5 would reach the median survival rate when they were 90 years old (50% of the patients in the group died by the age of 90), with the Q1 group reaching the median survival at 92 years of age - a difference of three years (Fig. 5a). This was more pronounced in AusDiab males with the median survival rate of Q5 (age = 83) almost eight years earlier than Q1 (age = 90) (Fig. 5c). In contrast, the AusDiab females had a median survival rate ranging between Q1 (age = 92) and Q5 (age = 90) of 3 years (Fig. 5b). The p values from the log rank test indicated a significant difference among five groups’ survival curves in both the whole population (p = 1.3 × 10⁻⁰⁴), females (p = 1.9 × 10⁻⁰²), and males (p = 2.0 × 10⁻⁰⁴).

Fig. 5.

Survival analysis of incident CVE by mAgeΔ quintiles in the AusDiab cohort. Survival analyses were performed in the whole population (444 cases, a), female only (161 cases, b), and male only (283 cases, c). The Kaplan–Meier curves show the survival rate of the stratified population by mAge $\Delta$ quintile under the risk of incident CVE. The dotted lines indicate the median survival rate of each group.

To further examine the survival difference from all-cause mortality, we performed the same survival analysis on all-cause mortality with 17 years follow-up (Fig. 6). We observed the major difference between Q5 to Q1 in AusDiab men with a median survival difference between Q1 (age = 88) and Q5 (age = 84) of 4 years, but smaller differences in the total and women populations (Fig. 6). The log rank test revealed significant differences between Q1-Q5 groups for incident all-cause mortality in the whole population and males with p < 1.0 × 10⁻⁰⁴. However, no significant difference was observed in the female group (p = 8.1 × 10⁻⁰²).

Fig. 6.

Survival analysis of all-cause mortality by mAgeΔ quintiles in the AusDiab cohort. Survival analyses were performed in the whole population (1706 cases, a), female only (814 cases, b, and male only (892 cases, c). The Kaplan–Meier curves show the survival rate of the stratified population by mAgeΔ quintile under the risk all-cause mortality. The dotted lines indicate the median survival rate of each group.

Discussion

In this study, we derived lipidomic-based metabolic age scores from two large population-based cohorts: the AusDiab study (training cohort, n = 10,339) and the BHS (validation cohort, n = 4492). We employed both penalised linear and non-linear machine learning models to derive the scores and then evaluated their performance in terms of the proportion of variance in age captured and their association with disease outcomes and all-cause mortality. We demonstrate the mAgeΔ, the difference between mAge and chronological age, was strongly associated with prevalent and incident CVE, independent of chronological age. The subsequent survival analysis supported these associations and further demonstrated strong associations between mAgeΔ and all-cause mortality, which was stronger in men than women. These results suggest that mAgeΔ can identify a high-risk subset of the population that may be amenable to early drug and lifestyle intervention to improve their metabolic health and lower their cardiometabolic risk.

Penalised linear models provide optimal performance in the development of metabolic age scores

We assessed both penalised linear and non-linear models to predict age, motivated by the following considerations: 1) linear models have the potential advantage of lower over-fitting and ease of interpretation. 2) LASSO can be utilised to select lipid species for smaller models; 3) neural network may better capture the nonlinearity of the relationship between lipid species and age. The predicted age from the neural network within a 10-fold cross-validation in the AusDiab dataset explained 73% of the variance in age, which outperformed the ridge (68%) and LASSO (69%) models. However, we observed that both the ridge and LASSO models performed better than the neural network in the external validation in BHS, suggesting that the linear models were better suited to the lipidomics data and resulted in less overfitting of the models. Consistent with our findings, previous studies have demonstrated robust performance of penalised linear regression models in the development of biological age scores.^20,47 Further, the similar performance of ridge and LASSO demonstrated that we could reduce the number of lipids in the model without loss of performance.

Further evaluation of the associations of mAgeΔ from different machine learning models with cardiometabolic disease outcomes, showed comparable associations with both prevalent and incident CVE risk in the AusDiab cohort, but upon validation in the BHS cohort, mAgeΔ from ridge and LASSO remained significant, whereas mAgeΔ from neural networks did not. These findings suggest penalised linear models of lipidomics against age may be superior to neural network models of the same data.

Metabolic age delta represents lipid dysregulation that is independent of chronological age

Lipidomic and metabolomic studies have demonstrated a strong association between age and dysregulation of lipid metabolism.^25,26 To gain a deeper understanding of the lipid biology captured by mAge, we examined the associations of mAgeΔ with the lipidome. We observed strong positive associations of mAgeΔ with acylcarnitine, ceramide, phospholipid and triacylglycerol species, as well as negative associations with certain lipid species from lyso and ether phospholipid classes. Most of these lipid species have also appeared as the top predictors in the mAge modelling (Supplementary Fig. S3). When we plotted the effect size (beta-coefficients) of the associations with mAgeΔ against the corresponding beta-coefficients for chronological age, we observed the associations of the same lipid species with mAgeΔ correlated almost perfectly to the associations with chronological age. The correlation of the coefficients showing an R² of 0.99–1.00 for both ridge and LASSO. This indicates that mAgeΔ effectively captures the dysregulation of metabolic pathways that typically occur with ageing. Since mAgeΔ is constructed to be independent of chronological age, any biological variation it captures beyond chronological age represents unique, age independent metabolic information. The derivation of mAgeΔ - shown in Supplementary Note S1 - explains why the correlation between beta-coefficients of lipid species against chronological age and mAgeΔ is close to 1.0, and why mAgeΔ contains additional biological information that is independent of chronological age. Notably, our previous research²⁵ has demonstrated that the age (and mAgeΔ) associated lipid species can be mapped to several lipid metabolic pathways, including fatty acid oxidation (acylcarnitine species) and ether lipid metabolism (alkyl and alkenylphospholipid species). These same lipid species and pathways have been shown to be highly linked to obesity,²⁵ type 2 diabetes mellitus (T2DM)48, 49, 50 and CVD risk,51, 52, 53, 54 independent of age and have been demonstrated to be modifiable by exercise (acylcarnitine)⁵⁵ or dietary supplementation (ether lipids).⁵⁶

These findings suggest that mAge represents the metabolic status of each individual, encompassing both the metabolic dysregulation captured by chronological age and the metabolic dysregulation (in the same lipid metabolic pathways) that is not captured by chronological age. Therefore, it is expected that mAge can serve as a better predictor of metabolic health and cardiometabolic disease risk than chronological age itself.

Higher mAgeΔ identified individuals with increased risk of incident CVE and all-cause mortality

Although age is a major risk factor for CVE and many other age-related diseases, it does not accurately capture all age-related metabolic dysregulation. For example, elderly individuals who lead a healthy lifestyle and do not carry major genetic risk factors may have good metabolic health, while younger people may be at a high risk due to a combination of poor lifestyle and genetic factors. Thus, while chronological age is an important risk factor in epidemiological studies it lacks discrimination at the individual level, where a biological measurement of age is essential.⁵ Inspired by this, we introduced metabolic age score, representing the metabolic status of each individual based on the lipid metabolic pathways.

To assess the ability of mAge to identify individuals at increased risk, we stratified AusDiab into five groups (Q1-Q5) based on the values of mAgeΔ (the difference between mAge and chronological age). Subsequent logistic or Cox regression analyses demonstrated that the risk of major CVE in individuals in the Q5 group (highest mAgeΔ) was more than twice that of individuals in the Q1 group (smallest mAgeΔ). Furthermore, individuals in the Q5 group also had a 1.5-fold higher risk of incident all-cause mortality relative to those in the Q1 group. Survival curves revealed that males in the Q5 group reached a 50% survival rate due to CVE about six years earlier than males in the Q1 group. While the Q5 group included individuals with age ranging from 25 to 88 (Fig. 4b), those with a chronological age younger than 50 years had mAgeΔ between 5.2 and 45.5, indicating that they faced a higher risk of CVE and mortality.

Metabolic age is better suited as a health score rather than a disease biomarker

We developed the metabolic age score to demonstrate how such a score may effectively capture age related metabolic dysregulation, providing an accurate measure of an individual’s metabolic health status, that can be affected by lifestyle, environmental factors and disease over time. However, while mAge and mAgeΔ associate with multiple disease outcomes – and indeed with all-cause mortality – it is important to note that metabolic age is not intended to serve as a risk score for any specific disease outcome, but rather as a modifiable indicator of metabolic health across all ages. In our study, we evaluated the performance of mAgeΔ and a lipidome-based CVD risk score in predicting incident CVD. Our finding revealed that the lipidome-based CVD risk score (HR = 1.77, 95% CI: 1.42–2.21, p = 3.94 × 10⁻⁰⁷) significantly outperformed mAgeΔ (HR = 1.13, 95% CI: 1.04–1.23, p = 4.73 × 10⁻⁰³) in the BHS validation cohort (Supplementary Table S16). Additionally, other studies have proposed a range of different lipidomic risk scores targeting at diseases57, 58, 59 or mortality,^60,61 all of which have yielded promising outcomes. However, these outcome-specific scores do not capture a broad spectrum of metabolic health. Indeed, the primary focus of such scores is on predicting the likelihood of disease, rather than providing insights into the complex interplay of factors that contribute to metabolic health. Thus, we propose metabolic age as a healthy aging score rather than a disease-specific risk score.

In this study, we successfully defined a lipidomic-based age score and demonstrated its effectiveness as a measure of a metabolic health and a predictor of cardiometabolic disease risk, independent of age, in two large population cohorts. However, there were several limitations. Firstly, the strong relationship between mAgeΔ and IHD risk, observed in the AusDiab training set was weaker in the BHS validation set, likely due to differences in the age- and sex distribution of IHD cases in this cohort. We observed the higher ratio of male to female events and the higher proportion of male events in the 50–70 age group in the AusDiab compared to the BHS cohort. Therefore, an additional independent study is required to confirm the predictive performance of mAge in CVD. Another limitation of this study was the focus on cardiometabolic diseases. To comprehensively evaluate mAge, the relationship with other age-related diseases should be explored. Future analyses could also explore the associations between metabolic age and lifestyle/dietary factors as it is well recognised that the plasma lipidome is modifiable by interventions.^56,62, 63, 64, 65, 66

Conclusion

This study presented a comprehensive lipidomic-based score of metabolic age and assessed its relationship to diabetes, CVD and all-cause mortality. It is important to note that we do not propose mAge or mAgeΔ as new CVD biomarkers, rather we envisage these metabolic scores as useful guides to metabolic health, that can identify metabolic dysregulation and provide an avenue for early intervention. Thus, metabolic age has the potential to serve as a health score that is modifiable and may identify individuals at high risk of age-related disease.

Contributors

PJM led the study and revised the manuscript. TW analysed the data and wrote the manuscript. CG and KH developed LC-MS/MS methods and provided support for the LC-MS/MS analysis. CG, KH, GO, TGM, JW, AS, CY and AD provided input into the study design and statistical analyses. MC, NM and HBB and TGM supported the acquisition and processing of the lipidomic data for the cohorts. RKD provided suggestions for the study design. GFW, JH, JH, GC, JB, and EKM were key members of the BHS cohort and revised the manuscript. JES and DJM coordinated the AusDiab data and revised the manuscript. PJM and CG are the guarantors of this work and shall take the responsibility for the full access and integrity of the data. All authors have approved the final version of the manuscript.

Data sharing statement

All raw data used in the study are available from the corresponding authors upon reasonable request.

Declaration of interests

The mAge score is included in a provisional patent, Application number 2023900769 (Methods of assessing metabolic health) and has been licenced to Trajan Scientific and Medical.