Retinal Ganglion Cell Content Underlying Standard Automated Perimetry Size I to V Visual Sensitivities in the Non-Human Primate Experimental Glaucoma Model

Abstract

Purpose

To determine the relationship between visual sensitivities from white-on-white Goldmann size I to V stimuli and the underlying retinal ganglion cell (RGC) content in the non-human primate (NHP) experimental glaucoma model.

Methods

Normative data were collected from 13 NHPs. Unilateral experimental glaucoma was induced in seven animals with the least variable fields who were monitored using optical coherence tomography and 30-2 full-threshold standard automated perimetry (SAP). At varying endpoints, animals were euthanized followed by perfusion fixation, and 1-mm retinal punches were obtained from 34 corresponding SAP locations. RGCs were immunolabeled with an antibody against an RNA-binding protein (RBPMS) marker and imaged using confocal microscopy. RGC counts from each location were then related to visual sensitivities for each stimulus size, after accounting for ocular magnification.

Results

At the endpoint, the circumpapillary retinal nerve fiber layer thickness for experimental glaucoma eyes ranged from 47 to 113 µm. RGC density in control eyes was greatest for the 4.24° sample (18,024 ± 6869 cells/mm²) and decreased with eccentricity. Visual sensitivity at each tested location followed that predicted by spatial summation, with the critical area increasing with eccentricity (slope = 0.0036, R² = 0.44). The relationship between RGC counts and visual sensitivity was described using a two-line fit, where the intercept of the first segment and hinge points were dependent on eccentricity.

Conclusions

In NHPs, SAP visual thresholds are related to the underlying RGCs. The resulting spatial summation based structure–function model can be used to estimate RGC content from any standard white-on-white stimulus size.

Glaucoma is a multifactorial optic neuropathy characterized by progressive degeneration of retinal ganglion cells (RGCs) with associated irreversible loss of visual function.^1,2 The precise pathophysiology remains unknown; hence, clinical assessment is dependent on RGC-associated measures of in vivo structure and visual function. RGCs are not readily visualized in the clinical setting, but objective measures of ganglion cell–containing layers using methods such as optical coherence tomography (OCT) have become part of clinical care. OCT-derived circumpapillary retinal nerve fiber layer (RNFL) contains the majority of RGC axons, with in vivo thickness measures following those measured histologically³ and also correlated with total retrobulbar axon counts.^4,5 Similarly, the macula ganglion cell plus inner plexiform layer (GCIPL) thickness is a good indicator of RGC content when eccentricity is accounted for.^6,7 Although OCT is an essential tool for managing ocular pathology, thickness measures of the circumpapillary RNFL and macula GCIPL have a limited dynamic range.⁸ Hence, optic neuropathies cannot be diagnosed and monitored by objective measures alone.

The clinical standard for assessing visual function is standard automated perimetry (SAP), where luminance thresholds are quantified using white Goldmann size III stimuli (0.43° diameter) on a white background luminance of 10 cd/m².^9–11 Pointwise measures of visual sensitivity using these methods are shown to be related to the underlying RGC density.^12,13 In contrast to objective measures of structure, perimetric visual sensitivities have a larger dynamic range but also have greater variability.^14,15 Hence, confirmatory testing is needed for detection of disease or disease progression.^16–18

Several structure–function models have been described using data from in vivo imaging and SAP thresholds.^12,19–24 As expected, there is generally good agreement, but the relationships reflect the limitations and variability of both in vivo structural and functional measures. Although some studies have suggested a loss of visual function prior to structure,^24–28 others show otherwise,^29–32 and there is a need to improve how both structure and function are clinically assessed. To that end, the current work focuses on visual sensitivities as would be quantified clinically, and their relationship to the underlying RGC content. Sensitivity can have many meanings in vision and neuroscience, but for this manuscript visual sensitivity and thresholds refer to the white-on-white differential light sensitivity.

Using white-on-white perimetry, several strategies have been proposed to improve functional assessment. One approach has been to optimize stimulus size based on disease state. Psychophysically, the relationship between visual sensitivity and stimulus size is described using spatial summation, where the measured sensitivities are modeled to reflect the convergence of RGCs to cortical cells.^22,33 Spatial summation data are commonly fit with two segmental lines, with the slope of the first segment constrained to Ricco's law and connected at a hinge point, referred to as the critical area (A_c).³⁴ With glaucomatous RGC loss, the spatial summation curve is altered in that luminance thresholds are disproportionately higher for smaller than for larger areas, and the critical area is enlarged.³⁵ Both human and non-human primate (NHP) experimental glaucoma studies suggest that, within the central 10°, stimuli smaller than size III may have greater sensitivity to damage in early disease.^6,36 Furthermore, size V stimuli may have greater clinical value for patients with moderate to severe disease.³⁷

Hence, using stimuli of different sizes, white-on-white perimetry could be used to accurately detect and monitor visual function at all stages of neuropathy.^38,39 Although methods for equating visual sensitivity from different stimulus sizes have been described,⁴⁰ the histological association with underlying RGC content is less studied. Previously, the NHP experimental glaucoma model was used to establish the nonlinear model for relating visual sensitivity from size III stimuli to the underlying RGC density.^12,41,42 We have also demonstrated that RGC counts are related to visual sensitivity following spatial summation for the central macula region.⁶ Using histological techniques specific for RGCs, the current work aims to expand on this previous work, providing methods with which RGC content can be estimated for the central 30° using all stimulus sizes tested with standard full threshold white-on-white perimetry.

Methods

Subjects

Normative data for 30-2 perimetry using Goldmann size I through V stimuli were collected from 13 eyes of 13 healthy rhesus monkeys (Macaca mulatta). Seven animals, with the most reliable fields, defined as being able to complete size I through V perimetry in 7 consecutive days, were recruited into the unilateral experimental glaucoma arm of the study. All experimental and animal care procedures were reviewed and approved by the Institutional Animal Care and Use Committee of the University of Houston. The use of animals for this study adhered to the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research and the National Institutes of Health guidelines for the care and use of laboratory animals.

Animal Sedation

Prior to imaging or lasering, monkeys were sedated with an intramuscular injection of ketamine (20 mg/kg) and xylazine (0.8 mg/kg) and treated with a subcutaneous injection of atropine sulfate (0.04 mg/kg) to minimize salivation and maintain a healthy heart rate. While the monkeys were sedated, body temperature was maintained using a warm water blanket (Adroit Heat Therapy Pump and Warming Pad; Adroit Medical, Loudon, TN, USA), and heart rate and blood oxygen saturation were monitored continuously (perMAP + II; Ramsey Medical, Tampa, FL, USA).

Experimental Glaucoma Model

Unilateral experimental glaucoma was induced by scarring the trabecular meshwork using a 532-nm diode laser (VISULAS 532; Carl Zeiss Meditec, Jena, Germany). Contiguous laser burns (0.8 W, 0.5 second, 50-µm spot size) were applied to the trabecular meshwork through a laser gonioscopy lens (Ocular Kaufman; Ocular Instruments, Bellevue, WA, USA). Initially, the laser burns were applied to 180° of the drainage angle, followed by 90° applications at 2- to 3 week-intervals until sustained elevated intraocular pressure (IOP) was achieved. To minimize excessive elevation of IOP, 1 clock hour of the trabecular meshwork was left untreated. IOP was measured approximately every 2 weeks with Tono-Pen XL (Reichert Technologies, Depew, NY, USA).

Optical Coherence Tomography

Animals were imaged approximately every 2 weeks following the first laser session. After the animal was sedated, IOP was measured and pupils were dilated with 1% tropicamide. Prior to imaging, optical biometry measures (Lenstar LS 900; Haag Streit, Koeniz, Germany) were obtained after the insertion of an eyelid speculum. To maintain corneal hydration and optical clarity, a plano rigid gas-permeable lens was placed on the cornea, and OCT imaging (SPECTRALIS OCT; Heidelberg Engineering, Heidelberg, Germany) was obtained. Scans included a 24-line 20° radial scan and a 193-line 20° × 20° raster scan centered on the optic nerve head (ONH), and imaging was repeated when signal strength fell below 30 decibels (dB). OCT scans were exported as *.vol files and segmented using neural networks trained on a DeepLabv3+ background, as previously described.^43,44 In brief, borders of the inner limiting membrane (ILM), RNFL, Bruch's membrane, and the Bruch's membrane opening (BMO) were identified and used for analysis. Before extracting thickness measures, each scan and associated segmentation were rescaled to a 1:1 aspect ratio, incorporating individualized transverse scaling calculated using a three-surface schematic eye, using the optical biometry measures obtained at the scan session. Circumpapillary RNFL thickness was extracted from an interpolated scan path 550 µm from the BMO, and the minimum rim width (MRW) as the shortest distance from the BMO to the ILM.^45,46 Staging of disease was defined based on the percentage loss of RNFL and MRW compared to baseline.

Behavioral Perimetry

Visual sensitivity was quantified using static threshold perimetry with a clinical Humphrey Field Analyzer (HFA 750i; Carl Zeiss Meditec), attached to a NHP testing chamber, details of which have been previously described.⁴⁷ In brief, animals were seated in a primate chair and positioned such that the tested eye was at the correct viewing distance and centered on the fixation light-emitting diode (LED) of the perimeter. Each subject was trained to press a response lever to initiate a trial and given up to 700 ms to respond to the presented visual stimulus. True positives were reinforced with an orange drink; false positives and misses were not punished, but no juice reinforcement was offered. To maintain fixation, the central LED of the perimeter was used as a dimming stimulus, controlled through an external program. Approximately 20% of all trials were central fixation, and the remaining trials were released to the native perimeter full threshold algorithm, which was paused between trials. Using this protocol, animals worked approximately 2 hours daily, completing a single 30-2 visual field at each session and completing Goldmann size I to V testing for a single eye, nominally over the work week. Although the stimulus size used each day was not intentionally randomized, there was no specific order in which animals completed these each week. Reliable fields were considered those with less than 10% false positives on fixation trials and less than 10% false positive or false negatives on perimetry trials. Of the 13 animals trained on this paradigm, the seven animals with the best reliability and least variability of pointwise visual sensitivity measures had experimental glaucoma induced. Prior to lasering, these seven animals had between 149 and 598 days of visual field training, and following lasering they were monitored with perimetry to a time point when OCT structural measures were stable and reliable thresholds from size I through V stimuli could be collected in a single week (between 83 and 816 days after lasering). The visual sensitivity (dB) reported on the printouts and the corresponding differential light sensitivity (DLS) in candelas per square meter (cd/m²) were used for statistical analysis:

$$\begin{array}{c}\hfill \mathrm{Differential}\mathrm{light}\mathrm{sensitivity}\left(\mathrm{DLS}\right)=\frac{{10}^{\left(\frac{40-\mathrm{dB}}{10}\right)}}{\pi }\end{array}$$

Tissue Preparation

Following a series of reliable endpoint visual thresholds, animals were sedated, imaged with OCT, and euthanized. Animals were euthanized through an overdose (100 mg/kg) of sodium pentobarbital (Fatal-Plus; Vortech Pharmaceuticals, Dearborn, MI, USA). Following exsanguination, animals were perfusion fixed with 4% paraformaldehyde in phosphate buffer, and the eyes were then enucleated. The anterior segments were removed, and the globes were placed in 4% paraformaldehyde for at least 24 hours before further processing.

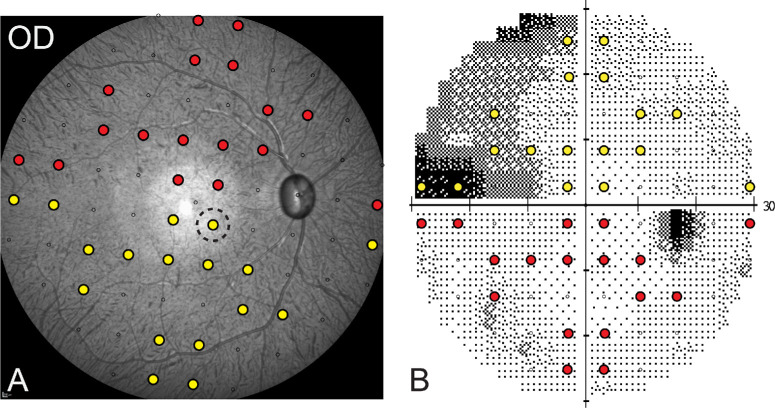
The endpoint 55° widefield scanning laser ophthalmoscope (SLO) image from each eye was used to register perimetry locations, matching the central fixation and blind spot from perimetry to the fovea and ONH from imaging. From this aligned mapping, circular retinal punches of 1-mm diameter were extracted from 34 SAP locations (see Fig. 1) and placed in phosphate-buffered saline (PBS) for immunohistochemistry. The 34 locations included six eccentricities: 4.24°, 9.48°, 12.72°, 17.49°, 21.21°, and 27.16°. After the tissue was washed, antigen retrieval was performed by placing the punches in 300 µL citrate buffer for 10 minutes at 86°C. The retinal punches were blocked with diluent (10% donkey serum, 0.05% sodium azide made in PBS, and Triton X-100, 0.5%–16%) overnight at 4°C and then incubated with a guinea pig polyclonal anti-RBPMS antibody (1:100 µL dilution), and a goat polyclonal anti-choline acetyltransferase (ChAT) antibody (1:100 µL dilution) for up to 7 days at 4°C. RBPMS labels all RGCs,⁴⁸ whereas ChAT was used to identify displaced amacrine cells in the ganglion cell layer. After the samples were washed, the punches were incubated with Cy3-conjugated donkey anti-guinea pig IgG antibody (1:300 µL dilution) and Alexa Fluor 647–labeled donkey anti-goat IgG antibody (1:300 µL dilution) and placed in the dark overnight at 4°C. The punches were washed in PBS and counterstained with 4′,6-diamidino-2-phenylindole (DAPI; 1:1000 µL PBS) in the dark for 1.5 hours. After a final wash in PBS, the choroid was removed, and the punches were mounted using VECTASHIELD medium (VectorLabs, Newark, CA, USA).

Figure 1.

(A, B) Endpoint widefield SLO image from an eye with experimental glaucoma (A), with corresponding visual field locations marked from a size III 30-2 field (B). The color locations indicate the regions punched for histological evaluation of RGC density (the dashed circle indicates the nominal size of the punched region).

Confocal Imaging

Flatmounts were imaged using a confocal microscope (ZEISS LSM800; Carl Zeiss Meditec) at 20× magnification. For each retinal flatmount, confocal z-stack images with an interval of 1 µm were acquired for six non-overlapping regions. The z-stacks were exported to a program written in MATLAB (MathWorks, Natick, MA, USA), and cells labeled for RBPMS were manually counted using a 250 × 250-µm bounding box with two inclusion and two exclusion borders and were used to calculate cell density (cells/mm²). The cell density for each 1-mm sampled punch was determined as the mean cell density for the six sampled regions. For comparison with visual sensitivity, the total cell count for each stimulus was determined after accounting for retinal magnification for that eye, calculated using a three-surface schematic eye. On average, retinal scaling for an emmetropic eye with an axial length of 19 mm is 219 µm/degree.

Nonlinear Model

Localized RGC density can be estimated with the nonlinear model (NLM), which was developed in the NHP using visual sensitivity measures from size III stimuli.^12,49 Although the model was developed using different histological methods compared to the present study, NLM estimates of RGCs should mirror those measured for size III stimuli in this experiment and were used for validation. The NLM equations used were as follows:

$$\begin{array}{c}\hfill \begin{array}{c}m=(0.054e)+0.95\hfill \\ b=(-1.5e)-14.8\hfill \\ gc=(s-b)/m\hfill \end{array}\end{array}$$ (1)

where RGC density (gc, in dB) for a specific sensitivity (s, in dB) can be estimated using a linear function where the slope (m) and intercept (b) are dependent on the stimulus eccentricity (e). RGC estimates from each sampled size III location were compared to the measured cell density using Bland–Altman analysis.

Statistical Analysis

Descriptive statistics are used to present the visual sensitivities and RGC densities at the different eccentricities. Bland–Altman analysis was used to compare the RGC density measured at each sampled location and the density estimated using the NLM. The relationship between logDLS and logRGC counts was assessed with a segmental linear regression model, for which the first slope was constrained to −1. Because visual sensitivity measures across disease states are not homoscedastic,¹⁴ robust regression was used. All statistical analyses were performed in Prism (GraphPad Software, Boston, MA, USA), and all plots were generated with SigmaPlot (Systat Software, San Jose, CA, USA).

Results

Perimetry

Of the 13 animals enrolled in the study, one was unable to provide repeatable thresholds with size I through V stimuli, and normative data are presented for the 12 reliable datasets. Seven of the 12 subjects with better reliability, based on consistency of perimetric thresholds, were later induced with experimental glaucoma. One of these animals was unable to maintain consistent fields, and for them, size I to V data were only collected from the experimental glaucoma eye with a 24-2 paradigm. All perimetric data used for analysis came from completed fields with 0% false-positive or false-negative errors. Table 1 shows the OCT structural data for each of the experimental glaucoma eyes.

Table 1.

Circumpapillary RNFL Thickness and ONH MRW for Each Experimental Glaucoma Eye at Baseline and Endpoint

Subject	Time Point	Circumpapillary RNFL Thickness (µm)	MRW (µm)
NHP_SS1	Baseline	126	306
	Endpoint	47	36
NHP_SS2	Baseline	128	300
	Endpoint	54	61
NHP_SS3	Baseline	120	307
	Endpoint	61	71
NHP_SS4	Baseline	117	327
	Endpoint	64	96
NHP_SS5	Baseline	133	334
	Endpoint	64	71
NHP_SS6	Baseline	137	338
	Endpoint	80	122
NHP_SS7	Baseline	131	308
	Endpoint	113	219

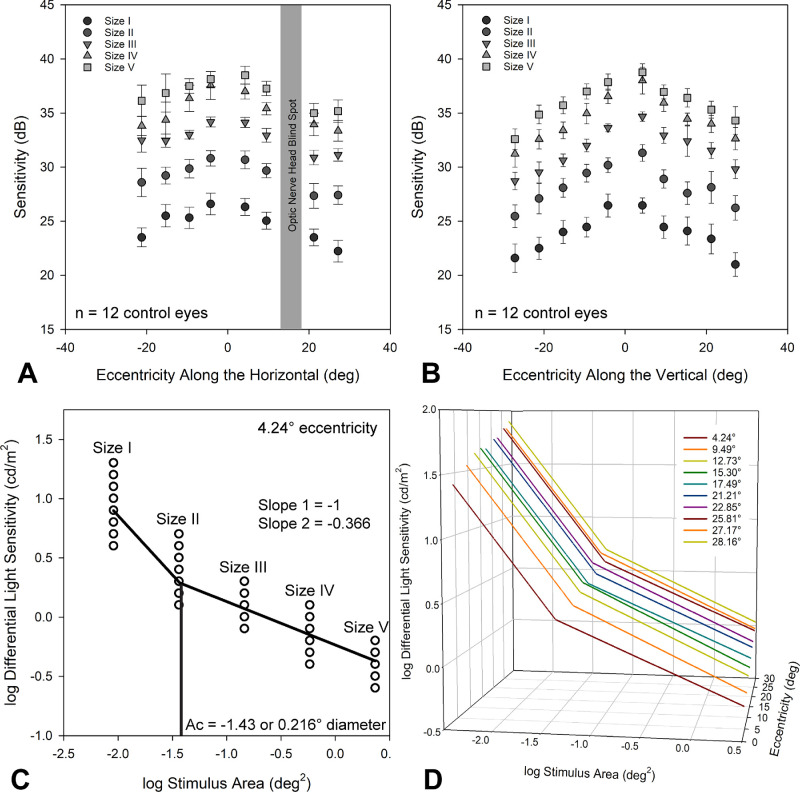
For control eyes, larger stimuli had higher sensitivity measures, and sensitivity measures followed the hill of vision as demonstrated by the mean data from the horizontal and vertical meridians (Figs. 2A, 2B). For each of the 10 30-2 eccentricities, the spatial summation relationship between differential light sensitivity and stimulus size was assessed using a two-line fit, with the slope of the first segment constrained to −1 (n = 12 control eyes) (Fig. 2C). The critical area (A_c), in log(deg²), and y-intercept were noted from these fits. As expected,^6,40,50 the A_c ranged from −1.43 to −1.28, increasing with eccentricity (slope = 0.0036, R² = 0.44). With increasing eccentricity, the spatial summation curve moved upward and to the right (Fig. 2D), as previously reported for human subjects.⁵⁰

Figure 2.

(A, B) Mean sensitivity (±95% CI) along the horizontal (A) and vertical (B) meridians of the 30-2 field for size I through V stimuli. (C) Spatial summation plot for the closest eccentricity evaluated. (D) Spatial summations plots for the 10 30-2 eccentricities, illustrating the change in y-intercept and critical area with eccentricity.

Retinal Ganglion Cell Density

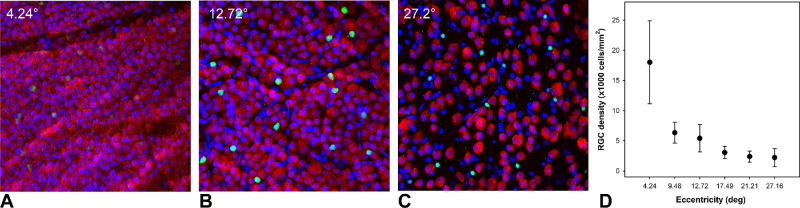
Immediately following the last scan session, animals were euthanized and perfusion fixed with 4% paraformaldehyde in phosphate buffer. The eyes were enucleated, the anterior segment of each eye was carefully removed, and the eyecups were placed in 4% paraformaldehyde for an additional 24 hours. Prior to sampling the retina, approximately five flaps were created to flatten the eyecup, and the posterior segment was oriented to match the endpoint SLO image (Fig. 1). Following, with the aid of the retinal vasculature, each of the predetermined locations (n = 34 for each eye) was then sampled using a 1-mm-diameter punch. Additional punches from each eye were obtained for antibody optimization but were not used for data analysis. For the control eyes, the average RGC density at the 4.24° eccentricity was 18,024 ± 6869 cells/mm², and it was 2226 ± 1504 cells/mm² at 27.16° (Fig. 3).

Figure 3.

(A–C) Single mid-ganglion cell layer images from confocal z-stacks of a control eye at 4.24° (A), 12.72° (B), and 27.2° (C) eccentricities, each acquired at 20× magnification. RGCs are labeled with RBPMS (red), displaced amacrine cells with ChAT (green), and cell nuclei with DAPI (blue). (D) Average ± SD cell densities of the seven control eyes for the six eccentricities sampled are shown.

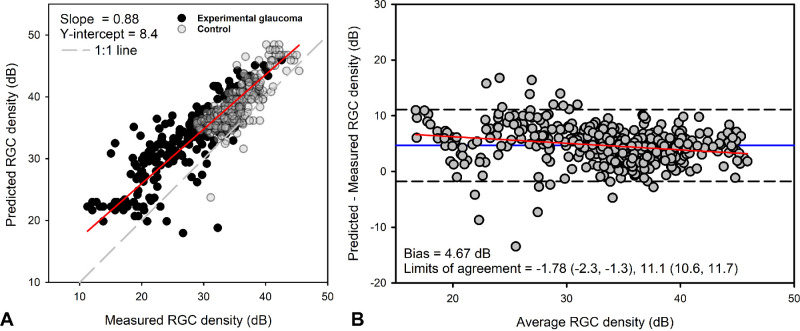
Comparison With Nonlinear Model

Cell densities were estimated for endpoint size III thresholds for both control and experimental glaucoma eyes using the NLM (Equation 1)¹² and compared to the densities quantified using confocal microscopy with Deming regression (slope = 0.88, P < 0.01) (Fig. 4A). The mean bias with Bland–Altman comparison was 4.67 dB (95% confidence interval [CI], 4.37–4.98) (Fig. 4B), with greater predicted RGC density compared to that measured, and 95% limits of agreement between −1.78 dB (95% CI, −2.30 to −1.25) and 11.12 dB (95% CI, 10.60–11.65). Although the Bland–Altman analysis suggests good agreement, there was greater variability in the predicted versus measured data for samples with lower RGC content. Further, the mean versus difference data showed a small but significant proportional bias (slope = −0.12, R² = 0.05, P < 0.01) (Fig. 4B, red line).

Figure 4.

(A) Retinal ganglion cell densities estimated using the nonlinear model were correlated with those measured. (B) Bland–Altman analysis with 95% limits of agreement showed a small proportional bias.

Stimulus Size and Visual Sensitivity

To determine the number of RGCs covered by each Goldmann size stimulus (I–V), individual ocular magnification using a three-surface schematic eye was used to determine the stimulus area on the retina. To avoid overfitting, visual sensitivities of 0 dB and regions with calculated cell densities of less than 5 cells were removed prior to fitting. When logDLS values from all stimulus sizes for both control and experimental glaucoma eyes were plotted as a function of the underlying RGC content, the data followed what would be predicted by spatial summation (Fig. 5), and were similar to macula 10-2 data reported previously using this animal model.⁶ A segmental two-line fit, with the slope of the first segment confined to −1, using robust regression, was fit to the control data (Fig. 5, blue line) and experimental glaucoma data (Fig. 5, red line). For the control data points, the y-intercept for the −1 slope section was at 1.414 logDLS, with the hinge point at 0.73 logRGC count, and the slope of the second function was −0.42. The experimental glaucoma data had a greater y-intercept of 1.85 logDLS, with the hinge at 0.79 logRGC count, and the slope of the second function was −0.49. Although the spatial summation curve for the experimental glaucoma data was vertically shifted, it was within the variability of the control eye data, and the hinge points were similar for the two datasets, F(1, 1027) = 3.343. Subsequently, for each eccentricity, two-line segmental functions were fit using robust regression for the combined control and experimental glaucoma data, which are summarized in Table 2.

Figure 5.

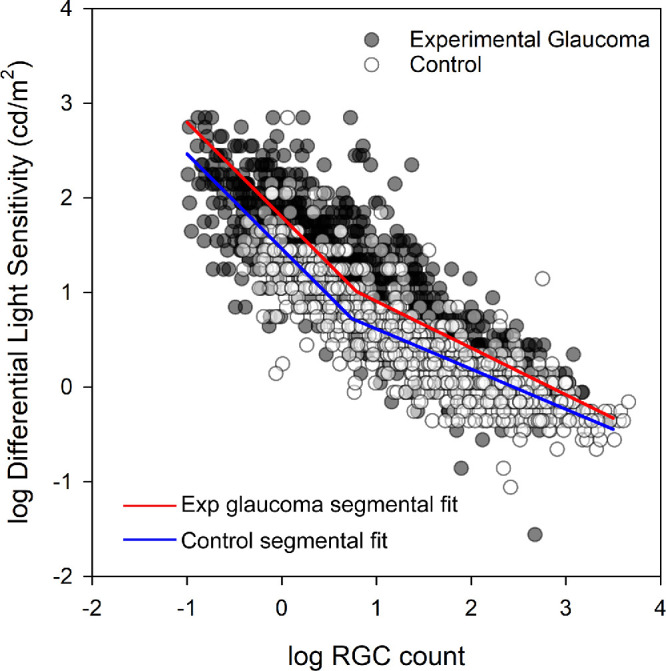
The relationship between logRGC counts and logDLS in control (open symbols) and experimental glaucoma (closed symbols) samples. The red and blue lines illustrate the segmental fits for the experimental glaucoma and control samples.

Table 2.

Coefficients for the logRGC Count and logDLS Robust Segmental Fit for Each Eccentricity Evaluated, and Robust Standard Deviation of the Residuals

Eccentricity (°)	Segment 1, Intercept (logDLS, cd/m2)	Hinge Point (log[Cell Count])	Segment 2 Slope	RSDR
4.24	2.063	1.426	−0.4934	0.3503
9.48	1.823	1.155	−0.4891	0.3036
12.72	1.757	0.9217	−0.5163	0.3371
17.49	1.537	0.7681	−0.4943	0.2743
21.21	1.578	0.8720	−0.4644	0.3262
27.16	1.602	0.8385	−0.4745	0.4179

The slope of the first segment was constrained to −1.

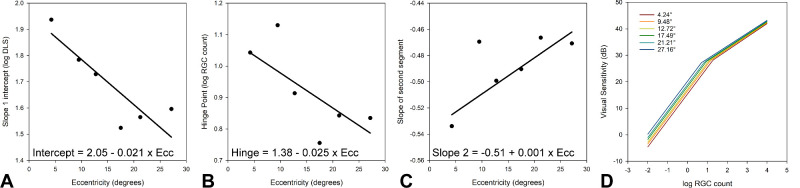
Each coefficient of the segmental fit (as defined in Equation 3) changed with eccentricity, and a linear best fit was used to generate equations to estimate each (Fig. 6, Equation 4). Using these equations, the relationships between logRGC count and visual sensitivity for each of the sampled 30-2 eccentricities are illustrated in Figure 6D.

Figure 6.

(A–C) Relationship between the intercept of the first segment (A), hinge point (B), and slope of the second segment (C) with eccentricity for a two-line segmental fit to the data illustrated in Figure 5. (D) Structure–function relationship for each histologically sampled eccentricity, using the coefficients estimated from the regressions A to C.

Two-line segmental fit:

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{Segment}1,\log \mathit{RGC}\mathrm{count}<\mathrm{hinge}:\hfill \\ log\mathit{DLS}=\mathrm{Segment}1\mathrm{intercept}-1\times \log \mathit{RGC}\mathrm{count}\hfill \\ \mathrm{Segment}2,\log \mathit{RGC}\mathrm{count}>\mathrm{hinge}:\hfill \\ log\mathit{DLS}=log\mathit{DLS}\mathrm{at}\mathrm{hinge}+\mathrm{slope}2\hfill \\ \times (log\mathit{RGC}count-\log \mathit{RGC}\mathrm{at}\mathrm{hinge})\hfill \\ \log \mathit{DLS}\mathrm{at}\mathrm{hinge}=\mathrm{Segment}1\mathrm{intercept}-1\hfill \\ \times log\mathit{RGC}countathinge\hfill \end{array}\end{array}$$ (3)

$$\begin{array}{c}\hfill \begin{array}{c}\mathrm{Slope}1\mathrm{intercept}=2.05-0.021\times \mathrm{eccentricity}\hfill \\ \mathrm{Hinge}\mathrm{point}=1.38-0.025\times \mathrm{eccentricity}\hfill \\ \mathrm{Slope}2=-0.5+0.001\times \mathrm{eccentricity}\hfill \end{array}\end{array}$$ (4)

Discussion

Standard automated perimetry using a white Goldmann size III stimulus on a 10 cd/m² white background is the clinical standard for assessing visual function in optic neuropathies. Although this testing protocol has a large dynamic range, it has limited sensitivity at both early and late stages of disease, and there is a need to improve the precision of testing across disease states.¹⁴ One potential approach is to optimize the stimulus size to be similar to or smaller than the critical area, based on stage of disease.³⁸ In this paradigm, smaller stimuli would be used at earlier stages of neuropathy, with larger stimuli potentially providing a better assessment of vision in advanced disease.^{37,38,51–54} The current work aimed to determine the underlying RGC content for visual thresholds of different stimulus sizes in control and experimental glaucoma eyes. Using the non-human primate experimental glaucoma model, we showed that the relationship between visual sensitivity and underlying RGC counts follows spatial summation and depends on eccentricity.

The correspondence between size III stimuli and RGC content has been studied in the NHP and presented as the NLM.¹² To validate the methods used in the current study, estimated RGC densities were compared to those measured for size III stimuli. Although the data showed good correspondence, they suggest that the published model overestimates cell density, and there was also a small, but statistically significant proportional bias (Fig. 4). The mean bias likely reflects differences in histological methods used for cell counts. The NLM was generated using histological samples taken from 16 predefined locations, assuming a 1-mm retinal distance to a 4° visual angle.⁴¹ The sections were prepared for light microscopy, and retinal cross-sections were stained with cresyl violet and used for cell counting. Ganglion cell density was estimated using Abercrombie's method, which requires sections to be smooth and of even thickness and assumes that all nuclei are spherical.⁵⁵ Further, because specific labels were unavailable, both RGC and displaced amacrine cells were included in counts, which also likely contributed to the overestimation of cell density. In contrast, the present study sampled a larger number of locations, using endpoint fundus imaging as a guide for sampling, and accounted for differences in ocular magnification. In addition, RGCs were labeled with RBPMS,⁴⁸ and cells were counted from flatmounts of retinal punches, likely resulting in more accurate quantification.

As expected, the highest cell densities were measured for samples closer to the fovea and decreased with eccentricity (Fig. 3). However, because cell densities were established for the entire punched region, the cell densities for the central 4.24° locations are less than the peak densities reported in the literature, which used smaller sampling windows.^6,56–60 The 1-mm punch size was selected as it was large enough to cover the entire Goldmann size V stimulus (1.72°) and account for normal fixational eye position variability in the primate model (∼0.33°).⁶¹ However, the 1-mm punched region spans a large region, and the central punched region included the peak cell density and regions where density starts to decrease. Because of these sampling techniques, it was not possible to account for displaced RGCs for the central 4.24° location.

The visual sensitivity data from the NHP control eyes followed a hill of vision similar to that of humans.^40,62 Our observations align with those previously reported comparing perceptive fields for normal monkey and human vision.⁶³ As expected, with an increase in stimulus size, there was an increase in visual sensitivity, and, with increasing eccentricity, there was an increase in the critical area of spatial summation.^64–66 The perimetric data would suggest that in the NHP there is an increase in threshold at the critical area with eccentricity. Although these data are consistent with human perimetric data,⁵⁰ they are in contrast with previous spatial summation literature showing that the increase in critical area is scaled to RGC dendritic coverage, maintaining constant sensitivity with eccentricity.^64,67–69

The relationship between visual sensitivity and RGC content from control and experimental glaucoma eyes also followed that of spatial summation. These findings support the hypothesis that spatial summation reflects the underlying RGC content and the cortical pooling of their responses.^22,70–72 The histological data show that the number of RGCs at the critical area decreases from approximately 12 at the fovea to 6 at a 30° eccentricity. This contrasts with most spatial summation models, which suggest a constant number of RGCs at A_c.⁷² Whereas previous models report a constant number of RGCs at A_c, a closer evaluation (e.g., data presented by Kwon and Liu³³) would suggest a similar decrease with eccentricity. It is possible that the observed decrease of RGCs at the critical area with eccentricity may reflect associated changes in optical quality.⁷³ Alternatively, the observed relationship could represent increased retinal convergence with eccentricity.⁷⁴ Specifically, although there is a one-to-one connection in the fovea, each ganglion cell pools from a larger number of photoreceptors with increasing eccentricity.

The spatial summation equations (Equation 4) resemble, and histologically support, the two-stage neural model, and in principle the “broken-stick” or “hockey-stick” models, each of which is a segmental fit.^{31,37,75–79} However, of these previous models, only the two-stage model directly relates visual thresholds with RGC counts, with a hinge point at 31 RGCs. Although similar, the current study suggests that the number of RGCs at the hinge point is half of that, and the histological data are different than previous segmental fits in that they show a dependence on eccentricity. In principle, the data (Fig. 5) and model also agree with that proposed by Garway-Heath et al.,²⁰ in which a curvilinear relationship was used to describe the relationship between differential light sensitivity and the underlying RGC content. Although the linear (Hood–Kardon) model does not include an inflection point, it is likely that the histological data following the hinge point would show good correspondence.²³

The spatial summation equation (Equation 3) for relating structure to function should be applicable to the entire glaucoma disease spectrum. Although the majority of control eye and experimental glaucoma data overlapped (Fig. 5), the vertical displacement of the spatial summation curves are suggestive of visual function loss prior to RGCs. This is similar to previous studies in this model, which showed that some regions had a significant loss of visual function yet had relatively normal cell densities.⁴¹ Further, using pattern electroretinograms, it has been shown that glaucoma suspects often have functional defects prior to loss of in vivo measures of circumpapillary RNFL thickness.⁸⁰ Hence, it is possible that the vertically shifted and slightly larger critical area for the glaucoma data points in Figure 5 represent dysfunctional RGCs, with increased intrinsic neural noise. Similarly, although animals were relatively stable at endpoint, disease progression in this animal model is fast compared to the human condition. For example, in this animal model, it has been reported that a substantial loss of RGC axons occurs before thinning of the circumpapillary RNFL.^4,5 Hence, it is also possible that damage of RGC axons at the optic nerve head are not fully reflected in the retinal flatmount cell counts.

There are several limitations to the presented work. The experiment was initially designed to include longitudinal data. However, due to disruptions from the COVID pandemic, there were many breaks in data collection, and longitudinal changes in thresholds could not be established. Although the NHP is a reliable model for visual thresholds, elevated pressures in this model are not treated. Hence, the influence of elevated IOP on visual sensitivity measures cannot be accounted for. An ideal protocol for adequate labeling of RGCs had to be determined for each animal, and any resulting differences in tissue shrinkage/expansion could not be accurately accounted for. Furthermore, although whole retinal labeling would have been ideal, we were only able to effectively label 2-mm-diameter retinal punches. As the samples were circular, these could not be accurately oriented, and therefore RGC displacement could not be accounted for. Although we do not expect this to have a significant impact for more peripheral locations, it could change the RGC counts for the central macula samples. The cell density and visual sensitivity data for both control and experimental glaucoma eyes are available for alternative hypotheses testing.

In conclusion, using the NHP experimental glaucoma model, we showed that visual sensitivity of white-on-white perimetry is dependent on the underlying number of RGCs and eccentricity and follows spatial summation. The resulting spatial summation model is expected to have good accuracy for estimating RGC content when using thresholds from stimuli at or smaller than the critical area.