Abstract
There is increasing evidence that biological systems are modular in both structure and function. Complex biological signaling networks such as gene regulatory networks (GRNs) are proving to be composed of subcategories that are interconnected and hierarchically ranked. These networks contain highly dynamic processes that ultimately dictate cellular function over time, as well as influence phenotypic fate transitions. In this work, we use a stochastic multicellular signaling network of pancreatic cancer (PC) to show that the variance in topological rankings of the most phenotypically influential modules implies a strong relationship between structure and function. We further show that induction of mutations alters the modular structure, which analogously influences the aggression and controllability of the disease in silico. We finally present evidence that the impact and location of mutations with respect to PC modular structure directly corresponds to the efficacy of single agent treatments in silico, because topologically deep mutations require deep targets for control.
Subject terms: Cancer, Regulatory networks
Introduction
Biologically, regulatory networks and protein–protein interaction networks are typically thought to be densely connected sub-regions of an overall sparse system1. Natural cellular functions such as signal transmission are carried out by so-called modules that are discrete entities with separable functionality from other modules2. For example, the ribosome is a module that is responsible for synthesizing proteins that are spatially isolated. A similar isolation is seen with the proteasome. Whereas, signaling systems through chemokines would be extended modules that are isolated through the binding of chemical signals to receptor proteins. These isolating features allow cells to achieve various objectives with minimal influence from cross-talk2. Yet, their connectivity allows complex guidance signals from one another.
More often, in silico models are being implemented in cancer research for the discovery of general principles and novel hypotheses that can guide the development of new treatments. Despite their potential, concrete examples of predictive models of cancer progression remain scarce. One reason is that most models have focused on single-cell type dynamics, ignoring the interactions between cancer cells and their local tumor microenvironment (TME). There have been a number of models that were used to study gene regulation at the single-cell scale, such as macrophage differentiation3–5, T cell exhaustion6, differentiation and plasticity of T helper cells7,8, and regulation of key genes in different tumor types9,10, including pancreatic cancers11.
These models are all great steps towards control-based treatment optimization, but it has been demonstrated that the TME has a critical effect on the behavior of cancer cells12. Ignoring the effect of cells and signals of the TME can generate confounding conclusions. For example, it was shown that in non-small cell lung cancer, the microenvironments of squamous tumors and adenocarcinomas are marked by differing recruitment of neutrophils and macrophages, respectively. Ex vivo experiments revealed the importance of the TME as a whole, especially when considering immunotherapy enhancement13. A similar observation has shown that removing pancreatic stellate cells from the TME in silico led to differing long-term outcomes because they form a protective layer around tumor cells11.
To study the interplay of cancer cells with components of the TME, modelers developed multicellular models including cancer, stromal, immune, cytokines, and growth factors14. These models are typically multiscale integrating interactions at different scales, making it possible to simulate clinically relevant spatiotemporal scales and, at the same time, simulate the effect of molecular drugs on tumor progression15–20. The high complexity of these models generates challenges for model validation such as the need to estimate too many model parameters.
While a multi-scale model would likely provide more realistic simulations, state-of-the-art control techniques require a network model specification such as Boolean networks (or their generalizations) to find optimal therapeutic interventions21. Implementation of Boolean networks (BNs) provides a coarse-grained description of signaling cascades without the need for tedious parameter fitting and can be simulated through stochastic discrete dynamical systems (SDDS22) to streamline the modeling process and increase efficiency. These models have a well-studied and effective track record for capturing various biological system dynamics23.
Pancreatic cancer is among the most lethal types of malignancies largely due to its difficulty in detecting. The pancreas is located deep within the body, and a standard doctor’s exam will likely not reveal a tumor. Additionally, there is an absence of detecting and imaging techniques for early-stage tumors. While PC only accounts for 3% of estimated new cases, it is the fourth highest cause of cancer-related death in the United States24, and there is only a 3% 5-year survival rate among its late-stage patients (~82% in Stages 3 and 4)25,26. PC is widely known for its resistance to most traditional therapy protocols. According to the Pancreatic Cancer Action Network (PanCAN), most patients receive fluorouracil (5-FU) or gemcitabine-based treatments that are anti-metabolites targeting thymidylate synthase and ribonucleotide reductase, respectively26.
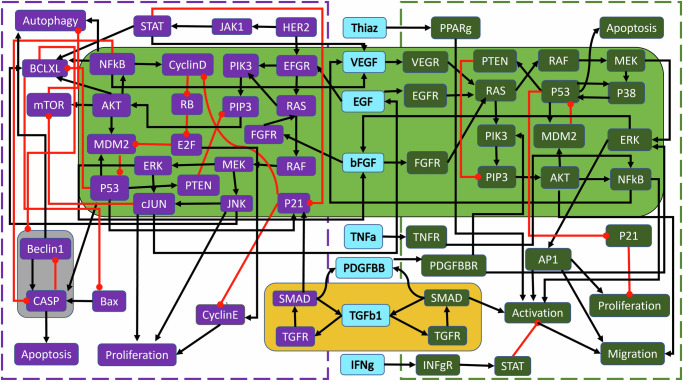
In prior work, we presented a multicellular model of pancreatic cancer (PC) based on a stochastic Boolean network approximation (Supplementary Fig. 1), and we used control strategies that direct the system from a diseased state to a healthy state by targeting and disrupting specific signaling pathways. The model consists of pancreatic cancer cells (PCCs), pancreatic stellate cells (PSCs), cytokine molecules diffusing in the local microenvironment, and internal gene regulations for both cell types11. We then used the PC model to study the impact of four common mutations: KRAS, TP53, SMAD4, and CDKN2A14,27,28. Throughout this writing, we will often denote PCC components with subscript c and PSC components with subscript s.
Using our PC model as a case study, readers will find the following: Figure 1 shows a workflow of our process for defining and analyzing modules, followed by a summary of the PC model dynamics and target efficacy in ‘Model dynamics and target efficacy’. Within the ‘Results’ section, we show that the modularity of GRNs is vulnerable to mutations, analogous perturbations to long-term dynamical outcomes occur that influence aggression and controllability, variance in topological rankings of the most phenotypically influential modules implies a strong relationship between structure and function, and we finally present evidence that the impact and location of mutations with respect to modular structure directly correspond to the efficacy of single-agent treatments in silico. Then, under the “Methods” section, we define the methods we have implemented.
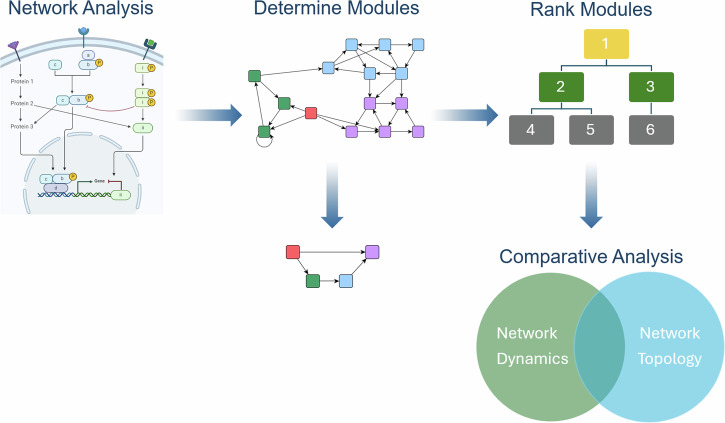
Fig. 1. Modularity workflow.
The workflow within this project begins with formal network analysis (previously conducted on a published PC model11,23,38). We then determine modules and reduce to non-trivial modules, rank the modules, and perform comparative analysis to understand the connection between dynamics and topology.
Results
Model dynamics and target efficacy
Prior work first completed a rigorous dynamical and network cascade analysis of the original non-mutant model11. We also identified numerous targets using various techniques for phenotype control including computational algebra29, feedback vertex set30,31, and stable motifs32, where each tactic provides a complimentary approach depending on the information available. We then sought to understand the impact of PC’s four most common gene mutations: KRAS (gain-of-function), TP53 (loss-of-function), SMAD4 (loss-of-function), and CDKN2A (loss-of-function)14,23,27,28. For ease of notation, we elected to use the abbreviations KRAS (K), TP53 (T), CycD (C), and SMAD (S). Each of these mutations can be computationally achieved by a functional knock-in or knock-out command, that permanently turns the given Boolean function ON/OFF. Detailed tutorials are included in our data repository.
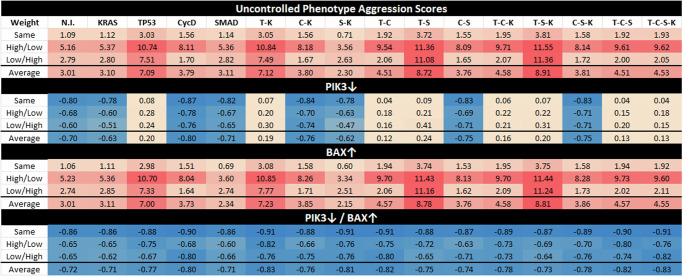
Within the various mutation combinations of the PC model, we used our stochastic simulator based on the SDDS framework (see the section “Stochastic discrete dynamical systems”) to derive aggressiveness scores from simulated long-term trajectory approximations (Supplementary Section 1)23. The estimates in Fig. 2 were tracked using phenotype expressions from only the PCC because the PSC is not considered malignant. Results showed that certain mutation combinations may indeed be more aggressive than others. We then performed statistical analysis on clinical gene expression data and derived survival curves that corroborated estimated aggressiveness scores.
Fig. 2. Aggression scores and target efficacy.
This figure shows aggression scores based on phenotype approximations by applying weights to trajectory probabilities. Here we include heat maps of aggression scores for each mutation combination (No mutation induced (N.I.), KRAS (K), TP53 (T), CycD (C), SMAD (S)), comparing cancer cell autophagy and proliferation while giving a negative weight to apoptosis. Row label “Same” indicates that the same weight was given to both autophagy and proliferation, “High/Low” indicates a high weight for autophagy but a low weight for proliferation, and “Low/High” indicates a low weight for autophagy but a high weight for proliferation. Scaling of the heat map ranges from orange (low score) to red (high score) based on the maximum and minimum values. Scaling shades of blue (cold) indicate non-aggressive or negative scores as a response to targets PIK3 knockdown (PIK3↓) and BAX agonist (BAX↑)23. See Supplementary Section 1 for more details.
Phenotype control theory techniques revealed that sets of targets contained nodes within both the PCC and the PSC, highlighting PIK3 and BAX as a strong combination23. Notice that cells in Supplementary Fig. 1 contain duplicate pathways. While targets are found in both the PSC and the PCC, targets such as PIK3c and PIK3s can be considered as one target biologically. This is because a PIK3 inhibitor would act systemically rather than locally. Thus, when inducing controls in Fig. 2, we assume systemic treatment. Here, we show a heatmap of projected mutation aggression compared to the application of target control. Note that as single agent targets, PIK3 knockdown (PIK3↓) and BAX agonist (BAX↑) are not universally effective. However, their combination is an effective control across all mutation combinations. We believe this can be explained by topological module rankings, detailed below.
The following key observations will be visited:
Network “depth” of KRAS mutation can break the standard modular structure
TP53 always directly impacts the module responsible for PCC apoptosis
Certain modules may not determine phenotypic states
Signaling from mutations to modules directly influences aggression
Topological ranking gaps correspond to aggression projections
Single-agent targets are insufficient to out-compete downstream mutations
Mutations perturb modular structure
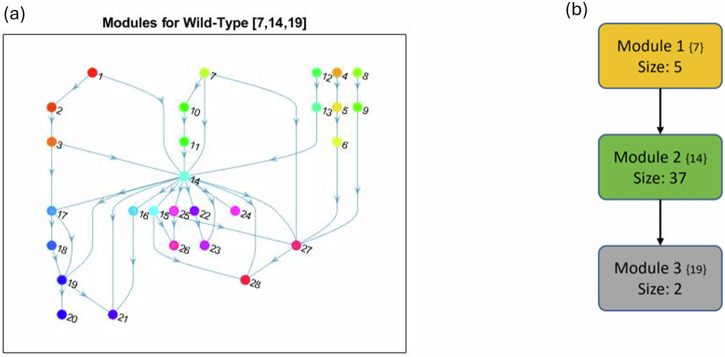
In1, the wild-type PC model from Supplementary Fig. 1 was first analyzed for modularity and revealed that the system contained three non-trivial modules. The module with the top hierarchical rank in Fig. 3, highlighted in yellow, is an autocrine loop of five nodes. Module 2, highlighted in green, contains 37 nodes spanning deep within both the PCC and PSC. The final module, highlighted in gray, is a negative feedback loop of only two nodes (referred to throughout as the ‘duplex module’)1.
Fig. 3. Wild-type PC wiring diagram with modules.
Shown are the highlighted modules (yellow, green, and gray) for the wild-type PC model in Supplementary Fig. 1, adapted from ref. 1. Black barbed arrows indicate signal expression, while red oval arrows indicate suppression. A simplified structure can be seen in Fig. 4b.
The overall wild-type modular structure from Fig. 3 was achieved using the graphs in Fig. 4. Notice that Fig. 4a contains all modules, both trivial and non-trivial. However, Fig. 4b is a reduced modular structure with only non-trivial nodes, including the cardinality of the modules as well as its original numbering from the condensation graph in curly brackets for easy reference. Figure 4a shows how phenotypes typically lie at the end (i.e. the bottom of the graph) because they are the dynamical endpoint: Apoptosiss(24), Proliferations(26), Migrations(28), Activations(27), Autophagyc(21), Apoptosisc(20), and Proliferationc(23). Thus, the condensation ordering begins with source (or input) nodes and expands distally to phenotypes because the ultimate flow of the multicellular network goes from the middle outward. We anticipate that, due to this structure, we must use targets sufficiently upstream of phenotypes to subvert the impact of mutations.
Fig. 4. Wild-type PC modular structure.
a Shown are the cumulative modules (trivial and nontrivial) ranked according to condensation. Node numbers are assigned by the MATLAB37 “conncomp” function that bins connected graph components. b The reduced modular structure is shown with only nontrivial nodes, including the cardinality of the modules (Size) and its original condensation numbering in brackets ({}).
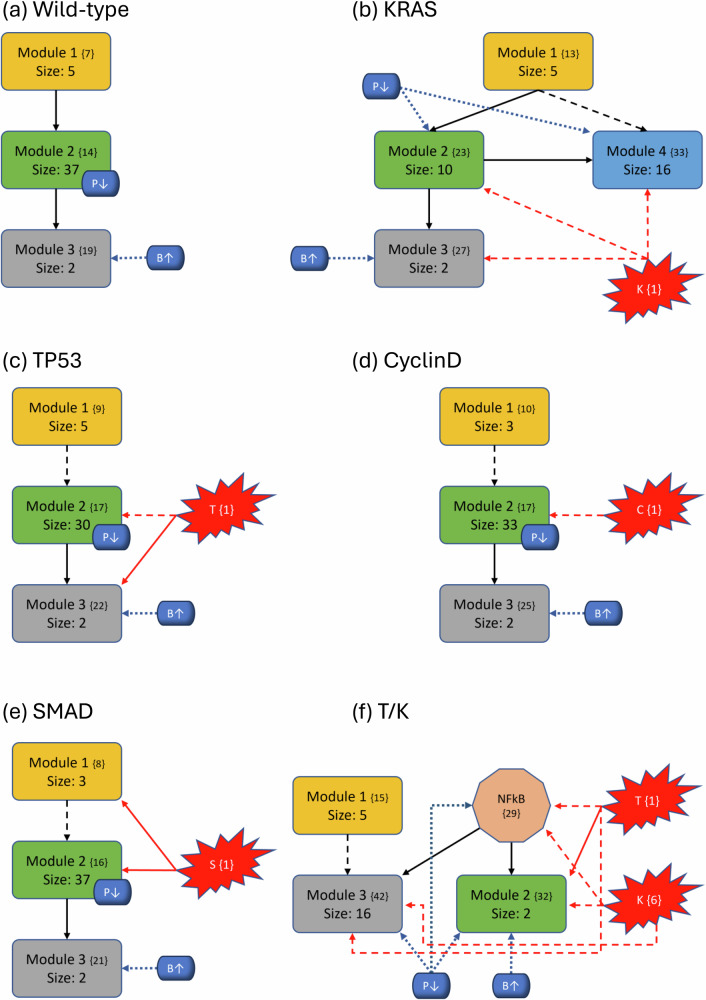
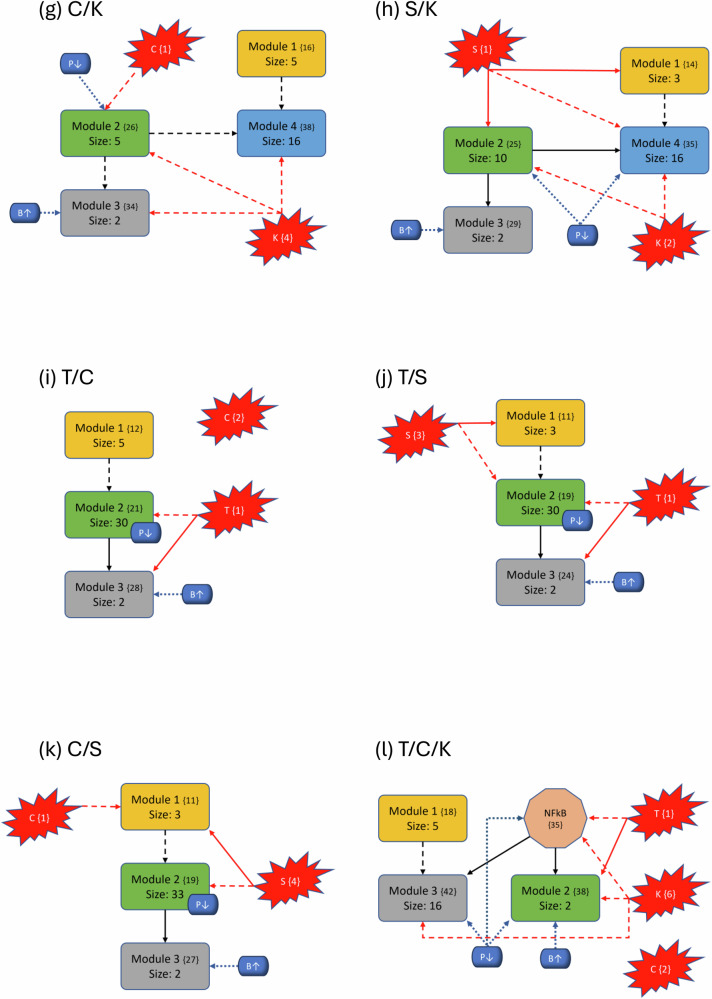
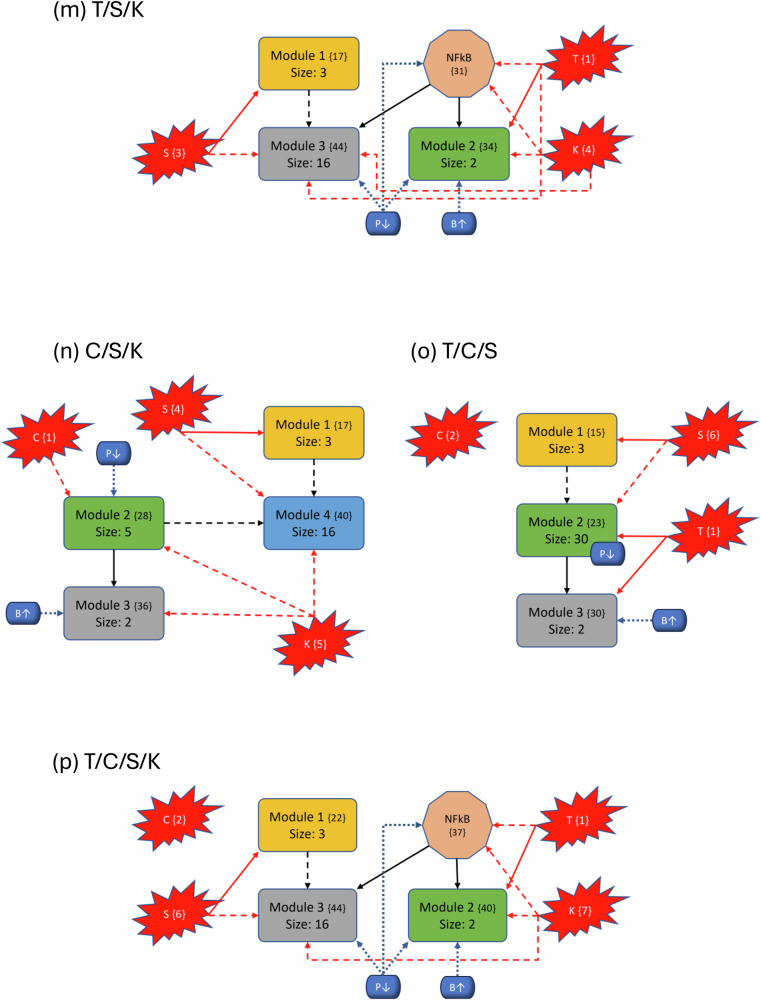
To better understand the impact of mutations on the modular structure, we constructed modules in the same manner as the wild-type after mutations were induced. We give a comprehensive breakdown of module structures for each mutation combination in Fig. 5. For example, to create Fig. 5b, we first produced the corresponding condensation graph (Supplementary Fig. 3) as previously described. We then identified the bins for each SCC and noted direct or indirect communications between each module. Lastly, we identified the location and influence of mutations that are indicated in red with respect to each module. We also included the PIK3 (P↓)/BAX (B↑) targets, indicated in blue with their respective locations and influences, to show the explicit topological impact of the intervention targets. Notably, mutations break SCCs and change the modularity structure both in the magnitude of the modules (total nodes within a module) and amount of modules. More details with tables, graphs, files, and tutorials are available in the Supplementary materials and data repository.
Fig. 5. Variants of PC modular structure.
Mutations are depicted with red “explosions” with their original module (condensation) numbers in brackets. Black arrows indicate communication between modules, red arrows indicate direct influence from mutations and dashed arrows indicate indirect communication. Modules are ranked in order, and curly brackets contain the original numeration from the condensation graph. Lastly, the PIK3 (P↓)/BAX (B↑) targets are shown in blue with respect to their location inside or outside modules to show their downstream modular effects. a–p Show each of the 16 mutation combinations and their respective modular influences.
In general, we maintain the three basic structures shown in Fig. 5a, b, and f. Some cases hold to the same structure as the wild-type, but notably, every instance of KRAS induction yields split modules—sometimes trivial (octagonal shape in Fig. 5f) and other times non-trivial (separate blue node). The former observation of a nontrivial node split arises when KRAS is combined with TP53. We posit that these phenomena are due to the location of KRAS in regard to its “depth” within the largest central module. Notice that Fig. 3 shows SMAD, TP53, and CyclinD are all located distally within their associated modules (Module 1 and all others in Module 2, respectively). Therefore, inducing their mutation merely shrinks the module size. When KRAS is induced, it is located more centrally within its original module and results in a broken component. For example, Fig. 5b shows a gained module that only contains elements from the PSC that have split from their strongly connected PCC counterparts. Additionally, mutations do not always influence modules directly (e.g. Fig. 5c), and there are scenarios where the mutation does not impact any modules at all (e.g. Fig. 5o). Mutations yield anywhere from 28 to 51 modules in total (including trivial nodes), but non-trivial modules remain at either three or four in total (Supplementary Fig. 2).
Modular structure correlates with aggression
The most aggressive scores from Fig. 2 are TP53, T/K, T/S, and T/S/K. The modularity structures for TP53 (Fig. 5c) and T/S (Fig. 5j) are unique in that the TP53 component always directly interacts with the duplex module that is responsible for apoptosis. Further, the structures for T/K (Fig. 5f) and T/S/K (Fig. 5m) are unique because (1) the duplex module is isolated from the standard downstream flow, and (2) the TP53 component influences all three downstream modules (versus only the trivial and duplex modules in T/C/K and T/C/S/K). This added layer of influence is what we believe drives a more aggressive prediction.
Figure 6 indicates the topological ranking for each module across every mutation combination using ‘toposort’. Rankings are calculated according to the module's overall percentile score (e.g. a rank of 5 among 28 total modules yields 18%). Thus, rankings of a higher percentile would indicate a greater impact (or stronger influence) on the final phenotypic state. Figures 7 and 8 show the importance of module rankings and the gaps (distance) between them.
Fig. 6. Toposort analysis.
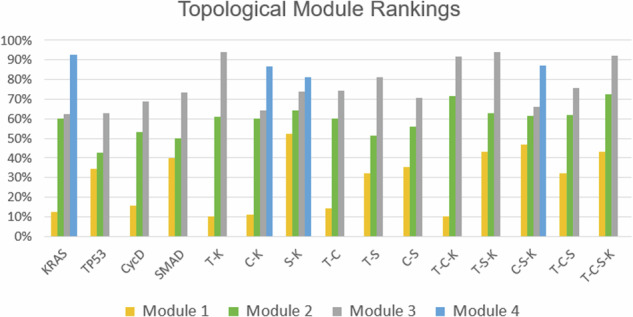
Shown are the overall topological rankings for each module among all mutation combinations. A table version is included in the data repository.
Fig. 7. Normalized toposort gaps between Modules 2 and 3.
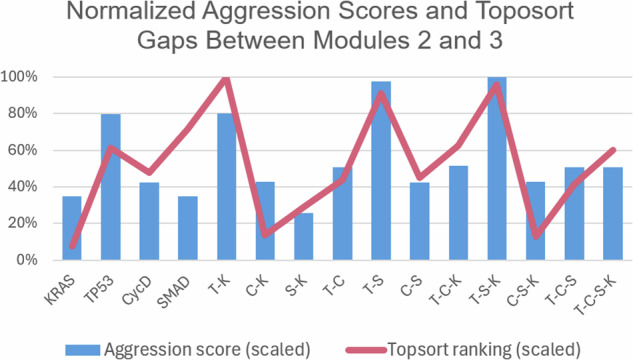
After comparing the toposort rankings and gaps across all modules (Fig. 6), the gaps between Modules 2 and 3 (i.e. the modules communicating to the PCC phenotypes) were identified as the most critical. Here we show a normalized scoring that indicates the largest variance (or distance) between Modules 2 and 3 best aligns with the predicted aggression scores from Fig. 2.
Fig. 8. Errors of normalized toposort gap rankings.
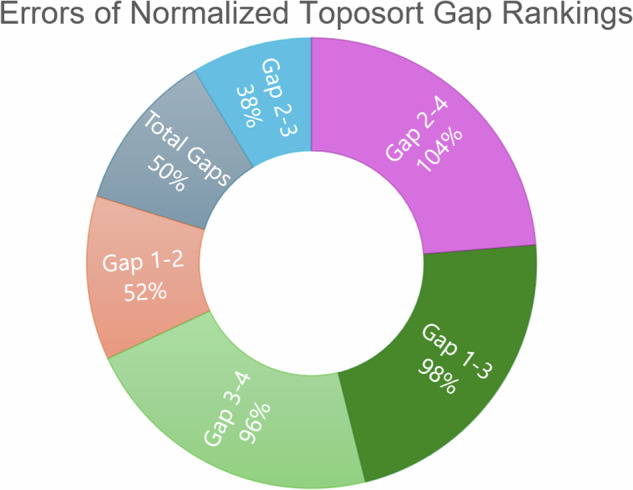
This chart is a comparison of average errors after ranking and normalizing toposort gaps, compared to the normalized aggression scores from Fig. 2. Gaps between Modules 2 and 3 best explain the predicted aggression scores, further shown in Fig. 7.
A compelling correlation is displayed in Fig. 7, which shows the normalized percentage difference between the rankings of Modules 2 and 3, compared to previously predicted aggression scores. We posit that a greater distance between the most influential modules indicates a more difficult system dynamic to overcome when attempting to apply phenotype control theory. This may be attributed to more competing signals to overcome when compared to a small gap between modules. That is, gaps leave more room for noise and therefore, link the topological structure to dynamical outcomes. This is further evidenced by comparing the average errors of all normalized module gaps, shown in Fig. 8, where Gaps 2–3 have the best fit to the aggression data. Indeed, greater gaps between these modules align with more aggressive scores.
Mutations impact target efficacy
In1, target analysis was performed on the wild-type PC model in Fig. 3. For an overview of some of the most prominent control techniques (see ref. 21). Using apoptosis as the desired attractor, one could control the entire system by regulating a total of three nodes within the top two modules. The module with the top hierarchical rank (yellow) is an autocrine loop with two fixed points and two 3-cycles. Therefore, the Feedback Vertex Set31 strategy yielded control of Module 1 by pinning TGFβ1. Next, Module 2 (green) was searched for targets using algebraic methods29 and revealed that pinning KRAS in both the PCC and PSC stabilized the module. The final module (gray) becomes constant after the initial three pinnings. That is, the entire wild-type system was found to be controllable by a single growth factor and systemic KRAS inhibition, both within the first two modules1.
However, KRAS is well-known for being unmanageable even though progress is being made towards its targetability33. Therefore, targeting PIK3 and BAX may be more achievable23,34,35. We showed in Fig. 2 that the single agent controls of PIK3 and BAX are insufficient to achieve PCC apoptosis across all mutation combinations. This is because TP53 directly influences the duplex module responsible for apoptosis signaling (Fig. 5). Since PIK3 is upstream of TP53, it must have helped to circumvent or out-compete the mutation (through help from BAX). Such a combination is effective topologically because PIK3 is heavily involved in communications between multiple modules (either directly inside influential modules or indirect communication to many modules), and BAX can override the deepest mutation signals.
Discussion
Systems biology is continually searching for general principles and tools for their identification. The approach of network modularity adds to the repertoire of techniques that provide structural and dynamic analysis across complex biological systems. We have shown here that the given definition of modules captures the drastic perturbing effect that mutational occurrence can have on normal biological mechanisms. A major limitation of most other approaches to modularity is their focus on a static representation of GRNs. Clearly, living organisms are dynamic and need to be modeled as such1,36. That is precisely what we advocate through the framework established in the section “Network modularity”.
However, it is important to note that the decomposition presented in1 does not preclude the existence of emergent properties. Each module is a complex dynamical system in itself. As we have shown, modules perturb other downstream modules, and their emergent properties propagate to other modules. That is, within each dynamical sub-system (module), the occurrence of mutations will have a direct and downstream effect. Likewise, as the dynamics of upstream modules vary through time, the downstream modules may see an emergence of altered dynamical properties.
What we have provided herein uses a new strategy of network modularity1 to investigate the link between structure and function, using a previously published pancreatic cancer network as a case study. Namely, this link was shown to be strongly related to the variance in topological rankings of the most phenotypically influential modules. We have identified that the location of mutations, with respect to network depth and module positioning, expressly influences aggression and controllability. Thereby, presenting evidence that the impact and location of mutations with respect to modular structure directly correspond to the efficacy of single-agent treatments in silico. These cumulative results help provide more clarity on the impact of mutations in PC and posit the viability of using network modularity to study dynamical systems.
Methods
Network modularity
Systems biology can often build complicated structures from simpler building blocks, even though these simple blocks (i.e. modules) traditionally are not clearly defined. The concept of modularity detailed in1 gives a structural decomposition that induces an analogous decomposition of the dynamics of the network, in the sense that one can recover the dynamics of the entire network by using the dynamics of the modules. First, we note that the wiring diagram of a Boolean network is either strongly connected or is composed of strongly connected components (SCCs). Using this decomposition, we will define a module of a BN as a subnetwork that is itself a BN with external parameters in the subset of variables that specify an SCC (example below). Naturally, this decomposition imposes a hierarchy among the modules that can be used for the purpose of control. In this work, we show one way to rank the modules to study their relevance with respect to the effectiveness and aggressiveness of treatment.
More precisely, for a Boolean network F and a subset of its variables S, we define a subnetwork of F as the restriction of F to S, denoted where for i = 1, ⋯ , m. We note that might contain inputs that are not part of S (e.g., when is regulated by variables that are not in S). Therefore, F∣S is a BN with external parameters. For the Boolean network F with wiring diagram W, let W1, …, Wm be the SCCs of W with variables Si. The modules of F are , and setting Wi ⟶ Wj where there exists a node from Wi to Wj gives a directed acyclic graph C = {(i, j)∣Wi ⟶ Wj}1.
The dynamics of the state-space for Boolean network F are denoted as , which is the collection of attractors. Further, if F is decomposable (say into subnetworks H and G), then we can write F = H ⋊ P G which is called the coupling of H and G by scheme P. In the case where the dynamics of G are dependent on H, we call Gnon-autonomous denoted as . Then we adopt the following notation: let A = A1 ⊕ A2 be an attractor of F with and 1.
Lastly, a set of controls u stabilizes a BN to attractor A if the only remaining attractor after inducing u is A. The decomposition strategy can be used to obtain controls for each module, which can then combine to control the entire system. That is, given a decomposable network F = F1 ⋊ PF2 and an attractor A = A1 ⊕ A2 with and , assume u1 is a control that stabilizes F1 in A1, and u2 is a control that stabilizes in A2. Then u = (u1, u2) is a control that stabilizes F in A given that either A1 or A2 are steady states1.
For an example, consider the network in Fig. 9a, which can be written as
| 1 |
Subnetworks are defined according to the dependencies of variables encoded by the wiring diagram1. For example, the subnetwork is the restriction of F to {x4, x5, x6} with external parameter x1. From the given wiring diagram, we derive two SCCs where Module 1 (red in Fig. 9b) flows into Module 2 (green in Fig. 9b). That is, F = F1 ⋊ F2 with
| 2 |
| 3 |
| 4 |
| 5 |
Suppose we aim to stabilize the system into y = 000000. First we see that either x1 = 0, x2 = 0 or x3 = 0 stabilize Module 1 (i.e. F1) to A1 = 000 by applying the Feedback Vertex Set method30,31. Likewise, x4 = 0, x5 = 0, or x6 = 0 stabilize Module 2 (i.e. ) to A2 = 000. Thus, we conclude that u = (x1 = 0, x6 = 0) achieves the desired result.
Fig. 9. Modularity example.
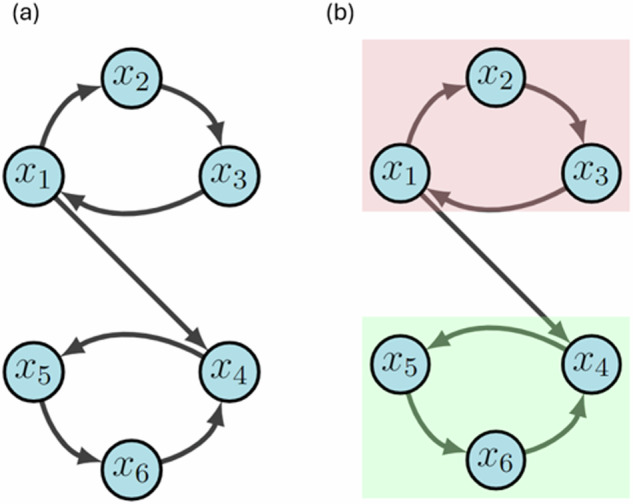
a We show two simple three-cycles connected by an intermediary edge. b The upper and lower modules are highlighted in red and green, respectively.
Topological sorting
To rank the modules of a Boolean network, we first formed the condensation graph C of its wiring diagram W which is obtained by contracting each strongly connected component into a single node (as in the middle panel of Fig. 1). Thus, the condensation graph is a directed, acyclic graph whose nodes represent the modules of the original graph W. To obtain the modules and their components we used the MATLAB37 function ‘condensation’ that returns the condensation graph C. Another MATLAB37 function called ‘conncomp’ bins nodes according to their corresponding strongly connected component. Two nodes belong to the same strong component only if there is a path connecting them in both directions. Condensation determines the nodes and edges in C by the components and connectivity in W such that: C contains a node for each strongly connected component in W, and C contains an edge between node I and node J if there is an edge from any node in component I to any node in component J of W.
We proceeded to then order the modules using the topological ordering of an acyclic graph, which is an ordering of the nodes in the graph such that each node appears before its successors. We use an implementation of the topological sorting algorithm called ‘toposort’ from MATLAB37. The algorithm is based on a depth-first search, where a node is added to the beginning of the list after considering all of its descendants and returns a new order of nodes such that i < j for every edge (ORDER(i), ORDER(j)) in the original graph W. For example, consider a directed graph whose nodes represent the courses one must take in school and whose edges represent dependencies that certain courses must be completed before others. For such a graph, the topological sorting of the graph nodes produces a valid sequence in which the tasks could be performed37. Finally, we ranked the modules based on the percentile scores (i.e., rank module k out of m modules).
Stochastic discrete dynamical systems
Synchronous updating schedules produce deterministic dynamics, where all nodes are updated simultaneously (i.e. in sync). The stochastic discrete dynamical systems (SDDS) framework developed by Murrugarra et al.22 incorporates Markov chain tools to study the long-term dynamics of Boolean networks. By definition, an SDDS on the variables x1, x2, …, xn is a collection of n triples denoted , where for k = 1, …, n,
fk: {0, 1}n → {0, 1} is the update function for xk
is the activation propensity
is the deactivation propensity
Consider the state-space S, consisting of all possible states of the system. If x = (x1, …, xn) ∈ S and y = (y1, …, yn) ∈ S, then the probability of transitioning from x to y is
| 6 |
where
| 7 |
Here we assume that P(xi → yi) = 0 for any yi ∉ {xi, fi(x)}. When propensities are set to p = 1, we have a traditional BN9. With this framework, we built a simulator that takes random initial states as inputs and then tracks the trajectory of each node through time. Long-term phenotype expression probabilities can then be estimated, as well as network dynamics with (and without) controls.
Supplementary information
Acknowledgements
D.P. was supported by the NIH Training Grant T32CA165990. D.M. was partially supported by a Collaboration grant (850896) from the Simons Foundation.
Author contributions
Conceptualization: D. P., Methodology: D. P. and D. M., Software: D. P., Formal analysis: D. P., Supervision: D. M., Writing—original draft: D. P., Writing—review and editing: D. P. and D. M.
Data availability
All data supporting the findings of this study are available within the paper and its supplementary information files on the repository.
Code availability
All code used for running simulations, statistical analysis, and plotting is available on a GitHub repository at https://github.com/drplaugher/PCC_Mutations. The repository also includes “How-To” documentation for reproducibility.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41540-024-00398-6.
References
- 1.Kadelka C, Wheeler M, Veliz-Cuba A, Murrugarra D, Laubenbacher R. Modularity of biological systems: a link between structure and function. J. R. Soc. Interface. 2023;20:20230505. doi: 10.1098/rsif.2023.0505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:47–52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 3.Palma A, Jarrah AS, Tieri P, Cesareni G, Castiglione F. Gene regulatory network modeling of macrophage differentiation corroborates the continuum hypothesis of polarization states. Front. Physiol. 2018;9:1659. doi: 10.3389/fphys.2018.01659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rex J, et al. Model-based characterization of inflammatory gene expression patterns of activated macrophages. PLoS Comput. Biol. 2016;12:e1005018. doi: 10.1371/journal.pcbi.1005018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Castiglione F, Tieri P, Palma A, Jarrah AS. Statistical ensemble of gene regulatory networks of macrophage differentiation. BMC Bioinform. 2016;17:119–128. doi: 10.1186/s12859-016-1363-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bolouri H, et al. Integrative network modeling reveals mechanisms underlying T cell exhaustion. Sci. Rep. 2020;10:1–15. doi: 10.1038/s41598-020-58600-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mendoza L, Xenarios I. A method for the generation of standardized qualitative dynamical systems of regulatory networks. Theor. Biol. Med. Model. 2006;3:1–18. doi: 10.1186/1742-4682-3-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tieri, P., Prana, V., Colombo, T., Santoni, D. & Castiglione, F. Multi-scale simulation of T helper lymphocyte differentiation. In Brazilian Symposium on Bioinformatics 123–134 (Springer, 2014).
- 9.Murrugarra, D. & Aguilar, B. Algebraic and Combinatorial Computational Biology Ch. 5, 149–150 (Academic Press, 2018).
- 10.Choi M, Shi J, Jung SH, Chen X, Cho K-H. Attractor landscape analysis reveals feedback loops in the p53 network that control the cellular response to DNA damage. Sci. Signal. 2012;5:ra83–ra83. doi: 10.1126/scisignal.2003363. [DOI] [PubMed] [Google Scholar]
- 11.Plaugher D, Murrugarra D. Modeling the pancreatic cancer microenvironment in search of control targets. Bull. Math. Biol. 2021;83:115. doi: 10.1007/s11538-021-00937-w. [DOI] [PubMed] [Google Scholar]
- 12.Vundavilli H, et al. In silico design and experimental validation of combination therapy for pancreatic cancer. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018;17:1010–1018. doi: 10.1109/TCBB.2018.2872573. [DOI] [PubMed] [Google Scholar]
- 13.DuCote TJ, et al. EZH2 inhibition promotes tumor immunogenicity in lung squamous cell carcinomas. Cancer Res. Commun. 2024;4:388–403. doi: 10.1158/2767-9764.CRC-23-0399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Aguilar B, et al. A generalizable data-driven multicellular model of pancreatic ductal adenocarcinoma. Gigascience. 2020;9:giaa075. doi: 10.1093/gigascience/giaa075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Padoan A, Plebani M, Basso D. Inflammation and pancreatic cancer: Focus on metabolism, cytokines, and immunity. Int. J. Mol. Sci. 2019;20:676. doi: 10.3390/ijms20030676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kleeff J, et al. Pancreatic cancer microenvironment. Int. J. Cancer. 2007;121:699–705. doi: 10.1002/ijc.22871. [DOI] [PubMed] [Google Scholar]
- 17.Gore J, Korc M. Pancreatic cancer stroma: friend or foe? Cancer cell. 2014;25:711–712. doi: 10.1016/j.ccr.2014.05.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Erkan M, Reiser-Erkan C, Michalski C, Kleeff J. Tumor microenvironment and progression of pancreatic cancer. Exp. Oncol. 2010;32:128–31. [PubMed] [Google Scholar]
- 19.Farrow B, Albo D, Berger DH. The role of the tumor microenvironment in the progression of pancreatic cancer. J. Surg. Res. 2008;149:319–328. doi: 10.1016/j.jss.2007.12.757. [DOI] [PubMed] [Google Scholar]
- 20.Feig C, et al. The pancreas cancer microenvironment. Clin. Cancer Res. 2012;18:4266–4276. doi: 10.1158/1078-0432.CCR-11-3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plaugher D, Murrugarra D. Phenotype control techniques for Boolean gene regulatory networks. Bull. Math. Biol. 2023;85:89. doi: 10.1007/s11538-023-01197-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Murrugarra D, Veliz-Cuba A, Aguilar B, Arat S, Laubenbacher R. Modeling stochasticity and variability in gene regulatory networks. EURASIP J. Bioinform. Syst. Biol. 2012;2012:5. doi: 10.1186/1687-4153-2012-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Plaugher D, Aguilar B, Murrugarra D. Uncovering potential interventions for pancreatic cancer patients via mathematical modeling. J. Theor. Biol. 2022;548:111197. doi: 10.1016/j.jtbi.2022.111197. [DOI] [PubMed] [Google Scholar]
- 24.Siegel RL, Miller KD, Wagle NS, Jemal A. Cancer statistics, 2023. CA Cancer J. Clin. 2023;73:17–48. doi: 10.3322/caac.21763. [DOI] [PubMed] [Google Scholar]
- 25.Bray F, et al. Global cancer statistics 2018: Globocan estimates of incidence and mortality worldwide for 36 cancers in 185 countries: Global cancer statistics 2018. CA Cancer J. Clin. 2018;68:394–424. doi: 10.3322/caac.21492. [DOI] [PubMed] [Google Scholar]
- 26.Pishvaian MJ, et al. Molecular profiling of patients with pancreatic cancer: initial results from the know your tumor initiative. Clin. Cancer Res. 2018;24:5018–5027. doi: 10.1158/1078-0432.CCR-18-0531. [DOI] [PubMed] [Google Scholar]
- 27.Wu C, Yang P-L, Liu B, Tang Y. Is there a cdkn2a-centric network in pancreatic ductal adenocarcinoma? OncoTargets Ther. 2020;13:2551–2562. doi: 10.2147/OTT.S232464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bryant KL, Mancias JD, Kimmelman AC, Der CJ. Kras: feeding pancreatic cancer proliferation. Trends Biochem. Sci. 2014;39:91–100. doi: 10.1016/j.tibs.2013.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vieira LS, Laubenbacher RC, Murrugarra D. Control of intracellular molecular networks using algebraic methods. Bull. Math. Biol. 2020;82:1–22. doi: 10.1007/s11538-019-00679-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mochizuki A, Fiedler B, Kurosawa G, Saito D. Dynamics and control at feedback vertex sets. II: a faithful monitor to determine the diversity of molecular activities in regulatory networks. J. Theor. Biol. 2013;335:130–146. doi: 10.1016/j.jtbi.2013.06.009. [DOI] [PubMed] [Google Scholar]
- 31.Zañudo JGT, Yang G, Albert R. Structure-based control of complex networks with nonlinear dynamics. Proc. Natl Acad. Sci. USA. 2017;114:7234–7239. doi: 10.1073/pnas.1617387114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zañudo JGT, Albert R. Cell fate reprogramming by control of intracellular network dynamics. PLoS Comput. Biol. 2015;11:e1004193. doi: 10.1371/journal.pcbi.1004193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rosenzweig A, et al. Management of patients with pancreatic cancer using the right track model. Oncologist. 2023;28:584–595. doi: 10.1093/oncolo/oyad080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hou P, et al. Tumor microenvironment remodeling enables bypass of oncogenic KRAS dependency in pancreatic cancer. Cancer Discov. 2020;10:1058–1077. doi: 10.1158/2159-8290.CD-19-0597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhao G, et al. Activation of the proapoptotic bcl-2 protein bax by a small molecule induces tumor cell apoptosis. Mol. Cell. Biol. 2014;34:1198–1207. doi: 10.1128/MCB.00996-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jimenez A, Cotterell J, Munteanu A, Sharpe J. A spectrum of modularity in multi-functional gene circuits. Mol. Syst. Biol. 2017;13:925. doi: 10.15252/msb.20167347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.MATLAB Version 9.12.0.2039608 (R2022a) Update 5 (The MathWorks Inc., Natick, MA, 2022).
- 38.Wang, Q. et al. Formal modeling and analysis of pancreatic cancer microenvironment. In Computational Methods in Systems Biology (eds Bartocci, E., Lio, P. & Paoletti, N.) 289–305 (Springer International Publishing, Cham, 2016).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data supporting the findings of this study are available within the paper and its supplementary information files on the repository.
All code used for running simulations, statistical analysis, and plotting is available on a GitHub repository at https://github.com/drplaugher/PCC_Mutations. The repository also includes “How-To” documentation for reproducibility.