Abstract
The recent SarsCov2 pandemic has disrupted healthcare system notably impacting intensive care units (ICU). In severe cases, the immune system is dysregulated, associating signs of hyperinflammation and immunosuppression. In the present work, we investigated, using a joint modeling approach, whether the trajectories of cellular immunological parameters were associated with survival of COVID‐19 ICU patients. This study is based on the REA‐IMMUNO‐COVID cohort including 538 COVID‐19 patients admitted to ICU between March 2020 and May 2022. Measurements of monocyte HLA‐DR expression (mHLA‐DR), counts of neutrophils, of total lymphocytes, and of CD4+ and CD8+ subsets were performed five times during the first month after ICU admission. Univariate joint models combining survival at day 28 (D28), hospital discharge and longitudinal analysis of those biomarkers’ kinetics with mixed‐effects models were performed prior to the building of a multivariate joint model. We showed that a higher mHLA‐DR value was associated with a lower risk of death. Predicted mHLA‐DR nadir cutoff value that maximized the Youden index was 5414 Ab/C and led to an AUC = 0.70 confidence interval (95%CI) = [0.65; 0.75] regarding association with D28 mortality while dynamic predictions using mHLA‐DR kinetics until D7, D12 and D20 showed AUCs of 0.82 [0.77; 0.87], 0.81 [0.75; 0.87] and 0.84 [0.75; 0.93]. Therefore, the final joint model provided adequate discrimination performances at D28 after collection of biomarker samples until D7, which improved as more samples were collected. After severe COVID‐19, decreased mHLA‐DR expression is associated with a greater risk of death at D28 independently of usual clinical confounders.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
In critically ill COVID‐19 patients, the initial response to SARS‐CoV‐2 infection is characterized by major immune dysfunctions similar to those in septic patients with bacterial infections. However, the exploration of the immune trajectories of these critically ill patients during their stay in intensive care units (ICU) and their relationship with survival has not been performed yet.
WHAT QUESTION DID THIS STUDY ADDRESS?
The present work aims to investigate, using a joint nonlinear modeling approach, whether the trajectories of cellular immunological parameters were associated with the survival in 538 patients included in the REA‐IMMUNO‐COVID (RICO) cohort from five ICU from Lyon academic hospitals.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
An exhaustive analysis of baseline covariates and immune biomarkers was performed where monocyte HLA‐DR emerged as the most interesting in terms of its association with 28‐day mortality.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
In routine care, a value of monocyte HLA‐DR below 5500 AB/C could be considered as an alarming sign, requiring a reconsideration of the patient's management.
INTRODUCTION
The appearance of severe acute respiratory coronavirus‐2 (SARS‐CoV‐2) has led to a rapidly spreading pandemic. Since the first cases of coronavirus disease‐19 (COVID‐19), more than 675 million cases and about 7 million deaths have been reported worldwide (by February 2023—Johns Hopkins University). Moreover, many intensive care units (ICUs) were overwhelmed due to an insufficient number of beds at the time of the outbreak peak. The local capacity to manage ICU beds availability in a given area was revealed of utmost importance. 1 , 2
In critically ill COVID‐19 patients, the initial response to SARS‐CoV‐2 infection is characterized by major immune dysfunctions associating a systemic inflammatory response and the development of altered innate and adaptive immune responses similar to those in septic patients with bacterial infections. 3 On myeloid side, elevation of the proportion of immature neutrophils and decreased HLA‐DR expression on monocytes (mHLA‐DR) have been reported, while adaptive immune response was markedly affected since severe lymphopenia, phenotypic, and functional T‐cell alterations have been associated with patients worsening.
The aim of the present work was thus to investigate, using a joint modeling approach, whether the kinetics (trajectories) of cellular immunological parameters were associated with the survival of COVID‐19 ICU patients. 4 Here, using a joint modeling approach prevents making the hypothesis that the marker does not change between measurements and neglecting measurement errors. Further, Latouche et al. in, 5 and Rizopoulos et al. in 6 have shown joint models should be used to handle endogenous time‐varying covariate. Indeed, modeling simultaneously the survival and the kinetics of biomarkers 4 , 7 with shared random effects is important to get precise and unbiased estimates of longitudinal and survival parameters, and thus enables to precisely characterize the association between these processes. 8 , 9 , 10 This approach also provides dynamic individual predictions, 11 accounting not only for the baseline information but also for the longitudinal data available until a certain time point, that is, until a given landmark time. For this purpose, we took advantage of the REA‐IMMUNO‐COVID (RICO) cohort that included more than 500 COVID‐19 ICU patients for which cellular immunological parameters were repeatedly monitored during 3 weeks after ICU admission. Figure 1 summarizes schematically the data at hand, the modeling strategy, and the model evaluation we performed.
FIGURE 1.
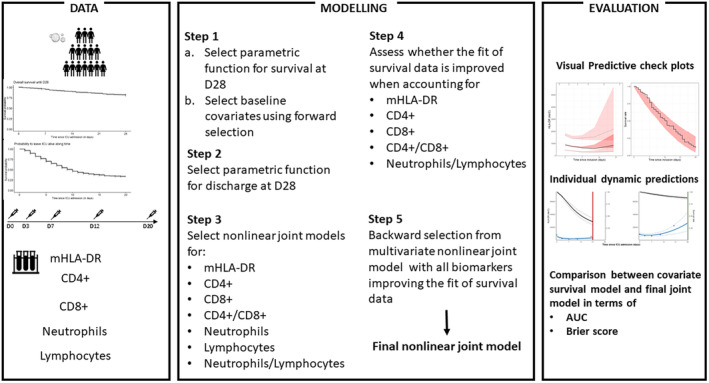
Scheme of the data used in this analysis, the modeling steps and evaluation procedures.
METHODS
Clinical study design, patient population, and approval
Between March 2020 and May 2022, critically ill patients admitted to five ICUs from Lyon academic hospitals (Hospices Civils de Lyon, Lyon, France) who presented with pulmonary infection with SARS‐CoV‐2 were prospectively included in RICO clinical study. Preliminary results from subgroups of the cohort were published previously. 12 , 13 , 14 , 15 , 16 This study was approved by an ethics committee (Comité de Protection des Personnes Ile de France 1 – N°IRB/IORG #: IORG0009918) under agreement number 2020‐A01079‐30. This clinical study was registered at ClinicalTrials.gov (NCT04392401). More details can be found in Section S1.1.
Patient characteristics
For each patient, demographics, comorbidities, time from onset of COVID‐19 symptoms to ICU admission, initial presentation of the disease in the ICU including the ratio of the arterial partial pressure of oxygen to the fractional inspired oxygen (PaO2/FiO2 ratio) at admission and organ supports were documented. Organ dysfunctions according to Sequential Organ Failure Assessment (SOFA) Score (range 0–24, with higher scores indicating more severe organ failures), and Simplified Acute Physiology Score II (SAPS II; range, 0–164, with higher scores indicating greater severity of illness) were documented on patients' admission in the ICU. Presence of acute respiratory distress syndrome (ARDS) was based on the Berlin criteria for ARDS. 17 Follow‐up included ICU length of stay, in‐hospital mortality, day‐28 (D28) mortality, day‐90 (D90) mortality, as well as occurrence of a secondary infection. Occurrence of secondary nosocomial infection was defined based on recommendation from “Comité technique des infections nosocomiales et des infections liées aux soins”. 18
Blood samples
Ethylenediaminetetraacetic acid (EDTA‐) anticoagulated blood was drawn five times during the first month after ICU admission: within the first 48 h after admission (Day 0: D0), between 72 h and 96 h after admission (D3), between D7 and D9 (D7), between D12 and D15 (D12), between D20 and D25 (D20). Blood was stored at 4–8°C and processed within 4 h after withdrawal.
Statistical analyses
As defined in the clinical protocol, primary study end point was patients' status (alive or deceased) 28 days after ICU admission. To model the survival and longitudinal data, submodels for each aspect were first defined separately before being modeled simultaneously. Another submodel was defined to consider the attrition phenomenon: the discharge from ICU submodel. Indeed, biomarker data were not collected in patients discharged from the ICU between D3 and D20.
Survival covariate model
Survival at D28 was modeled using a parametric proportional hazard model. Let be the survival time between inclusion and death, and be the censoring time between inclusion and the date of lost to follow‐up, here up to 28 days. The time‐to‐event was defined as the minimum between and . The D28 vital status indicator was either 1 if the patient died before D28 or 0 if the patient was censored (i.e., lost‐to‐follow‐up or still alive) at D28. Survival at D28 was modeled using a parametric proportional hazard model:
| (1) |
with the instantaneous probability of death at time t, the survival baseline hazard function, and the vector of regression coefficients associated with the baseline covariate vector . was selected among seven functions (Section S1.3.1).
Then, a forward covariate selection based on the Bayesian Information Criteria (BIC) was performed considering the following baseline patient characteristics: age, gender, body mass index (BMI), admission SOFA score, 19 admission Charlson index, 20 time elapsed between the first symptoms and ICU admission, presence of invasive or noninvasive mechanical ventilation before the third ICU day, and COVID wave based on the date of diagnostic or hospital admission (wave 1: from March 2020 to July 5th 2020, wave 2: from July 6th 2020 to January 3rd, 2021, wave 3: from January 4th 2021 to July 4th 2021 and wave 4: after July 5th 2021). These covariates were derived from a review of the existing literature, curated to capture the essential factors that have been consistently associated with survival in hospitalized patients presenting pulmonary infection with SARS‐CoV‐2. 21
Discharge model
The discharge model was defined and built in the same manner as the survival model. However, the censoring time was the time between inclusion and death, and was the discharge time. This allows to define the time to discharge and the D28 discharge indicator, respectively, as follows: and . The parametric proportional hazard function () has been selected among the same functions as for the survival baseline hazard function.
Univariate joint models
The biomarkers under study (i.e. mHLA‐DR, CD4+ and CD8+ lymphocyte counts, total neutrophil and lymphocyte counts) were first log‐transformed to ensure numerical stability and were then modeled using linear or nonlinear structural functions and shared random effects with the D28 survival covariate model described above. 22 , 23 , 24
Formally, denotes the biomarker measurement of subject at a given time , and the model was defined by the following equation:
| (2) |
where is the vector of individual parameters depending on fixed and random effects , with the variance–covariance matrix with diagonal elements ( the number of structural model parameters). is the residual error at time for subject i, and is the residual error variance model, selected among the following: constant: , proportional: and combined: .
The instantaneous risk of death was thus:
| (3) |
And the instantaneous chance of discharge was:
| (4) |
where represent the baseline hazard function for the discharge submodel. and were the link functions for survival and discharge submodels, respectively, that is, either the current value or the slope of the biomarker, and and were the link parameters associated to the link functions and , respectively.
We explored 9 mathematical functions to describe biomarkers' kinetics, based on visual inspection of the data on their natural scale (6 and 3 functions corresponding to convex and concave trajectories respectively, cf. Section S1.3.2). To best capture the link between the biomarker and the survival, we considered the following metrics: the current value or the slope of mHLA‐DR, CD4+ and CD8+ lymphocyte counts, CD4+/CD8+ ratio and neutrophil‐to‐lymphocyte ratio (NLR). Indeed, we modeled the biological entities and we explored the link with survival using metrics derived from these entities which clinicians use in clinical routine. Second, we explored whether it is the biomarker value at a given time that influenced the instantaneous risk or its change over a short period of time.
The best combination of mathematical function for the longitudinal data and link function within the survival covariate model was selected based on BIC, 25 ensuring relative standard errors (RSE) below 50%.
We also accounted for the attrition in the longitudinal data by using another joint model linking longitudinal data to the ICU discharge with, for a given model, the same link function as for the survival data.
Multivariate joint model
First, a screening of all biomarkers was performed by comparing the BIC of each biomarker univariate joint model when estimating the link coefficient effect (existence of a biomarker–survival association) versus fixing that coefficient to 0 (absence of a biomarker–survival association). Then, after inclusion in a multivariate joint model of all the remaining biomarkers, a backward selection was performed based on BIC, using two points decrease in BIC as stopping rule. 26
Evaluation
In order to assess the goodness‐of‐fit of the selected models to the data, visual predictive checks (VPC) plots were used. 27 Goodness‐of‐fit plots compare percentiles derived from 500 datasets simulated with the model to percentiles derived from the observed data. Using both the discharge and survival model made sure unrealistic trajectories were not simulated.
Using the survival covariate and the final joint model of survival and biomarker kinetic data, dynamic predictions were derived 28 at pre‐specified clinically relevant landmark times: D7, D12, and D20. These dynamic predictions were used to derive time‐dependent area under the receiver operating characteristic (ROC) curve (), corresponding to a cumulative sensitivity (or recall) and a dynamic specificity, for the prediction of D28 mortality. 29 , 30 , 31
The AUCs of the survival covariate model and the final joint model and the associated 95% confidence intervals (95% CI) were compared, for each landmark times, and at D28. 32 The discrimination and calibration of the survival covariate model and the final joint model were also evaluated with dynamic predictions‐derived Brier Scores (BS) 29 , 31 (cf. Section S1.4) which enable to quantify the error between the observations and the predictions: the smallest the , the smallest the error. This score was initially used to quantify the precision of meteorologic predictions. The scaled Brier Score (sBS) was also computed to assess the improvement, in terms of discrimination and calibration, of the final joint model over the covariate survival model.
Using the observed nadir and the final joint model predicted nadir for all patients, ROC curves at horizon D28 were plotted and cutoff values were derived according to the maximization of the Youden Index.
Softwares
Data management, VPCs (vpc package) 33 and time‐dependent AUCs (timeROC package) 30 , 34 were performed using R version 4.1.3 and data modeling was performed using Monolix 2018R2. 35
Ethics statement
This project was part of an ongoing prospective observational clinical study (RICO, REA‐IMMUNO‐COVID). It was approved by ethics committee (Comité de Protection des Personnes Ile de France 1 – N°IRB/IORG #: IORG0009918) under agreement number 2020‐A01079‐30. This clinical study was registered at ClinicalTrials.gov (NCT04392401).
RESULTS
Patients' characteristics
A total of 538 patients were included in the cohort, 383 (71%) were males. The baseline clinical characteristics are summarized in Table 1. Briefly, median [interquartile range (IQR)] age at admission was 65 [56;72] years old and median BMI was 29 [26;33] kg/m2. The median [IQR] Charlson Index and SOFA score were 2 [1;3] and 3 [1;5], respectively. The median [IQR] time between first symptoms and ICU admission was 9 [6;11] days. Thirty‐two percent of patients were on mechanical ventilation before the 3rd day of their ICU stay and 47% developed an ARDS during their ICU stay. Twelve percent of the patients were part of the first COVID wave, 35% of the 2nd, 32% of the 3rd and 21% of the 4th.
TABLE 1.
Baseline characteristics of the 538 patients included depending on their vital status at D28. The median and interquartile range is given for continuous covariates, and the percentage is given for categorical covariates.
| Alive, N = 425 | Dead, N = 94 | Censored, N = 19 | Overall population, N = 538 | Missing | |
|---|---|---|---|---|---|
| Continuous covariates – Median [Q1;Q3] | |||||
| Age (years) | 64 [54;70] | 71 [64;78] | 72 [57;74] | 65 [56;72] | 0 |
| Weight (kg) | 85 [74;97] | 80 [70;91] | 80 [68;90] | 84 [73;96] | 1 |
| Height (cm) | 170 [165;176] | 170 [164;174] | 168 [160;177] | 170 [164;176] | 6 |
| BMI (kg/m2) | 29 [26;33] | 28 [25;31] | 28 [27;33] | 29 [26;33] | 6 |
| Charlson index | 2 [1;2] | 3 [1;4] | 1 [1;2] | 2 [1;3] | 0 |
| Time between first symptoms and ICU admission (days) | 9 [7;11] | 7 [4;9] | 10 [3;11] | 9 [6;11] | 10 |
| Length of hospital stay (days) | 19 [11;41] | 14 [8;21] | 10 [8;16] | 18 [11;34] | 5 |
| Length of ICU stay (days) | 8 [4;21] | 12 [7;19] | 7 [3;10] | 9 [5;20] | 1 |
| SOFA score | 2 [1;4] | 4 [2;7] | 1 [0;4.5] | 3 [1;5] | 0 |
| SAPSII score | 30 [22;37] | 38 [30;47] | 30 [22;44] | 31 [24;40] | 0 |
| Glasgow coma scale | 15 [15;15] | 15 [15;15] | 15 [14.5;15] | 15 [15;15] | 1 |
| Categorical covariates – n (%) | |||||
| Male gender | 298 (70) | 75 (80) | 19 (53) | 383 (71) | 0 |
| Mechanical ventilation before 3rd day in ICU | 122 (29) | 45 (48) | 6 (32) | 173 (32) | 0 |
| Mac Cabe index | 209 | ||||
| Stage 1 a | 1 (0.4) | 3 (5.3) | 0 (0) | 4 (1) | |
| Stage 2 b | 20 (7.6) | 10 (18) | 2 (25) | 32 (10) | |
| Stage 3 c | 243 (92) | 44 (77) | 6 (75) | 293 (89) | |
| Preexisting immunological disease | 32 (7.5) | 17 (18) | 0 (0) | 49 (9) | 0 |
| Treatment by ARA II d | 59 (14) | 15 (16) | 2 (11) | 76 (14) | 0 |
| Origin | 0 | ||||
| Exterior | 260 (61) | 60 (64) | 12 (63) | 332 (62) | |
| COVID unit | 75 (18) | 8 (9) | 1 (5) | 84 (16) | |
| Hospital e | 76 (18) | 24 (26) | 6 (32) | 106 (20) | |
| Other | 14 (3) | 2 (2) | 0 (0) | 16 (3) | |
| ARDS f | 165 (41) | 69 (78) | 8 (42) | 242 (47) | 26 |
| Nosocomial infections | 117 (32) | 45 (57) | 5 (26) | 167 (36) | 79 |
| Vital status at day 90 | |||||
| Alive | 353 (93) | 0 (0) | 0 (0) | 353 (74) | 64 |
| Dead | 27 (7) | 94 (100) | 0 (0) | 121 (26) | |
| COVID wave g | 0 | ||||
| 1 | 51 (12) | 16 (17) | 0 (0) | 67 (12) | |
| 2 | 142 (33) | 36 (38) | 8 (42) | 186 (35) | |
| 3 | 142 (33) | 21 (22) | 9 (47) | 172 (32) | |
| 4 | 90 (21) | 21 (22) | 2 (11) | 113 (21) | |
Disease deadly within a year.
Life threatening disease at 5 years.
No threatening disease.
Angiotensin II Receptor Antagonist.
Except COVID unit.
Acute Respiratory Distress Syndrome.
COVID wave: 1: from March 2020 to July 5th 2020. 2: from July 6th 2020 to January 3rd 2021. 3: from January 4th 2021 to July 4th 2021. 4: after July 5th 2021.
Twenty‐eight days after admission, 94 (17%) patients had died (Figure 2) and 86 (16%) remained hospitalized in the ICU. The vital status at D28 was unknown for 19 (4%) patients and their outcome was consequently censored at the date of ICU discharge.
FIGURE 2.
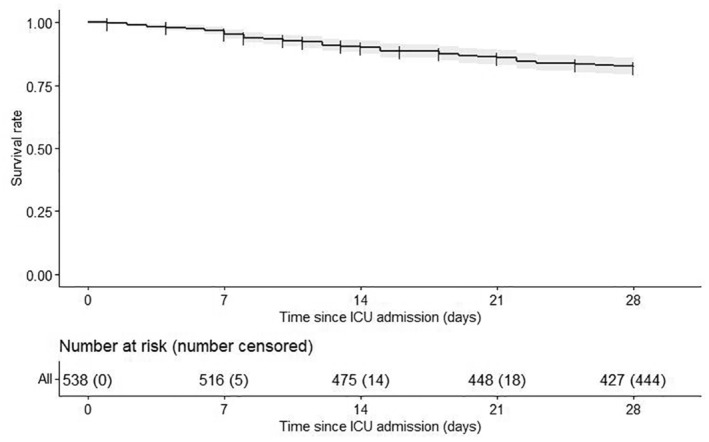
Kaplan–Meier of the overall survival until Day 28 (D28). The gray area around the survival curve represents the associated 95% confidence interval (95% CI). The numbers of patients at risk and the cumulative numbers of censored patients along time are displayed under the plot.
Ninety days after admission, 121 (22%) patients had died out of which 120 (99%) had died in the hospital. Nosocomial infections occurred for 167 (31%) patients.
Predictors of survival
Selection of clinical variables
Based on BIC, the survival curve was best described using an exponential baseline hazard function (Model selection steps detailed in Section S2.1; Table S1 and VPC in Figure S1). The selected model estimated the median length of survival at 401 days. Being older than 65 years old, having a higher Charlson Index and the presence of mechanical ventilation before the 3rd day of ICU were found as risk factors for death (Covariate selection detailed in Section S2.1; Tables S2–S6).
Selection of biomarkers
As shown in Figure 3, mHLA‐DR individual profiles exhibited a convex‐shaped kinetics. We selected the Stein‐Fojo model and the model predicted mHLA‐DR value at a given time rather than its slope as a link function in the survival model as it corresponded to the lowest BIC also ensuring RSE below 50% for all parameters (Section S2.2; Tables S7, S8; Figure S2).
FIGURE 3.
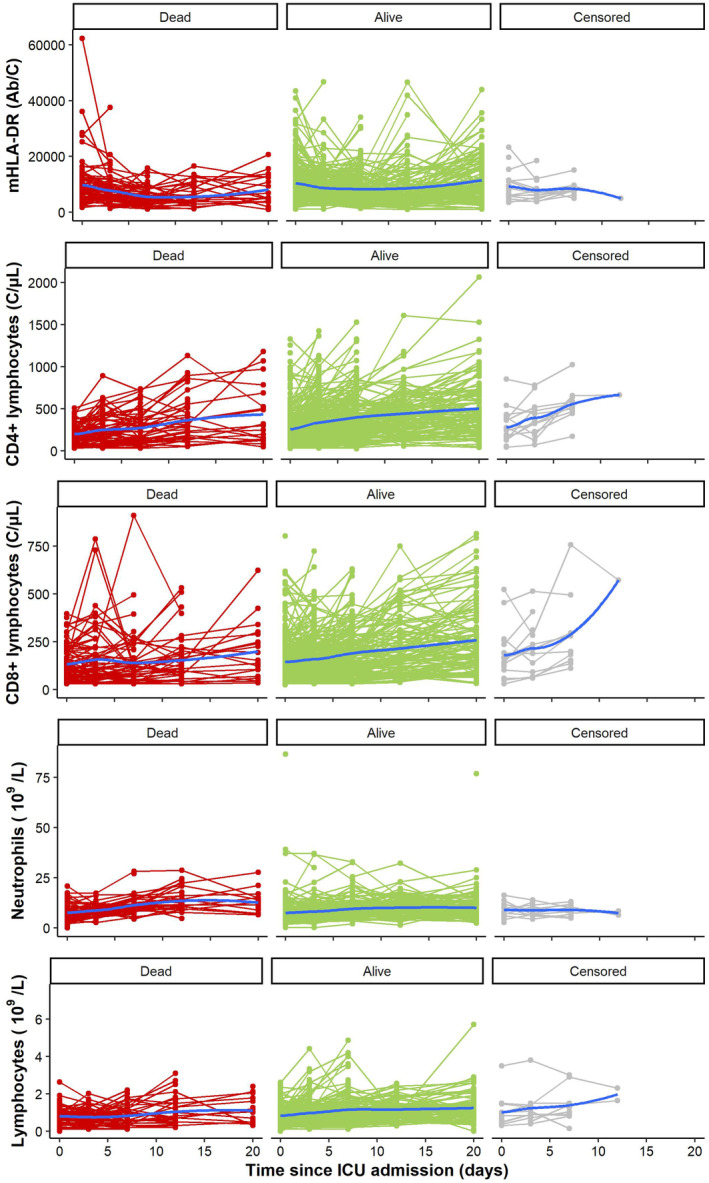
Spaghetti plots of mHLA‐DR, CD4+ lymphocytes, CD8+ lymphocytes, Neutrophils and lymphocytes according to vital status at Day 28 (D28). The blue curve represents the smoothed conditional mean at each time.
The individual profiles of all other immune parameters under study (i.e., absolute count of total lymphocytes, T CD4+ lymphocytes, T CD8+ lymphocytes and neutrophils) had concave‐shaped kinetics (Figure 3). A linear regression best characterized the CD4+ lymphocyte kinetics with the predicted CD4+ count at a given time as a link function in the survival model (Section S2.3; Tables S9, S10; Figure S3). The CD8+ lymphocyte kinetics (Section S2.4; Tables S11, S12; Figure S4) was also best described by a linear regression but with the model instantaneous slope as a link function in the survival model.
Once the structural model for both entities was selected accounting for patient survival, we derived CD4+ /CD8+ ratio and found the best link function of this metric with the survival was the instantaneous slope (Section S2.5; Tables S13, S14; Figure S5). The neutrophils kinetics was best described using a Bateman model with the biomarker value at a given time as link function (Section S2.6; Tables S15, S16; Figure S6) and the lymphocyte kinetics using a linear regression with the slope as link function (Section S2.7; Tables S17, S18; Figure S7). Here as well we used the models selected for both entities to derive NLR and explore the best link with survival, which happened to be the current value (Section S2.8; Tables S19, S20; Figure S8).
Only the univariate joint model with the mHLA‐DR level at a given time obtained a better BIC than fitting the longitudinal and survival data separately (Table 2).
TABLE 2.
Bayesian information criterion (BIC) of the selected univariate joint model for each biomarker and those same models with no link between the different biomarkers and survival. The lowest BIC is indicated in bold.
| Biomarker | Structural model | Link function | Association () | No association ( |
|---|---|---|---|---|
| HLA‐DR | Stein Fojo | Current value | 6273 | 6280 |
| CD4+ lymphocytes | Linear regression | Current value | 6659 | 6657 |
| CD8+ lymphocytes | Linear regression | Slope | 6470 | 6465 |
| CD4+/CD8+ | Slope | 41,729 | 41,724 | |
| Neutrophils | Bateman | Current value | ||
| Lymphocytes | Linear regression | Slope | ||
| Neutrophils/Lymphocytes | Current value | 12,499 | 12,497 |
Note: The instantaneous risk of death is modeled as with the median length of survival, the link function of the structural longitudinal model and the association coefficient between the longitudinal and the survival parts of the model.
Final joint model including mHLA‐DR instant value and selected clinical variables
We observed that a higher mHLA‐DR value was associated with a lower risk of death at D28 independently of selected clinical variables whose hazard ratios and confidence intervals were respectively of 1.079 [1.077;1.080], 1.349 [1.342;1.356], and 2.243 [2.196;2.292] for the age, Charlson Index and presence of mechanical ventilation before the 3rd day of ICU (all model parameters estimates, standard errors, and hazard ratios can be found in Section S2.2; Table S8).
A log‐logistic baseline hazard function was selected for the discharge, enabling to account for the longitudinal data attrition in the VPCs (Section S2.9; Tables S21, S22; Figure S9).
Finally, the observed mHLA‐DR nadir cutoff value that maximized the Youden index was 5107 Ab/C for prediction of mortality at D28 which led to an AUC [95% CI] of 0.65 [0.60;0.71], a sensitivity of 0.68 and a specificity of 0.63, whereas, using the final joint model predictions, the mHLA‐DR nadir cutoff value that maximized the Youden index was 5414 Ab/C and led to an AUC of 0.70 [0.65;0.75], a sensitivity of 0.76 and a specificity of 0.64.
Dynamic predictions of D28 mortality
Dynamic predictions of death at D28 computed with the final joint model had an adequate discrimination at landmark days 7, 12, and 20 post‐admission, with AUCs [95% CI] of 0.82 [0.77;0.87], 0.81 [0.75;0.87], and 0.84 [0.75;0.93], respectively. The latter were systematically greater than those obtained with the survival covariate model only (Table 3).
TABLE 3.
Area under the receiver operating characteristic (ROC) curve (AUC) and its confidence interval at 95% for the prediction of D28‐mortality using the HLA‐DR and survival data available at landmark time day 7, 12, and 20 up to horizon time day 28 for the survival model with baseline covariate only and the final joint model.
| Landmark | |||
|---|---|---|---|
| Day 7 | Day 12 | Day 20 | |
| Survival model | 0.80 [0.75;0.86] | 0.79 [0.72;0.86] | 0.79 [0.68;0.90] |
| Final joint model | 0.82 [0.77;0.87] | 0.81 [0.75;0.87] | 0.84 [0.75;0.93] |
In the same manner, the BS of the final joint model were systematically lower compared with those of the survival covariates model, highlighting the better calibration and discrimination abilities of the joint modeling approach (Section S2.10; Tables S23–S25).
Figure 4 shows the individual predictions from the final joint model in terms of mHLA‐DR evolution and survival rate compared with their outcome for six patients with different numbers of mHLA‐DR observations. Early steep decreasing mHLA‐DR kinetic profiles on the left led to rapidly decreasing predicted survival rates and death, whereas flat or rapidly increasing mHLA‐DR kinetic profiles on the right led to flat survival rates and survival at D28. Also, the prediction intervals decreased with the number of samples and increased with time since the last sample.
FIGURE 4.
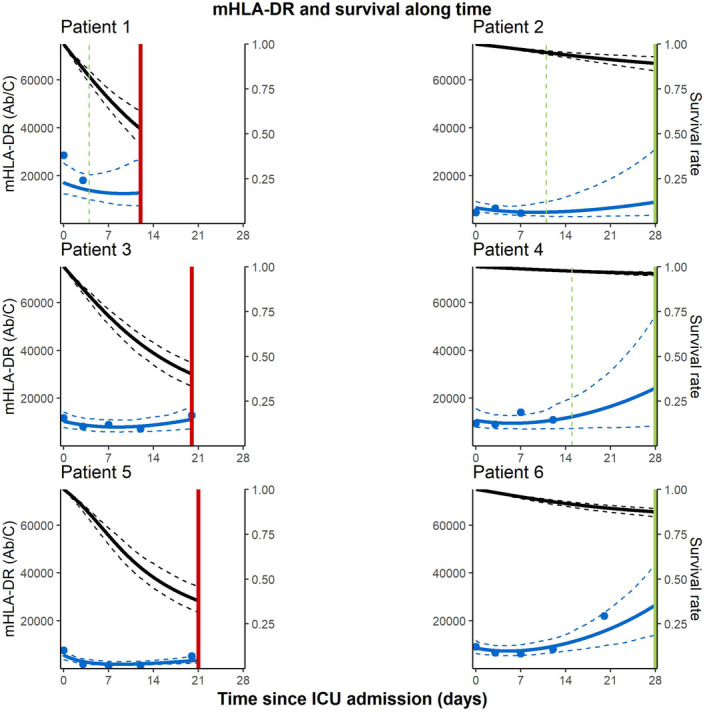
Individual fits of mHLA‐DR kinetics and survival rate for six patients. Solid vertical lines indicate the D28 vital status: green if the patient is still alive and red in case of death with the discharge time represented by dashed green vertical lines. The blue dots are observed levels of mHLA‐DR, the solid and dashed blue curves are the 2.5th, 50th, and 97.5th percentiles of model predicted mHLA‐DR levels and the solid and dashed black curves are the estimated 2.5th, 50th, and 97.5th percentiles of individual model predicted survival rates. Patients were selected to represent profiles with data up until D7, D12, and D20 each and for both survival status.
DISCUSSION
In the current work, we present a joint model quantifying the association between mHLA‐DR expression trajectory and the risk of death in critically ill COVID‐19 ICU patients.
The immune response in severe COVID‐19 is a complex and multifaceted process involving various components of the immune system. Severe COVID‐19 cases often exhibit lymphopenia, and dysfunction and exhaustion of T cells. This impairs the ability to clear the virus and compromises immune surveillance. 3 Decreased mHLA‐DR has also been reported. 36 Collectively, the interplay between dysregulated immune responses, excessive inflammation, lymphocyte dysfunction, and immunosuppression contributes to the complexity and severity of the immune response in severe COVID‐19 patients.
Beyond the use of biomarkers at a specific time point, the evaluation of immune parameters kinetics is also very important. The temporal immuno‐inflammatory trajectories of patients have been shown to be crucial in sepsis, where they help define patient's endotypes and enrich patient's groups with individuals most likely to respond to a given treatment. 37 , 38 , 39 , 40 , 41 It is necessary to apply holistic approaches including both patients' characteristics (e.g., age, comorbidities, initial severity) and the adjustment of risk over the course of days based on the evolution of relevant biomarkers. To this end, joint models are well appropriate as they enable the monitoring of multiple parameters over an extended period, facilitating early detection of changes and adaptation of treatment strategies.
To the best of our knowledge, the use of joint models has not been reported regarding immune parameters in severe COVID‐19 patients. As a first approach, we utilized data from the RICO study, 16 which monitored several cellular parameters over a period of 3 weeks in 538 COVID‐19 patients hospitalized in the ICU during the pandemic. mHLA‐DR emerged as interesting in terms of its association with 28‐day mortality. Decreased mHLA‐DR expression has been described on circulating monocytes from patients infected with SARS‐CoV‐2 both in lung and circulating cells in association with increasing severity. 42 While persistent decrease in mHLA‐DR has been repeatedly associated with increased risk of death and higher risk of secondary infections in patients with bacterial sepsis, no robust data were available so far in critically ill patients with COVID‐19. Consequently, our subsequent focus was on this particular marker.
The most important finding of this study is that, indeed, the analysis of mHLA‐DR expression or its kinetics over time using a joint model provided added value compared with the survival covariate model alone in terms of discrimination. Considering the evolution of mHLA‐DR levels up to day 7, day 12, or day 20 after ICU admission enables the prediction of vital status at day 28. Here, the joint model was not expected to subsequently shorten the time to assess the treatment effect as can be seen in cancer. But these specific landmark times are particularly relevant for COVID‐19 patients who tend to have prolonged ICU stays. Moreover, they align well with the recommended 10‐day dexamethasone treatment duration. 43 , 44 At the end of this treatment period, therapeutic decisions may differ, including discontinuation of dexamethasone or consideration of immunostimulation strategies. 45 , 46 , 47
Another notable result emerges from the current study. In addition to mHLA‐DR trajectories, the nadir (lowest point) during the entire monitoring period also appears to be of interest to predict D28 mortality. Therefore, in routine care, a value below 5500 AB/C could be considered as an alarming sign, requiring a reconsideration of the patient's management. However, it should be noted that the predictive performance of the joint model is superior to that of the nadir alone.
Our study has certain limitations due to its exploratory nature. The first limitation is related to the relatively low number of measurements per patient, averaging about 2.5 measurements. This limited number of measurements made it challenging to fit complex longitudinal models with multiple parameters. Another limitation, associated with the first one, is that the large 95% confidence intervals in modeling resulted in the lack of statistical significance in terms of the discrimination gain of the joint model compared with the survival model with baseline covariates only. However, the gain in discrimination was consistent and increased as the landmark times moved further from admission, indicating potential clinical relevance. Lastly, due to missing information, we were unable to incorporate certain parameters that could contribute to immune trajectories and patients' recovery, such as viral load, soluble markers, and treatment regimens. These factors should be considered and included in the design of future studies. Also, other inflammatory response biomarkers such as C‐reactive protein, tumor necrosis factors, interleukins, etc. were not systematically measured in all samples collected longitudinally in the present study, yet the samples are available and represent an interesting perspective, pending fund obtention.
In conclusion, this study showed that after severe COVID‐19 infection, decreased mHLA‐DR expression is associated with a greater risk of death at D28 independently of usual clinical confounders. Considering the nadir value of mHLA‐DR or gathering information about its kinetics until 7, 12, or 20 days after ICU admission improved the discrimination between survivors and non‐survivors. With further validation and refinements, the findings of this study open the door to enhancing individualized patient care based on their day‐to‐day immune trajectory monitoring.
AUTHOR CONTRIBUTIONS
G.B., C.T., G.M., C.L., J.B. and F.V. wrote this manuscript. C.T., G.M., C.L., J.B., and F.V. designed the research. G.B., C.T., G.M., C.L., J.B., and F.V. performed the research. G.B. analyzed the data. M.C., T.R., H.Y., J.‐C.R., F.W., M.‐C.D., F.D., M.B., A.‐C.L., L.A. collected clinical samples and clinical data. L.G., R.C., M.G., F.V., and G.M. were in charge of immunological analyses. All authors have read the final version of the manuscript and agreed to its submission.
FUNDING INFORMATION
This work was supported by funds from the Hospices Civils de Lyon, Fondation HCL and Claude Bernard Lyon 1 University/Région Rhône‐Alpes.
CONFLICT OF INTEREST STATEMENT
The authors declare no competing financial interests in relation to the work.
CONSENT TO PARTICIPATE
The committee waived the need for written informed consent because the study was observational, with a low risk to patients, and no specific procedure, other than routine blood sampling, was required. Oral information and non‐opposition to inclusion in the study were mandatory and were systematically obtained before any blood sample was drawn. This was recorded in patients' clinical files. If a patient was unable to consent directly, non‐opposition was obtained from the patient's legally authorized representative and reconfirmed from the patient at the earliest opportunity.
Supporting information
Appendix S1:
ACKNOWLEDGMENTS
This work was supported by funds from the Hospices Civils de Lyon, Fondation HCL and Claude Bernard Lyon 1 University/Région Auvergne Rhône Alpes. The authors would like to thank the clinical teams from all ICUs in HCL who were involved in the project while dedicated to their clinical duties during COVID‐19 pandemic as well as patients and their families who agreed to participate to this clinical study. The authors declare no competing financial interest.
The names of the individual members of the RICO study group as listed below should be searchable through their individual PubMed records:
Hospices Civils de Lyon, Lyon‐Sud University Hospital, Immunology Laboratory: Remi Pescarmona, Lorna Garnier, Christine Lombard, Magali Perret, Marine Villard.
Centre d'Investigation Clinique de Lyon (CIC 1407 Inserm): Marie Groussaud, Marielle Buisson, Laetitia Itah, Inesse Boussaha.
Hospices Civils de Lyon, Edouard Herriot Hospital, Immunology Laboratory: Françoise Poitevin‐Later, Christophe Malcus, Morgane Gossez.
RICO clinical investigators: Florent Wallet, Marie‐Charlotte Delignette, Frederic Dailler.
Hospices Civils de Lyon, Edouard Herriot Hospital, Medical Intensive Care Department: Marie Simon, Auguste Dargent, Pierre‐Jean Bertrand, Neven Stevic, Marion Provent.
Hospices Civils de Lyon, Edouard Herriot Hospital, Anesthesia and Critical Care Medicine Department: Laurie Bignet, Valérie Cerro.
Hospices Civils de Lyon, Croix‐Rousse University Hospital, Medical intensive Care Department: Jean‐Christophe Richard, Laurent Bitker, Mehdi Mezidi, Loredana Baboi.
The authors thank Lionel de la Tribouille for the use of the computer cluster services hosted on the “Centre de Biomodélisation UMR1137”.
Baudemont G, Tardivon C, Monneret G, et al. Joint modeling of monocyte HLA‐DR expression trajectories predicts 28‐day mortality in severe SARS‐CoV‐2 patients. CPT Pharmacometrics Syst Pharmacol. 2024;13:1130‐1143. doi: 10.1002/psp4.13145
The RICO study group members are present in the Acknowledgement section.
Julie Bertrand and Fabienne Venet contributed equally to this work and co‐last authors on that publication.
Contributor Information
Julie Bertrand, Email: julie.bertrand@inserm.fr.
for the RICO study group:
Remi Pescarmona, Christine Lombard, Magali Perret, Marine Villard, Marie Groussaud, Laetitia Itah, Inesse Boussaha, Françoise Poitevin‐Later, Christophe Malcus, Marie Simon, Auguste Dargent, Pierre‐Jean Bertrand, Neven Stevic, Marion Provent, Laurie Bignet, Valérie Cerro, Laurent Bitker, Mehdi Mezidi, and Loredana Baboi
DATA AVAILABILITY STATEMENT
De‐identified human/patient data and any additional information required to reanalyze the data reported in this article are available from the lead contact upon reasonable request.
REFERENCES
- 1. Serafim RB, Póvoa P, Souza‐Dantas V, Kalil AC, Salluh JIF. Clinical course and outcomes of critically ill patients with COVID‐19 infection: a systematic review. Clin Microbiol Infect. 2021;27(1):47‐54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Aziz S, Arabi YM, Alhazzani W, et al. Managing ICU surge during the COVID‐19 crisis: rapid guidelines. Intensive Care Med. 2020;46(7):1303‐1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Osuchowski MF, Winkler MS, Skirecki T, et al. The COVID‐19 puzzle: deciphering pathophysiology and phenotypes of a new disease entity. Lancet. Respir Med. 2021;9(6):622‐642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Zhudenkov K, Gavrilov S, Sofronova A, et al. A workflow for the joint modeling of longitudinal and event data in the development of therapeutics: tools, statistical methods, and diagnostics. CPT Pharmacometrics Syst Pharmacol. 2022;11(4):425‐437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Latouche A, Porcher R, Chevret S. A note on including time‐dependent covariate in regression model for competing risks data. Biom J. 2005;47(6):807‐814. [DOI] [PubMed] [Google Scholar]
- 6. Rizopoulos D. Joint Models for Longitudinal and Time‐to‐Event Data: with Applications in R. CRC Press; 2012:279 p. [Google Scholar]
- 7. Tardivon C, Desmée S, Kerioui M, et al. Association between tumor size kinetics and survival in patients with urothelial carcinoma treated with Atezolizumab: implication for patient follow‐up. Clin Pharmacol Ther. 2019;106(4):810‐820. [DOI] [PubMed] [Google Scholar]
- 8. Kerioui M, Bertrand J, Bruno R, Mercier F, Guedj J, Desmée S. Modelling the association between biomarkers and clinical outcome: an introduction to nonlinear joint models. Br J Clin Pharmacol. 2022;88(4):1452‐1463. [DOI] [PubMed] [Google Scholar]
- 9. Ibrahim JG, Chu H, Chen LM. Basic concepts and methods for joint models of longitudinal and survival data. J Clin Oncol. 2010;28(16):2796‐2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kerioui M, Mercier F, Bertrand J, et al. Bayesian inference using Hamiltonian Monte‐Carlo algorithm for nonlinear joint modeling in the context of cancer immunotherapy. Stat Med. 2020;39(30):4853‐4868. [DOI] [PubMed] [Google Scholar]
- 11. Rizopoulos D. Dynamic predictions and prospective accuracy in joint models for longitudinal and time‐to‐event data. Biometrics. 2011;67(3):819‐829. [DOI] [PubMed] [Google Scholar]
- 12. Tardiveau C, Monneret G, Lukaszewicz AC, et al. A 9‐mRNA signature measured from whole blood by a prototype PCR panel predicts 28‐day mortality upon admission of critically ill COVID‐19 patients. Front Immunol. 2022;13:1022750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Venet F, Gossez M, Bidar F, et al. T cell response against SARS‐CoV‐2 persists after one year in patients surviving severe COVID‐19. EBioMedicine. 2022;78:103967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Bidar F, Hamada S, Gossez M, et al. Recombinant human interleukin‐7 reverses T cell exhaustion ex vivo in critically ill COVID‐19 patients. Ann Intensive Care. 2022;12(1):21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Coudereau R, Waeckel L, Cour M, et al. Emergence of immunosuppressive LOX‐1+ PMN‐MDSC in septic shock and severe COVID‐19 patients with acute respiratory distress syndrome. J Leukoc Biol févr. 2022;111(2):489‐496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Venet F, Cour M, Rimmelé T, et al. Longitudinal assessment of IFN‐I activity and immune profile in critically ill COVID‐19 patients with acute respiratory distress syndrome. Crit Care. 2021;25(1):140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ferguson ND, Fan E, Camporota L, et al. The Berlin definition of ARDS: an expanded rationale, justification, and supplementary material. Intensive Care Med. 2012;38(10):1573‐1582. [DOI] [PubMed] [Google Scholar]
- 18. rapport_vcourte.pdf [Internet] . [cité 23 mai 2023]. Disponible sur: https://sante.gouv.fr/IMG/pdf/rapport_vcourte.pdf
- 19. Vincent JL, Moreno R, Takala J, et al. The SOFA (sepsis‐related organ failure assessment) score to describe organ dysfunction/failure. Intensive Care Med. 1996;22(7):707‐710. [DOI] [PubMed] [Google Scholar]
- 20. Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. J Chronic Dis. 1987;40(5):373‐383. [DOI] [PubMed] [Google Scholar]
- 21. Vardavas CI, Mathioudakis AG, Nikitara K, et al. Prognostic factors for mortality, intensive care unit and hospital admission due to SARS‐CoV‐2: a systematic review and meta‐analysis of cohort studies in Europe. Eur Respir Rev. 2022;31(166):1‐14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Lavielle M. Mixed Effects Models for the Population Approach: Models, Tasks, Methods and Tools. CRC Press; 2014:385 p. [Google Scholar]
- 23. Pinheiro J, Bates D, Lindstrom M. Model Building in Nonlinear Mixed Effects Models. 1994.
- 24. Desmée S, Mentré F, Veyrat‐Follet C, Sébastien B, Guedj J. Nonlinear joint models for individual dynamic prediction of risk of death using Hamiltonian Monte Carlo: application to metastatic prostate cancer. BMC Med Res Methodol. 2017;17(1):105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Park KY, Qiu P. Model selection and diagnostics for joint modeling of survival and longitudinal data with crossing hazard rate functions. Stat Med. 2014;33(26):4532‐4546. [DOI] [PubMed] [Google Scholar]
- 26. Raftery AE. Bayesian model selection in social research. Sociol Methodol. 1995;25:111‐163. [Google Scholar]
- 27. Post TM, Freijer JI, de Winter W, Danhof M, Ploeger BA, Bv PC. Accurate Interpretation of the Visual Predictive Check in Order to Evaluate Model Performance 1.
- 28. Riglet F, Mentre F, Veyrat‐Follet C, Bertrand J. Bayesian individual dynamic predictions with uncertainty of longitudinal biomarkers and risks of survival events in a joint modelling framework: a comparison between Stan, Monolix, and NONMEM. AAPS J. 2020;22(2):50. [DOI] [PubMed] [Google Scholar]
- 29. Lavalley‐Morelle A, Timsit JF, Mentré F, Mullaert J, Network TO . Joint modeling under competing risks: application to survival prediction in patients admitted in intensive care unit for sepsis with daily sequential organ failure assessment score assessments. CPT Pharmacometrics Syst Pharmacol. 2022;11(11):1472‐1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Blanche P, Dartigues JF, Jacqmin‐Gadda H. Estimating and comparing time‐dependent areas under receiver operating characteristic curves for censored event times with competing risks. Stat Med. 2013;32(30):5381‐5397. [DOI] [PubMed] [Google Scholar]
- 31. Blanche P, Proust‐Lima C, Loubère L, Berr C, Dartigues JF, Jacqmin‐Gadda H. Quantifying and comparing dynamic predictive accuracy of joint models for longitudinal marker and time‐to‐event in presence of censoring and competing risks. Biometrics. 2015;71(1):102‐113. [DOI] [PubMed] [Google Scholar]
- 32. Musoro JZ, Zwinderman AH, Abu‐Hanna A, Bosman R, Geskus RB. Dynamic prediction of mortality among patients in intensive care using the sequential organ failure assessment (SOFA) score: a joint competing risk survival and longitudinal modeling approach. Statistica Neerlandica. 2018;72(1):34‐47. [Google Scholar]
- 33. Post TM, Freijer JI, de Winter W, Danhof M, Ploeger BA, Bv PC. Accurate Interpretation of the Visual Predictive Check in Order to Evaluate Model Performance.
- 34. Blanche P, Latouche A, Viallon V. Time‐dependent AUC with right‐censored data: a survey. In: Lee MLT, Gail M, Pfeiffer R, Satten G, Cai T, Gandy A, eds. Risk Assessment and Evaluation of Predictions. Springer; 2013:239‐251 Lecture Notes in Statistics. [Google Scholar]
- 35. Monolix 2018R2 . Lixoft SAS. A Simulations Plus Company; 2018. [Google Scholar]
- 36. Benlyamani I, Venet F, Coudereau R, Gossez M, Monneret G. Monocyte HLA‐DR measurement by flow cytometry in COVID‐19 patients: an interim review. Cytometry A. 2020;97(12):1217‐1221. [DOI] [PubMed] [Google Scholar]
- 37. Lamontagne F, Agarwal A, Rochwerg B, et al. A living WHO guideline on drugs for covid‐19. BMJ. 2020;370:m3379. [DOI] [PubMed] [Google Scholar]
- 38. Snow TAC, Singer M, Arulkumaran N. Immunomodulators in COVID‐19: two sides to every coin. Am J Respir Crit Care Med. 2020;202(10):1460‐1462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Goyal M, Demchuk AM, Menon BK, et al. Randomized assessment of rapid endovascular treatment of ischemic stroke. N Engl J Med. 2015;372(11):1019‐1030. [DOI] [PubMed] [Google Scholar]
- 40. Bodinier M, Peronnet E, Brengel‐Pesce K, et al. Monocyte trajectories Endotypes are associated with worsening in septic patients. Front Immunol. 2021;12:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Sinha P, Meyer NJ, Calfee CS. Biological phenotyping in sepsis and acute respiratory distress syndrome. Annu Rev Med. 2023;74(1):457‐471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Schulte‐Schrepping J, Reusch N, Paclik D, et al. Severe COVID‐19 is marked by a dysregulated myeloid cell compartment. Cell. 2020;182(6):1419‐1440.e23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. The WHO rapid evidence appraisal for COVID‐19 therapies (REACT) working group . Association between Administration of Systemic Corticosteroids and Mortality among Critically ill Patients with COVID‐19: a meta‐analysis. JAMA. 2020;324(13):1330‐1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Dexamethasone in hospitalized patients with Covid‐19. N Engl J Med. 2021;384(8):693‐704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. van de Veerdonk FL, Giamarellos‐Bourboulis E, Pickkers P, et al. A guide to immunotherapy for COVID‐19. Nat Med Janv. 2022;28(1):39‐50. [DOI] [PubMed] [Google Scholar]
- 46. Maslove DM, Tang B, Shankar‐Hari M, et al. Redefining critical illness. Nat Med Juin. 2022;28(6):1141‐1148. [DOI] [PubMed] [Google Scholar]
- 47. Vincent JL, van der Poll T, Marshall JC. The end of “one size fits all” sepsis therapies: toward an individualized approach. Biomedicines Sept. 2022;10(9):2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1:
Data Availability Statement
De‐identified human/patient data and any additional information required to reanalyze the data reported in this article are available from the lead contact upon reasonable request.


