Joint modeling in presence of informative censoring on the retrospective time scale with application to palliative care research

Summary

Joint modeling of longitudinal data such as quality of life data and survival data is important for palliative care researchers to draw efficient inferences because it can account for the associations between those two types of data. Modeling quality of life on a retrospective from death time scale is useful for investigators to interpret the analysis results of palliative care studies which have relatively short life expectancies. However, informative censoring remains a complex challenge for modeling quality of life on the retrospective time scale although it has been addressed for joint models on the prospective time scale. To fill this gap, we develop a novel joint modeling approach that can address the challenge by allowing informative censoring events to be dependent on patients’ quality of life and survival through a random effect. There are two sub-models in our approach: a linear mixed effect model for the longitudinal quality of life and a competing-risk model for the death time and dropout time that share the same random effect as the longitudinal model. Our approach can provide unbiased estimates for parameters of interest by appropriately modeling the informative censoring time. Model performance is assessed with a simulation study and compared with existing approaches. A real-world study is presented to illustrate the application of the new approach.

1 Introduction

Palliative care specialty focuses on improving quality of life (QOL) for patients and is appropriate at any age and at any stage in a serious illness; it can be provided along with curative treatment (Kelley and Morrison, 2015). Palliative care research has led to a paradigm shift in clinical practice. This includes early integration of palliative care for seriously ill older adults, such as advanced cancer patients (Temel and others, 2010; Parikh and others, 2013; Bakitas and others, 2009) and a 3-fold increase in palliative care programs at hospitals with 50+ beds across the nation since 2000 (Dumanovsky and others, 2016). With the rapid growth, it is critical that high-quality palliative care research studies are appropriately performed to generate results that can inform clinical and nursing practice for palliative medicine to maximize its potential value throughout the health care system (Kelley and Morrison, 2015). However, despite the progress, there is still a lack of statistical analysis methods to appropriately analyze the longitudinal QOL data and survival data which are commonly seen in palliative care studies. One of the challenges is how to handle dropouts in palliative care studies when the data are analyzed with a joint model and QOL is modeled on a retrospective time scale from death (Chan and Wang, 2010; Li and others, 2013, 2017; Kong and others, 2018). Dropping out is often associated with QOL and survival. Such dropouts are called informative dropouts and lead to informative censoring. Missing QOL due to informative censoring is expected to be systematically different than uncensored QOL; noninformative censoring does not systematically mask low or high QOL. Both types of censoring can be observed in a typical palliative care study and should be treated differently in a statistical model because they have systematically different impacts on QOL data. To address this analysis issue in palliative care research, we propose a semiparametric model that jointly models longitudinal QOL data, death time and informative censoring time in the terminal trend model framework (Kurland and others, 2009; Li and others, 2017) to make efficient and valid inference.

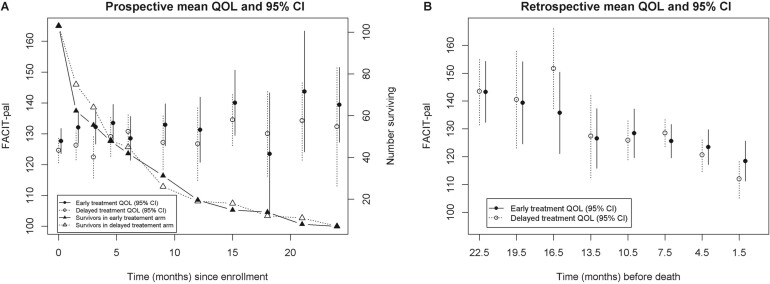
It is well known in the statistical literature that joint modeling of longitudinal data and survival data can improve efficiency and reduce bias (Hogan and Laird, 1997; Tsiatis and Davidian, 2004; Rizopoulos and Lesaffre, 2014; Dempsey and McCullagh, 2018; Elashoff and others, 2017). Joint models can be roughly classified based on whether the longitudinal data is modeled on the retrospective time scale from death, or prospectively from study entry, involving death as an event (Wulfsohn and Tsiatis, 1997; Hogan and Laird, 1997; Henderson and others, 2000; Li and others, 2010; Su and Hogan, 2010). The estimated longitudinal trajectories from the latter class do not have direct interpretation relative to death time(Kurland and Heagerty, 2005; Li and others, 2017). Another major issue, as Li and others (2017) pointed out (see Figure 1), is that longitudinal trajectories on the prospective time scale could be misleading for making inference on terminal trend. As shown in Figure 1, the longitudinal trajectories on the left panel (on prospective time scale) were clearly not correct patterns for terminal trends in the two treatment arms of a randomized trial, whereas the right panel (on retrospective scale) shows decreasing terminal trends as expected. Joint models on the prospective time scale could also extrapolate the longitudinal trajectories beyond death as pointed out by Kurland and Heagerty (2005) who proposed a partly conditional model that can address the risk of extrapolation beyond death by modeling the longitudinal data conditional on subjects being alive. Joint models on the retrospective time scale from death (Liu and others, 2007; Chan and Wang, 2010; Li and others, 2013; Chan and Wang, 2017; Li and others, 2017; Kong and others, 2018) often have a different target of inference (i.e., the terminal trend relative to death) than modeling the longitudinal data on the prospective time scale. Terminal trend models (TTM) (Kurland and others, 2009; Li and others, 2013, 2017) have been proposed for jointly analyzing longitudinal QOL data and survival data in palliative care studies and have advantages for estimating QOL on the retrospective time scale and interpreting the results for studies that have relatively short life expectancies. Under the assumption of noninformative censoring, there have been developments such as Chan and Wang (2017) which excluded the longitudinal data of subjects whose death times are censored from the analysis which results in efficiency loss and others (Liu and others, 2007; Li and others, 2013, 2017; Kong and others, 2018) that include all longitudinal data in the analysis. Although informative censoring have been extensively addressed in the literature for modeling the longitudinal data on the prospective time scale (Daniels and Hogan, 2008; Elashoff and others, 2017), informative censoring remains an unresolved issue for modeling longitudinal data on the retrospective time scale because the time points of the longitudinal measures are unknown on the retrospective time scale when death time is censored and the censoring time is associated with the longitudinal data and death time.

Fig. 1.

This figure is extracted from Li and others (2017) where the means and 95% CI of the QOL score (FACIT-pal) were presented on the prospective time scale (left panel) and on the retrospective time scale (right panel) for a two-arm randomized trial. Number of patients surviving at each time point was also presented in the left panel.

To fill this gap, we develop a new semiparametric model under the TTM framework for analyzing data in palliative care studies or other studies with relatively short life expectancy. The joint model has two submodels: a semiparametric mixed effect submodel for the longitudinal QOL data and a competing-risk survival submodel with piecewise hazards for the death time and dropout time. Dropout and death can be modeled as competing risks because the event of dropout prevents the event of death to occur in the study (Putter and others, 2007). The mixed effect submodel uses splines to model the longitudinal trajectory, making it flexible enough to approximate linear and nonlinear curves. The piecewise hazards for the death time and dropout time are also flexible to account for variation of hazard over time in palliative care studies. Both submodels share a common random effect that is used to handle the association between dropout time, QOL, and death time.

We will use a real-world study, the ENABLE III study (Bakitas and others, 2015), to illustrate our proposed method. The ENABLE III study was a two-arm randomized clinical trial comparing early palliative care with delayed palliative care for patients with advanced cancer to evaluate and test the benefit of introducing early palliative care versus delayed palliative care. The primary endpoint was QOL assessed by the 46-item Functional Assessment of Chronic Illness Therapy-Palliative Care (FACIT-pal), the higher the better. The treatment arm received palliative care immediately after enrollment (early treatment arm) and the control arm received standard care for the first 12 weeks and then switched to palliative care (delayed treatment arm). There were 207 patients enrolled in the study between October, 2009 and March, 2013 with 103 patients randomized to the early treatment arm and 104 patients randomized to the delayed treatment arm. QOL data were collected at baseline (i.e., enrollment) and at 6, 12, 18, and 24 weeks and every 12 weeks thereafter post enrollment until death, dropout or study completion. Survival data were collected as well. Given the strong association between QOL and survival for patients with short life expectancies, it is important to jointly model the QOL and survival data to estimate and test the treatment effect on QOL because better QOL in an arm could simply be due to longer survival in that arm.

This article is organized as follows. Models and notation are introduced in Section 2 with details on the longitudinal model and hazard models for the death time and the dropout time. Section 3 describes the calculation of the full log-likelihood function and the estimation procedure. A simulation study to assess the model performance is given in Section 4. A real study application is presented in Section 5 followed by a discussion in Section 6.

2 Model and notation

In this article, we focus on two-arm palliative care trials. The method can be naturally extended to trials with more than two arms or studies with binary independent variables. Let Y_i, D_i, W_i, and C_i denote the vector of longitudinal QOL measurements, death time, dropout time, and administrative censoring time (e.g., study completion) respectively for the ith subject. We will treat death and dropout as competing risks in our model. The administrative censoring time C_i can be calculated as the duration between the study completion time and the enrollment time. Let $T_i=\min (D_i,W_i,C_i)$ which is the observed event time and Δ_i take value of 0, 1, or 2, with ${\Delta }_i=0$ indicating a censored event (i.e., survived beyond the end of the study), ${\Delta }_i=1$ indicating a death and ${\Delta }_i=2$ indicating a dropout. Let A_i denote the binary treatment assignment in a two-arm palliative care trial and X_i denote a $P\times 1$ vector of potential confounders or covariates including baseline quality of life. We specify the following longitudinal model for QOL, constructed on a retrospective time scale starting from the death time:

$$Y_i(t^{*})={\beta }_{\mu }(t^{*})+A_i{\beta }_A(t^{*})+X_i^T{\psi }_X+Z(t^{*})U_i+{ϵ}_i(t^{*}),$$ (2.1)

where ${\beta }_{\mu }(t^{*})$ denotes the mean trajectory in the control group and the ${\beta }_A(t^{*})$ denotes the time-varying treatment effect at time $t^{*}$ counting backward from the time of death. Both of these functions are unspecified and assumed to be continuous. The time-varying coefficients allow for a flexible time-varying treatment effect during the terminal phase of life and testing the treatment effect at any specific time point prior to death. Here, ψ_X is the P-dimensional vector of coefficients of X_i. U_i is a scalar random effect following the standard normal distribution N(0, 1). The function $Z(t^{*})$ is an unspecified and continuous function of $t^{*}$. For identifiability of the model, the function $Z(t^{*})$ is constrained to be positive. Typical assumptions for mixed effects models are retained here. The residual error ${ϵ}_i(t^{*})$ is assumed to be normally distributed with mean $\mathrm{E}[{ϵ}_i(t^{*})]=0$ and $\text{var}[{ϵ}_i(t^{*})]={\tau }^2$, where ${ϵ}_i(t^{*})$ and ${ϵ}_i(s^{*})$ are independent for any $t^{*}\ne s^{*}$; The random effects U_i and residual error ${ϵ}_i(t^{*})$ are assumed independent.

Remark 2.1 (Flexible random effect) Notice that the term $Z(t^{*})U_i$ in model (2.1) has a normal distribution with mean of 0 and variance of $Z{(t^{*})}^2$. So model (2.1) is equivalent to the model below where $U_i^{*}(t^{*})$ is a random effect with the normal distribution $N(0,Z{(t^{*})}^2)$ and its variance $Z{(t^{*})}^2$ is a nonparametric function of $t^{*}$. Therefore, the model is flexible to account for a variety of different random effects with the nonparametric variance for the random effect $U_i^{*}(t^{*})$.

$$Y_i(t^{*})={\beta }_{\mu }(t^{*})+A_i{\beta }_A(t^{*})+X_i^T{\psi }_X+U_i^{*}(t^{*})+{ϵ}_i(t^{*}),$$

Remark 2.2 (Connection with prospective models) Let t denote time on the prospective time scale counting from enrollment. Model (2.1) can be rewritten on the prospective time scale as follows:

$$Y_i(t)={\beta }_{\mu }(D_i-t)+A_i{\beta }_A(D_i-t)+X_i^T{\psi }_X+Z(D_i-t)U_i+{ϵ}_i(t).$$

It is straightforward to see that QOL, $Y_i(t)$, depends on the death time through $D_i-t$ which measures how soon the subject will die after time t. Later we will see that QOL also depends on the death time through the random effect U_i. Let n_i denote the total number of follow-up longitudinal measurements, t_ij denote the measurement time of the jth measure on the prospective time scale and $t_{ij}^{*}$ denote the measurement time of the jth measure on the retrospective time scale for the ith subject; Note $t_{ij}^{*}=D_i-t_{ij}$. When D_i is censored, $t_{ij}^{*}$ cannot be observed which is a challenge for parameter estimation under informative censoring, such as dropouts, when modeling the longitudinal data on the retrospective time scale.

Let δ take values in {1, 2} with δ=1 indicating the event of death and δ=2 indicating the event of dropout. We use a piecewise-exponential competing-risk model for the time to event data $(T_i,{\Delta }_i)$. Dropout and death can be modeled as competing risks because the event of dropout prevents the event of death to occur in the study (Putter and others, 2007). The hazard function for the competing risk model is given by:

$${\lambda }_i^{\delta }(t)=\text{exp}({\alpha }_0^{\delta }(t)+A_i{\alpha }_A^{\delta }(t)+{\alpha }_U^{\delta }{U}_i), \text{for} \delta =1,2,$$

where ${\lambda }_i^{\delta }(t)$ is the hazard rate for type δ event at time t given treatment status A_i and frailty U_i. Here, we assume $({\alpha }_0^1(t),{\alpha }_0^2(t))$ and $({\alpha }_A^1(t),{\alpha }_A^2(t))$ are piecewise-exponential hazard; and ${\alpha }_U=({\alpha }_U^1,{\alpha }_U^2)$ are the coefficients of the frailty U_i for the two competing risks. Without loss of generality, we assume the piecewise-constant hazards, ${\alpha }_0^1(t)$ and ${\alpha }_A^1(t)$, have the same J breakpoints denoted by $\{t_1^{\alpha },\dots ,t_J^{\alpha }\},\hspace{0.17em}0<t_1^{\alpha }<\cdots <t_J^{\alpha }<\infty$. We also assume the piecewise-constant hazards of dropout, ${\alpha }_0^2(t)$ and ${\alpha }_A^2(t)$, have the same $J\prime$ breakpoints denoted by $\{t_1^{\gamma },\dots ,t_{J\prime }^{\gamma }\},\hspace{0.17em}0<t_1^{\gamma }<\cdots <t_{J\prime }^{\gamma }<\infty$. We can write the piecewise-constant hazards as follows:

$${\alpha }_0^1(t)=\sum _{j=1}^{J+1}{\eta }_0^j{\mathcal{B}}_j(t),{\alpha }_A^1(t)=\sum _{j=1}^{J+1}{\eta }_A^j{\mathcal{B}}_j(t),{\alpha }_0^2(t)=\sum _{j\prime =1}^{J\prime +1}{\gamma }_0^{j\prime }{\mathcal{B}}_{j\prime }^{\gamma }(t),{\alpha }_A^2(t)=\sum _{j\prime =1}^{J\prime +1}{\gamma }_A^{j\prime }{\mathcal{B}}_{j\prime }^{\gamma }(t),$$

where ${\mathcal{B}}_j(t)=1_{(t_{j-1}^{\alpha }\le t<t_j^{\alpha })}$ and ${\mathcal{B}}_{j\prime }^{\gamma }(t)=1_{(t_{j\prime -1}^{\gamma }\le t<t_{j\prime }^{\gamma })}$ are binary indicator functions, $t_0^{\alpha }=t_0^{\gamma }=0,\hspace{0.17em}{t}_{J+1}^{\alpha }=t_{J\prime +1}^{\gamma }=\infty$ and the coefficients: $\{{\eta }_0^j,{\eta }_A^j,{\gamma }_0^{j\prime },{\gamma }_A^{j\prime }\},j=1,\dots ,J+1,j\prime =1,\dots ,J\prime +1$ of the indicator functions determine the constant hazard on each piece. Note that this model shares the same random effect, U_i with the longitudinal model (2.1). We can add covariates, X_i, in the model as follows:

$${\lambda }_i^{\delta }(t)=\text{exp}({\alpha }_0^{\delta }(t)+A_i{\alpha }_A^{\delta }(t)+{\alpha }_U^{\delta }{U}_i+X_i^T{\alpha }_X^{\delta }), \text{for} \delta =1,2,$$ (2.2)

where ${\alpha }_X=({\alpha }_X^1,{\alpha }_X^2)$ are the parameters associated with X_i for the two competing risks, respectively. Notice that the above model can be also written in the form of a Cox model:

$${\lambda }_i^{\delta }(t)={\lambda }_0^{\delta }(t)\hspace{0.17em}\text{exp}(A_i{\alpha }_A^{\delta }(t)+{\alpha }_U^{\delta }{U}_i+X_i^T{\alpha }_X^{\delta }), \text{for} \delta =1,2,$$

where ${\lambda }_0^1(t)$ and ${\lambda }_0^2(t)$ are the baseline hazard functions for the two competing risks, respectively, in the Cox model, and ${\lambda }_0^1(t)=\text{exp}({\alpha }_0^1(t))$ and ${\lambda }_0^2(t)=\text{exp}({\alpha }_0^2(t))$.

Taken together, (2.1) and (2.2) form our joint model of longitudinal QOL, death time, and dropout time.

3 Parameter estimation with regression splines

Maximum likelihood estimation (MLE) will be used to estimate the parameters. We use regression splines to handle the nonparametric functions ${\beta }_{\mu }(t^{*}),\hspace{0.17em}{\beta }_A(t^{*})$, and $Z(t^{*})$. Without loss of generality, we use the same knots for the regression splines of the three functions and the knots will be placed at equally spaced quantiles of the observed times of the longitudinal measurements. In particular, ${\beta }_{\mu }(t^{*}),\hspace{0.17em}{\beta }_A(t^{*})$, and $Z(t^{*})$ will be approximated by linear splines with K knots:

$${\beta }_{\mu }(t^{*})={\beta }_0+\sum _{k=1}^K{\beta }_k{B}_k(t^{*}), {\beta }_A(t^{*})={\beta }_0^A+\sum _{k=1}^K{\beta }_k^A{B}_k(t^{*}),Z(t^{*})={\zeta }_0+\sum _{k=1}^K{\zeta }_k{B}_k(t^{*}),$$ (3.3)

where $B_k(t^{*})=(t^{*}-t^{k-1})1_{(t^{k-1}\le t^{*}<t^k)}+(t^k-t^{k-1})1_{(t^k\le t^{*})}$ are the linear spline basis functions, $t^0=0$ and $0<t^1<\dots <t^K<\infty$ are the knots which will be placed at the equally spaced sample quantiles of the data. Notice that the curves become flat after the last knot. Equation (2.1) can be rewritten as:

$$Y_i(t^{*})={\mathbb{X}}_i{(t^{*})}^T\beta +Z(t^{*})U_i+{ϵ}_i(t^{*}),$$ (3.4)

where ${\mathbb{X}}_i{(t^{*})}^T=(1,B_1(t^{*}),\dots ,B_K(t^{*}),1,A_i{B}_1(t^{*}),\dots ,A_i{B}_K(t^{*}),X_i^T)$ is a $(2K+P)$-dimensional vector of variables, $\beta ={({\beta }_0,{\beta }_1,\mathrm{\dots .}{\beta }_K,{\beta }_0^A,{\beta }_1^A,\dots ,{\beta }_K^A,{\psi }_X^T)}^T$. As defined previously, n_i denotes the number of measurements of the longitudinal outcome for the ith subject. Since ${ϵ}_i(t^{*})$ follows a normal distribution, conditional on U_i, the outcome variable vector $Y_i={(Y_i(t_{i1}^{*}),\dots ,Y_i(t_{i{n}_i}^{*}))}^T$ has a n_i-dimensional multivariate normal distribution $N({\mu }_i,V_i)$ with mean vector μ_i having its jth element equal to ${\mathbb{X}}_i{(t_{ij}^{*})}^T\beta +Z(t_{ij}^{*})U_i$ and covariance matrix $V_i={\tau }^2{I}_{n_i}$, where $I_{n_i}$ is the $n_i\times n_i$ identity matrix. Here, $t_{ij}^{*}$ denotes the measurement time of the jth measure on the retrospective time scale for the ith subject. Using equations (2.2)–(3.4), the log-likelihood function can be constructed to obtain MLE, given prespecified knots, for all the parameters denoted by $\theta =(\beta ,\zeta ,\Sigma ,\tau ,\{{\eta }_0^j,{\eta }_A^j,j=1,\dots ,J\},\{{\gamma }_0^j,{\gamma }_A^j,j=1,\dots ,J\prime \},{\alpha }_U,{\alpha }_X)$, where $\zeta =({\zeta }_0,{\zeta }_1,\dots ,{\zeta }_K)$. We will use equally spaced quantiles as candidates for knots and the optimal number of knots will be determined by using AIC (Akaike, 1974).

3.1 The log-likelihood function

Let $(y_i,t_i,{\delta }_i,x_i)$ denote the observed data for subject i, where y_i is the vector of observed longitudinal outcomes ${(y_i(t_{i1}^{*}),\dots ,y_i(t_{i{n}_i}^{*}))}^T$, t_i is the observed event time or censoring time and δ_i is the observed value of Δ_i. Due to the random effect U_i, we need to integrate over the distribution of U_i to calculate the log-likelihood function. To derive the log-likelihood function, we divide the subjects into six groups based on the value of δ_i and whether they have any longitudinal QOL measurements. Details of the derivation can be found in the Supplementary material available at Biostatistics online. For each of the six groups, we show the log-likelihood contribution of the ith subject if they are in that group. Group 1 consists of subjects who had death times observed (i.e., ${\delta }_i=1$) and had longitudinal QOL measurements. The log-likelihood contribution of subject i is given by:

$${\ell }_1^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_1^{i1}(\theta |u))\mathrm{d}u)-0.5(n_i+1)\hspace{0.17em}\text{log}(2\pi )+\text{log}(1-F_{C_i}(t_i)),$$ (3.5)

where

$$\begin{array}{c}{\ell }_1^{i1}(\theta |u)=-n_i\hspace{0.17em}\text{log}(\tau )-\frac{0.5{(y_i-{\mu }_i)}^T(y_i-{\mu }_i)}{{\tau }^2}-H_i(t_i,u)\\ \hspace{1em}+{\alpha }_U^{1}u+{\alpha }_0^1(t_i)+A_i{\alpha }_A^1(t_i)+x_i^T{\alpha }_X^1-{\Lambda }_i(t_i,u)-0.5u^2,\end{array}$$

$H_i(t,u)={\int }_0^t{\lambda }_i^2(v|U_i=u)dv,\hspace{0.17em}{\Lambda }_i(t,u)={\int }_0^t{\lambda }_i^1(v|U_i=u)\mathrm{d}v$ , and $F_{C_i}(t)$ is the cumulative distribution function (CDF) of C_i.

Group 2 consists of subjects who dropped out (${\delta }_i=2$) and had longitudinal QOL measurements before dropout. The log-likelihood contribution of subject i is given by:

$${\ell }_2^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_2^{i1}(\theta |u))\mathrm{d}u)-0.5(n_i+1)\hspace{0.17em}\text{log}(2\pi )+\text{log}(1-F_{C_i}(t_i)),$$ (3.6)

where

$$\begin{array}{c}{\ell }_2^{i1}(\theta |u)=-n_i\hspace{0.17em}\text{log}(\tau )\\ \hspace{1em}+\text{log}({\int }_{t_i}^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}(-\frac{0.5{(y_i-{\mu }_i)}^T(y_i-{\mu }_i)}{{\tau }^2}){\lambda }_i^1(s|U_i=u)\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\text{exp}({\Lambda }_i(t_i,u)-{\Lambda }_i(s,u))\mathrm{d}s)\\ \hspace{1em}-{\Lambda }_i(t_i,u)+{\alpha }_U^{2}u+{\alpha }_0^2(t_i)+A_i{\alpha }_A^2(t_i)+x_i^T{\alpha }_X^2-H_i(t_i,u)-0.5u^2.\end{array}$$

Group 3 consists of subjects who survived beyond the end of the study (${\delta }_i=0$) and had longitudinal QOL measurements. The log-likelihood contribution of subject i is given by:

$${\ell }_3^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_3^{i1}(\theta |u))\mathrm{d}u)-0.5(n_i+1)\hspace{0.17em}\text{log}(2\pi )+\text{log}(f_{C_i}(t_i)),$$ (3.7)

where

$$\begin{array}{c}{\ell }_3^{i1}(\theta |u)=-n_i\hspace{0.17em}\text{log}(\tau )\\ +\text{log}({\int }_{t_i}^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}(-\frac{0.5{(y_i-{\mu }_i)}^T(y_i-{\mu }_i)}{{\tau }^2}){\lambda }_i^1(s|U_i=u)\\ \hspace{1em}\hspace{1em}\hspace{0.17em}\text{exp}({\Lambda }_i(t_i,u)-{\Lambda }_i(s,u))\mathrm{d}s)\\ -{\Lambda }_i(t_i,u)-H_i(t_i,u)-0.5u^2,\end{array}$$

and $f_{C_i}(t)$ is the density function of C_i.

Group 4 consists of subjects who had death times observed (${\delta }_i=1$) but had no longitudinal QOL measurements. The log-likelihood contribution of subject i is given by:

$${\ell }_4^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_4^{i1}(\theta |u))\mathrm{d}u)-0.5\hspace{0.17em}\text{log}(2\pi )+\text{log}(1-F_{C_i}(t_i)),$$ (3.8)

where

$${\ell }_4^{i1}(\theta |u)=-H_i(t_i,u)+{\alpha }_U^{1}u+{\alpha }_0^1(t_i)+A_i{\alpha }_A^1(t_i)+x_i^T{\alpha }_X^1-{\Lambda }_i(t_i,u)-0.5u^2.$$

Group 5 consists of subjects who dropped out (${\delta }_i=2$) and had no longitudinal QOL measurements before dropout. The log-likelihood contribution of subject i is given by:

$${\ell }_5^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_5^{i1}(\theta |u))\mathrm{d}u)-0.5\hspace{0.17em}\text{log}(2\pi )+\text{log}(1-F_{C_i}(t_i)),$$ (3.9)

where

$${\ell }_5^{i1}(\theta |u)=-{\Lambda }_i(t_i,u)+{\alpha }_U^{2}u+{\alpha }_0^2(t_i)+A_i{\alpha }_A^2(t_i)+x_i^T{\alpha }_X^2-H_i(t_i,u)-0.5u^2.$$

Group 6 consists of subjects who survived beyond the end of the study (${\delta }_i=0$) but had no longitudinal QOL measurements. The log-likelihood contribution of subject i is given by:

$${\ell }_6^i(\theta )=\text{log}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_6^{i1}(\theta |u))\mathrm{d}u)-0.5\hspace{0.17em}\text{log}(2\pi )+\text{log}(f_{C_i}(t_i)),$$

where

$${\ell }_6^{i1}(\theta |u)=-{\Lambda }_i(t_i,u)-H_i(t_i,u)-0.5u^2.$$ (3.10)

Notice that the terms involving π, $F_{C_i}(t)$, and $f_{C_i}(t)$ can be ignored because they are constants with respect to the parameter vector θ. Thus, we just need to maximize the following objective function to compute the MLE:

$$\ell (\theta )=\sum _{h=1}^6\sum _{i\in \text{group} \mathrm{h}}\hspace{0.17em}\text{log}\hspace{0.17em}({\int }_{-\infty }^{\infty }\hspace{0.17em}\text{exp}\hspace{0.17em}({\ell }_h^{i1}(\theta |u))\mathrm{d}u).$$

Standard errors will be obtained using the observed Fisher information. Details of calculating the integrals with Gauss–Hermite quadrature (Takahasi and Mori, 1973) can be found in the Supplementary material available at Biostatistics online.

3.2 Computational challenge

An alternative way to obtain the MLE is to use an EM algorithm (Rizopoulos, 2012; Li and others, 2022) where the random effect U_i is treated as missing data. For joint models on the prospective time scale, the M-step of an EM algorithm typically has closed-form solutions for the coefficient and variance parameters of the longitudinal submodel and for the cumulative baseline hazard of survival submodel. And it can use one-step Newton–Raphson method to update the coefficient parameters of the survival submodel. All integrations can be calculated with Gauss–Hermite quadrature approximations (Li and others, 2022). The entire process of an EM algorithm for joint models on the prospective time scale is reasonably fast because it does not involve optimization, thanks to the closed-form solutions and one-step Newton–Raphson method in the M-step.

However, for our joint model on the retrospective time scale, due to the integrations with respect to $\mathrm{d}s$ in ${\ell }_2^{i1}(\theta )$ and ${\ell }_3^{i1}(\theta )$, the M-step of an EM algorithm does not have closed-form solutions for the coefficient parameters in the longitudinal submodel, and thus optimization is needed in each iteration of the M-step which is very computationally demanding. The root of this challenge comes from the unknown time origins of the terminal trends in groups 2 and 3 where death times are censored and thus the integrations with respect to death time is needed to construct the log-likelihood function. Because of the computational challenge for using an EM algorithm, we propose to directly maximize the log-likelihood function to obtain the MLE.

3.3 Choosing the optimal number of knots

The advantage of a regression splines approach is that it can transform a nonparametric or semiparametric model into a parametric model by approximating the nonparametric functions with linear combinations of the spline basis functions once the knots are determined. There are many ways for choosing the optimal number of knots such as AIC, BIC, cross-validation, and general cross validation. In our setting, since we have a log-likelihood function, it is natural to use AIC or BIC for selecting the optimal knots for ${\beta }_{\mu }(t^{*}),\hspace{0.17em}{\beta }_A(t^{*})$, and $Z(t^{*})$ because both AIC and BIC statistics are functions of the log-likelihood function. In the simulation Section 4 and the real study Section 5, we use AIC since it puts smaller penalty than BIC on the number of parameters. The set of knots that minimizes the AIC statistic will be our set of optimal knots.

4 Simulation

Model performance was evaluated by a simulation study where 100 datasets were randomly generated with 200 patients in each dataset. The binary treatment variable A_i was generated using a Bernoulli distribution with parameter p = 0.5. Two covariates were also generated with one from the Uniform distribution U(0, 1), denoted by X¹, and the other one from the Bernoulli distribution with the parameter p = 0.5, denoted by X². The death time and dropout time were generated based on the following two-piece piecewise hazard:

$${\lambda }_i^{\delta }(t)=\text{exp}({\alpha }_0^{\delta }(t)+A_i{\alpha }_A^{\delta }(t)+{\alpha }_U^{\delta }{U}_i+{\alpha }_1^{\delta }{X}^1+{\alpha }_2^{\delta }{X}^2), \text{for} \delta =1,2,$$

where ${\alpha }_0^1(t)={\eta }_0^1{1}_{(0\le t<t_1^{\alpha })}+{\eta }_0^2{1}_{(t_1^{\alpha }\le t)},\hspace{0.17em}{\alpha }_A^1(t)={\eta }_A^1{1}_{(0\le t<t_1^{\alpha })}+{\eta }_A^2{1}_{(t_1^{\alpha }\le t)},\hspace{0.17em}{\alpha }_0^2(t)={\gamma }_0^1{1}_{(0\le t<t_1^{\gamma })}+{\gamma }_0^2{1}_{(t_1^{\gamma }\le t)},\hspace{0.17em}{\alpha }_A^2(t)={\gamma }_A^1{1}_{(0\le t<t_1^{\gamma })}+{\gamma }_A^2{1}_{(t_1^{\gamma }\le t)},\hspace{0.17em}{t}_1^{\alpha }=t_1^{\gamma }=3,\hspace{0.17em}{\eta }_0^1=-2.5,\hspace{0.17em}{\eta }_0^2=-3,\hspace{0.17em}{\eta }_A^1=-1,\hspace{0.17em}{\eta }_A^2=-0.5,\hspace{0.17em}{\gamma }_0^1=-2.5,\hspace{0.17em}{\gamma }_0^2=-3,\hspace{0.17em}$${\gamma }_A^1=-1,\hspace{0.17em}{\gamma }_A^2=-0.5,\hspace{0.17em}{\alpha }_U^1=-1.5,\hspace{0.17em}{\alpha }_U^2=1.5,\hspace{0.17em}{\alpha }_1^1=-0.2,\hspace{0.17em}{\alpha }_2^1=0.1,\hspace{0.17em}{\alpha }_1^2=-0.2$, and ${\alpha }_2^2=0.1$. The parameter values were chosen to mimic the distribution of the six groups in the real data.

Here, ${\eta }_0^1$ and ${\eta }_0^2$ are the hazards of death for the first piece and second piece respectively in the control arm, and ${\eta }_0^1+{\eta }_A^1$ and ${\eta }_0^2+{\eta }_A^2$ are the hazards of death for the first piece and second piece respectively in the treatment arm. The parameters ${\gamma }_0^1$ and ${\gamma }_0^2$ can be interpreted as the hazards of dropout for the first piece and the second piece respectively in the control arm, and ${\gamma }_0^1+{\gamma }_A^1$ and ${\gamma }_0^2+{\gamma }_A^2$ are the hazards of dropout for the first piece and the second piece respectively in the treatment arm. The length of the study was set to be 25 months. Enrollment times are generated from the Uniform distribution U(0, 20) meaning that enrollment stops at 20 months and patients are entering the study at a stable speed which implies that the administrative censoring time follows the Uniform distribution U(5, 25).

After the death time was generated, the longitudinal data Y_i was generated with the following model:

$$Y_i(t^{*})={\beta }_{\mu }(t^{*})+A_i{\beta }_A(t^{*})+{\psi }_1{X}^1+{\psi }_2{X}^2+Z(t^{*})U_i+{ϵ}_i(t^{*}),$$

where ${\beta }_{\mu }(t^{*})=20-\frac{4}{1+\text{exp}(0.3t^{*})},\hspace{0.17em}{\beta }_A(t^{*})=10+4\hspace{0.17em}\text{exp}(-0.3t^{*}-0.5),\hspace{0.17em}Z(t^{*})=10-\frac{4}{1+\text{exp}(0.3t^{*})},\hspace{0.17em}{\psi }_1=2$, and ${\psi }_2=1$. And U_i and ${ϵ}_i(t^{*})$ were generated from the standard normal distribution N(0, 1) and $N(0,2^2)$ respectively. Here, the curves ${\beta }_{\mu }(t^{*})$ and ${\beta }_A(t^{*})$ were chosen such that they proportionally mimic trajectories in a real study (Bakitas and others, 2009; Li and others, 2013). The QOL measurements are assumed to be collected every 2 months until death, dropout, or study end. On average, there are 38.8%, 38.8%, 19.6%, 1.4%, 1.5%, and 0.0% of subjects in groups 1, 2, 3, 4, 5, and 6, respectively in the simulated data sets. In the estimation, the optimal number of knots for estimating ${\beta }_{\mu }(t^{*})$ and ${\beta }_A(t^{*})$ were selected using AIC (Akaike, 1974) within the range [2, 7]. We compared the proposed approach with the naive approach that only analyzed subjects whose death time were observed and another method (Li and others, 2017) assuming noninformative censoring (referred to as NIC herein). The average bias magnitude was calculated as the average of the bias magnitudes at 100 points equally taken within (0, 25).

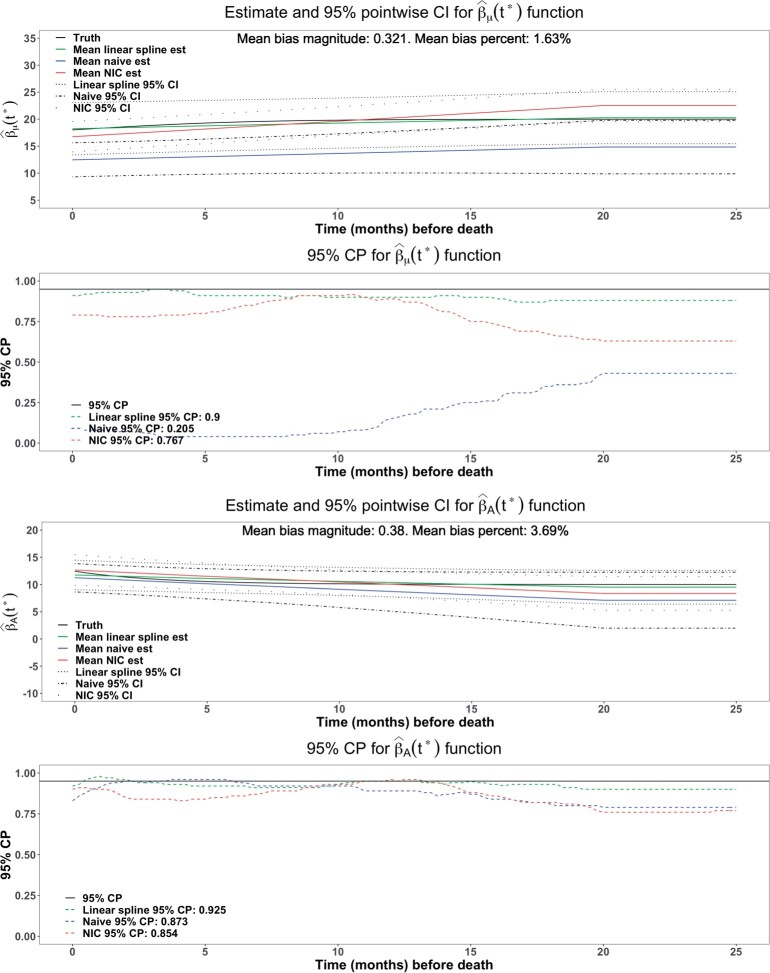
Figures 2 show that the estimates from the proposed approach (green curves) were virtually unbiased with the average bias magnitude over the interval (0, 25) being 0.321 (1.63%) for ${\widehat{\beta }}_{\mu }$ and 0.380 (3.69%) for ${\widehat{\beta }}_A$, whereas the naive approach (blue curves) had larger average bias magnitudes: 5.75 (29.3%) for ${\widehat{\beta }}_{\mu }$ and 1.59 (15.7%) for ${\widehat{\beta }}_A$, and NIC approach (red curves) also had much larger bias magnitudes: 1.36 (6.90%) for ${\widehat{\beta }}_{\mu }$ and 0.91 (8.89%) for ${\widehat{\beta }}_A$. The naive approach also had 35.3% wider point-wise 95% confidence intervals for β_A. The CP of point-wise 95% CI showed that proposed approach had a CP closer to the nominal level 95% than the NIC approach (0.900 vs 0.767 for ${\beta }_{\mu }$, 0.925 vs 0.854 for β_A). Hence, the proposed approach was more efficient than naive approach, and more accurate than both the naive approach and the NIC approach. The underestimated coverage probabilities from the naive method and the NIC method were likely due to their estimation bias.

Fig. 2.

Comparison with the naive method and NIC method for the estimate of ${\beta }_{\mu }$ and β_A. The proposed method, naive method and NIC method were colored as green, blue, and red, respectively. The mean bias, bias percentage, and CP were calculated from the average of 100 equally taken points.

For the parametric part of the model, estimates showed similar pattern (see Table 1) that the proposed approach produced nearly unbiased estimates with the CP of 95% CI around the nominal level of 95% whereas parameter estimates from the naive approach and the NIC approach had large biases and several CP’s of their 95% CI’s were significantly less than 95% although some are around or above 95%.

Table 1.

Simulation results for parameters in the model

Parameters	True	Bias	Naive bias	NIC bias	Bias (%)	Naive bias (%)	NIC bias (%)	CP $(\%)$	Naive CP (%)	NIC CP (%)
$et{a}_0^1$	–2.5	0.023	0.644	0.412	0.920	25.760	16.480	90	37	65
${\eta }_A^1$	–1.0	–0.062	0.140	0.259	–6.200	14.000	25.900	91	88	87
${\alpha }_U^1$	–1.5	–0.008	—	—	–1.733	—	—	90	—	—
τ	2.0	0.003	–0.003	0.028	0.150	–0.150	1.400	93	93	92
${\gamma }_0^1$	–2.5	–0.044	0.664	—	–1.760	26.560	—	95	35	—
${\gamma }_A^1$	–1.0	–0.117	0.089	—	–11.700	8.900	—	96	92	—
${\alpha }_U^2$	1.5	0.063	—	—	4.200	—	—	96	—	—
${\eta }_0^2$	–3.0	–0.040	0.090	–0.789	–1.333	3.000	–26.300	91	89	33
${\eta }_A^2$	–0.5	0.049	0.347	0.729	9.800	69.400	145.800	94	77	44
${\gamma }_0^2$	–3.0	–0.011	0.324	—	–0.367	10.800	—	91	79	—
${\gamma }_A^2$	–0.5	–0.108	0.067	—	–21.600	13.400	—	89	93	-
${\alpha }_1^1$	–0.2	–0.041	–0.016	0.051	–20.500	–8.000	25.500	94	95	94
${\alpha }_2^1$	0.1	–0.013	–0.020	–0.034	–13.000	–20.000	–34.000	91	95	89
${\alpha }_1^2$	–0.2	0.030	0.053	—	15.000	26.500	—	92	97	—
${\alpha }_2^2$	0.1	–0.009	–0.041	—	–9.000	–41.000	—	87	95	—
ψ 1	2.0	0.106	–0.276	0.048	5.300	–13.800	2.400	90	100	91
ψ 2	1.0	0.004	0.080	0.074	0.400	8.000	7.400	87	100	86

5 Application

As described in Section 1, we use the ENABLE III study (Bakitas and others, 2015) to illustrate the proposed model. It was a two-arm randomized clinical trial to investigate the effect of early introduction of palliative care (treatment arm) for advanced cancer patients versus delayed introduction (control arm). We jointly analyzed the longitudinal QOL data and the time-to-event data using the proposed approach. Unlike the previous analysis in (Li and others, 2017) where no dropout was defined because death times were extracted from cancer registries and study completion was used as the censoring time for subjects who survived beyond the study end, here a patient was considered a dropout if s/he did not have any data at the last visit and the dropout time was defined as the last visit time that had longitudinal QOL data. Based on the censoring status and the availability of longitudinal QOL data, there were 33.8%, 28.0%, 13.0%, 10.6%, 14.5%, and 0.0% patients in groups 1, 2, 3, 4, 5, and 6 respectively (as defined in Section 3.1). Two covariates, baseline QOL (QOL₀) and sex (Sex), were included in the submodels. The data were analyzed using the following submodels:

$$\begin{array}{c}{Y}_i(t^{*})={\beta }_{\mu }(t^{*})+A_i{\beta }_A(t^{*})+{\psi }_{1}Qo{L}_0+{\psi }_2\text{Sex}+Z(t^{*})U_i+{ϵ}_i(t^{*}),\\ {\lambda }_i^{\delta }(t)=\text{exp}({\alpha }_0^{\delta }(t)+A_i{\alpha }_A^{\delta }(t)+{\alpha }_U^{\delta }{U}_i+{\alpha }_1^{\delta }Qo{L}_0+{\alpha }_2^{\delta }\text{Sex}), \text{for} \delta =1,2,\end{array}$$

where the survival model is a three-piece exponential model with tertiles of observed times being the breakpoints for the pieces, ${\alpha }_0^1(t)=\sum _{j=1}^3{\eta }_0^j{\mathcal{B}}_j(t),\hspace{0.17em}{\alpha }_A^1(t)=\sum _{j=1}^3{\eta }_A^j{\mathcal{B}}_j(t),\hspace{0.17em}{\mathcal{B}}_j(t)=1_{(t_{j-1}^{\alpha }\le t<t_j^{\alpha })},\hspace{0.17em}{t}_1^{\alpha }=6.51$, and $t_2^{\alpha }=10.26$ are the tertiles of the observed death times, and ${\alpha }_0^2(t)=\sum _{j=1}^3{\gamma }_0^j{\mathcal{B}}_j^{\gamma }(t),\hspace{0.17em}{\alpha }_A^2(t)=\sum _{j=1}^3{\gamma }_A^j{\mathcal{B}}_j^{\gamma }(t),\hspace{0.17em}{\mathcal{B}}_j^{\gamma }(t)=1_{(t_{j-1}^{\gamma }\le t<t_j^{\gamma })},\hspace{0.17em}{t}_1^{\gamma }=3.19$, and $t_2^{\gamma }=9.15$ are the tertiles of observed dropout times.

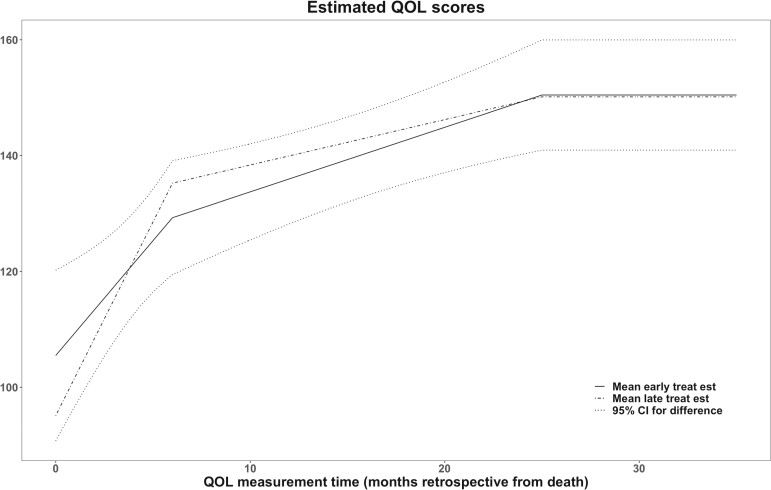
We followed the estimation procedure as described in Section 3 and determined the optimal number of knots for estimating ${\beta }_{\mu }(t^{*}),\hspace{0.17em}{\beta }_A(t^{*})$, and $Z(t^{*})$ over the range [2, 7] for the linear splines in the longitudinal submodel using AIC. The entire analysis took 8 h. The final model had 2 knots for the longitudinal submodel. The estimated trajectory of the longitudinal submodel is shown in Figure 3; QOL declines faster near end of life which is consistent with what has been observed in the literature (Bakitas and others, 2009; El-Jawahri and others, 2017; Bakitas and others, 2015). It also showed that the early treatment arm had better QOL but did not reach statistical significance based on pointwise Wald test which was consistent with the main finding (Bakitas and others, 2015) of the ENABLE III study.

Fig. 3.

Fitted QOL trajectories for early and late treatment arms with 95% in ENABLE III data.

The estimation results for parameters were presented in Table 2 and showed the longitudinal QOL was significantly associated with the baseline QOL (${\psi }_1=0.54$, p < 0.05). Patients with early treatment had lower hazard of death compared to late treatment group although this impact was not statistically significant according to the Wald tests for ${\eta }_A^1,\hspace{0.17em}{\eta }_A^2$, and ${\eta }_A^3$. Patients in the early treatment group tended to drop out faster compared to late treatment group, and this effect was statistically significant during the first 3 months but not significant after that according to the Wald tests for ${\gamma }_A^1,\hspace{0.17em}{\gamma }_A^2$, and ${\gamma }_A^3$.

Table 2.

Estimation of model parameters

Longitudinal model		Survival model		Dropout model
Parameters	Estimate(SE)	Parameters	Estimate(SE)	Parameters	Estimate(SE)
ψ 1	0.54 (0.07)	${\eta }_0^1$	–1.56 (0.60)	${\gamma }_0^1$	–2.18 (0.70)
ψ 2	4.31 (2.97)	${\eta }_A^1$	–0.29 (0.32)	${\gamma }_A^1$	0.79 (0.37)
τ	13.31 (0.42)	${\alpha }_U^1$	0.08 (0.03)	${\alpha }_U^2$	–0.07 (0.04)
		${\eta }_0^2$	–0.78 (0.63)	${\gamma }_0^2$	–2.94 (0.75)
		${\eta }_0^3$	–0.97 (0.64)	${\gamma }_0^3$	–2.99 (0.83)
		${\eta }_A^2$	–0.32 (0.43)	${\gamma }_A^2$	0.19 (0.57)
		${\eta }_A^3$	–0.27 (0.43)	${\gamma }_A^3$	0.30 (0.62)
		${\alpha }_1^1$	–0.015 (0.004)	${\alpha }_1^2$	–0.010 (0.005)
		${\alpha }_2^1$	0.61 (0.24)	${\alpha }_2^2$	0.51 (0.25)

6 Discussion

In this article, we proposed a novel and flexible semiparametric joint modeling approach under the TTM framework (Li and others, 2013, 2017) to account for informative censoring in palliative care studies where longitudinal QOL trajectories are often truncated by informative dropouts. The proposed method could serve as a useful data analysis tool for investigators in palliative research. The model was developed for analyzing data in two-arm clinical trials. However, it can be easily extended to trials with more than two arms and can also be used in observational studies to compare two longitudinal trajectories because potential confounders can be adjusted for in the model. The longitudinal QOL data are modeled on the retrospective time scale from death which can provide a direct estimate of the terminal trajectory and thus a convenient interpretation for palliative care investigators. The submodels for death time and dropout time are frailty models that share the same random effect with the submodel of longitudinal QOL. The piecewise hazard for both the death time and dropout time is a flexible feature of our approach that can accommodate a variety of different survival distributions and dropout patterns. It is worth noting that QOL data missing due to missed patients’ visits before dropout is assumed to be missing at random.

An improvement of the proposed approach over existing retrospective joint models (Chan and Wang, 2017; Kong and others, 2018; Li and others, 2017) is that it can handle informative censoring, such as informative dropouts, that are associated with low QOL. And the improvements were demonstrated in the simulation results where the proposed model had better performance with respect to bias and coverage probability in the presence of informative censoring. A possible extension of the proposed model is to use cubic splines (e.g., B-splines) instead of linear splines for the longitudinal submodel since cubic splines have more degrees of freedom. However, with cubic splines, it would be more time-consuming to calculate the integrals for groups 2 and 3 as described in Supplementary material available at Biostatistics online because there would be no explicit formulas for calculating the nested integrations. A second possible extension is to conduct sensitivity analysis to study the unverifiable assumption of conditional independence between the longitudinal trajectory and informative dropout in joint models (Daniels and Hogan, 2008; Harel and Schafer, 2009). There are existing approaches on sensitivity analysis (Creemers and others, 2010; Su and others, 2019) for traditional shared parameter models and those may be adapted under the TTM framework. Another possible extension is to remove the normality assumption on the distribution of the random effect U_i such that its distribution is unspecified. That way, the longitudinal model would have a fully nonparametric random effect (Wu and Zhang, 2006) which would give a little more flexibility over the current model.

There are two other factors that have significant impact on the computing time: the number of knots for the longitudinal model and the number of random effects. Due to the computational challenge, we only included one random effect U_i in the longitudinal submodel in (2.1). In theory, more than one random effects can be included like a typical mixed effect model. For example, we can use the longitudinal submodel as follows:

$$Y_i(t^{*})={\beta }_{\mu }(t^{*})+A_i{\beta }_A(t^{*})+X_i^T{\psi }_X+{\mathcal{Z}}_i{(t^{*})}^T{b}_i+{ϵ}_i(t^{*}),$$

where ${\mathcal{Z}}_i(t^{*})$ is the design matrix for the random effect b_i which could be a vector including random intercept and slopes. Correlations between b_i and U_i can be allowed to account for the dependence between the longitudinal outcome and the events (i.e., death and dropout). However, this will substantially increase the already-heavy computational burden due to the added integrations with respect to the different random effects. Note that we are also not treating the piecewise survival submodel as semiparametric because of the computational burden that would be added by selecting the optimal breakpoints for the survival submodel. In theory, the piecewise survival submodel can also be semiparametric if the breakpoints for the pieces are selected similarly as how the knots are selected for the longitudinal submodel.

Our model can be used for a variety of QOL measures. In addition to FACIT-pal, common QOL measures such as EORTC-QLQ-C30, McGill QOL questionnaire and EQ-5D can be modeled similarly. Furthermore, other continuous measures such as Edmonton Symptom Assessment Scale (Hui and Bruera, 2017), Karnofsky Performance Scale (Mor and others, 1984), and HADS Depression and Anxiety Scales (Snaith, 2003) can be also modeled. Notice that although our model can accommodate a broad range of patterns for the longitudinal trajectories by employing the linear splines, it assumes continuous longitudinal trajectories for the outcome variables. In the presence of sudden changes in the outcomes (e.g., for heart failure patients) which may cause noncontinuous longitudinal trajectories, the model may not provide optimal results in which case wavelet-based models (Morris and Carroll, 2006) could be adopted for the analysis.

Software

Software in the form of R code, together with a sample input data set and complete documentation is available on Github: https://github.com/quranwu/RetroJM.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by National Institutes of Health (R01GM123014, R01NR011871, R01HL158963, R01CA530191).