Abstract
We introduce a quantum information analysis of vibrational wave functions to understand complex vibrational spectra of molecules with strong anharmonic couplings and vibrational resonances. For this purpose, we define one- and two-modal entropies to guide the identification of strongly coupled vibrational modes and to characterize correlations within modal basis sets. We evaluate these descriptors for multiconfigurational vibrational wave functions which we calculate with the n-mode vibrational density matrix renormalization group algorithm. Based on the quantum information measures, we present a vibrational entanglement analysis of the vibrational ground and excited states of CO2, which display strong anharmonic effects due to the symmetry-induced and accidental (near-) degeneracies. We investigate the entanglement signature of the Fermi resonance and discuss the maximally entangled state arising from the two degenerate bending modes.
The calculation of anharmonic vibrational spectra remains a major challenge in computational molecular spectroscopy.1,2 For molecules with strong anharmonic couplings, a description of the nuclear motion beyond the harmonic approximation or a mean-field treatment is essential for the accurate prediction and interpretation of their spectra. Multiconfigurational vibrational methods are required to accurately treat correlated nuclear degrees of freedom described by complex potential energy surfaces (PESs). The resulting anharmonic wave functions can, however, no longer be as straightforwardly interpreted as those within the harmonic approximation. For this reason, an assignment of the vibrational eigenstates is commonly performed, based either on harmonic reference states or, less frequently, on mean-field wave functions obtained from vibrational self-consistent field (VSCF) calculations. However, in the case of strong anharmonicity, such an assignment of states fails to adequately characterize highly correlated vibrational states, such as resonant ones. These multiconfigurational vibrational wave functions can feature a high degree of entanglement between different vibrational modes and among different basis states of a given mode. Therefore, we propose vibrational quantum information measures for disentangling the entanglement structure of anharmonic wave functions in this Letter. We generalize the quantum information-based quantities introduced to electronic structure theory in refs (3−5) to vibrational wave functions. These information entropy measures can be applied for a diagnostic analysis of anharmonic molecular vibrations, as they provide both qualitative and quantitative insights to assess vibrational entanglement.
To reduce artifacts in the vibrational entanglement analysis, such as from an a priori restriction of the multiconfigurational wave function to a predefined excitation rank or due to the referencing to some zeroth-order wave function, we calculate the anharmonic vibrational wave functions with the vibrational density matrix renormalization group algorithm (vDMRG),6,7 because vDMRG does not impose a fixed predefined truncation of the chosen Hilbert space and allows for a systematic convergence toward the full vibrational configuration interaction (VCI) limit. As such, it is an ideal method for obtaining accurate anharmonic wave functions with a balanced description of correlation effects while enabling the treatment of dozens of coupled vibrational modes by virtue of its favorable scaling with system size. In the following, we define and calculate vibrational entanglement descriptors based on the flexible n-mode formulation of the vDMRG algorithm.8 Notwithstanding that, we emphasize that these descriptors can be applied to any kind of correlated second-quantized vibrational wave function regardless of the method chosen for solving the vibrational structure problem. Our vibrational entanglement analysis can be performed in general modal basis sets, irrespective of the PES parametrization scheme or the choice of vibrational coordinates.
n-mode vDMRG is a full-VCI-type method, which can be applied in conjunction with general single-particle basis sets while offering full flexibility with respect to both the functional form of the PES and its expansion coordinates. In a vDMRG calculation, the multiconfigurational many-body wave function is encoded as a matrix product state (MPS) as
| 1 |
where L is the overall number
of single-particle basis states σl mapped onto the DMRG lattice and  represents the corresponding many-body
basis state. The Mσiai-1ai are rank-three tensors with the index σi labeling the basis state of lattice site i, where for a given value of σi, Mσi is matrix of at most size m × m. The upper limit for the matrix dimension m is
commonly referred to as the bond dimension, and it is the key parameter
of any DMRG calculation, as it controls the compression degree of
the MPS wave function. Although an exact reconstruction of the full-VCI
wave function requires the bond dimension m to grow
exponentially with the basis size L of the system,9 we showed in previous work that for vDMRG calculations,
converged energies can be obtained already with rather small values
of m, i.e., m ≤ 100,6−8,10 hence effectively reducing the
exponential scaling of the MPS with system size to a polynomial one.
represents the corresponding many-body
basis state. The Mσiai-1ai are rank-three tensors with the index σi labeling the basis state of lattice site i, where for a given value of σi, Mσi is matrix of at most size m × m. The upper limit for the matrix dimension m is
commonly referred to as the bond dimension, and it is the key parameter
of any DMRG calculation, as it controls the compression degree of
the MPS wave function. Although an exact reconstruction of the full-VCI
wave function requires the bond dimension m to grow
exponentially with the basis size L of the system,9 we showed in previous work that for vDMRG calculations,
converged energies can be obtained already with rather small values
of m, i.e., m ≤ 100,6−8,10 hence effectively reducing the
exponential scaling of the MPS with system size to a polynomial one.
In our original formulation of vDMRG,6,10 the vibrational
wave function was restricted to vibrational Hamiltonians expressed
in a harmonic oscillator basis, with the PES being represented as
Taylor series around a reference geometry. While this canonical vDMRG
algorithm is an efficient method to characterize weakly anharmonic
vibrational systems, it is not well-suited to treating strong anharmonic
effects due to its inherently limited description of the vibrational
degrees of freedom, in terms of both the basis functions and the
PES parametrization. These drawbacks can be overcome by employing
a more general second quantization framework which is adaptable to
strongly anharmonic systems by adopting a more flexible representation
of the PES. The PES  can be expressed as a general many-body
expansion in which terms are grouped based on the number of degrees
of freedom on which they depend. If the PES is expanded in terms of
Cartesian normal mode coordinates Q =
(Q1, ..., QM), the so-called n-mode expansion11−13 is obtained
can be expressed as a general many-body
expansion in which terms are grouped based on the number of degrees
of freedom on which they depend. If the PES is expanded in terms of
Cartesian normal mode coordinates Q =
(Q1, ..., QM), the so-called n-mode expansion11−13 is obtained
| 2 |
where the terms in  depend on exactly n of
the M normal modes, while all other coordinates remain
fixed at their reference values. The one-body term
depend on exactly n of
the M normal modes, while all other coordinates remain
fixed at their reference values. The one-body term 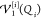 represents the anharmonic variation of
the PES upon change of the i-th coordinate. Similarly,
the two-body term
represents the anharmonic variation of
the PES upon change of the i-th coordinate. Similarly,
the two-body term 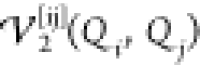 contains the variation of the potential
arising from simultaneously changing two coordinates i and j. The one-mode contributions
contains the variation of the potential
arising from simultaneously changing two coordinates i and j. The one-mode contributions 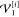 and
and 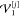 are removed from
are removed from 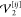 to ensure that the latter quantity includes
only the pure coupling between the modes. The n-mode
expansion becomes exact if carried out up to the M-th order. It has been shown, however, that even for strongly anharmonic
systems an accurate representation of the PES can be obtained by truncating
the expansion in eq 2 already at low orders.11,14−16 Furthermore, the PES expansion given in eq 2 enables one to encode the potential terms
in second quantization with general single-mode basis sets,17 allowing for basis functions which are more
suited to encode anharmonicity than harmonic oscillator functions,
such as the anharmonic mean-field eigenfunctions of a VSCF calculation.18−20
to ensure that the latter quantity includes
only the pure coupling between the modes. The n-mode
expansion becomes exact if carried out up to the M-th order. It has been shown, however, that even for strongly anharmonic
systems an accurate representation of the PES can be obtained by truncating
the expansion in eq 2 already at low orders.11,14−16 Furthermore, the PES expansion given in eq 2 enables one to encode the potential terms
in second quantization with general single-mode basis sets,17 allowing for basis functions which are more
suited to encode anharmonicity than harmonic oscillator functions,
such as the anharmonic mean-field eigenfunctions of a VSCF calculation.18−20
We denote a general single-mode basis function (commonly referred to as a modal) for mode i by φkii, where ki ∈ {1, ..., Ni} with Ni being the overall dimension of the basis set of a given mode. A basis state for the full M-body vibrational wave function expansion can then be constructed from a product of modals as
| 3 |
The many-body basis function ψk1,···, kM can be represented as an occupation number vector (ONV) with
| 4 |
where nkii denotes the occupation
of the ki-th modal φkii associated with the i-th mode. The multiconfigurational wave function 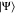 can then be efficiently encoded in n-mode vDMRG by mapping each modal basis function to a site
on the DMRG lattice. Hence, the n-mode MPS contains
a tensor for each basis function included in the expansion, as is
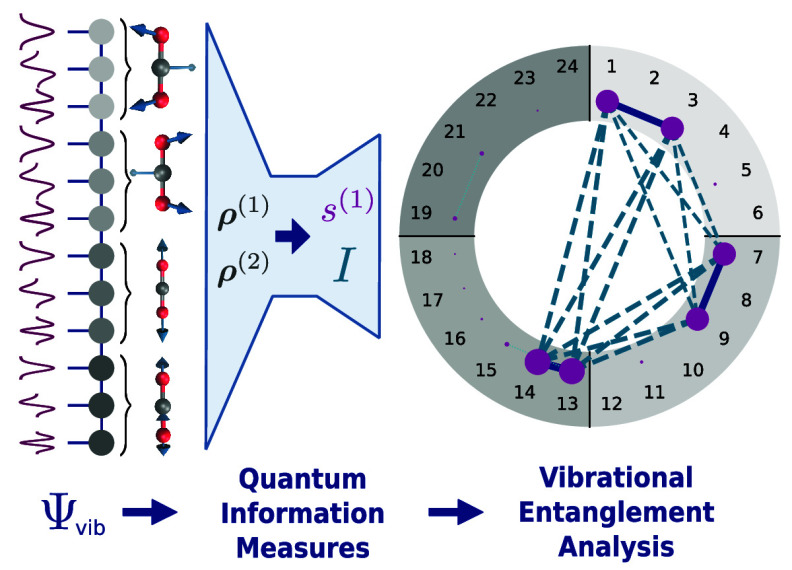
graphically illustrated in Figure 1 on the example of CO2.
can then be efficiently encoded in n-mode vDMRG by mapping each modal basis function to a site
on the DMRG lattice. Hence, the n-mode MPS contains
a tensor for each basis function included in the expansion, as is
graphically illustrated in Figure 1 on the example of CO2.
Figure 1.
Illustration of the n-mode MPS of CO2. In the diagrammatic tensor network notation, each filled circle denotes an MPS tensor with the adjoining lines representing the respective indices. For each of the four vibrational modes of CO2, the three lowest-energy VSCF eigenfunctions are included in the modal basis set.
Based on the general many-body basis introduced in eq 3, we now extend the definition of quantum information measures originally introduced in the context of electronic DMRG3−5 to vibrational wave functions (cf. also refs (21−23) for a discussion of electron correlation and orbital entanglement). Specifically, we define the vibrational analogues to the single- and two-orbital reduced density matrices (RDMs), the corresponding von Neumann entropies, and the orbital-pair mutual information. Toward this end, we partition the VCI expansion in n-mode second quantization into a system consisting of the ki-th modal of the i-th mode and an environment containing all remaining basis functions. In terms of this partition, the VCI expansion can be rewritten as
| 5 |
where we collected
all the modals different from the ki-th one in a single ONV 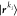 . The one-modal RDM can then be obtained
by tracing out all possible states of
. The one-modal RDM can then be obtained
by tracing out all possible states of 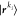 , i.e.
, i.e.
| 6 |
where 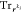 is the trace operator over the
is the trace operator over the 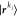 basis. The one-modal RDM can be understood
as an operator acting on the occupation-number basis of the φkii modal. Its matrix representation
in the σki ∈ {
basis. The one-modal RDM can be understood
as an operator acting on the occupation-number basis of the φkii modal. Its matrix representation
in the σki ∈ {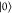 ,
, 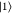 } basis reads
} basis reads
| 7 |
where we introduced the number operator n̂kii = b†kibki based on the creation and annihilation operators for modal φkii. For a single ONV, the diagonal elements of the one-modal RDM ρ(1)ki will be either 0 and 1, if the ki-th modal is occupied, or 1 and 0, if it is not contributing to the many-body state. For a general VCI wave function, the diagonal elements are between 0 and 1, and the deviation from the two extremal values increases with the degree of correlation of modal φkii with all other ones. This modal entanglement can be quantified with the von Neumann entropy, which we can introduce with respect to a specific basis function φkii as
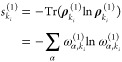 |
8 |
where the sum runs over the eigenvalues ω(1)α,ki of the RDM of the ki-th basis function. Based on the one-modal RDM given in eq 7, the single-modal von Neumann entropy can be conveniently calculated as
| 9 |
which allows for straightforward evaluation
by measuring the expectation value of the occupation n̂kii of modal φkii in the multiconfigurational
many-body wave function. The single-modal von Neumann entropy provides
a measure for the extent to which the state of the system, which here
corresponds to the ki-th modal, is affected by the state of the environment rki as it quantifies the interaction of a particular modal with
the modal “bath” in terms of the exchange of information.
At the same time, the single-modal entropy quantifies how much modal
φkii contributes
to the deviation of the many-body wave function from a pure product
state (i.e., a state where only one of the possible states σki ∈ {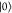 ,
, 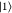 } of that modal is populated). For a pure
product state, we have s(1)ki = 0, whereas for a maximally entangled modal we obtain s(1)ki = ln 2 for
} of that modal is populated). For a pure
product state, we have s(1)ki = 0, whereas for a maximally entangled modal we obtain s(1)ki = ln 2 for 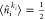 . We note here that in the quantum computing
community the von Neumann entropy is often defined as S = −Tr(ρlog2 ρ),24 hence based on a base-2 logarithm, with a maximum value
of 1 for a maximally mixed single-qubit state. However, the two definitions
merely differ by a constant multiplicative factor and in terms of
the resulting units (the entropy S with the base-2
logarithm is commonly measured in “bits” or “shannons”,
whereas the natural logarithm is given in “nats”25).
. We note here that in the quantum computing
community the von Neumann entropy is often defined as S = −Tr(ρlog2 ρ),24 hence based on a base-2 logarithm, with a maximum value
of 1 for a maximally mixed single-qubit state. However, the two definitions
merely differ by a constant multiplicative factor and in terms of
the resulting units (the entropy S with the base-2
logarithm is commonly measured in “bits” or “shannons”,
whereas the natural logarithm is given in “nats”25).
To quantify the entanglement between two specific modals, we begin by introducing the two-modal reduced density matrix. We now consider a pair of modals {φkii, φljj} as the system, where the modals can be basis functions of the same mode (i = j) or belong to different modes (i ≠ j). The two-modal RDM ρ(2)ki,lj is then defined as
| 10 |
where we have collected all residual modals
in a single ONV 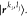 The representation of ρ(2)ki,lj in the standard ONV basis
The representation of ρ(2)ki,lj in the standard ONV basis 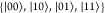 reads
reads
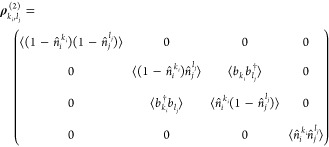 |
11 |
where the off-diagonal terms will vanish if the two modals belong to different modes as particle number symmetry is conserved. We can now define the two-modal entropy s(2)ki,lj as
| 12 |
where the sum runs over all eigenvalues ω(2)α,kilj of the two-modal RDM. The two-modal entropy provides a measure for how much the combined state of two modals is affected by the environment and quantifies the information that the modal-pair possesses about the remaining modal bath and vice versa. If the state of the modal-pair is not correlated to the state of the residual modals at all, the two-modal entropy is zero, whereas its maximum value is bound by s(2)ki,lj ≤ s(1)ki + s(1)lj ≤ ln 4.
To obtain the pure two-body correlation between modals φkii and φljj, we calculate their mutual modal information which we define as
| 13 |
Since the contribution of the two-modal entropy is subtracted from the single-modal entropies, the mutual modal information measures how strongly two modals are mutually correlated as all correlation with the remaining modal bath is removed. Iki,lj evaluates to zero for any uncorrelated pair of modals, whereas its maximum value amounts to Iki,lj = ln 2 for a maximally entangled pair of modals. The mutual information quantifies the total information one system (here, modal φkii) has about another (modal φljj) and vice versa, including all types of correlation, both classical and quantum. Note that alternative definitions of mutual information are sometimes employed in electronic structure theory and quantum information science, which effectively, however, only differ by a constant prefactor. Here we follow the convention that the quantum information measure will result in larger positive values if the system of interest is in a more strongly entangled state, whereas it will be lower bound by zero if the system does not possess any correlation at all.
The total quantum information encoded in the many-body wave function can be quantified as
| 14 |
where the sum runs over all single-mode basis functions of all modes. If Itot = 0, the vibrational wave function is in a pure product state, whereas its multiconfigurational character increases with larger values of Itot.
We emphasize that while our derivation of the modal information entropies follows similar steps as for the definition of the electronic one- and two-orbital entropies,3 we here account for distinguishable bosons in lieu of indistinguishable fermions. As a consequence, the form of the RDMs given in eqs 7 and 11 is inherently different from that in the electronic case. Furthermore, the vibrational entropies s(1)ki and s(2)ki,lj depend on both the mode and the basis function. We can, therefore, distinguish between inter- and intramode vibrational entanglement, which allows for a more differentiated look at the interaction patterns encoded in complex vibrational wave functions.
Although we focus on bipartite entanglement descriptors in this work, the extension of our approach to multipartite entanglement measures is possible in principle. However, already for tripartite systems, the proper characterization of entanglement has been subject to debate and many different quantification measures have been proposed, among them the so-called tangle,26 generalized Schmidt measures,27,28 measures based on normal forms,29 and geometric measures.30,31 These entanglement descriptors differ not only in their definition but also in the resulting classification of entangled states, depending on whether or not they are genuine multipartite entanglement measures. In the context of von Neumann entropy-based descriptors, the mutual information has been generalized to multipartite systems as32
| 15 |
where N is the number of subsystems considered. Calculating this expression would, however, require the evaluation of higher-order density matrices, which can be costly. Hence, for our purpose of introducing a cost-effective vibrational entanglement analysis, we solely rely on bipartite entanglement descriptors, as these enable an intuitive characterization of anharmonic vibrational wave functions at negligible computational cost by dissecting a complex many-body wave function into single-modal contributions and pairwise correlations.
To demonstrate our vibrational modal-entanglement analysis, we study CO2 as a classical example exhibiting strong anharmonic effects due to its Fermi resonance.33 CO2 possesses both symmetry-induced and accidental (near) degeneracies, as the two bending modes ν2 and ν̅2 are degenerate, while their overtone features almost the same harmonic energy as the fundamental transition of the symmetric stretching mode ν1 so that these modes are strongly coupled.34,35 We calculated the n-mode vibrational Hamiltonian of CO2 in second quantization with colibri(36) by applying the computational methodology introduced in ref (8). For this, we constructed an accurate anharmonic PES with up to 3-body coupling terms based on explicitly correlated CCSD(T)-F12/RI electronic structure single points37 obtained in the cc-pVTZ-F12 basis38 with the orca program39 through the interface available within colibri. As a primitive basis set, we chose an 11-point discrete variable representation (DVR) basis40 along each normal coordinate by equidistantly distributing the DVR points around the equilibrium geometry up to the 5th harmonic inversion point of each mode. We then transformed the second-quantized vibrational Hamiltonian into a modal basis, where we selected the six lowest-energy states of each mode as the single-particle basis set. Several choices for the modal basis function type are available in our computational framework, namely, harmonic oscillator eigenfunctions, (partially) random modal guesses, modals obtained by diagonalizing the anharmonic one-body potential, and modals calculated with our VSCF algorithm corresponding to the mean-field solution of the anharmonic Hamiltonian. For illustrative purposes, we compare two modal basis sets in this Letter, namely, optimized VSCF modals and unoptimized, noisy modals constructed from the diagonalization of the anharmonic one-body potential with a 20% uniform noise admixture. To obtain the correlated vibrational wave function in a given modal basis, we optimized the vibrational MPS with the n-mode vDMRG algorithm implemented in the QCMaquis program.6,8,41 To ensure that the multiconfigurational wave function was well converged to sub-cm–1 accuracy for the vibrational energy, the bond dimension of the MPS was dynamically adapted according to a truncation threshold of λcut ≤ 10–12, and the MPS was optimized until it fulfilled the chosen energy convergence threshold of ΔE ≤ 10–10 cm–1 from one DMRG sweep to the next. The excited states were calculated through a constrained optimization of the MPS tensors orthogonal to all lower-lying states. Once the MPS wave function optimization was converged, we measured the modal entropies by applying the corresponding operators in matrix form to the MPS. The energies of the fundamental vibrations of CO2 and the ν2 overtones as calculated in a VSCF modal basis are given in Table 1.
Table 1. Vibrational Wavenumbers of the Fundamental Frequencies and the First Resonance Polyad of CO2 (cm–1)a.
| State | Harmonic | VSCF | VCISDT | vDMRG | TBE | Exptl |
|---|---|---|---|---|---|---|
| ν1 | 1353.3 | 1341.2 | 1285.1 | 1285.1 | 1288.9 | 1285.4 |
| ν2 | 673.3 | 668.6 | 667.6 | 667.6 | 669.1 | 667.4 |
| ν3 | 2394.2 | 2352.3 | 2347.0 | 2347.0 | 2349.2 | 2349.2 |
| ν22 (l = 0) | 1346.6 | 1341.3 | 1388.7 | 1388.7 | 1389.3 | 1388.2 |
| ν2ν̅2 | 1346.6 | 1338.4 | 1336.6 | 1336.5 | 1339.6 | 1335.1 |
| ν22 (l = 2) | 1346.6 | 1341.3 | 1338.9 | 1336.6 |
Bold font highlights the wavenumbers of the Fermi doublet. l denotes the vibrational angular momentum of the ν22 states. For comparison, the theoretical best estimates (TBE) calculated by ref (34) and the experimental values from ref (42) are listed. The states ν2ν̅2 and ν22 (l = 2) have not been distinguished by Hirata and coworkers, whereas we calculated and characterized both states.
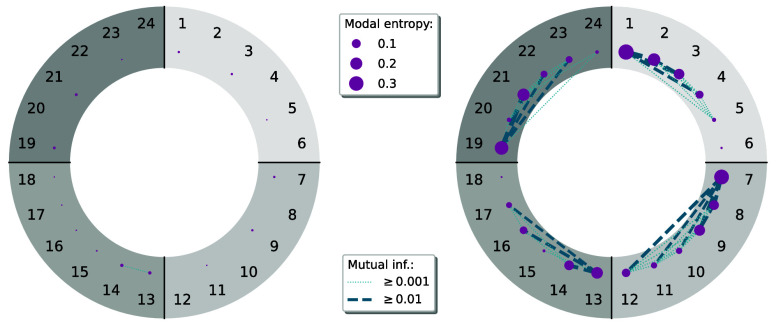
For the vibrational entanglement analysis, we visualize the single-modal entropy and the mutual modal information in entanglement diagrams, similar to what has been done first for electronic structure problems.43−45 For this purpose, we arrange the modals in a circular fashion with the modals belonging to the same mode being grouped together. The single-modal entropy and the mutual modal information are then represented as points and connecting lines, respectively, with their sizes and line strengths representing their numerical values. Entanglement diagrams of the zero-point vibrational ground state calculated in two different modal basis sets are shown in Figure 2. In these diagrams, the modals are arranged in correspondence to the MPS lattice ordering in Figure 1, except that we now include 6 basis functions per mode.
Figure 2.
Modal entanglement diagrams showing the single-modal von Neumann entropies (purple circles) and the mutual modal information (connecting lines) for the vibrational ground state of CO2 in an optimized VSCF modal basis (left) and an unoptimized, noisy modal basis (right). Each quarter of the circle is assigned to a vibrational mode, with the modes ordered with increasing energy as ν2, ν̅2, ν1, and ν3 from the lighter to the darker shaded segments, respectively. In each segment, the modal energy increases clockwise.
The vibrational entanglement analysis of the ground state wave function in the optimized VSCF modal basis contains very few correlation features. VSCF modals can encode the single-mode anharmonicity of the PES entirely such that the resulting product state would be exact in the absence of mode-coupling terms. They also absorb the mean-field coupling between the different modes through the VSCF procedure. As such, the vibrational ground state wave function can be well represented with an almost pure product state, which can be seen from the very small single-modal entropies and the absence of any strong correlation, as indicated by the lack of modal pairs with a large mutual modal information.
In the unoptimized noisy modal basis, however, distinct vibrational entanglement patterns can be observed. The modals possess a significant entropy, with higher values measured for the lower-energy modals than for the highly excited ones (as expected since low-energy basis functions usually contribute more to the ground state wave function than high-energy ones). Strong correlation patterns occur within the modal basis sets of all four modes. While the mutual modal information of modal pairs belonging to the same vibrational mode is considerably large, the intermode correlation is almost negligible. This is to be expected, as the noise in the modal basis increases intramode entanglement, while it does not change the strength of the anharmonic couplings between the different modes. Since both states are obtained for the same vibrational Hamiltonian, just expressed in different modal bases, the coupling between modes remains the same. Hence, while noisy modal bases result in higher (artificial) intramode correlation, they do not introduce additional intermode correlation. The intermode couplings, however, depend crucially on the expansion coordinates of the PES, meaning that a poor choice of coordinates can result in an artificially strongly coupled anharmonic Hamiltonian. For rather rigid molecules with a well-defined equilibrium structure, such as CO2, Cartesian normal modes are a natural choice for the PES expansion coordinates, but for more floppy molecules or weakly bound molecular clusters, other choices such as internal coordinates46 or local modes47 might be more suitable. The vibrational entanglement analysis can be exploited to monitor the extrinsic correlation that arises from the use of different vibrational coordinates and modal basis sets through the inter- and intramode correlation patterns. The ideal coordinate system minimizes intermode coupling strengths, while the optimal modal basis set minimizes the intramode correlation. The total correlation can be conveniently quantified through the total quantum information contained in the system, for instance, by measuring Itot for the vibrational ground state wave function.
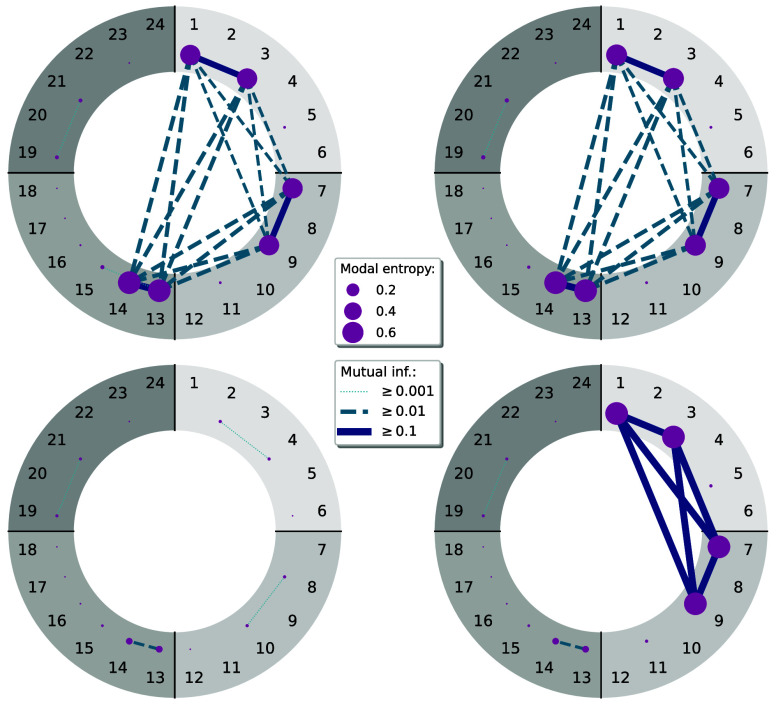
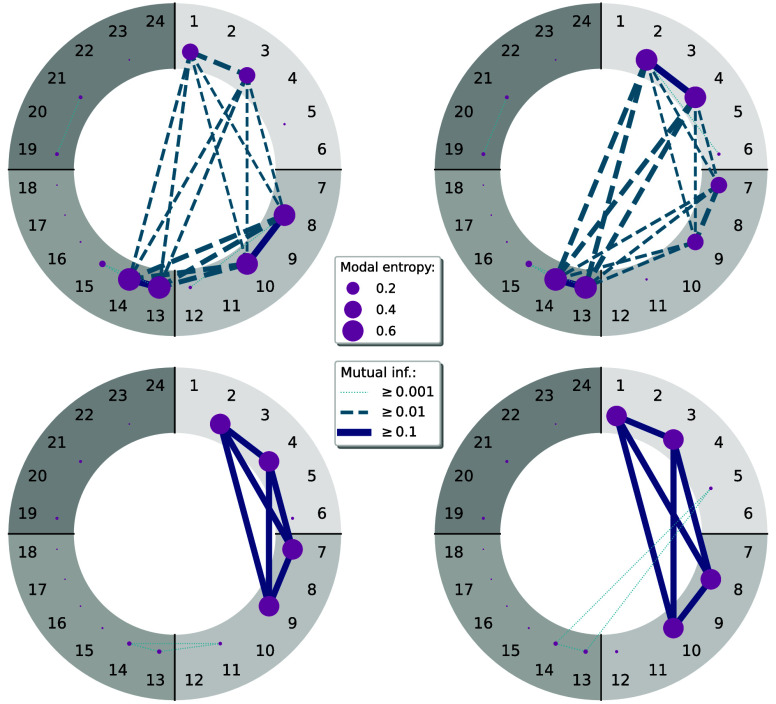
While the vibrational ground state in an optimized VSCF modal basis is nearly uncorrelated, the entanglement analysis of the excited states corresponding to the Fermi resonance shows striking entanglement patterns, as can be seen in the upper part of Figure 3, with the Fermi doublet displaying very similar entanglement signatures. In these resonant states, six modals have a significant entropy, namely, the ground state modals of the two bending vibrations ν2 and ν̅2, and the corresponding overtones, as well as the ground state modal and the fundamental excitation of the symmetric stretching mode ν1. These modals are strongly correlated, as indicated by their considerable pairwise mutual modal information, with the largest entanglement occurring between the modals belonging to the same vibrational mode. The total quantum information contained in these states is substantial, even though they are represented in an anharmonic, mean-field optimal modal basis. Hence, these vibrational wave functions are strongly multiconfigurational, with the large single-modal entropies distinctively characterizing the multiconfigurational state of the Fermi doublet. By analyzing the CI coefficients of the wave functions with the stochastic reconstruction of the complete active space (SRCAS) algorithm8,48 that reconstructs these coefficients from the vibrational MPS, we obtained ΨvDMRGν1 = 0.73ΨVSCFν1 – 0.48(ΨVSCFν22 + ΨVSCFν̅22) and ΨvDMRGν22,l = 0 = 0.68ΨVSCFν1 + 0.52(ΨVSCFν22 + ΨVSCFν̅22).
Figure 3.
Modal entanglement diagrams of the vibrational states around the Fermi resonance of CO2 in a VSCF modal basis. In the upper half, the Fermi doublet with states ν1 (left) and ν22 with l = 0 (right) is displayed, where l denotes the vibrational angular momentum quantum number of the ν22 overtone states. In the lower half, two additional near-degenerate states are shown, namely, the state ν2ν̅2 (left) and the state ν22 with l = 2 (right).
In addition to the Fermi doublet, we show two further
nearly degenerate
excited states in Figure 3. While these states are within the energy interval of the
Fermi resonance, their wave functions transform according to different
irreducible representations. These differences in symmetry can be
easily observed in the vibrational entanglement analysis through their
distinct entanglement signatures. Whereas for the state ν2ν̅2 there is very little correlation,
the state ν22 with l = 2 exhibits strong entanglement
between the ground state modals and the second overtones of the two
degenerate bending modes. In fact, the symmetry-induced degeneracy
of these two vibrational modes results in a nearly maximally entangled
state, where all four involved modals have a von Neumann entropy of s(1)ki ≈ ln 2. The entanglement
is evenly distributed, as the mutual modal information between all
strongly correlated modal pairs is almost equal, with 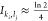 . If one only considers the two involved
modes ν2 and ν̅2, and regards
the two significant modals of each mode as the two possible states
of this mode, then one can draw a close analogy of this vibrational
state to a Bell state. The state of the vibrational resonance can
be reduced to
. If one only considers the two involved
modes ν2 and ν̅2, and regards
the two significant modals of each mode as the two possible states
of this mode, then one can draw a close analogy of this vibrational
state to a Bell state. The state of the vibrational resonance can
be reduced to 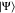 =
= 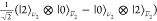 if one drops all modals except the ground
and overtone ones of the two bending modes. This corresponds exactly
to the Bell state |Ψ–⟩, which is a
maximally entangled two-qubit state. Due to the principle of monogamy
of entanglement,49 the involved modals
can thus not be significantly entangled with any other modals in this
state. In fact, the mutual information on bending modes ν2 and ν̅2 amounts to the maximum value Iν2,ν̅2 = ln 2.
if one drops all modals except the ground
and overtone ones of the two bending modes. This corresponds exactly
to the Bell state |Ψ–⟩, which is a
maximally entangled two-qubit state. Due to the principle of monogamy
of entanglement,49 the involved modals
can thus not be significantly entangled with any other modals in this
state. In fact, the mutual information on bending modes ν2 and ν̅2 amounts to the maximum value Iν2,ν̅2 = ln 2.
Distinct vibrational entanglement signatures of the resonances can not only be observed for the ν1 and ν22 states but also for higher excited states in the resonance polyad of CO2, as can be seen in Figure 4. The entanglement diagrams of the next-higher Fermi doublet display similarly characteristic correlation patterns as previously observed in Figure 3, with the main difference being that for one of the bending modes now the first and third excited modals are involved as expected due to the additional vibrational quantum in the bending mode. The symmetric stretching mode is more strongly correlated with the higher excited bending mode in both resonant states, as indicated by the larger mutual modal information. The entanglement diagrams of the ν32 overtones display a very similar correlation pattern as previously observed for the ν22(l = 2) state. Also here, the additional vibrational quantum in one of the bending modes can be seen directly in the modal entropies, as now the first and third excited modals are significantly correlated.
Figure 4.
Modal entanglement diagrams of the vibrational states in the second resonance polyad of CO2 in an excited-state VSCF modal basis of the ν22ν̅2 mean-field eigenstate. In the upper half, the Fermi doublet with an additional vibrational quantum in the bending mode is shown. In the lower half, the ν32 overtones are shown.
In this work, we introduced modal entropy descriptors that provide both qualitative and quantitative insights into correlated wave functions to assess vibrational entanglement and correlation effects. Degeneracies, whether symmetry-induced or accidental, result in distinct entanglement signatures that enable an intuitive visual assessment of the wave function characteristics. The modal entropy descriptors allow for a closer look at the multiconfigurational character of a given vibrational state and provide additional insights into the interactions encoded in a specific vibrational Hamiltonian. They could, in principle, also be exploited for the construction of suitable entanglement witnesses to experimentally verify whether a given vibrational state is entangled or not. For an experimental measurement, however, entanglement witnesses such as those based on the quantum Fisher information are likely to be more suitable candidates, as this quantity can be evaluated also for mixed quantum states and measured through spectroscopic observables.50
Although we performed the vibrational entanglement analysis on MPS wave functions calculated with the vDMRG algorithm in the present work, the modal entropy descriptors introduced in this Letter are completely general and can be easily transferred to other types of second-quantized multiconfigurational vibrational methods such as those based on vibrational configuration interaction or vibrational coupled cluster.51 As a consequence, the vibrational entanglement analysis can be applied to compare the results of different vibrational structure methods, PES parametrizations, vibrational coordinates, and modal basis sets. The quantum information descriptors can, for instance, be utilized to monitor the introduction of artificial inter- and intramode correlations caused by a poor choice of the expansion coordinates and the modal basis, respectively. The modal entropy descriptors can also be exploited to lower the computational costs of multiconfigurational anharmonic calculations or to further enhance their accuracy, e.g. by utilizing them (1) to determine the subset of strongly correlated vibrational modes that require treatment beyond the harmonic approximation or mean-field approach, (2) to select which modal basis functions to include in a multiconfigurational calculation (for instance, in the spirit of the AutoCAS algorithm52 for the automated selection of the active space orbitals in multiconfigurational electronic structure calculations), (3) to directly optimize the modal basis set with approaches inspired by orbital optimization schemes such as the QICAS method,53 (4) to optimize the ordering of both the modes and the modals on the DMRG lattice as is commonly done in electronic structure DMRG calculations,3,44,54 and (5) to establish a hierarchy of strongly correlated modes to guide the construction of tree tensor network states.55 We also note that, while we have applied the entanglement analysis to vibrational eigenstates in the present work, the modal entropy descriptors could also be straightforwardly exploited in time-dependent nuclear quantum dynamics simulations, for instance, to gain further insights into vibrational energy redistribution phenomena or to optimize the mode combination and layering scheme of the commonly employed multilayer multiconfigurational time-dependent Hartree ansatz.56,57
Acknowledgments
The authors gratefully acknowledge the financial support from the Swiss National Science Foundation through Grant No. 200021_219616.
The authors declare no competing financial interest.
References
- Puzzarini C.; Bloino J.; Tasinato N.; Barone V. Accuracy and Interpretability: The Devil and the Holy Grail. New Routes across Old Boundaries in Computational Spectroscopy. Chem. Rev. 2019, 119, 8131–8191. 10.1021/acs.chemrev.9b00007. [DOI] [PubMed] [Google Scholar]
- Bowman J. M., Ed. Vibrational Dynamics of Molecules; World Scientific: Singapore, 2022. [Google Scholar]
- Legeza Ö.; Sólyom J. Optimizing the density-matrix renormalization group method using quantum information entropy. Phys. Rev. B 2003, 68, 195116. 10.1103/PhysRevB.68.195116. [DOI] [Google Scholar]
- Legeza O.; Sólyom J. Quantum data compression, quantum information generation, and the density-matrix renormalization-group method. Phys. Rev. B 2004, 70, 205118. 10.1103/PhysRevB.70.205118. [DOI] [Google Scholar]
- Rissler J.; Noack R. M.; White S. R. Measuring orbital interaction using quantum information theory. Chem. Phys. 2006, 323, 519–531. 10.1016/j.chemphys.2005.10.018. [DOI] [Google Scholar]
- Baiardi A.; Stein C. J.; Barone V.; Reiher M. Vibrational Density Matrix Renormalization Group. J. Chem. Theory Comput. 2017, 13, 3764–3777. 10.1021/acs.jctc.7b00329. [DOI] [PubMed] [Google Scholar]
- Glaser N.; Baiardi A.; Reiher M. In Vibrational Dynamics of Molecules; Bowman J. M., Ed.; World Scientific, 2022; Chapter 3, pp 80–144. [Google Scholar]
- Glaser N.; Baiardi A.; Reiher M. Flexible DMRG-Based Framework for Anharmonic Vibrational Calculations. J. Chem. Theory Comput. 2023, 19, 9329–9343. 10.1021/acs.jctc.3c00902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schollwöck U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 2011, 326, 96–192. 10.1016/j.aop.2010.09.012. [DOI] [Google Scholar]
- Baiardi A.; Stein C. J.; Barone V.; Reiher M. Optimization of highly excited matrix product states with an application to vibrational spectroscopy. J. Chem. Phys. 2019, 150, 094113. 10.1063/1.5068747. [DOI] [PubMed] [Google Scholar]
- Carter S.; Culik S. J.; Bowman J. M. Vibrational self-consistent field method for many-mode systems: A new approach and application to the vibrations of CO adsorbed on Cu(100). J. Chem. Phys. 1997, 107, 10458–10469. 10.1063/1.474210. [DOI] [Google Scholar]
- Bowman J. M.; Carter S.; Huang X. MULTIMODE: A code to calculate rovibrational energies of polyatomic molecules. Int. Rev. Phys. Chem. 2003, 22, 533–549. 10.1080/0144235031000124163. [DOI] [Google Scholar]
- Toffoli D.; Kongsted J.; Christiansen O. Automatic generation of potential energy and property surfaces of polyatomic molecules in normal coordinates. J. Chem. Phys. 2007, 127, 204016. 10.1063/1.2805085. [DOI] [PubMed] [Google Scholar]
- Kongsted J.; Christiansen O. Automatic generation of force fields and property surfaces for use in variational vibrational calculations of anharmonic vibrational energies and zero-point vibrational averaged properties. J. Chem. Phys. 2006, 125, 124108. 10.1063/1.2352734. [DOI] [PubMed] [Google Scholar]
- Manzhos S.; Carrington T. Jr. A random-sampling high dimensional model representation neural network for building potential energy surfaces. J. Chem. Phys. 2006, 125, 084109. 10.1063/1.2336223. [DOI] [PubMed] [Google Scholar]
- Vendrell O.; Gatti F.; Lauvergnat D.; Meyer H.-D. Full-dimensional (15-dimensional) quantum-dynamical simulation of the protonated water dimer. I. Hamiltonian setup and analysis of the ground vibrational state. J. Chem. Phys. 2007, 127, 184302. 10.1063/1.2787588. [DOI] [PubMed] [Google Scholar]
- Christiansen O. A second quantization formulation of multimode dynamics. J. Chem. Phys. 2004, 120, 2140–2148. 10.1063/1.1637578. [DOI] [PubMed] [Google Scholar]
- Ratner M. A.; Gerber R. B. Excited vibrational states of polyatomic molecules: the semiclassical self-consistent field approach. J. Phys. Chem. 1986, 90, 20–30. 10.1021/j100273a008. [DOI] [Google Scholar]
- Bowman J. M. The self-consistent-field approach to polyatomic vibrations. Acc. Chem. Res. 1986, 19, 202. 10.1021/ar00127a002. [DOI] [Google Scholar]
- Hansen M. B.; Sparta M.; Seidler P.; Toffoli D.; Christiansen O. New formulation and implementation of vibrational self-consistent field theory. J. Chem. Theory Comput. 2010, 6, 235–248. 10.1021/ct9004454. [DOI] [PubMed] [Google Scholar]
- Boguslawski K.; Tecmer P.; Legeza Ö.; Reiher M. Entanglement Measures for Single- and Multireference Correlation Effects. J. Phys. Chem. Lett. 2012, 3, 3129–3135. 10.1021/jz301319v. [DOI] [PubMed] [Google Scholar]
- Boguslawski K.; Tecmer P. Orbital entanglement in quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1289–1295. 10.1002/qua.24832. [DOI] [Google Scholar]
- Ding L.; Mardazad S.; Das S.; Szalay S.; Schollwöck U.; Zimborás Z.; Schilling C. Concept of Orbital Entanglement and Correlation in Quantum Chemistry. J. Chem. Theory Comput. 2021, 17, 79–95. 10.1021/acs.jctc.0c00559. [DOI] [PubMed] [Google Scholar]
- Nielsen M. A.; Chuang I. L.. Quantum Computation and Quantum Information, 10th ed.; Cambridge University Press: Cambridge, 2010. [Google Scholar]
- International Organization for Standardization . Quantities and units Part 13: Information science and technology; 2008; Vol. IEC 80000–13:2008.
- Coffman V.; Kundu J.; Wootters W. K. Distributed Entanglement. Phys. Rev. A 2000, 61, 052306. 10.1103/PhysRevA.61.052306. [DOI] [Google Scholar]
- Acín A.; Andrianov A.; Costa L.; Jané E.; Latorre J. I.; Tarrach R. Generalized Schmidt Decomposition and Classification of Three-Quantum-Bit States. Phys. Rev. Lett. 2000, 85, 1560–1563. 10.1103/PhysRevLett.85.1560. [DOI] [PubMed] [Google Scholar]
- Eisert J.; Briegel H. J. Schmidt measure as a tool for quantifying multiparticle entanglement. Phys. Rev. A 2001, 64, 022306. 10.1103/PhysRevA.64.022306. [DOI] [Google Scholar]
- Verstraete F.; Dehaene J.; De Moor B. Normal forms and entanglement measures for multipartite quantum states. Phys. Rev. A 2003, 68, 012103. 10.1103/PhysRevA.68.012103. [DOI] [Google Scholar]
- Wei T.-C.; Goldbart P. M. Geometric measure of entanglement and applications to bipartite and multipartite quantum states. Phys. Rev. A 2003, 68, 042307. 10.1103/PhysRevA.68.042307. [DOI] [Google Scholar]
- Xie S.; Eberly J. H. Triangle Measure of Tripartite Entanglement. Phys. Rev. Lett. 2021, 127, 040403. 10.1103/PhysRevLett.127.040403. [DOI] [PubMed] [Google Scholar]
- Horodecki R. Informationally coherent quantum systems. Phys. Lett. A 1994, 187, 145–150. 10.1016/0375-9601(94)90052-3. [DOI] [Google Scholar]
- Fermi E. Über den Ramaneffekt des Kohlendioxyds. Z. Phys. 1931, 71, 250–259. 10.1007/BF01341712. [DOI] [Google Scholar]
- Rodriguez-Garcia V.; Hirata S.; Yagi K.; Hirao K.; Taketsugu T.; Schweigert I.; Tasumi M. Fermi resonance in CO2: A combined electronic coupled-cluster and vibrational configuration-interaction prediction. J. Chem. Phys. 2007, 126, 124303. 10.1063/1.2710256. [DOI] [PubMed] [Google Scholar]
- Yagi K.; Hirata S.; Hirao K. Vibrational quasi-degenerate perturbation theory: applications to fermi resonance in CO2, H2CO, and C6H6. Phys. Chem. Chem. Phys. 2008, 10, 1781. 10.1039/b719093j. [DOI] [PubMed] [Google Scholar]
- Glaser N.; Baiardi A.; Kelemen A. K.; Reiher M. qcscine/colibri: Release 1.0.0. 2023; 10.5281/zenodo.10276683, Development version. [DOI]
- Adler T. B.; Knizia G.; Werner H.-J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 2007, 127, 221106. 10.1063/1.2817618. [DOI] [PubMed] [Google Scholar]
- Peterson K. A.; Adler T. B.; Werner H.-J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 2008, 128, 084102. 10.1063/1.2831537. [DOI] [PubMed] [Google Scholar]
- Neese F. Software update: The ORCA program systemVersion 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. 10.1002/wcms.1606. [DOI] [Google Scholar]
- Colbert D. T.; Miller W. H. A novel discrete variable representation for quantum mechanical reactive scattering via the S-matrix Kohn method. J. Chem. Phys. 1992, 96, 1982–1991. 10.1063/1.462100. [DOI] [Google Scholar]
- Baiardi A.; Battaglia S.; Feldmann R.; Freitag L.; Glaser N.; Kelemen A. K.; Keller S.; Knecht S.; Ma Y.; Stein C. J.. et al. qcscine/qcmaquis: Release 3.1.3. 2023; 10.5281/zenodo.7907785, Development version. [DOI]
- Chedin A. The carbon dioxide molecule: Potential, spectroscopic, and molecular constants from its infrared spectrum. J. Mol. Spectrosc. 1979, 76, 430–491. 10.1016/0022-2852(79)90236-4. [DOI] [Google Scholar]
- Murg V.; Verstraete F.; Legeza O.; Noack R. M. Simulating strongly correlated quantum systems with tree tensor networks. Phys. Rev. B 2010, 82, 205105. 10.1103/PhysRevB.82.205105. [DOI] [Google Scholar]
- Barcza G.; Legeza O.; Marti K. H.; Reiher M. Quantum-information analysis of electronic states of different molecular structures. Phys. Rev. A 2011, 83, 012508. 10.1103/PhysRevA.83.012508. [DOI] [Google Scholar]
- Freitag L.; Knecht S.; Keller S. F.; Delcey M. G.; Aquilante F.; Bondo Pedersen T.; Lindh R.; Reiher M.; González L. Orbital entanglement and CASSCF analysis of the Ru-NO bond in a Ruthenium nitrosyl complex. Phys. Chem. Chem. Phys. 2015, 17, 14383–14392. 10.1039/C4CP05278A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson J.; Bright E.; Decius P. G.; Cross J. G.. Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill: New York, 1955; Vol. 102. [Google Scholar]
- Jacob C. R.; Reiher M. Localizing normal modes in large molecules. J. Chem. Phys. 2009, 130, 84106. 10.1063/1.3077690. [DOI] [PubMed] [Google Scholar]
- Boguslawski K.; Marti K. H.; Reiher M. Construction of CASCI-type wave functions for very large active spaces. J. Chem. Phys. 2011, 134, 224101. 10.1063/1.3596482. [DOI] [PubMed] [Google Scholar]
- Osborne T. J.; Verstraete F. General Monogamy Inequality for Bipartite Qubit Entanglement. Phys. Rev. Lett. 2006, 96, 220503. 10.1103/PhysRevLett.96.220503. [DOI] [PubMed] [Google Scholar]
- Hales J.; Bajpai U.; Liu T.; Baykusheva D. R.; Li M.; Mitrano M.; Wang Y. Witnessing light-driven entanglement using time-resolved resonant inelastic X-ray scattering. Nat. Commun. 2023, 14, 3512. 10.1038/s41467-023-38540-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christiansen O. Vibrational structure theory: new vibrational wave function methods for calculation of anharmonic vibrational energies and vibrational contributions to molecular properties. Phys. Chem. Chem. Phys. 2007, 9, 2942–2953. 10.1039/b618764a. [DOI] [PubMed] [Google Scholar]
- Stein C. J.; Reiher M. Automated Selection of Active Orbital Spaces. J. Chem. Theory Comput. 2016, 12, 1760–1771. 10.1021/acs.jctc.6b00156. [DOI] [PubMed] [Google Scholar]
- Ding L.; Knecht S.; Schilling C. Quantum Information-Assisted Complete Active Space Optimization (QICAS). J. Phys. Chem. Lett. 2023, 14, 11022–11029. 10.1021/acs.jpclett.3c02536. [DOI] [PubMed] [Google Scholar]
- Moritz G.; Hess B. A.; Reiher M. Convergence behavior of the density-matrix renormalization group algorithm for optimized orbital orderings. J. Chem. Phys. 2005, 122, 024107. 10.1063/1.1824891. [DOI] [PubMed] [Google Scholar]
- Larsson H. R. Computing vibrational eigenstates with tree tensor network states (TTNS). J. Chem. Phys. 2019, 151, 204102. 10.1063/1.5130390. [DOI] [PubMed] [Google Scholar]
- Vendrell O.; Meyer H.-D. Multilayer multiconfiguration time-dependent Hartree method: Implementation and applications to a Henon-Heiles Hamiltonian and to pyrazine. J. Chem. Phys. 2011, 134, 044135. 10.1063/1.3535541. [DOI] [PubMed] [Google Scholar]
- Mendive-Tapia D.; Meyer H.-D.; Vendrell O. Optimal Mode Combination in the Multiconfiguration Time-Dependent Hartree Method through Multivariate Statistics: Factor Analysis and Hierarchical Clustering. J. Chem. Theory Comput. 2023, 19, 1144–1156. 10.1021/acs.jctc.2c01089. [DOI] [PubMed] [Google Scholar]