Multimodal analysis of traction forces and the temperature dynamics of living cells with a diamond-embedded substrate

Abstract

Cells and tissues are constantly exposed to chemical and physical signals that regulate physiological and pathological processes. This study explores the integration of two biophysical methods: traction force microscopy (TFM) and optically detected magnetic resonance (ODMR) to concurrently assess cellular traction forces and the local relative temperature. We present a novel elastic substrate with embedded nitrogen-vacancy microdiamonds that facilitate ODMR-TFM measurements. Optimization efforts focused on minimizing sample illumination and experiment duration to mitigate biological perturbations. Our hybrid ODMR-TFM technique yields TFM maps and achieves approximately 1 K precision in relative temperature measurements. Our setup employs a simple wide-field fluorescence microscope with standard components, demonstrating the feasibility of the proposed technique in life science laboratories. By elucidating the physical aspects of cellular behavior beyond the existing methods, this approach opens avenues for a deeper understanding of cellular processes and may inspire the development of diverse biomedical applications.

1. Introduction

Cells and tissues are complex biological objects regulated by chemical and physical signals. Chemical stimulation is induced by sugars, fatty acids, amino acids, mineral salts, vitamins, hormones, and other necessary compounds for cell survival, growth, and other physiological processes [1]. Physical stimulation of cells is equally important and can be exerted in many forms, such as by applying an electric field, mechanical forces, dimensionality constraints, light, or even physical plasma [2–4]. One of the most prominent types of physical signals in organisms is the mechanical interaction between cells and their microenvironment. The ability of cells to sense forces and translate them into intracellular signals, as well as to exert forces back on the microenvironment, is called mechanotransduction. Cells can detect mechanical stimulation through several types of receptors, including the adhesion sites that are bound to the cytoskeleton [5]. Adherent cells adapt to the mechanical microenvironment through the dynamic rearrangement of their cytoskeleton and, in turn, exert the so-called traction forces back on their surroundings. These forces can be quantified by traction force microscopy (TFM) [6,7], which registers the deformations of a cellular substrate and transforms them into traction forces [8]. TFM is one of the most fundamental methods in cellular mechanobiology as it explains the role of substrate stiffness, cell contraction, migration, adhesiveness, and focal adhesion architecture in cellular mechanics [9,10] and reveals the role of mechanical signals in tissue dynamics [11,12] and cancer metastasis [13,14].

Another relevant physical factor that affects cells is temperature. Even in homeothermic organisms, the internal temperature varies owing to specific cell functions [15] and metabolism [16]. Furthermore, in vitro studies have indicated that increased temperature can affect myoblast proliferation [17]. Thermal heterogeneity has been observed in tumors [18] and at infection sites [19]; thus, temperature monitoring can be useful in diagnostics. Moreover, the stability of physiologically relevant temperature is crucial in live-cell microscopy to ensure the reliability and reproducibility of the study. Some of the most popular tools for temperature sensing are thermocouples, which are placed inside a Petri dish to measure the temperature of the cell medium. However, typical thermocouples are millimeter-sized, resulting in a significant thermal capacity, consequently resulting in a high inertia of their temporal response (∼300 ms) [20]. Their dimensions also make them impractical for local microscopy measurements. These problems were partially solved by the development of micro-thermocouples with lower inertia and greater measurement accuracy [21–23]. Recently, a new research field called micro- and nanothermometry has emerged, focusing on local temperature measurements [24]. Some of the tools used for such research include quantum dots [25], organic fluorophores [26], biomolecules [27], synthetic polymers [28,29], and diamonds. The latter have grown in popularity in various scientific fields; they use different types of color centers, with silicon-vacancy (SiV) [30] and nitrogen-vacancy (NV) centers [31] being the most popular.

In diamonds, a nitrogen-vacancy center is a defect in which one carbon atom is replaced by nitrogen and an adjacent lattice site is left empty, creating a vacancy, which may be neutral (NV⁰) or negatively charged (NV^-). NV^- color centers have high photostability and exhibit strong red fluorescence after green light excitation, making them useful as fluorescent markers in biological studies [32–35]. They are also paramagnetic; hence, they can be controlled by optically detected magnetic resonance (ODMR), which relies on the decrease of fluorescence intensity after the application of a microwave (MW) field with an appropriate frequency (∼2.87 GHz) [36]. ODMR allows the use of the NV⁻ centers for sensing electric [37] or magnetic [38–40] fields. Because of the linear temperature dependence of the ODMR frequency (-74.2 kHz/K at room temperature, see: Fig. 1(A)) [41], NV⁻ centers are also suitable as temperature sensors for use in biology [35,42–45].

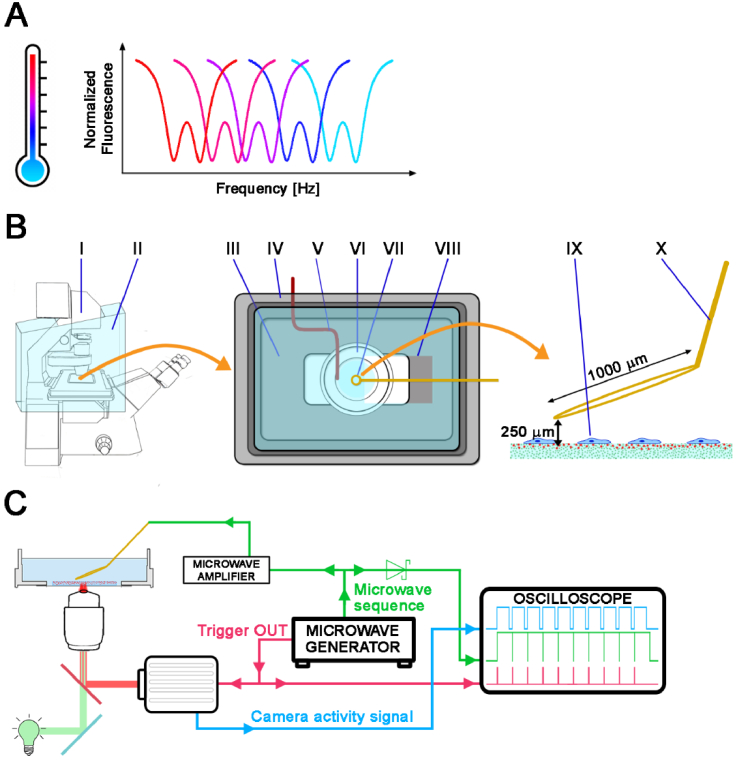
Fig. 1.

A: Illustration of the optically detected magnetic resonance (ODMR) temperature measurement: The ODMR resonance curves shift toward lower frequencies with increasing temperature. B: Scheme of the cell incubation equipment and the microscope setup: The left panel shows the fluorescence microscope (I) with a large incubation chamber (II). The middle panel presents the details of the incubator: (III) heated mini-incubator on-stage (bottom), (IV) incubator lid with window (top, not heated), (V) thermocouple placed inside the inner well of the dish, (VI) glass bottom dish with cells, (VII) microwave antenna, (VIII) opening in the lid to insert the antenna. The right panel schematically depicts the side view of the (IX) observed cells and (X) antenna loop wire. C: Scheme of the microwave setup. The microwave generator serves as the microwave source as well as the camera trigger. All signals were recorded on the oscilloscope.

Current studies of NV^- nanodiamonds as temperature sensors in biological research have adopted various methodological approaches. These methods primarily differ in their microscopy techniques: some studies have used confocal setups with point illumination, registering one diamond at a time [42,45,46], while others have used wide-field microscopes that register fluorescence from multiple diamonds [35,47]. In all cases, samples were illuminated with green lasers of various intensities, from 4.7 W/cm² [45] for point illumination to 3 kW/cm² for wide-field illumination [35]. The illumination intensity is crucial for live-cell experiments because intense laser light may cause phototoxic damage, leading to cell death. However, insufficient illumination decreases the contrast of the ODMR spectrum and the precision of the measured temperature. Another factor that influences ODMR quality is the type of fluorescence detector used. The described confocal microscopes were equipped with avalanche photodiodes (APDs) [42,45,46], whereas the wide-field setups were coupled with a single-photon detector [47] or an sCMOS camera [35], which also influenced the quality of the registered ODMR spectrum. Moreover, resonance can be registered and processed in various ways. In some studies, the microwave sequence consisted of two MW frequencies from the descending fragment of the ODMR spectrum and another two frequencies from the ascending fragment, which were registered multiple times and then averaged. The resonance position was found at the intersection of two linear functions fitted to each two-point set. In these studies, data acquisition took milliseconds to hundreds of milliseconds, and the precision of the temperature measurement was in the range of hundreds of millikelvins for nanodiamond-based temperature registration [42,46]. By contrast, the entire ODMR spectrum was measured in other studies, taking from 12 s [35] to 3–6 min [45]. Subsequently, the ODMR spectra were fitted with one or two Lorentzian curves, resulting in temperature precision ranging from millikelvins [35] to ∼1 Kelvin (K) [45]. The ODMR registration parameters affecting acquisition time play a pivotal role in live-cell imaging. Prolonged exposure to microwaves and heat generated by the antenna can elevate sample temperature, while exposure to illumination may induce phototoxic effects. Therefore, the precision of temperature measurements in live-cell imaging depends on the trade-off between the experimental conditions and cell viability.

Many experimental setups used in cell biophysics can measure only one physical factor at a time (e.g. substrate elasticity, mechanical deformation, and application of an electric current). Moreover, we did not find any reports linking the mechanical response of living cells to the local temperature. Therefore, our primary goal was to develop a wide-field microscope setup for simultaneous measurements of local relative temperature and cellular traction forces. This setup should be simple enough for application in life science laboratories with a focus on short measurement times and sufficient precision and accuracy for recording temperatures. Hence, we incorporated microwave equipment into an existing commercial wide-field microscope fitted with a mercury short-arc fluorescence lamp, dry 40x/0.6 objective, and a CMOS camera without any extensive modifications to the microscope. Moreover, we aimed to decrease the potentially adverse effects of the ODMR experiment on living cells that may be caused by intense light excitation, microwave irradiation, and long exposure times. These conditions are typical of standard measurements in physics and material science but are undesirable in experiments with living cells. One way to mitigate these effects is to keep the ODMR measurement time as short as possible. The final objective was to achieve sufficient precision in the temperature measurements (∼1 K in our case) to provide physiologically significant information, making it a good starting point for further development of the proposed ODMR-TFM method.

Here, we describe the preparation of an ODMR-TFM experimental material, the optimization of ODMR measurements, and a demonstration of ODMR-TFM measurements of cells that were heated or cooled down.

2. Materials and methods

2.1. Elastic substrate preparation

Elastic polyacrylamide (PA) substrates were prepared in two forms: first, in a glass bottom dish (Cellvis, #0 thickness) for microscopic observations and on standard glass slides for AFM measurements. For both types of substrates, glass was silanized using a mixture of 3-(trimethoxysilyl)propyl methacrylate (Sigma-Aldrich), glacial acetic acid (Chempur), and 96% ethyl alcohol in a 1:1:14 ratio for 20 min. Subsequently, the glass was rinsed three times with 96% ethyl alcohol to wash out any residues of chemicals [48]. A polymerization mixture of the blank 12 kPa substrate was prepared by mixing 7.5% acrylamide with 0.16% bis-acrylamide in DI water. The mixture of the 12 kPa substrate with diamonds was prepared similarly to the blank substrate but with the addition of a pre-sonicated and vortexed 25 µg/mL suspension of NV^- diamonds. The polymerization mixture of the ODMR-TFM substrate—the substrate used for the parallel measurement of temperature and cellular traction—was prepared like the substrate with NV^- diamonds, but with the addition of 2% green fluorescent carboxylate-modified polystyrene (PS) beads of 200 nm in diameter (excitation: 505 nm, emission: 515 nm, Thermo Fisher Scientific). Each type of polymerization mixture was mixed with 0.5% ammonium persulfate and 0.05% tetramethylethylenediamine (Bio-Rad) as polymerization agents. All substrates were prepared by upside-down polymerization, and the appropriate amount of polymerization mixture (18 µL for thin substrates, 22 µL for medium-thickness substrates, and 26 µL for thick substrates) was placed on a glass coverslip, on top of which a glass slide or the inner surface of a glass bottom dish was placed to allow upside-down polymerization. This procedure allowed for the sedimentation of microdiamonds. After 1 h of polymerization, the glass bottom dish attached to the coverslip was turned upright and filled with PBS, allowing the coverslip (which was initially at the bottom) to detach. After polymerization, the substrates were left to stand for 24 h to dissolve any residual acrylamide. Subsequently, the substrates were washed three times with PBS.

2.2. Diamond surface functionalization and particle size characterization

Tests of different surface terminations in various solvents were conducted on nonfluorescent microdiamonds (MSY 0.75–1.25, Pureon AG), which exhibit a size (D50 = 1 µm) and surface properties similar to those of NV⁻ microdiamonds but are less expensive. The final suspension used in the experiments was prepared from NV⁻ microdiamond powder with ∼3.5 ppm color centers (MDNV1umHi30 mg, Adámas Nanotechnologies). Hydrogenated and oxygenated surface terminations were prepared by treating diamond powders with hydrogen and oxygen plasma, using a plasma cleaner system (Diener Zepto). Briefly, the weighed diamond powder was placed in a glass dish in the chamber of the plasma cleaner system. After the air was pumped out, the chamber was filled with hydrogen or oxygen to hydrogenate or oxidate the surface, respectively. The plasma RF generator was operated at a pressure of 0.3 mbar with a 13.56 MHz frequency and 300 W power. The diamond powder was treated with plasma for 10 min.

Next, four nonfluorescent microdiamond suspensions were prepared at a concentration of 0.5 mg/mL, using the following solvents: (I) deionized water (passed through a 0.22 µm PS filter), (II) DMSO, (III) BSA (2.5% w/w, freshly prepared from lyophilized BSA and prefiltered DI water), and (IV) FBS solution (FBS qualified, Gibco). Suspensions of NV^- oxygenated microdiamonds were also prepared in prefiltered DI water at a concentration of 0.5 mg/mL. Before the dynamic light scattering (DLS) measurements, the samples were sonicated for 5 min in an ultrasonic bath and then vortexed twice for 15 s at 3000 rpm.

The hydrodynamic diameters were determined using a Zetasizer Nano ZS particle analyzer (Malvern Panalytical, UK) equipped with a 632.8 nm laser and a narrowband filter (ZEN9062). Each suspension was placed in a disposable polystyrene cuvette (outer dimensions of 12 × 12 × 45 mm) and measured at 25 °C using a backscatter configuration (scattered light collected at a 173° angle). Three measurements were conducted for each particle size distribution. The particles were analyzed in terms of their mean hydrodynamic diameter (Z-average), standard error of the mean (SEM), and the 10^th, 50^th, and 90^th percentiles (Di₁₀, Di₅₀, and Di₉₀) derived from the intensity-weighted particle size distributions. SEM was calculated from the standard deviation derived from the polydispersity index [49].

2.3. Characterization of ODMR-TFM substrates

Elasticity measurements were performed using a NanoWizard 3 NanoScience AFM system (JPK Instruments) in force-mapping mode. The experiments were performed in triplicate, using samples prepared independently on different days, and each experimental day involved examining all types of 12 kPa substrates. Force mapping was performed for each substrate in five areas of the sample. All experiments were performed in a drop of Hanks’ Balanced Salt Solution (HBSS, Cat. No. 55037C, Sigma-Aldrich, St. Louis, MO, USA). A spatial map of the force vs. distance (FD) curves was measured on a 16 × 16-point grid and a square surface of 30 × 30 µm. The position of the scanned area was controlled by an inverted optical microscope (IX71, Olympus). Force-distance curves were measured at a speed of 2 µm/s with a maximum applied force of 1.2 nN. To evaluate the elastic modulus of the substrates, a non-covered spherical polystyrene probe with a radius of 2.5 µm (Novascan) mounted on a triangular cantilever with a spring constant of 0.03 N/m was used. Before each measurement, the cantilever spring constant was calibrated using dedicated software (SPM software, JPK Instruments). The global elastic modulus of the substrates was calculated using the Hertz-Sneddon model.

High-resolution topographic images were obtained using the force-distance (FD)-based imaging mode (QI; JPK Instruments). In this method, a single FD curve measurement is performed at every pixel of the image and then translated from the selected trigger force into images of the substrate topography. The loading force ranged from 0.5 to 0.7 nN and was adjusted to obtain a clear contrast of the topography of the substrate. The topography images obtained were analyzed using the JPK Data Processing software.

The nanopit analysis started with a manual outline of the nanopit area to find its deepest point. The nanopit depth was compared to the closest surroundings (i.e., the envelope with a width of three pixels).

Confocal imaging was performed using a Zeiss LSM 710 confocal microscope with a Zeiss α Plan-Apochromat 63x/1.46 oil objective. The maximum projection of ODMR-TFM substrate was obtained by flattening all slices of the 3D data into X-Z image by retaining the maximum intensity value along Y-axis for each pixel.

2.4. ODMR registration setup

A generator (Rohde & Schwarz SMBV100A) connected to an amplifier (Mini-Circuits ZRL-3500+) linked to the MW antenna—a coaxial cable terminated in a wire loop of ∼1 mm in diameter made of 0.2 mm copper wire—was used to produce microwaves. Wide-field ODMR was registered through a time-lapse sequence of fluorescent images acquired for each subsequent MW frequency with a CMOS camera (ORCA-Flash 4.0 V2). The camera was triggered by the signal from the MW generator; therefore, each following frequency of the microwave sequence triggered the acquisition of the next image. To increase the image acquisition speed, the ODMR spectrum was registered with a field of view limited to 1024 × 1024 pixels. The regular ODMR sweep (regular sweep) consisted of 201 discrete frequencies with a 0.25 MHz step between 2845 and 2895 MHz. The irregular sequence (Irreg) consisted of 0.25 MHz steps between 2864 and 2874 MHz with three off-resonance frequencies at the beginning and the end of the sequence. The MW frequency was switched every 25 ms. However, because of the camera’s dead time, fluorescence was registered only for 18 ms. The MW antenna was positioned ∼250 µm above the substrate, using the InjectMan NI 2 micromanipulator (Eppendorf). NV^- diamond fluorescence was recorded using a custom fluorescence cube built using a 470/40 nm (excitation) bandpass filter, DMLP 567 nm dichroic mirror, and FELH 600 nm filter (emission).

2.5. Optimization of ODMR experiments

To measure the optical power density of the fluorescence lamp, the LD Plan-Neofluar 40x/0.6 objective (Zeiss) was focused on the top layer of the ODMR-TFM substrate to obtain a sharp image of the green fluorescent beads. The field diaphragm on the fluorescence path was partially closed to make its borders visible on the image, allowing the measurement of the illuminated field of view (this area was then used to calculate the optical power density). The ODMR-TFM substrate was removed from the microscope stage and replaced with a power meter (PM100D power meter with an S120 sensor, Thorlabs). The objective was refocused to register the maximum optical power of the focused light. The optical power was between 0% and 100% of the intensity of the fluorescence lamp (HXP120, Zeiss). The optical power registered by the power meter was then divided by the field of view measured at the initial stage.

The thickness of the substrate was measured by refocusing between the top and bottom surfaces of the substrate, using a dry objective (Zeiss, LD Plan-Neofluar 40x/0.6). Because of the differences between the refractive index of the PA substrate and that of the air ( $n_{air}$ ), the measured distance ( $\mathrm{\Delta }{h}_{Measured}$ ) was corrected using the formula (1), as previously reported [50]. The refractive index of the polyacrylamide gel was assumed to be the same as that of water ( $n_{water}$ ), and NA was the numerical aperture of the objective.

$$\mathrm{\Delta }{h}_{Corr}=\mathrm{\Delta }{h}_{Measured}\ast \sqrt{\frac{{n_{water}}^2-N{A}^2}{{n_{air}}^2-N{A}^2}}$$ (1)

The ODMR spectra of the three substrates with different thicknesses were collected at room temperature. They were used to examine five locations of similar thickness, each for three ranges: thin (20–40 µm), medium (50–70 µm), and thick (100–120 µm). The temperature measurement precision for a single measurement comes from the uncertainty of fitting the Lorentzian to the acquired ODMR spectra (least squares method) multiplied by the temperature response of NV^- diamonds [41]. The average temperature measurement precision in Fig. 3(C) comes from averaging precision values obtained for the measured locations, so error bars stand for their standard error multiplied by the Student’s t critical value for 5 repetitions.

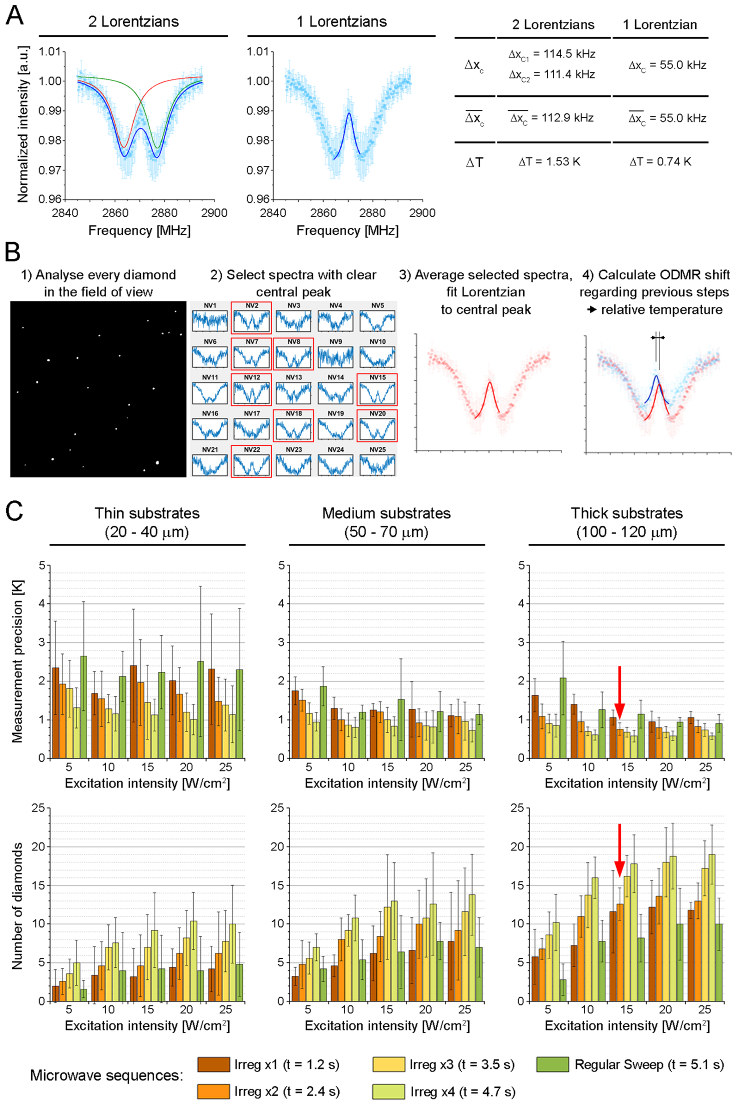
Fig. 3.

A: Precision of the determination of the center of the ODMR spectrum fitted by two Lorentzian functions compared to one Lorentzian function. $\mathrm{\Delta }{x}_c$ denotes the uncertainty of the position of the fitted Lorentzian peak (least square method), $\overline{\mathrm{\Delta }{x}_c}$ denotes the mean value of the measured $\mathrm{\Delta }{x}_c$ , the temperature uncertainty $\mathrm{\Delta }T$ was calculated assuming a slope of -74.2 kHz/K, according to Acosta et al. [41]. B: Sketch of the estimation of the relative temperature averaged in a field of view. C: Optimization of the ODMR experiment, effect of the excitation intensity and microwave sequences on the precision of the temperature measurement (top row) and the number of diamonds included in the analysis (bottom row). Optimized experimental conditions are marked in both rows by red arrows.

2.6. Temperature calibration of ODMR-TFM substrates

Temperature calibration of the ODMR-TFM substrate was performed in the range between 17 and 39 °C, using an incubator (Fig. 1(B)). A type-K thermocouple with an accuracy of ±1.5 °C was placed inside the glass bottom dish, on the left side of the inner well, touching the bottom coverslip. During the experiment, a glass bottom dish with an ODMR-TFM substrate was filled with the cell culture medium without phenol red to preserve the standard experimental conditions. Then, the temperature inside the dish was increased by 1 °C, confirmed by a stable thermocouple readout for 5 min. Hence, we assumed that the glass bottom dish with the substrate and the cell culture medium had the same temperature. The ODMR spectra were collected from three fields of view. For each time point, the reference full sweep and twice-averaged irregular sequence (see: ODMR registration setup) were measured. To avoid the potential local heating of diamonds, these two measurements were performed at a 1-minute interval.

2.7. Cell culture

MEF 3T3 cells were cultured in plastic T-25 bottles (NEST Biotechnology) in DMEM low-glucose medium (Bio West) supplemented with 10% FBS (Gibco) and 1% PS (BioWest), and kept at 37 degrees in standard 5% CO₂ incubator.

2.8. ODMR-TFM experiment

Before the ODMR-TFM experiments, the surface of the 12 kPa PA substrate was functionalized with type-I collagen. The polyacrylamide substrate was treated with a Sulfo-SANPAH solution (Thermo Fisher Scientific) for 5 min under UV light. The substrates were initially washed with a 10 mM HEPES solution in deionized water, and then they were washed three times with sterile PBS. Subsequently, the hydrogels were incubated with a solution of type I collagen (10 µg/mL) at 4 °C for 12 h [51,52]. After protein conjugation, dishes were washed three times with sterile PBS. MEF 3T3 cells were seeded at a concentration that allowed single-cell observation and cultured in a cell incubator for the next 12 h. Cells were seeded in DMEM low-glucose medium without phenol red dye (Bio West).

In each experiment, the local temperature was measured every 10 min. Each time point consisted of three separate measurements: a snapshot in transmitted light mode to locate the cell (here, DIC contrast), time-lapse ODMR signal collection, and the acquisition of Z-stack images of TFM beads. For most of the experiment duration, the microwave antenna was placed in the standby position approximately 3 mm above the substrate and moved to a distance of ∼250 µm only to register the ODMR signal. The Z-stack (i.e., a short series of images obtained in different focus positions) of the TFM beads was obtained because of the lack of focus stabilization in such a custom experiment. The collection of several slices allowed us to select properly focused TFM images to calculate cellular traction.

The heating experiment started at a low temperature (28.4 °C), which was maintained for seven consecutive time steps. Therefore, the temperature gradually increased to reach a difference of 1 °C between each time step. After reaching ∼37 °C, this temperature was maintained until the end of the experiment. Heating was performed using an on-stage mini-incubator as well as a large incubation chamber, which could be heated to the desired temperature. The cooling experiment started at 37 °C, which was maintained for seven consecutive time steps. However, neither incubator was equipped with cooling equipment. Hence, the incubator temperature was decreased by turning down the heat and placing ice packs inside the large incubation chamber. Ice packs were added several times to decrease the temperature by ∼1 °C every 10 min, and the cooling process was verified with a thermocouple placed inside the Petri dish. A final temperature of approximately 28 °C was maintained until the end of the experiment.

After ODMR-TFM acquisition, the cell culture medium was removed and replaced with Trypsin-EDTA solution concentrated 10 times, in order to detach cells from the substrate. After cell detachment, the Z-stack of fluorescent beads was collected in order to find the reference image of the non-contracted substrate. Our TFM routine is based on Fourier transform traction cytometry (FTTC) presented for the first time by Butler and co-workers [7]. Similarly to the conditions presented there, our images were analyzed with the particle image velocimetry (PIV) method with 64-pixel window size. The single-bead image occupied mostly 6 pixels in diameter, and there were between 12 and 20 beads in each PIV window. The TFM data were processed using custom Fourier Transform TFM software provided by Prof. Xavier Trepat of the Integrative Tissue and Cell Dynamics Group of the Institute for Bioengineering of Catalonia, Barcelona, Spain (an example of implementation: [53]).

3. Results

We used a standard wide-field inverted microscope setup (Zeiss Axio Observer Z1) equipped with a short-arc mercury fluorescence lamp and a CMOS camera for the experiments (Fig. 1(B–C)). The sample was heated in two ways: by warm air in the large microscope heating chamber (Fig. 1(B II)) and using a small incubator for Petri dishes (Fig. 1(B III)), which was placed on the microscope stage. The temperature of the sample was regulated using built-in thermocouples and temperature controllers (TempModule S and Heating Unit XL, Zeiss). The bottom part of the inner incubator was heated, while its lid (Fig. 1(B IV)) served as a partial passive heat barrier as it had a hole to place the microwave (MW) antenna above the sample. The actual temperature of the cell medium was measured using a thermocouple inserted into the dish on the left side of the well, touching its bottom (V). The MW antenna—a coaxial cable terminated in a wire loop of ∼1 mm diameter made of thin copper wire (Fig. 1(B VII))—was placed on the micromanipulator, which was able to lower the antenna to ∼250 µm above the substrate (Fig. 1(B X)). The MW generator served as the source of the microwaves and as a camera trigger (Fig. 1(C)). Three signals (MW sequence, camera activity signal, and camera trigger) were checked on the oscilloscope to verify the correctness of the ODMR measurements (Fig. 1(C)).

This work comprised three stages: optimization of the ODMR-TFM substrate (Fig. 2), optimization of the ODMR measurement conditions (Fig. 3), and a proof-of-principle experiment using the optimized ODMR-TFM (Fig. 4).

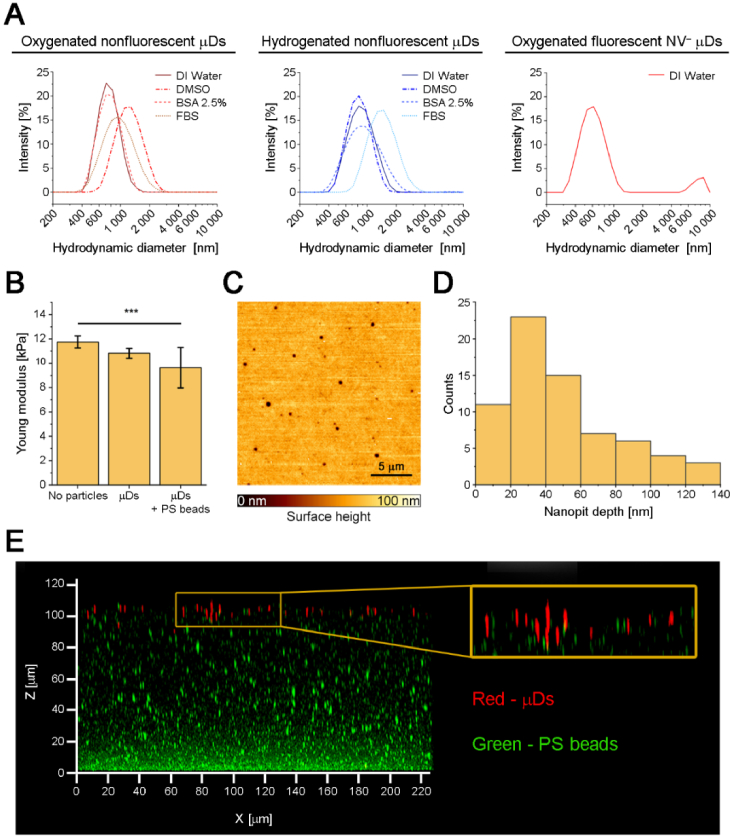
Fig. 2.

A: Hydrodynamic diameters of oxygenated and hydrogenated nonfluorescent and fluorescent microdiamonds suspended in various solvents. B: Young’s moduli of elastic substrate variants. C: Surface morphology of the ODMR–TFM substrate. D: Histogram of nanopit depths. E: Maximum projection of the ODMR–TFM substrate in the X-Z plane from a confocal scan. The yellow box presents a magnified fragment of the substrate surface, showing that microdiamonds are placed at slightly different depths.

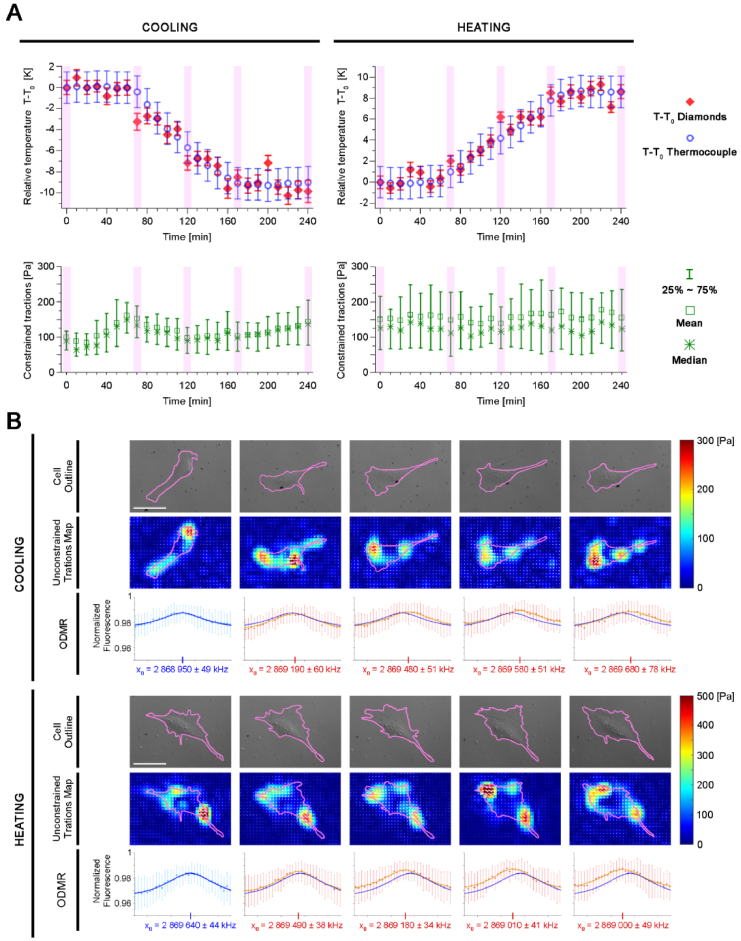
Fig. 4.

ODMR-TFM proof-of-principle experiments for cell cooling and heating. A: Plots of relative temperature measured with the thermocouple and microdiamonds (upper panel) and constrained tractions exerted by the observed cells (lower panel). The timepoints highlighted in purple in the plots are presented in more detail in panel B. B: Cell outlines, maps of unconstrained tractions, and ODMR shifts for the cooling and heating of cells. $x_0$ and $x_c$ denote the position of fitted Lorentzian peak in first and following time steps, respectively. Scalebar = 50 µm.

3.1. Development and characterization of an ODMR-TFM substrate

A polyacrylamide hydrogel of defined elasticity, containing both diamonds and fluorescent markers, was prepared. To register the ODMR signal under conditions of low illumination, short experiment duration, and low-aperture objective, we used microdiamonds (µDs) of ∼1 µm in diameter that contained numerous NV⁻ centers (∼10⁵ centers in each microdiamond) that emitted light in the red channel. However, such large markers are not suitable for TFM experiments; thus, we also used green fluorescent polystyrene (PS) beads of 200 nm in diameter to register cellular tractions in the green channel of the microscope.

To ensure the proper dispersion of µDs within the substrate, their surface termination was tested in various solutions. We tested oxygenated and hydrogenated nonfluorescent µDs in four solvents (Fig. 2(A), Table 1): deionized (DI) water (suitable for a PA polymerization mixture), DMSO (potentially dissolvable in a PA polymerization mixture), and two protein solutions, namely, bovine serum albumin (BSA; 2.5% w/w in water) and fetal bovine serum (FBS). The latter two solvents were chosen based on previous studies that reported that the creation of a protein corona can prevent the aggregation of nanodiamonds [54]. The results of DLS measurements are presented in Fig. 2(A) and Table 1 and reveal that most combinations of surface terminations and solvents worked properly. The only exceptions were oxygenated µDs in DMSO and hydrogenated diamonds in FBS, which exhibited a substantially higher hydrodynamic diameter than that of the other samples. However, the increased hydrodynamic diameters of µDs in protein solutions may also have been caused by the generation of the protein corona; thus, they do not necessarily indicate the aggregation of µDs. The lowest hydrodynamic diameter was observed for the oxygenated µD suspension in water rather than in protein solutions; thus, we used the water suspension in further experiments. NV⁻ µDs were oxygenated and suspended in DI water at a concentration of 0.5 mg/mL. The DLS measurement revealed that NV⁻ µDs were well-dispersed with a fraction of large aggregates (>6 µm in diameter) that represented less than 10% of the total measured DLS intensity. Thus, the suspension of oxygenated µDs in DI water was used to prepare elastic substrates.

Table 1. Dynamic light scattering (DLS) characterization of the hydrodynamic diameters of nonfluorescent (non-NV⁻) and fluorescent (NV⁻) diamonds. The quantitative characterization presents the average hydrodynamic diameter (Z_Ave), standard error of the mean (SEM), and the 10^th, 50^th, and 90^th quantiles (Di₁₀, Di₅₀, and Di₉₀).

NV− presence	Surface termination	Solvent	ZAve [nm]	SEM [nm]	Di10 [nm]	Di50 [nm]	Di90 [nm]
Non–NV−	-O	DI water	734	88	546	754	1060
		DMSO	1145	279	813	1220	1860
		BSA 2.5%	741	108	540	767	1100
		FBS	887	168	597	945	1540
	-H	DI water	818	187	578	864	1310
		DMSO	798	108	568	817	1200
		BSA 2.5%	851	192	548	907	1570
		FBS	1267	385	942	1430	2230
NV−	-O	DI water	735	202	484	713	1260

Substrates suitable for traction force microscopy must have a properly characterized Young’s modulus. As shown in Fig. 2(B), we compared the three applied substrate formulations that are intended to achieve a targeted elasticity of ∼12 kPa. The substrate without fluorescent particles had Young’s modulus of 11.7 ± 0.5 kPa, similar to those reported in the literature [55]. The substrate with added µDs was slightly softer, with Young’s modulus of 10.8 ± 0.4 kPa. The addition of fluorescent markers softened the substrate further to 9.6 ± 1.6 kPa, which was the final value considered in our TFM calculations. Even though the ODMR-TFM substrate with µDs and green fluorescent PS beads was slightly softer than that without added particles, it still had acceptable elasticity and was suitable for mechanobiology studies. The surface morphology of the substrate was also evaluated. AFM experiments revealed that substrates with µDs exhibited shallow nanopits up to 140 nm deep (Fig. 2(C–D)). The 3D morphology of the ODMR-TFM substrate is presented in Fig. 2(E), which shows that fluorescent microdiamonds are present in the top layer; however, they may be placed at slightly different depths. By contrast, fluorescent PS beads gathered at the bottom of the substrate; however, their concentration at the top was sufficient for the TFM experiments. Such a diverse placement of microdiamonds and PS beads may have been caused by the upside-down polymerization during which the heavy microdiamonds precipitated to the bottom, whereas low-density PS beads floated to the top of the substrate. Reversing the substrate back to the upright position after polymerization resulted in microdiamonds being placed in the top layer, and PS beads being placed in the bottom layer of the substrate. The pits in the substrate may have been caused by the presence of diamonds beneath them. This hypothesis may be verified by a possible combination of AFM and super-resolution microscopy, which is beyond the scope of this study. In summary, we demonstrated the production of a substrate with properly dispersed microdiamonds; the produced substrate was slightly softer than the reference one which lacked any particles but was still well-suited for the planned TFM and ODMR measurements. The nanopits in the substrate surface were shallow; however, they can be evaluated in further studies.

3.2. Optimization of ODMR measurement conditions

The next step in the development of the ODMR-TFM setup involved optimizing the experimental conditions of the ODMR. As illustrated in Fig. 3(A), the ODMR spectrum is split into two resonances, which is caused by diamond-lattice strain [36]. The literature presents several ways of determining the position of the ODMR, and thus, the readout of the relative temperature, as mentioned in the Introduction. This signal processing optimization demonstrates that utilizing a single Lorentzian component for the central dip between the split ODMR components yields superior resonance localization compared to the conventional double-Lorentzian fit. Such optimization not only enhances the precision of the temperature measurement but also reduces the duration of the experiment, both of which were among primary objectives of this study.

Assuming that live-cell imaging will be performed in the range of 20–45 °C, we probed the ODMR spectrum in the range of 2864–2874 MHz with a 0.25 MHz step with three additional points outside the resonance at the beginning and end of the spectrum. Here, we call this MW sequence an irregular sequence. We then compared it with a reference microwave sequence (called the regular sweep here) that was performed between 2845 and 2895 MHz with the same 0.25 MHz step. All these steps helped decrease the duration of the ODMR measurement as much as possible while maintaining the ∼1 K precision.

Figure 3(B) depicts the procedure for determining the average relative temperature in the field of view. The first step was to obtain the ODMR spectra for each visible particle. This was followed by the selection of particles (NV1, NV2, NV3, etc.) that produced ODMR signals of sufficient quality to allow a reliable determination of the resonance frequency, that is, (a) signals of at least 1% of the height of the dip H, (b) with a height uncertainty δH not larger than the height of the central dip δH/H < 1, and (c) that have an R² factor of the fitted Lorentzian ≥0.4 (Fig. S1). These criteria were chosen to include even the weakest ODMR signal in our analysis. The selected signals were averaged, and a Lorentzian was fitted to the averaged data to determine the resonance position. Microdiamonds with low-quality ODMR signals were not considered in further analysis. The low quality of these signals may have been due to the small size of the µD or the fluorescence of a defocused diamond. This procedure allowed the identification of the relative temperature in consecutive time steps.

To determine the optimal conditions for ODMR measurements (Fig. 3(C)), we examined the precision of temperature readings and the number of diamonds included in the analysis based on three parameters: a) the thickness of the substrate, b) the intensity of the optical excitation, and c) the type of microwave sequence. To determine the thickness of the substrate, we used substrates that were too thin (20–40 µm) for standard cell mechanobiology measurements, substrates of medium thickness (50–70 µm) that were just above the reliability threshold for mechanobiology studies, and thick substrates (100–120 µm) adequate for cell mechanobiology studies. As can be seen in Fig. 3(C), the temperature measurement precision improved with increasing substrate thickness. This is likely due to reduced defocusing effects arising from a mismatch between the objective correction and the glass bottom dish thickness, as we use #0 dishes, while the objective was corrected for a standard #1.5 coverslip.

The excitation intensities were chosen starting from the maximum available intensity of the fluorescence lamp (25 W/cm²), which was gradually reduced in 5 W/cm² steps. The results presented in Fig. 3(C) show that the temperature measurement precision improves with the increasing illumination of the sample.

Microwave sequence optimization involved comparing an irregular sequence targeting the central ODMR dip with a regular sweep sequence. Additionally, the influence of averaging the irregular sequence one, two, three, and four times, which took 1.2, 2.4, 3.5, and 4.7 s, respectively, was also assessed. Data provided in Fig. 3(C) show that increase of averaging improves the precision of temperature measurement and increases the number of diamonds included in analysis.

The optimization aimed to achieve a balance between precision, illumination intensity, and duration of the experiment. Our aim was to find conditions enabling temperature measurement precision of ∼1 K (including the uncertainty) while minimizing the illumination intensity and experiment time. We have found such conditions and marked them with red arrows in Fig. 3(C). This approach yielded a temperature precision of 0.76 ± 0.16 K and provided 12.6 ± 2.07 diamonds that meet the quality criteria of the ODMR spectrum. Importantly, averaging temperature data from multiple locations (diamonds) within the field of view enhanced the measurement reliability. This optimization successfully reduced the duration of the ODMR measurement to 2.4 seconds while maintaining accurate temperature measurements with moderate excitation intensity of 15 W/cm² and appropriate substrate thickness.

The temperature response of the microdiamonds was also verified (Fig. S2, Table S3). The temperature calibration resulted in slopes between -65.6 kHz/K and -71.2 kHz/K, which resemble those found in the literature. This confirms that our ODMR-based temperature setup exhibits appropriate linear characteristics. However, to calculate the relative temperature change, we used the slope value of -74.2 kHz/K from Acosta et al. [41], which was measured under more precisely controlled conditions than those of our study.

3.3. Proof-of-principle ODMR-TFM experiments

Finally, two proof-of-principle experiments for cooling and heating were conducted. Both 4-h experiments started with maintaining a stable temperature for 1 h, followed by a gradual change in temperature (∼1 K every 10 min), and keeping the final temperature until the end of the experiment. The bulk temperature of the sample during heating and cooling was determined by the thermocouple readout (i.e., the bulk signal from inside the dish). The cooling experiment started at 37.0 °C, while the heating experiment started at 28.4 °C. The upper panel of Fig. 4(A) presents the temperature measured by µDs (red squares) and the thermocouple (blue circles), while the lower panel shows the constrained tractions exerted by the cells (green bars) during the experiments. Because the values of the constrained tractions from the map did not meet the normality criteria, they are described here by the mean, median, and quartiles at each time point. The time points highlighted in purple in Fig. 4(A) are presented in more detail in Fig. 4(B). The thermocouple temperature measurement for sample cooling reveals a smooth decrease, whereas the µD measurement shows temperature drops at 70, 120, and 160 min, which were then followed by temperature stabilization. Thus, we regard the latter measurement as more reliable because the temperature drops coincide with the addition of ice packs to the large incubation chamber to cool down the surroundings of the microscope. Furthermore, the temperature measured by µDs had consistently lower error bars than the temperature measured by the thermocouple. Likewise, the heating experiment yielded more precise temperature measurements using µDs (i.e., smaller error bars). The µDs also responded to sample heating, showing the temperature dynamics throughout the experiment. In each experiment, a constant temperature was maintained for the first and last hours. Even if the thermocouple readouts were stable in these regions, the microdiamond readouts exhibited temperature fluctuations. Owing to the faster registration of temperature with the ODMR compared with the thermal inertia of the thermocouple, we can assume that the microdiamond registration is more reliable than the bulk thermocouple signal. The distribution of constrained cellular tractions in heated cells is wider in the lower panel of Fig. 4(A). This is due to the larger area of the observed cell, which exerts greater forces near the cell’s border and includes more pixels of low tractions closer to the center of the cell. Fig. 4(A) presents a quantitative description of constrained tractions that were computed over the area of cell body. Fig. 4(B) displays unconstrained traction maps to better assess the quality of the TFM experiments. The unconstrained traction maps for cooling and heating are of sufficient quality, exhibit low background noise, and demonstrate that parallel measurements of relative temperature and cellular tractions are possible using our setup. The ODMR spectra at each selected time point reveal a spectral shift to higher frequencies when cells are cooled and lower frequencies when cells are heated. The acquisition of each time step of the ODMR-TFM experiment took 20-30 seconds, since each component (bright-field image of cell, ODMR time-lapse registration and TFM z-stack) was collected manually one after another, however, the prospective automation of the procedure might decrease this time down to less than 10 seconds.

4. Discussion

In this study, we developed a microscopy imaging method for the hybrid sensing of cellular tractions (TFM) and local relative temperature (ODMR). In addition to the proof-of-principle experiment, we described the optimization of ODMR measurements. A simple setup based on a standard wide-field fluorescence microscope without extensive modifications was used. The experimental conditions were optimized to decrease the harmful effects of light and microwaves on living cells.

The current research began with the preparation of an ODMR-TFM substrate that contained fluorescent beads for TFM and microdiamonds for ODMR. The substrate was tested for its elastic properties, which are crucial in TFM experiments [6,7], and topography, which might affect cellular behavior. The custom-made ODMR-TFM substrate slightly differed in elasticity from the reference, however, this did not affect its applicability in TFM experiments as only a modification of the Young’s modulus was needed, which is used to calculate cellular tractions. Therefore, prospective adaptations of the ODMR-TFM methodology in other life science laboratories should also include the verification of nominal Young’s moduli of substrates of various compositions. The substrate was also sufficiently thick (>100 µm) to allow mechanobiological studies. Topography imaging of the substrate surface revealed the presence of shallow nanopits (up to 140 nm). The literature reports that nanopits can modify cell spread, adhesion, differentiation, or osteogenic induction on substrates [56–58]. However, in the published cases, the nanopits were deeper, regular, and densely packed. In contrast, in our study, the nanopits were shallower and sparsely located at random places on the substrate; thus, we do not expect them to have a substantial impact, although their effects may be evaluated in future studies if cell behavior is somehow altered.

Here, microdiamonds were not introduced directly into the cell, as in Kucsko et al., [42] or by culturing with a nanodiamond suspension [35], but were placed in the hydrogel just below the cells. This approach does not allow for any additional interactions between cells and diamonds, thus reducing the effects of external factors on the cells. Even if particular carbon-based materials can be absorbed more preferably by cells than other types of nanomaterial [59] and diamond particles exhibit high biocompatibility (see ref. [60] and references therein), the lack of additional direct interactions makes the experiment less prone to perturbations.

This research also aimed to optimize the ODMR experimental conditions in the context of live-cell imaging. Microthermometry of living cells using ODMR is a fairly new topic. Therefore, only a few studies have presented relevant experimental approaches. Likewise, no standard live-cell ODMR protocols are available, and the experimental conditions have rarely been optimized. Thus, here, we optimized the microwave sequence for ODMR, data processing, illumination intensity, and substrate thickness. We attained a short duration (2.4 s) and low illumination (15 W/cm²), which provided satisfactory precision in the temperature measurement (0.76 ± 0.16 K). The temperature precision is similar to that reported by Yukawa et al. [45]. However, we achieved it with a simpler (non-confocal) setup, shorter duration, and slightly higher illumination (4.7 W/cm² in [45]). However, the temperature precision we achieved is lower than that of the wide-field setup with an sCMOS camera by Simpson et al. [35]. They achieved a temperature determination precision that ranged in millikelvins; however, they also applied illumination that was 200 times more intensive (3 kW/cm²), and the duration of their experiment was four times longer than that presented here. Other studies [42,46] have also reported better temperature precision; however, they used more sophisticated confocal microscopes that probed only a small fraction of the field of view. In summary, the ∼ 1 K temperature precision we achieved is not the highest reported in the literature; however, it still provides relevant biological information about the thermal conditions of the cells, including information from several diamonds in the field of view, and was achieved with low illumination, in a short time, and on a simple wide-field microscope setup that did not require major modifications.

Thus, the final quality of the temperature measurement is derived from the interplay of several experimental conditions and the microscope equipment. To our knowledge, this is the first systematic study to optimize the experimental conditions of live-cell ODMR. However, the parameters optimized here can still be fine-tuned to increase the precision even further, while decreasing the heating produced by microwaves and the phototoxic effects due to illumination. Therefore, future studies should aim to determine to what extent light or microwave perturbations influence cellular function. In addition, we did not measure the biological effects of the ODMR experiment on living cells, such as the generation of free radicals or the induction of the apoptotic signaling pathway, although the optimization procedure aimed to keep the cells alive during the multi-hour experiment. Therefore, an evaluation of the negative biological effects of the optimized ODMR experiment is still needed. Addressing this issue can further enhance the applicability of ODMR to live-cell imaging.

We also expect that adaptations of the ODMR-TFM methodology in other life-science laboratories will strongly depend on the individual research aims. Among others, the experimental procedure might benefit from the modified design and delivery of the MW antenna. Here, the antenna was positioned on top of the sample, which requires an open container. When the antenna is placed in a manner that keeps the sample enclosed, the robustness of the experiment can be increased. The length, interval, and averaging of the microwave sequence can also be modified, especially for the different registered temperature range expected by a researcher. Yet another issue that can be addressed is the automation of the experimental procedure, since in our study, the bright-field image, ODMR time-lapse, and TFM z-stacks were collected manually one after another.

Moreover, our setup incorporated low aperture, 40x/0.6 dry objective of limited spatial resolution. In this configuration, the TFM maps give more information about the overall change in cellular mechanics, rather than high-resolution maps that can be colocalized with specific structures. However, it suits the multi-well plates protocols, which practically benefit from the lack of immersion oil. On the other hand, recent advances in high-resolution TFM allow for the acquisition of precise cell tractions maps, unveiling other aspects of cellular mechanobiology. Some authors mix beads of two different colors [61] or apply TIRF-SIM techniques [62], employing high-aperture objectives. In such setups, the TFM beads can be located just near the substrate’s surface [63]. Incorporating these advancements in ODMR-TFM methodology imposes the modification and further verification of the elastic substrate. These changes are required by the clear need for a higher bead density (TFM component) as well as the modified readout of the brighter ODMR spectrum collected by high-aperture objectives (ODMR component). The application of NV^- microdiamonds also eliminates the red and far-red fluorescent beads from the potential setup. Therefore, the experimental procedure tailored for individual research aims can be further optimized in order to mitigate the negative effects of microwaves and fluorescent light illumination. However, these potential customizations might come with the loss of setup simplicity and versatility, decreasing the chances of reproducing the experiments by many independent groups at the same time.

To our knowledge, this is the first study to apply local temperature measurements in the field of mechanobiology. Proof-of-principle ODMR-TFM experiments demonstrated that it is possible to simultaneously measure the local temperature in the field of view and cellular traction forces using a simple microscope setup. Thus, this method can be used in studies of hyper- and hypothermic conditions or even rapid temperature changes in the mechanical responses of cells and tissues because NV^- diamonds have low thermal inertia and provide a precise temperature readout from the field of view. The determination of local temperature in biological systems, especially at the level of single cells and tissues, is important in many research areas because biochemical reactions are usually temperature dependent. For example, cellular diffusion processes depend on local temperature and as a result, influence the rate of cellular metabolism [64,65]. Another example is shown by Harding and co-workers [66] where the authors describe the influence of temperature on the proliferation and differentiation of chicken skeletal muscle satellite cells derived from different muscle types. However, external temperature is not the only source that influences cellular processes, because the internal metabolic processes also generate heat [67,68]. These are only a few examples of relevant biological processes in which the determination of local temperatures is required. On the other hand, the TFM technique is employed with adherent cells where all processes, described above, occur as well. The ability of parallel determination of local temperatures and cellular/tissue traction forces will provide a great advantage in studies linking the processes of generation of cellular forces with internal biochemical regulatory mechanisms. One branch that in our opinion can considerably benefit from the ODMR-TFM experiments is the biology of inflammation and immune system. The role of mechanical interactions of immune cells with targets and the environment is the subject of numerous current studies [69,70] and the increase in temperature during diseases is also the known fact [71]. Therefore, the parallel observation of mechanical interactions and temperature changes can be a useful tool for investigating these processes, improving the knowledge of physiological and pathological processes.

5. Conclusion

In this study, we successfully combined the ODMR and TFM techniques to parallelly measure local relative temperature and cellular tractions in the field of view. Achieving this goal posed a challenge due to the adverse effect of intensive light illumination and strong microwave irradiation on living cells, both of which are utilized in ODMR experiments. The combined ODMR-TFM method also required the development and characterization of novel diamond-embedded elastic substrate.

To address this challenge, we optimized the ODMR experimental conditions, which reduced the sample illumination and shortened the experiment time. The experimental setup was constructed on the commercially available inverted fluorescence microscope, without extensive modification. Compared to the existing studies, we achieved significantly lower illumination and shorter experiment duration, facilitating multi-hour acquisitions while maintaining a temperature precision of approximately 1 Kelvin.

The simplicity of our setup enhances its reproducibility in other life-science laboratories, offering a promising avenue for further research in this field.

Supporting information

Supplement 1. Supplementary 1.

https://doi.org/10.6084/m9.figshare.25735506

Funding

Fundacja na rzecz Nauki Polskiej10.13039/501100001870 (project QUNNA within TEAM-NET programme); European Regional Development Fund10.13039/501100008530 (POIR.04.04.00-00-1644/18).

Disclosures

The authors declare no conflicts of interest.

Data availability

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Supplemental document

See Supplement 1 ^{(1.1MB, pdf)} for supporting content.