Abstract
Analysis of phylogenetic trees has become an essential tool in epidemiology. Likelihood-based methods fit models to phylogenies to draw inferences about the phylodynamics and history of viral transmission. However, these methods are often computationally expensive, which limits the complexity and realism of phylodynamic models and makes them ill-suited for informing policy decisions in real-time during rapidly developing outbreaks. Likelihood-free methods using deep learning are pushing the boundaries of inference beyond these constraints. In this paper, we extend, compare, and contrast a recently developed deep learning method for likelihood-free inference from trees. We trained multiple deep neural networks using phylogenies from simulated outbreaks that spread among 5 locations and found they achieve close to the same levels of accuracy as Bayesian inference under the true simulation model. We compared robustness to model misspecification of a trained neural network to that of a Bayesian method. We found that both models had comparable performance, converging on similar biases. We also implemented a method of uncertainty quantification called conformalized quantile regression that we demonstrate has similar patterns of sensitivity to model misspecification as Bayesian highest posterior density (HPD) and greatly overlap with HPDs, but have lower precision (more conservative). Finally, we trained and tested a neural network against phylogeographic data from a recent study of the SARS-Cov-2 pandemic in Europe and obtained similar estimates of region-specific epidemiological parameters and the location of the common ancestor in Europe. Along with being as accurate and robust as likelihood-based methods, our trained neural networks are on average over 3 orders of magnitude faster after training. Our results support the notion that neural networks can be trained with simulated data to accurately mimic the good and bad statistical properties of the likelihood functions of generative phylogenetic models.
Keywords: Deep learning, epidemiology, machine learning, phylogeography, phylodynamics
Viral phylodynamic models use genomes sampled from infected individuals to infer the evolutionary history of a pathogen and its spread through a population (Holmes and Garnett 1994; Volz et al. 2013). By linking genetic information to epidemiological data, such as the location and time of sampling, these generative models can provide valuable insights into the transmission dynamics of infectious diseases, especially in the early stages of cryptic disease spread when it is more difficult to detect and track (Holmes et al. 1995; Rambaut et al. 2008; Lemey et al. 2009; Pybus et al. 2012; Worobey et al. 2016, 2020; Lemey et al. 2021; Washington et al. 2021; Pekar et al. 2022). This information can be used to inform public health interventions and improve our understanding of the evolution and spread of pathogens.
Viral phylodynamic processes have long been studied through a variety of modeling frameworks. For instance, coalescent-based models (Drummond et al. 2005; Minin et al. 2008; Lemey et al. 2009; Volz 2012; Müller et al. 2017; Volz and Siveroni 2018) are backward-time population genetic processes that can estimate important population-level parameters, such as effective population sizes and interpopulation migration rates, for pathogens of concern. Birth–death-based models (Maddison et al. 2007; FitzJohn 2012; Kühnert et al. 2014; Beaulieu and O’Meara 2016) are forward-time branching processes that can model how lineages multiply, go extinct, change states, and are sampled. When applied to viral phylodynamics and beyond, coalescent and birth–death models both face their own theoretical and computational challenges. We note that coalescent and birth–death models are often used interchangeably to study the same evolutionary phenomenon (Morlon et al. 2010; Stadler 2010; Stadler et al. 2012, 2013; Seidel et al. 2020). In this study, we focus upon state-dependent birth–death processes to model viral phylodynamics because of their additional uses in modeling macroevolution (Maddison et al. 2007; MacPherson et al. 2022).
Birth–death models inherently correspond to the well-known Susceptible-Infectious-Recovered (SIR) model during an exponential growth phase, when nearly all individuals in the population are susceptible to infection (Anderson and May 1979). The simplest SIR models only track the number of susceptible, infected, and recovered individuals across populations over time, with more advanced models also allowing the movement of individuals among localized populations. The phylodynamic models we are interested in track the incomplete transmission tree (phylogeny) of sampled, infected individuals that emerges from host-to-host pathogen spread among populations over space and time. Within this broader context, we will refer to the state as location and the models as location-dependent birth–death (LDBDS) models that include serial sampling of taxa (Kühnert et al. 2016).
Analysts typically fit these birth–death models to data using likelihood-based inference methods, such as maximum likelihood (Maddison et al. 2007; Richter et al. 2020) or Bayesian inference (Kühnert et al. 2016; Scire et al. 2020). Likelihood-based inference relies upon a likelihood function to evaluate the relative probability (likelihood) that a given phylogenetic pattern (i.e. topology, branch lengths, and tip locations) was generated by a phylodynamic process with particular model parameter values. In this sense, the likelihood of any possible phylodynamic data set is mathematically encoded into the likelihood as a function of (unknown) data-generating model parameters.
Computing the likelihood requires high-dimensional integration over a large and complex space of evolutionary histories. Analytically integrated likelihood functions, however, are not known for LDBDS models. Methods developers instead use ordinary differential equation (ODE) solvers (Maddison et al. 2007; Kühnert et al. 2016) to numerically approximate the integrated likelihood. These clever approximations perform well statistically, but are too computationally expensive to use with large epidemic-scale data sets. Thus, while Nextstrain (Hadfield et al. 2018) and similar efforts have provided useful visualizations to policy makers during the COVID response, most phylogeographical methods are used forensically, providing insight on the past, and are not used to provide parameter estimates in response to emerging events to inform policy decisions in real-time due to the complexity and long run-times of these models.
As phylodynamic models become more biologically realistic, they will necessarily grow more mathematically complex, and, therefore, less able to yield likelihood functions that can be approximated using ODE methods. Because of this, phylodynamic model developers tend to explore only models for which a likelihood-based inference strategy is readily available. As a consequence, the lack of scalable inference methods impedes the design, study, and application of richer phylodynamic models of disease transmission, in particular, and richer phylogenetic models of lineage diversification, in general.
To avoid the computational limitations associated with likelihood-based methods, deep learning inference methods that are likelihood-free have emerged as a complementary framework for fitting a wide variety of evolutionary models (Bokma 2006). Deep learning methods rely on training many-layered neural networks to extract information from data patterns. These neural networks can be trained with simulated data as another way to approximate the latent likelihood function (Cranmer et al. 2020). Once trained, neural networks have the benefit of being fast, easy to use, and scalable. Recently, likelihood-free deep learning neural network methods have successfully been applied to phylogenetics (da Fonseca et al. 2020; Suvorov et al. 2020; Nesterenko et al. 2022; Solis-Lemus et al. 2022; Suvorov and Schrider 2022) and phylodynamic inference (Lambert et al. 2023; Voznica et al. 2022).
Here, we extend new methods of deep learning from phylogenetic trees (Lambert et al. 2023; Voznica et al. 2022) to explore their potential when applied to phylogeographic problems in geospatial epidemiology. Phylodynamics of birth–death-sampling processes that include migration among locations have been under development for more than a decade (Stadler 2010; Stadler et al. 2012; Kühnert et al. 2014, 2016; Scire et al. 2020; Gao et al. 2022, 2023). Given the added complexity of location-specific dynamics (e.g. location-specific infection rates) and recent successes in deep learning with phylogenetic time trees (Voznica et al. 2022) under state-dependent diversification models (Lambert et al. 2023), we sought to evaluate this approach when applied to viral phylodynamics and phylogeography by including location data when training deep neural networks with phylogenetic trees.
A current limitation of likelihood-free approaches is that it remains unknown how brittle the inference machinery is when the assumptions used for simulation and training are violated (Schmitt et al. 2022). For example, a brittle deep learning method would be more easily misled by model misspecification when compared to a likelihood-based method. Likelihood approaches may have some advantages because the simplifying assumptions are explicit in the likelihood function, while for trained neural networks, it is difficult to know how those same assumptions implemented in the simulation are encoded in data patterns in the training data and learned network weights. However, with complex likelihood models, there may be unexpected interactions among simplifying assumptions that can result in large biases when applied to real-world data (Gao et al. 2023). Characterizing the relative robustness and brittleness of these two inference paradigms is essential for those who wish to confidently develop and deploy likelihood-free methods of inference from real world data.
To explore relative robustness to model misspecification, we trained multiple deep convolutional neural networks (CNNs) with transmission trees generated from epidemic simulations. We were able to achieve accuracy very close to that of a likelihood-based approach and through several model misspecification experiments show that our CNNs are no more sensitive to model violations than the likelihood approach. Significantly, both methods consistently show similar biases induced by model violations in test data sets. We find that for the models tested here, the migration rate estimates are highly sensitive to misspecification of infection rate and sampling rates, but that estimates of the infection and sampling rates are fairly robust to misspecification of the migration models. We also show that the rate parameter estimates are fairly robust to misspecification of both the number of locations in the model and phylogenetic error. We also estimated prediction intervals for the rate parameters and compared and contrasted their performance to the Bayesian highest posterior density intervals. We show that they produce intervals that greatly overlap with highest posterior densities in all experiments, but have, on average, wider intervals making them relatively conservative. Finally, we compared a simulation-trained neural network to a recent phylodynamic study of the first wave of the COVID pandemic in Europe (Nadeau et al. 2021) and obtain similar inferences about the dynamics and history of SARS-CoV-2 in the European clade.
Methods
First, we define the SIR model which we assume here is approximately equivalent to the LDBDS model (Kühnert et al. 2016). Following that is a description of the simulation method to generate the training, validation, and test data sets of phylogenies under the model. The simulation and data processing pipeline is shown in Fig. 1. We next describe our implementation of simulation-trained deep learning inference with convolutional neural networks (CNN) as well as a likelihood-based method using Bayesian inference. We then describe our methods for measuring and comparing their performance when tested against data sets generated by simulations under the inference model as well as several data sets simulated under models that violate assumptions of the inference model. Finally, we describe how we tested our simulation-trained CNN against a real-world data set.
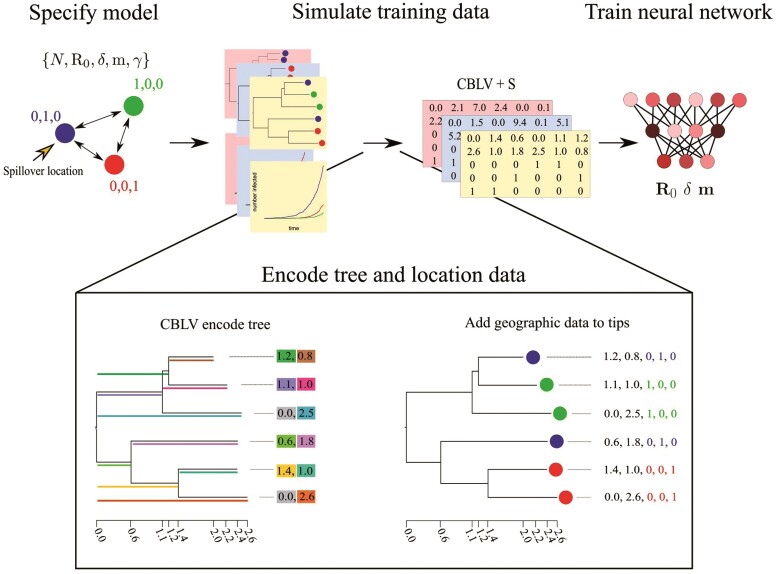
Figure 1.
Simulation and tree encoding pipeline for generating training data. 1) Specify a model, for example, an SIR model with serial sampling and migration among 3 locations (colored circles). 2) Run simulations of outbreaks under the model to generate population trajectories and phylogenetic trees. 3) Encode trees and location data into the Compact Bijective Ladderized Vector + States (CBLV+S) format. 4) Train the neural network with CBLV+S training data.
Model Definition
We first define a general location-dependent SIR stochastic process used for simulations and likelihood function derivation in the format of reaction equations we specified in MASTER (Vaughan and Drummond 2013). MASTER allows users to simulate phylodynamic data sets under user-specified epidemiological scenarios, for which MASTER simultaneously simulates the evolution of compartment (population type) sizes and tracks the branching lineages (transmission trees in the case of viruses) from which it samples over time. Reaction equations 1 through 4 specify the SIR compartment model with migration and serial sampling where , , and denote the number of individuals in each compartment. The and compartments are indexed by geographic location using and . is the total population size in location and . We consider all local recoveries to lead to the same global compartment and absorbing state, . The symbols for each rate parameter is placed above each reaction arrow.
| (1) |
| (2) |
| (3) |
| (4) |
We parameterize the model with the basic reproduction number in location , , which is related to and by Equation (5),
| (5) |
In particular, our study considers a location-independent SIR model with sampling that assumes was equal among all locations, and a location-dependent SIR model with sampling that assumes varied among locations. During the exponential growth phase of an outbreak, the location independent and dependent SIR models are equivalent to thelocation-independent birth–death-sampling (LIBDS)and location-dependent birth–death-sampling (LDBDS) models, respectively, which are often used in viral phylogeography (Kühnert et al. 2014, 2016; Douglas et al. 2021).
Each infectious individual transitions are recovered at rate . We assumed that sampling a virus in an individual occurs at rate in location and immediately removes that individual from the infectious compartment and places them in the recovered compartment. Thus the effective recovery rate in location is . The above reactions correspond to the following coupled ordinary differential equations.
| (6) |
When the migration rate is constant among locations and the model is a location-independent SIR model, or equivalently, LIBDS, and we set at the beginning of the outbreak, the equation set (6) reduces to
The number of infections and the migration of susceptible individuals is at negligible levels on the timescales investigated here. The infection rate is, therefore, approximately constant and the migration of susceptible individuals can be safely ignored requiring only migration of infectious individuals to be simulated.
At the beginning of an outbreak, it is often easier to know the recovery period from clinical data than the sampling rate that requires knowing the prevalence of the disease. Therefore, we treat the average recovery period as a known quantity and use it to make the other 2 parameters (the sampling rate and the basic reproduction number ) identifiable. This was done by fixing the corresponding rate parameter in the likelihood function to the true simulated value for each tree, and by adding the true simulated value to the training data for training the neural network.
Simulated Training and Validation Data Sets
Epidemic simulations of the SIR+migration model that approximates the LIBDS process were performed using the MASTER package (v. 6.1.2) (Vaughan et al. 2014) in BEAST 2 (v. 2.6.6) (Bouckaert et al. 2019). We used standard tools (Chollet et al. 2015; Abadi et al. 2016) to train neural networks with these simulated data to learn about latent populations from the shape of sampled and subsampled phylogenies. In addition to the serial sampling process, at the end of the simulation 1% of infected lineages were sampled. In MASTER, this was approximated by setting a very high sampling rate and very short sampling time such that the expected number sampled was approximately 1%. This final sampling event was required to make a 1-to-1 comparison of the likelihood function used for this study (see Likelihood method description below) that assumes at least one extant individual was sampled to end the process. Coverage statistics from our Markov chain Monte Carlo (MCMC) samples closely match expectations (see Likelihood method description below; Fig. 2c). Simulation parameters under LIBDS and LDBDS models for training the neural network under the phylogeography model were drawn from the following distributions:
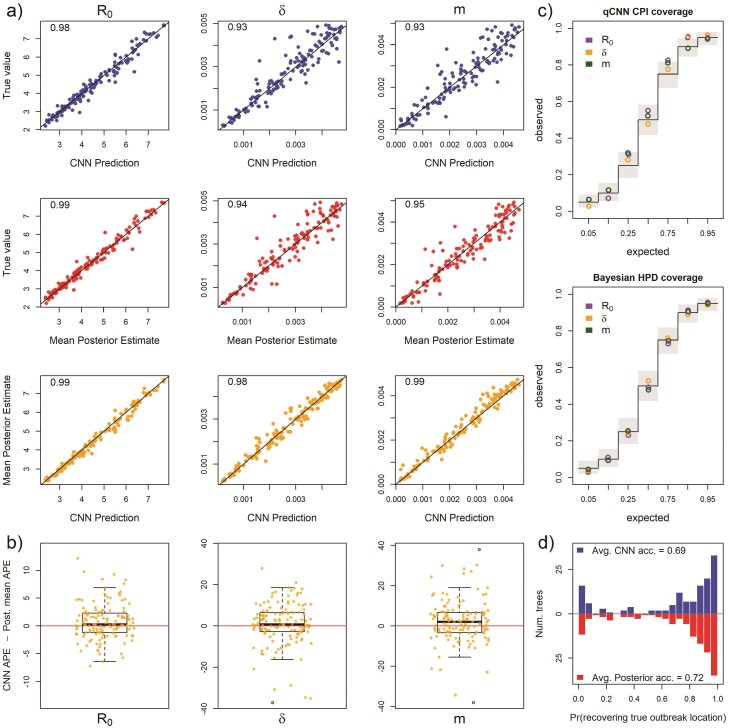
Figure 2.
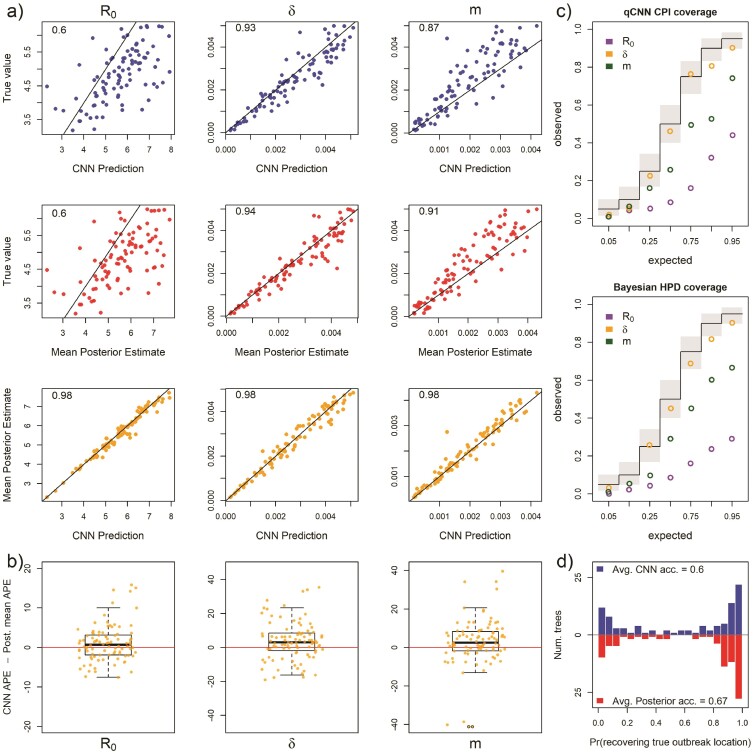
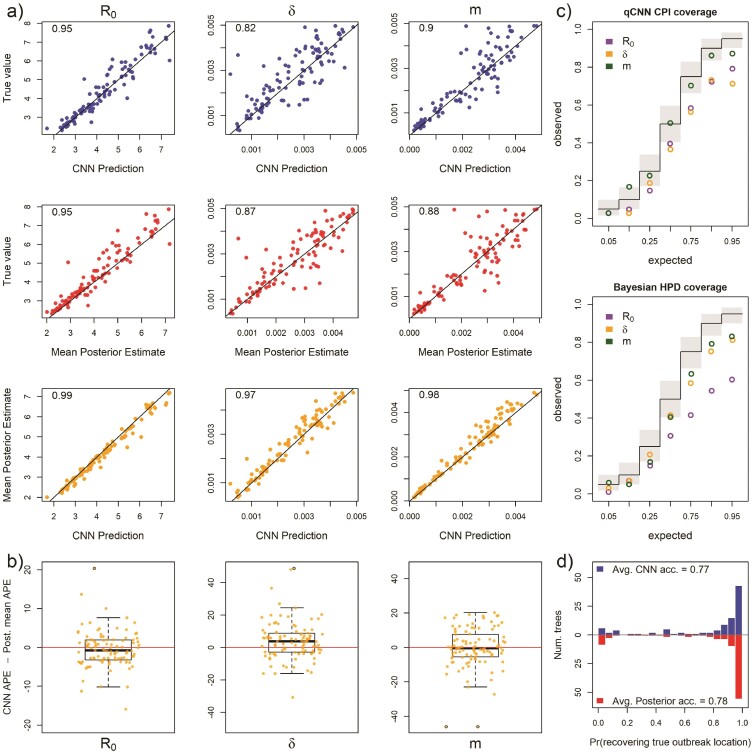
Inference under the true simulating model. a) Scatterplot of CNN predictions and posterior mean estimates from Bayesian analyses against the true values (top 2 rows in blue and red, respectively) of the basic reproduction number, R0, the sampling rate, , and the migration rate, m for 138 test trees. In the upper-left corners of the scatter plots are the correlations of the plotted data. The bottom row in orange shows scatter plots of the CNN estimates against the posterior mean estimates for the same trees. b) The difference in the APE of estimates for the 2 inference methods. Boxes show the inner 50% quantile of the data while whiskers extend 1.5 IQR. Dots with black circles were truncated to the length of whiskers for visualization purposes. c) Coverage plots show the expected frequency of coverage for each of the categories and the observed frequencies (black steps and colored circle, respectively). Gray boxes are the expected 95% confidence intervals at each of the expected coverage values that follows a Beta distribution. d) Histograms of the probabilities of inferring the correct outbreak origin location.
| (7) |
All 5 locations had initial population sizes of 1,000,000 susceptible individuals and 1 infected individual in a randomly sampled spillover location. Simulations were run for 100 time units or until 50,000 individuals had been infected to restrict simulations to the approximate exponential phase of the outbreak. For the experiments comparing the CNN to the likelihood-based method under the LIBDS model, if this population threshold was reached, the simulation was rejected. This ensured the LIBDS model used in the likelihood-based analyses are equivalent to more complex density-dependent SIR models. This criterion was not enforced for simulations under the LDBDS model. After simulation, trees with 500 or more tips were uniformly and randomly downsampled to 499 tips and the sampling proportion was recorded for training the neural networks and to adjust estimates of .
We simulated 410,000 outbreaks under these LIBDS settings to generate the training, validation, and test sets for deep learning. Any simulation that generated a tree with less than 20 tips was discarded, leaving a total of 111,157 simulated epidemiological data sets. Of these, 104,157 data sets were used to train and 7000 were used to validate and test each CNN. A total of 193,110 LDBDS data sets were simulated, with 186,110 used to train and 7000 used to validate and test the LDBDS CNNs.
To make phylodynamic inferences about the first wave of the SARS-CoV-2 epidemic in Europe, we used the LDBDS model on the data set from Nadeau et al. (2021). Training simulation parameters for the LDBDS process were drawn from the same distributions as LIBDS except R0, which was unique for each location. We assume that the variability of R0 among different pathogens (simulated outbreaks) is greater than the variability of the same pathogen’s R0 among different locations within the same simulation. To implement this assumption, all R0 was drawn from a joint distribution to narrow the magnitude of differences among locations within simulations to be within 6 of each other but expand the magnitude of differences between simulations to range from 0.9 to 15:
For the empirical analysis, population sizes at each location were also set to 500,000 and instead of running the simulations for 100 time units, time was scaled by the recovery period, , and was drawn from a uniform distribution:
Simulated Test Data Sets With and Without Model Misspecification
All simulation models used for training and testing are listed in Table 1. We first simulated a test set of 138 trees under the training model to compare the accuracy of the CNN and the likelihood-based estimates when the true model is specified. These data sets were simulated by random draws of parameter values from the same distributions described above for generating the training data set.
Table 1.
Models used in this study. All simulations assume an SIR compartmental epidemic model. N = 5 is the number of locations, R0 is the basic reproduction number, is the sampling rate, m is the migration rate, is the recovery rate (treated as data), and is the phylogenetic tree + locations (also treated as data)
| Description | Simulation model parameters and data |
|---|---|
| Generate training data | |
| Misspecify | |
| Misspecify | |
| Misspecify | |
| Misspecify number of locations | |
| Tree error | |
| Analyze Nadeau et al. (2021) dataset |
Sensitivity to model misspecfication for each of the 3 rate parameters, , , and , was tested. All sensitivity experiments used the same LIBDS model for inference for both the CNN and the Likelihood-based methods. Sensitivity experiments were conducted by simulating a test data set of trees that were generated by an epidemic process that was more complex than or different from the LIBDS model.
The tree data set for the misspecified R0 experiment consisted of simulating outbreaks where each location had a unique R0 drawn from the same distribution as above. Likewise, the misspecified sampling model test set was generated by simulating outbreaks where each location had a unique sampling rate, , drawn from the same distribution used for the global sampling rate described above. For the misspecified migration model, a random pair of coordinates, each drawn from a uniform(0,5) distribution in a plane, were generated for the 5 locations, and a pairwise migration rate was computed such that pairwise migration rates were symmetric and proportional to the inverse of their euclidean distances and the average pairwise migration rate was equal to a random scalar that was also drawn from a uniform distribution (see Equation (7) above).
The tree set for the misspecified number of locations experiment was generated by simulating outbreaks among 10 locations instead of 5. After simulations, 6 locations were chosen at random and re-coded as being sampled from the same location.
To generate a test set where the time tree used for inference has incorrect topology and branch lengths, we implemented a basic pipeline of tree inference from simulated genetic data to mimic a worst case real-world scenario. We simulated trees under the same settings as before. Phylogenetic error was introduced in 2 ways: the amount of site data (short sequences) and misspecification of the DNA sequence evolution inference model using seq-gen (v. 1.3.2) (Rambaut and Grassly 1997). We simulated the evolution of a 200 base-pair sequence under an HKY model with = 2, equal base frequencies and 4 discretized-gamma(2, 2) rate categories for among site rate variation. The simulated alignment as well as the true tip dates (sampling times) was then used to infer test trees. Test tree inference was done using IQ-Tree (v. 2.0.6) (Minh et al. 2020) assuming a Jukes–Cantor model of evolution where all transition rates are equal. The inference model also assumed no among-site rate variation. The number of shared branches between the true transmission tree and the test tree inferred by IQ-Tree was measured using gotree (v. 0.4.2) (Lemoine and Gascuel 2021). Polytomies were resolved using phytools (Revell 2012) and a small, random number was added to each resolved branch. These trees were then used for likelihood inference and CNN prediction.
Deep Learning Inference Method
The resulting trees and location metadata generated by our pipeline were converted to a modified CBLV format (Compact Bijective Ladderized Vector; Voznica et al. (2022)), which we refer to as the CBLV+S (+State of character, e.g. location) format (Fig. 1). The CBLV format uses an in-order tree traversal to translate the topology and branch lengths of the tree into an matrix where n is the maximum number of tips allowed for trees. The matrix is initialized with zeroes. We then fill the matrix starting with the root then proceed to the tip with largest root-to-tip distance rather than starting with that tip as in Voznica et al. (2022). We chose this to separate the the zero value of the root age from the zeroes used to pad matrices where the tree has less than the maximum number of tips, though we expect this to make marginal to no difference in performance. The CBLV representation gives each sampled tip a pair of coordinates in “tree-traversal space.” Our CBLV+S format associates geographic information corresponding with each sampled taxon by appending each vector column with a one-hot encoding vector of length states (e.g. ) to yield a CBLV+S matrix. The CBLV+S format allows for multiple characters and/or states to be encoded, extending the single binary character encoding format introduced by Lambert et al. (2023). Our study uses CBLV+S to encode a single character with location-states. In addition to the the CBLV+S data, we also include a few tree summary statistics and known simulating parameters; the number of tips, mean branch length, the tree height, and the recovery rate and the subsampling proportion. Trees were rescaled such that their mean branch length was the default for phylodeep (Voznica et al. 2022) before training and testing of the CNN. The mean pre-scaling branch length and tree heights were also fed into the neural networks. Trees were not rescaled for the likelihood-based analysis. Recall that tree height did not vary for the LIBDS CNN training set but did for the LDBDS training set (see simulation time settings above). Varying the time-scale for the LDBDS model was necessary for analyzing real-world data where time-scales of outbreaks can vary considerably.
Our CNNs were implemented in Python 3.8.10 using keras v. (2.6.0) and tensorflow-gpu (v. 2.6.0) (Chollet et al. 2015; Abadi et al. 2016). CNNs consist of one or more layers specifically intended for structural feature extraction. CNNs utilize a filter, akin to a sliding window, that executes a mathematical operation (convolution) on the input data. When dealing with structured data like the CBLV+S matrix, multiple 1D filters slide across the matrix’s columns, embedding each scanned window into an N-dimensional vector representation. This architectural design imparts CNNs with translation invariance, enabling them to recognize and learn repeating patterns throughout the input space, regardless of their specific location. Stacking multiple convolutional layers enables CNNs to decipher hierarchical structures within the data. See Alzubaidi et al. (2021) and Khan et al. (2020) for reviews of the subject.
For each model, LIBDS and LDBDS, we designed and trained 2 CNN architectures, one to predict epidemiological rate parameters and the other to predict the outbreak location resulting in 4 total CNNs trained by 2 training data sets (LIBDS and LDBDS). We used the mean-squared-error for the regression neural loss function in the network trained to estimate epidemiological rates, and the categorical cross-entropy loss function for the categorical network trained to estimate outbreak location. We assessed the performance of the network by randomly selecting 5000 samples for validation before each round of training. We measured the mean absolute error and accuracy using the validation sets. We used these measures to compare architectures and determine early stopping times to avoid overfitting the model to the training data. We also added more simulations to the training set until we could no longer detect an improvement in error statistics. After comparing the performance of several networks, we found that the CNN described in Supplementary Figure S1 performed the best. In brief, the networks have 3 parallel sets of sequential convolutional layers for the CBLV+S tensor and a parallel dense layer for the priors and tree statistics. The 3 sets of convolution layers differed by dilation rate and stride lengths. These 3 segments and the dense layer were concatenated and then fed into a segment consisting of a sequential set of dense layers, each layer gradually narrowing to the output size to either 3 or 5 for the rates and origin location networks, respectively, for the LIBDS model, and 7 and 5 for the 7 rates and 5 locations, respectively, for the LDBDS model.
All layers of the CNN used rectified linear unit (ReLU) activation functions, which is a standard non-linear function that evaluates to 0 for values of less than 0 and is linear for values above 0. We used the Adam optimizer algorithm for batch stochastic gradient descent (Kingma and Ba 2017) with batch size of 128. We selected the number of epochs by monitoring the mean absolute error and accuracy of the validation data set. This set was not used in training or testing. These metrics suggested stopping after 15 epochs for the regression network and 10 epochs for the root location network would maximize accuracy/minimize error for out-of-sample test data. The output layer activation for the network that predicted the , and m parameters was linear with 3 nodes. For the output layer predicting the outbreak location, the activation function was softmax with 5 nodes for the 5 locations. The input layer and all intermediate (latent) layers were the same for all 4 networks, namely the CBLV+S tensor and the recovery rate, mean branch lengths, tree height, and number of tips in the tree. The LDBDS neural network was trained with simulated trees where varied among locations and had an output layer with 7 nodes; 5 for the each location’s and a node each for the sampling rate and the migration rate. We tested networks with max-pooling layers between convolution layers as well as dropout at several rates and found no improvement or a decrease in performance.
Likelihood-Based Method of Inference
We compared the performance of our trained phylodynamic CNN to likelihood-based Bayesian phylodynamic inferences. We specified LIBDS and LDBDS Bayesian models that were identical to the LIBDS and LDBDS simulation models that we used to train our CNNs. The most general phylodynamic model in the birth–death family applied to epidemiological data is the state-dependent birth–death-sampling process (Kühnert et al. 2016; Scire et al. 2020), where the state or type on which birth, death, and sampling parameters are dependent is the location in this context. The basic model used for experiments here is a phylogeographic model that is similar to the serially sampled birth–death process (Stadler 2010) where rates do not depend on location, which we refer to as the LIBDS model. The death rate, , is equivalent to the recovery rate, , in SIR models. Standard phylogenetic birth–death models assume the birth and death rates, and , are constant or time-homogeneous, while the SIR model’s infection rate is proportional to and and varies with time as changes. However, when the number of infected is small relative to susceptible people, as in the initial stages of an outbreak, the infection rate is approximately constant and approximately equal to the birth rate ;
| (8) |
The joint prior distribution was set to the same model parameter distributions that were used to simulate the training and test sets of phylogenetic trees in the first section with treated as known and the proportion of extant lineages sampled, , set to 0.01 as in the simulations. The likelihood was conditioned on the tree having extant samples (i.e. the simulation ran for the allotted time without being rejected). All simulated trees in this study had a stem branch and the outbreak origins were inferred for the parent node of the stem branch.
We used MCMC to simulate random sampling from the posterior distribution implemented in the TensorPhylo plugin (https://bitbucket.org/mrmay/tensorphylo/src/master/) in RevBayes (Höhna et al. 2016). After a burnin phase, a single chain was run for 7500 cycles with 4 proposals per cycle and at least 100 effective sample size (ESS) for all parameters. If the ESS was less than 100, the MCMC was rerun with a higher number of cycles. We also analyzed the coverage of the 5%, 10%, 25%, 50%, 75%, 90%, and 95% highest posterior density to verify that our simulation model and inference model are the same and that the MCMC simulated draws from the true posterior distribution. Bayesian phylogeographic analysis recovered the true simulating parameters at the expected frequencies (Fig. 2c), thus validating the simulations were working as expected and confirming that the MCMC was accurately simulating draws from the true posterior distribution.
Quantifying Errors and Error Differences
We measure the absolute percent error (APE) of the predictions from the CNN and the mean posterior estimate of the likelihood-based method. The formula for APE of a prediction/estimate, , of is
The Bayesian alternative to significance testing is to analyze the posterior distribution of parameter value differences between groups. In this framework, the probability that a difference is greater than zero can be easily interpreted. We, therefore, used Bayesian statistics to infer the median difference in error between the CNN and likelihood-based methods and the increase in median error of each method when analyzing misspecified data compared to when analyzing data simulated under the true inference model.
We used Bayesian inference to quantify population error by performing three sets of analyses: (i) inferred the population median APE under the true model (this will be the reference group for analysis 3), (ii) the effect of inference method—CNN or likelihood-based (Bayesian)—on error by inferring the median difference between the CNN estimate and the likelihood-based estimate, (iii) the effect of misspecification on error for each parameter by comparing the median error of estimates under misspecified experiments and the reference group defined by analysis 1. See Supplementary Figures S3–S13 and Supplementary Table S1 for summaries and figures for all analyses for this section.
To infer these differences between groups we used the R package BEST (Kruschke 2013). BEST assumes the data follow a t-distribution parameterized by a location parameter, , a scale parameter, , and a shape parameter, , which they call the “normality parameter” (i.e. if is large the distribution is more Normal). Because the posterior distribution does not have a closed form, BEST uses Gibbs sampling to simulate draws from the posterior distribution. 20,000 samples were drawn from the posterior distribution for each BEST analysis. BEST uses automatic posterior predictive checks to indicate that a model adequately describes the data distributions. Posterior predictive checks indicate the BEST model adequately fits each data set analyzed below.
Inferring the median APE
Before inferring differences between groups, we inferred the population median APE for predictions of R0, , and from test data simulated under the inference model using the CNN and likelihood-based methods. Histograms of the sampled log-transformed APE appears to be symmetric with heavy tails so we fit the log APE to the BEST model. This implies that the sampled APE scores are drawn from a log-t distribution. The log-t distribution has a mean of and median of , we, therefore, focus our inference on estimating posterior intervals for the population median APE from the sampled APE values for each parameter estimated by the CNN method and likelihood-based method that we denote APECNN, and APELike, respectively. The data analyzed here and likelihood assumed by BEST is
The priors were set to the vague priors that BEST provides by default,
Ninety-five percent of highest posterior density for the median APE, , was estimated by the following transformation of simulated draws from the posterior distribution
In summary, the results we present are 95% highest posterior density from the posterior distributions of the median error, .
Inferring the relative accuracy of the CNN and likelihood-based method
To quantify the difference in error between the CNN and the likelihood-based method, we fit the difference in sampled APE scores, APE, between the CNN method and the likelihood-based method to the BEST model. Histograms of APE appear symmetric with weak to strong outliers making the BEST model a good candidate for inference from this data. The data and likelihood are
We used the same default priors as above.
Because, is not log-transformed, it is drawn from a t-distribution and the marginal posterior of the parameter is an estimate of the population mean, . Because the mean and the median are equivalent for a t-distribution, we again report the posterior distribution of the median difference, to simplify the results.
In summary, the results we present are 95% highest posterior density from the posterior distribution of the median difference between the 2 methods, .
When comparing CNN to the likelihood-based approach, positive values for indicate the CNN is less accurate, and negative indicate the likelihood-based estimates less accurate. We emphasize that this quantity is the median difference in contrast to the difference in medians, , reported in the next section.
Inferring sensitivity to model misspecification
Finally, to quantify the overall sensitivity of each rate parameter to model misspecification under each inference method, we infer the difference in median APE, of predictions under a misspecified model relative to predictions under the true model. In other words, we are inferring differences in medians between experiments. For example, to infer the sensitivity of the CNN’s inference of the sampling rate, , to phylogenetic error, we inferred the difference between the median APE of the CNN’s predictions for misspecified trees and the median APE of CNN predictions for true trees. The data are concatenated as below.
We inferred the difference between group median APE scores, denoted , by assuming that the model parameters conditioned on the observed APE from the 2 groups, and , follow a posterior distribution that is proportional to
where log and log follow t distributions with means and and standard deviations and , respectively, while sharing a common normality parameter, .
The posterior sample of is obtained by transforming samples from the joint marginal posterior distribution of and with the following equation,
The 2 components of the likelihood are each t-distributed and share the parameter, which means we assume both samples are drawn from a similarly shaped distribution (similarly heavy tails).
The prior distribution for the parameters of the model were set to the defaults for BEST,
As before, interpretation of the posterior distribution of the difference in medians is straightforward: the more positive the difference in median APE from the misspecified model test set and the median APE from the true model test set, the more sensitive the parameter is to model misspecification in the experiment.
CNN Uncertainty Quantification
To estimate support intervals for our parameter estimates, we applied a technique known as Conformalized Quantile Regression (CQR) as part of our training procedure (Romano et al. 2019). CQR generates support intervals that are predicted to contain the true data generating parameter value at a desired frequency (typically 95%), known as the intended coverage level for the interval. CQR has 2 phases.
The first phase uses quantile regression (Koenker and Bassett Jr 1978) to predict upper and lower bounds and construct an uncalibrated support interval for a specified coverage level. In more detail, the first phase constructs and trains a quantile CNN (qCNN) using the same input dataset that was used to train the initial CNN to predict true data generating parameters as point estimates. Whereas the initial CNN learned to predict point estimates by minimizing a MSE loss function, the qCNN instead minimizes the standard mean pinball loss function used to estimate quantiles (Steinwart and Christmann 2011; Romano et al. 2019). Briefly, the pinball loss score is an asymmetric linear penalty function where the errors when the true value, , is below the predicted are weighted by and those above by :
For instance, with , the loss is minimized by predicting higher values ensuring more of the labels, , fall below where the loss score of . This behavior is inversely mirrored for lower values, instead favoring true values of to be above . Pairing predictions of and can be used to construct an interval with an expected coverage rate. In practice, these uncalibrated interval estimates may not always provide the expected coverage on test data sets, as shown in Figure 3 (left). This discrepancy underscores the importance of the next phase of CQR: calibration (Vovk et al. 2009; Lei et al. 2018; Romano et al. 2019; Sousa et al. 2022; Vovk et al. 2022).
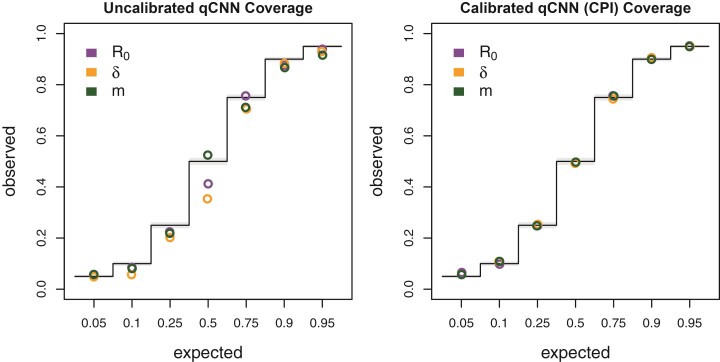
Figure 3.
Coverage of uncalibrated qCNN quantile predictions (left) and calibrated qCNN that produce CPI on the right. The observed coverage of 5000 samples tested at 7 different predicted coverage levels (labeled horizontal). See Figure 2c for more details on coverage plots.
The second phase calibrates the initial, uncalibrated support interval to produce the desired coverage properties. The chief task of this phase is to find adjustment terms for the lower and upper bounds (quantiles) that extend, shrink, and/or shift the uncalibrated intervals to attain the targeted coverage (Romano et al. 2019). We call these adjusted intervals calibrated probability intervals (CPI). For example, the 95% CPI estimated for a new individual dataset will have a 95% chance of containing the true data generating parameter value. To perform the calibration, the previously trained qCNN is used to predict lower and upper bounds from a new calibration dataset that was not part of the initial qCNN training dataset. Predictions from the calibration dataset are then used to separately quantify the degree to which each of the lower and upper bounds are too small or too large, and to compute upper and lower adjustment terms that, when added to all estimated quantiles in the calibration set, produce the correct coverage for the calibration data and future data. CQR is one form of conformal prediction that is an active and rapidly progressing field of research on distribution-free uncertainty quantification in machine learning and statistics. See Angelopoulos and Bates (2022) for a general overview of conformal prediction methods.
To create a calibration data set, we simulated 108,559 more datasets (trees with states) to estimate adjustment terms for the upper and lower qCNN-estimated quantiles. After calibration, we clipped intervals to the prior boundary for intervals that extended beyond the prior distribution’s range. To examine the consistency of quantile regression for neural networks trained on different quantiles, we trained 7 different quantile networks to predict the same inner quantiles used for validating our Bayesian analysis and simulation model: {0.05, 0.25, 0.5, 0.75, 0.9, 0.95}. We checked the coverage of these adjusted CPIs on another simulated test dataset of 5000 trees (Fig. 3, right).
Real Data
We compared the inferences of a LDBDS simulation trained neural network to that of a phylodynamic study of the first COVID wave in Europe (Nadeau et al. 2021). These authors analyzed a phylogenetic tree of viruses sampled in Europe and Hubei, China using a location-dependent birth–death-sampling model in a Bayesian framework using priors informed by myriad other sources of information. We simulated a new training set of trees under an LDBDS model where depends on the geographic location, and the sampling process only consists of serial sampling and no sampling of extant infected individuals. We estimated 95% CPIs for model parameters with a simulated calibration dataset of 101,219 trees using CQR as above and confirmed accurate coverages with another dataset of 5000 trees.
We then analyzed the whole tree from Figure 1 in (Nadeau et al. 2021) as well as the European clade, which Nadeau et al. (2021) labeled as A2 in the same figure. We note that our simulating model is not identical to the inference model used in (Nadeau et al. 2021). We model migration with a single parameter with symmetrical migration rates among locations and all locations having the same sampling rate. Nadeau et al. parameterize the migration process with asymmetric pairwise migration rates and assume location-specific sampling rates. We also do not include the information the authors used to inform their priors as that requires an extra level of simulation and training on top of simulations done here, and is thus beyond the scope of this study.
The time tree from (Nadeau et al. 2021) was downloaded from GitHub (https://github.com/SarahNadeau/cov-europe-bdmm). The recovery rate assumed in (Nadeau et al. 2021) was 0.1 days−1, which was set to 0.05 to bring the recovery rate to within the range of simulating values used to train the CNN. Consequently, the branch lengths of the tree were then scaled by 2. The number of tips, tree height, and average branch lengths were measured from the rescaled trees and fed into the network. The full tree and A2 clade were then analyzed using the LDBD CNN and compared to the posterior distributions from (Nadeau et al. 2021).
Hardware Used
Simulations were run on a 16 core Intel(R) Xeon(R) Platinum 8175M CPU @ 2.50GHz. For each simulation, an XML file with random parameter settings was generated using custom scripts. These XML files were the inputs for MASTER which was run in the BEAST2 platform. Neural network training and testing and predictions were conducted on an 8 core Intel(R) Core(TM) i7-7820HQ CPU @ 2.90GHz laptop with a NVIDIA Quadro M1200 GPU for training.
Results
Comparing Deep Learning to Likelihood
Our first goal in this study was to train a CNN that produced phylodynamic parameter point estimates that were as accurate as likelihood-based Bayesian posterior mean estimates under the true model. This will serve as a reference for quantifying level of sensitivity in our misspecification experiments. Using viral phylogenies like those typically estimated from serially sampled DNA sequences, we focused on estimating important epidemiological parameters—the reproduction number, , the sampling rate, , the migration rate, , and the outbreak origin.
Our CNN produced estimates that are as accurate as the mean posterior estimates under the true simulating model. We compared the APE of the network predictions to the APE of the mean posterior estimate of the Bayesian LIBDS model (Fig. 2). The APE is straight-forward to interpret, for example, an APE of < 10 means the estimate is within 10 percentage points (ppts) of the true value. For the 3 epidemiological rate parameters, , , and , both methods made very similar predictions for the 138 time tree test set (Fig. 2a). The 2 methods appear to produce estimates that are more similar to each other than to the ground truth labels (compare bottom row scatter plots in orange to the blue and red scatter plots in panel a). Fig. 2b shows that the inferred median difference in APE, , between the method’s estimates for the 3 parameters is close to 0 ( 95% highest posterior density is < 4 ppts; Supplementary Table S1; Supplementary Fig. S3).
We also compared the performance of uncertainty quantification using quantile-CNN-based CQR (Romano et al. 2019) to that of Bayesian highest posterior densities for each of the experiments. We trained 7 qCNNs to predict inner-quantiles at 7 different levels to compare with the Bayesian highest posterior densities; = {0.05, 0.1, 0.25, 0.5, 0.75, 0.9, 0.95}. We then used another simulated dataset to calibrate predicted intervals that we refer to as CPIs which theoretically have correct coverage properties (Romano et al. 2019) like the highest posterior densities. For the test dataset of 138 trees, the CPIs had coverages that matched well with expectations to a comparable degree to the Bayesian highest posterior density (Fig. 2c) though more variable. To further confirm that our CQR procedure was adequately calibrating the qCNN estimates, we confirmed correct coverages of CPIs for a much larger dataset with 5000 trees (Fig. 3). On average, the widths of CPIs in the set of 138 trees shown in (Fig. 2) was about 20%–40% wider than that of the corresponding highest posterior density and Jaccard similarity index ranging from 0.66 to 0.75 suggesting a high degree of overlap between the intervals (Supplementary Fig. S4 and Supplementary Table S2). These results indicate the probability level of the CPI, that is, 95% can be safely interpreted as the probability a parameter falls within the CPI. The wider intervals suggest the basic CQR method employed here is somewhat less precise and thus more conservative than the Bayesian method.
Our trained CNN provides nearly instantaneous estimates of model parameters. While the run time of the likelihood approach employed in this study scales linearly with the size of the tree, the neural network has virtually constant run times that are more than three orders of magnitude faster. Because simulation-trained neural networks have a one-time cost of simulating the training data set and then training the neural network, these methods are often called amortized-approximators (Bürkner et al. 2022). This means the time savings are not recouped until a certain number of trees have been analyzed. For example, here over 524 trees would need to be analyzed to realize the cost savings of simulating data and training our neural network (Fig. 4). This illustrates the importance of simulation optimization and generality for likelihood-free approaches to inference.
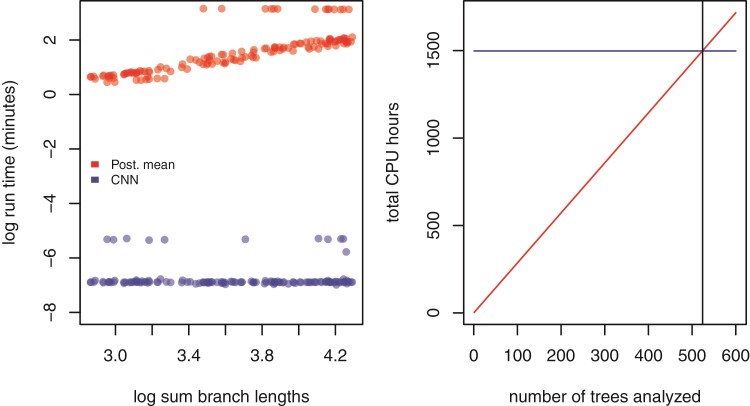
Figure 4.
Left: Estimates of time to complete analysis of each of 138 trees relative to tree size. Right: The number of trees (524; gray vertical line) needed to analyze for total analysis time of Bayesian method (red, diagonal line) to equal that of the entire simulation and CNN training and inference pipeline (blue, nearly horizontal line).
Comparing Sensitivity to Model Misspecification
To test the relative sensitivity of CNN estimates and the likelihood-based mean posterior estimate to model misspecification, we simulated several test data sets under different, more complex epidemic scenarios and compared the decrease in accuracy (increase in APE).
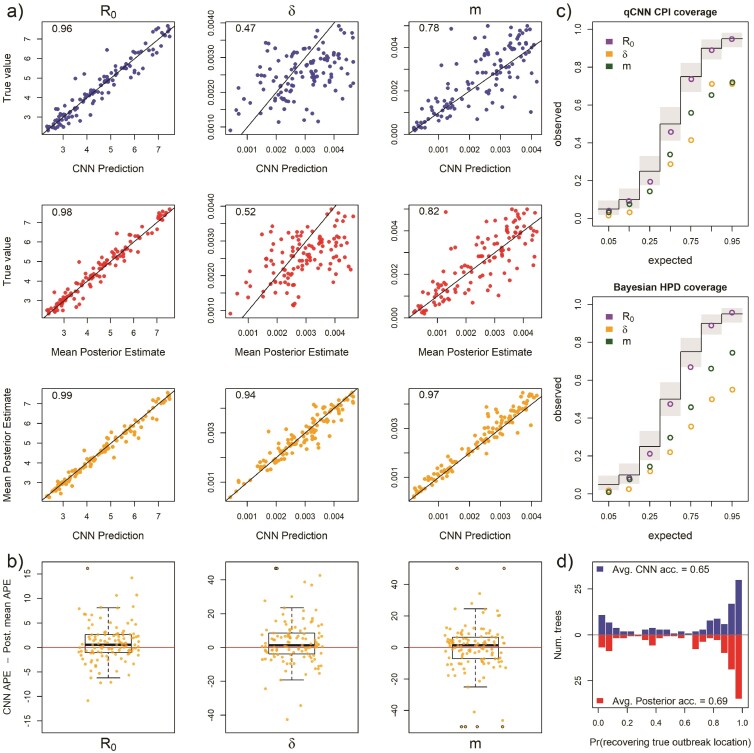
Our first model misspecification experiment tested performance when assuming all locations had the same R0 when, in fact, each location had different values. The median APE for all 3 parameters increased to varying degrees (Supplementary Fig. S5a) compared to the median APE measured in Fig. S3. We found that both methods converged on similar biased estimates for R0. In both the CNN and Bayesian method, estimates of were relatively robust to misspecifying R0. In contrast, the migration rate showed much more sensitivity to this model violation in both methods with both methods also converging on similarly biased estimates (Fig. 5a). The median difference in error between the 2 methods is close to zero for all rate parameters ( 95% highest posterior density < 6 ppts; Supplementary Table S1) (Supplementary Fig. S5b. For both methods of uncertainty quantification, the coverage declined by similar amounts for all 3 parameters with showing little to no sensitivity to R0 misspecification (Fig. 5c and Supplementary Table S2). The patterns of coverage are also somewhat less regular across the qCNN quantiles than the highest posterior densities for the migration rate parameter likely due in part to the fact that each inner quantile qCNN was trained independently and thus have independent errors. The relative interval widths and Jaccard similarity indexes did not change appreciably from predictions under the true model (Supplementary Fig. S4 and Supplementary Table S2). Our CNN appears to be slightly more sensitive than the Bayesian approach when predicting the outbreak location. Nevertheless, their distributions are quite similar (Fig. 5d).
Figure 5.
For 93 test trees where the R0 parameter was misspecified: the simulating model for the test data specified 5 unique R0s among the 5 locations while the inference methods assumed one R0 shared among locations. Because of this, the estimates for R0 are plotted against mean of the 5 true R0 values. See Figure 2 for general details about plots.
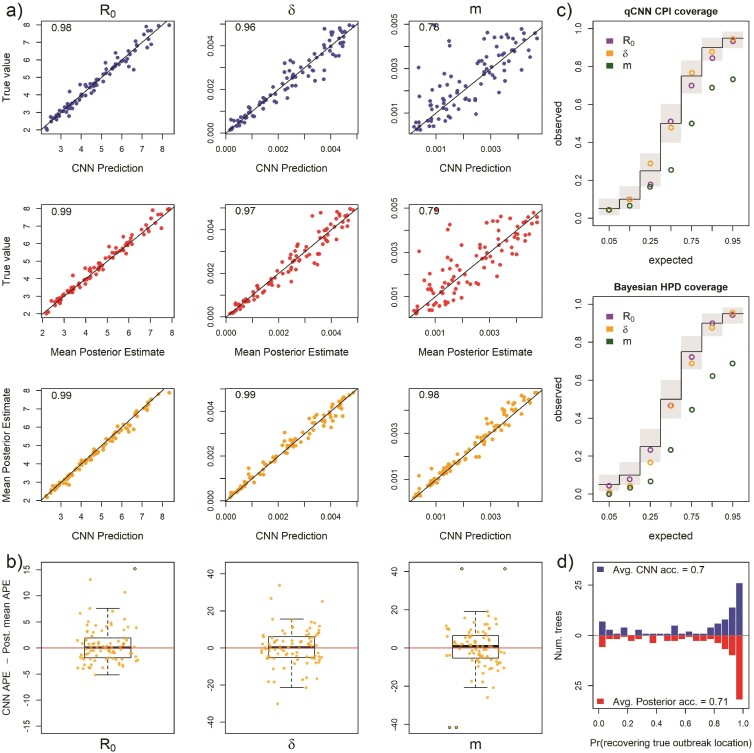
Next, we measured method sensitivity when the sampling process of the test trees violates assumptions in the inference model. In this set, each location had a unique and independent sampling rate, , rather than a single shared among locations. The median APE only increased for and m (Supplementary Fig. S7a). As expected, estimates of were highly biased for both methods (Fig. 6a). Panel a also shows that R0 is virtually insensitive to sampling model misspecification, but that migration rate, again, is highly sensitive in both the CNN and likelihood method. The median difference in error between the 2 methods is close to 0 for all the rate parameters ( 95% highest posterior density < 5 ppts; Supplementary Table S1, Supplementary Fig. S7) (Fig. 6a). For both methods coverage declined for and m, while R0 showed little to no sensitivity to misspecification (Fig. 6c and Supplementary Table S2). The relative widths and degree of overlap was again similar to the experiments above (Supplementary Fig. S8, Supplementary Table S2). We again also see greater irregularity among CPI levels in coverage, notably at inner-quantile level 0.9. The location of outbreak prediction is also somewhat sensitive in both methods, with the CNN showing a slightly larger mean difference, but the overall distribution of accuracy of all the test trees again is similar (Fig. 6d).
Figure 6.
For 118 test trees where the sampling rate parameter was misspecified: the simulating model for the test data specified 5 unique sampling rates among the 5 locations while the inference methods assumed one sampling rate shared among locations. The estimates of are plotted against the mean true values of . See Figure 2 for general details about plots.
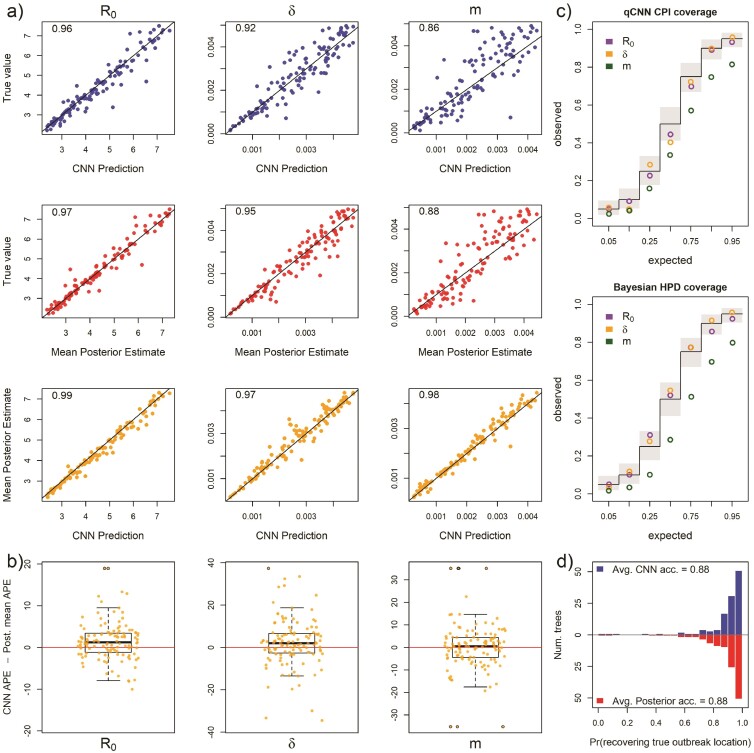
To explore sensitivity to migration model underspecification, we simulated a test set where the migration rates between locations is free to vary rather than being the same among locations as in the inference model. This implies 5! unique location-pairs and thus unique migration rates in the test data set. Results show that for both methods, the parameters R0 and are highly robust to this simplification (Supplementary Fig. S9a). Though estimates of a single migration rate had a high degree of error (Fig. 7a), the two methods still had similar estimates with the difference in APE centered near zero (Fig. 7b). The inferred median difference in APE was close to zero ( 95% highest posterior density < 3 ppts; Supplementary Table S1; Supplementary Fig. S9b). For both methods, the coverage only declined significantly for the migration rate and the decrease was again similar in magnitude across quantiles (Fig. 7c and Supplementary Table S2). Again, relative widths and degree of overlap of CPI and highest posterior density were similar to previous experiments (Supplementary Fig. S10, Supplementary Table S2). There was a slight but similar decrease in accuracy in predicting the outbreak location for both methods (Fig. 7d).
Figure 7.
For 90 test trees where the migration rate parameter was misspecified: the simulating model for the test data specified 5! (120) unique migration rates among the unique pairs of the 5 locations while the inference methods assumed all migration rates were equal. The infered migration rate is plotted against the mean pairwise migraiton rates of test data set. See Figure 2 for general details about plots.
When testing the sensitivity of the 2 methods to arbitrary groupings of locations, we found that both methods showed equal sensitivity to the same parameters (Fig. 8 Panels a and b). In particular, the migration rate showed a modest increase in median APE and R0 and sample rate showed virtually no sensitivity to arbitrary grouping of locations (Supplementary Fig. S11a). The inferred median difference between method APE’s was again close to zero ( 95% highest posterior density < 4 ppts; Supplementary Table S1; Supplementary Fig. S11b). For both methods, the coverage declined modestly only for the migration rate (Fig. 8c and Supplementary Table S2). Relative widths and interval overlap showed virtually no change (Supplementary Fig. S12 and Supplementary Table S1). These results suggest that, for at least the exponential phase of outbreaks, rate parameters do not vary among locations, these models have a fair amount of robustness to the decisions leading to geographical division of continuous space into discrete space. The outbreak location showed higher accuracy in both methods due to the fact that the test data were no longer a flat distribution; the 6 combined locations should contain 60% of the outbreak locations (Fig. 8d).
Figure 8.
For 101 test trees where the number of locations was misspecified: the simulating model for the test data specified an outbreak among 10 locations with 6 locations subsequently combined into a single location while the inference methods assumed 5 locations with no arbitrary combining of locations. See Figure 2 for general details about plots.
Finally, we explored the relative sensitivity of our CNN to amounts of phylogenetic error that are present in typical phylogeographic analyses. Our simulated phylogenetic error produced trees with average Jaccard similarity indexes between the inferred tree and the true tree of about 0.5 with 95% of simulated trees having distances within 0.36 and 0.72. We again compared inferences derived from the true tree and the tree with errors using the CNN and the Bayesian LIBDS methods. Results show that migration rate was minimally affected but R0 and were to some degree sensitive to phylogenetic error (Fig. 9a; Supplementary Fig. S13a), with both methods again showing similar degrees of sensitivity (Fig. 9b). The inferred median difference was, yet again, small ( 95% highest posterior density < 6 ppts. Supplementary Table S1, Supplementary Fig. S13b). Coverages of declined for both methods in a similar way across quantiles. Again the 90% inner quantile showed some inconsistency with its neighboring quantiles. In this case, its coverage for was slightly higher than the 95th inner quantile. The CPIs for appear much less sensitive (Fig. 9c and Supplementary Table S2). Although the relative widths of the CPIs and highest posterior densities were similar to previous experiments, the degree of overlap decreased somewhat by about 5%–10% (Supplementary Fig. S14 and Supplementary Table S2). One difference between this experiment and the others is that trees are data instead of model parameters. It is interesting that the point estimates from the 2 methods show similar biases while the coverages seem to depart somewhat. Inference of the origin location was very similar for both methods (Fig. 9d).
Figure 9.
For 118 test trees where the time tree was misspecified: the true tree from the simulated test set was replaced with an inferred tree from simulated DNA alignments under the true tree. See Figure 2 for general details about plots.
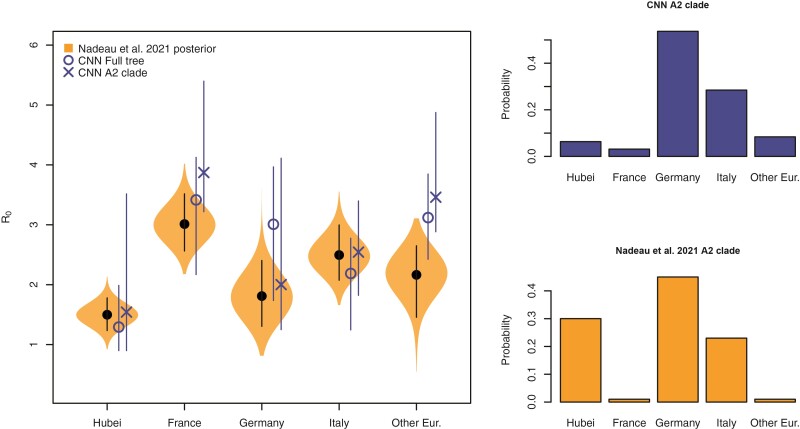
Analysis of SARS CoV-2 Tree
We next compared our likelihood-free method to a recent study investigating the phylodynamics of the first wave of the SARS CoV-2 pandemic in Europe (Nadeau et al. 2021). Despite simulating the migration and the sampling processes differently from Nadeau et al. (2021), our CNN produces similar estimates for the location-specific R0 and the origin of the A2 clade (Fig. 10). Whether the full tree or just the A2 clade is fed into the network, the predicted R0 for each location was not far from the posterior estimates of Nadeau et al. (2021). For the most part the R0 95% CPI for each location overlaps to a high degree with the 95% highest posterior density and is roughly 1.5 times wider indicating that our CNN estimates are relatively conservative. For Hubei, the interval width of the a2 clade is much wider than the estimate using the whole tree. This is not surprising because there are no samples from Hubei in the a2 clade. We also obtained estimates for the sampling rate and migration rate from our CNN and CPIs from our calibrated qCNN. Because Nadeau et al. (2021) specify location-specific rates and informative priors for these rates, making a direct comparison of these results with the single parameter for each of migration and sampling rates is more challenging to interpret. Supplementary Figure S15 shows the CNN’s estimates are within the range of posterior distributions estimated in Nadeau et al. (2021), however, overlap could be explained in large part by wide posterior distributions.
Figure 10.
LDBDS CNN comparison to (Nadeau et al. 2021) inference. Left violin plots show the posterior distributions of R0 for each location in Europe as well as Hubei, China (orange). The black dot and line within each violin plot shows the posterior mean and 95% highest posterior density respectively. The blue X and O marks the LDBDS CNN prediction from analyzing the full tree and the A2 (European) clade, respectively. Vertical blue lines give the 95% CPI for the CNN estimates of R0. Right barplots show the LDBDS CNN prediction (top, blue) and posterior inference (bottom, orange) from (Nadeau et al. 2021) of the ancestral location of the A2 (European) clade (see Figure 1 (Nadeau et al. 2021)).
The spillover-location-prediction-CNN produced probability estimates of the A2 clade ancestral location that mostly agreed with that of Nadeau et al. (Fig. 10, right histograms). The only significant discrepancy in the European origin prediction is that Nadeau et al.’s analysis suggests a much higher probability that the most recent common ancestor of the A2 clade was in Hubei than our CNN predicts. This is likely because our CNN only used the A2 clade to predict A2 origins which has no Hubei samples to infer the origin of the A2 clade while Nadeau et al. (2021) used the whole tree. Notwithstanding this difference, among European locations, both methods predict Germany is the most likely location of the most recent common ancestor followed by Italy.
Discussion and Conclusions
Inference models are necessarily simplified approximations of the real world. Both simulation-trained neural networks and likelihood-based inference approaches suffer from model under-specification and/or misspecification. When comparing inference methods, it is important to assess the sensitivity of model inference to simplifying assumptions. In this study, we show that newer deep learning approaches and standard Bayesian approaches behave and misbehave in similar ways under a panel of phylodynamic estimation tasks where the inference model is correct as well as when it is misspecified.
By extending new approaches to encode phylogenetic trees in a compact data structure (Voznica et al. 2022; Lambert et al. 2023), we have developed the first application of phylodynamic deep learning applied to phylogeography with serial sampling. Our approach is similar to that of Lambert et al. (2023) in which they analyzed a binary state-dependent birth-death model with exclusively extant sampling. By training a neural network on phylogenetic trees generated by simulated epidemics, we were able to accurately estimate key epidemiological parameters, such as the reproduction number and migration rate, in a fraction of the time it would take with likelihood-based methods. Like Voznica et al. (2022) and Lambert et al. (2023), we found that CNN estimators perform as well or nearly as well as likelihood-based estimators under conditions where the inference model is correctly specified to match the simulation model. The success of these separate applications of deep learning to different phylodynamic problems is a testament to the versatility of the CBLV encoding of trees.
We compared the sensitivity of deep learning and likelihood-based inference to model misspecification. Because deep-learning methods of phylogenetic and phylodynamic inference are new, few studies compare how simulation-trained deep learning methods fail in comparison to likelihood methods in this way (Flagel et al. 2019). We assume that when the inference model is correctly specified to match the simulation model, the trained CNN will, at best, produce noisy approximations of likelihood-based parameter estimates. In reality, issues related to training data set size, learning efficiency, and network overfitting may cause our CNN-based estimates to contain excess variance or bias when compared to Bayesian likelihood-based estimators. Our results from 5 model misspecification experiments show that both methods of inference perform similarly when the simulating model and the inference model assumptions do not perfectly match. These similarities exist not only in aggregate, when comparing method performance across datasets but also when comparing performance for each individual dataset. This suggests that the CNN and likelihood methods are truly estimating parameters using functionally equivalent criteria, despite the fact that CNN heuristically learns these criteria through data patterns, while likelihood precisely and mathematically defines these criteria through the model definition itself.
Results of comparative sensitivity experiments like this are important because if likelihood-free methods using deep neural networks can easily be trained to yield estimates that are as robust to model misspecification as likelihood-based methods, then analysis of a large space of more complex outbreak scenarios for which tractable likelihood functions are not available can be developed and applied to real world data. Additionally, sufficiently realistic, pre-trained neural networks can yield nearly instantaneous inferences from data in real time to inform analysts and policy makers. For example, modeling how viruses move and are unevenly sampled among host populations can impact phylogeographic inferences (Layan et al. 2023). Unfortunately, inference under accurate models currently requires sophisticated but computationally demanding likelihood-based methods that may constrain other model design choices (Maio et al. 2015; Müller et al. 2018). Deep learning may prove useful for exploring this important area of model space, particularly in those areas where likelihood-based methods development is most difficult.
We also tested location-dependent SIR simulation trained neural networks against results from a previous publication fitting a similar model—location-dependent birth-death-sampling (LDBDS) model—on real-world data using a Bayesian method. Our CNN predicted location-specific R0 and outbreak origin in Europe were similar to that inferred in (Nadeau et al. 2021). This result and our model misspecification experiments suggest that simulation-trained deep neural networks trained on phylogenetic trees can find patterns in the training data that generalize well beyond the training data set.
Our study extends the results of Voznica et al. (2022) and Lambert et al. (2023) in several important ways. Our work showed that the new compact bijective ladderized vector encoding of phylogenetic trees can easily be extended with one-hot encoding to include metadata about viral samples. Using this strategy, we trained a neural network to not only predict important epidemiological parameters such as R0 and the sampling rate but also geographic parameters such as the migration rate and the location of outbreak origination or spillover. We anticipate that more diverse and complex metadata can be incorporated to train neural networks to make predictions about many important aspects of epidemiological spread such as the relative roles of different demographic groups and the overlap of different species’ ranges.
This approach can be readily applied to numerous compartment models used to describe the spread of different pathogens among different species, locations, and demographic groups, for example, SEIR, SIRS, SIS, etc. (Ponciano and Capistrán 2011; Volz and Siveroni 2018; Bjørnstad et al. 2020; Chang et al. 2020; O’Dea and Drake 2022) as well as modeling super-spreader dynamics as in (Voznica et al. 2022). Here, we focused on one phase of outbreaks (the exponential phase), but there are many other scenarios to be investigated, such as when the stage of an epidemic differs among locations (e.g. exponential, peaked, declining). With likelihood-free methods, the link between the underlying population dynamics from which viral genomes are sampled and inferred phylogenetic trees can easily be interrogated. More complex models will require larger trees to infer model parameters. In this study, we explored trees that contained fewer than 500 tips, but anticipate that larger trees will demonstrate even greater speed advantages of neural networks over likelhood-based methods either through subsampling regimes (Voznica et al. 2022) or by including larger trees in training datasets.
With the fast, likelihood-free inference afforded by deep learning, the technical challenges shift from exploring models for which tractable likelihood functions can be derived toward models that produce realistic empirical data patterns, have parameters that control variation of those patterns, and are efficient enough to generate large training data sets. A growing number of advanced simulators are rapidly expanding the possibilities for deep learning in phylogenetics. For example, FAVITES (Moshiri et al. 2019) is a simulator of disease spread through large contact networks that tracks transmission trees and simulates sequence evolution. Gen3sis, MASTER, SLiM, and VGsim are flexible simulation engines for generating complex ecological, evolutionary, and disease transmission simulations (Vaughan and Drummond 2013; Haller and Messer 2019; Hagen et al. 2021; Overcast et al. 2021; Shchur et al. 2022). Continued advances in epidemic simulation speed and flexibility will be essential for likelihood-free methods to push the boundaries of epidemic modeling sophistication and usefulness.
There are several avenues of development still needed to realize the potential of likelihood-free inference in phylogeography using deep learning. The current setup is ideal for simulation experiments, but it is more difficult to ensure that the optimal parameter values for empirical data sets are within the range of training data parameters. Standardizing input tree height, geographical distance, and other parameters help make training data more universally applicable. Simulation-trained neural networks are often called amortized methods (Bürkner et al. 2022; Schmitt et al. 2022) because the cost of inference is front-loaded, that is, it takes time to simulate a training set and train a neural network. The total cost in time per phylogenetic tree amortizes as the number of trees analyzed by the trained model increases. These methods are, therefore, important when a model is intended to be widely deployed or be responsive to an emerging outbreak where policy decisions must be formulated rapidly. Because amortized approximate methods require multiple analyses to realize time savings, researchers need to generate training data sets over a broad parameter and model space so that trained networks can be applied to new and diverse data sets.
Our analysis introduces a simple approach to estimate the ancestral state corresponding to the root node or stem node of a phylogeny. More sophisticated supervised learning approaches will be needed to train neural networks to predict the ancestral locations for internal nodes other than the root. The topologies and branch lengths of random phylogenies in the training and test datasets will vary from tree to tree. Our approach relies on the fact that all trees contain a root node, meaning all trees can help predict the root node’s state. However, few (if any) trees in the training dataset will contain an arbitrary clade of interest within a test dataset, suggesting to us that naive approaches to train networks to estimate ancestral states for all internal nodes will probably fail. We are unaware of any existing solutions for generalized ancestral state estimation using deep learning, and expect the problem will gather more attention as the field matures.
Quantifying uncertainty is crucial to data analysis and decision making, and Bayesian statistics provide a framework for doing so in a rigorous way. It is essential to understand how uncertainty estimation with likelihood-free methods compare to likelihood-based methods when confronted with the mismatch of models and real-world data-generating processes. We quantified uncertainty using CQR (Romano et al. 2019) by training neural networks to predict quantiles and then calibrating those quantiles to produce the expected coverage. We refer to the resulting intervals as CPI and demonstrate that they predict well the coverage of true values on a test dataset (Fig. 3) and behave in similar ways to Bayesian methods when the model is or is not misspecified (Figs. 2–9). Despite having the same (correct) coverage as the Bayesian highest posterior density, the interval length was 20%–50% wider on average making them a more conservative (less precise) estimation procedure. Though this can likely be improved with more training data for qCNNs, there are more fundamental challenges for uncertainty quantification with quantile regression and conformalization.
Methods for estimating more precise intervals is an active vein of research among machine learning researchers and statisticians (Barber et al. 2020; Chung et al. 2021; Sousa et al. 2022; Gibbs et al. 2023). For example, although intervals estimated by the qCNN are conditional on each data point, the calibration of quantiles through CQR involves estimating marginal calibration terms that shift all quantiles by the same amount. If the error in the quantile coverage is not constant across the prediction range, then a more adaptive procedure should yield more precise intervals (Sousa et al. 2022; Gibbs et al. 2023).
We also compared the consistency among CPI estimates at different inner-quantiles to that of highest posterior densities at those same quantiles. We find that independently trained neural networks for each coverage level can potentially lead to inconsistencies where narrower, nested inner quantiles can have close to or higher coverage than wider quantiles (e.g. Fig. 9c). Overall, our results suggest CQR is approximately consistent with likelihood-based methods and similarly sensitive to model misspecification, while there is room for improvement. Methods where all quantiles of interest can be estimated jointly (Chung et al. 2021) may be a fruitful avenue of research for such improvements.
Another important challenge of inference with deep learning is the problem of convergence to a location on the loss function surface that approximates the maximum likelihood well. There are a number of basic heuristics that can help such as learning curves but more rigorous methods of ascertaining convergence is the subject of active research (Bürkner et al. 2022; Schmitt et al. 2022).
With recent advances in deep learning in epidemiology, evolution, and ecology (Battey et al. 2020; Schrider and Kern 2018; Voznica et al. 2022; Radev et al. 2021; Lambert et al. 2023; Rosenzweig et al. 2022; Suvorov and Schrider 2022), biologists can now explore the behavior of entire classes of stochastic branching models that are biologically interesting but mathematically or statistically prohibitive for use with traditional likelihood-based inference techniques. Beyond epidemiology, we anticipate that deep learning approaches will be useful for a wide range of currently intractable phylogenetic modeling problems. Many phylogenetic scenarios—such as the adaptive radiation of anoles (Patton et al. 2021) or the global spread of the grasses (Palazzesi et al. 2022)—involve the evolution of discrete traits, continuous traits, speciation, and extinction within an ecological or spatial context across a set of co-evolving species. Deriving fully mechanistic yet tractable phylogenetic model likelihoods for such complex scenarios is difficult, if not impossible. Careful development and applications of likelihood-free modeling methods might bring these phylogenetic scenarios into renewed focus for more detailed study. Although we are cautiously optimistic about the future of deep learning methods for phylogenetics, it will become increasingly important to diagnose the conditions where phylogenetic deep learning underperforms relative to likelihood-based approaches, and to devise general solutions to benefit the field.
Acknowledgements
We are grateful to Jacob McCord, Mark Lowell, Michael May, Fábio Mendes, Sarah Swiston, Sean McHugh, Walker Sexton, and Mariana Braga for helpful comments on the research.
Contributor Information
Ammon Thompson, Participant in an Education Program Sponsored by U.S. Department of Defense (DOD) at the National Geospatial-Intelligence Agency, Springfield, VA 22150, USA.
Benjamin J Liebeskind, National Geospatial-Intelligence Agency, Springfield, VA 22150, USA.
Erik J Scully, National Geospatial-Intelligence Agency, Springfield, VA 22150, USA.
Michael J Landis, Department of Biology, Washington University in St. Louis, Rebstock Hall, St. Louis, MO 63130, USA.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.25338/B8SH2J.
Funding
This research was supported in part by an appointment to the Department of Defense (DOD) Research Participation Program administered by the Oak Ridge Institute for Science and Education (ORISE) through an interagency agreement between the U.S. Department of Energy (DOE) and the DOD. ORISE is managed by ORAU under DOE contract number DE-SC0014664. All opinions expressed in this paper are the author’s and do not necessarily reflect the policies and views of DOD, DOE, or ORAU/ORISE. M.J.L. was supported by the National Science Foundation (DEB 2040347), by the Fogarty International Center at the National Institutes of Health (R01 TW012704) as part of the joint NIH-NSF-NIFA Ecology and Evolution of Infectious Disease program, and by an internal grant awarded by the Incubator for Transdisciplinary Futures at Washington University.
Data Availability
Data available from the Dryad Digital Repository: https://doi.org/10.25338/B8SH2J (Thompson et al. this issue) and code is available on github: https://github.com/ammonthompson/phylogeo_epi_cnn
References
- Abadi M., Agarwal A., Barham P., Brevdo E., Chen Z., Citro C., Corrado G.S., Davis A., Dean J., Devin M., Ghemawat S., Goodfellow I., Harp A., Irving G., Isard M., Jia Y., Jozefowicz R., Kaiser L., Kudlur M., Levenberg J., Mane D., Monga R., Moore S., Murray D., Olah C., Schuster M., Shlens J., Steiner B., Sutskever I., Talwar K., Tucker P., Vanhoucke V., Vasudevan V., Viegas F., Vinyals O., Warden P., Wattenberg M., Wicke M., Yu Y., Zheng X. 2016. TensorFlow: large-scale machine learning on heterogeneous distributed systems. arXiv 10.48550/arXiv.1603.04467.
- Alzubaidi L., Zhang J., Humaidi A.J., Al-Dujaili A., Duan Y., Al-Shamma O., Santamaría J., Fadhel M.A., Al-Amidie M., Farhan L. 2021. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J. Big Data 8(1):53. doi: 10.1186/s40537-021-00444-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., May R.M. 1979. Population biology of infectious diseases. Part I. Nature 280(5721):361–367. [DOI] [PubMed] [Google Scholar]
- Angelopoulos A.N., Bates S. 2022. A gentle introduction to conformal prediction and distribution-free uncertainty quantification. arXiv 2107.07511v6.
- Barber R.F., Candès E.J., Ramdas A., Tibshirani R.J. 2020. The limits of distribution-free conditional predictive inference. arXiv 10.48550/arXiv.1903.04684.
- Battey C.J., Ralph P.L., Kern A.D. 2020. Predicting geographic location from genetic variation with deep neural networks. eLife 9:e54507. doi: 10.7554/eLife.54507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaulieu J.M., O’Meara B.C. 2016. Detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Syst. Biol. 65(4):583–601. doi: 10.1093/sysbio/syw022 [DOI] [PubMed] [Google Scholar]
- Bjørnstad O.N., Shea K., Krzywinski M., Altman N. 2020. The SEIRS model for infectious disease dynamics. Nat. Meth. 17(6):557–558. doi: 10.1038/s41592-020-0856-2. [DOI] [PubMed] [Google Scholar]
- Bokma F. 2006. Artificial neural networks can learn to estimate extinction rates from molecular phylogenies. J. Theor. Biol. 243(3):449–454. [DOI] [PubMed] [Google Scholar]
- Bouckaert R., Vaughan T.G., Barido-Sottani J., Duchêne S., Fourment M., Gavryushkina A., Heled J., Jones G., Kühnert D., Maio N.D., Matschiner M., Mendes F.K., Müller N.F., Ogilvie H.A., du Plessis L., Popinga A., Rambaut A., Rasmussen D., Siveroni I., Suchard M.A., Wu C.-H., Xie D., Zhang C., Stadler T., Drummond A.J. 2019. BEAST 2.5: An advanced software platform for Bayesian evolutionary analysis. PLoS Comput. Biol. 15(4):e1006650. doi: 10.1371/journal.pcbi.1006650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bürkner P.-C., Scholz M., Radev S. 2022. Some models are useful, but how do we know which ones? Towards a unified Bayesian model taxonomy. arXiv 2209.02439.
- Chang S.L., Piraveenan M., Pattison P., Prokopenko M. 2020. Game theoretic modelling of infectious disease dynamics and intervention methods: a review. J. Biol. Dyn. 14(1):57–89. doi: 10.1080/17513758.2020.1720322 [DOI] [PubMed] [Google Scholar]
- Chollet F. et al. 2015. Keras. https://keras.io.
- Chung Y., Neiswanger W., Char I., Schneider J. 2021. Beyond pinball loss: quantile methods for calibrated uncertainty quantification. arXiv 10.48550/arXiv.2011.09588.
- Cranmer K., Brehmer J., Louppe G. 2020. The frontier of simulation-based inference. Proc. Natl. Acad. Sci 117(48):30055–30062. doi: 10.1073/pnas.1912789117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Fonseca E.M., Colli G.R., Werneck F.P., Carstens B.C. 2020. Phylogeographic model selection using convolutional neural networks. bioRxiv. doi: 10.1101/2020.09.11.291856 [DOI] [PubMed] [Google Scholar]
- Douglas J., Mendes F.K., Bouckaert R., Xie D., Jiménez-Silva C.L., Swanepoel C., de Ligt J., Ren X., Storey M., Hadfield J., Simpson C.R., Geoghegan J.L., Drummond A.J., Welch D. 2021. Phylodynamics reveals the role of human travel and contact tracing in controlling the first wave of COVID-19 in four island nations. Virus Evol. 7(2):1–10. doi: 10.1093/ve/veab052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Rambaut A., Shapiro B., Pybus O.G. 2005. Bayesian coalescent inference of past population dynamics from molecular sequences. Mol. Biol. Evol. 22(5):1185–1192. [DOI] [PubMed] [Google Scholar]
- FitzJohn R.G. 2012. Diversitree: comparative phylogenetic analyses of diversification in R. Meth. Ecol. Evol. 3(6):1084–1092. doi: 10.1111/j.2041-210X.2012.00234.x [DOI] [Google Scholar]
- Flagel L., Brandvain Y., Schrider D.R. 2019. The unreasonable effectiveness of convolutional neural networks in population genetic inference. Mol. Biol. Evol. 36(2):220–238. doi: 10.1093/molbev/msy224 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J., May M.R., Rannala B., Moore B.R. 2022. New phylogenetic models incorporating interval-specific dispersal dynamics improve inference of disease spread. Mol. Biol. Evol. 39(8):msac159. doi: 10.1093/molbev/msac159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J., May M.R., Rannala B., Moore B.R. 2023. Model misspecification misleads inference of the spatial dynamics of disease outbreaks. Proc. Natl. Acad. Sci 120(11):e2213913120. doi: 10.1073/pnas.2213913120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs I., Cherian J.J., Candès E.J. 2023. Conformal prediction with conditional guarantees. arXiv 10.48550/arXiv.2305.12616.
- Hadfield J., Megill C., Bell S.M., Huddleston J., Potter B., Callender C., Sagulenko P., Bedford T., Neher R.A. 2018. Nextstrain: real-time tracking of pathogen evolution. Bioinformatics 34(23):4121–4123. doi: 10.1093/bioinformatics/bty407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagen O., Flück B., Fopp F., Cabral J.S., Florian H., Pontarp M., Rangel T.F., Pellissier L. 2021. Gen3sis: a general engine for eco-evolutionary simulations of the processes that shape Earth’s biodiversity. PLoS Biol. 19(7):e3001340. doi: 10.1371/journal.pbio.3001340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haller B.C., Messer P.W. 2019. SLiM 3: forward genetic simulations beyond the Wright–Fisher Model. Mol. Biol. Evol. 36(3):632–637. doi: 10.1093/molbev/msy228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höhna S., Landis M.J., Heath T.A., Boussau B., Lartillot N., Moore B.R., Huelsenbeck J.P., Ronquist F. 2016. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65(4):726–736. doi: 10.1093/sysbio/syw021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes E.C., Garnett G.P. 1994. Genes, trees and infections: molecular evidence in epidemiology. Trends Ecol. Evol. 9(7):256–260. [DOI] [PubMed] [Google Scholar]
- Holmes E.C., Nee S., Rambaut A., Garnett G.P., Harvey P.H. 1995. Revealing the history of infectious disease epidemics through phylogenetic trees. Philos. Trans. R. Soc. London. Series B: Biol. Sci 349(1327):33–40. [DOI] [PubMed] [Google Scholar]
- Khan A., Sohail A., Zahoora U., Qureshi A.S. 2020. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 53(8):5455–5516. doi: 10.1007/s10462-020-09825-6 [DOI] [Google Scholar]
- Kingma D.P., Ba J. 2017. Adam: a method for stochastic optimization. arXiv. https://arxiv.org/abs/1412.6980
- Koenker R., Bassett G. Jr. 1978. Regression quantiles. Econ. J. Econ. Soc.: 33–50. [Google Scholar]
- Kruschke J.K. 2013. Bayesian estimation supersedes the t test. Experiment. Psychol 142(2):573–603. doi: 10.1037/a0029146 [DOI] [PubMed] [Google Scholar]
- Kühnert D., Stadler T., Vaughan T.G., Drummond A.J. 2014. Simultaneous reconstruction of evolutionary history and epidemiological dynamics from viral sequences with the birth–death SIR model. J. R. Soc. Int 11(94):20131106. doi: 10.1098/rsif.2013.1106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühnert D., Stadler T., Vaughan T.G., Drummond A.J. 2016. Phylodynamics with migration: a computational framework to quantify population structure from genomic data. Mol. Biol. Evol. 33(8):2102–2116. doi: 10.1093/molbev/msw064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert S., Voznica J., Morlon H. 2023. Deep learning from phylogenies for diversification analyses. Syst. Biol. XX(X):syad044. [DOI] [PubMed] [Google Scholar]
- Layan M., Müller N.F., Dellicour S., De Maio N., Bourhy H., Cauchemez S., Baele G. 2023. Impact and mitigation of sampling bias to determine viral spread: evaluating discrete phylogeography through CTMC modeling and structured coalescent model approximations. Virus Evol. 9(1):vead010. doi: 10.1093/ve/vead010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei J., G’Sell M., Rinaldo A., Tibshirani R.J., Wasserman L. 2018. Distribution-free predictive inference for regression. J. Am. Stat. Assoc. 113(523):1094–1111. doi: 10.1080/01621459.2017.1307116 [DOI] [Google Scholar]
- Lemey P., Rambaut A., Drummond A.J., Suchard M.A. 2009. Bayesian phylogeography finds its roots. PLoS Comput. Biol. 5(9):e1000520. doi: 10.1371/journal.pcbi.1000520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemey P., Ruktanonchai N., Hong S.L., Colizza V., Poletto C., Van den Broeck F., Gill M.S., Ji X., Levasseur A., Oude Munnink B.B., Koopmans M., Sadilek A., Lai S., Tatem A.J., Baele G., Suchard M.A., Dellicour S. 2021. Untangling introductions and persistence in COVID-19 resurgence in Europe. Nature. doi: 10.1038/s41586-021-03754-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemoine F., Gascuel O. 2021. Gotree/Goalign: toolkit and Go API to facilitate the development of phylogenetic workflows. NAR Genom. Bioinform 3(3):lqab075. doi: 10.1093/nargab/lqab075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacPherson A., Louca S., McLaughlin A., Joy J.B., Pennell M.W. 2022. Unifying phylogenetic birth–death models in epidemiology and macroevolution. Syst. Biol. 71(1):172–189. doi: 10.1093/sysbio/syab049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddison W.P., Midford P.E., Otto S.P. 2007. Estimating a binary character’s effect on speciation and extinction. Syst. Biol. 56(5):701–710. doi: 10.1080/10635150701607033 [DOI] [PubMed] [Google Scholar]
- Maio N.D., Wu C.-H., O’Reilly K.M., Wilson D. 2015. New routes to phylogeography: a Bayesian structured coalescent approximation. PLoS Genet. 11(8):e1005421. doi: 10.1371/journal.pgen.1005421 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minh B.Q., Schmidt H.A., Chernomor O., Schrempf D., Woodhams M.D., von Haeseler A., Lanfear R. 2020. IQ-TREE 2: new models and efficient methods for phylogenetic inference in the genomic era. Mol. Biol. Evol. 37(5):1530–1534. doi: 10.1093/molbev/msaa015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minin V.N., Bloomquist E.W., Suchard M.A. 2008. Smooth skyride through a rough skyline: Bayesian coalescent-based inference of population dynamics. Mol. Biol. Evol. 25(7):1459–1471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morlon H., Potts M.D., Plotkin J.B. 2010. Inferring the dynamics of diversification: a coalescent approach. PLoS Biol. 8(9):e1000493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moshiri N., Ragonnet-Cronin M., Wertheim J.O., Mirarab S. 2019. FAVITES: simultaneous simulation of transmission networks, phylogenetic trees and sequences. Bioinformatics 35(11):1852–1861. doi: 10.1093/bioinformatics/bty921 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller N.F., Rasmussen D.A., Stadler T. 2017. The structured coalescent and its approximations. Mol. Biol. Evol. 34(11):2970–2981. doi: 10.1093/molbev/msx186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller N.F., Rasmussen D., Stadler T. 2018. Mascot: parameter and state inference under the marginal structured coalescent approximation. Bioinformatics 34(22):3843–3848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadeau S.A., Vaughan T.G., Scire J., Huisman J.S., Stadler T. 2021. The origin and early spread of SARS-CoV-2 in Europe. Proc. Natl. Acad. Sci 118(9):e2012008118. doi: 10.1073/pnas.2012008118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesterenko L., Boussau B., Jacob L. 2022. Phyloformer: towards fast and accurate phylogeny estimation with self-attention networks.
- O’Dea E.B., Drake J.M. 2022. A semi-parametric, state-space compartmental model with time-dependent parameters for forecasting COVID-19 cases, hospitalizations and deaths. J. R. Soc 19:20210702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overcast I., Ruffley M., Rosindell J., Harmon L., Borges P.A.V., Emerson B.C., Etienne R.S., Gillespie R., Krehenwinkel H., Mahler D.L., Massol F., Parent C.E., Patiño J., Peter B., Week B., Wagner C., Hickerson M.J., Rominger A. 2021. A unified model of species abundance, genetic diversity, and functional diversity reveals the mechanisms structuring ecological communities. Mol. Ecolo. Res 21:2782–2800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palazzesi L., Hidalgo O., Barreda V.D., Forest F., Höhna S. 2022. The rise of grasslands is linked to atmospheric co2 decline in the late palaeogene. Nat. Commun. 13:293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patton A.H., Harmon L.J., del Rosario Castañeda M., Frank H.K., Donihue C.M., Herrel A., Losos J.B. 2021. When adaptive radiations collide: different evolutionary trajectories between and within island and mainland lizard clades. Proc. Natl. Acad. Sci 118(42):e2024451118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pekar J.E., Magee A., Parker E., Moshiri N., Izhikevich K., Havens J.L., Gangavarapu K., Malpica Serrano L.M., Crits-Christoph A., Matteson N.L., Zeller M., Levy J.I., Wang J.C., Hughes S., Lee J., Park H., Park M.-S., Ching K.Z.Y., Lin R.T.P., Mat Isa M.N., Noor Y.M., Vasylyeva T.I., Garry R.F., Holmes E.C., Rambaut A., Suchard M.A., Andersen K.G., Worobey M., Wertheim J.O. 2022. The molecular epidemiology of multiple zoonotic origins of SARS-CoV-2. Science 0(0):eabp8337. doi: 10.1126/science.abp8337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponciano J.M., Capistrán M.A. 2011. First principles modeling of nonlinear incidence rates in seasonal epidemics. PLoS Comput. Biol. 7(2):e1001079. doi: 10.1371/journal.pcbi.1001079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus O.G., Suchard M.A., Lemey P., Bernardin F.J., Rambaut A., Crawford F.W., Gray R.R., Arinaminpathy N., Stramer S.L., Busch M.P., Delwart E.L. 2012. Unifying the spatial epidemiology and molecular evolution of emerging epidemics. Proc. Natl. Acad. Sci 109(37):15066–15071. doi: 10.1073/pnas.1206598109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radev S.T., Graw F., Chen S., Mutters N.T., Eichel V.M., Bärnighausen T., Köthe U. 2021. OutbreakFlow: model-based Bayesian inference of disease outbreak dynamics with invertible neural networks and its application to the COVID-19 pandemics in Germany. PLoS Comput. Biol. 17(10):e1009472. doi: 10.1371/journal.pcbi.1009472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A., Grassly N.C. 1997. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci 13:235–238. [DOI] [PubMed] [Google Scholar]
- Rambaut A., Pybus O.G., Nelson M.I., Viboud C., Taubenberger J.K., Holmes E.C. 2008. The genomic and epidemiological dynamics of human influenza a virus. Nature 453(7195):615–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revell L.J. 2012. Phytools: an R package for phylogenetic comparative biology (and other things). Meth. Ecol. Evol. 3(2):217–223. doi: 10.1111/j.2041-210X.2011.00169.x23467194 [DOI] [Google Scholar]
- Richter F., Haegeman B., Etienne R.S., Wit E.C. 2020. Introducing a general class of species diversification models for phylogenetic trees. Statistica Neerl 74(3):261–274. doi: 10.1111/stan.12205 [DOI] [Google Scholar]
- Romano Y., Patterson E., Candes E. 2019. Conformalized quantile regression. In: Wallach H., Larochell H., Beygelzimer A., dAlche-Buc F., Fox E., Garnett R., editors, Advances in neural information processing systems. Vol. 32. Vancouver, Canada: Curran Associates, Inc. [Google Scholar]
- Rosenzweig B.K., Hahn M.W., Kern A. 2022. Accurate detection of incomplete lineage sorting via supervised machine learning. bioRxiv. doi: 10.1101/2022.11.09.515828 [DOI] [Google Scholar]
- Schmitt M., Bürkner P.-C., Köthe U., Radev S.T. 2022. Detecting model misspecification in amortized Bayesian inference with neural networks. arXiv 10.48550/arXiv.2112.08866.
- Schrider D.R., Kern A.D. 2018. Supervised machine learning for population genetics: a new paradigm. Trends Genet. 34(4):301–312. doi: 10.1016/j.tig.2017.12.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scire J., Barido-Sottani J., Kühnert D., Vaughan T.G., Stadler T. 2020. Improved multi-type birth–death phylodynamic inference in BEAST 2. bioRxiv 2020.01.06.895532. [Google Scholar]
- Seidel S., Stadler T., Vaughan T.G. 2020. Estimating disease spread using structured coalescent and birth–death models: a quantitative comparison. bioRxiv. doi: 10.1101/2020.11.30.403741 [DOI] [Google Scholar]
- Shchur V., Spirin V., Sirotkin D., Burovski E., Maio N.D., Corbett-Detig R. 2022. VGsim: scalable viral genealogy simulator for global pandemic. PLoS Comput. Biol. 18(8):e1010409. doi: 10.1371/journal.pcbi.1010409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solis-Lemus C., Yang S., Zepeda-Nunez L. 2022. Accurate phylogenetic inference with a symmetry-preserving neural network model. arXiv 10.48550/arXiv.2201.04663. [DOI] [PMC free article] [PubMed]
- Sousa M., Tomé A.M., Moreira J. 2022. Improved conformalized quantile regression. arXiv 10.48550/arXiv.2207.02808.
- Stadler T. 2010. Sampling-through-time in birth–death trees. J. Theor. Biol. 267(3):396–404. doi: 10.1016/j.jtbi.2010.09.010 [DOI] [PubMed] [Google Scholar]
- Stadler T., Kouyos R., von Wyl V., Yerly S., Böni J., Bürgisser P., Klimkait T., Joos B., Rieder P., Xie D., Günthard H.F., Drummond A.J., Bonhoeffer S.; The Swiss HIV Cohort Study. 2012. Estimating the basic reproductive number from viral sequence data. Mol. Biol. Evol. 29(1):347–357. doi: 10.1093/molbev/msr217 [DOI] [PubMed] [Google Scholar]
- Stadler T., Kühnert D., Bonhoeffer S., Drummond A.J. 2013. Birth–death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV). Proc. Natl. Acad. Sci. 110(1):228–233. doi: 10.1073/pnas.1207965110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinwart I., Christmann A. 2011. Estimating conditional quantiles with the help of the pinball loss. Bernoulli. 17(1):211–225. doi: 10.3150/10-BEJ267 [DOI] [Google Scholar]
- Suvorov A., Schrider D.R. 2022. Reliable estimation of tree branch lengths using deep neural networks. bioRxiv. doi: 10.1101/2022.11.07.515518. https://www.biorxiv.org/content/early/2023/02/21/2022.11.07.515518 [DOI]
- Suvorov A., Hochuli J., Schrider D.R. 2020. Accurate inference of tree topologies from multiple sequence alignments using deep learning. Syst. Biol. 69(2):221–233. doi: 10.1093/sysbio/syz060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson A., Liebeskind B., Scully E.J., Landis M.J. This issue. Deep learning phylogeography. Dryad. doi: 10.25338/B8SH2J [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan T.G., Drummond A.J. 2013. A stochastic simulator of birth–death master equations with application to phylodynamics. Mol. Biol. Evol. 30(6):1480–1493. doi: 10.1093/molbev/mst057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan T.G., Kühnert D., Popinga A., Welch D., Drummond A.J. 2014. Efficient Bayesian inference under the structured coalescent. Bioinformatics 30(16):2272–2279. doi: 10.1093/bioinformatics/btu201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E.M. 2012. Complex population dynamics and the coalescent under neutrality. Genetics 190(1):187–201. doi: 10.1534/genetics.111.134627 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E.M., Siveroni I. 2018. Bayesian phylodynamic inference with complex models. PLoS Comput. Biol. 14(11):e1006546. doi: 10.1371/journal.pcbi.1006546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volz E.M., Koelle K., Bedford T. 2013. Viral phylodynamics. PLoS Comput. Biol. 9(3):e1002947. doi: 10.1371/journal.pcbi.1002947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vovk V., Nouretdinov I., Gammerman A. 2009. On-line predictive linear regression. Ann. Stat 37(3):1566–1590. [Google Scholar]
- Vovk V., Gammerman A., Shafer G. 2022. Conformal prediction: general case and regression. In: Vovk V., Gammerman A., Shafer G., editors, Algorithmic learning in a random world. Cham: Springer International Publishing. p. 19–69. doi: 10.1007/978-3-031-06649-82. [DOI] [Google Scholar]
- Voznica J., Zhukova A., Boskova V., Saulnier E., Lemoine F., Moslonka-Lefebvre M., Gascuel O. 2022. Deep learning from phylogenies to uncover the epidemiological dynamics of outbreaks. Nat. Commun. 13(1):3896. doi: 10.1038/s41467-022-31511-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washington N.L., Gangavarapu K., Zeller M., Bolze A., Cirulli E.T., Schiabor Barrett K.M., Larsen B.B., Anderson C., White S., Cassens T., Jacobs S., Levan G., Nguyen J., Ramirez J.M., Rivera-Garcia C., Sandoval E., Wang X., Wong D., Spencer E., Robles-Sikisaka R., Kurzban E., Hughes L.D., Deng X., Wang C., Servellita V., Valentine H., De Hoff P., Seaver P., Sathe S., Gietzen K., Sickler B., Antico J., Hoon K., Liu J., Harding A., Bakhtar O., Basler T., Austin B., MacCannell D., Isaksson M., Febbo P.G., Becker D., Laurent M., McDonald E., Yeo G.W., Knight R., Laurent L.C., de Feo E., Worobey M., Chiu C.Y., Suchard M.A., Lu J.T., Lee W., Andersen K.G. 2021. Emergence and rapid transmission of SARS-CoV-2 B.1.1.7 in the United States. Cell 184(10):2587–2594. doi: 10.1016/j.cell.2021.03.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worobey M., Watts T.D., McKay R.A., Suchard M.A., Granade T., Teuwen D.E., Koblin B.A., Heneine W., Lemey P., Jaffe H.W. 2016. 1970s and “patient 0” HIV-1 genomes illuminate early HIV/aids history in North America. Nature 539(7627):98–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worobey M., Pekar J., Larsen B.B., Nelson M.I., Hill V., Joy J.B., Rambaut A., Suchard M.A., Wertheim J.O., Lemey P. 2020. The emergence of SARS-CoV-2 in Europe and North America. Science 370(6516):564–570. doi: 10.1126/science.abc8169 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data available from the Dryad Digital Repository: https://doi.org/10.25338/B8SH2J (Thompson et al. this issue) and code is available on github: https://github.com/ammonthompson/phylogeo_epi_cnn