Abstract
Background
The evaluation of brain tumor recurrence after surgery is based on the comparison between tumor regions on pre-operative and follow-up magnetic resonance imaging (MRI) scans in clinical practice. Accurate alignment of MRI scans is important in this evaluation process. However, existing methods often fail to yield accurate alignment due to substantial appearance and shape changes of tumor regions. The study aimed to improve this misalignment situation through multimodal information and compensation for shape changes.
Methods
In this work, a deep learning-based deformation registration method using bilateral pyramid to create multi-scale image features was developed. Moreover, morphology operations were employed to build correspondence between the surgical resection on the follow-up and pre-operative MRI scans.
Results
Compared with baseline methods, the proposed method achieved the lowest mean absolute error of 1.82 mm on the public BraTS-Reg 2022 dataset.
Conclusions
The results suggest that the proposed method is potentially useful for evaluating tumor recurrence after surgery. We effectively verified its ability to extract and integrate the information of the second modality, and also revealed the micro representation of tumor recurrence. This study can assist doctors in registering multiple sequence images of patients, observing lesions and surrounding areas, analyzing and processing them, and guiding doctors in their treatment plans.
Keywords: Bilateral pyramid, deformable registration, non-corresponding regions, brain tumor
Introduction
Glioblastoma multiforme (GBM) is one of the most common and aggressive primary brain tumors in adults. It is characterized by a poor prognosis and a high degree of invasiveness, with over 80% of patients experiencing local tumor recurrence near the original resection cavity after surgical intervention (1). This suggests that residual glioblastoma cells inevitably persist in the tumor infiltration zone (edema) following surgery or radiation therapy. In this context, identifying imaging features within the tumor infiltration zone that contributes to recurrence is crucial for the treatment and prognosis of patients with diffuse glioblastoma. Furthermore, glioblastomas vary in size and shape and often cause significant deformation (mass effect) by compressing surrounding tissues. One approach to discovering these imaging features is to first register pre-operative and post-recurrence structural brain magnetic resonance imaging (MRI) scans of patients and then analyze the imaging characteristics of the tissue that evolves into tumor recurrence (2,3). Therefore, accurately mapping the correspondence between pre-operative and post-recurrence brain tumor scan images is essential.
The best way to locate brain tumors is with multimodal imaging information (4). Initially, surgical resection of visible tumor regions is the most common treatment for brain tumors. In most cases, surgery is the sole necessary treatment, with the specifics of the surgical plan depending on the size and location of the tumor. Subsequently, radiation therapy is employed, using X-rays and other forms of radiation to destroy cancer cells in malignant tumors or slow the progression of benign brain tumors. It is recommended to combine post-surgical radiotherapy and chemotherapy (5). Finally, supportive care is required, including psychological support, antiedema therapy, and antiepileptic treatment. Despite employing these standard treatments, brain tumors still recur (6-8). Therefore, a method to reveal the location of brain tumor recurrence is of paramount importance for selecting appropriate treatment methods and subsequent personalized therapy.
Registration is a fundamental operation in medical image analysis, aiming to establish spatial correspondence between 2 (or more) images (9,10). In critical steps of various clinical tasks such as tumor monitoring and prognosis (11), pathological changes (e.g., tumor recurrence growth) or mass effect can induce alterations in intracranial anatomical structures. Pathological medical images often exhibit numerous nonlinear local deformations. Therefore, brain tumor image registration heavily relies on deformable image registration to establish dense nonlinear correspondences between image pairs. However, due to the shape and appearance variations in pathological tumor images, deformable image registration remains a challenging problem, particularly for image pairs involving tissue changes influenced by pathology (12). Registration between pre-operative and follow-up MRI scans of patients with diffuse gliomas still faces the following issues:
Brain tumors often lead to substantial deformations of brain anatomical structures.
Lack of correspondence between tumors in pre-operative scans and resection cavities in follow-up scans (13).
Inconsistent intensity distributions between acquired scans, where tissue marked as edema in pre-operative scans is known to include infiltrative tumor cells, which may transform into recurrent tumors in follow-up scans.
To solve these issues, it is necessary to establish spatial correspondence between pre-operative and post-recurrence MRI brain scans by accurate deformable registration algorithms. This would enable the mapping of information from the follow-up recurrent scans to the pre-operative scans, thus elucidating subtle imaging phenotypic features that can be used for the detection of future occult case recurrences (14). Image appearance variations stem from 2 sources: firstly, pre-scans encompass tumor and mass effect deformations; secondly, post-scans typically include the tumor resection cavity (the location where the tumor existed in the pre-scan) and reveal signs of tumor infiltration and recurrence. Additionally, consideration needs to be given to the subsequent scans post-tumor resection and the relevant relaxations of the deformations induced by these previous mass effects (15).
In this paper, we discuss a registration method to address the issue of lacking correspondence between scans and demonstrate that the results are significantly more accurate compared to traditional registration methods.
Inspired by the DIRAC framework (16), we introduce a novel bilateral pyramid network in the study. In the first stage, with information from both modalities separately, we extract the most relevant information from each type of imaging contrast. In the second stage, we make reasonable morphological predictions of the tumor core within the network through forward-backward consistency constraints, which allows for the expansion of the distribution of brain tumors while excluding pathological regions.
We briefly review the recent methods for learning-based medical image registration, with a particular focus on deep learning approaches. Traditional image registration methods (17-20) typically rely on multi-resolution strategies and iterative estimation of target transformations along with smooth regularization. Although traditional image registration methods excel in registration accuracy and diffeomorphism (i.e., invertibility and topology preservation), the runtime of the registration process depends on the degree of misalignment between input images and can be quite time-consuming, especially for high-resolution 3-dimensional (3D) images. This has spurred a trend toward faster deep registration methods based on deep learning (21). Recent unsupervised deep learning-based image registration (DLIR) methods have demonstrated good registration speed and quality across various deformable image registration tasks. De Vos et al. developed a patch-based end-to-end unsupervised deformable image registration network (DIRNet) (22), where a spatial transformer network (STN) was used to estimate the deformation field (23). However, the deformation field estimated by STN is unconstrained, which can lead to severe distortions. To overcome this limitation, VoxelMorph was proposed. It estimates the deformation field using an encoder-decoder convolutional neural networks (CNN) and regularizes the deformation field with a penalty. They treat the image registration problem as a pixel-level image transformation problem, attempting to learn pixel-wise spatial correspondences from a pair of input images (24).
To register images with significant deformations, stacking multiple networks and deep registration methods from coarse to fine have been widely used. For instance, Zhao et al. designed a recursive cascade network where multiple VoxelMorph cascades are employed to progressively deform images (25). Kim et al. introduced CycleMorph, consisting of 2 registration networks that exchange inputs in a cyclically consistent manner. It can be extended to a large-scale multi-scale implementation, allowing the model to better capture different levels of transformation relationships (26). However, this comes at the cost of high complexity and computational burden due to the need for multiple models. Additionally, the sequential combination of multiple networks can result in the accumulation of interpolation artifacts, potentially affecting the quality of the deformation field. In contrast to cascade-based approaches, pyramid-based methods have unequal deformation components at each level. Low-resolution levels have a large receptive field to handle significant deformation components, whereas high-resolution levels have a smaller receptive field to handle minor deformation components. Through this coarse-to-fine strategy, large deformations can be decomposed into multi-level components, and each level can be considered a refinement of the previous one, enabling promising registration performance. Mok et al. proposed a Laplacian pyramid framework (LapIRN) to leverage the image deformations from the previous level, mimicking the traditional multi-resolution strategy (27). Also, a few works have focusing on transformer architectures, because their substantially larger receptive field enables a more precise comprehension of the spatial correspondence between moving and fixed images (28,29).
In recent years, non-iterative coarse-to-fine registration methods have been proposed, which employ a single network in a single pass to perform coarse-to-fine registration, even outperforming approaches that use multiple cascaded networks or iterations (30-32). Additionally, Liu et al. introduced the innovative deformable registration network, named im2grid, incorporating multiple Coordinate Translators alongside hierarchical features extracted from a CNN encoder. This network systematically produces a deformation field in a progressive coarse-to-fine manner (33). In a similar vein, Chen et al. proposed a distinct yet effective approach by introducing an innovative Deformer module within a multi-scale framework for deformable image registration. The Deformer module is meticulously designed to simplify the mapping process from image representation to spatial transformation, achieving this by expressing displacement vector predictions as a weighted summation of multiple bases (34). Specifically, the Dual-stream Pyramid Registration Network (Dual-PRNet) was designed to incorporate a dual-stream network that computes 2 meaningful feature pyramids separately and directly estimates the sequential deformation fields in feature space in a single pass. Refinements of the registration field and convolution features are performed in a hierarchical, sequential, and coarse-to-fine manner, offering an effective way to progressively, and more accurately, align 2 volumes in feature space (30). However, it shares a common issue with previous schemes, namely, the inadequacy of single modal information for tumor imaging. Therefore, recent research has focused on fusing multi-modal images through variants of the Inception model (35) and extracting the most relevant information from each type of imaging contrast. Nevertheless, it coarsely combines 4 modalities of brain tumor images without elucidating which modality’s features extraction played a critical role.
To better delineate the tumor’s location and extent, as well as its post-resection biologic activity, and address the issue of the lack of correspondence between pre-operative and post-recurrence images, Mok and Chung proposed DIRAC, which jointly estimates bidirectional deformation fields and precisely localizes regions with missing correspondences (16). By excluding regions lacking correspondence in the similarity metrics during training, it improves the target registration error (TRE) of markers in pre-operative and post-recurrence images. However, the segmented tumor core within the network lacks corresponding post-processing to adapt to the tumor’s edge and edema location.
How the bilateral pyramid leverages multimodal information and expands the tumor core is explained in Methods. In Results, the results of the ablation study and the comparison with the other popular models are summarized and analyzed.
Methods
Our goal was to establish dense nonlinear correspondences between pre-operative and post-recurrence scans of the same patient, wherein regions with no effective correspondences are excluded from similarity metrics during the optimization process. Our approach was built upon the previous deep learning deformable registration (DLDR) method (36), incorporating multi-modal information to enhance feature extraction in tumor regions, and employs morphological operations to extend the boundaries of non-corresponding voxels in the resection and recurrent regions in the 2 images located by forward-backward consistency constraints.
Model overview
The overview of our method is depicted in Figure 1. First, we train our approach on the 3D clinical dataset from the BraTS-Reg challenge (15), which consists of 160 pairs of pre-operative and follow-up brain MRI scans from patients with gliomas at different time points. Given that the BraTS-Reg challenge provides multi-parametric MRI sequences for each case at each time point, including native pre-contrast (T1), contrast-enhanced T1-weighted (T1ce), T2-weighted (T2), and fluid-attenuated inversion recovery (FLAIR) MRI, we leverage 2 MRI modalities to extract rich semantic features. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
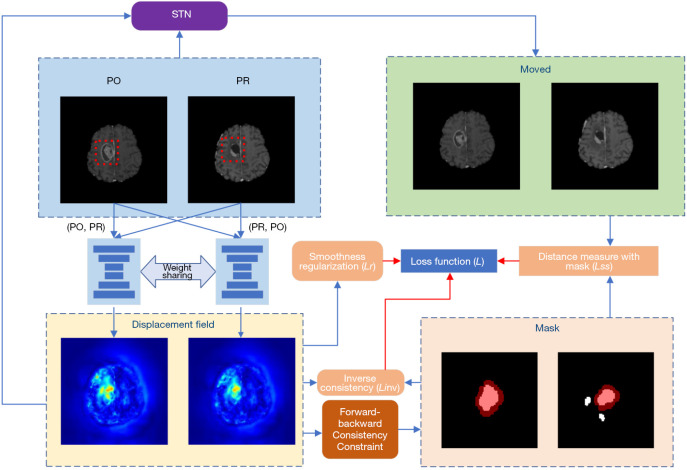
Figure 1.
Overview of the proposed method. Our method jointly estimates the bidirectional de-formation field and locates regions (denoted as masks) where no correspondence exists. During training, regions where no correspondence exists are excluded from the similarity measure. In the mask area in the lower right corner, white is the initial non-corresponding area, and red is the area after morphological operations. The red box represents the tumor risk area. STN, spatial transformation network; PO, pre-operative; PR, post-recurrence.
Our network is built upon the DIRAC framework, which parameterizes the deformable registration problem as a bidirectional registration problem: PO and PR denote the pre-operative (baseline) scan B and post-recurrence (follow-up) scan F defined on a 3D mutual space domain. We define it as and , where represents a set of learnable parameters, represents the displacement field that aligns B to F, namely, , and defines the anatomically corresponding locations for each voxel , except for non-corresponding voxels. To accommodate large deformations caused by tumor mass effects and anatomical variations, we also incorporate a conditional image registration module into the network for widespread use in smooth regularization. This module enables the network to undergo a single training phase to obtain multiple regularization parameters’ influence on the deformation field, allowing us to select the optimal regularization hyperparameters, thus saving significant human and computational resources compared to grid search.
Although DIRAC employs a multi-resolution optimization strategy, using bidirectional displacement fields and forward-backward consistency to constrain regions of non-correspondence between registered images, the standard DIRAC method does not effectively leverage multi-modal information. Additionally, it uses a fixed bias of 0.0015 for computing the weighted average deformation measure in each direction, which does not adapt well to different individuals’ characteristics. In contrast, our approach excludes the expanded regions of non-correspondence from the similarity metric and effectively utilizes multi-modal tumor-related information.
Bilateral pyramid network
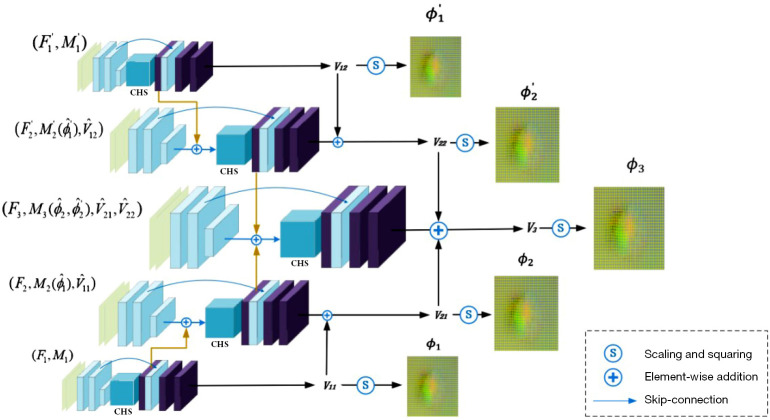
Our bilateral pyramid network is set on the cLapIRN architecture, but has been enhanced through the introduction of bilateral design, as illustrated in Figure 2. Our input data consists of 2 modalities and their multi-resolution images. Specifically, we start by creating an input image pyramid by downsampling the input images using trilinear interpolation. Here, we employ a 3-level Laplacian pyramid network, denoted as , corresponding to . represents downsampled images with a scale factor of , and represents downsampled images of another modality with a scale factor of . Both modalities of images start from the coarsest resolution images , and pass through a CNN-based registration network to obtain the corresponding 3-channel vector fields and deformation fields for the lowest resolution. For the second-level pyramid, we first upscale the deformation field from the first pyramid level by a factor of 2 to obtain , which warps the input of the second level. Additionally, we upsample the 3-channel vector field from the first pyramid level by a factor of 2 and concatenate it with , to form a 5-channel input. The output velocity field of the second level is obtained by adding the second pyramid level’s upsampled velocity field to the output of the first pyramid level. The deformation field at the second level is then integrated from the velocity field . In contrast, the input at the third level consists of an 8-channel input, formed by combining and the upsampled 3-channel vector field from the second pyramid level. The combination of vector fields from both upper and lower modalities is achieved through mean fusion, leveraging the complementary information from both modalities. Finally, we obtain the ultimate deformation field through the third level, which is at full resolution. This bilateral input introduces information from both modalities, enhancing the extraction of tumor region features. For example, the inclusion of the FLAIR modality allows for effective consideration of features related to tumor edema areas, which are crucial for subsequent extraction of non-corresponding regions.
Figure 2.
Overview of the proposed 3-level bilateral pyramid image registration networks. The bottom-to-top process represents the multi-scale feature extraction of one modality, while the top-to-bottom process corresponds to the feature extraction of another modality. It is built on the basis of LapIRN (27). For clarity and simplicity, we depict the 2D formulation of our method in the figure. CHS, conditional hyperparameter search module; LapIRN, Laplacian pyramid framework; 2D, 2-dimensional.
In the CNN from low to high resolution, lower-level networks extract image features through decoders, and these features are embedded into the next-level network via skip connections. This significantly increases the network’s receptive field and nonlinearity, enabling the learning of complex nonlinear correspondences at finer levels. In the 5-layer CNN-based registration network, each layer’s architecture remains consistent, comprising a feature decoder, hyperparameter search module, feature encoder, and skip connection from feature encoder to feature decoder to prevent the loss of low-level features when learning the target deformation field.
Post-processing of non-corresponding areas
The network extends the forward-backward consistency constraint to strengthen the localization of regions lacking correspondence between baseline and follow-up scans. Specifically, we performed effective post-processing on the binary mask created within the network based on pixel differences and a threshold , which is used to label voxels without correspondence.
| [1] |
| [2] |
Here, is a threshold to determine whether voxels have correspondence or the displacement field is inaccurately estimated, and represents the forward–backward (inverse consistency) error from to . is set to 0.015, and represents the number of non-zero voxels in image F. denotes an average filter of size , and represents a convolution operator with zero-padding. As the estimated registration field may exhibit fluctuations during the learning process, we apply an average filter to the estimated forward error to stabilize the binary mask estimation and mitigate the impact of contour artifacts on the mask estimation.
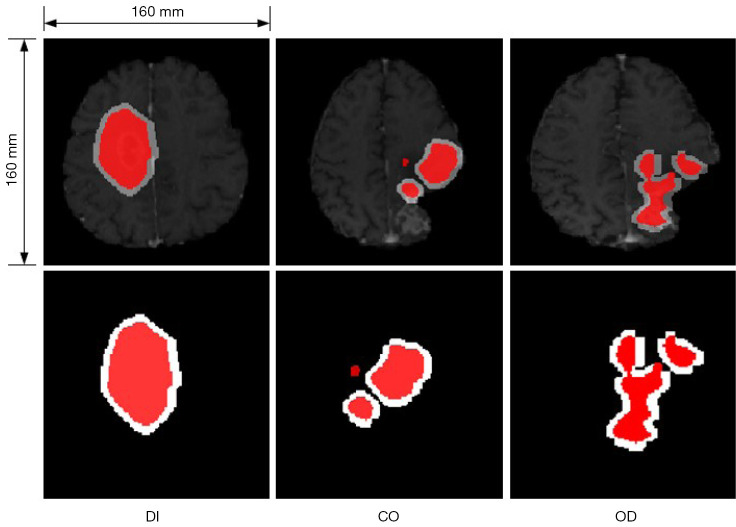
Due to small noise, holes, and non-connectivity in the shape of the obtained binary mask, which are important factors affecting similarity assessment, we designed several post-processing steps for the segmentation. These post-processing steps include various morphological operations or combinations thereof, as shown in Figure 3. The first is referred to as ‘OD’, which involves applying an opening operation followed by dilation to the mask. Performing an opening operation first effectively eliminates small image noise, disconnects edge fragments, and smooths the edges. Subsequently, dilation on the processed mask compensates for the eroded mask edges from the opening operation, preserving the original shape and approximate size. The second operation is called ‘CO’, which consists of a closing operation followed by an opening operation. The closing operation is used to fill holes in the mask, connect neighboring edges, and then an opening operation further removes noise and smooths the image edges. We use rectangular structuring elements in opening and closing operations with size [5,5], and cross-shaped structuring elements in dilation operations with size [10,10]. Alternative to the morphological operations, we additionally considered enlarging the mask region by a certain scale, referred to as ‘DI’. This approach roughly simulates the process of uniform tumor edge expansion and serves as a control group compared to the previous 2 groups.
Figure 3.
The picture above is a schematic diagram of three post-processing methods for masks, they are DI, CO, and OD from left to right. The red regions represent the non-corresponding area output by the network, and white represents the mask after the respective post-processing method is applied. DI, CO, and OD represent 3 post-processing methods for masks.
Loss function
In the deformation fields and , is the identity transform. The objective of our proposed method is to compute the optimal deformation field that minimizes the dissimilarity metrics between and , as well as B and within the regions of effective correspondence. The objective function is as follows:
| [3] |
Specifically, we employ a masked negative normalized cross-correlation (NCC) to measure dissimilarity, excluding regions without effective correspondence. The definitions of and are as follows:
| [4] |
| [5] |
In this step, we utilize masked negative NCC with a similarity pyramid (27) as the dissimilarity function, which is calculated at each resolution level. To encourage smooth solutions and penalize unreasonable ones, we employ a diffusion regularizer during training. , , and are hyperparameters that balance the loss functions. During training, we sample following the conditional registration framework. In the inference phase, we divide it into 20 groups with intervals of 0.5 and select the optimal result.
Results
Data and experiments setup
The dataset we utilized is a 3D clinical dataset from the BraTS-Reg challenge (15), comprising 160 pairs of preoperative baseline and follow-up brain MRI scans for adult patients with diffuse intrinsic pontine glioma [World Health Organization Central Nervous System (WHO CNS) grades 3–4]. For each patient, multiple MRI sequences, including T1, T1ce, T2, and FLAIR images, were provided. Clinical experts meticulously annotated landmarks within the scans, describing various anatomical positions within the entire region.
We applied standard preprocessing techniques, such as rigid registration to a common anatomical template (Montreal Neurological Institute, MNI), resampling to an isotropic resolution of 1 mm3, skull stripping, and brain extraction. For learning-based methods, during the training phase, we further resampled the scans to 160×160×80 with an isotropic resolution of 1.5×1.5×1.94 mm3 and upsampled the solutions to 1 mm3 isotropic resolution at the evaluation stage using bilinear interpolation. We conducted 5-fold cross-validation, dividing the 140 pairs of scans equally into 5 folds. There are 4 folds (122 pairs of scans) for training, an additional 20 pairs of scans for validation, and 1 fold (28 pairs of scans) for testing.
We built our approach on the official implementation of 3D DIRAC and used the default parameters provided in (16). We set , , and to 0.3, 0.5, and 0.01, respectively, during the validation phase. Our training takes about 130,000 iterations. Network weights were updated using the Adam optimizer with a batch size of 1 and a learning rate value α of 1e−4. Our network was implemented using PyTorch 1.10 (37) and deployed on the same machine equipped with an Nvidia RTX 3080Ti GPU (Nvidia, Santa Clara, CA, USA).
Measurement
The registration accuracy was assessed in terms of median absolute error (MAE) and robustness based on manually annotated landmarks. MAE is calculated between landmark coordinates in the preoperative and deformed follow-up scans, where lower MAE typically indicates more accurate registration. We registered each pre-operative scan to its corresponding follow-up scan of the same patient, propagated the landmarks using the obtained deformation field from the follow-up scan, and measured the average TRE of paired landmarks in millimeters. The definitions of MAE are as follows:
| [6] |
represents the estimated anatomical landmark in the baseline scan, and represents the true landmark in the baseline scan.
Robustness is a success rate metric within the (0, 1) range, describing the percentage of landmarks whose MAE improved after registration. Robustness (15) is defined as follows:
| [7] |
| [8] |
Where is the set of successfully registered landmarks, is a pair of images to be registered, and is the set of all pairs of images to be registered.
Additionally, the smoothness of the displacement field was evaluated by the number of negative Jacobian determinants. Voxel p is considered smooth and invertible if the Jacobian determinant is positive and a lower percentage of negative Jacobian determinants indicates a smoother displacement field (38).
Comparative experiment of different methods
We compared our method with several top-ranking registration methods in the 2022 BraTS-Reg Challenge, including DIRAC, NICE-Net (39), and 3D Inception-Based TransMorph (35). Additionally, we compared our method with 2 traditional methods, Elastix (40), and 2 classic deep learning methods, HyperMorph (41) and cLapIRN (36). Given the adoption of cost function masking strategy, our experiments were based on the cost functions of tumor core segmentation maps for both methods. To ensure an objective and effective comparison, the experimental parameters were kept consistent with those of the original methods.
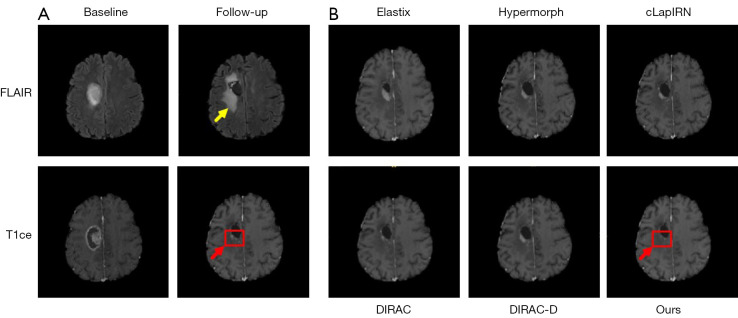
Figure 4 is an example of registration results achieved by the 3 different methods.
Figure 4.
An example of registration resulted by 3 different methods. The left part (A) is a pair of images to be registered for 2 modalities, with the aim of registering the baseline image onto the follow-up image. The tumor area is marked by the red arrow while the tumor edema is marked by the yellow arrow. The right part (B) are the registration results of 3 different methods. They show varying degrees of mismatch in region of the tumor which is marked by red box. FLAIR, fluid-attenuated inversion recovery; T1ce, contrast-enhanced T1-weighted; LapIRN, Laplacian pyramid framework.
Quantitative comparison results are presented in Table 1. Our network differs from 3D Inception-Based TransMorph in that it fuses the information of the 4 modalities at the input end through the Inception module when leveraging multimodal information. However, this introduces unnecessary modal information, but also indirectly highlights the necessity of incorporating multimodal image information. NICE-Net effectively addressed substantial deformations between preoperative and follow-up scans through a coarse-to-fine registration network, emphasizing the importance of feature extraction at multiple scales.
Table 1. Comparison of results achieved by the top-ranking registration methods.
| Method | TRE (mm)↓ | Robustness↑ | ↓ |
|---|---|---|---|
| Elastix | 4.54±3.22 | – | – |
| 3D Inception-Based TransMorph | 2.24±1.52 | 0.82±0.26 | 0.17±0.28 |
| NICE-Net | 1.98±1.46 | 0.83±0.16 | 0.16±0.21 |
| Hypermorph | 2.64±2.00 | 0.81±0.27 | 0.27±1.57 |
| cLapIRN | 2.03±1.31 | 0.80±0.25 | 0.23±0.18 |
| DIRAC | 1.91±1.06 | 0.82±0.24 | 0.14±0.20 |
| DIRAC-D | 1.88±1.01 | 0.82±0.23 | 0.09±0.16 |
| Ours | 1.82±0.94 | 0.85±0.18 | 0.19±0.24 |
Results are provided as mean ± standard deviation. ↑, higher is better; ↓, lower is better. TRE, target registration error.
In terms of TRE and robustness, our method achieved the best performance among all baseline models, especially with an improvement of 3.3% in terms of average target error compared to other methods. Paired t-tests indicated that the decrease of TRE and the increases of robustness in our method were statistically significant (P<0.05) compared to the other 6 deep learning-based methods. This is attributed to the superiority of the bilateral pyramid input in extracting features from multimodal image data and the effectiveness of handling errors in non-corresponding regions constrained by the network. Furthermore, this also reveals that the underlying causes leading to non-corresponding regions are more related to tumor edema.
However, in terms of Jacobian determinant, our method is relatively poor among the tested models. Paired t-tests indicated that the difference of Jacobian determinant between our method and the other 6 deep learning-based methods were statistically significant (P<0.05). Our proposed method is deficient in terms of deformation field smoothness, which is attributed to not considering voxels at the boundaries when extending the non-corresponding regions. When the region is extended, some voxels in the extended region will be excluded from the loss function, resulting in an unsmooth deformation field in this region.
Discussion
To demonstrate the superiority and effectiveness of our designed network, we conducted ablation experiments on the multimodal inputs and post-processing of masks in the bilateral pyramid network. We present the evaluation performance of the backbone network in Table 2, where the D suffix indicates the introduction of the T2 modality through single-sided fusion input, the TT suffix indicates bimodal inputs with T1ce and T2, and the TF suffix indicates bimodal inputs with T1ce and FLAIR. DI, CO, and OD represent 3 post-processing methods for masks, namely, dilation, first closing operation followed by opening operation, and first opening operation followed by dilation, respectively. The design of DI serves as a contrast to CO and OD. We conducted comprehensive experiments on various combinations in both stages as detailed in the Table 2.
Table 2. The ablation study of MRI modalities and post-processing of masks on the BraTS-Reg 2022.
| Method | Modality | TRE (mm)↓ | Robustness↑ | ↓ |
|---|---|---|---|---|
| DIRAC | T1ce | 1.91±1.06 | 0.82±0.24 | 0.14±0.20 |
| DIRAC-D | T1ce-T2 | 1.88±1.01 | 0.82±0.23 | 0.09±0.16 |
| DIRAC-TT | T1ce-T2 | 1.87±0.98 | 0.82±0.23 | 0.13±0.18 |
| DIRAC-TF | T1ce-FLAIR | 1.85±0.95 | 0.80±0.24 | 0.14±0.12 |
| DIRAC-TT-DI | T1ce-T2 | 1.86±1.01 | 0.83±0.23 | 0.15±0.14 |
| DIRAC-TT-CO | T1ce-T2 | 1.84±0.99 | 0.84±0.19 | 0.15±0.16 |
| DIRAC-TT-OD | T1ce-T2 | 1.84±0.98 | 0.85±0.22 | 0.13±0.15 |
| DIRAC-TF-DI | T1ce-FLAIR | 1.86±1.13 | 0.85±0.22 | 0.11±0.18 |
| DIRAC-TF-CO | T1ce-FLAIR | 1.85±1.08 | 0.82±0.23 | 0.13±0.20 |
| DIRAC-TF-OD | T1ce-FLAIR | 1.82±0.94 | 0.85±0.18 | 0.19±0.24 |
Results are provided as mean ± standard deviation. The D suffix indicates the introduction of the T2 modality through single-sided fusion input, the TT suffix indicates bimodal inputs with T1ce and T2, and the TF suffix indicates bimodal inputs with T1ce and FLAIR. DI, CO, and OD represent 3 post-processing methods for masks. ↑, higher is better; ↓, lower is better. MRI, magnetic resonance imaging; TRE, target registration error; T1ce, contrast-enhanced T1-weighted; FLAIR, fluid-attenuated inversion recovery.
Our network architecture is an improvement based on DIRAC. To introduce crucial multimodal information from the tumor region, we used a bilateral pyramid network to extract information from different modalities for fusion. It can be observed that introducing the T2 modality effectively reduced the average TRE from 1.91 to 1.87 mm. With the introduction of the FLAIR modality, TRE further improved to 1.85 mm, indicating the FLAIR modality’s effectiveness in extracting features from the tumor region. Moreover, in the model with inputs of T1ce and T2, using bilateral inputs reduced TRE from 1.88 to 1.87 mm, demonstrating the helpfulness of bilateral inputs in feature extraction from the images. In terms of robustness and smoothness of the deformation field, introducing bilateral networks controlled them within an acceptable error range.
Building on the introduction of the second modality, we further applied 3 post-processing techniques to the non-corresponding regions constrained by the network. It can be observed that when introducing the second modality as T2, both CO and OD improved TRE by 1.6%, with varying degrees of enhancement in network robustness compared to the baseline model. Conversely, when the second modality was FLAIR, our model achieved the best overall result with a TRE of 1.82 mm, representing a 3.3% reduction compared to the DIRAC-D. Network robustness also increased by 3.7%. Although it sacrificed some smoothness of the deformation field, it remained within a controllable range. Figure 4 displays qualitative examples of the registration results for each method and the regions estimated by our method to have no correspondence. The results indicate that our method effectively utilizes information from the second modality through bilateral networks to accurately locate regions with no valid correspondences. It applies reasonable post-processing to eliminate mask errors and expand them. Additionally, during the training phase, it explicitly excludes these regions in similarity measurements, further reducing artifacts and registration errors for patients.
Conclusions
We have proposed a deformable registration method with bilateral pyramid input for pre-operative and post-recurrence brain scan registration, which can jointly register, segment, and post-process regions without correspondence. We introduced a novel post-processing method for segmentation maps to address errors in non-corresponding regions. Compared to other deep learning-based methods, our study offers a way to utilize multimodal patient image data effectively and provides significant insights into the origins and patterns of tumor recurrence. In contrast to traditional methods, our approach inherits the runtime advantages of deep learning-based methods and does not require any manual interaction or supervision, demonstrating great potential in fully automatic patient-specific registration.
Supplementary
The article’s supplementary files as
Acknowledgments
Funding: This research was supported by the National Key Research and Development Program of China (No. 2019YFE120100), 2020 Major Scientific Research Problems And Medical Technology Program of China Medical Education Association (No. 2020KTZ003), the National Natural Science Foundation (NSF) of China (No. 11975312), Anhui Provincial Natural Science Foundation (Grant No. 2108085MF232), and the Anhui Provincial Department of Education University Coordination Project “Research on Intelligent Recommendation Based on Multimodal Knowledge Graph and Dynamic Heterogeneous Graph Neural Network” (Project No. GXXT-2022-046).
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Footnotes
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1821/coif). The authors have no conflicts of interest to declare.
References
- 1.Han X, Bakas S, Kwitt R, Aylward S, Akbari H, Bilello M, Davatzikos C, Niethammer M. Patient-Specific Registration of Pre-operative and Post-recurrence Brain Tumor MRI Scans. Brainlesion 2019;11383:105-14. 10.1007/978-3-030-11723-8_10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Provenzale JM, Mukundan S, Barboriak DP. Diffusion-weighted and perfusion MR imaging for brain tumor characterization and assessment of treatment response. Radiology 2006;239:632-49. 10.1148/radiol.2393042031 [DOI] [PubMed] [Google Scholar]
- 3.Waldman AD, Jackson A, Price SJ, Clark CA, Booth TC, Auer DP, Tofts PS, Collins DJ, Leach MO, Rees JH, National Cancer Research Institute Brain Tumour Imaging Subgroup . Quantitative imaging biomarkers in neuro-oncology. Nat Rev Clin Oncol 2009;6:445-54. 10.1038/nrclinonc.2009.92 [DOI] [PubMed] [Google Scholar]
- 4.Lapointe S, Perry A, Butowski NA. Primary brain tumours in adults. Lancet 2018;392:432-46. 10.1016/S0140-6736(18)30990-5 [DOI] [PubMed] [Google Scholar]
- 5.Kumar LA, Satapathy BS, Pattnaik G, Barik B, Patro CS, Das S. Malignant brain tumor: Current progresses in diagnosis, treatment and future strategies. Annals of R.S.C.B. 2021;25:16922-32. [Google Scholar]
- 6.Parvez K, Parvez A, Zadeh G. The diagnosis and treatment of pseudoprogression, radiation necrosis and brain tumor recurrence. Int J Mol Sci 2014;15:11832-46. 10.3390/ijms150711832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mendes M, Sousa JJ, Pais A, Vitorino C. Targeted Theranostic Nanoparticles for Brain Tumor Treatment. Pharmaceutics 2018;10:181. 10.3390/pharmaceutics10040181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu Z, Wang S, Dong D, Wei J, Fang C, Zhou X, Sun K, Li L, Li B, Wang M, Tian J. The Applications of Radiomics in Precision Diagnosis and Treatment of Oncology: Opportunities and Challenges. Theranostics 2019;9:1303-22. 10.7150/thno.30309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. IEEE Trans Med Imaging 2013;32:1153-90. 10.1109/TMI.2013.2265603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ou Y, Akbari H, Bilello M, Da X, Davatzikos C. Comparative evaluation of registration algorithms in different brain databases with varying difficulty: results and insights. IEEE Trans Med Imaging 2014;33:2039-65. 10.1109/TMI.2014.2330355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Haskins G, Kruger U, Yan P. Deep learning in medical image registration: a survey. Mach Vis Appl 2020;31:8. 10.1007/s00138-020-01060-x [DOI] [Google Scholar]
- 12.Meng M, Bi L, Fulham M, Feng DD, Kim J. Enhancing medical image registration via appearance adjustment networks. Neuroimage 2022;259:119444. 10.1016/j.neuroimage.2022.119444 [DOI] [PubMed] [Google Scholar]
- 13.Dean BL, Drayer BP, Bird CR, Flom RA, Hodak JA, Coons SW, Carey RG. Gliomas: classification with MR imaging. Radiology 1990;174:411-5. 10.1148/radiology.174.2.2153310 [DOI] [PubMed] [Google Scholar]
- 14.Akbari H, Rathore S, Bakas S, Nasrallah MP, Shukla G, Mamourian E, Rozycki M, Bagley SJ, Rudie JD, Flanders AE, Dicker AP, Desai AS, O'Rourke DM, Brem S, Lustig R, Mohan S, Wolf RL, Bilello M, Martinez-Lage M, Davatzikos C. Histopathology-validated machine learning radiographic biomarker for noninvasive discrimination between true progression and pseudo-progression in glioblastoma. Cancer 2020;126:2625-36. 10.1002/cncr.32790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Baheti B, Waldmannstetter D, Chakrabarty S, Akbari H, Bilello M, Wiestler B, Schwarting J, Calabrese E, Rudie J, Abidi S, Mousa M. The brain tumor sequence regis-tration challenge: establishing correspondence between pre-operative and follow-up MRI scans of diffuse glioma patients. arxiv: 2112.06979. 2021.
- 16.Mok TCW, Chung ACS. Unsupervised Deformable Image Registration with Absent Correspondences in Pre-operative and Post-recurrence Brain Tumor MRI Scans. In: Wang L, Dou Q, Fletcher PT, Speidel S, Li S, editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. Lecture Notes in Computer Science, Springer, 2022;13436:25-35. [Google Scholar]
- 17.Thirion JP. Image matching as a diffusion process: an analogy with Maxwell’s demons. Med Image Anal 1998;2:243-60. 10.1016/S1361-8415(98)80022-4 [DOI] [PubMed] [Google Scholar]
- 18.Ou Y, Sotiras A, Paragios N, Davatzikos C. DRAMMS: Deformable registration via attribute matching and mutual-saliency weighting. Med Image Anal 2011;15:622-39. 10.1016/j.media.2010.07.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: efficient non-parametric image registration. Neuroimage 2009;45:S61-72. 10.1016/j.neuroimage.2008.10.040 [DOI] [PubMed] [Google Scholar]
- 20.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal 2008;12:26-41. 10.1016/j.media.2007.06.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xiao H, Teng X, Liu C, Li T, Ren G, Yang R, Shen D, Cai J. A review of deep learning-based three-dimensional medical image registration methods. Quant Imaging Med Surg 2021;11:4895-916. 10.21037/qims-21-175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.de Vos BD, Berendsen FF, Viergever MA, Staring M, Išgum I. End-to-End Unsupervised Deformable Image Registration with a Convolutional Neural Network. In: Cardoso M, Arbel T, Carneiro G, Syeda-Mahmood T, Tavares JMRS, Moradi M, Bradley A, Greenspan H, Papa JP, Madabhushi A, Nascimento JC, Cardoso JS, Belagiannis V, Lu Z, editors. Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. DLMIA ML-CDS 2017 2017. Lecture Notes in Computer Science(), Springer, 2017;10553:204-12. [Google Scholar]
- 23.Jaderberg M, Simonyan K, Zisserman A. Spatial transformer networks. Advances in neural information processing systems. Part of Advances in Neural Information Processing Systems 28 (NIPS 2015).
- 24.Balakrishnan G, Zhao A, Sabuncu MR, Guttag J, Dalca AV. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE Trans Med Imaging 2019. [Epub ahead of print]. doi: . 10.1109/TMI.2019.2897538 [DOI] [PubMed] [Google Scholar]
- 25.Zhao S, Dong Y, Chang EI, Xu Y. Recursive cascaded networks for unsupervised medical image registration. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2019:10600-10. [Google Scholar]
- 26.Kim B, Kim DH, Park SH, Kim J, Lee JG, Ye JC. CycleMorph: Cycle consistent unsupervised deformable image registration. Med Image Anal 2021;71:102036. 10.1016/j.media.2021.102036 [DOI] [PubMed] [Google Scholar]
- 27.Mok TCW, Chung ACS. Large Deformation Diffeomorphic Image Registration with Laplacian Pyramid Networks. In: Martel AL, Abolmaesumi P, Stoyanov D, Mateus D, Zuluaga MA, Zhou SK, Racoceanu D, Joskowicz L. Medical Image Computing and Computer Assisted Intervention – MICCAI 2020. MICCAI 2020. Lecture Notes in Computer Science(),Springer, 2020;12263:211-21. [Google Scholar]
- 28.Chen J, Frey EC, He Y, Segars WP, Li Y, Du Y. TransMorph: Transformer for unsupervised medical image registration. Med Image Anal 2022;82:102615. 10.1016/j.media.2022.102615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ma T, Dai X, Zhang S, Wen Y. PIViT: Large Deformation Image Registration with Pyramid-Iterative Vision Transformer. In: Greenspan H, Madabhushi A, Mousavi P, Salcudean S, Duncan J, Syeda-Mahmood T, Taylor R. Medical Image Computing and Computer Assisted Intervention – MICCAI 2023. Lecture Notes in Computer Science, vol 14229. Springer, 2023:602-12. [Google Scholar]
- 30.Kang M, Hu X, Huang W, Scott MR, Reyes M. Dual-stream pyramid registration network. Med Image Anal 2022;78:102379. 10.1016/j.media.2022.102379 [DOI] [PubMed] [Google Scholar]
- 31.Lv J, Wang Z, Shi H, Zhang H, Wang S, Wang Y, Li Q. Joint Progressive and Coarse-to-Fine Registration of Brain MRI via Deformation Field Integration and Non-Rigid Feature Fusion. IEEE Trans Med Imaging 2022;41:2788-802. 10.1109/TMI.2022.3170879 [DOI] [PubMed] [Google Scholar]
- 32.Meng M, Bi L, Feng D, Kim J. Non-iterative Coarse-to-Fine Registration Based on Single-Pass Deep Cumulative Learning. In: Wang L, Dou Q, Fletcher PT, Speidel S, Li S, editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. Lecture Notes in Computer Science, Springer, 2022;13436:88-97. [Google Scholar]
- 33.Liu Y, Zuo L, Han S, Xue Y, Prince JL, Carass A. Coordinate Translator for Learning Deformable Medical Image Registration. Multiscale Multimodal Med Imaging (2022) 2022;13594:98-109. 10.1007/978-3-031-18814-5_10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Chen J, Lu D, Zhang Y, Wei D, Ning M, Shi X, Xu Z, Zheng Y. Deformer: Towards Displacement Field Learning for Unsupervised Medical Image Registration. In: Wang L, Dou Q, Fletcher PT, Speidel S, Li S, editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. Lecture Notes in Computer Science, Springer, 2022;13436:141-51. [Google Scholar]
- 35.Abderezaei J, Pionteck A, Chopra A, Kurt M. 3D Inception-Based TransMorph: Pre- and Post-operative Multi-contrast MRI Registration in Brain Tumors. In: Bakas S, Crimi A, Baid U, Malec S, Pytlarz M, Baheti B, Zenk M, Dorent R, editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2022. Lecture Notes in Computer Science, Springer, 2022;14092:35-45. [Google Scholar]
- 36.Mok TC, Chung AC. Conditional Deformable Image Registration with Convolutional Neural Network. In: de Bruijne M, Cattin PC, Cotin S, Padoy N, Speidel S, Zheng Y, Essert C, editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. Lecture Notes in Computer Science(),Springer, 2021;12904:35-45. [Google Scholar]
- 37.Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L, Desmaison A. Pytorch: An imperative style, high-performance deep learning library. NIPS'19: Proceedings of the 33rd International Conference on Neural Information Processing Systems 2019;32:8036-37. [Google Scholar]
- 38.Ashburner J. A fast diffeomorphic image registration algorithm. Neuroimage 2007;38:95-113. 10.1016/j.neuroimage.2007.07.007 [DOI] [PubMed] [Google Scholar]
- 39.Meng M, Bi L, Feng D, Kim J. Brain Tumor Sequence Registration with Non-iterative Coarse-To-Fine Networks and Dual Deep Supervision. In: Bakas S, Crimi A, Baid U, Malec S, Pytlarz M, Baheti B, Zenk M, Dorent R, editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2022. Lecture Notes in Computer Science, Springer, 2022;13769:273-82. [Google Scholar]
- 40.Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging 2010;29:196-205. 10.1109/TMI.2009.2035616 [DOI] [PubMed] [Google Scholar]
- 41.Hoopes A, Hoffmann M, Greve DN, Fischl B, Guttag J, Dalca AV. Learning the Effect of Registration Hyperparameters with HyperMorph. J Mach Learn Biomed Imaging 2022:1:003. [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.