Abstract
Distance distribution information obtained by pulsed dipolar EPR spectroscopy provides an important contribution to many studies in structural biology. Increasingly, such information is used in integrative structural modeling, where it delivers unique restraints on the width of conformational ensembles. In order to ensure reliability of the structural models and of biological conclusions, we herein define quality standards for sample preparation and characterization, for measurements of distributed dipole–dipole couplings between paramagnetic labels, for conversion of the primary time-domain data into distance distributions, for interpreting these distributions, and for reporting results. These guidelines are substantiated by a multi-laboratory benchmark study and by analysis of data sets with known distance distribution ground truth. The study and the guidelines focus on proteins labeled with nitroxides and on double electron–electron resonance (DEER aka PELDOR) measurements and provide suggestions on how to proceed analogously in other cases.
INTRODUCTION
The combination of site-directed spin labeling (SDSL) of proteins1,2 and nucleic acids3,4 with pulsed dipolar EPR spectroscopy (PDS)5,6 has developed into an important tool in structural biology.7,8 This methodology is applicable to a broad range of samples, accesses a distance range typically between 15 and 80 Å that matches the dimension of individual macromolecules and their complexes, and can provide distance distributions rather than just mean distances.9,10 The latter is particularly important, since many biomacromolecular systems are partially disordered.11 The SDSL/PDS approach is an ensemble measurement technique that provides unique information on, e.g., the extent of such disorder, conformational changes in proteins,12,13 and the time scale of the conformational change.14 In conjunction with modeling of the conformational distribution of the spin label itself15-18 and integration with data from other techniques, the SDSL/PDS approach can be used for generating structural models of biological entities.19-28 In that, a number of issues require careful consideration to ensure reliability of the data and the derived conclusions. These considerations include potential perturbation of the biomolecular structure by the labels,29 studying the ensemble in a glassy frozen matrix, measurements at the sensitivity limit of EPR, and computation of the distance distribution by solving an ill-posed problem. The utility of the SDSL/PDS approach in integrative ensemble structural biology will depend on the ability to provide reliable distance distribution restraints. In fact, setting such standards is a requirement for the ability of the EPR community to contribute to integrative structural biology projects in the future.30 Based on discussions within the community, driven mainly by Thomas Prisner, it became clear that this goes hand in hand with a repository for the raw data and the analyzed data. In turn, such a data repository requires a white paper, which defines the community standards for sample preparation and characterization, for PDS measurements, for data analysis, and for archiving data and metadata. In addition, these standards will help reviewers in assessing manuscripts, which, in a feedback loop, will help adopting the standards. In order to be able to define them, a multi-laboratory ring test was performed that tested the performance of current approaches and revealed some weaknesses that we then addressed in our guidelines. The concrete discussions and the writing of the paper were organized by Olav Schiemann, together with Marina Bennati and Gunnar Jeschke. The discussions and writing were streamlined by forming three workgroups: (1) “Instrumentation, sample preparation and measurements”, (2) “Data analysis”, and (3) “Data interpretation” headed by Thomas Prisner/Bela Bode, Gunnar Jeschke, and Hassane Mchaourab/Enrica Bordignon, respectively. The multi-laboratory ring test was designed and headed by Olav Schiemann, with the samples being prepared by Caspar Heubach from his lab. All participants were involved in the discussions and writing down the results of their respective workgroups. The outputs from the workgroups and the ring test were compiled by Gunnar Jeschke and Olav Schiemann and converted into a first draft. The first draft was commented on and improved to the final paper by all participants.
The small-angle scattering community published first guidelines in 2012,31 updated them in 2017,32 and established the small-angle scattering biological data bank for storing primary data, models, and metadata.33 The community of integrative structural biology published a paper on handling and archiving its data in 2019,30 and the community of Förster resonance energy transfer (FRET) defined the limits of precision and accuracy of single-molecule FRET measurements in a multi-laboratory ring test in 2018.34 Beyond being a requirement for quality assessment, such guidelines also produce awareness of best practices. The open-data approach will help to provide transparency.
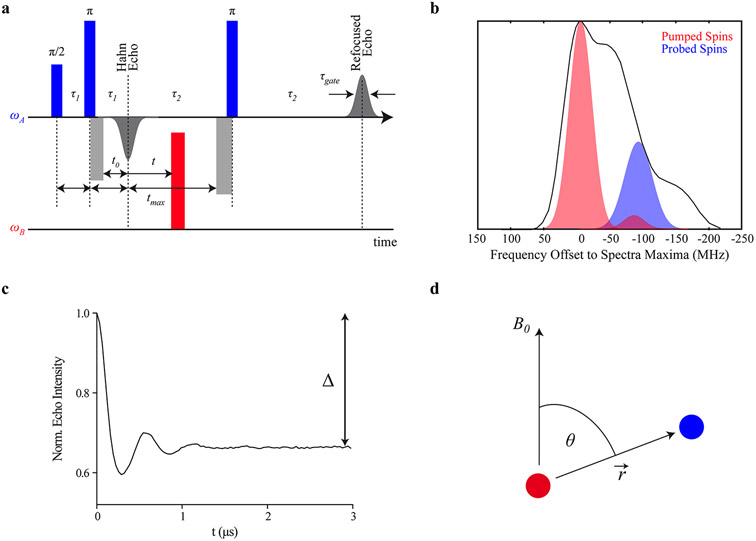
Here, we focus on nitroxide spin labels, which are the most common, well-established and commercially available labels for introducing electron spins into diamagnetic biomolecules. Nevertheless, the presented guidelines apply in analogy also to other types of labels.35-39 We also focus on the experiment that is mostly used for PDS, i.e., the four-pulse double electron–electron resonance experiment (PELDOR or DEER, Figure 1a).40,41 It consists of a remote-detection echo, produced by one -pulse and two -pulses at the observer frequency and a pump pulse, commonly of flip angle , at a second frequency (Figure 1b). The second observer pulse is applied after a delay with respect to the first pulse. Subsequent free evolution of the spin system produces a primary Hahn echo (PE) with maximal intensity at a further delay . The third observer pulse is applied at a delay from the maximum of this echo. Accordingly, a refocused echo (RE) appears at a delay after this last observer pulse. The signal phase is adjusted such that the RE has maximum positive amplitude. If data is acquired with quadrature detection, this phase correction can be performed during post-processing.
Figure 1.
Four-pulse PELDOR/DEER experiment. (a) The DEER/PELDOR pulse sequence with rectangular pulses of the same length. (b) Frequency-domain Q-band (~34 GHz) spectrum of a nitroxide spin label (black) along with the excitation profiles of 16 ns pump and probe pulses (in red and blue, respectively). The pump pulse is set to the maximum of the nitroxide spectrum and the probe pulse is set in this case 100 MHz lower in frequency. The excitation bandwidths are calculated for pulse lengths of 16 ns for both pump and probe pulses. (c) Background-corrected Q-band time trace with the modulation depth indicated. (d) Schematic representation of two spins (red and blue spheres) connected via a distance vector . is the angle between this distance vector and the applied magnetic field .
The DEER signal is recorded as the integral of the RE as a function of the variable delay between the PE and the pump pulse. The maximal observable evolution time is limited by the potential overlap of the pump pulse with length and the last observer pulse with length and is thus given by . Since electron spin transverse magnetization relaxes with phase memory time during the whole sequence length, is limited to a small multiple of . The time period is sampled with the increment . The pulse lengths determine the shortest accessible distance, since all observer pulses as well as the pump pulse must have a sufficient bandwidth to excite the dipolar doublet.42
In a two-spin system A-B, the inversion of the B spin by the pump pulse leads to a change in the local magnetic field at the A spin by the dipolar coupling between the two spins. Thus, a phase change of the RE ensues, which is observed as a dipolar modulation (Figure 1c). Therein, is given by
| (1) |
where is the magnetic constant, and are the values of the two spins, is the Bohr magneton, is the reduced Planck constant, is the spin–spin distance, and is the angle between the inter-spin vector and the magnetic field (Figure 1d). In the glassy frozen solution typically used for biosystems, all molecular orientations are equally probable, leading to a uniform distribution of . The inverse cube dependence of on requires long for measuring long distances. However, the choice of requires a compromise, since a longer leads to a lower signal-to-noise ratio (SNR).
In order to obtain the probability distribution of distances in a doubly spin-labeled molecule, one aims at measuring isolated spin pairs. In practice, even at the lowest accessible concentrations, dipolar coupling to spins in other molecules is not negligible. As a result, the overall dipolar signal factorizes into the intramolecular contribution of the A-B spin-pair and the intermolecular contribution from B spins in other molecules,
| (2) |
For molecules homogeneously distributed in three dimensions, is determined by the overall spin concentration and the fraction of spins inverted by the pump pulse ,
| (3) |
where the numerical constant is 1.0027 mmol , with being the Avogadro constant. For homogeneous distributions with lower dimension , the intermolecular contribution is a stretched exponential function with fractal dimension , e.g., for systems embedded in lipid bilayers and for the homogeneous three-dimensional distribution typically encountered for soluble proteins.43-45 If possible, the signal is recorded such that the dipolar modulation is completely damped at time , allowing robust separation of the intermolecular contributions.46
The intramolecular contribution can be generalized to a system where spins B are coupled to the same observer spin A,
| (4) |
For an isolated spin pair () that is randomly oriented with respect to the magnetic field, the modulation depth is equal to the inversion efficiency if orientation selection is weak or the correlations of the two spin labels’ orientations can be neglected, as is typically the case for nitroxide labels at surface sites at measurement frequencies up to Q-band (~34 GHz).47
The primary signal is a vector of voltage amplitudes given at discrete times , where is an integer. In order to obtain the distance distribution as a vector at discrete distances, the equation
| (5) |
needs to be solved for , where is the kernel matrix computed by integrating eq 4 over a uniform distribution of . This inverse problem is ill-posed, meaning that small variations in , due to noise or systematic deviations of the signal from eqs 2-4, translate into large errors in .9 Therefore, the solution needs to be stabilized. This is achieved by fitting a parametrized model,43 which reduces the number of free parameters, by regularization,10 by neural network processing,48 or by truncated singular value decomposition (SVD).49,50 Until recently, the standard method for solving this problem has followed a two-step approach, where is first separated into and by fitting a model of to the final section of . In a second step eq 5 is solved with a kernel corresponding to , only.51 Recent software packages either fit a parametrized model including 43 or use nested subspace optimization to analyze the data in a single step52 or analyze background and distance distribution by a single neural network.48 Because of the nature of these signal processing techniques, noise in does not linearly transform into noise in . Therefore, uncertainty estimates must be obtained by numerical analysis.52-54
BENCHMARK SAMPLES
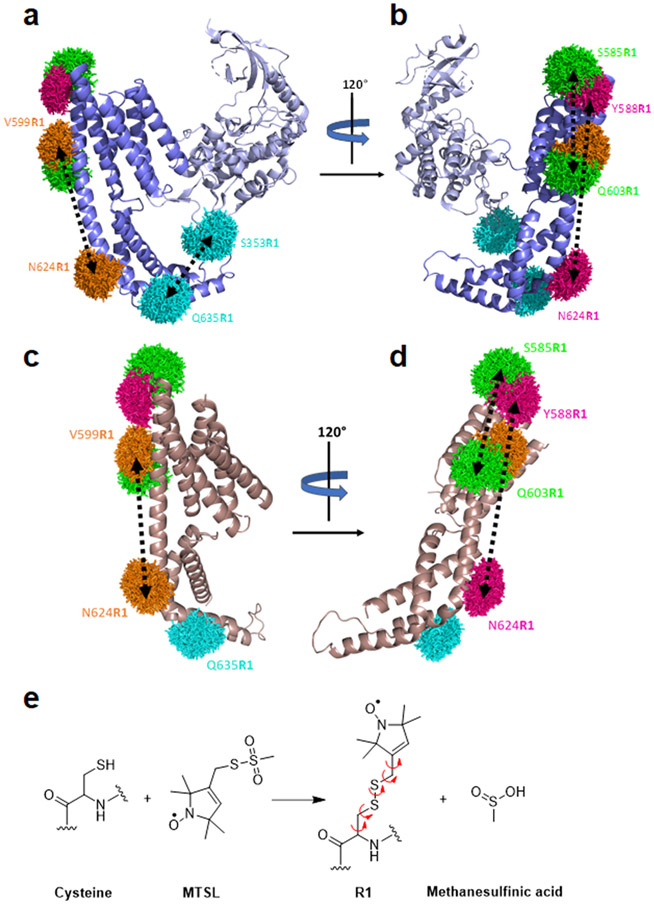
Building on the spin-labeling approach for native cysteines introduced by Berliner et al.,55 Hubbell’s group was the first to introduce SDSL, in which nitroxide spin labels were attached to thiol groups of genetically engineered cysteines at selected positions within a protein.56,57 Here, the Yersinia outer protein O from Yersinia enterocolitica without its membrane anchor (YopO89–729) was chosen as the model system for the present ring test (Figure 2) because it is soluble, stable, can be expressed and purified according to established protocols, and contains only one wild-type (wt) cysteine which can be mutated to alanine (C219A) without loss of function.22 In the following, YopO89–729 containing mutation C219A is named YopO. Two crystal structures are available for wt YopO, one with actin bound (PDB-ID: 4ci6; Figure 2a,b)58 and one for its isolated guanine-nucleotide dissociation inhibitor (GDI) domain without actin (PDB-ID: 2h7o; Figure 2c,d).59
Figure 2.
Structure of YopO and the spin labeling positions. (a–d) The rotamer clouds (mtsslWizard)18 of the R1 pairs are depicted in the same color code for the constructs: S353R1/Q635R1, cyan; V599R1/N624R1, orange; S585R1/Q603R1, green; and Y588R1/N624R1, pink. The distance within the pairs is indicated with a black dashed arrow. (a) Crystal structure of YopO89–729 shown without the bound actin (PDB-ID: 4ci6). The kinase domain is shown in gray and the GDI domain in blue. (b) The same structure as in (a) but rotated by 120°. (c) Crystal structure of the isolated GDI domain (PDB-ID: 2h7o). Note, the GDI domain does not include position S353. (d) The same structure as in (c) but rotated by 120°. (e) Labeling reaction of MTSL with a cysteine giving the spin-labeled residue R1. The leaving group methanesulfinic acid reacts further with oxygen to methanesulfonic acid. The rotatable bonds of R1 are indicated by curly arrows.
The GDI domain contains an -helix (helix 14) that is 43 amino acids long, providing the scaffold for spanning the typical PELDOR/DEER distance range from 15 to 60 Å. Into this -helix, three pairs of cysteines were introduced, i.e., S585C/Q603C, V599C/N624C, and Y588C/N624C, for which the number of intervening amino acids is 18, 25, and 36, respectively. A fourth pair, S353C/Q635C, has one cysteine in -helix 14 and the second in a loop of the kinase domain. The three cysteine pairs within the -helix were expected to yield rather narrow distance distributions with increasing mean distance, whereas the fourth pair with one cysteine in a flexible loop would yield a broad distance distribution.
All four YopO mutants were expressed, purified, and labeled with (2,2,5,5-tetramethylpyrroline-1-oxyl-3-methyl)-methanethiosulfonate (MTSL or MTSSL, Figure 2e),55 providing the four constructs S585R1/Q603R1, V599R1/N624R1, Y588R1/N624R1, and S353R1/Q635R1, where R1 stands for the spin-labeled cysteine side chain (Supporting Information (SI), section S1.1). All laboratories A to G were blind as to the sample identity and were asked to run four-pulse DEER/PELDOR experiments with rectangular pulses at Q-band frequencies and to analyze data in terms of distance distributions using Tikhonov regularization as implemented in DeerAnalysis. While each lab was provided with aliquots from the same batch for each sample, the spectrometer setups varied across the laboratories (SI, sections S1.1 and S1.2).
PELDOR/DEER MEASUREMENTS AND DISTANCE DISTRIBUTIONS
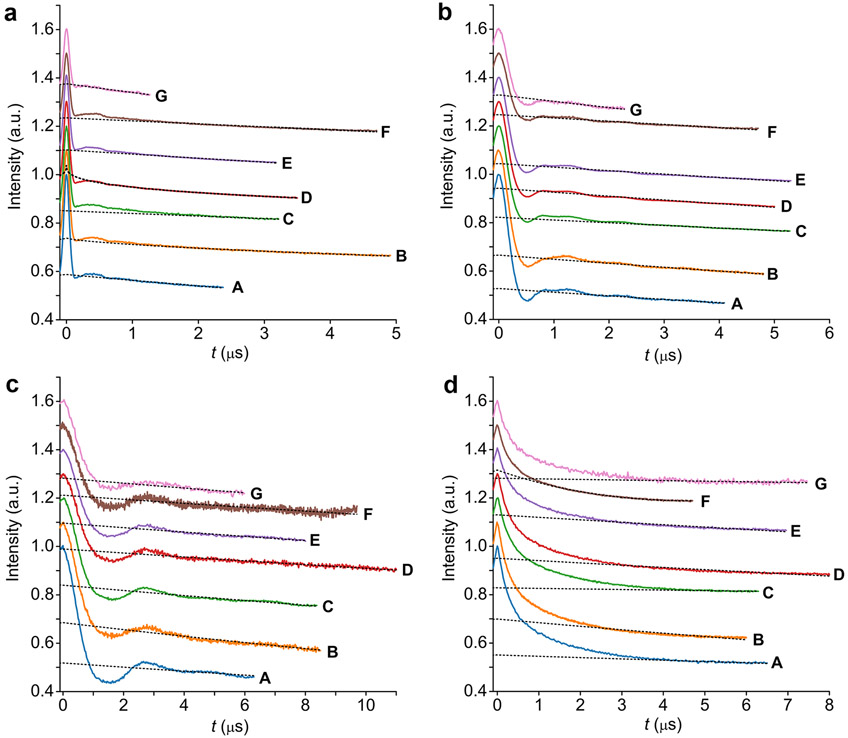
The original time traces from each laboratory A–G are shown in Figure 3 (SI, section 1.2).
Figure 3.
Q-band PELDOR/DEER time traces. Time traces for (a) S585R1/Q603R1, (b) V599R1/N624R1, (c) Y588R1/N624R1, and (d) S353R1/Q635R1. The time traces are color-coded according to the laboratories A–G. The time traces are shifted relative to each other for better visibility. The background fits done in DeerAnalysis (Versions 2015–2019) are overlaid as gray dotted lines.
All time traces were recorded with an SNR larger than 30 with respect to the modulated part and, in most cases, well above 100 (SI, section S1.2.1). Tests on simulated data with known ground-truth distance distributions show that this SNR is sufficient for reliable analysis (SI, section S1.2.2). The dipolar evolution time windows are in each case longer than the resolved dipolar modulation or, in the case of S353R1/Q635R1, where no distinct oscillations could be observed, the time window length is of the order of 5 or longer. Intentionally, ring test instructions did not specify required trace length. Thus, individual laboratories made different decisions regarding this parameter. This point will be addressed below by formulating a guideline. The background decays of the time traces are nearly parallel to each other as expected for samples from the same batch for very similar experimental settings. Slight differences can arise from variations in the excitation bandwidth of the pump pulse (SI, section 1.2.3).7
To extract the modulation depths and distance distributions, all laboratories relied on two-step analysis with the commonly used program DeerAnalysis (SI, section S1.3).51 Division of the raw time traces by the fitted background decay (all laboratories used a homogeneous 3D background) yielded time traces (so-called form factors) with an average modulation depth of 35% ± 8% (SI, Figure S8 and Table S12). The variation in is partly due to the different background fits, as also reflected by the different shapes of the Fourier transforms of the form factors (SI, Figure S9), and also owing to different experimental settings, e.g., pump pulse length and resonator type. This highlights that counting of spins within a molecule via requires careful calibration of the spectrometer, resonator, and pulse parameters with standard samples.60
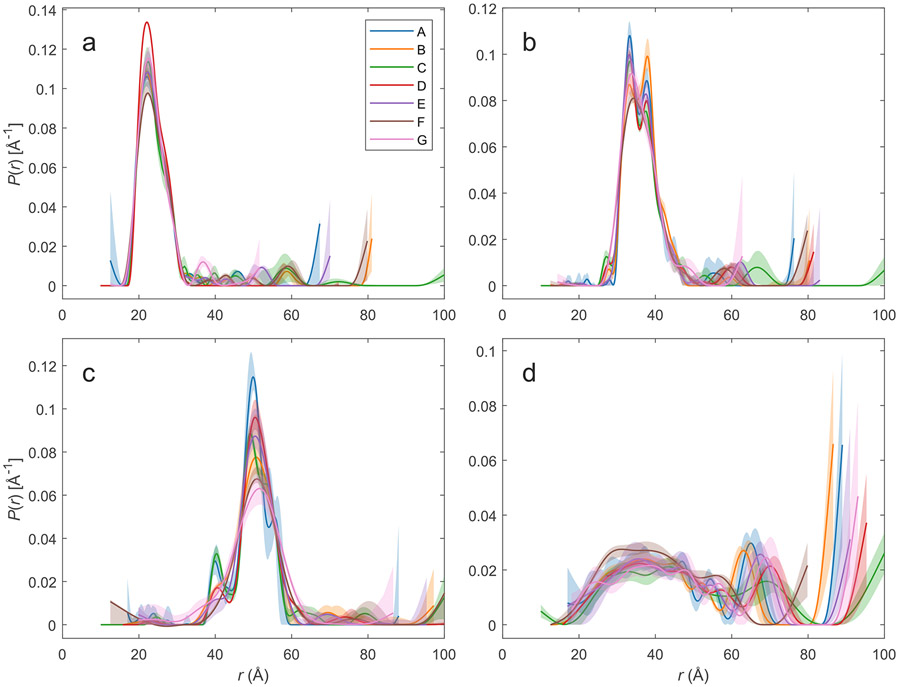
The laboratories provided L-curves10 that differ considerably because of different SNR and trace length. In each case, a regularization value close to the intersection of both legs was chosen (L-curve corner criterion) (SI, Figure S10 and Table S14). The resulting distance distributions are shown for each sample as overlays in Figure 4. They include uncertainty estimates from the validation tool in DeerAnalysis (transparent areas). As can be inferred from Figure 4, the distance distributions belonging to the same sample agree quite well with each other, except for features near the upper limit of the distance range that arise from uncertainty in background separation. This uncertainty is the larger the shorter the trace is. Except for S353R1/Q635R1, validation recognizes that these features are insignificant. For the very broad distribution of S353R1/Q635R1, both the edge of the distribution toward long distances (65–75 Å) and the presence or absence of very long distances (>80 Å) differ between laboratories. This problem again arises from uncertain background separation, combined with different trace lengths. Note also that uncertainty estimates do not always overlap at shorter distances, especially for Y588R1/N624R1, but to a lesser extent also for V599R1/N624R1.
Figure 4.
Overlays of the normalized distance distributions as obtained by Tikhonov regularization with DeerAnalysis. The distance distributions are color-coded according to laboratories A-G that processed them and uncertainty bands from DeerAnalysis validation are indicated as transparent areas: (a) S585R1/Q603R1, (b) V599R1/N624R1, (c) Y588R1/N624R1, and (d) S353R1/Q635R1.
In order to obtain further insight, all data sets were additionally analyzed by neural network analysis with DEERNet 2.0,61 by multi-Gauss fitting with DD, by one-step Tikhonov regularization with automatic selection of the regularization parameter by the Akaike information criterion (AIC) with DeerLab and by a comparative analysis that compares neural network analysis and regularization (SI, section S2; Figures S11-S14). In general, all approaches yield similar distance distributions, but differ considerably in their uncertainty estimates, which do not cover the full variation between laboratories in the case of DEERNet and exceed this variation substantially in the cases of multi-Gauss fitting. The one-step Tikhonov analysis by DeerLab underestimates the optimal regularization parameter for data of laboratories E and F for S353R1/Q635R1, leading to an overestimate of uncertainty in these cases. Comparative analysis appears to provide the most realistic uncertainty estimate, except perhaps for Y588R1/N624R1 where most of the data from the different laboratories agree better than indicated. Variation in the distance distributions between laboratories stems mostly from uncertainty of background separation due to different trace lengths. In addition, overlap of excitation bands of observer and pump pulses leads to an end-of-trace artifact in time domain that is not accounted for in the standard kernel and can thus distort the distance distribution.52
Quantification of distance distributions in terms of only their mean distance and width is of general interest, too, because some modeling approaches require restraints in this form.62 We have performed such analysis on the primary data provided by laboratories A-G by simultaneously fitting a Gaussian distribution and three-dimensional homogeneous background in DeerAnalysis (Table 1). We found that inference of the mean and standard deviation of the distribution from such a fit is numerically more stable than inference from results of regularization or neural network analysis. For samples S585R1/Q603R1, V599R1/N624R1, and Y588R1/N624R1, this analysis proved to be very stable with 95% confidence intervals of the mean distance smaller than 1 Å and confidence intervals of the standard deviation of the Gaussian smaller than 2 Å. These values compare favorably to the uncertainty of about 3 Å in rotamer modeling of the spin label.18 The width of the distance distributions for constructs S585R1/Q603R1, V599R1/N624R1, and Y588R1/N624R1 is, with 4.3, 4.5, and 4.9 Å, respectively, fairly narrow and fits to the -helix being rather rigid. In contrast, for construct S353R1/Q635R1 uncertainties of the mean distance and standard deviation are as large as 5.1 and 7.8 Å, respectively. Without additional restraints and ensemble modeling, the only conclusion that should be drawn is that the distribution is broad, indicating a high degree of flexibility, with a mean distance between 40 and 50 Å.
Table 1.
Statistics of the Distance Distributions
| S585R1/Q603R1 |
V599R1/N624R1 |
Y588R1/N624R1 |
S353R1/Q635R1 |
|||||
|---|---|---|---|---|---|---|---|---|
| lab | a | b | a | b | a | b | a | b |
| A | 23.5 | 3.8 | 36.2 | 4.3 | 50.5 | 4.7 | 39.5 | 26.9 |
| B | 23.8 | 4.1 | 36.7 | 4.2 | 50.2 | 5.5 | 44.8 | 24.2 |
| C | 23.1 | 4.7 | 35.9 | 4.7 | 50.4 | 4.8 | 47.3 | 24.4 |
| D | 23.6 | 4.1 | 36.0 | 4.6 | 51.0 | 4.3 | 40.9 | 29.3 |
| E | 23.8 | 4.7 | 35.9 | 4.3 | 50.8 | 4.5 | 41.9 | 25.7 |
| F | 23.7 | 5.2 | 36.0 | 4.7 | 51.2 | 4.3 | 42.6 | 17.6 |
| G | 23.5 | 3.7 | 35.9 | 4.5 | 50.6 | 6.0 | 42.8 | 20.8 |
| average:c | 23.6 | 4.3 | 36.1 | 4.5 | 50.7 | 4.9 | 42.8 | 24.1 |
| CI (95%):d | 0.5 | 1.0 | 0.6 | 0.4 | 0.7 | 1.3 | 5.1 | 7.8 |
Mean distance (Å).
Standard deviation of the mean distance (Å).
Average of the parameter in the respective column (Å).
Twice the standard deviation of the average value in this column (Å).
Beyond the mean distance and the distribution width, one may aim at analyzing the different peaks in the distance distributions (Figure 4). However, the intensity distribution of these peaks and the number of peaks resolved varies across the different laboratories. Importantly, already the uncertainty bands of individual laboratories indicate that these are not stable features (Figure 4). This highlights that such an analysis requires a very good SNR, several resolved modulation periods, reduction or fitting of the end-of-trace artifact, and checks for reproducibility. In any case, only features exceeding the uncertainty bands should be interpreted and even such an analysis would need to be corroborated by additional data, e.g., from other spin labels or further biophysical methods.
COMPARISON WITH CRYSTAL STRUCTURES
PELDOR/DEER measures the distance between the spin centers, i.e., the N–O groups. Hence, comparison with a crystal structure or structural model has to take into account the length and conformational flexibility of the R1 side chain (Figure 2e). Usually, this is done by means of in silico labeling programs, such as mtsslWizard,18 MMM,62 or ALLNOX.63 Using the two crystal structures of YopO as input, the distance distributions in Figure S15 were calculated (SI, section S3). The mean distance increases from S585R1/Q603R1 via V599R1/N624R1 to Y588R1/N624R1 and, together with the width of the distributions, matches the experimental data well (Table 2). The average deviation between the experimental and in silico mean distances lies between 3.6 and 7.5 Å. The distance differences between the in silico distributions using the two different crystal structures, arise from the -helix 14 being extended and straight in PDB-ID 2h7o, but slightly bent at amino acid 606 in PDB-ID 4ci6 (Figure S16). As the differences between experiment and simulation exceed the combined uncertainties, at least for S585R1/Q603R1, the solution structure may slightly deviate from the crystal structures.22 For construct S353R1/Q635R1, there is no agreement between the experimental distribution and the in silico prediction, strongly suggesting that the loop and/or the GDI and kinase domain are trapped in one conformation in the crystal, whereas the structure of YopO in solution is much more flexible in this region. Such differences between crystal and solution structures have been observed in many cases.13 This is a demonstration of PDS in frozen solution better capturing conformational flexibility than observed in crystallography.
Table 2.
Comparison of Experimental and In Silico-Derived Mean Distances and Distribution Widths
| S585R1/Q603R1 |
V599R1/N624R1 |
Y588R1/N624R1 |
S353R1/Q635R1 |
||||||
|---|---|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | a | b | ||
| PELDOR/DEER | 23.6 | 4.3 | 36.2 | 4.5 | 50.5 | 4.7 | 42.8 | 24.1 | |
| mtsslWizard | 4ci6 | 30.0 | 4.8 | 41.1 | 4.5 | 58.0 | 4.5 | 24 | 5 |
| 2h7o | 29.7 | 4.8 | 39.2 | 4.7 | 54.4 | 4.9 | – | – | |
| MMM | 4ci6 | 29.5 | 4.9 | 40.9 | 4.3 | 56.8 | 4.7 | 23 | 4 |
| 2h7o | 35.0 | 4.1 | 37.8 | 4.6 | 54.8 | 4.8 | – | – | |
| differenceexp/in silicoc | 7.5 | 0.4 | 3.6 | 0.0 | 5.5 | 0.0 | 19.3 | 19.6 | |
Mean distance (Å).
Standard deviation of the mean distance (Å).
Averaged difference between the in silico and experimental mean distances and distribution widths, both in (Å).
GUIDELINES
Based on the benchmark test and discussions evolving around it, the following guidelines for sample preparation, PELDOR/DEER measurements, data analysis, and data interpretation have been agreed on by all authors as representatives of the wider community. Extended guidelines are provided in the SI, section S4.
Spin Labeling.
To ensure high quality of the data, complete removal of free label should be achieved. Even though residual unbound label only contributes to the background, this can easily dominate the signal, especially if a protein-bound label has a shorter phase memory time (). Less than 10% free label is usually acceptable. Quality control and assessment of modulation depth require that protein concentration and labeling efficiency are known. Ambient-temperature cw X-band EPR spectra measured in the liquid state can reveal whether all spin label is bound. It is good practice to test by such spectra for unspecific labeling of the wildtype protein or of the cys-less construct used.
Check for Integrity of Protein Structure and Function.
Integrity of secondary and tertiary structure and/or protein function needs to be checked with respect to the wildtype. If the structure and/or function of the protein is compromised, other labeling sites, and other strategies for spin-labeling can be tested, e.g., insertion of unnatural amino acids.39 In some cases, native paramagnetic centers can be exploited.64
Cryoprotection.
To minimize structural changes and aggregation upon sample freezing,46 either a cryoprotectant should be added, or rapid freeze quench techniques may be applied.65,66 Adding 10–50% v/v glycerol or ethylene glycol suffices for water-soluble proteins,56 although lower concentrations can also be used, especially for membrane proteins. The cryoprotectant may compete with weak protein–protein interactions, so that cryoprotection needs to be optimized if such interactions are under study.67 In most cases, the frozen ensembles resemble the conformations sampled by biomolecules in solution very well.68 If the system is partially or fully disordered or the detailed distribution shape is of concern, different freezing methods should be tested and compared.
Prolonging Phase Memory Time and Diamagnetic Dilution.
The phase memory time limits and thus the largest accessible distances and the distance resolution. At given , the SNR scales with , where typically ranges between 1 and 2. At too high local concentration, instantaneous diffusion mechanisms govern .69-71 Long phase memory times are achieved by diluting samples to the limit where nuclear spin diffusion governs . Deuteration of the solvent, including the cryoprotectant72-75 and, if possible, of the biomolecule can increase significantly.76,77 For aggregates and fibrils,78 as well as membrane proteins in membrane or membrane-mimetic environments72,79 (except nanodiscs), the local concentration can still be higher than the 20–50 bulk concentrations that are usually required for obtaining high-quality data. In such cases, diamagnetic dilution is required, which can also counteract adverse effects on the time traces from aggregation,80 reduce multi-spin effects for oligomeric proteins,81 or disentangle intra- and intermolecular distances.82
Intermolecular Background.
If the assumption of a homogeneous three-dimensional distribution of the doubly labeled molecules is not safe, it should be checked whether singly labeled samples exhibit the expected mono-exponential decay of their PELDOR/DEER signal. This may be required for membrane proteins, fibrils,78 and for in-cell samples, if excluded volume effects are significant,83 or if protein aggregation is suspected.84
Data Reproducibility.
Each study should establish by repeats, usually in the form of triplicates, that the applied methodology leads to reproducible distance distributions. In biological repeats, the labeled biomolecule is freshly prepared and labeled. In cases where a large series of double mutants is part of the study, it is unrealistic to have biological repeats for each member of the series. When the conclusions are derived from the whole series, such repeats are not necessary for all samples, as bad samples can be identified by other means. However, when conclusions are based on the behavior of one or two samples, they are essential. Technical repeats are required to substantiate conclusions when samples of the same protein batch are prepared under different conditions, such as pH, buffer, interaction with effector or ligand, concentration, environment (in buffer, cell extract, cells, membrane type), and if conclusions are derived from the effect of these parameters. If data quality is borderline, repeats of the PELDOR/DEER measurement of the same sample can help to detect sources of uncertainty stemming from the setup of the experiment. If possible, such technical repeats should involve thawing and refreezing the sample or freezing a second sample prepared from the same solution.
Assessing Local Spin Concentration, Multi-spin Effects, and Orientation selection.
While sample characterization as described above can provide an estimate of the bulk spin concentration, the intermolecular PELDOR/DEER background is sensitive to the local concentration near the observer spins.9 The local spin concentration is related to the fraction of spins inverted by the pump pulse by eq 3. Typical values of for 100% labeling efficiency at both sites are 0.3–0.6 at X-band and 0.3–0.5 at Q-band with a 150 W amplifier when pumping at the maximum of the nitroxide spectrum. The value can be calibrated for a given spectrometer, resonator, and given pulse sequence parameters.47 This then allows to determine whether bulk and local spin concentration are the same, provided that the fraction of cryoprotectant is the same during calibration and actual measurement.
Furthermore, is related to the modulation depth . For well-isolated and doubly labeled molecules, is the product of and the labeling efficiency 85 if orientation selection is weak or the correlation of the two spin labels’ orientations can be neglected.86 A modulation depth lower than expected usually implies . Vice versa, a modulation depth higher than expected indicates that more than one B spin contributes to modulation of the signal acquired on the A spin. Processing data from multi-spin systems with a two-spin kernel gives rise to ghost peaks87 and diminished contributions from longer distances.88 To counteract this effect, the inversion efficiency , the labeling efficiency or both simultaneously can be reduced.89
Correlated spin label orientations combined with orientation selection by the microwave pulses invalidate integration over a uniform distribution of for obtaining the kernel in eq 5.86,90 Such orientation selection can be suppressed by averaging traces acquired at different fields .91-93
Measurement Parameters.
In Table 3, typical experimental parameters are collected for PELDOR/DEER experiments using nitroxide spin labels, deuterated solvents, and a 3 mm Q-band dielectric resonator in combination with a 150 W traveling wave tube (TWT) amplifier. In cases where a multimodal or very broad distribution of the phase memory time is expected to originate from a broad conformer ensemble, several values of should be tested.94,95
Table 3.
Typical Parameters for PELDOR/DEER Measurements on Nitroxides with High-Power Q-Band Spectrometers
| temp, | 50a |
| [ns] | 12–16 |
| [ns] | 12–32 |
| [ns] | 12–16 |
| [MHz] | 80–100 |
| [ns] | 8–20 |
| [ns] | 200–400 (first observable maximum of the refocused echo decay) |
| few , limited by , minimal SNR, and maximal | |
| sequence repetition time (SRT) [ms] | ~5 (≥80% of echo recovery) |
| [ns] | as long as the longest pulse length |
| SNR (w.r.t. modulation depth) | >20b |
| phase cycle | 2-step (or 8-step for coherent MW sources) |
| ESEEM modulation average | 8 steps of 16 ns |
| total acquisition time | 1–72 |
Measurement at 80 K is feasible, but entails a substantial reduction of the available .
If an SNR of 20 cannot be achieved at the required trace length, data with an SNR down to 10 can still provide useful restraints.
General Guidelines on Data Analysis.
The mathematically ill-posed nature of the PELDOR/DEER data processing problem creates much scope for sample-specific parameter variation and subjective decision making. This should be avoided; we therefore recommend using automated data analysis workflows that leave no room for bias from subjective decisions. If the software running the workflow offers options to the user, the choices must be reported and the reasoning behind them explained. To ensure reproducibility, the software should be freely accessible (ideally, open-source and under version control).
The popular two-step approach to PELDOR/DEER data processing (background fitting and elimination followed by distance distribution extraction) still used in the ring test is discouraged for future work because the separation between the background and the form factor can be subjective and single-step methods have now become available. Accordingly, we recommend using such single-step methods as illustrated on the ring test data in the SI that simultaneously account for both the distance distribution and the background. This is the norm for neural networks48 and fully parametric models43 and possible for regularization methods with a nested optimization approach.52
Pre-processing of PELDOR/DEER Data.
It is preferable to detect primary data in quadrature, because correcting the phase of the averaged signal during data processing is more accurate than (only) phasing the echo during the experiment setup. After phase correction, the deviation of the imaginary part from zero is expected to be white noise; systematic deviations indicate experimental problems that compromise data quality.
The time shift between the first point of the primary data and the zero time of dipolar evolution cannot be exactly predicted from pulse timings. It should be either determined by measurements on high-quality standard samples or directly from the data, which requires pulse timings that ensure ns.
Conversion of Time-Domain Data to Distance Distributions.
It must be checked that data conforms to the standard kernel, which assumes dilute A-B spin pairs, the absence of orientation selection or correlation, the absence of exchange coupling,96,97 and at most weak overlap of observer and pump excitation bands. If some of these assumptions break down and a non-standard kernel is used, this kernel has to be specified.
For the time increment of PELDOR/DEER data, we recommend a value of 8 or 12 ns in order to avoid aliasing of large dipolar frequencies stemming from short distances. Analysis of individual features in distance distributions requires that at least the widths of all features can be quantified, which requires that exceeds two periods of the slowest dipolar oscillation. With eq 1 and , corresponding to the singularities of the Pake pattern, this puts an upper limit to such interpretation. For a mean distance to be quantifiable, at least one period of its dipolar frequency must be recorded. An extended discussion is provided in section S4.1 of the SI.
Regularization parameters10,51 or SVD truncation levels49 should be determined by a criterion that has no element of user discretion52 and reported. In general, all details necessary for reproducing data analysis must be provided. This includes any prior information measured or estimated independently, which is used to constrain the distance distribution, such as spin concentration, modulation depth range, or minimum and maximum distance.
Specifying Data Quality and Uncertainty.
Preferably, the noise level should be estimated by acquiring several PELDOR/DEER traces and computing the standard deviation. This is most easily done by storing scans separately. Alternatively, noise can be estimated from the deviation of a good fit to the time-domain data mentioned above.97,98 If phase drifts and phase noise are negligible, the noise level can be estimated from the root-mean-square amplitude of the imaginary part after phase correction.
Uncertainties in the distance distributions and the model parameters should be specified in the form of 95% confidence intervals, using any of the techniques described for regularization approaches,52,53 truncated singular value decomposition,50 neural networks48 or fitting of parametrized models.54 Note that the confidence intervals do not necessarily include model bias. Therefore, comparison between results of two or more approaches is commendable.
REPORTING CHECKLIST
The following should be reported in publications:
Data confirming the identity, purity, labeling efficiency, and structural/functional integrity of crucial and selected mutants
Sample conditions: concentration, tube size, sample volume, amount and type of cryoprotectant, freezing procedure, deuteration
Whether diamagnetic dilution was used along with the way the mixture has been prepared
Spectrometer and resonator
Measurement temperature
Pulse lengths of pump and probe pulses
Positions of pump and probe pulses with respect to the EPR spectra
Frequency offsets of pump and probe pulses with regard to resonator frequency
Parameters describing the shape of the pulses (if they are not rectangular)
The delays used ( and ), shot repetition time, the time increment in the primary data, accumulation time, total number of averages (i.e., echoes per point)
Nuclear modulation averaging procedure, if any
Procedure for reducing orientation selection, if any
Measures to reduce multi-spin effects, if any
Modulation depth
Time offset of the zero time of dipolar evolution in the primary data
Equation for a custom kernel, if applicable
Information on global fitting of several data sets, if applicable
Software used for distance distribution analysis, including version number
Regularization parameter and criterion for its selection, if regularization was used
Truncation level and criterion for its selection for singular-value decomposition methods
Prior information used to constrain the distance distribution
DATA DEPOSITION CHECKLIST
Data should be deposited in an openly accessible public repository and include the following:
Primary data as measured, preferably with quadrature detection
Distance distribution, including upper and lower limit of the 95% confidence interval
Fit of the primary data, if one-step analysis (preferred) was used
Background-corrected data and their fit, if two-step analysis was used
Log file of the data analysis software, if any; otherwise, a list of the settings of the software or processing script
If data is not deposited, it should be archived locally and provided upon reasonable request. In addition, all these data should be documented in main text or supplementary figures.
DERIVING AND INTERPRETING RESTRAINTS FROM DISTANCE DISTRIBUTIONS
Here, we focus on the interpretation of distance information derived from MTSL-labeled proteins. We assume that the distance distribution has been reliably extracted from the PELDOR/DEER trace as described above.
Determinants of the Distance Distributions: Spin-Label Rotamers versus Protein Dynamics.
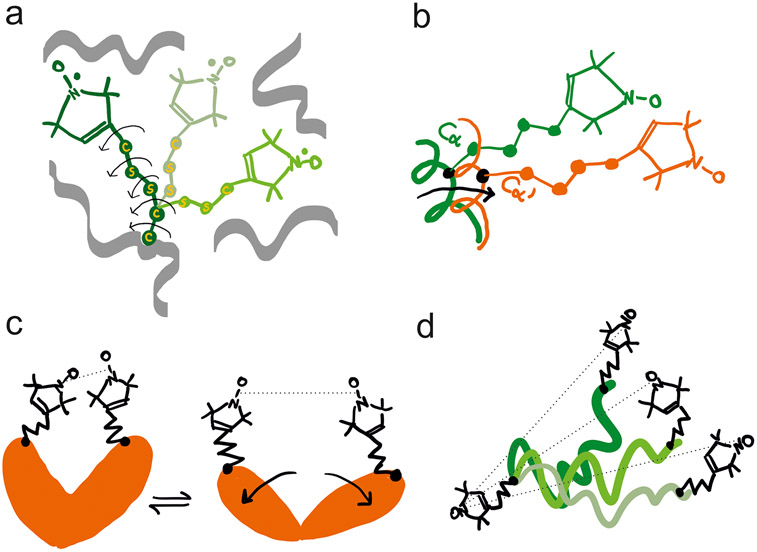
DEER/PELDOR measures the distribution of pairwise N–O to N–O distances of the two dipolar-coupled spin labels in solid state. Hence, the distribution width reflects the frozen disorder of the spin label rotamers. In the case of MTSL, the N–O group bearing five-membered ring is attached to the atom via five potentially rotatable bonds (giving the R1 side chain)16,99,100 and the distribution of label rotamers contributes appreciably to the distance distribution (Figure 5a). Steric hindrance by the internal structure of R1 and its interactions with the backbone and neighboring side chains can induce different anisotropic distributions of the rotamers at each site.101-104 In addition, restricted backbone dynamics and the protein’s conformational heterogeneity can broaden the distance distribution and/or result in distinct distance components (Figure 5b-d). Deconvolution of these contributions, i.e., label rotamers and protein conformers, is a critical step for structurally and mechanistically relevant interpretation of PELDOR/DEER data. Distance distributions can be simulated using one of the many rotamer libraries available (see section below) in conjunction with known crystal, NMR or cryo-EM structures or with properly constructed models. Comparison between predicted and experimental distributions can serve to test the models and, e.g., can inform on the local dynamics in response to changes in biochemical conditions, e.g., binding of ligands.
Figure 5.
Schematic representation of the most common determinants of the width of the MTSL-derived distance distributions in PELDOR/DEER. (a) The five potentially rotatable bonds enable distinct rotamers to be populated at a specific site, based on the steric hindrance imposed by neighboring side chains and backbone atoms. Three rotamers are shown with arrows highlighting the rotatable bonds in one of them. (b) Small translational or rotational motion of the backbone to which the rotamers are attached can also induce broadening or appearance of shoulders in the distance distribution toward another spin-labeled site. (c) The protein adopts two distinct conformations (for example with and without a ligand bound) which can be monitored by PELDOR/DEER. Equilibria between two conformations can also be identified by the appearance of two peaks in the distance distribution. (d) If MTSL is attached to intrinsically disordered proteins or to a dynamic region of a protein, a broad distribution of distances is expected in frozen state. Such disorder is correlated with the large-amplitude motions of the backbone to which MTSL is attached.
Examples of Distance Distributions and Their Interpretation.
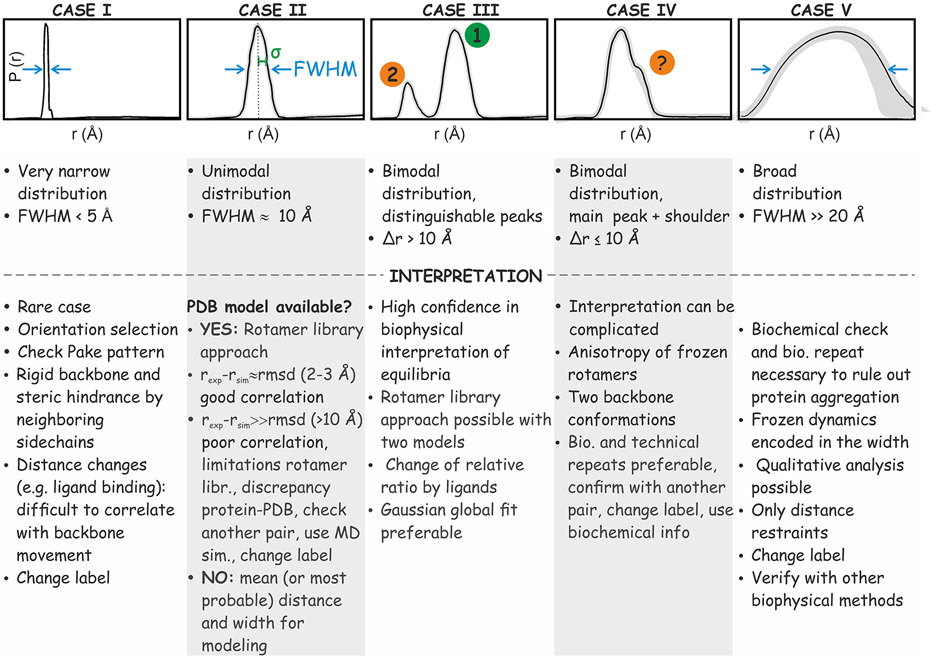
Figure 6 showcases five examples of distance distributions that, separately or in combination, represent the majority of experimentally encountered distributions. Cases I, II and V are unimodal distributions that differ by the full-width at half-maximum (FWHM). At one extreme, the narrow case I is rather favorable for detection of small-amplitude conformational changes. It arises from labels attached to rigid backbones and rigidly held in a defined orientation by tight molecular interactions. Due to the limitations of the available rotamer library approaches (see below), the agreement of case I with predictions may be unsatisfactory. Consequently, it may be difficult to interpret, e.g., ligand-induced changes in the mean distance in terms of a protein’s backbone motion. In fact, slight changes in the micro-environment can induce large shifts in the mean distance by rotamer redistribution. Changes in the solution-state cw EPR line shape or in water accessibility upon ligand binding can reveal such redistribution.105 Furthermore, such a narrow distribution may induce orientation correlation. Hence, it is advisable that the data is collected at multiple magnetic fields or resonance offsets.91-93
Figure 6.
Classification of distance distributions encountered with MTSL-labeled proteins described in detail in the text. The main characteristics are related to the full width at half-maximum (FWHM) of the distance peaks, and by the presence of distance peaks separated by . The most important aspects to be considered in interpretation are briefly summarized below each distance distribution.
At the opposite extreme, case V is one of the most difficult to interpret. The distribution is broad with a FWHM larger than 20 Å, indicating protein or protein complex disorder. Conclusions about residual structure in such cases require additional experiments and biochemical validation or modeling based on a large set of restraints. A critical control is to exclude protein precipitation and aggregation by size exclusion chromatography, dynamic light scattering or DEER/PELDOR on singly labeled samples. Assuming that the labeled mutant is functional and aggregation-free, broad distributions reflect intrinsic disorder. Quantitative interpretation of these distributions requires modeling106 which may be aided by molecular dynamics simulations.107 Comparative analysis under different conditions however may yield qualitative insight. A broad distance distribution is a common feature of intrinsically disordered proteins (IDPs) (Figure 6, case V)108 and is expected also when the two labels are attached to structured domains, which are linked via a disordered region.81 In some cases, altering the linker or adding side groups on the nitroxide-containing ring can help disentangling intrinsic flexibility of the label from protein backbone dynamics. Interpretation of the mean distance is difficult; however, useful distance restraints can be retrieved, e.g., “20–60 Å” or “>30 Å” or pairs of mean distance and standard deviation. Among the constructs in the ring test, S353R1/Q635R1 corresponds to case V.
Case II is the conceptually simplest one with a unimodal distribution of about 10 Å width. It is encountered when both R1 side chains sample many rotamers. Here, predicted rotamer distributions enable the deconvolution of spin label from backbone conformer distribution. The well-defined mean distance can be used directly in modeling. Starting from such a distribution, it is straightforward to read off the amplitude of distance changes induced in response to different biochemical conditions. Among the constructs in the ring test, S585R1/Q603R1 corresponds to case II.
Case III corresponds to multi-modal distributions, illustrated here by two distinct and large-amplitude peaks. Typically, the peaks are relatively narrow and their mean distances differ by more than 10 Å. Such well-separated peaks are unlikely to arise from rotamer sub-ensembles. Thus, case III is explained by multiple conformations of the protein’s backbone or of domain arrangement. Often, addition of ligands or other changes in conditions can alter the equilibrium between the conformers and can thus identify their contributions to the distribution.24-26,109 In that case, multi-Gaussian global fitting of the set of PELDOR/DEER time traces can be used to determine the free energy difference of the equilibrium.27,28 As for case II, the rotamer library approach can be used if a model or structure exists. Similarly, these peaks, once their origin has been established, can be used as constraints in modeling.21
Case IV corresponds to a main peak with a shoulder which has been proven to be reliable by uncertainty analysis. Like case III, case IV may originate from protein equilibria, but now with overlapping distance distributions of label conformers. This can be tested by altering biochemical conditions and observing the shift in the distance distribution. The caveat is that shoulders can also arise from anisotropy of the spin label rotamers at one or both sites.103 Hence, in order to confirm the relevance of shoulders in terms of backbone conformation, other closely related spin label pairs should be investigated or the persistence of such shoulders should be verified with spin labels linked to the backbone by different tethers, especially those with rigid attachment.110 Biological and technical repeats are advisable and other biophysical or structural information should be used to confirm the existence of a second backbone conformation. Among the constructs in the ring test, V599R1/N624R1 corresponds to case IV. Construct Y588R1/N624R1 is complex, being borderline between cases II and IV with a minor peak at 40 Å (borderline to case III) appearing in data from several laboratories with various data analysis approaches. Further experiments would be required in this case to assign the contributions.
Simulation of Distance Distributions.
Distance distributions can be used to test hypotheses on structure, if these hypotheses can be formulated in terms of a three-dimensional model. To that end, the distance distributions expected for this model are computed by rotamer library approaches, such as MMM,16,62 mtsslWizard,18 or ALLNOX,63 or by MD methods such as the molecular dynamics dummy spin-label method MDDS111 or the CREST/MD17 approach. Tests with MMM and mtsslWizard show that agreement of mean distances between experiment and model in the 2–4 Å (root-mean-square deviation) range can be expected if the model fits.18 Larger deviations for several distance distributions indicate local flexibility at the sites of attachment of the label or, for instance, a solution structure that differs from the crystal structure. In case of such deviations, molecular dynamics computations can be useful to better estimate the uncertainty of the rotamer library predictions for the case at hand.17,112,113
Structure Modeling.
Detailed guidance on modeling is beyond the scope of this paper. In general, modeling can be based on direct fitting of primary data,19 fitting of full distance distributions,62 or parametrization of the distributions.22,114,115 Typical applications are rigid-body protein docking,19 modeling of transitions between conformations,116 or ab initio coarse-grained modeling of structures.20-22 For transitions between conformations, the quality of the starting structural model needs to be carefully evaluated by an independent set of DEER distance restraints. The mean and the most probable distance are likely very similar in case II (Figure 6) but can differ if shoulders or multiple peaks are present in the distance distributions (cases III and IV) or if a broad distribution is asymmetric (case V). Depending on the task at hand, it is important to use not only mean distances, but also the widths of the distributions.22 It is important that enough restraints are used in the model calculation, and it can be useful to overdetermine the problem so that restraints can be left out in turn to add certainty to the final solution.19,107,117 Integrative modeling that includes constraints from other biophysical methods is required in many cases.20-22,62
CONCLUSION
The combination of site-directed spin labeling with distance distribution measurements by pulsed dipolar EPR spectroscopy, in particular with PELDOR/DEER, has become a valuable component in integrative structural biology. To fully exploit the potential of this approach, good practice in sample preparation, measurements, data analysis, and estimation of structural restraints and their uncertainty is required. Our benchmark test demonstrates that measurements and data analysis are robust and well reproducible across measurement conditions used in different laboratories but, at the same time, illustrates the limitations in interpreting distance distributions at the current stage. The results, together with discussions among all authors, allow us to propose guidelines on sample preparation, PELDOR/DEER measurements, data analysis, reporting, and data deposition or archiving. Furthermore, we provide some guidance on the interpretation of the different categories of distance distributions and on the use of tools to create coarse-grained models of proteins in different conformational states. We hope that our results and guidelines will foster the use of site-directed spin labeling EPR and PELDOR/DEER in the wider structural biology community.
Supplementary Material
ACKNOWLEDGMENTS
We acknowledge the DFG (German Research Foundation) priority program SPP 1601 for funding multiple projects (O.S., G.J., E.B., M.D., T.F.P., and M.B.) related to the present work together with the funding of many collaborations outside Germany, particularly the NSF (National Science Foundation)-funded SharedEPR. J.E.L. thanks The Royal Society for a University Research Fellowship. We thank the Leverhulme Trust (RPG-2018-397) and the BBSRC (BB/R013780/1 and BB/T017740/1) for funding.
Footnotes
Supporting Information
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.1c07371.
Methods and materials, original DEER/PELDOR data, details on data analysis, and details on good practice (PDF)
The authors declare no competing financial interest.
Contributor Information
Olav Schiemann, Institute of Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany.
Caspar A. Heubach, Institute of Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany
Dinar Abdullin, Institute of Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany.
Katrin Ackermann, EaStCHEM School of Chemistry, Biomedical Sciences Research Complex, and Centre of Magnetic Resonance, University of St Andrews, St Andrews KY16 9ST, U.K..
Mykhailo Azarkh, Department of Chemistry and Konstanz Research School Chemical Biology, University of Konstanz, 78457 Konstanz, Germany.
Elena G. Bagryanskaya, N.N. Vorozhtsov Novosibirsk Institute of Organic Chemistry, 630090 Novosibirsk, Russia
Malte Drescher, Department of Chemistry and Konstanz Research School Chemical Biology, University of Konstanz, 78457 Konstanz, Germany.
Burkhard Endeward, Institute of Physical and Theoretical Chemistry and Center of Biomolecular Magnetic Resonance, Goethe University, 60438 Frankfurt am Main, Germany.
Jack H. Freed, Department of Chemistry and Chemical Biology, and ACERT, National Biomedical Center for Advanced Electron Spin Resonance Technology, Cornell University, Ithaca, New York 14853-1301, United States
Laura Galazzo, Faculty of Chemistry and Biochemistry, Ruhr University Bochum, 44801 Bochum, Germany.
Daniella Goldfarb, Department of Chemical and Biological Physics, Weizmann Institute of Science, Rehovot 76100, Israel.
Tobias Hett, Institute of Physical and Theoretical Chemistry, University of Bonn, 53115 Bonn, Germany.
Laura Esteban Hofer, Department of Chemistry and Applied Biosciences, ETH Hönggerberg, 8093 Zürich, Switzerland.
Luis Fábregas Ibáñez, Department of Chemistry and Applied Biosciences, ETH Hönggerberg, 8093 Zürich, Switzerland.
Eric J. Hustedt, Department of Molecular Physiology and Biophysics, Vanderbilt University, Nashville, Tennessee 37232, United States
Svetlana Kucher, Faculty of Chemistry and Biochemistry, Ruhr University Bochum, 44801 Bochum, Germany.
Ilya Kuprov, School of Chemistry, University of Southampton, Southampton SO17 1BJ, U.K..
Janet Eleanor Lovett, SUPA School of Physics and Astronomy and BSRC, University of St Andrews, St Andrews KY16 9SS, U.K..
Andreas Meyer, Max Planck Institute for Biophysical Chemistry, 37077 Göttingen, Germany.
Sharon Ruthstein, Department of Chemistry, Bar Ilan University, Ramat Gan 5290002, Israel.
Sunil Saxena, Department of Chemistry, University of Pittsburgh, Pittsburgh, Pennsylvania 15260, United States.
Stefan Stoll, Department of Chemistry, University of Washington, Seattle, Washington 98195, United States.
Christiane R. Timmel, Department of Chemistry, Centre for Advanced Electron Spin Resonance, University of Oxford, Oxford OX1 3QR, U.K.
Marilena Di Valentin, Department of Chemical Sciences, University of Padova, 35131 Padova, Italy.
Hassane S. Mchaourab, Department of Molecular Physiology and Biophysics, Vanderbilt University, Nashville, Tennessee 37232, United States
Thomas F. Prisner, Institute of Physical and Theoretical Chemistry and Center of Biomolecular Magnetic Resonance, Goethe University, 60438 Frankfurt am Main, Germany
Bela Ernest Bode, EaStCHEM School of Chemistry, Biomedical Sciences Research Complex, and Centre of Magnetic Resonance, University of St Andrews, St Andrews KY16 9ST, U.K..
Enrica Bordignon, Faculty of Chemistry and Biochemistry, Ruhr University Bochum, 44801 Bochum, Germany.
Marina Bennati, Max Planck Institute for Biophysical Chemistry, 37077 Göttingen, Germany.
Gunnar Jeschke, Department of Chemistry and Applied Biosciences, ETH Hönggerberg, 8093 Zürich, Switzerland.
REFERENCES
- (1).Todd AP; Cong J; Levinthal F; Levinthal C; Hubell WL Site-directed mutagenesis of colicin E1 provides specific attachment sites for spin labels whose spectra are sensitive to local conformation. Proteins: Struct., Funct., Genet 1989, 6, 294–305. [DOI] [PubMed] [Google Scholar]
- (2).Fanucci GE; Cafiso DS Recent advances and applications of site-directed spin labeling. Curr. Opin. Struct. Biol 2006, 16, 644–653. [DOI] [PubMed] [Google Scholar]
- (3).Shelke SA; Sigurdsson ST Site-Directed Spin Labeling of Nucleic Acids. Eur. J. Org. Chem 2012, 2012, 2291–2301. [DOI] [PubMed] [Google Scholar]
- (4).Bagryanskaya EG; Krumkacheva OA; Fedin MV; Marque SRA Development and Application of Spin Traps, Spin Probes, and Spin Labels. Methods Enzymol. 2015, 563, 365–396. [DOI] [PubMed] [Google Scholar]
- (5).Borbat PP; Freed JH Dipolar Spectroscopy – Single-Resonance Methods. In Encyclopedia of Magnetic Resonance; Harris RK, Wasylishen R, Eds.; John Wiley & Sons: Chichester, 2017; Vol. 6, pp 465–494. DOI: 10.1002/9780470034590.emrstm1519 [DOI] [Google Scholar]
- (6).Jeschke G. Dipolar Spectroscopy – Double-Resonance Methods. In Encyclopedia of Magnetic Resonance; Harris RK, Wasylishen R, Eds.;John Wiley & Sons: Chichester, 2016; Vol. 5, pp 1459–1475. DOI: 10.1002/9780470034590.emrstm1518 [DOI] [Google Scholar]
- (7).Jeschke G. DEER distance measurements on proteins. Annu. Rev. Phys. Chem 2012, 63, 419–446. [DOI] [PubMed] [Google Scholar]
- (8).Krstić I; Endeward B; Margraf D; Marko A; Prisner TF Structure and Dynamics of Nucleic Acids. Top. Curr. Chem 2011, 321, 159–198. [DOI] [PubMed] [Google Scholar]
- (9).Jeschke G; Koch A; Jonas U; Godt A Direct Conversion of EPR Dipolar Time Evolution Data to Distance Distributions. J. Magn. Reson 2002, 155, 72–82. [DOI] [PubMed] [Google Scholar]
- (10).Chiang Y-W; Borbat PP; Freed JH The determination of pair distance distributions by pulsed ESR using Tikhonov regularization. J. Magn. Reson 2005, 172, 279–295. [DOI] [PubMed] [Google Scholar]
- (11).Drescher M. EPR in Protein Science Intrinsically Disordered Proteins. Top. Curr. Chem 2011, 321, 91–119. [DOI] [PubMed] [Google Scholar]
- (12).Mchaourab HS; Steed PR; Kazmier K Toward the Fourth Dimension of Membrane Protein Structure: Insight into Dynamics from Spin-Labeling EPR Spectroscopy. Structure 2011, 19, 1549–1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Jeschke G. The contribution of modern EPR to structural biology. Emerging Top. Life Sci 2018, 2, 9–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Hett T; Zbik T; Mukherjee S; Matsuoka H; Bönigk W; Klose D; Rouillon C; Brenner N; Peuker S; Klement R; Steinhoff H-J; Grubmüller H; Seifert R; Schiemann O; Kaupp UB Spatiotemporal Resolution of Conformational Changes in Biomolecules by Combining Pulsed Electron-Electron Double Resonance Spectroscopy with Microsecond Freeze-Hyperquenching. J. Am. Chem. Soc 2021, 143, 6981–6989. [DOI] [PubMed] [Google Scholar]
- (15).Sale K; Song L; Liu YS; Perozo E; Fajer P Explicit treatment of spin labels in modeling of distance constraints from dipolar EPR and DEER. J. Am. Chem. Soc 2005, 127, 9334–9335. [DOI] [PubMed] [Google Scholar]
- (16).Polyhach Y; Bordignon E; Jeschke G Rotamer libraries of spin labelled cysteines for protein studies. Phys. Chem. Chem. Phys 2011, 13, 2356–2366. [DOI] [PubMed] [Google Scholar]
- (17).Spicher S; Abdullin D; Grimme S; Schiemann O Modeling of spin-spin distance distributions for nitroxide labeled bio-macromolecules. Phys. Chem. Chem. Phys 2020, 22, 24282–24290. [DOI] [PubMed] [Google Scholar]
- (18).Hagelueken G; Abdullin D; Schiemann O mtsslSuite: Probing biomolecular conformation by spin labeling studies. Methods Enzymol. 2015, 563, 595–621. [DOI] [PubMed] [Google Scholar]
- (19).Hilger D; Polyhach Y; Padan E; Jung H; Jeschke G High-resolution structure of a Na+/H+ antiporter dimer obtained by pulsed EPR distance measurements. Biophys. J 2007, 93, 3675–3683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Boura E; Różycki B; Chung HS; Herrick DZ; Canagarajah B; Cafiso DS; Eaton WA; Hummer G; Hurley JH Solution Structure of the ESCRT-I and -II Supercomplex: Implications for Membrane Budding and Scission. Structure 2012, 20, 874–886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Duss O; Michel E; Yulikov M; Schubert M; Jeschke G; Allain FH-T Structural basis of the non-coding RNA RsmZ acting as protein sponge. Nature 2014, 509, 588–592. [DOI] [PubMed] [Google Scholar]
- (22).Peter MF; Tuukkanen A; Heubach CA; Selsam A; Duthie F; Svergun GD; Schiemann O; Hagelueken G Studying conformational changes of the Yersinia type-III-secretion effector YopO in solution by integrative structural biology. Structure 2019, 27, 1416–1426. [DOI] [PubMed] [Google Scholar]
- (23).Park SY; Borbat PP; Gonzalez-Bonet G; Bhatnagar J; Pollard AM; Freed JH; Bilwes AM; Crane BR Reconstruction of the Chemotaxis Receptor-Kinase Assembly. Nat. Struct. Mol. Biol 2006, 13, 400–407. [DOI] [PubMed] [Google Scholar]
- (24).Timachi MH; Hutter CAJ; Hohl M; Assafa T; Böhm S; Mittal A; Seeger MA; Bordignon E Exploring conformational equilibria of a heterodimeric ABC transporter. eLife 2017, 6, e20236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Van Eps N; Caro LN; Morizumi T; Kusnetzow AK; Szczepek M; Hofmann KP; Bayburt TH; Sligar SG; Ernst OP; Hubbell WL Conformational equilibria of light-activated rhodopsin in nanodiscs. Proc. Natl. Acad. Sci. U. S. A 2017, 114, E3268–E3275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Barth K; Rudolph M; Diederichs T; Prisner TF; Tampe R; Joseph B Thermodynamic Basis for Conformational Coupling in an ATP-Binding Cassette Exporter. J. Phys. Chem. Lett 2020, 11, 7946–7953. [DOI] [PubMed] [Google Scholar]
- (27).Verhalen B; Dastvan R; Thangapandian S; Peskova Y; Koteiche HA; Nakamoto RK; Tajkhorshid E; Mchaourab HS Energy transduction and alternating access of the mammalian ABC transporter P-glycoprotein. Nature 2017, 543, 738–741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Dastvan R; Mishra S; Peskova YB; Nakamoto RK; Mchaourab HS Mechanism of allosteric modulation of P-glycoprotein by transport substrates and inhibitors. Science 2019, 364, 689–692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Kapsalis C; Wang B; El Mkami H; Pitt SJ; Schnell JR; Smith TK; Lippiat JD; Bode BE; Pliotas C Allosteric activation of an ion channel triggered by modification of mechanosensitive nanopockets. Nat. Commun 2019, 10, 4619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Berman HM; Adams PD; Bonvin AA; Burley SK; Carragher B; Chiu W; DiMaio F; Ferrin TE; Gabanyi MJ; Goddard TD; Griffin PR; Haas J; Hanke CA; Hoch JC; Hummer G; Kurisu G; Lawson CL; Leitner A; Markley JL; Meiler J; Montelione GT; Phillips GN; Prisner TF; Rappsilber J; Schriemer DC; Schwede T; Seidel CAM; Strutzenberg TS; Svergun DI; Tajkhorshid E; Trewhella J; Vallat B; Velankar S; Vuister GW; Webb B; Westbrook JD; White KL; Sali A Federating Structural Models and Data: Outcomes from A Workshop on Archiving Integrative Structures. Structure 2019, 27, 1745–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Jacques DA; Guss JM; Svergun DI; Trewhella J Publication guidelines for structural modelling of small-angle scattering data from biomolecules in solution. Acta Crystallogr., Sect. D: Biol. Crystallogr 2012, 68, 620–626. [DOI] [PubMed] [Google Scholar]
- (32).Trewhella J; Duff AP; Durand D; Gabel F; Guss JM; Hendrickson WA; Hura GL; Jacques DA; Kirby NM; Kwan AH; Perez J; Pollack L; Ryan TM; Sali A; Schneidman-Duhovny D; Schwede T; Svergun DI; Sugiyama M; Tainer JA; Vachette P; Westbrook P; Whitten AE Publication guidelines for structural modelling of small-angle scattering data from biomolecules in solution: an update. Acta Cryst. Sect. D-Struct. Biol 2017, 73, 710–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Kikhney AG; Borges CR; Molodenskiy DS; Jeffries CM; Svergun DI SASBDB: Towards automatically curated and validated repository for biological scattering data. Protein Sci. 2020, 29, 66–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Hellenkamp B; Schmid S; Doroshenko O; Opanasyuk O; Kühnemuth R; Adariani SR; Ambrose B; Aznauryan M; Barth A; Birkedal V; Bowen ME; Chen H; Cordes T; Eilert T; Fijen C; Gebhardt C; Götz M; Gouridis G; Gratton E; Ha T; Hao P; Hanke CA; Hartmann A; Hendrix J; Hildebrandt LL; Hirschfeld V; Hohlbein J; Hua B; Hübner CG; Kallis E; Kapanidis AN; Kim J-Y; Krainer G; Lamb DC; Lee NK; Lemke EA; Levesque B; Levitus M; McCann JJ; Naredi-Rainer N; Nettels D; Ngo T; Qiu R; Robb NC; Röcker C; Sanabria H; Schlierf M; Schröder T; Schuler B; Seidel H; Streit L; Thurn J; Tinnefeld P; Tyagi S; Vandenberk N; Vera AM; Weninger KR; Wünsch B; Yanez-Orozco IS; Michaelis J; Seidel CAM; Craggs TD; Hugel T Precision and accuracy of single-molecule FRET measurements – a multi-laboratory benchmark study. Nat. Methods 2018, 15, 669–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Shelke S; Sigurdsson S Site directed Nitroxide Spin Labeling of Biopolymers. Struct. Bonding (Berlin, Ger.) 2011, 152, 121–162. [Google Scholar]
- (36).Goldfarb D. Gd3+ spin labeling for distance measurements by pulse EPR spectroscopy. Phys. Chem. Chem. Phys 2014, 16, 9685–9699. [DOI] [PubMed] [Google Scholar]
- (37).Fleck N; Heubach CA; Hett T; Haege FR; Bawol PP; Baltruschat H; Schiemann O SLIM: A short-linked, highly redoxstable trityl label for high sensitivity in cell EPR distance measurements. Angew. Chem., Int. Ed 2020, 59, 9767–9772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Bertran A; Henbest KB; De Zotti M; Gobbo M; Timmel CR; Di Valentin M; Bowen AM Light-Induced Triplet-Triplet Electron Resonance Spectroscopy. J. Phys. Chem. Lett 2021, 12, 80–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Fleissner MR; Brustad EM; Kalai T; Altenbach C; Cascio D; Peters FB; Hideg K; Peuker S; Schultz PG; Hubbell WL Site-directed spin labeling of a genetically encoded unnatural amino acid. Proc. Natl. Acad. Sci. U. S. A 2009, 106, 21637–21642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Martin RE; Pannier M; Diederich F; Gramlich V; Hubrich M; Spiess HW Determination of End-to-End Distances in a Series of TEMPO Diradicals of up to 2.8 nm Length with a New Four-Pulse Double Electron Electron Resonance Experiment. Angew. Chem., Int. Ed 1998, 37, 2833–2837. [DOI] [PubMed] [Google Scholar]
- (41).Pannier M; Veit S; Godt A; Jeschke G; Spiess HW Deadtime free measurement of dipole–dipole interactions between electron spins. J. Magn. Reson 2011, 213, 316–325. [DOI] [PubMed] [Google Scholar]
- (42).Banham JE; Baker CM; Ceola S; Day IJ; Grant GH; Groenen EJJ; Rodgers CT; Jeschke G; Timmel CR Distance measurements in the borderline region of applicability of CW EPR and DEER: A model study on a homologous series of spin-labelled peptides. J. Magn. Reson 2008, 191, 202–218. [DOI] [PubMed] [Google Scholar]
- (43).Stein RA; Beth AH; Hustedt EJ A Straightforward Approach to the Analysis of Double Electron-Electron Resonance Data. Methods Enzymol. 2015, 563, 531–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Milov AD; Ponomarev AB; Tsvetkov YD Electron-electron double resonance in electron spin echo: Model biradical systems and the sensitized photolysis of decalin. Chem. Phys. Lett 1984, 110, 67–72. [Google Scholar]
- (45).Milov AD; Salikhov KM; Shirov MD Application of the double resonance method to electron spin echo in a study of the spatial of the spatial distribution of paramagnetic centers in solids. Fiz. Tverd. Tela 1981, 23, 975–982. [Google Scholar]
- (46).Jeschke G; Polyhach Y Distance measurements on spin-labelled biomacromolecules by pulsed electron paramagnetic resonance. Phys. Chem. Chem. Phys 2007, 9, 1895–1910. [DOI] [PubMed] [Google Scholar]
- (47).Polyhach Y; Bordignon E; Tschaggelar R; Gandra S; Godt A; Jeschke G High sensitivity and versatility of the DEER experiment on nitroxide radical pairs at Q-band frequencies. Phys. Chem. Chem. Phys 2012, 14, 10762–10773. [DOI] [PubMed] [Google Scholar]
- (48).Worswick SG; Spencer JA; Jeschke G; Kuprov I Deep neural network processing of DEER data. Sci. Adv 2018, 4, eaat5218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (49).Srivastava M; Freed JH Singular Value Decomposition Method to Determine Distance Distributions in Pulsed Dipolar Electron Spin Resonance. J. Phys. Chem. Lett 2017, 8, 5648–5655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (50).Srivastava M; Freed JH Singular Value Decomposition Method To Determine Distance Distributions in Pulsed Dipolar Electron Spin Resonance: II. Estimating Uncertainty. J. Phys. Chem. A 2019, 123, 359–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (51).Jeschke G; Chechik V; Ionita P; Godt A; Zimmermann H; Banham J; Timmel CR; Hilger D; Jung H DeerAnalysis2006 – A Comprehensive Software Package for Analyzing Pulsed ELDOR Data. Appl. Magn. Reson 2006, 30, 473–498. [Google Scholar]
- (52).Fábregas Ibáñez L; Jeschke G; Stoll S DeerLab: a comprehensive software package for analyzing dipolar electron paramagnetic resonance spectroscopy data. Magn. Reson 2020, 1, 209–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (53).Edwards TH; Stoll S A Bayesian approach to quantifying uncertainty from experimental noise in DEER spectroscopy. J. Magn. Reson 2016, 270, 87–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).Hustedt EJ; Marinelli F; Stein RA; Faraldo-Gomez JD; Mchaourab HS Confidence Analysis of DEER Data and Its Structural Interpretation with Ensemble-Biased Metadynamics. Biophys. J 2018, 115, 1200–1216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Berliner LJ; Grunwald J; Hankovszky HO; Hideg K A novel reversible thiol-specific spin label: Papain active site labeling and inhibition. Anal. Biochem 1982, 119, 450–455. [DOI] [PubMed] [Google Scholar]
- (56).Hubbell WL; Gross A; Langen R; Lietzow MA Recent advances in site-directed spin labeling of proteins. Curr. Opin. Struct. Biol 1998, 8, 649–656. [DOI] [PubMed] [Google Scholar]
- (57).Hubbell WL; López CJ; Altenbach C; Yang Z Technological advances in site-directed spin labeling of proteins. Curr. Opin. Struct. Biol 2013, 23, 725–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (58).Lee WL; Grimes JM; Robinson RC Yersinia effector YopO uses actin as bait to phosphorylate proteins that regulate actin polymerization. Nat. Struct. Mol. Biol 2015, 22, 248–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (59).Prehna G; Ivanov MI; Bliska JB; Stebbins CE Yersinia virulence depends on mimicry of host Rho-family nucleotide dissociation inhibitors. Cell 2006, 126, 869–880. [DOI] [PubMed] [Google Scholar]
- (60).Bode BE; Margraf D; Plackmeyer J; Dürner G; Prisner TF; Schiemann O Counting the Monomers in Nanometer Sized Oligomers. J. Am. Chem. Soc 2007, 129, 6736–6745. [DOI] [PubMed] [Google Scholar]
- (61).Keeley J; Choudhury T; Galazzo L; Bordignon E; Feintuch A; Goldfarb D; Eggeling A; Fabregas Ibanez L; Jeschke G; Kuprov I Neural networks in double electron-electron resonance: a practical guide. arXiv [physics.chem-ph] 2106.07465, submitted 14 Jun 2021; https://arxiv.org/abs/2106.07465 (accessed 24 Sep 2021). [Google Scholar]
- (62).Jeschke G. MMM: A toolbox for integrative structural modelling. Protein Sci. 2018, 27, 76–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Beasley KN; Sutch BT; Hatmal MM; Langen R; Qin PZ; Haworth IS Computer Modeling of Spin Labels: NASNOX, PRONOX, and ALLNOX. Methods Enzymol. 2015, 563, 569–593. [DOI] [PubMed] [Google Scholar]
- (64).Sameach H; Ruthstein S EPR Distance Measurements as a Tool to Characterize Protein-DNA Interactions. Isr. J. Chem 2019, 59, 980–989. [Google Scholar]
- (65).Georgieva ER; Roy AS; Grigoryants VM; Borbat PP; Earle KA; Scholes CP; Freed JH Effect of freezing conditions on distances and their distributions derived from Double Electron Electron Resonance (DEER): A study of doubly-spin-labeled T4 lysozyme. J. Magn. Reson 2012, 216, 69–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (66).Schmidt T; Jeon J; Okuno Y; Chiliveri SC; Clore GM Submillisecond Freezing Permits Cryoprotectant-Free EPR Double Electron–Electron Resonance Spectroscopy. ChemPhysChem 2020, 21, 1224–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Emmanouilidis L; Esteban-Hofer L; Damberger FF; de Vries T; Nguyen CKX; Fábregas Ibáñez L; Mergenthal S; Klotzsch E; Yulikov M; Jeschke G; Allain FH-T NMR and EPR reveal a compaction of the RNA-binding protein FUS upon droplet formation. Nat. Chem. Biol 2021, 17, 608–614. [DOI] [PubMed] [Google Scholar]
- (68).Grohmann D; Klose D; Klare JP; Kay CWM; Steinhoff H-J; Werner F RNA-Binding to Archael RNA Polymerase Subunits F/E: A DEER and FRET Study. J. Am. Chem. Soc 2010, 132, 5954–5955. [DOI] [PubMed] [Google Scholar]
- (69).Eaton SS; Eaton GR Relaxation Mechanisms. eMagRes. 2016, 5, 1543–1556. [Google Scholar]
- (70).Edwards DT; Huber T; Hussain S; Stone KM; Kinnebrew M; Kaminker I; Matalon E; Sherwin MS; Goldfarb D; Han S Determining the Oligomeric Structure of Proteorhodopsin by Gd3+-Based Pulsed Dipolar Spectroscopy of Multiple Distances. Structure 2014, 22, 1677–1686. [DOI] [PubMed] [Google Scholar]
- (71).Raitsimring AM; Salikhov KM; Umanski U; Tsvetkov YD The instantaneous diffusion of the ESE paramagnetic centers in solids. Fiz. Tverd. Tela 1974, 16, 756–763. [Google Scholar]
- (72).Dastvan R; Bode BE; Karuppiah MPR; Marko A; Lyubenova S; Schwalbe H; Prisner TF Optimization of Transversal Relaxation of Nitroxides for Pulsed Electron–Electron Double Resonance Spectroscopy in Phospholipid Membranes. J. Phys. Chem. B 2010, 114, 13507–13516. [DOI] [PubMed] [Google Scholar]
- (73).Canarie ER; Jahn SM; Stoll S Quantitative Structure-Based Prediction of Electron Spin Decoherence in Organic Radicals. J. Phys. Chem. Lett 2020, 11, 3396–3400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Huber M; Lindgren M; Hammarström P; Martensson LG; Carlsson U; Eaton GR; Eaton SS Phase memory relaxation times of spin labels in human carbonic anhydrase II: pulsed EPR to determine spin label location. Biophys. Chem 2001, 94, 245–256. [DOI] [PubMed] [Google Scholar]
- (75).Milov AD; Tsvetkov YD; Salikhov KM Phase relaxation of H-atoms stabilized in glassy matrices. Fiz. Tverd. Tela 1973, 15, 1187–1195. [Google Scholar]
- (76).El Mkami H; Ward R; Bowman A; Owen-Hughes T; Norman DG The spatial effect of protein deuteration on nitroxide spin-label relaxation: Implications for EPR distance measurement. J. Magn. Reson 2014, 248, 36–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (77).Schmidt T; Wälti MA; Baber JL; Hustedt EJ; Clore GM Long Distance Measurements up to 160 Å in the GroEL Tetradecamer Using Q-Band DEER EPR Spectroscopy. Angew. Chem., Int. Ed 2016, 55, 15905–15909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Pornsuwan S; Giller K; Riedel D; Becker S; Griesinger C; Bennati M Long-Range Distances in Amyloid Fibrils of -Synuclein from PELDOR Spectroscopy. Angew. Chem., Int. Ed 2013, 52, 10290–10294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Borbat PP; Ramlall TF; Freed JH; Eliezer D Inter-Helix Distances in Lysophospholipid Micelle-Bound alpha-Synuclein from Pulsed ESR Measurements. J. Am. Chem. Soc 2006, 128, 10004–10005. [DOI] [PubMed] [Google Scholar]
- (80).Endeward B; Butterwick JA; MacKinnon R; Prisner TF Pulsed Electron–Electron Double-Resonance Determination of Spin-Label Distances and Orientations on the Tetrameric Potassium Ion Channel KcsA. J. Am. Chem. Soc 2009, 131, 15246–15250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Riederer EA; Focke PJ; Georgieva ER; Akyuz N; Matulef K; Borbat PP; Freed JH; Blanchard SC; Boudker O; Valiyaveetil FIA Facile Approach for the In Vitro Assembly of Multimeric Membrane Transport Proteins. eLife 2018, 7, e36478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (82).Bleicken S; Jeschke G; Stegmueller C; Salvador-Gallego R; Garcia-Saez AJ; Bordignon E Structural Model of Active Bax at the Membrane. Mol. Cell 2014, 56, 496–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (83).Kattnig DR; Reichenwallner J; Hinderberger D Modeling Excluded Volume Effects for the Faithful Description of the Background Signal in Double Electron–Electron Resonance. J. Phys. Chem. B 2013, 117, 16542–16557. [DOI] [PubMed] [Google Scholar]
- (84).Yardeni EH; Mishra S; Stein RA; Bibi E; Mchaourab HS The Multidrug Transporter MdfA Deviates from the Canonical Model of Alternating Access of MFS Transporters. J. Mol. Biol 2020, 432, 5665–5680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Jeschke G; Sajid M; Schulte M; Godt A Three-spin correlations in double electron–electron resonance. Phys. Chem. Chem. Phys 2009, 11, 6580–6591. [DOI] [PubMed] [Google Scholar]
- (86).Larsen RG; Singel DJ Double electron–electron resonance spin–echo modulation: Spectroscopic measurement of electron spin pair separations in orientationally disordered solids. J. Chem. Phys 1993, 98, 5134–5146. [Google Scholar]
- (87).von Hagens T; Polyhach Y; Sajid M; Godt A; Jeschke G Suppression of ghost distances in multiple-spin double electron–electron resonance. Phys. Chem. Chem. Phys 2013, 15, 5854–5866. [DOI] [PubMed] [Google Scholar]
- (88).Junk MJN; Spiess HW; Hinderberger D DEER in biological multispin-systems: A case study on the fatty acid binding to human serum albumin. J. Magn. Reson 2011, 210, 210–217. [DOI] [PubMed] [Google Scholar]
- (89).Ackermann K; Pliotas C; Valera S; Naismith JH; Bode BE Sparse labeling PELDOR spectroscopy on multimeric mechanosensitive membrane channels. Biophys. J 2017, 113, 1968–1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (90).Weber A; Schiemann O; Bode B; Prisner TF PELDOR at S- and X-Band Frequencies and the Separation of Exchange Coupling from Dipolar Coupling. J. Magn. Reson 2002, 157, 277–285. [DOI] [PubMed] [Google Scholar]
- (91).Godt A; Schulte M; Zimmermann H; Jeschke G How Flexible Are Poly(para-phenyleneethynylene)s? Angew. Chem., Int. Ed 2006, 45, 7560–7564. [DOI] [PubMed] [Google Scholar]
- (92).Schiemann O; Cekan P; Margraf D; Prisner TF; Sigurdsson ST Relative Orientation of Rigid Nitroxides by PELDOR: Beyond Distance Measurements in Nucleic Acids. Angew. Chem., Int. Ed 2009, 48, 3292–3295. [DOI] [PubMed] [Google Scholar]
- (93).Endeward B; Butterwick JA; MacKinnon R; Prisner TF Pulsed electron-electron double-resonance determination of spin-label distances and orientations on the tetrameric potassium ion channel KcsA. J. Am. Chem. Soc 2009, 131, 15246–15250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (94).Hagelueken G; Ingledew WJ; Huang H; Petrovic-Stojanovska B; Whitfield C; El Mkami H; Schiemann O; Naismith JH PELDOR Spectroscopy Distance Fingerprinting of the Octameric Outer-Membrane Protein Wza from Escherichia coli. Angew. Chem., Int. Ed 2009, 48, 2904–2906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Baber JL; Louis JM; Clore GM Dependence of Distance Distributions Derived from Double Electron–Electron Resonance Pulsed EPR Spectroscopy on Pulse-Sequence Time. Angew. Chem., Int. Ed 2015, 54, 5336–5339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (96).Margraf D; Cekan P; Prisner T; Sigurdsson S; Schiemann O Ferro- and antiferromagnetic exchange coupling constants in PELDOR spectra. Phys. Chem. Chem. Phys 2009, 11, 6708–6714. [DOI] [PubMed] [Google Scholar]
- (97).Abdullin D; Brehm P; Fleck N; Spicher S; Grimme S; Schiemann O Pulsed EPR Dipolar Spectroscopy on Spin Pairs with one Highly Anisotropic Spin Center: The Low-Spin FeIII Case. Chem. - Eur. J 2019, 25, 14388–14398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (98).Bahrenberg T; Yang Y; Goldfarb D; Feintuch A rDEER: A Modified DEER Sequence for Distance Measurements Using Shaped Pulses. Magnetochemistry 2019, 5, 20. [Google Scholar]
- (99).Fajer MI; Li H; Yang W; Fajer PG Mapping Electron Paramagnetic Resonance Spin Label Conformations by the Simulated Scaling Method. J. Am. Chem. Soc 2007, 129, 13840–13846. [DOI] [PubMed] [Google Scholar]
- (100).Sarver JL; Townsend JE; Rajapakse G; Jen-Jacobson L; Saxena S Simulating the dynamics and orientations of spin-labeled side chains in a protein-DNA complex. J. Phys. Chem. B 2012, 116, 4024–4033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (101).Mchaourab HS; Lietzow MA; Hideg K; Hubbell WL Motion of Spin-Labeled Side Chains in T4 Lysozyme. Correlation with Protein Structure and Dynamics. Biochemistry 1996, 35, 7692–7704. [DOI] [PubMed] [Google Scholar]
- (102).Langen R; Oh KJ; Cascio D; Hubbell WL Crystal Structures of Spin Labeled T4 Lysozyme Mutants: Implications for the Interpretation of EPR Spectra in Terms of Structure. Biochemistry 2000, 39, 8396–8405. [DOI] [PubMed] [Google Scholar]
- (103).Abdullin D; Hagelueken G; Schiemann O Determination of nitroxide spin label conformations via PELDOR and X-ray crystallography. Phys. Chem. Chem. Phys 2016, 18, 10428–10437. [DOI] [PubMed] [Google Scholar]
- (104).Cunningham TF; Pornsuwan S; Horne WS; Saxena S Rotameric preferences of a protein spin label at edge-strand -sheet sites. Protein Sci. 2016, 25, 1049–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (105).Bordignon E; Steinhoff H-J Membrane Protein Structure and Dynamics Studied by Site-Directed Spin-Labeling ESR. Biol. Magn. Reson 2007, 27, 129–164. [Google Scholar]
- (106).Ritsch I; Esteban-Hofer L; Lehmann E; Emmanouilidis L; Yulikov M; Allain FH-T; Jeschke G Characterization of Weak Protein Domain Structure by Spin-Label Distance Distributions. Front. Mol. Biosci 2021, 8, 636599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (107).Tesei G; Martins JM; Kunze MBA; Wang Y; Crehuet R; Lindorff-Larsen K DEER-PREdict: Software for efficient calculation of spin-labeling EPR and NMR data from conformational ensembles. PLoS Comput. Biol 2021, 17, e1008551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (108).Kurzbach D; Platzer G; Schwarz TC; Henen MA; Konrat R; Hinderberger D Cooperative unfolding of compact conformations of the intrinsically disordered protein osteopontin. Biochemistry 2013, 52, 5167–5175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (109).Borbat PP; Surendhran K; Bortolus M; Zou P; Freed JH; Mchaourab HS Conformational Motion of the ABC Transporter MsbA Induced by ATP Hydrolysis. PLoS Biol. 2007, 5, 2211–2219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (110).Jarvi AG; Ghosh S; Bogetti X; Singewald K; Saxena S Going the dHis-tance: Site-Directed Cu2+ Labeling of Proteins and Nucleic Acids. Acc. Chem. Res 2021, 54, 1481–1491. [DOI] [PubMed] [Google Scholar]
- (111).Islam SM; Roux B Simulating the distance distribution between spin-labels attached to proteins. J. Phys. Chem. B 2015, 119, 3901–3911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (112).Lillington JED; Lovett JE; Johnson S; Roversi P; Timmel CR; Lea SM Shigella flexneri Spa15 crystal structure verified in solution by double electron electron resonance. J. Mol. Biol 2011, 405, 427–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (113).Corey RA; Ahdash Z; Shah A; Pyle E; Allen WJ; Fessl T; Lovett JE; Politis A; Collinson I ATP-induced asymmetric preprotein folding as a driver of protein translocation through the Sec machinery. eLife 2019, 8, e41803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (114).Jeschke G. MMM: Integrative ensemble modeling and ensemble analysis. Protein Sci. 2021, 30, 125–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (115).Marinelli F; Fiorin G Structural Characterization of Biomolecules through Atomistic Simulations Guided by DEER Measurements. Structure 2019, 27, 359–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (116).Puljung MC; DeBerg HA; Zagotta WN; Stoll S Double electron-electron resonance reveals cAMP-induced conformational change in HCN channels. Proc. Natl. Acad. Sci. U. S. A 2014, 111, 9816–9821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (117).Krug U; Alexander NS; Stein RA; Keim A; Mchaourab HS; Sträter N; Meiler J Characterization of the Domain Orientations of E. coli 5’-Nucleotidase by Fitting an Ensemble of Conformers to DEER Distance Distributions. Structure 2016, 24, 43–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.