Causal evidence for cholinergic stabilization of attractor landscape dynamics

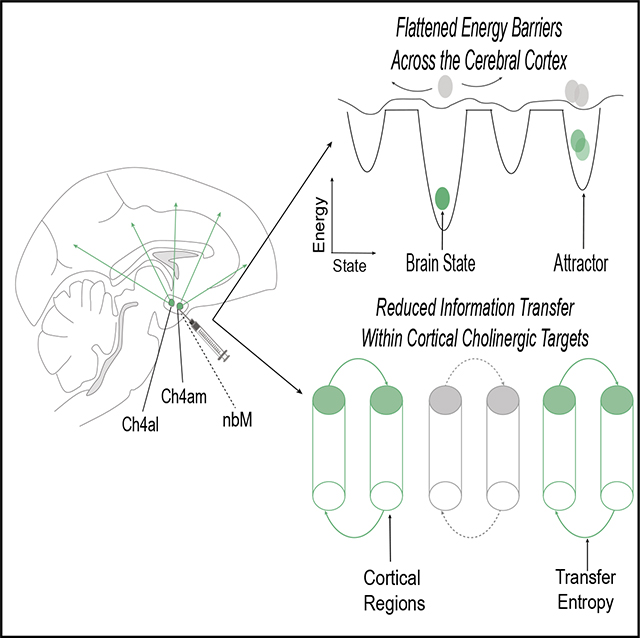
SUMMARY

There is substantial evidence that neuromodulatory systems critically influence brain state dynamics; however, most work has been purely descriptive. Here, we quantify, using data combining local inactivation of the basal forebrain with simultaneous measurement of resting-state fMRI activity in the macaque, the causal role of long-range cholinergic input to the stabilization of brain states in the cerebral cortex. Local inactivation of the nucleus basalis of Meynert (nbM) leads to a decrease in the energy barriers required for an fMRI state transition in cortical ongoing activity. Moreover, the inactivation of particular nbM sub-regions predominantly affects information transfer in cortical regions known to receive direct anatomical projections. We demonstrate these results in a simple neurodynamical model of cholinergic impact on neuronal firing rates and slow hyperpolarizing adaptation currents. We conclude that the cholinergic system plays a critical role in stabilizing macroscale brain state dynamics.

In brief

Taylor et al. found that the cholinergic system is important for stabilizing brain state dynamics, which builds upon a body of work emphasizing the importance of the ascending arousal system in modulating global brain state reconfigurations.

Graphical abstract

INTRODUCTION

Individual neurons in the cerebral cortex each have a vast number of structural connections, yet their firing patterns remain relatively flexible and context dependent across multiple time-scales.^1–3 A popular means for characterizing these complex patterns is to use statistical techniques that estimate a low-dimensional state-space,^4–7 which is a statistical approximation that permits the identification of brain states and the transitions between them.^5,8–10 Within this state-space perspective, brain dynamics form smooth trajectories that tend toward locations, known as “attractors,” that appear as deepened “wells” along a distributed attractor landscape (Figure 1A). Through this lens, the computations required for perception, cognition, and action are proposed to emerge through the realization of specific trajectories across the attractor landscape.⁷

Figure 1. The cholinergic system deepens attractor landscapes.

(A) Graphical representation of the effects of acetylcholine (ACh) on facilitating attractor landscape topography, in which brain states are particular locations in a low-dimensional state space. Neuromodulatory neurotransmitters are proposed to alter the topography of the landscape;^11,12 specifically, ACh has been linked to the deepening of attractors.¹³

(B) Sagittal graphical representation of a macaque brain with nbM subnuclei projection patterns (Ch4_AM and Ch4_AL) with inhibition injection from muscimol.

(C) Time series extracted from symmetric ROIs following inactivation of the left nbM (recreated from original Turchi et al. data).

(D) Graphical representation of the influence of the cholinergic system on MSD and “activation energy” required to move; given that ACh acts to deepen the wells of the attractors and stabilize brain states, we predict that inhibition of the nbM will lead to a relative flattening of the energy landscape estimated from fMRI data.

By way of analogy, we can conceptualize brain states evolving across an attractor landscape as a ball rolling along a hilly landscape (Figure 1A); the ball can easily roll across the landscape if the topography is relatively flat, whereas the ball could get “stuck” within a deepened well.^4,13 This approach affords a low-dimensional (topographic) representation of systems-level neural dynamics (Figure 1C). Extending the analogy, transitions to different brain states can be operationalized as the “activation energy” required to reach a particular state; e.g., the amount of energy that would need to be exerted to move a ball from one location to another along a hilly landscape (Figure 1A). Importantly, there are robust ways to quantify the amount of energy required to transition to a brain state; i.e., by calculating the inverse log probability of the likelihood of a particular transition at a given delay in time (Figure 1A). In this instance, energy is a descriptive term that does not refer to the metabolic energy required to enact a transition to a different brain state but rather describes the likelihood of a brain state occurring. Deep wells in the attractor landscape designate stable brain states, whereas a relatively flat landscape is associated with relatively easy shifting between states.

In previous work, we used this approach to confirm a theoretical prediction;¹⁴ namely, that the topography of the attractor landscape estimated from human resting-state fMRI data should be differentially modulated by distinct arms of the ascending neuromodulatory arousal system.^13,14 Specifically, we showed that peaks in blood flow within the noradrenergic locus coeruleus were followed by a relative flattening of the attractor landscape,¹³ whereas peaks in blood flow within the cholinergic nucleus basalis of Meynert preceded deepening of the attractor landscape.¹³ While these results were well matched to the cognitive capacities typically linked to these two neuromodulatory systems,^15–19 the results were inherently descriptive. A more powerful test of our hypothetical framework requires causal intervention (Figure 1B), with the prediction that inhibition of the neuromodulatory system should shift the topography of the attractor landscape toward the opposite extreme (Figure 1D).

RESULTS

The cholinergic nucleus basalis of Meynert causally alters attractor landscape topography

To test for causal evidence of cholinergic attractor deepening, we leveraged macaque (n = 2) fMRI recordings in which the nucleus basalis of Meynert (nbM) was reversibly inactivated by unilateral injection of muscimol (agonist of GABA_A receptors) into two different sub-regions: either Ch4_AM (a subdivision of the nbM that contains magnocellular cholinergic cells that innervate medial cortical regions) or Ch4_AL (a subdivision of the nbM with projections to the lateral cortex and visual areas; Turchi et al.). Sham trials in which no injections were performed were used as controls. Following injections (or sham trials), fMRI (cerebral blood volume) signals were recorded across the whole brain (the primary results of this study were published in Turchi et al.²⁰), allowing us to quantify changes in brain state associated with cholinergic inhibition. In the original study, nbM inhibition caused a reduction in intra-hemispheric signal amplitude, with only minimally altered functional connectivity patterns observed at the whole brain level.²⁰ However, the original analyses were limited to zero-lagged coordination between brain regions, whereas the attractor landscape perspective is concerned with how brain states change over short windows of time, not the overall, time-averaged behavior of the system per se, suggesting that the two signatures might co-exist in the same data.

To test whether cholinergic inhibition flattened energy barriers, we required a means to characterize the dynamics of brain state transitions. Based on previous work,¹³ we estimated the amount of brain state change (mean-squared displacement [MSD] in 266 cortical region of interest [ROI] fMRI time series) for a series of pre-defined temporal delays (repetition time [TR]) at 30 randomly spaced points across the time series (results were replicated with 10–100 random time points). We next calculated the likelihood that each brain state occurred by estimating the probability of signal displacement at a specific time lag. We then estimated the energy of each brain state transition as the natural logarithm of the inverse probability of each brain state occurring at a particular displacement and temporal delay. In this framework, highly likely changes in fMRI signal correspond to lower-energy transitions.

Based on previous theoretical¹⁴ and empirical¹³ work, we predicted that inhibiting the nbM would impair the ability to deepen attractor wells (Figures 1D). That is, the attractor landscape should become “flatter” following nbM inhibition, in that it will become easier for the brain to shift into new states and not remain “stuck” in its previous configurations. Despite a lack of significant differences in zero-lagged inter-regional correlations (all p > 0.05; STAR Methods; i.e., replicating the main result in Turchi et al.), we confirmed our hypothesis that inhibition of the nbM was associated with a decrease in energy barrier for large brain state transitions later in time relative to control scans (significant across all time bins except for TR = 6–7, MSD = 2; Figure 2A). In contrast to the intra-hemispheric effects observed in the original study,²⁰ attractor landscape flattening was apparent in both hemispheres, irrespective of the hemisphere in which the nbM was inhibited (Figure S1), and also across inhibition sites in both monkeys (Figure S2), suggesting that the observed effects in attractor landscape topography may relate both to the primary effect of nbM inhibition as well as compensatory effects that can enact inter-hemispheric changes,¹⁴ such as interhemispheric non-cholinergic projections between nbM cells,²¹ compensatory activation of other neuromodulatory systems,^13,22–24 or a drop in bilateral inter-hemispheric cortical projections; however, the precise mechanism is outside the scope of this study.

Figure 2. Lesions of the cholinergic nbM lead to energy landscape flattening.

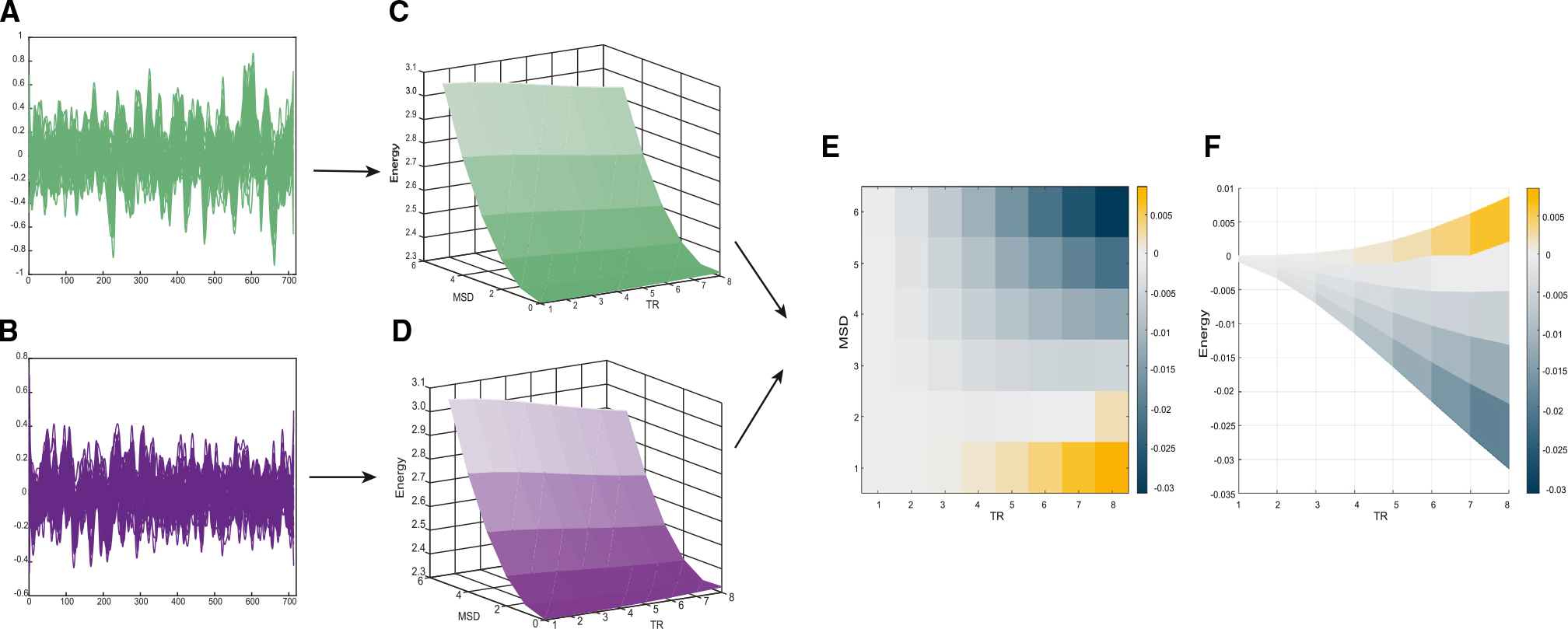
(A) Plot of an example time series across control sessions for both monkeys for 50 regions.

(B) Plot of an example time series across inhibition sessions for both monkeys for 50 regions.

(C) Plot of the average (both monkeys) attractor landscape (changes in fMRI signal activity being measured in relation to MSD value and time represented by TRs) during no inhibition.

(D) Plot of the average (both monkeys) attractor landscape (changes in fMRI signal activity being measured in relation to MSD value and time represented by TRs) during nbM inhibition.

(E) 2D plot of the average difference (of both monkeys) in attractor landscape (changes in fMRI signal activity being measured in relation to MSD value and time represented by TRs) between the nbM being inhibited vs. no inhibition; significantly (p < 0.05, paired t test) different MSD energy values are represented on the colored 2D plot beneath the difference in the attractor plot.

(F) 2D plot of the average difference (both monkeys) in attractor landscape between the nbM inhibition versus no inhibition; energy is represented on the y axis, with the time represented on the x axis (across all MSD). Differences in MSD energy are represented on the color bar.

To quantify the level of “flatness” in the attractor landscape, we calculated the gradient of the topography following nbM inhibition and control conditions. Due to the complex topography of the landscapes, results were represented as a difference in slopes per MSD and TR bin, which we then plotted onto an array (Figure S4). Inhibiting the nbM led to a marked reduction in the slope of the landscape following cholinergic inhibition compared to the control conditions (p < 0.05, permutation tested). These effects were particularly evident at medium-to-long delays (TR = 2–8, 9.7 × 10⁻³ ± 9.1 × 10⁻³ vs. 8.3 × 10⁻³ ± 7.1 × 10⁻³), with maximal slope reduction at MSD = 6 and TR = 8 s. We confirmed that these results were not due to chance by permuting data labels 5,000 times to estimate a null distribution; differences in landscape topography were considered significant if the original differences (between stimulation and sham) were more extreme than 99.9% of the null distribution. Our results therefore provide causal evidence of the hypothesis that cholinergic projections to the cerebral cortex from the nbM deepen energy wells in an attractor landscape representing brain state transitions, potentially by facilitating inter-regional communication between target regions.^13,14

Cholinergic inhibition interrupts information flow between cholinergic projection targets

The prediction that cholinergic mechanisms should deepen attractors is based in part on the relatively segregated (as opposed to diffuse) projections from the nbM to the cerebral cortex.¹⁴ That is, cholinergic axons from each nbM subnucleus project to a distributed, but constrained, set of regions that differs according to each nbM subnucleus;¹⁵ the Ch4_AL projects to the primary visual cortex, anterior auditory association cortex, and medial pre-frontal cortex (among others), whereas the Ch4_AM projects to the retrosplenial cortex, secondary somatosensory cortex, and subgenual cingulate cortex (among others; Figure 3A). As a specific sub-division of the nbM becomes active, the release of acetylcholine (ACh) to this set of regions should augment ongoing glutamatergic signaling in those targeted regions, particularly when considered relative to the remaining (non-targeted) regions that presumably did not receive a cholinergic boost in the same window. A key prediction is thus that communication between the cortical targets of nbM sub-regions should be selectively impaired during inhibition, relative to pairs of regions that are not within the downstream projections of the specific subnucleus of the nbM.

Figure 3. Decreased information transfer between targets of lesioned cholinergic projections.

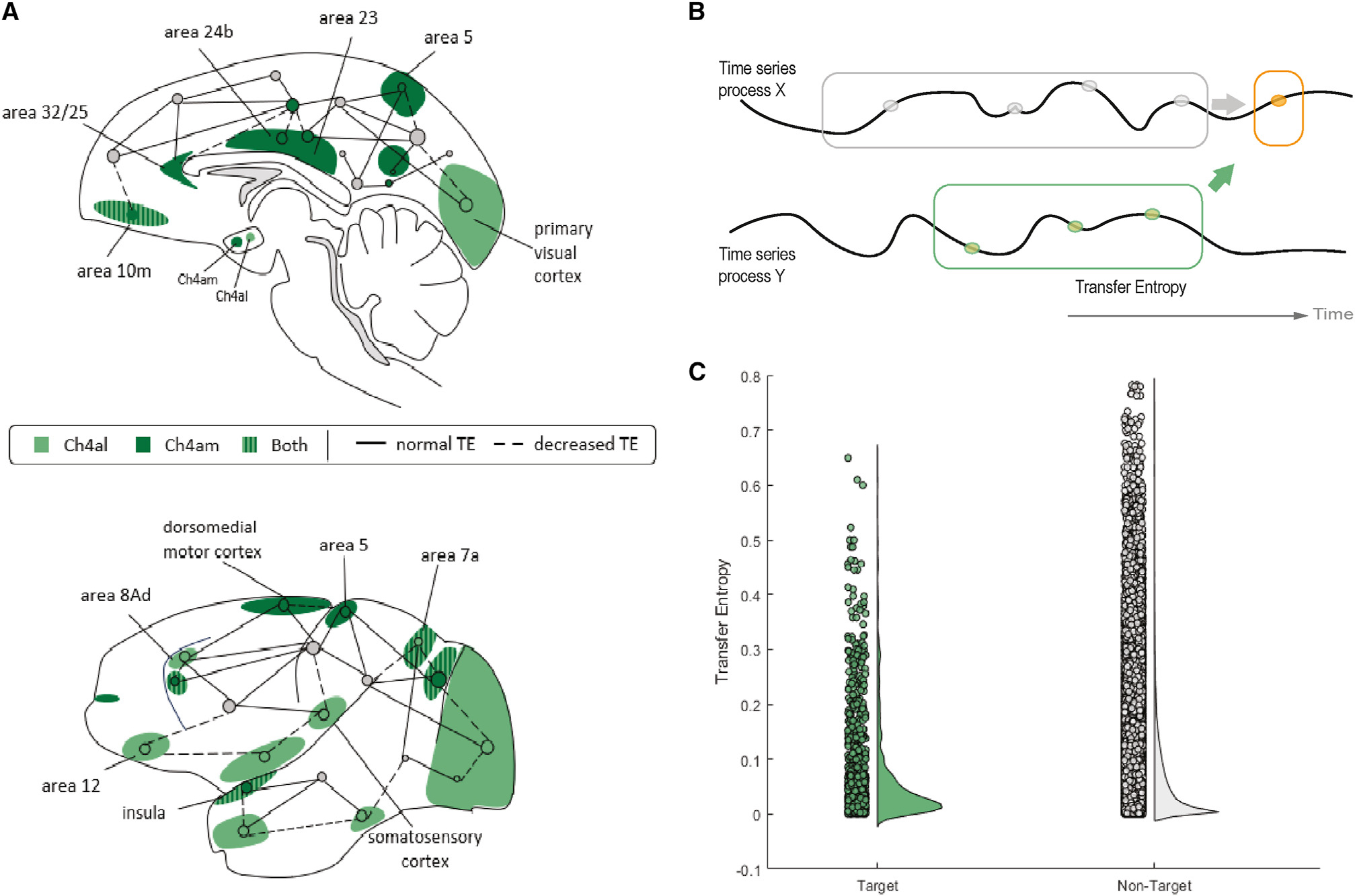
(A) Midline and lateral sagittal graphical representation of the distinct regions to which the Ch4_AL and Ch4_AM sub-regions of the nucleus basalis of Meynert (nbM) project, with dashed lines representing the regions that had a relative decrease in TE between other regions in the brain (p < 0.05, paired t test).

(B) Graphical representation of information theoretical analysis; TE (orange arrow) describes information on the next instance ${\mathrm{X}}_{\mathrm{n}+1}$ (gray) of a target region that is provided by the past (${\mathrm{Y}}_{\mathrm{n}+1}$, orange) of another time series Y in the context of the target’s history.

(C) Decreased TE between pairs of regions with targeted projections from Ch4_AL and Ch4_AM when compared to pairs not targeted by Ch4_AL and Ch4_AM [gray dots] (p = 0.0216, paired t test).

To test this hypothesis, we required a term that tracked inter-regional coupling while also accounting for time delays. To achieve this aim, we employed a technique from information theory, transfer entropy (TE), to estimate the amount of information flow between pairs of regions.²⁵ Briefly, TE models the “information” transferred from a source process Y to the updates of a target process X by estimating the amount of information Y provides about the next state in the future of X in the context of the targets’ past (Figure 3B). Using the Java Information Dynamics toolkit (JIDT),²⁶ TE is calculated as the expected mutual information from realizations of the source process Y over a delay u to a given target process X, conditional on the past of the target. In this way, TE can be calculated between all pairs of cortical time series for each source and target region.

As predicted, we found that GABAergic inhibition of the nbM led to a smaller relative TE between regions that were within each nbM sub-region’s projection targets, relative to pairs of regions outside the projections of each nbM sub-region (p = 0.0216; Figure 3C). This indicates that regions that are innervated by the nbM cannot interact with one another during epochs of inhibition of the nbM and thus refines the causal evidence for the role of the nbM in mediating dynamic brain state reconfigurations^13,24 (see Figure S2 for additional comparisons).

Cholinergic modulation of the neural mass model drives deepened attractors

To further demonstrate the dynamical basis of our hypothesis for the action of ACh on stabilizing attractor landscapes while retaining pairwise correlations (original Turchi et al. results), we constructed a minimal dynamical system capable of reproducing the primary outcomes observed across both studies. The model consisted of two mutually inhibiting Wilson-Cowan-like²⁷ neural masses (Figure 4) modulated by adaptation and excitability. The dynamics consisted of noisy excursions around two stable fixed points separated by a saddle node with occasional noise-driven jumps between fixed points (STAR Methods). We tuned the adaptation variable so that it narrowed the basin of attraction of each fixed point but did not lead to a bifurcation; i.e., conserved the stability of all fixed points.

Figure 4. Computational evidence for cholinergic deepening of attractor wells.

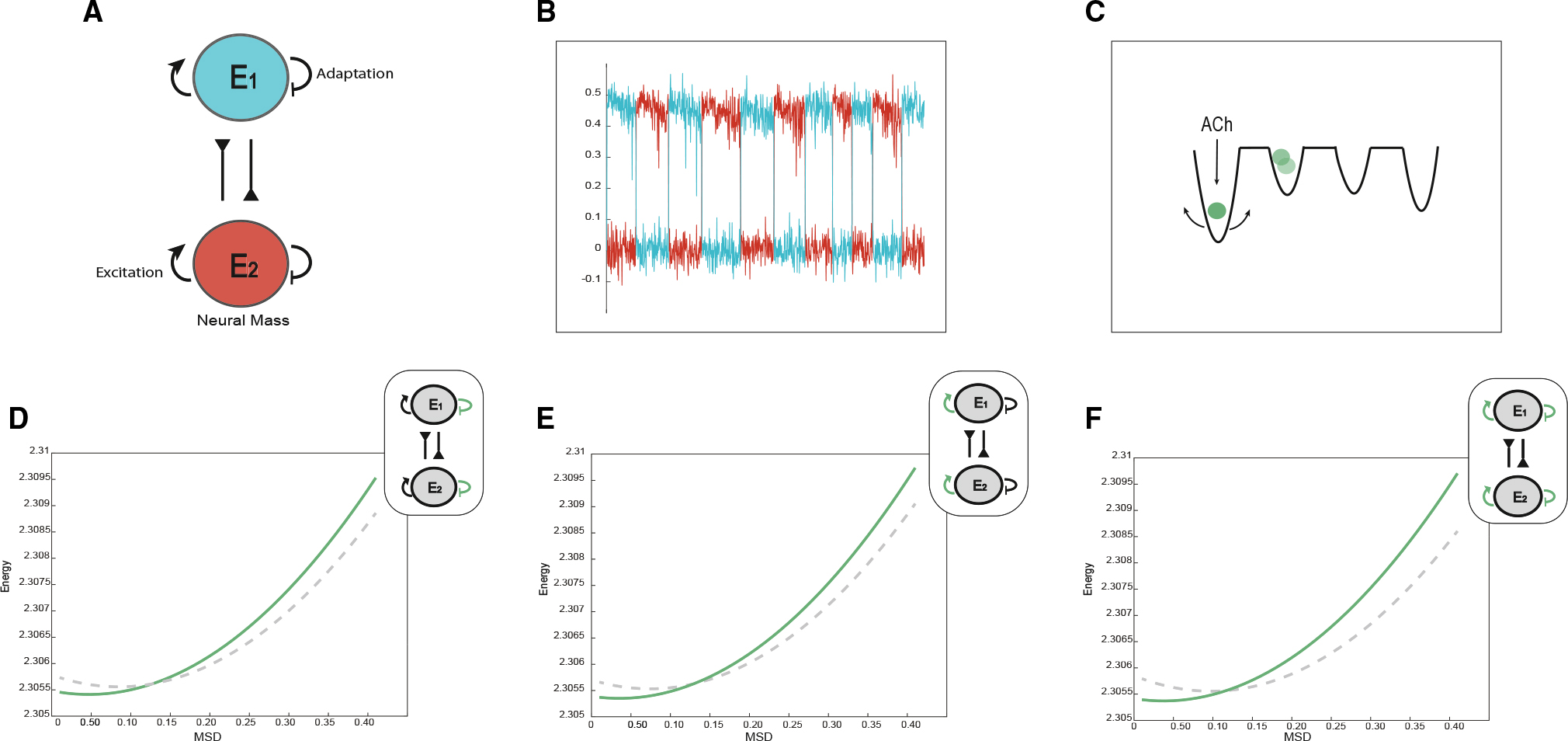
(A) Graphical representation of the neural mass model with adaptation manipulation.

(B) Plot of the down-sampled time series of the two neural mass populations.

(C) Graphical representation of role of the cholinergic system in facilitating deepened attractor landscapes.

(D) A plot of attractor landscape averaged across time as adaptation is decreased (the dashed line represents d = 0.25, and green represents d = 0.05).

(E) A plot of attractor landscape averaged across time as excitability is increased (the dashed line represents a = 0.9, and green represents a = 1.1).

(F) A plot of attractor landscape averaged across time as excitability is increased and adaptation is decreased (the dashed line represents a = 0.9, d = 0.25, and green represents a = 1.1, d = 0.05).

To model the action of ACh on these neural masses, we simulated two complimentary impacts of ACh on neural dynamics. The first effect involved a reduction in adaptation, which was intended to mimic the closure of hyperpolarizing potassium channels²⁸); the second increased the excitability of targeted neurons, leading to greater inhibition through the mutual inhibitory connections of the competing neural masses, a process akin to cholinergic divisive normalization.^29–31 Specifically, to model adaption, we reduced the contribution of the firing rate to the accumulation of adaptation (from d = 0.25 [Figure 4D, gray] to d = 0.05 [Figure 4D, green]), which led to elongated dwell times. To model excitability, we implemented a simple form of divisive normalization by increasing the excitability of both masses (from a = 0.9 [gray] to a = 1.1 [green]; Figure 4F), which, through the (mutual) inhibitory connections between nodes, effectively led to greater inhibition of the competing mass whose strength scaled with the firing rate of the first node.

To demonstrate the utility of our attractor landscape framework, we subjected the time series outputs of our simple model to the same analysis used in the macaque resting state fMRI data. In keeping with our proposed mechanism, heightened cholinergic input led to a deepened and stabilized attractor landscape. The effect was consistent for both reduced adaptation and heightened excitability, suggesting that the main effect of ACh is to deepen the resultant energy landscape, making each fixed point more robust to adaptation. Consistent with the simultaneous impact of both reduced adaptation and increased excitability, the combination of reducing adaptation and increasing excitability (d = 0.25 and a = 0.9 [gray], d = 0.05 and a = 1.1 [green]; Figure 4H) also led to a similar deepening in attractor landscape topography. By direct implication, blocking ACh would have the opposite effect; i.e., flattening the energy barrier between attractors. Importantly, these effects were all evident despite no change in the zero-lagged correlation between the time series of the masses. Therefore, we conclude that this simply mechanistic model of ACh is able to permit both the key result of our study (namely, weakened attractor stability) while also recapitulating the main effect observed in the original study.²⁰

DISCUSSION

In this study, we demonstrated causal evidence that the cholinergic system stabilizes macroscopic brain states, as direct GABAergic inhibition of the cholinergic system drove a flattening of the brain’s attractor landscape. We then mechanistically validated this finding in a bistable neural mass model. These results support previous work showing that phasic bursts in the cholinergic nbM lead to a deepened energy landscape (Figure 2). Together, our results advance our understanding of how the cholinergic forebrain constrains the formation of the brain state dynamics that form the basis of cognitive and affective brain states.^8,11

The cholinergic system exhibits complex topographical projections to distributed sets of cortical populations, with the degree of overlap dependent upon the overall interconnectivity among the same cortical regions.^15,32 The dynamic topological sequelae of this organization are directly illustrated by our demonstration of a decrease in information flow (quantified using TE) among areas that are innervated by the nbM (Figure 3).³³ Without the cholinergic system innervating these specific areas, the impact of incoming signals from other surrounding areas (i.e., “noise”) will likely have a greater influence, resulting in a decrease in shared information (i.e., information flow) between these specific areas. Thus, this result clarifies the role of the cholinergic system in facilitating complex and adaptive communication within segregated networks in the cerebral cortex.

To demonstrate the mechanistic validity of our hypothesis, we constructed a simple bistable neural mass model^27,34 of the cholinergic deepening of the attractor landscape (Figure 4). Based on a wide array of cellular neuroscience findings, we proposed that the cholinergic system deepens the macroscale attractor landscapes through the closure of the slow hyperpolarizing potassium channels responsible for adaptation²⁸ and through increasing the excitability of neurons, which, through the action of mutual inhibition, had an effect akin to divisive normalization.^29–31 These effects modeled the action of the cholinergic reduction of adaptation for each mass, which, in turn, resulted in elongated dwell times. These changes can be understood in terms of attractor landscape as the increasing energy barrier separating the two stable fixed points (Figure 4), an effect that was replicated by increasing the excitability of each neural population and reducing adaptation and increasing excitability in tandem. Importantly, these dynamics occurred in the context of unaltered zero-lag correlations between nodes (by construction). In this way, we were able to create a simple model that recapitulated both our results and those of the original study.²⁰ We therefore conclude that the cholinergic system is causally related to deepened energy wells within the context of attractor landscapes defined on whole-brain functional neuroimaging data. It is important to note that, while we proposed a microcircuit mechanism for the cholinergic system facilitating deepen attractor landscapes, we attempted to explicate the microcircuit mechanism through the lens of a neural mass model, which incorporates an average neural population activity. As such, the precise mechanism relating to blood-oxygen-level-dependent-related changes observed in fMRI is underdetermined. Whether similar signatures will occur when interrogating the brain in finer detail, such as in layer-specific or cell-type-specific brain networks, remains an important open question for future experiments.

Given the complex and diverse impacts of the cholinergic system, the precise microcircuit properties that mediate these cholinergic effects remain somewhat enigmatic, and often we rely upon inferred measures of brain activity that have been linked to cholinergic modulation to explicate its mechanisms of actions. For instance, divisive normalization^29–31 and temporal prolongation^35,36 are measures that have been extensively linked to cholinergic modulation. We now briefly detail the role of ACh in each of these computational signatures.

Normalization arises when the amount of inhibition within a population of cells is proportional to the total activity in the population, so that, if the excitability of one subset of a population is increased, the others receive greater inhibition.³⁷ This process has been suggested as a neural mechanism of focused attention.³⁷ ACh has been shown to facilitate normalization by heterogeneous cholinergic receptor expression, which both promotes excitability in one cortical layer and inhibits interneurons, causing nonlinear integration of output neural activity.^38,39 While not entirely equivalent, we proposed that increasing excitability in subsets of neural populations (exemplified in our model through a microscale mechanism) would likely be an interpretable microcircuit mechanism that underlies cortical normalization.

Temporal prolongation instead refers to the augmentation of the intrinsic timescale of cortical neurons; i.e., the stabilization of cortical activity. Through the prolongation of NMDA dendritic spike generation, which shifts cortical pyramidal neurons into a “sustained depolarized state,” ACh is thought to facilitate shortening of membrane time constants, which further tunes temporal discrimination across distant synaptic inputs.^35,36,40,41 In practice, temporal prolongation and normalization are likely inter-related in that any modulatory input that drives stabilization through either influencing the temporal scale of activity and/or the balance of excitation/inhibition (normalization) would lead to a stable attractor; which we have evidenced both through our experimental findings and our neural mass model.

Given the proposed importance of the cholinergic system in cognitive and adaptive behaviors,^42–46 it is important that we design future experiments that investigate the interactions between the selective cholinergic manipulations in the nbM and sustained focus within cognitively challenging tasks^47,48 as well as the encoding of contents into episodic memory.⁴³ Based upon our findings, we anticipate that specific task-relevant networks (such as the ventral attention⁴⁹ and default networks⁵⁰) will be supported by patterns of cholinergic innervation and, thus, that these sub-networks should be recruited in distinct cognitive scenarios. Future work should attempt to characterize the distinct cognitive capacities in manipulating cholinergic tone so as to determine whether there are specific overlapping circuits that facilitate these different capacities.

Limitations of the study

The proposed mechanism of cholinergic attractor landscape deepening requires further interrogation through additional empirical experiments and more sophisticated computational modeling approaches. For instance, a potential limitation of our approach is that there are heterogeneous groups of cells within the nbM, each of which could have also been inactivated through muscimol injection, resulting in interaction of cholinergic and glutamatergic inhibition that could cloud the interpretation of our results.²⁰ This concern could be mitigated by using more precise causal approaches, such as opto- or chemogenetics, that target specific populations of cells within a target region. In addition, there are other compensatory neuromodulatory mechanisms that could be contributing to the results of this study, and future work should attempt to modulate the multiple arms of the neuromodulatory system to further explicate their combined role in brain dynamics. To this end, more nuanced computational models would allow us to consider the influence of normalization and prolongation at a more fine-grained scale by building a model that incorporates the cellular structural complexity of a range of different cholinergic receptors,^47,51,52 layer-specific modulation,^47,53–55 and the summation of the cholinergic systems’ influence across these heterogeneous layer-specific modulations. Given the heterogeneity of receptor expression across the neuroaxis, there is reason to expect that the impact of ACh on neural dynamics may be similarly heterogeneous.^30,38,56 Ultimately, we anticipate that models with these features will provide more robust fits to electrophysiological and functional neuroimaging data than simplified models, particularly in cognitive contexts that recruit cholinergic engagement.

In conclusion, we provided causal evidence of the cholinergic system mediating deep-well attractor landscapes in brain state shifts. Our findings build upon a body of work highlighting the importance of the ascending arousal system in modulating global brain state reconfigurations.^{2,13,14,24,57} They further emphasize the importance of considering the influence of neuromodulatory systems in adaptive neural reconfigurations and their implication for overall brain function.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, A/Prof. James M. Shine (mac.shine@sydney.edu.au).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• All fMRI data recorded is accessible upon reasonable request from the lead contact. All neural mass model data is available within the following repository, https://doi.org/10.5281/zenodo.11324156

• All original code is publicly available through the following repository, https://doi.org/10.5281/zenodo.11324156

• Any additional information required to reanalyse the data reported in this work paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS

Guidelines established by the Institute of Animal Research and approved by the National Institute of Mental Health (NIMH) Animal Care and Use Committee, were followed for all experimental procedures.

Two female rhesus monkeys (Macaca mulatta, 4–5 years old, 4.5–5.5-kgs at start of experiment) participated in the study. Both participants were socially housed, with a different female conspecific companion, in light (fixed 12hr light/dark cycle), humidity and temperature-controlled rooms. They received meals of nuts, fruits, and primate chow, and had access to water (ad libitum). Their healthy was consistently monitored by veterinary staff.

METHOD DETAILS

MRI acquisitions

We acquired an existing dataset of two macaque monkeys that had unilateral injections of muscimol (agonist of GABA_A receptors, with 18mM–44mM, 1.8–2.46 μL) into either Ch4_AM (centered on anterior-medial cluster of Ch4_AM) or Ch4_AL (targeted lateral regions of the Ch4_AL); with no manipulation as controlled trials. The two monkeys underwent resting-state functional MRI scanning across the whole brain (we were provided with a sub-sample two monkeys, 21 scans of unilateral inactivation of Ch4_AM (MonkeyF, left hemisphere 11 scans) and 33 scans of unilateral inactivation of Ch4_AL (MonkeyZ, left hemisphere 15 scans), further 20 scans of no injection for control), obtaining cerebral blood volume as fMRI signal (4.7T/60cm vertical scanner, custom-built transmit-receiver RF coil, functional MRI acquired with EPI, TR = 2.5s, TE = 14ms, voxel = 1.5mm isotropic, 42 sagittal slices, FOV = 96mm, each scan acquisition of 30mins; the primary results of this study were published in Turchi et al. 2018). All fMRI scans underwent standardized pre-processing from Turchi et al., 2018 methods; which included slice-timing correction, correction of magnetic field inhomogeneities, motion co-registration, 2mm spatial smoothing, skull-stripping and removal of the first seven time frames of the time-series (AFNI/SUMA package https://afni.nimh.nih.gov/afni), regions of interest were defined through the anatomical parcellation D99 atlas.⁵⁸

Brain-state attractor landscape analysis

In order to evaluate the changes of fMRI signal activity in relation to inhibition of the nbM, we utilised the approach introduced in Munn et al., 2021 (code for this analysis available https://doi.org/10.5281/zenodo.11324156). Briefly, this approach estimates the likelihood that a given brain state ${\mathrm{x}}_{{\mathrm{t}}_0}$ will changes into another distinct brain state ${\mathrm{x}}_{{\mathrm{t}}_0+\mathrm{t}}$, within a given time window $\mathrm{t}$. We inferred the attractor landscape by examining the likelihood of changes in the instantaneous fMRI signal (brain-state) for a given temporal delay (TR = repetition time) for each of 266 cortical ROIs at 30 random, equally-spaced starting time-points across the timeseries. Changes in fMRI signal were quantified using the fMRI signal mean-squared displacement (MSD) across varying time-lags $\mathrm{t}$ (30 randomly spaced start points). First, we calculated the mean squared displacement (MSD), which measures the average $<{>}_{\mathrm{r}}$ deviation of the signal activity for $\mathrm{r}$ nodes

$${\mathrm{M}\mathrm{S}\mathrm{D}}_{\mathrm{t},{\mathrm{t}}_0}={⟨{\left|{\mathrm{x}}_{{\mathrm{t}}_0+\mathrm{t}}-{\mathrm{x}}_{{\mathrm{t}}_0}\right|}^2⟩}_{\mathrm{r}}.$$

Then, we estimated the probability of a fMRI signal displacement at a time-lag $\mathrm{t}$, $\mathrm{P}\left({\mathrm{M}\mathrm{S}\mathrm{D}}_{\mathrm{t}}\right)$. The probability distribution was calculated from ${\mathrm{M}\mathrm{S}\mathrm{D}}_{\mathrm{t},{\mathrm{t}}_0}$ samplings by a Gaussian kernel density estimation $\left(\mathrm{K}\right)$,

$$\mathrm{P}\left(\mathrm{M}\mathrm{S}{\mathrm{D}}_{\mathrm{t}}\right)=\frac{1}{4\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}} \mathrm{K}\left(\frac{\mathrm{M}\mathrm{S}{\mathrm{D}}_{\mathrm{t},{\mathrm{t}}_0\left(\mathrm{i}\right)}}{4}\right)$$

and we calculated the probability distribution for $\mathrm{t}$ between 1 and 8 TR and MSD between 0 and 5. We parameterised the MSD range by taking the maximal MSD value for the histogram of all MSD values across the timeseries. We determined the TR range by taking the autocorrelation of the timeseries and taking the maximal time of the autocorrelation. We then calculated the energy, $\mathrm{E}$, of fMRI signal MSD attractor state at a given time-lag $\mathrm{t}$, as the natural logarithm of the inverse probability:

$$\mathrm{E}=\mathrm{l}\mathrm{n}\left(\frac{1}{\mathrm{P}\left(\mathrm{M}\mathrm{S}{\mathrm{D}}_{\mathrm{t}}\right)}\right)$$

This approach indicates that a highly probable relative change in fMRI signal (calculated by $\mathrm{M}\mathrm{S}\mathrm{D}$) corresponds to a low energy (i.e., small $\mathrm{E}$), and an unlikely change in fMRI signal requires a higher energy (i.e., large $\mathrm{E}$).¹³ The attractor landscapes are represented as the energy for a given MSD at a given temporal displacement (TR).

We calculated an average attractor landscape for each condition (left hemisphere injection, right hemisphere injection and control) for each monkey. Then, we calculated the difference between the attractor landscapes by taking the difference between the nbM inhibition attractor landscape normalised by the control attractor landscape for each monkey. We ran paired t-tests to determine the significantly different points between the nbM inhibition compared to the control. To further investigate the attractor landscape, we also ran the above calculations by concatenating the time-series for all the same conditions (all runs for the left and right hemisphere injection, and control) and running the attractor landscape across the concatenated time-series, which reproduced the results. We established no significant difference in the attractor landscape when comparing between left and right hemisphere injection conditions (See Figure S2). In addition, we calculated the difference between ipsilateral and contralateral hemispheric attractor landscapes, by calculating the attractor landscape across ipsilateral (same hemisphere as inhibitory hemisphere injection) and contralateral ROIs (opposite hemisphere to inhibitory hemisphere injection) for both left and right hemisphere injection conditions. We ran a paired t test of the difference between hemispheric attractor landscape for either ipsilateral/contralateral ROIs and corresponding hemisphere control attractor landscape (i.e., ipsilateral left ROIs with left hemisphere control condition ROIs) (see Figure S3). We calculated whether there were differences between ipsilateral/contralateral left hemisphere inhibition versus ipsilateral/contralateral right hemisphere inhibition attractor landscapes (paired t test); and corrected for multiple comparisons with equivalent hemisphere control attractor landscapes (see Figure S3).

To determine the difference in the ‘flatness’ of the attractor landscape between nbM inhibition and control, we calculated the topography gradient for both nbM inhibition and control for each monkey. We used an inbuilt MATLAB (Version 2022b) ‘gradient’ function, which calculates the slope of a given vector field for $\mathrm{f}\left({\mathrm{x}}_1,\dots .{\mathrm{x}}_{\mathrm{n}}\right)$ and separately $\mathrm{f}\left({\mathrm{y}}_1,\dots .{\mathrm{y}}_{\mathrm{n}}\right)$, which in this case were the points of $\mathrm{x},\mathrm{y}$ on our attractor landscape plots:

$${\nabla }_{\mathrm{x}}\mathrm{f}(\mathrm{x})=\left(\frac{\delta \mathrm{f}}{\mathrm{\delta }{\mathrm{x}}_1},\frac{\delta \mathrm{f}}{\mathrm{\delta }{\mathrm{x}}_2},\dots \cdot \frac{\delta \mathrm{f}}{\mathrm{\delta }{\mathrm{x}}_{\mathrm{n}}}\right)$$

We then determined the maximal difference in the slope for the inhibition of the nbM compared to control.

Information theoretic analysis

The information-theoretic measures we employed on this data are based upon a Shannon entropy model of information storage and transfer of information.⁶⁰ This “information dynamics” approach considers how information in a variable ${\mathrm{X}}_{\mathrm{n}+1}$ at a given time, $n+1$, can be modeling by considering samples of this and other processes at the previous time points. Past information from a process $\mathrm{X}$ that contributes to its own future state is considered information storage, and information that contributes from other sources $\mathrm{Y}$ is considered information transfer between $\mathrm{X}$ and $\mathrm{Y}$.

We were interested in how information transfer between different regions in the brain changed during cholinergic inhibition. More specifically, transfer entropy models the information transferred from a source process $\mathrm{Y}$ (one region of interest) to the updates of a target process $\mathrm{X}$ (another region of interest), by estimating the amount of information $\mathrm{Y}$ provides about the next state in the future $\mathrm{X}$ in the context of the targets’ past.²⁵ This is quantified as the expected mutual information from realizations of the previous value ${\mathrm{Y}}_{\mathrm{n}}$ of the source process to realizations of the next value in the target process ${\mathrm{X}}_{\mathrm{n}+1}$ conditioned on the previous state ${\mathrm{X}}_{\mathrm{n}}^{(\mathrm{k},\mathrm{\tau })}=\left\{{\mathrm{X}}_{\mathrm{n}-(\mathrm{k}-1)\mathrm{\tau }},\dots ,{\mathrm{X}}_{\mathrm{n}-\mathrm{\tau }},{\mathrm{X}}_{\mathrm{n}}\right\}$ of the target:

$${\mathrm{T}}_{\mathrm{Y}\to \mathrm{x}}(\mathrm{k},\mathrm{\tau })=\mathrm{I}\left({\mathrm{Y}}_{\mathrm{n}};{\mathrm{X}}_{\mathrm{n}+1}\mid {\mathrm{X}}_{\mathrm{n}}^{(\mathrm{k},\mathrm{\tau })}\right)$$

We used an auto-embedding function to set the $(\mathrm{k},\mathrm{\tau })$ parameters to maximize active information storage of the target with additional bias correction^61,62 (with maximum allowed values of $\mathrm{k}=10$ and $\mathrm{\tau }=2$). We obtained a TE value for each region-to-region edge across the runs for each condition (we computed a single TE using the time-series for all runs in the same condition) for each monkey. We calculated the difference in region-to-region specific TE by grouping the regions based of Ch4_AL and Ch4_AM projection patterns during inhibition and performed a paired $\mathrm{t}$ test between the region-to-region TE that had passed a statistical significance permutation test with a 0.05 threshold (1000 iterations for each TE edge). We also performed paired $\mathrm{t}$ test between the region-to-region TE for comparison between inhibition of acetylcholine and ‘sham’ injection (for which results are presented in Figure S2).

Excitatory-inhibitory neural mass model

To clarify the relationship between our hypothesised cholinergic mechanisms and the attractor landscape analysis we built a toy (bistable) system consisting of two Wilson-Cowan excitatory masses with mutual inhibition. In order to reduce our system to the phase plane we did not explicitly model inhibition. To capture the cholinergic effects on population level neuronal dynamics we added a slow adaptation variable to each mass leading to the following four dimensional system of equations.

$${\mathrm{\tau }}_{\mathrm{E}}{\dot{\mathrm{E}}}_1=-{\mathrm{E}}_1+\left(1-{\mathrm{E}}_1\right)\mathrm{f}\left(\mathrm{a}{\mathrm{E}}_1-{\mathrm{E}}_2-{\mathrm{H}}_1\right)$$

$${\mathrm{\tau }}_{\mathrm{H}}{\dot{\mathrm{H}}}_1=-{\mathrm{H}}_1+{\mathrm{b}\mathrm{E}}_1$$

$${\mathrm{\tau }}_{\mathrm{E}}{\dot{\mathrm{E}}}_2=-{\mathrm{E}}_2+\left(1-{\mathrm{E}}_2\right)\mathrm{f}\left(\mathrm{a}{\mathrm{E}}_2-{\mathrm{E}}_1-{\mathrm{H}}_2\right)$$

$${\mathrm{\tau }}_{\mathrm{H}}{\dot{\mathrm{H}}}_2=-{\mathrm{H}}_2+\mathrm{b}\mathrm{E}{\mathrm{E}}_2$$

Where $\mathrm{f}(\mathrm{x})={\left(1+{\mathrm{e}}^{-\mathrm{\alpha }(\mathrm{\delta }\mathrm{*}\mathrm{x}-\mathrm{\theta })}\right)}^{-1}$ is a sigmoidal activation function. The structure of this model is similar to a number of previous models of bistable neuronal phenomena and shares many of their dynamical properties.^34,35,40,63 The parameters of the model are given in table. Following standard separation of timescales arguments⁶⁴ we leveraged the fact that ${\mathrm{\tau }}_{\mathrm{E}}\ll {\mathrm{\tau }}_{\mathrm{H}}$ allowing us partition the dynamics of the system into two phases. In the first phase we treat adaptation as constant and allow the firing rates to (rapidly) converge to their equilibrium values given by the intersection of the nullclines ${\dot{\mathrm{E}}}_1={\dot{\mathrm{E}}}_2=0$. The nullclines had three intersections (see Figure S7) defining the fixed points (${{\mathrm{E}}_1}^{\mathrm{*}},{{\mathrm{E}}_2}^{\mathrm{*}}$) of the system. In the second slow phase, adaptation converged to its equilibrium value ${\mathrm{H}}_1=\mathrm{b}{{\mathrm{E}}_1}^{\mathrm{*}}$, ${\mathrm{H}}_2=\mathrm{b}{{\mathrm{E}}_2}^{\mathrm{*}}$. For all parameter settings included in the simulations the system had two stable fixed points separated by a saddle node (i.e., the value of the Jacobian at the two stable fixed points had a positive determinant and negative trace, separated by a fixed point with a negative determinant.⁶⁵ Adaptation modulated the basin of attraction of each fixed point but did not change their stability. To study the dynamics of the system under noise converted the above system of ordinary differential equations into a system of stochastic differential equations with additive Gaussian noise $\mathrm{d}\mathrm{W}=\mathrm{\sigma }\sqrt{\mathrm{d}\mathrm{t}}\mathrm{N}(0,1)$. Because the fixed points did not change their stability, large jumps in state space were noise driven. To study the hypothesised role of acetylcholine of the attractor landscape of our model we swept the a (excitability) and b (adaptation) parameter between a range of 0.5–1.5 with low values for b parameter and high values a parameter mimicking a highly cholinergic state. All simulations were run in the Brain Dynamics Toolbox (Version 2022b., MATLAB, Version 2022b)⁵⁹ using the Euler-Maruyama solver with a timestep of $\mathrm{d}\mathrm{t}=0.001$. For computational efficiency we then down sampled the simulated time-series by an order of 1000 (into ~10ms time-bins) and ran the down sampled time-series for both neural populations (together) through the above-mentioned attractor landscape analysis (running standardized optimisation of the TRs bins and range of MSD for the following timeseries).

Table of parameters and corresponding values for the simple toy model of acetylcholine modulation of neural masses

Parameter	Values
τE	1
τH	1000
a	0.9–1.1
d	0.05–0.25
σ	0.1
α	1.5
δ	6

QUANTIFICATION AND STATISTICAL ANALYSIS

We calculated an average attractor landscape for each condition (left hemisphere injection, right hemisphere injection and control) for each monkey. Then, we calculated the difference between the attractor landscapes by taking the difference between the nbM inhibition attractor landscape normalised by the control attractor landscape for each monkey. We ran paired t-tests to determine the significantly different points between the nbM inhibition compared to the control. To further investigate the attractor landscape, we also ran the above calculations by concatenating the time-series for all the same conditions (all runs for the left and right hemisphere injection, and control) and running the attractor landscape across the concatenated time-series, which reproduced the results. We established no significant difference in the attractor landscape when comparing between left and right hemisphere injection conditions (See Figure S2). In addition, we calculated the difference between ipsilateral and contralateral hemispheric attractor landscapes, by calculating the attractor landscape across ipsilateral (same hemisphere as inhibitory hemisphere injection) and contralateral ROIs (opposite hemisphere to inhibitory hemisphere injection) for both left and right hemisphere injection conditions. We ran a paired t test of the difference between hemispheric attractor landscape for either ipsilateral/contralateral ROIs and corresponding hemisphere control attractor landscape (i.e., ipsilateral left ROIs with left hemisphere control condition ROIs) (see Figure S3). We calculated whether there were differences between ipsilateral/contralateral left hemisphere inhibition versus ipsilateral/contralateral right hemisphere inhibition attractor landscapes (paired t test); and corrected for multiple comparisons with equivalent hemisphere control attractor landscapes (see Figure S3). We obtained a TE value for each region-to-region edge across the runs for each condition (we computed a single TE using the time-series for all runs in the same condition) for each monkey. We calculated the difference in region-to-region specific TE by grouping the regions based of Ch4_AL and Ch4_AM projection patterns during inhibition and performed a paired t test between the region-to-region TE that had passed a statistical significance permutation test with a 0.05 threshold (1000 iterations for each TE edge). We also performed paired t test between the region-to-region TE for comparison between inhibition of acetylcholine and ‘sham’ injection (for which results are presented in Figure S2).

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental models: Organisms/strains
Rhesus macaque (Macaca mulatta)	NIMH/NIH	N/A
Deposited data
Raw and pre-processed data	Turchi et al.20	N/A
Atlas-based regions of interest	Reveley et al.58	N/A
Analyzed data	This paper	https://doi.org/10.5281/zenodo.11324156
Model data	This paper: Github data	https://doi.org/10.5281/zenodo.11324156
Software and algorithms
MATLAB	MathWorks	https://mathworks.com/products/matlab.html
Brain Dynamics Toolbox	Heitmann et al.59	https://bdtoolbox.org/
Java Information Dynamics Toolkit (jidt)	Lizier26	https://github.com/jlizier/jidt

Highlights.

• ACh inhibition impairs brain state transitions while preserving correlations

• ACh inhibition leads to flattened energy barriers between brain state attractors

• ACh inactivation decreases information flow between targeted cortical regions

• Cholinergic model of firing rates and adaptation currents reproduces findings