Integrated Risk Assessment of Mountainous Long-Distance Oil and Gas Pipelines Based on Multisource Spatial Data

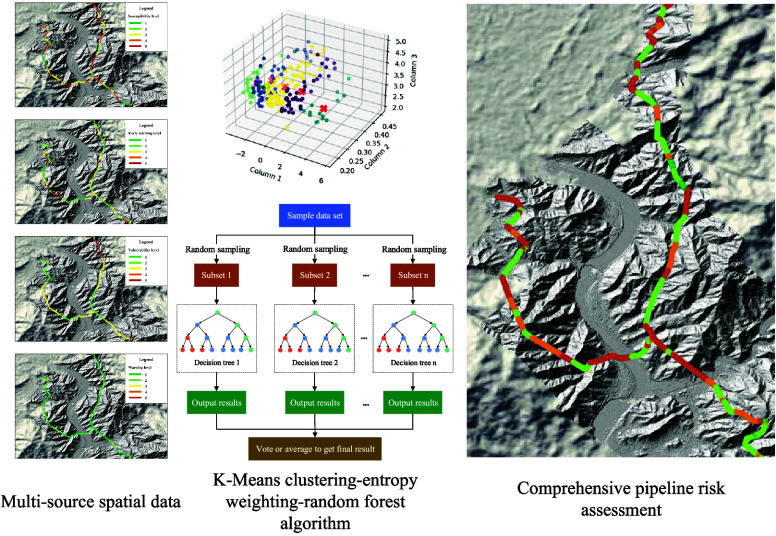
Abstract

Pipeline risk assessment is crucial for pipeline safety management and operation. The aim of this study is to develop a comprehensive assessment model that accurately evaluates pipeline risks and ensures the safe and reliable operation of the pipeline system. The model is based on multisource spatial data and is primarily applicable to long-distance oil and gas pipelines that traverse complex geological conditions in mountainous areas. The research is conducted using the example of the Jinliwen natural gas pipeline in Zhejiang Province, China. By analyzing the geological data of the study area and the potential risks that the pipeline may encounter, a comprehensive risk assessment indicator system for the pipeline was developed using slope units to divide pipeline sections. The pipeline risk levels are classified using the K-means clustering-entropy weighted-random forest algorithm. The model is evaluated using accuracy (Acc), precision (Pre), recall (R), F1-score, and the ROC curve. The results show that the model has an accuracy of 0.917, a precision of 0.92, a recall of 0.916, an F1-score of 0.914, and an AUC (Area Under Curve) of 0.93, indicating its strong predictive capability. The risk assessment results demonstrate a strong consistency when compared with actual incident events. This indicates that the constructed model effectively reflects the influencing factors of pipeline risk, providing a basis for pipeline risk assessment and disaster prevention and mitigation efforts in similar regions.

1. Introduction

Long-distance oil and gas pipelines have the advantages of high efficiency, low cost, and low energy consumption. They are an extremely economical and efficient transportation method for the transportation of oil, gas, and other resources.^1,2 With the continuous rise of socio-economic development, the petroleum industry, and the increasing demand from the population, human society’s consumption of oil, natural gas, and other energy sources has reached unprecedented levels. As a result, an increasing number of oil and gas pipelines have been put into operation.^3,4 However, long-distance oil and gas pipelines generally have characteristics such as crossing vast territories, shallow burial depths, complex external environments, and the presence of flammable, explosive, and toxic substances. They are susceptible to threats from third-party interference and geological hazards. These pipelines have multiple potential risks, and in the event of an accident, the consequences can be difficult to estimate.^5,6 Therefore, there is an urgent need for research on the types of risks that long-distance pipelines may encounter. It is important to consider the influencing factors of various risks and develop an accurate and universally applicable comprehensive risk assessment model for long-distance pipelines.

There is no doubt that a comprehensive risk assessment is critical to the safe operation of pipelines. The significance is mainly reflected in the following aspects: improving pipeline safety, optimizing resource allocation, formulating effective pipeline safety policies, and promoting the sustainable development of the pipeline industry.⁷ Therefore, in the absence of a clear comprehensive risk assessment method for long-distance oil and gas pipelines, this study focuses on researching risk types, influencing factors, and method selection to construct a comprehensive risk assessment model for long-distance pipelines. The model is developed by combining professional knowledge and practical experience.

Recently, there have been many studies on pipeline risk assessment. These studies aim to enhance the safety and reliability of long-distance pipeline systems, reduce accident risks, and optimize risk management strategies. Cui et al.⁸ proposed a pipeline third-party damage risk assessment model based on Bayesian networks and game theory. In their model, effective analysis has been conducted on both inadvertent third-party harm and deliberate malicious behavior. Hong et al.⁹ conducted an analysis of geological hazard risks faced by long-distance pipelines when crossing mountainous areas. They fully considered the role of rainfall factors in the occurrence of water-related geological hazards and constructed a meteorological early warning model. This model improved the accuracy of predicting such hazards. Mazumder et al.¹⁰ developed a feasible alternative approach to computationally intensive analysis methods for determining failure risks of steel oil and gas pipelines based on the XGBoost algorithm. Although the aforementioned studies have achieved significant results, they primarily focus on specific risks faced by long-distance pipelines (such as third-party damage, landslides, debris flows, earthquakes, and collapses). There is a lack of research on the comprehensive risk assessment of long-distance pipelines in mountainous areas.

Indeed, some scholars have begun to use machine learning methods for pipeline risk assessment, such as artificial neural networks,^11,12 support vector machines,^13,14 random forests,^15,16 and XGBoost.¹⁷ While these methods can learn from large amounts of data and extract patterns and features related to pipeline risks, they do require substantial data support and rely on prior data. For unsupervised classification problems, clustering algorithms are currently the most commonly used methods.¹⁸ Clustering algorithms aim to partition the samples in a data set into groups or clusters based on their similar features, without the need for pre-existing labels or specified category information.¹⁹Among them, K-means clustering is a simple and efficient clustering algorithm, with relatively low computational complexity. In K-means clustering, each sample is assigned to a cluster, and the center of each cluster is considered as the representative of that cluster. This allows for an intuitive understanding of the clustering results.²⁰

Furthermore, when conducting risk assessment studies on pipelines, researchers generally employ common methods for segmenting the pipeline, including equal-length segmentation, expert-based segmentation, and system node segmentation.^21,22 However, these segmentation methods have certain limitations. The equal-length segmentation method may not consider the variations in characteristics between pipeline segments, while the feature-based segmentation method may lead to significant differences in segment lengths.²³The commonly used pipeline segmentation methods are often based on simplified assumptions, which overlook the complex correlations and interactions between the pipeline and its surrounding environment.²⁴ There are various associations and interactions between the pipeline system and its surrounding environment, such as geological conditions and soil types. These factors can have a significant impact on pipeline risks. Therefore, it is essential to take them into account when segmenting the pipeline.²⁵ Slope units are divided based on geological conditions, using ridge lines and valley lines as boundaries. This approach not only adheres to the characteristics of river channel development but also has a higher likelihood of preserving the integrity of geological landforms.²⁶ Therefore, segmenting the pipeline based on slope units can lead to more accurate and effective analysis, helping to identify and manage potential risks.

From the review of previous research, it is evident that studies related to pipeline risk assessment have made significant progress and have become more mature. Researchers have developed various methods and models to assess the risks associated with pipeline systems. These methods and models include statistical-based approaches, machine learning-based methods, and physical models. Researchers select and apply appropriate methods and models for pipeline risk assessment based on the specific requirements of the problem and the availability of data. A detailed review of existing research is shown in Table 1.

Table 1. Detailed Review of Existing Research.

		pipe segment division method
references	research purposes	equal distance division	expert experience division	system node division	division of geological conditions
Cui8	Pipeline Third-Party Damage Risk Assessment	√
Hong28	Pipeline water damage geological hazard warning				√
Mazumder10	Pipeline Failure Risk Assessment			√
Li21	Pipeline Failure Risk Assessment	√
Wen23	Pipeline landslide risk assessment			√
Xiong22	Pipeline landslide risk assessment		√
this study	Comprehensive Pipeline Risk Assessment				√

However, most of the aforementioned studies focus on specific risks faced by pipelines, such as geological hazards, third-party interference, and pipeline failures, lacking comprehensive research on the integrated risks of long-distance pipelines in mountainous areas. This single risk assessment approach may not comprehensively consider the mutual interactions and cumulative effects of multiple risk factors. To address this issue, this study collects and consolidates information from various data sources, including pipeline basic information, operational data, environmental data, and more. Based on multisource spatial data, this study considers the risks faced by long-distance pipelines in mountainous areas and quantifies their impact on the pipeline system. Subsequently, by establishing an appropriate indicator system and utilizing a multimethod fusion model, the data related to various risk factors are integrated to comprehensively assess the risks of the pipeline system. Furthermore, most of the aforementioned studies use relatively long pipeline segments as the unit for risk assessment, overlooking the complex correlations and interactions between the pipeline and its surrounding environment. When pipelines traverse through flat terrain with minimal changes in the surrounding environment, the impact on risk assessment may not be as significant. However, when pipelines traverse through mountainous areas, the topography and geological conditions are typically more complex and diverse compared to flat terrain. If long pipeline segments are used as the unit for risk assessment, it would undoubtedly disrupt the integrity of natural slopes, and long segments would not be conducive to the placement of artificial defenses for high-risk units. So, when pipelines traverse through areas with complex geological conditions, it is indeed beneficial to divide the pipeline into shorter segments using slope units. This allows for better consideration of variations in topography and geological conditions along the pipeline route.²⁷ This approach allows for a more detailed and accurate assessment, enabling a more comprehensive capture of potential risk factors.

Therefore, this study focuses on the risk assessment of long-distance oil and gas pipelines in mountainous areas. It explores the development of a pipeline risk assessment model based on the fusion of multisource data. The aim is to establish a more comprehensive and accurate risk assessment model that provides valuable information to evaluate potential risks. This research can assist decision-makers in formulating more effective risk management strategies. The contributions of this article are as follows:

• This study employed hydrological analysis methods and curvature analysis methods to divide the slope units around the pipeline in mountainous areas. Based on the division results, the pipeline was segmented. This segmentation method helps consider geological variations, improves assessment accuracy, facilitates maintenance, and supports the implementation of risk management measures.

• A comprehensive pipeline risk assessment indicator system was constructed, which includes 25 indicators from four aspects: real-time fiber optic monitoring, risks related to third-party interference, susceptibility to geological hazards, and early warning for water-related hazards. This multisource data-based comprehensive pipeline risk assessment method offers advantages such as comprehensiveness, accuracy, and timeliness. It can integrate information from multiple data sources and provide more comprehensive, accurate, and timely pipeline risk assessment results.

• The proposed method utilizes K-means clustering for sample data clustering, entropy weight method for weight calculation, and random forest for model training and prediction. This approach takes advantage of unsupervised clustering, entropy weight calculation, and the random forest classifier, reducing reliance on prior knowledge and improving classification accuracy. It enables a more objective and accurate classification of risk levels for pipeline segments, providing robust support for pipeline risk assessment.

2. Materials and Methods

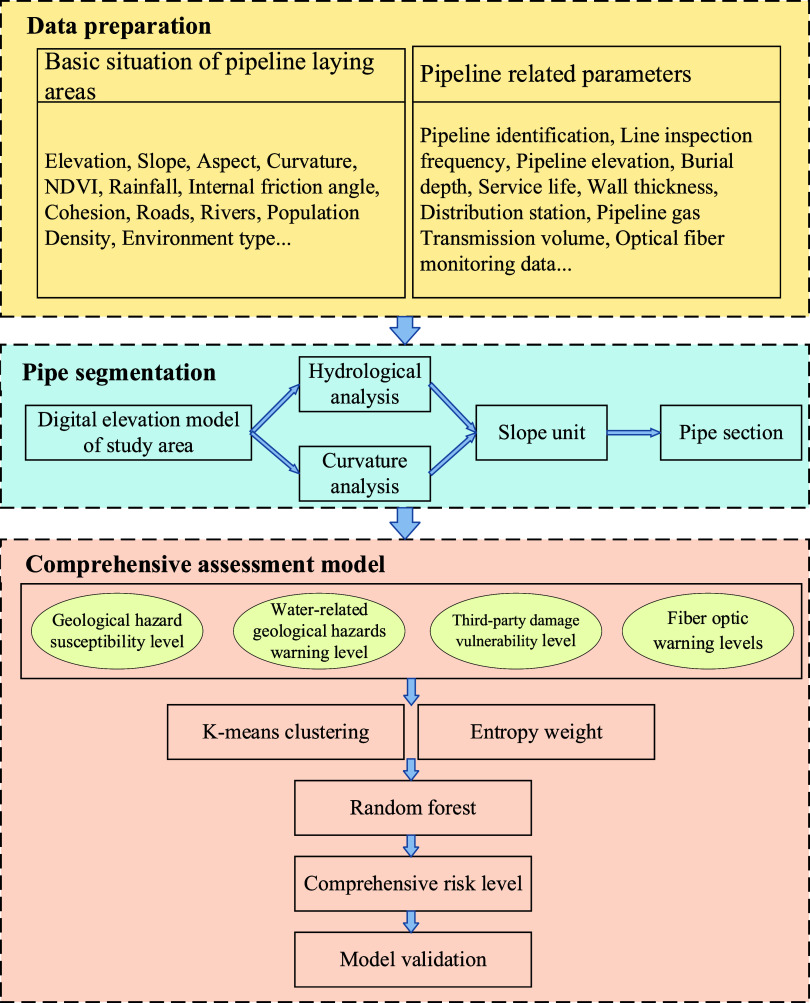
The comprehensive pipeline risk assessment model constructed in this study includes four key stages (Figure 1):

• Through detailed field investigations and high-resolution satellite image analysis, data from various sources were collected and integrated to gather research area information, including pipeline basic information, operational data, and environmental data.

• Based on high-precision digital elevation model (DEM) data of the research area, slope units were divided using hydrological analysis methods and curvature analysis methods. Any unreasonable units were corrected during the process of dividing the slope units. Based on the well-divided slope units, the segmentation of pipeline segments was completed.

• By utilizing various data sources and techniques, a comprehensive assessment model was constructed. The collected data was used to determine the susceptibility to geological hazards, water-related hazard warning levels, third-party interference vulnerability, and fiber optic system warning levels for each pipeline segment. The pipeline segments were classified and ranked using K-means clustering and entropy weight method. The fusion of multisource spatial data was accomplished by inputting the attributes and risk levels of pipeline segments into the Random Forest (RF) algorithm for training. This process determined the comprehensive risk level of the pipeline and completed the construction of the model.

Figure 1.

Pipeline comprehensive risk assessment process.

The constructed pipeline risk assessment model in this study was validated using metrics such as accuracy (Acc), precision (Pre), recall (R), F1-score, and the Receiver Operating Characteristic (ROC) curve. The trained model was then used to perform a comprehensive risk assessment of all pipeline segments.

2.1. Data Preparation

The risks faced by pipelines mainly include geological hazards and third-party damage, where geological hazards are influenced by multiple factors such as meteorological conditions, topography, and previous rainfall. The process is complex and characterized by high uncertainty. Third-party damage accidents are sudden and random, making it difficult to achieve early warning and prevention. Based on the potential risks identified for the studied pipeline and the geological characteristics of the research area, a comprehensive review of the literature was conducted to extract evaluation indicators used in risk assessments. After removing overlapping and similarly worded indicators, this study selected a total of 25 indicators from four aspects: real-time fiber optic monitoring, risks related to third-party interference, susceptibility to geological hazards, and early warning for water-related hazards. These indicators were used to construct the comprehensive pipeline risk assessment indicator system (Table 2).

Table 2. Pipeline Comprehensive Risk Assessment Index System.

first-level indicator	secondary indicators	indicator properties	indicator source
geological hazard susceptibility level	elevation	+	high-precision DEM
	slope	+	high-precision DEM
	aspect		high-precision DEM
	planar curvature	+	high-precision DEM
	profile curvature	+
	Normalized difference vegetation index (NDVI)	–	Resource and Environmental Sciences and Data Center
	Topographic wetness index (TWI)	+	Resource and Environmental Sciences and Data Center
	rainfall	+	National Earth System Science Data Center
	distance from the road	–	Resource and Environmental Sciences and Data Center
	distance from the river	–	Resource and Environmental Sciences and Data Center
Water-related geological hazard warning level	internal friction angle	–	National Geological Data Center
	cohesion	–	National Geological Data Center
	cumulative rainfall in 7 days	+	Meteorological department measured data
	24-h rainfall forecast	+	Meteorological department measured data
Third-party damage vulnerability level	pipeline identification	+	field survey data
	patrol frequency	+	field survey data
	pipe elevation	+	Pipeline construction parameters
	burial depth	+	Pipeline construction parameters
	service life	–	Pipeline construction parameters
	wall thickness	+	Pipeline construction parameters
	degree of modernization	+	Resource and Environmental Sciences and Data Center
	distribution station distance	–	Pipeline construction parameters
	pipeline gas flow	–	field survey data
	population density	–	World Population Organization Web site
	exposure distance	–	field survey data
Fiber optic warning levels	optical fiber real-time monitoring data	+	actual data

Note: “+” in the table represents a positive correlation with the first-level indicator, and “–” represents a negative correlation with the first-level indicator.

The selection criteria for each secondary indicator and their positive or negative correlation with the primary indicators are as follows:

• (1)Elevation: Elevation refers to the vertical distance of a point on the Earth’s surface relative to a reference horizontal plane. It is commonly used to describe the vertical position or altitude of a geographic location. In high-altitude areas, the terrain is typically steep, climate conditions are often harsh, and rock formations and soil are generally weaker and less stable.²⁹ Therefore, there is usually a positive correlation between elevation and susceptibility to geological hazards.
• (2)Slope: Slope refers to the degree of inclination of the ground or terrain in the horizontal direction. It is used to describe the steepness or inclination of the ground. Steeper slopes increase the self-weight pressure of soil and rocks on the surface and also increase the force of gravity acting on the soil mass, thereby increasing the risk of geological hazards such as landslides and collapses.²⁹ When the slope exceeds a certain threshold, the shear strength of the soil or rock may not be able to resist the force of gravity, leading to instability and collapse. Therefore, there is generally a positive correlation between slope and susceptibility to geological hazards.
• (3)Aspect: Aspect refers to the direction of the slope or terrain, i.e., the orientation of the slope. It describes the inclination trend of the ground or the directional characteristics on a horizontal plane. In certain cases, the selection of aspect may have an adverse impact on the collection of rainfall moisture and the path of runoff.²⁹ Therefore, this aspect has some influence on the formation and development of geological hazards.
• (4)Planar curvature: Planar curvature describes the magnitude and direction of curvature of a surface at a particular point. It is used to describe the degree of bending of the surface on a plane near that point.³⁰ Larger planar curvature indicates a higher degree of curvature of the terrain or surface at a specific point, making the soil or rock more prone to instability under external forces and potentially increasing the risk of landslides and collapses. Therefore, there is usually a positive correlation between planar curvature and susceptibility to geological hazards.
• (5)Profile curvature: Profile curvature refers to the curvature radius of a curve or surface along the tangent line at a particular point. It is used to describe the degree of curvature of a curve or surface near that point.³⁰ In areas with significant profile curvature, the stress distribution of slopes may be uneven, leading to localized stress concentration. This can make the soil or rock more vulnerable to instability under external forces, increasing the risk of sliding or collapsing. Therefore, there is usually a positive correlation between profile curvature and susceptibility to geological hazards.
• (6)Normalized difference vegetation index (NDVI): NDVI is an index used to assess vegetation condition and vitality. Higher NDVI values typically indicate abundant vegetation coverage, which means that vegetation roots can increase soil shear strength and inhibit soil erosion and surface runoff, thereby reducing the risk of geological hazard development.²⁹ Therefore, there is usually a negative correlation between NDVI and susceptibility to geological hazards.
• (7)Topographic wetness index (TWI): TWI is an index used to describe the degree of surface or terrain wetness. It is based on terrain features and calculates a value reflecting the surface wetness by considering factors such as rainfall, slope, and soil water-holding capacity.³¹ When the topographic wetness index is higher, it may indicate more surface water accumulation. Water saturation can decrease the shear strength of soil, thereby increasing the likelihood of geological hazards. Therefore, there is usually a positive correlation between TWI and susceptibility to geological hazards.
• (8)Rainfall: Rainfall is typically measured as the amount of water per unit area and is known as precipitation. Heavy or continuous rainfall can lead to water accumulation and soil saturation, reducing the shear strength of the soil and increasing the risk of hazard occurrence.²⁹ Especially in steep slopes, loose soil, or areas affected by human excavation and embankment, increased rainfall can significantly increase the potential danger of landslides and collapses. Therefore, there is usually a positive correlation between rainfall and susceptibility to geological hazards.
• (9)Distance to roads: Distance to roads refers to the straight-line distance or actual path distance between a point or area and the nearest road. It is used to measure the distance relationship between a location and the road network in geographic space.³¹ Being closer to roads may increase the risk of geological hazard occurrence. Road construction activities such as excavation, retaining walls, and embankments may disrupt the stability of the original geological formations, leading to geological hazards. Additionally, the drainage systems of roads can cause water infiltration into the soil, increasing soil saturation and further exacerbating the development of geological hazards. Therefore, there is usually a negative correlation between distance to roads and susceptibility to geological hazards.
• (10)Distance to water system: Distance to water system refers to the straight-line distance or actual path distance between a point or area and the nearest water body, such as rivers, lakes, or oceans. It is used to measure the distance relationship between a location and water bodies in geographic space.²⁹ Areas closer to water systems may be more affected by changes in groundwater levels, which can lead to changes in soil moisture and stability, thereby influencing the development of geological hazards. Therefore, there is usually a negative correlation between the distance to water systems and the susceptibility to geological hazards.
• (11)Internal friction angle: The internal friction angle refers to the magnitude of the internal frictional resistance formed between soil particles when subjected to shear forces. A larger internal friction angle indicates a greater frictional resistance between soil particles, indicating better shear resistance and relatively higher stability of the soil.²⁸ In water-related geological hazards, the presence of water can have a certain influence on the internal friction angle of the soil. When the soil contains an appropriate amount of water, the water can lubricate the soil particles, reducing the internal frictional resistance between them and thereby decreasing the internal friction angle of the soil. In this case, the shear resistance of the soil decreases, making it prone to water-related geological hazards such as landslides and debris flows. Therefore, there is usually a negative correlation between the internal friction angle and the warning level of water-related geological disasters.
• (12)Cohesive strength of soil: The cohesive strength of soil refers to the mutual adhesive force between soil particles and is the soil’s ability to resist shear failure.²⁸ When the cohesive strength of the soil is high, there is a strong adhesive force between the soil particles, resulting in good cohesion and shear resistance of the soil. In this case, when the soil is subjected to external forces, the interaction between the particles is strong, maintaining the stability of the soil and reducing the likelihood of water-related geological hazards. Therefore, there is usually a negative correlation between the cohesive strength of the soil and the warning level of water-related geological disasters.
• (13)Cumulative rainfall in 7 days: The accumulated rainfall in the preceding period has a significant impact on the development of water-related geological hazards.²⁸ When there is a large amount of rainfall during this period, the soil’s water content increases, leading to higher soil saturation and a decrease in its shear strength. This makes the soil unstable and susceptible to water-related geological hazards such as landslides, debris flows, and slope collapses. The majority of water-related geological hazards in the study area occur on days with heavy rainfall, with 83.9% of these hazards occurring within 3 days of rainfall, indicating a high correlation between the accumulated rainfall in the preceding 7 days and the occurrence of geological hazards. Therefore, this study uses the rainfall in the preceding 7 days as a secondary indicator for water-related disaster warnings. There is typically a positive correlation between the accumulated rainfall in the preceding period and the warning level of water-related geological disasters.
• (14)Twenty-four hour forecasted rainfall: The forecasted rainfall is closely related to the development of water-related geological hazards. Accurate rainfall forecasts can help in implementing appropriate disaster prevention and emergency measures, thereby reducing or avoiding the occurrence of water-related geological hazards.²⁸ Therefore, this study uses the 24-h forecasted rainfall as a secondary indicator for water-related disaster warnings. There is usually a positive correlation between the forecasted rainfall and the warning level of water-related geological disasters.
• (15)Pipeline signage: Pipeline signage plays a crucial role in preventing third-party damage and enhancing the disaster resilience of pipelines. By promoting awareness and recognition, improving inspection efficiency, and raising public awareness, pipeline signage can reduce the occurrence of destructive behaviors and facilitate timely problem detection and mitigation measures, thereby enhancing the safety and disaster resilience of pipelines.³² The more numerous and clearer the pipeline signage, the stronger the capacity to withstand third-party damage. Therefore, there is typically a positive correlation between pipeline signage and the resilience against third-party disruptions.
• (16)Patrol frequency: Patrol frequency refers to the frequency of pipeline inspections, indicating how often pipelines are surveyed and examined within a certain period of time.³² A higher patrol frequency can enhance the pipeline’s resistance to damage and its ability to withstand disasters. By promptly identifying issues, reducing opportunities for damage, and responding to incidents in a timely manner, it effectively prevents third-party acts of sabotage and ensures the safety of the pipeline. Therefore, there is typically a positive correlation between patrol frequency and the pipeline’s resilience against third-party damage.
• (17)Pipeline elevation: Pipeline elevation refers to the vertical distance between the centerline or top of the pipeline and the sea level or ground surface.³² A higher pipeline elevation can reduce the likelihood of unintentional third-party damage to the pipeline, thereby enhancing the pipeline’s resilience against third-party sabotage and reducing the occurrence of accidents. Therefore, there is typically a positive correlation between pipeline elevation and the pipeline’s resilience against third-party damage.
• (18)Burial depth: Pipeline burial depth refers to the vertical distance between the bottom of the pipeline and the ground surface when it is buried.³² When the pipeline is buried at a greater depth, it becomes more difficult for third parties to accidentally come into contact with the pipeline or exert destructive forces upon it. Additionally, deeper burial provides better protection against geological and soil factors such as earthquakes, soil settlement, erosion, and scour. Therefore, there is typically a positive correlation between pipeline burial depth and the pipeline’s resilience against third-party damage.
• (19)Service life: Pipeline service life refers to the actual duration of time that a pipeline is put into operation and used. As the service life of a pipeline increases, it may experience a certain degree of aging and wear, thereby reducing its resilience and making it more susceptible to third-party damage.³² Therefore, there is typically a negative correlation between pipeline service life and its resilience against third-party damage.
• (20)Wall thickness: Pipeline wall thickness refers to the thickness of the pipe’s walls, which is the distance between the inner and outer walls of the pipe’s cross-section. A greater wall thickness can increase the strength and stiffness of the pipeline, making it more resistant to external forces. Additionally, a larger wall thickness can provide a better protective layer, reducing the impact of corrosion, wear, and damage on the pipeline.³³ Therefore, there is typically a positive correlation between pipeline wall thickness and its resilience against third-party damage.
• (21)Degree of modernization: The process of urbanization and modernization is often accompanied by improvements in the construction and management of related infrastructure. Urban planning and pipeline layout tend to become more scientific and standardized. With proper planning and layout, pipelines can reduce risk factors associated with third-party damage, such as construction activities, excavation, and mechanical operations.³³ Therefore, there is typically a positive correlation between the degree of modernization in the vicinity of pipelines and their resilience against third-party damage.
• (22)Distance to distribution stations: Distribution stations typically enhance the management and security monitoring of the pipeline’s surrounding environment. This includes strengthening security patrols, installing monitoring devices, and restricting activities around the pipeline. These measures allow for the timely detection of signs of pipeline damage, the implementation of preventive and repair measures, and the reduction of risks associated with third-party damage.³² Therefore, there is typically a negative correlation between the distance of a pipeline from distribution stations and its resilience against third-party damage.
• (23)Pipeline gas flow: Pipelines with high gas flow are often associated with significant economic interests. When a pipeline experiences failure, resulting in reduced or halted gas flow, it can have a greater negative impact on the related economic interests. Additionally, higher gas flow can subject the pipeline system to greater transportation pressure. If the pipeline is unable to withstand this pressure or does not receive proper maintenance and protection, it may increase the potential risk of damage to the pipeline.³⁴ Therefore, there is typically a negative correlation between pipeline gas flow and its resilience against third-party damage.
• (24)Population density: Population density refers to the number of people living or engaging in activities within a given area. A higher population density implies more frequent activities and a denser concentration of individuals, which may increase the potential risk of human-induced damage to pipelines. Additionally, higher population density means that more people are affected in the event of pipeline damage, increasing the likelihood of injuries or fatalities.³³ Therefore, there is typically a negative correlation between population density and the resilience of pipelines against third-party damage.
• (25)Exposure distance: Pipeline exposure distance refers to the length or distance of pipeline segments that are exposed on the surface or in other visible locations within the pipeline system. Longer exposure distances may increase the potential risk of third-party damage to the pipeline and reduce its resilience.³³ Therefore, there is typically a negative correlation between exposure distance and the resilience of pipelines against third-party damage.
• (26)Abnormal distribution count of COTDR: COTDR (Coherent Optical Time Domain Reflectometry) is a fiber optic sensing system based on coherent optical time domain reflectometry technology, used for the detection and monitoring of events or abnormal conditions within the fiber optic cable.³⁵ A higher count of abnormal distributions may indicate a greater number of abnormal conditions within the pipeline system, which may require further inspection and maintenance. Conversely, a lower count of abnormal distributions may indicate normal operation of the pipeline system with no significant abnormal conditions. Therefore, there is typically a positive correlation between the count of abnormal distributions of COTDR within a given time period and the fiber optic alert level.

2.2. K-Means Clustering Algorithm

The K-means clustering algorithm was employed in this study to classify pipeline segments. In the comprehensive risk assessment of pipelines, the primary indicator data of each pipeline segment were used as input, and the K-means algorithm was applied to divide the pipeline segments into different categories, thereby achieving segmentation of the pipeline. The K-means clustering algorithm is a distance-based unsupervised and dynamic clustering method.³⁶ It is easy to describe, simple, efficient, and suitable for handling large data sets. As a result, it is widely used in various risk assessments.³⁷⁻³⁹ The calculation of centroids in clustering algorithms provides a basis for risk factor classification. Clustering algorithms determine the similarity of data points based on the distances between them. The closer the data points are, the more similar they are, while the farther apart they are, the less similar they are. In cluster analysis, the Euclidean distance is commonly used as a calculation method for similarity. Its formula is as follows (eq 1)

1

In the equation, d represents the Euclidean distance from a sample point to a cluster center. b_i refers to the i_th data point, while a_j represents the j_th cluster center.

The data processing flow of the K-means clustering algorithm is as follows: First, specify the number of clusters, denoted as k. Then, select k data points from the data set as the initial cluster centers. Based on eq 1, calculate the distance between each data point and the k cluster centers. Then, based on the principle of minimizing distance, assign each data point to the nearest initial cluster center. Repeat this process until all data points are assigned to one of the k clusters. Calculate the mean of the new clusters, obtaining the cluster centers for the k clusters. Iterate this process until a certain termination condition is met. The termination condition can minimize the sum of distances between data points and their corresponding cluster centers, reach the maximum number of iterations, or achieve convergence of a criterion function. The criterion function associated with the Euclidean distance is given by eq 2.

2

In the equation, S represents the sum of squared errors (SSE), k denotes the number of clusters, and z^j represents the cluster center of the j_th cluster.

The key factors that influence the effectiveness of the K-means clustering algorithm are the number of clusters (k), the initial cluster centers, and the maximum number of iterations (μ). The selection of k significantly determines the performance of the algorithm. It can be determined based on specific requirements, prior knowledge, or through evaluation of clustering effectiveness using clustering validity metrics. The clustering results of the K-means algorithm can vary with different initial cluster center inputs, and the algorithm can also get trapped in local optima if the maximum number of iterations (μ) is set too small. In this study, a number of clusters (k) equal to 5 were selected, and a maximum of 100 iterations (μ) were set to stop the iteration when the objective function reached its optimal value.

2.3. Entropy Weight Method

In this study, the entropy weight method was used to rank the classified pipeline segments. After K-means clustering, the pipeline segments were divided into different categories. In order to further rank the pipeline segments within each category, which may have different characteristics and risk levels, this study utilized the entropy weight method to determine the weights of various indicators and ranked the pipeline segments based on their respective weight values. The entropy weight method is a way to determine the weights of indicators based on the degree of variation transfer. It reflects the practical value of the information entropy of indicators, making the calculated indicator weights more objective.⁴⁰ Entropy is used in information theory to measure the degree of stability in a structure. The larger the entropy value, the greater the impact on the overall system, and conversely, the smaller the entropy value, the smaller the impact.⁴¹ The use of the entropy weight method allows for the adjustment of subjective ratings of indicators, resulting in a more reasonable determination of indicator weights. The steps for calculating indicator weights based on the entropy weight method are as follows:

Construct the evaluation matrix. Normalize the constructed evaluation matrix R = [r_ij]_m×n, and denote it as R′ = [r′_ij]_m×n.

Calculate the information entropy for each indicator. The information entropy for the j_th evaluation indicator is given by

3

In the equation, the value range of H_j is [0, 1], k = 1/lnm, .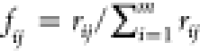

Calculate the entropy values for each indicator. Compute the information entropy for each indicator as H_1,H_2,···,H_n. Use the information entropy to determine the weights of each indicator as follows

4

2.4. Random Forest Model

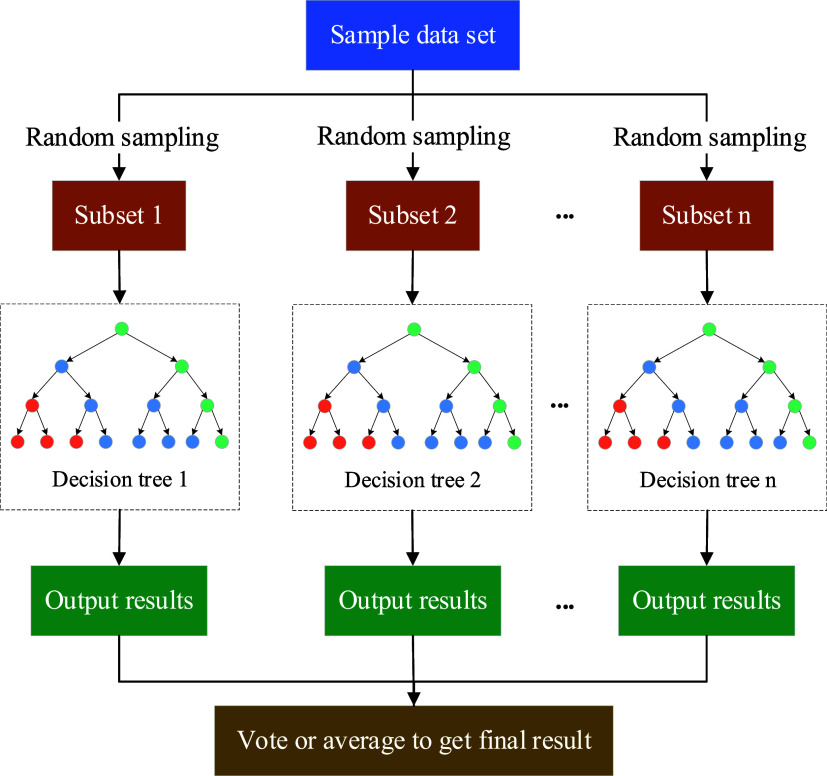
This paper utilizes the random forest algorithm to construct a comprehensive risk assessment model for pipelines based on existing pipeline classification data. The random forest model is a classification model that uses multiple decision trees as classifiers to train and predict samples.^42,43 The algorithm model is illustrated in Figure 2. This model combines the bagging algorithm, which operates on training samples, with the random subspace method, which operates on feature sets. It combines multiple decision trees together, randomly selects samples with replacements, and uses a subset of features as outputs. The prediction result is generated by voting based on the results of each tree. The final result is determined by taking the class with the highest vote count or by averaging the results. This approach achieves high accuracy and stability.^44,45

Figure 2.

Schematic diagram of random forest model.

2.5. Model Verification

This paper evaluates the performance of the model using Acc, Pre, R, F1-score, and the ROC curve. Acc represents the proportion of correctly predicted samples to the total number of samples. Pre is the proportion of true positive samples among the samples predicted as positive by the model. R is the proportion of true positive samples among the samples that are actually positive. The F1-score is a metric that comprehensively evaluates the performance of a classification model. It is based on the weighted average of precision and recall.^46,47 The ROC curve is a comprehensive metric that reflects specificity and sensitivity. The horizontal axis represents the false positive rate (FPR), and the vertical axis represents the true positive rate (TPR). The AUC value represents the area under the curve, with a higher value indicating better accuracy of the predictive model.

3. Case Study

3.1. Overview of the Study Area

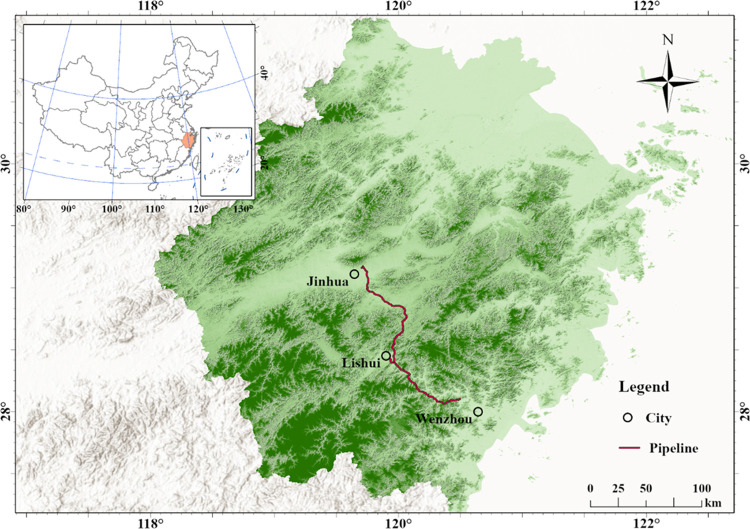
This paper selects the Jinliwen pipeline, which is a branch line of the operating West-East Gas Pipeline Phase II, as a case study. The study area is defined as a 1 km range along the pipeline route for conducting a comprehensive risk assessment of the pipeline. The Jinliwen natural gas pipeline has a total length of 219 km. It starts from the Jinhua Distribution Station and passes through counties and cities such as Wuyi, Yongkang, Jinyun County in Lishui, and Liandu District. The pipeline finally reaches its destination at the terminal station in Wenzhou, where it connects with the Yongtaiwen pipeline. The specific location of the pipeline is shown in Figure 3. The pipeline in the study area exhibits the following risk characteristics:

• Frequent geological hazards: The study area is characterized by mountainous and hilly terrain. The soil mainly consists of fine-grained clay, which is prone to natural hazards such as landslides, collapses, and mudslides.

• Temporal concentration: The study area is situated in the monsoon zone, where rainfall is significantly influenced by the monsoon. Rainfall is mainly concentrated during the flood season, and water-related hazards caused by precipitation occur primarily from June to September.

• Severity of damage: The study area has a long history of agriculture and robust industrial development. In the event of a pipeline leakage accident caused by third-party activities, it could result in resource wastage and environmental pollution and potentially lead to fire and explosion accidents, causing economic losses and human casualties.

Figure 3.

Study of pipeline location.

3.2. Pipe Segmentation

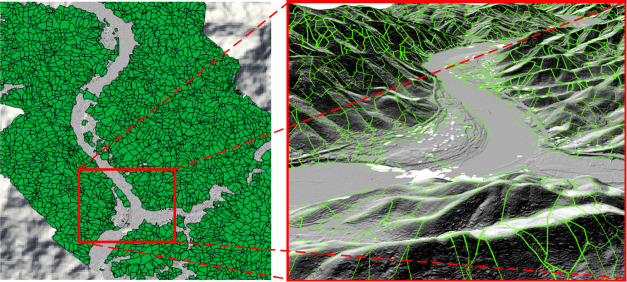
Due to the relatively long length of pipelines in mountainous areas, the risk conditions along the pipeline may vary, and the allocation of relevant safety resources should also consider the actual risks of different pipeline segments. Therefore, it is necessary to divide the pipeline into segments to assess and manage the risks of the pipeline accurately. The slope units play a significant role in traversing the terrain and landforms of mountainous areas, providing effective control over geological hazards such as landslides and collapses. Therefore, this study adopts an analysis method combining hydrology and curvature to divide the slope units, as shown in Figure 4. Based on the well-defined slope units, the pipeline is segmented into 2340 sections.

Figure 4.

Slope unit division.

3.3. Pipeline Index Evaluation

3.3.1. Geological Hazard Susceptibility Level

Geological hazards pose significant destructive risks to pipelines in mountainous areas, often resulting in severe casualties and property losses.⁴⁸ Therefore, various indicator data are collected and analyzed in advance in this study. A neural network is used to obtain the weights of each evaluation indicator. By weighting and combining all of the evaluation indicators, the susceptibility of geological hazards in the vicinity of the pipeline is determined. The susceptibility was classified into five categories: low, relatively low, moderate, relatively high, and high. A susceptibility zoning map was generated, and the geological hazard susceptibility levels for each pipeline segment are shown in Figure 5.

Figure 5.

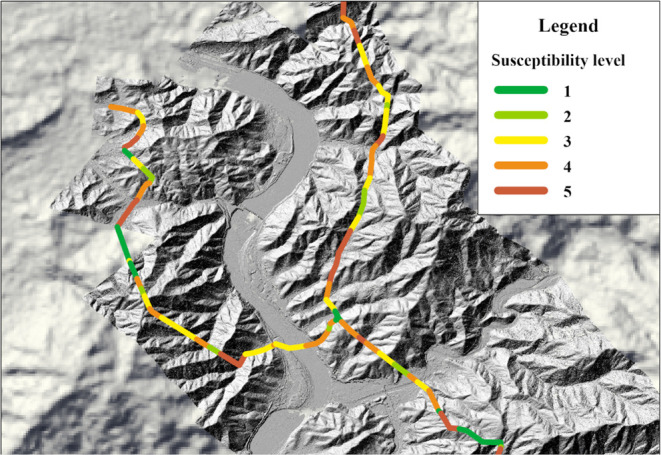
Susceptibility level of geological hazards in pipeline segments.

3.3.2. Water-Related Geological Hazard Warning Level

Based on the historical disaster data of the study area, it has been found that the most frequent type of disaster is water-related geological hazards. This is related to the geological and meteorological conditions of the study area. The predominant soil type within the area is fine-grained clay, and the characteristics of this type of soil, such as cohesion and internal friction angle, decrease with increasing moisture content. This makes the soil more susceptible to landslides, mudslides, and soil loosening hazards.⁴⁹ In fact, for complex mountainous slopes, the depth of damage caused by geological hazards varies, and it would be a significant challenge to fully consider the impact of different depths of damage on pipelines. The challenges are reflected in the following two aspects: a large-scale research area will double the workload, and the depth of disaster damage is difficult to define. Therefore, this study only considers the impact of damage at the depth of pipeline burial, which is uniformly set at 1.5 m. By referring to geotechnical exploration reports along the pipeline route, data on soil characteristics such as internal friction angle, cohesive strength, and soil density at burial depths have been collected. The corresponding soil characteristic data are then inputted into the pipeline segments divided based on slope units.

Based on meteorological statistics, the annual average rainfall is around 1100 mm, with rainfall being more concentrated during the flood season. Therefore, for water-related geological hazards with clear triggering factors and periodicity, the stability of each slope is calculated using the SHALSTAB model in this study. The stability levels are then coupled with rainfall data to calculate the warning index, resulting in the prediction of water-related geological hazard warning levels in the study area. For detailed calculation procedures, please refer to the article by Hong.²⁸ The warning levels for water-related geological hazards in each pipeline segment are shown in Figure 6.

Figure 6.

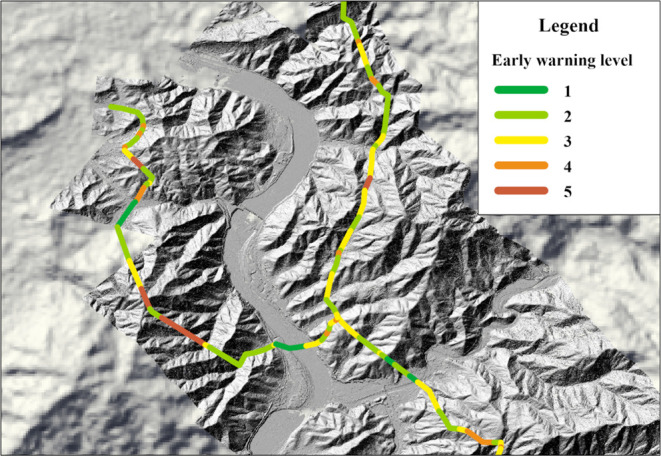
Early warning levels of water-related geological hazards in the pipeline segment.

3.3.3. Third-Party Damage Vulnerability Level

Third-party damage to pipelines primarily refers to actions by nonpipeline carriers or outsourced carrier units, resulting in damage or even destruction of pipeline facilities due to factors such as construction equipment, machinery, vehicles, intentional damage, and other reasons.⁵⁰ Long-distance pipelines traverse through complex natural environments, including urban and wilderness areas. The geological and geomorphological conditions along the pipeline route are intricate. These regions are prone to various construction and agricultural activities. Additionally, the increasing urbanization and associated illegal activities, such as unauthorized excavations and mechanical damage, pose a growing threat to the safe operation of the pipelines.⁵¹ Therefore, the vulnerability of pipelines to third-party damage is assessed based on relevant parameters of pipeline construction and on-site survey patrol data in this study. Expert knowledge and experience are used to score and classify the pipelines’ susceptibility to third-party damage, with five levels ranging from low to high vulnerability. For detailed calculation procedures, please refer to the article by Hong.⁵ The vulnerability levels of each pipeline segment are shown in Figure 7.

Figure 7.

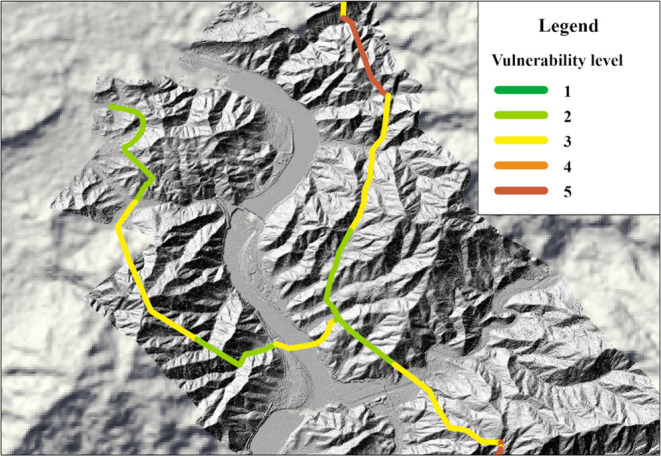
Third-party damage vulnerability levels for pipeline segments.

3.3.4. Fiber Optic System Warning Levels

Compared to the traditional manual patrol inspection method used in routine maintenance of long-distance pipelines, fiber optic-based pipeline safety warning technology offers real-time monitoring over long distances and provides accurate fault location capabilities. When incidents such as third-party construction events, manual mechanical excavation events, natural disaster damage, or oil and gas theft occur, coherent optical time domain reflectometry (COTDR) can be used to analyze the distribution characteristics in different monitoring environments. This allows for the identification of alarm types and accurate localization of the incident location.^52,53 According to the frequency of abnormal distribution observed in the COTDR data within a month, this study classified the warning levels for each segment of the fiber optic system. The higher the frequency of abnormalities, the more frequent the occurrence of third-party damage activities during that period, resulting in a higher warning level. The warning level of the fiber optic system can, to some extent, measure the risk of the pipeline. A higher alert level typically indicates a greater number of abnormal conditions or potential risks, requiring further inspection and maintenance to ensure the safe operation of the pipeline. Conversely, a lower warning level indicates that the pipeline system is in a normal state with lower risks. For detailed calculation procedures, please refer to the article by Lou.³⁵ The warning levels for each segment of the fiber optic system are shown in Figure 8.

Figure 8.

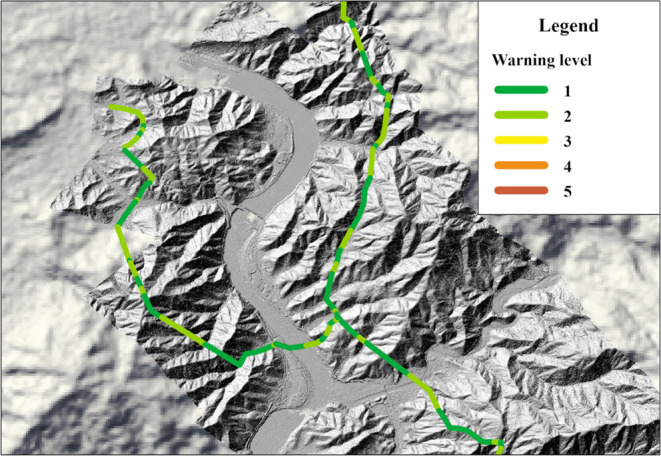
Fiber optic system segment warning levels.

3.4. Comprehensive Segment Risk Assessment

3.4.1. Cluster Analysis

By aggregating the levels of various indicators from Section 3.3, the geological hazard susceptibility level, water damage warning level, third-party damage vulnerability level, and fiber optic system warning level were determined for each pipeline segment. K-means clustering was applied to all pipeline segments that included these indicator levels for cluster analysis. The clustering results can be seen in Figure 9, and the number of segments in each cluster is listed in Table 3.

Figure 9.

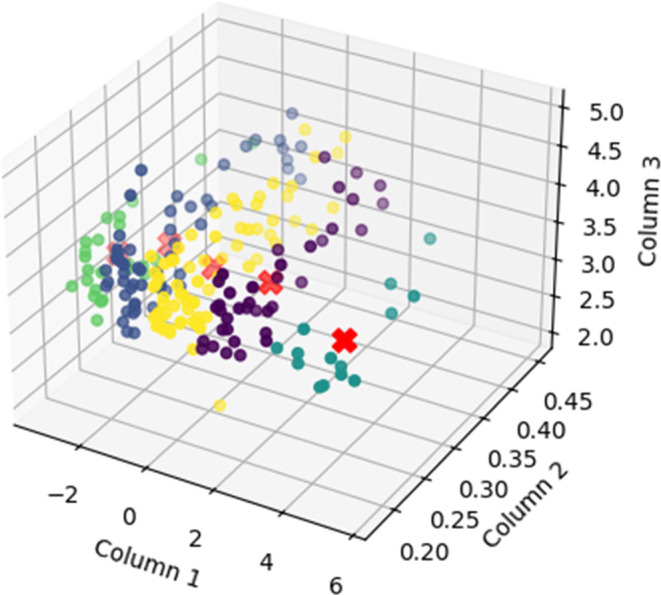
K-means clustering diagram.

Table 3. Risk Levels of Each Clustering Category.

cluster category	number of clusters	average risk index	comprehensive risk level
1	356	0.4778	4
2	483	0.865	5
3	370	0.383	3
4	492	0.311	2
5	639	0.276	1

3.4.2. Objective Weighting

By performing cluster analysis on all pipeline segments, they were divided into five categories. However, this alone cannot determine the overall risk level of the pipelines. Therefore, this paper utilizes the entropy weight method to objectively assign weights to each indicator and calculate the risk index for each pipeline segment.

″Information entropy” is used to characterize the degree of disorder in an information system. After the concept of information entropy was introduced, it was widely applied in various industries due to its strong objectivity. It has been particularly utilized in the suitability or hazard assessment of engineering disasters and various multicriteria decision-making cases. The heterogeneous evaluation of comprehensive pipeline risk is represented by the degree of disorder in the distribution of various evaluation indicators. Therefore, it is feasible to use the entropy weight method to determine the heterogeneity that affects pipeline risk. The heterogeneity can be measured by the geological hazard susceptibility level, water-related disaster warning level, third-party damage vulnerability level, and fiber optic system warning level of different pipeline sections. If the discrete values of the above indicators are large, the entropy value will be smaller, indicating a larger weight. Conversely, if the discrete values of the parameters are small, the entropy value will be larger, indicating a smaller weight. Therefore, the determination of the corresponding indicator weights can be achieved by studying the differences in the geological hazard susceptibility level, water-related disaster warning level, third-party damage vulnerability level, and fiber optic system warning level among different pipeline sections.

In this study, the entropy weight method is used to objectively assign weights to various indicators and calculate the risk index for each pipeline section. During the process of using the entropy weight method to determine the weights of primary indicators, the positive and negative correlations of the indicators were taken into consideration. The geological hazard susceptibility level, water-related disaster warning level, and fiber optic system warning level are positively correlated with the overall risk of pipelines and are defined as positive indicators. The third-party damage vulnerability level is negatively correlated with the overall risk of pipelines and is defined as a negative indicator. Through validation with actual accident events, it has been found that most accidents occur in pipeline sections with higher risk indices. The results calculated using the entropy weight method provide reasonable and feasible support for further research.

By comparing the average risk index of all pipeline segments within each clustering category, the risk level of that category can be determined. Based on the comparison, the risk levels of each clustering category are shown in Table 3.

3.4.3. Model Building

In this study, the entropy weight method is used to determine the comprehensive risk levels of pipeline segments, and some pipeline segments are used as training samples for the random forest model. The levels of various indicators and the comprehensive risk levels associated with these pipeline segments are considered important factors for training the random forest model. Once the model training is completed, it can be used to perform a comprehensive analysis and evaluation of all pipeline segments. This leverages the advantages of the random forest model, which can automatically learn and capture the relationships between different indicators and handle more complex data patterns. This improves the accuracy of risk assessment and the robustness against anomalous data.

The paper randomly selected 700 pipeline segments (including the overall risk level of the segments and the level of each indicator) to build a random forest model. Among them, 70% of the segments (490 data sets) were used for training, and 30% of the segments (210 data sets) were used for testing. The optimal model parameters were selected through a grid search algorithm (number of decision trees = 21, maximum tree depth = 8). After training, the confusion matrix for the test set is shown in Figure 10a, and the accuracy of the model is 0.917.

Figure 10.

(a) Confusion matrix for the test set. (b) The confusion matrix for all of the researched pipeline segments.

Finally, the paper utilized the trained random forest model to classify the overall risk levels of all pipeline segments. The confusion matrix for all of the researched pipeline segments is shown in Figure 10b. The classification results were then imported into ArcGIS to create a thematic layer for the overall risk (Figure 11). By analyzing the results of the comprehensive risk analysis for the pipelines, the number of segments in each risk level is presented in Table 4.

Figure 11.

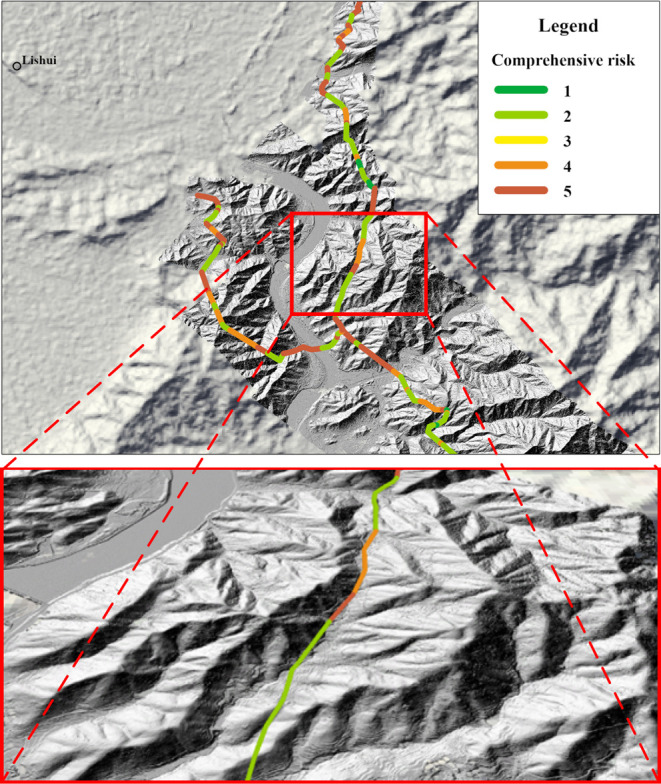
Pipeline comprehensive risk.

Table 4. Number of Segments in Each Risk Level.

comprehensive risk level of pipeline segments	quantity	percentage
1	656	28.0%
2	501	21.4%
3	379	16.2%
4	366	15.6%
5	438	18.7%

By comparing the risk assessment results from the entropy weight method and the random forest model, a statistical analysis of 89 historical disaster events in the study area is conducted. It is found that 70 of the historical disaster events are distributed in the high-risk and moderate-risk areas evaluated by the entropy weight method (Level 5 and Level 4), with an accuracy rate of approximately 78.7%. On the other hand, 74 of these events are distributed in the high-risk and moderate-risk areas evaluated by the random forest model, with an accuracy rate of approximately 83.1%. It can be concluded that the risk assessment of the random forest model is more in line with the actual situation and demonstrates better accuracy.

3.5. Model Verification

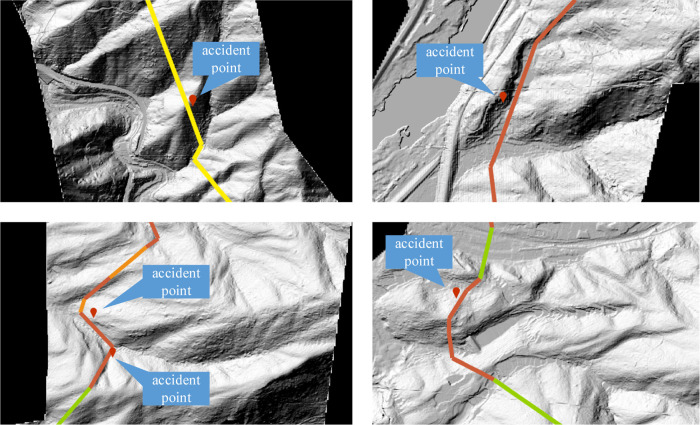
In this paper, the model performance was evaluated using Acc, Pre, R, F1-score, and the ROC curve. After testing, the performance metrics are shown in Table 5, and the results of the ROC curve are depicted in Figure 12. These indicate that the model has good predictive capability. The assessment results of the model for pipeline sections exhibit a high level of consistency when compared with historical incident events. Some of the comparative charts are shown in Figure 13.

Table 5. Model Accuracy Index.

risk level	precision	recall	F1-score
1	0.91	0.94	0.92
2	0.98	0.93	0.95
3	0.91	0.91	0.91
4	0.92	0.88	0.89
5	0.88	0.92	0.90

Figure 12.

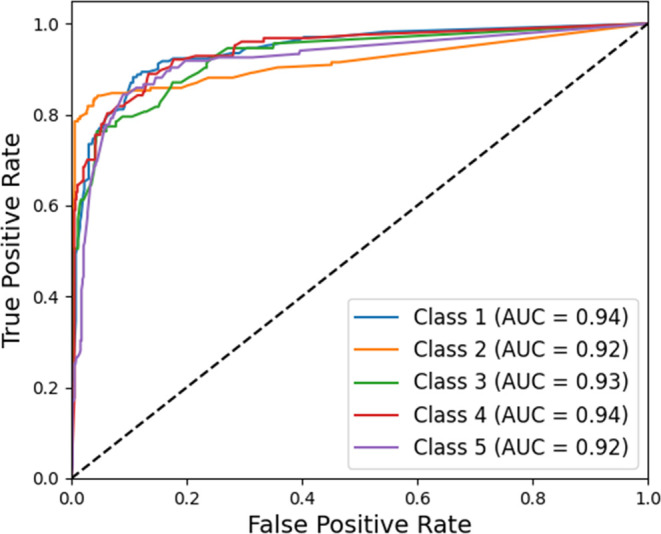
ROC curve.

Figure 13.

Historical accident events.

4. Results and Discussion

Based on the statistical data, it can be observed that compared to the results of K-means clustering, the classification results of the random forest model show a reduction in the number of pipeline segments classified as high risk (Level 5) and an increase in the number of segments classified as low risk (Level 1 and Level 2), while the classification of other risk levels remains consistent. Referring to historical accident event data, the classification results provided by the random forest model are more in line with the actual situation.

Two incidents occurred near pipeline segments, which were classified as low risk. Upon analysis, it was found that both accidents took place in areas with frequent human activities. In the case of accidents near low-risk segments, it was determined that they occurred due to a lack of awareness among residents in the pipeline vicinity, who ignored warning signs and engaged in unintentional construction activities. Another incident near a low-risk segment was attributed to outdated data. The geological conditions in that area had changed due to land development and urbanization activities, indicating that it should be reclassified as a medium to high-risk segment. Therefore, future research should consider incorporating indicators related to the intensity of human activities, residents’ safety awareness, and education level. Additionally, regular data updates are necessary to achieve a more accurate assessment of the comprehensive risk levels of pipeline segments.

Compared to previous studies on small-scale pipeline risk assessment, this study has a larger research scope, focusing on the region along the long-distance natural gas pipelines in mountainous areas. It primarily considers the influence of external factors in the study area on the pipelines rather than the pipelines themselves. On the other hand, in mountainous environments, the mechanical behavior of pipelines is more complex, requiring the establishment of relevant physical models for calculation and analysis. For long-distance pipelines, the complexity and computational effort of the models increase further. Therefore, factors such as pipeline mechanical performance, structural defects, and corrosion have not been considered at the moment. In the future, specific to mountainous pipelines, structural and mechanical analyses of the pipelines, detection and assessment of structural defects, and assessment of pipeline corrosion will be conducted. By comprehensively considering these factors’ impact on the pipelines, a more comprehensive pipeline risk assessment can be achieved.

Based on the model’s predicted results and validation results, the model tends to favor low-risk levels and has higher accuracy in predicting low-risk segments (all above 0.9). Upon analysis, for comprehensive pipeline analysis and evaluation, the number of samples in the low-risk category is usually greater than the number of samples in the high-risk category. This may cause the model to predict more samples as low-risk categories, leading to an overall underestimation of high-risk predictions. In the future, considerations will be given to strategies such as adjusting class weights, oversampling, or undersampling to balance the sample distribution and improve the accuracy of predictions for the high-risk category.

5. Conclusions

The paper proposes a pipeline risk assessment model based on the fusion of multiple data sources. The model divides the pipeline segments based on slope units and takes into account the factors of geological hazards and pipeline risk characteristics. It constructs a comprehensive risk assessment indicator system for pipelines, which includes 25 indicators in four aspects: real-time monitoring of fiber optics, third-party damage risk, susceptibility to geological hazards, and warning for water-related hazards. This model is of significant importance in ensuring the safety and reliable operation of pipeline systems.

• Dividing the pipeline segments based on slope units allows for a more accurate reflection of the geographical and geological characteristics of the pipeline system. Through a finer division, it becomes possible to capture small-scale geological changes and risks that exist within the pipeline system. This significantly improves the accuracy of the comprehensive analysis and assessment of the pipeline.

• The proposed pipeline risk assessment method, which incorporates multiple data sources, including real-time fiber optic monitoring, third-party damage risk, susceptibility to geological hazards, and warning for water-related hazards, offers several advantages in terms of comprehensiveness, accuracy, and timeliness. It enables the timely understanding of the pipeline system’s condition, identification of potential risks, and implementation of appropriate measures to reduce the occurrence of accidents.

• The proposed pipeline comprehensive risk classification method based on K-means clustering, entropy weight method, and random forest has the advantage of automatically learning features and performing classification from the data, reducing reliance on prior knowledge. By leveraging the strengths of multiple algorithms, it can better handle complex classification problems. The proposed method is capable of adapting to different data characteristics and classification requirements while considering multiple indicators and features, thereby providing more accurate and comprehensive pipeline risk classification results.

In future work, a more comprehensive risk assessment will be conducted, analyzing the potential threats to pipeline safety posed by human activities and incorporating relevant indicators. Additionally, a data management system will be established to regularly update data and enable timely evaluations, achieving a more precise assessment of the comprehensive risk levels of pipeline segments.

The authors declare no competing financial interest.