Abstract
The interaction of liquid water with hydrophobic surfaces is ubiquitous in life and technology. Yet, the molecular structure of interfacial liquid water on these surfaces is not known. By using a 3D atomic force microscope, we characterize with angstrom resolution the structure of interfacial liquid water on hydrophobic and hydrophilic silica surfaces. The combination of 3D AFM images and molecular dynamics simulations reveals that next to a hydrophobic silica surface, there is a 1.2 nm region characterized by a very low density of water. In contrast, the 3D AFM images obtained of a hydrophilic silica surface reveal the presence of hydration layers next to the surface. The gap observed on hydrophobic silica surfaces is filled with two-to-three layers of straight-chain alkanes. We developed a 2D Ising model that explains the formation of a continuous hydrocarbon layer on hydrophobic silica surfaces.
Keywords: interfacial water, hydrophobic surfaces, hydrophobic gap, 3D AFM, silica−water interfaces, self-assembled monolayers
The hydrophobic properties of extended surfaces are of relevance in a broad range of scientific fields, including tribology, geochemistry, molecular biology, and materials science. The interaction of water with a hydrophobic surface has implications for a variety of devices and technologies such as biosensors and water desalination devices. Consequently, many scientific contributions have been devoted to study the properties of water at a hydrophobic surface.1−9 However, our molecular-scale understanding of the structure of liquid water next to a smooth hydrophobic surface is far from satisfactory. Water contact angle (WCA) is the dominant technique to study the hydrophobicity of surfaces.10 This parameter provides a macroscopic property that does not give information on the local structure of liquid water near a solid surface. Vibrational sum frequency spectroscopy data supported the existence of water molecules with a single dangling OH bond next to the surface.11,12 On the other hand, X-ray reflectivity experiments supported the presence of a water density depletion layer (gap) next to hydrophobic surfaces.3,13−15 However, the reported thickness of the gap varied between experiments from 0.15 nm (a fraction of a water molecule)3,13 to 0.45 nm.14,15 A neutron reflectivity measurement performed in deuterated water reported a reduced water density region reaching 1.1 nm from the hydrophobic surface.16 However, molecular dynamics (MD) simulations did not support the existence of a gap larger than 0.2 nm.6−8,17 In fact, our incomplete understanding of the structure of liquid water on smooth hydrophobic surfaces comes from the limitations of the experimental methods applied to characterize those surfaces.
To resolve the above question and expand our understanding of the interaction of liquid water with a hydrophobic surface, we implement three-dimensional AFM (3D AFM) methods. Those methods provide real-space, atomic-scale resolution images of solid–liquid interfaces.18 To that purpose, a silicon dioxide film was functionalized with n-octadecyltrichlorosilane (OTS). Functionalization of silicon or silicon oxide surfaces with alkylsilane self-assembled layers (SAM) has been extensively applied in the last 25 years.19−22 Therefore, the functionalization protocols are well-established and routinely applied in biosensing and lithography applications. In fact, those are among the most commonly used hydrophobic surfaces in nanotechnology.
We show that on a hydrophobic silica surface, the interface has a layered structure with an interlayer distance of 0.45 nm (mean value). This distance coincides with the periodicity of straight-chain alkane layers adsorbed on a solid surface. The layered structure extends up to 1.2 nm from the surface of the OTS. Molecular dynamics simulations performed with a mixture of water and alkane molecules in the presence of the hydrophobic surface support these experimental data. In contrast, the structure of the interface measured by 3D AFM on a hydrophilic silica surface shows a considerably thinner interface (∼0.6 nm), with layers separated by 0.3 nm (mean value). The latter value is consistent with the geometry of hydration layers and with the presence of water molecules next to the silica surface.23
The combination of experimental and simulation findings demonstrates that liquid water is effectively separated from an extended hydrophobic surface by a gap of 1.2 nm. This gap is filled with alkane molecules that are spontaneously incorporated from the surroundings. The displacement of water by straight-chain hydrocarbons and the consequent formation of a water-depleted region are driven by hydrophobic interactions and the presence of alkanes in the environment. The presence of trace amounts of alkanes in ultrapure water and the surrounding air is unavoidable under standard conditions. Therefore, the above results represent a universal property that defines the interaction of liquid water with any extended hydrophobic surface.
1. Results and Discussion
Figure 1a shows diagrammatically how the xyz displacements are performed in 3D AFM. The atomic-scale resolution features revealed by 3D AFM have been validated on a variety of crystalline surfaces immersed in aqueous solutions.24−32 In some cases, interpretation of 3D AFM images remains challenging.33−36 However, for pure water, low-molarity aqueous solutions, and organic liquids, the contrast observed in 3D AFM data can be explained in terms of the liquid density variations through the interface (Figure 1b).33,36,37
Figure 1.
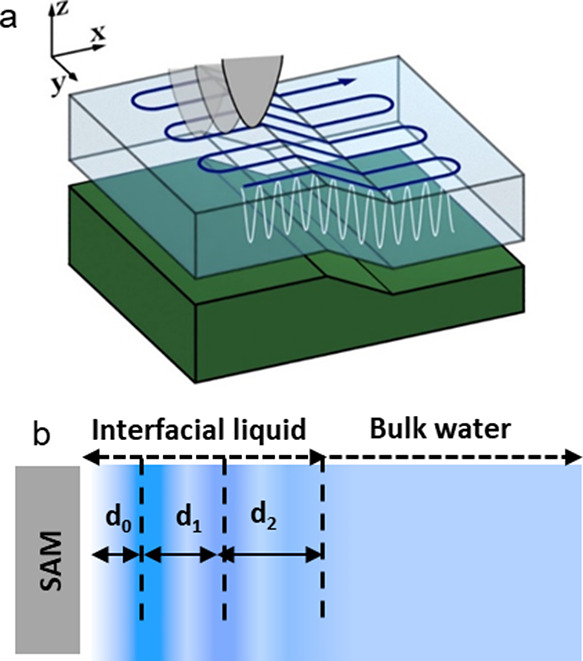
Diagrams of the 3D AFM and interfacial liquid layers. (a) Tip displacements in 3D AFM. (b) d0 is the distance between the first liquid layer and the solid surface; d1 and d2 are the distances between the liquid layers.
We apply tapping mode AFM38 to quantify the surface roughness and uniformity of the pristine and functionalized silicon surfaces in water before 3D AFM imaging (Figure S1, Supporting Information). The root-mean square roughness of pristine, OTS, and 3-aminopropyltriethoxysilane (APTES)-functionalized silica surfaces are, respectively, 0.5, 0.3, and 0.45 nm. Those values are consistent with the ones reported by others.20 Roughness values below 1 nm are characteristic of very smooth surfaces. We observe that the functionalized silica surfaces have a roughness lower than that of pristine silica surfaces. We measure the WCA on pristine and OTS and APTES-functionalized silica surfaces. The values are, respectively, 58°, 108°, and 42° (Figure S2, Supporting Information).
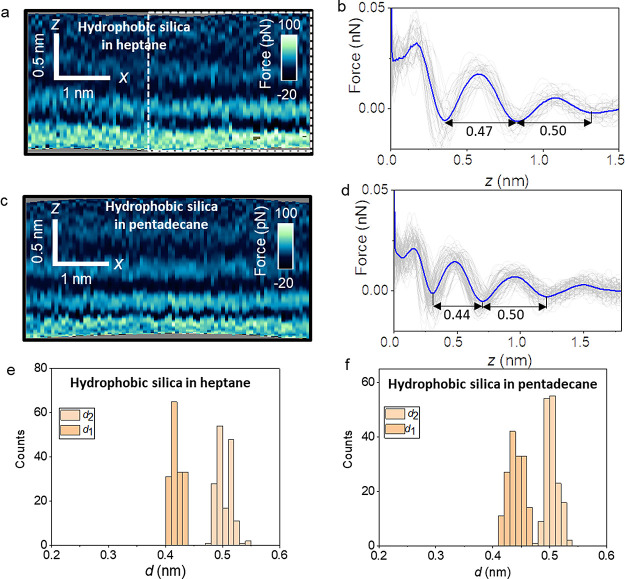
Figure 2a shows a representative 2D force map (z–x) of an OTS–water interface. The force map of the interface shows a layered structure characterized by the alternation of high (dark) and low (light) force regions. The layered structure extends about 1.2 nm from the outer methyl group of the OTS. At each position on the surface, we acquire a single force–distance curve F(z) perpendicular to the OTS surface (Figure 2b). Single force–distance curves are shown in gray. The F(z) plots extracted from the 2D maps show an oscillatory profile. The histograms of the distances d1 and d2 obtained from several experiments (600 force–distance curves) are shown in Figure 2c. The histograms show two distributions characterized by different median and mean values. The mean interlayer distances d1 and d2 are, respectively, 0.42 and 0.48 nm. Interfacial liquid layers typically exhibit d2 ≥ d1 because the order of the layer decreases with the distance to the solid surface.9,34,50 Additional 2D force maps for the OTS–water interface are shown in part 2 (Supporting Information).
Figure 2.
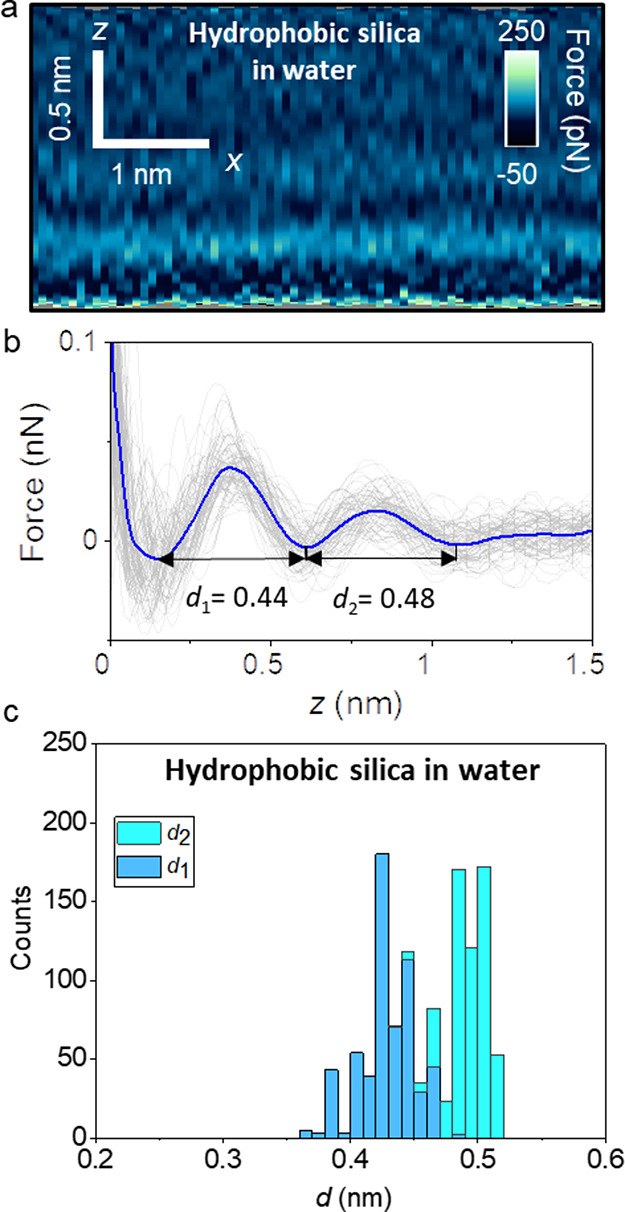
Interfacial liquid water structure on a hydrophobic silica surface (OTS). (a) 2D force maps (x, z) of an OTS–water interface (1 mM KCl). (b) Force–distance curves obtained from (a). (c) Histogram of d1 and d2 distances measured from several hydrophobic silica–water interfaces. About 600 force–distance curves are used to plot the histogram. The average force–distance curve is highlighted in blue. Individual force–distance curves are plotted in gray. Experimental parameters: f = 806 kHz, k = 9.2 N m–1, Q = 6.3, A0 = 150, and Asp = 100 pm.
The above 3D AFM results underline that the interfacial water structure on a hydrophobic surface (OTS) is characterized by interlayer distances above 0.4 nm. The periodicity of the liquid layers arises from entropic effects associated with the molecular packing of the liquid.34,39 The average diameter of a water molecule is 0.28 nm. Therefore, the measured values >0.4 nm are at odds with the presence of water (hydration) layers at the interface. In fact, the interlayer distance of hydration layers, as determined by different methods such 3D AFM,18,39 X-ray reflectivity,41 and MD simulations,6,7,42,43 ranges between 0.26 and 0.35 nm.
To identify the chemical species present at the OTS–water interfaces, we study first the interfacial structure of alkane liquids on the OTS surfaces. Based on the considerable number of studies which reported the spontaneous adsorption of alkanes from air onto graphite,44−47 graphene,48−50 van der Waals materials,50,51 and other surfaces,52,53 we hypothesize that hydrocarbons from the surroundings might be incorporated into liquid water.
Figure 3a–d shows the 2D maps and force–distance curves obtained by immersing the OTS surfaces in two organic liquids, heptane and pentadecane. Heptane and pentadecane molecules are examples of short and long straight-chain alkanes found in the contingent of volatile organic compounds often present in indoor air.56,57 For both organic liquids, the interlayer distances are in the range of 0.42–0.5 nm. The average chain lengths for heptane and pentadecane are, respectively, 0.76 and 1.8 nm. Therefore, from the above interlayer distance values, we infer that the alkanes align mostly parallel to the surface of the OTS, yielding layered structures with little dependence on alkane chain length. Figure 3e,f shows the histograms for d1 and d2 obtained from several OTS–alkane liquid interfaces. The distributions are very narrow (≤0.02 nm) and show negligible overlaps. Those distributions are associated with d1 and d2.
Figure 3.
Interfacial layer structure of organic liquids on hydrophobic silica surfaces. (a) 2D force maps (x, z) of a hydrophobic silica–heptane interface. (b) Force–distance curves obtained from the rectangle marked in panel (a). (c) 2D force maps (x, z) of a hydrophobic silica–pentadecane interface. (d) Force–distance curves obtained from panel (c). (e) Histogram of d1 and d2 distances measured on hydrophobic silica surfaces in heptane. (f) Histogram of d1 and d2 distances measured on hydrophobic silica surfaces in pentadecane. The average force–distance curve is highlighted in blue in (b) and (d). Individual force–distance curves are plotted in gray in (b) and (d). Experimental parameters for heptane (pentadecane): f = 590,776 (476,235) kHz, k = 8.2 N m–1, Q = 5.4 (4.6), A0 = 100 pm, and Asp = 60 pm.
Figure 4 compares the interlayer distance values for the OTS interfaces in three solvents: water, heptane, and pentadecane. The mean values of d1 and d2 are, respectively, 0.425 and 0.48 nm (water), 0.415 and 0.49 nm, and 0.43 and 0.49 nm (Figure 3d). For each layer, the 3D AFM data show very similar values (within the error bar) for the three interfaces. Those similarities suggest that the interfacial structure observed on the surface of the OTS immersed in water is not due to water itself but might instead arise from the adsorption of straight-chain alkanes or similar molecules.
Figure 4.
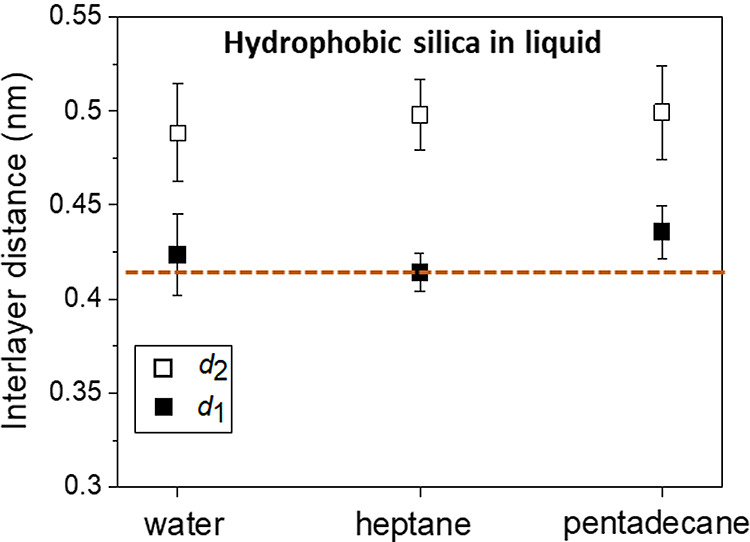
Average interlayer distance values of hydrophobic silica surfaces immersed in different liquids. The values are similar, independent of the physical properties of the liquid, water versus organic solvents. The horizontal dash line indicates the nominal diameter of a straight-chain alkane molecule (0.42 nm).
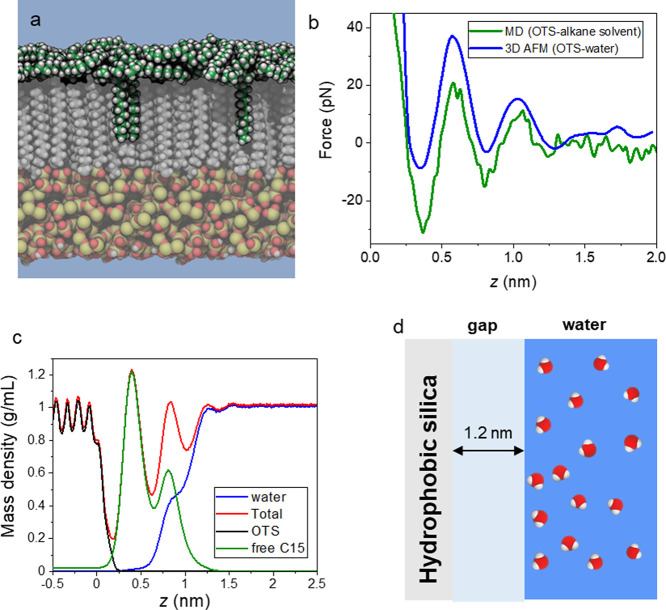
Next, we compare the force–distance curves (FDCs) measured on the OTS–water interfaces with the FDCs estimated in MD simulations. We constructed three simulation systems, one with a pristine OTS–water interface and two others with an OTS–water interface in the presence of straight-chain alkanes (heptane or pentadecane). Figure 5a shows a cross section of the OTS–water interface in the presence of alkane molecules after 600 ns of the MD simulation. Multiple layers of alkanes are visible on top of the OTS chains. We note that the structure of these layers fluctuates rapidly on the nanosecond time scale. We find that alkanes intercalate between OTS chains, preferentially at regions of lower OTS density, resulting in little dependence of the interfacial structure on the OTS functionalization density (Figure S7, Supporting Information). Consequently, there is little difference in the predicted FDCs for the OTS layers with densities of 4.0 and 5.0 chains/nm2 (Figure S8, Supporting Information). Most importantly, the simulations indicate that the water is expelled from the OTS surface. Figure 5b presents a comparison between the experimental and simulation FDCs. The computational force profile for the OTS–water with alkanes agrees (green) well with the corresponding experimental FDC (blue). In particular, the simulation reproduces the distance between force peaks and the number of peaks. On the other hand, the calculations using a model of an OTS–pure water interface do not even exhibit qualitative agreement with the experimental OTS–water force profile (Figure S9, Supporting Information).
Figure 5.
(a) MD snapshot of pentadecane molecules adsorbed on an OTS-functionalized silicon dioxide surface. C atoms are shown in green (pentadecane) or gray (OTS), while H, O, and Si atoms are shown in white, red, and yellow, respectively. The simulations included explicit water, represented as a blue background for clarity. (b) Comparison of force profiles determined by AFM for a nominally anodized OTS–water interface and by MD simulation using a model AFM tip asperity and octane solvent. The distance z is relative to the center of mass of the terminal CH3 groups of the OTS chains. The experimental force profile is shifted on the horizontal axis so that the first minimum coincides with that of the MD profile. (c) Mass density profiles for the system shown in (a). Within the OTS layer (z < 0), the oscillations correspond to the positions of the alkyl C atoms. At the interface (0 < z < 1.25 nm), the oscillations are associated with the structuring of pentadecane layers, which also coincides with the water-depleted region. The density of water reaches its bulk value 1.2 nm from the terminal C atom of the OTS chains. (d) Scheme of an OTS–water interface.
Currently, the experimental 3D AFM data do not distinguish the density profiles of the different chemical species forming the interface. However, the agreement obtained between the experimental data and the MD simulation enables us to plot the total and partial mass densities across an experimental OTS–water interface. Figure 5c shows total, water, and alkane densities as a function of distance from the interface, averaged over the simulation after equilibrium was reached. The water density is well below the bulk value for distances shorter than 1 nm. In that region, the oscillatory behavior observed in the 3D AFM curves can only be associated with the layering of hydrocarbons. We conclude that water molecules are effectively expelled from the OTS surface (Figure 5d).
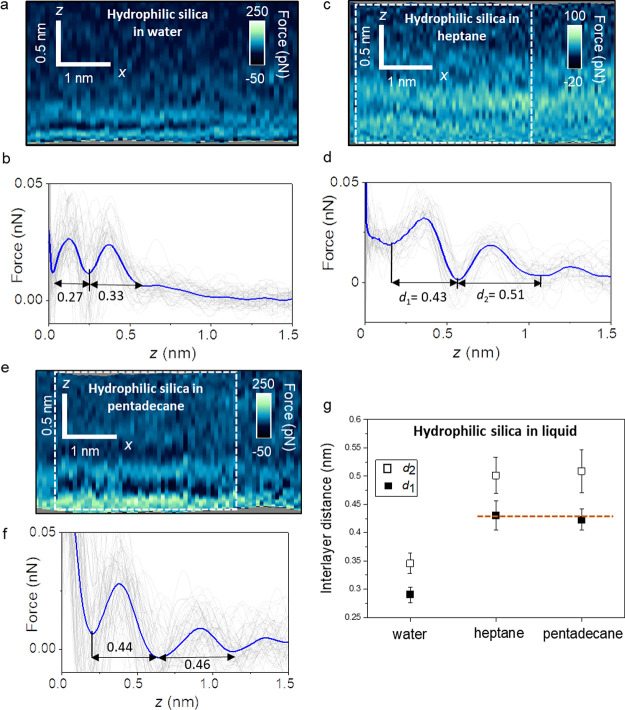
Lastly, we study the interfacial liquid water structure on a hydrophilic silicon oxide surface. For that purpose, a silicon oxide film was functionalized with APTES. An amino-terminated monolayer confers a marked hydrophilicity to silicon surfaces (Figure S2, Supporting Information). Figure 6a shows a 2D force map obtained on an APTES–water interface. Figure 6b shows the corresponding F(z) curves. The 2D maps show the presence of two solvation layers in addition to, probably, a layer of water molecules directly in contact with APTES. The interlayer distance varies between 0.3 and 0.34 nm. Those values are consistent with the average value expected for hydration layers based on theory and experiments.6−9 We have obtained similar results in other APTES–water experiments (Figure S4, Supporting Information).
Figure 6.
Interfacial liquid structure on a hydrophilic silica surface (APTES). (a) 2D force maps (x, z) of a hydrophilic silica–water interface (1 mM KCl). (b) Force–distance curves obtained from (a). Individual force–distance curves are plotted in gray. (c) 2D force maps of a hydrophilic silica–heptane interface. (d) Force–distance curves obtained from the rectangle marked in (c). (e) 2D force maps of a hydrophilic silica–pentadecane interface. (f) Force–distance curves obtained from the rectangle marked in (e). (g) Average interlayer distances for hydrophilic silica surfaces immersed in different liquids. The average force–distance curve is highlighted by a thick continuous line (blue) in panels (b), (d), and (f). Experimental parameters for water: f = 806 kHz, k = 9.2 N m–1, Q = 6.3, A0 = 150 pm, and Asp = 100 pm; heptane: f = 478 kHz, k = 9.2 N m–1, Q = 5.2, A0 = 150 pm, and Asp = 100 pm; and pentadecane: f = 594 kHz, k = 9.2 N m–1, Q = 3.5, A0 = 150 pm, and Asp = 120 pm.
We also study the interfacial structure of APTES with heptane and pentadecane liquids. The 2D force maps and force–distance curves (Figure 6c–f) show that the interfacial distances d1 and d2 are well above those found in water. Figure 6g summarizes the interfacial distances obtained on APTES surfaces immersed in water and alkane liquids. The data show a clear separation between the values measured in water (≤0.34 nm) and those measured in heptane and pentadecane (≥0.42 nm). They indicate that on a hydrophilic surface (APTES), the interfacial water structure is not affected by the presence of hydrocarbons in the environment. Furthermore, the values of d1 and d2 measured in APTES–heptane and pentadecane interfaces are very similar to the ones obtained for OTS in the same liquids (Figure 4). The last result indicates that the interfacial distances of the alkane liquids are independent of the hydrophilic or hydrophobic properties of the surface.
The interfacial liquid structure observed on an OTS is, perhaps surprisingly, independent of the chemical and physical properties of liquid, water (polar) versus heptane, and pentadecane (organic and nonpolar liquids). The interlayer distances are in all cases consistent with straight-chain alkane layers, which fully meets expectations for heptane and pentadecane solvents but indicates that the properties of the OTS–water interface cannot be explained by water alone. Indeed, the interfacial structure in water can be well-explained by the spontaneous migration of alkane-like contaminants from the environment to the OTS–water interface, similar to phenomena observed at aqueous interfaces of other hydrophobic materials.40,52−55 MD simulations corroborate this hypothesis reproducing the force–distance curves measured on an OTS–water interface only when the water includes straight-chain alkanes. The 3D AFM data show that the interfacial water structure depends on the properties of the SAM. An OTS–water interface is characterized by the presence of 2–3 layers separated by about 0.45 nm (mean value). On a hydrophilic surface (APTES), the interfacial structure is characterized by the presence of 2–3 layers separated by about 0.3 nm. The above results lead us to conclude that water is separated by a gap of about 1 nm from an extended hydrophobic surface. The gap is filled by molecules likely originating in the ambient environment with structures similar to straight-chain alkanes. The presence of hydrocarbons on hydrophobic surfaces exposed to indoor air or water should be considered to be unavoidable. Indoor air and purified water contain a trace amount of organic compounds. Among those organic compounds, linear alkanes with 15–26 carbon atoms have the highest affinity for interfaces between water and hydrophobic surfaces.49,58,59 The concentration of linear alkanes in air is very small (≈20 μg/m3),56 while purified water has a concentration of hydrocarbons of about 3 μg/L (3 ppb). On the other hand, numerous reports have provided evidence on the adsorption of alkanes from indoor air onto graphitic surfaces.44−50 On some graphite-like surfaces, those adsorbates form regular patterns (stripes) which cover large regions of the surface.48−51 The condensation of dissolved gas molecules in the water (mostly N2) was proposed to explain the formation of stripe structures on graphite surfaces.60−62 However, neither additional experimental data nor theoretical simulations supported the presence of structured N2 molecules on the graphite–water interface. The 3D AFM data were obtained by using ultrapure water and standard laboratory conditions (T = 300 K and ambient pressure). We plan to perform experiments as a function of pH, dissolved gases in water, and temperature to establish the environmental condition limits to obtain the above results.
The existence of a nearly complete interfacial hydrocarbon layer at aqueous interfaces of hydrocarbon materials can be theoretically justified as follows. We consider a grid of interfacial sites σi that can be unoccupied or occupied by single hydrocarbon molecules. The adsorption of these hydrocarbons at the interface can be modeled by using a formalism similar to the 2D Ising model
| 1 |
Here, H is the effective Hamiltonian, ΔGair→water is the hydration free energy of a single hydrocarbon molecule, ΔGwater→ads is the free energy of adsorption of an isolated molecule from the water phase, ΔGads→layer is the free energy of transferring an adsorbed molecule to the interfacial layer phase, b is the coordination number of a molecule in the layer phase, μ is the chemical potential of hydrocarbon molecules, and σi ∈ {0, 1} is the occupancy of surface site i. The second sum is over neighboring pairs of sites ⟨i, j⟩; hence, ΔGads→layer < 0 represents an adsorbate–adsorbate attraction. In the mean-field approximation, the above Hamiltonian can be written as
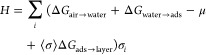 |
2 |
where ⟨σ⟩ is the mean occupancy of surface sites. From this, we obtain the mean-field partition function,
| 3 |
The partition function can then be used to compute the average site occupancy, which yields a self-consistent solution for ⟨σ⟩
| 4 |
where β = (kBT)−1. In addition, we have replaced the chemical potential with the ambient concentration in air (c) by
| 5 |
Eq 4 is a transcendental equation that is most easily solved by looking for intersections between the left and right sides. The left side is a straight line of unit slope, while the right side is sigmoid that approaches one as ⟨σ⟩ → ∞. The midpoint of the sigmoid shifts was left for increasing values of c. This means that, for large values of c, the only solution is ⟨σ⟩ ≅ 1, while for small values of c, the only solution is
| 6 |
For intermediate values of c, the sigmoid rises in the physical range 0 < ⟨σ⟩ < 1, and it is possible to have three solutions. This regime represents phase coexistence with the largest and smallest solutions corresponding to the coverage of the dense and dilute phases, respectively (the middle solution is an unstable stationary state).
The model given in eq 2 treats the surface as a grid of sites that can be occupied by at most a single molecule without specifying the size of these sites; therefore, without the inclusion of additional entropy terms, the size of a state in the model is the volume per molecule in the fully occupied interfacial layer. Hence, the reference concentration c0 is the mass density of the interfacial layer phase, which can be approximated by the mass density of the pure alkane (liquid or solid).
The difference between the two sides of eq 4 is plotted in Figure S10 of the Supporting Information, with zero values representing self-consistent solutions. For very small ambient concentrations, eq 4 has only one solution, which is associated with a very low coverage. However, above a critical concentration, a high-coverage solution appears, marking the transition from adsorption of dilute, isolated molecules to nucleation and growth of a nearly complete layer. For a straight-chain alkane with 24 carbons, we estimate c0 = 0.7991 g/mL, ΔGair→water = +5.6 kcal/mol (derived from a published Henry’s law constant60), ΔGwater→ads = −14.5 ± 0.3 kcal/mol, and ΔGads→layer = −7.6 ± 0.8 kcal/mol (see Figure S9 of the Supporting Information), giving a critical concentration for the transition to the layer phase of approximately 14 μg/m3.
These experiments and simulations together with the theoretical model underline that under ambient conditions, the spontaneous adsorption of hydrocarbons on hydrophobic surfaces is ubiquitous. To suppress or minimize the presence of hydrocarbons, hydrophobic–water interfaces would require electrochemical control.63 Those methods have not been implemented in any applications involving hydrophobic silica–water interfaces.19−22 In fact, the presence of trace amounts of alkanes in water (ultrapure or otherwise)64 or in air environments56,57 is unavoidable under the conditions used to conduct solid–water experiments. Therefore, the above findings should not be regarded as a contamination effect.
Based on previous results obtained on mild hydrophobic surfaces such as graphite,9 we propose that next to any extended hydrophobic surface, there is a 1.2 nm region of low density of water.
The formation of a water-depleted region is driven by minimization of the free energy of the system. In fact, this effect might be considered a variation of the hydrophobic interaction.2 In this variation, the hydrophobic surface acts as a template that favors the interaction of the solutes (straight-chain alkane molecules) dispersed in liquid water.
2. Conclusions
By combining three-dimensional AFM experiments and MD simulations, we demonstrate the existence of a water-depleted region next to a hydrophobic silica surface, which extends 1.2 nm into the water.
Angstrom-scale resolution images of hydrophobic silica–water interfaces reveal that the interface is characterized by the presence of two-to-three layers separated by 0.45 nm (mean value). The interlayer distance coincides with that of the adsorbed alkanes. Similar experiments performed on hydrophilic silica surfaces reveal an interface formed by one-to-two hydration layers. We conclude that straight-chain alkanes are the dominant molecular species that replace water in the gap region of a hydrophobic silica–water interface.
We develop a model of the experimental interface which involves three free energies, air–liquid, liquid–adsorbate, and adsorbate–monolayer. The model shows that the displacement of water by hydrocarbons and the consequent formation of a water-depleted region are driven by hydrophobic interactions and the presence of hydrocarbons in the environment. This behavior seems to capture the universal property of the interaction of liquid water with an extended hydrophobic surface under ambient conditions.
Many properties of alkane layers, for example, the dielectric constant, the WCA, or the vibrational modes, are similar to the properties of the OTS molecules. Those considerations might explain why the replacement of water with alkanes has not been reported before. However, there are other properties such as friction coefficients, electrical conductivities, or binding of solutes that might be significantly affected by the existence of a fluid-like alkane layer adsorbed on the hydrophobic surface.
3. Materials and Methods
3.1. 3D AFM Imaging
A homemade three-dimensional AFM40 was implemented on a Cypher S microscope (Asylum Research, Oxford Instruments). 3D AFM is performed in amplitude modulation38 by exciting the cantilever at its first eigenmode. At the same time that the cantilever oscillates with respect to its equilibrium position, a sinusoidal signal is applied to the z-piezo position to modify the relative z-distance between the sample and the tip. We have used z-piezo displacements with amplitudes of 2.0 nm and a period (frequency) of 10 ms (100 Hz). The z-piezo signal is synchronized with the xy-displacements in such a way that for each xy-position on the surface of the material, the tip performs a single and complete z-cycle. The z-data are read out every 10.24 μs and stored in 512 pixels (256 pixels half cycle). Each xy-plane of the 3D map contains 80 × 64 pixels. Hence, the total time required to acquire such a 3D AFM image is 52 s. Additional details on the experimental methods are found in the Supporting Information.
3.2. Molecular Dynamics Methods
Molecular dynamics simulations were performed using NAMD 2.1465 using hydrogen mass repartitioning66 and a 4-fs time step, with the temperature and pressure maintained at 295 K and 1 atm using the Langevin thermostat and Langevin piston barostat, respectively.67 Alkyl groups were represented with the CHARMM General Force Field,68 while amorphous SiO2 was represented using the CHARMM-compatible parameters of Emami et al.69 Water used the TIP3P model of CHARMM. The force profiles were efficiently estimated by applying the adaptive biasing force (ABF) method to the distance between an AFM tip asperity and an OTS surface. The SiO2 AFM tip asperity model was created as described in Figure S11 of the Supporting Information. FDCs were calculated for four different atomistic simulation systems, each including a patch of amorphous SiO2 conjugated with an OTS at different chain densities (4.0 or 5.0 chains/nm2) in different solvents (water, pentadecane, octane, and decane). Octane and decane exhibited faster diffusion than the heavier alkanes, allowing the FDCs to converge on an accessible time scale. The FDC in Figure 5b is derived from more than 30 μs of simulated time. The complete systems had a mean size of 4.05 nm × 4.18 nm × 14 nm and were periodic along all three axes. Larger scale simulations, such as that shown in Figure 5a, were performed with an 8.10 × 8.36 nm OTS surface, created by duplicating the smaller system in the x and y directions. The simulation protocols and construction of the simulation models are described in greater detail in the Supporting Information.
3.3. Hydrophobic and Hydrophilic Silica Surfaces
The formation of self-assembled monolayers on surfaces involves two steps, the chemisorption of the molecules and the spontaneous organization of ordered domains.70−74 The hydrophobicity and hydrophilicity of the silica surfaces were controlled by functionalization with self-assembled monolayers, respectively, OTS (hydrophobic) and APTES (hydrophilic). Details on the preparation of the silica surfaces are provided in the Supporting Information.
Acknowledgments
We thank Francisco M. Espinosa for technical support with the preparation of the silica surfaces and self-assembled monolayers. Financial support was received from Ministerio de Ciencia e Innovación grant PID2022-136851NB-I00/AEI/10.13039/501100011033 (R.G.) and the National Science Foundation grant DMR-1945589 (J.C.).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.4c05689.
Methods: protocol to acquire images and force–distance curves in 3D AFM; functionalization of the silica surfaces; details of MD and force-field codes; AFM tip model; thermodynamics of alkane adsorption; Figures S1: AFM images of the relevant surfaces; Figure S2: water contact angles; Figures S3–S4: 2D force (x, z) maps; Figure S5: FTIR spectrum; Figures S6 and S7: MD simulations alkanes on an OTS-functionalized silica surface; Figures S8 and S9: thermodynamics of alkane adsorption; Figure S10: tip asperity model; and Figure S11: MD snapshots of the assembly of alkane molecules on an OTS-functionalized silica surface (PDF)
Author Contributions
Conceptualization: R.G.; methodology: R.G., D.M.A., J.S., and J.C.; investigation: D.M.A., J.C., J.S., and R.G.; funding acquisition: R.G. and J.C.; supervision: R.G.; writing—original draft: R.G.; and writing—review and editing: R.G., D.M.A., J.C., and J.S.
The authors declare no competing financial interest.
Supplementary Material
References
- Israelachvili J.; Pashley R. The hydrophobic interaction is long range, decaying exponentially with distance. Nature 1982, 300, 341–342. 10.1038/300341a0. [DOI] [PubMed] [Google Scholar]
- Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- Poynor A.; Hong L.; Robinson I. K.; Granik S.; Zhang Z.; Fenter P. A. How water meets a hydrophobic surface. Phys. Rev. Lett. 2006, 97, 266101 10.1103/PhysRevLett.97.266101. [DOI] [PubMed] [Google Scholar]
- Kuna J. J.; Voïtchovsky K.; Singh C.; Jiang H.; Mwenifumbo S.; Ghorai P. K.; Stevens M. M.; Glotzer S. C.; Stellacci F. The Effect of Nanometer-Scale Structure on Interfacial Energy. Nat. Mater. 2009, 8, 837–842. 10.1038/nmat2534. [DOI] [PubMed] [Google Scholar]
- Biedermann F.; Nau W. M.; Schneider H. J. The Hydrophobic Effect Revisited—Studies with Supramolecular Complexes Imply High-Energy Water as a Noncovalent Driving Force. Angew. Chem., Int. Ed. 2014, 53, 11158–11171. 10.1002/anie.201310958. [DOI] [PubMed] [Google Scholar]
- Björneholm O.; Hansen M. H.; Hodgson A.; Liu L. M.; Limmer D. T.; Michaelides A.; Pedevilla P.; Rossmeis J.; Shen H.; Tocci G.; Tyrode E.; Walz M. M.; Werner J.; Bluhm H. Water at Interfaces. Chem. Rev. 2016, 116, 7698–7726. 10.1021/acs.chemrev.6b00045. [DOI] [PubMed] [Google Scholar]
- Brini E.; Fennell C. J.; Fernandez-Serra M.; Hribar-Lee B.; Lukšič M.; Dill K. A. How water’s properties are encoded in its molecular structure and energies. Chem. Rev. 2017, 117, 12385–12414. 10.1021/acs.chemrev.7b00259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monroe J.; Barry M.; DeStefano A.; Gokturk P.; Jiao A. S.; Robinson-Brown D.; Webber T.; Crumlin E. J.; Han S.; Shell M. S. Water structure and properties at hydrophilic and hydrophobic surfaces. Annu. Rev. Chem. Biomol. Eng. 2020, 11, 523–557. 10.1146/annurev-chembioeng-120919-114657. [DOI] [PubMed] [Google Scholar]
- Garcia R. Interfacial Liquid Water on Graphite, Graphene, and 2D Materials. ACS Nano 2023, 17, 51–69. 10.1021/acsnano.2c10215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drelich J.; Chibowski E.; Meng D. D.; Terpilowski K. Hydrophilic and superhydrophilic surfaces and materials. Soft Matter 2011, 7, 9804. 10.1039/c1sm05849e. [DOI] [Google Scholar]
- Scatena L. F.; Brown M. G.; Richmond G. L. Water at hydrophobic surfaces: weak hydrogen bonding and strong orientation effects. Science 2001, 292, 908–911. 10.1126/science.1059514. [DOI] [PubMed] [Google Scholar]
- Tyrode E.; Liljebla J. F. D. Water Structure Next to Ordered and Disordered Hydrophobic Silane, Monolayers: A Vibrational Sum Frequency Spectroscopy Study. J. Phys. Chem. C 2013, 117, 1780–1790. 10.1021/jp310732f. [DOI] [Google Scholar]
- Mezger M.; Sedlmeier F.; Horinek D.; Reichert H.; Pontoni D.; Dosch H. On the Origin of the Hydrophobic Water Gap: An Xray Reflectivity and MD Simulation Study. J. Am. Chem. Soc. 2010, 132, 6735–6741. 10.1021/ja910624j. [DOI] [PubMed] [Google Scholar]
- Chattopadhyay S.; Uysal A.; Stripe B.; Ha Y.; Tobin Marks J.; Karapetrova E. A.; Dutta P. How water meets a very hydrophobic surface. Phys. Rev. Lett. 2010, 105, 037803 10.1103/PhysRevLett.105.037803. [DOI] [PubMed] [Google Scholar]
- Uysal A.; Chu M.; Stripe B.; Timalsina A.; Chattopadhyay S.; Schlepütz C.; Marks T.; Dutta P. What X-rays Can Tell us about the Interfacial Profile of Water near Hydrophobic Surfaces. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 035431 10.1103/PhysRevB.88.035431. [DOI] [Google Scholar]
- Doshi D. A.; Watkins E. B.; Israelachvili J. N.; Majewski J. Reduced water density at hydrophobic surfaces: Effect of dissolved gases. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 9458–9462. 10.1073/pnas.0504034102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godawat R.; Jamadagni S. N.; Garde S. Characterizing hydrophobicity of interfaces by using cavity formation, solute binding, and water correlations. Proc. Natl. Acad. Sci. U. S. A. 2009, 106 (36), 15119–15124. 10.1073/pnas.0902778106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukuma T.; Garcia R. Atomic and Molecular-Resolution Mapping of Solid–Liquid Interfaces by 3D Atomic Force Microscopy. ACS Nano 2018, 12, 11785–11797. 10.1021/acsnano.8b07216. [DOI] [PubMed] [Google Scholar]
- Maoz R.; Cohen S. R.; Sagiv J. Nanoelectrochemical patterning of monolayer surfaces: toward spatially defined self-assembly of nanostructures. Adv. Mater. 1999, 11, 55–61. . [DOI] [Google Scholar]
- Onclin S.; Ravoo B.; Reinhoudt D. N. Engineering Silicon Oxide Surfaces Using Self-Assembled Monolayers. Angew. Chem., Int. Ed. 2005, 44, 6282–6304. 10.1002/anie.200500633. [DOI] [PubMed] [Google Scholar]
- Martínez R. V.; Martínez J.; Chiesa M.; Garcia R.; Coronado E.; Pinilla-Cienfuegos E.; Tatay S. Large-scale Nanopatterning of Single Proteins used as Carriers of Magnetic Nanoparticles. Adv. Mater. 2010, 22, 588–591. 10.1002/adma.200902568. [DOI] [PubMed] [Google Scholar]
- Janssen D.; De Palma R.; Verlaak S.; Heremans P.; Dehaen W. Static solvent contact angle measurements, surface free energy and wettability determination of various self-assembled monolayers on silicon dioxide. Thin Solid Films 2006, 515, 1433–1438. 10.1016/j.tsf.2006.04.006. [DOI] [Google Scholar]
- Gaigeot M. P.; Sprik M.; Sulpizi M. Oxide/water interfaces: how the surface chemistry modifies interfacial water properties. J. Phys.: Condens. Matter 2012, 24, 124106 10.1088/0953-8984/24/12/124106. [DOI] [PubMed] [Google Scholar]
- Fukuma T.; Ueda Y.; Yoshioka S.; Asakawa H. Atomic-Scale Distribution of Water Molecules at the Mica-Water Interface Visualized by Three-Dimensional Scanning Force Microscopy. Phys. Rev. Lett. 2010, 104, 016101 10.1103/PhysRevLett.104.016101. [DOI] [PubMed] [Google Scholar]
- Martin-Jimenez D.; Chacon E.; Tarazona P.; Garcia R. Atomically Resolved Three-Dimensional Structures of Electrolyte Aqueous Solutions near a Solid Surface. Nat. Commun. 2016, 7, 12164 10.1038/ncomms12164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umeda K.; Zivanovic L.; Kobayashi K.; Ritala J.; Kominami H.; Spijker P.; Foster A. S.; Yamada H. Atomic-Resolution Three-Dimensional Hydration Structures on a Heterogeneously Charged Surface. Nat. Commun. 2017, 8, 2111. 10.1038/s41467-017-01896-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Söngen H.; Reischl B.; Miyata K.; Bechstein R.; Raiteri P.; Rohl A. L.; Gale J. D.; Fukuma T.; Kühnle A. Resolving Point Defects in the Hydration Structure of Calcite (104) with Three-Dimensional Atomic Force Microscopy. Phys. Rev. Lett. 2018, 120, 116101 10.1103/PhysRevLett.120.116101. [DOI] [PubMed] [Google Scholar]
- Kuchuk K.; Sivan U. Hydration Structure of a Single DNA Molecule Revealed by Frequency-Modulation AFM. Nano Lett. 2018, 18, 2733–2737. 10.1021/acs.nanolett.8b00854. [DOI] [PubMed] [Google Scholar]
- Zhou S.; Panse K. S.; Motevaselian M. H.; Aluru N. R.; Zhang Y. Three-Dimensional Molecular Mapping of Ionic Liquids at Electrified Interfaces. ACS Nano 2020, 14, 17515–17523. 10.1021/acsnano.0c07957. [DOI] [PubMed] [Google Scholar]
- Su S.; Siretanu I.; van den Ende D.; Mei B.; Mul G.; Mugele F. Facet-Dependent Surface Charge and Hydration of Semiconducting Nanoparticles at Variable pH. Adv. Mater. 2021, 33, 2106229 10.1002/adma.202106229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakouzi E.; Stack A. G.; Kerisit S.; Legg B. A.; Mundy C. J.; Schenter G. K.; Chun J.; De Yoreo J. J. Moving beyond the Solvent-Tip Approximation to Determine Site-Specific Variations of Interfacial Water Structure through 3D Force Microscopy. J. Phys. Chem. C 2021, 125, 1282. 10.1021/acs.jpcc.0c07901. [DOI] [Google Scholar]
- Li Z.; Liu Q.; Zhang D.; Wang Y.; Zhang Y.; Li Q.; Dong M. Probing the hydration friction of ionic interfaces at the atomic scale. Nanoscale Horizons 2022, 7, 368–375. 10.1039/D1NH00564B. [DOI] [PubMed] [Google Scholar]
- Miyazawa K.; Kobayashi N.; Watkins M.; Shluger A. L.; Amano K.; Fukuma T. A relationship between three-dimensional surface hydration structures and force distribution measured by atomic force microscopy. Nanoscale 2016, 8, 7334–7342. 10.1039/C5NR08092D. [DOI] [PubMed] [Google Scholar]
- Hernández-Muñoz J.; Chacón E.; Tarazona P. Density functional analysis of atomic force microscopy in a dense fluid. J. Chem. Phys. 2019, 151, 034701 10.1063/1.5110366. [DOI] [PubMed] [Google Scholar]
- Hashimoto K.; Amano K.; Nishi N.; Onishi H.; Sakka T. Comparison of atomic force microscopy force curve and solvation structure studied by integral equation theory. J. Chem. Phys. 2021, 154, 164702. 10.1063/5.0046600. [DOI] [PubMed] [Google Scholar]
- Benaglia S.; Uhlig M. R.; Hernández-Muñoz J.; Chacón E.; Tarazona P.; Garcia R. Tip Charge Dependence of Three-Dimensional AFM Mapping of Concentrated Ionic Solutions. Phys. Rev. Lett. 2021, 127, 196101 10.1103/PhysRevLett.127.196101. [DOI] [PubMed] [Google Scholar]
- Qin X.; Dong M.; Li Q. Insight into the hydration friction of lipid bilayers. Nanoscale 2024, 16, 2402–2408. 10.1039/D3NR05517E. [DOI] [PubMed] [Google Scholar]
- Garcia R.; Perez R. Dynamic atomic force microscopy methods. Surf. Sci. Rep. 2002, 47, 197–301. 10.1016/S0167-5729(02)00077-8. [DOI] [Google Scholar]
- Hernández-Muñoz J.; Uhlig M. R.; Benaglia S.; Chacón E.; Tarazona P.; Garcia R. Subnanometer Interfacial Forces in Three-Dimensional Atomic Force Microscopy: Water and Octane near a Mica Surface. J. Phys. Chem. C 2020, 124, 26296–26303. 10.1021/acs.jpcc.0c08092. [DOI] [Google Scholar]
- Uhlig M. R.; Martin-Jimenez D.; Garcia R. Atomic-Scale Mapping of Hydrophobic Layers on Graphene and Few-Layer MoS2 and WSe2 in Water. Nat. Commun. 2019, 10, 2606. 10.1038/s41467-019-10740-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenter P.; Lee S. S. Hydration layer structure at solid–water interfaces. MRS Bull. 2014, 39, 1056–1061. 10.1557/mrs.2014.252. [DOI] [Google Scholar]
- Willard P.; Chandler D. The molecular structure of the interface between water and a hydrophobic substrate is liquid-vapor like. J. Chem. Phys. 2014, 141, 18C519. 10.1063/1.4897249. [DOI] [PubMed] [Google Scholar]
- Kanduč M.; Schlaich A.; Schneck E.; Netz R. R. Water-Mediated Interactions between Hydrophilic and Hydrophobic Surfaces. Langmuir 2016, 32, 8767–8782. 10.1021/acs.langmuir.6b01727. [DOI] [PubMed] [Google Scholar]
- Martinez-Martin D.; Longuinhos R.; Izquierdo J. G.; Marele A.; Alexandre S. S.; Jaafar M.; Gómez-Rodríguez J. M.; Bañares L.; Soler J. M.; Gomez-Herrero J. Atmospheric contaminants on graphitic surfaces. Carbon 2013, 61, 33–39. 10.1016/j.carbon.2013.04.056. [DOI] [Google Scholar]
- Wastl D. S.; Speck F.; Wutscher E.; Ostler M.; Seyller T.; Giessibl F. J. Observation of 4 nm Pitch Stripe Domains Formed by Exposing Graphene to Ambient Air. ACS Nano 2013, 7, 10032–10037. 10.1021/nn403988y. [DOI] [PubMed] [Google Scholar]
- Amadei C. A.; Lai C. Y.; Heskes D.; Chiesa M. Time dependent wettability of graphite upon ambient exposure: The role of water adsorption. J. Chem. Phys. 2014, 141, 084709 10.1063/1.4893711. [DOI] [PubMed] [Google Scholar]
- Kozbial A.; Zhou F.; Li Z.; Liu H.; Li L. Are graphitic surfaces hydrophobic?. Acc. Chem. Res. 2016, 49, 2765–2773. 10.1021/acs.accounts.6b00447. [DOI] [PubMed] [Google Scholar]
- Gallagher P.; Li Y.; Watanabe K.; Taniguchi T.; Heinz T. F.; Goldhaber-Gordon D. Optical Imaging and Spectroscopic Characterization of Self-Assembled Environmental Adsorbates on Graphene. Nano Lett. 2018, 18, 2603–2608. 10.1021/acs.nanolett.8b00348. [DOI] [PubMed] [Google Scholar]
- Temiryazev A.; Frolov A.; Temiryazeva M. Atomic-force microscopy study of self-assembled atmospheric contamination on graphene and graphite surfaces. Carbon 2019, 143, 30–37. 10.1016/j.carbon.2018.10.094. [DOI] [Google Scholar]
- Uhlig M. R.; Benaglia S.; Thakkar R.; Comer J.; Garcia R. Atomically Resolved Interfacial Water Structures on Crystalline Hydrophilic and Hydrophobic Surfaces. Nanoscale 2021, 13, 5275–5283. 10.1039/D1NR00351H. [DOI] [PubMed] [Google Scholar]
- Pálinkás G.; Kálvin P.; Vancsó K.; Kandrai M.; Szendrő G.; Németh M.; Németh A.; Pekker J. S.; Pap P.; Petrik K.; Kamarás L.; Tapasztó P.; Nemes-Incze P. The composition and structure of the ubiquitous hydrocarbon contamination on van der Waals materials. Nat. Commun. 2022, 13, 6770. 10.1038/s41467-022-34641-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preston D. J.; Miljkovic N.; Sack J.; Enright R.; Queeney J.; Wang E. N. Effect of hydrocarbon adsorption on the wettability of rare earth oxide ceramics. Appl. Phys. Lett. 2014, 105, 011601 10.1063/1.4886410. [DOI] [Google Scholar]
- Balajka J.; Hines M. A.; DeBenedetti W. J. I.; Komora M. High-affinity adsorption leads to molecularly ordered interfaces on TiO2 in air and solution. Science 2018, 361, 786–789. 10.1126/science.aat6752. [DOI] [PubMed] [Google Scholar]
- Seibert S.; Klassen S.; Latus A.; Bechstein R.; Kühnle A. Origin of Ubiquitous Stripes at the Graphite-Water Interface. Langmuir 2020, 36, 7789–7794. 10.1021/acs.langmuir.0c00748. [DOI] [PubMed] [Google Scholar]
- Arvelo D. M.; Uhlig M. R.; Comer J.; Garcia R. Interfacial layering of hydrocarbons on pristine graphite surfaces immersed in water. Nanoscale 2022, 14, 14178–14184. 10.1039/D2NR04161H. [DOI] [PubMed] [Google Scholar]
- Brown S. K.; Sim M. R.; Abramson M. J.; Gray C. N. Concentrations of Volatile Organic Compounds in Indoor Air – A Review. Indoor air 1994, 4, 123–134. 10.1111/j.1600-0668.1994.t01-2-00007.x. [DOI] [Google Scholar]
- Halios C. H.; Landeg-Cox C.; Lowther S. D.; Middleton A.; Marczylo T.; Dimitroulopoulou S. Chemicals in European residences – Part I: A review of emissions, concentrations and health effects of volatile organic compounds (VOCs). Sci. Total Environ. 2022, 839, 156201 10.1016/j.scitotenv.2022.156201. [DOI] [PubMed] [Google Scholar]
- Azhagiya Singam E. R.; Zhang Y.; Magnin G.; Coates I.; Thakkar R. H.; Comer J. Thermodynamics of Adsorption on Graphenic Surfaces from Aqueous Solution. J. Chem. Theory Comput. 2019, 15, 1302–1316. 10.1021/acs.jctc.8b00830. [DOI] [PubMed] [Google Scholar]
- Thakkar R.; Gajaweera S.; Comer J. Organic contaminants and atmospheric nitrogen at the graphene–water interface: a simulation study. Nanoscale Adv. 2022, 4, 1741–1757. 10.1039/D1NA00570G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y. H.; Yang C. W.; Fang C. K.; Ko H. C.; Hwang I. S. Interface-Induced Ordering of Gas Molecules Confined in a Small Space. Sci. Rep. 2014, 4 (1), 7189. 10.1038/srep07189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schlesinger I.; Sivan U. Three-Dimensional Characterization of Layers of Condensed Gas Molecules Forming Universally on Hydrophobic Surfaces. J. Am. Chem. Soc. 2018, 140, 10473–10481. 10.1021/jacs.8b04815. [DOI] [PubMed] [Google Scholar]
- Yang C. W.; Miyazawa K.; Fukuma T.; Miyata K.; Hwang I.-S. Direct comparison between subnanometer hydration structures on hydrophilic and hydrophobic surfaces via three-dimensional scanning force microscopy. Phys. Chem. Chem. Phys. 2018, 20, 23522–23527. 10.1039/C8CP02309C. [DOI] [PubMed] [Google Scholar]
- Sander R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmospheric Chemistry and Physics. 2015, 15, 4399–4981. 10.5194/acp-15-4399-2015. [DOI] [Google Scholar]
- Bonagiri L. K. S.; Panse K. S.; Zhou S.; Wu H. N.R.; Zhang Y. Real-space charge density profiling of electrode–electrolyte interfaces with angstrom depth resolution. ACS Nano 2022, 16, 19594–19604. 10.1021/acsnano.2c10819. [DOI] [PubMed] [Google Scholar]
- Zhao P.; Bai Y.; Liu B.; Chang H.; Cao Y.; Fang J. Process optimization for producing ultrapure water with high resistivity and low total organic carbon. Proc. Safety Environ. Control 2019, 126, 232–241. 10.1016/j.psep.2019.04.017. [DOI] [Google Scholar]
- Phillips J. C.; Hardy D. J.; Maia J. D. C.; Stone J. E.; Ribeiro J. V.; Bernardi R. C.; Buch R.; Fiorin G.; Hénin J.; Jiang W.; McGreevy R. M. C. R.; Radak K.; Skeel R. D.; Singharoy A.; Wang Y.; Roux B.; Aksimentiev A.; Luthey-Schulten Z.; Kalé L. V.; Schulten K.; Chipot C.; Tajkhorshid E. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Comput. Chem. 2020, 153, 044130 10.1063/5.0014475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopkins C. W.; Le Grand S.; Walker R. C.; Roitberg A. E. Long-time-step molecular dynamics through hydrogen mass repartitioning. J. Chem. Theory Comput. 2015, 11, 1864–1874. 10.1021/ct5010406. [DOI] [PubMed] [Google Scholar]
- Feller S. E.; Zhang Y. H.; Pastor R. W.; Brooks B. R. Constant pressure molecular dynamics simulations-the Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
- Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A. D. Jr. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emami F. S.; Puddu V.; Berry R. J.; Varshney V.; Patwardhan S. V.; Perry C. C.; Heinz H. Force field and a surface model database for silica to simulate interfacial properties in atomic resolution. Chem. Mater. 2014, 26, 2647–2658. 10.1021/cm500365c. [DOI] [Google Scholar]
- Sagiv J. Organized monolayers by adsorption. 1. Formation and structure of oleophobic mixed monolayers on solid surfaces. J. Am. Chem. Soc. 1980, 399, 92–98. 10.1021/ja00521a016. [DOI] [Google Scholar]
- Love J. C.; Estroff L. A.; Kriebel J. K.; Nuzzo R. G.; Whitesides G. M. Self-assembled monolayers of thiolates on metals as a form of nanotechnology. Chem. Rev. 2005, 105, 1103–1170. 10.1021/cr0300789. [DOI] [PubMed] [Google Scholar]
- Casalini S.; Botolotti C. A.; Leonardi F.; Biscarini F. Self-assembled monolayers in organic electronics. Chem. Soc. Rev. 2017, 46, 40–71. 10.1039/C6CS00509H. [DOI] [PubMed] [Google Scholar]
- Ricci M.; Spijker P.; Voïtchovsky K. Water-induced correlation between single ions imaged at the solid–liquid interface. Nat. Commun. 2014, 5, 4400. 10.1038/ncomms5400. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.