Biomolecular condensates can function as inherent catalysts

SUMMARY

We report the discovery that chemical reactions such as ATP hydrolysis can be catalyzed by condensates formed by intrinsically disordered proteins (IDPs), which themselves lack any intrinsic ability to function as enzymes. This inherent catalytic feature of condensates derives from the electrochemical environments and the electric fields at interfaces that are direct consequences of phase separation. The condensates we studied were capable of catalyzing diverse hydrolysis reactions, including hydrolysis and radical-dependent breakdown of ATP whereby ATP fully decomposes to adenine and multiple carbohydrates. This distinguishes condensates from naturally occurring ATPases, which can only catalyze the dephosphorylation of ATP. Interphase and interfacial properties of condensates can be tuned via sequence design, thus enabling control over catalysis through sequence-dependent electrochemical features of condensates. Incorporation of hydrolase-like synthetic condensates into live cells enables activation of transcriptional circuits that depend on products of hydrolysis reactions. Inherent catalytic functions of condensates, which are emergent consequences of phase separation, are likely to affect metabolic regulation in cells.

INTRODUCTION

Biomolecular condensates concentrate condensate-specific biomolecules to regulate diverse cellular functions¹ such as stress responses and ribosomal biogenesis^2–5. Condensates form via composite processes that combine phase separation and reversible associations such as stoichiometric binding and non-stoichiometric percolation transitions also known as sol-gel transitions^6–8. We refer to the collection of processes that contribute to condensate formation as condensation^1,9,10. Multivalent macromolecules, such as intrinsically disordered proteins (IDPs), drive condensation. Partitioning of client molecules and ligands can influence cellular functions of condensates and the driving forces for condensation^11–19.

Condensation, which involves spontaneous phase separation as a key driving process, results in the coexistence of two or more phases^10,20–27. The differences in solvent and biomolecular compositions between the condensate interiors and coexisting dilute phases result in unique interphase physicochemical properties. These come about due to the establishment of phase equilibria whereby the chemical and / or electrochemical potentials of each species are equalized, thus giving rise to asymmetric partitioning of these species in coexisting dense and dilute phases^8,28. Interphase properties including electric potentials such as Donnan potentials are set up by differential partitioning of solution ions across condensate interiors and coexisting dilute phases^28–31. Other interphase potentials such as proton motive forces are set up by pH gradients as was recently shown for nucleoli, whereby the interiors are more acidic when compared to the surrounding nucleoplasm^9,10. Interphase electric potential gradients give rise to an electric double layer at condensate interface²², and these have measurable consequences such as zeta potentials³² and strong interfacial electric fields³³.

The presence of unique interphase and interface properties, including asymmetries of ionic and hydration properties across coexisting phases and the implied presence interfacial electric potentials^{14,22,25–27}, suggests that distinct functionalities can be enabled by the unique chemical environments within condensates and at their interfaces. This hypothesis derives from analogies with what has been shown in colloid chemistry and micron-sized water droplets^34–38. A chemically active emulsion would imply that condensate functions are not solely determined by their capacity to store and compartmentalize biomolecules^39,40, but they will also contribute as enablers of biochemical reactions through their distinct interphase and interfacial physicochemical properties.

The unique physicochemical environments created within condensates and their interfaces inspired us to draw parallels with proteins enzymes, wherein catalytic activities can be attributed, at least partially, to the local environments within the enzyme active sites. This includes the distinctive solvent environment and electric fields created by unique structural alignments of functional residues^41–44. We reasoned that the physicochemical properties within condensate interiors and interfaces might share similarities to those within the catalytic sites of enzymes. Therefore, while enzymes are nanoscale catalysts, we conjectured that condensates have the potential to function as mesoscale catalysts. Accordingly, we tested whether the unique chemical features of condensates can induce spontaneous catalytic functions.

We present the results of assays and mass spectroscopy experiments used to evaluate the catalytic functions of different types of biomolecular condensates that possess distinct physicochemical features. The capability of condensates to catalyze hydrolysis reactions was evaluated both in vitro and in living cells. The underlying driving forces that mediate catalysis were studied using density functional theory and examined via vibrational stark effects. Using de novo designs of IDPs that were guided by coarse-grained simulations we uncover a decoupling of the contribution from the dense phase chemical environments and the interfacial electric fields to the kinetics of enzymatic reactions catalyzed by condensates. To explore whether the catalytic functions of condensates can drive cellular processes, we implemented RNA sequencing and constructed synthetic gene circuits to assess how catalytic functions of condensates affect downstream cellular processes. Overall, we find that condensates formed by catalytically inactive IDPs have the emergent property of being able to function as inherent catalysts of biochemical reactions such as hydrolysis of ATP.

RESULTS

We first utilized two programmable model systems based on polypeptides with repeating units namely, resilin-like polypeptides (RLPs) and elastin-like polypeptides (ELPs). RLPs undergo phase transitions driven by intra/inter-molecular interactions based on electrostatic and pi-based interactions^45,46, while ELPs undergo phase transitions driven by hydrophobicity based on the release of water molecules from the protein backbone^12,47. Therefore, the condensates formed by RLPs and ELPs arise from different driving forces, and they are defined by different chemical environments^22,48.

Hydrolysis reactions can be catalyzed by condensates:

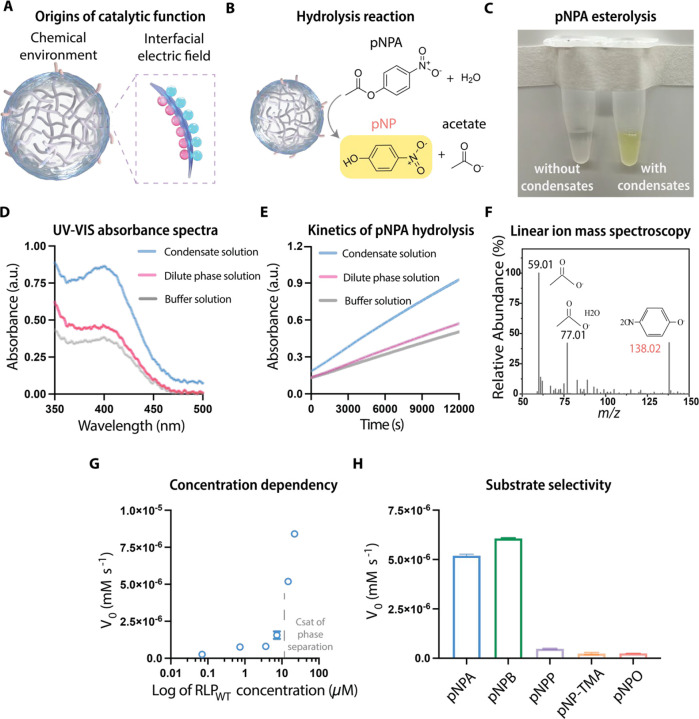
Hydrolysis is a crucial biochemical process in live cells (Figure 1A). As a reaction it enables energy production and is a key driver of cellular signaling^49,50. Enzyme catalyzed hydrolysis by ATPases involves the binding of ATP, the substrate within the active site and cleavage of a bond by a water molecule⁵¹. Hydrolysis typically requires an alkaline environment⁵², and this matches the dense phase environments of RLP condensates²². Accordingly, we first explored the effects of condensates formed by the RLP_WT protein (amino acid sequence: Ser-Lys-Gly-Pro-[Gly-Arg-Gly-Asp-Ser-Pro-Tyr-Ser]₂₀-Gly-Tyr) on ester hydrolysis. Phase transitions of RLP_WT were triggered by reducing the ionic activity of the solution (Figure S1A, S1B). We applied a chromogenic assay using para-nitrophenyl acetate (pNPA), which is a widely used substrate for the evaluation of esterase activity⁵³. Hydrolysis of pNPA decomposes the substrate to acetate and para-nitrophenolate (pNP) (Figure 1B), and product release can be directly monitored by UV-visible absorption spectroscopy at a wavelength of 410 nm, which is the absorption wavelength of phenol. We evaluated the pNPA hydrolysis reaction using an absorption scan under three different solution conditions: solution with condensates (c_RLP > c_sat), solution without condensates (c_RLP < c_sat), and the buffer solution without protein. Here, c_RLP and c_sat are the bulk and saturation concentrations of RLP, respectively. In solutions with condensates, the colorless pNPA turned yellow after 120 min of incubation at room temperature (Figure 1C). This was evident from the appearance of a product absorption band at 410 nm (Figure 1D). In the solution without condensates and in the buffer solution, a similar intensity of the absorption was observed with a much lower signal compared to the solution with condensates. The weak signals in condensate-free or buffer solutions derive from the spontaneous hydrolysis of pNPA. Overall, our results suggest that the presence of condensates help catalyze the hydrolysis of pNPA (Figure 1E).

Figure 1. Biomolecular condensates can function as catalysts of hydrolysis.

A, Biomolecular condensates possess a unique chemical environment in the dense phase and an electric field at their interface.

B, The hydrolysis reaction of p-nitrophenol acetate (pNPA) results in the formation of p-nitrophenol (a yellow product) and acetate.

C, Image visualization of the catalytic reaction with a change of color in the solution with condensates. The samples containing 0.5 mM pNPA with or without condensates were incubated at room temperature for 120 min.

D, UV-Vis absorbance spectrums of 1) the solution containing condensates and pNPA, 2) the solution containing only the dilute phase of a phase separated sample and pNPA, 3) the buffer solution containing pNPA. The final concentration of pNPA was 0.5 mM.

E, Time-dependent absorbance tracking of pNPA reaction with the same experimental setup as in d. N = 4 independent experimental trail. Each data point represents mean ± SD.

F, A sample spectrum of linear ion mass spectroscopy analysis of the supernatant of the condensate solution containing pNPA after incubation of 120 min at room temperature. The same analysis was performed three times with different samples and the results were consistent.

G, Protein concentration-dependent initial rate (V₀) of the pNPA catalytic reaction. The protein concentration at which a sharp transition of the initial rate happened aligned with the saturation concentration of the RLP_WT.

H, Evaluation of the catalytic specificity of RLP_WT condensates using different substrates by comparing their initial rate at the same substrate concentration of 0.5 mM. The evaluated substrates were p-nitrophenyl butyrate (pNPB), p-nitrophenyl phosphate (pNPP), p-nitrophenyl octanoate (pNPO) and p-nitrophenyl trimethylacetate (pNP-TMA).

To test if the reaction products are concordant with hydrolysis of pNPA, we used linear ion mass spectroscopy to analyze the supernatant of the condensate solution with pNPA after 120 min of incubation at room temperature. Distinct peaks at m/z values of 138, 77, and 59 were observed (Figure 1F). These correspond to p-nitrophenol, acetate, and acetate hydrate, confirming the esterolysis of pNPA in the solution with condensates. To evaluate whether the catalytic reaction is governed by condensate formation, we applied the pNPA assay to solutions containing different concentrations of RLP_WT and quantified the initial velocity (V₀). The bulk concentration of RLP_WT is not correlated with V₀. Instead, we find that once the concentration of RLP_WT crosses the saturation concentration (c_sat), V₀ increases exponentially (Figure 1G and Figure S1C). This observation suggests that the catalytic function requires the formation of condensates.

To shed light on the mechanism by which condensates influence pNPA hydrolysis, we asked if the RLP_WT condensate acts as a catalyst instead of a reactant. As a catalyst, the material of the condensates should not be produced or destroyed by the pNPA decomposition reaction⁵⁴. We quantified the dense phase concentration using a sedimentation assay and compared the physical forms of the dense phase using confocal phase contrast imaging. Across samples, with and without pNPA after 120 min of incubation at room temperature (Figure S2A), we did not observe significant differences in the dense phase concentrations or areas of the condensates (Figure S2B, S2C). These observations suggest that the reaction does not consume the components of the condensates and the constituents of the condensate are not chemically active⁵⁵ during the reaction period.

Condensates can mediate hydrolysis of substrates with distinct side groups:

To explore whether the hydrolysis reactions catalyzed by condensates are substrate-specific, we employed different compounds as substrates. These compounds have distinct chemical groups next to the ester bond (Figure S3). We first tested the ability of RLP_WT condensates to catalyze hydrolysis of nitrophenyl esters with different sidechains, including p-nitrophenyl butyrate (pNPB), p-nitrophenyl trimethylacetate (pNP-TMA) and p-nitrophenyl octanoate (pNPO). By subtracting spontaneous hydrolysis rates of the substrates in the buffer from the signal generated by the RLP_WT condensate-dependent hydrolysis reactions, we found that all the substrates show certain level of increase in their hydrolysis rates. the The rate of hydrolysis reactions influenced by RLP_WT condensates depends on the lengths of sidechains of the different substrates (Figure 1h). At the same substrate concentration, pNPB, which contains a shorter side chain than pNPA, showed a higher initial hydrolysis rate than pNPA. In contrast, pNP-TMA and pNPO, which contain a longer side chain than pNPA, showed a lower initial hydrolysis rate than pNPA.

To further explore the capability of condensates to catalyze hydrolysis of a distinct chemical group, we investigated whether the RLP_WT condensates enable the hydrolysis of p-nitrophenyl phosphate (pNPP), the hydrolysis of which is a dephosphorylation process. Surprisingly, we found that RLP_WT condensates can also catalyze dephosphorylation (Figure S4). These findings suggest that condensates have broad substrate specificity and can catalyze different reactions. This lends credence to the idea that the unique chemical features of condensates provide a favorable environment for enhancing the rates of reactions.

Interfacial electric fields help lower the free energy barrier for hydrolysis reactions:

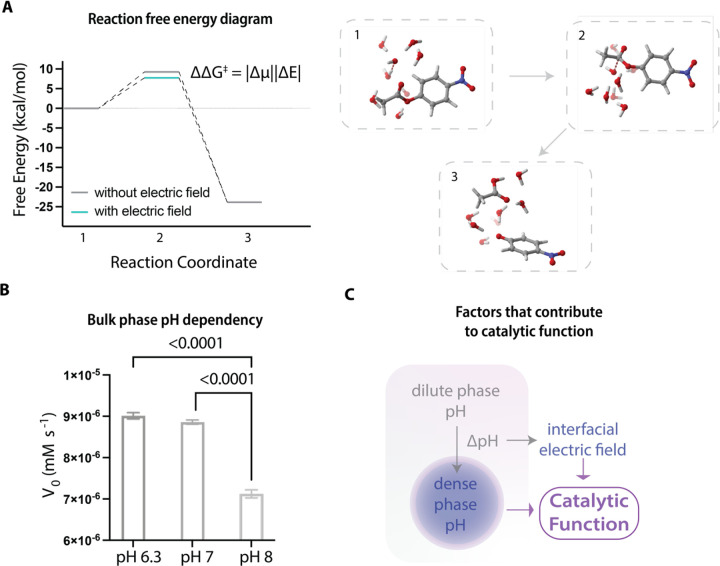
The fact that condensates can catalyze different chemical reactions implies that the catalytic feature of condensates are influenced by the unique electrochemical features defined by the environments of condensate solution²². Specifically, we hypothesized that interfacial electric fields of condensates might lower the activation free energy that must be crossed for reactions to occur^56,57. To explore the physical basis of this possibility, we studied the influence of external electric field strengths on the rates of pNPA hydrolysis using Density Functional Theory (DFT)⁵⁸. We evaluated the difference in dipole moment between the initial substrate and the transition state of the substrate to quantify the field-induced change of the reaction barrier (see STAR Methods for details). Under the influence of an electric field strength of ~10 MV/cm (a typical value in the protein environment⁵⁹), the free energy barrier (ΔΔG‡) decreases from 9.26 kcal/mol to 7.73 kcal/mol at the intermediate state (Figure 2A). This decrease of barrier should correspond to an approximate 13-fold increase in the rate of pNPA hydrolysis, and this is comparable to the observations in our experiments. This result suggests that interfacial electric fields of condensates are likely to play an important role in catalyzing chemical reactions.

Figure 2. Evaluation of the role of interfacial electric fields on driving hydrolysis reactions.

A, The reaction free energy diagram calculated based on DFT shows the effect of external electric fields on lowering the free energy barrier of the transition state of pNPA hydrolysis. The right panel shows the entire hydrolysis reaction pathway calculated with an explicit first solvation shell (with 7 H₂O molecules) combined with a conductor-like polarizable continuum model (CPCM).

B, The bulk phase pH dependency of catalytic behavior of RLP_WT condensates. RLP_WT condensates under different bulk phase pH conditions can generate different interphase pH gradients cross the phases, while maintaining a similar dense phase alkaline pH. This gives rise to distinct initial rates for pNPA catalysis.

C, The dominating factors contributing to the catalytic functions of condensates are the dense phase chemical environment and the interfacial electric field.

To modulate the interfacial field and evaluate its contribution to the catalytic functions, we first altered the bulk phase environmental pH to evaluate its effect on pNPA hydrolysis by RLP_WT condensates. This experiment was motivated by previous discoveries showing that the dense phase pH of RLP_WT condensates does not shift significantly upon a change in the bulk phase pH²². Accordingly, decreasing the bulk phase pH of the solution containing RLP_WT condensates (with an alkaline dense phase) will generate an increased interphase pH gradient between the dilute and dense phases²². This, in turn, should lead to a stronger interfacial electric field. Therefore, by testing the catalytic behavior of RLP_WT condensates at different bulk phase pH conditions, we sought to understand the contributions of the bulk environment and the interfacial electric field to the catalytic functions. In accord with our hypothesis, when compared to condensates prepared in solutions that are more basic, we observed a significantly higher initial rate of hydrolysis from RLP_WT condensates in solutions that are more acidic (Figure 2B), even though a basic bulk environment is favorable for the hydrolysis of pNPA. This observation implies that 1) a larger interphase pH gradient, which in turn enhances the strength of the interfacial electric fields, promotes the catalytic performance of condensates formed by RLP_WT, and 2) the bulk solution phase contributes minimally to the catalytic activity of condensates. Taken together, our data suggest that condensation, which generates two coexisting phases delineated by an interface, defines an environment that catalyzes hydrolysis. The performance of condensates as catalysts is enhanced by increasing the interphase pH gradient and consequently the interfacial electric field (Figure 2C).

Decoupling the contributions of dense phases and the interfacial electric field to the catalytic capability of condensates:

Next, we set out to isolate the contributions of the microenvironment of the dense phase versus the interface to the catalytic functions of condensates. We employed the pNPP assay for further investigations due to its low background signal and the important role of dephosphorylation reactions in cellular processes^60–62 (Figure 3A and Figure S4). We first used the condensates formed by an ELP with a sequence of [Val-Pro-Gly-Val-Gly]₆₀. This sequence lacks charged residues. A limited pH gradient across the dilute and dense phases was found in the ELP condensates²², suggesting a limited electric potential gradient between phases. Accordingly, as expected, the ELP condensates were incapable of mediating catalytic functions (Figure S5A).This suggests that ionizable residues are necessary to generate interphase electric potentials²⁸, which in turn generate from the interfacial electric fields that contribute to inherent catalytic functions.

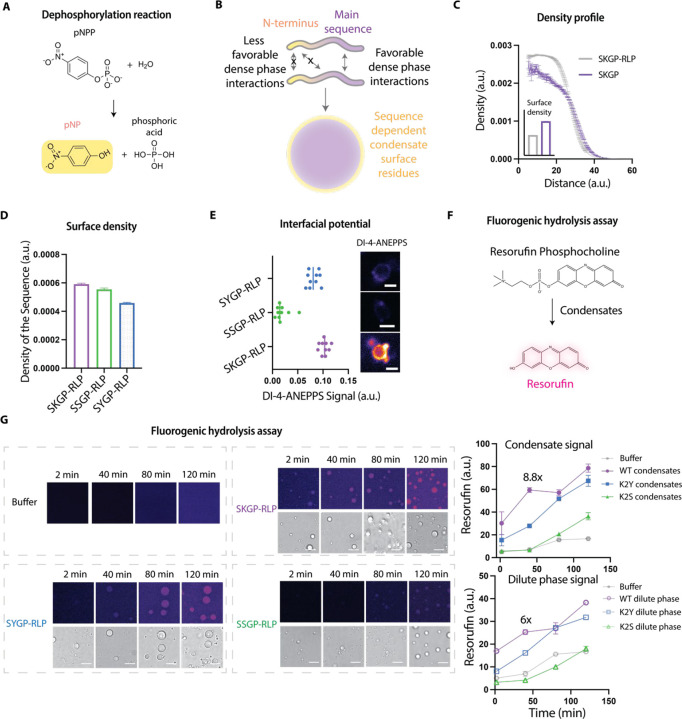
Figure 3. Decoupling the contribution of the dense phase chemical environment and the interfacial electric field to the catalytic function of condensates.

A, The hydrolysis reaction of p-nitrophenol phosphate (pNPP) results in the formation of p-nitrophenol (a yellow product) and phosphoric acid.

B, Schematic showing that regions of an IDP can have different intrinsic preferences for interacting localizing to the dense phase versus preferentially localizing to the interfaces of condensates.

C, Radial density plots of the N-terminal region (first four residues) and full-length protein from simulations of the full-length RLP_WT. Each data point represents mean ± SE. Inset shows the comparison of the density of the N-terminal sequence and the full-length sequence at the interface of the condensates based on the radial density plots. Bar graph shows the mean ± SE.

D, Comparison of the density of the N-terminal sequence at the condensate interface for different N-terminal sequences: Ser-Lys-Gly-Pro, Ser-Ser-Gly-Pro, and Ser-Tyr-Gly-Pro. Bar graph shows the mean ± SE.

E, Evaluation of the interfacial electric field of different sequences (SKGP-RLP, SSGP-RLP, SYGP-RLP) using ratiometric DI-4-ANEPPS fluorescence assay. The insets show the sample ratiometric images of condensates (at similar size) with DI-4-ANEPPS.

F, Fluorogenic hydrolysis reaction of resorufin phosphocholine generates fluorescent resorufin.

G, Comparison of the resorufin signal of the fluorogenic assay using different condensates formed by RLPs with different N-terminal sequences namely, SKGP-RLP, SSGP-RLP, and SYGP-RLP. The excitation was set at 550 nm with a WLL laser, and the emission detector was set at 570–600 nm on a HYD detector. The highest fluorescence signal within a 15 μm z range was identified for quantification of the resorufin signal. The grey line represents the spontaneous hydrolysis of resorufin phosphocholine in the same buffer solution. Scale bar is 5 μm. Each data point represents mean ± SE.

To understand how interfaces contribute to catalytic reactions, we explored whether we could design IDP sequences to modulate the surface charges of condensates without changing dense phase environments. We hypothesized that the surface charge density of condensates will define the strength of the interfacial electric field^63,64, thereby modulating the catalytic behaviors. Similar to colloidal particles in a solution containing electrolytes^65,66, the first layer of ions within the Stern layer⁶⁷, which is governed by the surface charge of the colloid particle, will organize the assembly of the second layer of ions that screens the first layer within the shear plane. This gives rise to the electric double layer that defines the strength of the interfacial electric field.

We hypothesized that if certain regions of IDPs preferentially partition to the interface of the condensate, then we should be able to tune the surface charges of condensates⁶⁸ thereby disrupting interfacial ion organization (Figure 3B). To this end, we first employed a coarse-grained simulation approach using LaSSI⁶⁹, which is a Monte-Carlo simulation engine that has been used to model phase behaviors of low-complexity sequences and the internal organization of condensates^14,70. The simulations helped us explore if there is a defined region of RLP_WT that has a higher preference of localizing to condensate surface. The repetitive nature of the RLP sequence mediates strong homotypic interactions. We focused our attention on the N-terminus (Ser-Lys-Gly-Pro), which lacks sticker residues^71,72 and is distinct from the repetitive main sequence. We hypothesized that the N-terminus should interact weakly with repetitive elements within the dense phase and that the charged Lys residue in the N-terminus might drive a preference for the N-terminus to localize to the condensate surface.

We performed simulations using the full-length protein and analyzed the resulting radial density profiles. This analysis focused on the localization preferences of the N-terminus versus the rest of the sequence. As expected, the N-terminus shows a decreased density in the dense phase (Figure 3C) and an increased density at the interface when compared to either the C-terminus or the full protein. This observation suggests that the specific sequence of the N-terminus (Ser-Lys-Gly-Pro) may promote its localization to the interface.

Next, we made variants containing different N-terminal sequences by replacing the charged residue, Lys, in the N-terminus sequence with a Ser or Tyr. This sets up a hierarchy whereby the wild-type (SKGP) N-terminus, which contains a Lys residue, would have the weakest interaction with the main repeat, followed by the N-terminus with a Ser residue (SSGP), and the N-terminus with a Tyr residue (SYGP), which should have the strongest interaction with the main repeat. Indeed, we observed that the density of the N-terminal sequence motif in the interface was significantly diminished for the variants when compared to the WT sequence, with the N-terminus containing a Tyr showing the lowest preference for localization to the interface (Figure 3D). This finding confirms that the relative interaction strengths between distinct sequence regions can affect the spatial preferences of each region within a condensate⁷⁰. This also provides a fundamental ability to program the interfaces of condensates without disrupting interactions within dense or dilute phases, thereby allowing us to isolate contributions from the interfacial electric field to catalytic behaviors.

We investigated the effects of distinct sequences on the interfacial electric field and the catalytic behaviors of the resulting condensates. We hypothesized that removal of the charged residue at the interface of condensates modifies surface electrostatics and ion alignments^73,74, thereby changing the strength of the interfacial electric field and catalytic capabilities. To ensure that the modification of a single-amino acid residue at the N-terminus does not affect the internal properties of condensates, we first measured the dense phase concentrations of these condensates and did not observe significant differences (Figure S5B). This suggests that the homotypic interactions between the main repetitive sequences stabilize the dense phase. Next, we probed the pH of these condensates using a previously established method²² and found that the N-terminus sequence does not significantly affect the dense phase pH (Figure S5C), confirming that the main repetitive sequences determine the chemical environments of the dense phase.

To investigate how the interfacial properties of condensates change due to single mutations in the N-terminus, we used a ratiometric DI-4-ANEPPS dye, which undergoes a structural change and fluoresces upon experiencing a local electric field^22,75,76. The ratiometric feature of ANEPPS allows us to quantify the electric field strength without considering the concentration-dependent effect of the dye⁷⁵. We compared condensates of similar sizes and found a noticeable difference in the interfacial signal between the WT (SKGP), K2S (SSGP), and K2Y (SYGP) sequences. The interfacial potentials are strongest for WT, followed by K2Y, and weakest for K2S, with an over 5-fold lower signal generated by K2S (Figure 3E). This observation suggests that the interfacial alignment of ions, which can be modulated by interfacial electrostatics dictated by the protein sequence, will perturb local ion density and modulate the strength of the interfacial electric field.

Sequences that encode the same dense phase chemical environments of condensates while enabling distinct interfacial features enable the quantification of contributions of interfacial electric fields to the catalytic functions of condensates. To study this feature at a single condensate level, we designed a fluorogenic assay using resorufin phosphocholine as the substrate. Hydrolysis of this substrate removes the phosphocholine and yields a fluorescent resorufin (Figure 3F). We tracked the catalytic behaviors of condensates formed by different sequences as a function time (Figure 3G). We specifically compared the resorufin signal in different condensates but with similar size (r =1–3 μm). The resorufin signal of condensates formed by RLP_WT was significantly higher than that of condensates formed by the mutants K2S and K2Y. The most significant difference was recognized at 40 min with an 8.8-fold catalytic product difference between the condensates of RLP_WT and the condensates formed by K2S (Figure 3G). This signal difference between different types of condensates possessing similar dense phase environments suggests that the resorufin is not specifically partitioned into the condensates. Instead, the trends in resorufin signals, which reflect the catalytic activity of different condensates, correlate with their differences in interfacial potentials. Similarly, the dilute phase of RLP_WT condensates also showed the highest signal. This is concordant with the phase separation generating coexisting phases, thereby generating distinct dense and dilute phases that are delineated by distinct, system-specific interfaces. Taken together with data for ELP versus RLP condensates, our observations suggest that the interphase physicochemical properties defined by differences between coexisting dilute and dense phases, and the interfacial electric fields are key determinants of catalytic properties of condensates.

Condensation regulates catalytic behavior by creating distinct solvent environments:

Water molecules are key components of hydrolysis reactions. In addition to the surface electrostatics that depends on interfacial electric fields as described by the Gouy-Chapman-Stern formalism⁷⁷, the total field generated by the two-phase system will also be influenced by the solvent dipoles that are mediated by solvent-solute interactions⁷⁸. An example of this is the Onsager reaction field at an electrochemical interface⁷⁹. Similarly, due to the same solvent polarity-dependent field, the abundance of free water molecules that can form hydrogen bonds with solutes or substrates has also been correlated with the rates of hydrolysis reaction with a lower water activity mediating a faster hydrolysis reaction^80,81. We reasoned that the differences in the properties of water across coexisting phases, which we refer to as interphase water potentials⁸², and the distinct features of interfacial hydration might be key determinants of the catalysis of hydrolysis by condensates. Accordingly, we tested the hypothesis that the impact of different condensates on catalyzing hydrolysis can be explained by differences in “interphase waters”, which refers to differences in water organization and the properties of water affected by condensate formation within the two-phase system. To test for this effect, we employed stimulated Raman scattering (SRS) microscopy^83–88 to help make inferences regarding the hydrogen-bonding environment based on the availability of free water molecules compared to biomolecule-bound water⁸³.

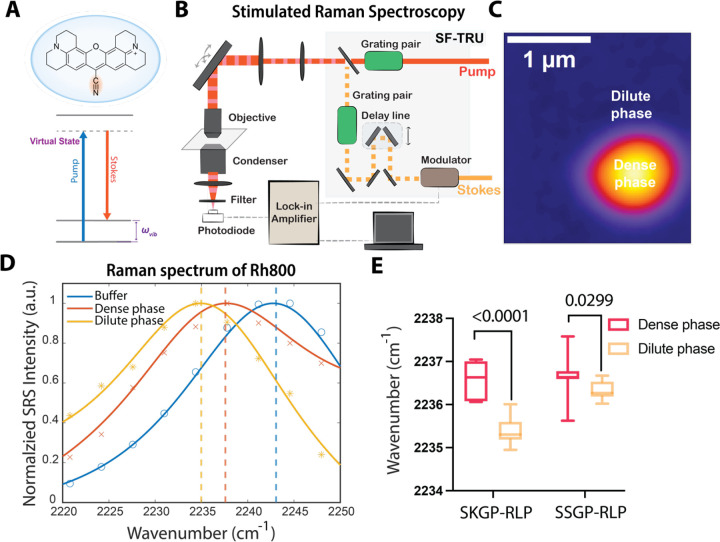
To the condensate solution, we added Rh800 (Figure 4A and 4B), which is a Raman probe with a nitrile group that is sensitive to local water environment^83,89. The Raman frequency of C≡N vibration (${\overline{v}}_{C\equiv N}$) for Rh800 redshifts with increasing bound water components in the local environment⁹⁰. Based on this setup, we first evaluated condensates formed by RLP_WT (Figure 4C). Compared to the original resonance of Rh800 in a pure buffer solution, we analyzed the ${\overline{v}}_{C\equiv N}$ on the both sides of the interface and observed red-shifts of the ${\overline{v}}_{C\equiv N}$ between the dense phase and the dilute phase of the condensates. This points to a substantial decrease of water activity in the condensate solution⁸³. A significant difference between the ${\overline{v}}_{C\equiv N}$ of the dilute and the dense phases further confirms the existence of a strong interfacial electric field, pointing to a notable contribution of the solvent dipole to the interfacial field.

Figure 4. Characterization of water environments using hyperspectral stimulated Raman Spectroscopy.

A, Chemical structure of nitrile bearing Rh800 and the energy diagram of the stimulated Raman process.

B, Microscope setup for stimulated Raman imaging with Rh800 probe for condensate samples.

C, A representative image showing the fluorescence signal of Rh800 in a condensate with spatially defined dense and dilute phases.

D, Normalized SRS spectrums of condensate buffer (50 mM Tris, 150 mM NaCl), the dilute phase and the dense phase of condensates formed by RLP_WT.

E, Comparison of SRS peak frequency of C≡N of Rh800 evaluated for the dilute and the dense phases of condensates formed by different sequences. Unpaired T-test shows the p-value.

Next, we applied the same assay to evaluate condensates formed by K2S sequences. When compared to condensates formed by K2S sequence, condensates formed by WT sequence showed a 3-fold larger redshift of ${\overline{v}}_{C\equiv N}$ corresponding to a larger water gradient across the interface (Figure 4D). This explains our observation of a stronger interfacial field for WT condensates when compared to K2S condensates. Our observations of the lowered water activity due to the existence of condensates with appropriate interfacial characteristics aligns with previous studies, which found that the solution environment with an increased quantity of bound water molecules favors hydrolysis reactions because this helps lower the activation energy and entropy of the reaction^80,91. Taken together, the analysis of vibrational frequency of Rh800 in different condensate solutions points to a critical role of water molecules in defining the interfacial electric field whereby rate enhancements of hydrolysis reactions are partially determined by the changes in water activities due to condensation.

Condensate-dependent hydrolysis is generalizable:

We next asked if condensates formed by naturally occurring IDPs also possess catalytic functions. To explore whether the catalysis of hydrolysis by condensates might be a generic feature, especially if the IDPs feature ionizable residues, which are essential for mediating the asymmetric ion distribution in the coexisting phases²⁸, we reconstituted different condensates formed by IDRs of the Dead-Box helicase 4 (Ddx4) from nuage bodies⁹², the prion-like low complexity domain of hnRNP A1 (A1-LCD) from stress granules⁷², and the nucleolar protein Ly-1 antibody reactive (LYAR)⁹. We used the pNPP assay to evaluate whether condensates formed by naturally occurring IDPs can catalyze reactions. We found that compared to the dilute phase protein and the buffer solution, solutions containing condensates formed by Ddx4 and LYAR were able to catalyze the decomposition of pNPP, while A1-LCD condensates showed minimal functionality as catalysts (Figure S6). Ddx4 condensates showed the most significant activation with an over 4-fold increase of catalytic products after 150 min incubation at room temperature. The distinct catalytic behaviors of condensates formed by Ddx4 and LYAR versus A1-LCD can be explained by the high fraction of charged residues and polyampholytic character of the IDRs of Ddx4⁹² and LYAR⁹. In contrast, the A1-LCD has a low fraction of charged residues⁷².

We also explored whether facsimiles of native condensates formed via heterotypic protein-RNA interactions could mediate catalytic functions. For this, we selected condensates formed by nucleophosmin 1 (NPM1) and mature rRNA⁹ (mat-rRNA). Recently, King et al., showed that these condensates are formed via asymmetric complex coacervation and defined by an interphase pH gradient, whereby the interior has a pH of 6.5 and the coexisting dilute phase has a pH of 7.1⁹. This interphase pH gradient should set up a strong interfacial electric field that enables catalytic activity. To test for this, we used the pNPP assay and assessed the catalytic functions of NPM1 + mat-rRNA condensates. Compared to the solutions containing only NPM1 protein, mat-rRNA, and buffer, the solution containing the NPM1-rRNA condensates was able to accelerate the decomposition of pNPP (Figure S6). These observations suggest that the inherent catalytic functions of condensates are encoded in the sequence grammars of the biomolecules and the partitioning features defined by the driving forces for condensation. Our findings regarding the catalytic activities of NPM1 + mat-rRNA condensates are likely to have broad implications for activities at the interface between granular components of nucleoli and the nucleoplasm.

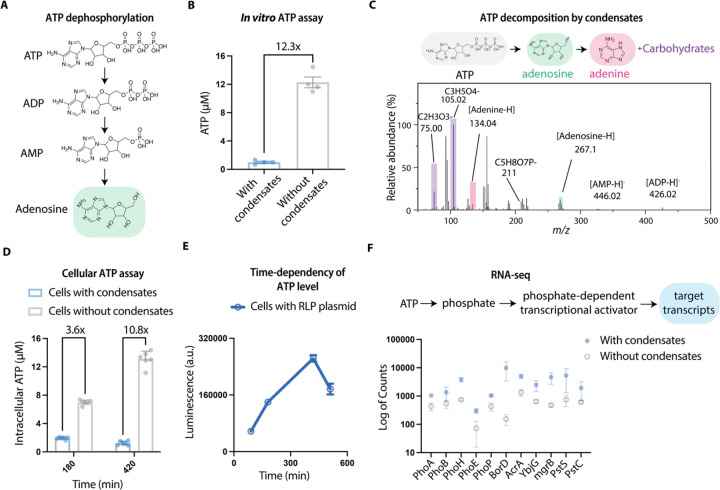
Condensates decompose ATP to adenine and carbohydrates:

Catalysis of dephosphorylation reactions is one of the main chemical pathways for energy generation in biology⁹³. Considering the broad substrate specificity of condensate catalytic behavior, we explored whether condensates could facilitate the dephosphorylation reactions of adenosine triphosphate (ATP), a process typically mediated by ATPases⁹⁴ (Figure 5A). We tested this possibility with RLP_WT condensates and characterized the decomposition of ATP using a bioluminescence-based ATP quantification assay (see Figure S7A for calibration). After incubating condensates with ATP for 30 minutes at room temperature, we found that over 95% of the ATP was decomposed by condensates (Figure 5B). To probe products of the decomposition reaction of ATP, we employed linear ion mass spectroscopy and characterized the supernatant of the reaction solution. Surprisingly, we not only found the existence of ADP and AMP, which are typical products of ATP dephosphorylation reactions⁹⁵, but we also detected distinct peaks at m/z ratios of 134.05, 105.02, 75.00 that correspond to adenine and different carbohydrates (Figure 5C). This surprising finding suggests that the RLP_WT condensates facilitate the dephosphorylation of ATP and they also contribute to the bond breakage of adenosine to form adenine and different carbohydrates. This observation implies an important role of condensate-based catalysts in generating cellular energy and it points to the critical importance of interphase electric potentials and that accompanying interfacial electric fields^22,57, which are the only possible energy source that can be implicated in the breakdown of adenosine. As noted earlier, our DFT calculations provide a mechanistic explanation for how strong electric fields can align substrates and lower the barrier for reactions. This highlights the fact that condensate-specific microenvironments and interfacial properties jointly contribute to the ability of condensates to catalyze reactions.

Figure 5. Condensates can catalyze the decomposition of ATP.

A, The dephosphorylation pathway of ATP to ADP, AMP, and adenosine.

B, Quantification of the decomposition of ATP based on solutions with or without condensates with an ATP-dependent luminescence assay. N = 4 independent experiment. Bar graph shows the mean ± SD.

C, A sample spectrum of linear ion mass spectroscopy analysis of the supernatant of the condensate solution containing 0.1 mM ATP after incubation of 30 min at room temperature.

D, Quantification of intracellular ATP level at different time points for cells with or without condensates. Cells with or without condensates were incubated into rich medium for different periods and their intracellular ATP levels were quantified using an ATP-dependent luminescence assay. N = 5 independent experiment. Bar graph shows the mean ± SD.

E, Time-dependent tracking of the intracellular ATP level at different cellular stages. The decrease of the ATP level aligns with the time needed to form condensates. N = 4 independent experiment. Data point represents the mean ± SD.

F, RNA-seq analysis of mRNA abundance depending on phosphate-activated transcriptional activator for cells with or without condensates.

Next, we asked if synthetic condensates could function as catalysts in living cells. We transformed E. Coli BL21 cells (DE3) with an isopropyl ß-D-1-thiogalactopyranoside (IPTG) inducible pET24 plasmid encoding the RLP_WT⁴⁵. We implemented a cellular ATP assay to probe the change in ATP concentration in cells with or without condensates. To decouple the effects of protein overexpression, we compared ATP levels in cells with or without induction of the expression of a cyan fluorescent protein based on the same plasmid backbone. We did not detect a decrease in ATP level upon protein expression (Figure S7B). This aligns with a previous observation that the induction of pET based vectors in BL21(DE3) results in the accumulation of ATP and metabolites caused by excessive energy generation from the expression system⁹⁶. To understand the effects of condensates on cellular ATP, we cultured cells with or without condensates in the rich 2 x YT medium and tracked cellular ATP levels. After three hours of culturing, the cells containing condensates showed a 4.4-fold lower ATP level than those without condensates (Figure 5D).

Next, we leveraged the leaky expression nature of the T7 promoter to track the correlation between condensate formation and the decrease of cellular ATP levels, thereby fully excluding the possible metabolic burden caused by overexpression on the consumption of ATP^97,98. We applied differential interference contrast imaging to track condensate formation and correlated the results with the time-dependency of ATP levels of cells grown in the nutrient-rich 2 x YT medium. We observed a gradual increase of ATP levels alongside exponential cellular growth before condensate formation and a sharp decrease (>30%) of ATP levels (Figure 5E) at a time point that aligns with condensate formation (Figure S7C). These observations confirm that the catalytic functions of condensates remain operative in living cells and points to a role for condensates as modulators of cellular energy sources.

Condensate-mediated ATP decomposition activates phosphate-dependent cellular pathways:

To evaluate whether the condensate-mediated ATP decomposition can activate specific cellular pathways, we implemented RNA-sequencing to quantify the targeted transcriptome correlated with the consequences of ATP decomposition. We specifically assessed free phosphate-dependent cellular pathways in E. Coli^99–103, in which free phosphate binds to the transcription factor and activates downstream gene expression. We prepared cells with or without condensates from log-phase culture and analyzed them using RNA-sequencing. We found that the gene clusters driven by phosphorylated PhoB and PhoP transcription factors^101,104,105 are significantly upregulated (p-value < 0.048) when comparing cells with condensates and cells without condensates (Figure 5F). This suggests that the catalytic effects of condensates generate global changes of cellular environments that affect cellular pathways.

Catalytic functions of condensates modulate intra- and inter-cellular communication:

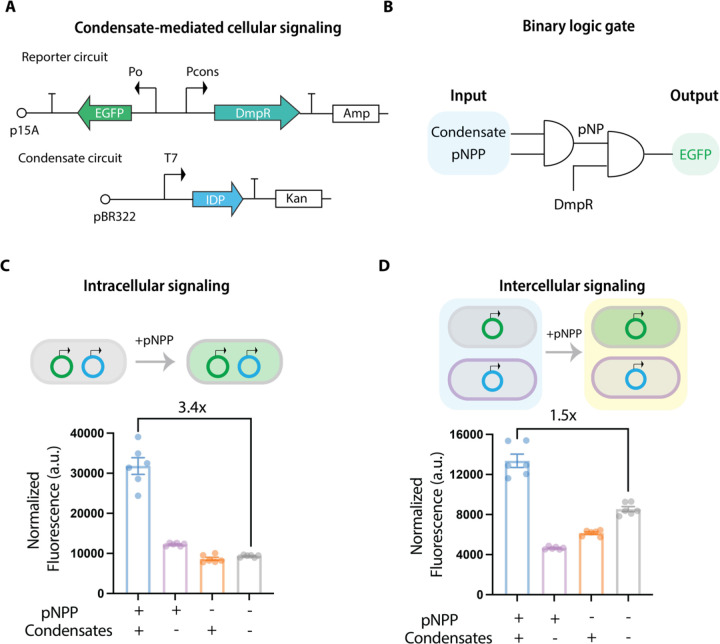
The capability of condensates to modulate intracellular catalytic reactions suggests a potential role of condensates on cellular signaling through their inherent catalytic functions. To test this possibility, we designed and engineered a synthetic gene circuit that can be activated by the catalytic product of condensate-mediated hydrolysis reactions. We elected to use the phenol product generated from the pNPP reaction to drive a downstream gene circuit (Figure 6A). To connect the phenol generation with a downstream cellular response, we implemented a σ₅₄-dependent phenol-responsive transcription regulator DmpR¹⁰⁶, which specifically drives the activation of the phenol degradation pathway in bacteria¹⁰⁷, to regulate the expression of an enhanced green fluorescent protein (EGFP) (Figure 6B). This serves as the downstream reporter, thereby establishing a logical AND gate signaling cascade initiated by the chemical activity of condensates.

Figure 6. Catalytic functions of condensates mediate the activation of a synthetic signaling circuit.

A, A reporter circuit was built using DmpR, a phenol activated transcription activator as a sensor, to drive the expression of EGFP, which serves a reporter protein for the cellular signaling. A condensate circuit was built to generate the cellular signaling event, which is mediated by condensates-mediated pNPP degradation to produce phenol. The coupling of these two circuits can be used to detect whether condensates have the capability to drive cellular signaling through degradation of pNPP from the culture medium.

B, The designed gene circuit follows a binary logic gate cascade with the formation of condensates and the existence of pNPP as the inputs to generate pNP, which activates DMPR to drive the expression of EGFP protein as the output.

C, Evaluation of the capability of condensates to mediate intracellular signaling with two circuits transformed into the BL21 (DE3) cells. The fluorescence signal was normalized to the cellular density. N = 6 independent experiment. Bar graph shows the mean ± SD.

D, Evaluation of the capability of condensates to mediate intercellular signaling with the condensate circuit transformed into the E. Coli. BL21 (DE3) cells and the reporter circuit transformed into the E. Coli. DH5α cells. The fluorescence signal was normalized to the cellular density. N = 6 independent experiment. Bar graph shows the mean ± SD.

We confirmed the activity of the DmpR circuit by monitoring the EGFP response in cell cultures with or without the phenol product. The cell culture with 100 μM phenol showed a 3-fold higher normalized EGFP signal compared to the culture without phenol (Figure S7D). We next tested whether condensates could modulate intracellular signaling. We transformed the E. Coli. BL21 (DE3) cells with two distinct plasmids, one encoding the RLP_WT and the other encoding the DmpR-regulated reporter circuit. We examined the EGFP response based on conditions with or without condensates and with or without pNPP. We triggered the formation of condensates by adding IPTG and then transited the cells from rich medium containing IPTG to minimum medium containing pNPP to test the signaling function. By doing so, we could evaluate the functions of condensates based on the hysteretic feature of condensate formation¹⁰⁸, which can act as a memory component to establish a sustained chemical function. We observed that the culture with cells containing condensates and no pNPP, as well as the culture containing cells without condensates but containing pNPP showed a negligible change in the normalized EGFP signal compared to the control (Figure 6C). However, the cell culture with induced condensates and the presence of pNPP showed a 3.4-fold higher normalized EGFP signal compared to the control (Figure 6C). This demonstrates that the catalytic capability of condensates is robust enough to modulate intracellular signaling.

We further explored whether robust chemical activity of condensates could be used to control different populations of cells based on intercellular signaling. Such capability to modulate intercellular communication is of fundamental interest in synthetic biology^109–111. We transformed the E. Coli. BL21 (DE3) cells with the plasmid encoding the RLP_WT as the signaling cell and the E. Coli. DH5α with the reporter circuit as the sensor cell. We then co-cultured the two populations of cells in one culture (Figure 6D). Specifically, we incubated log-phase BL21 (DE3) cells with or without condensates with DH5α cells in M9 medium containing pNPP in an equal volume fraction and tracked the activated EGFP signal. We found that only the BL21 (DE3) cells with condensates could activate the EGFP signal in the DH5α cells (Figure 6D). To test the robustness of the signal, we varied the volume fraction between the BL21 (DE3) cells with condensates and the DH5α cells under a fixed total cell density. We found that increasing the fraction of BL21 (DE3) cells in the multicellular population could further increase the EGFP signal (Figure S7E), even though the absolute quantity of DH5α cells was decreased. This observation suggests that the rate limiting step for the intercellular signaling was the activation of gene circuits. Our results show that condensates can mediate cellular signaling thereby establishing that the catalytic potentials of condensates can directly affect cellular processes. This provides a new design principle for the construction of synthetic biological networks using the sustained chemical functions of biomolecular condensates. It also highlights the fact that condensates are unlikely to be passive storage depots that are in any way incidental to cellular functions¹¹². Instead, we argue that catalytically active condensates have a direct influence on the regulation of biochemical reactions in cells. The question of interest is how are inherent catalytic functions of condensates managed or leveraged in cells and not whether condensates have any functions.

DISCUSSION

In this work, we showed that biomolecular condensates can catalyze hydrolysis reactions and do so without the input of energy. Our data are consistent with sequence-dependent dense phase chemical environments and condensate-specific interfacial electric fields being the defining features of condensates^20,22,28,113 that enable condensates to function as mesoscale versions enzymes. In enzymes, the creation of unique catalytic environments is made possible by the types of chemistries that are present in active sites,^41,57 and for condensates the chemistries that preferentially accumulate in the coexisting phases help determine interphase electric potentials ²⁸and interfacial electric fields.

A surprising finding is that the RLP-based condensates can catalyze the full decomposition of ATP. In sharp contrast to the hydrolysis of ATP by ATPase, which catalyzes the decomposition of ATP to ADP or AMP, the condensates we studied are capable of decomposing ATP all the way to adenine, which requires the removal of the ribose sugar molecule from adenosine. This appears to be realized by free hydroxyl radicals generated by the ability of condensates to drive spontaneous redox reactions²². The free radicals can lead to the hydrolytic release of ribose¹¹⁴. A recent study also showed that how the redox environment of condensates can regulate protein activity in condensates through mediating disulfide bond formation¹¹⁵. These findings emphasize the critical importance of understanding the role of free radicals on the chemical functions of condensates and also the role of free solvated electrons generated by redox reactions²².

Using a synthetic biology approach¹¹⁶ as a proof-of-principle, we demonstrated that the catalytic functions of condensates are prevalent in living cells. Moreover, such chemical functions are robust enough to lead to global effects in a cell and in a population of cells. This finding further highlights that condensates cannot be viewed as chemically inert entities or as entities that are incidental to cellular functions¹¹². Instead, they are biochemically active. We deployed a series of IDPs of native proteins including those from Ddx4, hnRNP A1 and LYAR. These were compared to condensates formed by synthetic IDPs such as RLP and ELP. The IDPs we studied are known as the drivers of phase separation for the formation of many condensates in mammalian cells . We found that the condensates formed by highly charged IDPs including the RLPs, and IDRs from Ddx4 and LYAR were able to catalyze reactions, while condensates formed by IDPs with lower charge contents, such as the A1-LCD and the non-charged ELP were less capable of catalyzing reactions. This can be rationalized by the possibility that charge contents of IDPs correlates with the extent of asymmetric ion distribution upon phase transition^117–125. This conjecture is supported by the active catalytic behavior of the condensates formed by complex coacervation between NPM1 and mat-rRNA. Asymmetrical partitioning of solution ions across the coexisting phases will define a chemical environment for the dense phase that is distinct from the dilute phase^9,10,28. This gives rise to interphase electric potentials that is essential for generating interfacial electric fields^9,10,28. Considering that native condensates, especially RNP granules are enriched in charged biomacromolecules^{3,4,39,40,126}, such as RNAs and oppositely charged proteins, the asymmetric partitioning of ions and protons will set up gradients and interfacial electric fields that provide the impetus for the biochemical activities of condensates^22,127,128.

A key feature driving the catalytic reaction is the interfacial electric double layer, which is defined as the Gibbs dividing plane in the interphase region where charge separation occurs^129–131. The existence of an interphase electric potential gradient can also lead to an interfacial potential gradient²², which is correlated with the formation of a double layer³³. However, the emergence of an electric field at the interface is governed by various mechanisms, suggesting its widespread occurrence^65,132. For example, within condensates the homogeneity of the bulk solvent is likely to be altered due to a combination of confinement, solvent-macromolecule interactions, and the presence of additional internal interfaces. In addition to the interiors of condensates, properties of the solvent are also likely to be altered by the interface that delineates coexisting phases^14,70. This leads to anisotropic forces acting on the solvent^65,133, which results in a net orientation of the solvent dipoles and the alignment of excess charges at the phase boundary thereby enabling the formation of an electrically active interface. This, together with the passive response by the solvents in the dense phase, collectively establishes an electric double layer in a two-phase system.

In our study, we probed the water availability using stimulated Raman spectroscopy by coupling with a H-bonding dependent frequency vibrational probe. Our results suggest that the field effect induced by the organization of water molecules or vice versa is critical to the chemical features of condensates^134–137. The relevant organizational effects include the fact that dipole moments of water molecules depend significantly on sizes of water clusters^136,138. Our findings also underscore the importance of understanding the internal and interfacial organization of water molecules as drivers of condensate functions⁸².

Our study uncovers diverse factors that can affect the inherent catalytic behaviors of condensates. Our results suggest that condensates serve as versatile crucibles that mediate diverse chemistries. This does not require that condensates be formed by molecules with an intrinsic enzymatic functionality. Instead, just the formation of condensates is sufficient, providing they generate high enough interfacial fields via significant interphase electric potentials. Given that condensates are defined by their unique interphase potentials that arise from differences in chemical environments across coexisting phases and the ubiquitous existence of condensates¹³⁹, our discovery of inherent chemical functions of condensates suggests a possible role of condensates in maintaining cellular chemical homeostasis and managing cellular resources.

STAR METHODS

Expression and purification of IDPs

Construction of RLP genes

The RLP_WT gene was a gift from Chilkoti lab^45,46. The RLP_WT gene was modified through site-directed mutagenesis to generate mutants at the N-terminus using Q5 Site-Directed Mutagenesis kit (New England Biolabs). The cloned genes were transformed into NEB^® 5-alpha Competent E. coli (High Efficiency) (New England Biolabs) and selected on a 2x YT plate with kanamycin. A single colony was picked and grown in 2x YT liquid medium (MilliporeSigma) containing 45 μg/mL Kanamycin at 37 °C for 18 h overnight (shaking at ~225 r.p.m.). The cloned plasmids were then purified using QIAprep Spin Miniprep Kit (QIAGEN) and the DNA sequences of the purified plasmids were verified with Sanger sequencing service (Genewiz, Azenta Life Sciences).

Expression of synthetic IDPs

BL21 (DE3) competent E. Coli (New England Biolabs) was transformed with RLP genes (RLP_SKGP-WT, RLP_SYGP-WT, RLP_SSGP-WT) or ELP genes (ELP_VPGVG-60) and the transformed cells were selected by plating with Kanamycin. A single colony was picked and grown in 2x YT liquid medium (MilliporeSigma) containing 45 μg/mL Kanamycin at 37 °C for 18 h overnight (shaking at ~225 r.p.m.). The overnight cell culture was inoculated into 1 L 2× YT liquid medium supplied with 45μg/mL Kanamycin. The bulk culture was first incubated at 37 °C (shaking at ~225 r.p.m.) until the OD₆₀₀ of cell culture reaching 0.5. The expression of IDPs was then induced by adding 0.5 mM final concentration of IPTG. For all the ELP proteins, the cell culture was incubated for another 18 h at 25 °C (shaking at ~225 r.p.m.). For all RLP proteins, the cell culture was incubated for another 18 h at 37 °C (shaking at ~225 r.p.m.).

Purification of ELP protein

Purification of ELP protein was modified based on an established protocol using the lower critical solution temperature (LCST) feature of ELP¹⁴⁰. Each liter of the ELP cell culture was pelleted by centrifugation (Eppendorf CR22N) at 2,000 g for 20 min at 4 °C. Each pellet from 1 liter of cell culture was resuspended into 35 mL 1×PBS and lysed by sonication (3 min total time, each cycle with 10 sec on and 40 sec off, 75 % amplitude) in an ice bucket. 1 tablet of cOmplete^™ Protease Inhibitor Cocktail (Roche) and 500 units of Benzonase Nuclease (MilliporeSigma) were then added into the cell lysate and incubated at room temperature for 1 h. The cell lysate was centrifuged at 20,000 g for 25 min at 4 °C to separate the soluble and the insoluble phases. The supernatant, which contains the soluble ELP, was collected in a new tube. The ELP phase transition was then induced by adjusting the NaCl concentration to 1 M and heating in a 40 °C water bath for 20 min. The turbid ELP solution was then pelleted by centrifugation at 20,000 g for 25 min at 40 °C. The insoluble ELP pellet was physically disrupted using pipette tip and dissolved in 20 mL fresh 1×PBS at 4 °C for at least 3 h with rocking. The dissolved ELP was centrifuged at 20,000 g for 25 min at 4 °C and the supernatant was collected. This completed a full round of ELP purification based on its LCST phase behavior. Another two rounds of temperature-dependent purification were performed before isolating the protein with AKTA size exclusion chromatography (cytiva). Protein purity was then determined on an SDS-PAGE gel (Bio-Rad, Any kD Mini-PROTEAN TGX Precast Protein Gels). This process would lead to a purity over 95%. The purified ELP was dialyzed into milli-Q water overnight at 4 °C. The dialysis water was changed three times.

The dialyzed sample was then frozen at −80 °C for 1 h and lyophilized for three days to remove all water. The lyophilized dry powder was stored at −80 °C.

Purification of RLP protein

Purification of RLP proteins was modified based on an established protocol using the upper critical solution temperature (UCST) feature of RLP^46,141. Each liter of the overnight cell culture was pelleted by centrifugation at 2,000 g for 20 min at 4 °C (Eppendorf CR22N). Each pellet was resuspended in 30 mL Resuspension buffer (50 mM Tris, pH 7.5) and lysed by sonication (3 min total time, each cycle with 10 sec on and 40 sec off, 75 % amplitude) in an ice bucket. The cell lysate was centrifuged at 20,000 g for 25 min at 4 °C to separate the insoluble and the soluble phases. The insoluble pellet from each liter of bacterial culture was dissolved in 10 mL Urea buffer (50 mM Tris, 500 mM NaCl, 8 M Urea, pH 7.5) supplied with 500 units Benzonase Nuclease (MilliporeSigma) at room temperature for at least 2 h with rocking. The sample was then pre-warmed to 40 °C in a water bath for 30 min and centrifuged at 20,000 g for 25 min at 40 °C. The supernatant was collected and dialyzed into Resuspension buffer (50 mM Tris, pH 7.5). The dialysis buffer was changed one time over 3 h. Both the soluble and insoluble fractions in the dialysis bag were collected and centrifuged at 20,000 g for 25 min at 4 °C. The insoluble pellet was dissolved in Urea buffer (50 mM Tris, 500 mM NaCl, 8 M Urea, pH 7.5) at room temperature for at least 1 h with rocking. The sample was then warmed to 40 °C and centrifuged at 20,000 g for 25 min at 40 °C. The supernatant was collected, and its purity was determined on a SDS-PAGE gel (Bio-Rad, Any kD Mini-PROTEAN TGX Precast Protein Gels). This completes a round of UCST based purification. Another two rounds of temperature-dependent purification were performed before isolating the protein with AKTA size exclusion chromatography (cytiva). The final purity of the purified protein is higher than 95%.

The purified RLP protein was then processed in two different methods for storage. For liquid stock preparation, the concentration of the RLP stock protein was first adjusted to the concentration below its C_sat using Urea buffer and dialyzed into High salt buffer (50 mM Tris, 500 mM NaCl, pH7.5) at room temperature. The dialysis buffer was changed three times over 4 h. The dialyzed sample was first verified its capability to phase separate upon dilution. If not able to phase separate upon dilution, the concentration of the dialyzed sample was adjusted by the Pierce^™ Protein Concentrators PES, 10K MWCO (ThermoFisher). Once it is verified, the protein stock was aliquoted into PCR tubes and frozen by liquid nitrogen and stored at −80 °C. For dry powder preparation, the rest of the purified RLP protein was dialyzed into milli-Q water at 4°C . The dialysis water was changed three times overnight. The dialyzed sample was then frozen at −80 °C for 1 h and lyophilized for three days to remove all water. The lyophilized dry powder can be stored at −80 °C. We did not find a performance difference between samples stocked by different methods. The dry powder sample is more convenient for the preparation of RLP protein solution below C_sat.

Expression and purification of A1-LCD: BL21-CODONPlus RIPL E. Coli. cells (Agilent Technologies 230280) transfected with Δhexa_His-TEV-A1-LC 1 were grown in LB broth (Sigma: L3522) in Erlenmeyer flasks with ≥ 5-fold head volume at 37 °C (shaking at 220 r.p.m.) until OD600 ~0.6 was reached. Cultures were then chilled for 15 min in an ice bath before adding 0.35 mM IPTG. Induced cultures were grown for additional 6 hours at 37 °C. Cells were harvested by centrifugation as described previously for synthetic IDPs, flash frozen, and stored as pellets in 50 mL Falcon tubes at −80 °C.

The cell pellet was resuspended to homogeneity in 35 mL supplemented lysis buffer (50 mM MES, 500 mM NaCl, 14.3 mM BME (β-Mercaptoethanol), 200 μM PMSF (phenylmethylsulfonyl fluoride) pH 6). Lysis buffer was then supplemented with: 500U DNAaseI (Sigma - 4536282001), 500U RNAse A (Sigma - 10109169001), 5 mg Lysozyme (Sigma - 62971–10G-F), and one protease inhibitor tablet (Sigma - 40694200). The cell suspension was lysed via sonication on a Branson 550 sonicator with an L102C horn attachment using five series of the following 20-round cycle: 1 second on / 2 second off at 30% power. The lysate was then pelleted through centrifugation for 30 min at 38,000 g. The lysate pellet was resuspended in a resuspension buffer (6 M GdmCl, 20 mM Tris, 15 mM imidazole, 14.3 mM BME, and 200 μM PMSF; pH 7.5) via repeat pipetting and pulses of sonication until the solution was visibly homogenous. This solubilized pellet was spun at 38,000g for 30 minutes at room temperature and the supernatant was applied to a gravity column with 5 mL bed volume of HisPur NiNTA resin (Thermo Fisher Scientific) equilibrated with resuspension buffer. The Ni-NTA resin was washed with 75 mL wash Buffer (20 mM Tris, 30mM imidazole, 4 M Urea, 14.3mM BME, and 200 μM PMSF; pH 7.5), then protein was eluted in elution buffer (20 mM Tris, 350mM imidazole, 4 M Urea, 14.3mM BME, and 200 μM PMSF; pH 7.5). Peak fractions from Ni-NTA affinity purification were pooled and diluted 1:1 in dilution buffer (20 mM Tris and 14.3 mM BME; pH 7.5). To this, 1 mg of TEV protease was added, and the mixture was dialyzed overnight in dialysis buffer (20 mM Tris, 2 M urea, 50 mM NaCl, 0.5 mM EDTA, and 1 mM DTT; pH 7.5) at room temperature. After 16 h, the protein solution was filtered through a 0.22 μm filter, then further purified via ion exchange chromatography on an ÄKTA Pure fast protein liquid chromatography (FPLC) module using a HiTrap SP 5mL column (Cytiva – 17115201). The column was equilibrated with buffer A (20 mM Tris, 2 M urea, 50 mM NaCl, and 14.3 mM BME; pH 7.5) and protein was bound then subjected to a contiguous gradient protocol with from 0.05M NaCl to 1 M NaCl. Fractions containing A1-LCD were pooled then further purified and buffer exchanged using size exclusion chromatography - HiLoad 16/600 Superdex 200pg column (Cytiva - 28989335) into the following storage buffer: 20mM MES and 4 M GdmCl at pH 5.5. Lastly, protein was pooled and concentrated in Amicon Ultra 3 MWCO (molecular weight cut-off) concentrator columns (Millipore-Sigma UFC 500396), according to the manufacturer’s suggestions. Concentrated protein was stored at 4°C for further usage.

Expression and purification of DDX4-NT: BL21 E. coli. cells (NEB) transfected with His-SUMO-DDX4-NT 2, a gift from Professor Lewis E. Kay, were grown in the same manner as A1-LCD. Cells were lysed in the same manner as A1-LCD with a different lysis buffer (20 mM Sodium Phosphate, 750 mM NaCl, 20 mM Imidazole, 14.3 mM BME, and 0.2 mM PMSF; pH 7.5). The supernatant was spun for 25 min at 38,000g and transferred into an equilibrated HisTrap FF Crude 5mL column (Cytiva – 11000458) with an ÄKTA Pure fast protein liquid chromatography (FPLC) module. The Ni-NTA column was washed in 75 mL lysis buffer then protein was eluted in elution buffer (0.02 M Sodium Phosphate, 0.5 M NaCl, 0.35 M Imidazole, 0.0143 M BME, 0.0002 M PMSF; pH 7.5). Peak fractions from this affinity purification were pooled and diluted 5-fold in dilution buffer (0.02 M Sodium Phosphate, 0.0143 M BME; pH 7.5). This solution was further purified via ion exchange chromatography using a continuous gradient purification protocol with a HiTrap Heparin HP 5mL column (Cytiva – 17040703), Buffer A (0.02M Sodium Phosphate, 0.1M NaCl, 0.0143M BME; pH 7.5), and Buffer B (0.02 M Sodium Phosphate, 0.1 M NaCl, 0.0143 M BME; pH 7.5) on the ÄKTA Pure FPLC module. Peak fractions containing SUMO-DDX4 protein were pooled and cleaved of SUMO tags during an overnight dialysis in the presence of 0.02x ULP1 Protease in cleavage buffer (0.02 M Sodium Phosphate, 0.3 M NaCl, 0.001M DTT (Dithiothreitol), pH 7.5). DDX4-NT was purified to ≥98% using size exclusion chromatography - HiLoad 16/600 Superdex 200pg column (Cytiva - 28989335) on the ÄKTA Pure FPLC module in storage buffer (0.022M Sodium Phosphate, 1.1M NaCl, 0.0143M BME, pH 7.5). The DDX4-NT solution was supplemented with 10% glycerol and concentrated in Amicon Ultra 3 MWCO (molecular weight cut-off) concentrator columns (Millipore-Sigma UFC 500396) and concentrated protein was aliquoted into single-use volumes (typically 10 μL), flash froze in liquid nitrogen, and stored at −80 °C. Each step of the purification was assessed in the same manner as described for A1-LCD.

Expression and purification of LYAR: Expression was carried out in the same way as described for A1-LCD. Cells were lysed in supplemented lysis buffer (20mM Sodium Phosphate, 500mM NaCl, 20mM Imidazole, 14.3mM BME, 200μM PMSF, pH 7). Supernatant was recovered from a 25-minute spin at 38,000g and transfered into a 10 mL volume of equilibrated HisPur Ni-NTA resin (Fisher - 88222) in a gravity column. The Ni-NTA column was washed in lysis buffer until no contaminant protein was detected by Bradford assay. Protein eluted in 20 mL elution buffer (20 mM Sodium Phosphate, 500 mM NaCl, 350 mM Imidazole, 14.3 mM BME, 200 μM PMSF; pH 7). Peak fractions from this affinity purification were pooled and diluted five-fold in dilution buffer (20 mM Sodium Phosphate, 14.3 mM BME; pH 7). This solution was further purified via ion exchange chromatography using a contiguous gradient purification protocol with a His-Trap Heparin HP 5mL column (Cytiva – 17040703), Buffer A (20 mM Sodium Phosphate, 100 mM NaCl, 14.3 mM BME; pH 7), and Buffer B (20 mM Sodium Phosphate, 100 mM NaCl, 14.3 mM BME; pH 7) on the ÄKTA Pure FPLC module. Peak fractions containing His-LYAR were pooled and purified to ≥95% using size exclusion chromatography - HiLoad 16/600 Superdex 75pg column (Cytiva - 28989333) on the ÄKTA Pure FPLC module in storage buffer (22mM Sodium Phosphate, 1.1M NaCl, 14.3mM BME, pH 7.5). The LYAR solution was supplemented with 10% (v/v) glycerol and concentrated in Amicon Ultra 3 MWCO (molecular weight cut-off) concentrator columns (Millipore-Sigma UFC 500396). Concentrated protein was aliquoted into single use volumes (typically 5 μL), flash frozen in liquid nitrogen and stored at −80 °C.

Expression and purification of NPM1: Expression was carried out in the same way as described for DDX4-NT and LYAR. Cells were lysed in supplemented lysis buffer (20 mM sodium phosphate, 500 mM NaCl, 20 mM imidazole, 14.3 mM BME, 200 μM PMSF, pH 7). Supernatant was recovered from a 25-minute centrifuge at 38,000 g and bound to a 10 mL volume of equilibrated HisPur Ni-NTA resin (Fisher - 88222) in a gravity column. The Ni-NTA column was washed in lysis buffer until no contaminant protein was detected by a Bradford assay. Protein eluted in 20 mL elution buffer (20 mM sodium phosphate, 500 mM NaCl, 350 mM imidazole, 14.3 mM BME, 200 μM PMSF; pH 7). Peak fractions from this affinity purification were pooled and diluted five-fold in dilution buffer (20 mM sodium phosphate, 14.3 mM BME; pH 7). Peak fractions containing His-MBP-Tev-NPM1 were pooled and cleaved of MBP during an overnight dialysis in the presence of 0.025x TEV protease in cleavage buffer (20 mM Sodium phosphate, 300 mM NaCl, 1 mM DTT, pH 7.5). This solution was further purified via ion exchange chromatography using a continuous gradient purification protocol with a HiTrap SP 5 mL column (Cytiva – 17115201), Buffer A (20mM sodium phosphate, 100mM NaCl, 14.3mM BME; pH 7), and Buffer B (20mM sodium phosphate, 100mM NaCl, 14.3mM BME; pH 7) on the ÄKTA Pure FPLC module. Peak fractions containing NPM1 were pooled and purified to ≥95% using size exclusion chromatography - HiLoad 16/600 Superdex 75pg column (Cytiva - 28989333) on the ÄKTA Pure FPLC module in storage buffer (22 mM sodium phosphate, 1.1 M NaCl, 14.3 mM BME, pH 7.5). The NPM1 solution was supplemented with 10% (v/v) glycerol and concentrated in Amicon concentrators. Concentrated protein was aliquoted into single use volumes (typically 5 μL), flash frozen in liquid nitrogen and stored at −80 °C.

Purification of Mature rRNA (mat-rRNA): Mature rRNA (mat-rRNA) is a mixture of rRNAs (18S and 28S) and was purified using the same protocol described previously¹⁴². Briefly, rRNA was first purified from 50 μL packed volume of stage VI Xenopus oocytes Xenopus oocytes via TRIzol reagent extraction (Fisher - 15596026). A pellet of precipitated rRNA was reconstituted in 100 μL 4 °C ddH2O. Gel electrophoresis was carried out to confirm that the dominate RNA species were the 18s and 28s rRNA. rRNA Concentration was measured by absorbance at 260 nm on a Nanodrop 2000 and immediately aliquoted into single use volumes (typically 5 μL), flash-frozen in liquid nitrogen and stored at −80 °C.

Condensate formation for LYAR and DDX4: To prepare LYAR and DDX4 condensates, we mixed 3 μL of 2320 μM DDX4 (in 8 mM NaH₂PO₄, 12 mM Na₂HPO₄, 1 M NaCl) with 27 μL low-salt solution (8 mM NaH₂PO₄, 12 mM Na₂HPO₄, 0 M NaCl) into a 1.5 mL microcentrifuge tube and incubated for 30 min at room temperature before subjecting to catalytic assay. The corresponding buffer was used as base line to assess the spontaneous hydrolysis activity of the substrate in this buffer.

Condensate formation for A1 LCD: To prepare A1 LCD condensates⁷², we mixed 27 μL of 100 μM A1-LCD (in 20 mM HEPES buffer, pH 7.0) with 3 μL of salt buffer (20 mM HEPES buffer with 3 M NaCl, pH 7.0) into a 1.5 mL microcentrifuge tube with a final concentration of 90 μM A1-LCD in 20 mM HEPES buffer with 300 mM NaCl. The condensate solution was incubated for 30 min at room temperature before subjecting to catalytic assay. The corresponding buffer was used as base line to assess the spontaneous hydrolysis activity of the substrate in this buffer.

Condensate formation through complex coacervation of NPM1 and rRNA: To prepare NPM1+mat-rRNA condensates, we mixed a 0.1x volume of 200 μM NPM1 (in mM NaH₂PO₄, 12 mM Na₂HPO₄, 1 M NaCl) with a 0.9x volume of low-salt solution (8 mM NaH₂PO₄, 12 mM Na₂HPO₄, 0 M NaCl) containing mat-rRNA at 11.12ng/μL. The condensate solution was incubated for 30 min at room temperature before subjecting to catalytic assay. The corresponding buffer was used as base line to assess the spontaneous hydrolysis activity of the substrate in this buffer.

Catalytic activity assay

To prepare RLP proteins for the catalytic activity assay, a frozen protein stock was freshly thawed to room temperature before dilution. For the condensates-forming condition, each reaction contained 60 μL protein stock and 140 μL Dilution buffer (50 mM Tris, pH was adjusted to meet the specific testing condition described in the manuscript). For the dilute-protein (no condensates formation) condition, each reaction contained 10 μL protein stock, 50 μL High Salt buffer (50 mM Tris, 500 mM NaCl, pH 7.5) and 140 μL Dilution buffer (50 mM Tris, pH was adjusted to meet the specific testing condition described in the manuscript). The well-mixed protein solutions were incubated at room temperature for 30 min to allow condensates formation before adding substrates.

To prepare ELP condensates for the catalytic activity assay, lyophilized ELP powder was weighted to prepare a stock solution in Dilution buffer (50 mM Tris, pH 7.5). After the powder was fully dissolved, NaCl concentration was adjusted using a high concentration NaCl stock solution (50 mM Tris, pH 7.5, 2 M NaCl) to realize a final salt concentration at 150 mM NaCl.

To prepare chemical stock solutions, a 100× chemical stock was freshly prepared before every experiment. 4-nitrophenyl phosphate (pNPO) was prepared in water. 4-nitrophenol (4-NP), 4-nitrophenyl acetate (pNPA), 4-nitrophenyl trifluoroacetate, 4-nitrophenyl trimethylacetate were prepared in acetonitrile. 4-nitrophenol butyrate (pNPB) and 4-nitrophenyl octanoate were prepared in dimethyl sulfoxide (DMSO).

To initiate the catalytic reaction after protein incubation, 2 μL of a 100× chemical stock solution was added per 200 μL of diluted protein sample on a flat-bottom transparent 96-well plate (Corning, COSTAR). For control reaction without chemical, the same volume of corresponding solvent was added. The plate was sealed with a transparent film and immediately transferred to a plate reader for recording. The absorbance was measured at 410 nm and 385 nm with 25 flashes on a TECAN Infinite M200 plate reader or a TECAN Multimode plate reader (TECAN). The reaction was evaluated at 25 °C with a 3-min kinetic interval for at least 70 cycles.

From the measured absorbance at 410 nm for all catalytic reactions, the concentration of 4-Nitrophenol, the product of the hydrolysis reactions, was calculated based on a standard curve which was obtained experimentally under the same condition. The baseline of 4-nitrophenol from chemical self-hydrolysis was subtracted from the catalytic reaction. The initial rate (V₀) was calculated from the linear portion of the activity plot ([4-Nitrophenol] versus time) by performing a linear regression using Graphpad. For Michaelis-Menten fitting, the means of V₀ values were plotted as a function of substrate concentrations, and the plot was fitted to the Michaelis-Menten equation by using the built-in non-linear regression on Prism Graphpad. The fitted Michaelis Menten equation was Y=V_max*X/(K_m+X). All measurements were replicated at least 4 times.

Absorbance scan

The absorbance scan of 0.8 mM pNPA hydrolysis reaction catalyzed by RLP_SKGP-WT condensates was conducted at 25 °C at pH 7.5. The reaction condition and the buffer composition were identical to the aforementioned catalytic activity assay. At different incubation time points, measurements were taken using the UV-VIS function on Nanodrop one (Thermo Scientific).

Fluorogenic hydrolysis activity assay

The condensate solutions were prepared as described in previous sections. Resorufin phosphocholine was added into the condensate solution at a final concentration of 50 μM. The reaction solution was transferred into a 384 well plate (PerkinElmer) and incubated in H301-K stage (okolab) at 30°C. The 10 % excitation was set at 550 nm with a WLL laser, and the emission detector was set at 570–600 nm on a HYD detector. An autofocus function was set to image a z range of 15 μm and the image with the highest fluorescence signal was used for quantification. ImageJ (Fiji) was used for quantification based on Particle Analysis function.

In vitro ATP dephosphorylation assay

To evaluate the level of dephosphorylation of ATP by RLP_SKGP-WT condensates in vitro, protein samples were prepared by the same method as in the aforementioned catalytic activity assay. The ATP stock solution (prepared from adenosine 5’-triphosphate disodium salt hydrate) was added to initiate the reaction with a final concentration of 10 μM. The reaction was incubated at 30 °C for 30 min or 90 min. The ATP quantification was performed by using the Luminescent ATP Detection Assay Kit (Abcam) following the manufacturer’s protocol. In brief, the reaction was terminated by adding the detergent and incubated for 5 min. The substrate solution was then added into the sample and incubated for 15 min in the dark. The luminescence was recorded on the TECAN Infinite M200 plate reader with a 2000 ms integration time (Luminescence mode). For the ATP calibration standard, the ATP standard solutions were freshly prepared for each assay under the same experimental condition.

Mass spectrometry analysis of catalytic reactions

The same catalytic reaction assay was performed as described in previous sections. The condensate samples and controls were centrifuged at 15,000 g for 10 min at room temperature. The supernatant of the centrifuged solution was extracted for analysis. The supernant of the samples were analyzed by LTQ-XL linear ion trap mass spectrometer (Thermo-Fisher). The nano-ESI mode was employed for sample introduction. Samples were tested in positive ion mode with an applied voltage at 1.2 kV.

E. Coli. intracellular ATP assay

To measure the level of intracellular ATP upon the formation of RLP_SKGP-WT condensates, the BL21 (DE3) competent E. coli was transformed with the RLP_SKGP-WT plasmid and the transformed cells were selected on a Kanamycin plate. A single colony of the plated BL21 E. coli was picked and grown in 2 mL 2× YT liquid medium supplied with 4 % glucose and 45 μg/mL Kanamycin at 37 °C overnight. Each liquid culture was back diluted at a ratio of 1:100 with fresh 2× YT liquid medium supplied with 45 μg/mL Kanamycin. After a 1.5-hour incubation at 37 °C, the culture was either induced with Isopropyl β-d-1-thiogalactopyranoside (IPTG) to produce RLP_SKGP-WT protein or not induced. At post-induction time points of 3 and 7 h, OD₆₀₀ of each sample was measured and adjusted to the same cellular density using 1×PBS after washing with 1×PBS. The quantification of ATP level was conducted using the Luminescent ATP Detection Assay Kit (Abcam) following the manufacturer’s protocol. In brief, the reaction was terminated by adding the detergent and the sample was shaken in an orbital shaker for 5 min. The substrate solution was then added, and the sample was transferred to the TECAN Multimode plate reader for a 3-minute shaking, followed by a 12-minute dark adaption. The luminescence was recorded with 2000 ms integration time using the Luminescence mode.

Intra- or inter-cellular communications with DmpR circuit

To evaluate whether the catalytic activities of condensates can mediate intracellular functions, the BL21 (DE3) competent E. Coli was co-transformed with two plasmids: one plasmid carrying the RLP_SKGP-WT gene and another plasmid carrying the DmpR gene circuit. The DmpR gene circuit consists of a phenol-inducible DmpR transcriptional activator¹⁴³ that can turn on eGFP reporter expression in a 4-nitrophenol concentration dependent manner. After selecting the transformed BL21 (DE3) cells by plating with both Ampicillin and Kanamycin, a single colony was picked and grown in 2 mL 2× YT liquid medium supplied with 4 % glucose, 100 μg/mL Ampicillin and 45 μg/mL Kanamycin at 37 °C overnight. The cell culture was back diluted at a ratio of 1:100 with fresh 2× YT liquid medium supplied with 100 μg/mL Ampicillin and 45 μg/mL Kanamycin. After a 1.5-hour incubation, RLP_SKGP-WT protein production was either induced or not induced with 0.5 mM IPTG. At 3 h post induction, each cell culture was measured for OD₆₀₀ and adjusted to the a saturated cell density OD₆₀₀ at 1.5 using M9 Minimal Salts liquid medium (Sigma-Aldrich) supplied with 0.4 % (w/v) sodium acetate, 0.01 % (w/v) thiamine, 2 mM MgSO₄ and 0.1 mM CaCl₂. eGFP fluorescence, absorbances at 600 nm and 410 nm were monitored with a 5-min kinetic interval at 37°C for 500 cycles on a TECAN Spark plate reader.

To evaluate whether the catalytic activities of condensates can mediate intercellular signaling, the BL21 (DE3) competent E. coli. was transformed with RLP_SKGP-WT plasmid and the DH5α competent E. coli. (NEB) was transformed with the DmpR gene circuit. A single colony of the RLP_SKGP-WT-harboring BL21 (DE3) cells and a single colony of the DmpR-harboring DH5α cells were picked and each grown separately in 2 mL 2× YT liquid medium supplied with 4 % glucose and appropriate antibiotic at 37 °C overnight. The cell culture was back diluted at a ratio of 1:100 with fresh 2× YT liquid medium with appropriate antibiotic. After a 1.5-hour incubation, the BL21 (DE3) cells carrying the RLP_SKGP-WT plasmid were either induced or not induced with 0.5 mM IPTG. At 3 h post induction for BL21 cell culture (4.5 h post dilution for 5-alpha cell culture), each cell culture was measured for OD₆₀₀ and adjusted to the same cellular density using M9 Minimal Salts liquid medium (Sigma-Aldrich) supplied with 0.4 % (w/v) sodium acetate, 0.01 % (w/v) thiamine, 2 mM MgSO₄ and 0.1 mM CaCl₂. Each sample was prepared by mixing two cell populations at a volume ratio of 1:2, 1:1, 2:1 with the same total volume. eGFP fluorescence, absorbances at 600 nm and 410 nm were monitored with a 5-min kinetic interval at 37°C for 500 cycles on a TECAN Spark plate reader.

Confocal microscopy for in vitro condensates

Analysis of condensate quantity and chemical environments were performed using LEICA STELLARIS 8 FELCON confocal microscopy (LEICA). For characterization of the chemical environments of the condensates, we followed the previous published protocols²² using SNARF^™−4F 5-(and-6)-Carboxylic Acid (ThermoFisher) and DI-4-ANEPPS (Thermofisher) dyes for the characterizations of internal apparent pH and the relative strength of interfacial electric fields. The images were processed through ImageJ with Image Calculator to quantify the ratio of fluorescent signals between each channels.

Rh800 assay for characterization of water environments using hyperspectral SRS microscopy

Construction of Hyperspectral SRS microscopy: Hyperspectral stimulated Raman scattering microscopy was constructed by sending a dual-output femtosecond laser system (InSight X3, Spectra-Physics) through a commercial Spectral Focusing Timing and Recombination Unit (SF-TRU, Newport Corporation) and coupled into a multiphoton laser scanning microscope (FVMPE-RS, Olympus). The pump beam is tunable in the range of 680–1300 nm, while the Stokes beam is fixed at 1045 nm. Inside SF-TRU, the stokes beam passes through a resonant electro-optic amplitude modulator (EOM), which modulates the stokes beam at a 10 MHz resonant frequency. A motorized delay stage (DL125, Newport) is inserted on the Stokes path to adjust the temporal overlap between two beams. A separate grating pair is installed in each beam path for spectral focusing. The pulse width for the pump and the Stokes were calculated to be 4 ps and 3.5 ps, respectively. The existence of grating pairs also reduces the pump tuning range to be 790–910 nm (corresponding to a Raman shift range of 1300–3100 cm⁻¹). The two synchronized beams are spatiotemporally overlapped and then coupled into the microscope for SRS imaging. A 25x water objective (XLPlan N, N.A. 1.05, MP, Olympus) was used with a high N.A. condenser lens (oil immersion, N.A. 1.4, Olympus) to collect the pump and stokes beams passing through the samples. A large-area (10 mm × 10 mm) Si photodiode (S3590–09, Hamamatsu) was placed after a telescope to detect pump beam intensity loss after filtering out the Stokes beam with two high-optical-density band-pass filters (FESH0950, Thorlabs). A 64 V DC power supply was used to reverse-biased the photodiode, and the output current of the detector was electronically prefiltered by a band-pass filter (Mini-Circuits, 9.5–11.5 MHz, 50 Ω) before being sent to a fast lock-in amplifier (HF2LI, 50 MHz, Zurich Instruments) with 50 Ω termination for signal demodulation. The in-phase X-output of the lock-in amplifier is fed back into the analogue interface box of the microscope to form SRS images. The fast acquisition of the SRS spectrum in each window was achieved by simply adjusting the arrival time of the Stokes beam through a motorized delay stage inside SF-TRU. The delay stage position was calibrated to wavenumber by comparing hyperspectral SRS spectra with spontaneous Raman spectra of d-DMSO.

Sample preparation for hyperspectral SRS microscopy: Condensates were prepared as described and incubated for the same amount of time before characterization. Rh800 (Sigma-Aldrich) was mixed with condensates with a final concentration of 100 μM for hyperspectral SRS imaging. The central wavelength of the pump beam was 850 nm. Pump power of 24 mW and Stokes power of 34 mW was used for hyperspectral SRS imaging of the Rh800 stained condensates with pixel dwell time set to be 8 μs and corresponding time constant from lock-in amplifier to be 6 μs. SRS spectra in the range of 2210 cm⁻¹- 2255 cm⁻¹ were obtained for segmented region of interests for condensates and dilute phase. The corresponding central vibrational frequencies ${\overline{v}}_{C\equiv N}$ were determined from the 14-point spectra using deconvolution methods reported before⁸³.

LaSSI Simulations

To evaluate whether the Simulations were performed using LaSSI, a lattice-based Monte Carlo engine⁶⁹. Monte Carlo moves are accepted or rejected based on the Metropolis–Hastings criterion so that the probability of accepting a move is equal to min (1, exp(–βΔE)), where β = 1 / kT. Here, kT is the simulation temperature, and ΔE is the change in total system energy associated with the attempted move. Total system energies were calculated using a nearest neighbor model and previously derived interaction parameters¹⁴. For each variant and simulation temperature, 300 distinct chain molecules composed of 166 beads each were placed in a cubic lattice with a length of 140 lattice units. Previous calibrations have shown that the numbers of molecules used in these simulations are adequate to avoid problems due to finite size effects¹⁴. The simulations were allowed to equilibrate such that the chains formed a single condensate with a coexisting dilute phase before any analysis was performed. This process was facilitated by initializing the system in a smaller box with side length 40 lattice units. Simulations were performed for 3 × 10¹⁰ Monte Carlo steps and analyzed every 5 × 10⁷ steps. Radial densities were determined by calculating the center-of-mass of the system and partitioning the system into radial bins, centered at the center-of-mass, each with radius 1/4 of a lattice unit. Radial densities were normalized by the exact number of lattice sites within each radial bin. Radial densities were further scaled based on the number of beads being analyzed. For example, when determining radial densities for the full-length proteins, densities were divided by 166 (the chain length). In contrast, when determining radial densities for the N-termini, the first four residues of the protein were used, so the densities were divided by 4. For each set of conditions, three independent simulations were performed.

Density functional theory calculations

To understand the role of electric field on catalyzing the hydrolysis reactions, we investigated the influence of the external electric field strength on the rate of PNPA hydrolysis computationally using density functional theory (DFT). It has been shown computationally that PNPA hydrolysis is likely concerted with the tetrahedral intermediate being the transition state, and the reaction is well-studied experimentally^144,145. In the presence of an electric field, the free energies is modulated by −μ·E, where μ is the dipole moment of any species and E is the electric field. The barrier height changes for this reaction due to the electric field is given by

$$\Delta G‡(E)=G_{TS}-G_{\text{reactant}}=G_{TS}(E=0)-G_{\text{reactant}}(E=0)-\Delta \mu \cdot E$$ (1)

where Δμ = μ_TS − μ_reactant is the difference in dipole between the reactant and the transition state. From this, the field-induced reaction barrier change is expressed as ΔΔG^‡ = −Δμ · E. By employing the Arrhenius equation, the expected rate change was calculated through the equation,

$$\frac{k(E)}{k(E=0)}=\text{exp}\left(\beta \mathrm{\Delta \Delta }{G}^{‡}\right)=\text{exp}(-\beta \Delta \mu \cdot E).$$ (2)

All computations were performed with Q-Chem 6.0⁵⁸. The dense phase environment was modeled using the conductor-like polarizable continuum model (CPCM), a standard implicit solvation model to model these reaction systems^146,147

We investigated a model with an explicit solvent cage¹⁴⁴ along with implicit solvation treatment. We found that without adding an explicit solvent cage, the barrier height was too low (1–2 kcal/mol) for various exchange-correlation functionals and basis sets employed. Therefore, an explicit solvent cage consisting of seven water molecules was added around the reaction complex, following a published study¹⁴⁴. To model the system, the 6–31++G** basis set and B3LYP exchange-correlation functional was first used to compute optimized gas-phase geometries for reactant, transition state, and product. The optimized gas-phase geometries with implicit solvation were studied via CPCM, the def2-TZVPD basis set, and ωB97X-V exchange-correlation function. The solvation-free energies and dipoles for the reaction system were obtained for the reactant, transition state, and product configurations. The dipoles for the reactant and transition state and change in barrier height due to a changing electric field were computed for several dielectric constants ε since we cannot measure the precise dielectric constant. Modulating the dielectric constant does not change the qualitative conclusions. We reported the free energy changes based on ε = 3.2, the average dielectric constant for proteins¹⁴⁸ and the electric field of 10 MV/cm (a typical value in the protein environment⁵⁹)