Unravelling the thermodynamic properties of soil ecosystems in mature beech forests

Abstract

Thermodynamics is a vast area of knowledge with a debatable role in explaining the evolution of ecosystems. In the case of soil ecosystems, this role is still unclear due to difficulties in determining the thermodynamic functions that are involved in the survival and evolution of soils as living systems. The existing knowledge is largely based on theoretical approaches and has never been applied to soils using thermodynamic functions that have been experimentally determined. In this study, we present a method for the complete experimental thermodynamic characterization of soil organic matter. This method quantifies all the thermodynamic functions for combustion and formation reactions which are involved in the thermodynamic principles governing the evolution of the universe. We applied them to track the progress of soil organic matter with soil depth in mature beech forests. Our results show that soil organic matter evolves to a higher degree of reduction as it is mineralized, yielding products with lower carbon but higher energy content than the original organic matter used as reference. These products have higher entropy than the original one, demonstrating how the soil ecosystem evolves with depth, in accordance with the second law of thermodynamics. The results were sensitive to soil organic matter transformation in forests under different management, indicating potential applicability in elucidating the energy strategies for evolution and survival of soil systems as well as in settling their evolutionary states.

Introduction

Forests play a crucial role in protecting our primary resources as water and soil. They shape the soil in a unique way and are the habitat of a high diversity of plants, macro-fauna, and microorganisms. The entire ecosystem may evolve over the millennia if it is not disturbed. Owing to its complexity, monitoring, and parametrizing the evolutionary state of forest ecosystems remain an important goal in science, especially in predicting their sensitivity to the complex climate and environmental conditions nowadays¹. The consciousness about the importance of understanding how forests and forest soils evolve can be considered as historical, with the first publication on this topic dating back to 1900². Since then, there have been continuous efforts to study and understand forest soils and their evolution.

The term thermodynamics was coined in 1849. It has been a subject with widespread impact across many fields of knowledge, including ecology. It has led to the development of different theories aiming to explain the evolution of ecosystems using the thermodynamic functions and principles as a tool, and to the bloom of differing theories resulting in intense scientific debates throughout the entire twentieth century^3–7 till now^8–10. Most of these theories are based on thermodynamic functions that have not yet been experimentally determined for soil reactions.

Before the beginning of thermodynamics in 1849, since the eighteenth century, there has been technological progress in designing devices to detect and measure the heat from living systems that adopted the name of calorimeters. The first calorimeter was designed in 1789 by Antoine Lavoisier to measure the heat involved in the respiration process of a guinea pig¹¹. The measurement of heat is the first step in the thermodynamic characterization of living systems. These techniques have evolved towards different thermal and calorimetric analyses to characterize and measure the energy content of different organic substrates, such as the soil organic matter, (SOM)^12–14 as well as the heat derived from metabolic reactions^15,16. Their application to living systems is referred to as bio-calorimetry. They have helped to quantify thermodynamic state functions that describe the metabolism of cells and microorganisms, beginning to be applied to soil in 1972^17,18. Curiously, the blooming of thermodynamic theories trying to explain the evolution of ecosystems as soils did not interact with the results arising from the development of biocalorimetry, which is responsible for the beginning of a new and still young discipline called bio-thermodynamics. It involves much research that provided and developed different models for quantifying the thermodynamic state functions for microbial metabolism through an intense research activity along the twentieth century, yielding the main equations connecting the enthalpies of the metabolic and combustion reactions of organic substrates with the degree of reduction of those substrates^19,20 and the subsequent connections to the Gibbs energy and entropy^21–23. This research and the models and equations that were generated are widely used in microbiology but have not been applied to soil reactions until recently^24,25 as a possible tool to unravel the thermodynamic characterization of soils.

The application of thermal analysis and calorimetry to soil in the twenty-first century to measure the heat involved in SOM and soil microbial metabolism is responsible for creating and introducing the term bioenergetics of the soil system, which is of growing interest in soil science^26,27. By measuring the energy content of soil we can gain insight into the energy strategies of soil survival and evolution, as well as the persistence of soil organic matter (SOM) by interpreting experimental thermodynamic data rather than relying on theoretical studies.

The first step to achieve this goal is the measurement of the energy source for the soil biota, which is the energy contained in the SOM. This has been reported for the first time in terms of the heat of combustion, Q_SOM, in 2020^24,28. Although the heat content of organic substrates is traditionally determined by bomb calorimetry²⁹, this method is not suitable for mineral soils because of the interaction of the soil organic matter with the mineral matrix that inhibits the combustion reaction in the device^30,31. This is probably why this goal has not been investigated in depth. The development of more sensitive devices, such as simultaneous thermogravimetry and differential scanning calorimetry (TG-DSC), provides a new option to calculate the Q_SOM^24,28. The other way to approach that energy is by the chemical formulation of SOM as recently done too^32,33.

Here, an approach to the experimental quantification of SOM energy content by direct measurement of that energy with a TG-DSC and by the chemical formulation of SOM is presented. We show how the measurement of that energy as the heat of combustion of SOM, Q_SOM, leads to the complete thermodynamic characterization of soils from beech forest ecosystems. Thermodynamic characterization is performed by quantifying the traditional state variables involved in the first and second laws of thermodynamics ruling the universe, enthalpy, entropy and Gibbs energy. They are quantified along a vertical gradient from the soil surface to 10 cm depth to track how the thermodynamic variables evolve as SOM mineralizes. We also tested their possible sensitivity to the forest management.

Evolution of SOM elemental and thermal properties with depth

SOM percentages and the carbon, C, hydrogen, H, oxygen,O, and nitrogen, N, percentages of of SOM decreased with increased soil depth (Table 1). Pearson’s correlation analysis gave significant correlations among all these elements defining the SOM formula (Table S1). The close link among the soil elements validates the SOM empirical formula to obtain the degree of reduction of SOM, E_formula (Table 2). There is a clear trend of E_formula to increase with soil depth in most of the samples indicating the evolution of SOM to a higher degree of reduction as mineralization proceeds. E_formula yields the enthalpy of combustion of SOM, ∆_cH⁰_SOM, by the Patel–Erickson (P&E)³⁴, ∆_cH⁰(SOM)_P&E, and Sandler–Orbey²¹ (S&O) models, ∆_cH⁰(SOM)_S&O (Table 2). Both data rows followed a normal distribution and were compared by a pair-sample t-test. Results yielded significant differences but the difference among values is small, with a constant ratio of 0.019 which is exactly the ratio between the Sandler–Orbey and Patel–Erikson coefficients^21,34.

Table 1.

Elemental composition of the soil organic matter (C, H, N, O), soil organic matter content (SOM) and heat of combustion of SOM, Q_SOM, determined by simultaneous TG-DSC after Baraldi’s correction.

Samples	H (%)	C (%)	N (%)	O (%)	SOM (%)	QSOM (kJ/g SOM)
AZT14LF	2.08	16.33	0.79	17.95	37.17	18.70
AZT 14 M0/5	0.74	3.15	0.22	3.34	7.46	20.49
AZT14M5/10	0.54	2.14	0.17	2.51	5.37	17.41
AZT15LF	2.2	16.91	0.94	10.14	30.19	17.70
AZT15M0/5	0.72	3.98	0.32	4.35	9.38	18.10
AZT15M5/10	0.62	2.58	0.25	3.06	6.52	18.07
AZT16LF	2.5	18.8	0.97	13.60	35.88	17.94
AZT16M0/5	0.94	5.9	0.47	5.52	12.84	18.33
AZT16M5/10	0.84	3.75	0.35	5.27	10.22	17.91
AZT22LF	1.97	13.8	0.83	8.89	25.5	19.51
AZT22M0/5	0.99	4.86	0.43	4.23	10.52	21.84
AZT22M5/10	0.83	2.93	0.28	4.31	8.36	21.66
ARAFACLF	2.66	22.05	1.05	16.72	42.49	18.13
ARAFACM0/5	0.78	5.22	0.28	3.55	9.84	21.73
ARAFACM5/10	0.66	3.28	0.18	2.89	7.02	22.68
ARALACLF	2.55	20.37	1.18	16.20	40.31	19.47
ARALACM0/5	0.87	4.7	0.32	4.47	10.37	18.83
ARALACM5/10	0.88	4.22	0.27	3.95	9.33	18.00
ARAFBCLF	3.01	26.1	1.36	15.50	45.98	20.42
ARAFBCM0/5	1.21	9.7	0.49	7.26	18.67	22.20
ARAFBCM5/10	1.08	7.26	0.36	4.19	12.89	23.60
LIZ19LF	3.9	32.18	1.47	24.63	62.19	18.06
LIZ19M0/5	0.91	3.91	0.31	3.98	9.12	24.50
LIZ19M5/10	0.84	3.25	0.29	4.41	8.8	24.44
LIZ17LF	3.3	27.99	1.08	21.76	54.14	18.16
LIZ17M0/5	0.77	2.55	0,2	3.03	6.56	25.62
LIZ17M05/10	0.72	2.14	0.17	2.95	5.98	26.01
LIZ18LF	3.13	26.18	1.21	19.75	50.28	18.77
LIZ18M0/5	0.92	4.29	0.34	4.11	9.67	22.02
LIZ18M5/10	0.82	3.2	0.28	3.58	7.89	22.98

The uncertainty in estimation of SOM enthalpy of combustion with the S&O model was determined with the experimental DSC data for ∆_cH⁰(SOM)_DSC. It was found that the absolute average deviation (AAD) for enthalpy of combustion of SOM calculated through the S & O model²¹ is 13.6%.

Table 2.

E_formula data determined from the elemental composition (C, H, N, O) of the samples.

Samples	Eformula	− ∆cH0(SOM)P&E kJ/C-mol	− ∆cH0(SOM)S&O kJ/C-mol	− ∆cH0(SOM)DSC kJ/C-mol	EDSC
AZT14LF	3.88	432	424	511	4.68
AZT 14 M0/5	5.26	585	574	582	5.34
AZT14M5/10	5.30	590	579	525	4.81
AZT15LF	4.66	518	508	379	3.47
AZT15M0/5	4.55	506	496	512	4.69
AZT15M5/10	5.13	570	560	548	5.02
AZT16LF	4.51	501	492	411	3.76
AZT16M0/5	4.51	502	492	479	4.39
AZT16M5/10	4.61	512	503	586	5.37
AZT22LF	4.74	528	518	433	3.96
AZT22M0/5	5.14	572	561	568	5.20
AZT22M5/10	5.21	579	568	741	6.80
ARAFACLF	4.31	479	470	419.	3.84
ARAFACM0/5	4.78	532	522	492	4.50
ARAFACM5/10	5.12	570	559	582	5.34
ARALACLF	4.30	479	470	463	4.24
ARALACM0/5	4.81	535	525	499	4.57
ARALACM5/10	5.11	568	558	478	4.38
ARAFBCLF	4.49	499	490	432	3.96
ARAFBCM0/5	4.38	487	478	512	4.70
ARAFBCM5/10	4.91	547	536	503	4.61
LIZ19LF	4.30	479	470	419	3.84
LIZ19M0/5	5.27	587	575	686	6.29
LIZ19M5/10	5.10	567	556	794	7.28
LIZ17LF	4.24	472	463	422	3.86
LIZ17M0/5	5.83	649	637	791	7.25
LIZ17M05/10	5.96	663	651	872	8.00
LIZ18LF	4.30	478	469	433	3.96
LIZ18M0/5	5.13	571	560	596	5.46
LIZ18M5/10	5.42	603	592	680	6.23

− ∆_cH⁰(SOM)_P&E and − ∆_cH⁰(SOM)_S&O are the enthalpies of SOM combustion determined from E_formula values by the Pattel and Ericksson (P&E) and Sandler and Orbey (S&O) correlations respectively. Note these values are negative because combustion is an exothermic reaction. − ∆_cH⁰(SOM)_DSC are the enthalpies of SOM combustion determined directly by integration of the DSC plots converted to C mol by the C/SOM ratio of the samples. E_DSC (S&O) is the degree of reduction of SOM determined from ∆_cH⁰(SOM)_DSC by the S&O correlation.

Heat of combustion of SOM, Q_SOM, and SOM content were experimentally determined by TG-DSC (Table 1). SOM content was significantly correlated with the SOM elemental composition (Table S1) which strengthens the SOM formula given for the soil samples. Q_SOM was directly and experimentally obtained in kJ/g SOM and converted to kJ/C-mol by normalizing Q_SOM to the C/SOM ratio of the samples to yield the enthalpy of combustion of SOM, ∆_cH⁰(SOM)_DSC (Table 2). The three values for ∆_cH⁰(SOM) obtained by the different procedures did not fix the required conditions of normality and homoscedasticity for parametric statistics. They were compared by the paired sample Wilcoxon signed rank test (PSWSR) for that reason which yielded not significant differences between the ∆_cH⁰(SOM)_DSC data, and the ∆_cH⁰(SOM)_P&E and ∆_cH⁰(SOM)_S&O values from the SOM formula (n = 30, p < 0.05) (Table 2).

Complete experimental thermodynamic characterization of SOM

SOM combustion reactions

The results above reinforce both experimental procedures to obtain the enthalpy of combustion of SOM, ∆_cH⁰(SOM)_, an essential step towards completing the thermodynamic characterization. That involves calculating the Gibbs energy, ∆G, and entropy changes, ∆S, for the SOM combustion reaction, ∆cG⁰(SOM) and ∆cS⁰(SOM), respectivelyThe S&O model was applied instead of P&E in this case, as it provides an equation connecting E with the Gibbs energy too²¹. The values of E obtained by applying the S&O correlation to the ∆_cH⁰(SOM)_DSC, E_DSC, did not differ significantly from the E_formula data when compared by the PSWSR test (n = 30, p < 0.05). E_formula and E_DSC (Table 2) were also significantly correlated (n = 30, r = 0.785, p < 0.001). Both E data follow the same trend with soil depth indicating SOM conversion to a higher degree of reduction as it mineralizes in most of the samples. ∆_cH⁰(SOM)_DSC is significantly correlated to E_formula (n = 30, r = 0.785, p < 0.001). If the intercept of the linear fit is fixed to zero, the slope is 113.35 kJ/mol e^-.

There are two ways to calculate the Gibbs energy: Path 1 involves the use of SOM formulation, while Path 2 involves measuring the ∆_cH⁰(SOM)_DSC directly. Figure 1 provides an overview of both paths. To calculate the Gibbs energy by the SOM formula (Path 1) one must first calculate the molar entropy of SOM, S⁰(SOM), and the entropy change of the SOM combustion reaction, ∆_cS⁰(SOM). It was possible by Battley’s model²² applied to the SOM formula, and by the Hess law applied to the adjusted combustion reaction (Table 3). Both, S⁰(SOM) and ∆_cS⁰(SOM), increased with soil depth, that is, with increased degree of reduction, E, of the SOM (Table 3).

Figure 1.

Summary of the two paths leading to the complete thermodynamic characterization of SOM combustion.

Table 3.

Data of the molar entropies of the samples, S⁰(SOM), obtained by Battey’s equation and the entropy change for the SOM combustion reaction, ∆_cS⁰(SOM), obtained by the Hess Law, given in J/C-mol K, together with the Gibbs energies yielded by Eq. (9) for each of the enthalpies of combustion in Table 2 through path 1 [∆_cG⁰(SOM)_P&E, ∆_cG⁰(SOM)_S&O], and the Gibbs energy obtained by Sandler and Orbey model by path 2 [∆_cG(SOM)_DSC] all of them given in kJ/C-mol.

Samples	S0(SOM)	∆cS0(SOM)	∆cG0(SOM)P&E	∆cG0(SOM)S&O	∆cG0(SOM)DSC
AZT14LF	36.29	127.01	− 432	− 461	− 516
AZT 14 M0/5	50.74	161.00	− 585	− 623	− 589
AZT14M5/10	55.05	174.99	− 590	− 632	− 530
AZT15LF	29.52	97.02	− 518	− 537	− 383
AZT15M0/5	43.66	144.67	− 506	− 540	− 517
AZT15M5/10	53.69	172.50	− 571	− 612	− 554
AZT16LF	31.67	105.60	− 501	− 523	− 415
AZT16M0/5	38.19	126.82	− 502	− 531	− 484
AZT16M5/10	54.50	180.26	− 513	− 558	− 592
AZT22LF	32.09	104.86	− 528	− 548	− 437
AZT22M0/5	43.64	138.87	− 572	− 603	− 573
AZT22M5/10	63.70	204.92	− 579	− 631	− 750
ARAFACLF	30.31	102.92	− 479	− 500	− 424
ARAFACM0/5	32.78	105.84	− 532	− 554	− 497
ARAFACM5/10	43.22	137.12	− − 570	− 601	− 589
ARALACLF	31.67	107.62	− 479	− 501	− 467
ARALACM0/5	42.02	136.41	− 535	− 567	− 504
ARALACM5/10	44.97	143.21	− 568	− 601	− 483
ARAFBCLF	27.24	90.96	− 499	− 517	− 436
ARAFBCM0/5	30.21	101.23	− 487	− 508	− 518
ARAFBCM5/10	31.00	98.52	− 546	− 566	− 508
LIZ19LF	30.46	103.43	− 478	− 500	− 423
LIZ19M0/5	49.75	157.71	− 586	− 624	− 693
LIZ19M5/10	58.63	189.06	− 567	− 614	− 803
LIZ17LF	30.05	102.48	− 472	− 493	− 426
LIZ17M0/5	61.80	192.15	− 648	− 695	− 800
LIZ17M05/10	69.31	215.80	− 663	− 717	− 882
LIZ18LF	30.08	102.18	− 478	− 499	− 437
LIZ18M0/5	46.23	147.39	− 571	− 605	− 602
LIZ18M5/10	54.81	173.15	− 603	− 645	− 687

Equation 9 (Fig. 1) provided the Gibbs energy change for the combustion reaction of SOM, ∆_cG⁰(SOM)_P&E and ∆_cG⁰(SOM)_S&O, which were determined using ∆_cH⁰(SOM)_P&E and ∆_cH⁰(SOM)_S&O data respectively (Table 2) obtained from E_formula. These Gibbs energy data (Table 3) determined from ∆_cH⁰(SOM)_P&E and ∆_cH⁰(SOM)_S&O followed a normal distribution and were compared by a pair- sample t-test giving significant differences, but correlated (n = 30, p < 0.05) as observed with the enthalpies of combustion.

The second path (Path 2) towards the Gibbs energy (Fig. 1) uses the S&O model connecting the E_DSC data (given by the S&O model too) with the Gibbs energy by Eq. (10). By this option, ∆_cS⁰ (SOM)would be obtained by Eq. (9). Application of the S&O model for the Gibbs energy yields a new row for these values, ∆_cG⁰(SOM)_DSC, that are not normally distributed. Comparison with the ∆_cG(SOM)_P&E and ∆_cG(SOM)_S&O data by the PSWSR test yielded no significant differences between ∆_cG(SOM)_S&O obtained by Path 1 and ∆_cG(SOM)_DSC data by path 2 (Fig. 1) (Table 3). Therefore, the Gibbs energy change for the combustion reaction of SOM can be calculated by either of the two paths using the Sandler and Orbey correlation. The three rows of Gibbs energy values are closely and significantly correlated (Table S2).

∆_cG(SOM)_DSC, obtained by TG-DSC can be used to determine ∆_cS⁰(SOM) by Eq. (9). The resulting values for these ∆_cS⁰(SOM) data were found to be significantly different from those obtained by the Battley’s model with the SOM formula, but still significantly correlated (n = 30, r = 0.885, p < 0.0001). These results are in Table S3 while Fig. 1 summarizes the entire procedure and outcomes.

Molar entropy, S⁰(SOM), is correlated to the enthalpy of combustion, suggesting the possibility to provide an equation to quantify the molar entropy of SOM for different soil ecosystems. The best correlation was obtained when plotting the S⁰_SOM values in Table 3 versus the enthalpy of combustion given by the TG-DSC, ∆_cH⁰(SOM)_DSC in Table 2. The relation obtained is:

S⁰(SOM) = 0.0856 ∆_cH⁰(SOM)_DSC—4.0729 (n = 30, r = 0.895, p < 0.0001). Also, for the entropy change of SOM combustion: ∆_cS⁰(SOM) = 0.2541 ∆_cH⁰(SOM)_DSC—0.2865 (n = 30, r = 0.884, p < 0.0001).

All the Gibbs energy data showed the same trend of becoming more negative with increasing soil depth.

SOM formation reactions

Results for the SOM combustion reaction opens the possibility to extend the thermodynamic characterization to the thermodynamic variables involved in the SOM formation reaction, enthalpy of formation, ∆_fH(SOM), entropy change of SOM formation, ∆_fS(SOM), and the Gibbs energy, ∆_fG(SOM).

Thermodynamic properties of formation of SOM were calculated through a combination of P&E and Battley models, and through the S&O model (Table S4). The enthalpy of formation, Δ_fH, values calculated through P&E and S&O models were compared by the PSWSR test. Results indicated that the obtained data were significantly different at the p < 0.05 level, but also closely correlated (r = 0.999, p < 0.0001) and with an average absolute deviation (AAD) of 6.1%. The Δ_fH values are negative for all the analysed SOM samples (between − 90 to − 320 kJ/C-mol). This implies that the total energy content of SOM is lower than that of its constituent elements and that the formation of SOM releases energy.

Entropy of formation, Δ_fS, values were calculated with the Battley and S&O models (Table S4). The results given by the two models are significantly different by the PSWSR test at p < 0.05. Nevertheless, they are in reasonable agreement with an AAD of 7.0% and significantly correlated (n = 30, r = 0.985, p < 0.0001) (Table S4). The Δ_fS values range between − 115 and − 355 J/C-mol K. Both turns more negative with increased soil depth.

Gibbs energies of formation, Δ_fG, of SOM were calculated through a combination of P&E and Battley models, and the S&O model (Table S4). The Δ_fG values given by the two models are in reasonably good agreement with an AAD of 5.9% and significantly correlated (n = 30, r = 0.997, p < 0.0001). All the Δ_fG values are negative (between − 55 and − 225 kJ/C-mol). This is due to the negative Δ_fH of SOM (Table S4). The negative Δ_fG indicates a lower usable energy content than in the constituent elements.

Evolution of the SOM thermodynamic properties with soil depth and sensitivity to forest management

The observed thermodynamic SOM properties indicates that SOM increases the degree of reduction, the molar entropy and turns Gibbs energy of SOM combustion and SOM formation more negative as soil depth increases at the forest soil ecosystems studied. These changes cause depletion of soil C. A more negative Gibbs energy of combustion indicates that SOM from deepest soil layers has a stronger tendency to spontaneously combust with increasing temperature than the SOM from the soil surface. The resulting evolution of the entropy indicates that entropy increases as SOM evolve to a higher degree of mineralization. That means that SOM evolves following the second law of thermodynamics contributing to increase the entropy of the universe.

The degree of reduction of LF soil layers was consistent across all sampling sites, varying from 3.8 to 4.74, which is similar to the degree of reduction of carbohydrates (E = 4). E values became more variable as soil mineralized, ranging from 4.8 to 5.9 in the deepest mineral layers.

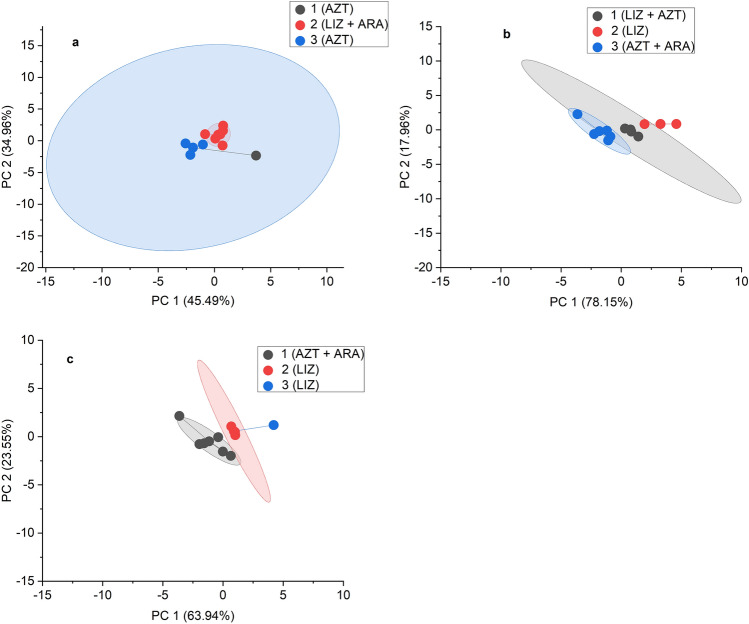
To analyze the variability of thermodynamic properties related to forest management, PCA and K-clustering were applied to the different soil layers and the following properties: SOM, C, Q_SOM, E_formula, ∆cH⁰(SOM)_(DSC), S⁰(SOM), and ∆_cG⁰(SOM)_S&O. The variance of SOM properties could be explained by two principal components (PC) for all soil layers. PC1 accounted for 45.49% of the variance and PC2 34.96% for LF layers. This contribution changed to 78.15 for PC1 and 17.96% for PC2 in mineral soils from 0–5 cm depth, and to 63.94% for PC1 and 23.55% for PC 2 in the deepest soil layers (5–10 cm depth).

SOM, C, and Q_SOM (direct integral of the DSC plot) had the highest contribution to PC2 and the thermodynamic variables to PC1 in all samples. K-clustering plots (Fig. 2) show the distribution of samples within three groups based on the different forest management practices. LIZ samples were taken from undisturbed forests for centuries, AZT samples were from forests under weak management, and ARA samples were from forests under stronger management.

Figure 2.

Results for the PCA and K-Klustering applied to the samples from different soil layers. Thermodynamic properties of mineral soil samples distinguished among soils from the undisturbed forest (LIZ samples) and those from the forests under heaviest management (ARA samples).

The study found that the properties analyzed did not seem to be affected by the intensity of the forest management in LF samples (Fig. 2a). LIZ LF samples share the same group with ARA samples. However, ARA samples from 0–5 cm are in a different group (group 3 overlapping with 2 AZT samples) from those of LIZ and AZT sharing groups 1 and 2. Two of the LIZ samples constitute group 2 overlapping with two AZT samples under weak management but not with the ones under the heaviest management (ARA) (Fig. 2b). Samples AZT and ARA at a depth of 5–10 cm (Fig. 2c) belonged to a different group (group 3) than those of LIZ samples (groups 1 and 2). The study suggests that the thermodynamic properties of SOM could be used to detect trends associated with forest management. However, it is unclear whether they are sensitive enough to differentiate between different levels of forest management intensity.

Discussion

The statistical results indicated that the proposed procedures for the calculation of the thermodynamic SOM properties can serve as good proxies for the state variables that explain the thermodynamic evolution of soil ecosystems. The significant correlation between the enthalpy of combustion and E, obtained through two different experimental procedures, gave a slope value of − 113.35 kJ/mol e⁻, similar to the values reported for different organic substrates ranging from − 108 to − 118 kJ/mol e⁻²⁰.

The approach to the thermodynamics of SOM combustion provides information about the energy budget in the different soil layers, how the degree of reduction of SOM evolves with increasing soil depth, and how it affects to the SOM sensitivity to temperature by the Gibbs energy change of the SOM combustion reaction through the Gibbs–Helmholtz equation (Eq. 9). The results suggest that SOM evolves to a higher degree of reduction with soil depth, turning the Gibbs energy of combustion more negative. Therefore, accumulating driven force to spontaneously combust as temperature increases. As the Gibbs energy is traditionally linked to the rate of the reaction^35,36, if it becomes more negative with increased depth, it should combust faster as temperature increases according to Eq. (9). This perspective could help to understand the role of SOM nature in the sensitivity to temperature³⁷, parametrizing the concept of SOM recalcitrance based on the degree of reduction of SOM, E^27,33, and discerning among the different existing models explaining the evolution of SOM nature as it mineralizes³⁸. Based on the results in this paper, SOM evolves with increased depth to a more reduced state than the original source, as found by other authors³⁹ and the resulting SOM would be more sensitive to temperature than the original reference according to Eq. (9).

The molar entropies obtained from Battley²² and Sandler–Orbey²¹ models are all positive, which agrees with the third law of thermodynamics⁴⁰. Entropy values from Battley’s model²² and the entropy change of SOM combustion enlarged with soil depth, suggesting that SOM would evolve according to the second law of thermodynamics, thereby contributing to increase the entropy of the universe⁸. From a chemical perspective, entropy increases with softer solids, containing larger atoms, and with solids with complex molecular structures, such as SOM. The observed increment in entropy may be due to a less rigid nature of SOM compared to the reference material (partially decomposed tree leaves with a more rigid structure). The molar entropies reported in this study were consistent with those reported for live matter and organic substrates⁴¹.

The thermodynamic variables characterizing SOM combustion became more variable among the different sampling sites as SOM mineralizes, resulting in differing groups within the samples between undisturbed forest sites and those under forest management. This shows the sensitivity of the soil thermodynamic properties to dissimilar soil conditions. Therefore, they could be sensitive to different evolutionary states attached to diverse soil ecosystems. The observed trend is consistent with previous findings in soils from seminatural oak forests reporting the role of SOM microbial decomposition on the geographical variability of the SOM thermodynamic properties²⁴.

The thermodynamic characterization of the SOM combustion enables the completion of the SOM thermodynamic characterization by calculating the state variables of the SOM formation reaction. This provides additional information about the properties and structure of SOM. The enthalpies of formation obtained for all the analysed soil samples are negative, becoming more negative with soil depth and the degree of SOM mineralization. This implies that the total energy content of SOM is lower than that of its constituent elements as in the case of organic substrates derived from plants⁴¹. Therefore, the SOM formation reaction releases energy. This could be explained by the oxidation of less electronegative C and H by more electronegative O and N. Electronegativity expresses the tendency of an atom to attract electrons⁴⁰. When electrons travel from less electronegative elements to more electronegative ones, they become more tightly bound to their nuclei and release energy. This interaction may be favoured in soils by the interaction of SOM with the soil minerals, resulting in high- energy organic-metal bonds between SOM and the soil mineral matrix as soil depth increases. In general, negative enthalpies of formation are interpreted as more stable and less reactive material. Therefore, these enthalpies of formation could assess about SOM chemical stability^42,43. The obtained values ranged within those reported for live matter^20,29,41 and evidence that deep soil would contain more stable and less chemically reactive SOM structures than topsoil.

The entropy change of SOM formation becomes more negative with soil depth. These negative values indicate a higher level of organization of atoms in SOM than in its constituent elements. It is also associated with less chemically reactive materials. The SOM empirical formula comprises of C, H, O, and N atoms. In their elemental form, C is solid graphite, while H, O, and N are diatomic gasses H₂, O_2, and N₂. In SOM these atoms exist in organic molecules that are much larger and more organized than the pure elements, resulting in less dispersion of atoms. This organization could be the origin of the negative entropies of formation. In general, lower entropy is linked to dissipative structures⁴⁴ in agreement with the observed evolution of the entropy change of SOM combustion, following the definition of life forms as dissipative structures too^9,45. A dissipative structure is defined as an organized state or structures that are maintained through dissipation of free energy and generation of entropy⁴⁴. Based on the obtained results, soil ecosystems would keep SOM according to that postulate.

What the soil system would achieve with the observed evolution of all these thermodynamic variables is to balance the carbon losses as SOM mineralizes with the preservation of the energy in the resulting SOM substrates. Although the SOM produced by the mineralization of the original C sources has less C than the original one, it has more energy stored by a material that would be less chemically reactive but more sensitive to combustion with temperature than the original one.

Experimental entropies and enthalpies could be useful tools in determining the stability of SOM in different soil ecosystems and the impact of management practices. These tools could help to validate the theoretical approaches developed since the early twentieth century to explain the evolution and survival strategies of soil ecosystems^10,46.

In this paper, TG-DSC and elemental SOM composition show up as choices for determining the energy content of SOM as the heat of combustion. This approach leads to the complete thermodynamic characterization of SOM and yields the entropies for SOM and SOM combustion and formation reactions, as well as their respective Gibbs energies. It is a first step to be able to study the evolution of soil ecosystems by classic thermodynamic functions. These results suggest that the ecosystems studied follow the thermodynamic laws, increasing entropy as SOM evolves from a less to a more mineralized state. The accumulation of Gibbs energy turns SOM into a more reduced state that the original reference (poorly degraded SOM on the soil surface) in accordance with the concept of live matter as dissipative structures^44,45. The experimental approaches are sensitive enough to detect differences among soil samples from various locations, and therefore could be useful in studying diverse soil ecosystems and their evolutionary states.

Methods

Soil samples

Soil samples were collected in three mature beech forests from three different locations: Lizardoia (LIZ samples), Aztaparreta (AZT samples) and Sierra de Aralar (ARA samples) (Navarra, Spain). The sampling collection was designed for 3 and 4 plots at each location. The soils were taken at 6 points equally distributed within each plot following a systematic sampling. It consists in the random selection of a sampling point within the plot close to its centre followed by the selection of six sampling points that must be located at about 5 m from the centre. The first sampling point is at a northerly direction (0°), and the following ones at intervals of 60° in a clockwise direction (60°, 120°, 180°, 240° and 300°). Excessive proximity to trees or other elements that distort the nature of the sample has been avoided.

At each sampling point, samples were collected following a depth gradient and distinguishing the organic horizons (LF) from the mineral soil taken from 0–5 cm and 5–10 cm depth (Samples LF, 0/5 and 5/10 respectively). These three soil samples from each of the 6 points are combined into one for each depth per plot and stored in polyethylene bags.

All soil samples were sieved at 2 × 2 mm and dried at 105 °C for 24 h before elemental and thermal measurements.

Soil elemental composition and thermal properties

Elemental analysis of carbon, C, hydrogen, H, and nitrogen, N, were done with a LECO analyser.

The soil organic matter was measured by a simultaneous TG-DSC (TGA-DSC1 Mettler Toledo) at a scan of temperature from 50 to 1000 °C in the case of mineral soil samples, and from 50 to 600 °C for the organic layer at the soil surface, at a temperature rate of 10 °C per minute and under an air flow of 50 ml per minute after previous calibration of the device according to the company instructions. It is determined as the mass lost from 180 to 600 °C and directly calculated from the TG trace.

Oxygen, O, was indirectly measured by subtracting the sum of C, H, N elements from 100% after normalizing to the SOM content^29,47.

Calculation of the heat of combustion of SOM by TG-DSC

The heat of combustion of SOM, Q_SOM, was directly determined by DSC under airflow at the same conditions reported for the mass loss. TG-DSC gives the pattern of the heat released by the material during the combustion as DSC curves representing the energy in watts versus temperature or time in seconds. The total heat dissipated along with the combustion is determined by integration of the DSC plots normalized to the soil mass combusted given by the simultaneous TG from 180 to 600 °C (SOM). This value is used for the determination of the molar enthalpy of combustion of SOM by TG-DSC, ∆_cH⁰(SOM)_DSC, after Baraldi’s correction⁴⁸ (1.839 kJ/g) and normalization to the soil C content given by the elemental analysis by two procedures²⁴. The first one is by obtaining a conversion factor from the linear fit between C and SOM, which informs about the extent at which C is attached to the SOM composition. The other procedure, after demonstrating the C-SOM connection, is by the C/SOM ratio obtained for each sample. Values for the Q_SOM in kJ/C-mol obtained by these procedures were compared to check which of both may be more convenient. This value is assumed to represent the enthalpy of SOM combustion, ∆_cH⁰(SOM) _DSC, in kJ/C-mol.

Calculation of the enthalpy of combustion of SOM by elemental analysis

It is attempted to provide an empirical formula for SOM samples from their elemental composition. The C, H, N and O content of the soil samples are converted into unit C formulas as C-mol (empirical formula) by the following general Equation⁴¹:

$$nJ=\frac{W_J}{W_C}.\frac{M_C}{M_J}$$ 1

where W_J and W_C are the mass fractions of element J and carbon in the SOM respectively, and M_J and M_C are the molar masses of element J of SOM and the carbon. Therefore, the formula for SOM adopts the form: C_nCH_nHO_nON_nN where n_J is the atomic coefficient of each element J in the SOM formula given by Eq. (1). This possibility for SOM involves the existence of a correlation of each of the SOM elements to the SOM quantity in soils, informing about the extent at which each of the determined elements takes part in SOM. The last is important for [H] to discern the influence of water on [H] elements and the effect of inorganic material.

The connection to the energy of the SOM substrate can be settled by different models linking energy with the degree of reduction or degree of oxidation of carbon. The degree of reduction is given by the number of electrons transferred to oxygen during combustion to CO₂ (g), H₂O(v), and N₂(g). Carbon is +4, [O] is − 2, [H] is +1, [N] is zero assuming it is converting to N₂⁴¹. Thus, the number of electrons transferred, E_formula, can be determined as follows:

$$E_{\text{formula}}=4n_C+n_H-2n_O-0n_N$$ 2

where n_C, n_H, n_O, and n_N are the number of C, H, O, and N in the SOM empirical formula.

E (also called degree of reduction, λ, by other authors²³) can be used to obtain the enthalpy of combustion of SOM through the following equations attached to different models (Patel-Erickson³⁴; Sandler and Orbey²¹):

$${\mathrm{\Delta }}_c{H}^0{\left(\mathit{SOM}\right)}_{P\&E}=-111.14E$$ 3

$${\mathrm{\Delta }}_c{H}^0{\left(\text{SOM}\right)}_{\text{S}\&\text{O}}=-109E$$ 4

Equations (2–4) are used to obtain the molar enthalpy of combustion of SOM, Δ_cH⁰_SOM, from the empirical formula, to be compared to the values given by TG-DSC.

Calculation of the molar entropy of SOM and entropy change for the SOM combustion

SOM formulation allows the calculation of the molar entropy of SOM by Battley’s model²² through the following equation:

$$S_m^0=0.187\sum {(S}_m^0(J)/a_j)n_j$$ 5

where $S_m^0$ is the molar entropy of a substrate, nj is the number of atoms of element j in the empirical formula of any biological substrate, and aj is the number of atoms per molecule of element j in its standard state elemental form⁴¹. If applied to SOM, Eq. (5) can be written as follows:

$$S^0(SOM)=0.187\left(n_C,S_C^0,+,n_H,\frac{S_{H2}^0}{2},+,n_O,\frac{S_{O2}^0}{2},+,n_N,\frac{S_{N2}^0}{2}\right)$$ 6

Values of the standard entropies, S⁰m for the SOM elements and the products of SOM combustion are shown in Table 4.

Table 4.

Standard molar entropies for the elements of SOM (C, O₂, H₂ and N₂) and the products of SOM combustion (CO₂ and H₂O).

	S0C	S0O2	S0 H2	S0N2	S0mCO2(g)	S0mH2O(v)
S0m (J/mol K)	5.740	205.15	130	191.6	213.7	188.8

The entropy change for the SOM combustion reaction, ∆_cS⁰(SOM), can be determined by the Hess’s law, applied to each of the samples as follows³⁸:

$$C_{\mathit{nC}}{H}_{\mathit{nH}}{O}_{\mathit{nO}}{N}_{\mathit{nN}}\left(\text{s}\right)+\left[n_c+1/4n_H-1/2n_O\right]O_2(g)=n_{c}C{O}_2(g)+1/2n_H{H}_{2}0(v)+1/2n_N{N}_2(g)$$ 7

where the entropy change is:

$${\mathrm{\Delta }}_c{S}^0\left(\mathit{SOM}\right)=\sum S_{\mathit{products}}^0-\sum S_{\mathit{reactants}}^0$$

Calculation of the Gibbs energy change of SOM combustion

The Gibbs energy change for SOM combustion, ∆_cG⁰(SOM), is determined by two procedures:

From SOM empirical formula: Once determined the Δ_cH⁰(SOM) and the ∆_cS⁰(SOM)_, the Gibbs energy change can be calculated by the following equation:

$${\mathrm{\Delta }}_c{G}^0\left(\mathit{SOM}\right)={\mathrm{\Delta }}_c{H}^0\left(\mathit{SOM}\right)-T\mathrm{\Delta }c{S}^0\left(\mathit{SOM}\right)$$ 9

where T is the temperature.

From the Δ_cH⁰(SOM) data given by the TG-DSC, by applying the Sandler and Orbey²¹ correlation for the Gibbs energy (Sandler and Orbey²¹):

$${\mathrm{\Delta }}_{c}G\mathrm{\Delta }=-110.23E$$ 10

The ∆_cG⁰(SOM) values are compared among the two different Eqs. (9 and 10). Alternatively, the procedure 2) yields the ∆_cS⁰(SOM ) through Eq. (9). The obtained values for ∆_cS⁰(SOM)by the two different procedures were compared too, to discern the best approach to the entropy of SOM.

Calculation of enthalpies, Gibbs energies and entropies of formation of SOM

Standard enthalpies of combustion of SOM calculated thorough the Patel-Erickson Eq. (3) were used to calculate standard enthalpies of formation of SOM based on the Patel-Erickson model, Δ_fH(SOM)_P&E. This was done through the Hess’s law. Δ_cH(SOM)_P&E is the enthalpy change of reaction (7). When we apply Hess’s law to reaction (7), we find:

$${\mathrm{\Delta }}_{C}H(SOM)=n_C{\mathrm{\Delta }}_{f}H(CO2)+\frac{1}{2}{n}_H{\mathrm{\Delta }}_{f}H(H2O)-{\mathrm{\Delta }}_{f}H(SOM)$$ 11

where Δ_fHX is standard enthalpy of formation of substance X. Thus, Δ_fH(SOM) can be found if the Eq. (11) is rearranged into:

$${\mathrm{\Delta }}_{f}H(SOM)=n_C{\mathrm{\Delta }}_{f}H(CO2)+\frac{1}{2}{n}_H{\mathrm{\Delta }}_{f}H(H2O)-{\mathrm{\Delta }}_{C}H(SOM)$$ 12

This equation was used to find Δ_fH(SOM)_P&E from Δ_cH(SOM)_P&E.

Standard entropy of formation of SOM, Δ_fS(SOM)_B, was found through the alternative Battley Equation²². If the coefficient 0.187 in the Battley Eq. (5) is changed to − 0.813, then it gives standard entropy of formation:

$${\mathrm{\Delta }}_f{S(SOM)}_B=-0.813\sum {(S}_m^0(J)/a_j)n_j$$ 13

Finally, Δ_fH(SOM)_P&E and Δ_fS(SOM)_B were combined to give standard Gibbs energy of formation of SOM, Δ_fG(SOM)_PEB, through the equation:

$${\mathrm{\Delta }}_f{G(SOM)}_{\mathit{PEB}}={\mathrm{\Delta }}_f{H(SOM)}_{P\&E}-T{\mathrm{\Delta }}_f{S(SOM)}_B$$ 14

where T is temperature. Therefore, Δ_CH(SOM)_P&E was given by the Patel-Erickson equation. It was converted into Δ_fH(SOM)_P&E through Hess’s law. Then, Δ_fS(SOM)_B was found through the alternative Battley equation. Finally, Δ_fH(SOM)_P&E and Δ_fS(SOM)_B were combined to give Δ_fG(SOM)_PEB.

Standard thermodynamic properties of formation were also calculated based on the Sandler–Orbey model. Standard enthalpy of combustion of SOM calculated through the Sandler–Orbey Eq. (4), Δ_CH(SOM)_S&O, was converted into standard entropy of formation of SOM, Δ_fH(SOM)_S&O, through Eq. (12).

Standard Gibbs energy of combustion of SOM based on the Sandler–Orbey model, Δ_CG(SOM)_S&O, in Eq. (10) was used to find standard Gibbs energy of formation of SOM based on the Sandler–Orbey model, Δ_fG(SOM)_S&O. This was done through the Hess’s law, which gave an equation analogous to Eq. (12) for enthalpy:

$${\mathrm{\Delta }}_{f}G(SOM)=n_C{\mathrm{\Delta }}_{f}G(CO2)+\frac{1}{2}{n}_H{\mathrm{\Delta }}_{f}G(H2O)-{\mathrm{\Delta }}_{C}G(SOM)$$ 15

Finally, Δ_fH(SOM)_S&O and Δ_fG(SOM)_S&O were combined to give standard entropy of formation of SOM based on the Sandler–Orbey model, Δ_fS(SOM)_S&O, through the equation:

$${\mathrm{\Delta }}_f{S(SOM)}_{S\&O}=\frac{{\mathrm{\Delta }}_f{H(SOM)}_{S\&O}-{\mathrm{\Delta }}_f{G(SOM)}_{S\&O}}{T}$$ 16

Therefore, Δ_CH(SOM)_S&O was given by the Sandler–Orbey model in Eq. (4). It was converted into Δ_fH(SOM)_S&O through Hess’s law. Then, Δ_CG(SOM)_S&O was found through the Sandler–Orbey model given by Eq. (10). It was then converted into Δ_fG(SOM)_S&O through Hess’s law. Finally, Δ_fH(SOM)_S&O and Δ_fG(SOM)_S&O were combined to find Δ_fS(SOM)_S&O by Eq. (16).

Statistical analysis

Uncertainties

The uncertainty in the standard enthalpy of combustion of SOM determined by DSC, δ[Δ_CH_SOM(DSC)], is 5%. Thus, it is given by the equation:

$$\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(DSC)\right]=0.05·{\mathrm{\Delta }}_C{H}_{\mathit{SOM}}(DSC)$$ 17

This uncertainty is passed to the calculated number of electrons transferred to oxygen during combustion, [E_DSC(S&O)], which is found from ∆_cHSOM_(DSC) with Eq. (4). Therefore, the uncertainty in the number of electrons transferred to oxygen during combustion δ[E_DSC(S&O)] is given by the equation:

$$\left[E_{\mathit{DSC}},\left(S,\&,O\right)\right]=E_{\mathit{DSC}}\left(S,\&,O\right)·\sqrt{{\left(\frac{\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},\left(D,S,C\right)\right]}{{\mathrm{\Delta }}_C{H}_{\mathit{SOM}}\left(D,S,C\right)}\right)}^2+{\left(\frac{\delta \left[C,o,e,f\right]}{\mathit{Coef}}\right)}^2}$$ 18

where δ[Coef] is the uncertainty in the coefficient − 109 in Eq. (4), Coef. The absolute average deviation (AAD) for Δ_CH_SOM(S&O) calculated with Eq. (4) was found to be 12.7%, which was set as the relative error in the coefficient 109. Therefore, δ[Coef]/Coef = 12.7%. Once this is substituted into the Eq. (18) above, it simplifies into:

$$\delta \left[E_{\mathit{DSC}},\left(S,\&,O\right)\right]=0.136·E_{\mathit{DSC}}\left(S,\&,O\right)$$ 19

This means that the uncertainty in number of electrons transferred to oxygen during combustion, E_DSC(S&O), calculated from DSC enthalpy data with the Sandler–Orbey model is 13.6%.

The uncertainty in the standard enthalpy of combustion calculated through the Patel-Erickson model, δ[Δ_CH_SOM(P&E)], is 5.36% ⁴⁹. This means that:

$$\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(P\&E)\right]=0.0536·{\mathrm{\Delta }}_C{H}_{\mathit{SOM}}(P\&E)$$

This uncertainty is passed to the standard enthalpy of formation calculated through the Patel-Erickson model⁴⁹. Thus, since enthalpies of inorganic oxides have been determined very accurately⁴⁷. The uncertainty in the standard enthalpy of formation calculated from the Patel-Erickson model, δ[Δ_fH⁰(P&E)], is given by the equation:

$$\delta \left[{\mathrm{\Delta }}_f,H_{\mathit{SOM}},(P\&E)\right]=\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(P\&E)\right]$$

For the Sandler–Orbey model, no uncertainty was reported in the literature. Thus, it was calculated in this research, with the experimental DSC enthalpies of combustion and empirical formulas of SOM. The empirical formulas of SOM were used to find the enthalpies of combustion of SOM through the Sandler–Orbey model²¹. These were then combined with the experimental DSC values, to find the deviation. The absolute average deviation (AAD) for Δ_CH_SOM(S&O) was found to be 12.7%. This means that the uncertainty in enthalpy of SOM determined with the Sandler–Orbey model, δ[Δ_CH_SOM(S&O)], is:

$$\delta \left[{\mathrm{\Delta }}_f,H_{\mathit{SOM}},(S\&O)\right]=0.127·{\mathrm{\Delta }}_C{H}_{\mathit{SOM}}(S\&O)$$

The uncertainty in standard molar entropies calculated through the Battley equation, δ[S_m⁰(B)], is 19.7%²²:

$$\delta \left[S_m^0,\left(B\right)\right]=0.197·S_m^0\left(B\right)$$

This uncertainty is passed to the standard entropy of formation and standard entropy of combustion. Entropies of the constituent elements and their oxides have been measured very accurately⁵⁰. Thus, the uncertainty in standard entropy of formation, δ[Δ_fS⁰(B)], and uncertainty in standard entropy of combustion, Δ_CS(SOM), are given by the equations:

$$\delta \left[{\mathrm{\Delta }}_f,S^0,(B)\right]=\delta \left[S_m^0,\left(B\right)\right]$$

$$\delta \left[{\mathrm{\Delta }}_C,S,(SOM)\right]=\delta \left[S_m^0,\left(B\right)\right]$$

The uncertainties in enthalpies were combined with those in entropies, to find the uncertainties in Gibbs energies. Thus, the uncertainty in standard Gibbs energy of formation given by a combination of Patel-Erickson and Battley models is, δ[Δ_fG], and uncertainty in standard Gibbs energy of combustion calculated with a combination of the Patel-Erickson and Battley models, δ[Δ_CG_SOM(P&E)], uncertainty in standard Gibbs energy of combustion given by the Sandler–Orbey model for enthalpy and Battley model for entropy, δ[Δ_CG_SOM(S&O)], and standard Gibbs energy of combustion given by DSC enthalpy and Battley entropy model, δ[Δ_CG_SOM(DSC)], are given by the equations:

$$\delta \left[{\mathrm{\Delta }}_f,G,(PEB)\right]=\sqrt{{\left\{\delta ,\left[{\mathrm{\Delta }}_f,H_{\mathit{SOM}},(P\&E)\right]\right\}}^2+{\left\{T,·,\delta ,\left[{\mathrm{\Delta }}_f,S^0,(B)\right],·,\frac{1kJ}{1000J}\right\}}^2}$$

$$\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{SOM}},(P\&E)\right]=\sqrt{{\left\{\delta ,\left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(P\&E)\right]\right\}}^2+{\left\{T,·,\delta ,\left[{\mathrm{\Delta }}_C,S^0,(SOM)\right],·,\frac{1kJ}{1000J}\right\}}^2}$$

$$\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{SOM}},(S\&O)\right]=\sqrt{{\left\{\delta ,\left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(S\&O)\right]\right\}}^2+{\left\{T,·,\delta ,\left[{\mathrm{\Delta }}_C,S^0,(SOM)\right],·,\frac{1kJ}{1000J}\right\}}^2}$$

$$\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{SOM}},(DSC)\right]=\sqrt{{\left\{\delta ,\left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},(DSC)\right]\right\}}^2+{\left\{T,·,\delta ,\left[{\mathrm{\Delta }}_C,S^0,(SOM)\right],·,\frac{1kJ}{1000J}\right\}}^2}$$

The uncertainty in entropy was multiplied by the conversion factor (1 kJ/1000 J) to bring its units in agreement in kJ for enthalpy.

The uncertainty in standard Gibbs energy of combustion calculated from experimental DSC enthalpy with the Sandler–Orbey model, δ[Δ_CG_DSC(S&O)], is given by the equation:

$$\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{DSC}},\left(S,\&,O\right)\right]={\mathrm{\Delta }}_C{G}_{\mathit{DSC}}\left(S,\&,O\right)·\sqrt{{\left(\frac{\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},\left(D,S,C\right)\right]}{{\mathrm{\Delta }}_C{H}_{\mathit{SOM}}\left(D,S,C\right)}\right)}^2+{\left(\frac{\delta \left[C,o,e,f\right]}{\mathit{Coef}}\right)}^2+{\left(\frac{\delta \left[C,o,e,f\right]}{\mathit{Coef}}\right)}^2}$$

where δ[Coef] is the uncertainty in the coefficient -109 in Eq. (4), Coef, and δ[Coef]/Coef = 12.7%, while δ[Δ_CG_DSC(S&O)]/[Δ_CG_DSC(S&O)] = 5%. Once this is substituted into the equation above, it simplifies into:

$$\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{DSC}},\left(S,\&,O\right)\right]=0.186·{\mathrm{\Delta }}_C{G}_{\mathit{DSC}}\left(S,\&,O\right)$$

This means that the uncertainty in standard Gibbs energy of combustion calculated from experimental DSC enthalpy with the Sandler–Orbey model, Δ_CG_DSC(S&O), is 18.6%.

The uncertainty in standard entropy of combustion calculated from experimental DSC enthalpy and Gibbs energy found from the DSC enthalpy through the Sandler–Orbey model, δ[Δ_CS_SOM(S&O)], is:

$$\delta \left[{\mathrm{\Delta }}_C,S_{\mathit{SOM}},(S\&O)\right]=\sqrt{{\left\{\frac{\delta \left[{\mathrm{\Delta }}_C,H_{\mathit{SOM}},\left(D,S,C\right)\right]·\frac{1000J}{1kJ}}{T}\right\}}^2+{\left\{\frac{\delta \left[{\mathrm{\Delta }}_C,G_{\mathit{DSC}},\left(S,\&,O\right)\right]·\frac{1000J}{1kJ}}{T}\right\}}^2}$$

The conversion factor (1000 J/1 kJ) was used to convert kJ from units of enthalpy and Gibbs energy into J in the units for entropy.

Tables with the thermodynamic variables and their uncertainties are provided as supplementary material as Tables S4, S5 and S6.

Thermodynamic functions determined by formulation and TG-DSC by the different models were compared by pair sample t-test and by the paired sample Wilcoxon signed rank test (PSWSR) depending on the row of data fulfilled or not the parametric conditions. The existing correlation among the different soil data was tested by Pearson’s correlation at p < 0.05. Sensitivity of soil elemental, thermal and thermodynamic properties to SOM evolution and different sampling sites was studied by PCA and K-Cluster analysis. The entire statistical study was performed by Origin Lab software.

Author contributions

CPC, JMV and YLC are responsible for the sampling design, travel, and collection of samples at the sampling sites and preparation of soils for the measurements. NB is responsible for designing soil analysis, interpretation of results, and design of the procedure for the thermodynamic characterization of the soil organic matter combustion reaction. MP is responsible for all calculations to achieve the thermodynamic functions for the soil organic matter formation reaction and determination of uncertainties. All authors have equally contributed to writing the paper providing information from their respective tasks.

Data availability

All data are presented in the article and the supplementary material.

Competing interests

The authors declare no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-67590-w.