Characterizing normal perinatal development of the human brain structural connectivity

Abstract

Early brain development is characterized by the formation of a highly organized structural connectome, which underlies brain's cognitive abilities and influences its response to diseases and environmental factors. Hence, quantitative assessment of structural connectivity in the perinatal stage is useful for studying normal and abnormal neurodevelopment. However, estimation of the connectome from diffusion MRI data involves complex computations. For the perinatal period, these computations are further challenged by the rapid brain development, inherently low signal quality, imaging difficulties, and high inter‐subject variability. These factors make it difficult to chart the normal development of the structural connectome. As a result, there is a lack of reliable normative baselines of structural connectivity metrics at this critical stage in brain development. In this study, we developed a computational method based on spatio‐temporal averaging in the image space for determining such baselines. We used this method to analyze the structural connectivity between 33 and 44 postmenstrual weeks using data from 166 subjects. Our results unveiled clear and strong trends in the development of structural connectivity in the perinatal stage. We observed increases in measures of network integration and segregation, and widespread strengthening of the connections within and across brain lobes and hemispheres. We also observed asymmetry patterns that were consistent between different connection weighting approaches. Connection weighting based on fractional anisotropy and neurite density produced the most consistent results. Our proposed method also showed considerable agreement with an alternative technique based on connectome averaging. The new computational method and results of this study can be useful for assessing normal and abnormal development of the structural connectome early in life.

1. INTRODUCTION

Structural connectivity of the brain underlies our cognitive abilities and influences the progression of neuropathologies (Collin & Van Den Heuvel, 2013; Fornito et al., 2015). Metrics computed from a graph representation of the structural connectome can be strong markers of brain disorders (Cao et al., 2013; Wheeler & Voineskos, 2014). Studying brain connectivity can be particularly useful for understanding and characterizing early brain development, where the brain is vulnerable to diseases and environmental factors. To name three examples, prenatal exposure to maternal stress (Chen & Baram, 2016; Scheinost et al., 2017), congenital heart disease (Schmithorst et al., 2018), and various brain malformations (Jakab et al., 2015; Meoded et al., 2011) may disrupt the development of the connectome.

Diffusion‐weighted magnetic resonance imaging (dMRI) is the method of choice for non‐invasive quantitative assessment of structural brain connectivity (Shi & Toga, 2017; Tymofiyeva et al., 2014). Over the past decade, the accuracy and reliability of this approach as well as our understanding of the potentials and limitations of this technique have improved (Fornito et al., 2013; Jones, 2010; Sotiropoulos & Zalesky, 2019; Zhang et al., 2022). However, the great majority of prior works on structural connectivity have focused on pediatric and adult brains. Comparatively, much less is known about the structural brain networks very early in life. Quantitative assessment of structural connectivity in the perinatal stage is challenged by several factors:

• Low data quality. Image acquisition for this age range is challenged by such factors as subject motion, increased MRI distortions, and overall low data quality (Cordero‐Grande et al., 2018; Malamateniou et al., 2013; Pecheva et al., 2018). Subject motion is likely to be high unless sedation is used or the subject is scanned in natural sleep, which is not feasible in most settings. Even with advanced retrospective motion correction techniques, subject motion can significantly impact the data quality. Additionally, compared with adult brain imaging, the signal to noise ratio is inherently lower due to higher free water content of the brain tissue in the perinatal period (Dubois et al., 2021; Pietsch et al., 2019).

• Rapid brain development and high inter‐subject variability. During the perinatal period, brain undergoes a rapid increase in size and significant transformations in the cellular and microstructural makeup (Dubois et al., 2021). Different brain structures and white matter tracts emerge, develop, and mature at different time points and with different rates during this short period (Dubois et al., 2014; Ouyang et al., 2019). As a result, the structural connectome develops in complex ways.

• Technical and methodological challenges. Another set of difficulties are imposed by the lack of dedicated computational tools, paucity of postmortem material for deriving the gold standard, and overall limited existing knowledge regarding brain development at this early stage. These factors make it especially difficult to develop and validate new computational methods for quantitative structural connectivity analysis in the perinatal stage.

In addition, application of advanced dMRI‐based methods such as computation of complex fiber orientations and anatomically‐constrained tractography require high‐quality data, preferably dense multi‐shell measurements. Moreover, in order to study the development of the connectome with postmenstrual age (PMA), the data should include a sufficient number of subjects at each PMA. Such data have become available only recently through initiatives such as the Human Connectome Project (HCP) (Bastiani et al., 2019).

Because of the limitations mentioned above, prior works on perinatal structural connectivity suffer from a number of important shortcomings. Methodologically, most of these studies have used a diffusion tensor model to estimate the local orientation of fascicles in each voxel (de Almeida et al., 2021; Ramirez et al., 2022; Van Den Heuvel et al., 2015). This choice has been dictated, in part, by the fact that a small number of measurements (usually 15–30) in a single shell has been available (de Almeida et al., 2021; Ratnarajah et al., 2013; Zhao et al., 2019). This can significantly influence the computed connectome and the derived connectivity metrics. Moreover, a deterministic tractography algorithm has often been used, which restricts the reconstruction of different white matter tracts especially in the neonatal brain where local white matter anisotropy is low (Dubois et al., 2021; Smyser et al., 2019). The overwhelming majority of prior works have not used anatomical information to prune false streamlines, which can substantially reduce the accuracy and reproducibility of the results. Leveraging anatomical information can lead to drastic reductions in tractography error, which can be especially important in perinatal imaging given the low data quality. Another important shortcoming of prior works is that they have used unreliable measures, such as the number of streamlines, to define the connection strength (Shi et al., 2012). Moreover, microstructure‐informed filtering of the streamlines has not been utilized. A number of advanced methods for filtering the tractogram to better match the brain microstructure have been proposed in recent years (Daducci et al., 2014; Ocampo‐Pineda et al., 2021; Smith et al., 2013). These methods can effectively filter the massive tractogram data such that the streamline counts/weights are closer to an anatomically valid measure of connection strength. While these have been shown to be essential to ensure accuracy of connectivity quantification, they have not been applied to study the perinatal brain. Moreover, most prior works on perinatal brain connectivity have explored a very narrow age range with a limited number of subjects, which limits the accuracy of these studies in characterizing the complex development of the structural connectome with age.

This represents a critical gap in knowledge as it is well known that adult‐like topological structures and a highly structured brain connectome develop very early in life (Bayer & Altman, 2005; Kostović & Jovanov‐Milošević, 2006; Marami et al., 2017; Ouyang et al., 2019; Silbereis et al., 2016; Van Den Heuvel et al., 2015). Hence, there is an urgent need for methods and resources to enable accurate and reproducible quantitative assessment of structural brain connectivity in the perinatal stage. Such methods can significantly enhance our understanding of perinatal brain development and improve our knowledge of the neurodevelopmental processes that shape the structure and function of the brain for the rest of life.

In order to address this gap in methodology, the goal of this work is to develop and evaluate a new computational framework for assessing the normal development of brain's structural connectivity in the perinatal stage. The central idea of our proposed method is spatial alignment (also referred to as registration or spatial normalization) and averaging of imaging data from subjects of the same age. We think this approach holds the key to mitigating the impact of poor subject data quality due to such factors as low signal to noise ratio and motion effects that we mentioned above. By averaging the data from subjects within the same age range, this approach also enables improved characterization of the developments in structural connectome in the presence of high inter‐subject variability while accounting for rapid changes over time. We strive to achieve precise spatial registration of white matter structures between subjects by computing the registration transforms based on maps of diffusion tensor and fiber orientation distribution (FOD). Accurate alignment and averaging of tissue microstructure and FOD generate spatio‐temporal atlases. As shown by prior works, such atlases can portray the developmental trends in fetal and neonatal brains and amplify important details that may not be clearly seen in individual subject images (Calixto Nunez et al., 2024; Ciceri et al., 2024; Khan et al., 2019; Oishi et al., 2019). Therefore, we expect that spatio‐temporal averaging in the image space should be effective in characterizing the changes in structural connectivity that take place due to brain development with age. To the best of our knowledge, no prior work has developed such a computational method to study the structural connectivity in the perinatal stage. Furthermore, unlike prior studies, our framework utilizes the state of the art techniques for data pre‐processing, micro‐structure and fiber orientation estimation, streamline tractography, and tractography post‐processing. To enable these computations, we use densely‐sampled multi‐shell dMRI data that allow us to compute accurate FOD and whole‐brain tractograms and to apply microstructure‐informed tractography filtering using advanced models of tissue microstructure. The new method, applied to high‐quality data used in this work, is expected to reconstruct normative structural connectivity metrics that can serve as reference baselines for reliable assessment and comparison of normal and abnormal brain development at this critical stage. We demonstrate the effectiveness of the proposed computational framework by applying it to a large cohort of subjects scanned between 33 and 44 weeks of PMA and analyzing important metrics of structural connectivity.

2. MATERIALS AND METHODS

2.1. Data

We used the MRI data from the second release of the Developing Human Connectome Project (dHCP) study (Bastiani et al., 2019). All subjects included in this analysis were healthy, that is, without major focal brain lesions or any clinically significant abnormalities based on expert evaluation of structural MRI. To conduct our analysis, we considered PMAs between 33 and 44 weeks. This period is characterized by interhemispheric synchronization and a gradual resolution of the subplate that corresponds to the establishment of permanent brain circuitry (Kostović & Judaš, 2010). The PMA is the summation of gestational age (interval between the initial day of the last menstrual period and the day of delivery) and chronological age. The PMA was rounded to the nearest week. For PMA of 35 weeks, for example, we used subjects scanned between 34.5 and 35.5 postmenstrual weeks. For PMAs around 38 weeks, the dHCP dataset contained many more subjects than needed for our analysis. Our recent work as well as works of other researchers have shown minimal or no changes in the quality of spatio‐temporal atlases when more than 15 subjects are used in each age group (Karimi & Gholipour, 2022; Pietsch et al., 2019). Hence, we used at most 15 subjects for each PMA. For the earliest age of 33 weeks only seven subjects were available, but that was still sufficient for our analysis.

2.2. Data preprocessing

Structural MRI data for each subject included T1w and T2w multi‐slice fast spin‐echo images acquired with an in‐plane resolution of 0.8 mm, slice thickness of 1.6 mm, and slice overlap of 0.8 mm in axial and sagittal directions. The dMRI data was collected with a set of spherically optimized directions at four b‐values: $b=0$ ($n=20$), $b=400$ ($n=64$), $b=1000$ ($n=88$), and $b=2600$ ($n=128$). Preprocessing of raw structural data included bias correction with the N4 algorithm (Tustison et al., 2010), motion corrected volumetric reconstruction of the multi‐slice acquisitions, brain extraction using BET from the FSL software package (Jenkinson et al., 2005), and tissue segmentation using the DRAW‐EM algorithm developed for neonatal brains (Makropoulos et al., 2014, 2018). A fetal neuroanatomist (L.V.) and an MD with 3 years of experience in fetal and neonatal neuroimaging (C.C.) carefully inspected and verified the segmentations. Preprocessing of the raw dMRI data included susceptibility‐induced distortion correction, correction of eddy current‐induced distortions and subject motion, followed by super‐resolution volume reconstruction and registration to structural images. The details of the preprocessing operations are described in Bastiani et al. (2019) and Makropoulos et al. (2018). We denoised the dMRI data and resampled all dMRI and anatomical data (i.e., T2 images and tissue segmentations) to an isotropic resolution of 1 mm. Denoising was performed with a method based on Marchenko‐Pastur Principal Component Analysis (Veraart et al., 2016). We used the implementation of this method in MRtrix (Tournier et al., 2019).

2.3. Computational pipeline

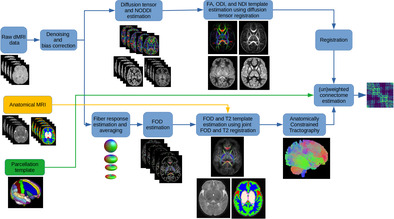
Figure 1 shows the data processing pipeline for computing population‐averaged age‐specific connectomes. The pipeline has two main branches. One branch uses FOD‐based registration to compute a tractogram for each age. The other branch uses diffusion tensor‐based registration to compute maps of micro‐structural biomarkers. The FOD‐based alignment could have been used to also compute atlases of micro‐structural biomarkers. However, we found that a diffusion tensor‐based registration resulted in sharper and more detailed micro‐structural biomarker maps. Different steps of the pipeline are described below. Note that this pipeline is applied separately for each age group to compute a separate structural connectome for every week between 33 and 44 postmenstrual weeks.

FIGURE 1.

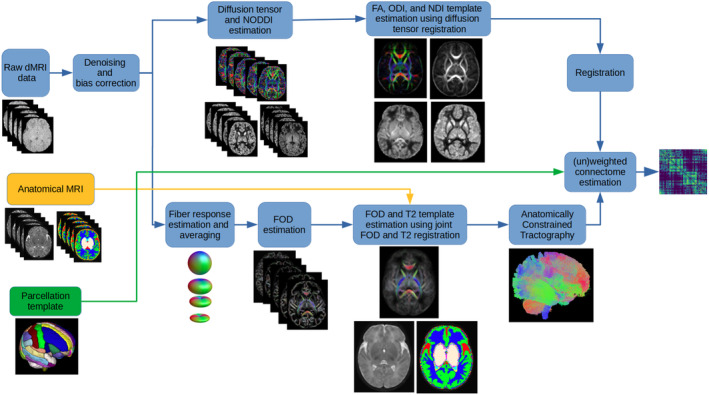
The proposed computational pipeline for computing population‐averaged age‐specific structural connectomes. dMRI, diffusion‐weighted magnetic resonance imaging; FA, fractional anisotropy; MRI, magnetic resonance imaging; NDI, neurite density index; NODDI, neurite orientation dispersion and density imaging; ODI, orientation dispersion index.

2.3.1. Computing age‐specific FOD templates and tractograms

We used the multi‐shell multi‐tissue constrained spherical deconvolution (MSMT‐CSD) (Jeurissen et al., 2014) for FOD estimation. This method is based on deconvolving the dMRI signal with signature response functions from white matter, gray matter, and cerebrospinal fluid (CSF). We first estimated these response functions separately for each subject in an age group. To compute the response functions, we used the method proposed in Dhollander et al. (2016). This method first computes a segmentation of the brain tissue to identify voxels that consist purely of white matter, gray matter, and CSF. Then, the signals from these voxels are used to estimate response functions for each of the three tissue types. Subsequently, we computed average response functions for that age. The average response functions were used to estimate the FOD images for each subject in the age group. A white matter FOD template was then estimated using symmetric diffeomorphic registration of the white matter FOD maps of all subjects in the age group. To compute the registration, we used the method proposed in (Raffelt et al., 2011). This method uses a point spread function (PSF) representation of the FODs. Specifically, each FOD is represented as a weighted sum of equally distributed PSFs. The computed deformation is applied to each PSF separately and, subsequently, the reoriented PSFs are used to compute the reoriented FOD as a weighted sum. The main advantage of this method is that it applies the correct rotation to the PSFs such that the reoriented FOD is consistent with the nonlinear deformation. This is essential for properly aligning the white matter structures between different brains. The deformations computed based on the white matter FODs were also used to warp the T2 images and tissue segmentation maps. Voxel‐wise averaging and majority voting, respectively, were used to estimate a T2 template and a tissue segmentation template for that age.

Anatomically‐constrained tractography (Smith et al., 2012) was then applied using the FOD and tissue segmentation templates. We used a probabilistic streamline tracing method (Tournier et al., 2010). This tractography method is based on a second‐order integration of FOD. In addition to the FOD at the current streamline tracing point, it also takes into account the FOD at a number of candidate next points, and takes the next step so as to maximize the joint probability. We empirically set the maximum angle between successive streamline tracing steps to 30° and the FOD amplitude cut‐off threshold of 0.01 as the stopping criterion. We randomly seeded all voxels in the brain volume and generated a total of five million valid streamlines. The Spherical‐deconvolution Informed Filtering of Tractograms 2 (SIFT2) algorithm (Smith et al., 2015) was subsequently applied on the computed tractogram. The SIFT2 algorithm computes a cross‐sectional area multiplier for each streamline such that, after applying the multiplier, the streamline density is reflective of the density of the underlying white matter fiber.

2.3.2. Computing age‐specific templates of tissue micro‐structure biomarkers

There is no consensus on the proper weighting of the edges in a structural connectome. It is possible to compute the edge weight/strength values based on tractography data alone, for example in terms of the streamline count. However, there is growing evidence in favor of utilizing biomarkers of tissue micro‐structure integrity to weight the connections (Qi et al., 2015; Yeh et al., 2021). In this work, we used biomarkers derived from the diffusion tensor and the Neurite Orientation Dispersion and Density Imaging (NODDI) models (Zhang et al., 2012).

We estimated the diffusion tensor with the iterative weighted least squares method of Veraart et al. (2013) using the measurements in the $b=1000$ shell. We computed the fractional anisotropy (FA) image from the diffusion tensor image. We fitted the NODDI‐Watson model to the full multi‐shell data and computed the Orientation Dispersion Index (ODI) and the Neurite Density Index (NDI) (Zhang et al., 2012). As suggested by Guerrero et al. (2019), we lowered the initial value of parallel diffusivity from $1.7\times {10}^{-9}{m}^2/s$ to $1.4\times {10}^{-9}{m}^2/s$ in order to better fit neonatal brain data.

Subsequently, we computed a template for these biomarkers using a nonlinear diffusion tensor‐based alignment algorithm (Zhang et al., 2006). This algorithm divides the image into patches and computes affine registration transforms for each patch. To ensure smoothness of the transformation across the boundaries of neighboring patches, a smoothness constraint is introduced into the optimization objective. We used the implementation of this algorithm in the DTI‐TK software package. These templates were then registered to the T2 template map for the same age group using affine registration. Note that the T2 and FOD templates were co‐registered by design, as shown in Figure 1. Hence, after being registered to the T2 template, these biomarker templates could be used to weight the streamlines computed based on the FOD template.

2.3.3. Computing the structural connectome

To define the connectome nodes, we used the Edinburgh Neonatal Atlas (ENA50) (Blesa et al., 2020). This atlas included 107 regions of interest (ROIs) from 53 structures with bilateral presentation in addition to the corpus callosum. We only utilized the cortical gray matter parcellations, subcortical gray matter structures, and cerebellar parcellations, resulting in a total of 98 nodes. Table 1 in the Supporting Information shows the names of these nodes and the abbreviated names that are used in this paper. In order to form brain lobes, we merged the relevant nodes in this atlas. Table 2 in the Supporting Information displays the names of these lobes and the abbreviations that we use in this paper. We registered the parcellation to our computed age‐specific templates using deformable registration of the T2 image from the ENA50 atlas to the T2 template computed by our pipeline.

Using the gray matter parcellations as graph nodes and the streamlines as edges, we computed the structural connectomes. We computed the mean of microstructural biomarkers along streamlines connecting each pair of nodes to obtain $w_{\mathrm{FA}}\left(i,j\right)$, $w_{\mathrm{NDI}}\left(i,j\right)$, and $w_{1-\mathrm{ODI}}\left(i,j\right)$, which were used to weight the connections. The negative sign for ODI is standard practice and it is used because ODI is a measure of fiber dispersion, whereas one should assign larger weights to higher microstructural integrity.

The procedure described above follows the state of the art approach for computing the structural connectome (Smith et al., 2020). The results presented in this paper mostly follow this analysis. Nonetheless, we also present and discuss the connectivity results after applying a connectome normalization operation that has been used in some prior studies on perinatal brain too (Batalle et al., 2017). This normalization aims to ensure that different connectomes are equal in terms of the total network strength. It normalizes each connectome as $w_{\mathit{nX}}\left(i,j\right)=w_X\left(i,j\right)/\sum _{\forall i,j}{w}_X\left(i,j\right)$, where $X$ refers to the connectome weighting (FA, NDI, or 1‐ODI). The rationale behind this normalization strategy is that it may facilitate comparison of the connectomes in terms of network topology by reducing the influence of total network strength. In other words, this normalization is meant to equalize the total network strength for all connectomes, thereby making the graph metrics independent of the total network strength. This experiment will determine whether such normalization can enhance the capability of the computed connectome to describe the topological and organizational properties of the brain.

We also performed the connectivity analysis at a higher nodal resolution. It is well known that nodal resolution may significantly influence the structural connectivity metrics (Messé, 2020; Qi et al., 2015; Zalesky, Fornito, Harding, et al., 2010). In order to investigate how this factor may impact the results of our pipeline, in addition to the ENA50 atlas with 98 parcellations we also used the UNC Cedars Infant Atlas (UNC FC atlas, (Shi et al., 2018)) with 223 parcellations to define the connectome nodes. We followed the same processing steps explained above to compute the connectomes with this alternative cortical parcellation.

2.3.4. Computing the connectivity metrics

After computing the connectome as described above, we computed five standard and widely‐used structural connectivity measures: characteristic path length (CPL), global efficiency (GE), local efficiency (LE), clustering coefficient (CC), and small‐worldness index (SWI). CPL and GE are measures of network integration, which quantifies brain's ability to incorporate information across distant brain regions (Rubinov & Sporns, 2010). CC and LE are measures of network segregation, which reflects the capability for specialized processing to occur within interconnected groups of brain regions (Rubinov & Sporns, 2010). SWI is a measure of network topology.

2.3.5. Comparison with connectome‐level averaging methods

The main rationale behind our method is that averaging of subjects' data for each PMA may suppress the subject‐level variability and amplify the changes in connectivity metrics with PMA. Our method achieves this via spatial alignment and averaging in the image space. An alternative approach is to perform the averaging in the connectome space (Betzel et al., 2019). In this approach, connectomes are computed separately for each individual subject and then averaged to compute a group‐representative connectome.

This averaging can be accomplished in various ways. Here, we applied four different ways of implementing this approach, as described by Betzel et al. (2019): (1) Simple average: In this approach, the non‐zero elements of subject connectomes are simply averaged to compute the corresponding elements of an average connectome. (2) Consensus‐based uniform thresholding with $\tau =0.50$: Only the connections that are present in at least half of the subjects are retained and the rest are set to zero. (3) Consensus‐based uniform thresholding with a threshold $\tau =\mathrm{Avg}$: Here, the value of $\tau$ is chosen such that the binary density of the average connectome is as close as possible to the average binary density of the subject connectomes. (4) Length‐preserved averaging. Using a single threshold, as in methods 2 and 3, can result in a biased averaging because it is more likely to retain the shorter connections and eliminate the longer ones (Betzel et al., 2019). To overcome this shortcoming, an alternative method is to divide all subject‐level connections into $N$ non‐overlapping bins based on their length and to retain a variable fraction of connections in each bin. Different fractions of connections are kept depending on their lengths such that the distribution of the connection lengths in the group‐averaged connectome will match that of the subjects.

We refer to Betzel et al.'s paper for details of implementation of these methods (Betzel et al., 2019). After generating the group‐representative networks for each age, we computed the connectivity metrics and performed age regression similarly as for our proposed method. Even though we have applied all four methods, we mostly focus on the results of length‐preserved averaging method since it is the preferred way of averaging the connectomes according to the arguments presented in Betzel et al. (2019).

We compared our method with length‐preserved connectome averaging method in terms of the changes in structural connectivity with PMA and brain asymmetry, described further below. Moreover, we compared these methods in terms of the similarity between the age‐specific average connectomes and the connectomes of the individual subjects in the same age subgroup. It can be argued that a good average connectome should have a high similarity to the connectomes of individual subjects of the same age. In the literature, different ways of comparing connectomes and quantifying the similarity between connectome matrices have been proposed (Sotiropoulos & Zalesky, 2019; Zalesky, Fornito, & Bullmore, 2010). In this work, we followed two approaches outlined below.

• Our first evaluation approach was based on scalar connectivity measures. Specifically, we relied on GE, LE, CPL, CC, and SWI. For example, for GE, we computed the difference between GE of each subject and the GE of the age‐specific average connectome for our method and the length‐preserved connectome averaging method. We then performed a paired t‐test to determine if the absolute differences were significantly different between the two methods.

• The second approach that we followed was based on pairwise classification of connectomes. Specifically, we followed the method proposed by Petrov et al. (2018). We represented each connectome with a feature vector that consisted of the connectome weights and eight topological features as described in Petrov et al. (2018). Let us use $f\left(C\right)$ to denote the feature vector computed for connectome $C$. Let us also denote the connectome for subject $i$ as $C_{\mathrm{sub}}^i$ and the average connectome $j$ as $C_{\mathrm{avg}}^j$ (i.e., each $j$ corresponds to a different age between 33 and 44 weeks). Following (Petrov et al., 2018), we computed the difference in the feature vectors as $\Vert f\left(C_{\mathrm{sub}}^i\right)-f\left(C_{\mathrm{avg}}^j\right)\Vert$, where we used ${\mathrm{\ell }}_1$‐norm, ${\mathrm{\ell }}_2$‐norm, and ${\mathrm{\ell }}_{\infty }$‐norm to obtain a pair‐wise feature vector of size three. We trained a support vector machine (SVM) classifier on this feature vector. The SVM was trained to predict class “1” if the subject connectome $i$ was the same age as average connectome $j$, and class “0” otherwise. We trained the SVM on 120 subjects. We then applied the trained SVM on the remaining 46 subjects (3 or 4 test subjects per PMA) and computed the classification accuracy. For technical details, such as SVM implementation and training, we followed Petrov et al. (2018).

2.3.6. Age regression

We used general linear models (GLMs) to estimate the effect of age on the structural brain connectivity measures using the network measures as dependent variables and PMA as the independent variable. We used the R statistics package to perform all GLM analyses. We considered a $p$ value of less than 0.05 to be statistically significant.

2.3.7. Edge‐wise association with age

We assessed the correlations between the individual connections and PMA to characterize the changes in connectivity weights with age. This edge‐wise association analysis was performed on un‐normalized as well as normalized FA‐, NDI‐, and (1‐ODI)‐weighted connections. For this analysis, we only considered the connections that were common to all ages. We used the Spearman's rank correlation coefficient ($\rho$) to quantify the association between edge‐wise connection strengths with PMA. We used the Bonferroni correction to account for multiple comparisons in order to control the family‐wise error rate at 0.05. Furthermore, we assessed the correlation between the PMA and connection strengths between the lobes. Similar to the node‐wise analysis, we only considered the connections that were common to all PMAs. We computed the Spearman's rank correlation coefficient to assess the association between lobe‐wise connections and PMA. We applied the false discovery rate (FDR) correction to control the family‐wise error rate at 0.05.

2.3.8. Asymmetry in brain connectivity

In order to analyze the differences between the structural connectivity in the left and right brain hemispheres, we computed the laterality index $\mathrm{LI}=\frac{\text{Right}-\text{Left}}{\text{Right}+\text{Left}}$ for FA‐, NDI‐, and (1‐ODI)‐weighted connections. LI <0 indicates leftward asymmetry, whereas LI >0 indicates rightward asymmetry. Furthermore, we performed linear regression analyses to assess the effect of age on the asymmetry of the brain connectivity.

3. RESULTS

3.1. Spatio‐temporal atlases

Figure 2 shows selected views of the atlases reconstructed by our computational pipeline for PMAs of 35 and 43 weeks. The atlases portray a detailed representation of the brain's structure. To ensure accuracy, an expert visually assessed the atlases to confirm that they were free from errors and artifacts, verify the orientation of the FODs, and determine the correctness of the computed tractograms. Figure 1 in the Supporting Information shows the FOD atlases for all 12 PMAs between 33 and 44 weeks.

FIGURE 2.

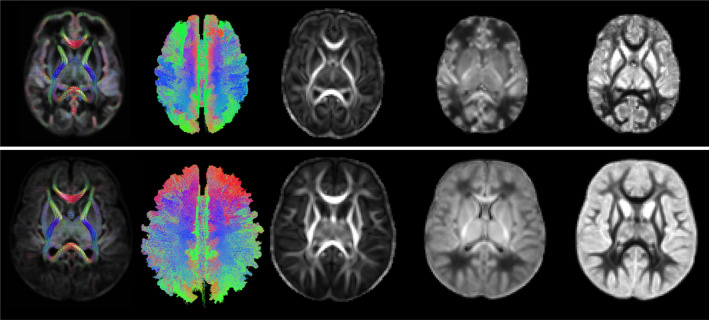
From left to right: Example FOD atlas, tractogram, FA, NDI, and ODI atlases generated by our computational pipeline for 35 weeks (top) and 43 weeks (bottom). FA, fractional anisotropy; FOD, fiber orientation distribution; NDI, neurite density index; ODI, orientation dispersion index.

3.2. Similarity between subject connectomes and average connectomes

Here, we present the results of the two comparisons between individual subject connectomes and age‐specific average connectomes described in Section 2.3.5. Table 1 shows the difference between subject connectomes and age‐specific average connectomes of the same age in terms of connectivity metrics. It shows the results for our method and length‐preserved connectome averaging, separately for each of the three connection strength weightings. The results clearly show that the average connectomes computed with our method are closer to the individual subject connectomes within the age subgroup. In terms of most measures, the average connectome computed with our method has a smaller difference with individual connectomes. In terms of GE, LE, and CPL most of the differences between our method and length‐preserved connectome averaging are statistically significant. The results presented in this table have been pooled across all ages. When looking at individual age subgroups separately, the results were similar in that the connectome computed by our method was closer to the individual subject connectomes.

TABLE 1.

Mean of the absolute difference in five connectivity measures between the individual subject connectomes and the age‐specific average connectomes. Results are shown separately for three connection strength weightings. An asterisk indicates a statistically significant difference ($p=.05$) between the proposed method and length‐preserved connectome averaging method.

	Proposed method					Length‐preserved connectome averaging
	$\mid \mathrm{\Delta GE}\mid$	$\mid \mathrm{\Delta LE}\mid$	$\mid \mathrm{\Delta CPL}\mid$	$\mid \mathrm{\Delta CC}\mid$	$\mid \mathrm{\Delta SWI}\mid$	$\mid \mathrm{\Delta GE}\mid$	$\mid \mathrm{\Delta LE}\mid$	$\mid \mathrm{\Delta CPL}\mid$	$\mid \mathrm{\Delta CC}\mid$	$\mid \mathrm{\Delta SWI}\mid$
FA	0.047	0.045*	0.630*	0.055	0.007	0.047	0.050	0.685	0.056	0.007
NDI	0.046*	0.048*	0.611*	0.064	0.007	0.051	0.053	0.679	0.067	0.008
1‐ODI	0.090*	0.092*	0.739*	0.096	0.008	0.130	0.144	0.772	0.101	0.008

In the SVM‐based classification evaluation, for the average connectomes computed with our method, the classification accuracy, sensitivity, and specificity were, respectively 0.77, 0.76, and 0.79. For the connectomes computed with length‐preserved connectome averaging, classification accuracy, sensitivity, and specificity values were 0.70, 0.68, and 0.71. In this analysis, for each individual connectome we considered only the closest average connectome to be the correct match. For example, a subject of age 38.6 weeks should only be matched with the average connectome of age 39 weeks. We could relax this by accepting all matches with an age difference of within 1 week to be correct. In this relaxed analysis, a subject of age 38.6 weeks is considered to be correctly classified if it is matched to an average connectome of 38 weeks or 39 weeks. With this relaxed evaluation, for our method the classification accuracy, sensitivity, and specificity were 0.83, 0.85, and 0.82, respectively. For length‐preserved connectome averaging the accuracy, sensitivity, and specificity were, respectively 0.77, 0.79, and 0.76. These results also show that the average connectomes computed with our method are closer to the individual subject connectomes.

3.3. Association between connectivity metrics and PMA

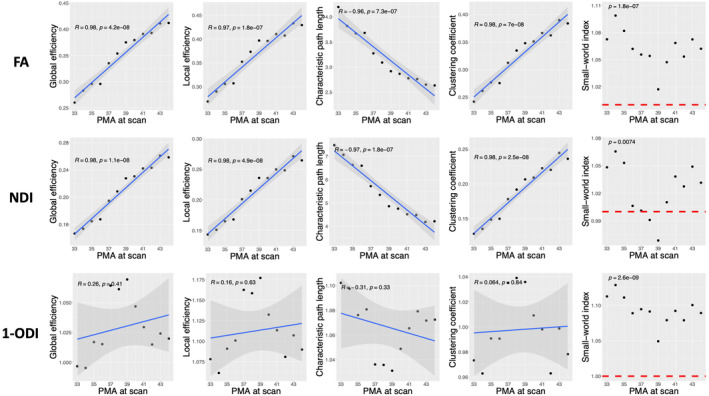
Figure 3 shows the observed trends in GE, LE, CPL, and CC as a function of PMA. Overall, the plots in this figure depict an increase in GE, LE, and CC and a decrease in CPL. For ODI‐weighted connectome, linear correlations are relatively strong ($\mid R\mid \in \left[0.61,0.70\right]$). For connectomes weighted by FA and NDI, on the other hand, there are unmistakable strong linear correlations with $\mid R\mid \ge 0.97$. GE is positively correlated with PMA in the connectomes weighted by FA (R = .99, p < .001), NDI (R = .98, p < .001), and 1‐ODI (R = .70, p = .011). Similarly, LE is positively correlated with PMA in the connectomes weighted by FA (R = .99, p < .001), NDI (R = .98, p < .001), and 1‐ODI (R = .68, p = .014). CPL is negatively correlated with PMA in the connectomes weighted by FA (R = −.97, p < .001), NDI (R = −.97, p < .001), and 1‐ODI (R = −.68, p = .014). Lastly, CC is positively correlated with PMA in the connectomes weighted by FA (R = .98, p < .001), NDI (R = .97, p < .001), and 1‐ODI (R = .61, p = .035). The last column in Figure 3 shows the SWI values computed with different connectome weighting schemes. For SWI, instead of the correlation with PMA, we are interested in knowing whether the computed values are larger than one, which would indicate small‐world network properties. We used one‐sample t‐tests to test the hypothesis that SWI was significantly larger than one. As shown in the figure, these tests show that SWI for the connectome weighting based on FA, NDI, and (1‐ODI) is significantly larger than one.

FIGURE 3.

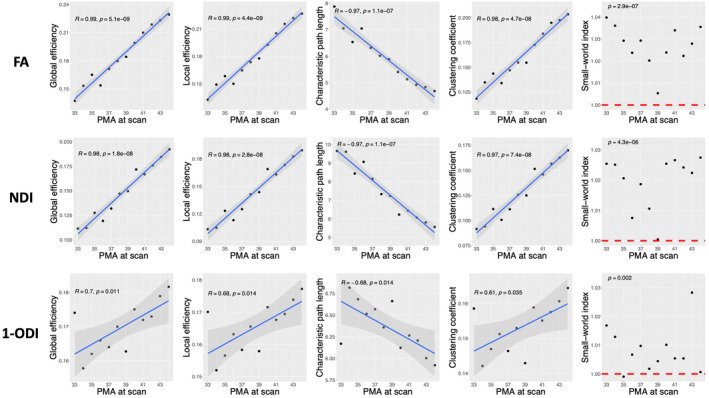
Plots of different structural connectivity measures, computed with the parcellation nodes defined with the ENA50 atlas, versus PMA for the connectome edge weighting based on FA, NDI, and 1‐ODI. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

Results of the analysis with the length‐preserved connectome averaging method are shown in Figure 4. In terms of the trends in GE, LE, CPL, and CC, the results are surprisingly similar to those computed with our method, especially for the connectomes weighted based on FA and NDI. Specifically, for the FA‐ and NDI‐weighted connectomes, the trends are in the same directions as those in Figure 3 and they are all statistically significant. For the (1‐ODI)‐weighted connectome, on the other hand, although the trends are in the same direction as Figure 3, they are much weaker and none are statistically significant at $p=.05$. In terms of SWI, the results computed with the two methods are consistent in the sense that SWI is significantly larger than one for all three connection weighting methods.

FIGURE 4.

Plots of different structural connectivity measures versus PMA for the connectomes computed with the length‐preserved connectome averaging technique. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

Table 2 presents a summary of the results for all four connectome averaging methods described in Section 2.3.5. The results of all four methods are highly similar for FA and NDI connection weighting. With (1‐ODI)‐weighting, the Simple Average method shows opposing but statistically insignificant trends in GE and LE. For the remainder of this paper, we present the results only for the length‐preserved averaging technique because it is the preferred method (Betzel et al., 2019) and because the other three methods show largely similar results.

TABLE 2.

Summary of the PMA regression results. ENA50 column shows the results of our proposed method with the parcellation nodes defined with the ENA50 atlas. The other four columns present the results of four different ways of implementing connectome‐level averaging, including length‐preserved averaging (column 2), simple average (column 3), consensus‐based uniform thresholding with $\tau =0.50$ (column 4), and consensus‐based uniform thresholding with a threshold $\tau =\mathrm{Avg}$ (column 5).

		ENA50		Length‐preserved		Simple average		Consensus $\tau =0.5$		Consensus $\tau =\mathit{Avg}$
		p‐value	R	p‐value	R	p‐value	R	p‐value	R	p‐value	R
FA	GE	<.0001	.9854	<.0001	.9777	<.0001	.9905	<.0001	.9671	<.0001	.9766
	LE	<.0001	.9858	<.0001	.9699	<.0001	.9907	<.0001	.9481	<.0001	.9872
	CPL	<.0001	−.9728	<.0001	−.9603	<.0001	−.9775	<.0001	−.9586	<.0001	−.9592
	CC	<.0001	.9772	<.0001	.9753	<.0001	.9894	<.0001	.9517	<.0001	.9746
	SWI	<.0001	/	<.0001	/	.1098	/	<.0001		1.0000	/
NDI	GE	<.0001	.9813	<.0001	.9829	<.0001	.9926	<.0001	.9756	<.0001	.9809
	LE	<.0001	.9794	<.0001	.9770	<.0001	.9920	<.0001	.9639	<.0001	.9692
	CPL	<.0001	−.9730	<.0001	−.9700	<.0001	−.9829	<.0001	−.9620	<.0001	−.9638
	CC	<.0001	.9750	<.0001	.9798	<.0001	.9914	<.0001	.9661	<.0001	.9648
	SW	<.0001	/	.0074	/	.8537	/	.0293	/	1.0000	/
1‐ODI	GE	.0111	.7008	.4092	.2628	.7368	−.1086	.2748	.3431	.7386	.1079
	LE	.0144	.6826	.6256	.1572	.4145	−.2600	.4607	.2358	.9868	.0054
	CPL	.0140	−.6850	.3283	−.3091	.5306	−.2012	.3217	−.3131	.3532	−.2942
	CC	.0353	.6098	.8440	.0638	.6820	.1323	.6498	.1464	.5419	−.1958
	SW	.0020	/	<.0001	/	.0012	/	<.0001	/	.0005	/

3.4. Node‐wise associations with age

Figure 5 shows the association between connection strength and PMA for different connection weighting schemes. For the connectomes that have been computed based on FA and NDI weighting, all connections show a positive correlation with PMA, which means all connections become stronger with age. Analysis with the connectome weighting based on 1‐ODI paints a largely similar picture, with the exception of a few sporadic connections that show a significant decrease in strength with PMA. These results show a consistent increase in the strength of the connections that seem to be primarily driven by improved neural density, reduced dispersion, and increased myelination. Figure 6 shows the corresponding plots for the length‐preserved connectome‐level averaging method. The plots for connection weighting based on FA and NDI are very similar to those presented for the proposed method in Figure 5, in the sense that all significantly changing connections show an increase in strength and that there are many such connections between all brain lobes considered. However, for connection weighting in terms of 1‐ODI, no connection shows a significant increase or decrease with PMA for this method, which is quite unlike the results for our method as shown in Figure 5.

FIGURE 5.

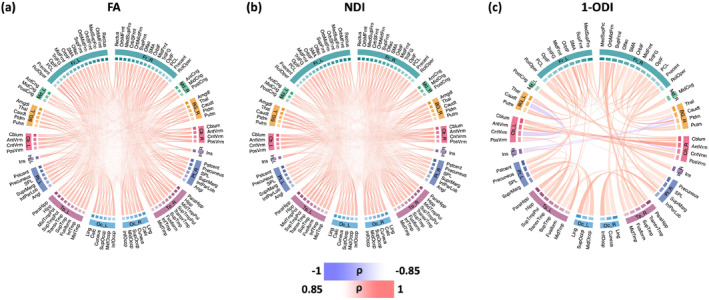
These plots show the connectome edges that are significantly correlated with PMA, quantified in terms of Spearman's rank correlation coefficient ($\rho$) after Bonferroni correction. The color intensity of the edges is proportional to $\rho$. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

FIGURE 6.

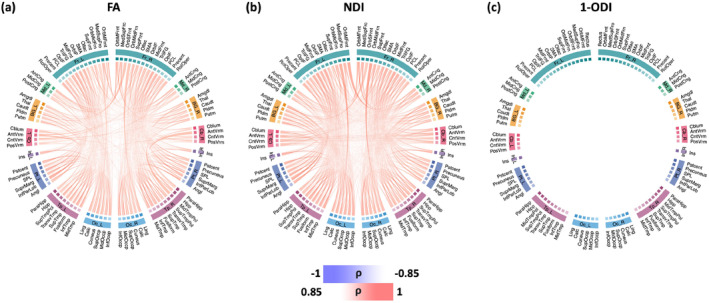
Connectome edges that are significantly correlated with PMA, quantified in terms of Spearman's rank correlation coefficient ($\rho$) after Bonferroni correction for the length‐preserved connectome averaging method. The color intensity of the edges are proportional to $\rho$. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

3.5. Correlation between PMA and connections between the lobes

Figure 7 shows the change in the connection strength between different brain lobes in the connectomes weighted with FA, NDI, and 1‐ODI. The connectomes weighted with FA and NDI display a near‐uniform increase in the connection strength with PMA. The (1‐ODI)‐weighted connectome shows an overall similar pattern of increasing connection strength with a few sporadic decreasing connection strengths. Figure 8 shows the results for the length‐preserved connectome averaging method. For connection weighting in terms of FA and NDI, connections show increasing strength with PMA, similar to our method. For connection weighting in terms of 1‐ODI, on the other hand, there are fewer connections that show a significant change in strength with PMA and most of those show a decrease in strength, which is very different from the results observed with our proposed method that show mostly positive correlations with PMA.

FIGURE 7.

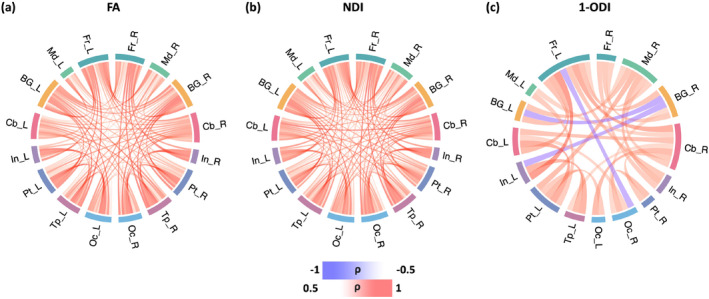
Lobe‐wise connections that are significantly correlated with PMA. These connectomes show the Spearman's rank correlation coefficient ($\rho$) after FDR correction. The color intensity of the edges is proportional to $\rho$. FA, fractional anisotropy; FDR, false discovery rate; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

FIGURE 8.

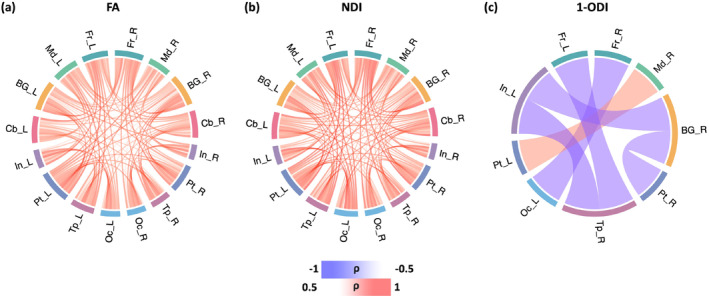
Lobe‐wise connections that are significantly correlated with PMA for the length‐preserved connectome averaging method. These connectome plots show the Spearman's rank correlation coefficient ($\rho$) after FDR correction. The color intensity of the edges is proportional to $\rho$. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

Figure 9 shows the results of statistical significance tests to compare our method and length‐preserved connectome averaging method in terms of the age‐related changes in lobe‐wise connection strengths. It shows the connections for which the Spearman's rank correlation coefficient are significantly different between the two methods. For (1‐ODI)‐weighting, our method shows a much larger number of stronger age‐related changes in lobe‐wise connection strengths. For FA‐ and NDI‐weighting, on the other hand, the results are mixed and each of the two methods reconstructs significantly stronger age‐related changes in a different subset of lobe‐wise connections.

FIGURE 9.

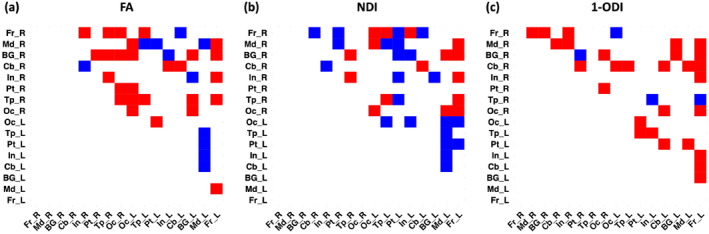
Significant differences between our method and length‐preserved connectome averaging method in terms of the Spearman's rank correlation coefficient of lobe‐wise connection strength with PMA. Blue squares indicate significantly larger correlation for the connectome averaging method, whereas red squares show significantly larger correlation for our proposed method. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

3.6. Brain asymmetry

The results of asymmetry analysis are presented in Figure 10. The asymmetry patterns revealed by the FA‐, NDI‐, and (1‐ODI)‐weighted connectomes, although complex, display remarkable similarities, as shown in Figure 10a–c. The connections between the frontal and temporal lobes and the other lobes show right‐ward asymmetry, while the connections between medial and occipital lobes and the other lobes display left‐ward asymmetry. Figure 10d–f shows the correlation between connection asymmetry and PMA. The patterns for FA‐ and NDI‐weighted connectomes are largely similar, but markedly different from the (1‐ODI)‐weighted connectome. Connections among occipital, temporal, and parietal lobes, insula, and cerebellum show an increase in right‐ward asymmetry, while the connections among medial and frontal lobes and BG show slight increases in left‐ward asymmetry. The sharpest changes occur between cerebellum and insula in the FA‐ and NDI‐weighted connectomes. With (1‐ODI) weighting, only two significantly changing connections are observed, which are also observed with FA and NDI weighting.

FIGURE 10.

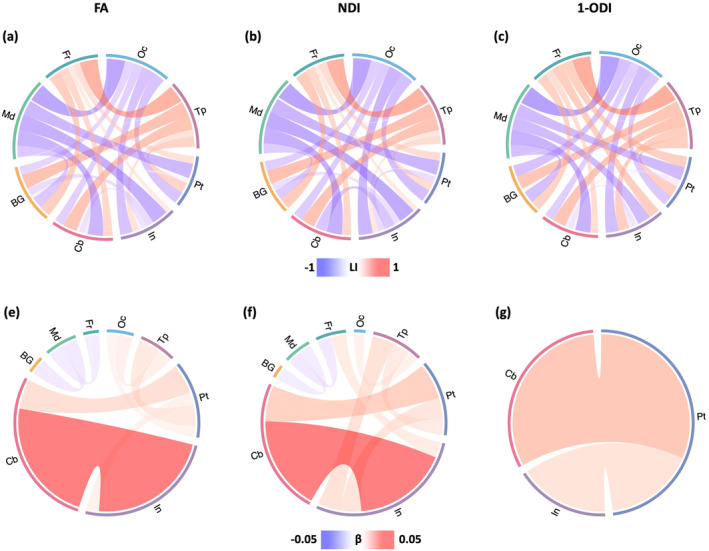
Top: Brain asymmetry quantified in terms of the laterality index (LI). The connections with leftward asymmetry are colored in blue, while the connections with right asymmetry are in red. The color intensity and thickness of the links are proportional to the LI value. Bottom: Correlation between LI and PMA. The color intensity and thickness of the links are proportional to the regression slope $\beta$. A blue color indicates an increasing leftward asymmetry with PMA, while red indicates increasing rightward asymmetry. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

The corresponding results for length‐preserved connectome averaging method are presented in Figure 11. In terms of brain asymmetry, the results are interestingly very similar to those obtained for the proposed method. There are very few minor differences between the laterality patterns discovered with the two methods, such as a left‐ward asymmetry in the connections between cerebellum and insula in our results, which is not observed in the results obtained with connectome‐level averaging. Otherwise, the results are almost identical. In terms of the change in brain asymmetry with PMA, the results are different from those obtained with our method. Moreover, unlike our method that shows consistent results between FA and NDI weighting, the results with length‐preserved connectome averaging are not consistent between these two weighting schemes.

FIGURE 11.

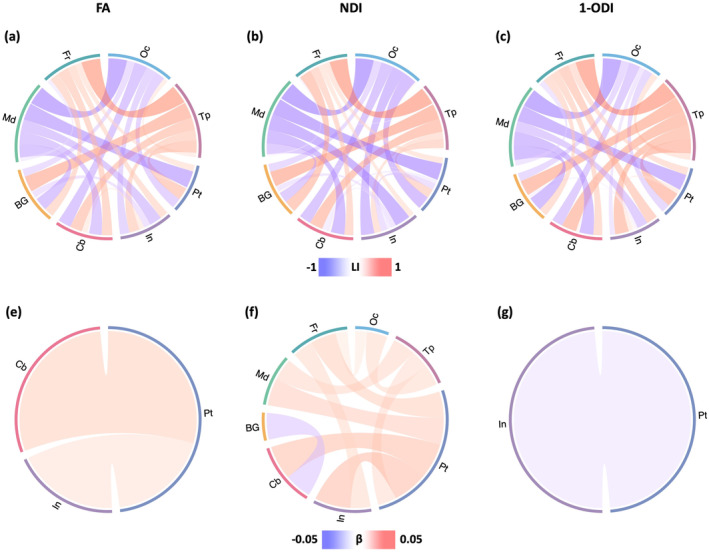
Analysis of brain asymmetry patterns for length‐preserved connectome averaging method. Top: Brain asymmetry quantified in terms of the laterality index (LI). The connections with leftward asymmetry are colored in blue, while the connections with right asymmetry are in red. The color intensity of the links is proportional to the LI value. Bottom: Correlation between LI and PMA. The color intensity is proportional to the regression slope $\beta$. A blue color indicates an increasing leftward asymmetry with PMA, while red indicates an increasing rightward asymmetry. FA, fractional anisotropy; NDI, neurite density index; ODI, orientation dispersion index; PMA, postmenstrual age.

3.7. Connectome normalization

Figure 2 in the Supporting Information shows the change in GE, LE, CPL, and CC as a function of PMA, as well as SWI, for the connectomes normalized in terms of total strength, computed as explained in Section 2.3.3. Overall, these observed trends do not agree with those shown for the original (i.e., un‐normalized) connectomes shown in Figure 3. The correlations with PMA are much weaker and often the opposite of the trends that we observe for un‐normalized connectomes. The only statistically significant trend was the decrease in GE for the NDI‐weighted connectome, which is the opposite of the trend observed for the un‐normalized connectomes. Overall, the trends in GE, LE, CPL, and CC for FA‐ and NDI‐weighted connectomes, although mostly not significant, were all the opposite of those for the unnormalized connectomes shown in Figure 3. The SWI results were similar to those for the un‐normalized connectomes.

Figure 3 in the Supporting Information shows the correlation between connection strengths and PMA in the connectomes that are normalized in terms of the total network strength. Compared with the results shown in Figure 5, the normalized connectomes display a more complex picture with significant regional variations in maturation. The normalized FA‐weighted connectome, for instance, shows an increase in strength for some connections, including within the right frontal lobe and between precentral and lingual. On the other hand, the connection strength decreases for several connections, including connections within the cerebellum, between BG and cerebellum, between frontal lobe and posterior cingulate, between medial lobe and BG and hippocampus, as well as inter‐hemisphere connections. The normalized NDI‐weighted connectome shows more increasing connection strengths in the left than in the right hemisphere. Specifically, connection strengths increase between the frontal lobe, insula, temporal, and occipital lobes in the left hemisphere. In the right hemisphere, a few connections become stronger between the frontal lobe and other regions. Inter‐hemispheric connections, on the other hand, show much slower rates of change. The normalized (1‐ODI)‐weighted connectome shows a strengthening of the connections within the frontal lobe and between the frontal lobe and putamen, but a weakening of connections between BG and cerebellum and between the occipital and temporal lobes. Figure 4 in the Supporting Information shows the corresponding plots for the length‐preserved connectome averaging method. For connection weighting based on FA and NDI, there are many positive and fewer negative correlations with PMA. There are some similarities with those of our method (Figure 3 in the Supporting Information), but also many differences. For example, for NDI weighting, the length‐preserved connectome averaging method shows many more strengthening connections between the frontal and occipital lobes within each of the two hemispheres. For connectome weighting based on 1‐ODI, no connections show an increasing or decreasing strength with PMA, which is again quite different from the results of our method.

Figure 5 in the Supporting Information shows the association between lobe‐wise connection strengths and PMA in the connectomes that have been normalized in terms of the total network strength. Similar to Figure 3 in the Supporting Information, and unlike Figure 7, the relations displayed in this figure are complex and do not lend themselves to a simple description. Both FA‐ and NDI‐weighted connectomes display weakening connections between multiple lobes within and across the two brain hemispheres, although a few of the connections become stronger such as the connection between the insula and cerebellum in the left hemisphere. With (1‐ODI)‐weighting, similarly, most connections become weaker, except for a few connections between the left frontal lobe and other lobes. Figure 6 in the Supporting Information shows the results for length‐preserved connectome averaging method. The results are different among the three connection weighting schemes and they are also different from those shown in Figure 5 in the Supporting Information for our proposed method. Overall, these results show that normalizing the connectomes based on the total connectome strength leads to more divergent results between the different connection weighting schemes and group‐wise averaging methods.

3.8. Parcellation resolution

Figure 7 in the Supporting Information shows the connectivity metrics for the connectomes computed with the parcellation nodes defined with the UNC FC atlas with 223 nodes. The trends in GE, LE, CPL, and CC as a function of PMA are largely consistent with those observed with the ENA50 atlas shown in Figure 3. For FA‐ and NDI‐weighted connectomes, $\mid R\mid >.95$, while for the (1‐ODI)‐weighted connectome $\mid R\mid \in$[.52, .65]. For SWI, on the other hand, the results are different. Unlike Figure 3 where SWI >1, for this alternative atlas with 223 nodes the SWI values are mostly smaller than one for all three weighting methods.

Table 3 in Supporting Information summarizes some of the main results from the above‐explained experiments. It shows the $p$ and $R$ values for our proposed method with the ENA50 atlas parcellation (without and with total network strength normalization) and with the UNC FC atlas parcellation (without normalization) as well as the results obtained with the length‐preserved connectome‐level averaging.

4. DISCUSSION

In this work, we proposed a computational framework for quantitative assessment of the development of structural connectome in the perinatal stage. We computed the structural connectome and connectivity metrics using three micro‐structural biomarkers (i.e., FA, NDI, and 1‐ODI) for connection weighting. Our results showed that the proposed framework could unveil strong relationships between several important measures of brain connectivity and PMA. Our analysis of the correlation between connection strength and PMA showed a consistent and widespread increase in node‐wise and lobe‐wise connection strengths in the connectomes weighted with FA and NDI.

Several prior studies have examined the development of structural connectivity from infancy to adolescence using graph theoretical approaches (Baker et al., 2015; Bhroin et al., 2020; Hagmann et al., 2010; Ouyang et al., 2022). There have also been a few studies on the structural connectivity in preterm neonates (Batalle et al., 2017; Brown et al., 2014; de Almeida et al., 2021; Ratnarajah et al., 2013; Van Den Heuvel et al., 2015). However, all prior works have been conducted on individual subjects. To the best of our knowledge, our work is the first to develop a methodology to assess the development of the structural connectome in the perinatal stage using spatio‐temporal normalization and averaging in the image space. Even though connectome averaging methods have existed in the past, they have not been applied to study the perinatal brain. Moreover, our method works differently as it carries out the averaging in the image domain. Therefore, our results provide new insights into the normal development of the structural connectome in this critical period.

Comparisons of our results with those of the length‐preserved connectome averaging method of Betzel et al. (2019) show overall good agreement between these two methods. For example, both methods show similar trends in GE, LE, CPL, and CC as a function of PMA for the connectomes computed with FA and NDI weighting. Our method shows significant linear trends in these measures for connection weighting based on 1‐ODI, but for the connectome averaging method these trends are not statistically significant. Similarly, both methods show uniformly increasing connection strengths with PMA between the nodes and lobes for connectome weighting based on FA and NDI. For this analysis too, with (1‐ODI) weighting our method shows results that are largely consistent with FA and NDI weighting (Figure 5), whereas connectome averaging method does not show this (Figure 6). Another striking similarity is observed in terms of the asymmetry patterns portrayed by the two methods as shown in Figures 10a–c and 11a–c. In our opinion, given the fundamental differences between the way the two methods work, these similarities in the results may be interpreted as confirmation for both methods. They show that group averaging in the image space and connectome space can be effective approaches to studying structural connectivity in the perinatal stage.

Some of the observations in this study are consistent with the findings of prior works. Increases in local efficiency and global efficiency (Batalle et al., 2017; Bhroin et al., 2020; Song et al., 2017) and a decrease in characteristic path length (Brown et al., 2014; Van Den Heuvel et al., 2015) with PMA have been reported in prior studies. The increase in global efficiency and decrease in characteristic path length indicate an increase in network integration, which translates into improved ability of the brain to integrate information from distant regions of the brain and enhanced efficiency of communication between those regions (Rubinov & Sporns, 2010; Sporns, 2016). The increase in local efficiency, on the other hand, indicates an increase in network segregation, which means an increased ability of the brain to support specialized information processing by interconnected clusters of brain regions (Rubinov & Sporns, 2010; Sporns, 2016). Some studies have also found that the clustering coefficient increases with PMA (e.g., Brown et al., 2014). This is consistent with our results for the connectomes weighted by FA, NDI, and 1‐ODI.

Some prior works have reported results that are qualitatively similar to ours. For example, some studies have found positive correlations between local efficiency, global efficiency, and characteristic path length with PMA in connectomes weighted by FA and NDI (Batalle et al., 2017; Bhroin et al., 2020; Van Den Heuvel et al., 2015). Some of our findings, on the other hand, do not agree with those reported in the literature. Perhaps most prominently, our SWI computations are not consistent with those reported in some prior works. The SWI values reported in the literature are typically in the range 1–5 (de Almeida et al., 2021; Ratnarajah et al., 2013; Van Den Heuvel et al., 2015), although some studies have computed SWI <1 on a few individual neonatal brains (Ramirez et al., 2022; Van Den Heuvel et al., 2015). Moreover, some studies have reported that SWI increases with age in the perinatal stage (Batalle et al., 2017; Brown et al., 2014; Van Den Heuvel et al., 2015). Our analysis did not reveal such a trend. As shown in Figure 3 and several other figures in the paper and the Supporting Information, our computed SWI values were very close to 1 and mostly below 1.1. Moreover, as shown in Figure 7 in the Supporting Information, with the higher nodal parcellation our computed SWI values decreased and were mostly in the range 0.90–1. This observation also disagrees with prior studies that show SWI increases with nodal parcellation resolution (Zalesky, Fornito, Harding, et al., 2010). We think the difference between our results and previous perinatal brain studies (de Almeida et al., 2021; Marami et al., 2017; Ratnarajah et al., 2013; Shi et al., 2012; Van Den Heuvel et al., 2015) may be mainly because of the methodological differences. Unlike previous works, our method relies on anatomically‐constrained tractography, microstructure‐informed filtering of the streamlines, and microstructure‐based weighting, which represent the state of the art methodology for computing the structural connectome. Most prior works have not used any of these techniques. It has been shown that these methodological differences can impact the quantitative results (Bastiani et al., 2012; Li et al., 2012; Qi et al., 2015), which may explain the difference between our results and those of prior works. The SWI values reported in this paper have been computed using the definition (C/C _r )/(L/L _r ). In this equation, C and L, respectively, denote the clustering coefficient and characteristic path length for the brain network, while C _r and L _r denote the same for a random network (Humphries et al., 2006). We experimented with other definitions of SWI (Neal, 2017; Telesford et al., 2011). However, the results did not consistently show small world properties. Moreover, we also used other weighting methods such as the inverse of the streamline length, and we did not observe consistent small‐world properties. Therefore, we think our results raise new questions about the quantification of small‐world properties of the perinatal brain networks and warrant further research on this topic.

Several prior works have analyzed the change in connection strengths with PMA. Zhao et al. found increasing connection strengths across the brain lobes and hemispheres in their analysis of structural connectivity between 32 and 42 weeks PMA (Zhao et al., 2019). Batalle et al. observed significant increases in average FA‐weighted and NDI‐weighted connection strengths (Batalle et al., 2017). In terms of individual connections, they observed significant increases in many connections in the connectomes weighted with FA and NDI and decreases in the connectome weighted by 1‐ODI. Their results with FA‐ and (1‐ODI)‐weighting included several connections with opposite changes. Therefore, there are important differences between some of those results and our findings, which show uniform increases in terms of FA and NDI and near‐uniform increases in terms of 1‐ODI (Figure 5). There are other qualitative differences between our results and those of (Batalle et al., 2017). For example, in the normalized NDI‐weighted connectome, we observed increasing connection strengths between the frontal and occipital lobes and decreasing connection strengths between the frontal and medial lobes in both hemispheres (Figure 5 in Supporting Information). No such changes were observed by Batalle et al. (2017). Brown et al. assessed the change in the connection strength in terms of streamline count and FA with PMA (Brown et al., 2014). Their study included 47 subjects between 27 and 45 weeks PMA, with 23 of the subjects scanned twice. They observed that in terms of streamline count and FA, respectively, 664 and 1009 of the connections changed significantly with PMA and that most of these changes had a positive slope. For FA‐weighted connectome, 83% of those 1009 connections significantly increased in strength while 17% of them showed a significant decrease. As shown in Figure 5a, in our results all significantly changing connection strengths have a positive correlation. It is possible that this is due to the suppression of unreliable and noisy results by our framework, which may be impossible to achieve when data from individual subjects are considered. The results of connectome averaging technique (Figure 6a) seem to support this hypothesis as they are also based on aggregating data from multiple subjects.

For our method as well as for the connectome averaging method, the results show higher agreement between connection weighting in terms of FA and NDI and much less agreement between these two and connection weighting in terms of 1‐ODI. For example, FA‐ and NDI‐weighting show stronger and more similar temporal trends in connectivity metrics as well as more consistent and widespread increases in node‐wise and lobe‐wise connection strengths. Comparatively, far less consistent results are observed with (1‐ODI)‐weighting. This may be due to two factors. First, FA and NDI may be inherently more appropriate for determining the strength of structural connections. FA is a composite metric that basically quantifies the anisotropy of a diffusion tensor fit to the dMRI measurements. The NODDI model is meant to offer more specific information about the microstructure by disentangling the factors that may contribute to a change in FA. An increase in FA may be due to increased NDI, a decrease in ODI, or other factors such as myelination (Beaulieu, 2014). In white matter, voxels with a single dominant fiber orientation with strong bending or fanning show low FA, but so do voxels that contain crossing fibers. Zhang et al. (2012) show that both NDI and ODI are weakly correlated with FA. However, they argue that ODI may be a good indicator of bending or fanning, whereas NDI may be a good indicator (even better than FA) for myelination. Therefore, NDI may be intrinsically better suited than ODI for determining the strength of structural connections. Secondly, estimation of ODI may be more challenging and suffer from higher variability. This was shown in a comprehensive recent study that quantified intra‐ and inter‐session/scanner variability in microstructure mapping and found consistently higher variability for ODI than for FA and NDI (Cai et al., 2021). For example, the intra‐session variability in ODI was 4.6%, compared with 3.3% and 3.6% for FA and NDI, respectively. These higher estimation errors may have contributed to the lower consistency in the results obtained with ODI.

A comparison of the results obtained without and with normalization in terms of the total network strength shows that such normalization leads to less consistent results. For example, the correlation between network connectivity measures with PMA as well as the correlation between node‐wise and lobe‐wise edge strengths with PMA were stronger and more consistent for the unnormalized connectomes than for the normalized connectomes. We made similar observations for the length‐preserved connectome averaging method. This suggests that normalizing the connectomes in terms of the total strength may not be the proper approach for analyzing the development of perinatal brain. Increased fiber density and myelination during the perinatal stage result in a strengthening of the structural connections in this stage. Microstructural measures such as FA and NDI can effectively quantify these changes. Normalizing the connectomes in terms of network strength, on the other hand, essentially removes the effects of these developments. Therefore, we think these observations suggest that unnormalized connectomes better represent the development of structural connectivity at the perinatal stage.

Very few studies have assessed the asymmetry in brain's structural connectivity in the perinatal stage. Ratnarajah et al. observed differences in local and global efficiency between the left and right brain hemispheres in a population of 124 neonates between 36.9 and 42.7 gestational weeks (Ratnarajah et al., 2013). However, their regression analysis did not reveal any asymmetries in local/global efficiency or betweenness centrality for a large set of brain structures considered. Our results, shown in Figure 10, are novel. They show significant left laterality in the connections ending in the occipital and medial lobes and significant right laterality in the connections ending in the frontal and temporal lobes. Our results are consistent with previous research on neonates, with rightward asymmetry for temporal lobes (Hill et al., 2010; Lehtola et al., 2019; Li et al., 2014, 2015), rightward asymmetry for the frontal lobe (Vannucci et al., 2019), and leftward asymmetry for occipital lobe (Gilmore et al., 2007; Lehtola et al., 2019; Vannucci et al., 2019). Similar patterns have been reported for adult brains with significant asymmetry in frontal, temporal, and occipital lobes (Good et al., 2001; Toga & Thompson, 2003). Remarkably, the main observations from all three weighting schemes are very similar.

5. LIMITATIONS

This study suffers from a number of limitations that may be addressed in future works. One of the limitations of our evaluations is the lack of measures of reproducibility or variability such as coefficient of variation (CV) or intra‐class correlation coefficient (ICC). To compute such statistics for our methods, scan‐rescan imaging data from the same subjects or scans of matched subjects would be needed, which were unavailable to us. When such imaging data are available, assessing reproducibility of the results reported in this paper can be very useful in characterizing the advantages and limitations of the proposed computational framework. This is especially important for our study because the limited number of data points used in our regression analysis may have the tendency to produce false positives (Button et al., 2013).

There are also methodological limitations in our proposed computational framework that may be improved in future works. For example, we have used the same brain parcellation atlas (either the ENA50 atlas or the UNC FC atlas) for all postmenstrual ages between 33 and 44 weeks. As we explained in Section 2.3.3, we warped the same atlas, based on deformable registration of T2 images, to align with each gestational age. This is a common practice that has been followed by prior studies on perinatal connectivity analysis (Ramirez et al., 2022; Shi et al., 2012; Zhao et al., 2019). Nonetheless, it may be advisable to develop age‐specific parcellations, or to manually refine the parcellation after registering to age‐specific templates. There is also often high inter‐expert variability in assessing the correctness and quality of the results of medical image analysis computations. Employing a larger number of experts (than two, in this work) may be beneficial.

6. CONCLUSION

This work has proposed a novel computational framework for quantitative assessment of the development of brain's structural connectome in the perinatal stage based on dMRI scans. The new framework relies on accurate alignment of white matter structures across many subjects using tensor‐ and FOD‐based registration. This approach makes it possible to reduce the inter‐subject variability and to reconstruct the developmental trajectories of the normal brain. Our experimental results, on 166 neonates between 33 and 44 postmenstrual weeks, show that the proposed framework can unveil relationships between several important measures of brain connectivity and PMA. Connectome edge weighting based on FA and NDI are especially effective in uncovering strong trends in the structural connectivity measures. Our results show significant increases in network integration and segregation in the perinatal stage. They also portray significant changes in connection strength and asymmetry between many nodes and lobes within and across brain hemispheres. The trends reconstructed in this work are stronger and more consistent than the results reported in prior works on perinatal structural brain connectivity that have been based on subject‐wise analysis. Moreover, comparisons with alternative methods based on connectome‐level averaging in this paper showed high agreement with our method. Our method showed more consistent results, for example in terms of the changes in the connectivity measures and connection weights with PMA in connectomes weighted with 1‐ODI. The normative developmental trends that have been discovered in this work can be used as reference baselines for comparing and contrasting normal and abnormal brain development in future works. Future works may also extend the proposed framework to analyzing brain connectivity in longitudinal and population studies.

FUNDING INFORMATION

National Institutes of Health (NIH): R01HD110772, R01NS128281, R01NS106030, R01EB031849, R01EB032366, R01HD109395. National Science Foundation (NSF): 212306.

CONFLICT OF INTEREST STATEMENT

The authors have no conflicts of interest.

Supporting information

DATA S1: Supplementary Information.

Wu, Y. , Vasung, L. , Calixto, C. , Gholipour, A. , & Karimi, D. (2024). Characterizing normal perinatal development of the human brain structural connectivity. Human Brain Mapping, 45(11), e26784. 10.1002/hbm.26784

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in dHCP at https://www.developingconnectome.org/.