Evaluating the effects of the CERES-Rice model to simulate upland rice (Oryza sativa L.) yield under different plant density and nitrogen management strategies in Fogera Plain, Northwest Ethiopia

Abstract

This study assessed the optimal nitrogen (N) fertilizer rate and planting density for the well-adapted upland rice cultivar NERICA_4 on the Fogera Plain. The primary objective was to evaluate the effects of varied planting densities and N-fertilizer rates on upland rice yield and other agronomic parameters. A two-year field study (2020 and 2021) was conducted at the Fogera Rice Research Field Station, testing nine plant densities (75, 87, and 98; 72, 82, and 91; 70, 79, and 89 plants per m² and two N rates (115 and 138 kg N ha⁻¹). The Crop Simulation Model Crop Environment Resource Synthesis (CSM-CERES-Rice) within the Decision Support System for Agrotechnology Transfer (DSSAT) framework was calibrated and validated using site-specific weather, soil, crop, and agronomic management data from the experiment. Results on the subsequent RMSE, RMSEn, and d index values during the calibration phase were 0.074 t ha⁻¹, 1.82 %, and 0.86 of grain yield; 0.307 t ha⁻¹, 3.36 %, and 0.87 of by-product yield; 0.489 t ha⁻¹, 3.74 %, and 0.79 of top dry biomass yield; and 0.28, 8.24 %, and 0.63 of leaf area index values, respectively. Whereas results on the corresponding RMSE, RMSEn, and d index values during the evaluation phase were: 0.58 t ha⁻¹, 1.33 %, and 0.90 of grain yield; 0.69 t ha⁻¹, 0.58 %, and 0.99 of by-product yield; 0.678 t ha⁻¹, 4.36 %, and 0.67 of top dry biomass yield; and 0.75, 13.92 %, and 0.74 of leaf area index, respectively. The findings of the long-term simulation showed that a 23 % increase in grain yield was achieved with 138 kg N ha⁻¹ and 87 plants per m² of planting density, as compared to 115 kg N ha⁻¹ and 75 plants per m² of plant density. The recommended optimum plant density and N fertilizer rate were 138 kg N ha⁻¹ with PD2 of plant density for upland rice production in the Fogera Plain.

1. Introduction

Rice (Oryza sativa L.) is one of the world's most crucial staple cereal crops, providing over 21 % of the global population's caloric intake and playing a vital role in food security and human nutrition [1,2]. It ranks third among cereal crops, following wheat (Triticum aestivum L.) and maize (Zea mays L.) [3]. Since its recent introduction to Ethiopia, rice has become an integral part of the national economy and a key component in cereal production, contributing significantly to agricultural output [4]. Often referred to as the “millennium crop,” rice is expected to continue being pivotal in maintaining food security [5]. Ethiopia has significant potential for rice production, with over 30 million hectares of land suitable for cultivation [6]. Despite the rapid increase in rice production and the country's immense potential, the current average productivity of 2.8 t ha⁻¹ remains well below the global average of 4.7 t ha⁻¹ [7].

Rice production is influenced by several factors, including the choice of cultivar, planting dates, plant density, fertilizer application, and water management [8,9]. Nitrogen fertilization and plant density are particularly important in optimizing rice yield and nutrient use efficiency [10]. Research suggests that combining optimal nitrogen application with appropriate plant density is essential to minimize nitrogen losses and maximize upland rice yields [11]. Optimal nitrogen fertilization not only boosts yields but also offers significant economic benefits [12]. It is crucial to determine a nitrogen application rate that balances crop yield with environmental considerations. Studies have shown that wider planting patterns combined with high nitrogen rates are effective management strategies for increasing rice production [13,14]. Optimal planting density is influenced by multiple factors, including plant genetics, the length of the growing season, sowing methods, soil fertility, seed size, moisture availability, photoperiod, planting pattern, and weed pressure [15]. According to Mohammad et al. [16], planting density is a critical agronomic practice affecting various aspects of rice production. Effective crop management strategies can provide valuable insights for enhancing rice production, although traditional agronomic research methods often lack the timeliness and specificity required, making them costly and time-consuming [17]. Furthermore, typical cropping systems in major rice-growing regions are complex, necessitating the use of a variety of Crop Simulation Models (CSMs) and technologies to ensure long-term sustainability [18].

Regular, multi-season, and multi-location studies are essential for providing farmers and policymakers with the information needed to make informed decisions [19]. These studies, under varying agro-environmental conditions and management strategies, help evaluate models effectively [19,20]. Rice yield was simulated under different agronomic management methods and changing climate scenarios [21], and more effective rice management systems under irrigated environments were discovered [22]. CSMs and decision support systems are a possibility for solving this challenge in modern agriculture, where the integration of biophysical and management factors leads to sustainable practices. In spite of the use of CSMs for plant density, N management practices in the Ethiopian rice cropping system have received little attention. Studies have shown that the CSM-CERES (Crop Environment Resource Synthesis)-Rice model serves as a useful research and decision-support tool. This model was introduced to enhance decision-making, and its effectiveness has been assessed for rice-wheat cropping systems to increase resource and land use efficiency [23,24]. Although research has found the efficacy of the CSM-CERES-Rice model in evaluating different plant density and nitrogen fertilizer application techniques [8,25], the CSM-CERES-Rice is a parts of the Decision Support System for Agrotechnology Transfer (DSSAT) model, one of the latest advanced crop models [26], allows for the integration of crop management and environmental (soil and climate) data, which are essential for evaluating yield gaps and optimizing crop management strategies [27,28]. The rapid expansion of rice production in Fogera Plain, Ethiopia, requires an inquiry study that will optimize planting density and N management techniques in an integrated approach. However, the present studies aim to determine the effects of the CSM-CERES-Rice model to simulate upland rice production under various plant density and N management strategies in Fogera Plain. Therefore, the objectives of this study were to (1) evaluate the effectiveness of the CSM-CERES-Rice model in estimating upland rice yield and (2) determine the response of upland rice yield to different plant densities and nitrogen concentrations under rainfed conditions in the Fogera Plain.

2. Materials and methods

2.1. Description of the study area

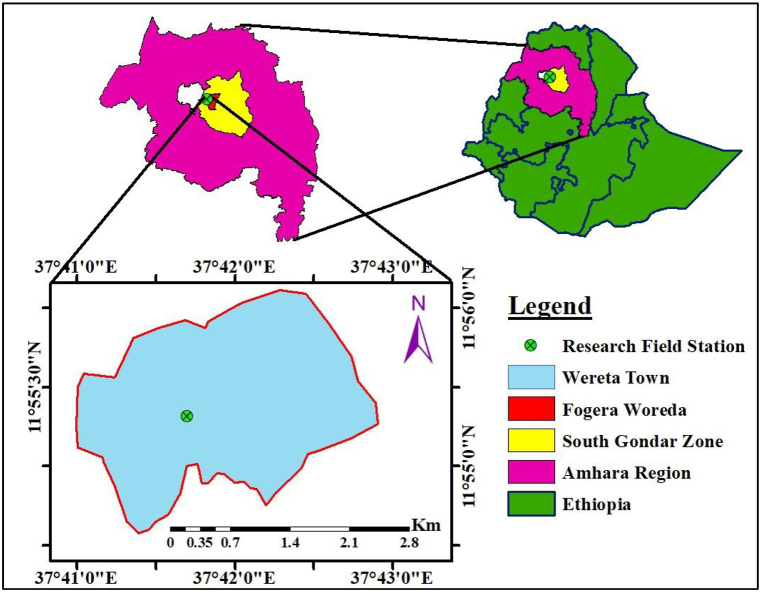
The study was carried out in Fogera Plain, Ethiopia, as shown in Fig. 1, which is located within latitudinal and longitudinal ranges between 10°58′N and 12°47′N and 36°45′E and 38°14′E, respectively, at an altitude of 1819 m above sea level, as revealed [29]. The averaged annual minimum and maximum air temperatures are 11.5 °C and 28.20 °C, respectively, and the annual mean temperature is 18.3 °C. Rainfall in the area is unimodal, usually from June to September, and the average annual rainfall is about 1259 mm. The soil's pH is 5.9, with a clay content ranging from 62 to 71 %. Its contents include 0.22 % total available N, 12.64 ppm available P (Olsen), 0.93 cmol (+) kg⁻¹ exchangeable K, 3 % organic carbon, and 52.9 cmol (+) kg⁻¹ CEC, as indicated by Aleminew et al. [4].

Fig. 1.

Map of study Aeea in Fogera Plain Ethiopia.

2.2. Description of the CERES-Rice model

The CERES-Rice model, part of the Decision Support System for Agrotechnology Transfer (DSSAT), is a sophisticated simulation tool designed to predict the growth, development, and yield of rice crops under various environmental conditions and management practices [19,30]. This model integrates data on weather, soil characteristics, crop management practices, and genetic factors to simulate the complete life cycle of rice from planting to harvest. By employing a detailed understanding of physiological processes, the CERES-Rice model can analyze the impact of variables such as water availability, nutrient levels, and climate conditions on rice productivity [17]. This enables the model to provide valuable insights into how different management strategies can optimize rice yield and sustainability. Additionally, the model allows for the adjustment of cultivar-specific genetic coefficients, ensuring that simulated outputs can be accurately calibrated and validated against observed data from specific study areas.

In this study, the DSSAT version 4.7 (DSSATv4.7) tool was utilized to investigate the effects of varying plant densities and nitrogen fertilizer rates on upland rice yield in the Fogera Plain. The model inputs included detailed information from the experimental setup, such as soil properties, crop management practices, and daily climate data (precipitation, minimum and maximum temperatures, and solar radiation). Key information regarding planting dates, planting methods, plant distribution, population density, row spacing, planting depth, cultivar selection, and fertilizer application was sourced from the nearby Fogera National Rice Research and Training Centre. For a deeper understanding of the model's capabilities.

2.3. Field experiment

A field experiment was conducted at the Fogera National Rice Research Training Centre on the field station during the 2020 and 2021 cropping seasons using a well-adapted upland rice cultivar (NERICA_4) in the Fogera Plain area [31], Phenological development and yield component data were collected throughout the growing season. Direct sowing was done by hand at 20, 25, and 30 cm of row spacing, with 80, 100, and 120 kg ha⁻¹ seed rates applied concurrently.

A factorial experiment consisted of nine levels of plant density of 75, 87, and 98; 72, 82, and 91; 70, 79, and 89 per m², combined with two levels of N fertilizer rates (115 and 138 N kg ha⁻¹), using a randomized complete block design (RCBD) replicated three times. All phenological and biophysical parameters were collected from a respective net plot area of 4.2, 3.9, and 3.6 m². Plant harvesting was done at physiological maturity, and all plots were made into soil bunds and separated by 0.5-m-wide strips of bare soil to avoid lateral movement of water and nutrients within plots.

2.4. Model inputs

The model's required inputs concerning the suggested crop management, soil physical and chemical properties, and weather data were described as follows:

2.4.1. Crop data

Leaf area index: The leaf area index of functioning leaves was measured at a maximum tillering phase. Data for the leaf area index was collected using the leaf area index calculator Hemisphere software tool reported by Jiangui et al. [32]. Which captures photographs of the vegetation ground cover over agricultural crops using top-of-canopy digital photography.

Tops dry weight (g): The total top dry weight was taken after harvesting and measured by weighing after the sun-dried total top weight (by-product + grain) of the net plot, and it's reported as converted into tons per hectare.

By-product weight (g): Total by-product yield was taken from the deducted total of dry biomass yield and converted into tons per hectare.

Grain Yield (t ha⁻¹): Grain yields were harvested at a net plot area of 4.2, 3.9, and 3.6 m², and they were first dried in the sun for up to 3 days in the field, then threshed manually and cleaned, and then the final weights were taken by digital balance. The grain yield per hectare was computed for each treatment from the yield of the net plot area. A digital moisture meter was used to record the moisture percentage of the grain. Finally, grain yields were adjusted at 11 % moisture using a digital tool as indicated by Singh et al. [33].

2.4.2. Soil data

A soil sample was taken before seeds were sown at the experimental site in 2020, and its required physicochemical characteristics were determined in the Amhara Design and Supervision Enterprise Laboratory Service, as indicated in Table 1. Between 0 and 30 cm depth, the soil's CEC is 44.26 (meq/100g⁻¹soil); the average field capacity (FC) and permanent wilting point (PWP) are 33.46 and 23.02 %, respectively; the average total nitrogen is 0.12 %, and the available phosphorus is 18.4 ppm. Table 2 shows the results of the soil study at the experimental site where the rice experiment was carried out and the reported data for three depths of layers (0–5, 5–15, and 15–30 cm) (Table 1).

Table 2.

Calibrated Genetic-coefficients of rice cultivar using CERS-Rice model in Fogera plain.

GC	Genetic coefficient description	Tested cultivar (NERICA_4)
P1	Juvenile phase coefficient (growth degree day in °C)	463
P2O	Critical photoperiod (hour length)	11.71
P2R	Photoperodism coefficient (growth degree day in °C)	138.84
P5	Grain filling duration coefficient (growth degree day in °C)	465.35
G1	Spikelet number coefficient	76.0
G2	Single grain weight (g)	0.023
G3	Tillering coefficient	1
G4	Temperature tolerance coefficient	83

Table 1.

Physical and chemical soil properties in Fogera Plain, Ethiopia.

Parameter	Soil depth (cm)
	0–5	5–15	15–30
Clay (%)	62	62	64
Silt (%)	23	21	21
Sand (%)	15	17	15
Bulk density (g cm−3)	1.18	1.14	1.13
Organic carbon	1.30	1.27	1.04
Total available N (%)	0.12	0.13	0.10
Av. P (ppm)	20.11	17.87	16.74
Soil pH(H2O) 1; 1.25	6.35	6.26	6.16
Field capacity (FC) (%)	37.48	33.15	29.76
Permanent wilting point(PWP) (%)	22.64	22.77	23.66
CEC (meq/100g−1 soil)	41.2	46.4	45.2

CEC= Cation exchange capacity.

2.4.3. Climate data

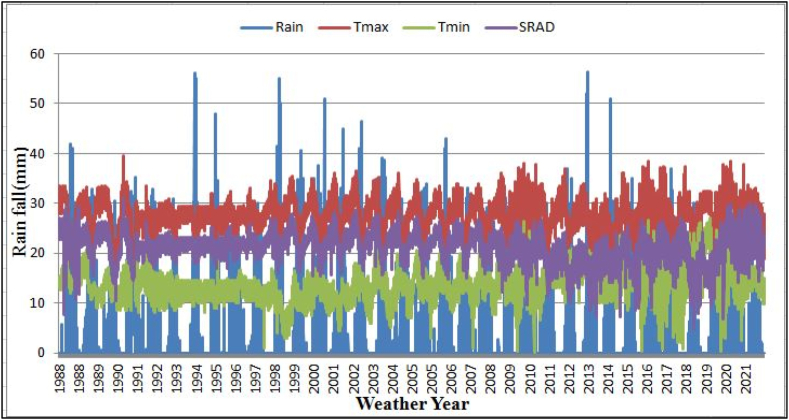
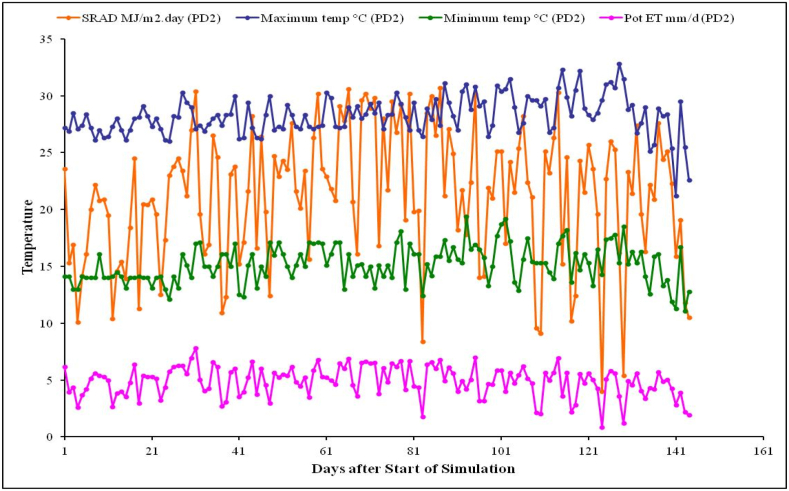
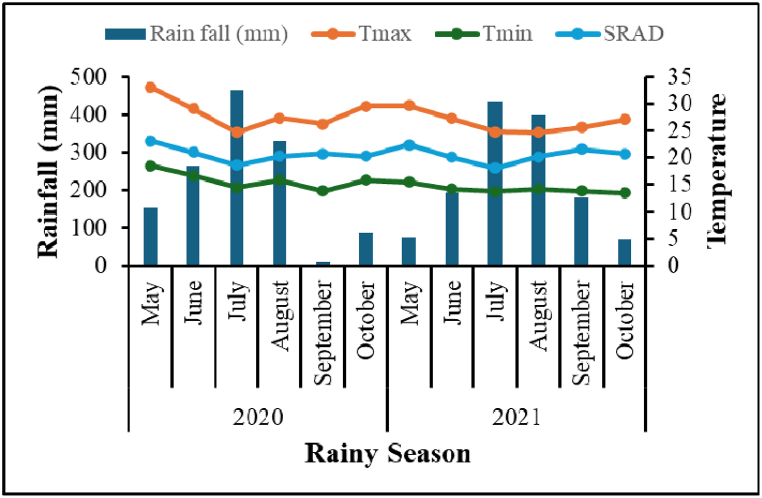
For the study area, daily weather data for the baseline period of 33 years, from 1988 to 2021, were obtained from the National Meteorological Agency of Ethiopia, as indicated in Fig. 3. The Weatherman climate data management tool integrated into the DSSAT model was used to estimate solar radiation, this tool uses inputs such as sunshine hours, longitude, and latitude data specific to the study area. As indicated in Fig. 4, weather output analyses were displayed in the validation simulation process. Furthermore, as depicted in Fig. 2, the mean air temperature (Tmax and Tmin), solar radiation, and total rainfall for the 2020 cropping season were 28.4 and 15.8 °C, 17.28 MJm⁻² day⁻¹, and 1308.2 mm, respectively, throughout the rainy season (June to September). The similar averages for temperature, solar radiation, and rainfall for the 2021 cropping season were 26.5 and 14.5 °C, 20.52 MJm⁻² day⁻¹, and 1351.56 mm, respectively. Fig. 2 reveals the inverse relationship between temperature and rainfall data collected during the 2020 and 2021 cropping seasons in the Fogera Plain.

Fig. 3.

Observed weather data (1988–2021) in Fogera Plain.

Fig. 4.

Weather output analysis for the evaluation simulation model in 2021 in Fogera Plain.

Fig. 2.

Mean monthly rainfall. Maximum, minimum temperature, and solar radiation in Fogera Plain.

2.5. Model calibration and validation

The model calibration process involved running the model with these coefficients in a Generalized Likelihood Uncertainty Estimation (GLUE) of 10,000 iterations for development and growth. Four biophysical attributes were used for calibration purposes in the 2020 cropping season. The 2021 main cropping season data sets were used for model validation, following a similar calibration process. The sensitivity analysis tool was also used to further refine the coefficients. This iterative process included running the model with each relevant genetic coefficient, comparing outputs with measured data, adjusting the coefficients, and repeating until satisfactory fits were achieved. The calibrated genetic coefficient values of P and G parameters for the upland rice cultivar (NERICA_4) are presented in Table 2. The CERES-Rice model was run under the normal conditions measured in the field experiment. All the calibrated traits were used to simulate each of the treatments in the study area. Then, graphical analysis and statistical measurements were carried out, as reported by Confalonieri et al. [34]. Simulated and measured values of total dry biomass yield, by-product yield, leaf area index, and grain yield were graphically compared using the Easy Grapher tool in the DSSAT model, and the values of physiological parameters were compared to those measured and simulated values. The performance of the CERES-Rice model to simulate the effects of upland rice traits was carried out during calibration, and evaluation was assessed using the following statistical indices: Abera [35], Gijsman and Ritchie [36], Fayed et al. [37], Wilmot et al. [38]. The root mean square error (RMSE) is the “best” measure as it summarizes the mean difference in the units of measured and simulated values [39]. In the case of RMSEn, a simulation can be considered excellent if it is smaller than 10 %, good between 10 and 20 %, fair between 20 and 30 %, and poor if it is larger than 30 % [40]. D values range between 0 and 1, where 0 indicates no agreement and 1 indicates perfect agreement between predicted and measured data, according to Akhter et al. [41]. In addition, the deviations in phenology and growth yields were presented as follows:

$$\text{RMSE}=\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\text{Pi}-\text{Oi}}{\mathrm{N}}\right)2}$$ (1)

The residuals measure how far the data points are apart from the regression line. It tells us how concentrated the data is around the line of best fit. RMSE values that are close to 0 indicate perfect fits between simulated and observed data.

$$\text{RMSEn}=\frac{100}{O}\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\text{Pi}-\text{Oi}}{\mathrm{N}}\right)2}$$ (2)

where N is the mean of the observed variables. RMSEn gives the measure (%) of the relative difference between simulated and observed data. Less value indicates a good fit for the model. Normalized RMSE: a simulation can be considered excellent if RMSEn is less than 10 %, good between 10 and 20 %, fair between 20 and 30 %, and poor if it is greater than 30 % [41].

$$\mathrm{d}=1-\left[\frac{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{P}}_{\mathrm{i}}-{\mathrm{O}}_{\mathrm{i}}\right)}^2}{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left(\left|{\mathrm{P}}_{\mathrm{i}}+{\mathrm{O}}_{\mathrm{i}}\right|\right)}^2}\right]$$ (3)

where n is the number of observations, Pi is the calculated value for the ith measurement, and Oi is the observed value for the ith measurement.

$$\Delta \mathrm{X}(\%)=\frac{{\mathrm{X}}_{\text{Simulated}}-{\mathrm{X}}_{\text{Observed}}}{{\mathrm{X}}_{\text{Observed}}}\times 100$$ (4)

where, X = any variable of interest.

3. Results and discussion

3.1. Results

3.1.1. Calibrtion and evaluation

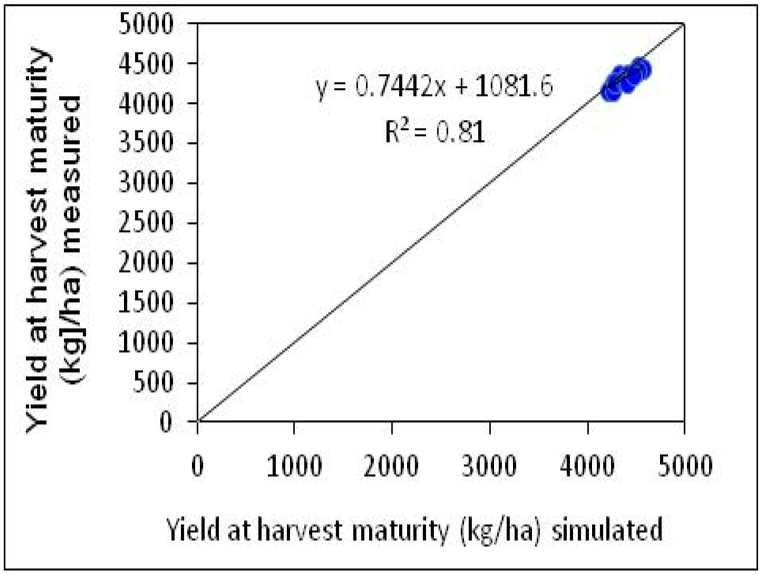
Grain Yield:Table 3 displays the results of the CERES-Rice model's calibration and evaluation in grain yield simulation. During the calibration phase, the grain yield's absolute root mean square error (RMSE) was 0.074 t ha^⁻1, while the evaluation phase exhibited an RMSE of 0.58 t ha⁻¹. The data in Table 3 indicate noticeable differences between the absolute RMSE, normalized RMSE (RMSEn), and the D index in the calibration and evaluation phases of the model. Specifically, the RMSEn for grain yield was 1.82 % during calibration and 1.33 % during evaluation. The model's D index, a measure of agreement between the observed and simulated values, was 0.86 during calibration and 0.90 during evaluation. Table 3 demonstrates a significant agreement between the simulated and measured grain yield values. This agreement is further supported by Fig. 5, where a regression coefficient of 0.81 indicates a strong and close correlation between the simulated and measured values.

Table 3.

Model evaluation under the effects of plant density and N fertilizer rates in Fogera Plain.

Model evaluation	Crop characteristics	Sample numberr	Mean values		Standard deviation (SD)		RMSE	RMSEn (%)	D index
			SIM	OBS	SIM	OBS
Calibration (2020)	Top dry biomass yield (t ha−1)	18	13.532	13.069	0.464	0.477	0.489	3.74	0.79
	By-product yield (t ha−1)	18	9.400	9.139	0.390	0.437	0.307	3.36	0.87
	LAI max	18	3.60	3.41	0.002	0.003	0.280	8.24	0.63
	Grain Yield (t ha−1)	18	4.131	4.075	0.103	0.091	0.074	1.82	0.86
Validation (2021)	Top dry biomass (t ha−1)	18	16.182	15.541	0.516	0.469	0.678	4.36	0.67
	By-product yield (t ha−−1)	18	11.812	11.854	0.423	0.461	0.690	0.58	0.99
	LAI max	18	6.14	5.41	0.001	0.002	0.750	13.92	0.74
	Grain Yield (t ha−1)	18	4.370	4.334	0.101	0.084	0.580	1.33	0.90

Key: SIM = simulated, OBS = observed, and SD = standard deviation.

Fig. 5.

Comparison of grain yield between simulated and measured values during the evaluation model in the 2021 cropping season in Fogera Plain.

For each crop variable in the calibration and evaluation simulations, as detailed in Table 3, the grain yields were accurately fitted and compared with the standard deviation (SD) and root mean square error (RMSE). Table 4, Table 5 illustrate the percentage deviations of grain yields during calibration and evaluation. The simulated and measured values for nitrogen fertilizer rates of 115 kg N ha⁻¹ and 138 kg N ha⁻¹, and plant densities (PD1 to PD9) showed deviations ranging from −0.98 % to 3.27 % and 0.14 %–2.82 %, and from −1.62 % to 1.55 % and 0.34 %–2.50 %, respectively. The findings indicate that grain yield increases with higher plant densities and increased nitrogen fertilization, as reflected in the calibration and evaluation values using 138 kg N ha^⁻1 and a plant density corresponding to PD2. Significant impacts on grain yields under different plant densities and nitrogen fertilizer levels are evident in Table 4, Table 5, highlighting the effectiveness of the CERES-Rice model in simulating upland rice yields under varying agronomic conditions.

Table 4.

Measured and simulated data for top dry biomass, by-product yield, leaf area index, and grain yield during calibration model in 2020 under different plant density and N rates in Fogera Plain.

Nitrogen Rates	Plant Density	Top dry biomass (t ha−1)			By-product (t ha−1)			LAIX			Grain Yield (t ha−1)
		SIM	OBS	Dev (%)	SIM	OBS	Dev (%)	SIM	OBS	Dev (%))	SIM	OBS	Dev (%)
N1 (115)	PD1	13.221	12.627	4.70	9.111	8.755	4.07	3.37	3.06	10.31	4.110	4.022	2.19
	PD2	13.426	13.101	2.48	9.214	8.945	3.01	3.47	3.56	−2.50	4.212	4.106	2.58
	PD3	13.560	13.436	0.92	9.300	9.461	−1.70	3.54	3.39	4.39	4.260	4.125	3.27
	PD4	12.938	12.327	4.96	8.912	8.412	5.94	3.26	3.01	8.20	4.025	4.065	−0.98
	PD5	13.208	12.614	4.71	9.084	8.719	4.19	3.38	3.54	−4.41	4.123	4.045	1.93
	PD6	13.314	12.788	4.11	9.154	8.773	4.34	3.47	3.39	2.42	4.160	4.165	−0.12
	PD7	12.684	12.482	1.62	8.747	8.677	0.81	3.15	3.19	−1.16	3.937	3.955	−0.46
	PD8	12.880	12.376	4.07	8.876	8.563	3.66	3.26	3.18	2.52	4.004	3.963	1.03
	PD9	13.144	12.614	4.20	9.041	8.705	3.86	3.39	3.23	4.99	4.103	4.059	1.08
N2 (138)	PD1	13.940	13.262	5.11	9.769	9.332	4.68	3.80	3.38	12.49	4.171	4.080	2.23
	PD2	14.174	13.536	4.71	9.904	9.508	4.16	3.90	3.58	9.00	4.270	4.178	2.20
	PD3	14.412	13.871	3.90	10.067	9.782	2.91	4.04	3.40	18.82	4.345	4.339	0.14
	PD4	13.640	13.162	3.63	9.569	9.291	2.99	3.69	3.73	−1.15	4.071	4.021	1.24
	PD5	13.904	13.649	1.87	9.759	9.684	0.77	3.83	3.56	7.74	4.145	4.115	0.73
	PD6	14.061	13.623	3.22	9.838	9.666	1.78	3.90	3.41	14.47	4.223	4.107	2.82
	PD7	13.461	13.017	3.41	9.462	9.182	3.05	3.63	3.51	3.54	3.999	3.985	0.35
	PD8	13.688	13.111	4.40	9.624	9.303	3.45	3.77	3.67	2.81	4.064	3.966	2.47
	PD9	13.918	13.649	1.97	9.777	9.741	0.37	3.90	3.55	9.92	4.142	4.058	2.07

Key: SIM = simulated, OBS = observed, Dev = deviation, Plant density per m² (PD1–9) (1 = 75, 2 = 87, 3 = 98, 4 = 72, 5 = 82, 6 = 91, 7 = 70, 8 = 79, and 9 = 89) and N1 and N2 (nitrogen rates), respectively.

Table 5.

Measured and simulated data for top dry biomass, by-product yield, leaf area index, and grain yield during evaluation model in 2021 under different plant densities and N rates in Fogera Plain.

Nitrogen Rates	Plant Density	Top dry biomass (t ha−1)			By-product (t ha−1)			LAIX			Grain Yield (t ha−1)
		SIM	OBS	Dev (%)	SIM	OBS	Dev (%)	SIM	OBS	Dev (%)	SIM	OBS	Dev (%)
N1 (115)	PD1	15.674	15.127	3.6	11.404	11.430	−0.23	5.61	4.55	23.16	4.270	4.244	0.61
	PD2	15.766	15.601	1.1	11.426	11.438	−0.10	5.58	5.06	10.30	4.340	4.328	0.28
	PD3	15.833	15.436	2.6	11.468	11.486	−0.16	5.63	4.89	15.11	4.365	4.347	0.41
	PD4	15.597	14.827	5.2	11.344	11.310	0.30	5.57	4.51	23.42	4.253	4.287	−0.79
	PD5	15.691	15.114	3.8	11.416	11.424	−0.07	5.67	5.04	12.59	4.275	4.267	0.19
	PD6	15.740	15.288	3.0	11.424	11.353	0.63	5.63	4.89	15.18	4.316	4.387	−1.62
	PD7	15.516	14.982	3.6	11.308	11.339	−0.27	5.65	4.69	20.55	4.208	4.177	0.74
	PD8	15.575	14.876	4.7	11.326	11.390	−0.56	5.57	4.68	19.02	4.250	4.185	1.55
	PD9	15.670	15.114	3.7	11.398	11.389	0.08	5.67	4.73	19.90	4.272	4.281	−0.21
N2 (138)	PD1	16.681	15.762	5.8	12.219	12.279	−0.49	6.67	5.88	13.47	4.462	4.402	1.36
	PD2	16.793	16.036	4.7	12.286	12.393	−0.86	6.66	5.98	11.41	4.508	4.470	0.85
	PD3	16.850	16.371	2.9	12.300	12.289	0.09	6.55	6.23	7.49	4.550	4.461	2.00
	PD4	16.616	15.662	6.1	12.218	12.333	−0.93	6.70	6.10	7.38	4.398	4.383	0.34
	PD5	16.692	16.149	3.4	12.225	12.355	−1.05	6.68	6.05	10.32	4.466	4.387	1.80
	PD6	16.743	16.123	3.8	12.237	12.314	−0.63	6.61	5.91	11.90	4.506	4.429	1.74
	PD7	16.55	15.517	6.7	12.184	12.243	−0.48	6.73	6.01	12.05	4.366	4.307	1.37
	PD8	16.607	15.611	6.4	12.212	12.319	−0.87	6.70	6.17	8.64	4.395	4.288	2.50
	PD9	16.675	16.149	3.3	12.214	12.295	−0.66	6.68	6.05	10.45	4.461	4.380	1.85

Key: SIM = simulated, OBS = observed, Dev = deviation, Plant density per m² (PD1–9) (1 = 75, 2 = 87, 3 = 98, 4 = 72, 5 = 82, 6 = 91, 7 = 70, 8 = 79, and 9 = 89) and N1 and N2 (nitrogen rates), respectively.

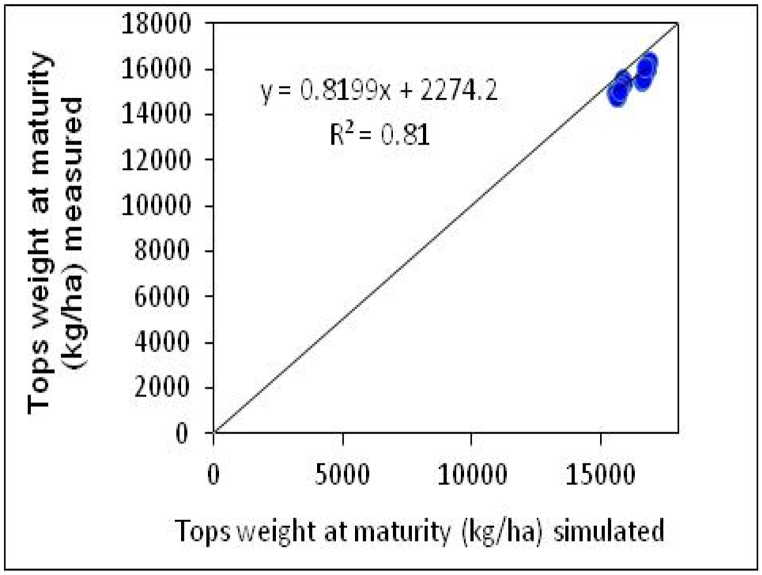
Top dry biomass yield:Table 3 presents the impact of the CERES-Rice model on the top dry biomass yield in relation to plant density and nitrogen (N) fertilizer rates. The results indicate that for the upland rice cultivar NERICA_4, the RMSE values for the top dry biomass yields during calibration and evaluation were 0.489 t ha⁻¹ and 0.678 t ha⁻¹, respectively. Under various planting densities and nitrogen fertilizer rates, the normalized RMSE (RMSEn) for top dry biomass yields was 3.74 % during calibration and 4.36 % during evaluation. The D index values were 0.79 and 0.67 for the calibration and evaluation phases, respectively, indicating a reasonable fit between the simulated and observed values on the harvest dates. A comparison of the simulated and measured top dry biomass yield values, as detailed in Table 5, shows that the model provides a satisfactory representation of actual biomass production. Regression analysis, as shown in Fig. 6, yielded a coefficient of determination (R²) of 0.81, suggesting a strong correlation between the simulated and measured values.

Fig. 6.

Comparison of top dry biomass yield between simulated and measured values during the evaluation model in the 2021 cropping season in Fogera Plain.

The percentage differences between the simulated and measured top dry biomass yields during the calibration and evaluation phases varied by nitrogen application rates (N115 and N138 kg ha⁻¹) and plant densities (PD1 to PD9). The disparities ranged from 1.1 % to 5.2 % during calibration and 2.9 %–6.7 % during evaluation. Additionally, the percentage differences ranged from −4.41 % to 10.31 % during calibration and from −1.15 % to 18.82 % during evaluation, reflecting the model's sensitivity to changes in nitrogen rates and plant densities (Table 4, Table 5).

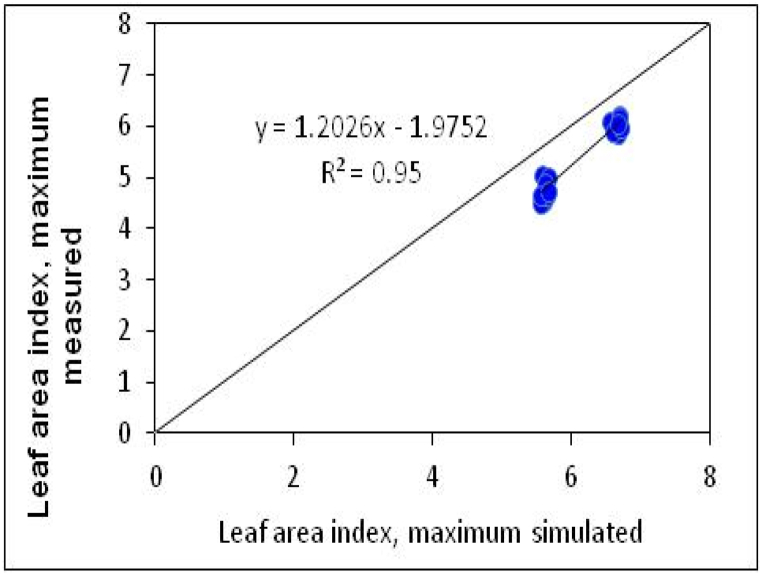
Leaf area index (LAI): The effects of plant density and nitrogen (N) fertilizer rates on the leaf area index (LAI) of upland rice (NERICA_4) were evaluated using the CERES-Rice model, as presented in Table 3. The results indicate that the RMSE values for LAI during calibration and evaluation were 0.28 and 0.75, respectively. The normalized RMSE (RMSEn) and D index at the maximum tillering stage were 8.24 % and 13.92 %, and 0.63 and 0.74, respectively, as shown in Table 3. Fig. 7 demonstrates a regression coefficient (R²) of 0.95, indicating a very close relationship between the simulated and measured LAI values. The results suggest that an increase in plant density, particularly the densely planted density (PD3), and an increase in the N fertilizer rate to 138 kg N ha^⁻1 both contribute to a higher LAI in the studied areas of the Fogera Plain.

Fig. 7.

Comparison of leaf area index between simulated and measured values during evaluation in the 2021 cropping season in Fogera Plain.

The deviations between the simulated and measured LAI values under different N fertilizer rates (115 and 138 kg N ha^⁻1) and plant densities (PD1 to PD9) during calibration and evaluation ranged from −1.15 % to 18.82 %, −4.41 %–10.31 %, 12.59 %–23.16 %, and 7.38 %–13.47 %, respectively, as presented in Table 4, Table 5 These deviations illustrate the model's ability to capture the effects of varying N rates and plant densities on LAI, although some differences between simulated and measured values remain, reflecting the inherent variability and complexity of crop-environment interactions.

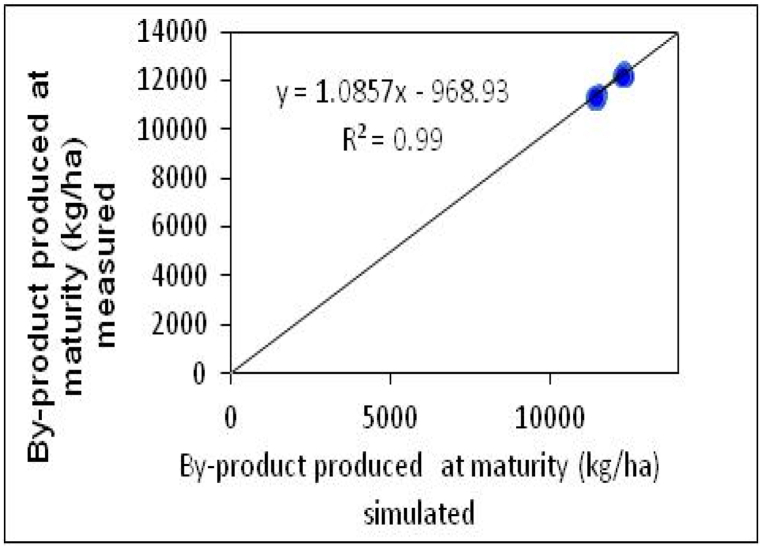
By-product yield: The effects of nitrogen (N) fertilizer rates and plant density on the by-product yield of upland rice, as evaluated using the CERES-Rice model, are detailed in Table 3. The calibration and evaluation phases showed that the absolute root mean square error (RMSE) for by-product yield was 0.307 t ha⁻¹ and 0.69 t ha⁻¹, respectively. The normalized RMSE (RMSEn) and D index values for both phases indicated significant agreement between the simulated and measured by-product yields, with RMSEn values of 3.36 % for calibration and 0.58 % for evaluation, and D index values of 0.87 and 0.99, respectively. The regression analysis, as illustrated in Fig. 8, demonstrates a high degree of correlation between the simulated and measured data, with a regression coefficient (R²) of 0.99, indicating a very close match. This suggests that the CERES-Rice model is highly accurate in predicting by-product yields under varying N fertilizer rates and plant densities. Table 4 indicates that an increase in the N fertilizer rate to 138 kg N ha⁻¹ and a dense plant population density at PD2 resulted in higher by-product yields. The deviations between the simulated and measured values for both N fertilizer rates (115 and 138 kg N ha⁻¹) and plant densities (PD1 to PD9) were −1.70 %–5.94 % for calibration and 0.34 %–4.68 % for evaluation, as detailed in Table 4, Table 5 These deviations illustrate the model's sensitivity to changes in nitrogen rates and plant densities, affirming its reliability in simulating by-product yields under different agronomic conditions.

Fig. 8.

Comparison of by-product yield between simulated and measured values during evaluation in the 2021 cropping season in Fogera Plain.

3.2. Discussion

In this study, we used the GLUE (Generalized Likelihood Uncertainty Estimation) and sensitivity analysis tools within the CERES-Rice model to evaluate the effects of different plant densities and nitrogen fertilizer rates on the growth and yield of upland rice in the Fogera Plain. For the upland rice cultivar NERICA_4, the model accurately simulated grain yield, top dry biomass yield, by-product yield, and leaf area index (LAI). Chisanga et al. [42] demonstrated that the soil and genetic coefficient traits of the CERES-Maize model were accurately estimated using the GLUE technique. Similarly, we estimated growth and developmental parameters by iterating through GLUE and sensitivity analysis events, confirming the reliability of our findings for upland rice in the Fogera Plain. We calibrated the genetic coefficients for each growth and development parameter across eight categories, following the model's guidelines [41].

This study integrated the GLUE method with a systematic approach to model calibration. The calibration and evaluation simulations for the upland rice (NERICA_4) cultivar showed acceptable grain yield values, with RMSE of 0.074 t ha⁻¹, RMSEn of 1.82 %, and a D index of 0.86 for calibration, and RMSE of 0.58 t ha⁻¹, RMSEn of 1.33 %, and a D index of 0.90 for evaluation. Calibration and evaluation results for dry biomass yield, by-product yield, and LAI were similarly satisfactory. The simulation results for the following variables were shown: by-product yield (RMSE of 0.307 t ha⁻¹, RMSEn of 3.36 %, D index of 0.87 for calibration; RMSE of 0.69 t ha⁻¹, RMSEn of 0.58 %, D index of 0.99 for evaluation); dry biomass yield (RMSE of 0.489 t ha⁻¹, RMSEn of 3.74 %, D index of 0.79 for calibration; RMSE of 0.678 t ha⁻¹, RMSEn of 4.36 %, D index of 0.67 for evaluation); and LAI (RMSE of 0.28, RMSEn of 8.24 %, D index of 0.63 for calibration; RMSE of 0.75, RMSEn of 13.92 %, D index of 0.74 for evaluation). These findings align with previous research by Mohammed and Misganaw [43], and Chisanga et al. [42], which reported similar levels of model accuracy. Findings confirmed by Tari et al. [44] found that the grain yield model evaluation showed an RMSE of 0.58 t ha⁻¹, RMSEn of 11.9 %, and a D index of 0.92. Similarly, Mirakhori et al. [45] reported that the CERES-Rice model simulated rice grain yield with RMSEn values of 8.0 % and 6.0 %, and biological yield with RMSEn values of 10.0 % and 9.0 %, with R² values of 0.82 and 0.95 for various nitrogen levels (0, 90, 120, and 150 kg N ha⁻¹). Akhter et al. [41] noted an RMSE of 1.3 t ha⁻¹ for grain yield, with observed yields ranging from 2.9 to 6.7 t ha⁻¹ and simulated yields ranging from 2.6 to 7.3 t ha⁻¹. Akinbile [28] reported that the CERES-Rice model simulated grain yield, leaf and stem biomass yield, and total above-ground biomass yield with slightly higher values than observed field values.

The findings of the present study indicated excellent accuracy in measured grain yields compared to simulated dry biomass yield and LAI, particularly when using the method shown in Fig. 5. The deviations in grain yield across various nitrogen fertilizer rates (115 and 138 kg N ha⁻¹) and plant densities (PD1 to PD9) ranged from −0.98 % to 3.27 %, 0.14 %–2.82 %, −1.62 %–1.55 %, and 0.34 %–2.50 % for calibration and evaluation simulations, respectively. The by-product yields varied from −1.70 to 5.94 %, 0.37–4.68 % during calibration and −0.56 to 0.63 % and −1.05 to 0.09 % for evaluation; the variations for top dry biomass yields were 0.92–4.96 %, 1.87–5.11 % during calibration and 1.1–5.2 %, and 2.9–6.7 % during evaluation. The LAI's variations were as follows: 10.30–23.42 %, 7.38–13.47 %, −1.15 to 18.82 %, and −4.41 to 10.31 % during calibration and evaluation, respectively. Similar results confirmed the findings of Akhter et al. [41], who indicated that the reported deviation ranges for biomass (−4.3 to 14.6 %), teff (−0.10 to 8.70 %), and barley grain yield (−13 to 15.1 %) were found in the validation data. Tari et al. [44] found that the Aqua Crop model replicated above-ground biomass yield more closely than grain yield, with validation errors ranging from 0.4 to 5.8 %. According to Hsiao et al. [46], the Aqua Crop model's estimation of maize biomass yield ranged from −0.4 to 21.9 %. Depending assumptions made about soil water intakes, the model may have overstated grain and biomass yields, or the actual values may have been lower than expected results based on the input of weather and soil parameters. The observed values for the essential calibration and evaluation simulation results showed that grain yield produced in tandem with dense plant population patterns and increasing nitrogen fertilizer rates. These increased grain yield the results were obtained with plant densities of PD3 (4.34 t ha⁻¹) and PD2 (4.47 t ha⁻¹) and nitrogen fertilizer rates of N138 kg ha⁻¹.

3.3. Conclusions

This study underscores the significance of integrating field experiments with simulation models like CERES-Rice to determine optimal planting densities and nitrogen (N) fertilizer rates for upland rice under varying conditions. Despite unpredictable factors such as weather and soil fertility, the CERES-Rice model, calibrated with extensive soil, weather, and crop management data, effectively identified the best combination of 138 kg N ha⁻¹ and 87 plants m² for maximizing grain yield in the Fogera Plain, resulting in a 23 % increase in yield. This model's accuracy in simulating grain yield, biomass, and LAI demonstrates its value in optimizing resource use and guiding agricultural practices. Future research should focus on further calibration and validation of the CERES-Rice model across diverse agro-ecological zones to enhance its robustness and provide precise recommendations. Integrating the model with other decision-support systems and real-time data will improve predictive accuracy and support adaptive management strategies. Adopting the recommended N fertilizer rates and planting densities can significantly increase rice yields and resource efficiency, contributing to sustainable agricultural development in Northwest Ethiopia and similar regions.

Data availability statement

The data that supports this study's findings is available from the corresponding author upon reasonable request.

CRediT authorship contribution statement

Sisay Tefera: Writing – original draft, Visualization, Validation, Software, Project administration, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Kindie Tesfaye: Writing – review & editing, Supervision, Conceptualization. Tilahun Tadesse: Writing – review & editing, Supervision. Teferi Alem: Writing – review & editing, Supervision. Dereje Ademe: Writing – review & editing, Validation, Software, Methodology, Supervision, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.