Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jul 3;8(7):1349–1358. doi: 10.1021/acsearthspacechem.4c00040

Ethynyl Radical Hydrogen Abstraction Energetics and Kinetics Utilizing High-Level Theory

Laura N Olive 1, Alexandra D Heide 1, Justin M Turney 1, Henry F Schaefer III 1,*
PMCID: PMC11261607  PMID: 39045226

Abstract

graphic file with name sp4c00040_0011.jpg

The ethynyl radical, C2H, is found in a variety of different environments ranging from interstellar space and planetary atmospheres to playing an important role in the combustion of various alkynes under fuel-rich conditions. Hydrogen-atom abstraction reactions are common for the ethynyl radical in these contrasting environments. In this study, the C2H + HX → C2H2 + X, where HX = HNCO, trans-HONO, cis-HONO, C2H4, and CH3OH, reactions have been investigated at rigorously high levels of theory, including CCSD(T)-F12a/cc-pVTZ-F12. For the stationary points thus located, much higher levels of theory have been used, with basis sets as large as aug-cc-pV5Z and methods up to CCSDT(Q), and core correlation was also included. These molecules were chosen because they can be found in either interstellar or combustion environments. Various additive energy corrections have been included to converge the relative enthalpies of the stationary points to subchemical accuracy (≤0.5 kcal mol–1). Barriers predicted here (2.19 kcal mol–1 for the HNCO reaction and 0.47 kcal mol–1 for C2H4) are significantly lower than previous predictions. Reliable kinetics were acquired over a wide range of temperatures (50–5000 K), which may be useful for future experimental studies of these reactions.

Keywords: ethynyl radical, hydrogen abstraction, kinetics, focal point analysis, theoretical study

1. Introduction

The ethynyl radical, C2H (2Σ+), is known to be a key intermediate in a number of diverse environments. It has been observed in both combustion reactions1,2 and planetary atmospheres.3,4 Additionally, it is one of the most abundant polyatomic radicals in interstellar space.5−8 In combustion environments, the ethynyl radical is a common intermediate in fuel-rich hydrocarbon combustion processes of various alkynes that can take place at temperatures in excess of 1800 K.9 Furthermore, it plays an important role as a key precursor in the synthesis of polyynes, polycyclic aromatic hydrocarbons (PAHs), and soot particles.1,10−13 It is also a reactive species in Titan’s atmosphere where the temperature is altitude-dependent (70 K at the tropopause and 94 K at the surface). To better understand the importance of these reactions involving the ethynyl radical in these drastically different environments, there is a need to accurately model the reactions of C2H with a variety of reactants over an extremely broad range of temperatures.

Hydrogen-atom abstraction is among the most prevalent reactions for the ethynyl radical and is commonly the main reaction pathway or a feasible alternative.14−16 The sizable dissociation energy of acetylene’s sp-hybridized C–H bond thermodynamically drives these hydrogen abstraction reactions. Large rate constants have been calculated by kinetic studies for the reaction of C2H with different saturated hydrocarbons over a broad range of temperatures, implying moderately low barriers for abstraction.2,9,17−19 Theoretical results corroborate this claim with moderate to low reported barrier heights for several hydrogen atom donors.14,20 At this time, most experimental and theoretical studies involving ethynyl radical hydrogen abstractions have focused on hydrocarbon hydrogen atom donors. Over the years, numerous studies have been done on these types of reactions with a wide variety of small molecules or radicals.2,11,14,15,21−30 However, little work has been done on larger molecules.

Reactions involving nitrogen containing radicals and their kinetics in the gas phase are also of considerable interest due to the role these species play in the formation and removal of NOx pollutants in combustion processes.31 NCO plays a key intermediate in combustion, however, very little is known of the kinetics of the reactions of NCO with hydrocarbons.19,32 No previous experimental studies on C2H + HNCO have been reported, but a theoretical study in 2003 by Chen and Ho31 addressed the reaction mechanisms for NCO and C2H2 at the CCSD(T)/6-31++G**//B3LYP/6-31++G** level of theory and they were able to find a direct pathway for the NCO + C2H2 → C2H + HNCO reaction.

Additionally, nitrous acid, HONO, has been detected in the interstellar medium,33 and the reaction involving CN has been explored theoretically34 with MP2 and CCSD(T); however, no study has been reported involving C2H. Furthermore, the kinetics of the pyrolysis and oxidation of methanol, CH3OH, which could be considered as an alternative, more environmentally friendly fuel or fuel additive to gasoline, have been of great interest in the last several years.35 Hydrogen abstraction reactions could happen at two different sites for CH3OH. The hydrogen could be abstracted off the hydroxyl, −OH, group (reaction R1), or the methyl, −CH3, group (reaction R2).

1. R1
1. R2

In 2011, a theoretical paper by Tri and Huê studied the C2H + CH3OH reaction mechanism with B3LYP and the 6-311++G(d,p) and 6-311++G(3df,2p) basis sets.36 They investigated 12 different reaction pathways and found that the formations of C2H2 + CH3O and C2H2 + CH2OH were the most favorable.

A recent study by Bowman et al. investigated numerous C2H hydrogen abstraction reactions with highly accurate ab initio methods.15 In the present study, a similar computational approach will be utilized to investigate the C2H + HX → C2H2 + X reactions, where HX = HNCO, trans-HONO, cis-HONO, C2H4, and CH3OH. Our study will provide high-level ab initio characterization of hydrogen abstraction reactions of the ethynyl radical with various medium sized molecules including HNCO, trans-HONO, cis-HONO, C2H4, and CH3OH. A composite approach will be implemented to converge the energies within subchemical accuracy (≤0.5 kcal mol–1). These highly accurate energetics will be used to compute reliable rate constants with canonical transition state theory that can be used in future kinetic studies.

2. Theoretical Methods

Full geometry optimizations and corresponding harmonic vibrational frequency computations were performed on each of the stationary points for the C2H + HX, where HX = HNCO, trans-HONO, C2H4, and CH3OH (reaction R1), reactive surfaces using the explicitly correlated CCSD(T)-F12a method37 in conjuction with the cc-pVTZ-F12 basis set38,39 as implemented in Molpro 2010.40 A restricted open-shell Hartree–Fock (ROHF) reference was used for all open-shell computations to avoid issues with spin contamination that are sometimes prevalent with the ethynyl radical. For the C2H + HX, where HX = cis-HONO and CH3OH (reaction R2), reactive surfaces, full geometry optimizations and corresponding harmonic vibrational frequency computations were performed on each of the stationary points at the MP241/aug-cc-pVTZ42 level of theory as implemented in Psi4.43 Single point energy computations were performed on the MP2/aug-cc-pVTZ geometries with CCSD(T)-F12a/cc-pVTZ-F12 in Molpro 2010.

The electronic energies of the CCSD(T)-F12a/cc-pVTZ-F12 stationary points were computed according to the focal point analysis (FPA) of Allen and co-workers.44,45 For the present study, methods that describe electron correlation up to CCSDT(Q)46 and basis sets as large as aug-cc-pV5Z47 were used. Single point energy computations were performed on the CCSD(T)-F12a/cc-pVTZ-F12 optimized geometries with CCSD(T)48,49/aug-cc-pVXZ (where X = D, T, Q, 5)42 in Molpro 2010, and CCSDT50/aug-cc-pVDZ and CCSDT(Q)/aug-cc-pVDZ as implemented in MRCC 2018.51 As shown in Table 1, there is excellent convergence to the complete basis set (CBS) limit. The CCSD(T)/CBS energies were obtained through extrapolation of the Hartree–Fock (HF) and correlation energies. The three-parameter exponential function by Feller is used to extrapolate to the HF/CBS limit.52

2. 1

The two-parameter cubic function of Helgaker et al.53 is used to extrapolate the correlation energies (Ecorr) to the CBS limit.

2. 2

The focal point energies were obtained with the following formula:

2. 3

Additional corrections were made to account for approximations made during the focal point computations. To account for the core-correlation neglected under the frozen-core approximation, the CCSD(T)/aug-cc-pCVQZ energy with all electrons correlated was computed and the difference between the energies with and without the core–electrons was determined (δCORE). A scalar relativistic correction (δREL) was obtained at the X2C–CCSD(T)/aug-cc-pCVTZ-X2C level of theory.54 The clamped-nuclei approximation was treated with the diagonal Born–Oppenheimer correction (δDBOC)55,56 performed at the ROHF/aug-cc-pVTZ level of theory. Spin–orbit coupling constants (δSO) were included for the NCO and CH3O products in order to account for the splitting of the electronic ground state.57,58 Lastly, zero-point vibrational energies (δZPVE) were obtained from the CCSD(T)-F12a/cc-pVTZ-F12 harmonic vibrational frequencies. All of these corrections were added together to obtain the relative enthalpies at 0 K using the following equation:

2. 4

Using canonical transition state theory,59,60 the rate constants were computed over a wide range of temperatures

2. 5

where QTS(T) and QR(T) are the partition functions of the transition state and reactants, respectively, and ΔH⧧ is the reaction barrier height from eq 4. The transmission coefficient, κ(T), was determined with an asymmetric Eckart potential barrier using the relative enthalpies of the prereactive complex, transition state, and products for each reaction, and the imaginary harmonic vibrational frequency corresponding to the reaction mode of the transition state.61

Table 1. Representative Incremental Focal Point Table for the Products of the C2H + HNCO → C2H2 + NCO Reaction Relative to the Reactants (kcal mol–1)a.

basis set HF +δMP2 +δCCSD +δ(T) +δT +δ(Q) net
aug-cc-pVDZ –23.32 +4.64 –4.01 +0.30 –0.10 –0.05 [−22.54]
aug-cc-pVTZ –23.54 +4.52 –4.20 +0.27 [−0.10] [−0.05] [−23.09]
aug-cc-pVQZ –23.34 +4.76 –4.11 +0.26 [−0.10] [−0.05] [−22.58]
aug-cc-pV5Z –23.33 +4.80 –4.08 +0.25 [−0.10] [−0.05] [−22.51]
CBS limit [−23.34] [+4.83] [−4.05] [+0.25] [−0.10] [−0.05] [−22.46]
Open in a new tab
a

Additional focal point tables can be found in the Supporting Information. δ denotes the change in the relative energy with respect to the previous level of theory. The numbers in [ ] are obtained by the extrapolation schemes found in the Theoretical Methods section.

Bowman and co-workers demonstrated that an Eckart tunneling model provides accurate kinetics in agreement with experimental results for hydrogen abstraction reactions involving the ethynyl radical;15 therefore, Eckart tunneling was used here. Additionally, other studies have achieved past success in accurately describing the tunneling of hydrogen transfer reactions at moderate to high temperatures using Eckart tunneling.62−64 In this work, pressure dependence will not be taken into account.

3. Results and Discussion

3.1. Energies and Geometries

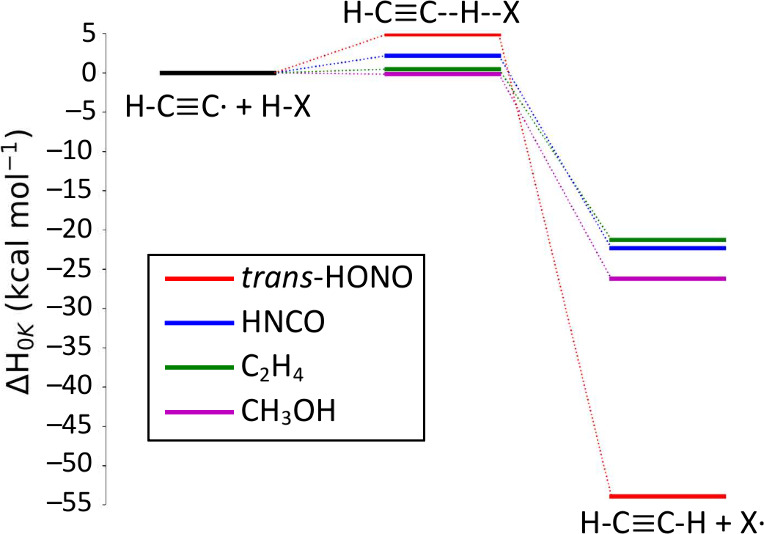
Table 2 shows the reaction enthalpies at 0 K for the C2H hydrogen-abstractions involving HNCO, trans-HONO, C2H4, and CH3OH (reaction R1). The last column of Table 2 demonstrates excellent agreement between our computed reaction enthalpies and the reaction enthalpies reported in the Active Thermochemical Tables (ATcT) (Version 1.122r) of Ruscic and co-workers.65,66 The mean absolute error (MAE) between the two is 0.19 kcal mol–1. The root-mean-square error (RMSE) is 0.25 kcal mol–1. The largest deviation is found for the CH3OH + C2H → CH3O + C2H2 reaction with a difference of 0.48 kcal mol–1.

Table 2. Enthalpies at 0 K (ΔH0 K in kcal mol–1 for Products Relative to Reactants (C2H + HX → C2H2 + X)a.

donor CBSb δT(Q) δCORE δREL δDBOC δZPVE δSO total ATcTc Δ|E|d
HNCO –22.31 –0.15 0.08 –0.16 0.00 0.63 –0.14 –22.05 –22.02 0.03
trans-HONO –53.93 0.15 –0.47 0.02 0.00 0.53   –53.69 –53.82 0.13
C2H4 –21.25 0.13 –0.17 –0.02 –0.04 –1.24   –22.58 –22.68 0.10
CH3OHe –26.22 0.21 –0.20 –0.14 0.47f –1.49 –0.41 –28.25 –27.77 0.48
Open in a new tab
a

δ denotes various corrections. See the Theoretical Methods section for details.

b

CBS denotes the CCSD(T)/CBS relative energy.

c

Enthalpies obtained from the ATcT.65,66

d

Absolute value of the difference between total and ATcT.

e

CH3OH + C2H → CH3O + C2H2.

f

DBOC correction not included in the final total.

Figure 1 depicts the geometries of the hydrogen abstraction transition states found for each reaction studied in this research. Table 3 shows the reaction enthalpies of the CCSD(T)-F12a/cc-pVTZ-F12 transition states relative to their respective reactants. According to the results in Table 2, the energetics of the products are expected to be accurate within 0.48 kcal mol–1; however, the relative energetics of the transition states are highly dependent on the employed level of theory. Because of this, we expect the barrier heights to be reliable well within chemical accuracy (1 kcal mol–1). Of the corrections listed in Table 3, δZPVE is the largest suggesting that obtaining accurate barrier heights not only requires accurate electronic energies, but also reliable vibrational frequencies. Additionally, δREL is small, but not negligible for these reactions which involve first and second row atoms. The diagonal Born–Oppenheimer corrections for the reaction enthalpies and transition state barriers were consistently small (≤0.2 kcal mol–1) for almost all of the reactions. However, for the CH3OH + C2H → CH3O + C2H2 reaction where δDBOC is computed as 0.47 kcal mol–1. Bartlett and co-workers proposed that δDBOC can be utilized as a diagnostic for the presence of a nearby conical intersection.67 Typically for most well-behaved systems without a nearby conical intersection, the δDBOC is small, but this is not true in the proximity of a conical intersection. The EDBOC becomes nonintegrable over domains that include a conical intersection because the second-derivative of the T̂n operator blows up, as shown by Meek and Levine.68 It is recommended that DBOC not be included when employing mixed quantum-classical methods and approximate quantum dynamical methods. Therefore, the δDBOC was not included in determining the final reaction enthalpy and transition state barrier of the CH3OH + C2H → CH3O + C2H2 reaction.

Figure 1.

Figure 1

Open in a new tab

Qualitative geometries of C2H + HX transition states.

Table 3. Enthalpies at 0 K (ΔH0 K in kcal mol–1 for Transition States Relative to Reactants (C2H + HX → C2H2 + X)a.

donor CBSb δT(Q) δCORE δREL δDBOC δZPVE total
HNCO 4.06 –0.19 0.14 –0.14 0.23 –1.90 2.19
trans-HONO 6.38 –0.96 0.03 0.23 –0.01 –0.76 4.91
C2H4 1.74 –0.11 –0.01 –0.01 0.02 –1.17 0.47
CH3OHc 1.49 –0.28 0.01 –0.21 0.11d –1.28 –0.27
Open in a new tab
a

δ denotes various corrections. See the Theoretical Methods section for details.

b

CBS denotes the CCSD(T)/CBS relative energy.

c

CH3OH + C2H → CH3O + C2H2.

d

DBOC correction not included in the final total.

As shown in Table 3, the C2H + CH3OH reaction has a very slightly submerged transition state barrier of −0.27 kcal mol–1, suggesting that this reaction will be rapid even at low temperatures. The C2H + HNCO and C2H + trans-HONO reactions have low barriers less than 5 kcal mol–1, meaning these reactions will likely proceed more slowly than the barrierless reaction.

Table 4 compares the reaction enthalpies (ΔrH), the barrier heights (ΔH⧧), important transition state features (shown in Figure 2), and the imaginary mode frequency (ω⧧) of the transition state of the C2H + HX, where HX = HNCO, trans-HONO, C2H4, and CH3OH (reaction R1), reactions. To better determine if these hydrogen abstraction reactions follow the Evans–Polanyi principle, the reactions have been listed in order of decreasing exothermicity (ΔrH). The Evans–Polanyi principle observes that the activation energy between two similar reactions is inversely proportional to the reaction exothermicity.69,70 The reactions studied here, in general, appear to follow the Evans–Polanyi principle; however, the C2H + trans-HONO reaction seems to be an exception. One might expect the abstraction of the hydrogen from trans-HONO to have a submerged barrier of around −2 kcal mol–1. Instead, the barrier height for trans-HONO is 4.91 kcal mol–1. The interaction between the nitrogen of trans-HONO and the terminal carbon of C2H could potentially be causing the unexpected ΔH⧧ increase.

Table 4. Reaction Enthalpies (ΔrH), Reaction Barrier Heights (ΔH⧧), and Transition State Imaginary Frequencies (ω⧧) for C2H + HX Hydrogen Abstractions at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 Level of Theory.

donor ΔrH ΔH⧧ RCH ΔRXH (%)a θ1 θ2 ω⧧
trans-HONO –53.7 4.9 1.480 17.7 176.2 133.2 1703i
CH3OHb –27.8 –0.3 1.540 6.8 174.4 134.4 794i
C2H4 –22.6 0.5 1.653 4.7 173.4 168.7 267i
HNCO –22.1 2.2 1.500 9.1 168.2 145.9 947i
Open in a new tab
a

ΔRXH = (RXH,TS – RXH,eq)/RXH,eq.

b

CH3OH + C2H → CH3O + C2H2.

Figure 2.

Figure 2

Open in a new tab

General representation of the transition state geometrical features.

To better understand the relationship between the reaction rates and how closely the transition states match the isolated reactants, Hammond’s postulate is assessed. The Hammond idea states that the geometry of the transition state resembles either the reactants or products depending on the exothermicity of the reaction, and this was also taken into consideration in this study. In order to determine how closely the transition state resembles the isolated reactants, the distance between the terminal carbon of the ethynyl radical and the hydrogen that is being abstracted in the transition state (RCH), was considered. The percent change between the XH bond length in the donor bond and the transition state (ΔRXH) was also taken into account. The transition state will more closely resemble the reactants than the products if the ΔRXH value is less than 50%. The reactions in this study do follow Hammond’s postulate. For example, the ΔRXH value of the C2H + HNCO reaction is 9.1%, and the energy difference of the reactants and transition state is 2.2 kcal mol–1 while the energy difference of the transition state and products is 24.3 kcal mol–1. Energetically, the transition state lies closer to the reactants than the products, which corresponds to the calculated ΔRXH value that is less than 50%.

3.1.1. C2H + HNCO

A previous study by Chen and Ho investigated the C2H + HNCO → C2H2 + NCO reaction at the CCSD(T)/6-311++G**//B3LYP/6-311++G** level of theory.31 They found that the reaction proceeded through a transition state barrier of 6.23 kcal mol–1 and ended with the products at −21.79 kcal mol–1 relative to the reactants.

As seen in Figure 3, the reaction pathway found in this study is qualitatively similar to that of Chen and Ho. As laid out in Table 5, our transition state barrier of 2.19 kcal mol–1 is 4.04 kcal mol–1 lower than that of Chen and Ho. However, the ending products of −22.05 kcal mol–1 relative to reactants show less than a 0.3 kcal mol–1 difference. The bond lengths of the transition state geometry are also similar to that of Chen and Ho with the largest difference being 0.14 Å for the H–C bond between HNCO and C2H. However, there is an 11.5° difference for the CNH angle in HNCO. Chen and Ho did not report rate constants for this reaction.

Figure 3.

Figure 3

Open in a new tab

Potential energy surface of the C2H + HNCO → C2H2 + NCO reaction at 0 K at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 level of theory.

Table 5. Comparison of the C2H + HNCO → C2H2 + NCO Abstraction at Different Levels of Theorya.
  ΔH⧧ ΔHr RCH RNH θCHN
Chen and Hob 6.23 –21.79 1.644 1.071 129.29
this workc 2.19 –22.05 1.500 1.096 117.77
Open in a new tab
a

Enthalpies are given in kcal mol–1; bond distances are given in Å; and angles are given in degrees.

b

CCSD(T)/6-31++G**//B3LYP/6-31++G**.

c

CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12.

3.1.2. C2H + HONO

Both the trans and cis isomers of HONO were considered for this study; however, only the reaction pathway involving the trans isomer was characterized at the highest level of theory implemented in this study. The study that investigated the CN + HONO reaction found that the trans isomer is 0.45 kcal mol–1 lower in energy than the cis isomer with an isomerization barrier of 9.46 kcal mol–1 at the CCSD(T)/aug-cc-pVTZ//UMP2/6-311++G(d,p) level of theory.34

There have been no previously reported theoretical studies or experimental measurements involving the C2H + HONO → C2H2 + NO2 reaction. As shown in Figure 4, the reaction pathway involving the trans isomer found in this work at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 level of theory proceeds through a transition state barrier of 4.91 kcal mol–1. Due to the stabilities of the ethylene and nitrogen dioxide, the energy of the products is −53.69 kcal mol–1 relative to the reactants. In Figure 5, the reaction pathway involving the cis isomer found in this work at the CCSD(T)-F12a/cc-pVTZ-F12//MP2/aug-cc-pVTZ level of theory proceeds through a prereactive complex at −0.91 kcal mol–1 followed by a submerged transition state barrier of −3.62 kcal mol–1 and ends with the products at −56.17 kcal mol–1 relative to the reactants.

Figure 4.

Figure 4

Open in a new tab

Potential energy surface of the C2H + trans-HONO → C2H2 + NO2 reaction at 0 K at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 level of theory.

Figure 5.

Figure 5

Open in a new tab

Potential energy surface of the C2H + cis-HONO → C2H2 + NO2 reaction at 0 K at the CCSD(T)-F12a/cc-pVTZ-F12//MP2/aug-cc-pVTZ level of theory.

3.1.3. C2H + CH3OH

There have been no previously reported experimental measurements involving the C2H + CH3OH → C2H2 + CH3O/CH2OH reactions. One previous study by Tri and Huê investigated the C2H + CH3OH reaction mechanism theoretically and determined the potential energy surfaces of 12 different reaction pathways.36 They determined that the pathways that formed C2H2 + CH3O and C2H2 + CH2OH were the most favorable with submerged barrier heights of −4.01 and −0.14 kcal mol–1, and ended with the products at −32.32 and −38.45 kcal mol–1, respectively, at the B3LYP/6-311++G(3df,2p)//B3LYP/6-311++G(d,p) level of theory. For the C2H + CH3OH → C2H2 + CH3O reaction, they were able to locate a prereactive complex at −4.06 kcal mol–1, but they did not report a prereactive complex for the C2H + CH3OH → C2H2 + CH2OH reaction.

As shown in Figure 6, the C2H + CH3OH → C2H2 + CH3O reaction proceeds through a prereactive complex at −6.45 kcal mol–1 and then through a very slightly submerged transition barrier of −0.27 kcal mol–1, and ends in the products at −28.25 kcal mol–1 relative to the reactants, which is qualitatively in agreement to that of Tri and Huê. The prereactive complex energy was determined at the CCSD(T)-F12a/cc-pVTZ-F12 level of theory with no additional corrections.

Figure 6.

Figure 6

Open in a new tab

Potential energy surface of the C2H + CH3OH → C2H2 + CH3O reaction at 0 K at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 level of theory. The asterisk (∗) denotes the energy is at the CCSD(T)-F12a/cc-pVTZ-F12 level of theory with no additional corrections.

Additionally, the C2H + CH3OH → C2H2 + CH2OH reaction was also investigated for this study; however, no direct transition state was found for CH2OH production at our highest-level of theory. The reported transition state geometry of Tri and Huê appears to be in Cs symmetry (Figure 7a) with a Ha–O–C-Hb dihedral angle of 180.0°. Calculations at the MP2/aug-cc-pVTZ level of theory determined a transition state with a Ha–O–C-Hb dihedral angle of 45.9° (Figure 7b). This floppy dihedral angle made this transition state difficult to optimize and locate.

Figure 7.

Figure 7

Open in a new tab

Qualitative geometries of C2H + CH3OH methyl abstraction transition state. Bond distances are given in Å, and angles are given in degrees.

As shown in Figure 8, the C2H + CH3OH → C2H2 + CH2OH reaction pathway characterized at the CCSD(T)-F12a/cc-pVTZ-F12//MP2/aug-cc-pVTZ level of theory proceeds through a prereactive complex at −1.64 kcal mol–1 followed by a submerged transition state barrier of −2.58 kcal mol–1 and ends with the products at −37.63 kcal mol–1 relative to the reactants. MP2/aug-cc-pVTZ gives an imaginary mode of 32i for the prereactive complex, but we believe this mode is an artifact of the level of theory and will likely disappear at a more rigorous level of theory. In terms of chemical reactivity, it appears this reaction pathway where the hydrogen is abstracted from the methyl group will likely prevail because it has a lower barrier height compared to the hydrogen being abstracted from the hydroxyl group. However, Tri and Huê report that the reaction pathway where the hydrogen is abstracted from the hydroxyl group has a lower transition state barrier; therefore, it would be beneficial to further study this reaction pathway in a future study.

Figure 8.

Figure 8

Open in a new tab

Potential energy surface of the C2H + CH3OH → C2H2 + CH2OH reaction at 0 K at the CCSD(T)-F12a/cc-pVTZ-F12//MP2/aug-cc-pVTZ level of theory.

3.1.4. C2H + C2H4

A previous study by Temelso and co-workers studied the C2H + C2H4 → C2H2 + C2H3 reaction with the B3LYP, BHLYP, MP2, and CCSD(T) methods in conjunction with the cc-pVXZ (where X = D, T, Q) basis sets.71 However, CCSD(T)/cc-pVDZ was the highest level of theory reported for the barrier height. They found that the reaction proceeds through a transition barrier of 1.7 kcal mol–1, and ends in the products at −19.5 kcal mol–1 at the CCSD(T)/cc-pVDZ level of theory using an ROHF reference. They also calculated the ΔH(0 K) at the CCSD(T)/cc-pVTZ level of theory and determined it to be −22.6 kcal mol–1, which is in excellent agreement with our results.

As shown in Figure 9, the reaction pathway characterized in this study is qualitatively similar to that of Temelso and co-workers. Our transition state barrier of 0.47 kcal mol–1 is 1.23 kcal mol–1 lower than that of Temelso and co-workers, but their ending product energy of −22.6 kcal mol–1 relative to reactants at the CCSD(T)/cc-pVTZ level of theory is in excellent agreement with our results. The transition state geometries are quite similar as shown in Table 6, with the largest difference being the CHC angle. Temelso and co-workers report a linear angle while we predict a 168.7 degree angle. Rate constants were not reported for this reaction by Temelso and co-workers.

Figure 9.

Figure 9

Open in a new tab

Potential energy surface of the C2H + C2H4 → C2H2 + C2H3 reaction at 0 K at the CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12 level of theory.

Table 6. Comparison of the C2H + C2H4 → C2H2 + C2H3 Abstraction at Different Levels of Theorya.
  ΔH⧧ ΔHr RCH RCH(2) θCHC
this workb 0.5 –22.6 1.653 1.133 168.7
Temelsoc 1.7 –22.6d 1.610 1.155 180.0
Dash and Rajakumare 0.3 –21.9 1.653 1.136 172.0
Dash and Rajakumarf 2.3        
Dash and Rajakumarg –1.4 –23.0      
Open in a new tab
a

Enthalpies are given in kcal mol–1; bond distances are given in Å; and angles are given in degrees. RCH(2) is the C–H bond distance to H that is being abstracted from C2H4.

b

CCSDT(Q)/CBS//CCSD(T)-F12a/cc-pVTZ-F12.

c

CCSD(T)/cc-pVDZ with an ROHF reference.

d

CCSD(T)/cc-pVTZ with an ROHF reference.

e

M06-2X/6-31+G(d,p).

f

CCSD(T)/cc-pVTZ//M06-2X/6-31+G(d,p).

g

G3(MP2)//M06-2X/6-31+G(d,p).

Additionally, Dash and Rajakumar studied the C2H + C2H4 → C2H2 + C2H3 reaction and computed the CCSD(T)/cc-pVTZ and G3(MP2) electronic energies at each stationary point. However, they employed the M06-2X/6-31+G(d,p) level of theory to optimize the geometries and determine the harmonic vibrational frequencies.20 The transition state barrier is quite different at each level of theory as seen in Table 6. The M06-2X/6-31+G(d,p) pathway is in good agreement with our results, but the CCSD(T)/cc-pVTZ//M06-2X/6-31+G(d,p) transition state barrier of 2.25 kcal mol–1 is 1.78 kcal mol–1 higher than our transition state barrier. The G3(MP2)//M06-2X/6-31+G(d,p) pathway predicts a submerged transition state barrier of −1.43 kcal mol–1. The transition state geometries are quite similar and the largest difference is the CHC angle again. Rate constants were reported by Dash and Rajakumar and will be discussed in the Kinetics section.

3.2. Kinetics

The rate constants computed in this study using the rigid-rotor harmonic oscillator approximation can be found in Table 7. The Theoretical Methods section contains the methods used for obtaining these rate constants. The abstractions from cis-HONO and CH3OH (both reactions R1 and R2) have submerged barriers, and as such the rate constants for these reaction will likely be large at all temperatures. Because of this, we have only examined the rate constants for the abstractions from HNCO, trans-HONO, and C2H4.

Table 7. Rate Constants for C2H + HX → C2H2 + X Abstractions in cm3 molecule–1 s–1.

T (K) HNCO trans-HONO C2H4
50 3.93 × 10–16 6.20 × 10–18 2.45 × 10–14
100 1.06 × 10–15 8.39 × 10–18 1.07 × 10–13
150 3.22 × 10–15 1.66 × 10–17 2.67 × 10–13
175 5.33 × 10–15 2.46 × 10–17 3.77 × 10–13
200 8.41 × 10–15 3.66 × 10–17 5.07 × 10–13
225 1.27 × 10–14 5.44 × 10–17 6.57 × 10–13
250 1.84 × 10–14 8.02 × 10–17 8.29 × 10–13
275 2.57 × 10–14 1.17 × 10–16 1.02 × 10–12
295 3.29 × 10–14 1.56 × 10–16 1.19 × 10–12
298 3.40 × 10–14 1.62 × 10–16 1.22 × 10–12
300 3.48 × 10–14 1.67 × 10–16 1.24 × 10–12
325 4.61 × 10–14 2.34 × 10–16 1.48 × 10–12
350 5.95 × 10–14 3.22 × 10–16 1.74 × 10–12
375 7.55 × 10–14 4.35 × 10–16 2.03 × 10–12
400 9.40 × 10–14 5.76 × 10–16 2.35 × 10–12
500 1.99 × 10–13 1.52 × 10–15 3.90 × 10–12
1000 1.88 × 10–12 2.58 × 10–14 2.10 × 10–11
1500 6.78 × 10–12 1.17 × 10–13 6.03 × 10–11
2000 1.66 × 10–11 3.23 × 10–13 1.29 × 10–10
3000 5.68 × 10–11 1.25 × 10–12 3.82 × 10–10
4000 1.32 × 10–10 3.10 × 10–12 8.19 × 10–10
5000 2.51 × 10–10 6.10 × 10–12 1.47 × 10–9
Open in a new tab

Quantitatively accurate kinetic models require highly accurate barrier heights of reaction. This makes the rate constants highly dependent on the calculated barrier heights. Additionally, the reaction barriers are low, therefore, variational effects are likely to be important which could be beneficial to explore in a future study.

3.2.1. C2H + C2H4

The computed rate constants from this study for the C2H + C2H4 hydrogen abstraction reaction are plotted in Figure 10 (solid red line). Additionally, the canonical variational transition state theory (CVT) theoretical rate constants of Dash and Rajakumar, as well as various experimental rate constants have been included. The rate constants of Dash and Rajakumar were obtained from the sum of the individual rate coefficients associated with abstraction (C2H + C2H4 → C2H2 + C2H3) and addition (C2H + C2H4 → C2H4CCH) channels. The sum of the individual rate coefficients at the G3(MP2)//M06-2X/6-31+G(d,p) and CCSD(T)/cc-pVTZ//M06-2X/6-31+G(d,p) levels of theory are given by the dashed purple line and dashed pink line, respectively. The rate constants for only the abstraction channel by Dash and Rajakumar at the CCSD(T)/cc-pVTZ//M06-2X/6-31+G(d,p) level of theory are given by the red dotted line. Our computed rate constants for the abstraction channel are in good agreement with theirs at the CCSD(T)/cc-pVTZ//M06-2X/6-31+G(d,p) level of theory. Dash and Rajakumar observed a strong negative temperature dependence for their computed rate constants, and the hydrogen abstraction contribution to the total rate constant is negligible below 250 K. Above 1000 K, the abstraction and addition reactions are in competition with each other. However, this competition is outside of the scope of the present study but it could be beneficial to explore the effects in the future. A negative temperature dependence was also reported in earlier experimental studies, but not to the same degree as that of Dash and Rajakumar. The experiments were performed using supersonic expansion methods. Opansky and Leone used transient infrared laser absorption spectroscopy,9 Chastaing et. al used CRESU (laval nozzle expansion),72 and Vakhtin et al. used pulsed nozzle expansion methods.73

Figure 10.

Figure 10

Open in a new tab

Experimental and theoretical rate constants for the C2H + C2H4 → C2H2 + C2H3 reaction. Theoretical rate constants are illustrated as solid curves and experimental rate constants are given as points.9,18,20,72,73

4. Conclusion

The energetics of ethynyl radical hydrogen abstraction reactions involving HNCO, trans-HONO, cis-HONO, C2H4, and CH3OH have been determined using highly accurate ab initio methods. Subchemical accuracy was achieved through various additive energy corrections, and shows excellent agreement with the available Active Thermochemical Table values. Additionally, accurate transition state barriers have been determined for the reactions involving HNCO, trans-HONO, C2H4, and CH3OH (reaction R1) in this study. The reaction pathways involving cis-HONO and CH3OH (reaction R2) have been determined at the CCSD(T)-F12a/cc-pVTZ-F12//MP2/aug-cc-pVTZ level of theroy. The reactions with CH3OH (reactions R1 and R2) and cis-HONO have submerged barriers below the relative enthalpies of the reactants. Abstractions of trans-HONO, HNCO, and C2H4 have barriers between 0.5 and 5.0 kcal mol–1. The reactions appear to follow the Evans–Polanyi principle and a strong correlation between the barrier height and reaction enthalpy was seen. One exception to the Evans–Polanyi principle was found with the C2H + trans-HONO reaction, which is believed to be due to the interaction between the nitrogen in trans-HONO and the terminal carbon of the ethynyl radical. This interaction raises the barrier height of the transition state to almost 5 kcal mol–1.

Reliable kinetics were obtained for a subset of the above reactions implementing an Eckart tunnelling model. The computed rate constants for the C2H + C2H4 → C2H2 + C2H3 reaction are in good agreement with those computed by Dash and Rajakumar. However, there appears to be a potential competition between the abstraction and addition channels of this reaction which could explain the disagreement between the computed rate constants and experiment. The kinetics of the reactions with trans-HONO and HNCO have not yet been explored, so the results presented in this study may aid in future experimental studies.

Acknowledgments

The authors acknowledge support from the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Division of Chemistry, Computational and Theoretical Chemistry (CTC) Program under Contract DE-SC0018412. This material is based on work supported by the National Science Foundation Graduate Research Fellowship under Grant 1842396.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsearthspacechem.4c00040.

  • Cartesian coordinates, harmonic vibrational frequencies, rotational constants, and wave function diagnostics (PDF)

The authors declare no competing financial interest.

Supplementary Material

sp4c00040_si_002.pdf (742.2KB, pdf)

References

  1. Lindstedt R. P.; Skevis G. Chemistry of Acetylene Flames. Combust. Sci. Technol. 1997, 125, 73–137. 10.1080/00102209708935656. [DOI] [Google Scholar]
  2. Ceursters B.; Nguyen H. M. T.; Nguyen M. T.; Peeters J.; Vereecken L. The reaction of C2H radicals with C2H6: Absolute rate coefficient measurements for T = 295–800 K, and quantum chemical study of the molecular mechanism. Phys. Chem. Chem. Phys. 2001, 3, 3070–3074. 10.1039/b103415b. [DOI] [Google Scholar]
  3. Yung Y. L.; Allen M.; Pinto J. P. Photochemistry of the atmosphere of Titan: Comparison between model and observations. Astrophys. J., Suppl. Ser. 1984, 55, 465–506. 10.1086/190963. [DOI] [PubMed] [Google Scholar]
  4. Gladstone G. R.; Allen M.; Yung Y. L. Hydrocarbon Photochemistry in the Upper Atmosphere of Jupiter. Icarus 1996, 119, 1–52. 10.1006/icar.1996.0001. [DOI] [PubMed] [Google Scholar]
  5. Wootten A.; Bozyan E. P.; Garrett D. B.; Loren R. B.; Snell R. L. Detection of C2H in cold dark clouds. Astrophys. J. 1980, 239, 844–854. 10.1086/158168. [DOI] [Google Scholar]
  6. Glassgold A. E.; Lucas R.; Omont A. Molecular ions in the circumstellar envelope of IRC+10216. Astron. Astrophys. 1986, 157, 35–48. [Google Scholar]
  7. Cherchneff I.; Glassgold A. E. The formation of carbon chain molecules in IRC+10216. Astrophys. J. Lett. 1993, 419, L41–L44. 10.1086/187132. [DOI] [Google Scholar]
  8. Beuther H.; Semenov D.; Henning T.; Linz H. Ethynyl (C2H) in massive star formation: Tracing the initial conditions?. Astrophys. J. Lett. 2008, 675, L33–L36. 10.1086/533412. [DOI] [Google Scholar]
  9. Opansky B. J.; Leone S. R. Rate coefficients of C2H with C2H4, C2H6, and H2 from 150 to 359 K. J. Phys. Chem. 1996, 100, 19904–19910. 10.1021/jp9619604. [DOI] [Google Scholar]
  10. Kiefer J. H.; Von Drasek W. A.; Von Drasek W. A. The mechanism of the homogeneous pyrolysis of acetylene. Int. J. Chem. Kinet. 1990, 22, 747–786. 10.1002/kin.550220710. [DOI] [Google Scholar]
  11. Boullart W.; Devriendt K.; Borms R.; Peeters J. Identification of the Sequence CH(2Π) + C2H2 → C3H2 + H (and C3H + H2) Followed by C3H2 + O → C2H + HCO (or H + CO) as C2H Source in C2H2/O/H Atomic Flames. J. Phys. Chem. 1996, 100, 998–1007. 10.1021/jp951995o. [DOI] [Google Scholar]
  12. Hansen N.; Klippenstein S. J.; Westmoreland P. R.; Kasper T.; Kohse-Höinghaus K.; Wang J.; Cool T. A combined ab initio and photoionization mass spectrometric study of polyynes in fuel-rich flames. Phys. Chem. Chem. Phys. 2008, 10, 366–374. 10.1039/B711578D. [DOI] [PubMed] [Google Scholar]
  13. Sun Y.-L.; Huang W.-J.; Lee S.-H. Formation of Polyynes C4H2, C6H2, C8H2, and C10H2 from Reactions of C2H, C4H, C6H, and C8H Radicals with C2H2. J. Phys. Chem. Lett. 2015, 6, 4117–4122. 10.1021/acs.jpclett.5b01910. [DOI] [PubMed] [Google Scholar]
  14. Nguyen H. M. T.; Chandra A. K.; Carl S. A.; Nguyen M. T. Quantum chemical study of hydrogen abstraction reactions of the ethynyl radical with hydrogen compounds (C2H + HX). J. Mol. Struct.: THEOCHEM 2005, 732, 219–224. 10.1016/j.theochem.2005.07.023. [DOI] [Google Scholar]
  15. Bowman M. C.; Burke A. D.; Turney J. M.; Schaefer H. F. Conclusive determination of ethynyl radical hydrogen abstraction energetics and kinetics. Mol. Phys. 2020, 118, e1769214. 10.1080/00268976.2020.1769214. [DOI] [Google Scholar]
  16. Tarr A. M.; Strausz O. P.; Gunning H. E. Reactions of the ethynyl radical. Part 1.—Hydrogen abstraction from alkanes. Trans. Faraday Soc. 1965, 61, 1946–1959. 10.1039/TF9656101946. [DOI] [Google Scholar]
  17. Laufer A. H. Reactions of ethynyl radicals. Rate constants with CH4, C2H6, and C2D6. J. Phys. Chem. 1981, 85, 3828–3831. 10.1021/j150625a023. [DOI] [Google Scholar]
  18. Lander D. R.; Unfried K. G.; Glass G. P.; Curl R. F. Rate constant measurements of C2H with CH4, C2H6, C2H4, D2, and CO. J. Phys. Chem. 1990, 94, 7759–7763. 10.1021/j100383a003. [DOI] [Google Scholar]
  19. Park J.; Hershberger J. F. Kinetics of NCO + hydrocarbon reactions. Chem. Phys. Lett. 1994, 218, 537–543. 10.1016/0009-2614(94)00037-9. [DOI] [Google Scholar]
  20. Dash M. R.; Rajakumar B. Abstraction and addition kinetics of C2H radicals with CH4, C2H6, C3H8, C2H4, and C3H6: CVT/SCT/ISPE and hybrid meta-DFT methods. Phys. Chem. Chem. Phys. 2015, 17, 3142–3156. 10.1039/C4CP04677C. [DOI] [PubMed] [Google Scholar]
  21. Peeters J.; Ceursters B.; Nguyen H. M. T.; Nguyen M. T. The reaction of C2H with H2: Absolute rate coefficient measurements and ab initio study. J. Chem. Phys. 2002, 116, 3700–3709. 10.1063/1.1436481. [DOI] [Google Scholar]
  22. Peeters J.; Van Look H.; Ceursters B. Absolute Rate Coefficients of the Reactions of C2H with NO and H2 between 295 and 440 K. J. Phys. Chem. 1996, 100, 15124–15129. 10.1021/jp960201i. [DOI] [Google Scholar]
  23. Van Look H.; Peeters J. Rate Coefficients of the Reactions of C2H with O2, C2H2, and H2O between 295 and 450 K. J. Phys. Chem. 1995, 99, 16284–16289. 10.1021/j100044a013. [DOI] [Google Scholar]
  24. Ceursters B.; Minh Thi Nguyen H.; Peeters J.; Nguyen M. T. Experimental and theoretical study of the reaction of the ethynyl radical with acetylene (HCC+HCCH). Chem. Phys. 2000, 262, 243–252. 10.1016/S0301-0104(00)00337-2. [DOI] [Google Scholar]
  25. Sengupta D.; Peeters J.; Nguyen M. T. Theoretical studies on C2H+NO reactions: Mechanism for HCN+CO and HCO+CN formation. Chem. Phys. Lett. 1998, 283, 91–96. 10.1016/S0009-2614(97)01298-0. [DOI] [Google Scholar]
  26. Carl S. A.; Nguyen H. M. T.; Nguyen M. T.; Peeters J. An experimental and theoretical study of the reaction of ethynyl radicals with nitrogen dioxide (HC≡C+NO2). J. Chem. Phys. 2003, 118, 10996–11008. 10.1063/1.1573192. [DOI] [Google Scholar]
  27. Ceursters B.; Thi Nguyen H. M.; Peeters J.; Tho Nguyen M. Experimental and theoretical study of the gas phase reaction of ethynyl radical with methane (HC≡C+CH4). Chem. Phys. Lett. 2000, 329, 412–420. 10.1016/S0009-2614(00)01033-2. [DOI] [Google Scholar]
  28. Carl S. A.; Elsamra R. M. I.; Kulkarni R. M.; Nguyen H. M. T.; Peeters J. No Barrier for the Gas-Phase C2H + NH3 Reaction. J. Phys. Chem. A 2004, 108, 3695–3698. 10.1021/jp0377580. [DOI] [Google Scholar]
  29. Nguyen H. M. T.; Carl S. A.; Peeters J.; Nguyen M. T. Theoretical study of the reaction of the ethynyl radical with ammonia (C2H + NH3): Hydrogen abstraction versus condensation. Phys. Chem. Chem. Phys. 2004, 6, 4111–4117. 10.1039/b404337e. [DOI] [Google Scholar]
  30. Sumathi R.; Peeters J.; Nguyen M. T. Theoretical studies on the C2H+O2 reaction: Mechanism for HCO+CO, HCCO+O and CH+CO2 formation. Chem. Phys. Lett. 1998, 287, 109–118. 10.1016/S0009-2614(98)00148-1. [DOI] [Google Scholar]
  31. Chen H.-T.; Ho J.-J. Theoretical Study of Reaction Mechanisms for NCX (X = O, S) + C2H2. J. Phys. Chem. A 2003, 107, 7004–7012. 10.1021/jp022613z. [DOI] [Google Scholar]
  32. Rim K. T.; Hershberger J. F. Temperature Dependence of the Product Branching Ratio of the CN + O2 Reaction. J. Phys. Chem. A 1999, 103, 3721–3725. 10.1021/jp990373q. [DOI] [Google Scholar]
  33. Coutens A.; Ligterink N. F. W.; Loison J.-C.; Wakelam V.; Calcutt H.; Drozdovskaya M. N.; Jørgensen J. K.; Müller H. S. P.; van Dishoeck E. F.; Wampfler S. F. The ALMA-PILS survey: First detection of nitrous acid (HONO) in the interstellar medium. Astron. Astrophys. 2019, 623, L13. 10.1051/0004-6361/201935040. [DOI] [Google Scholar]
  34. Wang D.-Q.; Li J.-L.; Huang X.-R.; Geng C.-Y.; Sun C.-C. Diatomic radical–molecule reactions CN+HONO: Mechanistic study. J. Mol. Struct.: THEOCHEM 2008, 857, 20–26. 10.1016/j.theochem.2008.01.030. [DOI] [Google Scholar]
  35. Jodkowski J. T.; Rayez M.-T.; Rayez J.-C.; Bérces T.; Dóbé S. Theoretical Study of the Kinetics of the Hydrogen Abstraction from Methanol. 2. Reaction of Methanol with Chlorine and Bromine Atoms. J. Phys. Chem. A 1998, 102, 9230–9243. 10.1021/jp980846d. [DOI] [Google Scholar]
  36. Tri T. Q.; Huê N. T. M. Mechanism of reaction between ethynyl radical with methanol. Tap Chi Hoa Hoc 2011, 49, 286–290. [Google Scholar]
  37. Knizia G.; Adler T. B.; Werner H.-J. Simplified CCSD(T)-F12 methods: Theory and benchmarks. J. Chem. Phys. 2009, 130, 054104. 10.1063/1.3054300. [DOI] [PubMed] [Google Scholar]
  38. Peterson K. A.; Adler T. B.; Werner H.-J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 2008, 128, 084102. 10.1063/1.2831537. [DOI] [PubMed] [Google Scholar]
  39. Hill J. G.; Peterson K. A. Correlation consistent basis sets for explicitly correlated wavefunctions: Valence and core–valence basis sets for Li, Be, Na, and Mg. Phys. Chem. Chem. Phys. 2010, 12, 10460–10468. 10.1039/c0cp00020e. [DOI] [PubMed] [Google Scholar]
  40. Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M. Molpro: A general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. 10.1002/wcms.82. [DOI] [Google Scholar]
  41. Møller C.; Plesset M. S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
  42. Dunning T. H.; Peterson K. A.; Wilson A. K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 2001, 114, 9244–9253. 10.1063/1.1367373. [DOI] [Google Scholar]
  43. Smith D. G. A.; Burns L. A.; Simmonett A. C.; Parrish R. M.; Schieber M. C.; Galvelis R.; Kraus P.; Kruse H.; Di Remigio R.; Alenaizan A.; James A. M.; Lehtola S.; Misiewicz J. P.; Scheurer M.; Shaw R. A.; Schriber J. B.; Xie Y.; Glick Z. L.; Sirianni D. A.; O’Brien J. S.; Waldrop J. M.; Kumar A.; Hohenstein E. G.; Pritchard B. P.; Brooks B. R.; Schaefer H. F.; Sokolov A. Y.; Patkowski K.; DePrince A. E.; Bozkaya U.; King R. A.; Evangelista F. A.; Turney J. M.; Crawford T. D.; Sherrill C. D. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. 10.1063/5.0006002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. East A. L. L.; Allen W. D. The heat of formation of NCO. J. Chem. Phys. 1993, 99, 4638–4650. 10.1063/1.466062. [DOI] [Google Scholar]
  45. Császár A. G.; Allen W. D.; Schaefer H. F. In pursuit of the ab initio limit for conformational energy prototypes. J. Chem. Phys. 1998, 108, 9751–9764. 10.1063/1.476449. [DOI] [Google Scholar]
  46. Bomble Y. J.; Stanton J. F.; Kállay M.; Gauss J. Coupled-cluster methods including noniterative corrections for quadruple excitations. J. Chem. Phys. 2005, 123, 054101. 10.1063/1.1950567. [DOI] [PubMed] [Google Scholar]
  47. Woon D. E.; Dunning T. H. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. 10.1063/1.464303. [DOI] [Google Scholar]
  48. Bartlett R. J. Many-Body Perturbation Theory and Coupled Cluster Theory for Electron Correlation in Molecules. Annu. Rev. Phys. Chem. 1981, 32, 359–401. 10.1146/annurev.pc.32.100181.002043. [DOI] [Google Scholar]
  49. Purvis G. D.; Bartlett R. J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. 10.1063/1.443164. [DOI] [Google Scholar]
  50. Noga J.; Bartlett R. J. The full CCSDT model for molecular electronic structure. J. Chem. Phys. 1987, 86, 7041–7050. 10.1063/1.452353. [DOI] [Google Scholar]
  51. Kállay M.; Nagy P. R.; Mester D.; Rolik Z.; Samu G.; Csontos J.; Csóka J.; Szabó P. B.; Gyevi-Nagy L.; Hégely B.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Ganyecz Á. The MRCC program system: Accurate quantum chemistry from water to proteins. J. Chem. Phys. 2020, 152, 074107. 10.1063/1.5142048. [DOI] [PubMed] [Google Scholar]
  52. Feller D. The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water. J. Chem. Phys. 1993, 98, 7059–7071. 10.1063/1.464749. [DOI] [Google Scholar]
  53. Helgaker T.; Klopper W.; Koch H.; Noga J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. 10.1063/1.473863. [DOI] [Google Scholar]
  54. Cheng L.; Gauss J. Analytic energy gradients for the spin-free exact two-component theory using an exact block diagonalization for the one-electron Dirac Hamiltonian. J. Chem. Phys. 2011, 135, 084114. 10.1063/1.3624397. [DOI] [PubMed] [Google Scholar]
  55. Sellers H.; Pulay P. The adiabatic correction to molecular potential surfaces in the SCF approximation. Chem. Phys. Lett. 1984, 103, 463–465. 10.1016/0009-2614(84)85277-X. [DOI] [Google Scholar]
  56. Handy N. C.; Yamaguchi Y.; Schaefer H. F. The diagonal correction to the Born–Oppenheimer approximation: Its effect on the singlet–triplet splitting of CH2 and other molecular effects. J. Chem. Phys. 1986, 84, 4481–4484. 10.1063/1.450020. [DOI] [Google Scholar]
  57. Bolman P. S. H.; Brown J. M.; Carrington A.; Kopp I.; Ramsay D. A. A re-investigation of the à 2Σ+ – X̃ 2 Πi band system of NCO. Proc. R. Soc. London A 1975, 343, 17–44. 10.1098/rspa.1975.0050. [DOI] [Google Scholar]
  58. Cooper D. L. Spin–orbit coupling constants for the 2E states of CH3O and CH3F+. J. Chem. Phys. 1982, 76, 2765–2766. 10.1063/1.443228. [DOI] [Google Scholar]
  59. Eyring H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
  60. Truhlar D. G.; Garrett B. C.; Klippenstein S. J. Current Status of Transition-State Theory. J. Phys. Chem. 1996, 100, 12771–12800. 10.1021/jp953748q. [DOI] [Google Scholar]
  61. Johnston H. S.; Heicklen J. Tunnelling corrections for unsymmettical Eckart potential energy barriers. J. Phys. Chem. 1962, 66, 532–533. 10.1021/j100809a040. [DOI] [Google Scholar]
  62. Zhang F.; Dibble T. S. Impact of tunneling on hydrogen-migration of the n-propylperoxy radical. Phys. Chem. Chem. Phys. 2011, 13, 17969–17977. 10.1039/c1cp21691k. [DOI] [PubMed] [Google Scholar]
  63. Sirjean B.; Dames E.; Wang H.; Tsang W. Tunneling in Hydrogen-Transfer Isomerization of n-Alkyl Radicals. J. Phys. Chem. A 2012, 116, 319–332. 10.1021/jp209360u. [DOI] [PubMed] [Google Scholar]
  64. Sha Y.; Dibble T. S. Tunneling effect in 1,5 H-migration of a prototypical OOQOOH. Chem. Phys. Lett. 2016, 646, 153–157. 10.1016/j.cplett.2016.01.011. [DOI] [Google Scholar]
  65. Ruscic B.; Pinzon R. E.; Morton M. L.; von Laszevski G.; Bittner S. J.; Nijsure S. G.; Amin K. A.; Minkoff M.; Wagner A. F. Introduction to Active Thermochemical Tables: Several “Key” Enthalpies of Formation Revisited. J. Phys. Chem. A 2004, 108, 9979–9997. 10.1021/jp047912y. [DOI] [Google Scholar]
  66. Ruscic B.; Pinzon R. E.; von Laszewski G.; Kodeboyina D.; Burcat A.; Leahy D.; Montoy D.; Wagner A. F. Active Thermochemical Tables: Thermochemistry for the 21st century. J. Phys.: Conf. Ser. 2005, 16, 561–570. 10.1088/1742-6596/16/1/078. [DOI] [Google Scholar]
  67. Bartlett M. A.; Liang T.; Pu L.; Schaefer H. F.; Allen W. D. The multichannel n-propyl + O2 reaction surface: Definitive theory on a model hydrocarbon oxidation mechanism. J. Chem. Phys. 2018, 148, 094303. 10.1063/1.5017305. [DOI] [Google Scholar]
  68. Meek G. A.; Levine B. G. Wave function continuity and the diagonal Born-Oppenheimer correction at conical intersections. J. Chem. Phys. 2016, 144, 184109. 10.1063/1.4948786. [DOI] [PubMed] [Google Scholar]
  69. Brønsted J. N. Acid and Basic Catalysis. Chem. Rev. 1928, 5, 231–338. 10.1021/cr60019a001. [DOI] [Google Scholar]
  70. Evans M. G.; Polanyi M. Inertia and driving force of chemical reactions. Trans. Faraday Soc. 1938, 34, 11–24. 10.1039/tf9383400011. [DOI] [Google Scholar]
  71. Temelso B.; Sherrill C. D.; Merkle R. C.; Freitas R. A. High-Level ab Initio Studies of Hydrogen Abstraction from Prototype Hydrocarbon Systems. J. Phys. Chem. A 2006, 110, 11160–11173. 10.1021/jp061821e. [DOI] [PubMed] [Google Scholar]
  72. Chastaing D.; James P. L.; Sims I. R.; Smith I. W. M. Neutral-neutral reactions at the temperatures of interstellar clouds Rate coefficients for reactions of C2H radicals with O2, C2H2, C2H4 and C3H6 down to 15 K. Faraday Discuss. 1998, 109, 165–181. 10.1039/a800495a. [DOI] [Google Scholar]
  73. Vakhtin A. B.; Heard D. E.; Smith I. W.; Leone S. R. Kinetics of C2H radical reactions with ethene, propene and 1-butene measured in a pulsed Laval nozzle apparatus at T = 103 and 296 K. Chem. Phys. Lett. 2001, 348, 21–26. 10.1016/S0009-2614(01)00975-7. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

sp4c00040_si_002.pdf (742.2KB, pdf)

Articles from ACS Earth & Space Chemistry are provided here courtesy of American Chemical Society

RESOURCES