Retrospective for the Dynamic Sensorium Competition for predicting large-scale mouse primary visual cortex activity from videos

Abstract

Understanding how biological visual systems process information is challenging because of the nonlinear relationship between visual input and neuronal responses. Artificial neural networks allow computational neuroscientists to create predictive models that connect biological and machine vision. Machine learning has benefited tremendously from benchmarks that compare different model on the same task under standardized conditions. However, there was no standardized benchmark to identify state-of-the-art dynamic models of the mouse visual system. To address this gap, we established the SENSORIUM 2023 Benchmark Competition with dynamic input, featuring a new large-scale dataset from the primary visual cortex of ten mice. This dataset includes responses from 78,853 neurons to 2 hours of dynamic stimuli per neuron, together with the behavioral measurements such as running speed, pupil dilation, and eye movements. The competition ranked models in two tracks based on predictive performance for neuronal responses on a held-out test set: one focusing on predicting in-domain natural stimuli and another on out-of-distribution (OOD) stimuli to assess model generalization. As part of the NeurIPS 2023 competition track, we received more than 160 model submissions from 22 teams. Several new architectures for predictive models were proposed, and the winning teams improved the previous state-of-the-art model by 50%. Access to the dataset as well as the benchmarking infrastructure will remain online at www.sensorium-competition.net.

1. Introduction

Understanding visual system processing is a longstanding goal in neuroscience. One way to approach the problem are neural system identification approaches which make predictions of neuronal activity from stimuli or other sources quantitative and testable (reviewed in Wu et al., 2006). Various system identification methods have been used in systems neuroscience, including linear-nonlinear (LN) models (Simoncelli et al., 2004; Jones & Palmer, 1987; Heeger, 1992a,b), energy models (Adelson & Bergen, 1985), subunit models (Liu et al., 2017; Rust et al., 2005; Touryan et al., 2005; Vintch et al., 2015), Bayesian models (Walker et al., 2020; George & Hawkins, 2005; Wu et al., 2023; Bashiri et al., 2021), redundancy reduction models (Perrone & Liston, 2015), and predictive coding models (Marques et al., 2018). In recent years, deep learning models, especially convolutional neural networks (CNNs) trained on image recognition tasks (Yamins et al., 2014; Cadieu et al., 2014; Cadena et al., 2019; Pogoncheff et al., 2023) or predicting neural responses (Cadena et al., 2019; Antolík et al., 2016; Batty et al., 2017; McIntosh et al., 2016; Klindt et al., 2017; Kindel et al., 2019; Burg et al., 2021; Lurz et al., 2021; Bashiri et al., 2021; Zhang et al., 2018b; Cowley & Pillow, 2020; Ecker et al., 2018; Sinz et al., 2018; Walker et al., 2019; Franke et al., 2022; Wang et al., 2023; Fu et al., 2023; Ding et al., 2023), have significantly advanced predictive model performance. More recently, transformer-based architectures have emerged as a promising alternative (Li et al., 2023; Azabou et al., 2024; Antoniades et al., 2023).

In machine learning and beyond, standardized large-scale benchmarks foster continuous improvements in predictive models through fair and competitive comparisons (Dean et al., 2018). Within the realm of computational neuroscience, several benchmarks have been established recently. An early effort was the Berkeley Neural Prediction Challenge¹, which provided public training data and secret test set responses to evaluate models of neurons from primary visual cortex, primary auditory cortex and field L in the songbird brain. More recent efforts include Brain-Score (Schrimpf et al., 2018, 2020), Neural Latents ‘21 (Pei et al., 2021), Algonauts (Cichy et al., 2019, 2021; Gifford et al., 2023) and SENSORIUM 2022 (Willeke et al., 2022). However, with the exception of the Berkeley Neural Prediction Challenge, which is limited to 12 cells, no public benchmark existed that focused on predicting single neuron responses in the early visual system to video (spatio-temporal) stimuli.

Since we all live in a non-static world, dynamic stimuli are more relevant and our models should be able to predict neural responses over time in response to these time-varying inputs (Sinz et al., 2018; Wang et al., 2023; Batty et al., 2017; McIntosh et al., 2016; Zheng et al., 2021; Qiu et al., 2023; Hoefling et al., 2022; Vystrčilová et al., 2024). Even though recent high-throughput recording techniques have led to the release of large datasets like the MICrONS calcium imaging dataset (MICrONS Consortium et al., 2021) and Neuropixel datasets from the Allen Brain Observatory (de Vries et al., 2020; Siegle et al., 2021), the absence of a withheld test set and the corresponding benchmark infrastructure hinders a fair comparison between different models.

To fill this gap, we established the SENSORIUM 2023 competition, with the goal to compare large-scale models predicting single-neuron responses to dynamic stimuli. The NeurIPS 2023 competition received over 160 model submissions from 22 teams and resulted in new state-of-the-art predictive models that improved over the competition baseline by 50%. Moreover, these models also led to a 70% improved predictions on out-of-domain stimuli, suggesting that more predictive models on natural scenes also generalize better to other stimuli.

2. Sensorium Competition Overview

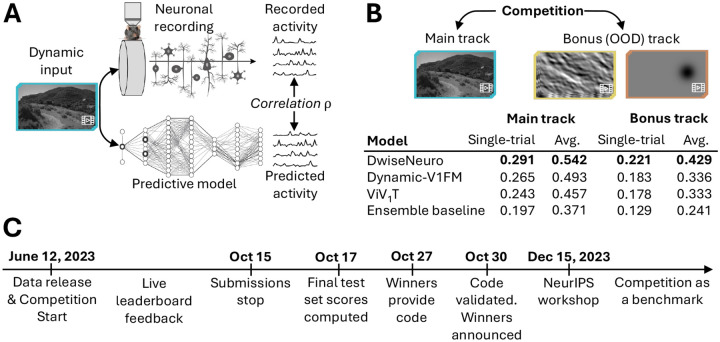
The goal of the competition was to advance models that predict neuronal responses of several thousand neurons in mouse primary visual cortex to natural and artificially generated movies. We collected and released a comprehensive dataset consisting of visual stimuli and corresponding neuronal responses for training (Section 3). This dataset included a dedicated test set, for which we released only the visual stimuli but withheld the neuronal responses to be able to compare models in a fair way (Fig. 1A). To assess model performance, participants submitted their predictions on the test set to our online benchmark website for evaluation and ranking against other submissions.² The test set consisted of two parts: a live test set and a final test set. The live test set was used during the competition to give feedback to the participants on their model’s performance via a leaderboard. The final test set was used only after the end of submissions to determine the final winners (Fig. 1C). From each team only the best-performing submission on the live test set was evaluated on the final test set. To facilitate participation from both neuroscientists and machine learning practitioners, we developed user-friendly APIs that streamline data loading, model training, and submission.³

Figure 1: A schematic illustration of the SENSORIUM competition.

A: Competition idea. We provide large-scale datasets of neuronal activity in the mice visual cortex in response to natural videos. The competition participants were tasked to find the best models to predict neuronal activity for a set of videos for which we withheld the ground truth. B: Tracks and leaderboard. C: Timeline.

The competition consisted of two tracks: The main track and the bonus track (Fig. 1B). The main track entailed predicting responses on natural movie stimuli, the same type of stimuli available for model training, but different movie instances. The bonus track required predicting out-of-distribution (OOD) stimuli for which no ground truth responses of the neurons were provided in the training set. This bonus track tests a model’s ability to generalize beyond the training data.

The competition ran from June 12 to October 15, 2023, culminating in a NeurIPS 2023 conference workshop where the winning teams presented their approaches and insights. The benchmark platform will continue to track advancements in developing models for the mouse primary visual cortex. In the following, we describe the dataset (Section 3) and evaluation metrics (Section 4), the baseline (Section 5) and winning models (Section 6) and report on the results and learnings (Section 7).

3. Dataset

We recorded⁴ neuronal activity in response to natural movie stimuli as well as several behavioral variables, which are commonly used as a proxy of modulatory effects of neuronal responses (Niell & Stryker, 2010; Reimer et al., 2014). In general terms, neural predictive models capture neural responses $\mathbf{\text{r}}\in {ℝ}^{n\times t}$ of n neurons for t timepoints as a function f_θ(x,b) of both natural movie stimuli $\mathbf{\text{x}}\in {ℝ}^{w\times h\times t}$, where w and h are video width and height, and behavioral variables $\mathbf{\text{b}}\in {ℝ}^{k\times t}$, where k = 4 is the number of behavioral variables (see below).

Movie stimuli.

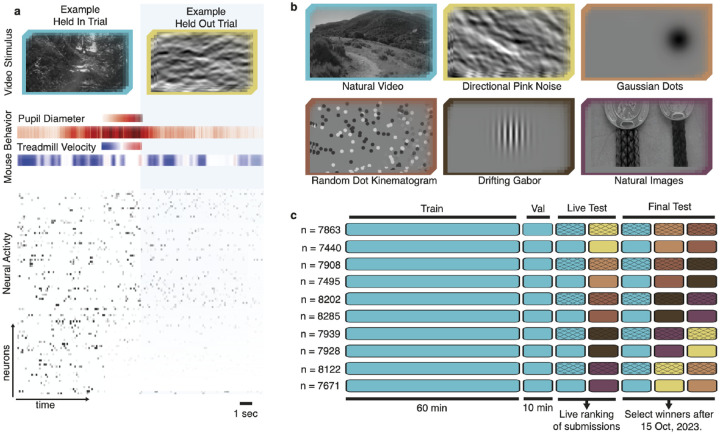
We sampled natural dynamic stimuli from cinematic movies and the Sports-1M dataset (Karpathy et al., 2014), as described by MICrONS Consortium et al. (2021). Following earlier work (Wang et al., 2023), we showed five additional stimulus types for the bonus track (Fig. 2b): directional pink noise (MICrONS Consortium et al., 2021), flashing Gaussian dots, random dot kinematograms (Morrone et al., 2000), drifting Gabors (Petkov & Subramanian, 2007), and natural images from ImageNet (Russakovsky et al., 2015; Walker et al., 2019). Stimuli were converted to grayscale and presented to mice in clips lasting ~ 8 to 11 seconds, at 30 frames per second.

Figure 2: Overview of the data.

a, Example stimulus frames, behavior (pupil position not depicted) and neural activity. b, Representative frames from natural video and five OOD stimuli. c, Stimulus composition (color) and availability for all five scans in ten animals. n is number of neurons per scan. The crossed elements were used for live and final test sets in the competition evaluation.

Neuronal responses.

Using a wide-field two-photon microscope (Sofroniew et al., 2016), we recorded the responses of excitatory neurons at 8 Hz in layers 2–5 of the right primary visual cortex in awake, head-fixed, behaving mice using calcium imaging. Neuronal activity was extracted as described previously (Wang et al., 2023) and upsampled to 30 Hz to be at the same frame rate as the visual stimuli. We also released the anatomical coordinates of the recorded neurons.

Behavioral variables.

We measured four behavioral variables: locomotion speed, recorded from a cylindrical treadmill at 100 Hz and resampled to 30 Hz, and pupil size, horizontal and vertical pupil center position, each extracted at 20 Hz from video recordings of the eye and resampled to 30 Hz.

Datasets and splits.

Our complete dataset consists of ten recordings from ten different animals, in total containing the activity of 78,853 neurons to a total of ~1200 minutes of dynamic stimuli, with ~120 minutes per recording. The recordings were collected and released explicitly for this competition. None of them had been published before. Each recording had four components (Fig. 2c):

• Training set: 60 minutes of natural movies, one repeat each (60 minutes total).

• Validation set: 1 minute of natural movies, ten repeats each (10 minutes total).

• Live test set: 1 minute of natural movies and 1 minute of OOD stimuli, ten repeats each (20 minutes total). Each OOD stimulus type is presented only in one of the five recordings.

• Final test set: 1 minute of natural movies and 2 minutes of OOD stimuli, ten repeats each (30 minutes total). Each OOD stimulus type is presented in two of the five recordings.

For the training set and validation set, the stimulus frames, neuronal responses, and behavioral variables are released for model training and evaluation by the participants, and are not included in the competition performance metrics. For the five mice included in the competition evaluation, the train and validation sets contain only natural movies but not the OOD stimuli. For the other five mice, all stimuli and responses, including test sets and OOD stimuli, were released.

Code and data availability.

The competition website and data are available at https://www.sensorium-competition.net/. Starter kit and benchmark code are available at https://github.com/ecker-lab/sensorium_2023.

4. Competition evaluation

Similar to SENSORIUM 2022, we used the correlation coefficient between predicted and measured responses to evaluate the models. Since it is bounded between −1 and 1, the correlation coefficient is straightforward to interpret. Because neuronal responses fluctuate from trial to trial, the correlation between model predictions and single-trial neuronal responses typically do not reach the upper bound of 1 even for a perfect model. This trial-to-trial variability can be reduced by averaging over repeated presentations of the same stimulus. However, in this case, also the contributions from behavioral states are reduced since these cannot be repeated easily during uncontrolled behavior. We therefore computed two metrics: single-trial correlation and correlation to average.

Single-trial correlation,

ρ_st, on the natural video final test set was used to determine competition winners for the main track. We also computed the single-trial correlation metric for each of the five OOD stimulus types in the test sets separately. The average single-trial correlation across all five final OOD test sets were used to determine the competition winner for the bonus track. Single trial correlation is sensitive to variation between individual trials and computes correlation between single-trial model output (prediction) o_ij and single-trial neuronal responses r_ij, as

$${\rho }_{\text{st}}=\text{corr}\left({\mathbf{\text{r}}}_{\text{st}},{\mathbf{\text{o}}}_{\text{st}}\right)=\frac{{\sum }_{i,j}\left(r_{ij}-\overline{r}\right)\left(o_{ij}-\overline{o}\right)}{\sqrt{{\sum }_{i,j}{\left(r_{ij}-\overline{r}\right)}^2{\sum }_{i,j}{\left(o_{ij}-\overline{o}\right)}^2}},$$ (1)

where r_ij is the i-th frame of j-th video repeat, o_ij is the corresponding prediction, which can vary between stimulus repeats as the behavioral variables are not controlled. The variable $\overline{r}$ is the average response to all the videos in the corresponding test subset across all stimuli and repeats, and $\overline{o}$ is the average prediction for the same videos and repeats . The single-trial correlation ρ_st was computed independently per neuron and then averaged across all neurons to produce the final metric.

Correlation to average,

ρ_ta, provides a more interpretable metric by accounting for trial-to-trial variability through averaging neuronal responses over repeated presentations of the same stimulus. As a result, a perfect model would have a correlation close to 1 (not exactly 1, since the average does not completely remove all trial-to-trial variability). However, correlation to average does not measure how well a model accounts for stimulus-independent variability caused by behavioral fluctuations.

We calculate ρ_ta in the same way as ρ_st, but we first average the responses and predictions per frame across all video repeats, where ${\overline{r}}_i$ is a response averaged over stimulus repeats for a fixed neuron:

$${\rho }_{\text{ta}}=\text{corr}\left({\mathbf{\text{r}}}_{\text{ta}},{\mathbf{\text{o}}}_{\text{ta}}\right)=\frac{{\sum }_i\left({\overline{r}}_i-\overline{r}\right)\left({\overline{o}}_i-\overline{o}\right)}{\sqrt{{\sum }_i{\left({\overline{r}}_i-\overline{r}\right)}^2{\sum }_i{\left({\overline{o}}_i-\overline{o}\right)}^2}},$$ (2)

The initial 50 frames of predictions and neuronal responses were excluded from all metrics calculations. This allowed a “burn-in” period for models relying on history to achieve better performance.

5. Baseline models

SENSORIUM 2023 was accompanied by three model baselines, representing the state of the art in the field at the beginning of the competition:

GRU baseline is a dynamic model with a 2D CNN core and gated recurrent unit (GRU) inspired by earlier work (Sinz et al., 2018), but with more recently developed Gaussian readouts (Lurz et al., 2021), which improves performance. Conceptually, the 2D core transforms each individual frame of the video stimulus into a feature space which is subsequently processed by a convolutional GRU across time. The Gaussian readout then learns the spatial preference of each neuron in the visual space (“receptive field”), by learning the position at which a vector from the feature space is extracted by bilinear interpolation from the four surrounding feature map locations. This latent vector is multiplied with a weight vector learned per neuron (“embedding”) and put through a rectifying nonlinearity to predict the activity of the neuron at each time step.

Factorized baseline is a dynamic model (Vystrčilová et al., 2024; Hoefling et al., 2022) with a 3D factorized convolution core and Gaussian readouts. In contrast to the GRU baseline, where the 2D CNN core does not interact with the temporal component, the factorized core learns both spatial and temporal filters in each layer.

Ensembled baseline is an ensembled version of the above factorized baseline over 14 models. Ensembling is a well-known tool to improve the model performance in benchmark competitions (Allen-Zhu & Li, 2023). As we wanted to encourage participants to focus on novel architectures and training methods beyond simple ensembling, only entries outperforming the ensembled baseline were considered candidates for competition winners.

Training.

All baseline models were trained with batch size 40 in the following way: For each of the 5 animals 8 video snippets consisting of 80 consecutive video frames starting at a random location within the video were passed and the gradient accumulated over all animals before performing optimizing step. We used early stopping with a patience of 5.

6. Results and Participation

In the four-month submission period, out of 44 registered teams, 22 teams submitted a combined total of 163 models (main track: 22 teams, 134 submissions, bonus track: 5 teams and 29 submissions). The strong baseline models were surpassed in both tracks by 48% and 70%, respectively (Table 1). Notably, the winning model – DwiseNeuro – outperformed all other models on both tracks by a fairly decent margin, and the difference seemed even stronger on the out-of-domain data than on the main track. In contrast, the runner-up solution – Dynamic-V1FM – had somewhat of an edge over the third place – ViV1T – on the main track, but both were on par on the out-of-domain data (Table 1). In the following we describe the three winning teams’ approaches.

Table 1:

Model performance of competition winners and baselines on both tracks.

	Main track		Bonus track
Model	single-trial ρst ↑	average ρta ↑	single-trial ρst ↑	average ρta ↑
DwiseNeuro	0.291	0.542	0.221	0.429
Dynamic-V1FM	0.265	0.493	0.183	0.336
ViV1T	0.243	0.457	0.178	0.333
Ensemble baseline	0.197	0.371	0.129	0.241
Factorized baseline	0.164	0.321	0.121	0.223
GRU baseline	0.106	0.207	0.059	0.106

6.1. Place 1: DwiseNeuro

Architecture.

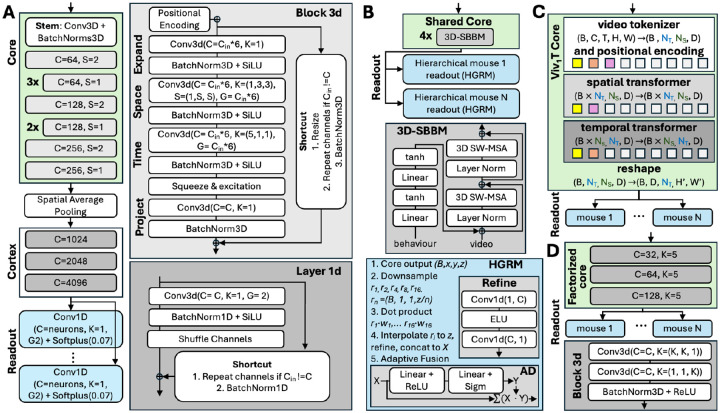
DwiseNeuro consists of three main parts: core, cortex, and readouts. The core consumes sequences of video frames and mouse behavior activity in separate channels, processing temporal and spatial features. Produced features are aggregated with global average pooling over space. The cortex processes the pooled features independently for each timestep, increasing the channels. Finally, each readout predicts the activation of neurons for the corresponding mouse.

Core.

The first layer of the module is the stem. It is a point-wise 3D convolution for increasing the number of channels, followed by batch normalization. The rest of the core consists of factorised inverted residual blocks (Tan & Le, 2019; Sandler et al., 2018) with a narrow -> wide -> narrow channel structure (Fig. 3A). Each block uses (1) absolute positional encoding (Vaswani et al., 2017) to compensate for spatial pooling after the core, (2) factorized (1+1) convolutions (Tran et al., 2018), (3) parameter-free shortcut connections interpolating spatial sizes and repeating channels if needed, (4) squeeze-and-excitation mechanism (Hu et al., 2018) to dynamically recalibrate channel-wise features, (5) DropPath regularization (Larsson et al., 2016; Huang et al., 2016) that randomly drops the block’s main path for each sample in the batch. Batch normalization is applied after each layer. SiLU activation (Elfwing et al., 2018) is used after expansion and depth-wise convolutions.

Figure 3: Architectures of winning solutions.

Across all subplots: C: number of output channels in convolution layers, C_in: number of input channels, K: size of convolution kernels, S: stride, G: number of groups for convolution channels, B: batch size. Core: green, readout: blue. A: DwiseNeuro. The core is based on 3D factorised convolutions. The only solution whose readout was not based on the Gaussian readout (Lurz et al., 2021). B: Dynamic-V1FM. The core is transformer-based, the Gaussian readout is extended to look in different resolution to the core output, then to fuse different resolutions. Here w represents the readout linear weights learnt for each neuron. C: ViV1T. The idea is to replace the core with a spatiotemporal transformer. D: Ensembled factorized baseline.

Cortex.

Spatial information accumulated through positional encoding was compressed by spatial global average pooling after the core, while the time dimension was unchanged. The idea of the “cortex” is to smoothly increase the number of channels before the readout and there is no exchange of information across time. First, the channels are split into two groups, then each group’s channels are doubled as in a fully connected layer. Next, the channels are shuffled across the groups and concatenated. The implementation uses 1D convolution with two groups and kernel size one, with shuffling as in Zhang et al. (2018a). This procedure is repeated three times. Batch normalization, SiLU activation, and shortcut connections with stochastic depth were applied similarly to the core.

Readout.

The readout is independent for each session, represented as a single 1D convolution with two groups and kernel size 1, 4096 input channels and the number of output channels equal to the number of neurons per mouse. It is followed by softplus activation as in Hoefling et al. (2022).

Training.

The main changes compared to the baseline are introducing CutMix data augmentation (Yun et al., 2019), removing normalization, and padding the frames to 64 × 64 pixels. For more details on the training recipe, see Appendix A.1.

Code.

Code is available at https://github.com/lRomul/sensorium

6.2. Place 2: Dynamic-V1FM

Architecture.

Dynamic-V1FM (Dynamic V1 Functional Model), follows the pipeline proposed by Wang et al. (2023). It incorporates a shared core module across mice and an unshared readout module for individual mice. The shared core module comprises four blocks of Layer Norms and 3D window based multi-head self-attention (MSA), inspired by the 3D swin transformer block (Liu et al., 2022) combined with a two-layer behavioral multi-layer perceptron (MLP) module (Li et al., 2023). The readout module is a Hierarchical Gaussian Readout Module (HGRM), which extends the Gaussian readout module (Lurz et al., 2021) by introducing a multi-layer design before the final linear readout (Fig. 3B).

Ensemble Strategy.

As the readout module could support up to five levels of features and original layer is not downsampled and is always used as a base, four combinations of low-resolution features were traversed, resulting in $C_4^4+C_4^3+C_4^2+C_4^1=1+4+6+4=15$ models, where $C_n^k$ is a binomial coefficient $C_n^k=\frac{n!}{k!(n-k)!}$ with n elements and k combinations. Feature enhancement modules were also added to the low-resolution part of these 15 models, but the performance improvement was insignificant. As another set of 15 candidate models, they were included in the subsequent average ensemble strategy. A model with the original Gaussian readout module was also trained as a baseline. The aforementioned 31 models were trained with a fixed random seed of 42, followed by an average ensemble of their predictions. For the final results of both competition tracks (the main track and the out-of-distribution track), the same model and ensemble strategy were used.

Code.

Code is available at https://github.com/zhuyu-cs/Dynamic-VFM.

6.3. Place 3: ViV1T

Architecture.

The Vision Transformer (ViT, Dosovitskiy et al. 2021) was shown to be competitive in predicting mouse V1 responses to static stimuli (Li et al., 2023). Here, a factorized Transformer (ViV1T) core architecture was proposed, based on the Video Vision Transformer by Arnab et al. (2021), to learn a shared visual representation of dynamic stimuli across animals. The ViV1T core contains three main components: (1) a tokenizer that concatenates the video and behaviour variables over the channel dimensions and extracts overlapping tubelet patches along the temporal and spatial dimensions, followed by a factorized positional embedding which learns the spatiotemporal location of each patch; (2) a spatial Transformer which receives the tubelet embeddings and learns the spatial relationship over the patches within each frame; (3) a temporal Transformer receives the spatial embedding and learns a joint spatiotemporal representation of the video and behavioural information. This factorized approach allows to apply the self-attention mechanism over the space and time dimensions separately, reducing the size of the attention matrix and, hence, compute and memory costs. Moreover, the vanilla multi-head attention mechanism is replaced by the FlashAttention-2 (Dao, 2023) and parallel attention (Wang, 2021) to further improve model throughput.

Training.

The model was trained on all labeled data from the five original mice and the five competition mice. To isolate the performance differences solely due to the core architecture, the same shifter module, Gaussian readout (Lurz et al., 2021), data preprocessing and training procedure as the factorized baseline were employed. Finally, a Bayesian hyperparameter search (Akiba et al., 2019) of 20 iterations was performed to find an optimised setting for the core module (see Table 3).

Ensemble.

The final submission was an average output of 5 models, initialized with different seeds.

Code.

Code is available at https://github.com/bryanlimy/ViV1T.

7. Discussion

Different competition submissions explored different architectures. All winners employed architectures distinct from the baseline, but stayed roughly within the core-readout framework (Antolík et al., 2016; Klindt et al., 2017). Successful strategies included:

• Two out of three winning teams utilized transformer-based cores.

• Two teams also modified the readouts, but no team explicitly modeled temporal processing or interaction between neurons in the readout.

• However, the “cortex” module of the winning solution introduced several layers of nonlinear processing after spatial average pooling, effectively allowing all-to-all interactions.

• The winning solution kept the factorized 3D convolutions while introducing methods from computer vision models, such as skip connections and squeeze-and-excitation blocks.

These observations suggest that classic performance-boosting methods from computer vision are also helpful to boost the performance for neural predictive models. However, the impact of such architectural changes on the biologically meaningful insights, such as in Franke et al. (2022); Burg et al. (2021); Ustyuzhaninov et al. (2022), still needs to be validated and requires additional research.

Another observation is that all three winning solutions included a mechanism for all-to-all interaction: the winning solution in the “cortex”, the other two by using a transformer-based core. Thus, although the CNN has originally been modeled after primary visual cortex (Fukushima, 1980), it does not seem to provide the best inductive bias for modeling, at least mouse V1. Long-range interactions appear to be important. The current data does not allow us to resolve whether these long-range interactions actually represent visual information, as expected from lateral connections within V1 (Gilbert & Wiesel, 1983, 1989), or from more global signals related to the animal’s behavior (which is also fed as input to the core). This will be an interesting avenue for future research.

Moving from static images to dynamic inputs in SENSORIUM 2023 increased the participation threshold markedly because of the higher demands on compute and memory. As a result, many models cannot be trained on freely available resources such as Colab or Kaggle anymore (Table 2).

Table 2:

Training time for a single model (before ensembling).

Model	GPU	GPU memory	Batch Size	Wall Time
DwiseNeuro	2 × RTX A6000	48 Gb	32	12h
Dynamic-V1FM	8 × 2080Ti GPU	11 Gb	32	24h
ViV1T	1 × Nvidia A100	40 Gb	60	20h
Factorized baseline	1 × RTX A5000	24 Gb	40	8h
GRU baseline	1 × RTX A5000	24 Gb	40	10h

8. Conclusion

Predictive models are an important tool for neuroscience research and can deliver important insights to understand computation in the brain (Doerig et al., 2023). We have seen that systematically benchmarking such models on shared datasets can boost their performance significantly. With the SENSORIUM benchmark we have successfully established such an endeavor for the mouse visual system. The 2023 edition successfully integrated lessons from 2022, such as including an ensemble to encourage participants to focus on new architectures. However, there are still ways to go to achieve a comprehensive benchmark for models of the visual system. Future iterations could include, among others, the following aspects:

• Use chromatic stimuli in the mouse vision spectrum (Hoefling et al., 2022; Franke et al., 2022).

• Establish a benchmark for combining different data collection protocols (Azabou et al., 2024) or modalities (Antoniades et al., 2023).

• Focus not only on the predictive performance on natural scenes, but also on preserving biologically meaningful functional properties of neurons (Walker et al., 2019; Ustyuzhaninov et al., 2022).

• Extend beyond the primary visual cortex.

• Include more comprehensive measurements of behavioral variables.

• Include active behaviors of the animals.

We invite the research community to join us in this effort by continuing to participate in the benchmark and contribute to future editions.

A. Winning solutions

A.1. Place 1 - DwiseNeuro

Analysis of Improvements.

All of the score numbers are in for the main track during the competition live phase. An early model with depth-wise 3D convolution blocks achieved a score of ≈0.19. Implementing techniques from the core section, tuning hyperparameters, and training on ten mice instead of five data boosted the score to 0.25. Removing normalization improved the score to 0.27. The cortex and CutMix (Yun et al., 2019) increased the score to 0.276. Then, the β value of Softplus was tuned, resulting in a score of 0.294. Lastly, adjusting drop rate and batch size parameters helped to achieve a score of 0.3. The ensemble of the basic and distillation A.1 training stages achieved a single-trial correlation of 0.2913. This is just slightly better than the basic training.

• Learning rate warmup for the first three epochs from 0 to 2.4e-03

• cosine annealing last 18 epochs to 2.4e-05

• Batch size 32, one training epoch comprises 72000 samples

• Optimizer AdamW with weight decay 0.05

• Poisson loss

• Model EMA with decay 0.999

• CutMix with alpha 1.0 and usage probability 0.5

• The sampling of different mice in the batch is random by uniform distribution

A.2. Place 2 - The Runner-up Solution Dynamic-V1FM

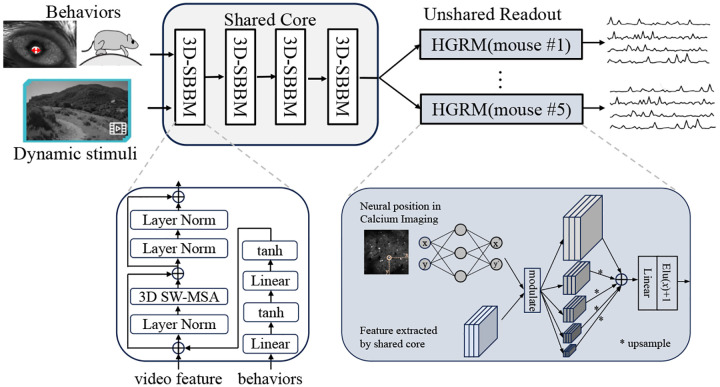
Figure 4:

The overall architecture of Dynamic-V1FM. The core module consists of four 3D-SBBMs that process video and behavioral information, as detailed in the lower left. The unshared readout module includes five levels of features before linear readout in the lower right.

Experiments

Training Details.

We trained Dynamic-V1FM using the training set of ten mice data provided by the competition, and tested it with only five mice data required for submission. Note that we did not employ any pre-training strategy and directly performed the evaluations required by the competition after training. During training, we used truncated normal initialization for the core module and the same initialization strategy for the readout module as Lurz et al. (2021). The whole model was optimized by AdamW optimizer (Loshchilov & Hutter, 2017) with (β₁, β₂) = (0.9, 0.999), weight_decay = 0.05, and a batch size of 32. Each batch contained 30 frames of randomly sampled data. The peak learning rate was 1e⁻³, linearly warmed up with ratio $\frac{1}{3}$ for the first 600 iterations, then kept constant for the first 80 epochs and decreased to 1e⁻⁶ in the last 100 epochs with a cosine strategy. All the models used in the ensemble strategy shared the same training setting.

Experimental Results.

On the live-test evaluation, the improvement of the core module, replacing 3D convolution with 3D swin transformer, resulted in an R² improvement of 0.045 (from 0.188 to 0.233). Enhancements in the readout module, replacing Gaussian readout to Hierarchical Gaussian readout, further improved the model by 0.018 (from 0.233 to 0.251). The final ensemble strategy yielded an overall prediction score of 0.276.

Discussions

We shall provide some thoughts on the V1FM design. Using combined data sets from multiple mice and a shared core module for training is an efficient approach, although the subject-specific readout module strategy increases the difficulty of training the core module. This design could be viewed as a stronger regularization that may weaken the performance of the whole model. This problem might be alleviated by designing a new shared readout module that also relies on subject-specific information, such as mice identities and behavioral data. Specifically, we can use a readout module with dynamic weights (Chen et al., 2020) which is adjusted by mice identities and pupil size.

A.3. Place 3 - ViV1T

Table 3:

ViV1T core hyperparameter search space and their final settings. We performed Hyperband Bayesian optimization (Li et al., 2017) with 20 iterations to find the setting that yield the best single trial correlation in the validation set. The resulting ViV1T model contains 12M trainable parameters, about 13% more than the factorized baseline.

hyperparameter	search space	final value
Core
embedding dim.	uniform, min: 8, max: 512, step: 8	112
learning rate	uniform, min: 0.0001, max: 0.01	0.0048
patch dropout	uniform, min: 0, max: 0.5	0.1338
drop Path	uniform, min: 0, max: 0.5	0.0505
pos. encoding	none, learnable, sinusoidal	learnable
weight decay	uniform, min: 0, max: 1	0.1789
batch size	uniform, min: 1, max: 64	6
Spatial Transformer
num. blocks	uniform, min:1, max: 8, step: 1	3
patch size	uniform, min: 3, max: 16, step: 1	7
patch stride	uniform, min: 1, max: patch size, step: 1	2
Temporal Transformer
num. blocks	uniform, min: 1, max: 8, step: 1	5
patch size	uniform, min: 1, max: 50, step: 1	25
patch stride	uniform, min: 1, max: patch size, step: 1	1
multi-head attention (MHA) layer
num. heads	uniform, min: 1, max: 16, step: 1	11
head dim.	uniform, min: 8, max: 512, step: 8	48
MHA dropout	uniform, min: 0, max: 0.5	0.3580
feedforward (FF) layer
FF dim.	uniform, min: 8, max: 512, step: 8	136
FF activation	Tanh, Sigmoid, ELU, GELU, SwiGLU	GELU
FF dropout	uniform, min: 0, max: 0.5	0.0592

Table 4: Core parameters for the baseline architectures.

Compared to the GRU baseline, the amount of channels in the core was increased sequentially.

Baseline	Core	Layers	Channels	Input Spatial Kernels	Spatial Kernels
GRU	Rotation-equivariant	4	8	9 × 9	7 × 7
3D Factorized	3D factorized	3	32, 64, 128	11 × 11	5 × 5

A.4. Baseline architectures parameters

The GRU baseline used rotation-equivariant core from Ecker et al. (2018) with 8 rotations, resulting in 64 channels totally (8 channels × 8 rotations = 64). Inspired by Sinz et al. (2019) we used the GRU module after the core. It had 64 channels, and both input and recurrent kernels were 9 × 9. For the 3D Factorized baseline, we used the core inspired by Hoefling et al. (2022); Vystrčilová et al. (2024). The temporal kernels were 11 × 1 in the 1st layer and 5 × 1 afterwards, same as the spatial ones (Tab. 4).

The Ensembled baseline cores were same as for the 3D Factorized baseline.

A.5. Stability analysis

Table 5:

We used seeds 8, 16, 42, 64, 128, 512, 1024, 2048, 4096, 16384, 32768, 131072, 262144, 104857 to ensemble the factorized benchmark. Here we provide the individual performance of the models on the final test set to analyse how much performance depended on the seed.

	Main track
Seed	single-trial ρst ↑	average ρta ↑
8	0.1932	0.3650
16	0.1642	0.3210
42	0.1887	0.3569
64	0.1780	0.3380
128	0.1839	0.3479
512	0.1799	0.3402
1024	0.1865	0.3528
2048	0.1672	0.3178
4096	0.1734	0.3305
16384	0.1880	0.3571
32768	0.1933	0.3661
131072	0.1852	0.3513
262144	0.1839	0.3488
1048576	0.1943	0.3674
mean	0.1828	0.3472
std	0.0094	0.0159