Electrically Controlled High Sensitivity Strain Modulation in MoS₂ Field-Effect Transistors via a Piezoelectric Thin Film on Silicon Substrates

Abstract

Strain can modulate bandgap and carrier mobilities in two-dimensional (2D) materials. Conventional strain-application methodologies relying on flexible/patterned/nanoindented substrates are limited by low thermal tolerance, poor tunability, and/or scalability. Here, we leverage the converse piezoelectric effect to electrically generate and control strain transfer from a piezoelectric thin film to electromechanically coupled 2D MoS₂. Electrical bias polarity change across the piezo film tunes the nature of strain transferred to MoS₂ from compressive (∼0.23%) to tensile (∼0.14%) as verified through Raman and photoluminescence spectroscopies and substantiated by density functional theory calculations. The device architecture, on silicon substrate, integrates an MoS₂ field-effect transistor on a metal-piezoelectric-metal stack enabling strain modulation of transistor drain current (130×), on/off ratio (150×), and mobility (1.19×) with high precision, reversibility, and resolution. Large, tunable tensile (1056) and compressive (−1498) strain gauge factors, electrical strain modulation, and high thermal tolerance promise facile integration with silicon-based CMOS and micro-electromechanical systems.

Critical properties of 2D materials, specifically transition metal dichalcogenides (TMDs), such as bandgap,^1,2 absorption coefficient,³ carrier effective mass,⁴ electrical⁵ and thermal conductivities,⁶ dielectric constant,⁷ and carrier mobility,⁸ exhibit a strong flake-thickness (number of layers) dependence. However, because of the non-viability of conventional doping techniques, modulating these properties of a 2D material exfoliated or grown at a specific thickness is challenging. Due to their ultrathin nature and high tensile strength, strain application can alter their structural parameters and enable tuning of various mechanical, optical, thermal, or electrical properties. For example, uniaxial tensile strain can reduce the optical bandgap of monolayer MoS₂ by 120 meV/%.^9,10

Several strain application strategies such as flexible/bendable substrates (polydimethylsiloxane (PDMS),¹¹ polyethylene terephthalate (PET),¹² polyimide (PI)¹³), tensile/compressive capping layers,^14,15 patterned substrates,¹⁶ and atomic force microscopy (AFM) based localized indentation,^17,18 have been reported. However, such flexible substrates cannot be employed for applications involving high-temperature processing, which can affect their quality and rigidity and also leave significant organic residues. Patterned/distorted substrates can impart only fixed strain without tunability or reversibility, similar to tensile/compressive capping layers, and AFM tips are unsuitable for device-level applications.

Electrically controlled strain modulation in 2D material based devices is absent in the strain application methods discussed above. Piezoelectric and electrostrictive materials demonstrate coupled electrical and mechanical properties with mechanical actuation on the order of nanoseconds^19,20 and low fatigue over multiple cycles enabling high endurance device applications.^21,22 The converse piezoelectric effect can transfer strain from an electrically biased piezoelectric material to another material in close proximity. This could be employed for electrically controlled strain transfer from a piezoelectric thin film to a 2D material.^23,24 Such a piezo film-based strain sensor can further be integrated on a conventional, rigid Si substrate with high thermal tolerance and compatibility with existing CMOS and MEMS device technologies.

In this work, we report an all-electrical, highly controllable transfer of strain onto an atomically thin 2D material (MoS₂) by conjugating it with a piezoelectric thin film (having large piezoelectric coefficients) on a Si substrate. Electrical modulation of the magnitude and nature of strain is examined by Raman and photoluminescence (PL) spectroscopy measurements, while piezoresponse force microscopy (PFM) reinforces the material-level strain transfer. The device architecture consists of a strain-tunable field-effect transistor (FET), in which the two- and three-terminal electrical transport parameters of the ultrathin MoS₂ flake are readily modulated by the piezo biasing. Thus, we demonstrate significant strain-induced modulation of two-terminal MoS₂ current (130× across 6 V of piezo bias) and three-terminal field-effect parameters such as the on/off current ratio (7 × ), threshold voltage (shift of 0.44 V) and mobility (1.19 × ). The electrical bias-controlled strain transfer feature offers easy, fast, and precise strain tunability at high resolution, in comparison to conventional mechanical techniques. We demonstrate large strain gauge factors for both compressive (−1498) and tensile (1056) strains, indicating efficient sensing of piezo-induced strain in MoS₂.

Device Architecture

A mixed-dimensional heterostructure device was designed for transferring electrically induced strain in a piezoelectric thin film to the 2D material flake via the converse piezoelectric effect, as depicted in Figure 1a. From bottom up, the device architecture consists of three major components, (i) a bottom metal electrode (M)–piezoelectric thin film (P)–top metal electrode (M) MPM stack on an Si/SiO₂ substrate, (ii) an intermediate dielectric layer (Al₂O₃) over the top electrode that couples the bottom MPM stack to, (iii) a micromechanically exfoliated and source/drain metallized MoS₂ flake FET on top of the dielectric layer. Ti/Pt was used for the MPM electrodes, while source/drain contacts on MoS₂ used Ni/Au metal stacks. Further fabrication details are available in Supporting Information S1. A 3D schematic, vertical cross-section, and optical microscope image are shown in Figure 1. Cross-section transmission electron microscope image of a representative device and AFM scan of the ∼2.4 nm thick MoS₂ flake are available in Supporting Information sections S2 and S3, respectively.

Figure 1.

Device architecture. (a) Pictorial representation of the converse piezoelectric effect based all-electrical strain transfer from a piezoelectric thin film to the 2D material. (b) Schematic of the Si substrate based piezoelectric thin film-2D material electromechanical device and (c) a vertical cross-section of the device showing the metal–piezoelectric–metal (MPM) stack at the bottom and the MoS₂ field-effect transistor (FET) with source (S)–drain (D) contacts on top, coupled through the intermediate Al₂O₃ dielectric layer. V_T (V_B) indicates voltage applied to the top (bottom) electrode, and V_P is the piezo voltage, V_P = V_B – V_T. (d) Optical microscope image of the as-fabricated device with different regions marked. T and B are top and bottom electrodes of the MPM stack, and P represents the sandwiched piezoelectric thin film. (e) XRD plots of LSCO/PNNZT film and platinized Si substrate for reference and (f) strain hysteresis loop of the PNNZT film obtained by piezoresponse force microscopy.

The piezoelectric thin film, a complex perovskite oxide 0.50Pb(Ni_1/3Nb_2/3)O₃–0.35PbTiO₃–0.15PbZrO₃ (PNNZT), was grown using pulsed laser deposition (PLD) at 750 °C. Single-phase targets of PNNZT were used to produce 350–500 nm films, and their quality was ascertained through X-ray diffraction (XRD) (Figure 1e, and discussed in Supporting Information S4). PNNZT was chosen for its sizable piezoelectric voltage coefficient d₃₃ (both electric field and surface displacement along the z-direction) value of ∼250 pm/V, which is higher than those of common piezoelectric films (Pb(Zr,Ti)O₃ (PZT, 100 pm/V)²⁵ or BaTiO₃ (BTO, 20 pm/V)²⁶). The electromechanical response of PNNZT films was evaluated using the PFM technique (Figure 1f), and extracted values of d₃₃ were around 150 to 250 pm/V (Supporting Information S4). Further, a large remnant polarization of 29.5 μC/cm² was obtained.

Nature of Strain Transfer

Bias voltages applied to top (V_T) and bottom (V_B) electrodes result in an out-of-plane electric field, E⃗ = = 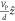, where d is the thickness and V_P = V_B – V_T is the potential difference across the piezoelectric film, ranging from 0 (V_P = 0 kV) to about ±150 kV/cm (V_P = ±6 V). If the polarization of the ferroelectric domains in PNNZT is aligned with the direction of the electric field, out-of-plane as well as in-plane deformations can be produced, depending on the correlated d₃₃ and d₃₁. The resulting nature of compressive and tensile strain transferred onto the MoS₂ flake was examined with bias-dependent Raman spectroscopy using a 532 nm laser.

The two prominent Raman active modes of MoS₂, E′ and A^′₁, are sensitive to strain application that distorts its hexagonal Brillouin zone. In Figure 2a, as V_P is increased in the negative direction, the E′ mode of three-layer (3L) MoS₂ shifts to higher frequencies at a rate of 0.26 ± 0.05 cm^–1/V. On the other hand, for increasing positive V_P, E′ shows a red shift at 0.15 ± 0.02 cm^–1/V. First-principles based calculations have shown a stiffening (softening) of phonon modes with compressive (tensile) strain.⁴ This trend in the shift in E′ mode with compressive/tensile strain is consistent with MoS₂ flakes strained by other techniques.^23,27 In addition, for monolayer (1L) MoS₂, by monitoring the direction of shift of the A excitonic peak (K – K transition) energies in the bias-dependent PL spectra, the nature of strain transfer with applied V_P can be reconfirmed. For increasing positive V_P in Figure 2c, the A peak shows a significant shift toward lower energies, whereas for higher negative V_P values, the PL peak shifts are smaller. This observation²⁸ correlates well with density functional theory (DFT) based first-principles calculations of strained MoS₂ bandstructure (Supporting Information S5). The decrease in bandgap of monolayer MoS₂ is much steeper for tensile strain (uniaxial and biaxial) than for compressive strain.²⁹ Hence, the direction of peak shifts in bias-dependent Raman and PL spectra indicates that a positive (negative) V_P leads to the tensile (compressive) straining of MoS₂.

Figure 2.

Physical evidence of strain transfer. (a) Raman spectra (using λ = 532 nm laser) of MoS₂ under unstrained (V_P = 0 V), and strained (V_P = −6 V and V_P = 6 V) conditions. The two characteristic modes have been fit using Lorentzian functions. (b) Raman shifts of E′ and A modes with piezo biasing, showing a red shift for positive V_P and blue shift for negative V_P corresponding to tensile and compressive strains, respectively. (c) Photoluminescence peak positions of monolayer MoS₂ for varying V_P. The A excitonic peak shifts by −30 meV when V_P of 4 V is applied. (d) Pictorial depiction of PFM imaging on an MoS₂ flake on top of the Al₂O₃/piezoelectric stack and PFM strain loop demonstrating the bias-dependent localized displacement of the MoS₂ flake in response to the vertical electric field. (e) Schematic representation of the nature of strain transferred to MoS₂ as determined by the polarity of V_P. The unstrained physical dimensions are denoted by the dotted lines, and the V_P-induced strained dimensions are represented by solid lines.

To directly probe the strain transfer from the piezoelectric layer to MoS₂, PFM measurements were performed on the MoS₂/Al₂O₃/PNNZT stack. The strain-loop in Figure 2d shows the electric-field-induced deformation of the PNNZT film can be sensed at the 2D material surface. The hysteresis strain-loop of an MoS₂ flake on a non-piezoelectric Si/SiO₂ substrate exhibits no evidence of straining (Supporting Information S6) and serves as a control experiment. Figure 2e shows a schematic summarizing the nature of strain transfer with piezo biasing.

Electrical Characteristics

The top electrode of the MPM stack is capacitively coupled to the MoS₂ channel through the Al₂O₃ dielectric. Hence, it also acts as the gate electrode of an FET with an n-type MoS₂ channel with source and drain electrodes on top. The series connection of the MPM stack and the FET through the shared top (gate) electrode gives rise to the possibility of studying strain- and field-effect driven transport in MoS₂ individually and in combination, through different biasing schemes (Figure 3a). Specifically, measuring the source-drain current (I_DS) while (i) grounding the top electrode (V_T = 0 V) and sweeping the bottom electrode bias (varying V_B) leads to strain-dependent transport, while (ii) sweeping V_T and V_B together with a fixed V_P offset ((iii), zero offset) voltage results in field-effect transport under a fixed strain value ((iii), just the field-effect transport with no strain-effect), and (iv) grounding V_B and sweeping V_T gives the combined effect of simultaneously varying field-effect and strain on MoS₂ transport. The top and bottom electrodes are biased for all electrical measurements and are never kept floating (unbiased).

Figure 3.

Strain modulated two-probe electrical transport. (a) Various biasing conditions to deconvolve the interplay between strain-effect and field-effect in the coupled MPM-MoS₂ FET device. (b) (i) Two-terminal I_DS–V_DS characteristics (biasing scheme i in (a)) showing the modulation of drain current with strain applied by varying V_P at zero V_T (no field-effect). The output trace for the unstrained case, V_P = 0 V, is shown by the black dotted line. (ii) Analytical current model based fit lines of the V_P = −3, 0, +3 V traces overlaid on the scatter data points. A 37× enhancement of the drain current at 3 V and 3.5× reduction at −3 V is obtained with the piezo biasing. (c) Plot of the normalized change in resistance with V_P for compressive (left plot, in blue) and tensile (right plot, in red) strains extracted for two V_DS values. The electrical gauge factor in (d) is calculated from the slopes of the respective V_DS plots in (c). (e) Switching between the unstrained (V_P = 0 V) and strained (V_P = 1 V) drain current values over multiple cycles.

Of these four schemes, we look at the first one investigating strain-dependent two-terminal transport in Figure 3b. Current–voltage (I_DS–V_DS, V_DS is source-drain voltage) curves were obtained at different V_B values for a fixed V_T = 0 V (V_P = V_B – V_T = V_B). Since V_T = 0 V, any change in carrier concentration in MoS₂ due to field-effect will be negligible. I_DS increases as V_P is increased from −3 to +3 V. Specifically, a V_P increase from 0 to +3 V (tensile strain) increases I_DS and decreasing it from 0 to −3 V (compressive strain) decreases I_DS. The I_DS trace for V_T = V_B = 0 V is highlighted to clearly distinguish the change in the current with V_P. A 6 V change in piezo-bias modulates I_DS by nearly 130×.

From the two-probe output characteristics, the change in channel resistance (ΔR = R(V_P) – R₀ = R(V_P) – R(V_P = 0)) with piezo voltage can be determined at different V_DS values. The normalized change in resistance with piezo voltage (Figure 3c) for both compressive and tensile strains at V_DS = −0.25 and −0.05 V and linear fits to the plots provide a measure of the sensitivity of the material as a strain sensor. This metric, gauge factor GF, is conventionally calculated as the change in normalized resistance with applied strain (ϵ), GF = . To account for change in channel resistance with piezo biasing, we define an electrical GF (EGF = 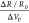). EGF reaches a maximum value of −202 V^–1 for negative V_P and a maximum value of 80 V^–1 for positive V_P. Further, repeatable output characteristics of two additional devices are available in section S7 of the Supporting Information

Ten back-to-back V_DS sweeps (0 to −0.2 V) show low (<7%) standard deviation error in I_DS for fixed V_P values of 0 and −1 V, indicating good repeatability (Supporting Information S8). Further, Figure 3e shows distinct I_DS values for multiple switching cycles between unstrained (V_P = 0 V) and strained (V_P = −1 V) conditions, indicating good time stability and current (strain) resolution of the device.

Next, MoS₂ FET performance under varying strain was evaluated using biasing schemes shown in Figure 3a (ii) and (iii). In both cases, the top and bottom electrodes were connected and swept together but with a fixed offset (V_B = V_T + V_offset), where V_offset = V_P ≠ 0 in case (ii) and V_offset = V_P = 0 V in case (iii). V_offset ensures a fixed electric field (strain) between the top and bottom electrodes, while V_T and V_B are swept together varying the gate field for the MoS₂ channel on top. V_offset = 0 V implies zero electric field (strain) for the MPM stack and gives us the unstrained, control, MoS₂ transistor performance. Transfer characteristics (I_DS – V_T) of the MoS₂ transistor, in Figure 4a, show significant I_DS modulation with varying V_P (strain) below the threshold voltage (V_Th). The complete transfer characteristics, including the forward and reverse sweeps, are shown in Supporting Information S9. The hysteresis width is not significantly affected by V_P. On the other hand, for a control sample without the top electrode, the hysteresis width is significantly larger, as discussed in Supporting Information S9. The top electrode set at 0 V (below V_Th) in the measurements in Figure 3b (scheme i in Figure 3a) holds the channel in the electrostatic off-state, thereby rendering the strain-effect more prominent. Figure 4b shows that I_DS values before, during, and at the end of several I_DS–V_T sweeps for different offset voltages (strain values) are nearly identical, highlighting the reversibility of the strain modulation. Corresponding I_DS–V_T traces are given in Supporting Information S9.

Figure 4.

Strain-tunable field-effect transistor. (a) Transfer characteristics (I_DS–V_T (gate bias)) of the MoS₂ transistor at different values of piezo (offset) bias (strain). The biasing scheme displayed in the inset, also shown in Figure 3(a) (ii), was implemented for the measurements. The top and bottom electrodes were tied together and swept with different fixed offset biases, where the offset bias is essentially the piezo voltage V_P that fixes the strain value for a given I_DS–V_T sweep. (b) Dynamic evolution of the drain current at V_T = 0 V, just below the threshold voltage, when V_P is increased from 0 to 3 V, then decreased to −3 V, and finally set at 0 V, indicating good reversibility of the strain modulation. (c, d) Modulation of the extracted FET parameters with V_P. Both I_on and I_off show an increasing trend with increasing V_P (−3 to +3 V); however, the modulation of I_off (5.18×) is substantially higher than that of I_on (1.2×). Threshold voltage shifts to the left (negative direction) with increasing piezo voltage, and the mobility can be tuned by 1.19× with V_P. In short, all FET parameters, I_on, I_off, V_Th, and μ, can be increased or decreased, in the strained-FET, with respect to the V_P = 0 V FET, thereby highlighting strain as an additional knob to modulate field-effect parameters.

Figure 4 panels c and d depict the substantial tuning of FET parameters with piezo biasing. The on-current (I_on), the off-current (I_off), and the corresponding on–off ratio (I_on/I_off) can be modulated by nearly 1.2, 5.18, and 150 times, respectively, across a 6 V piezo voltage range. The V_Th for each transfer characteristic was obtained from linear extrapolation at the maximum transconductance point, g_m = dI_DS/dV_G. V_Th shifts to lower values with increasing V_P, which leads to an increase in I_on. Field-effect electron mobility values were extracted at V_Th using μ = 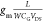, where L and W are the length and width of the channel and C_G is the capacitance of the Al₂O₃ gate dielectric (301 nF/cm²). The unstrained mobility value of 21 cm²V⁻¹s⁻¹, at an offset (V_P) of 0 V, can be tuned from 1.1× to 0.9× (1.19× overall) using piezo bias (Figure 4d). Mobility values decrease (increase) for positive (negative) V_P corresponding to the tensile (compressive) strain. This modulation in mobility could be attributed to the effect of strain on the MoS₂ channel and the impact of strain and strain-induced polarization charges on the contact resistance and Schottky barrier height (discussed later). The increase in I_on and left shift in V_Th with tensile strain are consistent with computational studies³⁰ and mechanical strain transfer reports³¹ for MoS₂ transistors. Further analysis of biasing schemes iii and iv in Figure 3a showing the impact of just varying the field-effect and combining it with a varying strain-effect is available in Supporting Information S10.

We performed first-principles based DFT calculations to understand the effect of compressive and tensile strain on the MoS₂ properties. To account for the mixed nature of strain that could be transferred from the piezoelectric layer to MoS₂, both uniaxial and biaxial strains were employed on a unit cell of 3L-MoS₂. Details of the strain-application methodology and the evolution of MoS₂ bandstructure with strain are available in section S5 of the Supporting Information For the unstrained case (inset in Figure 5a), there are two prominent valleys in the lowest energy conduction band, at K and at Q′ (along K–Γ), separated by 92 meV. The valence band maximum is at Γ, hence for the unstrained case, the bandgap is along Γ → Q′. Under the influence of uniaxial/biaxial in-plane tensile strain, the bandgap is along Γ → K since the decrease in K point energy is much more significant. Biaxial strain leads to a steeper change in bandgap (−76 meV/%) compared to uniaxial (−19 meV/%). Next, for increasing compressive strain, the bandgaps increase slightly and remain along Γ → Q′. These calculated changes in the bandgap values directly correlate with the strain-dependent photoluminescence peak positions in Figure 2c. For example, the PL peak red shifts by 30 meV at V_P = 4 V. The piezoresistive bandgap decrease with tensile strain is mainly due to lowering of the conduction band minimum (CBM). This reduces the electron Schottky barrier height (ϕ_B) and hence the I_DS (Figure 5c).

Figure 5.

Effect of strain on MoS₂ bandstructure and contacts and performance benchmarking. (a) Calculated strain-dependent bandgap of 3L-MoS₂ from first principles. The electronic bandstructure for unstrained 3L-MoS₂ is shown in the inset of (a). The two lowest energy transitions are marked for K and Q′ valleys. For both uniaxial and biaxial tensile strains, the bandgap along Γ → K shows a significant decrease, while for compressive straining of the unit cell, the bandgap occurs along Γ → Q′ and shows a comparatively smaller increase. (b) Change in Schottky barrier height with piezo bias obtained from (i) extracted V_P-dependent Schottky barrier height values from the fits to I_DS–V_DS characteristics in Figure 3b and (ii) calculations using eq 2. (c) Representative band diagrams depicting the changes in bandgap and electron effective mass with compressive and tensile strains due to the piezoresistive effect and the Schottky barrier modulation due to accumulation of strain-induced polarization charges through the piezotronic effect. (d) Benchmarking of the gauge factor of our device with 2D materials and other quasi-2D and bulk materials reported in the literature. The all-electrical tuning of strain along with the ability to achieve both compressive and tensile strain response is highlighted. In all plots, regions highlighted by yellow and light blue colors refer to tensile and compressive strains, respectively.

In addition, we have also calculated the strain-tuned electron effective mass 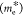around K and Q′ CBM (Supporting Information Figure S8). Under tensile and compressive strains, decreases at their respective band minima. The sharper decrease with increasing tensile strain could also improve I_DS and lower ϕ_B.

To extract the strain-dependent ϕ_B from the two-probe current (Figure 3b(i)), we employ the modified thermionic equation for back-to-back Schottky source and drain barriers,.³²

1

2

Here, S is the device area, A* is the strain-independent Richardson’s constant,³³ and T, q, and k_B are the absolute temperature, electronic charge, and Boltzmann’s constant, respectively. The ideality factor η₁ was fixed at 1, and η₂ was varied to account for nonidealities of bias-dependent series and shunt resistances. Figure 3b(ii) shows the thermionic equation based fit lines overlaid on corresponding scatter data points for V_P = −3, 0, and 3 V. The extracted ϕ_B for each V_P trace is used to calculate strain-induced change in ϕ_B (Δϕ_B) w.r.t. V_P = 0 V. Δϕ_B can also be calculated using eq 2 considering no applied strain at V_P = 0 V. Figure 5b plots Δϕ_B for varying V_P (strain) extracted from the fits as well as eq 2. Δϕ_B > 0 for compressive strain and becomes negative for tensile strain. Odd-layered MoS₂ flakes are inherently piezoelectric due to broken inversion symmetry. The resulting polarization charge due to structural deformation at the source/drain electrodes could additionally increase (compressive) or decrease (tensile) ϕ_B and influence I_DS via the peizotronic effect. Energy band diagrams showing ϕ_B lowering (increase) due to tensile (compressive) strain via the piezoelectric and piezotronic effects are shown in Figure 5c.

Performance benchmarking of our all-electrical MoS₂ strain sensor requires mapping of the piezo voltage to strain values. For this, we have mapped V_P to mechanical strain values by comparing reported strain-dependent E′ Raman peak shifts with V_P-dependent shifts obtained in this study. For negative V_P, the correlated compressive strain per unit negative V_P is 0.10–0.14% per V.^11,27,34 For tensile strain per unit positive V_P, the correlated strain values are 0.06–0.08% per V. Hence, total applied strain varies from −0.23% to +0.14% for V_P ranging from −3 to +3 V. These correlated values can be used to calculate the conventional strain gauge values for our devices (Supporting Information S11). Additional analysis shows that a strain precision of 0.002% at V_DS = −0.05 V was obtained by applying V_P (Supporting Information S11). Moreover, the Raman-based strain correlation also helps in estimating a strain resolution of 0.045% for tensile and 0.078% for compressive strain, respectively, based on the repeated drain current sweep measurements for V_P = 0 and V_P = 1 V (Supporting Information S12).

Gauge factor values calculated by the change in resistance method for different 2D materials and quasi-2D and bulk systems are benchmarked in Figure 5d. 2D materials show significantly larger values compared to silicon/metal based sensors³⁵⁻³⁷ due to their high tensile strength and large band edge density of states. Unlike most reported literature, our devices can show negative (−1498) and positive (1056) GFs. 2D materials exhibit high GFs at ultrathin flake thicknesses.^{12,27,38−41} Also, for the case of 2D WSe₂ and SnS₂, improved GFs have been obtained through ultraviolet illumination⁴² or reduced temperatures,⁴³ respectively. Nanowire, nanobelt, and microwire structures of ZnSnO₃, ZnO, SiC, or Si also exhibit considerable GFs, however, at the cost of large thicknesses.⁴⁴⁻⁴⁸ Further, anisotropic 2D ReS₂ could exhibit large GFs due to a strong dependence of electrical properties on strain.^49,50 It should be noted that employing the change in current method can lead to GF values reaching 28000 in our devices.^31,37,51

Further, a comprehensive benchmarking table in section S12 of the Supporting Information compares different straining strategies for MoS₂ and evaluates their implementation feasibility with respect to the substrate used, strain resolution, measurement precision over several cycles, and ease of integration for applications such as CMOS and MEMS systems. This work is the only all-electrical study of strain transfer on 2D materials with device applications. Also, for device fabrication processes that require high-temperature deposition or processing, piezoelectric thin film based straining could be more useful than flexible polymers.

In summary, we have demonstrated a novel electromechanical device by coupling a piezoelectric thin film on a Si substrate with an atomically thin 2D material. Electrically induced strain through the piezo film has been used to tune the physical and electrical properties of the 2D monolayer and three-layer MoS₂ over a wide range, with a high degree of ease, reversibility, precision, and resolution. Specifically, the shift in characteristic Raman modes, variation in photoluminescence peaks, and the piezoresponse strain loop demonstrate the physical nature of the strain transfer. In addition, the efficient modulation of two- and three-terminal electrical characteristics with the piezo voltage-induced strain demonstrates a strain-tuned 2D MoS₂ field-effect transistor. As a strain sensor, the advantage of controlling the nature of strain by simply using bias polarity helps in realizing large positive (tensile) and negative (compressive) gauge factors. The strain transfer reliability could be further improved using 2D crystalline materials such as hBN as the dielectric and graphene for source/drain contacts. Further, emerging nitride based piezoelectric materials such as AlN and AlScN can also be explored in our device architecture.⁵²⁻⁵⁴ Thus, our work provides an interesting and exciting platform for coupling the semiconducting properties of 2D materials and piezoelectric polarization in complex perovskite oxide thin films on silicon substrates, which will be useful for future CMOS and MEMS applications. This piezoelectric straining method has also been tested for other 2D materials such as ReS₂, making it a universal technique for strain-dependent electronic and optoelectronic studies. Besides technological relevance, it offers a new path for exploring localized strain-effects in 2D systems and exotic strain-derived phenomena such as exciton funneling and the anisotropy-induced bulk photovoltaic effect.^55,56

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.4c00357.

• Details of device fabrication and characterization and DFT calculations, cross-section TEM of device, AFM image of the flake, growth and characterization of the piezoelectric film, strain-dependent DFT bandstructure calculations, PFM analysis on non-piezo substrate, results from additional devices, multiple I-V sweeps, analysis of transfer characteristics, details of control samples, comparison of strain- and field-effects, strain gauge and precision calculations, and benchmarking (PDF)

The authors declare no competing financial interest.