Evaluation of relative biological effectiveness for diseases of the circulatory system based on microdosimetry

Abstract

In the next decade, the International Commission on Radiological Protection (ICRP) will issue the next set of general recommendations, for which evaluation of relative biological effectiveness (RBE) for various types of tissue reactions would be needed. ICRP has recently classified diseases of the circulatory system (DCS) as a tissue reaction, but has not recommended RBE for DCS. We therefore evaluated the mean and uncertainty of RBE for DCS by applying a microdosimetric kinetic model specialized for RBE estimation of tissue reactions. For this purpose, we analyzed several RBE data for DCS determined by past animal experiments and evaluated the radius of the subnuclear domain best fit to each experiment as a single free parameter included in the model. Our analysis suggested that RBE for DCS tends to be lower than that for skin reactions, and their difference was borderline significant due to large variances of the evaluated parameters. We also found that RBE for DCS following mono-energetic neutron irradiation of the human body is much lower than that for skin reactions, particularly at the thermal energy and around 1 MeV. This tendency is considered attributable not only to the intrinsic difference of neutron RBE between skin reactions and DCS but also to the difference in the contributions of secondary γ-rays to the total absorbed doses between their target organs. These findings will help determine RBE by ICRP for preventing tissue reactions.

INTRODUCTION

In the latest set of general recommendations [1], the International Commission on Radiological Protection (ICRP) has recommended the dose limits for tissue reactions (formerly termed deterministic effects) in equivalent dose, which is the product of absorbed dose and the radiation weighting factor, w_R. This is based on the assumption that the w_R values for stochastic effects are higher than the relative biological effectiveness (RBE) for tissue reactions. However, ICRP recently decided to change such equivalent dose limits to absorbed dose limits in the next set of general recommendations [2]. Taken together, the International Commission on Radiation Units and Measurements (ICRU) and ICRP recently suggested that RBE weighting of absorbed dose in relation to the specific health effects could be applied for the protection and operational quantities, as appropriate [3]. Thus, the evaluation of RBE for various types of tissue reactions would be needed to prepare the next ICRP general recommendations to be published in the next decade [4].

To estimate RBE for tissue reactions, we recently proposed a mathematical model applicable to any radiation field [5]. It is based on the microdosimetric kinetic (MK) model [6], which was originally developed for calculating the cell surviving fraction for various types of radiation. Importantly, this model can determine not only the mean value but also the uncertainty of RBE by analysing several experimental data taken from different papers. Using the model, we evaluated the means and uncertainties of RBE for skin reactions and dermal cell survival [5]. It was confirmed that the past evaluation of RBE for tissue reactions made by ICRP [7] and the US National Council on Radiation Protection and Measurements (NCRP) a few decades ago [8] are still supported, the recent experimental data for the skin being taken into account [5].

In this study, we applied this model for evaluating RBE to diseases of the circulatory system (DCS) by analysing animal experimental data taken from several papers [9–13]. We set out to deal with DCS because ICRP recently classified DCS as a tissue reaction with an approximate threshold dose of 0.5 Gy [14], but has not recommended RBE for DCS. The mechanisms of radiation-induced DCS such as the potential target organs/tissues and cellular responses have been intensively discussed [15–19]. In addition, evidence has accumulated for a causal association between radiation exposure and DCS, particularly at high dose [20]. Thus, DCS represents among the most important tissue reactions to be considered in the next ICRP general recommendations.

The basic calculation procedures for evaluating RBE for DCS are the same as those done previously for skin reactions (5). Thus, we here describe procedures briefly, while highlighting the differences between those for skin reactions and DCS. The evaluated RBE values for DCS shall be compared with the corresponding experimental data as well as the previously evaluated RBE values for skin reactions. Then, the appropriate weighting factors for preventing tissue reactions are discussed by calculating the means and uncertainties of RBE for DCS and skin reactions in a human phantom irradiated by mono-energetic neutrons.

MATERIAL AND METHODS

Model principles

The original MK model expresses the surviving fraction of cells, S(D), by the linear-quadratic (LQ) function of absorbed dose D [6]. However, the quadratic term of surviving fraction and radiotherapy toxicity is known to become smaller with increasing dose [21–24]. We therefore introduced a certain threshold dose level, D_t, for replacing the linear and LQ functions as written by:

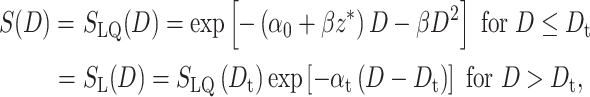(1)

where α₀ is the linear coefficient of the surviving fraction with the limit of linear energy transfer (LET) → 0, β is the quadratic coefficient independent of radiation quality, and α_t is the linear coefficient of the surviving fraction at higher doses, satisfying the condition:

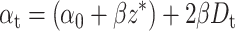(2)

to make S_L(D) asymptotic to S_LQ(D) at D_t. z^* is the saturation-corrected dose-mean specific energy introduced in the MK model by Kase et al. [25], which can be determined by

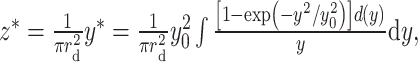(3)

where y is lineal energy, y^* is the saturation-corrected lineal energy, r_d is the radius of a subnuclear structure referred to as a domain, y₀ is a so-called saturation parameter indicating the lineal energy above which the saturation correction due to the overkill effect becomes very important, and d(y) is the dose probability density in the domain.

To reduce the number of parameters used in the model, we introduced the relationship:

(4)

where (α/β)_c is a constant value of the α/β ratio evaluated from clinical data, and is the saturation-corrected specific energy for a typical clinical radiation field. Then, RBE for test radiation as a function of the reference radiation dose D can be calculated by

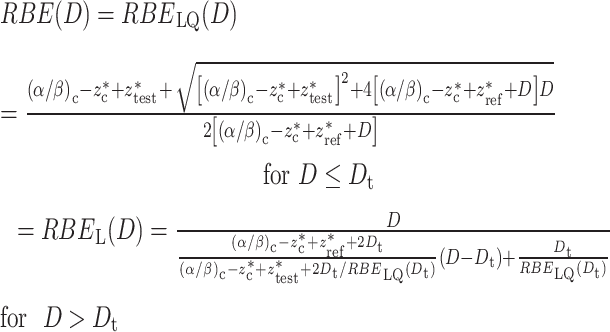(5)

where and 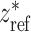are the saturation-corrected specific energies for the test and reference radiations, respectively.

Parameter determination for DCS

The parameters y₀ and r_d in Eq. (3) as well as D_t and (α/β)_c in Eq. (5) are independent of the radiation field and need to be determined for evaluating the RBE for each tissue reaction. Among them, y₀, D_t and (α/β)_c for DCS are assumed to be the same as those for skin reactions, which are 100 keV/μm, 7 Gy and 10 Gy, respectively. This assumption allows us to analyze the difference of RBE between DCS and skin reactions based on a significance test of evaluated r_d values for two diseases. y₀ of 100 keV/μm can be considered adequate irrespective of biological endpoints because it is widely used when expressed in LET. The sensitivity of calculated RBE to D_t and (α/β)_c was investigated by changing the parameters, although it was non-significant for skin reactions (5).

The domain radius, r_d, was independently determined from the least-square fitting of RBE for DCS measured by several animal experiments [9–13]. Table 1 summarizes the basic features of each experiment. These data were selected from ~450 articles found on PubMed with the search terms RBE and cardiovascular or circulatory system. Selection criteria were that the study employed ≥2 types of radiation, and included sufficient information on the experimental setups.

Table 1.

Experimental data used in the determination of the best-fit r_d value for DCS

Reference	Test radiation	Reference radiation	Animal species	Weight of Digimouse (g)	Reaction type	r d (μm)
Aarnoudse et al. 1977 [9]	15 MeV neutron	X-ray (200 kVp)	Rabbit (chinchilla)	3000	Plaque formation	0.173
Broerse et al. 1973 [10]	15 MeV neutron	X-ray (300 kV)	Rat	300	Capillary endothelium	0.233
Hoel et al. 2017 [11]	Fission neutron	γ-ray from 60Co	Mouse (B6CF1)	24.287*	Cardiovascular disease mortality	0.237
Yang et al. 1978 [12]	Fission neutron	γ-ray from 60Co	Mouse (B6CF1)	24.287*	Ultrastructure of the coronary arteries and aorta	0.227
Yang et al. 1984 [13]	High-energy Ne and Fe ions	X-ray (225 kVp)	Neonatal rat	6	Hemorrhage in brain	0.284
					Mean	0.231
					SD	0.039

^*Original weight of Digimouse [27]

Prior to the least-square fitting, the saturation-corrected specific energies 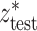, 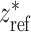and 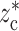in Eq. (5) must be determined for each experimental condition. They were calculated by the Particle and Heavy Ion Transport code System, PHITS [26], coupled with the mesh-type mouse phantom named Digimouse [27]. Since the target animal size is important to characterize the radiation fields, particularly for neutron exposures [28, 29], the size of Digimouse was adjusted to that of the actual experimental animals by scaling its weight using PHITS-based Application for Radionuclide Dosimetry in Meshes[30]. In the PHITS simulations, the size-adjusted Digimouse was irradiated by the test, reference and typical clinical radiations in the isotropic exposure scenario, and the dose probability densities of lineal energy, d(y), in the murine whole body were calculated using the updated microdosimetric function [31]. Note that the sizes of the target animals are generally small so that the heterogeneity of the radiation fields inside them can be ignored. In these calculations, we chose 0.25 μm for the domain radius and 10 MV X-rays for the typical clinical radiation, though these choices little affected the final calculation results as discussed in our previous paper [5].

The calculated d(y) for the test, reference and clinical radiation fields were converted to , and , respectively, using Eq. (3), and substituted into Eqs. (4) and (5) for calculating the RBE value in each experimental condition. In these calculations, r_d is the only free parameter and its numerical value was determined with the least-square fitting by minimizing the square of the differences between the measured and calculated RBE values. Then, the mean and standard deviation (SD) of the domain radii evaluated from each paper, and , respectively, were calculated and compared with the corresponding data for skin reactions. For comparison, a two-sided unpaired t-test was performed.

Calculation of RBE for mono-energetic neutron irradiation of human phantom

For discussing the appropriate values to be weighted on the absorbed dose for preventing tissue reactions, the means and uncertainties of RBE for DCS and skin reactions were calculated for mono-energetic neutron exposures to the human body. In this calculation, we performed the PHITS simulations by irradiating neutrons from 1 meV to 10 GeV to the ICRP mesh-type adult male reference phantom [32] under the isotropic exposure scenario and calculated d(y) in the brain, heart wall, blood (circulating the whole body) and skin of the phantom. The brain and heart wall were selected as the potential targets for cerebrovascular and cardiovascular diseases, respectively. Blood was selected for representing the tissues spread over the whole body. The domain radii were set to and 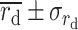, i.e. 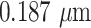0.231 μm and 0.231 0.039 μm for DCS and and 0.187 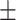0.052 μm for skin reactions. We also performed similar PHITS simulations for exposure to ⁶⁰Co γ-rays (reference radiation) and 10 MV X-rays (clinical radiation). Then, the mean values and the uncertainties of RBE were deduced from the calculated d(y) using Eqs. (3)–(5). Note that the domain radius and RBE are anti-correlated, and thus, d(y) calculated by setting the domain radius to 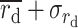gives the minimum value within the RBE uncertainty.

RESULTS

Table 1 summarizes the best-fit r_d obtained from each paper, together with their means and SD. The mean r_d of 0.231 μm for DCS was higher than 0.187 μm for skin reactions, indicating that RBE for DCS tends to be lower than that for skin reactions in the same radiation field. Their difference was borderline significant based on the two-sided unpaired t-test (P = 0.064) due to rather large variances of r_d best-fit to each experiment.

Figure 1 compares the measured and calculated RBE for DCS. The calculated results obtained by setting r_d to 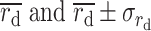previously evaluate for skin reactions are also shown. The calculated RBE rapidly decreases with increasing dose below ~10 Gy, while becoming asymptotic to certain values at higher dose. This is because the equation for representing the surviving fraction changes from the LQ to linear functions at 7 Gy in our model. The determination of the coefficients, R², was 0.88 and − 0.83, respectively, when evaluated from DCS and skin reactions were employed.

Fig. 1.

RBE calculated by Eqs. (3)–(5) in comparison with the corresponding experimental data [9–13] as a function of the reference radiation dose. The calculation was performed by setting r_d to and 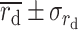for DCS obtained from this study and those for skin reactions determined by our previous study [5]. The reference radiation of the experimental data taken by Broerse et al. [10] shown in Panel (A) was 300 kV X-ray instead of 200 kVp X-ray.

Figure 2 shows the dependence of the calculated RBE for DCS on (α/β)_c and D_t. Although RBE data only for fission neutrons against ⁶⁰Co γ-rays are shown in this figure, were re-evaluated for each (α/β)_c and D_t using all experimental data listed in Table 1. Note that D_t was fixed to 7 Gy when (α/β)_c was the variable, while (α/β)_c was fixed to 10 Gy when D_t was the variable.

Fig. 2.

Dependence of the calculated RBE for DCS on (A) (α/β)_c and (B) D_t for fission neutrons against ⁶⁰Co γ-rays. The experimental data are taken from Refs. [11, 12]. The values in the parentheses are R² obtained by analyzing all experimental data listed in Table 1.

Figure 3 shows the incident-energy dependence of the calculated RBE for DCS and skin reactions for mono-energetic neutron exposures to the ICRP mesh-type adult male reference phantom, together with neutron w_R. Here, ⁶⁰Co γ-rays served as the reference radiation at the absorbed dose of (A) 0.5 and (B) 5 Gy to the target organs (blood for DCS and skin for skin reactions). The uncertainties of RBE estimated by setting r_d to 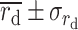are presented as error bars. Figure 4 shows the target-organ dependence of the calculated RBE for DCS: as expected from Fig. 1, RBE becomes smaller with increasing dose of reference radiation. Note that 0.5 Gy was selected because it is the ICRP threshold for DCS [14], while 5 Gy was selected because this level of dose can be reached during radiotherapy for cancer, e.g. to the heart or aorta following thoracic irradiation [33].

Fig. 3.

Calculated RBE for DCS and skin reactions for the isotropic irradiation of mono-energetic neutrons to the ICRP mesh-type adult male reference phantom. ⁶⁰Co γ-rays served as the reference radiation with the absorbed doses of (A) 0.5 and (B) 5 Gy in the target organs, which were blood and skin for DCS and skin reactions, respectively, for the data shown in this figure. The radiation weighting factor, w_R, assigned to the neutron is also plotted.

Fig. 4.

Target-organ dependence of the calculated RBE for DCS for the isotropic irradiation of mono-energetic neutrons to the ICRP mesh-type adult male reference phantom. ⁶⁰Co γ-rays served as the reference radiation with the absorbed doses of (A) 0.5 and (B) 5 Gy in the target organs, which are specified in the parentheses in the legends.

DISCUSSION

The present model suggests that there is a borderline significant difference between RBE for DCS and skin reactions in the same radiation field. The similarity is probably attributable to common underlying mechanisms, which could be, e.g. inflammation at low dose and cell death at high dose [18]. Given that the mean r_d for DCS is larger than that for skin reactions, a significant difference could be reached if more experimental data would be available.

As can be seen in Fig. 2, the dose dependence of RBE becomes less significant with increasing (α/β)_c and D_t. The R² values are rather insensitive to those parameters except for (α/β)_c below 10 Gy. Such tendency supports our assumption that (α/β)_c and D_t for DCS are the same as those for skin reactions, i.e. (α/β)_c = 10 Gy and D_t = 7 Gy, whereas the α/β ratio of slow turnover tissues such as the heart is considered 2–4 [14].

It is evident from Fig. 3 that the ICRP neutron w_R for stochastic effects is much larger than the neutron RBE for tissue reactions. The RBE for DCS for mono-energetic neutron irradiation of the human body was also significantly lower than the corresponding RBE for skin reactions, particularly at the thermal energy and around 1 MeV. This tendency is considered attributable not only to the intrinsic difference of neutron RBE between the two diseases but also to the difference in the contributions of secondary γ-rays to the total doses between their target organs, which are generally higher for more deep-seated organs [28, 29]. This dose profile can also explain the difference in RBE between the target organs selected for DCS as shown in Fig. 4; the mean shielding thickness from the body surface is thinner for the brain and thicker for the heart wall than blood. Therefore, the dependence of RBE not only on the absorbed dose but also on the anatomical location of the target organs must be carefully considered in discussing the appropriate weighting factors for preventing tissue reactions including DCS.

The reason for creating the peaks of RBE around 1 MeV is that z^* of recoil protons produced by neutron elastic scattering with hydrogen reaches the maximum around the energy. The peak energies are slightly shifted to higher energies with increasing the organ depth because neutrons tend to be moderated before arriving at the target organ. The tiny peaks observed at 20 MeV are mostly attributed to higher cross sections of the ¹²C(n,3α) reaction around the energy. The increase of RBE at the thermal energy observed only for skin reactions is considered attributable to 0.58 MeV protons produced by low-energy neutron capture reaction with nitrogen. Noted that RBE for skin reactions obtained from this study are generally smaller than those calculated in our previous study (5) because neutrons were delivered only to a small piece of skin in their exposure scenario; the γ-ray contributions to the skin dose were less important than the whole body exposure. For example, γ-rays contributed ~58% and 90% of the total dose of the thermal neutron irradiation in the skin and the blood, respectively. The representative exposure scenario should therefore be discussed also in determining the neutron RBE weighting factor for preventing tissue reactions.

CONCLUSION

The domain radii used in an MK model specialized for RBE estimation of tissue reactions were evaluated by analyzing several RBE data for DCS determined by past animal experiments. The mean domain radius for DCS obtained from this study was larger than the that for skin reaction obtained from the previous study, and the difference was borderline significant due to rather large variances of the evaluated domain radii best fit to each experiment. The means and uncertainties of RBE for DCS and skin reactions were also calculated for mono-energetic neutron irradiation of the human body, using PHITS coupled with the ICRP reference adult male phantom. The calculation results suggest that RBE depends on the anatomical locations of target organs and exposure scenarios, and such dependence should be taken into account in determining the neutron RBE weighting factor for preventing tissue reactions. To get more insights into whether the use of the cell survival model is adequate to estimate RBE for DCS, more RBE data for vascular cell survival would be needed.

CONFLICT OF INTEREST

None.

PRESENTATION AT A CONFERENCE

None.

CLINICAL TRIAL REGISTRATION NUMBER IF REQUIRED

None.