Strategy for randomised clinical trials in rare cancers

Short abstract

Proving that a new treatment is more effective than current treatment can be difficult for rare conditions. Data from small randomised trials could, however, be made more robust by taking other related research into account

The need for randomised trials to establish that treatments are effective is well established. However, because the effects of new treatments are usually modest compared with standard treatment, large numbers of patients are needed to detect any genuine benefits. This means that, even for common cancers, studies often have to be multicentred to ensure enough patients are recruited in a reasonable time. The strategy for testing new treatments in rare cancers, where it is impossible to accrue large number of patients, is unclear. We extend Lilford and others' proposal that a bayesian statistical approach, using related information from earlier studies, would be useful in designing and subsequently summarising small randomised controlled trials.¹ We suggest a scoring system for pooling this evidence and detail how this may be combined with hypothetical scenarios to assist in the design of, and justification for, a small randomised controlled trial.

Problems of small trials

Randomised controlled trials are regarded as the standard when comparing a new treatment with the standard treatment for a particular cancer. However, to be considered clinically worth while in clinical trials, these (essentially) very toxic regimens typically need to show relative reductions in the risk of death of 20-30%. For studies to have sufficient statistical power (≥80%) to detect treatment effects of this magnitude, several hundreds of deaths (typically 200 to 500) need to be observed. This implies trial sizes that are unrealistically large for rare cancers. Furthermore, even if a much larger treatment effect could be expected, estimates derived from the resulting (small) randomised controlled trial would lack the precision needed for clinical decisions.

Thus, investigators who wish to test new treatments for rare cancers tend to conduct either single arm studies of tumour response rates or comparative studies using historical controls. Alternatively, investigators may attempt to conduct small, underpowered, randomised controlled trials. These give rise to estimates of outcome that have unacceptably large confidence intervals and thus fail to provide clear answers. On these grounds, protocol review boards may regard such trials as unethical.² However, some have argued that in situations such as rare diseases, small randomised trials are the “only way that any unbiased measurements of effectiveness can be made.”³

Summary points

Treatments for rare cancers are difficult to evaluate in randomised trials as there are too few patients to detect any genuine treatment differences

Combination of previous data with trial data by bayesian techniques could help overcome this problem

Data from related studies are scored and weighted according to pertinence, validity, and precision

The method of combining data increases the robustness of information from small trials and can be used to help design and provide justification for such trials

One suggested solution to the problem is to use bayesian statistical approaches.⁴ These involve quantifying the information available about the outcome of interest in the form of a prior probability distribution at the design stage and combining this with the trial data to give a posterior distribution. Conclusions are then drawn from the posterior distribution. The key step in a bayesian approach is summarising the information available before the trial. This will often be from single arm studies or studies of response rate rather than survival.

Designing a new trial

Suppose we wish to design a randomised controlled trial to compare a new treatment with the standard treatment for a rare cancer, with the primary endpoint being overall survival. In such a case we would typically estimate the corresponding survival curves by the Kaplan-Meier technique and use the hazard ratio to estimate the magnitude of the treatment difference.⁵ It is customary when designing any trial to summarise the available information related to the question under consideration and to specify what would be regarded as a clinically important difference between the treatments being compared. In addition, there is a need to specify the type of patients eligible for the trial and quantify the number of patients that are likely to be recruited in a reasonable time frame.

Summarising and weighting information

For our model we assume that the evidence available at the planning stage of the proposed trial is from several studies, each providing relevant information according to three main criteria: pertinence, validity, and precision.

Pertinence

Pertinence summarises how close the information is to that which we wish to obtain during the proposed trial. The component parts to a full assessment of pertinence are the precise cancer investigated, the treatment(s) evaluated, and the endpoint measure. Table 1 lists six pertinence levels for these components with a score from 0 (no pertinence) to 1 (fully pertinent) for each. The minimum of the component scores provides an overall pertinence score (PS) for each study. By using the minimum score, we fully acknowledge whatever is the most serious defect of each study. An alternative would be to use the product of the scores, but this gives pertinence greater influence than validity (see below), which has only one component.

Table 1.

Proposed scales and scores for assessing the three components of pertinence of study relevant to small randomised controlled trial under design

Cancer	Treatment	Endpoint	Component score
Same disease and stage	Same as proposed standard and experimental treatments	Overall survival	1
Same disease, different stage or type of patient	Same standard treatment, similar experimental treatment (eg different dose)	PFS, DFS, or EFS; adjustment factor available	0.9
Different site, same biology/histology	Similar standard and experimental treatments	PFS, DFS, or EFS; adjustment factor unavailable	0.8
Same site, different biology/histology		Response rate validated as a surrogate endpoint	0.5
Different site, some similarity	Some similarity in standard or experimental treatment, or both	Response rate not validated as surrogate end point	0.3
Different disease	Unrelated treatments	Unrelated end points	0

DFS=disease-free survival, PFS=progression-free survival, EFS=event-free survival.

The adjustment factor (table 1) enables hazard ratios calculated from, for example, event-free survival to be converted to hazard ratios for overall survival when these are not reported. The adjustment factor is calculated as the ratio of two hazard ratios obtained from other studies that report ratios for both event-free survival and overall survival. If other end points are quoted, their relevance will depend on whether they have been validated as a surrogate for overall survival.⁶,⁷

Validity

Validity measures the quality of the available studies and depends on their design. It is maximal for properly designed and conducted randomised controlled trials and minimal for case reports. Table 2 gives a proposed classification and suggested validity scores.

Table 2.

Proposed scores for assessing the validity of study relevant to small randomised controlled trial under design

Design	Validity score
Randomised controlled trial:
No major flaws	1
Questionable quality	0.8
Major flaws	0.6
Non-randomised trial:
Prospective controlled	0.4
Single arm study:
With prespecified historical controls	0.3
No historical controls	0.2
Case study:
Series	0.1
Single report	0.05

Precision

Precision indicates how reliably the hazard ratio is determined. It depends on the number of events reported in each group. The more events there are, the more precise the ratio. Note that the study specific hazard ratio should be obtained, even from single arm studies without a control group. If necessary, this can be obtained by comparing the results with those from historical control group(s) mentioned in the study report or on some other clearly explained basis.

Correction factor

Once each study has been scored, the precision and validity scores are used as a correction factor to down weight the information. This is done by multiplying the number of events by the two scores in turn. This adjusted number of events reflects the added uncertainty associated with the methodological limitations of the study or with its limited pertinence to the question of interest. Other correction factors for the estimated hazard ratio may also be introduced at this stage–for example, to take into account the overestimate of treatment effects that is typically observed in uncontrolled studies.

Prior and posterior distribution

The adjusted numbers of events from each study are used to calculate the weighted mean prior log hazard ratio (LHR_Prior). The prior distribution is then constructed as a normal distribution with mean μ_Prior=LHR_Prior and standard deviation σ_Prior=√(4/m_Prior), where m_Prior is the adjusted number of events (deaths) from all the studies. If no prior information exists, a subjective prior distribution can be elicited from the investigators or other experts.^8–10

If μ_Data is the log hazard ratio based on actual deaths (m_Data), then (following Parmar et al¹¹) the posterior distribution has a normal distribution with mean μ_Posterior=(m_Prior μ_Prior+ m_Data μ_Data)/(m_Prior+ m_Data) and standard deviation σ_Posterior=√[4/(m_Prior+ m_Data)]. At the planning stage, μ_Data and m_Data are obtained from hypothetical scenarios, but once the trial is completed they are obtained from the actual data.

Using scenarios

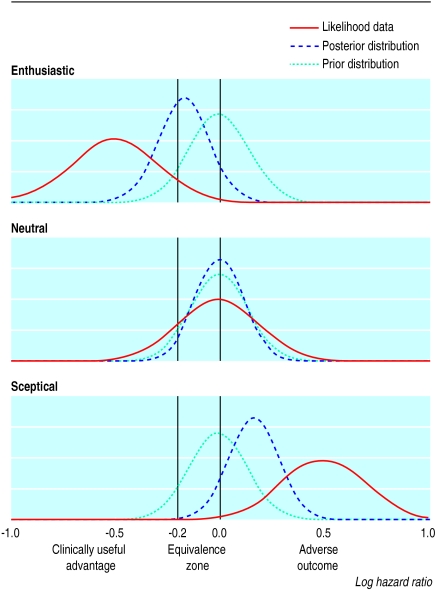
Once we have constructed the prior distribution and determined the number of patients likely to be recruited, the next step is to consider (at least) three hypothetical scenarios for the outcome of the trial: enthusiastic (experimental treatment is clearly better), neutral (treatment is the same), and sceptical (treatment worse than the control). These correspond to datasets with log hazard ratios that are negative, zero, or positive (figure). The prior distribution is combined with the hypothetical datasets to give a posterior distribution. For example, when the data from the enthusiastic scenario are combined with the prior distribution, which assumes no difference between treatments in this example, the final results suggest an almost 50% probability of a clinically useful advantage to the experimental treatment (see the area under the posterior distribution curve of the figure).

Figure 1.

Prior and posterior distributions and likelihood “data” for enthusiastic, neutral, and sceptical scenarios. The peak of each distribution corresponds to the most likely value of the true log hazard ratio, as estimated from the prior studies or the “data” or both (see text). The prior distribution in this example assumes that the two treatments are identical (log hazard ratio=0)

These scenarios can be presented to the protocol review board to help show that useful conclusions can be drawn from the proposed “small” trial. If the trial is given the go ahead, the posterior distribution is obtained from the real data combined with the prior distribution derived in the planning stage¹² or one modified by new information that becomes available during the trial.¹³

Discussion

Our proposed approach offers one way to overcome the problem of evaluating new treatments for rare conditions in randomised trials. Inferences based on the posterior distributions obtained in the approach provide a fuller description of the improved state of knowledge than is available from merely quoting P values or confidence intervals. An example of how the model could be applied in practice for supratentorial primitive neuroectodermal tumour, a rare childhood cancer, is available in our companion paper (see bmj.com).

The pertinence and validity scores that we have suggested to grade the usefulness of prior evidence should be modified as necessary to suit each project, although the investigators should clearly state the scoring systems that they use. Other scoring systems have been proposed,¹⁴,¹⁵ but a key feature of ours is that it reflects the relevance to a specific research question and is not simply a measure of overall quality. When all prior information derives from randomised trials, our approach reduces to a standard meta-analysis. When no suitable prior information is available, a distribution can be constructed by eliciting the opinions of experts.

We are not proposing an alternative to conducting trials of adequate size when these are feasible nor providing a justification for single centre studies where multicentre studies are clearly the best option. Rather, we hope that our proposals will contribute to the establishment of a clear strategy for randomised clinical trials in rare cancers and other conditions.