Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jul 8;128(28):6693–6703. doi: 10.1021/acs.jpcb.4c01417

Insights and Challenges in Correcting Force Field Based Solvation Free Energies Using a Neural Network Potential

Johannes Karwounopoulos †,‡, Zhiyi Wu , Sara Tkaczyk §,∥, Shuzhe Wang , Adam Baskerville , Kavindri Ranasinghe , Thierry Langer §, Geoffrey P F Wood , Marcus Wieder ¶,⊥,*, Stefan Boresch †,*
PMCID: PMC11264272  PMID: 38976601

Abstract

graphic file with name jp4c01417_0006.jpg

We present a comprehensive study investigating the potential gain in accuracy for calculating absolute solvation free energies (ASFE) using a neural network potential to describe the intramolecular energy of the solute. We calculated the ASFE for most compounds from the FreeSolv database using the Open Force Field (OpenFF) and compared them to earlier results obtained with the CHARMM General Force Field (CGenFF). By applying a nonequilibrium (NEQ) switching approach between the molecular mechanics (MM) description (either OpenFF or CGenFF) and the neural net potential (NNP)/MM level of theory (using ANI-2x as the NNP potential), we attempted to improve the accuracy of the calculated ASFEs. The predictive performance of the results did not change when this approach was applied to all 589 small molecules in the FreeSolv database that ANI-2x can describe. When selecting a subset of 156 molecules, focusing on compounds where the force fields performed poorly, we saw a slight improvement in the root-mean-square error (RMSE) and mean absolute error (MAE). The majority of our calculations utilized unidirectional NEQ protocols based on Jarzynski’s equation. Additionally, we conducted bidirectional NEQ switching for a subset of 156 solutes. Notably, only a small fraction (10 out of 156) exhibited statistically significant discrepancies between unidirectional and bidirectional NEQ switching free energy estimates.

Introduction

The importance of solvation in biological processes cannot be overestimated. Among other things, the correct description of the interaction of water with biological macromolecules and small molecule substrates is crucial for understanding ligand binding and, therefore, for computational techniques to predict binding affinities.1−4 The accuracy of the molecular-mechanical force field used in free energy difference calculations is one of the limitations of such methods. For this reason, several large-scale studies have focused on the computation of solvation free energy differences.5−8 The comparison of the predictions with experimental data helps to identify the strengths and weaknesses of the force field used.

Recently, we calculated solvation free energy differences for most of the compounds in the FreeSolv database using the CHARMM General force field (CGenFF).9 We have now completed analogous calculations with the Open force field (OpenFF), and these results are presented in detail below. Overall, the agreement with the experimental data is acceptable (for OpenFF 2.0 root mean squared error (RMSE) = 1.33 kcal/mol, mean absolute error (MAE) = 1.01 kcal/mol; for CGenFF RMSE = 1.76 kcal/mol, MAE: 1.12 kcal/mol). However, especially for CGenFF, there are a sizable number of molecules with significant discrepancies between the computed and experimentally determined solvation free energies.

Neural network potentials (NNP) are a recent development that allow a more accurate description of intra- and intermolecular interactions at an affordable cost. The use of NNPs in free energy simulations may, therefore, improve the accuracy of such calculations.10−13 However, although NNPs are fast compared to quantum chemical calculations, they are significantly slower than classical mechanical force fields.14 Furthermore, it is unknown how to apply certain “tricks” used in free energy simulations, such as soft-core potentials,15−17 in combination with NNPs. One can avoid both complications by indirect pathways, frequently used to compute free energy differences with quantum mechanics (QM)/molecular mechanics (MM) hybrid potential energy functions.18−26 Indirect free energy calculations use a computationally cheaper description of the potential energy (e.g., an MM force field) and calculate the free energy contribution needed for changing to a more expensive description of the potential energy (e.g., a QM/MM potential). The calculation of the free energy differences between the different levels of theory was shown to be nontrivial.23,27−31 One way to calculate them reliably is through nonequilibrium switching techniques (NEQ).32−36 NNPs offer a tempting trade-off between accuracy and speed compared to MM and QM methods, which is why they can be applied as the high-level potential in such indirect cycles. An early example of using NNPs to refine classical free energy simulations is a study by Rufa et al.10 Recently, we investigated the convergence of the correction step required in indirect pathways, i.e., calculating the free energy difference between an MM and an NNP representation of a system.37 In both studies, the ANI-2x38,39 NNP was used. Simulations with ANI and hybrid ANI/MM simulations can be carried out efficiently using TorchANI(40) and NNPOPS.14

The computational framework of ref (37) is suitable for use in the gas phase and aqueous solution. In this work, we explore whether MM → NNP and MM → NNP/MM corrections can improve the agreement of computed solvation free energies with the experiment. There are very efficient implementations of ANI in OpenMM; furthermore, mixing MM and ANI is straightforward.40,41 Therefore, the MM → NNP/MM corrections can be integrated smoothly into our automated workflows to compute the solvation free energies with CGenFF9 and OpenFF 2.0 (see below and the SI). Nevertheless, ANI/MM simulations are costly; therefore, we focus on the molecules that performed poorly with CGenFF, OpenFF 2.0, or both. From the ASFE results obtained at the MM level of theory, we identified the 100 compounds for each force field exhibiting the highest discrepancies compared to their experimental values (selection was limited to molecules with elemental composition covered by the ANI-2x training set; i.e.: H, C, N, O, F, S, and Cl). Thus, we created a set comprising 156 compounds, where 41 were among the worst-performing compounds for both force fields. The remaining compounds exhibited poor performance for either CGenFF (56 compounds) or OpenFF (59 compounds).

Furthermore, one must consider the limitations of the ANI/MM hybrid potential function currently implemented in OpenMM-ML. First, ANI-2x has been trained against quantum chemical calculations using the DFT functional ωB97X with the 6-31G* basis set.39 To improve solvation free energies calculated by QM/MM approaches, a careful choice of the DFT method/basis set is required.42 Second, as pointed out in ref (14), the coupling between MM and ANI is analogous to “mechanical embedding” in QM/MM simulations. In other words, only the intramolecular interactions of the solute are described by the NNP, whereas the solute–solvent interactions remain classical. Therefore, one cannot expect improvements in all cases. Specifically, describing the solute by ANI may result in different preferred conformations (compared to the force field), which, in turn, may lead to a different solvation free energy. Thus, improvements, if any, can be expected only for larger and/or flexible solutes. These cases are of interest as they can help identify shortcomings of the force field.

The remainder of the article is organized as follows: First, we report ASFEs obtained with the OpenFF force field. For the 589 compounds from the FreeSolv database that ANI-2x can handle, we calculated end-state corrections from unidirectional nonequilibrium work (NEQ) simulations. Second, we also calculated endstate corrections for the data set of 156 poor-performing compounds for the earlier CGenFF results.9 The endstate corrections using CGenFF for the MM description were computed using not only unidirectional but also two-sided NEQ approaches, making it possible to gauge the reliability of the computationally cheaper one-sided method. Lastly, we briefly investigate the correlation between the magnitude of the end-state corrections and the conformational flexibility of the solutes.

Theory

Absolute Free Energy Calculations

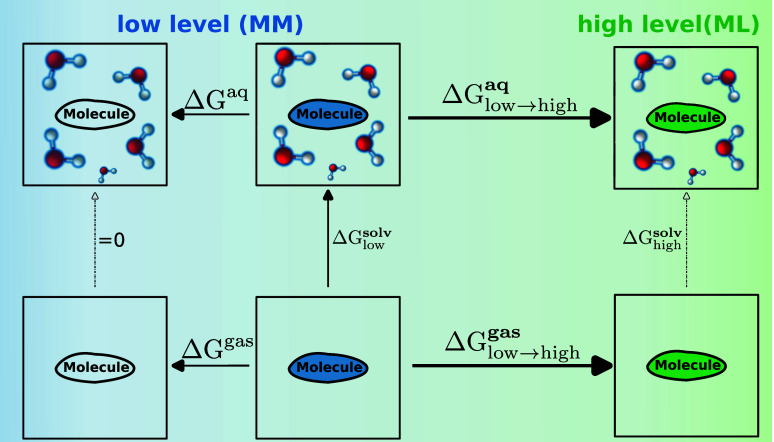
We calculated ASFEs using the alchemical pathway shown on the left side of Figure 1. Both protocols used in this work (see the Methods section below) involve (at least partial) annihilation of the solute’s nonbonded interactions, i.e., turning off both the nonbonded intramolecular interaction of the solute and its intermolecular interactions with its surroundings (solvent).44 The annihilation absolute free energy protocol requires a gas phase correction; the absolute solvation free energy of interest ΔGsolvMM is obtained as the difference between the annihilation protocol in the gas phase ΔGL1gas and in solution ΔGL1aq (ΔGsolvMM = ΔGL1gas – ΔGL1aq).43

Figure 1.

Figure 1

Open in a new tab

Free energy calculations between high and low levels of theory can be used to correct alchemical free energy calculations performed at a low level of theory. Left: The thermodynamic cycle used to compute an ASFE ΔGsolvlow at the MM level of theory using annihilation of the solute’s nonbonded interactions.43 Right: The indirect free energy cycle to correct ΔGsolvlow (in this work using either the CGenFF or the OpenFF force field) is from the MM to the NNP/MM level of theory.

Endstate Correction

Free energy estimates from NEQ work values (W) can be calculated using the Jarzynski equation45 or the Crooks fluctuation theorem.46 The Jarzynski equation recovers the free energy estimate between a target and a reference distribution based on an NEQ work process that starts at the reference and anneals to the target distribution. According to the Jarzynski equation, the free energy difference between two states 0 and 1 (W0→1) for NEQ work distributions is obtained as follows:

graphic file with name jp4c01417_m001.jpg 1

In our specific use case, state 0 indicates the potential energy function at the low level of theory, while 1 represents the same system at a higher level of theory. The subscript 0 in <>0 indicates that the NEQ switching simulations to obtain the work values W0→1 are started from equilibrium configurations sampled at the lower level of theory (state 0).

The Crooks fluctuation theorem recovers the equilibrium free energy estimate between the initial and final state based on NEQ work processes that transform the reference to the target potential and vice versa. Thus, one has to additionally carry out sampling at and NEQ switching simulations starting from the high level of theory or, in other words, compute work values in the 1 → 0 direction. The free energy between states 0 and 1 is then given by46

graphic file with name jp4c01417_m002.jpg 2

where f(x) denotes the Fermi function

graphic file with name jp4c01417_m003.jpg 3

and

graphic file with name jp4c01417_m004.jpg 4

Here, Q represents the canonical partition function of the respective state (0 and 1), and N is the number of work values in the forward and backward direction, respectively. Equation 2 is typically solved by searching iteratively for the value of C for which the argument of the logarithm becomes unity and, hence, the first term in eq 2 vanishes. As one sees from eq 4, the value of C found in this manner is essentially the sought free energy difference.

Methods

Overview of Calculations/Workflow

We performed ASFE calculations for most of the compounds in the FreeSolv database,47,48 a curated collection of experimental solvation free energies for 642 drug-like molecules. Compounds containing elements not covered in the ANI-2x training were removed, leaving 589 molecules for which an MM → NNP/MM endstate correction can be carried out. ASFEs were computed using two independent workflows, which we labeled as protocols EXS and UVIE. Here, we focus on the commonalities; additional details of each of the two protocols can be found in the SI. The UVIE protocol used the CGenFF force field49,50 and transformato(51,52) to calculate ASFEs at the MM level of theory. The results obtained with this approach have been previously described.9 In the EXS protocol, ASFEs at the MM level of theory were computed using openmmtools 0.23.053 and the Open Force Field (OpenFF 2.0).54 While the ASFEs at the MM level of theory were calculated with different methodologies/programs, the MM → NNP/MM end-state corrections were carried out quite similarly in both approaches, though specific adaptations were necessary.

Using the EXS protocol, endstate corrections were computed for all 589 molecules, i.e., the complete subset of the FreeSolv database, excluding any compounds that contained elements not covered by the training set of ANI-2x. These corrections were calculated only unidirectionally (eq 1). MM → NNP/MM corrections using the UVIE workflow were computed for the subset of the FreeSolv database (156 molecules), for which the force field results were in poor agreement with the experimental data (cf. the Introduction). These corrections were computed by uni- and bidirectional (Crooks’ theorem, eq 2) NEQ switching methods.

Endstate Correction with NNP

Equilibrium Simulations

MM Level of Theory

For each compound, a Langevin dynamics simulation was performed in the gas phase and in solution to generate equilibrium configurations from which the NEQ switches were started. OpenMM 8.041 was used with an integration time step of 1 fs. Molecules were solvated in TIP3P55 water, held rigid by the SETTLE algorithm,56 and simulations were performed under constant pressure conditions using a Monte Carlo barostat.57,58 The solutes themselves were fully flexible. The treatment of nonbonded interactions was slightly different in protocols UVIE and EXS; see the SI for details. Before each simulation, the geometry of the solute was optimized by using the L-BFGS minimizer.

NNP/MM Level of Theory

The NNP/MM simulations were carried out completely analogously to what was just described for the MM case. The only difference is the treatment of the intramolecular energetics of the small molecule, which was calculated using the ANI-2x potential instead of the respective MM force field.39 Specifically, the high-performance ANI-2x potential reimplementation, NNPOPS (v.0.4), was used in this work.14 To interpolate between the ANI-2x and the force field, we used the OpenMM-ML package.10

Nonequilibrium Switching Simulations

NEQ switching simulations of 5 ps length were initialized by randomly selecting 300 conformations (with replacement) from the equilibrium trajectories (either at the MM or NNP/MM endstate). For the total number of conformations saved in protocols EXS and UVIE, respectively, see the Supporting Information. The NEQ protocol consisted of an alternating sequence of propagation and perturbation steps in which the potential was slowly perturbed while propagating the coordinates. In each perturbation step, the coupling parameter λ = t/τ was used to scale the potential energy U = (1 – λ) UMM + λ UNNP/MM as a function of the current perturbation t ∈ [0, τ] and the total protocol length τ. Each propagation step consisted of a 1 fs integration step to propagate conformation x from xt to xt+1. The work value along a particular trajectory up to time t + 1 is calculated by using Wt = Ut+1(xt+1) – Ut(xt+1). Nonequilibrium switching simulations can be performed uni- and bidirectionally, i.e., employing either the Jarzynski or the Crooks equation. We used the exponential averaging (EXP) estimator and the Bennett Acceptance Ratio (BAR) estimator (both as implemented in pymbar(59)) to obtain free energies from unidirectional and bidirectional NEQ switching simulations, respectively. Errors were estimated via a bootstrapping procedure: Out of the pool of 300 work values, we randomly selected a subset (with replacement) for which ΔGMM→NNP was computed. This procedure was repeated 1000 times, and the standard deviation obtained in this manner was used as the error estimate.

NEQ switching simulations were performed both in aqueous solution and in the gas phase to obtain ΔGaqMM → NNP/MM and ΔGgasMM → NNP (see the right-hand side of Figure 1). The free energy difference (ΔGMM→NNP/MM) between levels of theory and thus the endstate correction value is obtained by ΔGcorrMM → NNP/MM = −ΔGgasMM → NNP + ΔGaqMM → NNP/MM. Thus, the corrected ASFE can be calculated as ΔGsolvNNP/MM = ΔGsolvMM + ΔGcorrMM → NNP/MM.

In the EXS protocol, corrections were computed using only unidirectional NEQ switching simulations, limiting the calculation of the free energy difference to the EXP estimator. By contrast, using protocol UVIE, also bidirectional NEQ calculations were performed, allowing the use of Crooks’ equation. Corrections obtained by Crooks’ equation are denoted as ΔGcorr, CrooksMM ↔ NNP/MM. Results are presented as the deviation of the computed result from the experimental reference value, i.e.,

graphic file with name jp4c01417_m005.jpg 5

The superscripts exp and calc denote the experimental and calculated solvation free energy, respectively. The subscript theory stands for either OpenFF or CGenFF at the MM level or the ANI-2x corrected result, indicated as OpenFF/ANI or CGenFF/ANI, respectively.

Multistate Equilibrium Free Energy Simulations

For 10 molecules out of the 156 molecule subset, we performed multistate equilibrium free energy simulations (MFES) using 11 equidistant λ windows (λ = 0.1, 0.2, ..., 1.0), with λ = 0 being the MM-endstate and λ = 1 being the NNP-endstate (protocol UVIE only). Sampling was performed for 5 ns from each equilibrium distribution, and 5,000 samples were collected. To ensure that the samples represent the stationary distribution, the initial 20% of each simulation was discarded, resulting in 4,000 samples per simulation and λ window. These were further pruned, and only every fifth sample was used to calculate the free energy difference of interest. From the combined set of 11 alchemical states, consisting of 800 samples each (11 × 800 in total), connecting the MM and NNP potentials, we calculated the free energy difference using the MBAR estimator, as implemented in the pymbar package.59 We monitored whether there was overlap between neighboring λ-states.

Results and Discussion

ASFE Results Using OpenFF 2.0

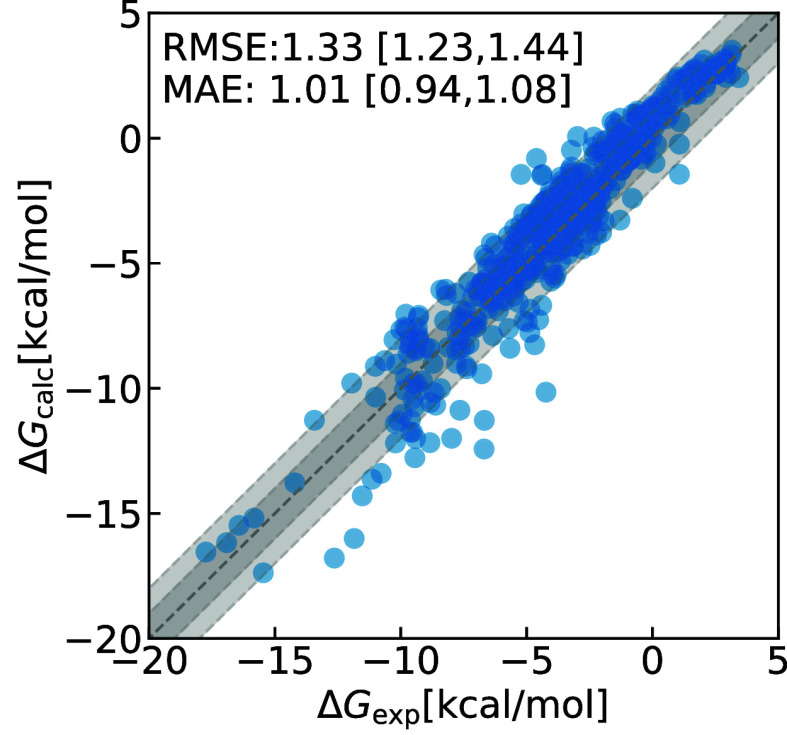
The performance of the classical ASFE results for 589 molecules of the FreeSolv database calculated with the EXS protocol (OpenFF 2.0) is good. A plot comparing experimental and calculated ASFEs is shown in Figure 2. Both RMSE: 1.33 [1.23, 1.44] kcal/mol and MAE: 1.01 [0.94, 1.08] kcal/mol are low. The values given in the brackets [] indicate the 95% confidence interval obtained via bootstrapping. The RMSE and MAE obtained with OpenFF 2.0 are better than the values for 621 molecules obtained with CGenFF (RMSE: 1.76 [1.52, 2.02] kcal/mol, MAE: 1.12 [1.02, 1.23] kcal/mol)9 (protocol UVIE), as well as the values obtained with the AMBER general force field (GAFF)60 for all 642 molecules as reported in the FreeSolv database (RMSE: 1.54 [1.39, 1.70], MAE 1.11 [1.03, 1.19] kcal/mol).47,48 Note that some improved results for GAFF have been reported recently.61,62

Figure 2.

Figure 2

Open in a new tab

Absolute solvation free energy calculations using the OpenFF force field. ΔGcalc are the calculated values using protocol EXS, while experimental values (ΔGexp) are taken from the literature.47 The dark and light gray areas depict the ±1 and ±2 kcal/mol confidence interval.

In Figure S1 in the Supporting Information, we compare the ASFEs calculated with these three force fields by presenting kernel density estimates (KDE)63,64 of the deviation between experimental and calculated ASFE, δΔG. These plots highlight a weakness of all three force fields which is not apparent from the RMSE and MAE: for all three, the peak of the KDE of δΔG is near −1 kcal/mol, indicating that on average ASFEs predicted by all three force fields are too positive (i.e., too hydrophobic) by about 1 kcal/mol. This finding is in line with earlier observations; see, e.g., Mobley et al.5

Endstate Corrections

Unidirectional Correction of the OpenFF ASFEs to ANI-2x/OpenFF (589 Compounds, Protocol EXS)

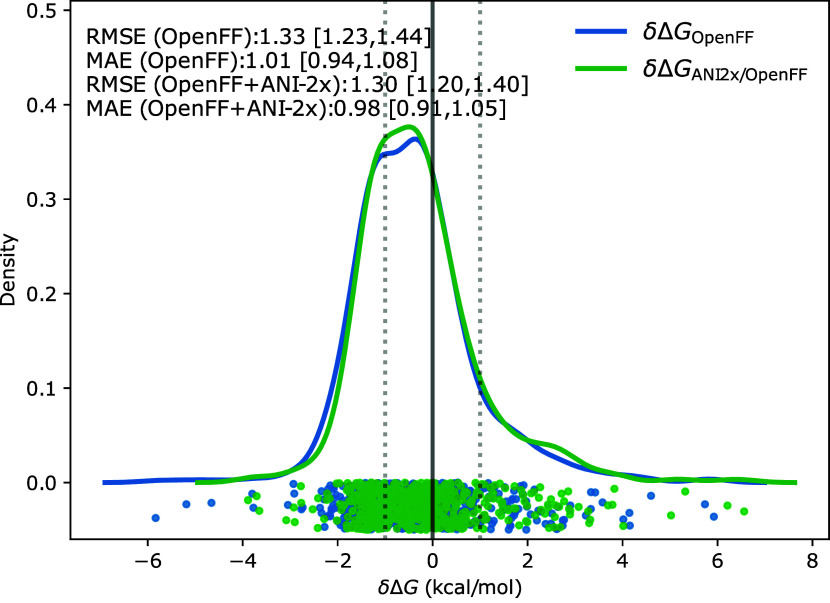
Using the EXS protocol, we computed unidirectional ΔGcorrMM→ NNP/MM corrections for the 589 (out of 642) molecules in the FreeSolv database that can be described by the ANI-2x NNP (cf. Methods). As indicated in the inset of Figure 3, the RMSE and MAE values for the MM and NNP/MM results are practically identical. Similarly, the correlation with the experiment remains unchanged (Pearson correlation is 0.95 in both cases, while the Spearman correlation increased marginally from 0.94 [0.93, 0.95] to 0.95 [0.94, 0.96]). All statistical descriptors (RMSE, MAE, etc.) discussed here and later in this article are summarized in a supplementary file (jp4c01417_si_002.csv). An alternative summary of the results is shown in Figure 3. Here, we superpose the KDE of δΔG (eq 5) between the experimental and calculated MM and NNP/MM corrected free energy estimates for the 589 molecules under investigation. The two KDEs are practically indistinguishable; if anything, the NNP/MM results (green curve) are shifted slightly toward more positive values.

Figure 3.

Figure 3

Open in a new tab

The KDE of δΔG for the NNP corrected free energy estimate for the 589 compounds of the FreeSolv database. Overlay of the KDE for δ ΔG (eq 5) of the MM (blue line, ΔGOpenFF) and the NNP/MM (green line, ΔGOpenFF/ANI2x) free energy estimates. Additionally, the plot shows dots indicating the individual deviations from the experimental values for the MM ASFE results (blue dots) and the NNP/MM corrected ASFE results using the unidirectional correction according to protocol EXS (green dots). The gray line displays the ideal behavior, δΔG = 0 with the two dotted gray lines indicating a deviation of ±1 kcal/mol.

If one studies the corrections more closely (for full details, see the data in file jp4c01417_si_002.csv in the SI), one notices that the absolute value of the correction |ΔGcorrMM→NNP/MM| for more than half of the molecules (294) is smaller than 0.5 kcal/mol. First, this indicates that the free energy difference between the MM and NNP/MM descriptions of interactions is very similar for these solutes. Second, based on the statistical uncertainty of the corrections (see jp4c01417_si_002.csv in the SI), 0.5 kcal/mol is a rough threshold indicating whether the MM → NNP/MM correction is statistically significant. While there are certainly systems for which the statistical error is very low and, thus, corrections of, e.g., ± 0.2 or ±0.3 kcal/mol are significant, such small (absolute values of the) corrections have a marginal impact on the agreement with the experiment at best. Even if one therefore considers only solutes for which the magnitude of the correction was larger than 0.5 kcal/mol, the resulting ASFEs had improved agreement with the experimental values in only approximately 60% of the cases. Overall, both the statistical descriptors and the KDE plots show that the effect of the MM → NNP/MM correction when applied to the full data set is statistically not significant.

Comparison of Corrections Using Different Force Fields (Protocol UVIE and Protocol EXS, 156 Molecule Subset)

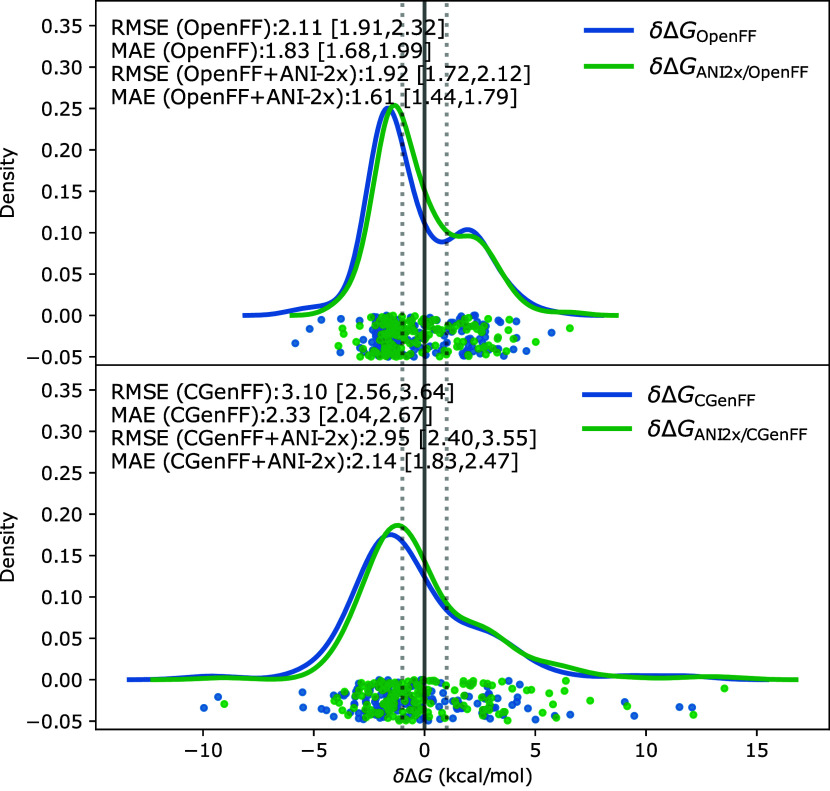
The results of the MM → NNP/MM corrections for the subset of 156 molecules for which the computed solvation energies are in poor agreement with the experiment when using either the CGenFF or the OpenFF 2.0 force field or both are summarized in Figure 4. Using the UVIE protocol, the MAE was reduced by 0.15 kcal/mol, from 3.10 [2.56, 3.64] kcal/mol to 2.95 [2.40, 3.55] kcal/mol. While the Pearson correlation coefficient improved slightly from 0.77 [0.69, 0.83] to 0.80 [0.72, 0.87], there was no change in the Spearman correlation (0.76 [0.66, 0.83] before and 0.76 [0.64, 0.83] after the correction). Applying the NNP correction to the ASFEs obtained with OpenFF (protocol EXS) gave a similar trend. The RMSE and MAE were reduced from 2.11 [1.91, 2.32] and 1.83 [1.68, 1.99] kcal/mol to 1.92 [1.72, 2.12] and 1.61 [1.44, 1.79] kcal/mol, respectively. The Pearson as well as the Spearman correlation improved slightly from 0.90 [0.87, 0.92] to 0.93 [0.90, 0.95] and from 0.91 [0.87, 0.93] to 0.92 [0.89, 0.94] respectively. While the numbers move slightly in the right direction, none of the improvements are statistically significant. The KDEs in Figure 4 provide similar information: for both protocols, the NNP/MM corrected results are shifted slightly toward the right, including the respective peak of the KDE, but one also sees that some results become even more too positive; i.e., one sees more green than blue dots toward positive values.

Figure 4.

Figure 4

Open in a new tab

The KDE of δ ΔG (eq 5) for the 156 compound subset. Top: KDE of the errors obtained with OpenFF 2.0 (blue line) and for the NNP corrected results (green line). Bottom: KDE of the errors for CGenFF (blue) and NNP corrected results (green). Results for the individual molecules are shown as dots: blue for the MM, and green for the NNP corrected values.

Table 1 provides some information in how many cases the NNP correction (ΔGcorrMM →NNP/MM) improved the agreement with the experimental values. In both protocols, this was the case for slightly over 60% of the solutes. However, even for this reduced subset of molecules, the (absolute value of the) correction is <0.5 kcal/mol in most cases; |ΔGcorrMM →NNP/MM| is larger than 0.5 kcal/mol for only about 25% of the compounds (37 for CGenFF, 46 for OpenFF). For these molecules, applying the MM → NNP/MM correction improves the agreement with experiment in almost 70% of the cases, a slightly higher percentage compared to the entire 156 molecule subset.

Table 1. Comparison of Improvements for the 156 Compound Subset.
  CGenFF OpenFF
Corrections improving the results [%] 62 63
Percentage of molecules with |ΔGcorr| > 0.5 kcal/mol [%] 24 29
Percentage thereof improving results [%] 68 67
Open in a new tab

Comparing Unidirectional with Bidirectional and MFES Results

In protocol UVIE, we computed the MM → NNP/MM correction not only unidirectionally, i.e., by using Jarzynski’s equation, but also carried out equilibrium simulations at the NNP/MM level of theory and backward switches in the NNP/MM → MM direction. Hence, we also calculated ΔGcorr, CrooksMM↔NNP/MM using Crooks’ equation. Therefore, we could investigate deviations of the unidirectional from bidirectional results. Out of the 156 compounds studied using the UVIE protocol the deviation between the Jarzynski and Crooks results, ΔCrooks = |ΔGcorr, CrooksMM↔NNP/MM – ΔGcorrMM→NNP/MM|, was larger than 1 kT only for 10 compounds, either in the gas phase or in aqueous solution, or both. For the three solutes, ΔCrooks was larger than 2 kcal/mol. Full details, together with the 2D structures of the ten molecules, are shown in Figure S3.

When using protocol UVIE, overlap between forward and backward work distributions was monitored routinely. We observed that there was no overlap between the distributions of forward and backward work values in the three cases where ΔCrooks > 2 kcal/mol plus one additional case. Poor or no overlap between forward and backward work distributions raises doubts about the reliability of even the Crooks results. Therefore, for these ten molecules we also computed the correction free energy by MFES (ΔGcorr, MFESMM↔NNP/MM) and inspected ΔMFES = ΔGcorrMFES – ΔGcorr, CrooksMM↔NNP/MM, the deviation between the MM → NNP/MM correction calculated with Crooks’ equation and MFES. The detailed results are also plotted in Figure S3. For the six molecules for which there is overlap, ΔMFES < 1 kcal/mol and most deviations are even within the 1 kT threshold. For the four molecules without overlap, the deviation is larger, as is to be expected (bottom panel of Figure S3).

These findings indicate that unidirectional methods are not sufficient in all cases, and in selected cases, even the bidirectional Crooks result may not be fully reliable. However, we observed problems only for 10 out of 156 molecules, i.e., for well below 10% of the system studied. Replacing the unidirectional corrections with the Crooks or MFES results would lead to only negligible changes in the overall RMSE, MAE, and correlation coefficients. Furthermore, the more accurate corrections (Crooks and/or MFES) do not necessarily improve the agreement with the experiment; see the spreadsheet jp4c01417_si_003.csv in the SI.

Investigating Large Corrections and Poor Convergence

Since ΔGcorrMM→NNP/MM was negligible in many, if not most, cases, it is of some interest to investigate when the correction is likely to be sizable. Furthermore, although it affects only a few systems (cf. the previous subsection), it is important to understand when and why unidirectional approaches (Jarzynski’s equation) may fail to converge. In trying to address these questions, one should keep in mind that the NNP/MM description used in this study applies only to the solute. While the solute’s interactions are treated by ANI-2x, the solute–solvent interactions are always classical. Any analysis, therefore, has to focus on the solute, i.e., the part of the system handled by the NNP.

Studies using the indirect cycle approach to compute free energy differences at the QM/MM level of theory have shown that convergence is difficult to achieve if there are different conformational preferences at the two levels of theory.32,34,65 We use the shorthand “different conformational preferences” to refer to situations, where the conformations sampled preferentially or exclusively at one level of theory are rare or never sampled at the respective other level of theory. Such cases are more likely for flexible solutes. The preferred conformation(s) of a solute, however, influences its solvation free energy, so for flexible solutes ΔGcorrMM→NNP/MM may also be larger.

To explore this hypothesis, we grouped the MM → NNP/MM corrections obtained for the 156 compound subset and protocol UVIE according to the number of rotatable bonds nrot (as reported by the CalcNumRotatableBonds function in the rdkit toolkit, https://www.rdkit.org/). This criterion is clearly far from perfect; e.g., aliphatic ring systems may have nrot = 0, yet they are often highly flexible. In Figure 5A, ΔGcorrMM→NNP/MM as a function of nrot is shown as box plots; all outliers (shown as diamonds) have numbers indicating the molecules in question (these are shown in Figure 5B). An analogous plot for EXS is shown in Figure S2 of the Supporting Information. Solutes that are outliers in both protocols are highlighted in purple. Ignoring for the moment the outliers, there appears to be a slight trend toward larger corrections as nrot increases. Given that changing from an MM to an NNP potential energy function affects only the intramolecular interactions of the solute, the ΔGcorrMM→NNP/MM correction is expected to be small for rigid molecules (low nrot, aromatic rings). Conversely, however, the correction does not have to be significant for flexible molecules. First, if the MM and the NNP descriptions of the solute intramolecular interactions lead to similar conformational preferences, there is little reason to expect large corrections. Furthermore, even if the MM and NNP descriptions of the solute do result in different conformational preferences, the solute–solvent interactions, which are described classically throughout, may still be similar.

Figure 5.

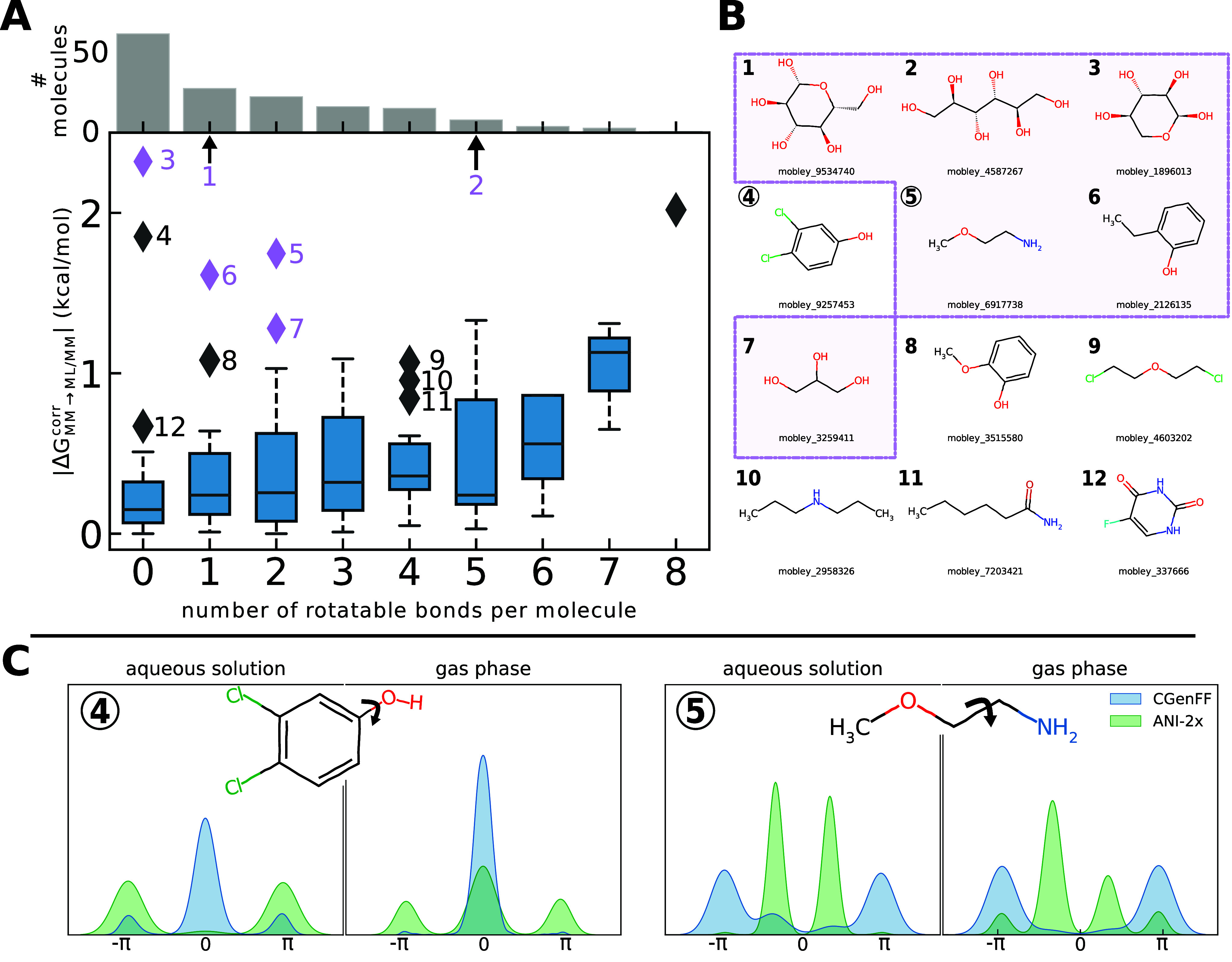
Figure 5

Open in a new tab

Panel A: Box plot of the unidirectional NNP correction (ΔGcorrMM→NNP/MM) as a function of the number of rotatable bonds for the 156 compound subset using protocol UVIE (an analogous plot for EXS is shown in Figure S2 in the Supporting Information). Molecules that are outliers in terms of ΔGcorrMM→NNP/MM are indicated as diamonds and labeled by numbers, starting with 1 for the compound having the highest correction value. Compounds that are also outliers when using protocol EXS are colored in purple. The bars at the top of the plot indicate how many molecules have this number of rotatable bonds. Panel B: Molecular structures of the outliers 1–12. Molecules in the purple box are also outliers when using protocol EXS. Panel C: Density of the indicated dihedral angle of compounds 4 (left side) and 5 (right side), respectively, in the gas phase and in aqueous solution when using CGenFF (blue) and ANI-2x (green).

Analyzing some outliers provides additional insight. The two solutes with the largest ΔGcorrMM→NNP/MM value have nrot = 1 (compound 1) and nrot = 5 (compound 2). Both have also large ΔGcorrMM→NNP/MM values using protocol EXS (see Figure S2) and converge poorly; see the previous subsection and Figure S3. The pyranose ring of compound 1 is an example where the nrot criterion fails; obviously, this cyclic structure is highly flexible, but this is not picked up by rdkit’s rotatable bond criterion. This is also the case for compound 3, which is reported as nrot = 0. Compound 2, on the other hand, is obviously flexible and has a large number of rotatable bonds. On the other hand, the ΔGcorrMM→NNP/MM value of compound 4 (nrot = 0) seems unexpected, as this is an aromatic ring. A possible explanation can be seen in Figure 5C, left panel, where the average population of the indicated C–C–O–H dihedral angle is plotted. Especially in aqueous solution, the distributions of this dihedral angle are quite different for the force field (blue) and for ANI-2x (green). The orientation of the hydroxyl group relative to the chlorine substituents may influence the solvation free energy of the molecule. An analogous plot is shown in the right panel of Figure 5C for compound 5. It has two rotatable bonds, one of which, as indicated, is populated quite differently when the solute is described by MM and NNP, respectively. Similarly to what was just discussed for compound 4, the different orientation of the hydroxyl group relative to the other substituent(s) when using MM and ANI-2x, respectively (data not shown), also seems to be the cause of the large ΔGcorrMM→NNP/MM corrections for compounds 6 and 8. Finally, compound 9, bis-2-chloroethyl ether, was discussed in some detail in ref (32), where it was found that the conformational preferences of the two relevant dihedral angles differ significantly between MM and the semiempirical QM method used.

Conclusion

Utilizing the ANI-2x potential, we employed an automated protocol to correct solvation free energies obtained with the OpenFF and CGenFF force fields. When the MM → NNP/MM correction is applied to the full subset of molecules that can be described by ANI-2x, the minuscule overall improvement in free energy is statistically not significant (see Figure 3). Focusing on the subset of molecules for which the error of the ASFE is highest using the MM protocols, we can observe some improvement and large corrections for a few molecules (Figures 4 and 5). Even here, however, the changes are statistically not significant, and for the systems where the corrections are >0.5 kcal/mol, they improve the agreement with the experiment only in less than 70% of the cases.

The majority of the results presented here were calculated using unidirectional NEQ protocols, i.e., Jarzynsky’s equation. The ANI-2x potential is sufficiently fast so that we could also carry out bidirectional NEQ switching and sampling for a sizable subset of the FreeSolv (156 molecules, protocol UVIE). Only a small subset (10 out of 156) showed statistically relevant deviations between the free energy estimate based on the forward NEQ switching trajectory and the forward and reverse NEQ switching trajectories. Given the limitations of mechanical embedding (see below), using unidirectional methods to compute the MM → NNP/MM corrections seems adequate.

There are important lessons to be learned from these results: The currently available coupling between MM and ANI corresponds to mechanical embedding in QM/MM.10,14 The description of the solute–solvent interactions remains classical at both levels of theory (MM and NNP/MM). This explains why different results are obtained depending on the MM force field used and why the corrections are tiny in most cases. As shown, large corrections are obtained primarily for flexible solutes. We, therefore, surmise that improving free energy estimates significantly will require advanced treatment of the interaction of the small molecule with its surroundings, i.e., moving beyond mechanical embedding.66−69 The importance of describing solute–solvent interactions as accurately as possible when calculating solvation free energy differences has been noted previously.70−72 An attempt to go beyond mechanical embedding for a handful of solutes is described in the SI; the data suggest that treating solute–solvent interactions at the NNP level of theory has significant effects, but the results clearly are not converged.

As an alternative to more advanced embeddings, treatment of the entire system with the NNP is a possibility. The performance of, e.g., ANI-2x in OpenMM is sufficient to allow nanosecond simulations of solute–solvent systems consisting of the solute and up to a thousand solvent molecules. Obviously, the success of direct free energy simulations at the NNP level of theory depends on several prerequisites. First, the NNP used has to reproduce the condensed phase properties of aqueous solutions correctly. In addition, protocols for the annihilation or decoupling of the solute need to be developed to ensure that end point catastrophes are avoided.

Acknowledgments

S.B. acknowledges financial support from the National Institutes of Health (1R01GM129519). M.W. acknowledges support from the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM132386 and the Sloan Kettering Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Data Availability Statement

All plots shown in this paper were produced using the Jupyter-notebook available on GitHub (https://github.com/JohannesKarwou/notebooks/blob/main/combinedDataset.ipynb). The notebook also contains the calculations of all statistics reported in this paper (RMSE, MAE, Pearson correlation, and Spearman’s rank correlation) and the corresponding bootstrapped errors. Python package used in this work (release v0.3): https://github.com/wiederm/endstate_correction.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c01417.

  • We describe in detail how ASFEs were calculated on the MM level of theory and how the endstate corrections to the ANI-2x potential were applied for the two respective protocols (UVIE and EXS). In Figure S2 we show the unidirectional NNP correction as a function of rotatable bonds for the 156 compounds subset using protocol EXS as well as the structures of the outliers observed. In Figure S3 we show several characteristics of the 10 compounds (of the 156 subset), for which the MM → NNP/MM correction differed by more than 1 kT when computed by Jarzynski’s and Crooks’ equation (PDF)

  • The ASFE on the MM and NNP/MM level for the 589 compounds of the FreeSolv database calculated using EXS are summarized in the spreadsheet jp4c01417_si_002.csv (CSV)

  • The ASFE values on the MM and NNP/MM level for the two force fields (OpenFF 2.0 and CGenFF) for the 156 compounds of the combined data set calculated with protocol EXS and UVIE are summarized in the spreadsheet jp4c01417_si_003.csv. In the case of the correction for CGenFF, unidirectional values are indicated with “Jar”, while bidirectional values are depicted with “Crooks” (CSV)

The authors declare the following competing financial interest(s): S.B. is a consultant for Exscientia.

Special Issue

Published as part of The Journal of Physical Chemistry Bvirtual special issue “Charles L. Brooks III Festschrift”.

Supplementary Material

jp4c01417_si_001.pdf (489.5KB, pdf)
jp4c01417_si_002.csv (85.3KB, csv)
jp4c01417_si_003.csv (20.2KB, csv)

References

  1. Chodera J. D.; Mobley D. L.; Shirts M. R.; Dixon R. W.; Branson K.; Pande V. S. Alchemical free energy methods for drug discovery: progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. 10.1016/j.sbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cournia Z.; Allen B.; Sherman W. Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57, 2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]
  3. Schindler C. E. M.; et al. Large-Scale Assessment of Binding Free Energy Calculations in Active Drug Discovery Projects. J. Chem. Inf. Model. 2020, 60, 5457–5474. 10.1021/acs.jcim.0c00900. [DOI] [PubMed] [Google Scholar]
  4. Cournia Z.; Chipot C.; Roux B.; York D. M.; Sherman W.. Free Energy Methods in Drug Discovery: Current State and Future Directions; American Chemical Society, 2021; pp 1–38. [Google Scholar]
  5. Mobley D. L.; Bayly C. I.; Cooper M. D.; Shirts M. R.; Dill K. A. Small molecule hydration free energies in explicit solvent: An extensive test of fixed-charge atomistic simulations. J. Chem. Theory Comput. 2009, 5, 350–358. 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Shivakumar D.; Deng Y.; Roux B. Computations of absolute solvation free energies of small molecules using explicit and implicit solvent model. J. Chem. Theory Comput. 2009, 5, 919–930. 10.1021/ct800445x. [DOI] [PubMed] [Google Scholar]
  7. Malde A. K.; Zuo L.; Breeze M.; Stroet M.; Poger D.; Nair P. C.; Oostenbrink C.; Mark A. E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. (PMID: 26598349) 10.1021/ct200196m. [DOI] [PubMed] [Google Scholar]
  8. Boulanger E.; Huang L.; Rupakheti C.; MacKerell A. D. J.; Roux B. Optimized Lennard-Jones Parameters for Druglike Small Molecules. J. Chem. Theory Comput. 2018, 14, 3121–3131. (PMID: 29694035) 10.1021/acs.jctc.8b00172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Karwounopoulos J.; Kaupang Å.; Wieder M.; Boresch S. Calculations of Absolute Solvation Free Energies with Transformato – Application to the FreeSolv Database Using the CGenFF Force Field. J. Chem. Theory Comput. 2023, 19, 5988–5998. 10.1021/acs.jctc.3c00691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Rufa D. A.; Macdonald H. E. B.; Fass J.; Wieder M.; Grinaway P. B.; Roitberg A. E.; Isayev O.; Chodera J. D.. Towards chemical accuracy for alchemical free energy calculations with hybrid physics-based machine learning/molecular mechanics potentials. bioRxiv (accessed 2024-05-21) 2020.
  11. Kulichenko M.; Smith J. S.; Nebgen B.; Li Y. W.; Fedik N.; Boldyrev A. I.; Lubbers N.; Barros K.; Tretiak S. The Rise of Neural Networks for Materials and Chemical Dynamics. J. Phys. Chem. Lett. 2021, 12, 6227–6243. 10.1021/acs.jpclett.1c01357. [DOI] [PubMed] [Google Scholar]
  12. Akkus E.; Tayfuroglu O.; Yildiz M.; Kocak A. Accurate Binding Free Energy Method from End-State MD Simulations. J. Chem. Inf. Model. 2022, 62, 4095–4106. 10.1021/acs.jcim.2c00601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Sabanés Zariquiey F.; Galvelis R.; Gallicchio E.; Chodera J. D.; Markland T. E.; De Fabritiis G. Enhancing Protein–Ligand Binding Affinity Predictions Using Neural Network Potentials. J. Chem. Inf. Model. 2024, 64, 1481–1485. 10.1021/acs.jcim.3c02031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Galvelis R.; Varela-Rial A.; Doerr S.; Fino R.; Eastman P.; Markland T. E.; Chodera J. D.; De Fabritiis G. NNP/MM: Accelerating Molecular Dynamics Simulations with Machine Learning Potentials and Molecular Mechanics. J. Chem. Inf. Model 2023, 63, 5701–5708. 10.1021/acs.jcim.3c00773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Beutler T. C.; Mark A. E.; van Schaik R. C.; Gerber P. R.; van Gunsteren W. F. Avoiding singularities and numerical instabilities in free energy calculations based on molecular simulations. Chem. Phys. Lett. 1994, 222, 529–539. 10.1016/0009-2614(94)00397-1. [DOI] [Google Scholar]
  16. Zacharias M.; Straatsma T. P.; McCammon J. A. Separation-shifted scaling, a new scaling method for Lennard-Jones interactions in thermodynamic integration. J. Chem. Phys. 1994, 100, 9025–9031. 10.1063/1.466707. [DOI] [Google Scholar]
  17. Lee T. S.; Lin Z.; Allen B. K.; Lin C.; Radak B. K.; Tao Y.; Tsai H. C.; Sherman W.; York D. M. Improved Alchemical Free Energy Calculations with Optimized Smoothstep Softcore Potentials. J. Chem. Theory Comput. 2020, 16, 5512–5525. 10.1021/acs.jctc.0c00237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gao J.; Xia X. A Priori Evaluation of Aqueous Polarization Effects through Monte Carlo QM-MM Simulations. Science 1992, 258, 631–635. 10.1126/science.1411573. [DOI] [PubMed] [Google Scholar]
  19. Luzhkov V.; Warshel A. Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem. 1992, 13, 199–213. 10.1002/jcc.540130212. [DOI] [Google Scholar]
  20. Gao J.; Freindorf M. Hybrid ab Initio QM/MM Simulation of N-Methylacetamide in Aqueous Solution. J. Phys. Chem. A 1997, 101, 3182–3188. 10.1021/jp970041q. [DOI] [Google Scholar]
  21. Valiev M.; Bylaska E. J.; Dupuis M.; Tratnyek P. G. Combined Quantum Mechanical and Molecular Mechanics Studies of the Electron-Transfer Reactions Involving Carbon Tetrachloride in Solution. J. Phys. Chem. A 2008, 112, 2713–2720. 10.1021/jp7104709. [DOI] [PubMed] [Google Scholar]
  22. Woods C. J.; Manby F. R.; Mulholland A. J. An efficient method for the calculation of quantum mechanics/molecular mechanics free energies. J. Chem. Pys. 2008, 128, 014109 10.1063/1.2805379. [DOI] [PubMed] [Google Scholar]
  23. Heimdal J.; Ryde U. Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys. Chem. Chem. Phys. 2012, 14, 12592–12604. 10.1039/c2cp41005b. [DOI] [PubMed] [Google Scholar]
  24. Lu X.; Fang D.; Ito S.; Okamoto Y.; Ovchinnikov V.; Cui Q. QM/MM free energy simulations: recent progress and challenges. Mol. Simul. 2016, 42, 1056–1078. 10.1080/08927022.2015.1132317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Giese T. J.; York D. M. Development of a Robust Indirect Approach for MM →QM Free Energy Calculations That Combines Force-Matched Reference Potential and Bennett’s Acceptance Ratio Methods. J. Chem. Theory Comput. 2019, 15, 5543–5562. 10.1021/acs.jctc.9b00401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Cui Q.; Pal T.; Xie L. Biomolecular QM/MM Simulations: What Are Some of the “Burning Issues”?. J. Phys. Chem. B 2021, 125, 689–702. 10.1021/acs.jpcb.0c09898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. König G.; Hudson P. S.; Boresch S.; Woodcock H. L. Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using non-Boltzmann Bennett reweighting schemes. J. Chem. Theory Comput. 2014, 10, 1406–1419. 10.1021/ct401118k. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Cave-Ayland C.; Skylaris C. K.; Essex J. W. Direct validation of the single step classical to quantum free energy perturbation. J. Phys. Chem. B 2015, 119, 1017–1025. 10.1021/jp506459v. [DOI] [PubMed] [Google Scholar]
  29. Genheden S.; Cabedo Martinez A. I.; Criddle M. P.; Essex J. W. Extensive all-atom Monte Carlo sampling and QM/MM corrections in the SAMPL4 hydration free energy challenge. J. Comput.-Aided Mol. Des. 2014, 28, 187–200. 10.1007/s10822-014-9717-3. [DOI] [PubMed] [Google Scholar]
  30. König G.; Brooks B. R. Correcting for the free energy costs of bond or angle constraints in molecular dynamics simulations. Biochimica et Biophysica Acta (BBA) - General Subjects 2015, 1850, 932–943. 10.1016/j.bbagen.2014.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ryde U. How Many Conformations Need to Be Sampled to Obtain Converged QM/MM Energies? the Curse of Exponential Averaging. J. Chem. Theory Comput. 2017, 13, 5745–5752. 10.1021/acs.jctc.7b00826. [DOI] [PubMed] [Google Scholar]
  32. Kearns F. L.; Hudson P. S.; Woodcock H. L.; Boresch S. Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities. J. Comput. Chem. 2017, 38, 1376–1388. 10.1002/jcc.24706. [DOI] [PubMed] [Google Scholar]
  33. Hudson P. S.; Woodcock H. L.; Boresch S. Use of Nonequilibrium Work Methods to Compute Free Energy Differences between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett. 2015, 6, 4850–4856. 10.1021/acs.jpclett.5b02164. [DOI] [PubMed] [Google Scholar]
  34. Wang M.; Mei Y.; Ryde U. Predicting Relative Binding Affinity Using Nonequilibrium QM/MM Simulations. J. Chem. Theory Comput. 2018, 14, 6613–6622. 10.1021/acs.jctc.8b00685. [DOI] [PubMed] [Google Scholar]
  35. Schöller A.; Kearns F.; Woodcock H. L.; Boresch S. Optimizing the Calculation of Free Energy Differences in Nonequilibrium Work SQM/MM Switching Simulations. J. Phys. Chem. B 2022, 126, 2798–2811. 10.1021/acs.jpcb.2c00696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schöller A.; Woodcock H. L.; Boresch S. Exploring Routes to Enhance the Calculation of Free Energy Differences via Non-Equilibrium Work SQM/MM Switching Simulations Using Hybrid Charge Intermediates between MM and SQM Levels of Theory or Non-Linear Switching Schemes. Molecules 2023, 28, 4006. 10.3390/molecules28104006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Tkaczyk S.; Karwounopoulos J.; Schöller A.; Woodcock H. L.; Langer T.; Boresch S.; Wieder M. Reweighting from Molecular Mechanics Force Fields to the ANI-2x Neural Network Potential. J. Chem. Theory Comput. 2024, 20, 2719–2728. 10.1021/acs.jctc.3c01274. [DOI] [PubMed] [Google Scholar]
  38. Smith J. S.; Isayev O.; Roitberg A. E. ANI-1, A data set of 20 million calculated off-equilibrium conformations for organic molecules. Scientific Data 2017 4:1 2017, 4, 1–8. 10.1016/B978-0-12-800720-4.00001-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Devereux C.; Smith J. S.; Huddleston K. K.; Barros K.; Zubatyuk R.; Isayev O.; Roitberg A. E. Extending the Applicability of the ANI Deep Learning Molecular Potential to Sulfur and Halogens. J. Chem. Theory Comput. 2020, 16, 4192–4202. 10.1021/acs.jctc.0c00121. [DOI] [PubMed] [Google Scholar]
  40. Gao X.; Ramezanghorbani F.; Isayev O.; Smith J. S.; Roitberg A. E. TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of the ANI Neural Network Potentials. J. Chem. Inf. Model. 2020, 60, 3408–3415. 10.1021/acs.jcim.0c00451. [DOI] [PubMed] [Google Scholar]
  41. Eastman P.; et al. OpenMM 8: Molecular Dynamics Simulation with Machine Learning Potentials. J. Phys. Chem. B 2024, 128, 109–116. 10.1021/acs.jpcb.3c06662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. König G.; Pickard F.; Huang J.; Thiel W.; MacKerell A.; Brooks B.; York D. A Comparison of QM/MM Simulations with and without the Drude Oscillator Model Based on Hydration Free Energies of Simple Solutes. Molecules 2018, 23, 2695. 10.3390/molecules23102695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Mey A. S. J. S.; Allen B. K.; MacDonald H. E. B.; Chodera J. D.; Hahn D. F.; Kuhn M.; Michel J.; Mobley D. L.; Naden L. N.; Prasad S.; Rizzi A.; Scheen J.; Shirts M. R.; Tresadern G.; Xu H. Best Practices for Alchemical Free Energy Calculations. LiveCoMS 2020, 2, 18378. 10.33011/livecoms.2.1.18378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shirts M. R.; Mobley D. L. In Biomolecular Simulations: Methods and Protocols; Monticelli L., Salonen E., Eds.; Humana Press: Totowa, NJ, 2013; pp 271–311. [Google Scholar]
  45. Jarzynski C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690. 10.1103/PhysRevLett.78.2690. [DOI] [Google Scholar]
  46. Crooks G. E. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361. 10.1103/PhysRevE.61.2361. [DOI] [Google Scholar]
  47. Mobley D. L.; Guthrie J. P. FreeSolv: a database of experimental and calculated hydration free energies, with input files. J. Comput. Aided Mol. Des. 2014, 28, 711–720. 10.1007/s10822-014-9747-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Duarte Ramos Matos G.; Kyu D. Y.; Loeffler H. H.; Chodera J. D.; Shirts M. R.; Mobley D. L. Approaches for Calculating Solvation Free Energies and Enthalpies Demonstrated with an Update of the FreeSolv Database. J. Chem. Eng. Data 2017, 62, 1559–1569. 10.1021/acs.jced.7b00104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Vanommeslaeghe K.; MacKerell A. D. Automation of the CHARMM general force field (CGenFF) I: Bond perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. 10.1021/ci300363c. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Vanommeslaeghe K.; Raman E. P.; MacKerell A. D. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. 10.1021/ci3003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wieder M.; Fleck M.; Braunsfeld B.; Boresch S. Alchemical free energy simulations without speed limits. A generic framework to calculate free energy differences independent of the underlying molecular dynamics program. J. Comput. Chem. 2022, 43, 1151–1160. 10.1002/jcc.26877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Karwounopoulos J.; Wieder M.; Boresch S. Relative binding free energy calculations with transformato: A molecular dynamics engine-independent tool. Front. Mol. Biosci. 2022, 9, 850. 10.3389/fmolb.2022.954638. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Chodera J.et al. choderalab/openmmtools: 0.23.1 (accessed 2024-05-21) 2023; https://zenodo.org/records/8102771.
  54. Boothroyd S.; et al. Development and Benchmarking of Open Force Field 2.0.0: The Sage Small Molecule Force Field. J. Chem. Theory Comput. 2023, 19, 3251–3275. 10.1021/acs.jctc.3c00039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Jorgensen W. L.; Chandrasekhar J.; Madura J. D. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
  56. Miyamoto S.; Kollman P. A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
  57. Åqvist J.; Wennerström P.; Nervall M.; Bjelic S.; Brandsdal B. O. Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chem. Phys. Lett. 2004, 384, 288–294. 10.1016/j.cplett.2003.12.039. [DOI] [Google Scholar]
  58. Chow K. H.; Ferguson D. M. Isothermal-isobaric molecular dynamics simulations with Monte Carlo volume sampling. Comput. Phys. Commun. 1995, 91, 283–289. 10.1016/0010-4655(95)00059-O. [DOI] [Google Scholar]
  59. Shirts M. R.; Chodera J. D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  61. Lee T. S.; Tsai H. C.; Ganguly A.; York D. M. ACES: Optimized Alchemically Enhanced Sampling. J. Chem. Theory Comput. 2023, 19, 472–487. 10.1021/acs.jctc.2c00697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Tsai H.-C.; Lee T.-S.; Ganguly A.; Giese T. J.; Ebert M. C.; Labute P.; Merz K. M.; York D. M. AMBER Free Energy Tools: A New Framework for the Design of Optimized Alchemical Transformation Pathways. J. Chem. Theory Comput. 2023, 19, 640–658. 10.1021/acs.jctc.2c00725. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Rosenblatt M. Remarks on Some Nonparametric Estimates of a Density Function. Annals of Mathematical Statistics 1956, 27, 832–837. 10.1214/aoms/1177728190. [DOI] [Google Scholar]
  64. Parzen E. On Estimation of a Probability Density Function and Mode. Annals of Mathematical Statistics 1962, 33, 1065–1076. 10.1214/aoms/1177704472. [DOI] [Google Scholar]
  65. Kearns F. L.; Warrensford L.; Boresch S.; Woodcock H. L. The Good, the Bad, and the Ugly: ”HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules (Basel, Switzerland) 2019, 24, 681. 10.3390/molecules24040681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Lier B.; Poliak P.; Marquetand P.; Westermayr J.; Oostenbrink C. BuRNN: Buffer Region Neural Network Approach for Polarizable-Embedding Neural Network/Molecular Mechanics Simulations. J. Phys. Chem. Lett. 2022, 13, 3812–3818. 10.1021/acs.jpclett.2c00654. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Zinovjev K. Electrostatic Embedding of Machine Learning Potentials. J. Chem. Theory Comput. 2023, 19, 1888–1897. 10.1021/acs.jctc.2c00914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Zeng J.; Tao Y.; Giese T. J.; York D. M. QDπ: A Quantum Deep Potential Interaction Model for Drug Discovery. J. Chem. Theory Comput. 2023, 19, 1261–1275. 10.1021/acs.jctc.2c01172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Zeng J.; Tao Y.; Giese T. J.; York D. M. Modern semiempirical electronic structure methods and machine learning potentials for drug discovery: Conformers, tautomers, and protonation states. J. Chem. Phys. 2023, 158, 124110. 10.1063/5.0139281. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Nerenberg P. S.; Jo B.; So C.; Tripathy A.; Head-Gordon T. Optimizing Solute–Water van der Waals Interactions To Reproduce Solvation Free Energies. J. Phys. Chem. B 2012, 116, 4524–4534. 10.1021/jp2118373. [DOI] [PubMed] [Google Scholar]
  71. Jämbeck J. P. M.; Lyubartsev A. P. Update to the General Amber Force Field for Small Solutes with an Emphasis on Free Energies of Hydration. J. Phys. Chem. B 2014, 118, 3793–3804. 10.1021/jp4111234. [DOI] [PubMed] [Google Scholar]
  72. He X.; Man V. H.; Yang W.; Lee T.-S.; Wang J.. A fast and high-quality charge model for the next generation general AMBER force field. J. Chem. Phys. 2020, 153. 10.1063/5.0019056 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4c01417_si_001.pdf (489.5KB, pdf)
jp4c01417_si_002.csv (85.3KB, csv)
jp4c01417_si_003.csv (20.2KB, csv)

Data Availability Statement

All plots shown in this paper were produced using the Jupyter-notebook available on GitHub (https://github.com/JohannesKarwou/notebooks/blob/main/combinedDataset.ipynb). The notebook also contains the calculations of all statistics reported in this paper (RMSE, MAE, Pearson correlation, and Spearman’s rank correlation) and the corresponding bootstrapped errors. Python package used in this work (release v0.3): https://github.com/wiederm/endstate_correction.

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES