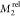Abstract
Magic-angle-spinning (MAS) nuclear magnetic resonance (NMR) experiments and molecular dynamics (MD) simulations were employed to investigate Na2O–B2O3–SiO2 and MgO–Na2O–B2O3–SiO2 glass structures up to ≈0.3 nm. This encompassed the {Na[p]}, {Mg[p]}, and {B[3], B[4]} speciations and the {Si, B[p], M[p]}–BO and {Si, B[p], M[p]}–NBO interatomic distances to the bridging oxygen (BO) and nonbridging oxygen (NBO) species, where the superscript indicates the coordination number. The MD simulations revealed the dominance of Mg[5] coordinations, as mirrored in average Mg2+ coordination numbers in the 5.2–5.5 range, which are slightly lower than those of the larger Na+ cation but with a narrower coordination distribution stemming from the higher cation field strength (CFS) of the smaller divalent Mg2+ ion. We particularly aimed to elucidate such Na+/Mg2+ CFS effects, which primarily govern the short-range structure but also the borosilicate (BS) glass network order, where both MD simulations and heteronuclear double-resonance 11B/29Si NMR experiments revealed a reduction of B[4]–O–Si linkages relative to B[3]–O–Si upon Mg2+-for-Na+ substitution. These effects were quantified and discussed in relation to previous literature on BS glasses, encompassing the implications for simplified structural models and descriptions thereof.
1. Introduction
Incorporating highly charged and/or small electropositive cations in oxide glasses, in particular rare-earth (RE3+) ions, often improves their thermal and mechanical properties.1−8 However, the high cost and toxicity of RE3+ species make Mg2+ an inexpensive and environmental-friendly alternative for glasses in a sustainable future society, as the cation field strength (CFS) of the small Mg2+ cation is only marginally lower than that of La3+. (The CFS scales as the charge divided by the square of the cation radius).9 There has been a decades-long and recently growing interest in exploring the structures of Mg2+-bearing aluminosilicate (AS) glasses10−15 and their correlation with physical properties.16−19 In contrast, there are comparatively few studies of incorporating Mg2+ into the other main glass family of ubiquitous technological and geological importance, i.e., borosilicate (BS) glasses.19−23 It also remains unclear as to whether the physical-property boosts observed for Mg2+-bearing AS glasses (relative to those with lower-CFS alkali/alkaline earth metal ions) also apply to the BS glass context. Results from MO–Na2O–B2O3–SiO2 glasses merely suggest that the larger Sr2+ and Ba2+ cations offer higher hardness and better elastic properties than their Mg2+ counterpart.22
These differences may be traced to the distinct effects from high-CFS Mg2+ and RE3+ incorporation in AS versus BS structures. While the physical glass properties are enhanced slightly from stronger Mg2+/RE3+–O bonds relative to those of lower-CFS M+/M2+ glass-network modifiers, all M–O bonds remain markedly weaker than their F–O counterparts, where F denotes a network forming species, F = {Si, Al, B}. Rather, the structure-strengthening effects and accompanying improved thermal/mechanical properties upon high-CFS Mz+ inclusion in AS glasses stem from the effects on the Al speciation, where the dominant AlO4 groups partially convert into higher-coordination yet network-forming AlO5 and AlO6 polyhedra,24,25 whose higher network cross-linking enhances the physical glass properties.5,7,25,26 Including high-CFS Mz+ cations in BS glasses, on the other hand, strongly alters their B speciations. B-bearing glass networks comprise both BO3 (B[3] coordinations) and BO4 (B[4]) groups,24,27 where large B[4] populations increase the network connectivity and boost many glass properties, such as the hardness and the glass transition temperature.22,26,28−31 However, high-CFS cations tend to promote B[3] formation at the expense of B[4],19,22,32−37 which lowers the overall glass-network connectivity and may thereby degrade physical properties. Yet, little is known about the precise structure–property relationships of high-CFS Mz+-bearing BS glasses, which are strongly dependent on the precise glass stoichiometry and likely also on the Mz+ size (alone);22 for example, incorporating Mg2+ into a few Na2O–B2O3–SiO2 glass compositions reduced their hardness and elastic properties, whereas these properties improved when instead introducing the larger high-CFS La3+ cation.22
By utilizing atomistic molecular dynamics (MD) simulations and magic-angle-spinning (MAS) nuclear magnetic resonance (NMR) spectroscopy, we report here on the structural alterations from Mg2+-for-Na+ substitutions in four Na2O–B2O3–SiO2 base-glass compositions. Besides the {B[p]} and {O[q]} speciations, we examine the local Na and Mg coordination environments and their distinctly different propensities for coordinating the bridging oxygen (BO; O[2] coordinations) and nonbridging oxygen (NBO; O[1]) species. We particularly aim to understand the dependence of the local glass structure on the Mz+ CFS, which besides Na+ and Mg2+ also involves results from Ca2+-bearing BS glass models along with previously published data from RE3+ cations in AS glasses.
We then move the spotlight from the first F[p] and M[p] coordination shells onto the F–O–F′ glass-network linkages, where the silicate and borate group intermixing was probed by computational modeling and heteronuclear double-resonance 11B/29Si MAS NMR experiments. Current B/Si interconnectivity insights partially stem from 17O triple-quantum MAS (3QMAS)38 experimentation.24,36,37,39,40 Although widely applied, it may not unambiguously discriminate between the B[3] and B[4] coordination numbers of the B–O–Si and B–O–B linkages (let alone quantify them, although such claims have been made36,37,40). The heteronuclear magnetic 11B–29Si dipolar interaction, which is mediated directly through space and scales as the inverse cube of the 11B–29Si distance,24,25,41,42 offers a more direct probing of the 11B[p]/29Si intermixing in BS glasses. However, its application is relatively sparse,43−49 mainly stemming from the requirement of dedicated glass syntheses from costly 29Si-enriched silica to enable high-quality experimental data for quantitative analyses, which is otherwise severely hampered or even precluded by the low natural abundance (4.7%) of the NMR-active 29Si isotope. The impact of Mg2+ incorporation on the relative degrees of B[3]–O–Si and B[4]–O–Si bonding in the Mg/Na-bearing BS glass networks is discussed in relation to current literature, as well as the implications for existing simplified BS-glass structure descriptions/models.
2. Materials and Methods
2.1. Borosilicate Glasses
Our study involved the eight BS glass compositions listed in Table 1, encompassing four ternary RNa2O–B2O3–KSiO2 glasses and four quaternary R[0.5MgO–0.5Na2O]–B2O3–KSiO2 analogs. They constitute a subset of a large BS glass ensemble examined previously.22,50,51 We adopt the glass nomenclature of ref (50), where each Na- and Mg/Na-based glass is denoted by NaK–R and MgNaK–R, respectively, with the {K, R} parameters defined by52,53
| 1 |
| 2 |
Each nominal glass composition in Table 1 is expressed in terms of its oxide equivalents and the atomic fraction of each element E in the (Mg)–Na–B–Si–O glass,
| 3 |
where nE is the corresponding stoichiometric amount.
Table 1. Borosilicate Glass Compositionsa.
| oxide
equivalents (mol %) |
atomic
fractions |
BO4 fractionsb |
NBO
fractionsc |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glass | MgO | Na2O | B2O3 | SiO2 | xMg | xNa | xB | xSi | xO | NMR | MD | NMR | MD |
| R = 0.75 | |||||||||||||
| Na2.0–0.75 | 20.0 | 26.7 | 53.3 | 0.114 | 0.151 | 0.151 | 0.584 | 0.604 | 0.547 | 0.038 | 0.054 | ||
| MgNa2.0–0.75 | 10.0 | 10.0 | 26.7 | 53.3 | 0.029 | 0.058 | 0.155 | 0.155 | 0.603 | 0.361 | 0.353 | 0.100 | 0.104 |
| Na4.0–0.75d | 13.0 | 17.4 | 69.6 | 0.078 | 0.104 | 0.208 | 0.610 | 0.623; 0.618 | 0.527 | 0.022; 0.022 | 0.039 | ||
| MgNa4.0–0.75d | 6.5 | 6.5 | 17.4 | 69.6 | 0.020 | 0.040 | 0.106 | 0.212 | 0.622 | 0.313; 0.310 | 0.301 | 0.074; 0.074 | 0.077 |
| R = 2.1 | |||||||||||||
| Na2.0–2.1 | 41.2 | 19.6 | 39.2 | 0.242 | 0.116 | 0.116 | 0.526 | 0.487 | 0.447 | 0.354 | 0.364 | ||
| MgNa2.0–2.1 | 20.6 | 20.6 | 19.6 | 39.2 | 0.065 | 0.129 | 0.123 | 0.123 | 0.560 | 0.402 | 0.364 | 0.373 | 0.382 |
| Na4.0–2.1 | 29.6 | 14.1 | 56.3 | 0.180 | 0.086 | 0.172 | 0.562 | 0.697 | 0.608 | 0.214 | 0.228 | ||
| MgNa4.0–2.1d | 14.8 | 14.8 | 14.1 | 56.3 | 0.094 | 0.047 | 0.090 | 0.180 | 0.589 | 0.459;0.445 | 0.444 | 0.249;0.251 | 0.253 |
Nominal ternary RNa2O–B2O3–KSiO2 (“NaK–R”) or quaternary R[0.5MgO–0.5Na2O]–B2O3–KSiO2 (“MgNaK–R”) glass compositions and their corresponding atomic fractions {xMg, xNa, xB, xSi, xO} defined by xE = nE/(nMg + nNa + nB + nSi + nO).
Fractional populations of B[4] coordinations, 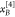 , as obtained either by 11B NMR
or by MD simulations, with the respective uncertainties of ±0.01
and ±0.005. The experimental
, as obtained either by 11B NMR
or by MD simulations, with the respective uncertainties of ±0.01
and ±0.005. The experimental  values listed to the left are reproduced
from Lv et al.,22 while those to the right
(in bold) are results from the present 29Si-enriched glasses;
the latter data are employed throughout the experimental analyses
of those glass specimens.
values listed to the left are reproduced
from Lv et al.,22 while those to the right
(in bold) are results from the present 29Si-enriched glasses;
the latter data are employed throughout the experimental analyses
of those glass specimens.
NBO fraction, xNBO, out of all BO and
NBO species, as either obtained
by MD simulations (uncertainty ±0.001) or calculated from eq 9 (±0.01) by using
the NMR-derived {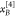 } data. The experimental xNBO values listed to the left and right (in bold) correspond
to the results presented by Lv et al.22 and those of the present 29Si-enriched glasses, respectively;
the latter data are assumed throughout this work.
} data. The experimental xNBO values listed to the left and right (in bold) correspond
to the results presented by Lv et al.22 and those of the present 29Si-enriched glasses, respectively;
the latter data are assumed throughout this work.
MD simulations were performed for all glass compositions in Table 1. The need for dedicated glasses synthesized from costly 29SiO2 to enable the heteronuclear 11B/29Si NMR experiments, however, limited them to three specimens: Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1.
The CFS of an Mz+ cation is defined according to9
| 4 |
where rM is the cation radius and rO = 1.36 Å. Table S1 lists the CFS values of the F = {Si, B[3], B[4]} network formers and the Mz+ = {Na+, Mg2+} network modifiers primarily targeted here, along with a few other Mz+ cations discussed in section 3. For consistency, we employed rM values for sixfold-coordinated Mz+ species (M[6]) throughout. The coordination number is not indicated for exclusively tetrahedrally coordinated Si ≡ Si[4] atoms.
2.2. Glass Preparation
The 29Si-enriched Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1 glasses were prepared in 250 mg batches from analytical grade 29SiO2 (99.8% 29Si), H3BO3, Na2CO3, and MgO precursors. After removing potential OH/H2O contaminations by preheating the 29SiO2 powder at 950 °C for 24 h, the precursors were mixed thoroughly in a mortar, transferred to a Pt crucible, and decarbonated at 950 °C for 2 h before being heated to final melt temperatures of 1000, 1100, and 1200 °C for the MgNa4.0–2.1, Na4.0–0.75, and MgNa4.0–0.75 batches, respectively. Those temperatures were deduced from multiple preparations using regular (nonenriched) SiO2 so as to ensure complete melting but minimal evaporation losses and close fictive temperatures to previous BS glass specimens of identical nominal compositions but prepared in larger batches (6 g) at ≈200 °C higher melting temperatures.22 The melt was held for 20 min and then quenched by immersing the crucible bottom in cold water.
All glass specimens were free of crystalline impurities. Their compositions are expected to be close to their batched/nominal counterparts listed in Table 1, as corroborated by the minute evaporation losses during heating of 1.0 wt % and 1.6 wt % for MgNa4.0–2.1 and MgNa4.0–0.75, respectively. Although the Na4.0–0.75 glass revealed a markedly higher loss (5.6% wt %) than the 1–2 wt % we normally observe,22,34 it mainly reflects accidental melt-loss prior to quenching. Indeed, relative to the batched B2O3 contents, the B2O3 masses determined from 11B MAS NMR experiments calibrated to H3BO3 as the standard (see refs (22) amd (34)) revealed marginal relative deviations from 0.6% for Na4.0–0.75 to 1.7% for MgNa4.0–0.75.
2.3. Molecular Dynamics Simulations
Atomistic MD simulations mimicking a melt-quench process were utilized to produce BS glass models with the stoichiometries from Table 1. The computations utilized the DLPOLY4.09 program,54 where NVT ensembles in a cubic box with periodic boundary conditions were simulated using a box size and number of atoms (6600–11600) to match the nominal chemical glass composition and the experimental density (Table S2). Each melt-quench protocol started from randomly positioned atoms, which were equilibrated for 100 ps at 3500 K, followed by a stepwise temperature reduction (5 K/ps) to 300 K. The equations of motion were integrated in steps of 0.2 fs by using the velocity Verlet integrator, while the temperature was controlled by a gentle stochastic thermostat with a 1.0 ps time constant and a 1.0 ps–1 Langevin friction constant. The structural data were sampled and averaged over the last 150 ps of a final 200 ps equilibration stage. The average value and uncertainty of each reported structural parameter were obtained by performing the melt-quench protocol four times. The selected system sizes, equilibration stages, and other simulation conditions provide well-converged and reliable structural parameters.34,55−57
All simulations utilized a polarizable shell-model potential.58−60 Every cation carries its full formal charge,58 but the O2– species are represented by core (OC) and shell (OS) portions with masses mC = 15.7994 u and mS = 0.2000 u, respectively, and corresponding charges zC = +0.8482e and zS = −2.8482e (obeying zC + zS = −2), where “u” is the atomic mass unit and e is the elementary charge. Each core–shell unit is connected by a harmonic potential with a force constant of 74.92 eV/Å 2.58 The interaction energy of two atom/ion species α and β separated by a distance rαβ was modeled by a modified Buckingham potential
 |
5 |
that accounted for all short-range OS–OS and cation–OS pair interactions.
It was evaluated out to rαβ = 0.8 nm. The B–O force field conforms to eq 5 with Cαβ ≡ 0 but also includes a repulsive 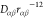 term.55,56Table S3 compiles all
term.55,56Table S3 compiles all 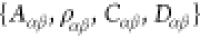 parameters, encompassing a three-atom potential
for constraining the O–Si–O intratetrahedral angles.
Long-range Coulombic interactions were calculated by a smoothed particle-mesh
Ewald summation54 with a 1.2 nm real-space
cutoff and an accuracy of 10–6.
parameters, encompassing a three-atom potential
for constraining the O–Si–O intratetrahedral angles.
Long-range Coulombic interactions were calculated by a smoothed particle-mesh
Ewald summation54 with a 1.2 nm real-space
cutoff and an accuracy of 10–6.
2.4. Solid-State NMR Experiments
All NMR experiments were performed with Bruker Avance-III spectrometers. The 29Si MAS NMR spectra were acquired at a magnetic field (B0) of 9.4 T (79.47 MHz 29Si Larmor frequency) using 4 mm zirconia rotors undergoing MAS at νr = 14.00 kHz and radio frequency (rf) pulses with a ≈70° flip angle (νSi = 84 kHz nutation frequency), relaxation delays of 3600 s, and 16 accumulated NMR signal transients. The 11B (spin-3/2) NMR spectra were recorded at B0 = 14.1 T (−192.5 MHz 11B Larmor frequency) and νr = 24.00 kHz using full 3.2 mm zirconia rotors and strong/short rf pulses (0.33 μs, 13° flip angle, νB = 105 kHz). The {B[3], B[4]} populations of each glass were determined from the integrated central-transition (CT) NMR-signal intensities,22,50 which were corrected for the satellite-transition centerband peak that overlaps with the main CT 11B[4] signal by using standard procedures.61 Every 11B NMR spectrum was corrected for probehead “background” signals by subtracting the result from the empty rotor recorded under otherwise identical experimental conditions. 29Si (δSi) and 11B (δB) shifts were referenced relative to neat tetramethylsilane (TMS) and BF3·OEt2, respectively.
The Van Vleck dipolar second moment(62) is proportional to the sum over the inverse sixth power of the interatomic distance of each heteronuclear Sj–Ik spin-pair in a structure:
| 6 |
Here, μ0 is the permeability
of vacuum, γI (γS) is the magnetogyric
ratio of spin species I (S), and NI and NS are the respective total numbers of I and
S nuclei in the glass obtained from its stoichiometry with 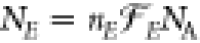 , where NA is
Avogadro’s number and
, where NA is
Avogadro’s number and 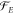 the natural isotopic abundance. I denotes the spin quantum number of the nuclide I, i.e., I = 1/2 (29Si) and I = 3/2 (11B) for the respective M2(B[p]–Si) and M2(Si–B[p]) entities. We
stress the unit of s–2 in eq 6, which is consistent with our previous work57,63,64 but differs from the original M2 definition with units of rad2/s2,62 which is most frequently encountered
in the literature (e.g., refs (19), (41), and (42)). The two dipolar second-moment
definitions are related by 4π2M2[s–2] = M2[rad2/s2]. Units aside, we comment that incorrect M2(S–I) expressions are stated in two
recent review articles,24,25 which should appear
as in ref (64) and eq 6.
the natural isotopic abundance. I denotes the spin quantum number of the nuclide I, i.e., I = 1/2 (29Si) and I = 3/2 (11B) for the respective M2(B[p]–Si) and M2(Si–B[p]) entities. We
stress the unit of s–2 in eq 6, which is consistent with our previous work57,63,64 but differs from the original M2 definition with units of rad2/s2,62 which is most frequently encountered
in the literature (e.g., refs (19), (41), and (42)). The two dipolar second-moment
definitions are related by 4π2M2[s–2] = M2[rad2/s2]. Units aside, we comment that incorrect M2(S–I) expressions are stated in two
recent review articles,24,25 which should appear
as in ref (64) and eq 6.
The M2(B[p]–Si) value of a given BS glass may be estimated from a 11B{29Si} REDOR NMR experiment65 that restores/“recouples” the MAS-averaged 11B[p]–29Si dipolar-interaction effects during a recoupling period (τrec) by a series of rotor-synchronized 180° rf pulses applied to 29Si, during which the 11B[p] NMR signal [S(τrec)] becomes attenuated (“dephased”) relative to that obtained by a spin–echo experiment [S0(τrec)]65 obtained by CT-selective 11B rf pulses.
All double-resonance 11B{29Si} REDOR NMR
experiments were performed at B0 = 14.1
T and νr = 9.00 kHz with each glass
powder centered to the 1/3 volume of a 4 mm zirconia rotor to reduce
the impact from rf inhomogeneity.41,66,67 All experiments were started by a saturation-recovery
rf-pulse comb followed by a 1.5 s relaxation delay. The 180°
dipolar recoupling pulses operated at νSi = 46 kHz
with the XY8 phase-cycling scheme to minimize rf-pulse errors.68 The 11B 90° and 180° spin–echo
rf pulses were 17.0 μs and 34.0 μs, respectively. The
dipolar recoupling period was sampled out to several ms at even integer
multiples n of the rotor period,  . Each M2(B[3]–Si) and M2(B[4]–Si) value was extracted from the respective integrated 11B[3] and 11B[4] NMR intensities
of the S0(τrec) and S(τrec) spectra, whereupon the resulting
{τrec, ΔS/S0} data (restricted to ΔS/S0 ⩽ 0.224,41,42) were fitted to the expression41,42,63
. Each M2(B[3]–Si) and M2(B[4]–Si) value was extracted from the respective integrated 11B[3] and 11B[4] NMR intensities
of the S0(τrec) and S(τrec) spectra, whereupon the resulting
{τrec, ΔS/S0} data (restricted to ΔS/S0 ⩽ 0.224,41,42) were fitted to the expression41,42,63
| 7 |
2–4 independent NMR-data blocks with 256–512 accumulated signal transients per block were acquired for each glass specimen. The average value of each M2(B[p]–Si) estimate and its uncertainty were extracted from these independent {M2(B[p]–Si)} best-fit results.
3. Results and Discussion
3.1. Boron and Oxygen Speciations
All
BS glasses considered herein comprise networks of interconnected SiO4, BO3 and [BO4]− groups,
where 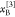 and
and 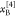 denote the respective fractional populations
of B[3] and B[4]. Table 1 lists each
denote the respective fractional populations
of B[3] and B[4]. Table 1 lists each 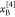 value obtained from either the 11B MAS NMR spectrum or MD simulations, whereas the corresponding BO3 fraction is given from the following normalization:
value obtained from either the 11B MAS NMR spectrum or MD simulations, whereas the corresponding BO3 fraction is given from the following normalization:
| 8 |
The experimental {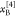 } data were reproduced from ref (22) except for the three 29Si-enriched Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1
specimens that were prepared specifically for the present study. Their
borate speciations match very well those of glasses prepared from
regular (non-29Si-enriched) SiO2,22 suggesting very close stoichiometries and fictive
temperatures for both specimens of each Na4.0–0.75, MgNa4.0–0.75,
and MgNa4.0–2.1 stoichiometry (see Table 1 and Figure 1). The MD simulations revealed O speciations solely
comprising NBO and BO sites, whereas “free O2– anions” (O[0]) are absent throughout and the “O
tricluster” (O[3]) populations remain <0.02%
out of each {O[q]} ensemble. Hence, the
fractional populations of NBO (xNBO) and
BO (xBO) species obey xNBO + xBO = 1.
} data were reproduced from ref (22) except for the three 29Si-enriched Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1
specimens that were prepared specifically for the present study. Their
borate speciations match very well those of glasses prepared from
regular (non-29Si-enriched) SiO2,22 suggesting very close stoichiometries and fictive
temperatures for both specimens of each Na4.0–0.75, MgNa4.0–0.75,
and MgNa4.0–2.1 stoichiometry (see Table 1 and Figure 1). The MD simulations revealed O speciations solely
comprising NBO and BO sites, whereas “free O2– anions” (O[0]) are absent throughout and the “O
tricluster” (O[3]) populations remain <0.02%
out of each {O[q]} ensemble. Hence, the
fractional populations of NBO (xNBO) and
BO (xBO) species obey xNBO + xBO = 1.
Figure 1.
11B MAS NMR spectra recorded at 14.1 T and 24.00 kHz MAS from (a) Na4.0–0.75, (b) MgNa4.0–0.75, and (c) MgNa4.0–2.1 glass specimens prepared from 29SiO2 (black traces) or from SiO2 with 29Si at natural abundance (red traces; reproduced from Lv et al.22). The glasses were prepared under similar conditions and reveal very similar 11B NMR spectra and borate speciations (Table 1).
The Na+/Mg2+ cations compensate
the negative
charges of the [BO4]− and NBO (O–) moieties, implying that the fractional populations
of B[4] and NBO anions are coupled according to 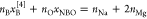 . Hence, xNBO is readily deduced from the glass stoichiometry and the 11B NMR-derived
. Hence, xNBO is readily deduced from the glass stoichiometry and the 11B NMR-derived 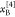 value as follows:
value as follows:
| 9 |
Equation 9 reflects the well-known dual “network modifier”
and “charge compensator” structural properties of the Mz+ cations in borate-based
glasses,24,27,52,53,69,70 which result in Mz+···O– and Mz+···[BO4]− structural motifs from the respective BO → NBO and B[3] → B[4] conversions. The borate speciation
of a BS-based glass depends strongly on both its stoichiometry and
CFSM.19,22,32−37 As expected from the higher CFSMg = 0.46 Å–2 than CFSNa = 0.18 Å–2,19,22,32,33 introducing Mg2+ to a NaK–R glass boosts the NBO content for fixed {K, R} parameters, while the B[4] population
is markedly reduced (Table 1). This effect is particularly drastic for the NaK–0.75 and Na4.0–2.1 glasses with 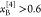 : when half of the Na+ ensemble
is replaced by Mg2+, a significant B[4] →
B[3] conversion occurs, rendering BO3 groups
most abundant in all MgNaK–R specimens.
: when half of the Na+ ensemble
is replaced by Mg2+, a significant B[4] →
B[3] conversion occurs, rendering BO3 groups
most abundant in all MgNaK–R specimens.
For a clear-cut discrimination between the Mz+ and F species, we employ the ancient “network modifier” terminology when referring to the M+/M2+ cations, although the categorical “modifier” and “charge-compensator” classification is oversimplified.56,57 For instance, both MD simulations and NMR experiments reveal that a significant/major portion of the {Na+} ensemble associates with the formally charge-neutral Si(O[2])4 and B(O[2])3 moieties via Na+···O–Si/B[3] fragments (rather than with the negatively charged [BO4]− and F–NBO moieties), rendering Na–BO contacts prevalent for all but very NBO-rich glasses.56,57
A long-standing problem of classical
MD simulations of B-bearing
glasses is their (in)accurate {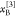 ,
, 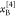 } predictions, which not only depend strongly
on the precise glass composition but also on thermal history of the
glass due to the temperature-dependent BO3 ⇄ BO4 equilibrium.71−73 The engineering of reliable B–O force fields
has received significant recent attention.74−81 The modeled BO4 and NBO populations listed in Table 1 were obtained with
the B–O interatomic potential parameters of refs (55) and (56), which have been validated
for Na- and Na/Ca-bearing borate and boro(phospho)silicate glasses
over large composition domains.34,55,56,82 Contrasting the modeled and experimental
BO4 populations of Table 1, however, reveals a highly variable performance. The
agreement is excellent for all MgNaK–R glasses (with relative deviations within
3%) but MgNa2.0–2.1, which along with all NaK–R models reveal markedly larger discrepancies
to experiments, typically by ≈10% but with a substantial deviation
of 17% for Na4.0–0.75. These errors stem from the distinctly
different
} predictions, which not only depend strongly
on the precise glass composition but also on thermal history of the
glass due to the temperature-dependent BO3 ⇄ BO4 equilibrium.71−73 The engineering of reliable B–O force fields
has received significant recent attention.74−81 The modeled BO4 and NBO populations listed in Table 1 were obtained with
the B–O interatomic potential parameters of refs (55) and (56), which have been validated
for Na- and Na/Ca-bearing borate and boro(phospho)silicate glasses
over large composition domains.34,55,56,82 Contrasting the modeled and experimental
BO4 populations of Table 1, however, reveals a highly variable performance. The
agreement is excellent for all MgNaK–R glasses (with relative deviations within
3%) but MgNa2.0–2.1, which along with all NaK–R models reveal markedly larger discrepancies
to experiments, typically by ≈10% but with a substantial deviation
of 17% for Na4.0–0.75. These errors stem from the distinctly
different 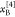 ranges between the NaK–R and MgNaK–R glasses. As noted in refs (34), (55), and (56) but more
clearly shown by Pedone and co-workers,82,83 MD simulations
with our B–O force field are prone to underestimating the BO4 population: although the deviations are insignificant for
glasses with
ranges between the NaK–R and MgNaK–R glasses. As noted in refs (34), (55), and (56) but more
clearly shown by Pedone and co-workers,82,83 MD simulations
with our B–O force field are prone to underestimating the BO4 population: although the deviations are insignificant for
glasses with 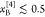 , they grow progressively for increasing
values of
, they grow progressively for increasing
values of 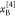 (Table 1).
(Table 1).
The underestimated (overestimated) modeled
BO4 (BO3) populations are reasons for concern
regarding reliable predictions
of some medium-range (0.3–1 nm) glass-structure
features. Gratifying, however, is the typically (very) good agreement
observed consistently relative to experimental data
on several interatomic-distance-related structural parameters, such
as the relative B[3]/B[4]···Na+ and P–O–B[p] contacts
in boro(phospho)silicate glasses,55,57 as well as
their B[p]–O–B[q] linkage statistics,34,50,55 which constitute the most sensitive medium-range structural parameters on the precise {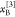 ,
,  } fractions; notwithstanding that the NMR/MD-derived
B[p]–O–B[q] populations do differ, all experimental
findings were reproduced qualitatively/semiquantitatively by the glass
models.34,50,55 Moreover,
the relative B[3]/B[4]–O–Si contacts
predicted by the glass models in section 3.5 agree very well with our experiments, encompassing the Na4.0–0.75 glass. Indeed, out of
the plethora of B–O force fields proposed to date (e.g., refs (74−81)), solely the herein utilized option55,56 has been assessed extensively against experimental interatomic-distance-related
parameters directly reflecting the medium-range glass
organization.
} fractions; notwithstanding that the NMR/MD-derived
B[p]–O–B[q] populations do differ, all experimental
findings were reproduced qualitatively/semiquantitatively by the glass
models.34,50,55 Moreover,
the relative B[3]/B[4]–O–Si contacts
predicted by the glass models in section 3.5 agree very well with our experiments, encompassing the Na4.0–0.75 glass. Indeed, out of
the plethora of B–O force fields proposed to date (e.g., refs (74−81)), solely the herein utilized option55,56 has been assessed extensively against experimental interatomic-distance-related
parameters directly reflecting the medium-range glass
organization.
3.2. MD-Derived Average F–O and M–O Distances
Here and in sections 3.3 and 3.4, we examine the MD-derived first coordination shells of the network formers and modifiers, paying particular attention to the structural bearings from Mg2+, thereby complementing our previous structural reports on large sets of Na+ and Na+/Ca2+ bearing borate and boro(phospho)silicate glasses with variable B, Si, and NBO contents.56,57
For each {Si, B[3], B[4]} network former, Table 2 compiles the average F[p]–O[q] interatomic distance,  (F[p]–O[q]), for each of O[1] and O[2], along with the corresponding {
(F[p]–O[q]), for each of O[1] and O[2], along with the corresponding { (F[p]–O)} result that represents the weighted average of
the F[p]–O[1]/O[2] distances over all {FOp} polyhedra. We stress that each F[p]–O/O[q] and M[p]–O/O[q] interatomic distance (“bond-length”)
discussed herein constitutes the arithmetic average across the entire F–O[q] (M–O[q]) bond ensemble in the structure.
(F[p]–O)} result that represents the weighted average of
the F[p]–O[1]/O[2] distances over all {FOp} polyhedra. We stress that each F[p]–O/O[q] and M[p]–O/O[q] interatomic distance (“bond-length”)
discussed herein constitutes the arithmetic average across the entire F–O[q] (M–O[q]) bond ensemble in the structure. 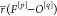 was not extracted from
the respective pair-distribution maximum, which constitutes the most probable F–O distance but is frequently reported
as
was not extracted from
the respective pair-distribution maximum, which constitutes the most probable F–O distance but is frequently reported
as  (F–O) (e.g., see
refs (60), (76), and (83−86)). Because the various Si/B[p]–BO/NBO
distances are governed by the high-CFS Si4+ and B3+ cations (Table S1), they remain similar
for all BS glasses regardless of the precise network modifier species.
All F[p]–O[q] distances in Table 2 conform well with those discussed by Stevensson
et al.56 for Na–(Ca)–B–Si–O
glasses, which agreed well with the sparsely available experimental
data. The direct dependence of each F–O distance
on the NBO content of the glass is evident when contrasting the
(F–O) (e.g., see
refs (60), (76), and (83−86)). Because the various Si/B[p]–BO/NBO
distances are governed by the high-CFS Si4+ and B3+ cations (Table S1), they remain similar
for all BS glasses regardless of the precise network modifier species.
All F[p]–O[q] distances in Table 2 conform well with those discussed by Stevensson
et al.56 for Na–(Ca)–B–Si–O
glasses, which agreed well with the sparsely available experimental
data. The direct dependence of each F–O distance
on the NBO content of the glass is evident when contrasting the  (Si–O) and
(Si–O) and  (B[3]–O) data from each
NaK–R glass with its MgNaK–R analog (in contrast with
(B[3]–O) data from each
NaK–R glass with its MgNaK–R analog (in contrast with  (B[4]–O); vide infra):
the distances in the Mg-bearing glass are marginally but consistently
shorter by ≈0.3 pm due to the slightly higher NBO contents
in those glasses coupled with the shorter F–NBO
distances relative to F–BO (Table 2).
(B[4]–O); vide infra):
the distances in the Mg-bearing glass are marginally but consistently
shorter by ≈0.3 pm due to the slightly higher NBO contents
in those glasses coupled with the shorter F–NBO
distances relative to F–BO (Table 2).
Table 2. MD-Derived Average F/M–O Bond Lengthsa.
 (B[3]–O[q]) (pm) (B[3]–O[q]) (pm) |
 (B[4]–O[q]) (pm) (B[4]–O[q]) (pm) |
 (Si–O[q]) (pm) (Si–O[q]) (pm) |
 (Na–O[q]) (pm) (Na–O[q]) (pm) |
 (Mg–O[q]) (pm) (Mg–O[q]) (pm) |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glass | xNBO | O | O[2] | O[1] | O | O[2] | O[1] | O | O[2] | O[1] | O | O[2] | O[1] | O | O[2] | O[1] |
| R = 0.75 | ||||||||||||||||
| Na2.0–0.75 | 0.054 | 135.33 | 135.45 | 134.00 | 142.53 | 142.59 | 134.69 | 163.96 | 164.03 | 160.29 | 257.9 | 260.8 | 238.4 | |||
| MgNa2.0–0.75 | 0.104 | 135.10 | 135.29 | 133.85 | 143.07 | 143.31 | 134.84 | 163.65 | 163.73 | 160.96 | 258.6 | 261.0 | 245.5 | 213.0 | 225.8 | 203.2 |
| Na4.0–0.75 | 0.039 | 134.90 | 134.97 | 133.88 | 142.09 | 142.13 | 134.71 | 163.58 | 163.64 | 160.09 | 258.5 | 261.7 | 236.4 | |||
| MgNa4.0–0.75 | 0.077 | 134.72 | 134.83 | 133.72 | 142.78 | 142.99 | 134.93 | 163.33 | 163.40 | 160.71 | 258.9 | 261.9 | 244.0 | 211.4 | 227.7 | 201.6 |
| R = 2.1 | ||||||||||||||||
| Na2.0–2.1 | 0.364 | 136.72 | 138.37 | 134.57 | 144.20 | 145.43 | 134.83 | 164.69 | 165.46 | 161.26 | 252.4 | 262.5 | 243.7 | |||
| MgNa2.0–2.1 | 0.382 | 136.26 | 137.56 | 134.54 | 144.60 | 146.17 | 135.21 | 164.49 | 165.09 | 161.69 | 255.9 | 262.5 | 248.6 | 210.3 | 228.3 | 206.0 |
| Na4.0–2.1 | 0.228 | 136.25 | 137.20 | 134.27 | 143.08 | 143.68 | 134.79 | 164.30 | 164.78 | 160.73 | 254.0 | 263.1 | 241.3 | |||
| MgNa4.0–2.1 | 0.253 | 135.85 | 136.63 | 134.25 | 143.66 | 144.59 | 135.13 | 164.02 | 164.37 | 161.31 | 257.3 | 263.4 | 246.9 | 209.6 | 228.7 | 204.3 |
| σb | 0.001 | 0.02 | 0.03 | 0.02 | 0.04 | 0.05 | 0.08 | 0.02 | 0.02 | 0.04 | 0.1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.1 |
Average F[p]–O[q] and M–O[q] distances between
the NBO (O[1] coordination) and BO (O[2]) species
for F = {Si[4], B[3], B[4]} and M = {Na, Mg}, where the latter involve
the entire {Na[p]} and {Mg[p]} ensembles. The  (B[p]–O),
(B[p]–O),  (Si–O), and
(Si–O), and  (M–O) values constitute
averages across all {O[1], O[2]} sites.
(M–O) values constitute
averages across all {O[1], O[2]} sites.
The data uncertainties are ±1σ, with σ given for each entity.
We next consider the F–O[1] and F–O[2] bond-length
variations. The large
CFS of the very small B3+ cation manifests as tightly confined
B[3]–O[1] and B[4]–O[1] bond lengths (134–135 pm throughout), which are
markedly shorter than those of Si–O[1] (161–162
pm; see Table 2). Nonetheless,
whereas the average B[3]–O[2] distances
are only a few pm longer than those of B[3]–O[1], the B[4]–O[2] bond lengths
are 7–8 pm longer (142–146 pm) than their B[4]–O[1] counterparts, which is consistent with previous
findings.75−77,84Table 2 confirms the anticipated feature of nearly
constant  (F[p]–O[1]) values regardless of the nSi/nB molar ratio
of the glass (related to K) or its NBO content (related
to R).56 In contrast,
all {
(F[p]–O[1]) values regardless of the nSi/nB molar ratio
of the glass (related to K) or its NBO content (related
to R).56 In contrast,
all { (F–O[2])} values increase slightly for increasing xNBO. For instance, contrast the bond lengths from each NaK–0.75 and MgNaK–0.75 structure
with those of its NBO-richer NaK–2.1 and MgNaK–2.1 counterpart:
(F–O[2])} values increase slightly for increasing xNBO. For instance, contrast the bond lengths from each NaK–0.75 and MgNaK–0.75 structure
with those of its NBO-richer NaK–2.1 and MgNaK–2.1 counterpart:  (F[p]–O[2]) is increased by 1–2 pm for
Si and slightly more for the two B[3] and B[4] coordinations (2–3 pm; Table 2). However, for the Mg2+/NBO-richer MgNaK–2.1 glasses, for which any bond-length effect from
Mg2+ is expected to be most pronounced, it is notable that
(F[p]–O[2]) is increased by 1–2 pm for
Si and slightly more for the two B[3] and B[4] coordinations (2–3 pm; Table 2). However, for the Mg2+/NBO-richer MgNaK–2.1 glasses, for which any bond-length effect from
Mg2+ is expected to be most pronounced, it is notable that  (B[3]–O[2])
is shorter by ≈1 pm than that for their NaK–2.1 analogs, whereas the reverse trend of a ≈1
pm longer
(B[3]–O[2])
is shorter by ≈1 pm than that for their NaK–2.1 analogs, whereas the reverse trend of a ≈1
pm longer (B[4]–O[2])
bond length is observed.
(B[4]–O[2])
bond length is observed.
We onward focus on the average M–O[1], M–O[2], and M–O distances listed in Table 2 for the Na+ and Mg2+ species, which are averages over all M[p] coordinations in the structure.
As expected, the
Na/Mg–O[1] bond lengths are significantly shorter
than their Na/Mg–O[2] counterparts. Marginal variations
of the average Mg–O[1] and Mg–O[2] distances are observed throughout, regardless of the precise B,
Si, or NBO content of the glass (Table 2). The mean Na–{O, O[1], O[2]} bond lengths predicted from the NaK–R glass models conform well to those discussed for Na- and
Na/Ca-bearing borate/BS glasses in ref (56). Notwithstanding that  (Na–O[2]) only varies
marginally among the eight glass structures (Table 2), the Na–O[1] distances
are markedly longer (by 5–8 pm) in each MgNaK–R glass relative to its NaK–R counterpart (Table 2). This is attributed primarily to the sharing
of many NBO sites in the MgNaK–R structure between Na+ and Mg2+, coupled with
the tighter control of Mg2+ to maintain a short Mg–O[1] bond (≈203 pm; Table 2), which lengthens
(Na–O[2]) only varies
marginally among the eight glass structures (Table 2), the Na–O[1] distances
are markedly longer (by 5–8 pm) in each MgNaK–R glass relative to its NaK–R counterpart (Table 2). This is attributed primarily to the sharing
of many NBO sites in the MgNaK–R structure between Na+ and Mg2+, coupled with
the tighter control of Mg2+ to maintain a short Mg–O[1] bond (≈203 pm; Table 2), which lengthens  (Na–O[1]) by 5–8
pm relative to the bond length of ≈240 pm of the Mg-free glasses.
(Na–O[1]) by 5–8
pm relative to the bond length of ≈240 pm of the Mg-free glasses.
3.3. MD-Derived {NaOp} and {MgOp} Speciations
Figure 2 plots the distributions
of {Na[p]} and {Mg[p]} coordinations observed from the glass models. As expected,
the larger Na+ cation exhibits higher coordination numbers
than Mg2+, which is mirrored in average coordination numbers 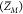 ranging over
ranging over 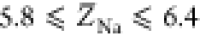 and
and 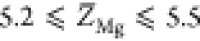 and corresponding distributions peaking
at Na[6] and Mg[5]. Along previous findings
from (boro)phosphosilicate glasses,56,64,87 substantial Na[5] and Na[7] populations are also present throughout all BS glass models (Figure 2). In contrast, the
{Mg[p]} ensemble is more strongly peaked
at p = 5, although significant contributions from
MgO4 and MgO6 polyhedra are encountered in all
structures, with the NaMg2.0–2.1 glass revealing nearly equal
Mg[5] and Mg[6] populations. The herein modeled
and corresponding distributions peaking
at Na[6] and Mg[5]. Along previous findings
from (boro)phosphosilicate glasses,56,64,87 substantial Na[5] and Na[7] populations are also present throughout all BS glass models (Figure 2). In contrast, the
{Mg[p]} ensemble is more strongly peaked
at p = 5, although significant contributions from
MgO4 and MgO6 polyhedra are encountered in all
structures, with the NaMg2.0–2.1 glass revealing nearly equal
Mg[5] and Mg[6] populations. The herein modeled 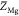 values accord well with those observed
by Pedone and co-workers from NBO-rich phosphosilicate86 and aluminoborosilicate83 glasses, all of which are higher than those reported in ref (85). Potential relationships
between
values accord well with those observed
by Pedone and co-workers from NBO-rich phosphosilicate86 and aluminoborosilicate83 glasses, all of which are higher than those reported in ref (85). Potential relationships
between 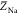 /
/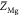 and the glass compositions are discussed
in section S1. The less dispersed distribution
of {Mg[p]} populations relative to {Na[p]} stems from the larger CFSMg and the higher capacity of Mg2+ to control its coordination
shell, as also mirrored in the respective standard deviation
and the glass compositions are discussed
in section S1. The less dispersed distribution
of {Mg[p]} populations relative to {Na[p]} stems from the larger CFSMg and the higher capacity of Mg2+ to control its coordination
shell, as also mirrored in the respective standard deviation 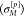 of the p-distribution
around its average value
of the p-distribution
around its average value 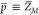 : it spans
: it spans 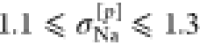 for Na+ but is consistently
smaller for Mg2+ (
for Na+ but is consistently
smaller for Mg2+ (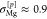 ) in the MgNaK–0.75
glasses and yet lower in their NBO-rich MgNaK–2.1
counterparts:
) in the MgNaK–0.75
glasses and yet lower in their NBO-rich MgNaK–2.1
counterparts: 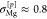 (Table 3).
(Table 3).
Figure 2.
MD-derived distributions of Na[p] (black
and red bars) and Mg[p] (green bars) coordination
numbers in each NaK–R and
MgNaK–R glass with (a) {K, R} = {2.0, 0.75}, (b) {K, R} = {4.0, 0.75}, (c) {K, R} = {2.0, 2.1}, and (d) {K, R} = {4.0, 2.1}. The black and red bars represent the coordination
numbers of Na in the NaK–R and MgNaK–R (“MgNa”)
glasses, respectively. The legends specify the average coordination
numbers 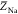 and
and  of Na+ and Mg2+,
respectively.
of Na+ and Mg2+,
respectively.
Table 3. Distributions of Na[p] and Mg[p] Coordinationsa.
| 100x[p]Na (%) |
100x[p]Mg (%) |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glass | Z̅Na | σ[p]Na | 4 | 5 | 6 | 7 | 8 | 9 | Z̅Mg | σ[p]Mg | 3 | 4 | 5 | 6 | 7 | 8 |
| R = 0.75 | ||||||||||||||||
| Na2.0–0.75 | 6.38 | 1.30 | 5.9 | 18.8 | 29.4 | 26.4 | 13.9 | 4.1 | ||||||||
| MgNa2.0–0.75 | 6.22 | 1.27 | 7.0 | 21.0 | 30.5 | 25.6 | 11.4 | 3.1 | 5.52 | 0.93 | 0.5 | 12.1 | 37.8 | 35.7 | 12.4 | 1.5 |
| Na4.0–0.75 | 6.11 | 1.27 | 8.0 | 22.6 | 31.6 | 23.0 | 10.5 | 2.6 | ||||||||
| MgNa4.0–0.75 | 5.90 | 1.26 | 9.9 | 26.0 | 32.0 | 20.0 | 7.8 | 1.8 | 5.17 | 0.91 | 1.4 | 21.7 | 43.2 | 27.2 | 5.6 | 0.9 |
| R = 2.1 | ||||||||||||||||
| Na2.0–2.1 | 5.81 | 1.11 | 9.8 | 30.6 | 34.3 | 18.1 | 5.5 | 1.0 | ||||||||
| MgNa2.0–2.1 | 6.03 | 1.18 | 8.0 | 24.9 | 33.0 | 23.0 | 8.4 | 1.8 | 5.33 | 0.79 | 0.0 | 13.0 | 48.2 | 32.3 | 6.2 | 0.4 |
| Na4.0–2.1 | 5.82 | 1.20 | 11.5 | 28.8 | 31.7 | 18.4 | 6.8 | 1.5 | ||||||||
| MgNa4.0–2.1 | 5.98 | 1.20 | 8.5 | 24.8 | 33.3 | 22.3 | 7.9 | 1.7 | 5.16 | 0.80 | 0.2 | 19.6 | 48.6 | 27.3 | 4.1 | 0.2 |
| σb | 0.02 | 0.01 | 0.3 | 0.4 | 0.4 | 0.5 | 0.2 | 0.2 | 0.02 | 0.02 | 0.2 | 1.1 | 1.1 | 0.9 | 0.7 | 0.2 |
MD-derived average coordination
number of Na+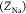 and Mg2+ (
and Mg2+ (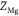 ) across the respective {Na[p]} and {Mg[p]} distributions,
where
) across the respective {Na[p]} and {Mg[p]} distributions,
where 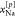 and
and  denote the corresponding fractional populations
of the Na[p] and Mg[p] coordination species and
denote the corresponding fractional populations
of the Na[p] and Mg[p] coordination species and 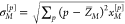 is the distribution width.
is the distribution width.
The data uncertainties are ±1σ, with σ given for each entity.
The herein observed 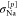 values from a rather modest Na–(Mg)–B–Si–O
glass ensemble agree well with those of previous MD-derived results
gathered from large sets of Na-bearing borate, boro(phospho)silicate,
and phosphosilicate glasses.56,64 Notably, the Ca2+ cation with an intermediate CFS between Na+ and
Mg2+ (Table S1) reveals
values from a rather modest Na–(Mg)–B–Si–O
glass ensemble agree well with those of previous MD-derived results
gathered from large sets of Na-bearing borate, boro(phospho)silicate,
and phosphosilicate glasses.56,64 Notably, the Ca2+ cation with an intermediate CFS between Na+ and
Mg2+ (Table S1) reveals 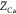 values close to and only marginally lower
than those of Na+. However, the
values close to and only marginally lower
than those of Na+. However, the 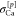 range is closer to that of Mg2+, spanning 0.8–0.9 in Na–Ca–Si–P–O
glasses64 and 0.8–1.1 in their B-bearing
counterparts.56 A general tendency is that
both
range is closer to that of Mg2+, spanning 0.8–0.9 in Na–Ca–Si–P–O
glasses64 and 0.8–1.1 in their B-bearing
counterparts.56 A general tendency is that
both 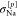 and
and 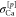 values increase concomitantly with the
B content of the glass (see Table 3 and ref (56)), whereas our rather sparse data available for Mg2+ merely suggests that
values increase concomitantly with the
B content of the glass (see Table 3 and ref (56)), whereas our rather sparse data available for Mg2+ merely suggests that 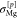 remains nearly constant for fixed-K MgNaK–R glasses
but depends on R, i.e., on the NBO content.
remains nearly constant for fixed-K MgNaK–R glasses
but depends on R, i.e., on the NBO content.
In oxide-based glasses,  decreases for increasing Mz+ CFS values. For instance, all high-CFS
La3+, Y3+, Lu3+, and Sc3+ cations (Table S1) manifest narrow p-distributions in AS glasses.5,88,89 Indeed, although the La3+ ion is markedly
larger than Mg2+—as is reflected in MD-derived average
coordination numbers of 6.0–6.6 in La2O3–Al2O3–SiO2 glasses88— CFSLa = 0.52 Å–2 is slightly higher than CFSMg = 0.46 Å–2, yielding a coordination spread of
decreases for increasing Mz+ CFS values. For instance, all high-CFS
La3+, Y3+, Lu3+, and Sc3+ cations (Table S1) manifest narrow p-distributions in AS glasses.5,88,89 Indeed, although the La3+ ion is markedly
larger than Mg2+—as is reflected in MD-derived average
coordination numbers of 6.0–6.6 in La2O3–Al2O3–SiO2 glasses88— CFSLa = 0.52 Å–2 is slightly higher than CFSMg = 0.46 Å–2, yielding a coordination spread of 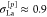 . Incidentally, the Sc3+ cation
with a substantial CFS of 0.68 Å–2 reveals
very similar {Sc[p]} populations in Sc2O3–Al2O3–SiO2 glasses compared to the {Mg[p]} populations of the present MgNaK–R glasses (Figure 2), with
. Incidentally, the Sc3+ cation
with a substantial CFS of 0.68 Å–2 reveals
very similar {Sc[p]} populations in Sc2O3–Al2O3–SiO2 glasses compared to the {Mg[p]} populations of the present MgNaK–R glasses (Figure 2), with 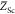 and
and 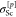 spanning 5.1–5.4 and 0.68–0.71,
respectively (see Figure 3 of Okhotnikov et al.89).
spanning 5.1–5.4 and 0.68–0.71,
respectively (see Figure 3 of Okhotnikov et al.89).
A frequently suggested but hitherto unsettled issue concerns the possibility that a subensemble of Mg2+ does not act as a network modifier but merely assumes a network-forming role in the guise of MgO4 tetrahedra.22,90−92 Yet, discriminating between those two distinct structural scenarios is not straightforward even from glass models because precise and reliable criteria are difficult to formulate given that all electropositive Mz+ cations coordinate a significant number of BO sites at the SiO4 and BOp moieties (section 3.4). Table 3 reveals that Mg[4] accounts for 12–22% of the Mg speciations of the present BS glasses. Even if {Mg[4]} would assume a partial network-forming role, it is likely to be only minor. Indeed, eq 9 rests on the assumption that all Na+/Mg2+ cations act as modifiers, where the excellent agreement between the MD-derived NBO populations and those obtained experimentally via eq 9 (Table 1) suggests that a vast majority of the Mg2+ cations (if not all) assume the expected network-modifying role. To widen the perspective, non-negligible Na[4] populations are also predicted in MD-derived oxide-glass models (see Table 3 and refs (56) and (87)), but a potential network-forming capacity of the archetypal Na+modifier has to our knowledge not yet been suggested.
3.4. CFS-Dependent Preferences for M–BO/NBO Bonding
We now examine the MD-derived BO/NBO partitioning in the first coordination shells of the Na+ and Mg2+ cations in each BS glass structure, i.e., the distribution of the O[2]/O[1] coordinations of the respective {NaOp} and {MgOp} ensembles presented in Table 4. Because CFSCa is intermediate between CFSNa and CFSMg (Table S1) and the relative preferences for M[p]–BO/NBO bonding are strongly CFS-dependent, Table 4 also includes modeled data from R[0.5CaO–0.5Na2O]–B2O3–KSiO2 glasses, denoted “CaNaK–R” and discussed in refs (22), (50), and (51). Each NBO and BO fraction in the first coordination shell of an Mz+ cation is denoted by x(M–NBO) and x(M–BO), respectively. It was determined from the MD-derived glass model, whereupon the corresponding preferences for M–NBO and M–BO bonding were calculated by P(M–NBO) = x(M–NBO)/xNBO, and P(M–BO) = x(M–BO)/xBO, with x(M–NBO) + x(M–BO) = 1.56,93 For nonpreferential M–BO/NBO bond formation, P(M–NBO) = P(M–BO) = 1 and the fractions of M–NBO and M–BO contacts match the respective xNBO and xBO values of the glass. The cases P(M–O[q]) > 1 and P(M–O[q]) < 1 mark the preference and reluctance of M–O[q] formation, respectively, with the deviation from unity of P(M–O[q]) conveying the degree of preference/reluctance.
Table 4. MD-Derived Fractional Populations and Preferences for {Na, Ca, Mg}–{BO, NBO} Bondinga.
|
x(M–O[1]) |
P(M–O[1]) |
x(M–O[2]) |
P(M–O[2]) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glass | xNBO | Na | Ca | Mg | Na | Ca | Mg | Na | Ca | Mg | Na | Ca | Mg |
| R = 0.75 | |||||||||||||
| Na2.0–0.75 | 0.054 | 0.128 | 2.39 | 0.872 | 0.92 | ||||||||
| CaNa2.0–0.75 | 0.083 | 0.114 | 0.408 | 1.37 | 4.91 | 0.886 | 0.592 | 0.97 | 0.65 | ||||
| MgNa2.0–0.75 | 0.104 | 0.155 | 0.565 | 1.50 | 5.44 | 0.845 | 0.435 | 0.94 | 0.49 | ||||
| Na4.0–0.75 | 0.039 | 0.124 | 3.20 | 0.876 | 0.91 | ||||||||
| CaNa4.0–0.75 | 0.064 | 0.131 | 0.446 | 2.05 | 6.95 | 0.869 | 0.554 | 0.93 | 0.59 | ||||
| MgNa4.0–0.75 | 0.077 | 0.165 | 0.623 | 2.14 | 8.07 | 0.835 | 0.377 | 0.90 | 0.41 | ||||
| R = 2.1 | |||||||||||||
| Na2.0–2.1 | 0.364 | 0.537 | 1.48 | 0.463 | 0.73 | ||||||||
| CaNa2.0–2.1 | 0.363 | 0.441 | 0.717 | 1.22 | 1.98 | 0.559 | 0.283 | 0.88 | 0.44 | ||||
| MgNa2.0–2.1 | 0.382 | 0.477 | 0.808 | 1.25 | 2.11 | 0.523 | 0.192 | 0.85 | 0.31 | ||||
| Na4.0–2.1 | 0.228 | 0.419 | 1.84 | 0.581 | 0.75 | ||||||||
| CaNa4.0–2.1 | 0.238 | 0.339 | 0.659 | 1.42 | 2.76 | 0.661 | 0.341 | 0.87 | 0.45 | ||||
| MgNa4.0–2.1 | 0.253 | 0.368 | 0.784 | 1.45 | 3.10 | 0.632 | 0.216 | 0.85 | 0.29 | ||||
| σb | 0.001 | 0.003 | 0.010 | 0.007 | 0.02 | 0.09 | 0.07 | 0.003 | 0.010 | 0.007 | 0.01 | 0.01 | 0.01 |
Fractional x(M–O[1]) and x(M–O[2]) populations out of the entire
O speciation for M = {Na, Ca, Mg}, along with the
corresponding preferences for M–O[p] bonding defined by P(M–O[p])=x(M–O[p])/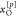 , where
, where 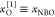 and
and 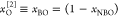 . The data from the CaNaK–R glasses were obtained from MD-generated
models presented in ref.50
. The data from the CaNaK–R glasses were obtained from MD-generated
models presented in ref.50
The data uncertainties are ±1σ with σ given for each entity.
The data of Table 4 confirm the well-documented propensities of Na+ and Ca2+ cations to coordinate NBO rather than BO species56,60,64,83,87,94−97 and that P(M–NBO) increases concurrently with the Mz+ CFS as follows:56,64,86,87P(Na–NBO) < P(Ca–NBO) < P(Mg–NBO). The precise P(M–NBO) value depends not only on the Mz+identity but also on the {R, K} parameters of the BS glass: all Na+, Ca2+, and Mg2+ cations strongly prefer NBO coordination, which accentuates for (i) increasing nSi/nB ratio (i.e., increasing K) and, in particular, (ii) decreasing xNBO (i.e., decreasing R). Consequently, all three network-modifier species manifest the overall strongest preference for M–NBO bond formation in the {K, R} = {4.0, 0.75} structures (Table 4).
Trend (ii) is unsurprising,
i.e., that the strongest preference
for M–NBO bonding occurs in NBO-poor BS glasses. It conforms to the frequently encountered feature of
oxide glasses in which their propensity for forming
a given structural moiety deviates the most from that predicted by
an unrestricted random/statistical distribution whenever its abundance is low. Some examples reported
by us and others encompass the following: (I) the clustering of rare-earth
cations in RE2O3–Al2O3–SiO2 (refs (93) and (98)) and Na2O–SiO2 (refs (99) and (100)) glasses (whereas if
RE2O3 oxides are added to molten SiO2, strong RE3+ clustering occurs at any concentration100,101); (II) the deviations from an
otherwise essentially random spatial distribution of 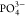 anions in Ca–Na–P–Si–O
glasses occur for low P contents (xP ≲
0.015), which manifest a minor P–P aggregation.102,103 (III) The preference for each of the two prevalent
P–O–B[4] and P–O–Si linkages in borophosphosilicate glasses is strongest in Si-rich and B-rich glass structures, respectively, i.e., when
the accompanying fractions of P–O–Si and
P–O–B[4] linkages dominate.55 Exceptions to this crude “rule of thumb”
do indeed exist, such as that the spatial distribution of Na+ cations in Na2O–(CaO)–B2O3–SiO2 glasses, which is most uniform in
Na-poor compositions but randomizes in modifier-richer glasses.57
anions in Ca–Na–P–Si–O
glasses occur for low P contents (xP ≲
0.015), which manifest a minor P–P aggregation.102,103 (III) The preference for each of the two prevalent
P–O–B[4] and P–O–Si linkages in borophosphosilicate glasses is strongest in Si-rich and B-rich glass structures, respectively, i.e., when
the accompanying fractions of P–O–Si and
P–O–B[4] linkages dominate.55 Exceptions to this crude “rule of thumb”
do indeed exist, such as that the spatial distribution of Na+ cations in Na2O–(CaO)–B2O3–SiO2 glasses, which is most uniform in
Na-poor compositions but randomizes in modifier-richer glasses.57
The stronger preference for NBO coordination of the higher-CFS Ca2+ and Mg2+ ions compared to that of Na+ (refs (56), (64), (83), (86), (87), and (96)) is also mirrored in the reduced P(Na–NBO) value in each MgNaK–R glass relative to that its ternary NaK–R analog, notwithstanding that some of the mixed-cation glasses manifest slightly larger x(Na–NBO) fractions than their NaK–R counterparts due to their higher NBO contents accompanying Mg2+ introduction (Table 4). Yet, except for the overall NBO-richest {K, R}={2.0, 2.1} glasses (xNBO ≈ 0.36), the low-CFS Na+ ion consistently features more BO than NBO contacts throughout all R = 0.75 glasses, for which NBO species accounts only for 11–17% of all Na–O bonds in each {NaOp} ensemble. That contrasts sharply with the {MgOp} speciation of the MgNa4.0–0.75 glass, for which NBO anions constitute 62% of all Mg–O[q] bonds despite the low NBO abundance (xNBO = 0.077), which is readily rationalized by the 2–3 times stronger Mg–NBO than Na–NBO affinity (Table 4).
The P(M–BO) < 1 values observed in Table 4 throughout all BS glass models and all three network modifier species mirror the as-expected reluctance of M–BO bond formation, which is accentuated for increasing Mz+ CFS values as follows: P(Na–BO) > P(Ca–BO) > P(Mg–BO). Although the much stronger propensity for M–NBO over M–BO contacts in oxide glasses is both intuitive and well documented by computational modeling,56,60,64,83,86,87,94,95 it is challenging to quantify the x(M–NBO) and x(M–BO) fractions using experiments. Yet, this was recently accomplished by exploiting double-resonance 17O{23Na} and 17O{27Al} NMR applied to an AS glass of composition 10.8Na2O–32.3CaO–13.0Al2O3–44.0SiO2.96 That yielded estimated x(M–BO)/x(M–NBO) ratios of 1.4 and 0.37 for Na+ and Ca2+, respectively,96 incidentally very close to those of 1.3 (Na+) and 0.40 (Ca2+) predicted herein for the M–BO/NBO partitioning of the NaCa2.0–2.1 glass (Table 4). However, given the by definition very local structural information encoded by the Na–O[q] contacts of the NaOp polyhedra—and M–O[q̅] bonds in general—coupled with the direct scaling of the x(Na–NBO) and x(Na–BO) fractions with the NBO content of the glass (e.g., see Table 4 and ref (56)), we discourage attempts to draw even qualitative conclusions about medium-range glass-structure features from {x(M–O[p])} data alone, encompassing inferences about the spatial Na+ distribution and its possible implications for the (sub)nanometer-scale glass organization.96,97
3.5. B[p]/Si Intermixing Probed by 11B{29Si} REDOR NMR and MD Simulations
3.5.1. Relative Degrees of B[3]–O–Si and B[4]–O–Si Bonding
The relative extents of B[3]–O–Si and B[4]–O–Si bonding in the Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1 structures were assessed by 11B{29Si} REDOR NMR experiments. Figure 3 displays the “dephasing” responses observed from the 11BO3 and 11BO4 resonances for increasing “dipolar recoupling” periods (τrec) of 11B[p]–29Si through-space interactions that are responsible for the NMR-signal dephasing.65,104 While the 11B[p]-resonance dephasing is unaffected by any B[p]–O–B[q] or Si–O–Si linkage of the structure, its rate increases concurrently with the number of 11B[p]–O–29Si linkages, thereby accelerating the progress toward the ΔS/S0 = 1 limit of “complete dephasing”24,25,41,42 (Figure 3a–c). As expected from the higher-coordination B[4] sites and previous 11B{29Si} REDOR NMR reports from other BS glasses,44,46 their resonances reach the complete limit of complete dephasing well before their 11B[3] counterparts (Figure 3a–c), except for the MgNa4.0–0.75 glass (vide infra).
Figure 3.

11B{29Si} REDOR NMR dephasing data (ΔS/S0) plotted against the recoupling/dephasing interval (τrec) and recorded at 14.1 T and 9.00 kHz MAS from the (a, d) Na4.0–0.75, (b, e) MgNa4.0–0.75, and (c, f) MgNa4.0–2.1 glasses. The top panels (a–c) displays the entire 11B[3] and 11B[3] dephasing curves, whereas the bottom panels (d–f) show zoomed-in views of the initial dephasing regimes. Note that the lines in (a–c) only serve to guide the eye, while those of (d–f) are best-fit results to eq 7 for the data ΔS/S0 ⩽ 0.20. All data uncertainties are within the symbol sizes.
Numerical fitting of the initial 11B[p] NMR-signal dephasing regime with “short” τrec values (Figure 3d–f) to eq 7 yields an estimate of the dipolar second moment M2(B[p]–Si), which reflects the “aggregate” 11B[p]–29Si contact in the structure24,41,42 and grows concomitantly with the net number of direct B[p]–O–Si bridges, N(B[p]–O–Si), i.e., the average number of Si atoms in the second coordination shell of the {B[p]} sites: M2(B[p]–Si) ≈ N(B[p]–O–Si). As highlighted by previous reports utilizing M2/dipolar-interaction-based NMR analyses to make inferences about bonding statistics/preferences,34,42,64 however, this relationship is only approximate because M2(B[p]–Si) involves a sum over all r(B[p]–O–Si) distances in the structure (eq 6). Although the analysis of section S2 reveals that M2(B[p]–Si) approximates well the targeted information about the (average) number of direct B[p]–O–Si linkages, other factors degrade quantitative assessments of B[4]–O–Si bonding relative to B[3]–O–Si, which becomes underestimated by ≈25%.
Table 5 compiles the experimental M2(B[p]–Si) data together with those extracted from the glass models via eq 6. The consistently lower experimental M2(B[p]–Si) values compared to their MD-derived counterparts (by 40–55%) stem primarily from experimental imperfections, in particular rf inhomogeneity.66,67 Consequently, we focus our comparisons on the relative M2(B[p]–Si) trends among the B[3]/B[4] coordinations encoded by each NMR- and MD-derived dipolar second-moment ratio (section S2):
| 10 |
Table 5 reveals a very good agreement between the experimental and
modeled 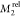 (B) values, whose deviations only amount
to a few percent. Even the largest discrepancy observed for the MgNa4.0–0.75
structure (16%) must be considered decent in view of the large number
of potential error sources that could degrade the agreement, notably
those of the MD-generated glass models.
(B) values, whose deviations only amount
to a few percent. Even the largest discrepancy observed for the MgNa4.0–0.75
structure (16%) must be considered decent in view of the large number
of potential error sources that could degrade the agreement, notably
those of the MD-generated glass models.
Table 5. 11B[p]–29Si Dipolar Second Moments and F–O–F′ Bonding Preferencesa.
| M2(B[3]–Si) | M2(B[4]–Si) | M2(Si–B[3]) | M2(Si–B[4])b |
P(Si–O–F)c |
P(B[3] −O–F)c |
P(B[4]–O–F)c | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| glass | (104 Hz2) | (104 Hz2) | Mrel2(B) | (104 Hz2) | (104 Hz2) | Mrel2(Si) | Si | B[3] | B[4] | B[3] | B[4] | B[4] |
| R = 0.75 | ||||||||||||
| Na2.0–0.75 | 5.13 | 7.58 | 1.48 | 9.32 | 16.61 | 1.78 | 0.95 | 0.90 | 1.16 | 0.66 | 1.38 | 0.50 |
| MgNa2.0–0.75 | 5.41 | 7.16 | 1.32 | 14.02 | 10.14 | 0.72 | 0.99 | 0.99 | 1.03 | 0.81 | 1.27 | 0.54 |
| Na4.0–0.75 | 7.08 | 9.51 | 1.34 | 6.70 | 10.04 | 1.50 | 0.99 | 0.94 | 1.09 | 0.76 | 1.38 | 0.40 |
| 3.92 ± 0.05 | 5.65 ± 0.05 | 1.44 ± 0.05 | 3.00 ± 0.04 | 6.99 ± 0.06 | 2.33 ± 0.08 | |||||||
| MgNa4.0–0.75 | 7.23 | 8.85 | 1.22 | 10.12 | 5.33 | 0.53 | 1.00 | 1.01 | 0.99 | 0.74 | 1.33 | 0.49 |
| 3.84 ± 0.03 | 4.02 ± 0.11 | 1.05 ± 0.06 | 5.30 ± 0.04 | 2.50 ± 0.07 | 0.47 ± 0.03 | |||||||
| R = 2.1 | ||||||||||||
| Na2.0–2.1 | 3.47 | 6.72 | 1.94 | 7.68 | 12.04 | 1.57 | 0.92 | 0.99 | 1.19 | 0.79 | 1.15 | 0.52 |
| MgNa2.0–2.1 | 3.78 | 6.51 | 1.72 | 9.63 | 9.49 | 0.99 | 0.97 | 0.99 | 1.11 | 0.81 | 1.20 | 0.54 |
| Na4.0–2.1 | 5.14 | 8.84 | 1.72 | 4.04 | 10.75 | 2.66 | 0.96 | 0.95 | 1.14 | 0.70 | 1.28 | 0.46 |
| MgNa4.0–2.1 | 5.55 | 8.45 | 1.53 | 6.18 | 7.51 | 1.22 | 0.99 | 0.98 | 1.07 | 0.72 | 1.29 | 0.49 |
| 3.37 ± 0.04 | 5.11 ± 0.04 | 1.51 ± 0.04 | 3.75 ± 0.04 | 4.55 ± 0.04 | 1.21 ± 0.03 | |||||||
| σd | 0.04 | 0.05 | 0.02 | 0.10 | 0.12 | 0.04 | 0.01 | 0.01 | 0.01 | 0.05 | 0.02 | 0.03 |
Heteronuclear 11B[p]–29Si dipolar second
moments, M2(B[p]–Si), calculated from the MD-derived glass model (eq 6) or obtained by fitting 11B{29Si} REDOR NMR data to eq 7 (data on line below the glass entry). 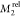 (B) = M2(B[4]–Si)/M2(B[3]–Si).
(B) = M2(B[4]–Si)/M2(B[3]–Si).
Preference factor P(F–O–F′) =P(F′–O–F) for F–O–F′ linkage formation of {F, F′} = {B[3], B[4], Si}. P(F–O–F′) is defined as the ratio between the as-observed number of F–O–F′ linkages in the glass model relative and that predicted from nonpreferential (statistical) {F, F′} intermixing.
The uncertainties of the MD-derived data are ±1σ, with σ given for each entity.
For a statistical/nonpreferential F–O–F′ linkage-formation among
{F, F′}={Si, B[3], B[4]} in a BS
structure devoid of NBO species, 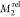 (B) is given by
(B) is given by  (stat) ≈ 1.18 (section S2). The MD derived
(stat) ≈ 1.18 (section S2). The MD derived 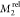 (B) data, and notably the experimental counterparts,
are markedly larger than
(B) data, and notably the experimental counterparts,
are markedly larger than 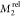 (stat) for all glasses but MgNa4.0–0.75,
in particular for the NBO-rich R = 2.1 members (Table 5). Two structural
factors account for these observations:
(stat) for all glasses but MgNa4.0–0.75,
in particular for the NBO-rich R = 2.1 members (Table 5). Two structural
factors account for these observations:
-
(i)
The NBO partitioning among Si, B[3], and B[4] species in BS glasses was discussed previously,34,50,56 suggesting a substantially stronger propensity for B[3]–NBO bonding relative to B[4]–NBO. Except for very NBO-rich glasses,105 the latter is even considered “forbidden” by most scientists in the field27,69,106−108 but remains frequently observed to minor extents in numerous MD-derived glass models.34,55,56,75,77,82 Consequently, a progressively growing NBO accommodation at the BO3 groups for increasing xNBO reduces the possibility of any B[3]–O–F linkage type, thereby boosting the
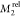 (B) values of all NBO-rich glasses (Table 5), while the relative dipolar second moment (eq 10) is independent of the degree of Si–NBO
bonding.
(B) values of all NBO-rich glasses (Table 5), while the relative dipolar second moment (eq 10) is independent of the degree of Si–NBO
bonding. -
(ii)
The second effect underlying the increased NMR/MD-derived
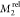 (B) values in any BS glass
is less influential but stems from a slightly higher preference for
B[4]–O–Si bridges than B[3]–O–Si
linkages. Owing to the difficulties in quantifying the preference
factor P(F–O–F′) for F–O–F′ bond formation by experiments, however, current quantitative
insights stem dominantly from computational modeling;55−57,64,109 see ref (50) for
experimental attempts to estimate the {P(B[p]–O–B[q])} subset. Table 5 lists the MD-derived {P(F–O–F′)} factors of the present BS glasses. Here, P(F–O–F′)
= 1 denotes a strictly nonpreferential F/F′ intermixing, whereas P(F–O–F′) > 1 and P(F–O–F′)
< 1 imply a preference and reluctance for F–O–F′ linkage formation, respectively. Although the
bonding preferences depend slightly on the glass composition, the
trends of Table 5 conform
well to those discussed previously for Na/Ca-bearing boro(phospho)silicate
glasses,34,50,55,56 revealing the strongest preference (reluctance) for
BO3–BO4 (BO4–BO4) pairs. While B[3]–O–B[3] linkages are also disfavored, all remaining Si–O–{Si,
B[3], B[4]} linkages form nearly statistically,
i.e., each fractional population is given roughly by the product of
the respective {xSi,
(B) values in any BS glass
is less influential but stems from a slightly higher preference for
B[4]–O–Si bridges than B[3]–O–Si
linkages. Owing to the difficulties in quantifying the preference
factor P(F–O–F′) for F–O–F′ bond formation by experiments, however, current quantitative
insights stem dominantly from computational modeling;55−57,64,109 see ref (50) for
experimental attempts to estimate the {P(B[p]–O–B[q])} subset. Table 5 lists the MD-derived {P(F–O–F′)} factors of the present BS glasses. Here, P(F–O–F′)
= 1 denotes a strictly nonpreferential F/F′ intermixing, whereas P(F–O–F′) > 1 and P(F–O–F′)
< 1 imply a preference and reluctance for F–O–F′ linkage formation, respectively. Although the
bonding preferences depend slightly on the glass composition, the
trends of Table 5 conform
well to those discussed previously for Na/Ca-bearing boro(phospho)silicate
glasses,34,50,55,56 revealing the strongest preference (reluctance) for
BO3–BO4 (BO4–BO4) pairs. While B[3]–O–B[3] linkages are also disfavored, all remaining Si–O–{Si,
B[3], B[4]} linkages form nearly statistically,
i.e., each fractional population is given roughly by the product of
the respective {xSi, 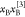 ,
, 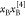 } molar fractions in the glass structure.
Nonetheless, along previous findings from boro(phospho)silicate glasses,34,50,55,56Table 5 conveys the
following subtle trend: P(Si–O–B[4]) > P(Si–O–B[3]) ≈ P(Si–O–Si) ≈ 1 [note
that P(F–O–F′) = P(F′–O–F)]. Hence, the slightly stronger propensity for forming
B[4]–O–Si linkages relative to B[3]–O–Si underlies the observed
} molar fractions in the glass structure.
Nonetheless, along previous findings from boro(phospho)silicate glasses,34,50,55,56Table 5 conveys the
following subtle trend: P(Si–O–B[4]) > P(Si–O–B[3]) ≈ P(Si–O–Si) ≈ 1 [note
that P(F–O–F′) = P(F′–O–F)]. Hence, the slightly stronger propensity for forming
B[4]–O–Si linkages relative to B[3]–O–Si underlies the observed 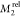 (B)
(B)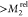 (stat) trend, notably so for the ternary
NaK–R glasses (sections 3.6 and S2).
(stat) trend, notably so for the ternary
NaK–R glasses (sections 3.6 and S2).
3.5.2. B[4] Environments with Variable Numbers of Si and B Neighbors
Figure 4a, c, and e shows the REDOR “reference” 11B NMR spectrum, S0(τrec), of each Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1 glass recorded at the shortest τrec = 0.22 ms value, along with two REDOR spectra [S(τrec)] observed for long dephasing periods of τrec={1.78, 2.67} ms. As expected from the ΔS/S0 dephasing data of Figure 3, the latter spectra manifest progressively diminished 11B[3] and (particularly) 11B[4] resonance intensities for increasing τrec, except for the MgNa4.0–0.75 specimen, which reveals comparable NMR-signal decays.
Figure 4.
Selected 11B{29Si} REDOR NMR spectra of the (a, b) Na4.0–0.75, (c, d) MgNa4.0–0.75, and (e, f) MgNa4.0–2.1 glasses for the as-indicated dipolar recoupling periods (τrec). (a, c, e) REDOR reference spectra [S0(0.22 ms)] shown together with the REDOR NMR spectra [S(τrec)] obtained for long dephasing intervals. (b, d, f) Zoomed-in view of the 11B[4] NMR spectral region (normalized to unity maximum intensity throughout), where two peaks attributed to 11 B[4](4Si) and 11B[4](3Si) moieties are marked as m = 4 and m = 3, respectively.
We now focus on the 11B[4] NMR-signal dephasing, which is more pronounced for the low-δB spectral region <−1 ppm, as is most transparent from the normalized NMR spectra presented in Figure 4b, d, and f. Along the 11B NMR spectral deconvolution results of the Na4.0–0.75 and NaMg4.0–0.75 glasses presented by Lv et al.,51 the two peak components at ≈ −1.8 ppm and ≈ −0.3 ppm are attributed to B[4](OSi)4 and B[4](OSi)3(OB) moieties, respectively,35−37,40,72 which are abbreviated as B[4](4Si) and B[4](3Si). Owing to its larger number of Si neighbors, the resonance decay of 11B[4](4Si) is stronger than that of its 11 B[4](3Si) counterpart. To adequately deconvolute the 11B[4] NMR signal region of the two Na4.0–0.75 and MgNa4.0–0.75 glasses, however, it was necessary to also include a minor peak at ≈1.2 ppm from 11B[4](2Si) environments (accounting for 9% and 17% out of all B[4](mSi) groups, respectively).51 These NMR signals are not clearly discernible in the REDOR spectra, but they are expected to decay even slower than the 11B[4](3Si) resonance, as is also hinted in Figure 4.
3.6. Effects from Mg2+ on the B[p]/Si Intermixing
Although all herein
discussed BS glasses but MgNa4.0–0.75 manifest a markedly larger
number of B[4]–O–Si linkages than B[3]–O–Si bridges, the partial replacement of Na+ by Mg2+ leads to a non-negligible reduction of 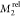 (B) throughout: contrasting the MD-derived M2(B[4]–Si) and M2(B[3]–Si) values of the NaK–R glass and its MgNaK–R counterpart in Table 5 reveals that the decrease of
(B) throughout: contrasting the MD-derived M2(B[4]–Si) and M2(B[3]–Si) values of the NaK–R glass and its MgNaK–R counterpart in Table 5 reveals that the decrease of  (B) stems from an increase of M2(B[3]–Si) at the expense of M2(B[4]–Si), altogether implying
that Mg2+-for-Na+ substitution is accompanied
by an increase (decrease) in the number of B[3]–O–Si
(B[4]–O–Si) linkages. The predictions of
the Na4.0–0.75 and MgNa4.0–0.75 glass models are corroborated
by the REDOR NMR experiments, which reveal a significant reduction
in M2(B[4]–Si) for the
MgNa4.0–0.75 glass (
(B) stems from an increase of M2(B[3]–Si) at the expense of M2(B[4]–Si), altogether implying
that Mg2+-for-Na+ substitution is accompanied
by an increase (decrease) in the number of B[3]–O–Si
(B[4]–O–Si) linkages. The predictions of
the Na4.0–0.75 and MgNa4.0–0.75 glass models are corroborated
by the REDOR NMR experiments, which reveal a significant reduction
in M2(B[4]–Si) for the
MgNa4.0–0.75 glass (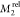 (B) = 1.05) relative to
(B) = 1.05) relative to 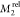 (B) = 1.44 for Na4.0–0.75 (yet the
experimental M2(B[3]–Si)
values of both glasses are nearly equal; Table 5). These effects are evident from the nearly
coincident 11B[p]{Si} REDOR
NMR dephasing curve observed for MgNa4.0–0.75 (Figure 3b,e), in sharp contrast to
those of the other two glasses for which the 11B[4] NMR-signal dephasing rate consistently exceeds that of 11B[3].
(B) = 1.44 for Na4.0–0.75 (yet the
experimental M2(B[3]–Si)
values of both glasses are nearly equal; Table 5). These effects are evident from the nearly
coincident 11B[p]{Si} REDOR
NMR dephasing curve observed for MgNa4.0–0.75 (Figure 3b,e), in sharp contrast to
those of the other two glasses for which the 11B[4] NMR-signal dephasing rate consistently exceeds that of 11B[3].
We stress that although a lower total number
of B[4]–O–Si linkages upon Mg2+ incorporation is indeed anticipated from the drastic decrease of
the BO4 population alone (Table 5), that effect is inconsequential for M2(B[4]–Si) because its value
is independent on {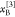 ,
, 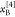 } (eq 6), in contrast to M2(Si–B[4]); see section 3.7. Notably, the MD-generated preference factors of Table 5 rationalize these quantitative trends of dipolar second moments and the number
of B[p]–O–Si bonds as originating from the more fundamental feature of a decrease in P(B[4]–O–Si)
upon the introduction of the high-CFS Mg2+ cation, which
for all NBO-poor (Mg)NaK–0.75 glasses is moreover
emphasized by a concomitant increase of P(B[3]–O–Si) (see section S2).
} (eq 6), in contrast to M2(Si–B[4]); see section 3.7. Notably, the MD-generated preference factors of Table 5 rationalize these quantitative trends of dipolar second moments and the number
of B[p]–O–Si bonds as originating from the more fundamental feature of a decrease in P(B[4]–O–Si)
upon the introduction of the high-CFS Mg2+ cation, which
for all NBO-poor (Mg)NaK–0.75 glasses is moreover
emphasized by a concomitant increase of P(B[3]–O–Si) (see section S2).
The weakened B[4]/Si contacts upon Mg2+-for-Na+ substitution reflect a general trend of a linearly decreasing fraction of B[4]–O–Si linkages (out of all B[4]–O–Si/B bridges) for increasing CFSM, as deduced from 11B[4] MAS NMR spectra deconvolutions.51 These CFS effects are also mirrored in the 29Si MAS NMR spectra of the Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1 glasses shown in Figure 5: as expected from amorphous (boro)silicates, the net 29Si resonance is broad but consistent with solely 29SiO4 groups.24,82,110−113 Hence, the 29Si MAS NMR information content is very limited, at best offering qualitative inferences.113,114 Even for the (almost) NBO-free Na4.0–0.75 and MgNa4.0–0.75 glasses, the net 29Si NMR peak stems from a plethora of unresolved 29Si(OB[3])p(OB[4])q(OSi)4–p−q resonances.
Figure 5.

29Si MAS NMR spectra recorded at 9.4 T and 14.00 kHz MAS from the Na4.0–0.75, MgNa4.0–0.75, and MgNa4.0–2.1 glasses. The higher structural complexity of the NBO-rich MgNa4.0–2.1 structure is mirrored in its ≈5 ppm wider resonance relative to that of its MgNa4.0–0.75 counterpart with a low NBO content, along with a more deshielded chemical shift at the peak maximum (i.e., a higher value of δSi).
The 29Si chemical-shift dispersion and
the precise value
of the most probable shift  located at the maximum NMR-peak intensity
depend predominantly on the {Si, B[3], B[4]}
distribution in the second coordination sphere of 29Si,
where a 3–5 ppm increase of δSi accompanies
each 29Si–O–Si → 29Si–O–B[4] bond replacement,
whereas 29Si–O–Si → 29Si–O–B[3] substitutions
leave the 29Si chemical shift essentially invariant.82,110−113 Hence, the markedly reduced number of Si–O–B[4] bonds in the MgNa4.0–0.75 structure and the concurrently
increased number of Si–O–B[3] and Si–O–Si
linkages rationalize its net 29Si resonance-displacement
toward lower shifts relative to Na4.0–0.75, while the evident
high-ppm “tail” of the NMR stems from the few(er) remaining 29Si–O–B[4] sites (Figure 5). The structural
complexity is accentuated further in the NBO-rich(er) MgNa4.0–2.1
glass, which additionally exhibits variable numbers
of Si–NBO bonds among the SiO4 groups. Besides rationalizing
the broader 29Si NMR peak, it accounts for the 5.8 ppm
higher
located at the maximum NMR-peak intensity
depend predominantly on the {Si, B[3], B[4]}
distribution in the second coordination sphere of 29Si,
where a 3–5 ppm increase of δSi accompanies
each 29Si–O–Si → 29Si–O–B[4] bond replacement,
whereas 29Si–O–Si → 29Si–O–B[3] substitutions
leave the 29Si chemical shift essentially invariant.82,110−113 Hence, the markedly reduced number of Si–O–B[4] bonds in the MgNa4.0–0.75 structure and the concurrently
increased number of Si–O–B[3] and Si–O–Si
linkages rationalize its net 29Si resonance-displacement
toward lower shifts relative to Na4.0–0.75, while the evident
high-ppm “tail” of the NMR stems from the few(er) remaining 29Si–O–B[4] sites (Figure 5). The structural
complexity is accentuated further in the NBO-rich(er) MgNa4.0–2.1
glass, which additionally exhibits variable numbers
of Si–NBO bonds among the SiO4 groups. Besides rationalizing
the broader 29Si NMR peak, it accounts for the 5.8 ppm
higher  value relative to that observed for MgNa4.0–0.75
(Figure 5), stemming
from a typically 7–12 ppm 29Si chemical-shift increase
for each BO → NBO bond replacement.82,110−113
value relative to that observed for MgNa4.0–0.75
(Figure 5), stemming
from a typically 7–12 ppm 29Si chemical-shift increase
for each BO → NBO bond replacement.82,110−113
It is known that Si-rich but Mz+-poor Mz/2O–B2O3–SiO2 glasses exhibit compositional regions of liquid immiscibility, which widen for high-CFS Mz+ cations.37,115−119 A glass-in-glass separation occurs upon cooling, typically identified as (or often merely assumed to involve) one Si-dominated phase coexisting with a B-rich borate/BS counterpart37,115−118 and manifested by 29Si MAS NMR peak displacement toward more negative chemical shifts117 near ≈ –110 ppm observed for vitreous SiO2.113 Incidentally, that is also observed for the MgNa4.0–0.75 glass (Figure 5) but is readily attributed to the significantly fewer Si–O–B[4] bonds in the MgNa4.0–0.75 structure relative to Na4.0–0.75 (note that both29Si–O–Si/B[3] environments resonate at near-equal shifts113). Notably, previous heteronuclear 11B/29Si NMR studies on the bearings from thermal annealing of BS glasses, which may induce structural inhomogeneities and/or phase separation, also reveal that the number of Si–O–B[3] bonds increases relative to Si–O–B[4],45−48 thereby mirroring the herein observed 29Si shielding accompanying Mg2+ incorporation into a Na2O–B2O3–SiO2 glass. However, backscatter scanning electron microscopy (SEM) images (not shown) did not indicate phase separation. Yet nanometer-scale inhomogeneities cannot be excluded, as they would remain undetected both over the ≳1 μm and <0.5 nm length scales probed by our SEM and NMR experimentation, respectively.
Remarkably, despite numerous reports on phase-separated BS glasses, the precise chemical compositions of the two (assumed) coexisting phases remain surprisingly poorly defined. Interestingly, all of the few studies using techniques that directly inform on the Si/B[p] intermixing (i.e., heteronuclear NMR) of annealed/phase-separated BS glasses do not point toward a categorical separation into Si-rich and B-rich phases, but merely to a significant reduction of the number of Si–O–B[4] linkages, while the number of Si–O–B[3] bonds remains invariant, or even increases,45−48 within one, or several, borosilicate phase(s). A recently reported elemental analysis of a phase-separated Na BS glass did reveal two such phases with distinct Si and B contents; however, both contents were substantial in each phase.119 This issue should be investigated further to better define what phases coexist in BS glasses attributed to exhibit nanometer-range structural inhomogeneities.
3.7. Relative Degrees of Si–O–B[3]/B[4] Bonding
This section discusses
the dipolar second moments {M2(Si–B[p])} listed in Table 5. They are accessible from the {M2(B[p]–Si)} set by
the general expression M2(S–I) for S–I spin-pairs,63 which for S = 1/2 (29Si) and I = 3/2 (11B) evaluates to
for S–I spin-pairs,63 which for S = 1/2 (29Si) and I = 3/2 (11B) evaluates to
| 11 |
where  for 11B, whereas 29Si constitutes ≈100% of all Si sites in the isotopically enriched
glasses
for 11B, whereas 29Si constitutes ≈100% of all Si sites in the isotopically enriched
glasses 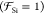 . Although the M2(Si–B[p]) and M2(B[p]–Si) values are
directly related for a given glass specimen, they nonetheless convey complementary information: while M2(B[p]–Si) is proportional
to the number of B[p]–O–Si
linkages at the BOp ensemble, M2(Si–B[p]) relates to the number of Si–O–B[p] bridges at {SiO4}.
. Although the M2(Si–B[p]) and M2(B[p]–Si) values are
directly related for a given glass specimen, they nonetheless convey complementary information: while M2(B[p]–Si) is proportional
to the number of B[p]–O–Si
linkages at the BOp ensemble, M2(Si–B[p]) relates to the number of Si–O–B[p] bridges at {SiO4}.
The crucial utility of eq 11 is its straightforward route to derive both M2(Si–B[3]) and M2(Si–B[4]) values, whose separate estimation is very difficult to accomplish accurately with current state-of-the-art heteronuclear NMR methodology. For instance, the less informative M2(Si–B) entity, i.e., the aggregate dipolar second moment across the entire {B[3], B[4]} ensemble, may be obtained from a 29Si{11B} REAPDOR NMR experiment,104 with the caveat that the experimental protocol along with its subsequent data analysis yield less accurate dipolar second-moment estimates than the M2(B[3]–Si) and M2(B[4]–Si) outcomes of 11B{29Si} REDOR NMR, from which moreover both M2(Si–B[3]) and M2(Si–B[4]) results are readily extracted via eq 11.57,63,64 Hence, sole11B{29Si} REDOR NMR application to a BS glass specimen unveils all four independent M2(B[3]–Si), M2(B[4]–Si), M2(Si–B[3]), and M2(Si–B[4]) results.
From its definition (eq 6), it follows that M2(B[p]–Si) is independent on 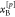 , while M2(Si–B[p]) scales linearly with the B[p] population of the glass but is independent of the
Si content. That feature rationalizes the excellent agreement observed
between the NMR/MD-derived
, while M2(Si–B[p]) scales linearly with the B[p] population of the glass but is independent of the
Si content. That feature rationalizes the excellent agreement observed
between the NMR/MD-derived 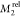 (Si) ≡ M2(Si–B[4])/M2(Si–B[3]) data for the Mg-bearing glasses of Table 5 (whose
(Si) ≡ M2(Si–B[4])/M2(Si–B[3]) data for the Mg-bearing glasses of Table 5 (whose 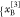 ,
, 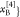 sets accord very well), whereas the significantly
underestimated MD-derived BO4 population of Na4.0–0.75
(section 3.1) accounts
for the lower modeled
sets accord very well), whereas the significantly
underestimated MD-derived BO4 population of Na4.0–0.75
(section 3.1) accounts
for the lower modeled  (Si) result. The direct M2(Si–B[p]) dependence
on
(Si) result. The direct M2(Si–B[p]) dependence
on  renders the
renders the 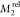 (Si) ratio a very sensitive probe of the
reduced Si–O–B[4] bonding in the glass structure
upon Mg2+ incorporation, as mirrored in the markedly lower
{
(Si) ratio a very sensitive probe of the
reduced Si–O–B[4] bonding in the glass structure
upon Mg2+ incorporation, as mirrored in the markedly lower
{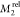 (Si)} values relative to their {
(Si)} values relative to their {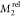 (B)} counterparts (Table 5) and underscoring the time/effort-saving
benefits of having both {M2(B[p]–Si)} and {M2(Si–B[p])} data available
from one sole NMR experiment and eq 11 (see refs (57), (63), and (64) for further examples.
(B)} counterparts (Table 5) and underscoring the time/effort-saving
benefits of having both {M2(B[p]–Si)} and {M2(Si–B[p])} data available
from one sole NMR experiment and eq 11 (see refs (57), (63), and (64) for further examples.
Both 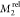 (B) and
(B) and 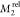 (Si) scale approximately as
(Si) scale approximately as 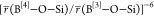 (eq 6 and section S2), while
(eq 6 and section S2), while 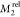 (Si) is additionally proportional to
(Si) is additionally proportional to 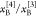 (eq 11). These parameter ratios are listed in Table S4, along with those of Prel(Si) ≡ P(Si–O–B[4])/P(Si–O–B[3]). Disregarding
the MgNa4.0–0.75 glass with much weaker Si/B[4] contacts, Prel(Si) > 1 holds throughout. When taken
together
with Nrel(stat) = 1.44 reflecting a nonpreferential/statistical
Si–O–B[3]/B[4] bond formation
(section S2), the product of the
(eq 11). These parameter ratios are listed in Table S4, along with those of Prel(Si) ≡ P(Si–O–B[4])/P(Si–O–B[3]). Disregarding
the MgNa4.0–0.75 glass with much weaker Si/B[4] contacts, Prel(Si) > 1 holds throughout. When taken
together
with Nrel(stat) = 1.44 reflecting a nonpreferential/statistical
Si–O–B[3]/B[4] bond formation
(section S2), the product of the 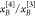 , Prel(Si),
and
, Prel(Si),
and 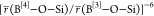 components is consistently slightly larger
than
components is consistently slightly larger
than 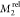 (Si) but yields overall good predictions
for all BS glasses (Table S4), despite
that the crude approximations made are only expected to capture the R = 0.75 glasses with low NBO contents (section S2). The good predictions also observed for the experimental
(Si) but yields overall good predictions
for all BS glasses (Table S4), despite
that the crude approximations made are only expected to capture the R = 0.75 glasses with low NBO contents (section S2). The good predictions also observed for the experimental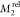 (Si) data are particularly gratifying because
they assumed the MD-derived
(Si) data are particularly gratifying because
they assumed the MD-derived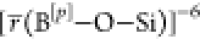 and Prel(Si)
parameters.
and Prel(Si)
parameters.
Notably, although illustrated in the context of
the M2(Si–B[p]) and 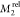 (Si) entities, the various glass composition/structure
parameters discussed above are readily replaced by their analogs underpinning
any M2(F–F′) entity reflecting the number of F–O–F′ linkages at FOp polyhedra that may interlink with
two (or several) FOp, F′Op′, and F″Op″ polyhedral
types.
(Si) entities, the various glass composition/structure
parameters discussed above are readily replaced by their analogs underpinning
any M2(F–F′) entity reflecting the number of F–O–F′ linkages at FOp polyhedra that may interlink with
two (or several) FOp, F′Op′, and F″Op″ polyhedral
types.
3.8. Inferred Si/B[p] Intermixing Versus Current BS Glass-Structure Descriptions
The findings herein of an overall larger extent of B[4]–O–Si than B[3]–O–Si bonding—yet with both linkage-types being abundant throughout all glasses (Table 5)—suggest BS glass networks with substantial {Si, B[3], B[4]} intermixing. When combined with previous inferences of the coexistence of all three B[3]–O–B[3], B[3]–O–B[4] and B[4]–O–B[4], linkages,34,50 the results portrays a network with all six F–O–F′ linkage-types among {Si, B[3], B[4]} encountered in significant populations, each scaling with the molar fractions of its constituents but with higher-than-statistical numbers of the most preferred B[3]–O–B[4] and Si–O–B[4] bonds, while B[4]–O–B[4] linkages are present but disfavored (Table 5).
Bray and co-workers introduced a structural description,52,53 herein referred to as the Yun–Dell–Bray–Xiao
(YDBX) model, which accurately reproduces the experimental {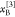 ,
, 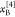 } fractions across the entire glass-formation
region of the Na2O–B2O3–SiO2 system and has found widespread recognition, particularly
within the NMR/glass community. Notwithstanding its success in predicting
the borate speciation, the YDBX model attempts—from routine 11B NMR experimental information alone—to furnish a very detailed (but oversimplified) structural description,
involving a (very) confined set of larger BOp/SiO4 molecular aggregates (“superstructural
units”27,70,120). Superstructural units are indeed known to build many crystalline
borate/BS phases,27 and numerous Raman
studies support their existence for glasses as well.28,110,120,121 While BS-based glass structures most likely do comprise some larger BOp/SiO4 molecular aggregates, it is difficult to reconcile the main body
of experimental reports with any dominating role thereof (except for
limiting cases, such as vitreous B2O327,122,123).
} fractions across the entire glass-formation
region of the Na2O–B2O3–SiO2 system and has found widespread recognition, particularly
within the NMR/glass community. Notwithstanding its success in predicting
the borate speciation, the YDBX model attempts—from routine 11B NMR experimental information alone—to furnish a very detailed (but oversimplified) structural description,
involving a (very) confined set of larger BOp/SiO4 molecular aggregates (“superstructural
units”27,70,120). Superstructural units are indeed known to build many crystalline
borate/BS phases,27 and numerous Raman
studies support their existence for glasses as well.28,110,120,121 While BS-based glass structures most likely do comprise some larger BOp/SiO4 molecular aggregates, it is difficult to reconcile the main body
of experimental reports with any dominating role thereof (except for
limiting cases, such as vitreous B2O327,122,123).
Indeed, 11B, 29Si, and 17O (3Q)MAS NMR reports suggest markedly more disordered BS networks than the (for a glass) exceptionally high medium-range order postulated by the YDBX model, notably its Si/B[3]/B[4]-intermixing predictions.36,37,39,40,47,108,110,111 We guide the reader to the thoughtful but critical remarks made by Möncke et al.47 Notably, the YDBX model predicts that only Si–O–Si/B[4] and B[3]–O–B[3]/B[4] bonds occur in the present NaK–0.75 glasses.52,53 Hence, Si–O–B[3] are absent, in sharp qualitative disagreement with the results for any glass of Table 5, encompassing direct experimental proof of significant Si–O–B[3] bonding in the Na4.0–0.75 glass, which is accentuated in the Mg-bearing glass structures. Furthermore, earlier findings from similar NMR experimentation compared to that employed herein suggested that SiO4 interlinks extensively with both BO3/BO4 moieties in BS glasses.44,46−49 The distinctly different Si/B[p] intermixing predicted by the YDBX model and experimental/modeling findings herein and in refs (36), (37), (39), (40), and (46−48) stems from the YDBX-postulated but grossly underestimated degree of Si–O–B[3] bonding (i.e., P(Si–O–B[3]) ≈ 0), whereas in fact P(Si–O–B[3]) ≲ P(Si–O–B[4]), yielding P(Si–O–B[4])/P(Si–O–B[3]) ≈ 1.2 (Table 5). Analogous contradictions with many experimental findings also plague the alternative branch of “random-network model” (RNM) descriptions69,106,107,124 originating from Zachariasen and Warren,125,126 which overestimate the structural disorder by largely ignoring F–O–F′ bonding preferences (see section 3.5 and comments in ref (50)).
To reconcile the orthogonal implications for the structural order from the too categorical RNM69,106,107,124 and “superstructural-unit”27,70,120 borate/BS glass descriptions, we recently highlighted a “hybrid” model thereof.50 While we are unaware of previous explicit outlines or discussions of a BS glass network being built from some superstructural units along with near-randomly intermixed BO3/BO4/SiO4 groups across a <1 nm scale, even the well established and noncontroversial structure of vitreous B2O3 conforms to such a hybrid structural picture. Here, superstructural B3O6 units (boroxol rings, which comprise ≈70% of all B[3] sites27,123) coexist with ring-interlinking BO3 groups.27,122,123 The introduction of network modifiers along with another network former (Si) naturally increases the structural disorder. This is, for instance, manifested by the strongly altered Si intermixing with both B[3] and B[4] accompanying the replacement of a low-CFS Na+ cation by Mg2+ (section 3.5) and also mirrored in B[3]–O–B[3]/B[4] and B[4]–O–B[4] populations somewhat closer to a statistical {B[p]–O–B[q]} intermixing in Mg-bearing BS glasses.50 Hence, all experimental/modeled results herein and in ref (50) as well as previous work36,37,39,40,47−49,110,111 are consistent with a hybrid random/superstructural-unit BS glass-network description, which nonetheless remains to be concretized from a quantitative standpoint.
4. Conclusions
We investigated the structural
alterations occurring across a subnanometer
scale when Mg2+ replaces Na+ in four RNa2O–B2O3–KSiO2 base glass compositions with K = n(SiO2)/n(B2O3) = {2.0, 4.0} and R=[n(MgO) + n(Na2O)]/n(B2O3) = {0.75, 2.1}. Na+ and Mg2+ exhibit average coordination numbers that vary across 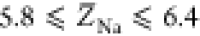 and
and 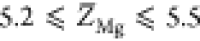 among the glasses, where Na[6] and Mg[5] coordinations are most abundant. A non-negligible
fraction (12–22%) of Mg[4] species is observed but
without evidence supporting a network-forming role of the MgO4 groups. The higher CFS of Mg2+ is manifested in
narrower distributions of coordination numbers {Mg[p]} compared with {Na[p]}, as well
as a 2–3 times stronger preference for NBO coordination relative
to Na+. Although all Mz+ species prefer M–NBO bonding over M–BO, the preference increases concurrently with
the CFS along the series P(Na–NBO) < P(Ca–NBO) < P(Mg–NBO),
where the precise preference factors also depend on the BS glass composition
and, in particular, on the NBO content. Hence, whereas Na+, Ca2+, and Mg2+ all exhibit the strongest
affinity for M–NBO bonding in the R = 0.75 glasses with low NBO contents (xNBO < 0.1), the fractions of M–BO bonds are significant for all glasses/cations,
amounting to roughly 86%, 57%, and 40% out of all BO/NBO species in
the first coordination shells of Na+, Ca2+,
and Mg2+, respectively.
among the glasses, where Na[6] and Mg[5] coordinations are most abundant. A non-negligible
fraction (12–22%) of Mg[4] species is observed but
without evidence supporting a network-forming role of the MgO4 groups. The higher CFS of Mg2+ is manifested in
narrower distributions of coordination numbers {Mg[p]} compared with {Na[p]}, as well
as a 2–3 times stronger preference for NBO coordination relative
to Na+. Although all Mz+ species prefer M–NBO bonding over M–BO, the preference increases concurrently with
the CFS along the series P(Na–NBO) < P(Ca–NBO) < P(Mg–NBO),
where the precise preference factors also depend on the BS glass composition
and, in particular, on the NBO content. Hence, whereas Na+, Ca2+, and Mg2+ all exhibit the strongest
affinity for M–NBO bonding in the R = 0.75 glasses with low NBO contents (xNBO < 0.1), the fractions of M–BO bonds are significant for all glasses/cations,
amounting to roughly 86%, 57%, and 40% out of all BO/NBO species in
the first coordination shells of Na+, Ca2+,
and Mg2+, respectively.
The partial replacement of Na+ by Mg2+ induces primarily the following structural alterations:
-
(i)
Significant BO3 → BO4 and BO → NBO conversions occur. Whereas BO4 accounts for 50–60% of the borate speciations of the Na2O–B2O3–SiO2 glasses, they only amount to 30–45% in the MgO–Na2O–B2O3–SiO2 structures.
-
(ii)
The average Na–NBO bond length is 5–8 pm longer in the MgNaK–R glasses relative to that of ≈240 pm in the absence of Mg2+. That effect likely stems from the sharing of many NBO sites between Na+ and Mg2+, where the stronger capacity of the high-CFS cation to maintain its short Mg–NBO distance (≈203 pm) perturbs the local Na coordination environment.
-
(iii)
All RNa2O–B2O3–KSiO2 glass structures reveal a clear preference for B[4]–O–Si linkages over B[3]–O–Si. Upon Mg2+-for-Na+ substitution, however, the preference for B[4]–O–Si is reduced (i.e., P(B[4]–O–Si) is decreased), whereas the propensity for B[3]–O–Si bridges either remain unaffected (for NBO-rich glasses; R = 2.1) or even increases (for NBO-poor glasses; R = 0.75). This results in P(B[4]–O–Si) ≈ P(B[3]–O–Si) for both MgNa2.0–0.75 and MgNa4.0–0.75 glasses, whereas B[4]–O–Si linkage formation remains (slightly) preferred for the R = 2.1 analogs. We stress that these bonding preferences are independent on the borate speciation. However, effects (i) and (iii) together account for effect (iv) below, namely
-
(iv)
a significant reduction in the number of B[4]–O–Si bonds in the quaternary MgNaK–R glasses. The former bridges dominate throughout all Na2O–B2O3–SiO2 glasses, notably so for the NBO-rich members, where the stronger propensity for B[3]–NBO over B[4]–NBO bonding leads to glass networks with 1.7–2 times more B[4]–O–Si linkages compared with B[3]–O–Si, as estimated from dipolar second moments obtained from either 11B{29Si} REDOR NMR experiments or MD simulations.
The diminished B[4]–O–Si bonding upon Mg2+ incorporation is most evident for the MgNa4.0–0.75 glass network, which exhibits similar numbers of B[4]–O–Si and B[3]–O–Si linkages, whereas the Na4.0–0.75 analog features ≈1.4 times more B[4]–O–Si bridges than B[3]–O–Si. The lower number of B[4]–O–Si linkages in the MgNa4.0–0.75 structure is also mirrored in its 29Si MAS NMR spectrum, whose broad resonance is centered around a chemical shift close to that of vitreous SiO2 but stemming from 29Si–O–Si as well as29Si–O–B[3] environments, both of which resonate at very similar chemical shifts.82,110−113 We found no indications of phase separation of the MgNa4.0–0.75 glass specimen, which most likely constitutes a single amorphous borosilicate phase with emphasized B[3]/Si contacts as compared to its NBO-richer MgNa4.0–2.1 counterpart or any NaK–R glass structure. The findings herein of reduced B[4]/Si contacts in the Mg-bearing glasses echo those deduced from heteronuclear 11B/29Si NMR experimentation on heat-treated BS glasses45−48 that are often taken to imply separation into Si and B dominated phases from face-value interpretations of routine infrared, Raman, or 29Si NMR spectra.
More detailed information about the borate environments and the Si/B[p] intermixing require reliable 11B MAS NMR spectral deconvolutions, which are far from straightforward concerning the 11B[3] resonances22,113 but could give more quantitative information about the M2(B[4]–Si) dipolar second moments for the B[4](2Si), B[4](3Si), and B[4](4Si) environments that coexist in the glass and together yielding each average M2(B[4]–Si) value. This topic, along with the prospects for realistic 11B NMR spectral deconvolutions, will be discussed in upcoming publications.
Acknowledgments
This research was funded by the Swedish Research Council (Grant VR2022-03652) and, in part, by the China Postdoctoral Science Foundation (project 2022M711445). We gratefully acknowledge a scholarship awarded by the China Scholarship Council to P.L. as a visiting Ph.D. student at Stockholm University, as well as Yang Yu for experimental help. The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS), partially funded by the Swedish Research Council through Grant 2022-06725.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.4c01840.
Discussion on the glass-composition dependence of Z̅Na and the relationship between the dipolar second moment M2(F–F′) and the number of F–O–F′ linkages in the glass; tables with cation field strengths, MD simulation parameters, the dependence on M2 on structural parameters, and MD-derived F–O–F′ bond lengths (PDF)
Author Present Address
4 Science Division, New York University Abu Dhabi, P.O. Box 129188, Abu Dhabi, United Arab Emirates
The authors declare no competing financial interest.
Supplementary Material
References
- Kohli J. T.; Shelby J. E. Formation and Properties of Rare Earth Aluminosilicate Glasses. Phys. Chem. Glasses 1991, 32, 67–71. [Google Scholar]
- Tanabe S.; Hirao K.; Soga N. Elastic Properties and Molar Volume of Rare-Earth Aluminosilicate Glasses. J. Am. Ceram. Soc. 1992, 75, 503–506. 10.1111/j.1151-2916.1992.tb07833.x. [DOI] [Google Scholar]
- Shelby J. E. Rare Earths as Modifiers in Oxide Glasses. Key Eng. Mater. 1994, 94–95, 43–80. 10.4028/www.scientific.net/KEM.94-95.43. [DOI] [Google Scholar]
- Iftekhar S.; Grins J.; Edén M. Composition-Property Relationships of the La2O3–Al2O3–SiO2 Glass System. J. Non-Cryst. Solids 2010, 356, 1043–1048. 10.1016/j.jnoncrysol.2010.01.017. [DOI] [Google Scholar]
- Iftekhar S.; Pahari B.; Okhotnikov K.; Jaworski A.; Stevensson B.; Grins J.; Edén M. Properties and Structures of RE2O3–Al2O3–SiO2 (RE = Y, Lu) Glasses Probed by Molecular Dynamics Simulations and Solid-State NMR: The Roles of Aluminum and Rare-Earth Ions for Dictating the Microhardness. J. Phys. Chem. C 2012, 116, 18394–18406. 10.1021/jp302672b. [DOI] [Google Scholar]
- Pahari B.; Iftekhar S.; Jaworski A.; Okhotnikov K.; Jansson K.; Stevensson B.; Grins J.; Edén M. Composition-Property-Structure Correlations of Scandium Aluminosilicate Glasses Revealed by Multinuclear 45Sc, 27Al and 29Si Solid State NMR. J. Am. Ceram. Soc. 2012, 95, 2545–2553. 10.1111/j.1551-2916.2012.05288.x. [DOI] [Google Scholar]
- Stevensson B.; Edén M. Structural Rationalization of the Microhardness Trends of Rare-Earth Aluminosilicate Glasses: Interplay between the RE3+ Field-Strength and the Aluminium Coordinations. J. Non-Cryst. Solids 2013, 378, 163–167. 10.1016/j.jnoncrysol.2013.06.013. [DOI] [Google Scholar]
- Rosales-Sosa G. A.; Masuno A.; Higo Y.; Watanabe Y.; Inoue H. Effect of Rare-Earth Ion Size on Elasticity and Crack Initiation in Rare-Earth Aluminate Glasses. J. Am. Ceram. Soc. 2018, 101, 5030–5036. 10.1111/jace.15760. [DOI] [Google Scholar]
- Dietzel A. Die Kationenfeldstärken und ihre Beziehungen zu Entglasungsvorgängen, zur Verbindungsbildung und zu den Schmelzpunkten von Silicaten. Z. Electrochem. 1942, 48, 9–23. 10.1002/bbpc.19420480104. [DOI] [Google Scholar]
- Lee S. K.; Cody G. D.; Mysen B. O. Structure and the Extent of Disorder in Quaternary (Ca-Mg and Ca-Na) Aluminosilicate Glasses and Melts. Am. Mineral. 2005, 90, 1393–1401. 10.2138/am.2005.1843. [DOI] [Google Scholar]
- Neuville D. R.; Cormier L.; Montouillout V.; Florian P.; Millot F.; Rifflet J.-C.; Massiot D. Structure of Mg and Mg/Ca Aluminosilicate Glasses: 27Al NMR and Raman Spectroscopy Investigations. Am. Mineral. 2008, 93, 1721–1731. 10.2138/am.2008.2867. [DOI] [Google Scholar]
- Kelsey K. E.; Allwardt J. R.; Stebbins J. F. Ca–Mg Mixing in Aluminosilicate Glasses: An Investigation using 17O MAS and 3QMAS and 27Al MAS NMR. J. Non-Cryst. Solids 2008, 354, 4644–4653. 10.1016/j.jnoncrysol.2008.05.049. [DOI] [Google Scholar]
- Guignard M.; Cormier L. Environments of Mg and Al in MgO–Al2O3–Si2O2 Glasses: A Study Coupling Neutron and X-Ray Diffraction and Reverse Monte Carlo Modeling. Chem. Geol. 2008, 256, 111–118. 10.1016/j.chemgeo.2008.06.008. [DOI] [Google Scholar]
- Lee S.; Kim H.; Kim J.; Mun K.; Ryu S. Extent of Disorder in Magnesium Aluminosilicate Glasses: Insights from 27Al and 17O NMR. J. Phys. Chem. C 2016, 120, 737–749. 10.1021/acs.jpcc.5b10799. [DOI] [Google Scholar]
- Allu A. R.; Gaddam A.; Ganisetti S.; Balaji S.; Siegel R.; Mather G. C.; Fabian M.; Pascual M. J.; Ditaranto N.; Milius W.; et al. Structure and Crystallization of Alkaline-Earth Aluminosilicate Glasses: Prevention of the Alumina-Avoidance Principle. J. Phys. Chem. B 2018, 122, 4737–4747. 10.1021/acs.jpcb.8b01811. [DOI] [PubMed] [Google Scholar]
- Smedskjaer M. M.; Mauro J. C.; Kjeldsen J.; Yue Y. Microscopic Origins of Compositional Trends in Aluminosilicate Glass Properties. J. Am. Ceram. Soc. 2013, 96, 1436–1443. 10.1111/jace.12298. [DOI] [Google Scholar]
- Ke X.; Shan Z.; Li Z.; Tao Y.; Yue Y.; Tao H. Toward Hard and Highly Crack Resistant Magnesium Aluminosilicate Glasses and Transparent Glass-Ceramics. J. Am. Ceram. Soc. 2020, 103, 3600–3609. 10.1111/jace.17048. [DOI] [Google Scholar]
- Gammond L. V. D.; Da Silva R. M.; Zeidler A.; Mohammadi H.; Youngman R. E.; Aitken B. G.; Florian P.; Neuville D. R.; Hennet L.; Fischer H. E.; et al. Structure and Related Properties of Amorphous Magnesium Aluminosilicates. Phys. Rev. Mater. 2022, 6, 125603. 10.1103/PhysRevMaterials.6.125603. [DOI] [Google Scholar]
- Bradtmüller H.; Uesbeck T.; Eckert H.; Murata T.; Nakane S.; Yamazaki H. Structural Origins of Crack Resistance on Magnesium Aluminoborosilicate Glasses Studied by Solid-State NMR. J. Phys. Chem. C 2019, 123, 14941–14954. 10.1021/acs.jpcc.9b03600. [DOI] [Google Scholar]
- Kuryaeva R. G. The State of Magnesium in Silicate Glasses and Melts. Glass Phys. Chem. 2009, 35, 378–383. 10.1134/S1087659609040051. [DOI] [Google Scholar]
- Stolyarova V. L.; Lopatin S. I.; Shugurov S. M.; Shilov A. L. Thermodynamic Properties of Silicate Glasses and Melts: VII. System MgO–B2O3–SiO2. Russ. J. Gen. Chem. 2010, 80, 2405–2413. 10.1134/S1070363210120029. [DOI] [Google Scholar]
- Lv P.; Wang C.; Stevensson B.; Yu Y.; Wang T.-S.; Edén M. Impact of the Cation Field Strength on Physical Properties and Structures of Alkali and Alkaline-Earth Borosilicate Glasses. Ceram. Int. 2022, 48, 18094–18107. 10.1016/j.ceramint.2022.03.022. [DOI] [Google Scholar]
- Hordieiev Y. S.; Karasik E. V.; Zaichuk A. V. Glass Formation in the MgO–B2O3–SiO2 System. Silicon 2023, 15, 1085–1091. 10.1007/s12633-022-01745-0. [DOI] [Google Scholar]
- Edén M.NMR of Glasses. In NMR of Inorganic Nuclei; Bryce D. L., Ed.; Comprehensive Inorganic Chemistry III, Vol. 9; Elsevier, 2023; pp 583–659. [Google Scholar]
- Edén M. Update on 27Al NMR Studies of Aluminosilicate Glasses. Annu. Rep. NMR Spectrosc. 2020, 101, 285–410. 10.1016/bs.arnmr.2020.07.002. [DOI] [Google Scholar]
- Zheng Q.; Potuzak M.; Mauro J. C.; Smedskjaer M. M.; Youngman R. E.; Yue Y. Composition-Structure-Property Relationships in Boroaluminosiliate Glasses. J. Non-Cryst. Solids 2012, 358, 993–1002. 10.1016/j.jnoncrysol.2012.01.030. [DOI] [Google Scholar]
- Wright A. C. Borate Structures: Crystalline and Vitreous. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol. B 2010, 51, 1–39. [Google Scholar]
- Chryssikos G. D.; Kamitsos E. I.; Karakassides M. A. Structure of Borate Glasses. Part 2. Alkali Induced Network Modifications in terms of Structure and Properties. Phys. Chem. Glasses 1990, 31, 109–116. [Google Scholar]
- Boekenhauer R.; Zhang H.; Feller S.; Bain D.; Kambeyanda S.; Budhwani K.; Pandikuthira P.; Alamgir F.; Peters A. M.; Messer S.; et al. The Glass Transition Temperature of Lithium Borosilicate Glasses Related to Atomic Arrangements. J. Non-Cryst. Solids 1994, 175, 137–144. 10.1016/0022-3093(94)90005-1. [DOI] [Google Scholar]
- Kato Y.; Yamazaki H.; Kubo Y.; Yoshida S.; Matsuoka J.; Akai T. Effect of B2O3 Content on Crack Initiation under Vickers Indentation Test. J. Ceram. Soc. Jpn. 2010, 118, 792–798. 10.2109/jcersj2.118.792. [DOI] [Google Scholar]
- Limbach R.; Winterstein-Beckmann A.; Dellith J.; Möncke D.; Wondraczek L. Plasticity, Crack Initiation and Defect Resistance in Alkali-Borosilicate Glasses: From Normal to Anomalous Behavior. J. Non-Cryst. Solids 2015, 417–418, 15–27. 10.1016/j.jnoncrysol.2015.02.019. [DOI] [Google Scholar]
- Yamashita H.; Inoue K.; Nakajin T.; Inoue H.; Maekawa T. Nuclear Magnetic Resonance Studies of 0.139MO (or M′2O)·0.673SiO2·(0.188 – x)Al2O3 xB2O3 (M = Mg, Ca, Sr and Ba, M′=Na and K) Glasses. J. Non-Cryst. Solids 2003, 331, 128–136. 10.1016/j.jnoncrysol.2003.08.086. [DOI] [Google Scholar]
- Maekawa T. Chemical Reactions Occurred in Oxide Glasses and Their Melts and Evaluation by Acid-Base Concept: NMR Investigation of Multi-Component Silicate Glasses. J. Ceram. Soc. Jpn. 2004, 112, 467–471. 10.2109/jcersj.112.467. [DOI] [Google Scholar]
- Yu Y.; Stevensson B.; Edén M. Direct Experimental Evidence for Abundant BO4–BO4 Motifs in Borosilicate Glasses from Double-Quantum 11B NMR Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 6372–6376. 10.1021/acs.jpclett.8b02907. [DOI] [PubMed] [Google Scholar]
- Angeli F.; Charpentier T.; de Ligny D.; Cailleteau C. Boron Speciation in Soda-Lime Borosilicate Glasses Containing Zirconium. J. Am. Ceram. Soc. 2010, 93, 2693–2704. 10.1111/j.1551-2916.2010.03771.x. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Solid-State NMR Study of Metastable Immiscibility in Alkali Borosilicate Glasses. J. Non-Cryst. Solids 2003, 315, 239–255. 10.1016/S0022-3093(02)01604-6. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Site Preference and Si/B Mixing in Mixed-Alkali Borosilicate Glasses: A-High Resolution 11B and 17O NMR Study. Chem. Mater. 2003, 15, 3913–3921. 10.1021/cm034427r. [DOI] [Google Scholar]
- Frydman L.; Harwood J. S. Isotropic Spectra of Half-Integer Quadrupolar Spins from Bidimensional Magic-Angle-Spinning NMR. J. Am. Chem. Soc. 1995, 117, 5367–5368. 10.1021/ja00124a023. [DOI] [Google Scholar]
- Wang S.; Stebbins J. F. Multiple-Quantum Magic-Angle Spinning 17O NMR Studies of Borate, Borosilicate, and Boroaluminate Glasses. J. Am. Ceram. Soc. 1999, 82, 1519–1528. 10.1111/j.1151-2916.1999.tb01950.x. [DOI] [Google Scholar]
- Du L.-S.; Stebbins J. F. Nature of Silicon-Boron Mixing in Sodium Borosilicate Glasses: A High-Resolution 11B and 17O NMR Study. J. Phys. Chem. B 2003, 107, 10063–10076. 10.1021/jp034048l. [DOI] [Google Scholar]
- Eckert H.Advanced Dipolar Solid State NMR Spectroscopy of Glasses. In Modern Glass Characterization; Affatigato M. Ed.; John Wiley & Sons, Ltd., 2015; pp 345–390. [Google Scholar]
- Eckert H. Spying with Spins on Messy Materials: 60 Years of Glass Structure Elucidation by NMR Spectroscopy. Int. J. Appl. Glass Sci. 2018, 9, 167–187. 10.1111/ijag.12333. [DOI] [Google Scholar]
- van Wüllen L.; Schwering G. 11B MQMAS and 29Si–{11B} Double-Resonance NMR Studies on the Structure of Binary B2O3–SiO2 Glasses. Solid State Nucl. Magn. Reson. 2002, 21, 134–144. 10.1006/snmr.2002.0054. [DOI] [Google Scholar]
- Wegner S.; van Wüllen L.; Tricot G. The Structure of Phosphate and Borosilicate Glasses and Their Structural Evolution at High Temperatures as Studied with Solid State NMR Spectroscopy: Phase Separation, Crystallisation and Dynamic Species Exchange. Solid State Sci. 2010, 12, 428–439. 10.1016/j.solidstatesciences.2009.03.021. [DOI] [Google Scholar]
- Martineau C.; Michaelis V.; Schuller S.; Kroeker S. Liquid-Liquid Phase Separation in Model Nuclear Waste Glasses: A Solid-State Double-Resonance NMR Study. Chem. Mater. 2010, 22, 4896–4903. 10.1021/cm1006058. [DOI] [Google Scholar]
- Venkatachalam S.; Schröder C.; Wegner S.; van Wüllen L. The Structure of Borosilicate and Phosphosilicate Glasses and its Evolution at Temperatures Above the Glass Transition Temperature: Lessons from In Situ MAS NMR. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol. B 2014, 55, 280–287. [Google Scholar]
- Möncke D.; Tricot G.; Winterstein-Beckmann A.; Wondraczek L.; Kamitsos E. I. On the Connectivity of Borate Tetrahedra in Borate and Borosilicate Glasses. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B 2015, 56, 203–211. 10.13036/1753-3562.56.5.203. [DOI] [Google Scholar]
- Möncke D.; Tricot G.; Winterstein A.; Ehrt D.; Kamitsos E. I. Preferential Bonding in Low Alkali Borosilicate Glasses. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B 2017, 58, 171–179. 10.13036/17533562.58.4.171. [DOI] [Google Scholar]
- Tricot G. The Structure of Pyrex® Glass Investigated by Correlation NMR Spectroscopy. Phys. Chem. Chem. Phys. 2016, 18, 26764–26770. 10.1039/C6CP02996E. [DOI] [PubMed] [Google Scholar]
- Lv P.; Stevensson B.; Yu Y.; Wang T.; Edén M. BO3/BO4 Intermixing in Borosilicate Glass Networks Probed by Double-Quantum 11B NMR: What Factors Govern BO4–BO4 Formation?. J. Phys. Chem. C 2023, 127, 20026–20040. 10.1021/acs.jpcc.3c03577. [DOI] [Google Scholar]
- Lv P.; Sun Z.; Wang F.; Yu Y.; Yang F.; Yue S.; Edén M.; Chen L.; Wang T. Cation Field-Strength Effects on Ion Irradiation-Induced Mechanical Property Changes of Borosilicate Glass Structures. J. Am. Ceram. Soc. 2023, 106, 5766–5780. 10.1111/jace.19213. [DOI] [Google Scholar]
- Yun Y. H.; Bray P. J. Nuclear Magnetic Resonance Studies of the Glasses in the System Na2O–B2O3–SiO2. J. Non-Cryst. Solids 1978, 27, 363–380. 10.1016/0022-3093(78)90020-0. [DOI] [Google Scholar]
- Dell W. J.; Bray P. J.; Xiao S. Z. 11B NMR Studies and Structural Modeling of Na2O–B2O3 – SiO2 Glasses of High Soda Content. J. Non-Cryst. Solids 1983, 58, 1–16. 10.1016/0022-3093(83)90097-2. [DOI] [Google Scholar]
- Todorov I. T.; Smith W.; Trachenko K.; Dove M. T. DL_POLY_3: New Dimensions in Molecular Dynamics Simulations via Massive Parallelism. J. Mater. Chem. 2006, 16, 1911–1918. 10.1039/b517931a. [DOI] [Google Scholar]
- Yu Y.; Stevensson B.; Edén M. Medium-Range Structural Organization of Phosphorus-Bearing Borosilicate Glasses Revealed by Advanced Solid-State NMR Experiments and MD Simulations: Consequences of B/Si Substitutions. J. Phys. Chem. B 2017, 121, 9737–9752. 10.1021/acs.jpcb.7b06654. [DOI] [PubMed] [Google Scholar]
- Stevensson B.; Yu Y.; Edén M. Structure–Composition Trends in Multicomponent Borosilicate-Based Glasses Deduced from Molecular Dynamics Simulations with Improved B–O and P–O Force Fields. Phys. Chem. Chem. Phys. 2018, 20, 8192–8209. 10.1039/C7CP08593A. [DOI] [PubMed] [Google Scholar]
- Yu Y.; Stevensson B.; Edén M. Structural Role of Sodium in Borosilicate, Phosphosilicate, and Borophosphosilicate Glasses Unveiled by Solid-State NMR and MD Simulations. J. Phys. Chem. C 2019, 123, 25816–25832. 10.1021/acs.jpcc.9b06823. [DOI] [Google Scholar]
- Sanders M. J.; Leslie M.; Catlow C. R. A. Interatomic Potentials for SiO2. J. Chem. Soc., Chem. Commun. 1984, 1271–1273. 10.1039/c39840001271. [DOI] [Google Scholar]
- Tilocca A.; de Leeuw N. H.; Cormack A. N. Shell-Model Molecular Dynamics Calculations of Modified Silicate Glasses. Phys. Rev. B 2006, 73, 104209. 10.1103/PhysRevB.73.104209. [DOI] [Google Scholar]
- Tilocca A.; Cormack A. N.; de Leeuw N. H. The Structure of Bioactive Silicate Glasses: New Insights from Molecular Dynamics Simulations. Chem. Mater. 2007, 19, 95–103. 10.1021/cm061631g. [DOI] [Google Scholar]
- Massiot D.; Bessada C.; Coutures J. P.; Taulelle F. A Quantitative Study of 27Al MAS NMR in Crystalline YAG. J. Magn. Reson. 1990, 90, 231–242. 10.1016/0022-2364(90)90130-2. [DOI] [Google Scholar]
- Van Vleck J. H. The Dipolar Broadening of Magnetic Resonance Lines in Crystals. Phys. Rev. 1948, 74, 1168–1183. 10.1103/PhysRev.74.1168. [DOI] [Google Scholar]
- Stevensson B.; Mathew R.; Yu Y.; Edén M. Two Heteronuclear Dipolar Results at the Price of One: Quantifying Na/P Contacts in Phosphosilicate Glasses and Biomimetic Hydroxy-Apatite. J. Magn. Reson. 2015, 251, 52–56. 10.1016/j.jmr.2014.12.002. [DOI] [PubMed] [Google Scholar]
- Mathew R.; Stevensson B.; Edén M. Na/Ca Intermixing around Silicate and Phosphate Groups in Bioactive Phosphosilicate Glasses Revealed by Heteronuclear Solid-State NMR and Molecular Dynamics Simulations. J. Phys. Chem. B 2015, 119, 5701–5715. 10.1021/acs.jpcb.5b01130. [DOI] [PubMed] [Google Scholar]
- Gullion T.; Schaefer J. Detection of Weak Heteronuclear Dipolar Coupling by Rotational-Echo Double-Resonance Nuclear Magnetic Resonance. Adv. Magn. Opt. Reson. 1989, 13, 57–83. 10.1016/B978-0-12-025513-9.50009-4. [DOI] [Google Scholar]
- Chan J. C. C.; Eckert H. Dipolar Coupling Information in Multispin Systems: Application of a Compensated REDOR NMR Approach to Inorganic Phosphates. J. Magn. Reson. 2000, 147, 170–178. 10.1006/jmre.2000.2191. [DOI] [PubMed] [Google Scholar]
- Nishimura K.; Fu R.; Cross T. A. The Effect of RF Inhomogeneity on Heteronuclear Dipolar Recoupling in Solid State NMR: Practical Performance of SFAM and REDOR. J. Magn. Reson. 2001, 152, 227–233. 10.1006/jmre.2001.2410. [DOI] [Google Scholar]
- Gullion T.; Baker D. B.; Conradi M. S. New, Compensated Carr-Purcell Sequences. J. Magn. Reson. 1990, 89, 479–484. 10.1016/0022-2364(90)90331-3. [DOI] [Google Scholar]
- Abe T. Borosilicate Glasses. J. Am. Ceram. Soc. 1952, 35, 284–299. 10.1111/j.1151-2916.1952.tb13051.x. [DOI] [Google Scholar]
- Krogh-Moe J. New Evidence on the Boron Co-ordination in Alkali Borate Glasses. Phys. Chem. Glasses 1962, 3, 1–6. [Google Scholar]
- Sen S.; Xu Z.; Stebbins J. F. Temperature Dependent Structural Changes in Borate, Borosilicate and Boroaluminate Liquids: High-Resolution 11B, 29Si and 27Al NMR Studies. J. Non-Cryst. Solids 1998, 226, 29–40. 10.1016/S0022-3093(97)00491-2. [DOI] [Google Scholar]
- Angeli F.; Villain O.; Schuller S.; Charpentier T.; de Ligny D.; Bressel L.; Wondraczek L. Effect of Temperature and Thermal History on Borosilicate Glass Structure. Phys. Rev. B 2012, 85, 054110. 10.1103/PhysRevB.85.054110. [DOI] [Google Scholar]
- Michel F.; Cormier L.; Lombard P.; Beuneu B.; Galoisy L.; Calas G. Mechanisms of Boron Coordination Change between Borosilicate Glasses and Melts. J. Non-Cryst. Solids 2013, 379, 169–176. 10.1016/j.jnoncrysol.2013.08.007. [DOI] [Google Scholar]
- Kieu L.-H.; Delaye J.-M.; Cormier L.; Stolz C. Development of Empirical Potentials for Sodium Borosilicate Glass Systems. J. Non-Cryst. Solids 2011, 357, 3313–3321. 10.1016/j.jnoncrysol.2011.05.024. [DOI] [Google Scholar]
- Inoue H.; Masuno A.; Watanabe Y. Modeling of the Structure of Sodium Borosilicate Glasses Using Pair Potentials. J. Phys. Chem. B 2012, 116, 12325–12331. 10.1021/jp3038126. [DOI] [PubMed] [Google Scholar]
- Lu X.; Deng L.; Kuo P.-H.; Ren M.; Buterbaugh I.; Du J. Effects of Boron Oxide Substitution on the Structure and Bioactivity of SrO-Containing Bioactive Glasses. J. Mater. Sci. 2017, 52, 8793–8811. 10.1007/s10853-017-0836-9. [DOI] [Google Scholar]
- Pacaud F.; Delaye J.-M.; Charpentier T.; Cormier L.; Salanne M. Structural Study of Na2O–B2O3–S iO2 Glasses from Molecular Dynamics Simulations Using a Polarizable Force Field. J. Chem. Phys. 2017, 147, 161711. 10.1063/1.4992799. [DOI] [PubMed] [Google Scholar]
- Deng L.; Du J. Development of Boron Oxide Potentials for Computer Simulations of Multicomponent Oxide Glasses. J. Am. Ceram. Soc. 2019, 102, 2482–2505. 10.1111/jace.16082. [DOI] [Google Scholar]
- Wang M.; Krishnan N. M. A.; Wang B.; Smedskjaer M. M.; Mauro J. C.; Bauchy M. A New Transferable Interatomic Potential for Molecular Dynamics Simulations of Borosilicate Glasses. J. Non-Cryst. Solids 2018, 498, 294–304. 10.1016/j.jnoncrysol.2018.04.063. [DOI] [Google Scholar]
- Sundararaman S.; Huang L.; Ispas S.; Kob W. New Interaction Potentials for Borate Glasses with Mixed Network Formers. J. Chem. Phys. 2020, 152, 104501. 10.1063/1.5142605. [DOI] [PubMed] [Google Scholar]
- Bertani M.; Pallini A.; Cocchi M.; Menziani M. C.; Pedone A. A new Self-Consistent Empirical Potential Model for Multicomponent Borate and Borosilicate Glasses. J. Am. Ceram. Soc. 2022, 105, 7254–7271. 10.1111/jace.18681. [DOI] [Google Scholar]
- Fortino M.; Berselli A.; Stone-Weiss N.; Deng L.; Goel A.; Du J.; Pedone A. Assessment of Interatomic Parameters for the Reproduction of Borosilicate Glass Structures via DFT-GIPAW Calculations. J. Am. Ceram. Soc. 2019, 102, 7225–7243. 10.1111/jace.16655. [DOI] [Google Scholar]
- Bertani M.; Bisbrouck N.; Delaye J.-M.; Angeli F.; Pedone A.; Charpentier T. Effects of Magnesium on the Structure of Aluminoborosilicate Glasses: NMR Assessment of Interatomic Potentials Models for Molecular Dynamics. J. Am. Ceram. Soc. 2023, 106, 5501–5521. 10.1111/jace.19157. [DOI] [Google Scholar]
- Swenson J.; Börjesson L.; Howells W. S. Structure of Borate Glasses from Neutron-Diffraction Experiments. Phys. Rev. B 1995, 52, 9310–9319. 10.1103/PhysRevB.52.9310. [DOI] [PubMed] [Google Scholar]
- Tuheen M. I.; Du J. Effect of Modifier Cation Field Strength on the Structures of Magnesium Oxide Containing Aluminoborosilicate Glasses. Int. J. Appl. Glass Sci. 2022, 13, 554–567. 10.1111/ijag.16599. [DOI] [Google Scholar]
- Pedone A.; Malavasi G.; Menziani M. Computational Insight into the Effect of CaO/MgO Substitution on the Structural Properties of Phospho-Silicate Bioactive Glasses. J. Phys. Chem. C 2009, 113, 15723–15730. 10.1021/jp904131t. [DOI] [Google Scholar]
- Xiang Y.; Du J. Effect of Strontium Substitution on the Structure of 45S5 Bioglasses. Chem. Mater. 2011, 23, 2703–2717. 10.1021/cm102889q. [DOI] [Google Scholar]
- Jaworski A.; Stevensson B.; Pahari B.; Okhotnikov K.; Edén M. Local Structures and Al/Si Ordering in Lanthanum Aluminosilicate Glasses Explored by Advanced 27Al NMR Experiments and Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2012, 14, 15866–15878. 10.1039/c2cp42858j. [DOI] [PubMed] [Google Scholar]
- Okhotnikov K.; Stevensson B.; Edén M. New Interatomic Potential Parameters for Molecular Dynamics Simulations of Rare-Earth (RE = La, Y, Lu, Sc) Aluminosilicate Glass Structures: Exploration of RE3+ Field-Strength Effects. Phys. Chem. Chem. Phys. 2013, 15, 15041–15055. 10.1039/c3cp51726h. [DOI] [PubMed] [Google Scholar]
- Kim K. S.; Bray P. J. 11B NMR Studies of Glasses in the System MgO–Na2O–B2O3. Phys. Chem. Glasses 1974, 15, 47–51. [Google Scholar]
- Watts S. J.; Hill R. G.; O’Donnell M. D.; Law R. V. Influence of Magnesia on the Structure and Properties of Bioactive Glasses. J. Non-Cryst. Solids 2010, 356, 517–524. 10.1016/j.jnoncrysol.2009.04.074. [DOI] [Google Scholar]
- Logrado M.; Eckert H.; Murata T.; Nakane S.; Yamazaki H. Structure-Property Relations in Crack-Resistant Alkaline-Earth Aluminoborosilicate Glasses Studied by Solid State NMR. J. Am. Ceram. Soc. 2021, 104, 2250–2267. 10.1111/jace.17629. [DOI] [Google Scholar]
- Stevensson B.; Jaworski A.; Edén M. The Structural Roles of Sc and Y in Aluminosilicate Glasses Probed by Molecular Dynamics Simulations. J. Non-Cryst. Solids 2017, 460, 36–46. 10.1016/j.jnoncrysol.2016.12.005. [DOI] [Google Scholar]
- Cormier L.; Neuville D. R. Ca and Na Environments in Na2O–CaO–Al2O3–SiO2 Glasses: Influence of Cation Mixing and Cation-Network Interactions. Chem. Geol. 2004, 213, 103–113. 10.1016/j.chemgeo.2004.08.049. [DOI] [Google Scholar]
- Tilocca A.; de Leeuw N. H. Structural and Electronic Properties of Modified Sodium and Soda-Lime Silicate Glasses by Car-Parrinello Molecular Dynamics. J. Mater. Chem. 2006, 16, 1950–1955. 10.1039/B517362K. [DOI] [Google Scholar]
- Sukenaga S.; Florian P.; Kanehashi K.; Shibata H.; Saito N.; Nakashima K.; Massiot D. Oxygen Speciation in Multicomponent Silicate Glasses Using Through Bond Double Resonance NMR Spectroscopy. J. Phys. Chem. Lett. 2017, 8, 2274–2279. 10.1021/acs.jpclett.7b00465. [DOI] [PubMed] [Google Scholar]
- Lee J.; Lee S. K. Probing the Homogeneous Distribution of Sodium Atoms in Silicate Glasses. Acta Mater. 2022, 241, 118413. 10.1016/j.actamat.2022.118413. [DOI] [Google Scholar]
- Christie J. K.; Tilocca A. Aluminosilicate Glasses as Yttrium Vectors for in situ Radiotherapy: Understanding Composition-Durability Effects Through Molecular Dynamics Simulations. Chem. Mater. 2010, 22, 3725–3734. 10.1021/cm100847p. [DOI] [Google Scholar]
- Johnson J. A.; Benmore C. J.; Holland D.; Du J.; Beuneu B.; Mekki A. Influence of Rare-Earth Ions on SiO2–Na2O–RE2O3 Glass Structure. J. Phys.: Condens. Matter 2011, 23, 065404. 10.1088/0953-8984/23/6/065404. [DOI] [PubMed] [Google Scholar]
- Kokou L.; Du J. Rare Earth Ion Clustering Behavior in Europium Doped Silicate Glasses: Simulation Size and Glass Structure Effect. J. Non-Cryst. Solids 2012, 358, 3408–3417. 10.1016/j.jnoncrysol.2012.01.068. [DOI] [Google Scholar]
- Afify N. D.; Mountjoy G. Molecular-Dynamics Modeling of Eu3+-Ion Clustering in SiO2 Glass. Phys. Rev. B 2009, 79, 024202. 10.1103/PhysRevB.79.024202. [DOI] [Google Scholar]
- Mathew R.; Turdean-Ionescu C.; Stevensson B.; Izquierdo-Barba I.; García A.; Arcos D.; Vallet-Regí M.; Edén M. Direct Probing of the Phosphate-Ion Distribution in Bioactive Silicate Glasses by Solid-State NMR: Evidence for Transitions between Random/Clustered Scenarios. Chem. Mater. 2013, 25, 1877–1885. 10.1021/cm400487a. [DOI] [Google Scholar]
- Stevensson B.; Mathew R.; Edén M. Assessing the Phosphate Distribution in Bioactive Phosphosilicate Glasses by 31P Solid-State NMR and MD Simulations. J. Phys. Chem. B 2014, 118, 8863–8876. 10.1021/jp504601c. [DOI] [PubMed] [Google Scholar]
- Gullion T.; Vega A. J. Measuring Heteronuclear Dipolar Couplings for I = 1/2, S > 1/2 Spin Pairs by REDOR and REAPDOR NMR. Prog. Nucl. Magn. Reson. Spectrosc. 2005, 47, 123–136. 10.1016/j.pnmrs.2005.08.004. [DOI] [Google Scholar]
- Chryssikos G. D.; Kamitsos E. I.; Patsis A. P.; Karakassides M. A. On the Structure of Alkali Borate Glasses Approaching the Orthoborate Composition. Mater. Sci. Eng., B 1990, 7, 1–4. 10.1016/0921-5107(90)90002-S. [DOI] [Google Scholar]
- Beekenkamp P.The Influence of the Coordination Number of Boron on the Properties of Alkali Borate Glasses. In Physics of Non-Crystalline Solids; Prins J. A., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1965; pp 512–524. [Google Scholar]
- Araujo R. J. Statistical Mechanical Model of Boron Coordination. J. Non-Cryst. Solids 1980, 42, 209–229. 10.1016/0022-3093(80)90023-X. [DOI] [Google Scholar]
- Smedskjaer M. M.; Mauro J. C.; Youngman R. E.; Hogue C. L.; Potuzak M.; Yue Y. Topological Principles of Borosilicate Glass Chemistry. J. Phys. Chem. B 2011, 115, 12930–12946. 10.1021/jp208796b. [DOI] [PubMed] [Google Scholar]
- Stevensson B.; Edén M. Exotic Structural Motifs in Aluminosilicate Glasses Quantified by Solid-State NMR and Molecular Dynamics Simulations. J. Non-Cryst. Solids 2021, 569, 120389. 10.1016/j.jnoncrysol.2020.120389. [DOI] [Google Scholar]
- Bunker B. C.; Tallant D. R.; Kirkpatrick R. J.; Turner G. L. Multinuclear Nuclear Magnetic Resonance and Raman Investigation of Sodium Borosilicate Glass Structures. Phys. Chem. Glasses 1990, 31, 30–41. [Google Scholar]
- Martens R.; Müller-Warmuth W. Structural Groups and Their Mixing in Borosilicate Glasses of Various Compositions – an NMR Study. J. Non-Cryst. Solids 2000, 265, 167–175. 10.1016/S0022-3093(99)00693-6. [DOI] [Google Scholar]
- Nanba T.; Nishimura M.; Miura Y. A Theoretical Interpretation of the Chemical Shift of 29Si NMR Peaks in Alkali Borosilicate Glasses. Geochim. Cosmochim. Acta 2004, 68, 5103–5111. 10.1016/j.gca.2004.05.042. [DOI] [Google Scholar]
- Edén M. Probing Oxide-Based Glass Structures by Solid-State NMR: Opportunities and Limitations. J. Magn. Reson. Open 2023, 16–17, 100112. 10.1016/j.jmro.2023.100112. [DOI] [Google Scholar]
- Yu Y.; Edén M. Structure-Composition Relationships of Bioactive Borophosphosilicate Glasses Probed by Multinuclear 11B, 29Si, and 31P Solid-State NMR. RSC Adv. 2016, 6, 101288–101303. 10.1039/C6RA15275A. [DOI] [Google Scholar]
- Karapetyan G. O.; Loboda V. V.; Tagantsev D. K. Influence of Ion Exchange on Liquid–Liquid Phase Separation in Alkali Borosilicate Glasses: Effect of Ion-Exchange-Induced Metastable Glass Homogenization. J. Non-Cryst. Solids 2000, 270, 154–162. 10.1016/S0022-3093(00)00069-7. [DOI] [Google Scholar]
- Hattori Y.; Wakasugi T.; Shiomi H.; Nishii J.; Kadono K. Li+ for Na+ Ion-Exchange-Induced Phase Separation in Borosilicate Glass. J. Mater. Res. 2012, 27, 999–1005. 10.1557/jmr.2012.33. [DOI] [Google Scholar]
- Boffy R.; Peuget S.; Schweins R.; Beaucour J.; Bermejo F. J. High Thermal Neutron Flux Effects on Structural and Macroscopic Properties of Alkali-Borosilicate Glasses Used as Neutron Guide Substrate. Nucl. Instr. Meth. B 2016, 374, 14–19. 10.1016/j.nimb.2015.10.011. [DOI] [Google Scholar]
- Motokawa R.; Kaneko K.; Oba Y.; Nagai T.; Okamoto Y.; Kobayashi T.; Kumada T.; Heller W. T. Nanoscopic Structure of Borosilicate Glass with Additives for Nuclear Waste Vitrification. J. Non-Cryst. Solids 2022, 578, 121352. 10.1016/j.jnoncrysol.2021.121352. [DOI] [Google Scholar]
- Sander S. A. H.; Syrowatka F.; Enke D.; Roggendorf H. Phase Relations in Heat Treated Sodium Borosilicate Glasses. Phys. Chem. Glasses: Eur. J. Glass Sci. Technol. B 2023, 64, 57–65. 10.13036/17533562.64.2.22. [DOI] [Google Scholar]
- Konijnendijk W. L.; Stevels J. M. The Structure of Borosilicate Glasses Studied by Raman Scattering. J. Non-Cryst. Solids 1976, 20, 193–224. 10.1016/0022-3093(76)90132-0. [DOI] [Google Scholar]
- Meera B. N.; Ramakrishna J. Raman Spectral Studies of Borate Glasses. J. Non-Cryst. Solids 1993, 159, 1–21. 10.1016/0022-3093(93)91277-A. [DOI] [Google Scholar]
- Hannon A. C.; Grimley D. I.; Hulme R. A.; Wright A. C.; Sinclair R. N. Boroxol Groups in Vitreous Boron Oxide: New Evidence from Neutron Diffraction and Inelastic Neutron Scattering Studies. J. Non-Cryst. Solids 1994, 177, 299–316. 10.1016/0022-3093(94)90544-4. [DOI] [Google Scholar]
- Joo C.; Werner-Zwanziger U.; Zwanziger J. W. The Ring Structure of Boron Trioxide Glass. J. Non-Cryst. Solids 2000, 261, 282–286. 10.1016/S0022-3093(99)00609-2. [DOI] [Google Scholar]
- Gupta P. K. The Random-Pair Model of Four-Coordinated Borons in Alkali-Borate Glasses. Collected Papers, XIV Int. Congr. Glass 1986, 1, 1–10. [Google Scholar]
- Zachariasen W. H. The Atomic Arrangement in Glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. 10.1021/ja01349a006. [DOI] [Google Scholar]
- Biscoe J.; Warren B. E. X-Ray Diffraction Study of Soda-Boric Oxide Glass. J. Am. Ceram. Soc. 1938, 21, 287–293. 10.1111/j.1151-2916.1938.tb15777.x. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.