Abstract
In the field of power ultrasonic vibration processing, the thin liquid layer nestled between the tool head and the material serves as a hotbed for cavitation shock wave emissions that significantly affect the material's surface. The precise manipulation of these emissions presents a formidable challenge, stemming from a historical deficit in the quantitative analysis of both the ultrasonic enhancement effect and the shock wave intensity within this niche environment. Our study addresses this gap by innovatively modifying the Gilmore-Akulichev equation, laying the groundwork for a sophisticated bubble dynamics model and a pioneering shock wave propagation model tailored to the thin liquid layer domain. Firstly, our study investigated the ultrasound enhancement effect under various parameters of thin liquid layers, revealing an amplification of ultrasound pressure in the thin liquid layer area by up to 7.47 times. The mathematical model was solved using the sixth-order Runge–Kutta method to examine shock wave velocity and pressure under different conditions. our study identified that geometric parameters of the tool head, thin liquid layer thickness, ultrasonic frequency, and initial bubble radius all significantly influenced shock wave emission. At an ultrasonic frequency of 60 kHz, the shock wave pressure at the measurement point exhibited a brief decrease from 182.6 to 179.5 MPa during an increase. Furthermore, rapid attenuation of the shock wave was found within the range of R0-3R0 from the bubble wall. This research model aims to enhance power ultrasonic vibration processing technology, and provide theoretical support for applications in related fields.
Keywords: Power ultrasonic, Ultrasonic cavitation, Shock wave, Thin liquid layers
Subject terms: Engineering, Mechanical engineering, Mathematics and computing, Applied mathematics, Fluid dynamics, Physics, Acoustics
Introduction
Cavitation shock wave, a type of cavitation effect, was initially discovered during the inspection of surface damage on ship turbine blades1,2. Researchers strive to regulate the intensity of these shock waves to prevent material damage by adjusting various parameters. Positive outcomes have been demonstrated in various applications such as using controlled picosecond laser pulses to create low-intensity cavitation shock waves in the laser treatment of biological tissues3. Moreover, the shock wave effect has been utilized in diverse fields including shock wave lithotripsy4,5, wafer surface cleaning6, textile cleaning7–9, and solid surface preparation10. However, in the domain of power ultrasonic vibration processing, the complexity of the processing environment has a significant impact on shock wave emission, which can lead to additional surface damage to the material. To address this issue, our study delves deeper into the generation and propagation of shock waves within thin liquid layers.
The study of cavitation shock waves is critical to understanding material erosion and the development of ultrasonic vibration machining technology. The establishment of the Gilmore equation11 and the Akulichev equation12 offers a theoretical foundation for the study of the formation and propagation of free interface shock waves. As technology advances, researchers are able to more accurately observe cavitation phenomena in the thin liquid layer. For example, Endo13 used photography to demonstrate the effect of liquid layer thickness on bubble size, while Moussatov14 found that ultrasonic pressure caused cavitation in thin liquid areas, producing an amplification effect. Cui15 conducted a study in 2006 on the dynamic response of driving spherical bubbles between parallel plates. He found that reducing the channel width to less than 10 bubble diameters decreased the resonance frequency and maximum response amplitude. In 2019, Matevz Dular16,17 investigated the cavitation damage on aluminum foil. The study confirmed that multiple impacts of shock waves resulted in the generation of larger single pits. In 2020, Bai18 conducted a review on the cavitation effect in thin liquid layers and emphasized that the cavitation effect of ultrasound is particularly severe in such regions. These theoretical and experimental studies provide a solid foundation for the research of this paper and guide our numerical simulation research on the behavior of cavitation shock waves in thin liquid layer environments.
In existing studies of cavitation shock waves, most models focus on environments with thicker liquid layers or entirely without liquid. However, the presence of a thin liquid layer—especially in power ultrasonic vibratory machining—significantly alters the emission and propagation of shock waves. The novelty of our research lies in our focus on this unique thin liquid layer environment. We have modified the Gilmore-Akulichev equation to quantitatively analyze the emission of cavitation shock waves in this context. Through numerical simulation, we discovered that the shock wave intensity is influenced by various factors such as the thickness of the liquid layer, the radius of the tool head, the initial radius of the cavitation bubble, and the ultrasonic frequency. The thin liquid layer environment offers a new perspective for our study because it changes the behavior of cavitation shock waves in several key ways. Firstly, the presence of a thin liquid layer significantly enhances the local amplification effect of the sound field, directly influencing the dynamics of bubble behavior and the subsequent intensity of shock waves. Secondly, the geometric constraints of the thin liquid layer limit the oscillation of bubbles and the propagation of shock waves, potentially leading to attenuation before reaching the material surface. Through these innovative analyses, our model not only provides a deeper understanding of the behavior of cavitation shock waves in thin liquid layer environments but also offers theoretical support for optimizing ultrasonic vibratory machining technology.
Methods
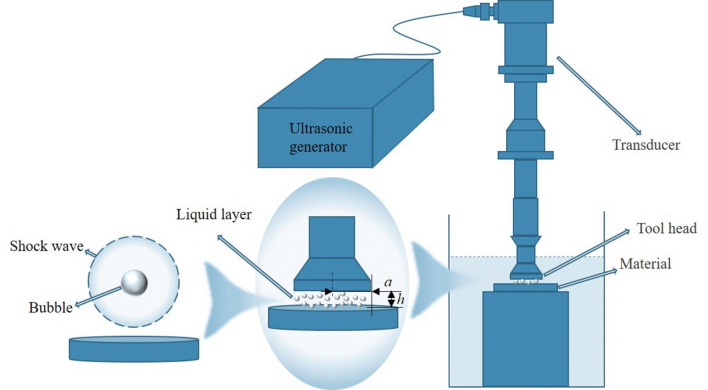
In the power ultrasonic vibration machining process, an ultrasonic generator outputs high-frequency current which is then converted into high-frequency vibration of the tool head through the transducer. This causes the fluid in the thin liquid layer area to be affected by the tool head, leading to a cavitation effect. During the rebound process of the bubble, if the speed of the bubble wall is much greater than the speed of sound, it compresses the surrounding fluid and generates a shock wave that propagates radially and ultimately acts on the material surface. The entire process of ultrasonic cavitation shock wave generation is represented in Fig. 1.
Figure 1.
Schematic Diagram of Power Ultrasonic Vibratory Processing and Thin Liquid Layer Cavitation Shock Waves.
The nonlinear oscillation process that describes the cavitation bubble in the thin liquid layer region is achieved by modifying the Gilmore equation. The original Gilmore equation11 is as
| 1 |
where is the speed of sound of the liquid at the bubble wall. is the difference between the enthalpy of the liquid at the bubble wall and at infinity. is the radius of the bubble. is the velocity of the bubble wall, . is the acceleration of the bubble wall. Then, we need to modify , in the original equations, taking into account the specific processing environment.
In power ultrasonic vibratory machining, high-frequency vibration of the tool head generates an ultrasonic field in the liquid, where the amplitude of the sound pressure in the liquid, ,can be given by the following equation.
| 2 |
where is the speed of sound of the liquid. is the density of the liquid. is the ultrasound frequency. is the Amplitude of the tool head. The phenomenon of reflection and superposition of the ultrasonic field during the propagation of the thin liquid layer results in local sound pressure amplification. The amplified sound pressure then acts on the liquid in the thin liquid layer area, resulting in a more intense cavitation effect. The amplified sound pressure, , can be calculated using the following formula14:
| 3 |
where is the amplification coefficient. The amplification coefficient is a measure of the ratio between the maximum pressure amplitude in the thin liquid layer and the sound pressure amplitude produced by the vibration of the tool head.
| 4 |
where is the Bessel function of the first kind and zero order. is the radius of the thin liquid layer. is the thickness of the thin liquid layer. characterizes the constructive interference of the incident and reflective waves propagating along the layer thickness describes the amplification associated with the radial focalization of pressure on the symmetry axis due to the zero-pressure lateral boundary condition.
In addition, during the high-frequency vibration of the tool head, the fluid experiences a material reaction force, which generates a pressure field around the bubble. This pressure field is important and should not be overlooked. Applying the kinetic energy theorem, we can derive the following:
| 5 |
where is the time required for the tool head to move down one amplitude distance. is the pressure of the tool head acting on the fluid after time . is the mass of the tool head. is the average velocity of the tool head in time .
Based on the geometry of the tool head and the vibration frequency, we can obtain , , , and , respectively:
| 6 |
| 7 |
| 8 |
| 9 |
Bringing Eqs. 6, 7, 8, and 9 into Eq. 5 and simplifying gives the impact pressure of the thin liquid layer by the tool head :
| 10 |
where is the density of the tool head. is the height of the tool head. tool head made of TC4 titanium alloy.
The bubbles in the thin liquid layer region undergo compression and rebound due to external pressure , resulting in the generation of a cavitation shock wave emission.
The pressure exerted on the bubble during compression can be obtained as
| 11 |
where is the surface tension of bubble. is the polytropic index. is the viscosity of liquid at ambient temperature. is the hydrostatic pressure. is the initial radius of bubble. We can get the modified , as
| 12 |
| 13 |
where and are the constants of the Tait equation.
The shock wave propagation model of the thin liquid layer is based on the Kirkwood-Bethe assumption that propagates outward at the speed of . We combine the function of the bubble wall radius changing with time obtained from the bubble dynamics equation with the Akulichev equation12 to calculate the pressure distribution of shock wave propagation at a distance outside the bubble wall radius. Numerical simulations are performed to determine the pressure . is the shock wave velocity at the bubble wall. The equation for shock wave pressure and velocity are as follows:
| 14 |
| 15 |
This study focuses on elucidating the role of thin liquid layer thickness and radius in influencing the effect of cavitation shock waves during power ultrasonic vibration processing. Its primary objective is to characterize the intensity of ultrasonic cavitation shock waves generated by micron-scale bubbles within the thin liquid layer region. The paper commences by conducting a comparative analysis of the ultrasonic enhancement effect under various parameters. Through problem-solving, the study derives the ultrasonic amplification coefficient (K) and the actual sound pressure amplitude within the thin liquid layer area. To accomplish this, the researchers employ the sixth-order Runge–Kutta method to numerically solve the modified bubble dynamics equation and shock wave propagation equation. This computational approach enables them to track the evolution of bubble behavior in the thin liquid layer region. Before initiating the solution process, establishing the initial conditions is imperative, as outlined in Table 1.
Table 1.
Values of relevant model parameters.
| Parameter | |||||
|---|---|---|---|---|---|
| Parameter | 1000 | 72.538 | 4510 | 1483 | 0.01 |
| 314 | 1.016 | 8 | 7 | 4/3 |
This paper utilizes the single-factor analysis method to compare the impact of various initial bubble radius and different ultrasonic frequencies on the intensity of shock waves. The study concludes by determining the pressure distribution around the bubble during the propagation process of shock waves.
Results and discussion
Ultrasonic field enhancement effects in thin liquid layers
To explore the enhanced impact of ultrasonic fields within thin liquid layers during power ultrasonic vibration processing, this study employed three distinct sizes of tool heads to administer vibrations across varying thicknesses of liquid layers. The frequency is set to 20 kHz in this study. This choice is based on Moussatov14 establishment of the ultrasonic enhancement effect model, where the frequency range was set at 15–30 kHz. Additionally, in the field of power ultrasonic vibration processing, 20 kHz is the most commonly used frequency parameter. Therefore, comparative analysis of the ultrasonic enhancement effect within this domain was conducted at a frequency of 20 kHz, with specific parameters outlined in Table 2. Through calculation of the ultrasonic field amplification coefficient, it was observed that the intensity of the ultrasonic field within the thin liquid layer area is significantly influenced by both the thickness and radius of the liquid layer.
Table 2.
Ultrasonic field enhancement effects with different thin liquid layer parameters.
| Parameter | Value | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 20 | |||||||||
| 0.015 | 0.01 | 0.005 | |||||||
| 0.005 | 0.003 | 0.001 | 0.005 | 0.003 | 0.001 | 0.005 | 0.003 | 0.001 | |
| 3 | 5 | 15 | 2 | 3.3 | 10 | 1 | 1.6 | 5 | |
| K | 1.48 | 2.48 | 7.47 | 0.49 | 0.82 | 2.45 | 0.12 | 0.2 | 0.59 |
| Effect | Enhance | Enhance | Enhance | Weaken | Weaken | Enhance | Weaken | Weaken | Weaken |
The findings from Table 2 suggest an intriguing inconsistency in the enhancement of the ultrasonic field within the thin liquid layer region. Specifically, when the radius (a) of the thin liquid layer is 0.015 m, enhancement of the ultrasonic field is observed across three different thicknesses (h). However, when the radius (a) is reduced to 0.01 m, enhancement occurs only at a thin liquid layer thickness (h) of 0.001 m. Furthermore, a further reduction in the radius (a) of the thin liquid layer leads to a weakening of the ultrasonic field within the thin liquid layer. This inconsistency indicates a complex relationship between the radius, thickness, and enhancement of the ultrasonic field, suggesting the need for further investigation to fully understand these dynamics.
The calculation results indicate a positive correlation between the ultrasonic amplification coefficient (K) and the ratio of radius to thickness (a/h). As depicted in Table 2, when the size of the tool head remains constant, proximity to the material surface amplifies the enhancement effect of the ultrasonic field. Utilizing a large-sized tool head for material surface processing, decreasing the thickness of the thin liquid layer results in a notable rise in sound pressure amplitude, thereby strengthening the impact of ultrasonic cavitation shock waves. This observation underscores the significance of considering both tool head size and liquid layer thickness in optimizing ultrasonic processing efficiency.
The conventional approach in previous research on power ultrasonic vibration processing typically involved increasing the ultrasonic frequency to enhance the cavitation effect. However, the findings presented here diverge from this convention by demonstrating that amplifying low-frequency ultrasound and intensifying cavitation shock wave impact can be achieved by enlarging the radius (a) of the thin liquid layer while simultaneously reducing its thickness (h). This discovery holds significant importance as it not only enhances processing efficiency but also contributes to reducing operational expenses. This shift in understanding could potentially reshape how power ultrasonic vibration processing is approached, offering a more cost-effective and efficient alternative to traditional methods.
Shock wave effects at different initial radius
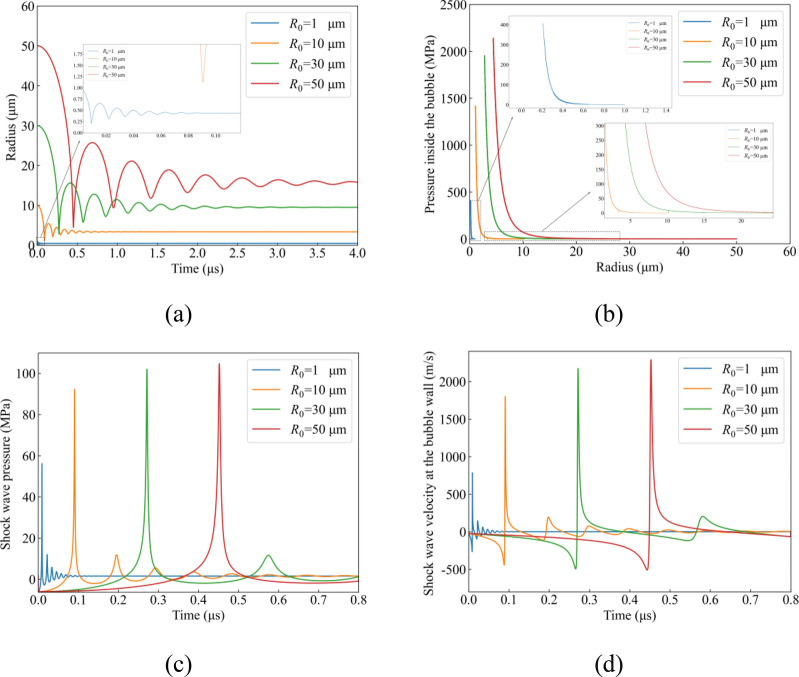
In the process of power ultrasonic vibration, bubbles within thin liquid layers tend to aggregate into clusters. Therefore, it's crucial to analyze the impact of ultrasonic cavitation shock waves produced by bubbles of different sizes in this region. In a study conducted by Tsochatzidis19, the influence of a 20 kHz ultrasonic frequency on liquid was investigated, resulting in bubble formation. The research found that bubbles with an average diameter of 10 μm are typically found within 40 mm from the bottom of the 20 kHz ultrasonic horn, while larger bubbles exceeding 50 μm are commonly located further away. In our study, the thickness of the thin liquid layer is much less than 40 mm. Burdin20 utilized laser technology to measure the size of bubbles generated by a 20 kHz ultrasonic frequency, finding an average size range of 10 to 50 μm. To further understand shock wave emissions from bubbles of varying sizes, we conducted a comparative simulation. Bubbles with initial radii of 1 μm, 10 μm, 30 μm, and 50 μm were selected. The parameters for the thin liquid layer were set at a radius (a) of 0.015 m and a thickness (h) of 0.005 m, with the ultrasonic frequency maintained at 20 kHz. A specific point for measuring shock waves was fixed at a predetermined distance from the bubble wall. The outcomes presented in Fig. 2 were obtained by numerically solving the relevant differential equations, offering insights into the behavior of shock waves emitted by bubbles of different dimensions within thin liquid layers subjected to power ultrasonic vibration.
Figure 2.
Dynamic evolution numerical simulation results for bubbles with different initial radius. (a) Bubble radius; (b) Pressure inside the bubble; (c) Shock wave pressure; (d) Shock wave velocity at the bubble wall.
In Fig. 2a, the chart illustrates the evolution of bubble radius over a specific time period for bubbles of different initial radii (R0). These curves provide insights into how bubbles expand or contract over time under the influence of an ultrasonic field, a critical aspect in studying the effects of ultrasonic cavitation. Specifically: Bubbles with an initial radius of 1 micron (R0 = 1 µm): This curve initiates at the smallest radius value and demonstrates the rapid expansion of the bubble due to the influence of ultrasound. Bubbles with an initial radius of 10 µm (R0 = 10 µm): This curve depicts a rapid initial growth phase, followed by a gradual decrease in growth rate, eventually reaching a steady state. Bubbles with initial radii of 30 microns (R0 = 30 µm) and 50 microns (R0 = 50 µm): These two curves exhibit rapid initial growth under the influence of ultrasound, followed by a gradual decrease in growth rate similar to the bubble with R0 = 10 µm. These observations highlight the varying dynamics of bubble expansion and contraction in response to ultrasonic stimulation, underscoring the complexity of ultrasonic cavitation phenomena.
Each curve in the graph represents simulation results detailing the dynamic behavior of bubbles under specific conditions: an ultrasonic frequency of 20 kHz and thin liquid layer parameters set at a radius (a) of 0.015 m and a thickness (h) of 0.005 m. These curves offer insights into the effect of bubble size on the ultrasonic cavitation shock wave phenomenon, crucial for optimizing the ultrasonic vibration machining process. By analyzing these curves, several conclusions can be drawn:
Effect of bubble size: The differences observed in the behavior of bubbles of varying sizes within the ultrasonic field indicate that the initial size of the bubble significantly influences its dynamic response and eventual stable state. Larger bubbles may exhibit slower growth rates or different stabilization behaviors compared to smaller ones.
Role of ultrasonic frequency and thin liquid layer parameters: The chosen ultrasonic frequency of 20 kHz, along with the specific parameters of the thin liquid layer, notably influence bubble behavior. These parameters are critical factors that may affect the quality and efficiency of material surface processing. Adjusting these parameters could potentially optimize the cavitation process for specific applications.
Ultrasonic cavitation shock wave effect: The dynamic changes observed in bubble behavior are closely tied to the intensity of ultrasonic cavitation shock waves. These shock waves play a crucial role in processes such as cleaning and processing material surfaces. Understanding and controlling the dynamics of bubble behavior can thus lead to improvements in the effectiveness of ultrasonic cavitation for various industrial applications.
In Fig. 2b, The chart shows the relationship between the pressure inside the bubble and the radius, which is an important part of studying the cavitation effect in ultrasonic vibration machining. Curves of different colors represent bubbles with different initial radius (R0), showing the behavior pattern of bubbles under the action of ultrasonic waves. Relationship between pressure and radius: The curve in the figure shows that as the radius of the bubble increases, the internal pressure first rises to a peak and then decreases as the radius further increases. This pressure change may be related to the compression and expansion of the gas inside the bubble in response to changes in external pressure under the action of ultrasound. Effect of initial radius: Each curve in the graph starts at a different initial radius, which shows that the initial radius has a significant impact on the behavior of the bubble. Smaller bubbles (e.g. R0 = 1 µm) need to undergo a larger radius change before reaching maximum pressure, while larger bubbles (e.g. R0 = 50 µm) reach maximum pressure after a smaller radius change. Maximum pressure point: The peak of each curve represents the maximum internal pressure of the bubble at a specific radius. This peak is important for understanding how bubbles collapse in an ultrasonic field, as this typically occurs when maximum internal pressure is reached.
In Fig. 2c, the blue curve represents the simulation results for a bubble with an initial radius of 1 µm, while the orange curve corresponds to a bubble with an initial radius of 10 µm. These curves illustrate how bubbles of different initial sizes respond to an ultrasonic field:
Blue curve (R0 = 1 µm): This curve depicts the response of a bubble with a smaller initial radius to the ultrasonic field. It exhibits multiple small peaks, indicating that the bubble undergoes several compressions and expansions before reaching equilibrium radius. The highest point on the curve indicates a pressure change of approximately 56 MPa, illustrating the pressure fluctuations experienced by smaller bubbles under the influence of ultrasonic waves.
Orange curve (R0 = 10 µm): In contrast to the blue curve, the orange curve reaches its peak pressure more slowly. Additionally, the maximum pressure observed is approximately 89 MPa, significantly higher than that of the smaller bubble. This suggests that bubbles with larger initial radii respond more slowly to the ultrasonic field and are capable of withstanding higher pressures.
Green curve (R0 = 30 µm): This curve has the highest peak pressure, almost reaching a peak pressure of 100 MPa. This could mean that larger bubbles are able to build up higher internal pressures before reaching the point of collapse.
Red curve (R0 = 50 µm): Although this curve is also close to the peak pressure of 100 MPa, it takes slightly longer to reach the peak than the green curve. This may indicate that, under certain conditions, there is an optimal initial radius range for bubble growth and pressure accumulation. All curves decrease rapidly after reaching the peak value, indicating that bubbles collapse rapidly after reaching maximum internal pressure. The small oscillations in the curve after the peak may represent pressure fluctuations following bubble collapse. The time to reach peak pressure and the pressure value change with increasing initial radius, indicating that the initial size of the bubble has a significant impact on its behavior in the ultrasonic field. Larger bubbles (such as 50 µm) take longer to build up pressure, while smaller bubbles (such as 1 µm) reach lower pressures more quickly.
In Fig. 2d, the observations regarding the behavior of bubbles of different initial sizes in the ultrasonic field provide valuable insights into their suitability for various applications: (R0 = 1 µm) rises sharply in the initial stage, decreases rapidly after reaching the peak, and then stabilizes. Fast response for applications requiring high pressures to be reached quickly. High pressures are of short duration and may not be suitable for applications requiring stable pressure over long periods of time. (R0 = 10 µm) The peak value is high, and the rise and fall are relatively mild. The pressure changes are relatively smooth and suitable for applications requiring mild pressure changes. Reaching peak speed is slow and may not be suitable for situations where a rapid pressure increase is urgently needed. (R0 = 30 µm) has a higher peak value and wider peak width, and the shock wave propagation lasts longer. (R0 = 50 µm) has the highest peak pressure and the widest peak width in the simulation. The shock wave propagates slowly, resulting in gradual pressure increases and decreases. This characteristic makes it suitable for applications requiring stable pressure over long periods of time and very smooth pressure changes. However, the slow increase in pressure may not be ideal for applications that require rapidly reaching a certain pressure level. General trend: All curves display a similar pattern of rising to a peak and then falling to a stable state, indicating that bubbles of different sizes generate shock waves in the ultrasonic field. Smaller bubbles (R0) cause shock waves to increase and decrease rapidly in velocity, while larger bubbles result in slower shock wave propagation and longer-lasting effects.
Integrating the data from Table 3 and Fig. 2, we performed a comparative analysis of bubble dynamics and the influence of shock waves across varying initial radius. The analysis indicated a direct correlation between the initial bubble radius and the equilibrium time, which extended from 0.13 µs for a 1 µm radius to 4.0 µs for a 50 µm radius. Concurrently, the minimum bubble radius experienced an increment from 0.21 to 4.46 µm, as depicted in Fig. 2a. In addition, there was a substantial rise in the peak internal pressure within the bubble, escalating from 407 to 2200 MPa, as illustrated in Fig. 2b. Complementing these findings, the apex shock wave pressure surged from 56 to 110 MPa, while the pinnacle shock wave velocity soared from 784 to 2700 m/s, as demonstrated in Fig. 2c,d. The maximum pressure within the bubble serves as the initial value for the shock wave in our study. This aligns closely with the findings of Burjan21, who experimentally recorded a shock wave pressure of 1300 ± 300 MPa and a speed range of 1500–2500 m/s. Similarly, Holzfuss22, through numerical simulation, reported a shock wave pressure exceeding 1300 MPa, with speeds ranging from 1500 to 5500 m/s. While variations in processing conditions and bubble size may impact shock wave intensity, our numerical simulation results fall within this reasonable range.
Table 3.
Shock wave generation at different initial radius.
| Initial radius of bubble | 1 | 10 | 30 | 50 |
|---|---|---|---|---|
| Minimum radius | 0.21 | 1.2 | 3.03 | 4.46 |
| Maximum internal pressure of a bubble | 407 | 1400 | 1900 | 2200 |
| Equilibrium time | 0.13 | 0.8 | 2.5 | 4.0 |
| Equilibrium radius | 0.56 | 3.34 | 9.54 | 15.66 |
| Maximum shock wave generation time | 0.009 | 0.09 | 0.27 | 0.45 |
| Shock wave pressure | 56 | 89 | 100 | 110 |
| Shock wave velocity at the bubble wall | 784 | 1700 | 2300 | 2700 |
Through comparison, it can be observed that the initial radius of the bubble has a significant impact on the cavitation shock wave effect. As the initial radius increases, the minimum radius Rmin a bubble can reach becomes larger, resulting in a longer oscillation period. This leads to an increase in the pressure inside the bubble, as well as the maximum pressure and maximum velocity of the shock wave generated when the bubble rebounds.
Shock wave effects at different ultrasonic frequencies
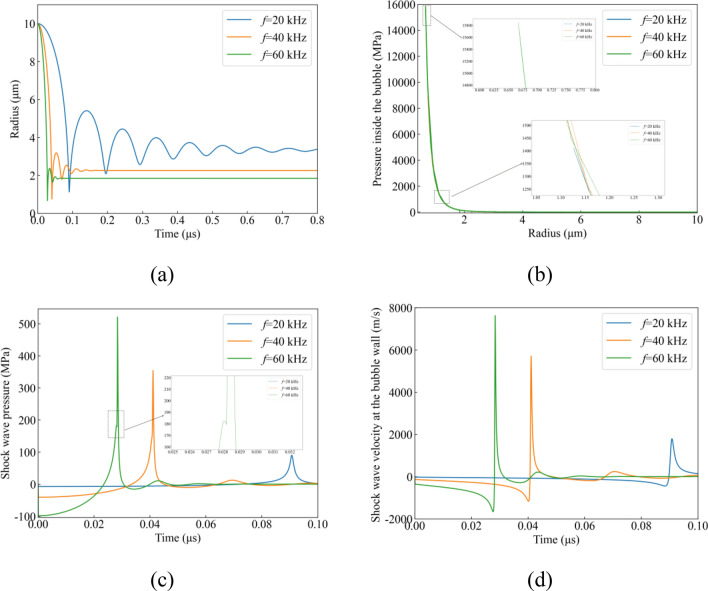
The influence of ultrasonic frequency on the ultrasonic field’s intensity is profound. By forecasting the shock wave intensity across various frequencies during power ultrasonic vibration processing, we can precisely modulate the shock wave’s impact and enhance the precision of the processing. In our investigation, we subjected a single 10 µm bubble to ultrasonic fields at frequencies of 20 kHz, 40 kHz, and 60 kHz. We then scrutinized the bubble’s response and the shock wave intensity under these varying frequencies. The thin liquid layer parameters were established at a = 0.015 m and h = 0.005 m, with the shock wave measurement point positioned at a specific distance from the bubble’s boundary. The insights presented in Fig. 3 were derived from the numerical resolution of the formulated differential equations.
Figure 3.
Dynamic evolution numerical simulation results at different ultrasonic frequencies. (a) Bubble radius, (b) Pressure inside the bubble, (c) Shock wave pressure, (d) Shock wave velocity at the bubble wall.
The analysis of Fig. 3 provides valuable insights into the behavior of a bubble with an initial radius of 10 μm and the corresponding shock wave generation under different ultrasonic frequencies:
20 kHz Frequency (Blue Curve)
Pronounced oscillations are observed, with peaks decreasing in amplitude over time, indicating repeated cycles of expansion and compression. The strong oscillations suggest a robust cavitation effect, suitable for applications requiring intense cleaning or surface treatment.
40 kHz Frequency (Orange Curve)
Oscillations are present but less pronounced than at 20 kHz, indicating a more controlled cavitation effect. This frequency offers a balance between intensity and control, potentially suitable for various processing applications.
60 kHz Frequency (Green Curve)
Minimal oscillations are observed post-peak, indicating a stable cavitation effect. Higher frequencies like 60 kHz provide a more consistent and less aggressive cavitation effect, suitable for delicate processing tasks where surface damage must be minimized.
In summary, all frequencies exhibit an initial spike in bubble radius, signaling cavitation onset. The main differences lie in the behavior post-peak. Lower frequencies (20 kHz) generate stronger cavitation effects with more violent oscillations, suitable for heavy-duty cleaning but potentially causing more wear on materials. Higher frequencies (60 kHz) offer a gentler cavitation effect, preferable for precision cleaning or delicate materials. This comparative analysis aids in understanding how ultrasonic frequency influences cavitation dynamics, facilitating optimized process design for various applications.
In Fig. 3b, The 20 kHz frequency shows a rapid increase in pressure as the radius decreases, stabilizing at higher radius. The initial sharp rise indicates a strong cavitation effect, with the bubbles rapidly collapsing and generating high pressure. The pressure increase at the 40 kHz frequency is also rapid, but slightly flatter than the 20 kHz curve. This indicates a milder cavitation effect and may be more suitable for applications requiring a balance of strength and control. The 60 kHz frequency, shows a similar pattern to the 40 kHz line, but the pressure increase is more gradual. This may indicate that higher frequencies may result in a more controlled cavitation process, suitable for precision cleaning or medical applications where excessive force may cause damage. All frequencies show a rapid increase in pressure as the radius decreases, which is a sign of cavitation. The key difference lies in the steepness of pressure increase and the plateau point, which vary with frequency. Here's a breakdown of how different frequencies affect pressure dynamics: Low Frequency (20 kHz): Steeper pressure increase: The pressure rises rapidly, leading to strong cavitation effects. Plateau point at higher pressure levels: The pressure stabilizes at relatively higher levels. Suitable for applications requiring intense cavitation effects, such as heavy cleaning or material processing, where robust and vigorous action is desired. High Frequency (60 kHz): More suitable for delicate applications where controlling cavitation effects is crucial to prevent damage.
Figure 3c,d demonstrate that as the maximum pressure inside the bubble rises from 1400 to 15,820 MPa, the maximum pressure of the shock wave increases from 89 to 520.9 MPa, and the shock wave velocity at the bubble wall increases from 1700 to 7670 m/s. Furthermore, the time taken for shock wave generation decreases from 0.09 to 0.03 μs. The increase in ultrasonic frequency and the ultrasonic enhancement effect in the thin liquid layer region led to a significant rise in the extreme values of bubble pressure, shock wave pressure, and shock wave velocity. Comparing this phenomenon to relevant literature on laser-induced cavitation, we find that while the principles of bubble generation differ, the generation and propagation process of the liquid environment and shock wave remain consistent. The maximum pressure limit inside the bubble at 60 kHz exceeds the 13.5 GPa reported by Liang23, but is still lower than the 20 GPa documented by Vassholz24. Notably, the shock wave speed at 60 kHz surpasses the research findings of Holzfuss22, Pecha25, and others. This discrepancy can be attributed to our research's consideration of the amplification effect of sound pressure in the thin liquid layer area, resulting in an increase in the sound pressure generated at 60 kHz and subsequently increasing the shock wave speed.
Table 4 showcases the data pertinent to the 40 kHz frequency. The simulations suggest that a higher ultrasonic frequency markedly improves the efficiency and impact of ultrasonic cavitation. This improvement is reflected in the diminished oscillation period and minimized bubble radius, alongside an escalation in internal bubble pressure. Additionally, there is an increase in both the pressure and velocity of the resultant shock wave, coupled with its accelerated formation time.
Table 4.
Shock wave generation at different ultrasound frequencies.
| Ultrasound frequency | 20 | 40 | 60 |
|---|---|---|---|
| Minimum radius | 1.2 | 0.77 | 0.69 |
| Maximum internal pressure of a bubble | 1400 | 8963 | 15,820 |
| Equilibrium time | 0.8 | 0.15 | 0.06 |
| Equilibrium radius | 3.34 | 2.26 | 1.84 |
| Maximum shock wave generation time | 0.09 | 0.04 | 0.03 |
| Shockwave pressure | 89 | 355.1 | 520.9 |
| Shock wave velocity at the bubble wall | 1700 | 5720 | 7670 |
| Shock wave dampening point | – | – | 0.028 |
Figure 3c reveals a notable dip in shock wave pressure at 60 kHz, where it momentarily decreased from 182.6 to 179.5 MPa during propagation, a pattern not observed at lower frequencies of 20 kHz and 40 kHz. This suggests that higher frequencies amplify the ultrasonic field within the thin liquid layer, boosting sound pressure and consequently dampening shock wave propagation due to increased resistance.
Pressure distribution around the bubble
The research focuses on investigating the effects of shock waves on materials resulting from cavitation rebounds within thin liquid layers. Simulations were conducted to evaluate the pressure distribution surrounding bubbles after shock wave generation, aiming to delineate the attenuation pattern during shock wave propagation. Specifically, the study examines the impact of ultrasonic cavitation shock waves on materials by subjecting bubbles with a radius of 10 μm to ultrasonic fields of 20 kHz, 40 kHz, and 60 kHz. The thin liquid layer is characterized by parameters a = 0.015 m and h = 0.005 m. Pressure measurements are taken at multiple points around the bubble, enabling a comparison of pressure distribution post-rebound across the three frequencies, as depicted in Fig. 4.
Figure 4.

Shock wave pressure at different measurement points.
Figure 4 illustrates that the bubble's shock wave, generated during the rebound process, compresses the surrounding fluid and creates a pressure field around the bubble. 20 kHz ultrasonic frequency: initial shock wave pressure is 137.9 MPa. At the propagation distance 9R0, the pressure drops to 15.17 MPa. This shows that at a frequency of 20 kHz, the shock wave pressure decreases significantly with distance. 40 kHz ultrasonic frequency: initial shock wave pressure is 534.8 MPa. At the same propagation distance 9R0, the pressure drops to 54.1 MPa. Compared with 20 kHz, the shock wave pressure attenuation at 40 kHz frequency is more severe. 60 kHz ultrasonic frequency: initial shock wave pressure is 802.7 MPa. At the propagation distance 9R0, the pressure drops to 79.77 MPa. At the frequency of 60 kHz, the initial value of the shock wave pressure is the highest, but the attenuation is also the fastest. At all three frequencies, the attenuation of shock wave pressure is greatest between R0-3R0 and then slows down between 3R0 and 10R0. At the position of 10R0, the difference in shock wave pressure at the three ultrasonic frequencies is smallest. It should be noted that the rapid attenuation trend of shock wave pressure shown in Fig. 4 aligns closely with the findings of Burjan21. The energy dissipation of shock waves and the nonlinear propagation contribute to this fast pressure decay. These data are useful for understanding how bubble shock waves affect the pressure field of the surrounding fluid at different ultrasonic frequencies. This analysis could help us design more effective ultrasound applications, such as using ultrasound to precisely control the pressure and propagation of shock waves in medical diagnosis or therapy.
The findings suggest that ultrasonic cavitation shock waves generated at frequencies of 20 kHz, 40 kHz, and 60 kHz follow a similar attenuation trend, primarily diminishing rapidly near the bubble wall. Interestingly, the pressure of the shock wave at a distance of 10 times the initial bubble radius (10R0) appears to be comparable across all frequencies. It's essential to emphasize that in the context of micron-scale bubbles, 10R0 represents an extremely small distance. When bubbles are situated far from the bubble wall, increasing the ultrasonic frequency doesn't notably alter the force exerted on the material by the resulting shock wave. Therefore, the primary factor influencing damage on the material surface is the shock wave effect generated by bubbles near the wall. By elevating the ultrasonic frequency, the impact load of the ultrasonic cavitation shock wave on the material can be effectively intensified, thereby enhancing material removal efficiency. These effects are chiefly achieved through the action of bubbles in close proximity to the material.
Shock wave effects at different R0/Requilibrium
During power ultrasonic vibration processing, the stability of the cavitation phenomenon is closely linked to the intensity of the shock wave. R0/Requilibrium is a crucial parameter that characterizes inertial cavitation in the thin liquid layer region. It signifies the degree of compression of the bubble and is specifically defined as the steady-state cavitation threshold. In the case of R0/Requilibrium, a value of at least 2 is generally considered indicative of inertial cavitation26. Our study explores R0/Requilibrium at various frequencies, along with the corresponding shock wave velocity, shock wave pressure, and maximum pressure within the bubble, as illustrated in Fig. 5. This section delves into the evolutionary rules of shock waves under varying R0/Requilibrium values. The thin liquid layer is characterized by parameters a = 0.015 m and h = 0.005 m.
Figure 5.
(a) The value of R0/Requilibrium at different ultrasonic frequencies, (b) Maximum internal pressure of a bubble, shock wave pressure, shock wave velocity at different R0/Requilibrium.
Figure 5a shows the variation of the value of R0/Requilibrium for different bubble sizes (10 μm, 30 μm, 50 μm) under varying ultrasonic frequencies (20 kHz, 40 kHz, 60 kHz). When subjected to a 20 kHz ultrasonic frequency, a bubble with an initial radius of 10 μm exhibits a R0/Requilibrium value of 2.99. At 40 kHz and 60 kHz ultrasonic frequencies, the R0/Requilibrium values increase to 4.46 and 5.38, respectively. This trend is consistent for bubbles with initial radii of 30 μm and 50 μm. The findings suggest that higher ultrasonic frequencies lead to smaller cavitation bubble radii. Larger bubbles in the thin liquid layer region have higher inertial cavitation thresholds, which increase with frequency, aligning with the research by J. Šponer27. The increase in R0/Requilibrium with frequency supports the hypothesis that higher ultrasonic frequencies will lead to more significant bubble collapses. The relatively higher values for larger bubbles indicate that they are more prone to achieving higher compression levels under the same frequency, which is consistent with the expected behavior of larger cavitation bubbles.
Figure 5b demonstrates that as the inertial cavitation threshold rises from 2.99 to 5.99, the maximum pressure within the bubble escalates from 1400 to 24,686 MPa, the shock wave pressure increases from 89 to 525.73 MPa, and the shock wave speed rises from 1700 to 9069 m/s. All these parameters increase with R0/Requilibrium, indicating that higher ultrasonic frequencies lead to more intense compression of the bubble, resulting in higher intra-bubble pressure and shock wave emission.
The data show a strong correlation between the value of R0/Requilibrium and the intensity of the resulting cavitation effects. Higher values of R0/Requilibrium correspond to higher internal pressures, shock wave pressures, and velocities.
Conclusions
This paper employs the Gilmore-Akulichev equation to formulate a bubble dynamics model and a shock wave propagation model for power ultrasonic vibration processing in thin liquid layer regions. The study conducts a comparative analysis of ultrasonic enhancement effects under varying thin liquid layer parameters. Numerical solutions, obtained through the sixth-order Runge–Kutta method, elucidate the dynamic evolution process of bubble radius, internal pressure, shock wave pressure, and shock wave velocity. Results are compared across different initial radius and ultrasonic frequencies. Furthermore, a simulation is performed to address the pressure distribution around the rebounding bubble, and shock wave attenuation outcomes are compared for diverse ultrasonic frequencies. The conclusions drawn are as follows:
In an ultrasonic field, the amplification factor (K) of a thin layer of liquid is directly related to the (a/h) value of that region. When the radius of the thin liquid layer (a) is 0.015 m, the amplification factor (K) of the ultrasonic pressure can reach the maximum value of 7.47. By adjusting the (a/h) value of the thin liquid layer, the effects of low-frequency ultrasonic waves and ultrasonic cavitation shock waves can be effectively enhanced. This enhancement helps improve processing efficiency and reduce processing costs.
At the micrometer scale, the effect of bubble initial radius on cavitation shock wave emission is observed. For example, when the initial radius is 50 μm, the shock wave pressure generated at a distance 1.5 times the radius is 110 MPa, while when the initial radius is 1 μm, it is 56 MPa. This indicates that the initial radius of the bubble plays an important role in the cavitation shock wave effect. As the initial radius increases, the minimum radius (Rmin) that the bubble can reach becomes larger, resulting in a longer oscillation period, an increase in the internal pressure of the bubble, and an increase in the maximum pressure and velocity of the shock wave generated during the rebound of the bubble. The significant influence of the bubble initial radius on the cavitation shock wave effect is revealed, especially at the micrometer scale. We find that a larger initial radius results in a larger (Rmin), resulting in higher shock wave pressure and velocity when the bubble rebounds. This discovery not only provides a new perspective for understanding cavitation phenomena, but also has important practical significance for designing and optimizing cavitation applications, such as ultrasonic cleaning and medical treatment. This work provides a new control method for technology that utilizes the cavitation effect, and is expected to promote the development of ultrasound technology in many fields.
When the initial radius of the bubble is 10 μm, the ultrasonic frequency of 60 kHz significantly increases the shock wave pressure generated by the bubble, reaching 520.9 MPa, which is much higher than 89 MPa at 20 kHz. By comparing three different frequencies (20 kHz, 40 kHz, 60 kHz), it is evident that higher ultrasonic frequencies greatly increase the efficiency of ultrasonic cavitation and shock wave emission. In addition, the high-frequency ultrasonic field inhibits the propagation of shock waves, and as the frequency increases, this inhibitory effect becomes more obvious. This study highlights the importance of ultrasonic frequency in enhancing the cavitation shock wave effect. We found that higher ultrasonic frequencies can not only increase the pressure of the shock wave, but also suppress its propagation, which is unprecedented in the field of ultrasonic applications. This discovery is of great significance to the understanding and utilization of ultrasonic cavitation phenomena.
Ultrasonic cavitation shock waves generated at three different frequencies (20 kHz, 40 kHz, 60 kHz) show an attenuation trend during propagation. They decay rapidly mainly in the range R0-3R0 from the bubble wall. At a distance of 10R0, the shock wave pressure was found to be similar. The comparison results show that the main factor causing different damages to the material surface is the shock wave effect generated by the bubbles close to the wall. By increasing the ultrasonic frequency, the impact load of the shock wave on the material can be effectively increased, thereby improving the material removal efficiency. The importance of ultrasonic frequency in material surface damage effects is highlighted. Our results show that increasing the ultrasonic frequency can significantly enhance the impact load of the shock wave on the material, which is crucial for improving material removal efficiency. In addition, we also discovered the attenuation trend of shock waves during propagation, which is of great significance for understanding and controlling the material removal mechanism during ultrasonic cavitation. This work not only provides a new theoretical basis for the application of ultrasonic cavitation technology, but also opens up a new way to achieve more efficient material processing. This innovative discovery is expected to attract widespread attention in the field of ultrasound technology and promote the further development of related technologies.
The inertial cavitation threshold is influenced by both the initial radius of the bubble and the ultrasonic frequency. With an increase in ultrasonic frequency, the inertial cavitation threshold also increases, leading to greater compression of bubbles and stronger shock wave emission. This higher threshold results in more intense compression of the bubble. Consequently, an increase in ultrasonic frequency causes a decrease in bubble size within the thin liquid layer region. Moreover, the maximum pressure inside the bubble, shock wave velocity, and shock wave pressure exhibits a significant correlation with the inertial cavitation threshold. More specifically, an increase in the inertial cavitation threshold directly results in stronger compression of the bubble, leading to more vigorous shock wave emission.
Acknowledgements
This work has been supported by the National Natural Science Foundation of China (Grant No. 51975540, 52005455, Nos.52375470) and; Postgraduate Education Innovation Project in Shanxi Province (Grant No. 2022Y577). The 18th Graduate Science and Technology Project of North University of China (Grant No.20221818). The Central Guidance on Local Science and Technology Development Fund of Shanxi Province (Grant No. YDZJSX2022C005).
Author contributions
T.G.: Conceptualization (equal); Data curation (equal); Formal analysis (equal); Investigation (equal); Methodology (equal); Software (equal); Validation (equal); Visualization (equal); Writing– original draft (equal). X.Z.: Formal analysis (equal); Investigation (equal); Writing– review & editing (equal). L.Y.: Formal analysis (equal); Investigation (equal); Project administration (equal); Resources (equal); Supervision (equal); Writing– review & editing (equal). Y.F.: Conceptualization (equal); Formal analysis (equal); Investigation (equal); Methodology (equal); Project administration (equal); Software (equal); Supervision (equal); Writing– review & editing (equal).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Arndt, R. E. A. Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech.13, 273–328. 10.1146/annurev.fl.13.010181.001421 (1981). 10.1146/annurev.fl.13.010181.001421 [DOI] [Google Scholar]
- 2.Escaler, X., Egusquiza, E., Farhat, M., Avellan, F. & Coussirat, M. Detection of cavitation in hydraulic turbines. Mech. Syst. Signal Process.20(4), 983–1007. 10.1016/j.ymssp.2004.08.006 (2006). 10.1016/j.ymssp.2004.08.006 [DOI] [Google Scholar]
- 3.Agrež, V., Mur, J., Petelin, J. & Petkovšek, R. Near threshold nucleation and growth of cavitation bubbles generated with a picosecond laser. Ultrason. Sonochem.92, 106243. 10.1016/j.ultsonch.2022.106243 (2023). 10.1016/j.ultsonch.2022.106243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Johnsen, E. & Colonius, T. Shock-induced collapse of a gas bubble in shockwave lithotripsy. J. Acoust. Soc. Am.124, 2008. 10.1121/1.2973229 (2011). 10.1121/1.2973229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Garg, M. et al. Role of hounsfield unit in predicting outcomes of shock wave lithotripsy for renal calculi: Outcomes of a systematic review. Curr. Urol. Rep.24(4), 173–185. 10.1007/s11934-023-01145-w (2023). 10.1007/s11934-023-01145-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang, S. et al. Elimination of blind zone in nanoparticle removal on silicon wafers using a double-beam laser shockwave cleaning process. Appl. Surf. Sci.10.1016/j.apsusc.2020.148057 (2021). 10.1016/j.apsusc.2020.148057 [DOI] [Google Scholar]
- 7.Song, W. D., Hong, M. H., Lukyanchuk, B. & Chong, T. C. Laser-induced cavitation bubbles for cleaning of solid surfaces. J. Appl. Phys.95, 2952–2956. 10.1063/1.1650531 (2004). 10.1063/1.1650531 [DOI] [Google Scholar]
- 8.Vouters, M., Rumeau, P., Tierce, P. & Costes, S. Ultrasounds: An industrial solution to optimise costs, environmental requests and quality for textile finishing. Ultrason. Sonochem.11, 33–38. 10.1016/S1350-4177(03)00113-5 (2004). 10.1016/S1350-4177(03)00113-5 [DOI] [PubMed] [Google Scholar]
- 9.Gallego-Juarez, J. A., Riera, E., Acosta, V., Rodríguez, G. & Blanco, A. Ultrasonic system for continuous washing of textiles in liquid layers. Ultrason. Sonochem.17, 234–238. 10.1016/j.ultsonch.2009.06.005 (2010). 10.1016/j.ultsonch.2009.06.005 [DOI] [PubMed] [Google Scholar]
- 10.Shchukin, D. G., Skorb, E., Belova, V. & Möhwald, H. Ultrasonic cavitation at solid surfaces. Adv. Mater.23, 1922–1934. 10.1002/adma.201004494 (2011). 10.1002/adma.201004494 [DOI] [PubMed] [Google Scholar]
- 11.Gilmore, F.R. The Growth or Collapse of a Spherical Bubble in a Viscous Compressible Liquid, Technical Report No. 26–4, California Institute of Technology, (1952).
- 12.Aкyличeв, B. A., Бoгycлaвcкий, ЮЯ, Иoффe, A. И & Hayгoльныx, КA. Излyчeниe cфepичecкиx вoлн кoнeчнoй aмплитyды. Aкycтичecкий жypнaл.13(3), 321–327 (1967). [Google Scholar]
- 13.Endo, K., Okada, T. & Najashima, M. A study of erosion between two parallel surfacesoscillating at close proximity in liquids. J. Lubr. Technol.84(4), 229–236 (1967). 10.1115/1.3616956 [DOI] [Google Scholar]
- 14.Moussatov, A., Granger, C. & Dubus, B. Ultrasonic cavitation in thin liquid layers. Ultrason. Sonochem.12, 415–422. 10.1016/j.ultsonch.2004.09.001 (2005). 10.1016/j.ultsonch.2004.09.001 [DOI] [PubMed] [Google Scholar]
- 15.Cui, J., Hamilton, M. F., Wilson, P. S. & Zabolotskaya, E. A. Bubble pulsations between parallel plates. J. Acoust. Soc. Am.119(4), 2067–2072. 10.1121/1.2172545 (2006). 10.1121/1.2172545 [DOI] [PubMed] [Google Scholar]
- 16.Dular, M., Delgosha, O. C. & Petkovšek, M. Observations of cavitation erosion pit formation. Ultrason. Sonochem.20, 1113–1120. 10.1016/j.ultsonch.2013.01.011 (2013). 10.1016/j.ultsonch.2013.01.011 [DOI] [PubMed] [Google Scholar]
- 17.Dular, M., Požar, T., Zevnik, J. & Petkovšek, R. High speed observation of damage created by a collapse of a single cavitation bubble. Wear418–419, 13–23. 10.1016/j.wear.2018.11.004 (2019). 10.1016/j.wear.2018.11.004 [DOI] [Google Scholar]
- 18.Bai, L. X., Yan, J. C., Zeng, Z. J. & Ma, Y. H. Cavitation in thin liquid layer: A review. Ultrason. Sonochem.66, 105092. 10.1016/j.ultsonch.2020.105092 (2020). 10.1016/j.ultsonch.2020.105092 [DOI] [PubMed] [Google Scholar]
- 19.Tsochatzidis, N. A., Guiraud, P., Wilhelm, A. M. & Delmas, H. Determination of velocity, size and concentration of ultrasonic cavitation bubbles by the phase-Doppler technique. Chem. Eng. Sci.56(5), 1831–1840. 10.1016/S0009-2509(00)00460-7 (2001). 10.1016/S0009-2509(00)00460-7 [DOI] [Google Scholar]
- 20.Burdin, F., Tsochatzidis, N. A., Guiraud, P., Wilhelm, A. M. & Delmas, H. Characterization of the acoustic cavitation cloud by two laser techniques. Ultrason. Sonochem.6, 43–51. 10.1016/S1350-4177(98)00035-2 (1999). 10.1016/S1350-4177(98)00035-2 [DOI] [PubMed] [Google Scholar]
- 21.Brujan, E. A., Ikeda, T. & Matsumoto, Y. On the pressure of cavitation bubbles. Exp Therm Fluid Sci32, 1188–1191. 10.1016/j.expthermflusci.2008.01.006 (2008). 10.1016/j.expthermflusci.2008.01.006 [DOI] [Google Scholar]
- 22.Holzfuss, J. Acoustic energy radiated by nonlinear spherical oscillations of strongly driven bubbles. Proc. R Soc. A Math. Phys. Eng. Sci.466, 1829–1847. 10.1098/rspa.2009.0594 (2010). 10.1098/rspa.2009.0594 [DOI] [Google Scholar]
- 23.Liang, X. X., Linz, N., Freidank, S., Paltauf, G. & Vogel, A. Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation. J. Fluid Mech.10.1017/jfm.2022.202 (2022). 10.1017/jfm.2022.202 [DOI] [Google Scholar]
- 24.Vassholz, M. et al. Pump-probe X-ray holographic imaging of laser-induced cavitation bubbles with femtosecond FEL pulses. Nat. Commun.12(1), 1–11. 10.1016/j.ultsonch.2023.106328 (2021). 10.1016/j.ultsonch.2023.106328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pecha, R. & Gompf, B. Microimplosions: Cavitation collapse and shockwave emission on a nanosecond time scale. Phys. Rev. Lett.84(6), 1328–1330. 10.1103/PhysRevLett.84.1328 (2000). 10.1103/PhysRevLett.84.1328 [DOI] [PubMed] [Google Scholar]
- 26.Church, C. C. Frequency, pulse length, and the mechanical index. Acoust. Res. Lett. Online6, 162–168. 10.1121/1.1901757 (2005). 10.1121/1.1901757 [DOI] [Google Scholar]
- 27.Šponer, J. Dependence of the cavitation threshold on the ultrasonic frequency. Czech. J. Phys.40, 1123–1132 (1990). 10.1007/BF01597973 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.