Abstract
Brain large-scale dynamics is constrained by the heterogeneity of intrinsic anatomical substrate. Little is known how the spatio-temporal dynamics adapt for the heterogeneous structural connectivity (SC). Modern neuroimaging modalities make it possible to study the intrinsic brain activity at the scale of seconds to minutes. Diffusion magnetic resonance imaging (dMRI) and functional MRI reveals the large-scale SC across different brain regions. Electrophysiological methods (i.e. MEG/EEG) provide direct measures of neural activity and exhibits complex neurobiological temporal dynamics which could not be solved by fMRI. However, most of existing multimodal analytical methods collapse the brain measurements either in space or time domain and fail to capture the spatio-temporal circuit dynamics. In this paper, we propose a novel spatio-temporal graph Transformer model to integrate the structural and functional connectivity in both spatial and temporal domain. The proposed method learns the heterogeneous node and graph representation via contrastive learning and multi-head attention based graph Transformer using multimodal brain data (i.e. fMRI, MRI, MEG and behavior performance). The proposed contrastive graph Transformer representation model incorporates the heterogeneity map constrained by T1-to-T2-weighted (T1w/T2w) to improve the model fit to structure-function interactions. The experimental results with multimodal resting state brain measurements demonstrate the proposed method could highlight the local properties of large-scale brain spatio-temporal dynamics and capture the dependence strength between functional connectivity and behaviors. In summary, the proposed method enables the complex brain dynamics explanation for different modal variants.
Keywords: Multimodal graph transformer, Graph contrastive representation, Neural graph differential equations
1. Introduction
Understanding how our brain dynamically adapts for mind and behaviors helps to extract fine-grained information for typical and atypical brain functioning. But how the microcircuit heterogeneity shapes the structure-function interactions remains an open question in systems neuroscience. Magnetic resonance imaging (MRI) makes it possible to infer the large-scale structural and functional connectivity and characterize the anatomical and functional patterns in human cortex. Electrophysiological methods reveal the dynamical circuit mechanisms at the structural and functional level with higher temporal resolution. Different neuroimaging modalities such as fMRI, dMRI and MEG enable us to estimate both static and functional connectivity during resting state and task experimental paradigms.
Existing studies of large-scale brain dynamics relate the structural and functional connectivity with dynamical circuit mechanisms. The biophysically based dynamical models explore the time-variant function connectivity with excitatory and inhibitory interactions which is interconnected through structural connections [6,20,22]. Microcircuit specialization could be summarized using graph model [3], showing insights into inter-individual brain architecture, development and dysfunction in disease or disorder states. Recently, the graph harmonic analysis based on Laplacian embedding [4] and spectral clustering [19] is introduced to inform the cortical architectural variation. Basically, the previous methods define the nodes of the graph with the harmonic components to quantify the density of anatomical fibers. However, the inter-areal heterogeneity of human cortex has not been widely studied. The next challenging is to decompose the spatio-temporal brain dynamics with multimodal data [21]. Rahim et al. [15] improve the Alzheimer’s disease classification performance with fMRI and PET modalities. The stacking method of multimodal neuroimaging data is explored in age prediction task [10]. Representational similarity analysis (RSA) [9] based methods use the common similarity space to associate multivariate modalities. Subsequent research uses Gaussian process to allow complex linking functions [2]. In order to associate the higher temporal resolution of Electrophysiological measurements at millisecond with the higher spatial resolution of MRI and fMRI at millimeter, we introduce the contrastive learning with the Graph Transformer model to learn the heterogeneous graph representation.
Contrastive methods measure the distribution loss with the discriminative structure and achieve the state-of-the-art performance in graph classification. Contrastive multiview coding (CMC) [18], augmented multi-scale DIM (AMDIM) [1] and SimCLR [5] take advantages of multiview mutual information maximization with data augmentation to learn better representations. The graph-level representation is further explored with the extension of the mutual information principle in [17]. Recently, the Graph Transformer based method [16] is proposed to explore the nodes relationship in node embedding learning. However, it is challenging to accurately represent the entire given graph.
Literature on previous multimodal based methods could not be directly applied to link structural connectivity, functional connectivity and behaviors for the following reasons. 1) Most of the existing methods use simple and direct correlational approaches to relate SC and FC. However, the linearity assumption violates the brain spatio-temporal dynamics in many cases. 2) The scanner availability and patient demands may cause the incomplete data problem which may affect the model’s performance. 3) As far as we know, little efforts has been made to study how the heterogeneity across human cortex affects the dynamical coupling strength of brain function with structure.
To address these issues, we develop a novel Graph Transformer based framework for associating the heterogeneity of local circuit properties and revealing the dependency of functional connectivity on anatomical structure. The proposed method consists of three parts, the Dynamical Neural Graph Encoder, the graph Transformer pooling with multi-head attention, and the contrastive representation learning model. The proposed method has the following advantages:
The proposed method provides insights into the brain spatio-temporal dynamical organization related to mind and behavior performance. Existing graph pooling methods may yield similar graph representation for two different graphs. To obtain accurate graph representation, the novel Graph Transformer use multi-head attention to acquire the global graph structure given multimodal inputs. Moreover, we use the contrastive learning model to associate structural and functional details of dMRI, fMRI and MEG.
The proposed method makes it possible to incorporate the areal heterogeneity map with functional signals using multimodal data from the human connectome project (HCP).
The proposed method is evaluated with the meta-analysis to explore the behavioral relevance of different brain regions and characterize the brain dynamical organization into low level functions region (i.e. sensory) and the complex function regions (i.e. memory).
2. Methods
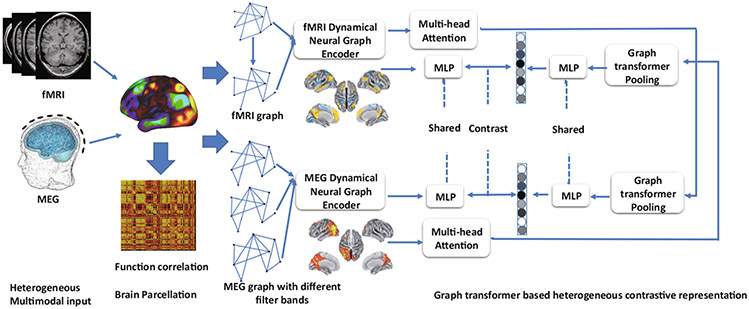
To explore the coupling strength of structural and functional connectivity, the heterogeneous Graph Transformer with contrastive learning is trained based on the multimodal brain measurements (i.e. MRI, fMRI and MEG). We use a graph to represent the heterogeneous graph representation, with the node type with brain ROIs and time points. The connection of different brain ROIs in spatial and temporal domain is denoted by the edge mapping . Given two types of multimodal graph representation and with different time points and and their multivariate value and . The dynamical neural graph encoder is used to represent the spatio-temporal dynamics within each modality. and . The adjacency matrices for each view are represented as and . We use and to represent the learned node representation within each modality. Then we use the Graph Transformer pooling layer together with the multi-head attention model to stack the entire node features. The overall framework is illustrated in Fig. 1.
Fig. 1.
Schematic illustration of the graph transformer representation learning
2.1. Dynamical Neural Graph Encoder for Single Modal Data
The dynamical brain network with neurons could be modeled as
| (1) |
where represents the internal states of neuron nodes at time . denotes the nonlinear dynamical function of each node. And represents the external stimuli for neurons.
To represent the dynamics of each single modality, we define a continuous neural-graph differential equation as follows,
| (2) |
where , and are graph encoder networks. is introduced to represent the value after discrete operation.
2.2. Multimodal Graph Transformer Module
To explore the relationship among different modalities, we introduce the multi-modal graph transformer layer. The previous pooling layer ignores the importance of nodes, we design a novel Graph Transformer pooling layer to keep the permutation invariance and injectiveness. The Graph Transformer module consists of a multi-head attention layer and a Graph Transformer pooling layer.
Graph Multi-head Attention.
Within each view, the inputs for the multi-head attention consists the terminal state of dynamical neural graph encoder. The inputs are transformed to query , key and value , where is the number of query vectors and represents the number of input nodes. and denotes the dimensionlity of corresponding key vector and value vector. The attention dot production is defined as . We define the output of the multi-head attention module as
| (3) |
where , and are parameter matrices. The output project matrices is defined as . Using the heterogeneous graph representation learned by graph encoder (GE), the graph multi-head attention block could be denoted by
| (4) |
Graph Transformer Pooling Together with Graph Multi-head Attention.
Inspired by traditional Transformer based method [12], we introduce a novel Graph Transformer pooling layer to learn the global representation of the entire graph, which is defined as follows:
| (5) |
where is any row-wise feed forward layer. is the seed matrix which could be directly optimized. is a layer normalization. In addition, we introduce the self-attention layer to explore the relationship between different nodes.
| (6) |
Together with graph encoder module, the overall framework is defined with the coarsened adjacency matrix
| (7) |
2.3. Contrastive Graph Representation Learning
Finally, we apply the shared projection head to the aggregated heterogeneous representation of each view. In the experiment, we use an MLP with two hidden layers as the projection head. The projected representations is defined as, and . For each view, the node representation are concatenated as follows,
| (8) |
The graph and node representations of the overall Graph Transformer module are defined as and . In the training stage, the cross modal mutual information between the node representation and graph representation is defined as,
| (9) |
where , , , represent the parameters of heterogeneous graph convolution and projection head. is the total numbers of graph. is the number of nodes. MI is denoted as the dot production .
3. Experimental Results
We evaluated the proposed method with resting state fMRI of 1200 subjects from Human Connectome Project (HCP). The resting state fMRI was preprocessed using the HCP minimal preprocessing pipeline [8]. The artefacts of the BOLD signal were further removed using ICA-FIX. The cortical surface was parcellated into N = 360 major ROIs using MMP1.0 parcellation [7]. We excluded 5 subjects with less than 1200 time points for resting-state fMRI data. Additionally, about 95 subjects have resting-state and/or task MEG (tMEG) data. We used 80% of the whole dataset for training and evaluation. The remaining dataset is used for testing. The corresponding resting-state MEG data were acquired in three 6 min runs. The preprocessing of MEG data followed the pipeline provided by HCP data [11]. The source reconstruction was performed using the FieldTrip toolbox. Then sensor data was bandpass filtered into 1.3 55 Hz and projected into source space by synthetic aperture magnetometry. After source reconstruction on the 8k-grid, the time courses were parcellated using MSMAll atlas [8]. The parcellated time courses were z-score normalized for both fMRI and MEG data. In addition, we used the ratio between T1 to T2 weighted maps from HCP dataset as the heterogeneity map. The parcellated diffusion MRI (dMRI) was analysed to generate the structural connectivity (SC) and compute the adjacency matrix for graph encoder module.
3.1. Heterogeneity Improves the Model Fit to FC
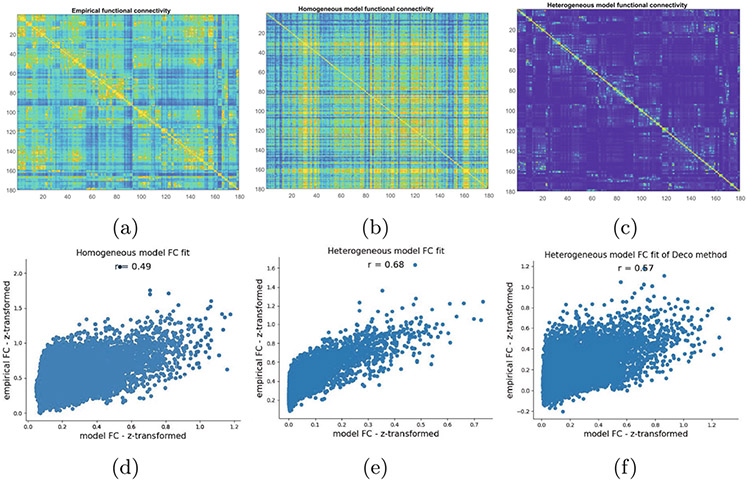
In the first experiment, we tested the similarity between empirical FC and heterogeneous FC patterns acquired by the proposed method compared with the homogeneous model. The empirical group averaged FC, particle-averaged homogeneous FC and heterogeneous FC are shown in Fig. 2. We used a simple non-neural model to introduce self-coupling heterogeneity strength based on the heterogeneity map , where and are heterogeneity parameters.
Fig. 2.
Heterogeneity map improves the model fit to functional connectivity (FC). (a) Empirical FC. (b) Homogeneous FC. (c) Heterogeneous FC. And (d-f) correlations between empirical FC and model FC, for the Homogeneous (d) Heterogeneous Graph Transformer (e) and Deco’s model (f).
Synaptic Dynamical Equations.
We introduced the biophysically-based computational model to simulate the functional dynamics for each node with the heterogeneity map .
| (10) |
where is the independent Gaussian white noise. represents the coupling matrix. is the learned representation using the proposed method. We incorporated the SC matrix and global coupling parameter with ,
| (11) |
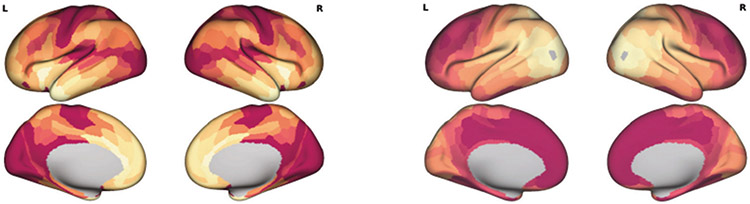
We used the squared Pearson correlation coefficient to evaluate the similarity between empirical FC and model fit FC for a single hemisphere. Figure 2 shows that the similarity of the proposed graph Transformer model is larger with than the homogeneous model (, dependent correlation test). The proposed model also yields higher FC similarity than Deco’s model [6] . The experimental result linking multiple modalities demonstrates the hypothesis that the T1w/T2w map shapes the microcircuit properties and spatio-temporal brain dynamics. The introduction of T1w/T2w heterogeneity with the proposed method could capture the dominant neural axis for microcircuit specialization is shown in Fig. 3. In summary, the proposed method with the prior of areal heterogeneity could inform the dynamical relationships among structure, function, and physiology.
Fig. 3.
T1w/T2w heterogeneity map (left) and the example surrogate heterogeneity map (right)
3.2. Functional Connectivity and Behaviors
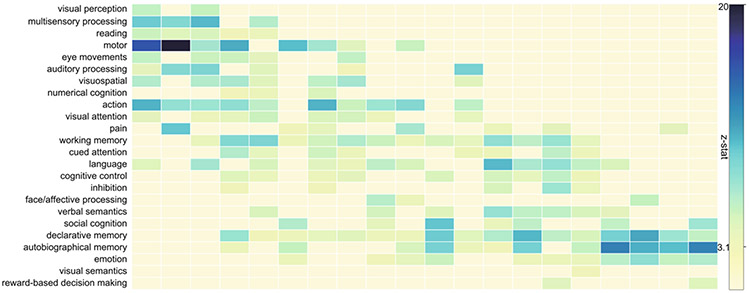
In the second experiment, we used a NeuroSynth meta-analysis [13] to assess the topic terms with the structural-functional coupling index in Fig. 4. The experimental results demonstrate the existence of behavior related global gradient spanning from lower to higher level cognitive functions. The evidence of global gradient reveals that higher coupling strength in sensory-motor areas which requires fast reacting (i.e. “visual perception”, “multisensory processing”, “motor/eye movement”). However, the coupling strength in high level cognitive regions (i.e. “autobiographical memory”, “emotion” and “reward-based decision making”) is low. Similar organization phenomenon could be found in the previous research [13,14].
Fig. 4.
Behaviorally relevant gradient shows brain organization
4. Conclusions
In the study, we propose a novel Graph Transformer based method for decoding the brain spatio-temporal dynamics. Different from most of the existing graph convolution method, the Graph Transformer model with multi-head attention guarantees the learning of global graph structure of multimodal data (i.e. dMRI, fMRI and MEG). The contrastive learning model makes it possible to associate multimodal graph representation and reveal how the heterogeneity map shapes the human cortical dynamics. The experimental results demonstrate the importance of regional heterogeneity and the corresponding intrinsic structure-function relationship within brain dynamical organization. Moreover, the proposed method provides insights into brain inter- and intra-regional coupling structure and the relationship between dynamical FC and human behaviors.
Supplementary Material
Acknowledgement.
This work was partially supported by NIH R01AG071243, R01MH125928, R01AG049371, U01AG068057, and NSF IIS 2045848, 1845666, 1852606, 1838627, 1837956, 1956002, IIA 2040588.
Footnotes
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1007/978-3-031-16431-6_33.
References
- 1.Bachman P, Hjelm RD, Buchwalter W: Learning representations by maximizing mutual information across views. arXiv preprint arXiv:1906.00910 (2019) [Google Scholar]
- 2.Bahg G, Evans DG, Galdo M, Turner BM: Gaussian process linking functions for mind, brain, and behavior. Proc. Natl. Acad. Sci 117(47), 29398–29406 (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bassett DS, Sporns O: Network neuroscience. Nat. Neurosci 20(3), 353–364 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Belkin M, Niyogi P: Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15(6), 1373–1396 (2003) [Google Scholar]
- 5.Chen T, Kornblith S, Norouzi M, Hinton G: A simple framework for contrastive learning of visual representations. In: International Conference on Machine Learning, pp. 1597–1607. PMLR; (2020) [Google Scholar]
- 6.Deco G, Ponce-Alvarez A, Hagmann P, Romani GL, Mantini D, Corbetta M: How local excitation-inhibition ratio impacts the whole brain dynamics. J. Neurosci 34(23), 7886–7898 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Glasser MF, et al. : A multi-modal parcellation of human cerebral cortex. Nature 536(7615), 171–178 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Glasser MF, et al. : The minimal preprocessing pipelines for the human connectome project. Neuroimage 80, 105–124 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guggenmos M, Sterzer P, Cichy RM: Multivariate pattern analysis for meg: a comparison of dissimilarity measures. Neuroimage 173, 434–447 (2018) [DOI] [PubMed] [Google Scholar]
- 10.Jas M, Engemann DA, Bekhti Y, Raimondo F, Gramfort A: Autoreject: Automated artifact rejection for MEG and EEG data. Neuroimage 159, 417–429 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Larson-Prior LJ, et al. : Adding dynamics to the human connectome project with meg. Neuroimage 80, 190–201 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee J, Lee Y, Kim J, Kosiorek A, Choi S, Teh YW: Set transformer: a framework for attention-based permutation-invariant neural networks. In: International Conference on Machine Learning, pp. 3744–3753. PMLR; (2019) [Google Scholar]
- 13.Margulies DS, et al. : Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci 113(44), 12574–12579 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Preti MG, Van De Ville D: Decoupling of brain function from structure reveals regional behavioral specialization in humans. Nat. Commun 10(1), 1–7 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rahim M, et al. : Integrating multimodal priors in predictive models for the functional characterization of Alzheimer’s disease. In: Navab N, Hornegger J, Wells WM, Frangi AF (eds.) MICCAI 2015. LNCS, vol. 9349, pp. 207–214. Springer, Cham: (2015). 10.1007/978-3-319-24553-9_26 [DOI] [Google Scholar]
- 16.Rong Y., et al. : Grover: self-supervised message passing transformer on large-scale molecular data. arXiv preprint arXiv:2007.02835 (2020) [Google Scholar]
- 17.Sun FY, Hoffmann J, Verma V, Tang J: InfoGraph: unsupervised and semi-supervised graph-level representation learning via mutual information maximization. arXiv preprint arXiv:1908.01000 (2019) [Google Scholar]
- 18.Tian Y, Krishnan D, Isola P: Contrastive multiview coding. arXiv preprint arXiv:1906.05849 (2019) [Google Scholar]
- 19.Von Luxburg U.: A tutorial on spectral clustering. Stat. Comput 17(4), 395–416 (2007) [Google Scholar]
- 20.Yang GJ, et al. : Altered global brain signal in schizophrenia. Proc. Natl. Acad. Sci 111(20), 7438–7443 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhao C, Gao X, Emery WJ, Wang Y, Li J: An integrated spatio-spectral-temporal sparse representation method for fusing remote-sensing images with different resolutions. IEEE Trans. Geosci. Remote Sens 56(6), 3358–3370 (2018) [Google Scholar]
- 22.Zhao C, Li H, Jiao Z, Du T, Fan Y: A 3D convolutional encapsulated long short-term memory (3DConv-LSTM) model for denoising fMRI data. In: Martel AL, et al. (eds.) MICCAI 2020. LNCS, vol. 12267, pp. 479–488. Springer, Cham: (2020). 10.1007/978-3-030-59728-3_47 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.