Unrolled Optimization via Physics-Assisted Convolutional Neural Network for MR-Based Electrical Properties Tomography: A Numerical Investigation

Abstract

Magnetic Resonance imaging based Electrical Properties Tomography (MR-EPT) is a non-invasive technique that measures the electrical properties (EPs) of biological tissues. In this work, we present and numerically investigate the performance of an unrolled, physics-assisted method for 2D MR-EPT reconstructions, where a cascade of Convolutional Neural Networks is used to compute the contrast update. Each network takes in input the EPs and the gradient descent direction (encoding the physics underlying the adopted scattering model) and returns as output the updated contrast function. The network is trained and tested in silico using 2D slices of realistic brain models at 128 MHz. Results show the capability of the proposed procedure to reconstruct EPs maps with quality comparable to that of the popular Contrast Source Inversion-EPT, while significantly reducing the computational time.

I. Introduction

Magnetic Resonance based Electrical Properties Tomography (MR-EPT) is a non-invasive imaging modality to extract the spatial distribution of the electrical conductivity and relative permittivity of living biological tissues by processing the magnetic field data acquired using a magnetic resonance (MR) scanner [1], [2], [3].

The knowledge of electrical properties (EPs) is relevant in several applications because they encode information about the typology and composition of biological tissues. Moving towards biomedical imaging, the values of EPs can be related to the health condition of biological tissues, hence variations from predicted reference values could reveal the presence of pathologies [2], [3], [4], [5], [6]. Indeed, the conductivity of healthy tissues differs significantly from that of pathological tissues [4]. This is useful as diagnostic tool for cancer and stroke in several biomedical applications [4], [5], [6], [7]. Additionally, the knowledge of the EPs allows for the evaluation of the electromagnetic (EM) fields inside tissues and this is very useful in all those medical applications wherein one needs to calculate tissue heating, that is related to the specific absorption rate induced by EM waves. Some examples are radiofrequency (RF) ablation and hyperthermia for cancer treatment [8], [9].

Different methods were proposed in the literature for MR-EPT. Most of them fall into two main groups: local derivative approaches [10], [11], [12], [13], [14] and global integral approaches [15], [16], [17], [18], [19], [20], [21], also known respectively as direct and iterative methods [2], [3], [22]. The main features, including advantages and limitations, of these methods are detailed in [22].

In the last few years, learning techniques have shown outstanding results on inverse problems, thanks to the rapid progress in the field of artificial intelligence. These techniques aim at making the reconstruction process as reliable as possible while reducing the computational time [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35]. They are very popular and widely used in several fields including biomedical imaging and diagnosis.

Among the above methods, learning approaches were proposed to deal with the inverse scattering problem (ISP) underlying MR-EPT. For instance, in [26] a feedforward approach employing a CNN was used to reconstruct the EPs with higher accuracy with respect to direct approaches. In [27] a two-step approach was proposed, where CNN-based reconstructions were solely used as initial guesses for 3D-Contrast source inversion based EPT (CSI-EPT). The procedure seeks to reduce the heavy computational load of 3D CSI-EPT without compromising quality. Nonetheless, convergence still required a huge number of CSI iterations and time. Moreover, in [27] the adopted end-to-end CNN does not incorporate any physical knowledge, compromising its generalizability to unseen cases.

Generalizability of out-of-distribution (OOD) data is a critical challenge in learning strategies. A possible strategy to make learning approaches more generalizable is acting on the training dataset creation [34], e.g., by increasing the size as well as the variety of the dataset the network was trained on ([32], [34] of the paper), or by using data augmentation during training, e.g., by transforming the input data.

Alternatively, one can introduce physical model information through the network [28], [29], [30], [33], [35], [36]. A first attempt to bridge the gap between learning approaches and problem physics was reported in [30], wherein a supervised descent method is proposed to update the inverted models by exploiting the descent directions collected from the training stage. Another further attempt is described in [36], where the EPT equations were combined with DL to iteratively reduce the error in the final reconstructions.

By taking advantage from the idea in [28], in this work, we propose an unrolled optimization based on a cascade of physics-assisted CNNs for MR-EPT, that explicitly considers the physics underlying the scattering model. Integrating physical knowledge into a deep learning (DL) approach is crucial for achieving physically meaningful results. Then, in the proposed strategy, the physics is introduced through the computation of the gradient descent direction of the cost function considering the misfit between the data and the scattering model, as in standard iterative optimization methods.

Unlike straightforward end-to-end learning procedures (as in [26], [27]) which discard the physics of the problem and aim at learning the relation between measured fields and electrical properties, the presented physics-assisted framework interleaves physics-based calculations (ensuring data consistency) with CNN (for a more reliable and fast contrast update).

The term “unrolled” refers to a cascade of CNNs with the same structure, imitating standard iterative optimization strategies. Moreover, it alleviates the limitations of iterative methods, such as the possibility during optimization to get trapped in local minima [37] and the high computational burden (as few rolls are required).

In the following, the proposed procedure is tested for brain EPs reconstructions. In particular, the current work is a numerical investigation of the performance of the proposed method in silico in the case of 2D realistic human head models. Also, a comparison with the performance obtained with the standard contrast source inversion CSI-EPT is given.

II. Method: Unrolled Optimization via Physics-Assisted CNNs

The proposed procedure involves a cascade of CNNs to mimic the overall iterative scheme of the minimization procedure underlying gradient based techniques (more details about the most common one, that is CSI-EPT, is reported in the supplementary materials (SM)). As such, the proposed approach is referred to as ‘unrolled’. This kind of algorithm allows to maintain the data consistency of iterative algorithms and it offers promises of reducing one of the main issues of DL techniques (i.e., the generalizability and the need for very large training sets).

The main idea is to consider the contrast function 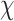(encoding the target EPs) as unique unknown and minimize the misfit between the data and the scattering model [38]. Then, the update of is performed by means of a CNN, trained for each roll separately (instead of using (S1.1a) as the popular iterative method CSI-EPT). From a mathematical point of view, the update is realized according to the following relation [28]:

where in 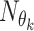identifies at each roll the k^th CNN and 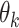are the learned parameters. Note that the functions 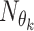correspond to CNNs with the same architecture but with different parameters 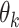, which are learnt separately at each roll (each roll identifies a single block, including a CNN). The inputs of the network at the roll are the complex contrast profile 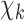and the descent gradient-determined direction 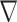_k (see Fig. 1), which enforces the physical model. Hereafter, we refer to the method as CNNs-EPT.

FIGURE 1.

Scheme of the proposed unrolled physics-assisted MR-EPT method. is the scattered magnetic field data. At the first roll, the input of the CNN 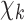is equal to the starting guess 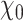, which is a homogenous contrast map. The starting guess is the same for both training and testing. Then, at the next roll, the input of the CNN is the output of the previous roll, i.e., the updated contrast map , and so on. The method uses a fixed structure (roll) which is repeated several times. Each roll interleaves physics-based calculations (full wave forward solver and gradient calculations in the light pink box) with a CNN (for the contrast update).

The update (1) is a key step of the proposed procedure, as the physics of the problem is maintained in the reconstruction framework. Indeed, unlike a straightforward end-to-end learning procedure, which discards the physics of the problem and aims at learning the relation between measured fields and EPs, the presented framework combines physics-based calculations (ensuring data consistency, see the light pink box in Fig. 1) with CNNs (for contrast update). This is a much easier task than a domain shift of end-to-end methods.

As the only unknown of the problem is the contrast function, the relevant cost function and the gradient direction 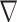_k are different from the ones in CSI-EPT. More details about the new cost functional as well as the gradient direction 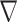_k are given in Section S2.A of SM.

During the training, starting from and 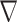_k, at each roll, the CNN learns an update of the contrast by minimizing a loss function (in particular, the half-mean-squared-error) between the predicted updated contrast and the ground truth (GT). Then, the output from the 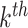roll becomes the initial guess for the next one and so on, iteratively.

Even if the proposed unrolled strategy computes at each 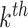roll the gradient 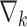, it is important to note that the proposed strategy can converge to a reliable solution in a few rolls compared to standard iterative ones. This means that the computation of the gradients is performed only a few times. Then, in the testing phase, the trained networks allow to quickly generate the EPs prediction.

The stopping criterion of the overall procedure is based on the evaluation of the difference between the contrast map in input and output. The iterative procedure stops, if no improvements are observed in terms of permittivity and conductivity reconstructions in terms of the computed normalized mean square error NMSE through the last two iterations, across all training data.

In the following numerical tests, three rolls were considered. Then the gradients were computed only three times, reducing the computational burden with respect to standard iterative methods. For more details about the CNN design, the reader is referred to Section S2 of SM.

III. Results

In this paper, a numerical investigation of the proposed strategy is presented against 2D realistic head models (more details on EM simulation setup, times and the involved brain models are in Section S3 of SM). All the performed tests are summarized in Table 1.

TABLE 1. Details of the Performed Numerical Analysis.

Test 1	Test 2	Test 3	Test 4
Test on noiseless and noisy data (DStest; training on DStrain,h in case of known transmit phase.	Test on noiseless and noisy data (DStest); training on DStrain,h in case of TPA.	Test on noisy data (DStest); training on DStrain,nh in case of TPA.	Comparison with CSI-EPT in case of noiseless data (DStest) and known transmit phase; training on DStrain,h.

TPA denotes the transceive phase assumption [15].

DS_test is the testing dataset which has 1080 2D slices (which includes 20 healthy head models and 20 head models with a tumor-like anomaly.

DS_train,h is the training dataset which consists of 100 healthy head models, i.e., 2700 2D slice.

DS_train,nh is the training dataset which includes (the same) 100 healthy models and additionally 10 head models with tumor-like anomalies, i.e., 2970 2D slices.

For Test 4 a hybrid two-step approach is also investigated, where the output of the proposed procedure was used as initialization for CSI-EPT.

In the following, the results from a test-case example are shown, i.e., on a head model with a tumor-like anomaly. As far as the case of pathology-free head models is concerned, the readers are referred to [29] for preliminary results.

To provide a quantitative understanding, the boxplots reporting the median of the mean absolute percentage error (MAPE) (see Section S4 of SM) over all the test data (with the 25th-bottom edge and 75th-top edge percentiles) and for the WM, GM, CSF, and tumor (when present) are shown. In case of noisy data, a white Gaussian noise with a SNR = 18 dB was superimposed on the real and imaginary parts of the total magnetic field, separately.

A. Test 1

Fig. 2 shows EPs reconstructions for each roll both for noiseless and noisy data of a single slice with a tumor-like pathology under the assumption that the transmit phase was known. These results show good conductivity and permittivity reconstructions, also at tissue boundaries, where the quality of the reconstructions improves from roll 1 to roll 3. In the presence of noise, the results show more blurring. The good performance is also confirmed by the NMSE (see Section S4 of SM for its definition) values reported in the figure. Indeed, the NMSEs at the third roll for conductivity and permittivity are equal to 0.05 and 0.01 without noise, 0.1 and 0.02 with noise, respectively. The results also show that such a network is able to infer the presence of the anomaly, even if the network was trained only on healthy brain maps. The MAPE trend across all the test population DS_test is reported in Fig. 2(d) and (e).

FIGURE 2.

Test 1: known transmit phase. EPs estimations through the three rolls for a slice of a brain model with tumor-like anomaly. Ground-truth (a); reconstructed EPs maps (conductivity top/permittivity bottom) noiseless (b) and with noise 18 dB (c). The NMSE values for the reconstructed slice are reported for all three rolls (red values) for the tissues considered all together. The reconstruction time for both cases (b) and (c) is about a few seconds. The boxplots showing the median MAPE (with the 25th-bottom edge and 75th -top edge percentiles), for WM, GM, CSF and tumor-like anomaly conductivity (d) and permittivity (e) reconstructions across all head models in DS_test respectively without and with noise (18 dB). CNNs were trained with DS_train,h. These boxplots reveal that the error drops as the number of rolls increases, for both noiseless and noisy cases. As far as GM, WM and CSF are concerned, the average error both for permittivity/conductivity at the third roll settles below 15% and 20% for the noiseless and noisy cases, respectively. Instead, for the tumor, the error settles around 10% for permittivity, for both noiseless and noisy cases. Performance is slightly worse in the case of conductivity, for which the tumor error is roughly 40%.

B. Test 2

Fig. 3 shows EPs reconstructions for each roll, both for noiseless and noisy data of the same pathological slice shown for Test 1, but using the TPA instead of the actual transmit phase. More details about TPA in SM Section III.

FIGURE 3.

Test 2: TPA. EPs estimation through the three rolls for a slice of a brain model with tumor-like anomaly, ground-truth (a); reconstructed EPs maps (conductivity top/permittivity bottom) noiseless (b) on the left and with noise 18 dB (c) on the right. The NMSE values for the reconstructed slice are reported for all three rolls (red values) for the tissues considered all together. The boxplots showing the median MAPE (with the 25th-bottom edge and 75th -top edge percentiles), for WM, GM, CSF and tumor-like anomaly conductivity (d) and permittivity (e) reconstructions across all head models in DS_test respectively without and with noise (18 dB). CNNs were trained with DS_train,h. Unlike Test 1, the MAPE trend shows that error does not always monotonically decrease, both without and with noise. This circumstance is probably related to the approximation underlying the TPA. However, the observed values in Fig. 3 are comparable to the range of values in Fig. 2, indicating that the introduced TPA did not significantly affect the results.

The NMSEs at the third roll for conductivity and permittivity are equal to 0.07 and 0.02 without noise and 0.12 and 0.02 with noise, respectively. As observed in the first test case, again the presence of noise leads to blurring in the results and higher NMSE values. Fig. 3(c) and (d) reports the MAPE trend for both noiseless and noisy cases.

C. Test 3

In the above tests, the proposed approach detects the tumor location and morphology, even though it was absent in the training dataset. We also investigated how the performance would change when tumors were included in the training set.

Fig. 4 shows EPs reconstructions for each roll, for noisy data of the pathological slice in Tests 1 and 2, assuming the TPA and also considering DS_train,nh. The displayed results show an improvement in the reconstructions, especially for the estimation of the tumor EPs. This is attributable to the fact that training in this case was done considering a different dataset (i.e DS_train,nh), which also includes pathological models.

FIGURE 4.

Test 3: TPA with noisy data and training with DS_train,nh. EPs estimation through the three rolls for a slice of a brain model with tumor-like anomaly, ground-truth (a); reconstructed EPs maps (conductivity top/permittivity bottom) with noise 18 dB (b). The NMSE values for the reconstructed slice are reported for all three rolls (red values) for the tissues considered all together. The boxplots comparing the third roll median MAPE (with the 25th-bottom edge and 75th -top edge percentiles) for CNNs trained with both DS_train,h and DS_train,nh, for WM, GM, CSF and tumor-like anomaly conductivity (c) and permittivity (d) reconstructions across all head models in DS_test with noise (18 dB). Focusing on the conductivity trend (c), the error decreases by about 5% for all tissues GM, WM and CSF. As far as the tumor is concerned, it is clearly seen that the error drops from around 45% to 15% when tumor models are also used in training. Conversely, for permittivity we do not observe an overall improvement. This is related to the training dataset, which is not enough wide.

In Fig. 4(c) and (d) the comparison of the MAPE obtained by training the CNNs-EPT both with the DS_train,h and with the DS_train,nh is shown, only for the third roll.

D. Test 4

In Fig. 5, a comparison of the proposed CNNs-EPT vs CSI-EPT only is shown, as well as the possibility of using, in a hybrid way the output of the proposed method as initial guess for CSI-EPT. As it is clear from the figure, the CNNs-EPT show for the tumor an underestimation of the conductivity and an over estimation of the permittivity, with respect to the ground-truth values. Starting from a homogeneous initial guess, CSI-only reconstructions show comparable accuracy to the CNNs reconstructions for the tumor. However, the CSI-only reconstruction time for a single slice is much higher: 1min for CSI-only vs few seconds for the cascade of three CNNs.

FIGURE 5.

Test 4: known transmit phase and noiseless data. EPs estimation from different EPT reconstruction approaches for a head model with tumor-like anomaly. Ground-truth (a); reconstructed EPs maps (conductivity top/permittivity bottom) noiseless (b)-(d), on the top. The NMSE values, for the reconstructed slice are reported (red values) for the tissues considered all together. Reconstruction time for case b) is about a few seconds, for case c) is about 1minute and for case d) is about the time for case b) plus the time to reach 980 iterations (i.e.,14s). The boxplots comparing the median MAPE (with the 25th-bottom edge and 75th -top edge percentiles) for three different reconstruction methods for WM, GM, CSF and tumor-like anomaly conductivity (e) and permittivity (f) reconstructions across all head models in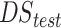. The hybrid technique improves tissues reconstruction for both conductivity and permittivity in WM, GM, and CSF. Notably, for the tumor, the error for the reconstructed conductivity decreases from 35% to 7% when the HYB is used instead of CNNs, whereas for the permittivity this decrease is from 8% to 6%. In Fig. 5(e) and (f), the variance of the CNNs-EPT reconstructions is larger. This is probably due to the fact that the training is performed using the dataset 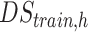. Then, in testing, the anomaly represents an OOD case for the CNNs. This issue is partially overcome when the HYB approach is considered. On the other hand, a wider and more varied training dataset can reduce the variability and improve the reconstructions (see results in test 3). Unlike the previous cases, in test 4 the noisy case is not considered as no further regularization technique is adopted. Indeed, the CSI-EPT algorithm fails in the case of noisy data (also in the more realistic case of TPA) as it needs to be properly equipped with a robust regularization technique.

The hybrid method (HYB in the following), i.e., the output of the CNNs used as input for CSI, further improve reconstruction quality. Additionally, providing CNNs as initial guess leads to a reduction in the reconstruction time (16s for the HYB vs 1min for CSI only for one slice, under the same stopping rule). Furthermore, by using the HYB the error arising from the low E-field region in the CSI reconstruction is also reduced. The boxplots with the MAPE for these three compared strategies are shown in Fig. 5(e) and (f).

IV. Discussion

Unlike most of the end-to-end learning approaches lacking physics information, the proposed strategy does incorporate the physics underlying the scattering model (i.e., the gradient descent direction) as an input to the CNNs. The presented results demonstrated the feasibility of CNNs-EPT to reconstruct conductivity and permittivity maps, starting from simulated data. It allows EPs reconstructions, for noiseless and noisy data as well as for known transmit phase and for TPA, with results comparable with the ones by CSI-based approaches but in a much shorter reconstruction time.

As shown in the boxplots, median MAPE values tend to decrease through the rolls, which confirms the effectiveness of the procedure. Simultaneously, the reconstructions get more detailed, especially at the tissue boundaries. First, only the actual transmit phase (assumed known) was considered; afterwards, the more realistic TPA was also added. The results demonstrate the method's ability to handle the TPA. Yet, tumor reconstructions for the cases trained with healthy models only are not yet accurate, even though the tumor is recognized by its spatial location within the brain and its shape. However, the reconstruction quality improves especially for the conductivity value, when DS_train,nh is considered. This suggests that both using physics and increasing the dataset improve generalizability.

The results presented demonstrate performance comparable to end-to-end methods presented in literature. For instance, if the same level of noise as in [26] is considered, for a head model (see Supplementary Table S9 in [26]), the average NMSE (for the main three tissues WM, GM and CSF considered together) is about 12% in the best network configuration. Contrary, in our procedure the NMSE is about 9%. Additionally, for the head model with a tumor inclusion with noisy data, the approach in [26] and the proposed one show that for the reconstructed tumor conductivity the NMSE is about 15%, while for the permittivity value is more accurate, as the NMSE is about 5%. It is important to note that in [26], two distinct trainings are performed to obtain conductivity and permittivity reconstructions, whereas the technique proposed in our work enables the direct reconstruction of contrast through a single network, saving time needed for training and testing. Lastly, the proposed method starts from a homogenous profile and does not exploit tissue contrast information as a priori knowledge, which was instead needed in [26]. On the other hand, unlike [27] which pertains to a 3D case, our technique is proposed and tested on a 2D geometry. However, in the case of TPA with noise, we compared our method against [27]. In this case we see that, the proposed strategy shows lower NMSE for conductivity and permittivity: in terms of conductivity for the head model the average NMSE is about 10% for our method, while it is about 55% for the one in [27]; for permittivity is about 3% versus 25%, respectively.

Ultimately, if compared with standard iterative methods, this approach allows significant computational advantages. With respect to CSI-EPT, it allows similar accuracy but faster reconstructions (2s versus 1min for a given 2D slice), which will be extremely relevant when moving to 3D-reconstructions (which take hours). The proposed learning procedure skips the computation of the step length adopted in CSI to guarantee the maximum decrease of the functional along the gradient direction. On the other hand, in CSI the full wave forward solver is not required at each roll. As far as the hybrid method is concerned, using the output of the proposed method as a convenient starting guess allows to reduce the number of iterations required for CSI to converge to the final solution (5422 versus 980).

Yet, the proposed method still presents some limitations. First of all, the method was tested on 2D simulated human brain data at 128 MHz, but other Larmor frequencies should be eventually considered. Second, the procedure should be extended and assessed in the case of a 3D scenario. This will require network adaptations to cope with 3D input data, as well as adaptations to the input patches to deal with the increased computational burden in training. Third, the rundown of reconstructed and (partially) shown head models was obtained starting from simulated data. This paper is a first numerical investigation, as done in many other recently published works [27], [33]. Future work should then be focused on translating this method to measured data, first in phantoms, where reference electrical properties values can be measured independently, and then in-vivo.

Moreover, as with most of the methods in the literature, the developed one does not include the RF shield in the Green's function. Then, future works should be devoted to the analytical or numerical inclusion of RF shields in the Green's function. In this respect, a possibility could be found in [15], in which the RF shield is numerically implemented to model the RF fields inside the MRI scanner, by using mirror currents.

Furthermore, CNNs are not the only possible architecture that can be used to resolve ISPs. Recurrent Neural Networks (RNN) are other common structures [25]. The real advantage of these kinds of networks is that they have a memory state, which allows them to mimic an iterative minimization procedure. In this regard, a future work may investigate the use of an RNN performing like the herein proposed unrolled CNNs-EPT.

Finally, this approach can also be adapted and extended to other imaging problems, e.g., microwave imaging [39], [40].

V. Conclusion

In this work, we presented a numerical investigation of a novel unrolled optimization method for MR-EPT reconstructions, which includes physics-assisted CNNs. Promising results are observed indicating substantial advantages in terms of computational time compared to iterative reconstructions (e.g., CSI-EPT). This computational improvement will be even more relevant when moving to 3D reconstructions in future studies. The presented analysis is for 2D MR-EPT reconstructions for noiseless reconstructions and reconstructions in presence of realistic noise levels. This work is therefore a necessary precursor before moving on to experimental data, where knowledge of ground-truth electrical properties is not available.

Statement of Contribution: S. Zumbo contributed to mathematics and modelling, data curation and analysis, interpretation of results, code writing and the manuscript writing. M. T. Bevacqua and S. Mandija contributed to the conception and design of the study, mathematics and modelling, interpretation of results and the manuscript writing. E. F. Meliadò, P. Stijnman, T. G. Meerbothe contributed to experiments. C.A.T. van den Berg and T. Isernia participated in the conception and design of the study, interpretation of results, manuscript writing. M. T. Bevacqua also supervised. All authors contributed to the article edition and approved the submitted version.

Conflicts of Interest: The authors of this manuscript declare no conflicts of interest.

Open Access funding provided by ‘Univ Mediterranea di Reggio Calabria’ within the CRUI CARE Agreement

Funding Statement

This work was supported in part by the project “RADIOAMICA: Open network per la radiomica/radiogenomica cooperativa basata su intelligenza artificiale” under Grant CUP C33C22000380006, in part by the PRIN project “DISCERN: aDvanced hybrId breaSt CancER imagiNg” under Grant CUP C53D23000430006, and in part by the Netherlands Organization for Scientific Research NWO; VENI under Grant 18078.