Model selection reveals selective regulation of blood amino acid and lipid metabolism by insulin in humans

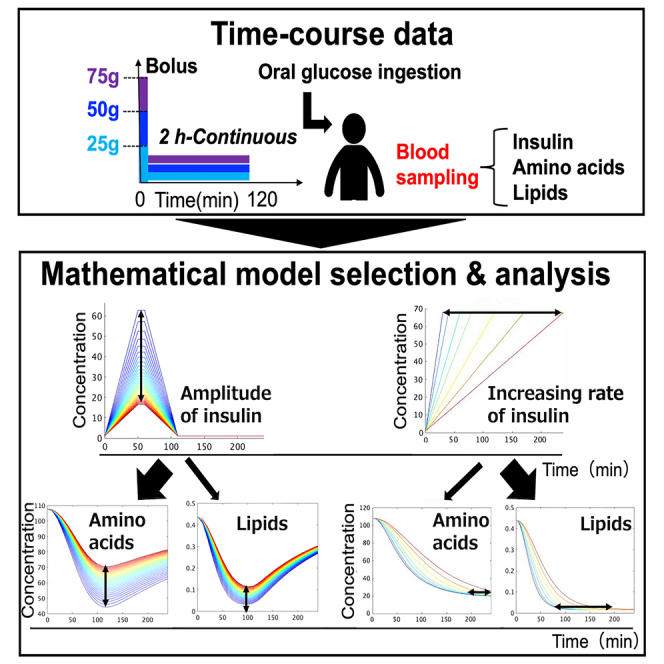
Summary

Insulin plays a crucial role in regulating the metabolism of blood glucose, amino acids (aa), and lipids in humans. However, the mechanisms by which insulin selectively regulates these metabolites are not fully understood. To address this question, we used mathematical modeling to identify the selective regulatory mechanisms of insulin on blood aa and lipids. Our study revealed that insulin negatively regulates the influx and positively regulates the efflux of lipids, consistent with previous findings. By contrast, we did not observe the previously reported insulin’s negative regulation of branched-chain aa (BCAA) influx; instead, we found that insulin positively regulates BCAA efflux. We observed that the earlier peak time of lipids compared to BCAA is dependent on insulin’s negative regulation of their influx. Overall, our findings shed new light on how insulin selectively regulates the levels of different metabolites in human blood, providing insights into the metabolic disorder pathogenesis and potential therapies.

Graphical abstract

Highlights

• •Mathematical model explored insulin’s regulation of blood AAs and lipids
• •Model selection revealed distinct regulatory structures for AAs and lipids
• •Insulin controls AAs by amplitude and lipids by rate adjustments

Biological sciences; Human metabolism; Mathematical biosciences

Introduction

Insulin is a hormone that plays a key role in regulating metabolism.^1,2 One of insulin’s primary functions is to regulate blood glucose levels, but it also has a role in regulating other blood metabolites such as amino acids (aa) and lipids.^3,4,5,6 Previous studies have shown that the regulation of these metabolites by insulin is selective and can vary over time after oral glucose ingestion.⁷ While there has been extensive research on the mathematical modeling of insulin’s regulation of blood glucose,^{8,9,10,11,12,13} there have been limited studies on its selective regulation of blood aa and lipids.^14,15,16,17 To address this gap, we utilized mathematical model selection to explore insulin’s selective regulatory mechanisms on blood aa and lipids, considering their temporal patterns after oral glucose ingestion.

Numerous studies have investigated how insulin regulates aa and lipids in the bloodstream.^4,18,19 Insulin reduces blood aa concentrations by limiting the release of aa into the bloodstream from skeletal muscle^18,20 and promoting protein synthesis in the liver and other tissues.³ Specifically, insulin inhibits the release of leucine, isoleucine, methionine, tyrosine, phenylalanine, and threonine^18,20 from skeletal muscle, while promoting protein synthesis from aa in the liver and other tissues.^3,4,7,18 In addition, insulin’s inhibitory effects on glycogenesis and urea synthesis have been shown to reduce the concentrations of arginine, citrulline, and ornithine in the blood.^4,21 These findings have been demonstrated through the use of various methods, including oral glucose ingestion studies.^{3,4,7,18,19,21} In the same metabolic group, leucine and isoleucine showed similar temporal patterns, while ornithine and citrulline showed different temporal patterns from leucine and isoleucine after glucose ingestion.⁷ These differences in the metabolic regulatory mechanisms of aa are reflected in their temporal patterns after glucose ingestion.⁷

Blood lipids consist of free fatty acids (FFAs) and ketone bodies, such as 3-hydroxybutyrate. Insulin plays a crucial role in regulating blood lipid metabolism. Insulin reduces the concentration of FFAs in the blood by inhibiting their efflux from adipose tissue into the blood and promoting their accumulation as triglycerides (TAGs) in adipose tissue.^5,6 During feeding, insulin inhibits the activity of hormone-sensitive lipases that regulate lipolysis in adipose tissue and also inhibits the synthesis and release of FFAs into the blood by degrading TAG.²² In addition, insulin indirectly regulates FFA synthesis from TAG by regulating blood glucose levels.⁵ For ketone bodies, insulin decreases their concentration in the blood by inhibiting ketogenesis in the liver.^23,24,25 Insulin also promotes the utilization of ketones, increasing their removal rate from the blood.²⁶ Taken together, aa and lipids such as FFA and ketone bodies have different temporal patterns, while lipids show similar temporal patterns to each other after glucose ingestion.⁷ These differences in metabolic regulatory mechanisms of lipids and AAs are reflected in their temporal patterns after glucose ingestion.⁷

Mathematical models can help identify the regulatory mechanisms of blood metabolites by insulin. By analyzing the temporal patterns of blood metabolites, mathematical models can estimate the model structure and parameters, allowing researchers to infer the selective regulatory mechanisms of insulin. While there have been studies using mathematical models for the metabolic regulation of insulin and glucose,^{8,9,10,11,12,13} there has been less research on the regulation of blood aa¹⁴ and lipids^15,16,17 by insulin. Several mathematical models have been developed for the kinetics of blood aa and lipids, but none have explained the differences in temporal patterns of these metabolites after oral glucose ingestion. One study estimated a phenomenological regulatory structure for blood aa without considering metabolic map information,²⁷ but comprehensive analyses of the selective regulation of AAs and lipids by insulin using mathematical model selection and detailed blood metabolite data have not been performed.

In this study, we used the time course data of blood metabolites and hormones from three healthy human subjects who ingested three doses of glucose with rapid or slow ingestion to identify the regulatory mechanisms of blood metabolites by insulin.^28,29 We used mathematical model selection to compare different regulatory models based on the metabolic map and statistically selected the best model. We found that branched-chain aa (BCAA) are positively regulated in terms of efflux, whereas lipids are positively regulated in terms of efflux but negatively regulated in terms of influx. This regulation pattern for BCAA is consistent with previous studies,³ whereas the negative regulation of insulin reported in a previous study⁴ was not necessary to explain the influx of aa in this study’s dataset. This suggests that insulin effectively stimulates the efflux of BCAA rather than inhibiting their influx. The regulation of lipid, citrulline, and methionine in the selected model is also consistent with a previous study.³ By using mathematical model selection and glucose dose-dependent time course data of blood metabolites, we were able to infer the effective mechanisms of selective metabolic regulation.

Results

Blood metabolites data

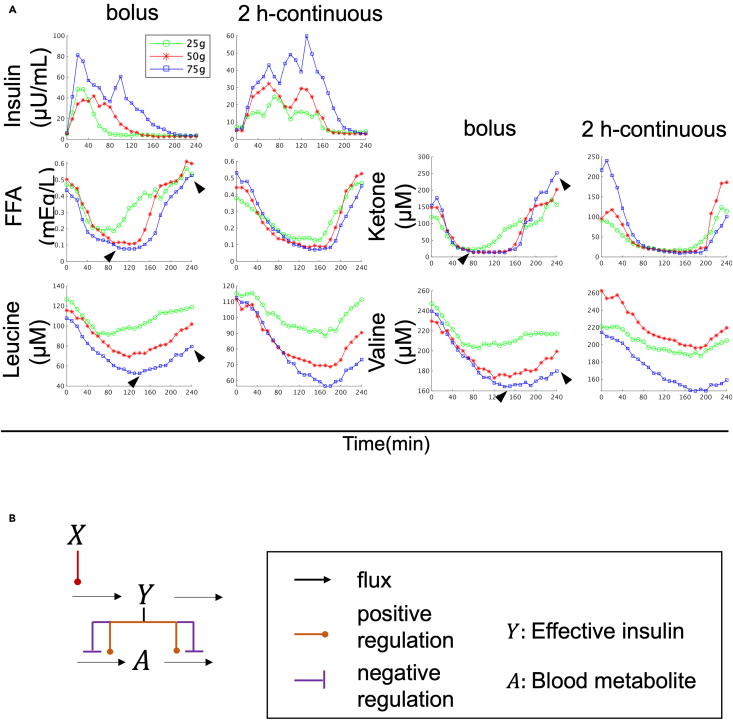
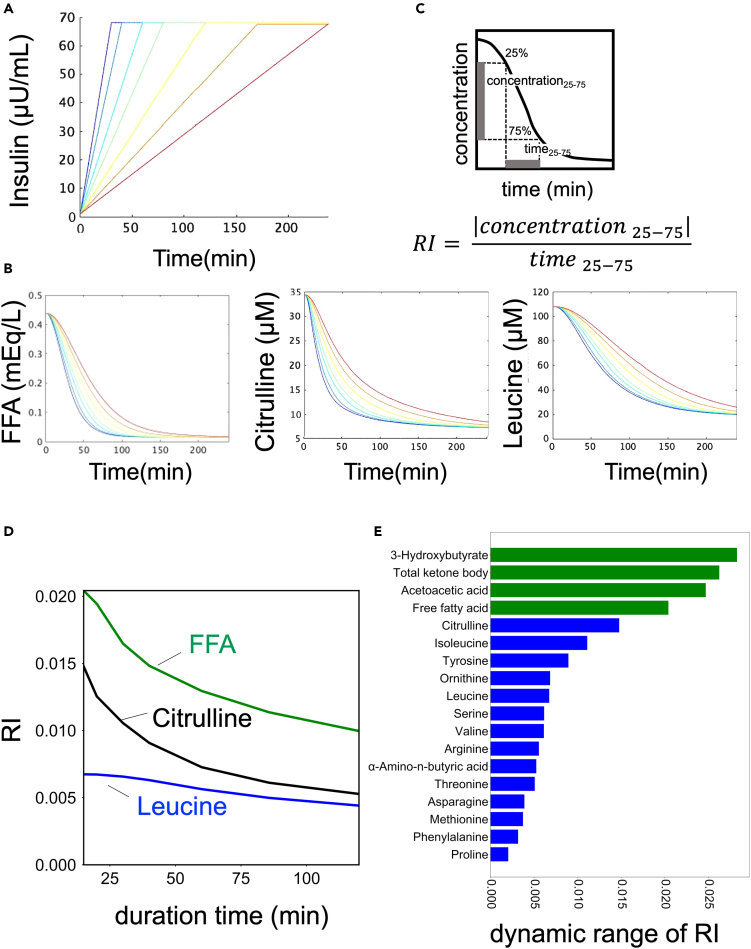
To perform model selection, we used a dataset from our previous study, which included the time course data of blood hormones and metabolites in three healthy human subjects.^7,28,29 The dataset included 14 aa such as leucine and valine, and 4 lipids including FFA and ketone bodies, which have distinct temporal patterns based on previous studies (Figures 1A and S2).^7,29 Lipids were found to peak earlier and return to fasting values faster than aa (Figure 1A, see Figure 1 legend). These temporal differences suggest that there are selective regulatory mechanisms for aa and lipids. Using this dataset, we performed model selection to explain the regulatory mechanisms by analyzing the time series data.

Figure 1.

Blood metabolites data and mathematical model structure for model selection

(A) Time course data on the mean values of blood insulin and blood metabolites by glucose ingestion.²⁹ The doses and ingestion patterns are indicated at the top. Green, red, and blue indicate three different doses: 25, 50, and 75 g, respectively. See text for arrowheads. For instance, in the case of a 75 g bolus, aa peaked later than 120 min and did not return to fasting values within 240 min, whereas lipids peaked earlier than 120 min and returned to fasting values within 240 min (Figure 1A, arrowhead).

(B) Model structure for model selection (see STAR methods).

Mathematical model structure for model selection

In this study, we developed a mathematical model using ordinary differential equations (Figures 1B and S3, see STAR methods) represented by the S-system, which is a type of power-law formalism.^30,31 As there could be multiple mechanisms of insulin action on blood aa and lipids, we developed several alternative models (Figure S3), each including blood insulin (X), effective insulin (Y), and blood metabolite (A) (Figure S3). These models differed in whether effective insulin regulated the influx or efflux of the blood metabolite (Figure S3, see STAR methods). We used time series data of blood insulin as input (Figures 1 and S3, see STAR methods) and constructed a regulatory model for each blood metabolite that best fit the population-averaged temporal pattern of each metabolite across three healthy human subjects. We estimated the parameters of each model separately to fit the time course data of each metabolite (Figures 1 and S4). The best model was selected by minimizing the Akaike information criterion (AIC), which takes into account the complexity of the model and its fit to the time course of each metabolite (see STAR methods). Note that since our previous study, using the same dataset, found that similar features among subjects and experimental conditions are dominant and distinguish metabolites (Equation 1 in Figure S1B),²⁹ the purpose of this study is to estimate parameters and select models that are common among experimental conditions for the population-averaged time series among subjects.

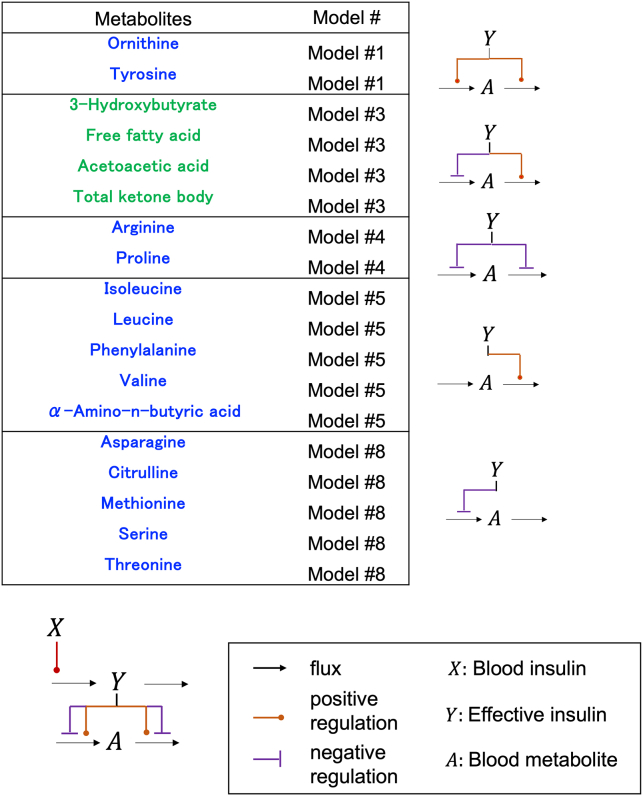
Selected model of each blood metabolite

The best models for the blood metabolites were divided into five groups based on their regulation by insulin (Figure 2; Table S1). In the models of ornithine and tyrosine (model #1), both the influx and efflux were positively regulated by effective insulin (Y) (Figures 2 and S5). In the lipid model (model #3), the influx was negatively regulated and the efflux was positively regulated by effective insulin (Figures 2 and S5), whereas the models for arginine and proline (model #4) showed that both the influx and efflux were negatively regulated by effective insulin (Figures 2 and S5). The models for BCAAs (model #5) showed that the influx was not regulated by effective insulin, but the efflux was positively regulated (Figures 2 and S5). In the models of aa such as serine and threonine (model #8), the influx was negatively regulated while the efflux was not regulated by effective insulin. Taken together, insulin positively regulates BCAA efflux, positively regulates lipid efflux, and negatively regulates influx. We compared our selected model structures with previous knowledge (Figure S5). For lipids, negative regulation of the influx and positive regulation of the efflux have been reported,^{5,22,23,24,25,26} consistent with the results of our selected model. For citrulline and methionine, negative regulation of the influx has been reported,⁴ consistent with our results (Figure S5). For BCAA, positive regulation of the efflux has been reported,³ consistent with our results. However, the negative regulation of influx by insulin has been reported,⁴ whereas it was dispensable in our model (Figure S5). Our results suggest that insulin may only effectively stimulate the efflux of BCAA, rather than inhibit the influx.

Figure 2.

The model structures of the selected model

The model structure with each number models are shown in Figure S4.

Model parameters reflecting the features of temporal pattern

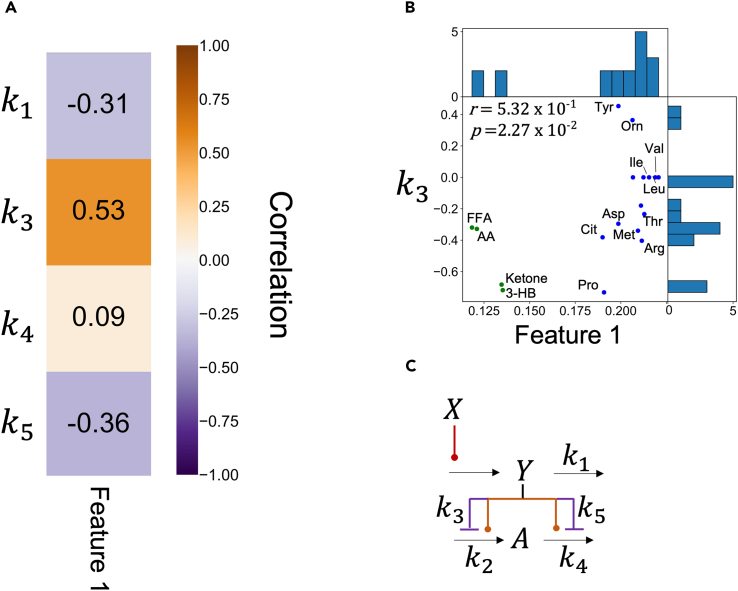
We analyzed the relationship between the estimated model parameters and experimental features extracted from our previous study using tensor decomposition (Figures 3 and S1B).²⁹ The features, called “Feature 1” and “Feature 2,” correspond to $y_{l_{4}m},l_4=1,2$, respectively (Equation 1 in Figure S1B).²⁹ Since Feature 1 represents the most dominant feature of the dataset, we focused on Feature 1 in this study. Feature 1 reflects the peak time of temporal patterns of blood metabolites, with higher Feature 1 values indicating later peaks of similar temporal patterns among individuals and experimental conditions (Figure S1B). One of the model parameters, $k_3$, was found to be strongly correlated with Feature 1, which are experimental features reflecting the peak time of temporal patterns of blood metabolites (Figure 3, correlation coefficient r = 0.53 for Feature 1; p < 0.05). Specifically, a greater negative strength of regulation on the influx of effective insulin (represented by a larger $k_3$ value) was associated with earlier peaks in both similar temporal patterns among experimental conditions. This is because insulin transiently increased after glucose ingestion (Figure 1), and the greater the strength of regulation of effective insulin on the influx, the more transient (i.e., earlier peak) the temporal patterns of the downstream metabolites (Figures 1, S1B, and S6). Lipids with a negative $k_3$ parameter, indicating a large strength of regulation of effective insulin on the influx, showed earlier peaks than BCAA with a $k_3$ parameter of 0, indicating no strength of regulation of effective insulin on the influx. These results suggest that the regulation of effective insulin on the influx contributes to earlier peaks in lipid temporal patterns compared to BCAA temporal patterns (Figures S1B and S6).

Figure 3.

Relationship between model parameters and physiological features

(A) Heatmap of correlation coefficients between model parameters and features.

(B) Scatterplot of k₃ with Feature 1 of the indicated metabolites. r and p indicate the correlation coefficient and p value, respectively. Abbreviations for the representative molecules as follows: Asp, aspartic acid; Cit, citrulline; FFA, free fatty acid; 3-OH, 3-hydroxybutyric acid; Ketone, Total ketone body; Glu, glutamic acid; His, histidine; Ile, isoleucine; Ins, insulin; Leu, leucine; Tyr, tyrosine; Val, valine. The dot colors correspond to the metabolic group (blue: AAs, green: lipids).

(C) Model diagram with model parameters.

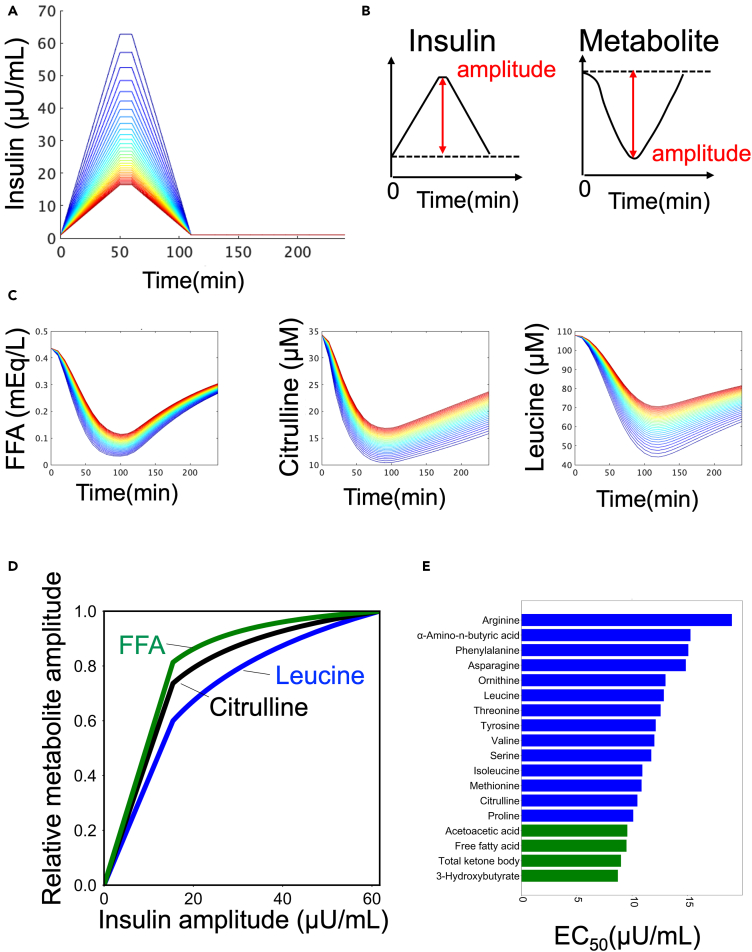
Regulation of the amplitude of AA and lipids by the amplitude of insulin

We previously found that the time course of different groups of blood metabolites in our study was characterized by “amplitude” and “rate”.⁷ Therefore, we examined which regulation by insulin in the model was responsible for the amplitude and rate of each metabolite (Figures 4 and 5). We used a mathematical model (Figure 4) to investigate how insulin regulates different temporal patterns of metabolites. We first determined how the amplitude of insulin affects the amplitude of metabolites. The amplitude of metabolites was quantified for various amplitudes of insulin (Figures 4B and 4C).³² The dose-response curves for all metabolites showed a monotonic increase as the amplitude of insulin increased (Figures 4D and S7B). We calculated the EC₅₀, which represents the half-maximal concentration of insulin required for half maximum amplitude of the metabolites (Figures 4E and S7C, see STAR methods). It should be noted that we normalized the amplitude of the metabolites corresponding to the maximum amplitude of insulin to 1.

Figure 4.

Regulation of the amplitude of the metabolites by the amplitude of insulin

(A) Temporal pattern of insulin with different amplitudes as input. The colors of the lines indicate different peaks.

(B) Definition of amplitudes in time series for insulin and metabolites.

(C) Temporal pattern of metabolites as outputs. The colors of the lines correspond to the colors of the inputs (A).

(D) The amplitudes of the indicated metabolite against the amplitudes of insulin in the simulation.

(E) EC₅₀s of metabolites against the amplitude of insulin. The color of the bar indicates the metabolic group (blue: AAs, green: lipids).

Figure 5.

Regulation of the rates of AAs and lipids by the increasing rate of insulin

(A) Temporal patterns of insulin with different increasing rates as input. The colors of the lines indicate different rates.

(B) The definition of RI in the time series for insulin and metabolites.

(C) Temporal pattern of metabolites as outputs. The colors of lines correspond to the colors of the inputs (B).

(D) The RI of the indicated metabolite against the rate of insulin in the simulation. The x axis of shows the duration of insulin, which is inversely proportional to the rate of insulin increase.

(E) Dynamic range of RI of metabolites. The color of the bar indicates the metabolic group (blue: AAs, green: lipids).

According to the results of our investigation using the mathematical model (Figure 4), we found that the EC₅₀ values for aa and lipids were 13.0 and 9.12 μU/mL, respectively (Figure 4E). Aa had larger EC₅₀ values compared to lipids, which means that they can respond to a wider range of insulin amplitudes than lipids (Figure 4E). Here, we calculated average values for each metabolic group. Conversely, lipids had smaller EC₅₀ values, indicating that they are more sensitive to the lower amplitude of insulin (Figure 4E). Taken together, our findings suggest that insulin can selectively regulate aa and lipids based on the amplitude of insulin, and citrulline shows intermediate characteristics between aa and lipids (Figures 4D and 4E).

Regulation of the rates of AAs and lipids by the increasing rate of insulin

Next, we examined how the increasing rate of insulin is linked to the rate of metabolites (Figures 5A and 5B). To quantify the rate of metabolites, we introduced an index called “the rate index (RI),” which represents the time duration required for a metabolite to transition from 25% to 75% of its maximum response (Figure 5C).³² We investigated how the rate of metabolites is affected by the increasing rate of insulin. The duration time of insulin was used as a measure of its increasing rate, with shorter durations indicating faster increasing rates (Figures 5A and 5C). The results showed that as the duration time of insulin increased (i.e., the increasing rate of insulin decreased), the RIs of metabolites also decreased, indicating that the rate of metabolites is influenced by the increasing rate of insulin (Figures 5D and S7D). The dynamic range of RI was calculated as a measure of how much information regarding the rate of increase of insulin is transferred to metabolites (Figure 5E). Lipids had a larger RI and a larger dynamic range than aa, suggesting that insulin can more finely control the rate of aa than lipids by changing the increasing rate of insulin (Figures 5D and 5E).

Model validation

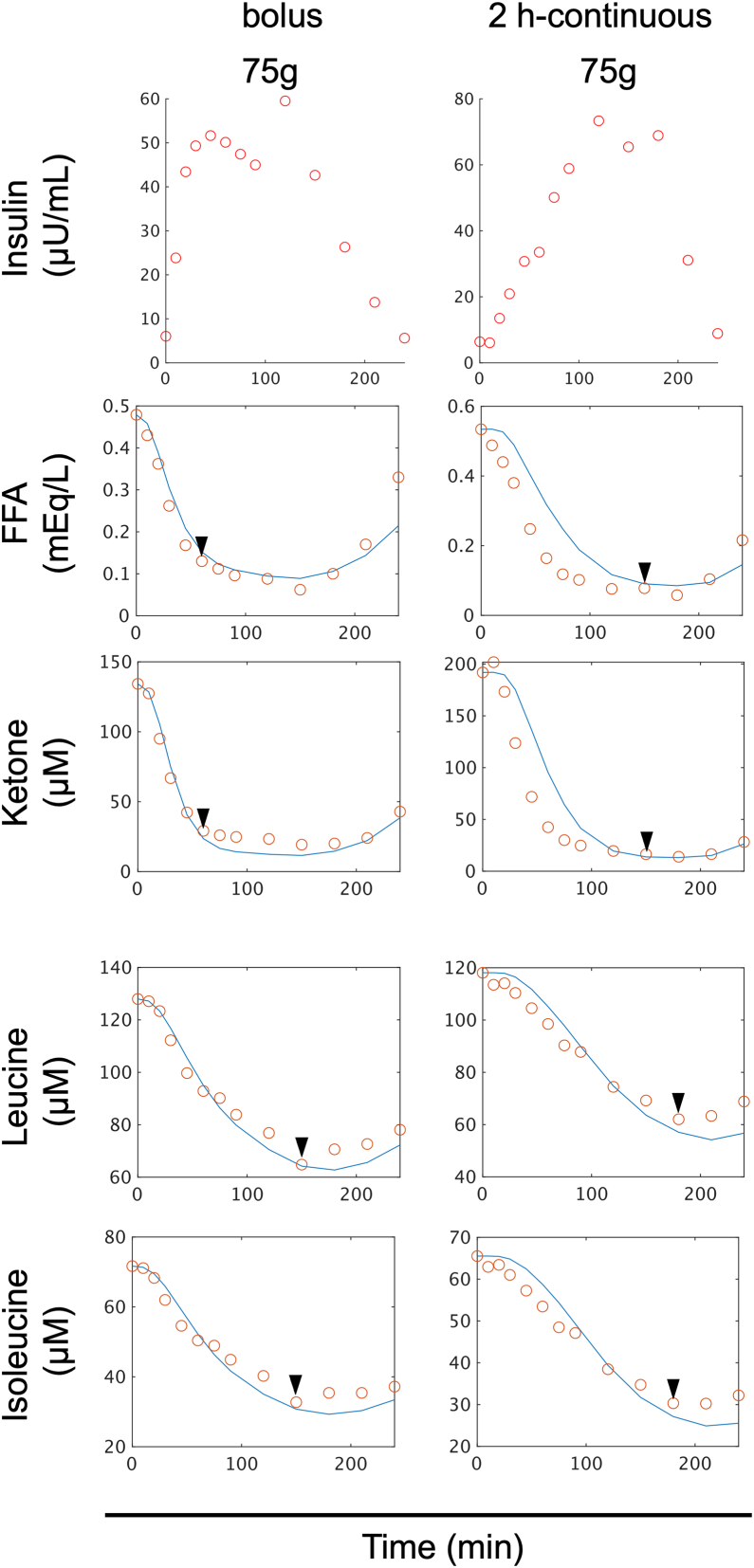
We examined the validity of the selected model for each metabolite by applying it to different datasets (Figure 6) from five healthy individuals who either ingested 75 g glucose rapidly or over 2 h, which are new datasets(Figure S8, see STAR methods). The selected model successfully reproduced the peaks at about 60 min for lipids such as FFA and ketones, and at 150 min for aa such as leucine and isoleucine for the bolus condition (Figure 6). For the 2 h continuous condition, the model reproduced the peak at about 120 min for lipids and at about 180 min for AAs, further confirming the validity of the model (Figure 6).We compared the experimental and simulated values using the selected model for each metabolite and found a high correlation (r > 0.9) for all metabolites (Figures S9 and S10), providing further evidence for the accuracy of the selected model.

Figure 6.

Model validation

Time course data on the mean values of blood insulin and blood metabolites in five individuals by glucose ingestion for validation. The doses and ingestion patterns are indicated at the top. The blue lines indicate the temporal patterns of simulations, and the red circles indicate the time course data of experiments. Before and after glucose ingestion, the concentration of blood insulin and 14 amino acids, including leucine and valine, and 4 lipids, including FFA and ketone bodies were measured at 14 time points from 10 min before fasting to 240 min after glucose ingestion (−10, 0, 10, 20, 30, 45, 60, 75, 90, 120, 150, 180, 210, 240 min).

Discussion

In this study, we developed a mathematical model to analyze changes in blood metabolites over time using data from three healthy human individuals who consumed three different doses of glucose at varying rates (Figures 1 and S4). The selected model structures varied between groups of blood metabolites, indicating that insulin selectively regulates different groups of metabolites (Figure 2). Interestingly, the same model structure was chosen for aa such as BCAA, as well as for lipids such as FFA and ketone bodies, suggesting that while the regulation of insulin is different between metabolic groups such as aa and lipids, it is similar within each metabolic group (Figure 2).

In this study, we analyzed the correlation between estimated model parameters and features extracted by tensor decomposition (Figures 3 and S1).²⁹ We found that the model parameter, $k_3$, was highly correlated with Feature 1; $k_3$ represents the strength of the negative regulation of effective insulin on the influx of metabolites. This indicates that the differences in the temporal patterns of aa and lipids (Figures 2 and S1B) can be explained by variations in the strength of the regulation of effective insulin on the influx. These findings demonstrate how data-driven features obtained by tensor decomposition can be used to drive hypotheses and uncover underlying physiological mechanisms.

Our study focused on examining the role of insulin in regulating the influx and efflux of blood metabolites in a mathematical model. Previous research has shown that insulin inhibits proteolysis in skeletal muscle, which leads to a decrease in the release of aa into the blood.⁴ In the liver, insulin activates S6 kinase through the AKT pathway, which promotes protein synthesis and causes an increase in aa usage for protein synthesis.³³ These findings suggest that insulin negatively regulates the influx of aa into the blood while positively regulating the efflux (Figure S5). However, the selected model structures indicated that insulin only positively regulates the efflux of aa from the blood and does not regulate the influx (Figures 2 and S5). This suggests that while insulin regulation of the efflux is physiologically effective, it is not essential for the influx of aa to reflect the dataset of this study. Further research is needed to better understand the contribution of insulin regulation to the influx of aa in the regulation of blood aa.

We found that insulin regulates the blood concentration of lipids such as FFA and ketone bodies through the positive regulation of their influx and the negative regulation of their efflux (Figure 2). This is consistent with previous studies showing that insulin inhibits fatty acid influx from adipose tissue into the blood,^5,6 leading to decreased blood FFA concentrations and increased triacylglycerol accumulation in adipose tissue (Figure S5).⁶ Additionally, insulin has been shown to inhibit ketone bodies synthesis^25,34 and increase their removal rate in the blood.²⁶ Our mathematical model selected the same structures (Figures 3 and S5), indicating that these regulations of insulin on blood lipids are consistent across multiple studies.^{5,22,23,24,25,26}

In this study, we investigated how insulin’s amplitude and rate regulate two components of metabolites (Figure 4). Differences in the temporal patterns of blood metabolites suggest different regulatory mechanisms by insulin.⁷ With respect to the amplitude component, we defined EC₅₀ as a measure of sensitivity to insulin and compared it among downstream metabolites (Figures 4 and S7). Lipids showed higher sensitivity to insulin than AAs against the amplitude of insulin, and citrulline showed intermediate sensitivity between lipids and AAs such as BCAA (Figure 4). We used experimental data to demonstrate a similar trend in sensitivity to insulin; that is, the EC₅₀ of aa is higher than that of lipids (Figure S7D). As a point of reference, in a previous study in which plasma aa concentrations were measured during normoglycemic insulin infusion in healthy young adult males at four different insulin infusion rates (6, 10, 30, and 400 mU/m²·min), the half-maximal response (a value with the same meaning as the EC₅₀ in this study) for aa was averaged about 30.9 μU/mL.¹⁸ The estimates from the model analysis of this study (13.0 μU/mL) did not deviate significantly. We also performed parameter sensitivity analysis of EC₅₀ in simulations for each model parameter (Table S2, see STAR methods). As the parameter sensitivity index, we compared the median value of each parameter for each of the 18 metabolites (Table S2). k₃ had the highest median value, indicating that the strength of the negative regulation of effective insulin on the influx of metabolites is the most important parameter controlling insulin sensitivity.

A previous study showed that insulin’s inhibition of lipolysis and ketogenesis is more sensitive than the inhibition of protein catabolism.²⁵ We also demonstrated that the sensitivity of citrulline to insulin was intermediate between that of aa and lipids.⁷ The mathematical model analysis in this study consistently explained the selective regulatory mechanisms for different sensitivities of the metabolites. For the rate component, we defined RI as a measure of the rate component and compared it among downstream metabolites (Figures 5 and S7). Lipids with a larger RI showed a larger dynamic range of increasing rate of insulin than aa with a smaller RI. Taken together, our results demonstrate that insulin can more tightly control aa than lipids by changing the amplitude of insulin, whereas insulin can more tightly control lipids than aa by changing the increasing rate of insulin.

In this study, we performed comprehensive analyses of the selective regulation of aa and lipids by insulin using a simple mathematical model selection and detailed blood metabolite data. Therefore, the strength of this study is that the analysis using a simple mathematical model reveals metabolite-specific differences in the response to glucose ingestion. Previous studies on individual metabolites proposed model structures that differ from this study.^35,36 We did not test a detailed model for each metabolite in this study because it is practically difficult and different from the aim of this study.

In our previous study, we investigated the different temporal patterns of how blood metabolites respond to glucose ingestion using a combination of hypothesis-driven⁷ and data-driven analyses.²⁹ We discovered that aa and lipids selectively decode the amplitude and increasing rate of insulin, respectively. However, we did not fully understand the mechanisms behind this selective decoding. In this study, we used mathematical modeling and time course data of blood metabolites after oral glucose ingestion to provide one explanation for the mechanism of selective regulation of the metabolites by insulin. Accordingly, we developed a mathematical model based on data from a single dose of glucose (75 g bolus), which is commonly used in clinical settings to assess glucose tolerance. Then we compared this model with a model based on multiple doses and durations of glucose (six experiments) data (Figure S11). The model using multiple doses and durations had a better fit (lower RSS value) for several molecules, including methionine, compared to the model using a single dose of glucose. This highlights the importance of using multiple datasets to validate mathematical models. The findings indicate that relying solely on data from a single dose of glucose (75 g bolus) is not enough to accurately capture the dynamics of blood metabolite changes. Instead, data from multiple doses and durations of glucose ingestion are required to better understand the temporal patterns of blood metabolites.

Limitations of the study

One limitation of this study was the small number of individuals and model structures used. The data were collected from only three individuals due to the time-consuming nature of the experiments, and population-averaged data were used to estimate the model structure without analyzing individual differences. In our previous study,⁷ we analyzed individual differences using blood data from 20 individuals. A larger number of individuals would allow for a more comprehensive analysis of individual differences using mathematical models.

For our additional analysis, we performed simulations not only for the population-averaged, but also for the time series per subject (Figure S12). The model selected for each subject’s varied, but for lipids, model #3 was selected, as was the model for the population-averaged. In contrast, aa such as BCAA were selected as models 5 and 8. This indicates that at least lipids, unlike aa, require two types of regulation: efflux inhibition and efflux promotion. In this study, the model analysis focused on the common features among subjects and experimental conditions because these features were domestic of the dataset.²⁹ In the future, studies that can discuss individual differences are expected. Additionally, the study assumed only eight simple candidate model structures and did not consider the interaction of insulin with glucose-mediated FFA^37,38,39 and mammalian target of rapamycin-mediated leucine.⁴⁰ While the model successfully reproduced blood aa and lipid concentrations, it is possible that the amplitude or rate of insulin altered insulin secretion, clearance, or feedback from FFA or leucine.

We investigated the identifiability of the parameters in the model structures selected for each metabolite (Figure S13).^41,42 For the lipid model, parameters k₃ and k₅ were shown to be identifiable, but k₁ and k₄ were found to be indistinguishable. For the aa model, including BCAA, parameters k₁ and k₅ were shown to be identifiable, but k₄ was indistinguishable for both leucine and isoleucine. Taken together, the parameters k₃ and k₅ representing insulin regulation showed that there are unique solutions in the range tested. We quantified EC₅₀ to determine the sensitivity of metabolites to insulin. Due to linear fitting, lipids showed smaller EC₅₀s than those of the amplitude of insulin, which was given as a simulation input (Figure 4). In this study, we did not argue strongly for the absolute values of EC₅₀s of metabolites, but at least for the fact that lipids have the smaller EC₅₀s than aa. (Figures 4 and S7). Further studies are needed to estimate the detailed regulatory structures for individual metabolites. To check the accuracy of our parameters, we transformed the Jacobian to the variance-covariance matrix of the model solutions in the estimated parameters for each metabolite and all models, and determined the standard deviation (Table S5). We confirmed that the parameters of the model selected in this study have low variability for all metabolites (Table S5, yellow). A priori identifiability is important in model analysis. For example, we found highly correlated pairs among the parameters of the selected model for lipids (Figure S14). This means that there is a possibility of redundancy among parameters in the model of this study. However, although we found correlations among the parameters, the small RSS pairs are locally distributed, indicating that the parameters selected in this study were appropriate as parameters reflecting the experimental data (Figure S15). In the future, study to develop mathematical model considering a priori identifiability will be conducted.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Metabolome data	This paper	Table S4
Software and algorithms
Source code	This paper	https://github.com/sfujita0601/ModelSelection_HumanOGTTDose
Python version 3.9	Python Software Foundation	https://www.python.org
MATLAB R2022a	MathWorks	https://jp.mathworks.com/products/matlab.html

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Shinya Kuroda (skuroda@bs.s.u-tokyo.ac.jp).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• •All data generated or analyzed during this study and the code files are included in this article and the article²⁹ and their supplementary materials files. The code files used in the simulation are freely available at https://github.com/sfujita0601/ModelSelection_HumanOGTTDose.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

Experimental model and study participant details

Subjects

The study involved three subjects for the “dataset for model construction” and five healthy subjects for the “dataset for model validation.” The profiles of the subjects are provided in Table S3. The “dataset for model validation” is provided in Table S4. Subjects have not been diagnosed with metabolic disorders, including diabetes, did not have chronic conditions affecting major organs such as the liver, kidney, heart, lungs, or digestive system, and did not regularly take medications known to influence metabolism.

Blood sampling

We used human blood samples obtained in our previous studied.^7,29 Briefly, after 10 h overnight fast, subjects underwent oral glucose tolerance test (OGTT) in the morning. An intravenous catheter was inserted into vein of the forearm and fasting samples were drawn twice. For ‘dataset for model construction’, three healthy subjects orally ingested a glucose solution containing 25, 50, or 75 g glucose (TRELAN-G75 (AJINOMOTO)). The ingestion method was rapid within a minute (bolus ingestion), and continuous over the course of 2 h (2-h-continuous ingestion). For continuous ingestion, we connected the tube to noncontact microdis-penser robot (Mr. MJ; MECT Corporation)⁴³ and glucose solution wasingested from tube.²⁸ Blood samples were obtained every 10 min until 240 min after glucose ingestion.²⁸ Subjects remained at rest throughout the test. Blood samples were rapidly centrifuged. For ‘dataset for model validation’, five healthy subjects orally ingested a glucose solution containing 75 g glucose within a few minute, and continuous over the course of 2 h. Blood samples were obtained at 10, 20, 30, 45, 60, 75, 90, 120, 150, 180, 210, 240 min after ingestion as described previously.⁷ Blood hormones and some metabolites were measured according to methods developed by LSI Medience Co., Ltd. The methods used to measure each of these molecules are described in our previous study.⁷ We considered the mean value of the time point prior to glucose ingestion and 0 min as the fasting value. Here, we set an interval of 1–2 months for each experiment, because these types of studies take a long period of time and require several hours and fasting by the subjects for each experimental condition.

Ethics committee certification

We followed Japan’s Ethical Guidelines for Epidemiological Research, and the study was approved by the Institutional Review Board and the Ethics Committee of Tokyo University Hospital (Approval No. 10264-(4)). Subjects were recruited through snowball sampling.

Method details

Model structure and parameter structure

We developed mathematical models to describe the temporal changes in blood metabolite concentrations (Figure 1). We developed a total of eight different models, assuming three types of regulation for each blood metabolite’s influx into and efflux from the blood: positive regulation, negative regulation, or no regulation (Figure S3). We excluded the case where there was no regulation for both influx and efflux. We estimated the model parameters for each model. The specific molecules targeted in our analysis are listed in Figure 2.

Each regulation type is based on the S-system model,^30,31 and the change in the concentration of a blood metabolite ($A$) is described by the following differential equation:

$$\frac{dY}{dt}=X-k_{1}Y$$ (Equation 1)

$$\frac{dA}{dt}={flux}_{A\text{in}}-{flux}_{A\text{out}}$$ (Equation 2)

$${flux}_{A\text{in}}=k_2{Y}^{k_3}\{\begin{array}{cc}{k}_3>0& \left(\text{if}\text{the}\text{positive}\text{regulation}\right)\\ k_3<0& \left(\text{if}\text{the}\text{negative}\text{regulation}\right)\\ k_3=0& \left(\text{if}\text{no}\text{regulation}\right)\end{array}$$ (Equation 3)

$${flux}_{A\text{out}}=k_4{Y}^{k_5}A\{\begin{array}{cc}{k}_5>0& \left(\text{if}\text{the}\text{positive}\text{regulation}\right)\\ k_5<0& \left(\text{if}\text{the}\text{negative}\text{regulation}\right)\\ k_5=0& \left(\text{if}\text{no}\text{regulation}\right)\end{array}$$ (Equation 4)

where $X$ is blood insulin concentration, $Y$ is effective insulin that effectively regulates blood metabolite concentration, and $A$ is blood metabolite concentration. To make the variable Y dimensionless, we applied a constant with a value of 1, ($\mu \mathrm{U}/\left(mL·t\right)$)), to the variable X (Equation 1). The term ${flux}_{A\text{in}}\left(k_2{Y}^{k_3}\right)$ represents the influx of metabolite $A$ into the blood and is determined by the positive regulation ($k_3>0$), negative regulation ($k_3<0$), or the reaction rate constant $k_2$, depending on the effective insulin $Y$. Similarly, the term ${flux}_{A\text{out}}\left(k_4{Y}^{k_5}A\right)$ represents the efflux of metabolite $A$ from the blood and is determined by the positive regulation ($k_5>0$), negative regulation ($k_5<0$), or the reaction rate constant $k_4$, depending on the effective insulin Y and blood metabolite concentration $A$.

Using the variables $X$, $Y$, and $A$, and assuming that $X$, $Y$, and $A$ are at steady state before glucose ingestion, we determined the initial conditions and parameters based on the estimated parameters and initial values:

$$X\left(0\right)=X_b,Y\left(0\right)=Y_b,A\left(0\right)=A_b\text{,}$$ (Equation 5)

$$\frac{dY}{dt}\left(0\right)=0\Rightarrow Y_b=\frac{X_b}{k_1}\text{,}$$ (Equation 6)

$$\frac{dA}{dt}\left(0\right)=0\Rightarrow k_2=k_4{Y}_b^{\left(k_5-k_3\right)}{A}_b\text{,}$$ (Equation 7)

where $X_b$, $Y_b$, and $A_b$ indicate the initial values of $X,Y\text{,}$ and $A\text{,}$ respectively. Therefore, there are four parameters to be estimated: $k_1$, $k_3\text{,}$ $k_4$, and $k_5$.

The unit of these parameters are follows: $k_1\left(1/t\right)\text{,}$ $k_2(\left(1/t)·(theunitofeachmetabolite)\right),k_3\left(dimensionless\right),k_4\left(1/t\right),k_5\left(dimensionless\right)$.

The measured blood insulin concentration was treated as continuous by linear interpolation between the measurement time points, as $X$ is used as a continuous value during the simulation, although the actual measured values were used.

Quantification and statistical analysis

Model selection

We used the residual sum of squares (RSS) as the objective function to minimize the differences between the experimental and simulated values, given by:

$${RSS}_k=\sum _{i\in Experiment}\sum _t{\left(\frac{A_{ikt}^{\mathit{exp}}-A_{ikt}^{sim}}{S.D.\left(A_{ik}^{\mathit{exp}}\right)}\right)}^2$$ (Equation 8)

In this equation, $A_{ikt}^{\mathit{exp}}$ and $A_{ikt}^{sim}$ represent the measured and simulated values, respectively, at time $t$ and metabolite k in experiment $i$, which can take the values 25B, 25C, 50B, 50C, 75B, or 75C. Each experiment is identified by the dose of glucose ingestion and the initial letters of the duration of ingestion (e.g., 25 g bolus ingestion is denoted as 25B, and 75-g-2-h-continuous is denoted as 75C).

To account for differences in the absolute values of the metabolites across experiments, we calculated the RSS with the same normalization used in our previous study,²⁹ where S.D.(·) is the function to calculate the standard deviation.

To find the global optimal solution, we performed parameter estimation using the Evolutionary Programming method.⁴⁴ We conducted 20 trials with a parent number of 20 and a generation number of 400. After obtaining the global optimal solution,⁴⁵ we further refined it using the simplex search method (MATLAB fminsearch) to find a local optimal solution. For each blood metabolite k, we performed parameter fitting for all eight models developed in Section model selection using the RSS calculated according to Equation 8. To statistically select the regulatory structure of each blood metabolite, we calculated the AIC based on the RSS of each model.

The AIC was computed using the following formula, taking into account that the models being compared have the same total number of data points N for the experimentally measured variables:

$${AIC}_k=N\ln \left({RSS}_k\right)+2K$$ (Equation 9)

where K is the number of parameters in the model that need to be estimated. The AIC provides a measure of the trade-off between the goodness of fit (represented by the RSS) and the complexity of the model (represented by the number of parameters). By considering both the fit to the data and the model complexity, the AIC allows us to compare and select the most appropriate model for each blood metabolite.

Parametaer identifiability

The parameter sets that produced the selected models were evaluated for identifiability. We iteratively changed the value of one parameter from its optimal value and re-estimated the remaining parameters.⁴¹ An increase in the cost function (RSS) of the model fit indicates that reliable parameter estimates are obtained and that the parameters are identifiable from the model structure and data.

Parameter accuracy

We computed the Jacobian of the model solution for each metabolite for all estimated parameters of the model, transformed it into a variance-covariance matrix by reference to nlparci function in MATLAB, and calculated the standard deviation for each parameter.

Parameter sensitivity analysis

We defined the individual model parameter sensitivity for each subject as follows:

$$M\left(f\left(x\right),x\right)=\frac{\partial logf\left(x\right)}{\partial logx}=\frac{x}{f\left(x\right)}·\frac{\partial f\left(x\right)}{\partial x}\text{,}$$ (Equation 10)

$$\frac{\partial f\left(x\right)}{\partial x}\approx \frac{f\left(x+\Delta x\right)-f\left(x-\Delta x\right)}{2\Delta x}\text{,}$$ (Equation 11)

$$f\left(x\right)={EC}_{50}\text{,}$$ (Equation 12)

where x is the parameter value and f(x) is EC₅₀. The differentiation is numerically approximated by central difference (Equation 8, and $x+\Delta x$ and $x-\Delta x$ were set so as to be increased [x (1.1x)] or decreased [x (0.9x)] by 10%, respectively. Finally, we defined the parameter sensitivity by the median of the individual parameter sensitivity for all metabolites. We examined the parameter sensitivity for four parameters. The higher the absolute value of parameter sensitivity, the larger the effect of the parameter on EC₅₀.

The temporal pattern similarity among molecules

In our previous study, we introduced the temporal pattern similarity among molecules (TPSM) as a measure of the similarity between their temporal patterns.⁷ The TPSM is defined as follows (Figure S7A):

$${\mathit{A}}_{\mathit{k}}^{\prime }=[A_{25B,\mathrm{k},-10}^{\prime },\cdots ,A_{25B,\mathrm{k},240}^{\prime },A_{50B,\mathrm{k},-10}^{\prime },\cdots ,A_{i,k,\mathrm{t}}^{\prime },\cdots ,A_{75C,k,240}^{\prime }]\text{,}$$ (Equation 13)

$${TPSM}_{kl}=\rho \left({\mathit{A}}_{\mathit{k}}^{\prime },{\mathit{A}}_{\mathit{l}}^{\prime }\right)\text{.}$$ (Equation 14)

where $A_{i\mathrm{k}t}^{\prime }$ represents the interindividual mean values of the difference from fasting at time t for metabolite k in experiment i. The vector ${\mathit{A}}_{\mathit{k}}^{\prime }$ represents the time-series connecting these values (Equation 10). The Pearson correlation coefficient, denoted as $\rho \left({\mathit{A}}_{\mathit{k}}^{\prime },{\mathit{A}}_{\mathit{l}}^{\prime }\right)$, is used to measure the similarity between ${\mathit{A}}_{\mathit{k}}^{\prime }$ and ${\mathit{A}}_{\mathit{l}}^{\prime }$. The ${TPSM}_{kl}$ (Equation 14) represents the temporal pattern similarity between molecule k and l, indicating how similar their temporal patterns are. Importantly, there were no molecular sets that exhibited a negative correlation.

Calculation of EC₅₀

To obtain the EC50 of all metabolites relative to insulin we performed linear fitting (Figure S7B). Half of the relative metabolite amplitude at insulin’s peak value of 15.432 was calculated as the EC50. It should be noted that although the time series for insulin and metabolites at a peak value of 0 is not depicted in Figure 4, we extrapolated the metabolite peak value to 0 for insulin in order to perform the calculation.

Published: May 16, 2024