Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2024 Jul 8;9(29):31694–31702. doi: 10.1021/acsomega.4c02393

Advancing Ionic Liquid Research with pSCNN: A Novel Approach for Accurate Normal Melting Temperature Predictions

Tao Liang 1, Wei Liu 1, Kai Tan 1, Anan Wu 1,*, Xin Lu 1,*
PMCID: PMC11270577  PMID: 39072063

Abstract

graphic file with name ao4c02393_0008.jpg

Ionic liquids (ILs), known for their distinct and tunable properties, offer a broad spectrum of potential applications across various fields, including chemistry, materials science, and energy storage. However, practical applications of ILs are often limited by their unfavorable physicochemical properties. Experimental screening becomes impractical due to the vast number of potential IL combinations. Therefore, the development of a robust and efficient model for predicting the IL properties is imperative. As the defining feature, it is of practice significance to establish an accurate yet efficient model to predict the normal melting point of IL (Tm), which may facilitate the discovery and design of novel ILs for specific applications. In this study, we presented a pseudo-Siamese convolution neural network (pSCNN) inspired by SCNN and focused on the Tm. Utilizing a data set of 3098 ILs, we systematically assess various deep learning models (ANN, pSCNN, and Transformer-CNF), along with molecular descriptors (ECFP fingerprint and Mordred properties), for their performance in predicting the Tm of ILs. Remarkably, among the investigated modeling schemes, the pSCNN, coupled with filtered Mordred descriptors, demonstrates superior performance, yielding mean absolute error (MAE) and root-mean-square error (RMSE) values of 24.36 and 31.56 °C, respectively. Feature analysis further highlights the effectiveness of the pSCNN model. Moreover, the pSCNN method, with a pair of inputs, can be extended beyond ionic liquid melting point prediction.

1. Introduction

Ionic liquids (ILs) are a class of liquids composed entirely of organic cations and inorganic/organic anions, which are typically in liquid state at temperatures below 100 °C.1 The unique chemical composition imparts various essential properties to ILs, including low volatility, high thermal stability, a wide liquid range, nonflammability, and high ionic conductivity.1 Consequently, ILs have recently attracted increasing and broad interest from both academia and industry.2−10 The distinctive chemical composition also bestows upon ionic liquids a crucial characteristic: the ability to tailor their physical, chemical, and biological properties to address specific challenges through modifications to the corresponding cations and/or anions. For example, the normal melting temperature (Tm) of methanaminium bromide can be systematically reduced from 237 to 111 and 13 °C by replacing bromide with nitrate and formate anions, respectively.11 Despite significant advances in synthetic chemistry that have accelerated IL production, the experimental screening of ILs remains impractical due to the vast number of potential combinations of organic cations and inorganic/organic anions.12

To tune the properties of ILs from a theoretical perspective, a profound understanding of the molecular structure and thermodynamics governing the ionic liquid system is necessary. Ab initio molecular dynamics and quantum chemical calculations offer a route to obtain reliable results,13 although these calculations are not feasible due to the prohibitive computational scaling of these methods. Quantitative structure–property relationship-based (QSPR) methods have been extensively employed to predict the physical and chemical properties of ILs and have achieved notable successes.12,14−18 Among the various properties, Tm is of great importance as a defining feature. Katritzky et al. developed a QSPR model for a data set of 126 pyridinium bromides using 6 descriptors, achieving an accuracy with a square correlation coefficient (R2) of 0.788.12 Since then, numerous attempts have been made to construct accurate QSPR models for estimating the Tm of ILs and have achieved certain successes(Table S1).14−18 However, several key factors have limited broad applications of these QSPR models: (1) QSPR-based models heavily depend on the quality and quantity of the data used for training. If the data set is limited or contains biases as in the case of previous investigations, the model’s predictions may not be reliable for broader applications; (2) The choice of molecular descriptors is crucial for QSPR models. If the selected descriptors are not truly representative of the molecular features influencing the property of interest, the model may not perform well in the blind test; (3) QSPR models often assume a linear relationship between descriptors and properties. It has been shown that the melting process of ILs is complicated and the descriptors are generally not linearly correlated with the Tm of ILs.19 Hence, more sophisticated methods are needed to better describe the correlation between the structure and the Tm values of ILs.

While tackling complex and nonlinear problems, modern machine learning methods (ML), supported by big data, have demonstrated superior efficiency and accuracy compared to traditional QSPR methods, achieving considerable success in predicting various properties of chemical materials.20,21 Over the past few decades, numerous ML models have been developed to predict the Tm values of ILs (Figure 1). Early ML efforts primarily focused on predicting the Tm of specific types of ILs due to a lack of sufficiently diverse data,22 and hence are lack of generalization capability in nature. Recently, Venkatraman et al.23 carefully compiled a comprehensive data set of 2212 ILs from the literature, facilitating ML models with generalization capabilities. Regression analyses, employing various ML methods, yielded prediction R2 values ranging from 0.53 to 0.67.23 Notably, the classification models revealed better accuracy (84%) in discriminating between ILs with Tm higher than 100 °C and those below 100 °C. Utilizing the same data set, Low et al.24 proposed a kernel ridge regression (KRR) model based on the extended connectivity fingerprint (ECFP4), Coulomb matrix, and molecular orbital energies derived from ab initio calculations, predicting the Tm of ILs with average mean absolute error (MAE), root-mean-square error (RMSE) and R2 of 29, 45 °C, and 0.74, respectively. This model, in contrast to the group contribution methods and traditional QSPR methods, is applicable to any type of ionic liquid.

Figure 1.

Figure 1

Open in a new tab

Various machine learning models for predicting the Tm of ionic liquids.

With the development of deep learning methods (DL), it is widely accepted that DL surpasses normal ML in handling complex and nonlinear problems. A benchmark investigation by Baskin et al.25 indeed demonstrated that nonlinear MLs outperform traditional linear models, and DLs outperform MLs. Furthermore, the Transformer, actively utilized in natural language processing, may offer a promising alternative for modeling the physical properties of ILs. In a recent development, Makarov et al.26,27 collected the largest and most comprehensive data set consisting of 3073 ILs. They utilized the Transformer Convolutional Neural Network (Transformer-CNN) equipped with a SMILES representation to predict the Tm of ILs. Two models, based on the whole data set, were developed with different cross-validation (CV) protocols (Component and Mixture). Reasonable accuracies have been achieved with R2 of 0.66 and 0.78,27 respectively. However, the generalization capability of these models needs further assessment due to the lack of sufficient external validation.

The Tm of ILs is controlled by both single-molecule properties and intermolecular interactions.1,28 Therefore, an effective model for predicting the Tm of ILs must accurately describe not only the properties of anions and cations themselves but also capture the complex and nonlinear correlations between them. In the field of computer vision, a specialized architecture, the Siamese convolutional neural network (SCNN) is designed for tasks that involve assessing the similarity or dissimilarity between pairs of inputs. SCNN is constructed to learn and extract features from pairs of input samples, making decisions based on their similarity.29 Compared to conventional artificial neural networks (ANNs) and Transformer-based methods, SCNNs focus on learning correlation between pair inputs and making predictions based on that. Consequently, they have demonstrated successful applications in image recognition,30 natural product identification,31 and bioactivity prediction.32 These characteristics suggest that SCNN is particularly well suited to predict the Tm of ILs using pairwise inputs of anions and cations. In this contribution, a pseudo-Siamese convolution neural network (pSCNN), inspired by SCNN, was developed to predict the Tm of ILs.

2. Methods

2.1. Data Set

To date, the most comprehensive data set, compiled by Makarov et al.,27 comprises 3073 records. As new data keep on appearing in journals and monographs, this work endeavors to enhance the data set’s comprehensiveness. Building upon the data set of Makarov et al.,27 journal articles,23 and NIST ILThermo database,11 we complied a more extensive data set. Several protocols have been adopted to ensure a relatively low noise level. For instance, when multiple melting point values were reported for a given IL, the most recent measurement was selected under the assumption that the recent measurement is more accurate due to the advances in experimental. In cases in which the melting point is presented as a range, the midpoint was adopted. Ionic liquids consisting of more than two types of ions were also excluded, aligning with the pSCNN’s capability to process pairs of inputs. The resultant data set comprises the Tm of 3098 ILs, featuring 203 distinct anions and 1760 unique cations. The cleaned data set was imported as a DataFrame in Python using the pandas package,33 serving as the foundation for various analyses and model selections in the subsequent sections.

Detailed analysis reveals that the Tm of 3098 ILs range from 177 to 592 K, with an average Tm of 357 K. Noted that the Tm distribution complies well with the standard normal distribution (Figure 2), suggesting the current data set is representative in terms of the Tm. However, further examination shows that majority of the cations are ammoniums (1096), imidazoliums (993), and pyridinums (372) based while majority of the anions are halides (1155), bistriflylimide (394), borates (168), and phosphates (168) based. The limited chemical diversity suggests a potential bias in the trained model, necessitating caution in its subsequent applications. Nevertheless, the current data set is the most comprehensive data set to the best of our knowledge.

Figure 2.

Figure 2

Open in a new tab

Distribution of the ionic liquid melting temperature in the whole data set (red line) and the standard normal distribution curve (green line).

2.2. Molecular Representation

For a predictive deep learning model in chemistry, a molecule is typically represented by an array of descriptors or a graph. One widely used molecular descriptor is the Extended Connectivity Fingerprint34 (ECFP), which has exhibited outstanding performance in virtual screening, particularly in identifying compounds with similar bioactivity.34 In this research, we employed ECFP4, which encodes functional groups up to two bonds away from the central atom and has demonstrated robust performance in virtual screening benchmarks.35 The ECFP4 fingerprints were encoded as 2048-bit one-hot vector using the implementation in RDKit.36

Molecular descriptors, encapsulating the structural, topological, and/or physicochemical properties of molecules, have been at the core of chemo-informatics and are always the first choice in data-driven deep learning approaches.37 As highlighted earlier, a robust model for predicting the Tm of ILs must accurately describe not only the properties of anions and cations themselves but also capture the complex and nonlinear correlations between them. Hence, Mordred38 molecular descriptors were also employed in this work to ensure a good description of anions and cations. 1631 molecular descriptors were calculated for each anion and cation in the data set by utilizing Mordred. These molecular descriptors were then subsequently analyzed using statistical criteria to minimize the impact of multicollinearity and prevent overfitting. All columns with low variance molecular descriptors and those containing missing values or empty columns were excluded. Pearson correlations were then applied to exclude columns with high correlation (>0.95). By excluding the molecular descriptors with low correlation (<0.05) with respect to the melting points of ILs, 178 and 47 features remained for cation and anion, respectively. Finally, the remaining features for cation and anion were combined together to keep a uniform input size as required by SCNN. In total, a set of molecular features consisting of 209 molecular descriptors for both anions and cations, were identified and used to train the pSCNN model.

2.3. Model

The pSCNN model consists of two networks as shown in Figure 3: a pseudo-Siamese convolution neural network and a fully connected multilayer perceptron (MLP). The pseudo-Siamese convolution neural network takes pairs of fingerprints or molecular descriptors as its input, which are fed into two independent subnetworks consisting of convolutional layers. Given that both anions and cations are organic/inorganic entities, these two subnetworks share identical architectures as in SCNN. However, the weights of the two networks are trained separately because anions and cations possess distinct properties and contribute differently to the melting of ILs. Through learning embeddings for input pairs, pSCNN can extract and create a feature space that maximizes the correlations between anions and cations. The learned and extracted features of anions and cations are then concatenated and fed into the MLP consisting of two dense layers for predictions, as shown in Figure 3.

Figure 3.

Figure 3

Open in a new tab

Schematic diagram of the proposed pSCNN model. pSCNN consists of two networks. The first one is a pseudo-Siamese convolution network for learning and extracting features of anions and cations. The extracted features are concatenated and fed into the MLP with two dense layers for prediction.

For model training, the 3098 ILs were randomly split into two sets: the training set and the testing set with a ratio of 2478/620. To ensure the generalization capability of the pSCNN model, the training set was then subjected to a 5-fold cross-validation. The final prediction is then made by taking the ensemble average of five trained models from the cross-validation process. The final model developed in this study and all data used in this work are publicly available at https://github.com/Anan-Wu-XMU/pSCNN/.

2.4. Statistical Metrics

The quality of the predictive model was evaluated using the mean absolute error (MAE, eq 1), the root-mean-square error (RMSE, eq 2), and the squared coefficient of correlation (R2, eq 3).

2.4. 1
2.4. 2
2.4. 3

where n is the number of ionic liquids, yexp is the experimental Tm, ypred is the predicted Tm, and 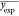Inline graphic is the mean values of all experimental Tm in the set.

3. Results and Discussion

3.1. Model Performance

The melting process of ILs is intricate and is still not well understood. However, certain facts are known: (1) both intramolecular and intermolecular factors are pivotal in the melting process; (2) van der Waals and electrostatic interactions assume distinct roles for different kinds of ILs; (3) Nonlinear entropy effects complicate the prediction of the Tm of ILs. Previous investigations have demonstrated that ANN can effectively handle complex nonlinear problem by correlating input features.39,40 Hence, the ANN models are included in this study for comparison. A summary of the performance of various models is presented in Table 1.

Table 1. Comparison of the Statistical Metrics of Different Models for Predictions of the Normal Melting Temperatures of the Ionic Liquids. For MAE and RMSE, the units are in °C.

descriptors method Nsample MAE RMSE R2
ECFP4a KRRa 2212 29.78 39.8 0.74
ECFP4 + QCa KRRa 2212 29.15 39.5 0.74
SMILESb transformer-CNFb 3073 27.3 35.8 0.77
consensus modelb 3073 26.4 34.9 0.78
ECFP4 ANN 3098 29.34 37.94 0.74
ECFP4 pSCNN 3098 29.85 38.33 0.74
mordred descriptors ANN 3098 26.25 34.11 0.79
mordred descriptors pSCNN 3098 24.36 31.56 0.82
Open in a new tab
a

QC: quantum chemistry descriptors derived from quantum chemical calculations, taken from ref (24).

b

Taken from ref (27).

For the KRR model based on ECFP4 reported by Low et al., the MAE and RMSE are 29.78 and 39.8 °C, respectively, with a moderate R2 of 0.74 (Table 1). The introduction of quantum chemical descriptors, intended to describe the interion interactions, yields only a slightly improved result, with MAE decreasing from 29.78 to 29.15 °C. However, using the same ECFP4 as descriptors, the deep learning models (ANN and pSCNN) do not outperform the conventional machine learning method as expected, even with a larger data set. For instance, ANN and pSCNN predict the Tm of ILs with MAEs of 29.34 and 29.85 °C, respectively (Table 1). Although DLs have generated various important breakthroughs in many areas, it is known that they are not friendly designed for application involving high-dimensional sparse data.41 Given the often sparse and highly dimensional nature of ECFP4, it is not surprising that both ANN and pSCNN do not outperform the conventional machine learning method in predicting the Tm of ILs using ECFP4 as descriptors. A closer inspection reveals that the feature space of halogen anions represented by ECFP4 is extremely sparse, with only 1 out of 2048 dimensions being nonzero. Since halogen anions are widely present in ILs (1155/3098), this will inevitably lead to the notorious “curse of dimensionality” in DLs,42 resulting in unsatisfied generalization performance, as shown above. Other molecular representations that do not generate sparse features (such as Mordred molecular descriptors) may yield better results.

The results of the ANN model using Mordred descriptors as input did improve compared to the ANN model based on the ECFP4 fingerprint. Its test MAE, RMSE, and R2 are 26.25, 34.11 °C, and 0.79, respectively, outperforming the best model in the literature (Table 1, Transformer-CNF). As reported by Makarov et al.,27 the Transformer-CNF model relies only on the augmented SMILES and can achieve the best accuracy among all general models reported to date (Table 1, i.e., MAE: 27.3, RMSE: 35.8 °C and R2: 0.77). As stated in Section 1, a robust model for predicting the Tm of ILs not only needs to accurately describe the properties of anions and cations themselves but also needs to describe the complex and nonlinear correlations between anions and cations. Transformer-CNF meets the above conditions to a certain extent. On the one hand, Transformer can effectively extract encoded chemical information from SMILES, allowing it to describe the properties of individual ions well. On the other hand, the intrinsic attention mechanism in the Transformer architecture can describe the correlation between anions and cations to a certain extent. However, systematic investigations43 show that the number of augmented SMILES plays a decisive role in the results, and it usually requires 20+ augmentations to achieve good enough results. 10-fold augmentation adopted by Makarov et al. may be insufficient.

In comparison to ANNs and transformer-based methods, SCNN is designed to learn and extract features from pairs of input samples and make decisions based on their correlation.29 Therefore, SCNN is particularly suitable for predicting the Tm of ILs provided that the properties of single ions can be well described. Using Mordred descriptors as input features, it is encouraging to see from Table 1 and Figure 4 that our pSCNN model has had the best accuracy so far. The introduction of the Siamese network does help to better learn and extract features from pairs of input samples as desired. The MAE and RMSE are significantly reduced from 26.25 and 34.11 °C (ANN/Mordred: Table 2) to 24.36 and 31.56 °C, respectively. The R2 value of 0.82 is one of the highest values among all general models (Table 1). This superior performance highlights the importance of choosing the proper model that matches the nature of the problem.

Figure 4.

Figure 4

Open in a new tab

Parity plot comparing the predicted melting point values (Tm,pred) with the corresponding experimental values (Tm,exp).

Table 2. Predicted Melting Points for 39 Newly Synthesized Ionic Liquidsa.

name Tm,expb Tm,pred(transformerCNN)c Tm,pred(transformerCNF)d Tm,pred(pSCNN)
1-butyl-3-methylimidazolium hydrogen sulfate 293 311 300 293.4
1-ethyl-3-methylimidazolium hydrogen sulfate 300 296 280 277.1
N-methyl-N-propylpyrrolidinium acetate 289.8 291 310 280.4
N-ethyl-N-methylmorpholinium bromide 445.6 413 440 420.5
1-butyl-3-methylimidazolium bromide 352.1 315 330 346.1
1-butyl-3-methylimidazolium trifluoromethanesulfonate 291.1 300 290 294.3
1-butyl-1-methylpiperidinium trifluoromethanesulfonate 309.1 330 350 348.6
1-butylpyridinium chloride 405.4 357 350 366.9
1-(2-Methoxyethyl)-1-methylpyrrolidinium hexafluorophosphate 307 311 300 313.1
1-butyl-1-methylpyrrolidinium bis(fluorosulfonyl)amide 253.5 288 270 277.2
1-ethyl-3-methylimidazolium bromide 350.2 354 360 348.6
1-butyl-3-methylpyridinium hexafluorophosphate 324.8 331 350 323.1
1-butyl-1-methylpiperidinium hexafluorophosphate 354.7 403 400 405.7
1-butyl-1-methylpyrrolidinium hexafluorophosphate 359.7 393 380 364.6
1-(2-hydroxyethyl)-3-methylimidazolium nonafluoro-1-butanesulfonate 251.5 293 280 322.4
1-(2-hydroxyethyl)-3-methylimidazolium perfluoropentanoate 294.8 271 280 285.0
1-ethyl-4-methylpyridinium bis((trifluoromethyl)sulfonyl)amide 288 298 290 287.4
1-ethyl-2-methylpyridinium bis((trifluoromethyl)sulfonyl)amide 289 281 290 293.4
N-(3-cyanopropyl)pyridinium tricyanomethanide 305.2 313 330 303.0
choline tosylate 378.1 393 380 389.8
1-ethylpyridinium 4-methylbenzenesulfonate 374.1 350 350 368.9
1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide 266.6 263 250 266.8
1-ethyl-3-methylimidazolium bis((trifluoromethyl)sulfonyl)imide 256 268 260 261.8
1-ethyl-3-methylimidazolium trifluoromethanesulfonate 262.6 299 270 270.9
1-ethyl-3-methylimidazolium 4-methylbenzenesulfonate 328.2 349 350 338.5
1-ethyl-3-methylimidazolium thiocyanate 266 283 280 276.4
1-ethyl-3-methyl-1H-imidazolium tricyanomethanide 274.9 274 270 281.2
1-ethyl-3-methylimidazolium dimethylphosphate 312.9 280 270 306.0
tetrabutylphosphonium bromide 376.1 370 380 393.5
1-ethyl-3-methylimidazolium bis((trifluoromethyl)sulfonyl)imide 259.1 268 260 260.6
1-ethyl-3-methylimidazolium tetrafluoroborate 284.1 270 270 281.5
N,N,N-triethylhexan-1-aminium trifluoromethanesulfonate 347.83 319 330 351.8
N,N,N-triethylhexan-1-aminium tricyanomethanide 290.03 270 280 300.1
N-decyl-N-methylmorpholinium trifluoromethanesulfonate 349.2 350 340 353.9
3-ethylthiazolium bis((trifluoromethyl)sulfonyl)amide 303.1 303 300 324.5
cetylpyridinium chloride 354.1 343 340 364.5
1-hexadecyl-1-methylpiperidinium acetylsalicylate 303.9 309 310 350.3
1-hexadecyl-1-methylpiperidinium chloride 365.9 393 390 374.1
3-methyl-1-octadecyl-1H-imidazolium bis((trifluoromethyl)sulfonyl)amide 328.1 306 300 318.0
MAE   17.8 16.3 13.4
RMSE   22.4 20.9 20.6
Open in a new tab
a

Units are in Kelvin (K).

b

Taken from ref (11).

c

Evaluated with the model in ref (26).

d

Evaluated with the model in ref (27).

3.2. Applicability Domain Analysis

For a predictive model, applicability domain analysis (ADAN) is also a crucial aspect to assess the reliability of the mode.44 To establish the boundaries within which the model predictions can be trusted, a probability-based and distance-oriented algorithm was applied. The query compound is considered as an outlier, and the prediction is marked as unreliable when the calculated average Euclidean distance with respect to the training set falls outside the 95% confidence interval boundary.

Figure 5 shows the applicability domain analysis for the pSCNN model, wherein the reliable prediction space is obtained by computing the 95 and 99% confidence interval boundaries. In the testing set, our analysis demonstrated that 34 ILs were outside the 95% confidence interval boundary (Figure 5, points in orange and red) with 7 ILs outside the 99% confidence interval boundary (Figure 5, points in red). Thus, the pSCNN model could account for nearly 95% reliable predictions across 620 compounds in the testing set. Such a performance is already satisfactory on the blind test.

Figure 5.

Figure 5

Open in a new tab

Boundaries of the applicability domain for the pSCNN model. Compounds positioned to the left of the gray dashed line fall within the 95% confidence interval, while those positioned to the left of the green dashed line are within the 99% confidence interval.

Upon close inspection of the ILs for which predictions were flagged as unreliable, it was revealed that these ILs contained cations or anions that were highly underrepresented in the calibration, and a majority of these ILs (25 out of 34) were even new ILs (Table S2). These ILs represent a significant challenge for melting point predictions. In such a stringent test, it is encouraging to see that our model can still produce reasonable predictions with MAE and RMSE of 30.4 and 37.0 °C, respectively. This suggests that by learning and extracting features from input pairs, our model has good generalization capability in predicting the Tm of ILs. In fact, this validation on outliers corresponds to the most rigorous “compounds out” adopted by Makarov et al.,26,27 both indicating the predictive power of the model for ionic liquids with novel ions. If the model is applied to predicting only a new combination of ions, the pSCNN model is expected to provide more accurate results. Thus, it may provide a simple yet efficient way to help experimentalists in advancing and customizing the synthesis of new IL. Note that predicting the Tm of a new IL by using the pSCNN model (including the feature generation) will take an average of 1.02 s on a workstation made of dual processor Intel Xeon Silver 4110@2.10 GHz.

3.3. Feature Importance

While the melting process of ILs is not fully understood, it is well recognized that factors primarily controlling the Tm of an ionic liquid include intermolecular forces (van der Waals and electrostatic), molecular symmetry, and the conformational degrees of freedom of a molecule.45

To further examine whether our model captures the essence of the problem being addressed, we analyzed feature importance based on permutation importance (see the Supporting Information (SI) for more information). Figure 6 shows the top 10 most important molecular descriptors that have a significant impact on Tm of ILs. Notably, all key features (Figure 6) are molecular descriptors related to either topological characters (IC3, IC2, IC5, and AATS0v) or electrostatic characters (PEOE_VSA7, VSA_Estat8, PEOE_VSA12, PEOE_VSA13, SlogP_VSA8, and Xc-3d). As the most important descriptors, ICx (IC3, IC2, and IC5) describe the connectivity and branching in the molecule. They are closely related to molecular shape and local symmetry, thus having a profound effect on the Tm of ILs. PEOE_VSAx (PEOE_VSA7, PEOE_VSA12, and PEOE_VSA13), on the other hand, quantify the van der Waals surface area of molecules with a specific charge range, aiming to capture direct electrostatic interactions46 that influence the Tm of ILs. SlogP_VSA8 is designed to capture the hydrophobic or lipophilic properties of a molecule,46 which is directly related to intermolecular van der Waals interactions and thus affects the melting point of the ionic liquid.

Figure 6.

Figure 6

Open in a new tab

Top 10 most important molecular descriptors that have a significant impact on the Tm of ILs.

All of these results clearly demonstrate that our pSCNN model, by learning and extracting features from pairs of input, indeed captures the essence of the problem being addressed. Thus, it can provide an accurate yet efficient way to predict the Tm of ILs.

3.4. External Validation and Perspective

Over the past few years, new data have continuously emerged in the journals and monographs. To further check the generalization performance of our pSCNN model, an independent test was conducted using 39 newly synthesized ILs, sourced from NIST ILThermo database.11 These ILs did not overlap with the ILs used in the development of the model. Results of the Transformer-CNF models were included for comparison.

ADAN (Figure S1) reveals that all 39 ILs are within the 95% confidence interval boundary, indicating that they should have good prediction results. The evaluations by our model indeed produced excellent results, with MAE and RMSE of 13.4 and 20.6 °C, respectively. These results are clearly superior to the two Transformer-CNF models26,27 with MAE and RMSE of 17.8, 22.4 °C and 16.3, 20.9 °C respectively (Table 2).

Detailed analysis showed that the majority of the prediction errors (23 out of 39) were less than 10 °C, which is an encouraging result for the design of new ILs. Large errors mainly occur when the occurrence rate of cations or anions is low. For instance, the largest error (71 °C, Table 2) was calculated for 1-(2-hydroxyethyl)-3-methylimidazolium nonafluoro-1-butanesulfonate, in which the 1-(2-hydroxyethyl)-3-methylimidazolium occurs only twice in the calibration. The cause of this high error may also be due to the fact that experimental measurements for ILs with very high (>200 °C) and low (<0 °C) Tm are often prone to errors.47

These results further strengthened the argument that, by learning and extracting features from pairs of input, the pSCNN model indeed captures the essence of the problem being addressed and hence can predict the Tm of ILs with good accuracy.

Considering that the synthesis of an ionic liquid is generally challenging and time-consuming, and the number of ionic liquids is virtually unlimited, it is therefore crucial to narrow down the potential pool of suitable ionic liquids to be synthesized. By taking combinations of all cations (1760) and anions (203) in our data set, we could evaluate the Tm of nearly 360,000 ILs (Figure 7) with satisfactory accuracy using our pSCNN model. This extensive data set, with diverse Tm’s ranging from −100 to 367 °C, may provide immense value for advancing and customizing the synthesis of new IL.

Figure 7.

Figure 7

Open in a new tab

Predicted melting points of all potential ILs generated by the pSCNN model.

4. Conclusions

Ionic liquids (IL) offer a broad spectrum of potential applications, owing to their distinctive and tunable properties, rendering them versatile across diverse fields. However, the practical applications of numerous ionic liquids are often constrained by their unfavorable physical or chemical properties. Due to the extensive number of potential combinations of anions and cations, the experimental screening of ionic liquids is impractical. Consequently, a robust and efficient method for predicting the properties of ionic liquids becomes imperative. In this study, we focused on predicting the normal melting temperature of ionic liquids, employing a pseudo-Siamese convolution neural network (pSCNN) inspired by SCNN. Utilizing a comprehensive data set of 3098 ILs, comprising 203 distinct anions and 1760 unique cations, we systematically assess various deep learning models (ANN, pSCNN, and Transformer-CNN), along with molecular descriptors (ECFP fingerprint and Mordred properties), for their performance in predicting the Tm of ILs. Noteworthy among the investigated modeling schemes, the pSCNN, in conjunction with filtered Mordred descriptors, demonstrates superior performance, yielding a mean absolute error (MAE) and root-mean-square error (RMSE) of 24.36 and 31.56 °C, respectively.

Subsequent feature analysis uncovered that the pivotal molecular descriptors influencing the melting process of ionic liquids are intricately associated with molecular symmetry, electrostatic interactions, and van der Waals forces. This observation highlights the effectiveness of the pSCNN model, which, by learning and extracting features from input pairs, effectively captures the essence of the addressed problem, explaining its superior performance. It is noteworthy that the same methodology can be extended to predict various other properties of ionic liquids.

By applying the pSCNN model to all combinations of anions and cations within our data set, we constructed an extensive database for advancing and customizing the synthesis of new IL. The final model developed in this study and all data used in this work are publicly available at https://github.com/Anan-Wu-XMU/pSCNN/.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (nos. 92161117 and 22373079) and the Natural Science Foundation of Fujian Province of China (grant no. 2021J01020).

Data Availability Statement

All materials for the prediction of the normal melting point of ionic liquid are publicly available at https://github.com/Anan-Wu-XMU/pSCNN/.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.4c02393.

  • Selected models for IL melting point prediction (Table S1); brief description of permutation feature importance analysis; Tm of ILs lay outside the 95% confidence interval boundary (Table S2); and boundaries of the applicability domain for the 39 ILs (Figure S1) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao4c02393_si_001.pdf (199.3KB, pdf)

References

  1. Freemantle M.An Introduction to Ionic Liquids; Royal Society of Chemistry, 2010. [Google Scholar]
  2. Lei Z. G.; Dai C. N.; Chen B. H. Gas Solubility in Ionic Liquids. Chem. Rev. 2014, 114 (2), 1289–1326. 10.1021/cr300497a. [DOI] [PubMed] [Google Scholar]
  3. Watanabe M.; Thomas M. L.; Zhang S. G.; Ueno K.; Yasuda T.; Dokko K. Application of Ionic Liquids to Energy Storage and Conversion Materials and Devices. Chem. Rev. 2017, 117 (10), 7190–7239. 10.1021/acs.chemrev.6b00504. [DOI] [PubMed] [Google Scholar]
  4. Zhang Q. H.; Zhang S. G.; Deng Y. Q. Recent advances in ionic liquid catalysis. Green Chem. 2011, 13 (10), 2619–2637. 10.1039/c1gc15334j. [DOI] [Google Scholar]
  5. Zhou Y.; Qu J. Ionic Liquids as Lubricant Additives: A Review. Acs Appl. Mater. Interfaces 2017, 9 (4), 3209–3222. 10.1021/acsami.6b12489. [DOI] [PubMed] [Google Scholar]
  6. Sahbaz Y.; Williams H. D.; Nguyen T. H.; Saunders J.; Ford L.; Charman S. A.; Scammells P. J.; Porter C. J. H. Transformation of Poorly Water-Soluble Drugs into Lipophilic Ionic Liquids Enhances Oral Drug Exposure from Lipid Based Formulations. Mol. Pharmaceutics 2015, 12 (6), 1980–1991. 10.1021/mp500790t. [DOI] [PubMed] [Google Scholar]
  7. Gupta K. M.; Jiang J. W. Cellulose dissolution and regeneration in ionic liquids: A computational perspective. Chem. Eng. Sci. 2015, 121, 180–189. 10.1016/j.ces.2014.07.025. [DOI] [Google Scholar]
  8. Hijo A. A. C. T.; Maximo G. J.; Costa M. C.; Batista E. A. C.; Meirelles A. J. A. Applications of Ionic Liquids in the Food and Bioproducts Industries. Acs Sustainable Chem. Eng. 2016, 4 (10), 5347–5369. 10.1021/acssuschemeng.6b00560. [DOI] [Google Scholar]
  9. Zhang J.; Sun B.; Zhao Y.; Tkacheva A.; Liu Z.; Yan K.; Guo X.; McDonagh A. M.; Shanmukaraj D.; Wang C.; et al. A versatile functionalized ionic liquid to boost the solution-mediated performances of lithium-oxygen batteries. Nat. Commun. 2019, 10 (1), 602 10.1038/s41467-019-08422-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hallett J. P.; Welton T. Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2. Chem. Rev. 2011, 111 (5), 3508–3576. 10.1021/cr1003248. [DOI] [PubMed] [Google Scholar]
  11. https://ilthermo.boulder.nist.gov/.
  12. Katritzky A. R.; Lomaka A.; Petrukhin R.; Jain R.; Karelson M.; Visser A. E.; Rogers R. D. QSPR correlation of the melting point for pyridinium bromides, potential ionic liquids. J. Chem. Inf. Comput. Sci. 2002, 42 (1), 71–74. 10.1021/ci0100503. [DOI] [PubMed] [Google Scholar]
  13. Izgorodina E. I.; Seeger Z. L.; Scarborough D. L. A.; Tan S. Y. S. Quantum Chemical Methods for the Prediction of Energetic, Physical, and Spectroscopic Properties of Ionic Liquids. Chem. Rev. 2017, 117 (10), 6696–6754. 10.1021/acs.chemrev.6b00528. [DOI] [PubMed] [Google Scholar]
  14. Sun N.; He X. Z.; Dong K.; Zhang X. P.; Lu X. M.; He H. Y.; Zhang S. J. Prediction of the melting points for two kinds of room temperature ionic liquids. Fluid Phase Equilib. 2006, 246 (1–2), 137–142. 10.1016/j.fluid.2006.05.013. [DOI] [Google Scholar]
  15. López-Martin I.; Burello E.; Davey P. N.; Seddon K. R.; Rothenberg G. Anion and cation effects on imidazolium salt melting points: A descriptor modelling study. ChemPhysChem 2007, 8 (5), 690–695. 10.1002/cphc.200600637. [DOI] [PubMed] [Google Scholar]
  16. Huo Y.; Xia S. Q.; Zhang Y.; Ma P. S. Group Contribution Method for Predicting Melting Points of Imidazolium and Benzimidazolium Ionic Liquids. Ind. Eng. Chem. Res. 2009, 48 (4), 2212–2217. 10.1021/ie8011215. [DOI] [Google Scholar]
  17. Gharagheizi F.; Ilani-Kashkouli P.; Mohammadi A. H. Computation of normal melting temperature of ionic liquids using a group contribution method. Fluid Phase Equilib. 2012, 329, 1–7. 10.1016/j.fluid.2012.05.017. [DOI] [Google Scholar]
  18. Mital D. K.; Nancarrow P.; Ibrahim T. H.; Jabbar N. A.; Khamis M. I. Ionic Liquid Melting Points: Structure-Property Analysis and New Hybrid Group Contribution Model. Ind. Eng. Chem. Res. 2022, 61 (13), 4683–4706. 10.1021/acs.iecr.1c04292. [DOI] [Google Scholar]
  19. Varnek A.; Kireeva N.; Tetko I. V.; Baskin I. I.; Solov’ev V. P. Exhaustive QSPR studies of a large diverse set of ionic liquids: How accurately can we predict melting points?. J. Chem. Inf. Model. 2007, 47 (3), 1111–1122. 10.1021/ci600493x. [DOI] [PubMed] [Google Scholar]
  20. Varnek A.; Baskin I. Machine Learning Methods for Property Prediction in Chemoinformatics:?. J. Chem. Inf. Model. 2012, 52 (6), 1413–1437. 10.1021/ci200409x. [DOI] [PubMed] [Google Scholar]
  21. Wu A.; Ye Q.; Zhuang X.; Chen Q.; Zhang J.; Wu J.; Xu X. Elucidating Structures of Complex Organic Compounds Using a Machine Learning Model Based on the 13C NMR Chemical Shifts. Precis. Chem. 2023, 1 (1), 57–68. 10.1021/prechem.3c00005. [DOI] [Google Scholar]
  22. Carrera G.; Aires-de-Sousa J. Estimation of melting points of pyridinium bromide ionic liquids with decision trees and neural networks. Green Chem. 2005, 7 (1), 20–27. 10.1039/b408967g. [DOI] [Google Scholar]
  23. Venkatraman V.; Evjen S.; Knuutila H. K.; Fiksdahl A.; Alsberg B. K. Predicting ionic liquid melting points using machine learning. J. Mol. Liq. 2018, 264, 318–326. 10.1016/j.molliq.2018.03.090. [DOI] [Google Scholar]
  24. Low K.; Kobayashi R.; Izgorodina E. I. The effect of descriptor choice in machine learning models for ionic liquid melting point prediction. J. Chem. Phys. 2020, 153 (10), 104101 10.1063/5.0016289. [DOI] [PubMed] [Google Scholar]
  25. Baskin I.; Epshtein A.; Ein-Eli Y. Benchmarking machine learning methods for modeling physical properties of ionic liquids. J. Mol. Liq. 2022, 351, 118616 10.1016/j.molliq.2022.118616. [DOI] [Google Scholar]
  26. Makarov D. M.; Fadeeva Y. A.; Shmukler L. E.; Tetko I. V. Beware of proper validation of models for ionic Liquids!. J. Mol. Liq. 2021, 344, 117722 10.1016/j.molliq.2021.117722. [DOI] [Google Scholar]
  27. Makarov D. M.; Fadeeva Y. A.; Shmukler L. E.; Tetko I. V. Machine learning models for phase transition and decomposition temperature of ionic liquids. J. Mol. Liq. 2022, 366, 120247 10.1016/j.molliq.2022.120247. [DOI] [Google Scholar]
  28. Valderrama J. O.; Faúndez C. A.; Vicencio V. J. Artificial Neural Networks and the Melting Temperature of Ionic Liquids. Ind. Eng. Chem. Res. 2014, 53 (25), 10504–10511. 10.1021/ie5010459. [DOI] [Google Scholar]
  29. Nandy A.; Haldar S.; Banerjee S.; Mitra S. In A Survey on Applications of Siamese Neural Networks in Computer Vision, In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June; IEEE, 2020; pp 1–5.
  30. Koch G.; Zemel R.; Salakhutdinov R. In Siamese Neural Networks for One-Shot Image Recognition, Proceedings of the 32nd International Conference on Machine Learning; JMLR, 2015.
  31. Wei W. W.; Liao Y. X.; Wang Y. F.; Wang S. Q.; Du W.; Lu H. M.; Kong B.; Yang H. W.; Zhang Z. M. Deep Learning-Based Method for Compound Identification in NMR Spectra of Mixtures. Molecules 2022, 27 (12), 3653 10.3390/molecules27123653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Fernández-Llaneza D.; Ulander S.; Gogishvili D.; Nittinger E.; Zhao H.; Tyrchan C. Siamese Recurrent Neural Network with a Self-Attention Mechanism for Bioactivity Prediction. Acs Omega 2021, 6 (16), 11086–11094. 10.1021/acsomega.1c01266. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. McKinney W. In Data Structures for Statistical Computing in Python, Proceedings of the 9th Python in Science Conference; van der Walt S.; Millman J., Eds.; 2010; pp 56–61.
  34. Rogers D.; Hahn M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50 (5), 742–754. 10.1021/ci100050t. [DOI] [PubMed] [Google Scholar]
  35. Riniker S.; Landrum G. A. Open-source platform to benchmark fingerprints for ligand-based virtual screening. J. Cheminf. 2013, 5, 26 10.1186/1758-2946-5-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Landrum G.rdkit: Open-Source Cheminformatics 2023. http://www.rdkit.org.
  37. Fernández-Torras A.; Comajuncosa-Creus A.; Duran-Frigola M.; Aloy P. Connecting chemistry and biology through molecular descriptors. Curr. Opin. Chem. Biol. 2022, 66, 102090 10.1016/j.cbpa.2021.09.001. [DOI] [PubMed] [Google Scholar]
  38. Moriwaki H.; Tian Y. S.; Kawashita N.; Takagi T. Mordred: a molecular descriptor calculator. J. Cheminf. 2018, 10, 4 10.1186/s13321-018-0258-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Almeida J. S. Predictive non-linear modeling of complex data by artificial neural networks. Curr. Opin. Biotechnol. 2002, 13 (1), 72–76. 10.1016/S0958-1669(02)00288-4. [DOI] [PubMed] [Google Scholar]
  40. LeCun Y.; Bengio Y.; Hinton G. Deep learning. Nature 2015, 521, 436–444. 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
  41. Jiang B. Y.; Deng C.; Yi H. M.; Hu Z. L.; Zhou G. R.; Zheng Y.; Huang S.; Guo X. Y.; Wang D. Y.; Song Y.. et al. In XDL: An Industrial Deep Learning Framework for High-dimensional Sparse Data, 1st International Workshop on Deep Learning Practice for High-Dimensional Sparse Data with Kdd (Dlp-Kdd 2019); ACM Digital Library, 2019.
  42. Altman N.; Krzywinski M. The curse(s) of dimensionality. Nat. Methods 2018, 15 (6), 399–400. 10.1038/s41592-018-0019-x. [DOI] [PubMed] [Google Scholar]
  43. Tetko I. V.; Karpov P.; Van Deursen R.; Godin G. State-of-the-art augmented NLP transformer models for direct and single-step retrosynthesis. Nat. Commun. 2020, 11, 5575 10.1038/s41467-020-19266-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Carrió P.; Pinto M.; Ecker G.; Sanz F.; Pastor M. Applicability Domain Analysis (ADAN): A Robust Method for Assessing the Reliability of Drug Property Predictions. J. Chem. Inf. Model. 2014, 54 (5), 1500–1511. 10.1021/ci500172z. [DOI] [PubMed] [Google Scholar]
  45. Katritzky A. R.; Jain R.; Lomaka A.; Petrukhin R.; Maran U.; Karelson M. Perspective on the relationship between melting points and chemical structure. Cryst. Growth Des. 2001, 1 (4), 261–265. 10.1021/cg010009s. [DOI] [Google Scholar]
  46. Labute P. A widely applicable set of descriptors. J. Mol. Graphics Model. 2000, 18 (4–5), 464–477. 10.1016/S1093-3263(00)00068-1. [DOI] [PubMed] [Google Scholar]
  47. Tetko I. V.; Lowe D. M.; Williams A. J. The development of models to predict melting and pyrolysis point data associated with several hundred thousand compounds mined from PATENTS. J. Cheminf. 2016, 8, 2 10.1186/s13321-016-0113-y. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao4c02393_si_001.pdf (199.3KB, pdf)

Data Availability Statement

All materials for the prediction of the normal melting point of ionic liquid are publicly available at https://github.com/Anan-Wu-XMU/pSCNN/.

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES